크레이그 내삽 보조정리

(The Craig interpolation lemma)

계산가능성과 논리 : George S. Boolos   Richard C. Jeffrey 저, 김영정.최훈.강진호 옮김, 문예출판사 (393-5681), 1996 (원서 : Computability and Logic, 3rd ed, Cambridge Univ. Press, 1989), page 292~302

문장 A 가 문장 C 를 함축한다면, 다음과 같은 문장 B 가 있게 되는데, 그 문장은 A 에 의해 함축되면서 C 를 함축하며 또 A 와 C 가 모두 포함하는 이름들만을 포함한다. 그 까닭은 분명하다. a₁, ..., a_m 음 A 에는 있으나 C 에는 없는 이름들이라고 하자. (a_i 들은 서로 별개의 것이라고 생각하자. 만약 m=0 이면 B=A 로 놓을 수 있다.) v₁, ..., v_m 은 완전히 새로운 m 개의 변수라고 하고, 모든 곳에서 A 의 a_i 를 각각 v_i 로 대입한 결과는 A^* 라고 하자. 그러면, (A→C) 가 타당하기 때문에 ∀v₁...∀v_m(A^*→C) 도 타당하고, 그러므로 또 (∃v₁...∃v_mA^*→C) 도 타당하다. 그러면 ∃v₁...∃v_mA^* 는 알맞은 B 이다. 왜냐하면 A 가 그것을 함축하면서 그것은 C 를 함축하고 또 그것에 나오는 모든 이름들이 A 와 C 에 모두 나오기 때문이다.

이름과 함축에 대한 이런 사실이 이름, 함수기호, 문장문자, 술어문자, 함축에 대한 사실로도 확장할 수 있을까 하는 의문이 생길 수 있다. 다시 말해서 문장 A 가 문장 C 를 함축한다면, 다음과 같은 문장 B 가, 곧 그 문장은 A 에 의해 함축되고 C 를 함축하며 또 A 와 C 가 모두 포함하는 이름, 함수기호, 문장문자, 술어문자들만을 포함하는 그런 문장 B 가 언제나 있을까 하는 의문 말이다.

방금 말한 이 질문에 대한 답은 없다 이다. A='∃xFx&∃x-Fx' 이고 C='∃x∃yx≠y' 라고 하자. A 는 C 를 함축하지만, A 와 C 에 모두 있는 이름, 함수기호 등만을 포함하는 문장은 없다. 따라서 A 에 의해 함축되면서 C 를 함축하는 문장이란 없다.

이 보기에서 C 는 '=' 를 포함한다. 그렇다면 우리가 '=' 는 무시한다고 가정하자. 그리고 이제 물어 보자. 문장 A 가 문장 C 를 함축한다면, 다음과 같은 문장 B, 다시 말해서 그 문장은 A 에 의해 함축되면서 C 를 함축하며 또 A 와 C 가 모두 포함하는 비논리적인 기호들만을 포함하는 문장 B 가 있는가? ('=' 는 논리적 기호이다. 9장 참조.)

우리는 A 에 의해 함축되면서 C 를 함축하며 또 A 와 C 가 모두 포함하는 비논리적인 기호들만을 포함하는 이차 양화문장을 쉽게 발견할 수 있다. 앞에서처럼 A 에는 나오지만 C 에는 나오지 않는 이름, 함수기호, 문장문자, 또는 '=' 를 뺀 술어문자를 새로운 개체 변항, 함수 변항, 문장변항, 또는 술어변항으로 알맞게 치환하고 그 결과를 존재양화하면 된다. (18장 참조.)

그러나 우리가 오직 일차 문장에만 관심이 있다고 가정하자. 일차 문장 A 가 일차 문장 C 를 함축한다면, 다음과 같은 일차 문장 B, 다시 말해서 그 문장은 A 에 의해 함축되면서 C 를 함축하며 또 A 와 C 가 모두 포함하는 비논리적인 기호들만을 포함하는 일차 문장 B 가 있는가?

크레이그 내삽 보조정리 (Craig interpolation lemma) 는 이 질문에 대해 그렇다 하고 대답하는 주장이다. (B 를 '내삽문장' 이라고 하는데 여기서 그 정리의 이름이 생겼다.)

크레이그 보조정리 증명은 네 부분으로 이루어져 있다. 첫 부분에서 우리는 A 와 C 가 명제 논리의 문장이라고 가정한다. 두번째 부분에서는 A 와 C 가 양화사도, 함수기호도, 또는 등호도 안 가질 것이다. 세번째 부분 (어려운 부분) 에서는 A 와 C 가 양화사를 안 갖는다는 가정을 뺀다 (여기서 한 증명은 드레벤과 퍼트남의 도움을 받았다). 마지막 부분에서는 A 와 C 가 함수기호와 '=' 를 안 갖는다는 가정을 뺀다. 처음부터 우리는 A 가 만족가능하고 또 C 는 타당하지 않다고 가정할 수 있다. 왜냐하면 A 가 만족가능하지 않다면 '∀-xx=x' 가 B 의 역할을 할 것이고 C 가 타당하다면 '∀-xx=x' 가 그럴 것이기 때문이다.

I 부

A 가 만족가능하고, C 가 타당하지 않고, A 는 C 를 함축하고, A 와 C 각각은 문장문자의 진리함수적 합성이라고 가정하자.

A 가 만족가능하므로 A 는 A 의 문장문자들에만 참거짓값을 부여하는 어떤 해석 에서 참이다. C 는 타당하지 않으므로 C 는 C 의 문장문자들에만 참거짓값을 부여하는 어떤 해석 에서 거짓이다. 여기서 A 와 C 모두가 포함하는 문장문장 P 가 적어도 하나 있어야만 한다는 사실이 따라나온다. 만약 그렇지 않다면 이나 이 부여하는 참거짓값을 어느 문장문자에나 그대로 부여하는 해석 가 있게 되고 그러면 (A)=1, (C)=0 이 되어 A 는 C 를 함축하지 않게 되기 때문이다.

T 는 문장 (P∨-P), F 는 문장 (P&-P) 라고 하자.

우리는 A 에는 있으나 C 에는 없는 문장문자 Q 가 적어도 하나 있다고 가정할 수 있다. (그렇지 않다면 B=A 로 놓을 수 있다.) A 에 나온 Q 를 모두 T 로 치환한 결과를 D₁ 이라고 하자. F 로 치환한 결과는 D₂ 라고 하자. 만약 가 A 를 해석하는데 (Q)=1 이라는 점에서만 와 다르다고 한다면 (만약 다른 점이 있다면), (A)=(D₁) 이라는 것에 주목하라. 만약 (Q)=0 이 유일한 차이점이라면 (A)=(D₂) 이다.

D=(D₁∨D₂)

라고 하자.

A 는 D 를 함축한다. 그 까닭은 이렇다. (D₁)=1 이지만 (C)=0 이라고 가정하자. 가 (Q)=1 이라는 점에서만 와 다르다고 (만약 다른 점이 있다면) 하자. 그러면 (A)=1 이고 C 는 Q 를 포함하지 않으므로 (C)=(C)=0 인데 이것은 A 가 C 를 함축한다는 가정에 모순된다. 유사한 방식으로 D₂ 는 C 를 함축한다. 그러므로 D〔=(D₁∨D₂)〕가  C 를 함축한다.

A 가 D 를 함축하고 D 가 C 를 함축하며 D 에 나오는 모든 문장문자는 A 에 나온다. 그런데 A 는 C 에는 나타나지 않는 문장문자를 D 보다 하나 더 가지고 있다. 따라서 한 단계의 D 를 다음 단계의 A 로 이용해서 이런 구성을 충분히 많이 되풀이 하면 다음과 같은 문장 B, 곧 A 에 의해 함축되고 C 를 함축하며 A 와 C 에 모두 들어 있지 않는 문장문자는 갖지 않는 문장 B 가 결국 생기게 된다.

II 부

A 가 만족가능하고, C 가 타당하지 않고, A 는 C 를 함축하고, A 와 C 각각은 문장문자들과, ('=' 가 아닌) 어떤 술어문자에 일련의 이름들을 덧붙여 생긴 원자문장들의 진리함수적 합성이라고 가정하자.

우리는 다음과 같은 방법을 써서 알맞은 B 를 얻을 수 있다. 먼저 A 와 C 에서 문장문자가 아닌 각 원자문장을 완전히 새로운 문장문자로 치환하고 (서로 다른 원자문장에는 서로 다른 문장문자를 치환하나, 원자문장이 A 또는 C 의 어디에 나오든 간에 같은 원자문장에는 같은 문장문자를 치환한다), 그 다음에 내삽문장을 얻기 위해 I 부를 적용하고, 마지막으로 거기에 나온 새 문장문자를 모두 본디의 것으로 치환한다. 이런 식으로 생긴 B 의 모든 이름, 문장문자, 술어문자가 A 와 C 에 나타날 뿐만 아니라, B 의 모든 원자문장과 역시 A 와 C 에 나타날 것이다.

(약간 미묘한 점이 하나 있다. 우리는 A^* 와 C^* 가 원자문장을 문장문자로 치환하여 A 와 C 에서 생긴 문장이라면 A^* 와 C^* 를 함축한다는 것을 알아야만 한다. 그러나 만약 (A^*)=1 이고 (C^*)=0 이라면 A 또는 C 의 어떠한 술어문자도 '=' 가 아니기 때문에 A 와 C 의 다음과 같은 해석  가 있게 된다. 즉 해석 에서 각 이름은 자신 을 지시하고, 또 해석 는 문장문자에 가 부여하는 것을 부여하고, Ra₁...a_n 을 치환한 문장문자 P 에 대해서 (P)=1〔0〕 일 경우 그리고 오직 그 경우에만 A 또는 C 의 모든 술어문자 R 이 a₁...a_n 에 대해서 참〔거짓〕이라고 규정한다. 그러면 (A)=1 이며 (C)=0 이 될 것이다. 따라서 만약 A^* 가 C^* 를 함축하지 않는다면 A 는 C 를 함축하지 않는데 이것은 우리의 가정에 위배된다.)

III 부

A 가 만족가능하고, C 가 타당하지 않고, A 는 C 를 함축하고, A 와 C 어느 것도 함수기호 및 '=' 를 갖지 않는다고 가정하자.

우리는 A 가 머리 표준 형식의 꼴이라고 가정할 수 있다. 를 C 의 부정과 동치인 머리 형식이라고 하자. (일반적 방법으로 머리 형식을 만들어도 새로운 비논리적 기호는 생기지 않는다.) A 가 C 를 함축하기 때문에 {A, } 는 만족가능하지 않다. 를 {A, } 로부터의 어떤 표준적 도출이라고 하자. 의 양화사 없는 문장의 어떤 유한한 집합은 만족가능하지 않다. m 을 다음과 같은 가장 작은 정수라고 하자. 곧 m 은 에서 m 행 다음에 오는 모든 문장을 없앤 결과가 그 도출에서 양화사가 없는 문장들이 만족불가능한 집합을 이루는 도출이 되는 그런 정수이다. 그리고 이런 도출을 도출 I 이라고 하자.

A 도  도 모두 함수기호를 가지고 있지 않으므로 에서, 따라서 도출 I 에서 UI 나 EI 를 적용할 때, 예화항은 이름이다. ('표준적 도출' 정의의 5항 참조.)

a₁, ..., a_n 은 A 에도  에도 없지만 도출 I 에 나타나는 이름들이라고 하자. 우리는 a₁, ..., a_n 이 도출 I 에서 나타나는 순서가 a₁, ..., a_n 이라고 가정한다. 그러므로 a_j 가 EI 를 적용해서 얻어지는 결론의 예화항일 때 a_i 가 그 결론보다 앞에 있는 문장에서 나온다면 i<j 이다.

이제 도출 I 을 다음과 같이 두 개의 도출, II 와 V 로 '쪼개겠다'. A 에 2 를 에 5를 부여하라. S 는 도출 I 에 있는 한 문장이라고 가정하고 또 I 에 있는 문장들 가운데 S 보다 앞선 각 문장에 2 또는 5 를 부여하지만 둘 다 부여하지는 않는다고 가정하라. S 에는 2 와 5 가운데 (I 에서) S 의 전제에 부여된 것을 부여하라. 도출 II〔 V 〕는  I 의 문장들 중 2〔 5 〕가 부여되어 있고  I 에서와 같은 순서로 배열되어 있는 문장들의 일련체이다. (우리는 III 부에서 옛 도출에서 새 도출을 여러 개 만들 것이다. 우리는 새 도출들에서 더 나중에 나온 문장들이 더 앞에 나온 문장들 중의 어떤 것에서 추론된 것인지를 규정할 때 가능한 한 새 도출의 주석 (annotation) 들이 옛 도출의 주석들과 일치한다고 가정하겠다. 물론 어떤 행들은 번호를 다시 매겨야만 한다. 왜냐하면 '빈 칸' 들을 몇 개 메우어야 하기 때문이다.)

도출 II〔 V 〕에서 양화사 없는 문장들의 연언은 만족가능하다. 그렇지 않다면 A〔 〕는 만족가능하지 않게 되는데, 우리는 만족가능하다고 가정하고 있기 때문이다. A^* 는 도출 II 의 양화사 없는 문장들의 연언이라고 하고, C^* 는 도출 V 에서 양화사 없는 문장들의 연언의 부정이라고 하자. A^* 는 만족가능하고, C^* 는 타당하지 않으며, A^* 는 C^* 를  함축한다. II 부에서 증명된 형태의 크레이그 보조정리로부터, A^* 에 의해 함축되고 C^* 를 함축하며 A^* 와 C^* 모두에 포함된 이름, 문장문자, 술어문자만을 포함하는 문장 B^* 가 있다는 사실이 따라나온다.

b₁, ..., b_k 는 B^* 에 나타나는 a_i 들로 된 것이라 하자 (a_i 들의 순서로 배열되어 있다). v_i, ..., v_k 는 k 개의 서로 다른 변항이라고 하고, B^v 는 B^* 에 있는 b_i 를 어디에서나 v_i 로 치환하여 B^* 로부터 생긴 식이라고 하자.

B=Q₁v₁...Q_kv_kB^v 라고 하는데, 이 때 b_i 가 도출 II 안에서 EI 를 적용해서 생긴 (즉, EI 를 적용한 전제와 그 결론인 모두 도출 II 에 있는 그러한 EI 에 적용해서 생긴) 예화 이름이라면 Q_i 는 ∃ 이다. 그렇지 않으면 Q_i 는 ∀ 이다.

=Q₁´v₁...Q_k´v_k-B^v 라고 하는데, 이 때 Q_i 가 ∃ 이면 Q_i´ 는 ∀ 이고 Q_i 가 ∀ 이면 Q_i′ 는 ∃ 이다. 따라서 는 B 의 부정과 동치인 머리 표준 형식이 된다.

우리는 이제 A 가 B 를 함축하고 B 는 C 를 함축한다는 것을 보여주어야만 한다. 우리는 이것을 { A, } 와 { B, } 가 모두 만족가능하지 않다는 것을 보여줌으로써 보여주겠다. 그러면 B 는 A 와 C 가 모두 가지고 있는 이름, 문장문자, 술어문자만을 가지므로, A 와 C 가 함수기호도 '=' 도 갖지 않는다는 전제 아래에서 크레이그 보조정리를 증명한 셈이 된다.

도출 III〔 도출 VI 〕을 다음과 같은 k+1 개 문장의 일련체라고 하자. 그 문장들 가운데 첫번째 것은  〔 B 〕이고 1과 k 사이에 임의의 i 에 대해서 i+1 번째 문장은 i 번째 문장에서 Q_i´v_i〔 Q_iv_i 〕를 제거하고 또 각 v_i 를 b_i 로 치환한 결과이다. 도출 III〔 VI 〕의 마지막 문장은 -B^*〔 B^* 〕일 것이다.

우리는 어떤 방식으로 도출 II 와 도출 III 을 '합해서' {A, } 로부터의 도출, 곧 도출 IV 를 만들 수 있다는 것을 보여줄 수 있다. 이 떄 도출 IV 는 도출 II 또는 도출 III 에 있는 바로 그 문장들을 포함한다. 그렇게 하면 {A, } 가 만족가능하지 않다는 것을 보여준 셈이 될 것이다. 왜냐하면 도출 IV 는 -B^* 를 포함하고 A^* 의 모든 연언지들을 포함한 도출이 될 것이며, 따라서 IV 의 양화사 없는 문장들의 집합은 만족가능하지 않게 될 것이기 때문이다. 마찬가지로, 도출 V 와 도출 VI 를 '합해서' {B, } 로부터의 도출, 곧 도출 VII 를 만들 수 있다는 것을 보여줄 수 있다. 도출 VII 은 도출 V 또는 도출 VI 에 있는 바로 그 문장들을 포함한다. 그러면 {B, } 가 만족가능하지 않다는 것을 보여준 셈이 될 것이다. 왜냐하면 도출 VII 은 B^* 를 포함하고 부정이 C^* 인 연언의 모든 연언지들을 포함한 도출이 될 것이며, 따라서 VII 의 양화사 없는 문장들의 집합은 만족가능하지 않게 될 것이기 때문이다.

합하는 절차를 기술하기 전에 정의가 필요하다. 도출 II, III, V, VI 의 어떤 문장이 만약 (그 도출에서) EI 에 적용한 결과라면 (그 도출에서의) 빨간 문장이라고 하자.

우리는 도출 II 에 나오는 빨간 문장의 어떠한 예화이름도 (다시 말해서 II 에서 EI 를 적용할 떄마다 결론으로 나오는 빨간 문장의 어떠한 예화이름도 - 이 점은 III, V, VI 에 대해서도 마찬가지다) 도출 III 의 빨간 문장들의 예화이름과 같지 않으며, 이것이 도출 V 와 VI 에서도 마찬가지로 성립한다는 것을 살펴봐야 한다.

II 와 III 에 대해서, 만약 b_i 가 III 에 나오는 어떤 빨간 문장의 예화이름이라면 v_i 는 에서 존재 양화되고, 따라서 B 에서 보편 양화된다. 그러므로 b_i 는 II 안에서 EI 를 적용한 (즉 자신의 전제와 결론이 모두 II 에 있는 그러한 EI 를 적용한) 결과의 예화이름이 아니다. 다시 말해서 b_i 는 II 의 어떠한 빨간 문장의 예화이름도 아니다. V 와 VI 에 대해서, 만약 b_i 가 VI 에 나오는 어떤 빨간 문장의 예화이름이라면 v_i 는 B 에서 존재양화되고, 따라서 b_i 는 II 안에서 EI 를 적용한 (즉 자신의 전제와 결론이 모두 II 에 있는 그러한 EI 를 적용한) 결과의 예화이름이다. b_i 가 또한 V 에서 어떤 EI 적용에 나오는 예화이름이라면, b_i 는 I 에서 서로 다른 두 EI 를 적용해 나오는 예화이름일텐데, 이것은 불가능하다.

이제 어떻게 합하는가를 말하겠다.

합하는 절차를 n 단계 (n=0 일 수도 있다) 끝냈다고 가정하자. 이 절차 동안 도출 II 와 III 에서 어떤 문장들을 없앴고 (하나도 없애지 않았을 수도 있으며), 결국 도출 IV 가 될 문장들의 새 일련체를 시작했다. 우리는 n+1 번째 단계에서 도출 II 와 III 에 남아있는 것들을 철저히 조사하여 각각의 도출에서 빨간 문장을 찾는다.

만약 도출 II 와 III 둘 다의 나머지에 빨간 문장들이 있다면 그 나머지에서 가장 앞에 나온 빨간 문장들을 보고서 둘 가운데 어느 것의 예화이름이 (a_i 들의 순서에서) 더 먼저인지 알아낸다. 방금 본 것처럼 두 이름 가운데 하나는 언제나 다른 이름보다 더 먼저일 것이다. 그러면 앞선 이름을 갖는 빨간 문장 위에 있는 모든 문장들을 그 빨간 문장과 함께 우리가 지금까지 도출 IV 로 만든 것 아래로 보낸다. 그리고 나서 단계 n+2 로 간다.

만약 II 에 남은 빨간 문장이 하나도 없다면, III 의 나머지를 우리가 지금까지 IV 로 만든 것 아래에 보탠다. 그러고 나서 II 의 나머지를 보탠다. 만약 II 의 나머지에 빨간 문장이 하나 있고 III 의 나머지에는 하나도 없다면, II 의 나머지를 우리가 지금까지 IV 로 만든 것 아래에 보탠다. 그러고 나서 III 의 나머지를 보탠다. 두 경우 모두 도출 IV 가 이제 끝났으므로 단계 n+2 는 없다.

이 상황의 그림은 아래 그림 23-1 에 있다.

우리가 '도출 IV' 라고 불렀던 문장들의 일련체는 실제로 {A, } 로부터의 도출이 되는데 그 도출의 양화사 없는 문장들은 만족가능하지 않은 집합을 이룬다. 왜냐하면 IV 의 문장들은 바로 II 와 III 의 문장들이고 둘 다 II〔 III 〕에 있는 두 문장은 항사 II〔 III 〕에서와 같은 순서로 IV 에 있기 때문이다. IV 의 모든 문장은 A 나 이거나 또는 EI 나 UI 를 통해서 앞선 문장들에서 따라나온다. 마지막으로 IV 에서 EI 를 적용할 때 언제나 전혀 새로운 이름들이 예화이름들로 쓰인다. 그 까닭은 이렇다. a_j 는 IV 에서 EI 를 적용할 때 결론 G 에 나오는 예화이름이고, G 는 II〔 III 〕의 문장이라고 가정하자. IV 의 G 위에 나오는 문장들의 이름들은 (a) A 또는 에 나오거나 (b) G 위에 II〔 III 〕에 나오는 문장에서 나오거나 (c) 예화이름이 a_j 보다 먼저인 III〔 II 〕의 어떤 빨간 문장의 위에 있거나 또는 그것과 같은 문장에 나오는 이름들뿐이다. 그리고 이 모든 이름들은 a_j 와 다른 이름들일 것이다.

도출 VII 은 IV 가 II 와 III 에서 만들어지는 것과 정확히 똑같이 V 와 VI 에서 만들어진다. 그러므로 그 도출은 {B, } 로부터의 도출인데 그것의 양화사 없는 문장들은 만족가능하지 않은 집합을 이룬다.

IV 부

A 가 만족가능하고, C 는 타당하지 않으며, A 는 C 를 함축한다고 가정하자.

우리는 A 또는 C 에 나오는 어떠한 함수기호도 '=' 오른쪽에 바로 나온다고 안전하게 가정할 수 있다. (22 장 참조.) 이제 다소 장황한 보조정리가 필요하다.

보조정리

다음과 같이 가정하자.

f₁, ..., f_m 은 m 개의 함수기호들이다.

F 는 문장이다.
F 의 모든 함수기호는 f₁, ..., f_m 가운데 하나이다.
R₁, ..., R_m 은 F 에 나오지 않는 m 개의 술어문자들이다.
만약 f_i 가 n 항 함수기호이면  R_i 는 n+1 항 술어문자이다.
E 는 모든 R_i  들과는 다르며 F 에 나오지 않는 이항 술어문자이다.

임의의 문장 G 에 대해서 처음에 식 s_n+1=f_i(s₁, ..., s_n) 이 G 에 나올 때마다 모두 식 R_is₁...s_ns_n+1 로 치환하고, 그 다음에 '=' 가 나올 때마다 모두 E 로 치환한 문장을 G^— 라고 정의하자.

그러면 F 가 타당한 꼭 그 경우 다음과 같은 문장들 모두의 연언 S 로부터 F^— 가 따라나온다.

∀xxEx,
∀x∀y(xEy→yEx),
∀x∀y∀z((xEy&yEz)→xEz),

그리고 각 n 과 각 n+1 항 R_i 에 대해서, 문장

∀x₁...∀x_n∃y∀z(R_ix₁...x_nz→yEz),

그리고 또 각 n 과 F^— 에 나오는 (E 와 다른) 각 n 항 술어문자 R 에 대해서 문장

∀x₁...∀x_n∀y₁...∀y_n((x₁Ey₁&...&x_nEy_n)→(Rx₁...x_n↔Ry₁...y_n)).

증명. 만약 f 가 n 항 함수기호라면

∀x₁...∀x_n∃y∀z(z=f(x₁, ..., x_n)↔y=z)

는 타당하다. 따라서 만약 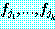가 f₁, ..., f_m 중 F 에 나오지 않는 것이라면 F 는

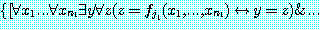
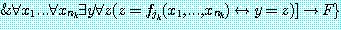
와 동치이다. 이 마지막 문장을 (1) 이라 부를텐데, (1) 은 전건이 타당한 문장들의 연언이고 후건이 F 인 조건문이다. (만약 k=0 이라면 (1)=F 이다.) 우선 22 장에서 기술했던 함수기호를 없애는 절차를 (f_i 대신 R_i 를 사용해서) (1) 에 적용하고, 그 다음에 (E 를 사용해서) '=' 를 없애는 절차를 적용하면 (2) 라는 문장이 하나 생기는데 그 문장은 (S→F^—) 와 같다. 22 장의 주요 결과에 의해 (1) 이 타당할 경우 그리고 오직 그 경우에만 (2) 가 타당하므로, F 가 타당한 꼭 그 경우 (S→F^—) 가 타당하고 따라서 꼭 그 경우 F^— 가 S 에서 따라나온다. 이상으로 이 보조정리는 증명되었다.

이제 조건문 (A→C) 를 생각해 보자. 그것을 F 라고 부르자. F 는 타당하다. f₁, ..., f_m 을 F 에 나오는 m 개의 함수기호들이라고 하자. R₁, ..., R_m 과 E 는 알맞은 새 술어문자라고 하자. 그리고 F^— 와 S 는 보조정리의 가정에서처럼 형성된다고 하자. 그러면 보조정리에 의해 F^— 는 S 에서 따라나온다.

F^— 는 조건문이다. 그 전건은 A^— 이고 후건은 C^— 이다. 따라서 S→(A^—→C^—) 는 타당하다.

우리는 S=S₁&...&S_i&S_i-1&...&S_j 라고 가정할 수 있다. 이 때 S₁...S_i 는 E와, A^— 는 포함하지만 C^— 는 포함하지 않는 술어문자들만을 포함하는 연언지들이다.

그러면 (S₁&...&S_i&A^—)→(S_i+1&...&S_j→C^—) 는 타당하다.

(S₁&...&S_i&A^—) 는 만족가능하다. 그 까닭은 이렇다. 만약 그것은 만족불가능하다면 -(A^—)〔 = (-A)^— 〕는 S 로부터 따라나오고 따라서 (보조정리에 의해) -A 는 타당하고 A 는 만족가능하지 않은데 이것은 가정에 위배된다. 마찬가지로

(S_i+1&...&S_j→C^—)

는 타당하지 않다.

이제 III 부에서 증명한 형태의 크레이그 보조정리를 적용할 수 있다. 그 보조정리가 함축하는 바는 다음과 같은 문장 B^@ 가 있다는 것이데, 그 문장은 (S₁&...&S_i&A^—) 에 의해 함축되고 (S_i+1&...&S_j→C^—) 를 함축하며 이들 문장 모두가 포함하는 이름, 문장문자, 술어문자들만을 포함한다. S₁, ..., S_i 가 이름이나 문장문자를 전혀 포함하지 않으며, E 를 제외하고는 A^— 는 포함하나 C^— 는 포함하지 않는 술어문자들만을 포함하기 때문에, B^@ 는 (역시 E 를 예외로 한다면) A^— 와 C^— 가 모두 포함하는 이름, 문장문자, 술어문자만을 포함한다.

B^@ 에 나오는 각 E 를 '=' 로 치환하고 각각의 식 R_is₁...s_ns_n+1 을 각각 식

s_n+1=f_i(s₁, ..., s_n)

으로 치환하여 B^@ 로부터 생긴 문장을 B 라고 하자. 그러면 B^—=B^@ 이다.

('=' 는 빼고) B 는 A 와 C 모두가 포함하는 술어문자, 이름, 문장문자들만을 포함한다. 만약 f_i 가 B 의 함수기호라면 R_i 는 B^— 에 있고 따라서 R_i 는 A^— 와 C^— 모두에 있으며 따라서 f_i 는 A 와 C 모두에 있다. 그러므로 B 는 또한 A 와 C 모두가 포함하는 함수기호들만을 포함한다.

우리는 (S₁&...&S_i&A^—) 가 B^— 를 함축하며 B^— 가

(S_i+1&...&S_j→C^—)

를 함축한다는 것을 안다. 여기서 알수 있는 것은 (A^—→B^—) 와 (B^—→C^—) 가 S 로부터 따라나온다는 사실이다. (A^—→B^—)=(A→B)^— 이고 (B^—→C^—)=(B→C)^— 이므로 (다시 보조정리에 의해) (A→B) 와 (B→C) 는 타당하고 그러므로 A 는 B 를 함축하고 B 는 C 를 함축한다.