덧셈은 있으나 곱셈이 없는 산수의 결정가능성

(The decidability of arithmetic with addition, but not multiplication)

계산가능성과 논리 : George S. Boolos   Richard C. Jeffrey 저, 김영정.최훈.강진호 옮김, 문예출판사 (393-5681), 1996 (원서 : Computability and Logic, 3rd ed, Cambridge Univ. Press, 1989), page 275~284

산수는 결정가능하지 않다. 그러나 곱셈이 없는 산수 는 프레스버거 (Presburger) 가 보여주었듯이 결정가능하다. (덧셈은 있으나) 곱셈이 없는 산수 는 곱셈 기호 '•' 를 포함하지 않는 산수의 정리들, 즉 에서 참인 L 의 '•' 이 없는 문장들이 정리인 이론이다. (곱셈은 있으나) 덧셈이 없는 산수 는 '+' 도 ' ′ ' 도 포함하지 않는 산수의 정리들이 정리인 이론이다. 곱셈이 없는 산수처럼, 덧셈이 없는 산수는 스콜렘이 보여주었듯이 결정가능하다. (만약 '+' 는 버리고 ' ′ ' 는 버리지 않는다면 우리는 근본적으로 산수와 차이점이 없는 결정불가능한 이론을 갖게 된다. 왜냐하면 덧셈은 다음수와 곱셈을 통해 정의할 수 있기 때문이다. 즉, a=i′, b=j′, c=k′′ 일 때 (a•c)′•(b•c)′=((a•b)′•(c•c))′ 인 꼭 그 경우 i+j=k 이다). 프레스버거가 얻어낸 결과를 증명하겠다.

'0', ' ´ ', '+' 만을 포함하는 문장이 에서 참인지 아닌지를 결정하는 방법을 보여주기 위해서 양의 정수든, 음의 정수든, 영이든 모든 정수들의 집합이 논의 영역인 해석 를 고려할 것이다. 는 '0' 에 영을, '1' 에 일을 부여한다. 는 '+' 에 (이제는 모든 정수에 대해 정의된) 덧셈 함수를 부여한다. 는 '-' 에 일상적인 뺄셈 함수를 부여한다. 는 i 가 j 보다 작을 경우 그리고 오직 그 경우에만 '<' 가 i, j 에 대해 참이라고 규정한다. 는 또한 무한히 많은 일항 술어문자 D₂, D₃, D₄, ... 에 대해 만약 i 가 m 에 의해 (나머지 없이) 나누어질 경우 그리고 오직 그 경우에만 D_m (m≥2) 이 i 에 대해서 참이라고 규정을 한다.

우리는 '0', '1', '+', '-', '<', 그리고 임의의 D_m 만을 포함하는 문장이 에서 참인지 아닌지를 결정하는 방법을 보여줄 것이다. 이것을 일단 보여주면 우리는 '•' 를 포함하지 않는 L 의 문장 S 가 에서 참인지 아닌지를 결정하는 방법을 보여준 셈이 된다. 왜냐하면 만약 S 가 에서 참일 경우 그리고 오직 그 경우에만 모든 ' ´ ' 을 '+1' 로 치환하고, S 에 나오는 모든 양화사 ∃v 와 ∀v 를 식 (0=v∨0<v) 에 대해 상대화 한 결과가 에서 참이기 때문이다. (∃v〔∀v〕를 문장 S 에서 식 F 에 대해 상대화한다는 것은 S 에서 ∃v...〔∀v...〕의 꼴의 모든 문맥을

∃v (F&...)〔∀v(F→...)〕

의 꼴로 고쳐 쓴다는 것이다.)

용어를 몇 가지 채택하자. 이 장에서는 항 이 '열린 항' 이 될 것이다. 즉, '0', '1', 변항, 또는 '+', 와 '-' 의 빈 칸들을 (더 짧은) 열린 항으로 채워 얻어진 표현이 될 것이다. 따라서 (열린) 항들은 (일상적인 뜻의) 항에서 이름에다 변항을 (영 개 또는 그 이상) 대입하여 생긴 표현들이다. 식 (문장) 에서는 '0', '1', '+', '-', '<', D₂, D₃, ... 이 유일한 비논리적 기호일 것이다. '지시체' 는 '에서의 지시체' 를 뜻할 것이다. '참' 은 ' 에서의 참' 을 뜻할 것이다. 우리는 만약 문장 ∀v₁...∀v_nr=s〔 문장

∀v₁...∀v_n(F↔G)〕

가 참이면 v₁, ..., v_n 이 r 이나 s〔 F 나 G 〕에 나오는 자유 변항의 전부라고 할 때 두 항 r 과 s 〔 두 식 F 와 G 〕는 외연이 같다 (coextensive) 고 말할 것이다.

만약 t 가 변항을 전혀 포함하지 않은 항이라면 우리가 t 가 주어졌을 때 t 의 지시체를 효율적으로 계산할 수 있다. 그러면 임의의 원자 문장이 주어졌을 때 우리는 마찬가지로 문장의 진리값을 계산할 수 있고, 따라서 양화사가 없는 어떠한 문장에 대해서도 똑같은 일을 할 수 있다. 우리는 S 가 주어졌을 때 S 와 외연이 같은 (즉 S 와 진리값이 같은) 양화사 없는 T 를 효율적으로 찾는 방법을 보여줌으로써 문장 S 가 참인지 아닌지를 결정할 수 있는 방법을 보여주겠다. 일단 T 가 발견되면 S 의 진리값이기도 한 T 의 진리값은 효율적으로 결정할 수 있다.

우리가 S 로부터 우리가 원하는 T 를 찾기 위해 쓰려고 하는 방법은 양화사를 없애기 라고 하는 것으로서, 그 방법이란 (x 뿐만 아니라 다른 자유 변항들도 포함할 수 있는) 양화사 없는 식 F 를 각각 (∃xF 와 외연이 같고 ∃xF 에서 자유롭게 나타나는 변항들만 자유롭게 나타나는) 양화사 없는 식 G 와 어떻게 연계시키느냐가 그 내용이다. 만약 양화사 없는 각 F 에 대해 양화사 없는 그런 G 를 찾을 수 있다면 각 문장 S 에 대해 S 와 외연이 같은 양화사 없는 문장 T 를 찾을 수 있을 것이다. 먼저 S 를 양화사 머리 표준 형식으로 만들고 그 다음에 머리에 붙어 있는 (일련의 양화사들 중에서) 각 보편 양화사 ∀v 를 -∃v - 로 치환한다. 그리고 나서 속박 변항이 없는 문장, 즉 양화사 없는 문장이 생길 때까지 양화사 없는 식들의 존재 양화식들을 계속해서 (어떠한 새로운 변항도 자유롭게 나타나지 않는) 외연이 같은 양화사 없는 식들을 치환하는 일을 문장 안에서부터 밖으로 계속한다.

F 를 양화사 없는 식이라고 하자. 우리는 식들을 외연이 같으면서 새로운 변항은 전혀 포함하지 않는 식들을 치환할 수 있도록 해주는 다음 서른 가지 조작을 순서대로 해서 ∃xF 와 외연이 갖고 ∃xF 에서 자유롭게 나오는 변항만 자유롭게 나오는 G 를 얻게 된다.

(1) F 를 선언 표준 형식으로 만들어라. 즉 F 를 F 에 포함된 원자식들과 F 에 포함된 원자식들의 부정의 연언들의 (논리적인 동치인) 선언으로 바꿔 써라.

원자식과 그 식의 부정은 다음 여섯 가지 꼴을 띤다.

(2) 각 r=s 를 (r<(s+1)&s<(r+1)) 로 치환하라.

(3) 각 r≠s 를 (r<s∨s<r) 로 치환하라. 

(4) 배분법칙을 써서 그 결과를 다시 선언 표준 형식으로 바꾸어라.

(5) 각 rs 를 s<(r+1) 로 치환하라.

(6) 각 -D_ms 를 (D_m(s+1)∨D_m(s+2)∨...∨D_m(s+(m-1))) 로 치환하라. (여기서 우리는 '(1+1)' 대신에 '2' 를,

'(1+(...+1)...)'
 
  m-1 개의 '1'

대신에 '(m-1)' 을 썼다.)

임의의 정수 m(≠0) 이 (임의의 정수 a 에 대하여) a, a+1, ..., a+(m-1) 가운데 정확히 하나를 나누기 때문에 이 결과는 본디 것과 외연이 같다.

(7) 그 결과를 다시 선언 표준 형식으로 바꾸어라.

이 시점에서 우리는 r<s 과 D_ms 꼴의 원자식들의 연언들의 선언인 식을 얻게 된다.

(8) 각 r<s 를 0<(s-r) 로 치환하라.

우리는 '(0-s)' 등을 줄여서 '-s' 등으로 쓸 것이다.

우리는 만약 항이 다음 다섯 가지 꼴들 가운데 하나이면 항이 표준 형식 을 띠고 있다고 말할 것이다: t 가 x 를 전혀 포함하지 않을 때

모든 항은 이런 표준 형식으로 된 항들 가운데 하나와 외연이 같다.

(9) 식에 나오는 모든 비표준 항들을 외연이 같은 표준 항들로 치환하라.

(10) 각 0<-kx〔0<kx+t, 0<-kx+t〕를 kx<0〔-t<kx, kx<t 〕로 치환하라.

이 시점에서 변항 x 를 포함하는 모든 부등식 (술어문자가 '<' 인 식) 은 t 가 x 를 포함하지 않는 항이고 k 가 양수일 때 t < kx 나  kx < t 꼴을 갖는다. 우리는 첫번째 꼴의 부등식을 하위 부등식이라고 하고, 두번째 꼴의 부등식을 상위 부등식이라고 하겠다.

우리는 이제 식들을 각 언언지가 하위 부등식을 많아야 하나 포함하는 식으로 계속해서 치환해 나간다.

(11) 모든 하위 부등식들이 왼쪽에 나오게끔 각 선언지에 나오는 연언지들의 순서를 다시 배열하라.

't₁<k₁x&t₂k₁≤t₁k₂' 가 성립하면 't₁k₂<k₁k₂x' 도 성립하고 't₂k₁<k₁k₂x' 도 성립하며 따라서  't₂<k₂x' 도 성립한다는 것에 주목하라.

('t₂k₁' 은 항 (t₂+(...+t₂)...) 를 가리킨다.)
                   
                   k₁ 개의 t₂

(12) 만약 연언 t₁<k₁x&t₂<k₂x 가 어떤 선언지에 나온다면 그 각각을

(t₁<k₁x&t₂k₁<t₁k₂)∨(t₁<k₁x&t₂k₁=k₁k₂)∨(t₂<k₂x&t₁k₂<t₂k₁)

로 치환하라.

(13) (2) 에서처럼 '=' 를 모두 없애라.

(14) 그 결과를 다시 선언 표준 형식으로 바꾸어라.

각 선언지에 나오는 하위 부등식의 최대수는 이제 하나가 줄어들었거나 또는 영 개나 한 개로 줄어들었다. (t₂k₁<t₁k₂ 는 x 를 포함하지 않기 때문에 하위 부등식이 아니라는 점을 주의하라.)

(15) 각 선언지에 하위 부등식이 많아야 하나 있을 때까지 (11)-(14) 를 반복하라.

(16) 각 선언지에서 상위 부등식들의 최대수를 비슷한 방식으로 많아야 하나로 줄여라.

m 이 n 을 나눌 경우 그리고 오직 그 경우에만 m 이 -n 을 나눈다는 것을 상기하라.

(17) 각

D_mkx〔 D_m-kx, D_m(kx+t), D_m(-kx+t) 〕

를 D_m(kx-0)〔 D_m(kx-0), D_m(kx--t), D_m(kx-t) 〕로 각각 치환하라.

m 이 y-z 을 나눌 경우 그리고 오직 그 경우에만 m 이 y 와 z 모두를 나누거나 m 이 y-1 과 z-1 모두를 나누거나 ... m 이 y-(m-1) 과 z-(m-1) 모두를 나눈다는 사실에 주목하라.

(18) 각 D_m(kx-t) 를

([D_m(kx-0)&D_m(t-0)]∨[D_m(kx-1)&D_m(t-1)]∨...
∨[D_m(kx-(m-1))&D_m(t-(m-1))])

로 치환하라.

(19) 그 결과를 다시 선언 표준 형식으로 바꾸어라.

이 시점에서 x 를 포함하는 D_ms 꼴의 모든 식들은, i 와 k 가 음수가 아닌 정수를 가리킬 때, D_m(kx-i) 의 꼴을 갖는다. 우리는 그런 식들을 합치 (congruence) 라고 부를 것이다. 우리는 이제 다음 물음을 따져 보아야 한다. 언제 m 이 kx-i 를 나누는가?

A_m,k,i 는 0≤y<m 이고 m 이 ky-i 를 나눈다는 성질을 만족하는 정수들 y 의 집합이라고 하자. m, k, i 가 주어졌을 때 우리는 0, 1, ..., m-1 가운데 어느 것이 (만약 있다면) A_m,k,i 에 속하는지 효율적으로 결정할 수 있다.

보조정리 1

m 이 kx-i 를 나눌 경우 그리고 오직 그 경우에만 A_m,k,i 속의 어떤 y 에 대해서 m 이 x-y 를 나눈다.

증명. m 이 kx-i 를 나눈다고 가정하자. 만약 x 를 m 으로 나눈다면 x=wm+y 와 0≤y<m 을 만족하는 정수들 y 와 w 가 생긴다. 그러므로 wm=x-y 이다. 그러므로 m 은 x-y 를 나눈다. 그러므로 m 은 -k(x-y)=ky-kx 를 나눈다. 그러므로 m 은

(ky-kx)+(kx-i)=ky-i

를 나눈다. 그러므로 y 는  A_m,k,i 속에 있다. 거꾸로 만약 y 가 A_m,k,i 속에 있고 m 이 x-y 를 나누면 m 은 k(x-y)=kx-ky 를 나누며, 따라서 m 이 ky-i 를 나누므로

(kx-ky)+(ky-i)=kx-i

를 나눈다.

그러므로 다음 단계가 정당화된다.

(20) 식에 나타나는 각 합치 D_m(kx-i) 에 대해 0, 1, ..., m-1 가운데 어느 것이 A_m,k,i 에 속하는지 결정하라. 만약 0, 1, ..., m-1 가운데 어느 것도 A_m,k,i 에 속하지 않는다면 각 D_m(kx-i) 를 0<0 으로 치환하라. 그렇지 않다면 각 D_m(kx-i) 를 {i₁, ..., i_j}=A_m,k,i 일 때(D_m(x-i₁)∨...∨D_m(x-i_j)) 로 치환하라.

(21) 그 결과를 다시 선언 표준 형식으로 바꾸어라.

이 시점에서 x 를 포함하는 모든 합치들은 D_m(x-i) 의 꼴을 띤다.

우리는 이제 우리 식을 다음과 같은 식 (*) 으로 치환하고 싶어한다. 즉, 이 식에서 모든 합치들은 여전히 D_m(x-i) 의 꼴이고, 만약 두 합치 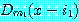과 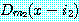가 그 식의 선언지들 가운데 어떤 하나에 나온다면 m₁ 과 m₂ 는 서로소이다라는, 즉 어떠한 정수>1도 m₁ 과 m₂ 를 동시에 나누지 못한다는 성질이 이 식에 대해서 참이 된다.

(22) 어떤 p₁, ..., p_k, e₁, ..., e_k 에 대해

m=m₁•...• m_k, m₁=p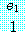, ..., m_k=p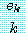, p₁<...<p_k

이고 p₁, ..., p_k 가 소수일 때 (모든 양의 정수는 소수들의 거듭제곱들의 유일한 집합의 곱이다), 각 D_m(x-i) 를

(D(x-i) & ... & D(x-i))

로 치환하라.

이제 a 가 b 를 나눈다면, a 가 x-y 를 나누고 b 가 x-z 를 나누는 꼭 그 경우에 a 가 z-y 를 나누고 b 가 x-z 를 나눈다는 사실에 주목하라.

(23) 만약 어떤 소수 p 와 e₁ ≤ e₂ 인 어떤 e₁, e₂ 에 대해서 m₁=p 과 m₂=p 일 때 어떤 한 선언지 안에 (두) 합치 D(x-i₁) 과 D(x-i₂) 가 나온다면, 그 선언지 안의 각 D(x-i₁) 을 D(i₂-i₁) 로 치환하고 연언지들의 모든 반복들을 없애라.

(24) 어떤 소수 p 와 어떤 e₁, e₂ 에 대해서 m₁=p 과 m₂=p 일 때 어떠한 선언지도 두 합치  D(x-i₁) 과 D(x-i₂) 를 포함하지 않을 때까지 조작 (23) 을 충분히 자주 반복하라.

이 시점에서 성질 (*) 을 갖는 식이 생긴다. 우리는 이제 각 선언지에 나오는 합치들의 수를 영 또는 하나로 줄이고 싶다.

(25) 식의 각 선언지에서 모든 합치들을 다른 연언지의 왼쪽으로 다시 써라. 이제 식의 각 선언지는 이런 꼴을 띤다.

D(x-i₁) & ... & D(x-i_k) & --...--.

이제 중국의 나머지 정리 (Chinese remainder theorem) 라고 하는 수론에서 나온 결과가 필요하다. 'rm(i, m_j)' 를 'i 를 m_j 로 나누었을 때 생긴 나머지' 의 뜻으로 쓰겠다. (m_j>0 일 경우 그리고 오직 그 경우에만 rm(i, m_j) 는 '정의된다', 다시 말해서 rm(i, m_j) 라는 수가 있다.)

중국의 나머지 정리

i₁, ..., i_k 가 임의의 자연수이고, m₁, ..., m_k 가운데 어떠한 두 수도 서로 소이고, 모든 1≤j≤k 에 대해서 i_j<m_j 라고 가정하자. m 이  m₁, ..., m_k 의 곱이라고 하자. 그러면 어떤 i<m 에 대해서 (모든 1≤j≤k 에 대해서) rm(i, m_j)=i_j 이다.

증명. (엔더튼) E(i)=<rm(i, m₁), ..., rm(i, m_k)> 라고 하자. 여러 정수들을 n 으로 나누어서 생길 수 있는 나머지는 n 개 있고 (곧 0, 1, ..., n-1), 그러므로 E 가 가질 수 있는 서로 다른 값들은 많아야  m₁• ...• m_k =m 개 있다. 우리는 어떤 i<m 에 대해서 E(i)=<i₁, ..., i_k> 라는 것을 보여야만 한다. 그리고 우리는 만약 i<a<m 이면 E(i)≠E(a) 임을 보여줄 수만 있다면 이것을 보여준 셈이 된다. 왜냐하면 그럴 경우 자연수 i<m 가운데 정확히 어떤 하나가 E(i) 의 투입값으로 주어질 때 <i₁, ..., i_k> 를 포함하여 E 의 모든 각 가능한 값이 E(i) 의 산출값이 되기 때문이다.

그러면 i<a<m 과 E(i)=E(a) 라고 가정하자. 그러면 0<a-i<m 이고 모든 1≤j≤k 에 대해서 rm(i, m_j)=rm(a, m_j) 이다. 그러므로 각 m_j 는 a-i 를 나눈다. 그러나 m₁, ..., m_k 가운데 어떠한 두 수도 서로 소이기 때문에 m 도 틀림없이 a-i 를 나눈다. 그러나 0<a-i<m 이므로 이것은 불가능하다. 이것으로 정리가 증명되었다.

프레스버거 정리의 증명으로 돌아가자.

모든 j(1≤j≤k) 에 대해서 i=rm(i_j, m_j), 곧 i_j 를 m_j 로 나눈 나머지가 i라고 하자. 그러면 i<m_j 이고, m_j 가 x-i_j 를 나눌 경우 그리고 오직 그 경우에만 m_j 는 x-i를 나눈다. 이제 모든 j(1≤j≤k) 에 대해

rm(i, m_j) = i

를 만족하는, 따라서 m_j 가 i-i를 나눈다는 성질을 만족하는 i 를 얻기 위해 중국의 나머지 정리를 적용하다.

m=m₁• ...• m_k 라고 하자. 그러면 m₁, ..., m_k 가운데 어떠한 두 수도 서로 소이므로 m 이 x-i 를 나누는 꼭 그 경우 m₁ 은 x-i 를 나누고 ... 그리고 m_k 는 x-i 를 나눈다. 그러나 m_j 가 x-i 를 나누는 꼭 그 경우 m_j 는 (x-i)+(i-i)=x-i를 나누고, 또 꼭 그 경우에 m_j 는 x-i_j 를 나눈다. 그러므로 m 이 x-i 를 나눌 경우 그리고 오직 그 경우에만 m₁ 은 x-i₁ 을 나누고 ... 그리고 m_k 는 x-i_k 를 나눈다.

(26) 각  D(x-i₁)&...&D(x-i_k) 를 알맞은 합치 D_m(x-i)  로 치환하라.

이 시점에서 각 선언지 속에 하위 부등식을 많아야 하나, 상위 부등식도 많아야 하나, D_m(x-i)  꼴의 합치도 많아야 하나만을 포함하는 선언 식 (F₁∨...∨F_j) 가 생기게 된다.

(27) 각 선언지를 다시 써서 x 를 포함하는 모든 연언지들이 왼쪽에 나타나게 하여라.

(28) ∃x(F₁∨...∨F_j) 를 (∃xF₁∨...∨∃xF_j) 로 다시 써라.

(29) 각 선언지 ∃xF_k 안에서, 양화사를 x 가 나오는 세 개 또는 그 미만의 연언지에만 제한해서 써라. 만약 하나도 없다면 양화사를 없애라.

따라서 F 를 G 로 치환하려는 절차에 대한 기술을 완성하기 위해서는 다음과 같은 성질을 갖는 양화사 없는 식 (**) 을 찾는 방법만 보여주면 되는데 왜냐하면 그러한 방법을 보여주는 조작 (30) 에 의해 우리가 얻고자 하는 G 를 얻을 수 있기 때문이다. 이 식은 하위 부등식 s<jx (여기서 j≥1 이고 x 는 s 에 나오지 않는다) 를 많아야 하나 포함하고 상위 부등식 kx<t 를 많아야 하나 포함하고 D_m(x-i) 꼴의 합치를 많아야 하나 포함하는 공집합이 아닌 연언을 (x 에 관련해서) 존재 양화시킨 어떠한 주어진 식과도 외연이 같으며, 새로운 자유 변항을 전혀 갖지 않는다.

(30) 앞으로 기술한 꼴로 된 존재 양화식들을 외연이 같고 양화사가 없는 알맞은 식들로 치환하라.

그렇게 하기 위해

가

와 외연이 같다는 것에 주목하자.

(물론 여기서 'jkx' 는 항 (x+(...+x)...) 을 가리킨다.)
                                 
                                  jk 개의 'x'

(B) 는 다시

와 외연이 같다. 왜냐하면 만약 jkm 이 x-jki 를 나누면 jk 는 x-jki 를 나누고 따라서 jk 는 x 를 나누고 따라서 어떤 x^* 에 대해서 x=jkx^* 이기 때문이다. (C) 는

의 꼴이다.

그런 어떠한 식도 양화사가 없고 (D) 와 같은 자유 변항들을 갖는 식

((s+1)<t&D_m((s+1)-i))∨...∨((s+m)<t&D_m((s+m)-i))

와 외연이 같다. 왜냐하면 임의의 두 정수 y 와 z 가 주어졌을 때 m 의 어떤 곱보다 i 만큼 더 큰 어떤 정수 x 가 엄밀하게 y 와 z 사이에 있을 경우 그리고 오직 그 경우에만 y+1, ..., y+m 은 그 자체가 z 보다 작고 m 의 어떤 곱보다 i 만큼 더 크기 때문이다.

(A) 보다 더 단순한 식들에 대해 말하면 ∃x(s<jx&kx<t) 가 ∃x(ks<jkx&jkx<jt) 와 외연이 같고 이것은 (D) 꼴의 식인

∃x(D_jk(x-0)&ks<x&x<jt)

와 외연이 같다. x 가 양수이면 jx≥x 이므로, 그리고 m 의 어떤 곱보다 i 만큼 큰 양의 정수들이 있으므로, ∃x(D_m(x-i)&s<jx) 는 양화사 없는 참인 식 '0<1' 과 외연이 같다. 마찬가지로,

∃x(D_m(x-i)&kx<t), ∃x(D_m(x-i), ∃xs<jx, ∃xkx<t

는 모두 '0<1' 과 외연이 같다.

우리는 이제 모든 경우에 성질 (**) 을 갖는 양화사 없는 식들을 찾는 방법을 보여준 셈이므로 우리 할 일을 다했다.