일항 논리 대 이항 논리

(Monadic versus dyadic logic)

계산가능성과 논리 : George S. Boolos   Richard C. Jeffrey 저, 김영정.최훈.강진호 옮김, 문예출판사 (393-5681), 1996 (원서 : Computability and Logic, 3rd ed, Cambridge Univ. Press, 1989), page 312~323

일항 (monadic) 식은 일차 논리의 식이며 그 식의 모든 비논리적인 기호들이 일항 술어문자인 식이다. 일항 식은 '=' 와 어떤 일항 술어문자가 동시에 있을 수 있다. 또 '=' 는 있지만 일항 술어문자는 전혀 없을 수도 있다. 또 어떤 일항 술어문자는 있을 수 있지만 '=' 는 없을 수 있다. 특히 마지막 경우를 순수 일항 식이라고 한다.

스콜렘-뢰벤하임 정리(12, 13장) 의 따름 정리 가운데 하나는, 만약 S 가 만족가능한 일차 논리의 문장이라면 S 는 그 논의 영역이 열거가능한 어떤 해석에서 참이라는 내용이다. 우리는 이 장에서 일항 문장과 관련된 정리를 증명하겠다.

정리 1

만약 S 가 만족가능한 일항 문장이라면, S 는 그 논의 영역의 원소가 많아야 2^k• r 개인 어떤 해석에서 참이다. 이 때 k 는 (일항) 술어문장의 개수이고 r 은 S 의 변항들의 개수이다.

우리는 22장에서 순수한 이항 문장이 타당한지 안한지를 결정할 수 있는 효율적인 절차가 없다는 것을 보았다 (그 문장은 비논리적 기호가 이항 술어문자들인 '=' 없는 문장이다). 우리는 이 장 끝에서 술어문자가 단 하나만 있는 순수 이항 문장의 타당성에 대한 결정 절차도 없음을 보이겠다. 한편 정리 1로부터 일항 문장이 타당한지 안 한지 결정할 수 있는 효율적 방법이 있다 는 내용의 정리가 따라나온다.

따라서 논리학의 역사와 결정가능성 개념은 다음과 같은 흥미로운 방식으로 연관되어 있다. 부울, 프레게, 그리고 다른 사람들의 업적과 함께 시작한 현대 논리학의 부흥이 지닌 중요한 특징은 타당한 추론의 개념이 눈에 띌 만큼 넓어졌다는 것이다. 타당성의 설명을 '고전', 곧 현대 이전의 논리학에 의존하던 추론들은 현대 논리학에 오면 일항 논리의 추론으로 다루어진다. 곧 그 전제들과 결론들이 일항 술어문자들만을, 그리고 혹은 등호까지 포함하는 식으로 기호화할 수 있는 추론으로 다루어진다.

모든 말은 동물이다.
따라서, 모든 동물을 타는 사람들은 누구나 모든 말을 탄다.

또는

모든 사람들은 사랑하는 사람들 모두를 사랑한다.
따라서, 아무도 전혀 사랑하지 않거나 아니면 모든 사람은 모든 사람을 사랑한다.

와 같이 직관적으로 타당한 추론들은 고전 논리학에서는 다룰 수 없으나, 현대의 논리학 이론은 일항 논리의 추론과 마찬가지로 타당하다고 인정한다. 단 그것을 기호화하는 데는 이항 술어문자들을 필요로 한다. 그러므로 이론의 설명력이 증가하는 대가로 타당한 추론의 현대적인 개념이 결정불가능한 결과를 낳게 된다. 왜냐하면, 앞으로 보겠지만, ('=' 을 제외한) 이항 술어문자가 추론들을 기호화하는 데 쓰이는 문장에서 허용되는 바로 그 때 결정불가능성이 나타나기 시작하기 때문이다.

일항 논리의 결정가능성이 어떻게 정리 1에서 따라나오는지 알아보기 시작하자. 우리는 각 일항 문장 S 가, S 가 만족가능할 경우 그리고 오직 그 경우에만 만족가능한 양홧 없는 문장 S^* 와 어떻게 효율적으로 연계되는지 보여주려고 한다. 따라서 일항 문장 G 가 타당한지 아닌지 말하기 위해서 12장 끝부분에서 기술한 절차를 적용하여 (-G)^* 의 만족가능성을 검사할 수 있을 것이다. G 가 타당할 경우 그리고 오직 그 경우에만 (-G)^* 는 만족가능하지 않기 때문이다.

k 를 S 에 있는 술어문자의 개수라고 하고 r 은 변항들의 개수라고 하자. m= 2^k• r 이라고 하고, a₁, ..., a_m 은 S 의 어디에서도 나타나지 않은 m 개의 이름들이라고 하자.

S 의 부분식 (subformula) 은 S 의 (연속된) 부분을 이루는 식이다. (S 는 자기 자신의 부분식이라고 생각된다.) 보기. 만약 S='(∀xFx∨∃yGy)' 라면, 'Fx', '∀xFx', 'Gy', '∃yGy', '∀xFx∨∃yGy)' 모두가 S 의 부분식들이다.

우리는 양화사 없는 식 H^* 를 S 의 각 부분식 H 와 귀납적으로 연계한다. 만약 H 가 원자식이면 H^*=H 이다. 만약 H 가 진리함수적 합성식이라면 H^* 는 H 를 이루는 각 식과 연계된 식들의 합성이다. 만약 H=∃vF 라면 H^*=F_va₁∨...∨F_va_m 이다(그리고 만약 H=∀vF 라면 H^*=F_va₁&...&F_va_m 이다). 그렇다면 S^* 는 양화사 없는 문장이다.

S^* 에 나오는 항들이 정확히 a₁, ..., a_m 이라는 사실과, S 와 S^* 는 논의 영역의 각 대상이 모두 a₁, ..., a_m 가운데 적어도 하나에 의해 지시되는 둘 모두의 어떠한 해석에서도 진리값이 같다는 사실에 주목하라. (이와 같이 논의 영역의 각 대상이 모두 어떤 이름에 의해 지시되는 해석을 '좋은 해석' 이라고 부르자.)

그러면 S 가 만족가능한 꼭 그 경우 (정리 1에 의해서) S 는 S 의 논의 영역의 원소가 많아야 m 개인 어떤 해석에서 참이고, 꼭 그 경우 S 가 어떤 좋은 해석에서 참이고, 꼭 그 경우 S^* 가 어떤 좋은 해석에서 참이고, 꼭 그 경우 (12장의 보조정리 III 에 의해서) S^* 가 만족가능하다. (S^* 가 만족가능한 꼭 그 경우 {S^*} 는 O.K. 이다.)

따라서 정리 1이 성립하면, 일항 논리는 결정가능하다. 이제 우리는 정리 1을 증명할 것이다. (우리가 할 증명은 로날드 젠슨 (R. Jenson) 에게 도움을 받았다.)

우리는 P₁, ..., P_k 가 k 개의 일항 술어문자이고 (k=0 일 수도 있다), v₁, ..., v_r 은 일항 문장 S 에 나타나는 r 개의 변항이고, 는 D 가 논의 영역인 S 의 모형이라고 가정하겠다.

D 의 각 d 에 대해서 s(d)=<j₁, ..., j_k> 라고 하자. 이 때 1 과 k 사이에 있는 각 i 에 대해서 P_i 가 d 에 대해 참 또는 거짓이라고 가 규정함에 따라 j_i=1 또는 0 이다. 그런 일련체 s(d) 는 많아야 2^k 개 있다. (만약 k=0 이면,  D 의 각 d 에 대해서 s(d) 는 빈 일련체인 < > 이다.)

우리는 s(c)=s(d) 일 경우 그리고 오직 그 경우에만 c 는 d 와 유사하다 (similar to) 고 할 것이다. 유사함은 분명히 D 에서의 동치 관계이다. 따라서 D 의 각 원소는 유사함 관계 아래에 있는 어떤 유일한 동치 집합에 속한다. 많아야 2^k 개의 동치 집합들이 있다.

우리는 이제 논의 영역의 원소가 많아야 2^k• r 개인 S 의 모형 를 구성할 수 있다. 우리는 집합 E 를 만드는데 어떻게 만드냐면, 만약 각각의 동치 집합에 적어도 r 개의 원소가 있다면 각 집합에서 r 개의 원소를 골라내서 만들고, 만약 r 보다 적은 수의 원소가 있다면 원소를 모두 골라내서 만든다. 그러면 E 는 많아야 2^k• r 개의 원소를 포함한다. 는 논의 영역이 E 인 해석이고, (E 의 어떠한 c 에 대해서도) 가 P_i 는 c 에 대해 참이라고 규정할 경우 그리고 오직 그 경우에만 는 (각각의 i 에 대해) P_i 가 c 에 대해 참이라고 규정한다. 는 그 이상은 어떠한 것도 더 규정하지 않는다.

우리가 (S)=1 임을 안다. 정리 1이 참임을 알기 위해서 우리는 (S)=(S) 임을 알아야 한다. 이 목적을 위해서 우리는 개념이 두 가지 필요하다. (유한한 두 일련체의) 정확히 비슷함 (exact likeness) 이라는 개념과 S 의 부분문장 이라는 개념이 그것이다.

c₁, ..., c_n 과 d₁, ..., d_n 이 D 의 원소들의 유한한 일련체들이라고 하자. 우리는 만약 모든 i(1≤i≤n) 에 대해서 c_{i 가} d_i 와 유사하고 모든 i 와 j(1≤i, j≤n) 에 대해서 c_i=c_j 인 꼭 그 경우 d_i=d_j 이면, c₁, ..., c_n 은 d₁, ..., d_n 과 정확히 비슷하다 고 할 것이다.

부분문장에 대해서는 다음과 같다. a₁, a₂, ..., a_r 이 r 개의 서로 다른 이름들의 일련체라고 하자. S 의 부분문장 은 S 의 부분식인 문장이거나 아니면 부분식으로부터 (자유) 변항에 이름을 대입해서 얻어질 수 있는 문장이다. 이 때 a₁ 은 언제나 v₁ 에 대입되고, a₂ 는 v₂ 에 대입되고, 등이다. 그렇다면 S 의 부분문장은 S 의 일부분일 필요는 없다. 왜냐하면 대입되는 이름들이 S 에 나타날 필요가 없기 때문이다. 예컨대, 만약 a₁='a', a₂='b', v₁='x', v₂='y' 이면 'Fa', '∀xFx', 'Gb', '∃yGy', '(∀xFx∨∃yGy)' 는 모두 '(∀xFx∨∃yGy)' 의 부분문장들이다. 그러면 S 의 부분문장들에 나타나는 유일한 이름들은 a₁, ..., a_r 이다.

(S) = (S) 라는 것을 보여주는 보조정리는 다음과 같다.

보조정리 1

G 는 S 의 부분문장이고, b₁, ..., b_n 은 G 에 나타나는 n 개의 (서로 다른) 이름들이고 (0≤n≤r), d₁, ..., d_n 은 D 의 원소들의 일련체이고, e₁, ..., e_n 은 E 의 원소들의 일련체이고, d₁, ..., d_n 은 e₁, ..., e_n 과 정확히 비슷하다고 가정하자. 그러면 G 가 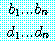에서 참일 경우 그리고 오직 그 경우에만 G 는 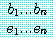에서 참이다.

증명. 증명은 G 의 복합도에 따른 귀납으로 한다. 복합도는 언제나처럼 G 에 연결사와 양화사가 나타나는 횟수로 측정한다.

만약 G 가 원자식이라면, G=P_ib₁ 이거나 G=b₁=b₁, G=b₁=b₂ 이다. 첫째 경우에는 G 가 에서 참인 꼭 그 경우  는 P_i 가 d₁ 에 대해 참이라고 규정하고, 꼭 그 경우 정확히 비슷함의 전제에 의해서 는 P_i 가 e₁ 에 대해 참이라고 규정하고, 꼭 그 경우 G 가 에서 참이다. 둘째 경우에는 G 가 과   모두에서 참이다. 셋째 경우에는 G 가 에서 참인 꼭 그 경우 d₁=d₂ 이고, 꼭 그 경우 정확히 비슷함의 전제에 의해서 e₁=e₂ 이고, 또 꼭 그 경우 G 가 에서 참이다.

만약 G=-H 이면, H 는 G 보다 복합도에서 낮고, 그러므로 우리는 보조정리가 H 에 대해 성립한다고 전제할 수 있다. 따라서 G 가 에서 참인 꼭 그 경우 H 가 에서 참이 아니며, 꼭 그 경우 H 가 에서 참이 아니며, 꼭 그 경우 G 가 에서 참이다.

G 가 더 단순한 문장들의 연언 또는 다른 진리함수적인 합성이거나 더 단순한 문장의 공허한 양화인 경우의 논증은 비슷하다.

v_j 가 H 에서 자유로울 때 G=∃v_jH 라고 가정하자. (G=∀v_jH 인 경우의 논증도 비슷하다.) 그러면 a_j 는 G 에 나타나지 않는다. 그러므로 b₁, ..., b_n 이 모두 G 에 나타나는 n 개의 이름들이라면 그것들은 a₁, ..., a_r 의 전부는 아니며 따라서 n<r 이다. b_n+1=a_j 라고 하자.

이제 만약 ∃v_jH 가 에서 참이면 D 의 어떤 d_n+1 에 대해서 는 에서 참이다. X=d_n+1 의 동치 집합이라고 하자. 만약 1 과 n 사이의 어떤 i 에 대해서 d_n+1=d_i 이면 e_n+1=e_i 라고 하자. 만약 1 과 n 사이의 어떠한 i 에 대해서도 d_n+1=d_i 가 아니라면 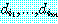은 d₁, ..., d_n 가운데 X 에 있는 m 개의 d_i 들이라고 하자 (0≤m≤n<r). 그러면 적어도 m+1(≤r) 개의 X 의 원소들이 있고, 따라서 적어도 m+1 개의 X∩E 의 원소들이 있고, 그러므로 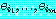모두와 구별되는 X∩E 의 원소가 하나 있는데, 우리는 그것을 e_n+1 로 잡는다. 어느 경우에도 e₁, ..., e_n, e_n+1 은 d₁, ..., d_n, d_n+1 과 정확히 비슷한 E 의 원소들의 일련체이며, 따라서 귀납 가설에 의해서 는 에서 참이며, 따라서 는 에서 참이다.

만약 다른 한편으로 가 에서 참이면 E 에 있는 어떤 e_n+1 에 대해서 는 에서 참이다. 비슷한 논증에 의해서 D 에는 e₁, ..., e_n, e_n+1 과 정확히 비슷한 d₁, ..., d_n, d_n+1 을 만족하는 d_n+1 이 하나 있으며, 따라서 귀납 가설에 의해서 는 에서 참이며 이로부터 는 에서 참이다. 이로써 보조정리 1이 증명되었다.

S 는 이름을 전혀 포함하지 않은 자기 자신의 부분문장이므로 보조정리 1로부터 (S)=(S) 가 따라나온다. 그러므로 정리 1이 증명되었다.

정리 1의 따름정리는

정리 2

만약 S 가 비논리적 기호들이 전혀 없는 문장이라면 (따라서 '=' 와 변항 등만이 있다면), S 가 만족가능한 경우, 논의 영역의 원소가 S 에 있는 변항들보다 더 많지 않은 어떤 해석에서 S 는 참이다.

증명. 그 때 S 는 일항 문장이고, k=0 이므로 2^k• r=1• r=r 이다.

정리 1의 또 다른 귀결은 순수 일항 문장에 대한 결과이다.

정리 3

만약 S 가 순수 일항 문장이라면, S 가 만족가능한 경우, k 가 S 에 있는 술어문자들의 수일 때 논의 영역의 원소가 많아야 2^k 개인 어떤 해석에서 S 는 참이다.

정리 3은 정리 1과 다음 정리에서 직접적으로 귀결된다.

정리 4

모든 순수 일항 문장은 술어문자들이 정확히 같고 변항이 단 한 개만 있는 순수 일항 문장과 동치이다.

증명. 정리 4는 모든 순수 일항 식 F 를, (a) F 와 동치이고, (b) F 와 술어문자와 자유변항이 같고, (c) 어떠한 변항 v_i 도 ∃v_i 와 ∀v_i 를 제외한 양화사의 범위에 나타나지 않는 순수 일항 식과 (귀납적으로) 연계할 수 있다는 사실에서 따라나온다. 만약 F 가 순수 일항 문장 이라면, 연계된 문장 H 는 F 와 술어문자가 같으며 어떠한 변항도 다른 변항을 포함하는 양화사의 범위에 나타나지 않는, F 와 동치인 문장이 될 것이다. 그러면 H 의 모든 변항들은 (이를테면) 'x' 라고 다시 쓸 수 있다.

우리는 임의의 순수 일항 원자식을 그 식 자체와 연계한다. 우리는 일항 식들의 임의의 진리함수적인 합성식을 그 일항 식과 연계된 식의 진리함수적 합성식과 연계한다. 이제 어떤 일항식 H 에 G 를 연계시켰을 때 F〔 =∃vH 〕를 어떤 식과 연계해야 하는가를 보이는 일만 남았다. (보편 양화는 명백히 대응쌍 (dual) 을 이용하여 다룰 수 있다.)

F 와 연계된 식을 찾기 위해서 우선 G 를 선언식 G₁∨...∨G_n 으로 다시 쓰는 일반적인 명제 연산 규칙을 이용해라. 이 때 각 G_i 는 원자식들, 원자식들을 진리함수적으로 합성한 식을 양화한 식들, 원자식과 그런 양화식을 부정한 식들의 연언이다. 우리는 각 G_i 가

B₁&...&B_j&C₁&...&C_m

의 꼴을 띤다고 가정할 수 있다. 이때 B₁&...&B_j 는 v 가 자유롭게 나타나는 G_i 의 연언지들이고 C₁&...&C_m 은 그 외의 다른 연언지들이다. 그러면 우리가 F 와 연계하는 식은

G′₁∨...∨G′_n

인데, 이때 G′_i 는 j>0 이면 (곧 v 가 G_i 의 최소한 한 연언지에서 자유롭다면)

∃v(B₁&...&B)&C₁&...&C_m

이고, 그렇지 않으면 G′_i 는 G_i 이다. 그러면 연계된 식은 성질 (a), (b), (c) 를 갖게 될 것이다.

우리는 이 장의 나머지에서 22장의 주요 결과를 써서 이항 술어문자가 단 하나만 있는 순수 이항 문장들의 타당성에 대한 결정 절차는 없다 는 것을 보임으로써 일항 논리와 이항 논리 사이의 경계를 날카롭게 할 것이다.

(에르브랑 (Herbrand) 과 처치의 힘을 빌린) 결정불가능성 증명은 두 부분으로 나뉜다. 첫째 부분은 임의의 순수 이항 문장 F 에 대해서 F 가 타당할 경우 그리고 오직 그 경우에만 타당하며 삼항 술어문자를 단 하나만 포함하는 순수 문장 G 를 구성하는 방법을 보여준다. 둘째 부분은 삼항 술어문자가 단 하나만 있는 임의의 순수 문장 G 에 대해서 G 가 타당할 경우 그리고 오직 그 경우에만 타당하며 이항 술어문자가 단 하나만 있는 순수 이항 문장 H 를 구성하는 방법을 보여준다.

F 에서 G 로 가기

A₁, ..., A_k 가 모두 F 에 나타나는 (이항) 술어문자들이라고 가정하자. v₁, ..., v_k 는 F 의 어디에서도 나타나지 않는 k 개의 (서로 다른) 변항들이라고 하자. B 는 F 에 나타나지 않는 삼항 술어문자라고 하자. 그리고 s 와 t 는 변항이라고 하자. 우리는 F 의 각 식 A_ist 를 Bv_ist 로 치환하고 그 치환한 결과에 ∀v₁...∀v_k 를 앞에 붙여서 F 로부터 G 를 만든다.

보기

만약 F='∀x∃y(Jyx&∀z(Jyz&Izz&Kwx)' 이면 G 는 '∀x₁∀x₂∀x₃∀x∃y(Lx₂yx&∀z(Lx₂yz&Lx₁zz&Lx₃wx))' 일 수 있다.

F 가 타당하면 G 도 역시 타당하다는 것은 분명하다. 왜냐하면 G 는 대입으로 F 에서 생긴 식에 보편 양화사를 앞에 불여서 얻어진 식이고, 대입은 타당성을 보존하는 조작하기 때문이다. 더욱 명백하게 하기 위해 G 가 거짓이 되는 해석 가 있다고 가정하자. D 를  의 논의 영역이라고 하자. 그리고 G^* 는 G 에서 ∀v₁...∀v_k 를 제거하고 v₁ 을 a₁ 로 치환하고, ..., v_k 를 a_k 로 치환하여 (a₁, ..., a_k 는 k 개의 이름들이다) 생긴 결과라고 하자. 그러면 G^* 를 에서 거짓이게끔 하는 d₁, ..., d_k 가 D 에 있다.  는 D 를 역시 논의 영역으로 하고, (각 i 에 대해) 가 B 를 d_i, c, e 에 대해 참이라고 규정할 경우 그리고 오직 그 경우에만 A_i 를 c, e 에 대해 참이라고 규정하는 해석이라고 하자. 그러면 F 는 G^* 가 에서 갖는 진리값과 같은 진리값, 곧 거짓을 에서 갖는다. 그러므로 F 는 타당하지 않다.

이제 F 가 타당하지 않다고 가정하자. 그러면 F 가 거짓이 되는 해석 가 있다. 13장의 따름정리 3에 의해서 우리는 의 논의 영역 D 가 자연수들의 집합이라고 가정할 수 있다. 이제 가 다음과 같은 해석이라고 하자. 곧 의 논의 영역도 역시 D 이고, 만약 1≤i≤k 이면, 가 A_i 를 c, e 에 대해 참이라고 규정할 경우 그리고 오직 그 경우에만 는 B 를 i, c, e 에 대해 참이라고 규정한다. (만약 i=0 이거나 i>k 이면 는 B 가 i, c, e 에 대해 참이라고 - 문제가 되지 않는다 - 규정한다.) 그러면 (위와 같은) G^* 는 F 가 에서 갖는 진리값과 같은 진리값 곧 거짓을 에서 갖는다. 그러므로 G 는 에서 거짓이며 따라서 타당하지 않다.

G 에서 H 로 가기

우리는 이제 단 하나의 삼항 술어문자 B 만을 가진 식 G 로부터, G 가 타당할 경우 그리고 오직 그 경우에만 타당하며 단 하나의 이항 술어문자 A 만을 가진 식 H 를 구성하는 방법을 알고 싶다.

우선 v₁, v₂, v₃, v₄ 는 G 의 어디에도 나타나지 않는 서로 다른 변항들이라고 하자. 그리고 A 는 G 에서 나타나지 않는 술어문자라고 하자. r, s, t 는 변항들이라고 하자. 그리고 Q(r, s, t) 는 식

∃v₁∃v₂∃v₃∃v₄(-Av₁v₁&Av₁v₂&Av₂v₃&Av₃v₄&Av₄v₁&
                          Av₁r&Av₂s&Av₃t&-Arv₂&-Asv₃&-Atv₄&Av₄r)

이라고 하자. 우리는 G 의 각 식 Brst 에 Q(r, s, t) 를 대입해서 G 로부터 H 를 얻는다.

G 가 타당하면 H 도 타당한 것은 분명하다. 왜냐하면 H 는 G 로부터 대입에 의해 얻어지기 떄문이다. 그 역을 위해서는 다음 보조정리를 이용한다.

보조정리 2

R 을 자연수들에 대한 삼항 관계라고 하자. 그러면 임의의 자연수 a, b, c 에 대해서 R(a, b, c) 일 경우 그리고 오직 그 경우에만 어떤 자연수 w, x, y, z 에 대해서

-S(w,w)&S(w,x)&S(x,y)&S(y,z)&S(z,w)&S(w,a)&S(x,b)
               &S(y,c)&-S(a,x)&-S(b,y)&-S(c,z)&S(z,a)

를 만족하는 자연수들에 대한 이항 관계 S 가 있다.

일단 보조정리 2가 옳다고 가정하자. 그러면 G 가 타당하지 않은 경우 G 는 우리가 모든 자연수들의 집합을 논의 영역으로 취할 수 있는 어떤 해석 에서 거짓이다. 가 B 를 a, b, c 에 대해 참이라고 규정할 경우 그리고 오직 그 경우에만 R(a, b, c) 는 성립한다고 보자. 보조정리 2의 결론에 있는 식을 S 라고 하자. 는 와 논의 영역이 같고, S(a, b) 가 성립할 경우 그리고 오직 그 경우에만 A 가 a, b 에 대해서 참이라고 규정한다고 하자. 그러면 (H)=(G)=0 이고 H 는 타당하지 않다.

보조정리 2의 증명. 자연수들에 대한 삼항 관계를 R 이라고 하자. 우리가 원하는 S 를 정의하기 위해 우리는 자연수들의 모든 삼중체 <x, y, z> 를 반복하지 않고 열거한다. 한 삼중체는 다음 네 가지 조건들 가운데 하나가 만족되면 그 열거에서 다른 삼중체 <a, b, c> 를 앞선다. (1) x+y+z<a+b+c 또는 (2) x+y+z=a+b+c 이고 x<a 또는 (3) x+y+z=a+b+c 이고 x=a 이고 y<b 또는 (4) x+y+z=a+b+c 이고 x=a 이고 y=b 이고 z<c. 그러므로 그 열거가 다음과 같이 시작할 것이다.

<0, 0, 0>
<0, 0, 1>
<0, 1, 0>
<1, 0, 0>
<0, 0, 2>
<0, 1, 1>
<0, 2, 0>
<1, 0, 1>
<1, 1, 0>
<2, 0, 0>
<0, 0, 3>
<0, 1, 2>
<0, 2, 1>
<0, 3, 0>
<1, 0, 2>
<1, 1, 1>
     :
     :

우리는 <0, 0, 0> 을 첫번째 삼중체, <0, 0, 1> 을 두번째 삼중체, <0, 1, 0> 을 세번째 삼중체 등으로 부를 것이다. 영번째 삼중체란 없다. 만약 n 번째 삼중체가

=<a, b, c>

라고 한다면, a, b, c 모두는 <n 이고, 또 만약 a<n 이고 w=4n+1 이라고 한다면, a<w-4 임에 주목하라. (왜냐하면 만약 a<n 이면 a+1≤n 이고 따라서 4a+4<4n+1 이고 거기서 a≤4a<w-4 이기 때문이다.) 그러면 분명히 만약 a, b, c 가 모두 <n 이고 w=4n+1, x=4n+2, y=4n+3, z=4n+4 라고 한다면 a, b, c 모두는 w-4, x-4, y-4, z-4 보다 작다.

우리는 S 를 이렇게 정의한다. 만약 <a, b, c> 가 n 번째 삼중체이면 (n≥1),

          u=4n+2 또는 u=a 인 꼭 그 경우 S(4n+1, u)
그리고 u=4n+2 또는 u=4n+3 또는 u=b 인 꼭 그 경우 S(4n+2, u)
그리고 u=4n+3 또는 u=4n+4 또는 u=c 인 꼭 그 경우 S(4n+3, u)
그리고 u=4n+4 또는 u=4n+1 또는 (u=a 이고 R(a, b, c)) 인 꼭 그 경우 S(4n+4, u) 이다.
          'S(t, u)' 는 다른 모든 경우에는 거짓이다.

다음을 주목하라.

또

우리는 R(a, b, c) 일 경우 그리고 오직 그 경우에만 어떤 w, x, y, z 에 대해서

-S(w,w)&S(w,x)&S(x,y)&S(y,z)&S(z,w)&S(w,a)&S(x,b)
               &S(y,c)&-S(a,x)&-S(b,y)&-S(c,z)&S(z,a)

임을 보여야만 한다.

'-S(w,w)&...&S(z,a)' 를 'Gw, x, y, z, a, b, c' 로 줄여 쓰자. 만약 R(a, b, c) 이면 어떤 w, x, y, z 에 대해서 Gw, x, y, z, a, b, c 인 것은 분명하다. 왜냐하면 만약 <a, b, c> 가 n 번째 삼중체이면, 그리고 w=4n+1, x=4n+2, y=4n+3, z=4n+4 이면, R(a, b, c) 인 경우에 Gw, x, y, z, a, b, c 가 되기 때문이다. (a<x-4 이고 그러면 a+1x 이기 떄문에 'S(a, x)' 는 성립한다. '-S(b, y)' 와 '-S(c, z)' 도 마찬가지다. 다른 연언지들이 성립한다는 것은 w, x, y, z 의 선택과 'S' 의 정의에서 보면 분명하다.)

그러므로 이제 Gw, x, y, z, a, b, c 라고 가정하자. 우리는 R(a, b, c) 임을 보여야 한다. Gw, x, y, z, a, b, c 이므로 S(w, x) 이고 -S(w, w) 이다. 그러므로 어떤 n≥1 에 대해서 w=4n+1 이다.

이제 S(w, x), S(x, y), S(y, z), S(z, w) 가 성립한다. 그러므로 (*) 에 의해서 x+3≥y+2≥z+1≥w 이고 따라서 x≥w-3 이다. 마찬가지로 y≥x-3 이고 z≥y-3 이다. 그러므로 x<w-4 도 y<x-4 도 z<y-4 도 아니다. S(w, x) 이고 xw-4 이므로 x=w+1=4n+2 이다. S(z, 4n+1) 이므로 z≠w+1 이고 z≠w+2 이다. S(x, y) 이고 yx-4 이므로 y=x 이거나 y=x+1 이다. 그리고 두 경우 모두 S(y, z) 이고 zy-4 이므로 z=y 이거나 z=y+1 이다. 그러나 y=x 이거나 z=y 이면 z=w+1 이거나 z=w+2 인데 두 경우 모두 불가능하다. 그러므로 y=x+1=4n+3 이고 z=y+1=4n+4 이다.

만약 우리가 n 번째 삼중체가 <a, b, c> 라는 것을 보여줄 수 있다면 우리는 R(a, b, c) 라고 결론지을 수 있다. 왜냐하면 <a, b, c> 가 n 번째 삼중체이면, 그 때 S(z, a) 일 경우 그리고 오직 그 경우에만 R(a, b, c) 인데 우리는 S(z, a) 가 성립한다는 것을 알고 있기 때문이다.

우리는 S(w, a), S(x, b), S(y, c) 임을 알고, -S(a, x), -S(b, y), -S(c, z) 임을 안다. 그러나 w=4n+1, x=4n+2, y=4n+3, z=4n+4 임을 알기에 우리는 또한 S(x, x), S(x, y), S(y, y), S(y, z), S(z, z) 임도 안다. 그러므로 a≠x, b≠x, b≠y, c≠y, c≠z 이다. 그러므로 S(w, a) 이고 a<w-4 이다. 그리고 S(x, b) 이고 b<x-4 이다. 그리고 S(y, c) 이고 c<y-4 이다. <r, s, t> 를 n 번째 삼중체라고 하자. 그러면 S(w, r), S(x, s), S(y, t) 이며 r<w-4, s<x-4, t<y-4 이다. (**) 에 의해서 r=a, s=b, t=c 이다. 그러므로 <a, b, c> 는 n 번째 삼중체이고 따라서 R(a, b, c) 이다.

연습문제

25.1 정리 3을 직접 증명하라. 다시 말해서 정리 1에서 도출하지 말고 증명하라

25.2 정리 1, 2, 3 에서 2^k• r, r, 2^k 값은 줄어들 수 없음을 보여라.

25.3 정리 1의 S 에 이름들이 나와도 괜찮다면 어떤 일이 생기는가?