산수의 비표준적 모형들

(Non-standard models of arithmetic)

계산가능성과 논리 : George S. Boolos   Richard C. Jeffrey 저, 김영정.최훈.강진호 옮김, 문예출판사 (393-5681), 1996 (원서 : Computability and Logic, 3rd ed, Cambridge Univ. Press, 1989), page 240~246

우리는 이제 산수의 모형을 주제로 삼으려고 한다. 우리는 산수의 모형이 적어도 하나, 즉 산수의 언어 L 에 대한 표준 해석 이 있다는 것을 안다. 물론 이 산수의 모형이 되는 것은 정의에 의해서이다. 즉, 산수란 다름 아닌 에서 참인 L 의 문장들의 집합이다. 우리는 이 산수의 유일한 모형인지 아닌지를 따져보려고 한다.

물론 문장들의 만족가능한 어떠한 집합도, 글자 그대로 말해서, 모형을 정확히 하나만 갖지는 않는다. 어떠한 모형에 대해서도, 논의 영역의 어떤 원소를 그 논의 영역에는 어디에도 없는 다른 대상으로 '치환' 해서 그 모형과 동일하지는 않지만 동형적인 (isomorphic) 다른 모형을 만들 수 있기 때문이다.

해석들의 동형성은 다음과 같이 정의한다. 한 해석 는 다음과 같은 경우에 해석 와 동형적이다.

(1) 와 는 같은 언어에 대한 해석이다.
(2) 와 는 같은 문장문자에 같은 진리값을 할당한다.
(3) 다음과 같은 세 조건을 만족하면서 의 논의 영역이 투입값 영역이고 의 논의 영역이 산출값 범위인 일대일 함수  가 있다.

(a) 만약 가 이름에 지시체 d 를 할당하면 는 그 이름에 (d) 를 할당한다.
(b) 만약 가 함수 기호에 n 항 함수 를 할당하면 는 그 함수 기호에 의 논의 영역에 있는 임의의 d₁, ..., d_n, d 에 대해서 (d₁, ..., d_n)=d 인 경우 그리고 오직 그 경우에만 ((d₁), ..., (d_n))=(d) 라는 조건을 만족하는 함수 를 할당하다.
(c) 만약 가 술어 문자에  n 항 특징함수 Φ 를 할당하면 는 그 특징함수에 의 논의 영역에 있는 임의의 d₁, ..., d_n 에 대해 Φ(d₁, ..., d_n)=φ((d₁), ..., (d_n)) 이라는 조건을 만족하는 특징함수 φ 를 할당한다.

와 동형적이다 라는 관계가 동치 관계이고, 같은 문장들은 동형적 해석들에서 진리값이 같다는 것을 검증하는 일은 독자들한테 남겨 두겠다.

만약 T 가 일관적 이론이고 그 이론에 대한 어떠한 두 모형도 동형적 이라면, T 는 모형을 정확히 한 개만 갖는 이상적 이론에 가까이 간 것이다. 그런 이론들은 '동형성에 의거하여' (up to isomorphism) 그 모형들을 '특징짓는다' 고 말하고 또 '본질적으로' 하나의 모형을 갖는다고 말한다. 그러면 다음과 같이 정의하자. 즉, 만약 (T 의 언어의 해석인) T 의 임의의 두 모형이 동형적이면 T 는 정언적 (categorical) 인 이론이다. 이제 우리는 산수가 정언적인지 아닌지 궁금해 할 수 있을 것이다.

모든 비일관적인 이론은 정언적이지만 (!), 일괄적인 정언적 이론도 있다. (P 만 포함하는 언어에서) ∃y∀xx=y&∀xPx 의 귀결들의 집합을 T 라고 하자. 그러면 T 는 정언적인데, 왜 그러냐면 T 의 임의의 모형 의 논의 영역은 원소를 정확히 하나만 포함할 것이고 P 가 그 원소에 대해 참이라고 가 규정할 것이데, 그러면 그런 어떠한 두 모형도 동형적이기 때문이다.

그러나 T 의 모든 모형들은 유한하다 (즉, 논의 영역이 유한하다). 그리고 이것은 우연이 아니다. 그 까닭은 이렇다. '위로의' 그리고 '아래로의' 스콜렘-뢰벤하임 정리에 따르면 무한한 모형을 가진 어떠한 이론도 논의 영역이 열거가능하게 무한한 모형을 갖고, 또 논의 영역이 열거가능하지 않게 무한한 모형도 갖는다. 열거가능하게 무한한 집합이 투입값 영역이고 열거가능하지 않게 무한한 집합이 산출값 범위인 일대일 함수란 결코 없으므로 일관적이면서 정언적인 이론들이란 모두 그 모형들의 논의 영역에 원소들이 (고정된) 유한한 수만큼 있는 이론들이다.

따라서 정언성이란 특별히 쓸모 있는 개념은 아니며, 산수는 모형의 영역이 무한하므로 산수는 정언적이 아니다. 알레프-영-정언성 (aleph-null-categoricity) 이 더 흥미 있는 개념이다. 논의 영역이 열거가능하게 무한하고 ('개수가 알레프-영 만큼이고') 또 T 의 모형인 어떤 언어의 어떠한 두 해석도 동형적이면 그 언어로 씌어진 이론 T 는 알레프-영-정언적이다.

T 가 모형이 결코 유한하지 않은 일관적인 이론이라고 가정하자. 만약 T 가 완전하지 않으면 T 는 알레프-영-정언적이 아니다. 왜냐하면 만약 T 로부터 (T 의 언어로 된) A 도 - A 도 따라나오지 않는다면, 스콜렘-뢰벤하임 정리에 의해 열거가능하게 무한한 논의 영역을 갖는다고 생각할 수 있는 T∪{A} 의 모형 가 있으며, 또 열거가능하게 무한한 논의 영역을 갖는 T∪{-A} 의 모형 도 있기 때문이다. 그러므로 T 의 동형적이 아닌 두 모형 와 가 있고 그 모형들은 모두 열거가능하게 무한한 논의 영역을 가지므로 T 는 알레프-영-정언적이지 않다.

m≠n 일 때마다 _Q m≠n 이다. 그러므로 Q 의 어떠한 모형도 무한하고 따라서 Q 를 확장한 이론의 어떠한 모형도 무한하다. 그리고 Q 의 일관적이면서 공리화가능한 어떠한 확장도 완전하지 않다. 그래서 Q 의 일관적이면서도 공리화가능한 어떠한 확장도 알레프-영-정언적이지 않다. 특히 Z 는 알레프-영-정언적이지 않다.

그러나 일관적이면서 알레프-영-정언적인 이론들도 존재한다. 간단한 보기를 들면 (단지 P 만을 포함하는 언어에서) ∀xPx 의 귀결들의 집합이 그런 이론이다. 더 흥미로운 보기는 연습문제 17.1에 있다. 그리고 산수는 Q 의 일관적인 확장이기는 하지만 공리화가능하지 않기 때문에, Z 와 달리 산수가 알레프-영-정언적일지도 모른다는 희망을 가져볼 수도 있을 것이다. 그러나 애석하게도, 산수가 결정가능하다거나 공리화가능하다는 희망처럼 이런 희망도 꺾이고 만다.

정리

산수는 알레프-영-정언적이지 않다.

증명. 우리는 논의 영역이 열거가능하게 무한하고 과 동형적이지 않은 산수의 모형인 L 의 해석 가 있다는 것을 보이겠다.

a 를 0 과는 다른 이름이라고 하자. A₀, A₁, A₂, ... 를 에서 참인 L 의 모든 문장들을 열거한 것이라고 하자. 문장들 {A₀, a≠0, A₁, a≠1, A₂, a≠2, ...} 의 집합 S 를 생각해 보자.

S 의 임의의 유한한 부분집합 S₀ 에 대해 다음과 같은 조건을 만족하는 수 n 이 있다. 즉, a≠n 은 S₀에 있지 않고, 그래서 a 에 지시체 n 을 할당한다는 점을 제외하고는 와 같은 해석이 S₀ 의 모형이다.

그러므로 S 의 모든 유한한 부분집합은 모형을 갖고, 따라서 조밀성 정리에 의해 S 는 모형을 가지며, 이에 따라 스콜렘-뢰벤하임 정리에 의해 S 는 논의 영역이 열거가능한 모형 를 갖는다.

임의의 m, n 에 대하여 만약 m≠n 이면 S 에서 m≠n 이다. 가 S 의 모형이므로 의 논의 영역이 열거가능하게 무한한 산수의 모형이다.

e 를 에서 a 의 지시체라고 하자. a≠0, a≠1, a≠2, ... 이 모두 에서 참이므로 어떠한 자연수 n 에 대해서도 e 는 에서 n 의 지시체와 동일하지 않다.

를 와 논의 영역이 같은 L 의 해석이라고 하자. 그 해석은 0, ′, +, • 에 가 할당하는 것과 같은 것을 할당한다 (그러나 a 에는 어떠한 지시체도 할당하지 않는다.) 는 에서 참인 L 의 문장들이 참이 되는 L 의 해석이다. 가 논의 영역이 열거가능하게 무한한 산수의 모형이므로 도 그렇다.

그러나  는 과 동형적이지 않다. 왜냐하면 의 논의 영역에 있는 원소 e 는 에서, 따라서 에서 어떠한 자연수 n 에 대해서도 n 의 지시체가 아니기 때문이다. 그러나 에서 그리고 결과적으로 과 동형적인 어떠한 해석에서도 어떤 자연수 n 에 대해서 논의 영역의 모든 각 원소가 n 에 의해서 지시된다.

똑같은 문장들이 에서 참인 것처럼 참이 되지만 과 동형적이 아닌 해석들을 산수의 비표준 모형 이라고 한다. 그러므로 우리가 방금 증명한 것은 논의 영역이 열거가능하게 무한한 산수의 비표준적 해석이 존재한다는 것이다.

산수의 비표준적 해석들은 어떠한 모습을 띠고 있는가? 가 산수의 비표준적 해석이라고 가정하다. 의 논의 영역에 있는 대상들을 수 라고 부르겠다. 는 0 에 어떤 수 z 를 할당하고 ′, +, • 에 각각 함수 s, , 를 할당한다. x<y 를 식 ∃w w′+x=y 라고 하자. 만약 (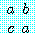a<b)=1 이면 한 수 c 가 다른 수 d 보다 작다 고 말하겠다.

먼저 어떠한 수 도 자신 보다 작지 않다. 그 까닭은 이렇다. 어떠한 (자연) 수도 자신보다 작지 않다. 그러므로 ∀x-x<x  는 에서 참이다. 따라서 에서도 참이다. 그러므로 어떠한 수 도 자신 보다 작지 않다. 이상과 같은 논증이 의 '모습' 에 대한 정보를 얻기 위한 주요 기법을 보여준다. 즉, 자연수가 어떤 성질을 갖고 있음을 살펴본다. L 의 어떤 문장이 에서 참이라고 결론짓는다. (똑같은 문장이 에서도 에서도 참이므로) 그 문장은 에서도 참임을 추론한다. 그 문장을 '의 견지에서' 해독한다. 이런 식으로 하여 임의의 두 수 가운데에서 정확히 하나가 다른 것 보다 작다 고 결론지을 수 있으며, 또 만약 한 수 가 다른 수 보다 작고 그 다른 수 는 세번째 수보다 작으면, 첫번째 수 는 세번째 수보다 작다 고 결론지을 수 있다. 그러므로 보다 작음이 수들의 선형 순서 (linear ordering) 인 것처럼 보다 작음 도 수 들의 선형 순서이다. 어떠한 수 c 도 sc 보다 작다.

0 은 가장 작은 수이다. 그러므로 z 도 가장 작은 수 이다. 0′ 은 가장 작은 수의 다음 수이다. 그러므로 sz 는 그 다음으로 가장 작은 수 이다. 그러므로 (자연)수의 수열과 동형적인 보다 작음 관계의 첫 조각 (initial segment) z, sz, ssz, sssz, ... 이 있다.

우리는 z, sz, ssz, sssz, ... 을 표준적 수 라고 부르겠다. 다른 것들은 모두 비표준적 이다. 표준적 수 는 딴 게 아니라 z 에 s 연산을 유한 번 적용하여 생길 수 있는 것들을 말한다. 어떠한 표준적 수 도 어떠한 비표준적 수보다 작다 (왜냐하면, 예를 들어 3은 0, 1, 2 를 제외한 어떠한 수보다 작기 때문이다.)

0을 제외한 어떠한 수도 어떤 유일한 수의 다음 수이다. 그러므로 z 를 제외한 어떠한 수 도 어떤 유일한 수 의 s 이다. 그러므로 수 에서 수 로 가는 함수 r 을 rz=z 그리고 rsc=c 라고 정의하자. 그러면 만약 c≠z 이면 src=c=rsc 이다.

만약 c 가 표준적이면 rc 와 sc 도 역시 표준적이고 만약 c 가 표준적이면 rc 와 sc 도 역시 비표준적이다. 더구나 c 가 비표준적이더라도 rc 는 c 보다 작다.

이제 수들 에 대한 동치 관계 eq 를 정의하겠다. 만약 c 와 d 가 수 이면, 어떤 표준적 (!) 수 e 에 대해 ce=d 이거나 de=c 인 경우 c eq d 라고 말하겠다. 직관적으로 말해서 c 와 d 가 서로간에 유한한 거리만큼 떨어져 있으면, 다시 말해서 r 이나 s 를 유한 번 적용해서 c 에서 d 를 얻을 수 있으면 c eq d 이다. 모든 표준적 수 는 모든 그리고 오직 표준적 수 와 eq 의 관계를 갖는다.

우리는 임의의 수 c 와 eq 관계에 있는 동치 집합을 c 의 구역 (block) 이라고 부르겠다. 그러면 c 의 구역은 {..., rrrc, rrc, rc, c, sc, ssc, sssc, ...} 이다. c 의 구역이 양쪽 방향으로 모두 무한할 경우 그리고 오직 그 경우에만 c 는 비표준적이다.

c 가 d 보다 작다 고, 그리고 c 와 d 가 서로 다른 구역에 있다고 가정하자. 그러면 sc 는 d 보다 작거나 같고 또 c 와 sc 는 같은 구역에 있기 때문에 sc 는 d 보다 작다. 마찬가지로 c 는 rd 보다 작다. 여기서 다음과 같은 결론이 따라나온다. 만약 구역 C 에 다른 구역 D 의 어떤 수 보다 작은 수가 하나라도 있다면 C 의 모든 수는 D 의 모든 수 보다 작다. 이런 경우 우리는 구역 C 는 구역 D 보다 작다 고 말하겠다. 한 구역 은 어떤 비표준적 수 를 포함할 경우 그리고 오직 그 경우에만 비표준적 이다. 표준적인 구역은 가장 작은 구역이다.

그러나 가장 작은 비표준적 구역이란 없다. 그 까닭은 이렇다. d 가 비표준적 수 라고 가정하자. 그러면 cc=d 이러나 ccsz=d 라는 조건을 만족하는 d 보다 작은 c 가 있다. (왜냐하면 어떠한 자연수 j≠0 에 대해서도 i+i=j 이거나 i+i+1=j 라는 조건을 만족하는 i<j 가 있기 때문이다.) cc=d 라고 가정하자. (다른 경우도 비슷하다.) 만약 c 가 표준적이면 cc=d 도 표준적이다. 그러므로 c 는 비표준적이다. 그리고 c 는 d 와 같은 구역에 있지 않다. 왜냐하면 만약 어떤 표준적 e 에 대해 ce=d 라고 한다면 ce=cc 이고 여기서 c=e 가 나오며 이것은 c 가 비표준적이라는 사실과 모순되기 때문이다. (덧셈 법칙들은 과 에서 성립한다.) 그러므로 c 의 구역은 d 의 구역 보다 작다. 마찬가지로 가장 큰 구역도 없다.

마지막으로, 만약 한 구역 C 가 다른 구역 E 보다 작으면, C 는 D 보다 작으며 D 는 E 보다 작은 세번째 구역 D 가 있다. 그 까닭은 이렇다. c 는 C 에 있고, e 는 E 에 있고, 그리고 c 는 e 보다 작다 고 가정하자. 그러면 c 는 d 보다 작고, d 는 e 보다 작으며, ce=dd 이거나 cesz=dd 라는 조건을 만족하는 d 가 있다. (오차의 여지가 1/2 이내인 평균 이 에 언제나 있다. d 는 에서 c 와 e 의 평균 이다.) ce=dd 라고 가정하자. (이 논증은 다른 경우에도 비슷하다.) 만약 d 가 C 에 있다면 어떤 표준적 f 에 대해서 d=cf 이고, 그러므로

ce=cfcf

이고, 그러므로 e=cff 이고 (덧셈 법칙), 이것으로부터 ff 가 표준적이므로 e 가 C 에 있다는 것이 따라나온다. 그러므로 d 는 C 에 있지 않고 마찬가지로 E 에도 있지 않다. 따라서 우리는 D 를 d 의 구역이라고 할 수 있다.

요약하면 이렇다. 산수의 임의의 비표준적 모형 의 논의 영역에 있는 원소들은 보다 작다 에 의해 선형적으로 순수 지워질 것이다. 이 순서는 자연수들의 수열과 동형적인 첫 조각을 가질 것이고 그 첫 조각 다음에는 각각이 모든 정수 (음수, 영, 양수) 의 수열과 동형적인 조각들의 일련체가 뒤따른다. 이 일련체에는 가장 앞에 있는 원소도 가장 뒤에 있는 원소도 없으며, 그 일련체에 있는 어떠한 두 조각 사이에도 세번째 조각이 있다. 그리고 만약 의 논의 영역이 열거가능하면 열거가능하게 많은 조각들이 있을 것이며 첫 조각이 아닌 조각들의 순서는 유리수들의 순서와 동형적일 것이다. (연습문제 17.1 참조.)

연습문제

17.1 알레프-영-정언적 이론의 재미있는 보기로 ('<' 만을 포함하는 언어에서) 다음과 같은 여섯 문장의 귀결들의 집합을 들 수 있다.

(1) ∀x -x<x,
(2) ∀x∀y∀z (x<y&y<z→x<z),
(3) ∀x∀y (x<y∨x=y∨y<x),
(4) ∀x∃y x<y,
(5) ∀x∃y y<x,
(6) ∀x∀y (x<y→∃z(x<z&z<y)).

 이 이론이 알레프-영-정언적임을 보여라. (힌트: 와 가 열거가능하게 무한한 모형들 가운데 둘이며, a₀, a₁, ...〔b₀, b₁, ...〕은 〔〕의 논의영역을 열거한 것이며, 〔〕는 '<' 에 관계 R〔S〕(의 특징함수) 를 부여한다는 것을 가정하자. a 들과 b 들 중 어느 하나도 빠뜨리지 않도록 다음과 같이 왔다갔다하여 논의 영역들 사이의 동형성을 귀납적으로 정의하라. 즉, a₀ 와 b₀ 을 짝지어라. a_n 이 아직 어느 b 와도 짝 지어지지 않았다고 가정하자. a_n 은 이미 짝지어진 a 들 중 어떤 것 (전혀 없을 수도 있다) 과 R 의 관계를 맺을 것이며, 이미 짝지어진 a 들 중 어떤 것 (전혀 없을 수도 있다) 은 a_n 과 R 의 관계를 맺을 것이다. (b₀, b₁, ... 의 열거 중) 다음의 조건을 만족하면서 아직 선택되지 않은 가장 앞선 b 를 a_n 과 짝지어라: 그 b 는 a_n 이 관계 R 을 맺고 있는 a 들과 짝지어진 b 들에 대해 관계 S 를 맺고 있으며 또한 a_n 에 대해 관계 R 을 맺고 있는 a 들과 짝지어진 b 들은 그 b 에 대해 관계 S 를 맺고 있다. 그리고 나서 지금까지 등한시됐던 가장 앞선 b 를 적절한 a 와 짝지어라. 이런 방식으로 계속하라.) 만약 의 논의 영역이 실수들의 집합이고 의 논의 영역이 유리수들의 집합이며 와 모두가 c 가 d 보다 작은 꼭 그 경우에 '<' 가 c, d 에 대해 참이라고 규정한다면 (그리고 이외의 어떤 것도 규정하지 않는다면) 는 에 대해 기초적으로 동치인 부해석이라는 결론을 내려라.

17.2 산수의 임의의 비표준적 모형 와 임의의 d 에 대하여 d 가 의 논의 영역에서 비표준적 수 인 경우 그리고 오직 그 경우에만 (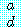S(a))=1 임을 만족하는 L 의 식 S(x) 는 없다는 것을 보여라.