스콜렘-뢰벤하임 정리 : George Boolos. Richard Jeffrey

스콜렘-뢰벤하임 정리

(The Skolem-Löwenheim theorem)

계산가능성과 논리 : George S. Boolos Richard C. Jeffrey 저, 김영정.최훈.강진호 옮김, 문예출판사 (393-5681), 1996 (원서 : Computability and Logic, 3rd ed, Cambridge Univ. Press, 1989), page 188~198

일반적으로 '스콜렘-뢰벤하임 정리' 라고 불리는 일군의 정리들은 일차 논리 언어에서 문장의 해석의 영역의 크기와 관련 있는 결과들을 모아 놓은 것이다. 이때 '크기' 는 원소들의 수(개수) 로 이해할 수 있다. 이 정리들은 전형적으로 다음과 같은 꼴로 되어 있다. 만약 이러이러한 (의미론적) 성질을 지닌 해석이 있다면, 저러저러한 크기의 영역을 가진 이러이러한 (의미론적) 성질을 지닌 해석이 있다. 예를 들어 가장 잘 알려져 있는 형태인 스콜렘-뢰벤하임 정리는 다음과 같다. 만약 한 문장 S 가 참이 되는 해석이 있다면 그 영역이 열거가능하면서 S 가 참이 되는 해석이 있다 (뢰벤하임, 1915). 이 정리는 우리가 12 장에서 증명한 스콜렘-뢰벤하임 정리에서 쉽게 나오는 귀결이다. 이 장에서는 이 형태 그리고 다른 형태들을 함축하는 강한 형태의 스콜렘-뢰벤하임 정리를 증명할 것이다.

25 장에서는 만약 S 가 k 개의 일항 술어문자들과 r 개의 변항들을 포함하고 또 등호 '=' 를 포함할 수는 있지만 이름이나 함수기호 또는 이항 이상의 술어문자는 포함하지 않는 문장(이른바 '일항' (monadic) 문장) 일 때, S 가 만약 어떤 해석에서 참이라면 S 는 영역의 원소의 개수가 2^k• r 개를 넘지 않는 해석에서 참이라는 것이 증명될 것이다. 그러므로 S 가 무한한 영역을 가진 해석에서 참인 일항 문장이라면 S 는 또한 유한한 영역을 가진 어떤 다른 해석에서도 참이다. 우리는 일항 문장에만 제한하는 것이 꼭 필요한가 그렇지 않은가를 궁금해 할 수 있다. 꼭 필요하다.

(a) = '∀x-xRx',
(b) = '∀x∃yxRy',
(c) = '∀x∀y∀z((xRy&yRz)→xRz)'

라고 하자. (1) 을 (a) 와 (b) 와 (c) 의 연언이라고 하자. 그렇다면 (1) 은 유한한 영역을 가진 어떠한 해석에서도 참이 아니지만 무한한 영역을 가진 어떤 해석에서 참이다.

(1) 이 유한한 영역을 가진 어떠한 해석에서도 참이 아니라는 것을 알기 위해서 ((1))=1 이라고, D= 의 영역이라고, 그리고 는 'R' 이 cSd 일 경우 그리고 오직 그 경우에만 c, d 에 대해 참이라고 가정하자. D 의 원소들의 배열 d₁, ..., d_n을 i<j≤n 일 때 d_iSd_j 이면 좋은 배열 (good sequence) 이라 부르자. d₁, ..., d_n 이 좋은 배열일 때 d₁, ..., d_n이 모두 서로 다름 에 주목하라. 왜냐하면 i<j 이지만 d_i = d_j 라면 d_iSd_i인데, 이것은 ((a)) = 1 이므로 불가능하기 때문이다. 우리는 각 양수 n 에 대해서 좋은 배열 d₁, ..., d_n이 있음을 귀납적으로 보여줌으로써 D 가 무한하다는 것을 보여줄 것이다. D 는 공집합이 아니므로 D 의 단 하나의 원소 d₁을 포함하는 좋은 배열이 있다는 것은 자명하다. d₁, ..., d_n이 좋은 배열이라고 가정하자. ((b)) = 1 이므로 D 의 어떤 d_n+1 에 대해서 d_nSd_n+1이다. 그러나 그러면 d₁, ..., d_n, d_n+1도 좋은 배열이다. 왜냐하면 i<n 이면 d_iSd_n이고 d_nSd_n+1이며 ((c)) = 1 이므로 d_iSd_n+1이 성립하고 그러므로 i<j≤n 이거나 i<j=n+1 이면 d_iSd_j라는 것이 성립하며 따라서 i<j≤n+1일 때는 d_iSd_j 라는 것이 성립하기 때문이다.

한편, (a) 어떠한 실수도 자기 자신보다 작지 않다. (b) 모든 각 실수는 어떤 다른 실수보다 작다. (c) 첫번째 실수가 두번째 실수보다 작고 두번째 실수가 세번째 실수보다 작다면 첫번째 실수는 세번째 실수보다 작다. (1) 은 따라서 모든 실수의 집합을 영역으로 갖고 c < d 일 경우 그리고 오직 그 경우에만 'R' 이 c, d 에 대해 참이라고 규정하는 해석 에서 참이다. 그러나 이 해석의 영역은 불필요하게 크다. 왜냐하면 (1) 은 모든 자연수의 집합을 영역으로 갖고 처럼 c<d 일 경우 그리고 오직 그 경우에만 'R' 이 c, d 에 대해 참이라고 규정하는 해석 에서도 역시 참이기 때문이다. 의 영역은 열거불가능하고 의 영역은 열거가능하다. 그러면 다른 질문이 절로 떠오른다. 어떤 해석에서 참이지만 열거가 불가능한 영역의 해석들에서만 참인 일차 논리 언어의 문장이라는 게 있을까?

이 장의 첫 문단에서 말한 뢰벤하임의 1915 년 정리는 이 질문에 대해 부정적으로 대답한다. 1919 년에 스콜렘은 뢰벤하임의 결과를 뢰벤하임 정리뿐만 아니라 12 장에서 증명한 다음과 같은 강한 명제까지 즉각적으로 함축하는 정리를 증명하여 뢰벤하임의 결과를 확장하였다. 그 강한 명제란 만약 문장들의 열거가능한 집합이 만족가능하면 그 집합의 모든 원소들을 참이 되게 하면서 열거가능한 영역을 가진 어떤 하나의 해석이 있다는 것이다. 스콜렘의 1919 년 정리는 어느 해석이든지 (우리는 9 장에서 열거불가능하게 많은 비논리적인 기호들에게 적절하게 대상을 부여할 수 있는 해석은 없고, 따라서 모든 해석은 많아야 열거가능하게 많은 문장들을 해석한다 (그 문장들의 진리값을 정의한다) 고 가정했다. 이 가정은 일차논리에로 제한함이 (스콜렘의 1919 년 형태의) 스콜렘-뢰벤하임 정리의 증명에 결정적인 것처럼 (18 장 참조) 마찬가지로 결정적이다. (연습문제 13.1 참조).) 그 영역이 열거가능하면서 기초적으로 동치인 부해석 (elementarily equivalent subinterpretation) 을 가지고 있다 는 내용이다.

'부해석' 이란 무엇이고 '기초적인 동치' 란 무엇인가? 와 가 같은 언어들에 관한 해석이고 또 다음 (1)~(5) 의 조건을 만족하는 경우 해석 를 해석 의 부해석 이라 부른다.

(1) 의 영역 E 는 의 영역의 부분집합이다.
(2) 는 이름들에 와 같은 지시대상들을 부여한다.
(3) 는 n 항 함수기호 f 에 다음과 같은 함수 를 부여한다: 함수 는 E 의 대상들의 일련체 c₁, ..., c_n 에 대해서만 산출값을 취하고 또 가 f 에 부여하는 함수가 일 때 (c₁, ..., c_n) = (c₁, ..., c_n) 이 성립한다.
(4) 는 문장문자에 와 같은 진리값을 할당한다.
(5) 가 n 항 술어문자 R 을 E 의 대상들의 일련체 c₁, ..., c_n 에 대해 참이라고 규정할 경우 그리고 오직 그 경우에만 는 R 을 그 일련체 c₁, ..., c_n 에 대해 참이라고 규정한다.

의 부해석의 영역이 될 수 있는 집합 E 는 어떤 집합인가? 무엇보다도 먼저 E 는 의 영역의 공집합이 아닌 부분집합이어야 한다. 구절 (2) 는 E 에 또 다른 요구조건을 부과한다. 즉, E 는 가 이름들에 할당하는 모든 지시대상들을 포함해야 한다. (3) 은 요구조건을 더 부과한다. 만약 c₁, ..., c_n이 E 에 있고 가 어떤 n 항 함수기호에 함수 를 할당한다면 (c ₁, ..., c_n) 도 또한 E 에 있어야 한다. 그렇지만 이 세 가지 요구조건이 만족된다면 E 를 영역으로 갖는 의 유일한 부해석이 있다. 공집합이 아니라면 가 항들에 할당하는 지시대상들의 집합은 이 세 가지 요구조건을 모두 만족하는 집합이다.

가 의 부해석이라면 는 와 같은 문장들을 해석한다. 그 같은 문장들은 양 해석에서 진리값이 꼭 같을 필요는 없지만 양 해석에서 모두 진리값을 갖는다. 구절 (2) 와 (3) 으로부터 가 각 항에 와 같은 지시대상을 할당한다는 것이 도출된다. 그리고 구절 (4) 와 (5) 로부터 원자문장들은 양 해석에서 진리값이 같고 따라서 모든 양화사 없는 문장들도 그렇다는 것이 도출된다.

두 해석 와 가 같은 문장들을 해석하고 어떤 문장이 에서 참일 경우 그리고 오직 그 경우에만 그 문장이 에서도 참이라면, 그 두 해석은 기초적 동치 라고 말한다. 이 정의는 약하게 할 수 있다. 즉, 그 두 해석은 같은 문장들을 해석하고 에서 참인 모든 문장들은 에서 참이다. 정의가 약화될 수 있는 이유는 와 가 S 를 해석하고 S 가 에서 참이면 S 의 부정은 에서 참이 아니며 따라서 에서도 참이 아니고 그러므로 S 는 에서 참이기 때문이다.

스콜렘은 어떠한 해석 에 대해서도 (A) 의 부해석이며 (B) 열거가능한 영역을 가지고 있고 (C) 와 기초적으로 동치인 해석 가 있다는 것을 보여주었다. 이것으로부터 다음이 도출된다: (일차) 언어의 모든 (열거가능하게 많은) 문장들의 해석이 주어진다면 그 영역이 아무리 크더라도 그 영역을 열거가능한 수의 원소들만 남아 있지만 원래의 해석에서 참이었던 바로 그 문장들이 축소된 해석에서도 참이 되는 방식으로 줄일 수 있다.

임의의 큰 모형들에 대한 관련된 결과들 - '위로의' (upward) 정리 - 과 우리가 증명하려는 것보다 훨씬 더 강한 '아래로의' (downward) 정리와 같은 것이 있지만 여기서는 증명하지 않겠다 (독자들은 창 (Chang) 과 카이슬러 (Keisler) 의 『모형이론』을 참조하라). 우리는 이제 스콜렘의 1919 년의 정리를 증명하고 따름정리로서 또 하나의 스콜렘-뢰벤하임 정리를 도출하겠다. 그 정리는 11 장의 강한 건전성 정리와 12 장의 보조정리 I 과 II, 그리고 방금 말한 부해석에 관한 사실로부터 직접적으로 도출된다.

정리

어떠한 해석 도 그 영역이 열거가능하면서 기초적으로 동치인 부해석 를 갖는다.

증명. Δ 를 에서 참인 모든 (양화사 머리) 문장들의 집합이라고 하자. 12 장의 보조정리 I 에 의해, Δ 로부터의 표준적 도출 가 있다. a 가 이름이고 f 가 함수기호이며 에 의해 각각 지시체와 함수를 부여받았다면, a=a, ∀xf(x, ..., x) = f(x, ..., x), ∀xx=x 모두는 Δ 와 에 나타난다. '표준적 도출' 의 정의 중 구절 5 에 의해 에 나타나는 모든 함수 기호들은 Δ 에 나타나고, 따라서 11 장의 강한 건전성 정리에 의해 의 모든 문장들을 참이게끔 하는 해석 이 있으며, 이 해석은 에 나타나지만 에 의해 어떠한 지시체도 부여받지 않는 그러한 이름들에 부여하는 것에 있어서만 와 다르다.

Γ 는 의 양화사 없는 문장들의 집합이라고 하자. 이 Γ 의 모형이기 때문에, Γ 에 나타나는 어떠한 항 t 도 에 의해 지시체를 부여받는다. 그리고 만일 t 가 에 의해 지시체를 부여받으면, t 는 에 의해 대상들을 부여받은 이름들과 함수기호들 - 이것들은 모두 에 나타난다 - 및 에 나타나는 다른 이름들로부터 형성된다. 따라서 ∀xx=x 가 에 있기 때문에 t=t 가 Γ 에 있다. 따라서 에 의해 지시체를 부여받는 항들은 Γ 에 나타나는 항들뿐이다.

E 를 이 항들에 부여한 지시체들의 집합이라고 하자. E 는 (어떤 항 t 에 대하여) t=t 가 Γ 에 있기 때문에 비어 있지 않다. E 는 Γ 가 열거가능하기 때문에 열거가능하다. 를 영역 E를 가진 의 부해석이라고 하자. 이 어떤 항에 지시체 d 를 부여한 경우 그리고 오직 그 경우에만 는 그 항에 d 를 부여한다. 그러므로 의 영역에 있는 모든 대상은 Γ 에 나타나는 어떤 항에 의해 ( 에 따라) 지시된다. Γ 의 모든 원소들은 양화사가 없고 에서 참이므로 의 부해석 에서 참이다. 따라서 는 Γ 와 짝이 맞는다 (12 장 참조). 따라서 12 장의 보조정리 II 에 의해, 는 에 있는 모든 문장들의 집합의 모형이고, 그러므로 Δ 의 모형이다.

만약 가 에서와 같은 이름들에 지시체를 부여한다는 것을 제외하고는 와 같다면, 는 열거가능한 영역을 가진 Δ 의 모형이고, 따라서 와 기초적으로 동치인 열거가능한 영역을 가진 부해석이다.

따름정리 1 (스콜렘, 1919)

만약 θ 가 만족가능하고 열거가능한 문장들의 집합이라면 θ 의 모형이면서 열거가능한 영역을 가긴 해석 가 있다.

따름정리 2 (뢰벤하임, 1915)

한 문장이 만족가능하면 그 문장은 열거가능한 영역을 가진 어떤 해석에서 참이다.

따름정리3

등호 '=' 를 포함하지 않는 한 문장이 만족가능하면 그 문장은 모든 자연수들의 집합을 영역으로 갖는 어떤 해석에서 참이다.

증명. 이 따름정리는 따름정리 2 와 다음의 두 사실로부터 도출된다. (a) '=' 를 포함하고 있지 않는 한 문장이 유한한 영역을 가지고 있는 어떤 해석 에서 참이라면 그 문장은 열거가능하게 무한한 영역을 가지고 있는 어떤 해석 에서 참이다. (b) 한 문장이 열거가능하게 무한한 영역을 가진 어떤 해석 에서 참이면 그 문장은 자연수들의 집합을 영역으로 갖는 어떤 해석 에서 참이다.

(a)의 증명. 가 유한한 영역 E 를 가진 해석이라고 가정하자. e 를 E 의 어떤 원소라고 하자. c₀, c₁, ... 을 E 에 있지 않은 대상들의 열거가능하게 무한한 일련체이라고 하자. D 를 E 의 모든 원소들과 모든 c_i 들을 포함하는 집합이라고 하자. d 가 D 에 있는 경우 d^* 를 다음과 같이 정의하자. 즉 d 가 E 에 있는 경우 d^*=d 이고, d 가 E 에 없는 경우 d^*=e 이다. 를 '모든 c_i 들을 e 와 구별불가능하게 만드는' 다음의 해석이라고 하자. 즉 의 영역은 D 이다. 는 가 이름들과 문장문자들에 부여하는 것을 모두 그것들에게 부여한다. 가 n 항 술어문자 R 을 d, ..., d에 대해 참이라고 명시할 경우 그리고 오직 그 경우에만 는 술어문자 R을 d₁, ..., d_n 에 대해 참이라고 명시한다. 그리고 는 다음이 성립하도록 n 항 함수기호 f 에 함수 를 부여한다. 가 f 에 부여하는 함수가 일 때, D 에 있는 어떠한 d₁, ..., d_n에 대해서도 (d₁, ..., d_n)=(d, ..., d) 이다. 이제 '=' 을 포함하지 않는 어떠한 문장 S 에 대해서도 (S)=(S) 임을 보이겠다.

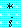이를 위해 D 에 있는 각각의 d 에 대하여 새로운 이름 a_d, 즉 에 의해 어떠한 지시체도 부여받지 않는 이름을 선택하라 (D 의 서로 다른 원소들에 대하여 서로 다른 이름들을 선택하라). 각각의 a_d 에 대하여 ₁(a_d)=d 인 것을 제외한다면 ₁은 와 똑같다고 하자. 그리고 각각의 a_d 에 대하여, ₁(a_d)=d^* 인 것을 제외한다면 ₁ 은 와 똑같다고 하자. 그러면 어떠한 이름 b 에 대해서도, ₁(b)=d 이면 ₁(b)=d^* 이다. 이제 1 과 n 사이의 어떠한 i 에 대해서도, ₁(t_i)=d_i 이고 ₁(t_i)=d이면,

₁(f(t₁, ..., t_n)) = (d₁, ..., d_n) = (d, ..., d) = ₁(f(t₁, ..., t_n))

이다. 따라서 어떠한 항 t 에 대해서도, ₁(t)=d 이면 ₁(t)=d^*라는 것이 귀납적으로 도출된다. 따라서 ₁(Rt₁, ..., t_n)=1 인 경우 그리고 오직 그 경우에만 ₁(Rt₁, ..., t_n)=1 이다. 따라서 '=' 을 포함하지 않는 모든 원자문장은 ₁에서 참인 경우 그리고 오직 그 경우에만 ₁ 에서 참이다. 모든 '=' 없는 문장이 ₁에서와 같은 진리값을 ₁ 에서 갖는다고 결론지을 수 있다면, 똑같은 것이 와 에 대해서도 성립한다고 결론지을 수 있다. 왜냐하면 a_d들 중 어떠한 것도 포함하지 않는 문장은 ₁에서 참인 경우 그리고 오직 그 경우에만 에서 참이고, ₁ 에서 참인 경우 그리고 오직 그 경우에만 에서 참일 것이기 때문이다. ₁ 에서와 같은 진리값을 ₁ 에서 갖는 문장들의 진리함수적 복합문장은 분명히 ₁ 에서와 같은 진리값을 ₁ 에서 갖기 때문에, ₁ 과 ₁ 에서 서로 반대되는 진리값을 갖는 어떤 가장 간단한 문장 S 가 존재한다면 S 는 ∃vH 와 ∀vH 두 형태들 중의 한 형태일 것임에 틀림없다. S=∃vH 라고 가정하자. (S=∀vH 일 경우에도 논증은 비슷하다.) 그러나 그러면 D 나 E 의 어떠한 원소도 ₁ 또는 ₁에 따라 각각 어떤 이름의 지시체이기 때문에, ₁(S)=1, 즉 ₁(∃vH)=1 인 꼭 그 경우 어떤 이름 a 에 대해여 ₁(H_va)=1 이며, 또 꼭 그 경우 (H_va 가 ∃vH 보다 더 간단하기 때문에) 어떤 이름 a 에 대하여 ₁(H_va)=1 이며, 똑 꼭 그 경우 ₁(∃vH)=1, 즉 ₁(S)=1 이 된다. 따라서 '=' 없는 어떠한 문장 S 도 ₁과 ₁에서 서로 반대되는 진리값을 갖지 않으며, 그러므로 와 도 마찬가지로 그러하다. 따라서 (a) 가 성립한다.

S 가 '=' 를 포함하지 않는다는 가정은 꼭 필요하다. '∃x∀yx=y' 는 정확히 한 원소만을 포함하는 영역을 가진 어떠한 해석에서도 참이지만, 더 큰 영역을 가진 어떠한 해석에서도 거짓이다.

(b)의 증명. d₀, d₁, d₂, ... 는 의 영역의 모든 원소들을 중복되지 않게 열거한 것이라고 하자. 그러면 에서 참인 동일한 문장들은 다음과 같은 해석 에서도 참이다. 의 영역은 자연수의 집합이며, 는 각각의 문장문자에 에서와 같은 진리값을 부여하고, 가 어떤 이름에 d_i 를 지시체로 부여하는 경우 그리고 오직 그 경우에만 그 이름에 수 i 를 부여하고, 가 어떤 술어문자를 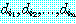에 대해 참이라고 명시하는 경우 그리고 오직 그 경우에만 그 술어문자가 자연수의 일련체 i₁, i₂, ..., i_n에 대해 참이라고 명시하고, 함수기호 f 에는 가 f 에 부여하는 함수로부터 위에서처럼 모든 곳에서 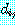를 i_j 로 '치환' 함으로써 함수를 부여한다.

한때 스콜렘-뢰벤하임 정리는 그 결과들이 변칙적인 것으로 여겨져서 철학적인 의문을 불러일으키는 것으로 생각되었다. 종종 '스콜렘의 역설' 이라고 불려지는 외견상의 변칙은 다음과 같은 내용이다. 즉, 자연수들의 집합들이 열거불가능하게 많이 존재한다고 말하는 듯한 어떤 한 문장이 참이 되는 어떤 해석들이 있다. 그런데 이 해석들의 영역들은 자연수들의 열거가능하게 많은 집합들만을 포함하고, 우리가 '(자연수들의) 집합' 이라고 번역하고 싶은 그 문장 속의 술어문자는 그 영역들 속의 (자연수들의) 집합들에 대해서만 참이다.

역설적이라고 생각되는 사태가 일어난다는 것을 부정할 수 없다. 그것이 어떻게 일어나는지를 알아 보기 위해서 우리는 우선 자연수들의 집합들의 집합인 E 가 열거가능하다는 것이 무엇인지에 대한 대안적인 설명이 필요하고 또 이것 때문에 약간의 정의가 필요하다.

우리는 x+y<i+j 이거나 (x+y=i+j 이고 x<i) 이면 순서 O 에서 자연수들의 (순서) 쌍 <x, y> 가 다른 쌍 <i, j> 를 앞선다고 말한 것이다. 우리는 <x, y> 가 순서 O 에서 (z+1) 번째 쌍이면 J(x, y)=z 라고 놓음으로써 쌍함수 (pairing function) J 를 정의한다. 그러면 J 는 자연수들의 쌍들의 집합에서부터 자연수들의 집합으로 가는 일대일 함수이다. 즉 J 는 투입값인 자연수들의 각 쌍에, 서로 다른 쌍에는 서로 다른 수들을 부여하면서, 유일한 자연수를 산출값으로 부여하고 또 모든 수를 어떤 쌍에 부여한다. (J 는 말하자면 회귀 함수이다.)

우리는 만약

∀z (z 는 자연수들의 집합이다 & z 는 E 속에 있다 → ∃x (x 는 자연수이다 & ∀y (y 는 자연수이다 → (y 는 z 속에 있다 ↔ J(x, y) 는 w 속에 있다))))

라면 자연수들의 집합 w 를 자연수들의 집합들의 집합인 E 의 열거자 (enumerator)라고 부를 것이다. 우리에게 필요한 열거자들과 열거가능성에 대한 사실은 E 가 열거자를 가지고 있을 경우 그리고 오직 그 경우에만 자연수들의 집합들의 집합인 E 가 열거가능하다 는 것이다.

(이유: E 가 열거가능하다고 가정하자. E 의 모든 원소들과 혹 자연수들의 어떤 다른 집합들까지 포함하는, 자연수들의 집합들의 열거를 e₀, e₁, e₂, ... 이라고 하자. 그러면 y 가 e_x에 있는 수들 J(x, y) 의 집합이 E 의 열거자가 된다. 반대로 w 가 E 의 열거자라면 e_x는 J(x, y) 가 w 에 속하는 그런 수들 y 의 집합일 때 e₀, e₁, e₂, ... 는 E 의 모든 원소들을 포함하는 열거이고 따라서 E 는 열거가능하다.)

우리는 이제 한 언어와 그것의 해석들 중에서 어떤 것을 살펴보려고 한다. 그 언어는 이름들 '0 ', '1 ', '2 ' 등과 하나의 이항 함수기호 'J ' 와 두 개의 일항 술어문자 'N ' 과 'S ' 와 하나의 이항 술어문자 '∈' 만을 포함한다. 우리가 관심을 가지고 있는 해석들은 그 영역이 모든 자연수들과 자연수들의 어떤 (아마도 모든) 집합들만을 포함하고 있고 그 외의 다른 것은 포함하지 않는 해석들이다. 그 해석은 각 숫자에 자신의 통상적인 지시대상을 부여한다. 그 해석은 J 에 (x, y 가 집합일지라도 투입값 x, y 에 대해서 어떤 임의적인 산출값 - 가령 17 - 을 취할 수 있도록 확장된) 쌍함수를 부여한다. 그리고 그 해석은 N 이 어떠한 수에 대해서도 참이고 S 는 수들의 어떤한 집합에 대해서도 참이며 ∈ 는 수 y 가 집합 z 에 속할 경우 그리고 오직 그 경우에만 y, z 에 대해서 참이라고 규정한다. 이러한 해석들 가운데 하나인 를 표준적 해석이라 부른다. 그것은 자연수들의 모든 집합을 포함하는 영역을 갖는 해석이다.

이러한 모든 해석들에서 문장

-∃w(S w&∀z(S z→∃x(N x&∀y(N y→(y∈z↔J (x, y)∈w)))))

(2)

는 진리값을 가질 것이다. 이 문장은 해석의 영역 안의 수들의 모든 집합들의 집합의 열거자가 그 해석의 영역 안에 없을 경우 그리고 오직 그 경우에만 그 해석들 중 하나에서 참일 것이다 (이상은 '열거자' 의 정의를 되돌아보면 알 수 있다). 우리는 영역 안의 수들의 모든 집합들의 집합의 열거자가 없을 경우 그리고 오직 그 경우에만 그 문장이 한 해석에서 참이라고 간단하게 말할 수 없다. 왜냐하면 양화사 '∃w' 는 그 해석의 영역의 원소들만을 값으로 갖거나 또는 '지시한다' 고 이해되기 때문이다.

알다시피 수들의 모든 집합들은 의 영역 안에 있기 때문에 의 영역 안의 수들의 모든 집합들의 집합의 열거자는 없다. 더구나 의 영역에는 그런 열거자는 없고 그래서 문장 (2) 는 에서 참이고 또 '에 관해' (over) 해석될 때 수들의 모든 집합들의 집합의 열거자가 있다는 것을 부정하기 때문에 '열거가 불가능하게 많은 집합들이 존재한다' 를 뜻한다고 말할 수 있다. 스콜렘-뢰벤하임 정리에 의해서 는 기초적으로 동치인 부해석 를 갖게 되는데 이 의 영역은 열거가능하고 따라서 수들의 열거가능하게 많은 집합들만을 포함한다. (0, 1, 2 등은 모두 의 영역 안에 있다. 왜냐하면 이것들은 가 '0 ', '1 ', '2 ' 등에 부여하는, 따라서 도 부여하는 지시대상들이기 때문이다.) 와 는 기초적으로 동치이기 때문에 (2) 는 에서 참인 문장이고 그러므로 다음과 같은 해석에서 참인데 그 해석의 영역에는 수들의 열거가능하게 많은 집합들만이 있고 그 해석에서 'S '는 그 영역에 속한 수들의 집합들에 대해서만 참이다. 이것이 스콜렘의 '역설'이다.

이 역설은 어떻게 해결할 수 있는가? 의 영역의 모든 집합들의 집합은 열거가능하기 때문에 정말로 열거자를 가지고 있지만 그 열거자들 중 어느 것도 의 영역 안에 있을 수 없다. (그렇지 않다면

(S w&∀z(S z→∃x(N x&∀y(N y→(y∈z↔J (x, y)∈w)))))

은 에서 그 열거자들 중의 하나에 대해서 참이 되고 따라서 (2) 는 에서 거짓이기 때문이다.) 그래서 (2) 가 에서 어떻게 참일 수 있는가에 대한 부분적 설명은 의 영역의 집합들의 집합이 열거가능하다는 주장을 '입증하는' 집합들 자신은 의 영역의 원소가 아니라는 것이다.

한 걸음 더 나아간 부분적 설명은, 한 문장이 무엇을 말하거나 뜻하거나 부정하는 것으로 이해해야 하느냐는 그 문장을 이루는 기호들의 기능인 것 못지않게 그 문장이 해석되는 해석의 (그리고 심지어 그 해석이 기술되거나 지시되는 방식의) 기능이라는 것이다. (2) 는 그 양화사가 표준적 해석 의 영역과 같은 모든 수들과 수들의 모든 집합들을 포함하는 집합에서 값을 가지는 것으로 이해될 때 '열거가 불가능하게 많은 집합들이 존재한다' 를 말하는 것으로 이해할 수 있다. 그러나 그 문장은 또한 그 양화사가 다른 영역들에서 값을 가질 때, 특히 셀 수 있는 영역들의 원소들을 값으로 가질 때는 그렇게 이해할 수 없다. 문장 (2) - 앞에서 본 기호들의 일련체 - 는 해석이 주어질 때에만 무엇인가를 '말한다'. (2) 가 열가가능한 영역을 가진 의 어떤 부해석 까지도 포함하는 모든 종류의 해석들에서 참이라는 사실은 놀라운 일일 수도 있고 심지어 재미있기까지 하다. 그러나 (2) 가 그것들에서 참이라는 사실이 덮어놓고 불가능하다고 생각해서는 안 된다. 문장 (2) 가 에 관해 해석될 때 그것은 단지 ' 의 영역은 의 수들의 집합들의 집합의 열거자들을 전혀 포함하지 않는다' 고 말하는 것이다. 그런데 이 말은 물론 참이다.

연습문제

13.1 해석들이 열거불가능하게 많은 일항 술어문자들에 대상을 할당하도록 허용되었다고 가정하자. 그러면 우리가 말했던 대로의 스콜렘-뢰벤하임 정리는 잘못이라는 것을 보여라.

13.2 만약 의 언어의 모든 식 F 와 의 논의 영역에 있는 모든 연속 o₁, ..., o_n 에 대하여

이면 의 하위해석 는 의 기초적인 하위해석 이라고 부른다. 여기서 F 는 기껏해야 n 개의 자유변항 v₁, ..., v_n 을 포함하고 a₁, ..., a_n은 가 아무런 지시체도 부여하지 않는 n 개의 이름들이고, F^* 는 F 에서 모두 자유롭게 나타난 v₁, ..., v_n 대신에 a₁, ..., a_n 을 (각각) 대입한 결과라고 가정하다. 임의의 해석 에는 열거가능한 논의 영역을 가진 기초적인 하위해석 가 있음을 보여라. 이 진술로부터 교재에서 증명한 꼴의 스콜렘-뢰벤하임 정리를 도출하라.

13.3 교재에서 증명한 꼴의 스콜렘-뢰벤하임 정리가 의존 선택 공리를 함축함을 보여라. (연습문에 11.5 참조)

풀이

13.1 이 실수들의 집합이라고 하자. 에 있는 각 r 에 대하여 A_r 은 일항 술어문자라고 하자. 는 각 A_r 이 r 그리고 오로지 r 에 대하여만 참이라고 규정하며 논의 영역이 인 해석이라고 하자. 각 r 에 대하여 ∃xA_rx 는 에서 참이고, 따라서 모든 동치인 기초적인 하위해석에서 참이다. 따라서 각 실수 r 은 틀림없이 모든 동치인 기초적인 하위해석 의 논의 영역에 속한다. 따라서 그런 각 의 논의 영역은 열거불가능하다.

13.3 X 가 공집합이 아닌 집합이고, X 에 있는 임의의 x 에 대해여 xRy 를 만족하는 y 가 X 에 있다고 가정하자. 는 논의 영역이 X이고, xRy 인 경우 그리고 오직 그 경우에만 'R' 이 x, y 에 대하여 참인 해석이라고 하자. ∀x∃yxRy 는 에서 참이다. 는 와 동치인 기초적 하위해석이고 논의 영역 E 가 열거가능하다고 하자. e₀, e₁, e₂, ... 는 E 를 열거한 것이라고 하자. ∀x∃yxRy 는 에서 참이다. 따라서 E 의 모든 e_i 에 대하여 e_iRe_j 를 만족하는 e_j 가 E 에 있을 것이다. f 를 다음과 같이 정의하라: f(0)=e₀ 이고, 각 n 에 대하여, f(n)Re_j 이며 모든 k < j 에 대하여 f(n)Re_k 가 아닐 꼭 그 경우 f(n+1)=e_j 이다. 의존 선택 공리는 f 의 존재를 보장하기 위해 필요하지 않다.