만약 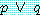 와
와 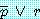 가 모두 참이면
가 모두 참이면 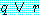 은 참이다. (1)
은 참이다. (1)
Resolution Proofs
이산수학 : Richard Johnsonbaugh 저서, 강홍식.김정인.이도훈.이명재 번역, 교보문고, 1999 (원서 : Discrete Mathematics 6th ed, Prentice-Hall, 1997), Page 45~49
분해 (resolution) 는 1965년 J. A. Robinson 에 의해 제안된 증명 기술이다. 이 기술은 하나의 법칙에 의존한다.
만약 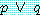 와
와 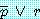 가 모두 참이면
가 모두 참이면 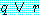 은 참이다. (1)
은 참이다. (1)
(1) 은 진리표를 작성하여 검증할 수 있다. 왜냐하면 분해는 하나의 단순한 법칙에 의존하며, 이것은 추론이나 정리 증명의 많은 컴퓨터 프로그램의 기초 (basis) 이다.
분해에 의한 증명에서 가설과 결론은 절 (clauses)
로 기술된다. 절은 변수이거나 변수의 부정을 나타내는 각 항목이 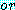 에 의해서 나누어진 항목들로 구성된다.
에 의해서 나누어진 항목들로 구성된다.
(예제
1)
표현
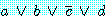
는 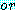 에 의해 나누어진
에 의해 나누어진 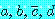 라는 항목으로 구성된 절이며 각 항목은 변수이거나 변수의 부정이다.
라는 항목으로 구성된 절이며 각 항목은 변수이거나 변수의 부정이다.
(예제
2)
표현
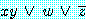
는 항목 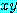 가 두 개의 변수로 구성되었기 때문에 비록
가 두 개의 변수로 구성되었기 때문에 비록 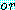 에 의해서 분리되었을 지라도 절은 아니다.
에 의해서 분리되었을 지라도 절은 아니다.
(예제
3)
표현
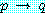
는 항목들이  에 의해 분리되어 있으므로 절이 아니다. 그러나 각 항목은 변수이다.
에 의해 분리되어 있으므로 절이 아니다. 그러나 각 항목은 변수이다.
분해에 의한 직접 증명은 결론이 유도될 때까지
새로운 문장을 유도하기 위하여 문장의 쌍으로 (1) 을 반복적으로 계속한다. 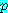 는 하나의 변수이나
는 하나의 변수이나  와
와  을 표현할 수 있다. 절에 (1) 이 적용될 때 결과
을 표현할 수 있다. 절에 (1) 이 적용될 때 결과 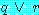 이 절임에 주의하라 (
이 절임에 주의하라 ( 와
와  은 각 항목이
은 각 항목이 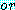 에 의해 구분되어 있으며, 각 항목은 변수이거나 변수의 부정이고
에 의해 구분되어 있으며, 각 항목은 변수이거나 변수의 부정이고 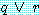 또한 변수나 변수의 부정으로 각 항목들이
또한 변수나 변수의 부정으로 각 항목들이 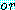 에 의하여 구성한다).
에 의하여 구성한다).
(예제
4)
분해를 이용하여 다음을 증명하라.
|
1. |
|
2. |
|
3. |
|
∴ |
1 과 2 의 표현으로부터 (1) 을 적용하여
4. 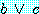
를 유도하며, 3 과 4 의 표현에 (1) 을 적용하여
5. 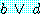
를 결론으로 유도한다. 주어진 가설 1, 2,
3 으로부터 결론 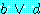 가 증명되었다.
가 증명되었다.
(1) 의 특별한 경우는 다음과 같다.
만약 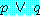 와
와 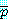 가 참이면
가 참이면  는 참이다.
는 참이다.
만약 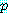 와
와 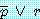 이 참이면
이 참이면  은 참이다. (2)
은 참이다. (2)
(예제
5)
분해를 이용하여 다음을 증명하라.
|
1. |
|
2. |
|
3. |
|
∴ |
표현 1 과 2 에 (2) 를 적용하면 4 가 유도된다.
4. 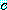
표현 3 과 4 에 (2) 를 결론 5 가 유도된다.
5. 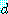
주어진 가설 1, 2, 3 을 가지고 결론 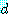 를 유도하였다.
를 유도하였다.
만약 가설이 절이 아니면 절이나 and 가 포함된
절인 표현 동치로 재배치해야 한다. 예를 들면, 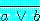 를 하나의 가설로 가정하자. bar 는 하나 이상의 변수에 걸쳐 있으므로 드모르간의
첫 번째 법칙 (예제 1.2.11) 을 이용하여
를 하나의 가설로 가정하자. bar 는 하나 이상의 변수에 걸쳐 있으므로 드모르간의
첫 번째 법칙 (예제 1.2.11) 을 이용하여
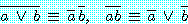
와 같은 bar 가 하나의 변수로 된 동치 표현을 얻는다.
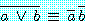 (3)
(3)
그러면 원래의 가설 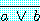 는
는 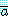 와
와  로 구성된 두 개의 가설로 재조정된다. 재조정은 개별적인 가설
로 구성된 두 개의 가설로 재조정된다. 재조정은 개별적인 가설 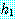 과
과 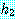 가
가 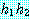 와 동치인 점에 의해 정당화되었다 (정의 1.4.9 를 보라). 드모르간의 법칙을
반복시키면 그 결과로 각 bar 는 오직 하나의 변수에 적용된다.
와 동치인 점에 의해 정당화되었다 (정의 1.4.9 를 보라). 드모르간의 법칙을
반복시키면 그 결과로 각 bar 는 오직 하나의 변수에 적용된다.
몇몇 변수의 and 로 구성된 항목이 or 에 분리된 항목들로 구성된 표현은 동치를 이용한 절의 and 로 구성된 동치 표현에 의해 재조정된다.
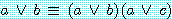 (4)
(4)
이 경우 하나의 가설 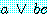 는 두 개의 가설
는 두 개의 가설 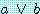 와
와 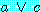 로 재조정한다. 첫 번째 드모르간의 법칙을 이용하면 (3) 과 (4) 는 각 절로
구성된 동치 가설을 얻을 수 있다.
로 재조정한다. 첫 번째 드모르간의 법칙을 이용하면 (3) 과 (4) 는 각 절로
구성된 동치 가설을 얻을 수 있다.
(예제
6)
분해에 의해서 다음을 증명하라.
|
1. |
|
2. |
|
∴ |
(4) 를 이용하여 가설 1 을 두 개의 가설로 재조정한다.
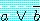
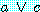
첫 번째 드모르간의 법칙을 이용하여 가설 2 를 두 개의 가설로 재조정한다.
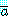

그러면 논법은 다음과 같이 된다.
|
1. |
|
2. |
|
3. |
|
4. |
|
∴ |
표현 1 과 3 에 (1) 을 적용시켜 직접적으로 결론

를 유도한다.
자동 추론 시스템에서 분해에 의한 증명은 반증에 의한 증명과 함께 결합된다. 절로서 부정된 결론을 적고 가설에 절들을 더한다. 그리고는 반복적으로 (1) 을 적용하여 반증을 유도한다.
(예제
7)
예제 4 를 반증에 의한 증명과 분해의 결합에 의해 다시 증명해 보자. 첫째로 결론을 부정하고 첫 번째 드모르간의 법칙을 이용하여
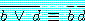
를 얻는다.  와
와  를 더하여 다음 가설을 얻는다.
를 더하여 다음 가설을 얻는다.
|
1. |
|
2. |
|
3. |
|
4. |
|
5. |
표현 1 과 표현 2 에 (1) 을 적용하여
6. 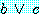
을 유도한다.
표현 3 과 표현 6 에 (1) 을 적용시켜
7. 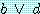
를 유도한다.
표현 4 와 표현 7 에 (1) 을 적용하여
8. 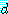
를 얻는다.
표현 5 와 표현 8 에 주어진 반증을 결합하면 증명은 완전하다.
분해는 정확 (correctness) 하며 완전한 반박이라는 것을 보였다. 분해가 정확하다는 것은 모순된 절들의 집합으로부터의 반증을 유도할 수 있다는 뜻이다. 분해가 완전한 반박이라는 것은 만약 절들의 집합이 모순이라면 분해는 반증을 유도할 수 있다는 뜻이다. 그러므로 만약 가설의 집합으로부터 결론이 도출된다면 분해는 가설과 결론의 부정에 의해 반증을 유도할 수 있다. 불행하게도 분해는 우리에게 반증을 유도하기 위하여 어느 절들을 결합하여야 하는지 제시하지 못한다. 자동 추론 시스템에서의 관건은 절들의 결합을 찾는 길잡이다. 분해와 자동 추론의 참고로는 [Gallier ; Genesereth ; and Wos] 가 있다.
( 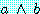 는
는 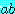 와 같이 표기한다)
와 같이 표기한다)