In the N Queens problem, the object is to place N queens on a chessboard in such a way that no two queens can take each other. Accordingly, no two queens can be placed on the same row, column, or diagonal.
To solve the problem, you'll number the rows and columns of the chessboard from 1 to N. To number the diagonals, you divide them into two types, so that a diagonal is uniquely specified by a type and a number calculated from its row and column numbers:
Diagonal = N + Column - Row (Type 1)
Diagonal = Row + Column - 1 (Type 2)
When you view the chessboard with row 1 at the top and column 1 on the left side, Type 1 diagonals resemble the backslash (íČ) character in shape, and Type 2 diagonals resemble the shape of slash (/). Figure 16.5 shows the numbering of Type 2 diagonals on a 4x4 board.
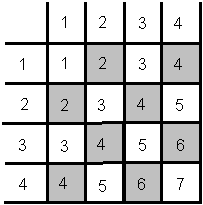
Figure 16.5: The N Queens Chessboard
To solve the N Queens Problem with a Visual Prolog program, you must record which rows, columns, and diagonals are unoccupied, and also make a note of where the queens are placed.
A queen's position is described with a row number and a column number as in the domain declaration:
queen = q(integer, integer)
This declaration represents the position of one queen. To describe more positions, you can use a list:
queens = queen*
Likewise, you need several numerical lists indicating the rows, columns, and diagonals not occupied by a queen. These lists are described by:
freelist = integer*
You will treat the chessboard as a single object with the following domain declaration:
board = board(queens, freelist, freelist, freelist, freelist)
The four freelists represent the free rows, columns, and diagonals of Type 1 and Type 2, respectively.
To see how this is going to work, let board represent a 4 )4 chessboard in two situations: (1) without queens, and (2) with one queen at the top left corner.
1. board without queens
board([], [1,2,3,4], [1,2,3,4], [1,2,3,4,5,6,7], [1,2,3,4,5,6,7])
2. board with one queen
board([q(1,1)], [2,3,4], [2,3,4], [1,2,3,5,6,7], [2,3,4,5,6,7])
You can now solve the problem by describing the relationship between an empty board and a board with N queens. You define the predicate
placeN(integer, board, board)
with the two clauses following. Queens are placed one at a time until every row and column is occupied. You can see this in the first clause, where the two lists of freerows and freecols are empty:
placeN(_, board(D, [], [], X, Y), board(D, [], [], X, Y)) :- !.
placeN(N, Board1, Result) :-
place_a_queen(N, Board1, Board2),
placeN(N, Board2, Result).
In the second clause, the predicate place_a_queen gives the connection between Board1 and Board2. (Board2 has one more queen than Board1). Use this predicate declaration:
place_a_queen(integer, board, board)
The core of the N Queens Problem lies in the description of how to add extra queens until they have all been successfully placed, starting with an empty board. To solve this problem, add the new queen to the list of those already placed:
[q(R, C)|Queens]
Among the remaining free rows, Rows, you need to find a row R where you can place the next queen. At the same time, you must remove R from the list of free rows, resulting in a new list of free rows, NewR. This is formulated as:
findandremove(R, Rows, NewR)
Correspondingly, you must find and remove a vacant column C. From R and C, you can calculate the numbers of the occupied diagonals. Then you can determine if D1 and D2 are among the vacant diagonals.
This is the place_a_queen clause:
place_a_queen(N, board(Queens, Rows, Columns,
Diag1, Diag2),
board([q(R, C)|Queens], NewR, NewS, NewD1,
NewD2)) :-
findandremove(R,
Rows, NewR),
findandremove(C,
Columns, NewC),
D1=N+S-R,
findandremove(D1, Diag1, NewD1),
D2=R+S-1,
findandremove(D2, Diag2, NewD2).
Program 7 is the complete program. It contains a number of smaller additions to define nqueens, so you only need to give a goal like:
nqueens(5)
to obtain a possible solution (in this case, for placing five queens on a 5 )5 board).
/* Program ch16e07.pro */
DOMAINS
queen = q(integer, integer)
queens = queen*
freelist = integer*
board = board(queens, freelist, freelist, freelist, freelist)