알고리즘과 튜링 기계

황제의 새마음 : Roger Penrose 저서, 박승수 옮김, 이화여대 출판부, 1996 (원서 : The Emperor's New Mind : Concerning Computers, Minds, and The Laws of Physics, Oxford Univ. Press, 1989)

알고리즘 개념의 배경

튜링의 개념

숫자 데이터의 2 진 코드화

처치-튜링 명제

자연수 이외의 수

만능 튜링 기계

힐베르트 문제의 해결 불가능성

알고리즘을 능가하는 방법

처치의 람다 계산법

알고리즘 개념의 배경

알고리즘이란 무엇이고 튜링 기계, 그리고 만능 튜링 기계란 정확히 무엇을 말하는 것인가? 왜 이 개념이 현대의 관점에서 보는 '생각하는 기계' 에서 가장 핵심적인 요소로 여겨지고 있는가? 알고리즘이 본질적으로 수행할 수 있는 일에 어떤 절대적 한계성이 있는 것일까? 이러한 질문에 정확히 접근하기 위해서는 알고리즘과 튜링 기계의 개념을 좀더 자세하게 알아볼 필요가 있다.

이제 여러 가지 주제를 다루는 가운데, 우리는 가끔은 수학 공식을 사용하여야 한다. 물론 어떤 독자들은 수식을 보면 흥미가 떨어지거나, 혹은 겁을 내는 사람도 있을 것이다. 만일 당신이 그러한 부류에 속한다면 염려하지 말고 적당히 넘어가기 바란다. 앞에 실은 '독자를 위한 노트' 에서 제시한 방법을 따르라고 조언하고 싶다. 여기에 제시하는 내용을 이해하는 데는 초등학교 수준 이상의 수학 실력을 필요로 하고 있지 않지만, 자세한 사항까지 이해하려면 깊은 생각이 필요할 것이다. 실제로 거의 모든 과정을 낱낱이 설명하였기 때문에 조심해서 따라가기만 하면 잘 이해할 수 있을 것이다. 그러나 개념만을 이해하기 위해서 적당히 훑더라도 많은 도움이 될 것이다. 한편 당신이 이 분야의 전문가라면, 다시 한 번 부탁하지만 그냥 자유롭게 읽어 주기 바란다. 그렇게 읽더라도 약간이나마 도움될 만한 가치가 있을 것이고, 혹 한두가지 흥미 있는 사항을 발견할 수 있을지도 모른다.

'알고리즘 (algorithm)' 이라는 단어는 AD 825 년에 'Kitab al jabr w' almuqabala' 라는 영향력 있는 수학 교과서를 저술한 9 세기 페르시아 수학자 알코와리즘 (Abu Ja'far Mohammed ibn Mûsâ al-Khowârizm) 의 이름에서 유래한다. 처음에는 더 정확하게 'algorism' 이라고 표기되었는데 요즈음 'algorithm' 으로 바뀐 것은 산수라는 의미의 'arithmetic' 에서 영향을 받은 것 같다. (대수학을 나타내는 'algebra' 도 위의 책 제목에 등장하는 아랍 단어 'al jabr' 에서 유래한다는 사실도 알아 둘 만하다.)

그러나 알고리즘의 예는 알코와리즘의 책보다 훨씬 이전부터 알려져 왔다. 가장 잘 알려진 예로서 고대 그리스 (기원전 300 년경) 시대에 만들어진 두 수의 최대 공약수를 구하는 유클리드 (Euclid) 알고리즘을 들 수 있다. 이것이 어떤 원리인가 살펴보기로 하자. 특정한 두 개의 수, 1365 와 3654 를 예로 들면 이해가 쉬울 것이다. 물론 최대 공약수란 두 수를 각각 나머지 없이 나눌 수 있는 가장 큰 수이다. 유클리드 알고리즘을 적용하려면 우선 큰 수를 작은 수로 나눈 뒤 나머지를 구한다. 3654 를 1365 로 나누면 근이 2 이고 나머지는 924 (= 3654 - 2730) 이다. 이제 원래의 두 수 대신 나머지값과 바로 전에 나눈 수 1365 를 넣는다. 그리고 이들 두 수, 924 와 1365 를 이용하여 똑같은 작업을 반복한다. 즉, 1365 를 924 로 나누어 나머지값 441 을 구하면 새로운 두 수는 441 과 924 가 되는 것이다. 이런 방법으로 나머지값이 없어질 때까지 계속하는 것이다. 이를 다시 정리하면,

3654 ÷ 1365 1365 ÷ 924 924 ÷ 441 441 ÷ 42 42 ÷ 21

나머지값 나머지값 나머지값 나머지값 나머지값

924 441 42 21 0

이 때 마지막으로 나눈 수 21 이 두 수의 최대 공약수가 된다.

우리가 최대 공약수 21 을 구하는 데 사용한 체계적 방법이 바로 유클리드 알고리즘이다. 우리는 방금 두 개의 특정한 수에다 이 방법을 적용했는데 실은 이 방법은 수의 크기에 관계없이 어떤 수에도 고아범위하게 적용할 수 있다. 아주 큰 수에는 이 방법이 시간이 오래 걸릴 것이고 크면 클수록 시간도 더 오래 걸릴 것이다. 그러나 어느 특정한 수를 택하더라도 이 과정은 결국 끝날 것이고 유한 개의 단게를 거쳐 명백한 답이 구해질 수 있다. 각각의 단계에서 어떤 계산을 할 것인가도 확실하고 언제 전체 과정이 끝나는가도 명명백백하다. 뿐만 아니라 전체 과정이 비록 무한 개의 자연수에 적용될 수 있더라도 유한 개의 과정으로 표시될 수 있다. '자연수' 는 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ..... 등 보통의 정수를 말한다. 실제로 유클리드 알고리즘의 전체 논리 연산을 간단하게 순서도로 그릴 수 있다.

한 가지 짚고 넘어갈 것은 위의 과정은 아직 가장 기본적인 단계까지는 설명되지 않았다는 것이다. 왜냐 하면 위에서는 이미 자연수 A 를 B 로 나눈 나머지 값을 구하는 기본 연산을 '안다' 고 가정해 놓고 있기 때문이다. 그 연산 자체도 우리가 학교에서 배운 방법에 의한 알고리즘을 따르고 있다. 그 과정이 실제로는 유클리드 알고리즘의 다른 과정에 비하여 훨씬 더 복잡하다고 볼 수 있지만 그 역시 순서도로 나타낼 수 있다. 그 계산이 복잡한 것은 우리가 자연수 표현에서 십진법을 사용하는데 있다고 볼 수 있다. 왜냐 하면 십진법의 구구단표를 열거해야 될 뿐 아니라 덧셈의 한자리 올림 등을 감안해야 되기 때문이다. 만일 우리가 어떤 수 n 을 표시하기 위하여 n 개의 특수한 마크를 사용한다면 (예를 들면, ●●●●● 는 5 를 표시) 나눗셈의 나머지를 구하는 것은 매우 간단한 알고리즘으로 표시할 수 있다. A 를 B 로 나눈 나머지를 구하기 위해서는 A 를 나타내는 표시로부터 더 이상 없앨 수 없을 때까지 B 만큼 씩을 계속 없애 나가면 된다. 그 때 마지막으로 남은 마크가 표시하는 수가 구하고자 하는 해가 되는 것이다. 예를 들면 17 을 5 로 나눈 나머지는 ●●●●●●●●●●●●●●●●● 로부터 ●●●●● 를 다음과 같이 잘라 나가면 된다.

그리고 이 경우 해는 2 가 되는 것이다.

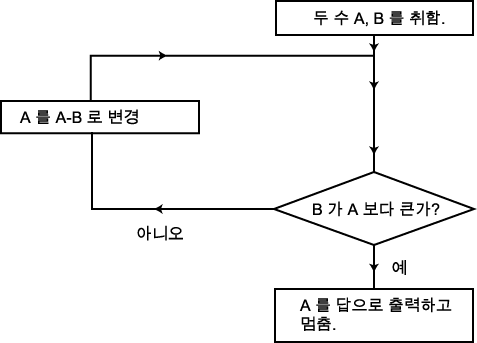
이러한 방법으로 나머지를 구하는 알고리즘은 다음과 같은 순서도로써 표시할 수 있다. 완전한 유클리드 알고리즘의 순서도를 구하기 위해서는 원래 순서도의 두 번째 줄의 오른편 상자를 위의 순서도로 대체시켜야 한다. 이렇게 알고리즘의 한 부분을 다른 알고리즘으로 대체시키는 것은 컴퓨터 프로그램에서 자주 사용하는 방법에 속한다. 위에서 본 나머지를 구하는 알고리즘은 부 프로그램 (subroutine) 의 한 예이다. 즉, 주알고리즘에서 부분적인 연산을 위하여 불러들이는 (보통 이미 알려진) 알고리즘을 뜻하는 용어이다.

물론 n 이라는 수를 표시하기 위하여 n 개의 표식을 사용하는 것은 특히 큰 수에서는 매우 비효율적이라 볼 수 있다. 그래서 우리는 일반적으로 좀더 간결한 십진법을 사용하는 것이다. 그렇지만 여기에서는 숫자 표시의 간결성 혹은 효율성 등을 염려하는 것이 아니다. 우리가 고려하고자 하는 것은 근본적으로 어떠한 연산을 체계적인 방법에 의해서 수행할 수 있는가 하는 것이다. 우리가 한 가지 형태의 숫자에 대해서 알고리즘을 구할 수 있으면 다른 형태의 숫자에 대해서도 알고리즘을 구할 수 있기 때문이다. 다만 세부적인 사항과 그 복잡도에 약간의 차이가 있을 따름이다.

유클리드 알고리즘은 수학에서 볼 수 있는 고전적ㆍ체계적 알고리즘의 하나에 지나지 않는다. 그러나 놀라운 것은 그것이 비록 고대에 기원을 두고 있지만 금세기에 들어서야 비로소 알려진 일반 알고리즘 개념에 정확하게 부합된다는 사실일 것이다. 실제로 일반 알고리즘에 대한 개념은 몇 가지 다른 형태의 형식으로 설명이 가능한데 이들은 모두 1930 년대에 제안된 것들이다. 이 중에서 가장 직접적이고 설득력이 있으며 또 역사적으로 중요하게 여겨지고 있는 것이 '튜링 기계' 라고 알려진 개념일 것이다. 이 '기계' 에 대해서는 좀더 자세한 기술이 필요하다.

튜링 '기계' 에 대해서 우선 염두에 두어야 할 사항은 그것이 실제 기계가 아니라 하나의 '추상 수학 개념' 이라는 것이다. 이 개념은 영국의 수학자요 암호 해독 전문가며 컴퓨터의 대가로 알려진 앨런 튜링이 Entscheidungsproblem 으로 알려진 아주 광범위한 수학 문제를 해결하기 위하여 1935~6 년경에 소개한 개념이다. 이 문제는 독일의 유명한 수학자 힐베르트 (David Hilbert) 가 1900 년 파리 국제수학회에서 일부 제기한 문제로서 힐베르트의 열 번째 문제라고도 불리는데 이 문제의 완전한 형태는 1928 년 볼로냐 국제학회에서 제시되었다. 힐베르트가 제기한 문제는 매우 엄청난 것이었는데 그것은 모든 수학 문제들을 풀 수 있는 일반적 알고리즘을 찾아 내는 것이었다. 더 엄밀히 말하면 그러한 알고리즘이 원칙적으로 존재할 수 있는가 하는 것에 대한 해답을 구한 것이다. 힐베르트는 또한 절대 불변하는 원칙과 공리로써 수학을 난공 불락의 기초 위에 세워 놓고자 하는 계획을 가지고 있었다. 그러나 튜링이 그의 위업을 달성하였을 때 힐베르트의 그 계획은 이미 오스트리아의 논리학자 괴델이 1931 년 증명한 놀라운 정리에 의해서 큰 타격을 입고 있었다. 제 4 장에서는 괴델이 발표한 정리와 그 중요성에 대해서 좀더 자세하게 다루고자 한다. 튜링이 관심을 갖고 있던 힐베르트의 문제 (Entscheidungsproblem) 는 어떤 특정한 수학 공리 체계를 초월한 것이었다. 그 문제란 (어떤 잘 정의된 계층에 속하는) 수학 문제 전부를 하나하나 전부 풀 수 있는 기계적인 프로그램이 원칙적으로 존재할 수 있는가 하는 것이다.

이 문제를 대답하는 데 어려운 점 중의 하나는 도대체 '기계적 프로그램' 의 정확한 의미가 무엇인가를 결정하는 것일 것이다. 그 개념은 당시 일반적인 수학적 개념의 한계를 넘어선 것이었다. 그 개념을 수식화하기 위하여 튜링은 기계 동작을 기본적인 식으로 나누어 정형화함으로써 '기계' 라는 개념이 어떻게 수식으로 표현될 수 있는가를 보이려고 하였다. 튜링은 인간의 두뇌도 하나의 '기계' 로 간주하였다. 그러므로 수학 문제를 푸는 수학자의 행동이 무엇이건 그것이 '기계적 프로그램' 으로 표시될 수 있다고 생각하였다.

인간의 사고를 그러한 관점으로 보았던 것이 튜링이 그의 중대한 이론을 개발하는 데 큰 도움을 주었는지는 모른다. 그러나 우리까지 그 관점을 전적으로 동의할 필요는 전혀 없다. 실제로 기계적 프로그램이 무엇인가를 정확히 정의함으로써 튜링은 수학적으로 명확하게 표기된 어떤 수식이 결코 기계적이 도리 수 없다는 것을 보여 주었다. 이러한 튜링의 노력이 이제 와서는 정신적 현상에 대한 그의 관점에 허점이 있음을 규명하는 데 간접적으로 쓰이게 되었다는 것은 좀 아이러니컬하다. 그러나 아직 그에 대한 이야기는 잠시 보류하기로 하고, 우선은 튜링의 기계적 프로그램이란 것이 도대체 무엇인가를 알고 넘어가기로 하자. 

튜링의 개념

어떤 유한의 계산 과정을 수행할 수 있는 장치가 있다고 가정하여 보자. 그러한 장치는 일반적으로 어떤 모양을 하고 있을까? 약간 이상적인 경우로 가정하고 그것의 실용성에 대해서는 너무 걱정하지 말기로 하자. 우리가 생각하는 것은 수학적으로 가상된 하나의 '기계' 이다. 그 기계는 (엄청나게 많을 수도 있지만) 유한 개의 서로 다른 상태를 가질 수 있다고 본다. 그것을 그 기계의 내부 상태 (internal states) 라고 부르자. 하지만 우리는 이 기계가 근본적으로 수행할 수 있는 계산의 크기에 대해서는 한계를 두지 않으려고 한다. 앞에서 제시한 유클리드 알고리즘의 예를 생각해 보자. 그 알고리즘이 다룰 수 있는 수의 크기에는 근본적으로 아무런 제한이 없다. 그 알고리즘 (혹은, 일반 계산 과정) 은 어떤 큰 수가 들어오더라도 똑같은 과정을 거친다. 아주 큰 숫자에 대해서는 그 과정을 수행하는 데 시간이 좀 오래 걸릴 수는 있다. 그리고 계산을 위하여 좀 많은 양의 '연습장' 이 필요할 수도 있다. 그러나 알고리즘 자체는 아무리 큰 수가 들어오더라도 똑같은 명령어들인 것이다.

그러므로 그 기계가 비록 제한된 내부 상태를 갖더라도 입력되는 숫자는 무한정 커질 수 있는 대비를 하여야 할 것이다. 그뿐 아니라 이 기계는 필요에 따라서는 무한정 외부 기억 장치 (우리 '연습장' 에 해당) 를 가져다 계산을 하고 또 무한정한 크기의 출력도 가능하다고 가정한다. 기계의 내부 상태가 유한하다는 가정 때문에 우리는 그 모든 외부 데이터 혹은 결과들을 기계 안에 내장시킬 수 없는 것이다. 그 대신 이 기계는 그 데이터 혹은 결과들 중에서 당장 필요한 내용만을 보고 그에 해당하는 명령을 수행하게 되는 것이다. 그리고는 그 결과를 외부 장치 등에 적어 놓기도 하며 약속된 다음 단계로 정확하게 넘어가게 되는 것이다. 입력ㆍ계산 과정에 필요한 기억 용량ㆍ출력 등의 크기에 제한이 없다는 점으로 인해서 이 기계가 실제로 만들어질 수 없는, 단지 수학적인 하나의 이상체라고 생각될 수도 있다 (그림 2.1). 그러나 매우 현실성이 있는 이상체이다. 현대 컴퓨터 기술의 놀라운 발달로 인하여 웬만한 경우의 계산에는 거의 무한정이라 할 수 있는 전자 기억 장치가 제공될 수 있는 것이다.

실제로 위에서 언급한 '외부' 기억 장치의 실체는 현대 컴퓨터의 내부 장치의 일부일 수 있다. 어떤 장치가 내부인가 외부인가는 단지 기술적인 문제일 뿐이다. 이러한 구분을 줄 수 있는 한 가지 방법은 하드웨어와 소프트웨어로 분류하는 것이다. 즉, 내부 장치는 하드웨어에 해당하고 외부 장치는 소프트웨어에 해당하게 한다거나 하는 것이다. 꼭 이 방법이 옳다는 말은 아니다. 그러나 어떤 방법으로 하건 간에 튜링의 수학적 이상체는 오늘날의 컴퓨터와 놀랍게도 유사하다고 볼 수 있다.

튜링이 구상했던 외부 데이터와 기억 장치는 마크가 되어 있는 테이프였다. 튜링 기계에 의해서 이 테이프가 불려 들어와서 필요에 따라 읽혀지기도 하고 명령에 따라 앞으로 혹은 뒤로 움직이게 된다. 이 기계는 또 필요하면 새로운 마크를 테이프에 쓰기도 하고 이미 있는 마크를 지우기도 함으로써 같은 테이프가 외부 기억 장치 역할 뿐 아니라 입력 장치 역할도 할 수 있는 것이다. 실제로 입력장치와 외부 기억 장치는 굳이 구분하지 않는 것이 편리하다. 왜냐 하면, 많은 계산 과정의 중간 결과는 새로운 데이터와 같은 역할을 하게 되기 때문이다. 앞서 보았던 유클리드 알고리즘에서도 우리는 A, B 로 표시되었던 원래 입력 데이터를 계산이 진행됨에 따라 새로운 값으로 계속 바꾸어 주었던 것이다. 마찬가지로 같은 테이프가 마지막 출력 (해답에 해당) 으로 사용될 수 있다. 그 테이프는 계산이 진행되는 동안 기계 속을 계속 앞뒤로 왔다갔다 하게 되는 것이다. 그 계산이 결국 끝나게 되면 그 기계는 정지 상태가 되고 계산된 답은 테이프 한쪽에 나타나게 된다. 좀더 정확을 기하기 위해서 기계를 중심으로 왼쪽편에 답이 씌어지고 오른편에 입력 데이터와 문제 등이 기입된다고 가정하기로 한다.

내 생각에, 유한한 기계에 의해서 무한한 길이의 테이프가 앞뒤로 움직인다는 사실이 웬지 마음에 걸린다. 그 테이프가 아무리 가벼운 물질로 만들어졌건 간에 무한 대의 테이프를 움직인다는 것은 매우 어렵기 때문이다. 그보다는 그 테이프가 외부 환경으로 고정되어 있고 그 위를 유한 기계가 움직인다고 보는 것이 타당할 것이다. (물론 현대의 전자공학에서는 '테이프' 혹은 '기계 장치' 가 실제 물리적으로 움직일 필요는 없다. 그러나 움직인다고 간주하는 것이 편리한 경우가 많이 있다.) 이러한 관점에서 보면 그 기계 장치는 모든 입력 데이터를 외부환경으로부터 받는다. 또 그 외부 환경을 '연습장' 으로 사용한다. 그리고 마지막으로 이 외부 환경에 결과를 써 넣게 되는 것이다.

튜링이 제시한 그림에서 '테이프' 는 양쪽으로 무한히 연속되는 네모칸들의 순서열이다. 각각의 네모칸은 비어 있든지 아니면 한 개의 표지가 되어 있다. 표지가 있거나 없는 네모칸을 사용한다는 것은 그 '환경' (즉, 테이프) 을 분석하면 이산 구조 (연속 구조가 아닌) 로서 설명할 수 있다는 것이다. 만일 우리가 원하는 것이 신뢰성 있고 절대적 법칙에 따라 동작하는 기계라면 이것은 타당한 선택이라고 볼 수 있다. 그런데 우리는 이 '환경' 이 우리가 사용하는 수학적 이상화 (mathematical idealization) 의 일환에 따라 (잠재적으로) 무한하다고 보고 있다. 그러나 어떤 특정한 경우에 대해서는 항상 입력치ㆍ계산, 그리고 결과치가 유한하다는 사실이다. 그러므로 테이프는 무한하더라도 그 위에는 유한한 개수의 표식만이 있을 수 있다. 양쪽 모두 어떤 특정한 점을 넘어서면 테이프 위에는 빈 칸만이 남게 되는 것이다.

이제 빈 칸을 '0' 으로, 표식 있는 칼을 1 로써 표시하겠다. 예를 들면 :

이 기계는 테이프를 한 칸씩 '읽을' 수 있다고 가정하자. 그리고 각각의 명령 수행 뒤에는 좌 혹은 우로 꼭 한 칸씩 움직인다고 가정하자. 그렇다고 일반성이 상실되는 것은 아니다. 한 번에 n 개씩 읽을 수 있는 기계나 k 만큼 움직일 수 있는 기계라도 한 칸씩 움직이는 기계로 쉽게 구현될 수 있는 것이다. 한 번에 k 만큼씩 움직이는 기계는 한 칸씩 움직이는 기계를 k 번 반복할 수 있고 한 칸씩 n 번 읽은 것을 모아 두었다가 마치 단번에 n 개를 읽은 것처럼 할 수 있기 때문이다.

이러한 기계가 도대체 구체적으로 어떤 일을 할 수 있는 것인가? 우리가 어떤 물건이 '기계적' 이라 부를 때 그 물건이 작동하는 가장 일반적인 방법은 무엇일까? 우리가 다루고 있는 기계의 내부 상태가 그 가짓수에서 유한하다는 사실을 기억하기 바란다. 이러한 유한성 이외에 다만 한 가지 알아야 할 것은 이 기계의 작동 방법이 그 때의 내부 상태와 입력 데이터에 의해서 완전하게 결정된다는 것이다. 여기서 입력이란 바로 앞에서 정한 두 개의 기호, '0' 과 '1' 중의 하나를 의미한다. 초기 상태와 입력이 주어지면 이 기계는 완전히 결정된 방법에 따라 작동하게 되는 것이다. 즉, 초기 상태를 새로운 상태 (혹은, 이전 그대로의 상태) 로 바꾸어 주고, 지금 읽어 들이고 있는 0 혹은 1 의 기호를 같은 혹은 다른 0 과 1 의 기호로 바꿔 주며, 현재의 테이프 위치에서 좌 혹은 우로 한 칸 움직인 후, 마지막으로 계산을 계속해서 수행할 것인가, 아니면 이를 중지하고 멈출 것인가를 결정할 수 있다.

이 기계의 작동을 좀더 자세히 볼 수 있게 하기 위하여 각각의 내부 상태에 0, 1, 2, 3, 4, 5, ... 와 같은 번호를 붙여 보기로 하자. 그러면 이 기계, 즉 튜링 기계는 다음과 같은 변환 규칙으로써 완전하게 기술될 수 있을 것이다.

화살표의 왼편에 있는 큰 글자는 이 기계가 지금 읽고 있는 테이프 위에 있는 기호를 의미하고 이 기호를 오른편의 큰 글자로 바꿔 주게 된다. R 은 이 기계가 오른편으로 한 칸 움직인다는 뜻이고 L 은 왼쪽으로 한 칸 간다는 뜻이다. (만약 튜링의 본래 기계에 제시된 것처럼 기계 대신 테이프가 움직인다고 가정하면 R 은 테이프가 한 칸 왼쪽으로 움직이고 L 은 오른쪽으로 한 칸 움직인다고 해석하면 된다.) 마지막의 STOP 은 계산이 모두 끝나서 기계가 정지 상태로 들어갔다는 것을 의미한다. 특별히 두 번째 규칙 01 → 131L 을 예로서 살펴보면 그 의미는 "만일 기계의 내부 상태가 0 이고 현재 테이프 내용이 1 이면 기계의 내부 상태는 13 으로 변하고 테이프의 내용은 그대로 1 로 유지하며 왼쪽으로 한 칸 움직여야 된다." 는 것이다. 마지막 규칙 2591 → 00R.STOP 은 내부 상태259 에서 테이프로부터 1 을 읽으면 상태는 다시 0 으로 바뀌고 테이프의 1 을 지우고 0 을 써 넣은 후 오른편으로 한 칸 간 다음 계산을 끝내라는 것이다.

내부 상태를 나타내는 0, 1, 2, 3, 4, 5, ... 라는 숫자 대신 테이프에서 사용하는 두 가지 기호 0 과 1 만을 사용한다면 더 적절할 것이다. 한 가지 방법은 n 이라는 상태를 표시하기 위하여 단순히 1 을 n 개 죽 나열하는 것이지만 이는 비효율적이다. 그 대신 이제는 우리에게 익숙해진 2 진법 체계를 사용하기로 하자.

여기에서 오른쪽 끝의 숫자는 보통 (십진법) 숫자처럼 홑자리 수이다. 그러나 그 바로 앞의 숫자는 '10' 자리 수가 아니라 '2' 자리를 나타내고 그 앞자리는 '100' 자리가 아니고 '4' 자리, 또 그 앞자리는 '1000' 자리가 아니라 8 자리가 되는 것이다. 즉, 왼쪽으로 한 자리 갈 때마다 다음과 같이 2 의 지수값이 하나씩 늘어난다고 볼 수 있다 : 1, 2, 4(= 2 × 2), 8(= 2 × 2 × 2), 16(= 2 × 2 × 2 × 2), 32(= 2 × 2 × 2 × 2 × 2) (뒤에서는 다른 목적 때문에 2 나 10 이 아닌 다른 수치 체계를 사용하게 된다. 예를 들면 3 진법에서는 십진법의 수 64 는 2101 로 표시되고 여기에서 각각의 자릿수는 3 의 지수가 된다. 즉, 64 = (2 × 3³) +3² +1 인 것이다.)

이러한 2 진 체계를 사용하면 앞에서 본 튜링 기계의 규칙은 다음과 같이 나타낼 수 있다 :

위에서는 R.STOP 대신 그냥 STOP 으로 줄여서 사용하였다. 그 이유는 L.STOP 이 절대 나올 수 없다고 가정함으로써 기계가 답을 제공할 때에는 꼭 현재 기계 위치의 왼쪽에 답이 나타나도록 가정할 수 있기 때문이다.

이제 이 기계가 2 진 표현으로 11010010 이라고 지명된 내부 상태에 있고 앞 페이지에 제시된 테이프 위의 어떤 위치에서 작업중에 있다고 가정하자. 여기에서 110100100 → 111L 의 규칙이 적용되는 과정을 살펴보면 다음과 같다.

지금 현재 읽혀지고 있는 기호 (0) 는 내부 상태를 표시한 문자열 오른편에 표시하여 보았다. 위에서 부분적으로 제시한 (내가 임의로 작성한) 튜링 기계에 따르면 지금 읽어 들어간 기호 '0' 은 '1' 로 대치되고 내부 상태는 '11' 로 바뀌게 된다. 그리고 기계는 왼편으로 한 칸 움직인다.

이제 이 기계는 새로운 기호 (여기에서는 다시 '0') 를 읽을 준비가 완료된 상태이다. 위의 규칙표에 의하면 여기에서 '0' 은 그대로 놓아 두고 내부 상태만 '100101' 로 바뀐 후 오른쪽으로 한 칸 움직이게 된다. 그러면 다시 '1' 을 읽어 들이고 규칙표 뒤쪽 어딘가에는 그에 대한 규칙, 즉 무엇을 쓰고 어떤 상태로 변하는가, 또 어느 쪽으로 기계가 움직이는가 등이 제시되어 있을 것이다. 이러한 과정이 계속 반복되다가 STOP 이라고 표시된 상태에 이르게 되면 (한 칸 오른칸으로 움직인 후) 멈추게 된다. 마치 벨을 울려서 기계의 오퍼레이터에게 작업이 끝났음을 알리는 상태를 상상해 보면 될 것이다.

튜링 기계가 항상 내부 상태 '0' 에서 작동을 시작하고 기계의 입력 기관이 위치한 곳으로부터 왼편에 있는 테이프는 전부 비어 있다고 가정하기로 하자. 또, 명령들과 데이터는 모두 그 오른편에 입력된다고 가정하자. 앞에서 언급했듯이 이 입력 데이터는 0 과 1 로만 이루어진 길이가 유한한 문자열이고 그 뒤는 모두 빈 칸 (0) 으로 채워진다. 기계가 STOP 상태에 도달하면 계산 결과는 입력 기관의 바로 왼편에 제시된다.

입력으로서 수치 데이터도 나타낼 수 있어야 하기 때문에 보통 숫자 (0, 1, 2, 3, 4, … 와 같은 자연수) 를 나타낼 수 있는 방법이 필요하다. 한가지 방법은 n 이라는 숫자를 표시하기 위하여 n 개의 1 로 된 문자열을 이용하는 것이다 (다만, 이 방법은 0 을 표시하는 데는 어려움이 있다.) :

1 → 1, 2 → 11, 3 → 111, 4 → 1111, 5 → 11111 등.

이러한 원시적인 수치 체계를 1 진법 체계라고 부른다. 그리고 기호 '0' 은 두 숫자 사이를 분별할 수 있는 빈 칸 역할을 담당하게 된다. 수많은 알고리즘이 한 개의 데이터보다는 여러 개의 데이터를 사용하는 경우가 많기 때문에 숫자들 사이를 구분할 수 있는 방법을 갖는 것이 매우 중요하다. 예를 들면, 유클리드의 알고리즘을 튜링 기계에 돌려 보려 하더라도 A 와 B 두 개의 입력 데이터를 주어야 할 것이다. 이 알고리즘에 대한 튜링 기게는 그리 어렵지 않게 작성될 수 있다. 관심있는 독자들은 연습삼아 다음 튜링 기계 (EUC) 가 0 으로 분리된 두 개의 1 진수에 대해서 실제로 유클리드 알고리즘을 수행하는지 확인해 보기 바란다.

00 → 00R, 01 → 11L, 10 → 101R, 11 → 11L, 100 → 10100R,

101 → 110R, 110 → 1000R, 111 → 111R, 1000 → 1000R, 1001 → 1010R,

1010 → 1110L, 1011 → 1101L, 1100 → 1100L, 1101 → 11L, 1110 → 1110L,

1111 → 10001L, 10000 → 10010L, 10001 → 10001L, 10010 → 100R,

10011 → 11L, 10100 → 00STOP, 10101 → 10101R.

이를 수행해 보기 전에 어쩌면 훨씬 간단한 기계부터 살펴보는 것이 현명할지도 모르겠다. 다음에 제시된 튜링 기계 UN+1 은 단순히 일진법 숫자에다 1 을 더하는 튜링 기계이다.

00 → 00R, 01 → 11R, 10 → 01STOP, 11 → 11R,

UN+1 이 실제로 작동하는가를 보기 위해서 다음과 같이 4 를 나타내고 있는 테이프에 적용해 보기로 하자.

ㆍㆍㆍ0 0 0 0 0 1 1 1 1 0 0 0 0 0ㆍㆍㆍ

처음에 이 기계의 입력 기관이 1 들의 왼편에 있는 어떤 0 위에 위치하고 있다고 가정하자. 초기 상태는 0 이고 입력되는 기호는 0 일 것이다. 첫 번째 명령에 따라서 이 0 을 그대로 놓아 둔 채 한 칸 오른쪽으로 움직일 것이다. 이 때 내부 상태는 0 으로 남아 있다. 이러한 동작이 첫 번째 1 이 입력될 때까지 반복될 것이다. 1 이 입력되면 두 번째 명령이 효과를 보게 된다. 1 은 그대로 둔 채 다시 오른편으로 한 칸 움직인다. 그러나 이제 내부 상태는 1 로 변한다. 네 번째 명령에 의해서 이제는 1 상태를 지속하며 입력된 1 을 그대로 놓아 두고 오른편으로 계속 움직인다. 이 동작은 1 들 다음에 나오는 첫 번째 0 이 입력될 때까지 계속된다. 첫 번째 0 이 입력되면 세 번째 명령에 따라 0 을 1 로 바꿔 주고 한칸 오른쪽으로 움직인 후 정지한다. (STOP 이 실제로는 R.STOP 이었음을 기억하기 바란다.) 결국 새로운 1 이 문자열 끝에 추가되고 원했던 바와 같이 입력된 4 는 5 로 바뀌게 된다.

약간 복잡한 예로서 다음 튜링 기계 UN×2 가 1 진법의 수를 2 배로 만들어 주는지 확인해 보기 바란다.

00 → 00R, 01 → 10R, 10 → 101L, 11 → 11R, 100 → 110R, 101 → 1000R,

110 → 01STOP, 111 → 111R, 1000 → 1011L, 1001 → 1001R, 1010 → 101L,

1011 → 1011L.

EUC 의 경우 어떠한 일이 벌어지는가 알아보기 위해서 적당한 두 개의 숫자, 예를 들면 6 과 8 을 대입하여 시도해 보기 바란다. 앞에서와 같이 튜링 기계의 처음 상태는 0 으로 그 입력 기관이 다음과 같은 테이프의 왼쪽에 위치한다고 가정하자.

ㆍㆍㆍ0 0 0 0 0 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0ㆍㆍㆍ

튜링 기계가 여러 과정을 거친 뒤 다음과 같은 테이프 상태의 1 들 오른편에서 동작을 멈출 것이다.

ㆍㆍㆍ0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0ㆍㆍㆍ

즉, 구하고자 하는 최대 공약수는 2 가 되는 것이다.

왜 EUC 혹은 UN×2 등이 우리가 원하는 작업을 실제로 수행하는가 하는 것에 대한 완전한 설명은 미묘한 문제를 내포하고 있기 때문에 그 기계 자체가 복잡한 것보다 이를 설명하는 것이 훨씬 복잡해진다. 실제로 이러한 문제는 컴퓨터 프로그램들이 공통적으로 안고 있는 보편적 문제에 속한다. (어떤 알고리즘적 프로그램이 어떻게 작성된 의도대로 수행될 수 있는가를 이해하려면 통찰력이라는 것이 필요하다. 그렇다면 '통찰력' 그 자체는 알고리즘적이라고 할 수 있는 것인가? 이 질문은 뒤에 우리가 중요하게 다룰 문제 중의 하나이다.) 여기에서는 EUC 나 UN×2 등의 예에 대해서 위에서 언급한 설명을 시도하지 않기로 하겠다. 실제로 EUC 를 확인해 본 독자들은 내가 임의로 본래의 유클리드 알고리즘을 간단한 형태로 변형하였다는 것을 눈치챌 수 있었을 것이다. 그래도 EUC 는 매우 복잡하여 22 개의 기본 명령과 11 개의 내부 상태가 존재한다. 그러나 이러한 복잡성의 주범은 기계 구성에 관한 명령들이다. 실제로 따져 보면 22 개의 명령 중에 단 세 개만이 테이프의 내용을 바꿔 주는 역할을 하는 것이다. (UN×2 를 보더라도 12 개의 명령 중에 테이프 내용을 바꿔 주는 명령어는 전체의 반 정도에 불과하다.)

숫자 데이터의 2 진 코드화

일진법 체계는 데이터의 크기가 커지게 되면 매우 비효율적이다. 그 때문에 우리는 앞서 언급한 대로 2 진수 체계를 주로 사용하기로 하겠다. 그러나 테이프에 있는 그대로 그 내용을 2 진수로써 직접 들여오는 것은 불가능하다. 현재로서는 필요한 숫자가 어디에서 끝나고 빈 칸에 해당하는 무한 개의 0 이 어디서부터 시작되는가를 알 방법이 없는 것이다. 즉, 그 2 진 숫자가 어디에서 끝나는가를 명시할 수 있는 표현 방법이 필요하다. 뿐만 아니라 유클리드 알고리즘에서 두 개의 숫자를 필요로 햇듯이 때때로 여러 개의 숫자를 표시할 필요가 생기게 된다. 현재로서는 숫자들 사이의 빈 칸을 표시하는 0 과 특정한 숫자 중간에 등장하는 0 을 구분할 방법이 없다. 게다가 우리는 테이프에 데이터뿐만 아니라 온갖 복잡한 명령어들도 입력시켜야 할 경우가 생길 수도 있다. 이러한 문제점을 해결하기 위하여 축약 (contraction) 이라 부르는 방법을 사용하고자 한다. 이 방법은 2 진 문자열을 그대로 2 진수로서 읽는 것이 아니고 일단 이를 0, 1, 2, 3, 4 등의 문자열로 바꾸는 것이다. 이를 위해서는 0 과 0 사이의 1 의 개수를 이용하여 이러한 문자열을 만들 수 있다. 예를 들어 다음과 같은 테이프 내용을 살펴보기로 하자.

01000101101010110100011101010111100110

이를 0 과 다음 0 사이를 분리하면 다음과 같은 문자열을 만들 수 있다.

이제 0 과 1 을 제외한 나머지 숫자들 2, 3, 4, … 등은 특별한 표식, 혹은 어떤 종류의 명령문으로 받아들일 수 있다. 실제로 2 를 두 개의 숫자를 분리하는 빈 칸의 역할을 하는 '쉼표(,)' 로서, 또 3, 4, 5, … 등은 원하는 바에 따라 '-', '+', '*', '다음에 나오는 번호로 JUMP', '이전 명령을 다음에 나오는 숫자만큼 반복' 등의 명령어를 표현한다고 가정할 수 있다. 이렇게 놓고 보면 위의 문자열은 0 과 1 로 이루어진 문자열들 2 이상의 숫자들에 의해서 분리된 형태를 취하고 있는데 0 과 1 로 이루어진 문자열은 2 진법으로 표현된 숫자를 나타낸다. 그러므로 위의 문자열은 (2 를 쉼표로 정하면) 다음과 같이 읽을 수 있다.

(2 진수 1001) 쉼표 (2 진수 11) 쉼표 ...

2 진수 1001, 11, 100, 0 에 대해서 그에 해당하는 아라비아 숫자 9, 3, 4, 0 을 대입하여 위의 문자열 전체를 다시 표시하면 다음과 같다.

9, 3, 4 (명령어 3) 3 (명령어 4) 0

이 과정을 통하여 우선 우리는 테이프상에서 표현하고자 하는 숫자의 끝마침을 할 수 있게 되었다. 즉, 마지막에 쉼표를 붙임으로써 오른쪽으로 끝없이 이어진 0 들로부터 그 숫자를 구분할 수 있게 되었다. 그뿐 아니라, 임의의 유한 개수의 (2 진수로 표시된) 자연수로 이루어진 수열도 쉼표로 각각을 구분함으로써 0 과 1 만으로 이루어진 하나의 커다란 문자열로써 표현할 수 있게 되었다. 이를 다음 예로써 다시 살펴보기로 하자.

5, 13, 0, 1, 1, 4,

이를 2 진수로 표시하면 다음과 같다.

101, 1101, 0, 1, 1, 100,

이를 확장 (expansion) (즉, 위에서 설명한 축약의 반대 과정) 을 통하여 다음과 같이 테이프 내용으로 바꿀 수 있다.

...000010010110101001011001101011010110100011000...

이를 위해서는 앞에서 구한 2 진수의 문자열에 다음과 같은 간단한 변환 규칙을 적용한 뒤 무한 개의 0 을 앞뒤에 분이면 된다.

0 → 0

1 → 10

, → 110

위의 테이프 내용을 다음과 같이 나누어 보면 위의 변환이 쉽게 이해될 것이다.

0000 10 0 10 110 10 10 0 10 110 0 110 10 110 10 110 10 0 0 110 00

이러한 표현 방법을 여기에서는 확장 2 진 표현법 (expanded binary notation) 이라 부르기로 하자. 예를 들면 13 의 확장 2 진 표현은 1010010 이다.

이 표현법에 대하여 한 가지 덧붙일 말이 있다. 이는 단지 기술적인 문제이지만 완벽을 기하기 위하여 밝혀 두려 한다. 자연수에 대한 2 진 혹은 십진수 표현을 할 때 대개의 경우 가장 왼쪽에 등장하는 0 은 숫자에 아무런 영향을 주지 않기 때문에 생략된다. 예를 들면 2 진수 00110010 은 110010 과 같은 수이고 십진법에서의 0050 은 50 과 같은 수인 것이다. 이러한 중복 표현은 0 이라는 수에도 적용되어 0 이외에도 000 혹은 00 으로 쓸 수 있는 것이다. 그뿐 아니라 논리적으로 말한다면 빈 칸도 0 이 되어야 한다! 보통의 표현 체계에서는 이러한 것이 큰 혼란을 초래하겠지만 위에서 제시한 방법을 사용하면 아무런 문제가 없다. 그러므로 두 개의 쉼표 사이에 있는 0 대신 그냥 연속된 쉼표 (, ,) 로 표현하면 된다. 연속된 쉼표는 두 개의 11 사이를 0 이 갈라 놓은 형태이다.

...001101100...

그러므로 앞의 예에서 본 여섯 개의 숫자는 다음과 같이 표시될 수 있다.

101, 1101, , 1, 1, 100,

이를 테이프 위에 확장 2 진 표현법으로 표시하면 아래와 같다 :

...00001001011010100101101101011010110100011000...

(이는 앞에서 본 문자열에서 0 이 하나 빠진 것이다.)

이제 유클리드 알고리즘의 튜링 기계를 확장 이진 표현으로 표시된 두 개의 데이터에 적용시키는 방법을 살펴보자. 예를 들어 앞에서 본 6 과 8 의 경우를 살펴보면,

...0000000000011111101111111100000...

과 같은 1 진 표현 방법 대신 6 과 8 의 2 진 표현인 110 과 1000 을 사용하고자 한다. 그 쌍은

6, 8, 즉 2 진 표현으로 100, 1000,

이를 확장하면 다음과 같은 테이프 내용을 얻을 수 있다.

...00000101001101000011000000...

이 예만을 놓고 보면 1 진 표현법에 비해서 별로 좋은 점을 볼 수 없을 것이다. 그러나 예를 들어 십진수 1583169 와 8610 을 택한다고 가정해 보자. 이 수들은 2 진법으로 각각,

110000010100001000001, 10000110100010

로 표시된다. 이를 테이프에 확장 2 진 표현법으로 나타내면 다음과 같다 :

...001010000001001000001000000101101000001010010000100110...

즉, 한 줄로 표시할 수 있는 것이다. 만약 1583169 와 8610 을 1 진수로 표시하려 하였다면 아마 이 책 한 권을 채우고도 남았을 것이다!

만약 확장 2 진 표현으로 입력된 데이터에 대하여 유클리드 알고리즘을 수행하는 튜링 기계를 만들고 싶다면 단순히 EUC 기계에다 확장 2 진 표현을 1 진수로 바꿔 주는 서브루틴만 부착하면 된다. 그러나 이 기계는 실로 매우 비효율적일 것이다. 왜냐 하면 1 진수의 비효율성은 '내부적' 으로는 그대로 남아 있어서 시간적으로도 느리고 계산에 필요한 외부 '연습장', 즉 테이프 왼편의 빈 칸이 엄청나게 많이 필요할 것이기 때문이다. 훨씬 효율적인 튜링 기계를 설계할 수도 있으나 여기에서는 다루지 않도록 하자.

튜링 기계에서 확장 이진 표현을 다루는 방법을 보이기 위해서 유클리드 알고리즘보다 훨씬 간단한 예를 살펴보도록 하겠다. 즉, 확장 2 진 표현의 자연수에 단순히 1 을 더하는 과정은 다음과 같은 튜링 기계 (XN+1) 로 처리될 수 있다.

00 → 00R, 01 → 11R, 10 → 00R, 11 → 101R, 100 → 110L, 101 → 101R,

110 → 01STOP, 111 → 1000L, 1000 → 1011L, 1001 → 1001L, 1010 → 1100R,

1011 → 101R, 1101 → 1111R, 1110 → 111R, 1111 → 1110R.

관심있는 독자들은 위의 기계가 실제로 맞게 동작하는가를 확인하기 위하여 167 이라는 가상의 데이터에다가 직접 적용해 보기 바란다. 167 의 2 진 표현은 10100111 이기 때문에 테이프에는 다음과 같은 확장 2 진 표현으로 표시될 것이다.

...0000100100010101011000...

2 진수에 1 을 더하기 위해서는 제일 마지막의 0 을 찾아서 1 로 바꿔 주고 그 0 다음에 나오는 모든 1 을 0 으로 바꿔 주면 된다. 예를 들면, 167 + 1 = 168 은 2 진 표현으로 다음과 같이 된다.

10100111 + 1 = 10101000.

그러므로 XN+1 튜링 기계는 위의 테이프를 다음과 같이 변환시킬 수 있어야 하는데, 참으로 이를 수행하는가 확인해 보기 바란다.

...0000100100100001100000...

앞의 예에서 본 바와 같이 가장 기본적인 계산인 1 더하기 연산도 확장 2 진 표현으로는 15 개의 규칙에 8 개의 내부 상태가 필요한 꽤 복잡한 기계가 되고 말았다. 1 진수 표기의 1 더하기 계산은 매우 간단했었다. 왜냐 하면 1 더하기 계산이라는 것이 실은 1 로 된 문자열 끝까지 가서 단순히 1 을 하나 덧붙이는 것에 지나지 않았기 때문이다. 그러므로 튜링 기계 UN+1 이 훨씬 단순한 것은 당연하다고 볼 수 있다. 하지만 아주 큰 숫자에 대해서는 처리해야 될 테이프의 길이 때문에 UN+1 기계는 지나치게 계산 속도가 느려지고 오히려 더 복잡한 기계인 XN+1 이 간단한 확장 2 진 표현 덕택에 효과적인 계산을 할 수 있다.

한 가지 덧붙이고 싶은 것은 어떤 계산은 확장 2 진 표현을 이용하는 기계가 1 진법을 사용하는 기계보다 오히려 외양적으로도 단순해진다는 것이다. 즉, 주어진 확장 이진 표현의 자연수를 2 배해 주는 튜링 기계 XN×2 를 살펴보자.

00 → 00R, 10 → 00R, 11 → 100R, 100 → 111R, 100 → 111R, 110 → 00STOP.

앞에서 제시한 바 있는 1 진법 튜링 기계 UN×2 는 이보다 훨씬 복잡했던 것을 기억하기 바란다. 이제 아주 기본적인 수준의 튜링 기계가 어떤 식으로 움직이는가에 대한 아이디어를 얻었을 것이다. 예상할 수 있겠지만 계산이 좀 복잡해지면 이러한 기계도 엄청나게 복잡해지게 된다. 그렇다면 이러한 기계의 궁극적인 한계는 무엇일까? 이제 이 문제를 검토해 보기로 하자.

처치-튜링 명제

간단한 튜링 기계를 작성하는 방법에 익숙해지면 여러 가지 다른 기본 연산들, 예를 들면, 두 수의 합, 두 수의 곱, 혹은 지수 계산 등도 모두 어떤 특정한 튜링 기계들로 풀 수 있음을 쉽게 확인해 볼 수 있을 것이다. 각각의 기계를 여기에 제시하는 것이 그렇게 어려운 일은 아니지만 생략하기로 하겠다. 나누기와 나머지처럼 계산의 결과가 두 개의 자연수로 주어지는 것, 혹은 결과가 임의의 크기인 유한 집합으로 주어지는 것도 모두 튜링 기계로 만들 수 있다. 그뿐 아니라 미리 지정된 계산을 하는 것이 아니고 무엇을 계산할 것인가를 테이프에 명령어 형태로 입력받을 수 있는 그러한 튜링 기계도 만들 수 있다. 그뿐 아니라 미리 지정된 계산을 하는 것이 아니고 무엇을 계산할 것인가를 테이프에 명령어 형태로 입력받을 수 있는 그러한 튜링 기계도 만들 수 있다. 때로는 수행되어야 할 명령이 그 기계가 앞에서 계산한 결과에 따라 달라질 수도 있다. ("만일 그 계산 결과가 어떤 값보다도 크면 이것을 수행하고 아니면 저것을 수행하시오.")

간단한 계산 혹은 논리 연산을 하는 튜링 기계가 만들어질 수 있다는 것이 완전히 이해가 된다면 이들을 알고리즘을 수행하는 복잡한 기계를 만드는 데 어떻게 이용할 수 있는가 하는 것도 쉽게 이해가 될 것이다. 그러한 것을 얼마 동안 실제로 연습해 본 사람이면 이러한 종류의 기계는 어떠한 기계적 작업 (mechanical operation) 이라도 수행할 수 있도록 만들 수 있다는 사실을 쉽게 확인할 수 있을 것이다. 수학적으로 말할 때, '기계적 작업' 이라는 것을 이러한 기계가 수행할 수 있는 작업으로 정의하는 것이 타당성을 갖게 되었다. 이러한 형태의 이론적 기계, 즉 튜링 기계에 의해서 수행될 수 있는 기계적 작업을 수학자들은 '알고리즘' 이라는 명사와 '계산 가능 (computable),' '재귀적 (recursive),' 혹은 '효과적 (effective)' 이라는 형용사를 사용하여 표현하고 있다. 어떤 계산 과정이 충분히 명료하고 기계적이라면 이를 수행할 수 있는 튜링 기계도 꼭 찾아낼 수 있다는 가정이 설득력을 갖게 된 것이다. 이것이 바로 튜링 기계 개념의 동기를 이해하는 데 가장 중요한 포인트이다.

그러나 한편으로는 이 기계가 불필요할 정도로 제약이 많게끔 설계되지 않았나에 대한 우려도 있을 수 있다. 단지 한 개의 2 진수 (0 혹은 1) 만을 읽어 들일 수 있다거나 테이프 하나에 좌나 우로 한 칸씩밖에 움직일 수 없다는 사실 등은 첫눈에도 좀 제약이 많다고 보여진다. 왜 네댓 개, 아니 천 개쯤의 테이프를 고집하는 대신 0 과 1 로 채워진 평면을 사용하거나 아니면 3 차원의 배열을 사용하면 어떨까? 좀더 복잡한 숫자 체계나 알파벳 기호를 사용하면 어떨까? 실제로 위의 어떤 변화를 취하더라도 근본적으로 무엇을 할 수 있나 없나 하는 문제에서는 아무런 영향을 끼치지 않는다. 물론 테이프를 여러 개 사용하는 예에서 보면 명백하듯이 이들로 인하여 작업의 경제적 효과는 얻을 수 있다. 위에서 제시한 변화를 한번에 다 해서 튜링 기계의 영역을 넓히더라도 수행 가능한 연산의 종류, 그리고 이에 따라 알고리즘 (혹은 '계산,' '효과적 계산 과정', '재귀적 연산') 에 속할 수 있는 것들은 이전과 하나도 변화가 없는 것이다!

튜링 기계가 필요에 따라서 빈 칸을 얼마든지 찾을 수 있는 한 테이프를 두 개 이상 가져야 할 필요가 없음을 알 수 있을 것이다. 이를 위해서 테이프 위의 데이터를 계속 옮겨다녀야 될지도 모른다. 이것은 '비능률적' 일지는 모르지만 근본적으로 무엇을 계산할 수 있는가 없는가라는 질문에는 영향을 미치지 않는다. 마찬가지로, 요즈음 인간 두뇌의 모형화와 관련하여 각광을 받고 있는 병렬 기법에서처럼 둘 이상의 튜링 기계를 동시에 작동시키더라도 근본적으로는 아무런 효과를 얻을 수 없다. (물론 어떤 경우에 처리 속도의 향상은 기대할 수 있다.) 서로 직접 교류할 수 없는 두 개의 기계는 서로 교류하는 두 개의 기계보다 더 많은 것을 수행할 수는 없다. 그리고 두 개의 기계가 서로 교류한다면 그것은 결과적으로 하나의 기계라 할 수 있는 것이다.

튜링이 테이프의 형태를 일차원으로 제한한 것은 어떠한가? 이 테이프가 '주변 상황 (environment)' 을 나타낸다는 관점에서 보면 그 모양이 일차원적인 직선보다는 2 차원의 평면, 혹은 3 차원의 공간이 더 적합할 듯 보인다. 평면이 '순서도' (유클리드 알고리즘의 예에서 본 것과 같은) 를 표현하기에는 1 차원 테이프보다 적합해 보일지도 모른다. 그러나 원칙적으로 순서도에 표시된 연산 과정을 '1차원' 형태로 기술하는 것은 아무런 어려움이 없다. (한 가지 방법은 순서도의 내용을 일반 대화식 언어로 기술하는 것이다.) 2 차원 평면 위에 표현하는 것은 단순히 우리가 편리하고 쉽게 이해할 수 있기 위한 것이지 근본적으로 어떤 것을 성취할 수 있는가 하는 문제에는 전혀 영향을 끼치지 않는다. 2 차원 평면 위의 기호나 물체의 위치, 심지어는 3 차원의 위치를 손쉽게 1 차원 테이프에 코드화할 수 있는 것이다. (실제로 2 차원 평면을 사용하는 것은 두 개의 테이프는 2 차원 평면에서 점을 지정하기에 필요한 두 개의 '좌표' 를 갖게 된다. 마찬가지로 세 개의 테이프는 3 차원상에서의 점의 좌표를 표시할 수 있다.) 다시 강조하지만 1 차원상의 코드는 '비능률적' 일지는 모르지만 무엇을 할 수 있는가라는 문제에 대해서는 영향을 받지 않는다.

이 모든 것에도 불구하고 튜링 기계의 개념이 진정 우리가 '기계적' 이라 부를 수 있는 모든 논리적 혹은 수학적 연산을 수행할 수 있는가에 대해서는 아직 의문이 있을 수 있다. 튜링이 그의 독창적 논문을 기술할 당시까지만 하더라도 이에 대해서는 현재보다 훨씬 불분명하였으므로 튜링은 자기의 입장을 다소 자세하게 서술할 필요가 있었다. 튜링의 주도 면밀한 변론은 새로운 사실로부터 지지를 얻게 되었는데 튜링과는 별도로 (실제로 약간 앞서) 미국의 논리학자 처치 (Alonzo Church) 가 클린 (Stephen C. Kleene) 의 도움을 받아 람다 계산법 (lambda calculus) 이라는, 이 역시 힐베르트의 '열 번째 문제' 를 풀기 위한 새로운 방법을 제안한 것이다 비록 튜링 기계에 비해서 완전한 기계적 방법이라는 측면에서는 훨씬 불분명하였지만 그 수학적 구조는 놀라울 정도로 간략하다는 이점이 있었다. (처치의 이 놀라운 계산법에 대해서는 이 장의 마지막에서 다루기로 한다.) 튜링과는 별도로 힐베르트 문제 (Gandy, 1988) 에 대한 또 다른 제안들이 있었는데 특히 폴란드계 미국인 논리학자 포스트 (Emil Post) 를 들 수 있다. (튜링보다 약간 늦었지만 처치에 비하여 튜링 기계에 더욱 유사한 아이디어에 근거하고 있다.) 얼마 후 이 모든 방법들이 완전히 동등하다는 것이 밝혀지게 되었다. 이러한 사실은 후에 '처치-튜링 명제' 라고 불리게 된 하나의 관점에 큰 활력소로서 작용하게 되었는데 그 관점이란 튜링 기계 (혹은 그와 동등한 다른 기계) 가 실제로 우리가 말하는 알고리즘적 (또는 효과적, 또는 재귀적, 또는 기계적) 과정을 수학적으로 정의한다는 것이다. 요즈음에는 초고속 전자 컴퓨터가 우리 생활에 친숙하게 되었기 때문에 이 명제의 원래 형태에 대하여 의문을 갖는 사람은 별로 없다. 그 대신 몇몇 사람들은 실세계의 물리 법칙을 따르는 물리적 시스템 (인간의 두뇌도 포함하여) 이 튜링 기계와 비교하여 논리적 혹은 수학적 연산 기능이 나을 것인가 못할 것인가, 아니면 똑같을 것인가에 대해서 의문을 갖기 시작하였다. 나의 개인적인 의견은 원래의 처치-튜링 명제에 대해서는 기꺼이 받아들일 준비가 되어 있다. 그러나 실제 물리적 시스템과 연관하는 것은 별개의 문제로서 이에 대해서는 이 책 뒷부분에서 자세히 다루고자 한다.

자연수 이외의 수

앞에서 우리는 자연수의 연산에 관하여 살펴보았고 하나의 튜링 기계가 내부적으로는 유한 개의 상태만을 가지면서도 임의의 크기의 자연수에 대하여 계산을 수행할 수 있다는 놀라운 사실을 확인하였다. 그러나 우리는 종종 이보다 더욱 복잡한 형태의 숫자들, 예를 들면 음수ㆍ소수ㆍ무한수 등을 필요로 하는 경우가 있다. 음수와 소수 (예를 들면 -597/26) 는 튜링 기계로 쉽게 처리될 수 있고 분자와 분모도 얼마든지 큰 숫자가 올 수 있다. 단지 '-' 나 '/' 같은 기호에 대한 코드만 있으면 되는데 앞에서 살펴본 확장 2 진 표현법을 사용하면 쉽게 해결될 수 있다 (예를 들면 '-' 는 '3' 을, '/' 는 '4' 를 쓰기로 하고 각각에 확장 2 진 코드 1110 과 11110 을 사용한다). 그러므로 음수와 소수는 자연수를 이용하여 표시가 되고 결과적으로 계산 가능성 여부도 아무런 문제가 제기되지 않는다.

마찬가지로, 유한 개의 숫자로 표시된 무한 숫자도 그것이 소수의 한가지 형태라고 보면 아무런 문제도 제기하지 않는다. 예를 들면, 무리수 π 를 3.14159265 로 표시하였다면 이는 314159265/100000000 라는 소수로 표현하면 된다. 하지만 다음과 같이 표현된 무한 숫자에 대해서는 문제가 발생한다.

π = 3.14159265358979...

튜링 기계의 입력 데이터와 출력값은 엄밀히 말해서 무한 숫자가 될 수 없는 것이다. 어떤 사람은 π 값을 3, 1, 4, 1, 5, 9, ... 와 같이 하나씩 출력하는 튜링 기계를 만들어서 계속 작동하게 하면 어떤가 하고 생각할지 모르겠다. 그러나 튜링 기계에서는 이와 같은 것은 허용되지 않는다. 튜링 기계의 결과를 보기 위해서는 기계가 멈출 때까지 (벨이 울릴 때까지) 기다려야만 한다. 기계가 아직 STOP 명령을 수행하기 전까지는 출력된 결과라 할지라도 바뀔 수 있기 때문에 그 결과를 믿을 수 없다. 기계가 일단 STOP 명령에 도달하면 출력된 결과는 필연적으로 유한한 것이다.

하지만 튜링 기계가 위에서 설명한 것과 아주 흡사하게, 그 결과를 한 글자씩 출력할 수 있게끔 할 수 있는 합법적 방법이 있기는 하다. π 와 같은 무한 수의 확장을 출력하기 위해서는 입력값 0 에 대하여 진수 3 을, 1 에 대해서는 소수 첫째자리 1 을, 2 에 대해서는 소수 둘째자리 4 를, 3 에 대해서는 1 을 출력하는 튜링 기계를 만들면 된다. 실제로, 막상 동작시키기에는 좀 복잡하지만, 이와 같이 π 값을 출력하는 튜링 기계가 존재한다. 1/2 = 1.414213562... 와 같은 무리수들도 마찬가지 방법으로 할 수 있다. 그런데 놀랍게도 어떤 무리수들은 그 어떤 튜링 기계로도 만들 수 없다는 것이 밝혀졌다.  이에 대해서 다음 장에서 더욱 자세히 살펴보기로 하자. 이러한 방법으로 만들어 낼 수 있는 수들을 계산 가능하다고 부르고 만들어 낼 수 없는 수들 (실제로 훨씬 많음) 을 계산 불가능하다고 부른다. 이에 관련된 이슈에 대해서는 뒷장들에서 다시 살펴보기로 한다. 이 내용은 실제 물리적 물체 (예를 들면 인간의 두뇌) 가 물리학적 관점에서 계산 가능한 수학적 구조로 적절하게 표시될 수 있는가 하는 문제와 연관되어 있다.

계산 가능성은 일반적으로 수학 분야에서 중요한 주제 중의 하나이다. 그런데 이것이 꼭 수에만 국한된다고 보면 안 된다. 대수학 혹은 삼각함수의 공식과 같은 수식 자체를 직접 대상으로 하여 작동하는 튜링 기계나 해석학의 형식 변환 (formal manipulation) 을 수행하는 튜링 기계도 가능하다. 다만 그 과정에 등장하는 모든 수학적 기호들을 0 과 1 의 나열로 표시할 수 있는 정확한 코드 체계가 필요하고 그 뒤에는 튜링 기계의 개념을 적용하면 된다. 이것이 바로 튜링이 '열 번째 문제', 즉 수학의 일반적인 문제들을 풀 수 있는 알고리즘적 방법을 구상할 때 마음 속에 두고 있던 것이다. 이에 대해서는 잠시 후 다시 보기로 하자.

만능 튜링 기계

아직 우리는 만능 튜링 기계 (universal Turing machine) 에 대해서는 설명하지 않았다. 이에 대한 자세한 내용은 비록 복잡할지 몰라도 그 배경에 깔려 있는 원리는 그다지 어렵지 않다. 기본 아이디어는 임의의 튜링 기계 T 의 명령어들을 테이프에 표현할 수 있도록 0 과 1 의 나열로 코드화하는 것이다. 이 테이프는 다시 만능 튜링 기계라고 불리는 어떤 특정한 튜링 기계 U 의 입력부 초반에 위치하게 되고 U 는 입력부 뒷부분에 위치한 데이터를 이용하여 마치 T 처럼 행동하게 된다. 만능 튜링 기계는 흉내내는 데는 만능이라 할 수 있다. 테이프 초반부에 있는 내용은 만능 기계 U 가 주어진 기계 T 를 똑같이 흉내내는데 필요한 모든 정보를 제공해 주는 것이다.

이것이 어떻게 수행되는가를 보기 위하여는 우선 튜링 기계를 체계적으로 숫자화할 수 있는 방법이 필요하다. 앞에서 보았던 어떤 특정한 튜링 기계의 명령어 리스트를 생각해 보기로 하자. 일단 이 리스트에 나타난 명령어들을 체계적인 방법으로 1 과 0 의 나열로 이루어진 코드로 바꿔 주는 것이 필요하다. 이것은 앞에서 기술한 바 있는 '축약' 과정을 이용하면 된다. 만일 R, L, STOP, 화살표 (→), 쉼표 (,) 등을 2, 3, 4, 5, 6 과 같은 숫자로 대치하면 각각은 축약 코드로 110, 1110, 11110, 111110, 1111110 으로서 나타낼 수 있다. 그리고 명령어에 등장하는 숫자 0 과 1 은 각각 0 과 10 이라는 코드를 사용하여 표시한다. 튜링 기계의 명령어에 큰 글자로 나타나는 0 혹은 1 과 작은 글씨의 0, 1 을 구분해 줄 필요는 없다. 왜냐 하면 큰 글자는 항상 맨 마지막 (오른쪽) 에 나오기 때문에 그 위치만 가지고도 분별이 가능하다. 예를 들면, 명령어 1101 은 2 진수의 1101 로 나타내고 테이프에는 1010010 이라는 코드로 표시된다. 특히 처음에 나오는 00 는 00 으로 받아들여지는데 이 경우 혼동될 염려가 없으므로 0 이라는 코드로 나타내든지 아니면 아예 생략해 버려도 무방하다. 코드 작업을 크게 단순화시키기 위해서 화살표와 화살표 좌측의 기호들을 생략해 버리고 명령어 코드 숫자의 순서에 의존하여 그 값을 다시 추정해 내는 방법도 있다. 다만 이 방법을 사용하기 위해서는 순서상에 빈 공간이 있으면 안 되기 때문에 곳곳에 가짜 순서값을 채워 넣어야 한다. (예를 들면, 튜링 기계 XN+1 의 경우 1100 에 대해서는 기계 동작 동안 그 경우가 발생하지 않기 때문에 1100 → 00R 과 같은 가짜 명령어를 채워 넣어 주어야 한다. 이 가짜 명령이 명령어 리스트에 포함되더라도 실제로 기계는 아무런 변화가 없다. 마찬가지로, XN×2 의 경우 가짜 명령어 101 → 00R 을 채워 주어야 한다.) 이러한 가짜 명령어가 없다면 그 위치 이후의 모든 코드가 망쳐져 버리기 때문이다. 또, L 혹은 R 에 의해서 명령어가 구분될 수 있기 때문에 쉼표도 꼭 필요한 것은 아니다. 그러므로 다음과 같은 간단한 코드를 사용하기로 한다.

0 혹은 0 → 0, 1 혹은 1 → 10, 110 → R, 1110 → L

11110 → STOP

예로서 튜링 기계 XN+1 (가짜 명령 1100 → 00R 포함) 의 코드를 살펴보기로 하자. 화살표와 화살표 좌측의 기호, 그리고 쉼표를 제외하면 다음과 같은 기호만 남는다.

00R  11R  00R  101R  110L  101R  01STOP  1000L  1011L  1001L  

1100R  101R  00R  1111R  111R  1110R

앞에서 언급한 대로 00 을 없애 버리고 01 을 단순히 1 로 바꿔 주면 다음과 같이 간략화할 수 있다 :

R11RR101R110L101R1STOP1000L1011L1001L1100R101RR1111R111R111OR.

이 기호들을 테이프 코드로 바꿔 주면 다음과 같다.

110101011011010010110101001110100101101011110100001110

100101011101000101110101000110100101101101010101011010

10101101010100110.

두 가지만 더 간소화 작업을 하자면, 제일 처음에 등장하는 110 은 그 앞에 끝없이 계속되는 공란 기호와 함께 생략할 수 있다. 왜냐 하면 이것이 표현하는 것은 00R 인데 이는 바로 명령문 00 → 00R 을 간략화한 것이다. 이 명령문은 이 책에서 모든 튜링 기계가 공통적으로 갖는다고 무언중에 가정한 것으로 기계가 일단 테이프 입력의 시작보다 충분히 왼쪽으로부터 시작하여 처음 기호가 나올 때까지 오른쪽으로 움직이라는 것이다. 마찬가지로 마지막의 110 도 그 뒤에 나오는 0 들과 함께 생략할 수 있다. 그 이유는 모든 명령어가 R, L, 혹은 STOP 으로 끝나게 되고 110 은 이들 코드의 마지막에 공통적으로 등장하기 때문이다. 그 결과로 얻어지는 2 진수가 바로 튜링 기계를 대표하는 숫자이다. 튜링 기계 XN+1 의 경우 다음과 같다 :

101011011010010110101001110100101101011110100001110100

101011101000101110101000110100101101101010101011010101

01101010100.

이 수를 일반 십진수로 나타내면 다음과 같다.

450813704461563958982113775643437908.

우리는 종종 기계의 번호가 n 인 튜링 기계를 n 번째 튜링 기계라고 부르고 이를 T_n 으로 표시한다. 그러므로 XN+1 은 450813704461563958982113775643437908 번째 튜링 기계가 되는 것이다!

튜링 기계들의 순서 목록에서 이렇게 많이 지나간 다음에야 겨우 자연수 (확장 2 진 표현) 에 하나를 더하는 정도의 아주 기본적인 튜링 기계를 발견할 수 있다는 것은 매우 충격적인 사실이다! (약간의 간소화 여지가 더 있긴 하지만 내가 여기에 제안한 코드화 방법이 터무니없이 비효율적인 방법이었다고 생각하진 않는다.) 실제로 이보다 작은 수의 튜링 기계 중에도 흥미있는 기계가 있기는 하다. 예를 들면, UN+1 기계는 다음과 같은 2 진수에 해당한다.

101011010111101010

이를 십진수로 고치면 불과 177642 밖에 되지 않는다! 그러므로 1 들로된 나열의 끝에 1 하나를 새로 붙이는 아주 단순한 튜링 기계 UN+1 은 177642 번째 튜링 기계가 되는 것이다. 재미있는 것은, 2 를 곱하는 작업은 어떤 표현법을 쓰건 위의 두 숫자 사이에 등장한다는 것이다. 왜냐하면 XN×2 의 숫자는 1456581339 이고, UN×2 의 숫자는 142923420919872026917547669 인 것이다.

이러한 숫자들의 크기와 연관시켜 생각해 보면 거의 대부분의 자연수가 실제 동작할 수 없는 튜링 기계라는 것이 별로 놀라운 사실이 아닐 것이다. 참고로 이 체계에 의한 처음 열세 개의 튜링 기계를 살펴보면 다음과 같다.

이중 T₀ 는 무엇을 만나건 무조건 파괴해 버리며 오른쪽 나아가는 기계이다. 절대로 멈추거나 뒤돌아보는 법도 없이. T₁ 도 궁극적으로는 이와 같은 효과를 거두지만 훨씬 솜씨가 떨어진다. 왜냐 하면 테이프의 기호를 하나 파괴할 때마다 뒤로 한 걸음 물러났다가 다시 나아가기 때문이다. T₀ 와 마찬가지로 T₂ 도 오른쪽으로 끝없이 나아간다. 다만 T₂ 는 훨씬 점잖아서 테이프의 내용을 하나도 바꾸지 않는다는 점이 다르다. 이들 모두 멈추는 법이라곤 없기 때문에 튜링 기계로서는 별로 쓸모가 없다. T₃ 는 처음 등장하는 쓸모 있는 기계이다. 이것은 처음 등장하는 (가장 왼쪽의) 1 을 0 으로 바꾼 뒤에 겸손하게도 정지를 하는 것이다.

T₄ 의 경우에는 심각한 문제가 있다. 이 기계는 테이프에서 최초의 1 을 발견하면 등록되지 않은 내부 상태로 들어가 버리기 때문에 다음에 무엇을 할 것인가에 대한 명령어가 존재하지 않는 것이다. T₈, T₉, T₁₀ 도 똑같은 문제에 봉착하게 된다. T₇ 에서는 더욱 근본적인 문제점에 봉착하게 된다. 이 기계에 해당하는 코드를 보면 110111110 으로서 다섯 개의 1 이 연달아 나오는데 이에 해당하는 해석이 존재하지 않는 것이다. 그러므로 이 기계는 최초의 1 을 발견하면 그 자리에서 아무것도 못하게 되는 것이다. (이와 같이 그 2 진 표현 속에 4 보다 많은 수의 1 이 연속해서 나오는 경우 그 기계를 오류 표기된 기계라고 부르기로 하자.) T₅, T₆, T₁₂  등은 T₀, T₁, T₂  와 비슷한 문제에 봉착한다. 그들은 멈추는 법이 없이 움직이는 것이다. 즉, T₀, T₁, T₂ , T₃, T₄, T₅, T₆, T₇, T₈, T₉, T₁₀, T₁₁, T₁₂  는 모두 불량품이라고 볼 수 있다. T₃ 과 T₁₁ 만이 뭔가 수행하는 기계지만 그나마도 별로 재미있는 작업을 하는 것은 아니다. T₁₁ 은 T₃ 보다도 더 보잘것없다. 이 기계는 처음 1 을 만나면 아무것도 못하고 그냥 정지하고 만다.

또 한가지 주목할 것은 위의 기계 리스트에는 중복되는 것들이 많다는 것이다. T₁₂ 는 T₆ 및 T₁ 과 동일하다. 왜냐 하면 T₆ 과 T₁₂ 의 내부 상태 1 로는 들어갈 수 없기 때문이다. 리스트에 이러한 중복이 많다거나 혹은 불량품이 많이 생성된다 하여 신경쓸 필요는 없다. 코드화 작업을 개선함으로써 불량품이나 중복되는 것을 훨씬 줄일 수는 있다. 그러나 그렇게 하려면 그 코드를 다 풀어헤쳐야 하며, n 이라는 숫자를 읽고 자신이 마치 n 번째 튜링 기계인양 흉내내야 하는 만능 튜링 기계를 훨씬 복잡하게 만들 게 될 것이다. 만일 이렇게 함으로써 모든 불량품이 제거되고 중복이 없어질 수만 있다면 할 만한 가치가 있을지도 모른다. 그러나 잠시 후 보겠지만 그것은 불가능하다. 그러므로 코딩 방법은 우리가 사용하던 것을 그대로 따르기로 하자.

테이프에 다음과 같은 기호의 나열이 있을 때 이를 2 진 표현된 자연수로 표시하는 것이 편리하다.

...0001101110010000...

앞에서 언급했듯이 왼쪽과 오른쪽으로는 0 이 끝없이 나오지만 1 의 개수는 한정되어 있다. 여기에서는 1 이 최소 한 개 이상 나타난다고 가정하기로 하자. 만일 최초의 1 과 최후의 1 을 포함하여 그 사이에 나오는 유한 개의 숫자만을 읽어 들인다고 한다면 위의 데이터가 표시하는 숫자는,

110111001

로서 십진수로는 441 이 될 것이다. 그러나 이 경우 2 진수의 마지막 숫자는 항상 1 이 되기 때문에 모든 자연수를 표현하고자 하는 우리 의도와는 달리 홀수만 나오게 된다. 그러므로 맨 마지막 1 은 제외하고 그 나머지만을 취하는 편법을 취하기로 한다. (이 경우 마지막 1 은 데이터의 끝을 표시하는 마크 역할을 하게 된다.) 그러므로 위의 예에 이를 적용하면,

11011100

이 되어 이를 십진수로 표시하면 220 이 된다. 이 방법은 0 을 표현하는데 다음과 같이 1 이 등장한다는 장점이 있다.

...0000001000000...

어떤 특정한 튜링 기계 T_n 에 0 과 1 의 문자열이 씌어진 테이프를 입력하였을 때 그 기계가 어떻게 동작하는가 생각해 보자. 그 기계에 주어진 문자열이 위에서 설명한 방법대로 어떤 자연수 m 을 나타내는 2 진수 표현이라고 가정하기로 한다. 튜링 기계 T_n 이 얼마간 작동한 후 정지 상태에 도달했다고 가정하자. 이 기계가 생성해 낸 2 진 숫자는 바로 계산의 결과가 될 것이다. 이 숫자를 위의 방법으로 해석하고 그 결과를 p 라고 가정하자. 이러한 관계, 즉 n 번째 튜링 기계가 입력 데이터 m 에 작동하여 p 를 생성하였다는 것을 다음과 같은 식으로 표현하기로 한다.

T_n(m) = p

이 관계를 약간 다른 방법으로 생각해 보자. 즉, n 과 m 의 순서쌍에 작용하여 p 를 생성하는 특정한 연산으로 보는 것이다. (그러므로 두 개의 숫자 n, m 이 주어졌을 때 p 를 알기 위해서는 n 번째 튜링 기계가 m 에 대하여 무엇을 생성하는가를 보면 된다.) 이 특정한 연산은 완전히 알고리즘적 과정이다. 그러므로 이는 어떤 특정한 튜링 기계 U 에 의해서 수행될 수 있다. 즉, U 는 순서쌍 (n, m) 을 받아들이고 p 를 생성하는 것이다. 튜링 기계 U 는 두 개의 입력값 n 과 m 을 받아들여야 하기 때문에 순서쌍 (n, m) 을 한 테이프에 표현할 수 있는 방법이 필요하다. 한 가지 방법은 n 은 그냥 보통의 2 진수로 표현해 주되 111110 이라는 문자열을 그 뒤에 붙여 주는 것이다. (튜링 기계를 표현할 때 여기에서 채택하고 있는 방법에 따르면 0, 10, 110, 1110, 11110 만이 나타날 수 있기 때문에 1 이 다섯 개 이상 연속적으로 나올 수 없다는 사실을 기억해 주기 바란다. 그러므로 T_n 이 정확히 기술되었다면 111110 을 n 이 끝났다는 표시로 사용할 수 있다.) 그 뒤에 나오는 숫자는 m 을 위에서 정한 방법에 따라 표현한 것이다 (즉, m 에 해당하는 2 진수 및 그 오른편에 1000...). 그러므로 뒷부분의 데이터는 바로 튜링 기계 T_n 이 사용할 입력값인 것이다.

예를 들어 n = 11 이고 m = 6 이라고 가정하면 U 가 사용할 테이프에는 다음과 같은 문자열을 사용하게 된다.

....000101111111011010000....

이를 분석해 보면,

...0000 (처음 공란들)

       1011 (11 의 2 진 표현)

  111110 (n 의 마침)

    110 (6 의 2 진 표현)

         10000... (나머지 공란들)

T_n 이 m 에 작동하는 각각의 단계에서 튜링 기계 U 가 할 일은 n 의 표현 구조를 분석하고 m (즉, T_n 의 '테이프') 을 적당히 대치시키는 것이다. 실제로 그러한 기계를 만드는 작업은 (지겹긴 하겠지만) 근본적으로 어려운 작업은 아니다. 그 자체의 명령어 리스트는 일단 n 에 코드화되어 있는 '리스트' 의 항목을 m 으로 표현된 입력을 처리해 나가는 단계별로 적당한 항목을 읽어 들일 수 있는 방법을 제공해 주는 것이다. 이 기계는 m 과 n 사이에서 앞뒤로 수없이 왔다갔다를 반복하게 되고 전체 과정도 엄청나게 느릴 것이다. 그렇더라도 그러한 기계의 명령어 리스트는 분명히 만들 수 있다. 이러한 기계를 만능 튜링 기계라고 부르는 것이다. 이 기계가 순서쌍 (n, m) 에 작동하는 것을 U(n, m) 로 표현한다면 각각의 (n, m) 쌍에 대하여 다음 식이 성립한다. 여기에서 T_n 은 정확하게 기술된 튜링 기계를 말한다.

U(n, m) = T_n (m)

U 기계는 n 값이 주어지면 정확하게 n 번째 튜링 기계를 흉내내게 되는 것이다.

U 자체도 튜링 기계이기 때문에 그 자신에 대한 숫자가 있을 것이다. 즉, 다음 식을 만족하는 u 가 존재할 것이다.

U = T_u ,

그렇다면 그 u 는 도대체 얼마나 큰 숫자일까? 실제로 이를 정확하게 표현하면 다음과 같다.

(혹은 다른 방법도 있겠지만 숫자의 크기는 비슷할 것이다.) 이 숫자는 물론 너무나 엄청나게 커 보인다. 실제로 이 숫자는 엄청나게 크다. 하지만 이 숫자를 상당히 줄일 수 있는 방법을 나는 아직 발견하지 못했다. 내가 제시한 코드화 방법이나 튜링 기계의 사양은 꽤 합당하고 간단한 것이지만 실제로 만능 튜링 기계를 코드화하려면 누구나 이같이 엄청나게 큰 숫자를 얻을 수밖에 없다.

나는 현대의 모든 범용 컴퓨터가 그 효과에서 만능 튜링 기계와 같다고 말한 적이 있다. 그 말은 그러한 컴퓨터의 논리 설계가 앞에서 제시한 만능 튜링 기계의 사양과 비슷하다는 뜻으로 한 말은 아니다. 나의 요지는 단지 적당한 프로그램 (입력 테이프의 처음 부분) 을 만능 튜링 기계에 전달함으로써 그것이 어떤 튜링 기계라도 흉내낼 수 있도록 만들어질 수 있다는 것이다. 위에 기술한 바에 따르면 프로그램은 단순히 하나의 숫자 (n) 형태를 취하고 있다. 그러나 다른 방법도 가능하고 이로 인하여 튜링의 오리지널 테마에 대한 여러 개의 변주곡이 존재하는 것이다. 실제로 내가 기술한 방법도 튜링의 원래 방법과는 다소 차이가 있다. 그러나 이 차이는 여기에서는 별로 중요하지 않다.

힐베르트 문제의 해결 불가능성

이제 튜링이 그의 아이디어를 내놓게 된 원래의 목적으로 돌아가 보기로 하자. 그것은 힐베르트의 개괄적인 '열 번째 문제,' 즉 광범위하면서도 잘 정의된 범주에 속하는 수학 문제들에 대하여 답할 수 있는 기계적 알고리즘이 존재하는가 하는 문제를 해결하는 것이다. 튜링은 그 문제가 "n 번째 튜링 기계가 m 이라는 숫자에 대하여 작동할 때 궁극적으로 정지할 것인가" 라는 문제로 귀결될 수 있음을 발견하였다. 이 문제는 정지 문제 (halting problem) 라고도 불린다. 어떤 수 m 에 대해서도 정지하지 않는 튜링 기계를 만들기는 아주 간단하다 (예를 들면, 위에서 살펴본 대로 n 이 1 이나 2 인 경우, 혹은 STOP 명령이 누락된 어떤 경우건 해당됨). 그리고 어떤 입력에 대해서도 항상 정지하는 경우 (예를 들면 n = 11) 도 많이 있는가 하면 어떤 입력에 대해서는 정지하고 어떤 입력에 대해서는 정지하지 않는 경우도 있을 수 있다. 소위 알고리즘이라는 것이 정지하지 않고 끝없이 계속된다면 그것은 아무 쓸모가 없다고 말할 수 있을 것이다. 그것은 아예 알고리즘이 아니다. 그러므로 튜링 기계 T_n 이 입력값 m 에 대해서 궁극적으로 어떠한 답이라도 내줄 것인가를 결정하는 것은 매우 중요한 문제이다! 만일 그렇지 않다면 (즉, 계산이 정지하지 않는다면) 다음과 같이 표기하기로 하자.

T_n(m) = □

(튜링 기계가 T₄ 나 T₇ 과 같은 불량품에서 본 것처럼 적합한 명령어가 없는 상태로 들어가는 경우도 위와 같이 표시하기로 한다. 그리고 좀 안됐지만 괜찮아 보이던 T₃ 기계도  이젠 불량품, 즉 T₃(m) = □ 라고 간주해야 되겠다. 왜냐 하면 어떤 계산의 결과를 수로 표시하려면 최소한도 1 이 하나는 있어야 되는데 T₃ 의 계산 결과는 항상 공란으로 남기 때문이다. T₁₁ 기계는 1 을 하나 생성하기 때문에 정당한 기계이다. 테이프에 1 하나가 있다는 것은 0 을 의미하기 때문에 모든 m 에 대해서 T₁₁(m) = 0 이라고 할 수 있다.)

튜링 기계가 언제 멈출 것인가를 판별할 수 있다는 것은 수학에서 매우 중대한 문제이다. 예를 들어 다음 식을 보자.

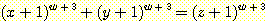
(수식을 혐오하는 독자는 이 식에 대하여 개의치 않아도 된다. 여기에서 이 식은 단지 한 가지 예이기 때문에 자세히 이해할 필요가 없다.) 이 식은 수학의 어쩌면 가장 유명한 미해결 문제와도 연관이 있다. 문제는 이러하다. 즉, 위의 등식을 만족시키는 자연수의 집합 x, y, z, w 가 존재하는가? 17 세기의 위대한 프랑스 수학자 페르마 (Pierre de Fermat, 1601-1665) 에 의해 '페르마의 마지막 정리 (Fermat's last theorem)' 라고 명명된 이 문제는 그가 고대 그리스 수학자 디오판투스 (Diophantus) 의 저서 Arithmetica 의 한쪽 페이지 여백 부분에 끄적거려 놓았는데 그의 주장은 그러한 집합이 절대 존재하지 않는다는 것이다. 데카르트와 동시대인으로서 직업이 법률가였던 페르마는 당시 가장 훌륭한 수학자였다. 그는 그 정리에 대해서 '실로 훌륭한 증명' 까지 있으나 페이지 여백이 너무 좁아 기재하지 못했다고 주장하고 있다. 그러나 현재까지 아무도 그러한 증명을 만들어 내지 못했고, 또 한편 그 주장이 틀리다는 반례도 찾아내지 못하고 있다.

네 개의 자연수 (w, x, y, z) 가 주어지면 위의 식이 만족하는가를 알아보는 것은 단순한 계산에 불과하다. 그러므로 모든 수들에 대해서 차례로 하나씩 식에다 대입하여 보고 등식을 만족할 때 정지하는 컴퓨터 알고리즘을 생각해 볼 수 있다. (유한 집합의 여러 개의 수를 계산적 방법으로 테이프상에 하나의 숫자로서 코딩하는 방법을 이미 앞에서 보았다. 그러므로 이 숫자를 하나씩 늘려 가면 모든 가능한 네 개의 수를 구할 수 있다.) 만약 이 알고리즘이 멈추지 않음을 보일 수만 있다면 페르마의 주장에 대한 증명을 얻을 수 있는 것이다.

이외에도 수많은 수학의 미해결 문제들이 튜링 기계의 정지 문제로 재구성될 수 있다. 그 중 하나가 '골드바흐 (Goldbach) 의 가설' 로서 모든 2 보다 큰 짝수는 두 개의 소수 (prime number) 의 합으로 나타낼 수 있다는 주장이다. 어떤 자연수가 소수인가를 확인하기 위해서는 그 수보다 작은 수로 나뉠 수 있는가를 시험하면 되기 때문에 유한한 계산이 필요한 알고리즘적 과정이다. 그러므로 짝수들 6, 8, 10, 12, 14, ... 에 대해서 모든 가능한 방법으로 다음과 같이 두 개의 홀수의 합으로 쪼갠 후 각각에 대해서 양쪽 모두 소수인가를 확인하는 튜링 기계를 고안할 수 있다.

6 = 3 + 3, 8 = 3 + 5, 10 = 3 + 7 = 5 + 5, 12 = 5 + 7,

14 = 3 + 11 = 7 + 7, ...

(확실히 2 + 2 를 제외하고는 두 개의 짝수로 된 쌍은 확인할 필요가 없다. 왜냐 하면 2 를 제외한 모든 소수는 홀수이기 때문이다.) 우리가 원하는 튜링 기계는 그와 같은 과정을 반복한 후 어떤 방법으로도 두 개의 소수의 합으로 표시할 수 없는 짝수에 봉착하였을 때에만 멈추는 것이다. 그 경우 우리는 골드바흐 가설의 반례, 즉 2 보다 큰 짝수이면서도 두 개의 소수의 합으로 표시될 수 없는 경우를 발견한 것이다. 그러므로 이 튜링 기계가 멈출 것인가를 알 수만 있으면 우리는 골드바흐의 가설이 옳은가도 알아 낼 수 있는 것이다.

그렇다면 당연히 제기되는 질문은 어떤 튜링 기계가 (특정한 입력 데이터에 대하여) 정지할 것인가 아닌가를 어떻게 판별하는가 하는 것이다. 많은 수의 튜링 기계에 대하여 이는 별로 어렵지 않은 문제일 것이다. 하지만 경우에 따라서는 앞의 예에서와 같이 그 답이 중요한 수학 문제를 해결하는 열쇠가 될 수 있는 것이다. 그러면 과연 일반화된 문제로서 '정지 문제' 를 풀 수 있는 완전 자동의 알고리즘적 해결 방법이 존재하는 것인가? 튜링은 그것이 절대 불가능하다는 것을 발견하였다.

그의 주장은 본질적으로 다음과 같다. 우선 그러한 알고리즘이 존재한다고 가정하자. 그 말은, 즉 어떤 튜링 기계 H 가 있어서 n 번째 튜링 기계에 m 이라는 입력이 주어졌을 때 그 기계가 궁극적으로 멈출 것인가를 판별해 줄 수 있다는 것이다. 그 기계가 멈춘다면 H 는 1 을 출력하고 그렇지 않으면 0 을 출력한다고 가정하자.

순서쌍 (n, m) 을 코드화할 때 만능 튜링 기계 U 에서 하던 방식으로 할 수도 있을 것이다. 그러나 이것은 약간의 기술적 문제에 봉착할 수 있다. 왜냐 하면 어떤 n 값 (예를 들면 n = 7) 에 대해서는 T_n 이 정확하게 표시될 수 없고 마커로 사용되는 11110 도 n 과 m 을 분리시키기에 부적합하기 때문이다. 이 문제를 극복하기 위하여 n 은 확장 2 진 코드로 표기되고 m 은 그냥 2 진 코드로 표기되었다고 가정하자. U(n, m) 과는 달리 H(n; m) 에서 세미콜론 (;) 기호를 사용한 것은 이러한 변화를 강조 하기 위한 것이다.

이제 모든 튜링 기계의 모든 가능한 입력에 대한 출력값을 갖는 무한 이차원 배열을 생각해 보자. 이 배열에서 n 번째 튜링 기계가 0, 1, 2, 3, 4, ... 와 같은 입력값에 대하여 출력된 결과를 표시한다.

위의 표에서 나는 약간 속임수를 써서 튜링 기계에 실제 수를 기입하지 않았다. 만일 제대로 했더라면 우선 너무나 지겨운 표가 됐을 것이다. 왜냐 하면 n 값이 11 이 되기 전에는 모든 출력값이 □ 가 됐을 것이고 n = 11 인 경우에도 모두 0 이었을 것이다. 이 표가 좀더 재미있게 보이기 위하여 앞에서보다 훨씬 효과적인 코드화 방법이 사용되었다고 가정하였다. 실제로 표에 있는 값들은 이 표가 대강 어떻게 생겼다는 인상만을 줄 수 있도록 임의로 기재한 값들이다.

내가 말하고자 하는 것은 이 표를 실제로 어떤 알고리즘을 사용하여 계산하였다는 것이 아니다. (실제로 그러한 알고리즘이 존재할 수 없다는 것이 곧 밝혀질 것이다.) 단지 그러한 표가 누군가, 예를 들면 신에 의해서 우리 앞에 펼쳐져 있다고 가정하자. 실제로 이러한 표를 계산하여 작성하고자 할 때 우선 문제가 되는 것은 □ 로 표시된 값들이다. 왜냐 하면 □ 로 표시되는 계산은 모두 끝없이 계속되는 것이기 때문에 언제 이를 기입해야 될지를 알 수 없기 때문이다.

그러나 우리가 만일 가상의 기계 H 를 사용한다고 가정하면 이러한 표를 작성하는데 그 위력을 톡톡히 발휘할 수 있을 것이다. 왜냐 하면 H 가 값이 나올 것인가 아닌가를 판별해 줄 것이기 때문이다. 그러나 여기에서는 H 를 대신 0 으로 대치해 주는 기계로서 사용하기로 하자. 이를 위해서는 T_n 을 m 값에 수행시키기 직전에 우선 H(n; m) 을 돌려보는 것이다. 만일 H(n; m) = 1 인 경우 (즉, T_n(m) 의 계산이 답을 생성할 경우) 에만 T_n 을 가동시키고 H(n; m) = 0 인 경우 [즉, T_n(m) = □] 에는 단순히 0 을 프린트하는 것이다. 이러한 계산 [즉, T_n(m) 에 앞서 H(n; m) 을 수행하는 것] 은 다음과 같이 표기될 수 있다.

T_n(m) × H(n; m)

(여기에서는 연산자 적용의 순서에 오랜 수학의 관례에 따라 오른편 항이 먼저 수행된다고 가정한다. 기호적으로 □ × 0 = 0 임을 주의하기 바란다.)

이제 위의 표는 다음과 같이 변한다 :

H 가 존재한다고 가정하면 이 표의 각 열은 계산 가능 수열임을 주의하기 바란다. (계산 가능 수열이라 함은 수열의 다음 값을 알고리즘을 이용하여 생성할 수 있는 무한 수열을 의미한다. 즉, 입력으로 m = 0, 1, 2, 3, 4, 5, ... 와 같이 자연수가 계속 주어지면 그에 따라 수열의 다음 값을 계산해 주는 튜링 기계가 있음을 의미함.) 이 표에 대해서 두 가지 사실에 주목하여 보자. 우선, 모든 계산 가능한 자연수의 수열이 위 표의 열들 가운데 어디엔가 (어떤 경우에는 여러 번) 등장한다는 사실이다. 이 성질은 이미 □ 를 제거하기 전의 원래 표에서도 성립하였다. 단지 '불량품' (최소 하나의 □ 를 생성하는) 기계들을 대체하기 위하여 몇 개의 새로운 열을 추가한 것으로 생각할 수 있다. 둘째로 H 라는 튜링 기계가 존재한다는 가정하에서 이 표는 T_n(m) × H(n; m) 이라는 계산 가능한 방법으로 (즉, 확실한 알고리즘에 의해서) 생성되었다는 것이다. 이는 다시 말하면 Q 라는 어떤 튜링 기계가 있어서 (n, m) 이라는 한쌍의 수가 입력으로 주어지면 그 표의 해당되는 값을 계산해 줄 수 있다는 것이다. 이를 위해서 n 과 m 의 값을 H 에서와 같이 Q 의 테이프에 코드화하여야 한다.

Q(n; m) = T_n(m) × H(n; m)

이제 칸토르 (Georg Cantor) 가 제안한 기발하고 강력한 대각선 짜르기라는 수법을 적용하려 한다. (칸토르의 대각선 짜르기의 원래 버전은 다음 단원에서 보게 될 것이다.) 표의 가운데 대각선에 굵은 글씨로 표기된 숫자들을 생각해 보자.

이 숫자들은 하나의 수열 0, 0, 1, 2, 1, 0, 3, 7, 1, ... 을 형성하는데 각각에 1 을 더하면 다음 수열이 된다 :

1, 1, 2, 3, 2, 1, 4, 8, 2, ...

이는 분명히 계산 가능 해결 방법에 속하고 위의 표가 계산 가능하게 생성되었다는 가정하에 새로운 계산 가능 수열 하나를 우리에게 제시하고 있다. 실제로 1 + Q(n; n), 즉

1 + T_n(n) × H(n; n)

의 식에 의해서 (m 과 n 의 값이 같으므로) 위의 수열이 생성된다. 그런데 앞에서 밝힌 바와 같이 이 표가 모든 가능한 계산 가능 수열을 포함하고 있으므로 위의 수열은 이 표 어디엔가 존재하여야 한다. 그러나 이것은 불가능하다. 왜냐 하면 이 수열은 첫 번째 열과는 첫 번째 값이 다르고, 두 번째 열과는 두 번째 값이 다르며, 이와 같이 모든 열에 대해서 최소한 하나의 값은 다르게끔 정의되었기 때문이다. 이는 분명히 모순이다. 이 모순으로 인해서 우리가 증명하려던 것, 즉 튜링 기계 H 는 실제로 존재할 수 없다는 것이 판명되었다. 어떤 튜링 기계가 멈출 것인가 아닌가에 대한 범용 알고리즘은 결코 존재하지 않는 것이다!

이를 다른 방법으로 설명하면, H 가 존재한다는 가정하에서 대각선 알고리즘 1 + Q(n; n) 을 계산하는 튜링 기계 (번호를 k 라고 하자) 가 존재한다. 그러므로,

1 + T_n(n) × H(n; n) = T_k(n)

그러나 n = k 를 대입하면 다음 식이 된다.

1 + T_k(k) × H(k; k) = T_k(k)

그러나 이는 불가능하다. 왜냐 하면 만일 T_k(k) 가 정지한다면 H(k ; k) 가 1 이 되기 때문에 다음과 같은 불가능한 등식이 나온다.

1 + T_k(k) = T_k(k)

또, T_k(k) 가 정지하지 않는다면 H(k ; k) 는 0 이 되기 때문에 마찬가지의 불가능한 등식,

1 + 0 = □

를 얻게 된다.

어떤 튜링 기계가 멈추는가 아닌가는 완벽하게 잘 정의된 수학 문제이다. (그리고 우리는 앞에서 여러 가지 중요한 수학 분야의 문제들이 튜링 기계의 정지성 문제로 전환될 수 있음을 보았다.) 그러므로 튜링 기계의 정지 여부의 질문에 대한 알고리즘이 존재하지 않는다는 사실을 보임으로써 튜링은 모든 수학의 문제를 풀 수 있는 범용 알고리즘이 존재할 수 없음을 증명하였다 (처치도 자기 나름의 다른 방식을 통해서 이를 보였다) 힐베르트의 「열 번째 문제」는 결국 답이 없었던 것이다!

이 말은 어떤 하나의 경우에 대하여 주어진 수학 문제의 결과가 참인지 아닌지를 알 수 없다거나 혹은 주어진 튜링 기계에 대하여 그것이 멈출 것인지를 알 수 없다는 말은 아니다. 창의력을 발휘하거나 아니면 단순히 상식에 의존하더라도 어떤 경우에는 그러한 문제에 답을 할 수 있다. (예를 들면 튜링 기계의 명령어 리스트 가운데 STOP 명령이 하나도 등장을 하지 않거나 아니면 STOP 명령만 있거나 하는 경우에는 상식적인 생각만 하더라도 그것이 정지할지 안 할지를 알 수 있다.) 그러나 모든 수학의 문제에 대하여 답할 수 있거나 모든 튜링 기계와 모든 데이터에 대해서 답할 수 있는 하나의 알고리즘은 존재하지 않는 것이다.

어쩌면 우리가 마치 결정 불가능한 수학 문제가 있다는 것을 보였다고 생각할지 모른다. 그러나 우리가 보인 것은 그게 아니다! 우리는 어떤 특별히 괴상한 튜링 기계가 있어서 그것이 특별히 괴상한 숫자에 대해서 멈출 것인가 아닌가를 아는 것이 원칙적으로 불가능함을 보인 것이 아니다. 잠시 후에 보게 되겠지만 오히려 그 반대이다. 우리가 말한 것은 어떤 하나의 문제에 대한 해결 불가능성을 지적한 것이 아니라 어떤 문제군에 대한 알고리즘적 해결 불가능에 대해서만 이야기한 것이다. 하나의 특정한 경우에 대해서는 그 대답은 항상 '네', 혹은 '아니오' 이다. 그러므로 그 특정 문제를 결정짓는 알고리즘, 즉 그 문제에 대하여 '네' 혹은 경우에 따라서 '아니오' 하고 대답하는 알고리즘은 분명 존재한다. 물론 문제는 어떤 알고리즘을 사용할 것인가를 알 수가 없다는 것이다. 그것은 어떤 명제들의 집합에 대한 체계적 결정 문제가 아니라 하나의 명제에 대한 수학적 진리값을 결정하는 문제이다. 알고리즘들이 자기들이 알아서 수학적 진리값을 결정하는 것은 아니다. 어떤 알고리즘이 맞는가 틀리는가는 항상 그 밖에서 결정해 주어야 되는 것이다.

알고리즘을 능가하는 방법

어떤 수학적 명제가 진실임을 결정하는 문제는 괴데르이 정리 (제 4 장) 에서 다시 다루기로 한다. 여기에서는 튜링의 주장이 실제로는 혹시 잘못 전달되었을지 모르지만 훨씬 건설적이고 덜 부정적이라는 것을 밝혀 두고 싶다. 물론 정지성을 결정할 수 없는 어떤 특정한 튜링 기계를 실제로 보여 준 것은 아니다. 실제로 그 내용을 잘 살펴보면 우리가 튜링 방법을 따라 만드는 '특히 괴상한' 기계에 대한 대답이 이미 그 과정 속에 암묵적으로 나와 있음을 알 수 있을 것이다.

그것이 왜 그런가 살펴보자. 만약 우리에게 어떤 알고리즘이 있어서 임의의 튜링 기계가 정지하지 않을 것임을 가끔 효과적으로 알려 줄 수 있다고 가정하여 보자. 앞에서 기술된 튜링의 프로시듀어는 그 알고리즘의 계산이 정지할 것인가 안 할 것인가를 결정하는 튜링 기계 계산 과정을 자세히 명시할 것이다. 그러나 그 과정에서 우리는 이 경우에는 답을 알 수 있게 되었다. 그 튜링 기계의 계산은 진정 멈추지 않는 것이다.

어떻게 그것이 가능한가 자세히 보기 위해서 가끔만 효과적인 어떤 알고리즘이 있다고 가정하여 보자. 전처럼 이 알고리즘 (튜링 기계) 을 H 로 표기하기로 한다. 그러나 이번에는 그 알고리즘이 어떤 튜링 기계가 정지하지 않는다는 것을 언제나 자신있게 말하지 못할 수도 있다는 것을 허용하는 것이다.

그러므로 T_n(m) = □ 인 경우에도 H(n; m) = □ 이 될 수도 있다. 이러한 H(n; m) 알고리즘이 실제로 많이 존재한다. (예를 들면 T_n(m) 이 정지하기만 하면 H(n; m) 으로 하여금 1 을 생성하게 할 수도 있다. 그러나 이 알고리즘은 별로 쓸모는 없을 것이다!)

위에 주어진 대로 튜링의 프로시듀어를 자세히 따라가기만 하면 된다. 다만 □ 를 모두 0 으로 바꾸는 대신에 □ 들을 몇 개 남겨 놓게 된다. 전과 마찬가지로 대각선 방법을 이용하여 대각선상의 n 번째 항을 구할 수 있다. (H(n; n) = □ 인 경우에는 항상 □ 가 나오게 된다. □ × □ = □, 1 + □ = □ 임을 주의할 것.)

1 + T_n(n) × H(n; n)

이는 완벽하게 올바른 계산이다. 그러므로 이는 어떤 튜링 기계로 수행될 수 있는데 이 기계의 번호를 k 라고 하자. 그러면,

1 + T_n(n) × H(n; n) = T_k(n)

대각선상에서 k 번째 항을 살펴보자면, 즉 n = k 인 경우,

1 + T_k(k) × H(k ; k) = T_k(k)

가 된다. 만약 T_k(k) 가 멈추면 모순이 발생한다. (왜냐 하면 T_k(k) 가 멈추면 H(k ; k) 값이 1 이 되는데 그 경우 위의 식은 1 + T_k(k) = T_k(k) 이 되어 불가능한 상황이 발생한다.) 그러므로 T_k(k) 는 멈출 수가 없다. 즉,

T_k(k) = □

그러나 그 알고리즘은 이 사실을 '알 수가' 없다. 왜냐 하면 H(k ; k) = 0 라는 식을 얻게 되면 또다시 모순이 발생하기 때문이다. (식으로 표시하면 다음과 같은 불가능한 경우가 발생한다. 즉, 1 + 0 = □)

그러므로 우리가 k 값을 찾을 수만 있다면 그 알고리즘을 능가하는, 하지만 우리가 이미 답을 알고 있는 특별한 계산 방법을 구할 수 있다. 그렇다면 어떻게 k 의 값을 구할 것인가? 이는 힘든 작업이다. 이를 위해서는 H(n; m) 과 T_n(m) 을 만드는 과정을 면밀히 조사하고 1 + T_n(n) × H(n ; n) 가 튜링 기계로써 어떻게 움직이는가도 조사해야 한다. 이 튜링 기계의 숫자를 구하면 그것이 k 이다. 이는 물론 매우 복잡한 과정이 되겠지만 가능은 하다. 그 복잡성 때문에 만일 그것이 알고리즘 H 를 능가하기 위하여 특별히 식을 구성하는 과정이 아니었다면 그 실제값에 관하여 별로 흥미도 갖지 않았을 것이다! 중요한 것은 우리에게 잘 정의된 프로시듀어가 있어서 어떤 H 에 대해서도 그에 해당하는 k 를 구할 수 있는데 이 경우 T_k(k) 가 H 보다 낫다는 것을 우리가 알고 있다는 것이다. 즉, 우리는 알고리즘보다 낫다는 것이다. 어쩌면 우리가 단순한 알고리즘보다는 낫다고 생각하면 좀 위로가 될지 모르겠다!

실제로 그 프로시듀어가 아주 잘 정의되었기 때문에 H 가 주어지면 k 를 구하는 알고리즘도 구할 수 있다. 그러므로 아직 만족하기에 앞서 이 알고리즘 역시 H 보다 나아질 수 있다는 것이다. 왜냐 하면 결과적으로 이것 역시 T_k(k) = □ 임을 '알 수' 있기 때문이다. 과연 그럴까? 위의 설명에서 알고리즘에 대하여 의인화된 '안다' 는 표현을 사용하는 것이 이해에 도움이 되었다. 그러나 실제로는 '아는' 것은 우리 사람이고 알고리즘은 단지 사람이 정해 준 규칙을 따르기만 하는 것이 아니었던가? 그렇지 않으면 우리 자신이 다만 두뇌가 구성된 방법에 따라, 혹은 환경이 결정해 준 대로 따르도록 프로그램된 규칙을 그대로 따르고 있는 것인가? 여기에서 이슈는 단순히 알고리즘 하나에 국한된 것이 아니고 사람들이 어떻게 참과 거짓을 판단하는가 하는 문제까지 포함하게 된다. 이는 우리가 후에 다시 자세히 살펴볼 주제가 될 것이다. 수학적 진리에 관한 문제는 제 4 장에서 다루어질 것이다. 지금쯤은 '알고리즘' 이나 '계산 가능성' 이라는 용어에 대하여 최소한도 감이 잡혔을 것이고 이와 관련된 이슈에 대해서도 일부 이해가 가능할 것이다.

처치의 람다 계산법

계산 가능성의 개념은 매우 중요하고 아름다운 수학적 개념이다. 그리고 그것이 수학의 근본 성질을 다룬다는 점에서 보면 1930 년대에 처음 등장했다는 것이 놀라울 정도로 근자에 와서 연구되기 시작한 분야이기도 하다. 이 개념은 수학의 모든 분야에 관련된다. (물론 거의 모든 수학자들이 계산 가능성에 대해서는 종종 염두에 두지 않는 것도 사실이다.) 이 개념이 놀라운 이유 중의 하나는 몇몇 잘 정의된 수학 문제들이 실제로 계산 불가능하다는 데 있다. (튜링 기계의 정지성 여부에 대한 문제가 그 한 예이고 그 밖에 제 4 장에서 다른 예를 볼 것이다.) 왜냐 하면 그와 같은 계산 불가능한 문제가 없었더라면 계산 가능성의 개념은 별로 수학적 흥미를 일으키지 않았을 것이기 때문이다. 수학자들은 따지고 보면 퍼즐을 좋아하는 사람들이다. 어떤 수학의 연산이 계산 가능한가를 밝히는 것은 그들에게 매우 흥미로운 퍼즐이 될 수 있는 것이다. 그리고 그러한 퍼즐에 대한 일반적 해답이 계산 불가능하다는 것이 그 퍼즐을 더욱 흥미롭게 만든다.

한 가지 확실히 밝혀 두어야 할 것은 계산 가능성이 순전하고 확실한 수학적 개념이라는 사실이다. 그것은 앞에서 기술한 튜링 기계에 의한 특정 구현의 차원을 넘는 훨씬 추상적인 개념인 것이다. 앞서 밝힌 바와 같이 튜링의 기발하고 독창적인 방법을 특징짓는다고 볼 수 있는 '테이프' 니 '내적 상태' 니 하는 것에 꼭 중요성을 부가할 필요는 없다. 계산 가능성의 개념을 표현할 수 있는 다른 방법들이 있는데 역사적으로 최초의 방법은 미국의 논리학자 처치가 클린의 도움으로 만든 람다 계산법 (lambda calculus) 이다. 처치의 방법은 튜링의 방법과는 완전히 달랐고 훨씬 추상적이었다. 실제로 처치가 자신의 아이디어를 기술한 수식들을 살펴보면 그것과 '기계적' 이라고 불릴 수 있는 그 무엇과는 어떤 연결성을 발견해 내기가 쉽지 않다. 처치 방법의 중심 아이디어는 실로 그 핵심에서 볼 때 추상적이다. 즉, 하나의 수학 연산을 사용하는데 처치도 실제로 그것을 추상화 (abstraction) 라 불렀던 것이다.

여기에서 처치의 방법을 간략하게 제시하는 것이 가치가 있다고 생각된다. 이는 계산 가능성이라는 개념이 어떤 특정한 계산 기계와는 독립적이라는 것을 보이기 위함도 있지만 또한 수학에서 추상적 개념이 얼마나 강력한 수단이 될 수 있는가를 보여 주기 때문이다. 수학적 개념에 대해서 이해하기 어려운 독자들이나 그러한 것에 별로 흥미가 없는 독자는 다음 장으로 건너뛰더라도 문맥 진행에 별 문제가 없을 것이다. 하지만 그러한 독자들도 잠시만 더 같이 인내함으로써 처치의 방법이 가져다 주는 마술과도 같은 명료함을 목격할 수 있을 것이다.

이 방법은 다음과 같이 표기되는 객체들이 이루는 '세계 (universe)' 에 관한 것이다.

a, b, c, d, ..., z, a', b', ..., z', a'', b'', ..., a''', ..., a'''', ...

위의 객체들은 수학의 연산 혹은 함수를 의미한다. (표지가 달린 기호는 단지 수없이 많은 함수들을 표기하기 위하여 편의상 붙인 것이다.) 이 함수의 '독립 변수 (argument)' 들, 즉 함수가 계산에 사용하는 값들도 역시 같은 종류들인 함수이다. 게다가 함수를 계산한 결과 역시 함수이다. (실로 처치의 체계는 개념상 놀라울 정도로 경제적이라 할 수 있다.) 그러므로 다음 식이 의미하는 것은 함수 b 에 함수 c 를 적용한 결과가 함수 a 가 된다는 것이다.

a = bc

이 방법에 따르면 함수가 두 개 이상의 독립 변수를 갖는 경우도 쉽게 표현할 수 있다. 예를 들어 f 라는 함수가 두 개의 독립 변수 p 와 q 를 갖는다고 하면 다음과 같이 표현하면 된다. (함수 fp 에 q 를 적용한 결과임.)

(fp)q

또, 세 개의 변수가 필요하면,

((fp)q)r

이와 같이 계속하면 된다.

이제 강력한 연산자인 추상화에 대해서 살펴보자. 이를 위해서 그리스 문자 λ (람다) 를 쓰고 그 바로 다음에 처치의 함수를 표시하는 변수 기호, 예를 들어 x 를 써 주는데 이 변수는 다만 '명목 변수 (dummy variable)' 역할을 한다. 그 바로 다음에 대괄호로 둘러싸인 식이 나오는데 그 식 안에 등장하는 모든 x 들은 식 바로 다음에 오는 것이 들어갈 수 있는 '빈 자리' 의 역할을 한다. 그러므로,

λx.[fx]

가 의미하는 것은 함수로서 만일 a 라는 값을 적용하면 fa 를 만들어 주는 함수이다. 즉,

(λx.[fx])a = fa

다시 말하면 λx.[fx] 는 단지 함수 f 를 의미할 따름이다. 즉,

λx.[fx] = f

이것에 대해서는 약간 더 깊은 고찰이 필요하다. 처음에는 그냥 현학적이고 당연스러워 보이는 수식 장난 같아서 그 요점을 놓치기 쉽다. 우리가 잘 아는 중ㆍ고등학교 수학 문제를 예로 들어 보자. 함수 f 가 어떤 각도의 사인값을 취하는 삼각함수 연산이라고 가정하여 보자. 추상화된 함수 'sin' 은 다음과 같이 정의된다.

λx.[sin x] = sin

(각도 x 가 어떻게 '함수' 가 될 수 있는가에 대해서는 전혀 염려할 필요가 없다. 잠시 후 수라는 개념도 함수가 될 수 있음을 보일 것인데 각도도 수로 간주할 수 있기 때문이다.) 지금까지는 참으로 '당연' 하다고 볼 수 있다. 그런데 만일 'sin' 이라는 개념이 아직 발명되지 않았고 단지 다음과 같이 sin x 의 전개식 (power series) 만을 알고 있다고 가정하자.

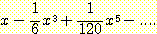
그렇다면 다음과 같이 sin 함수를 정의할 수 있다.

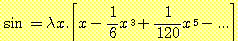
좀더 간단한 예를 들면 '세제곱의 6 분의 1' 이라는 함수는 이를 지칭하는 표준화된 함수 이름이 없다 할지라도 다음과 같이 정의할 수 있다.

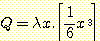
그리고 이 함수에 (a + 1) 이라는 값이 주어지면 다음과 같이 전개된다.

지금 다루는 내용과 좀더 관련 있는 예를 들어 보자면 처치의 기본 함수 연산만으로 구성된 다음과 같은 수식을 생각해 볼 수 있다.

λf.[f(fx)]

이 함수는 다른 함수를 받아서 이를 x 값에 두 번 반복하게 하는 역할을 한다. 예를 들면,

(λf.[f(fx)])g = g(gx)

여기에서 x 를 먼저 '추상화' 시켜 버리면,

λf.[λx[f(fx)]]

이를 다음과 같이 간략하게 표시하기도 한다.

λfx.[f(fx)]

이 연산은 g 라는 입력값을 주면 'g 를 두 번 반복한다.' 라는 함수를 생성한다. 실제로 이 함수는 처치가 자연수 '2' 를 표시하기 위하여 사용한 함수이다.

2 = λfx.[f(fx)]

그러므로 (2g)y = g(gy) 가 성립한다. 마찬가지로,

3 = λfx.[f(f(fx))],    4 = λfx.[f(f(f(fx)))], 등

처럼 되고, 0 과 1 도 다음과 같이 정의된다.

1 = λfx.[fx],    0 = λfx.[x]

실제로 처치의 2 와 3 등은 '두 번' 또는 '세 번' 의 의미에 가깝다고 볼 수 있다. 그러므로 3 이라는 연산을 함수 f 에 적용시킨 3f 는 'f 를 세 번 반복하라.' 는 의미이다. 만일 3f 에 y 를 대입하면, (3f)y = f(f(f(y))) 가 된다.

처치의 방법에서 아주 단순한 연산, 예를 들면 어떤 수에 1 을 더하는 계산이 표현될 수 있나를 살펴보기로 하자. 함수 S 는 다음과 같이 정의된다.

S = λabc.[b((ab)c)]

함수 S 가 실제로 처치의 방법으로 표현된 수에 1 을 더하는가를 확인하기 위하여 3 이라는 수를 적용시켜 보도록 하자:

S3 = λabc.[b((ab)c)]3 = λbc.[b((3b)c)]

= λbc.[b(b(b(bc)))] = 4              

위에서 (3b)c = b(b(bc)) 임을 이용하였다. S 를 어떤 자연수에 적용시키더라도 마찬가지로 성립함을 알 수 있을 것이다. (실제로 S 를 λabc[(ab)(bc)] 로 정의하였더라도 같은 결과를 얻었을 것이다.)

어떤 수를 2곱 하려면 어떻게 할까?  2곱 함수는 다음과 같이 정의할 수 있다 :

D = λabc.[(ab)((ab)c)],

여기에도 3 을 대입하여 확인하여 보자.

D = λabc.[(ab)((ab)c)] 3 = λbc.[(3b)((3b)c)]               

= λbc.[(3b)(b(b(bc)))] = λbc.[b(b(b(b(b(bc)))))] = 6

실제로 덧셈 (A), 곱셈 (M), 제곱 (P) 등의 기본 연산은 다음과 같이 정의될 수 있다 :

A = λfgxy.[((fx)(gx))y]

M = λfgx.[f(gx)]

P = λfg.[fg]

독자들은 위의 연산을 실제로 확인해 보든지 아니면 그대로 믿어 주기 바란다. 즉, m, n 이 처치의 함수로 표현된 두 자연수일 때 다음 식이 성립한다 :

(Am)n = m + n,    (Mm)n = m × n,    (Pm)n=n^m

마지막 줄의 제곱 함수는 놀라울 정도로 간단하다. m = 2 이고 n = 3 인 경우를 예로 들어 확인해 보도록 하자 :

뺄셈이나 나눗셈은 이들처럼 간단하지는 않다 (실제로 'm-n' 에서 m 이 n 보다 작은 경우나 'm ÷ n' 에서 m 이 n 으로 안 나누어지는 경우에는 예외 조항을 만들어야 한다). 사실 1930 년대 초에 미국의 수학자 클린 (S. C. Kleene) 이 처치의 계산법 내에서 뺄셈을 수행하는 방법을 발견함으로써 이 분야에 큰 이정표를 수립하였다 할 수 있다. 다른 연산들도 곧 이어서 발견되었다. 결국 1937 년에 처치와 튜링이 각자 독자적인 연구에 의해서 모든 계산 가능한 (알고리즘적인) 연산들, 즉 튜링 기게로 수행될 수 있는 연산들은 처치의 계산법에 의해서도 수행될 수 있고 그 역도 성립한다는 것이 밝혀졌다.

이는 실로 놀라운 사실로서 이 결과로 인하여 계산 가능성이라는 개념이 근본적으로 객관적이고 수학적인 특성을 갖는다는 것이 설득력을 얻게 되었다. 처치의 방법에서 계산 가능성이라는 개념은 외형상 계산기와는 전혀 연관성이 없는 것처럼 보일지도 모른다. 그럼에도 불구하고 그것은 실생활의 계산과도 깊은 관계를 가지고 있다. 특히 강력하면서도 유연함을 자랑하는 컴퓨터 언어인 리스프 (LISP) 는 본질적으로 처치의 람다 계산법의 기본 구조를 사용하고 있다.

앞서 잠시 언급한 바와 같이 계산 가능성을 정의하는 데 다른 방법들도 있다. 포스트가 제안한 계산기의 개념도 튜링 기계와 흡사한데 튜링과 비슷한 시기에 튜링과는 무관하게 독자적으로 개발된 것이다. 또, 그 편의성 때문에 지금도 많이 사용되고 있지만 허브랑 (J. Herbrand) 과 괴델에 의한 계산 가능성 (재귀성) 의 정의도 있다. 그보다 약간 먼저 커리 (H. B. Curry) 는 1929 년에, 또 쇤핀켈 (M. Schönfinkel) 은 1924 년에 각각 다른 방법을 제안하였는데 처치의 계산법은 이들 방법으로부터 일부 영향을 받았다고 할 수 있다. 계산 가능성에 대한 현대적 방법들 (예를 들면, 1980 년에 커틀랜드 [N. G. Cutland]에 의해서 제안된 무한 레지스터 기계) 는 훨씬 실용적이라는 점에서 튜링의 원래 기계와는 현저하게 다르다. 그러나 어떤 방법을 취하건간에 개념적으로는 똑같은 계산 가능성을 다루고 있는 것이다.

수많은 다른 수학적 개념들, 특히 심오한 아름다움과 근본적인 내용을 지니고 있는 수학 개념들에서 볼 수 있는 것처럼 계산 가능성이라는 개념도 그 나름대로의 플라톤적 실체를 소유한 것같이 여겨진다. 수학적 개념에 대한 플라톤적 실체의 신비에 대해서는 다음 두 단원에서 다루고자 한다.