
고급 문제 풀이 시스템
인공지능 : Elaine Rich 저서, 유석인.전주식.한상영 편역, 상조사, 1986 (원서 : Artificial Intelligence, McGraw-Hill, 1983, Artificial Intelligence (2nd ed, 1991)), Page 249~284
(5) 계층적 계획 (Hierarchical Planning)
(2) 흑판 기법 (Blackboard Approach)
제 3 장에서 논의한 기본적인 문제 풀이 기법과 제 5, 6 및 7 장에서 소개한 여러 가지 지식 표기법을 함께 사용함으로써 어려운 문제를 풀 수 있다. 풀고자 하는 문제를 작은 부분으로 나누어, 이 부분들을 각각 개별적으로 풀고, 이렇게 개별적으로 얻은 풀이를 결합하여 원래 문제에 대한 일관성있는 풀이를 찾는 방법도 효과적인 방법이다. 이 장에서는 이미 논의된 기본 요소를 사용하여 대규모의 문제 풀이 시스템을 구성하는 방법을 다룬다.
제 2 장에서, 일어날 상황을 점으로 표시한 상태 공간을 탐색하는 과정으로 문제 풀이 과정을 설명하였다. 탐색 과정에 의해, 초기 상태에서 출발하여 목표 상태에 도착할 때까지, 이용할 수 있는 일련의 연산 작용이 수행된다. 제 3 장에서 주어진 문제의 답을 찾기 위해 탐색 공간을 움직여 가는 방법을 설명하였다. 예를 들어, A* 알고리즘은 문제 공간을 표시한 그래프를 따라 수행되는 최적 우선 탐색을 보여 준다. A* 알고리즘에서 조사되는 각 노드는 완전한 문제 상태를 기술하며, 각 작용자는 문제 상태를 변화시키는 방법을 설명한다. 8-퍼즐과 같이 간단한 문제의 경우, 상태를 완전히 기술하는 노드는 합리적으로 쉽게 처리된다.
그러나 좀 더 복잡한 문제의 경우, 문제를 여러 작은 부분으로 분해하여, 각 부분을 개별적으로 처리하고, 각 부분의 해답을 하나의 완전한 풀이로 결합하는 방법이 더욱 중요해진다. 만약, 이렇게 할 수 없다면, 문제를 이루는 구성 요소들이 결합할 수 있는 상태의 수가 매우 커져, 주어진 시간내에 문제를 처리할 수 없게 된다. 이러한 분해를 수행하기 위해 사용될 두 가지 방법이 앞으로 논의된다.
첫번째 방법에서는 한 문제 상태에서 다른 문제 상태로 움직일 때, 전 상태를 다시 새로이 계산하는 것이 아니라, 변한 부분만 고려한다. 예를 들어, 어린이가 현재 있는 방에서 다른 방으로 갈 때, 두 방의 문과 창문의 위치는 변하지 않는다. 변한 물체와 변하지 않은 물체를 결정하는 방법의 문제인 골조 구조 문제의 중요성은 문제 상태가 복잡해질수록 더욱 더 커진다. 움직임이 수행되었을 때마다 8-퍼즐의 상태가 어떻게 변하는지를 이해하는 것은 어려운 일이 아니며, 또한 그다지 많은 일을 하지 않고도 만들어진 변화를 반영하고 있는 상태를 새로이 기록할 수 있다. 한 상태에서 다른 상태로의 전이를 나타내는 규칙을 사용하여, 장기판의 전체적인 위치를 변화시키는 방법을 기술할 수 있다. 그러나 집 주위를 돌아다니는 로보트의 움직임을 제어하는 문제의 경우, 상황은 훨씬 더 복잡해진다. 로보트의 위치 뿐만 아니라, 집 안에 있는 각 물체의 위치도 기술해야 하기 때문에 하나의 상태를 완전히 기술하기 위해서는 엄청나게 많은 사항을 표기해야 한다. 그러나 로보트가 방으로 탁자를 옮긴다면, 탁자와 그 위에 있는 물체의 위치만 변할 뿐, 집 내의 다른 물체들의 위치는 그대로이다. 하나의 전체 상태에서 다른 전체 상태로의 전이를 나타내는 규칙을 작성하는 대신, 상태의 변화된 부분만을 나타내는 규칙을 작성하는 것이 효과적이다. 이 때 나머지 부분에는 변화가 없다고 가정한다.
문제의 분해 방법을 사용하여 어려운 문제를 쉽게 풀 수 있는 두번째 방법은, 하나의 어려운 문제를 여러 개의 쉬운 문제들로 분해하는 것이다. A* 알고리즘을 사용하여 원래 문제를 완전히 독립적인 작은 문제들로 분해할 수 있다. 대부분의 문제들은 분해가 거의 가능한 (nearly decomposable) 문제로 볼 수 있는데, 이것은 문제를 서로의 상호 작용이 아주 적은 부분들로 나눌 수 있음을 의미한다. 예를 들면, 방에 있는 모든 가구를 방에서 들어내는 문제를 살펴 보자. 이 문제를 작은 문제들의 집합으로 분해할 수 있는데, 작은 각 문제들은 방에 있는 가구 하나를 들어내는 일을 포함하고 있다. 각 작은 문제에서, 서랍을 옮기는 작업을 가구 하나에 대해 개별적으로 고려할 수 있다. 그러나 책장이 침대 뒤에 있다면, 책장을 옮기기 전에 침대를 먼저 옮겨야 한다. 이렇게 분해가 거의 가능한 문제를 풀기 위해, 지금까지 논의한 기법을 사용하여 문제를 구성하는 작은 문제들을 각각 개별적으로 풀고, 작은 문제들 간의 잠재적인 상호 작용을 기록하고, 이들을 적절히 처리하는 방법을 사용한다.
앞으로 논의될 기법은 광범위한 많은 문제들에 사용될 수 있다. 여러 가지 기법들의 비교를 쉽게 하기 위해, 각 기법의 필요성이 명백하면서도 간단하고 또한 이해하기 쉬운 문제의 예를 찾아 살펴 보는 것도 효과적이다. 블럭 세계는 이러한 조건을 만족하는 종류의 문제이다. 각 기법이 논의됨에 다라, 블럭 세계에 대한 기술을 조금씩 수정할 필요가 있다. 그러나 일단 다음과 같이 블럭 세계를 정의하자. 블럭이 놓여 있는 평평한 면이 있다. 동일한 크기의 정사각형 블럭이 여러 개 있다. 이 블럭들을 함께 쌓을 수 있다. 블럭을 다룰 수 있는 로보트 팔이 있다. 수행될 행동에는 다음과 같은 것이 포함된다 :
UNSTACK (a, b) : 현재, 블럭 b 위에 있는 블럭 a 를 집는다. 로보트 팔은 아무 것도 가지고 있지 않아야 하고, 블럭 a 위에는 어떤 것도 놓여 있어서는 안된다.
STACK (a, b) : 블럭 b 위에 블럭 a 를 얹는다. 로보트 팔은 이미 블럭 a 를 가지고 있어야 하고, 블럭 b 의 표면에는 아무 것도 없어야 한다.
PICKUP (a) : 탁자 위에 놓여 있는 블럭 a 를 집어, 가지고 있는다. 블럭 a 를 집기에 앞서, 로보트 팔은 비어 있어야 하며, 블럭 a 의 표면에는 아무 것도 없어야 한다.
PUTDOWN (a) : 블럭 a 를 탁자 위에 놓는다. 로보트 팔은 반드시 블럭 a 를 가지고 있어야 한다.
이 문제에서 로보트 팔은 한 번에 하나의 블럭을 가질 수 있다. 또한 모든 블럭의 크기가 동일하기 때문에, 각 블럭의 표면에 접하여 얹을 수 있는 블럭의 수는 기껏해야 한 개이다.
연산 작용에 수행될 조건과 수행된 결과를 모두 규정하기 위해서, 다음과 같이 술어를 포함한 명제를 사용한다 :
ON (a, b) : 블럭 a 는 블럭 b 위에 있다.
ONTABLE (a) : 블럭 a 는 탁자 위에 있다.
CLEAR (a) : 블럭 a 위에 아무 것도 없다.
ARMEMPTY : 로보트 팔이 비어 있다.
블럭 문제에서는 논리적으로 참인 언명이 많다. 예를 들면,
[∃x HOLDING(x)] → ~ARMEMPTY
∀x ONTABLE(x) → ~∃y ON(x, y)
∀x [~∃y ON(y, x)] → CLEAR(x)
첫번째 언명은 만약 로보트 팔이 아무 것도 가지고 있지 않으면, 이것이 비어 있음을 의미한다. 두번째 언명은 만약 블럭이 탁자 위에 있으면, 이것은 다른 블럭의 위에 놓여 있지 않음을 의미하고, 세번째 언명은 자신의 위에 어떤 블럭도 놓여 있지 않는 블럭은 블럭 위에 아무 것도 없다는 것을 의미한다.
제 3 장에서 논의된 기본적인 기법을 바탕으로 하여 문제를 풀 때, 다음과 같은 기능을 수행할 수 있는 방법이 필요하다 :
앞으로 다루고자 하는 복잡한 시스템에서는 위 작업을 처리하는 방법뿐만 아니라, 다음 다섯번째 작업을 처리하는 방법도 또한 필요하다 :
특정한 계획 기법을 논의하기에 앞서, 위 다섯 가지 작업을 처리하는 기법에 대해 간단히 살펴 보자.
<적용할 규칙의 선택>
적용할 적절한 규칙을 선택하기 위해 가장 광범위하게 사용되는 기법은 먼저 원하는 목표 상태와 현재 상태간의 차이를 따로 뽑아내어, 이 차이를 줄일 수 있는 적절한 규칙을 찾아내는 기법이다. 만약 적절한 규칙이 여러 개 존재한다면, 다른 많은 경험적 방법을 사용하여 이들 중 하나를 선택한다. 이 기법은 GPS 에서 사용된 방법-목적 분석 방법을 기초로 한 것이다. 예를 들어, 만약 목표가 마당 주위에 하얀 울타리를 치는 것이고, 현재 마당은 갈색 울타리로 둘러싸여 있다면, 물체의 색깔을 변화시키는 작용자를 택해야 한다. 반면, 현재 울타리가 없으면 먼저 목재를 찾는 작용자를 택해야 한다.
<규칙의 적용>
앞에서 논의된 간단한 시스템에서는 규칙을 적용하는 것이 쉽다. 각 규칙은 이것을 적용함으로써 얻어지는 문제의 상태를 규정한다. 그러나 이제, 전체 문장 상태 중 이것의 작은 부분만을 규정하는 규칙을 처리할 수 있어야 한다. 실제로 이를 처리하기 위해 다양한 여러 가지 방법이 사용된다.

그림 1 간단한 블럭 문제의 기술
처리 방법의 한 가지는, 각 행동에 대해, 이를 적용함으로써 상태의 기술에 발생하는 변화를 기술하는 것이다. 이 경우, 그밖의 모든 것은 변화되지 않고 그대로 남아 있음을 알리는 언명이 필요하다. 이 방법을 사용한 시스템에서는 주어진 상태를, 이 상태에서 참인 사실들을 나타내는 술어를 포함한 명제들의 집합으로 기술한다. 서로 다른 각 상태는 술어를 포함한 명제의 부분으로 명확하게 표기된다. 예를 들어, 그림 1 은 S0 라 불리는 간단한 블럭 문제에서의 한 상태를 표기한 것이다.
이러한 상태 기술법은 비교 흡수 방법에 의한 정리 증명 과정을 사용하여 처리된다. 예를 들면, 다음과 같은 공리로 작용자 UNSTACK (x, y) 의 영향을 표기할 수 있다 (이 절에서 소개되는 공리에 사용된 변수들은 특별한 표시가 없는 한, 전체 한정 기호에 의해 한정되었다).
[CLEAR (x, s) ∧ ON (x, y, s)]
→ [HOLDING (x, DO (UNSTACK (x, y), s))
∧ CLEAR (y, DO (UNSTACK (x, y), s))]
여기서, DO 는 주어진 상태와 움직임에 대해, 이 움직임의 수행으로 인해 얻어지는 새로운 상태를 규정하는 함수이다. 위 공리는, 만약 CLEAR (x) 와 ON (x, y) 가 모두 상태 S 에 있다면, HOLDING (x) 와 CLEAR (y) 는 상태 S 에서 출발하여, UNSTACK (x, y) 에 대해 함수 DO 를 수행함으로써 얻어지는 상태에 있음을 표기한 것이다.
만약, 위에서 정의된 것처럼, 상태 S0 에서 UNSTACK (A, B) 를 수행한다면, S0 에 대한 주장 및 UNSTACK 에 대한 공리를 토대로 하여, UNSTACK 의 작용으로부터 얻어지는 상태 (S1 이라 하자) 에서
HOLDING (A, S1) ∧ CLEAR (B, S1)
이 됨을 증명할 수 있다.
그러나, 상태 S1 하에서의 상황에 대해 이외에 알고 있는 것은 무엇인가? B 가 여전히 탁자 위에 있음은 직관적으로 알 수 있지만, 지금까지 허용된 것들로부터는 이 사실을 추측할 수 없다. 이를 위해 골조 공리 (frame axiom) 라 불리는 규칙의 집합을 사용하는데, 골조 공리는 각 작용자에 대해 영향을 받지 않는 상태의 구성원을 기술한다. 예를 들면,
ONTABLE (z, s) → ONTABLE (z, DO (UNSTACK (x, y), s))
이 필요하다. 이 공리는 ONTABLE 관계가 작용자 UNSTACK 에 의해 전혀 영향을 받지 않음을 나타낸다. 또한, 만약 ON 관계에 관련된 블럭이 작용자 UNSTACK 에 관련된 블럭과 동일한 블럭이라면, ON 관계가 작용자 UNSTACK 에 의해 영향을 받는다는 것을 알릴 필요가 있다. 이는 다음과 같이 나타낸다.
[ON (m, n, s) ∧ NE (m, x)]
→ ON (m, n, DO (UNSTACK (x, y), s))
이 방법의 장점은 비교 흡수 방법이라는 한 가지 기법을 사용하여 상태를 기술하기 위해 필요한 모든 연산 작용을 수행할 수 있다는 점이다. 그러나 만약 문제 상태에 대한 기술법이 복잡하다면, 필요한 공리의 수가 엄청나게 커지는 단점이 또한 내재한다. 예를 들어, 블럭의 위치뿐만 아니라 블럭의 색깔에도 관심이 있다고 가정하면, 모든 연산 작용 (PAINT 는 제외) 에 대해, 다음과 같은 공리가 필요하다.
COLOR (x, c, s) → COLOR (x, c, DO (UNSTACK (y, z), s))
복잡한 문제를 처리하기 위해, 골조 공리를 가능한 한 적게 사용하는 기법이 필요하다. 이를 만족하는 한 가지 기법은 초기의 로보트 문제 풀이 시스템인 STRIPS 와 이것의 후속 시스템에 사용된 기법이다. 이 방법에서, 각 작용은 작용자에 의해 참으로 되는 새로운 술어를 포함한 명제의 리스트와, 작용자에 의해 거짓으로 되는 이전의 술어를 포함한 명제의 리스트로 기술된다. 이 두 개의 리스트를 각각 ADD 및 DELETE 라 부른다. 각 작용자를 위해 또 하나의 리스트가 규정되는데, 이것은 PRECONDITION 이란 리스트로서 작용자를 적용하기 위해 참이어야만 하는 술어를 포함한 명제들을 구성되어 있다. 그린 시스템 (Green's system) 에 사용된 골조 공리가 STRIPS 에 암시적으로 규정되어 있다. 작용자의 ADD 나 DELETE 리스트에 포함되어있지 않는 술어를 포함한 명제는 이 작용자에 의해 전혀 영향을 받지 않는다고 가정한다. 이는, 각 작용자를 규정할 때, 이 작용자와 관계되지 않는 것은 고려할 필요가 없음을 의미한다. 이는, 각 작용자를 규정할 때, 이 작용자와 관계되지 않는 것은 고려할 필요가 없음을 의미한다. 따라서, UNSTACK 과 COLOR 의 관계를 언급할 필요가 없다. 물론, 이것은 작용이 수행된 후에 완전한 전체적인 상태의 기술을 계산하기 위해, 간단한 정리 증명 기법과는 다른 어떤 기법이 사용되어야 함을 의미한다.
STACK (x, y) UNSTACK (x, y) PICKUP (x) PUTDOWN (x) |
그림 2
지금까지 논의한 블럭 세계의 작용에 대응하는 STRIPS 방식의 작용자가 그림 2 에 소개되었다. 이와 같이 간단한 규칙의 경우에는, PRECONDITION 리스트와 DELETE 리스트가 동일함을 알 수 있다. 블럭을 선택하기 위해 로보트 팔은 비어 있어야만 한다. 일단 로보트 팔이 블럭을 잡으면, 로보트 팔은 더 이상 비어 있는 것이 아니다. 그러나 이것이 항상 참인 것은 아니다. 로보트 팔이 블럭을 잡기 위해서는, 블럭 위에 다른 어떤 블럭도 놓여 있어서는 안된다. 블럭을 집은 후에도, 이 블럭의 위에는 아무 것도 없다. 이것이 PRECONDITION 과 DELETE 리스트를 각각 규정해야 하는 이유이다.
골조 공리를 암시적으로 만듦으로써 각 작용자에게 부가되는 정보의 양을 크게 감소시킬 수 있다. 이것은 물체가 가질 수 있는 새로운 특성이 시스템에 소개되었을 때, 이미 존재하고 있는 각 작용자에 이 새로운 공리를 첨가하기 위해 되돌아갈 필요가 없다는 것을 의미한다. 그러나 완벽한 전체적인 상태의 기술을 계산할 때 골조 공리를 사용함으로써 얻어지는 효과를 실제로 어떻게 얻을 수 있을까? 복잡한 상태의 기술인 경우, 상태의 대부분은 각 작용후에는 변하지 않고 그대로 남아 있음을 명심하라. 그러나 그린 시스템에서처럼 만약 상태를 술어를 포함한 명제의 일부로 명백히 표기한다면, 각 상태를 위한 모든 정보는 감소시켜야 한다. 이를 피하기 위해서, 명시적인 상태의 표기 기호를 개개 술어를 포함한 명제에서 삭제하고 대신 술어를 포함한 명제의 데이터 베이스를 수정하여, 이 데이터 베이스가 항상 현재의 상태를 기술하도록 한다. 예를 들어 그림 1 에 나타난 상황에서 출발한다면, 이것을 다음과 같이 표기할 수 있다.
ON (A, B) ∧ ONTABLE (B) ∧ CLEAR (A)
작용자 UNSTACK (A, B) 를 수행한 후의 상태의 기술은 다음과 같다.
ONTABLE (B) ∧ CLEAR (A) ∧ CLEAR (B) ∧ HOLDING (A)
이것은 작용자 UNSTACK 의 일부로 규정된 ADD 와 DELETE 리스트를 사용하여 얻어진 것이다.
간단히 하나의 상태 기술을 수정하는 방법은 주어진 일련의 작용자들로부터 얻어지는 효과를 기억하는 방법으로 적합하다. 그러나 적절한 일련의 작용자들을 탐색하는 과정동안 어떤 일이 발생할 수 있는가? 만약 부적절한 일련의 작용자들의 탐색된다면 다른 일련의 작용자들을 조사할 수 있도록 원래 상태로 회복할 수 있어야 한다. 이것은 탐색 그래프의 각 노드에 문제 상태를 기술한 전역적인 데이터 베이스에서 가능하다. 이 경우, 노드를 통과할 때마다 전역적인 데이터 베이스에 만들어진 변화를 각 노드에 기록하는 것만이 필요한 일이다. 만약 이 노드를 통해 후진한다면, 변화가 발생하지 않았던 것처럼 할 수 있다. 그러나 변화는, 현 노드에서 다른 노드로 이동하기 위해 적용되었던 작용자들의 ADD 와 DELETE 리스트에 정확히 명시적으로 기술된다. 따라서 탐색 그래프의 각 링크를 따라가면서 적용된 작용자들을 기록해야 한다. 그림 3 은 이러한 탐색 그래프와 각 링크를 따라가면서 적용된 작용자들을 기록해야 한다. 그림 3 은 이러한 탐색 그래프와 이에 대응하는 전역적인 데이터 베이스의 한 예를 나타낸다. 초기 상태는 그림 1 에 나타난 것이고, STRIPS 형태로 표기되어 있다. 후에 변화가 발생하지 않은 것처럼 하기 위해, 작용자뿐만 아니라, 이 작용자의 매개 변수도 규정해야 한다.
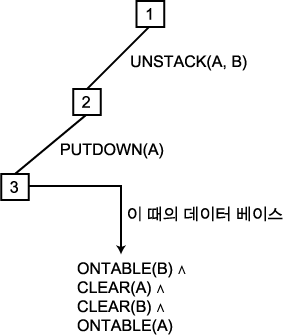
그림 3
이제, 앞에서 소개된 경로와는 다른 경로를 탐색한다고 가정하자. 먼저 작용자 PUTDOWN 의 DELETE 리스트에 포함되어 있는 각 술어를 포함한 명제를 전역적인 데이터 베이스에 첨가하고, PUTDOWN 의 ADD 리스트에 있는 각 명제들을 데이터 베이스에서 삭제함으로써, 먼저 노드 3 을 통해 후진한다. 이렇게 한 후의 데이터 베이스에는
ONTABLE (B) ∧ CLEAR (A) ∧ CLEAR (B) ∧ HOLDING (A)
가 포함되어 있다. 예상햇던 것처럼 이 기술은 이전에, 초기 상태에 UNSTACK 을 적용한 결과로 계산되었던 상태의 기술과 동일한 것이다. 만약 UNSTACK 의 ADD 와 DELETE 리스트를 사용하면서, 이 후진 과정을 반복 수행한다면, 출발 상태의 기술과 동일한 기술을 얻게 된다.
골조 공리의 암시적인 언명은 복잡한 문제에서 매우 중요한 역할을 하기 때문에, 앞으로 살펴 볼 모든 기법들은 이용 가능한 작용자에 대해 STRIPS 방식의 기술을 이용한다.
<풀이의 탐지>
계획 시스템을 사용하여 초기의 문제 상태를 목표 상태로 전이하는 일련의 작용자들을 찾았다면, 문제의 풀이를 찾는데 성공한 것이다. 이 때를 어떻게 알 수 있는 지 알아보자. 간단한 문제 풀이 시스템에서는 상태의 기술을 직접 비교하여 일치하는지를 살펴봄으로써 쉽게 이 질문에 답할 수 있다. 그러나 만약 전체 상태가 명확하게 기술되지 않고 관련된 성질들의 집합으로만 기술되었다면, 이 문제는 상당히 복잡해진다. 이 문제에 대한 해답을 찾는 방법은 상태의 표기법에 의해 좌우된다. 어떤 표기 방법이 사용된다 할 지라도, 하나의 표기된 상태가 다른 표기된 상태와 일치하는지 결정하기 위해 추론할 수 있어야 한다. 앞의 세 개의 장에서 복잡한 문제를 표기하기 위한 여러 가지 방법들을 논의하였으며, 이들 각 방법에 대해, 추론 기법을 또한 설명하였다. 이 모든 표기법들은 문제의 상태를 표기하는데 사용될 수 있었고, 대응하는 추론 기법들이 풀이가 발견된 때를 탐지하기 위해서도 사용되었다.
서술 논리 표기법은 이미 존재하는 많은 계획 시스템에 사용되어 왔다. 목표의 일부로 술어를 포함한 명제 P(x) 가 주어졌다고 가정하자. P(x) 가 초기 상태에서 만족하는 지를 조사하기 위해서는, 초기 상태를 기술한 주장과, 이 분야의 모델을 정의하는 공리가 주어졌을 때 P(x) 를 증명할 수 있는 지를 알아야 한다. 만약 이러한 증명을 얻을 수 있다면, 문제 풀이 과정을 마친다. 만약 그렇지 않다면, 문제를 풀 수 있는 일련의 작용자들을 찾아야 한다. 이 작용자들을 적용함으로써, 어덩진 공리와 상태의 기술을 사용하여 P(x) 를 증명할 수 있는지 질문함으로써, 이 일련의 작용자들을 조사할 수 있다.
<풀이가 아닌 경로의 탐지>
계획 시스템은 주어진 문제를 풀기 위한 일련의 작용자를 찾는 작업을 하기 때문에 풀이로 이끌지 못하는 경로를 조사하고 있는 경우를 알아야 한다. 풀이를 탐지하는데 사용되는 것과 같은 추론 기법이 이를 위해 사용될 수 있다.
만약 탐색 과정이 초기 상태로 부터의 전진 추론이면, 목표 상태에 도달할 수 없는 상태를 유도하는 경로를 삭제해 버릴 수 있다. 예를 들면, 고정된 양의 페인트가 공급되고 있다고 가정하자. 이 페인트들은 흰 색, 분홍 색, 빨간 색으로 구성되어 있다. 방의 벽은 밝은 빨간 색으로, 천장은 흰 색으로 칠하고자 한다. 빨간 색 페인트에 흰 색 페인트를 첨가하여 밝은 빨간 색 페인트를 만들 수 있다. 그러나 이렇게 하면 천장을 흰 색으로 칠할 수가 없다. 따라서 이 방법 대신 분홍 색 페인트와 빨간 색 페인트를 함께 혼합 사용하는 방법을 택한다. 또한 출발 상태보다 풀이에 더 가깝게 접근할 수 없을 것 같은 경로도 또한 제거할 수 있다.
만약 탐색 과정이 목표 상태로 부터의 후진 추론이라면 초기 상태에 도달할 수 없거나 진전이 만들어지지 않음이 확실해질 때 경로를 끝맺을 수 있다. 후진 추론에서 각 목표는 작은 목표들로 분해된다. 이들 분해된 각각의 작은 목표들은 다시 더 작은 목표들로 분해될 수 있다. 때때로 주어진 작은 목표들을 동시에 만족시킬 수 있는 방법이 존재하지 않음을 쉽게 탐지할 수 있다. 예를 들면 로보트 팔이 아무 것도 가지고 있지 않음과 동시에 어떤 블럭을 가지고 있는 것은 불가능하다. 이 두 목표를 동시에 참으로 만들고자 하는 경로는 즉시 탐색에서 삭제한다. 또한, 어떤 곳으로도 이끌지 못하는 경로도 탐색에서 삭제한다. 예를 들어, 목표 A 를 만족시키고자 할 때, 프로그램이 목표 A 뿐만 아니라, 목표 B 및 C 도 만족시키려 한다면, 어떤 진전도 불가능하다. 이렇게 되면, 원래 문제보다도 더 어려운 문제가 발생하게 되므로 이러한 경로는 탐색에서 제외시킨다.
<근사적인 풀이의 수정>
여기서 논의될 기법은 분해가 거의 가능한 문제를 푸는데 효과적으로 사용된다. 이러한 종류의 문제를 푸는 적합한 한 가지 방법은 이 문제들을 완전히 분해될 수 있는 것으로 가정하여, 부분적인 문제를 각각 개별적으로 풀고, 이로부터 얻어진 풀이를 하나로 결합시킨 것이 원래 문제의 풀이가 되는지 조사하는 방법이다. 물론 만약 그렇다면, 더 이상 다른 작업을 할 필요가 없다. 그러나 만약 그렇지 않다면, 여러 가지 방법을 사용하여 이를 처리할 수 있다. 가장 간단한 방법은 얻은 풀이를 버리고, 더 적절한 풀이를 찾는 것이다. 비록 이 방법은 간단하지만, 많은 노력이 소모된다.
이보다 효율적인 방법은 제안된 풀이에 대응하는 일련의 작용자들이 수행되었을 때 얻어지는 상황을 조사하여 원하는 목표 상태와 비교하는 것이다. 대부분의 경우, 이 두 상황간의 차이는 초기 상태와 목표 상태의 차이보다 작아진다. 다시 문제 풀이 시스템을 사용하여 이 새로운 차이를 제거하기 위한 방법을 찾는다. 첫번째 풀이와 두번째 풀이를 결합하여 원래 문제에 대한 풀이를 만든다.
거의 풀이에 가까운 것을 수정하는 더욱 효과적인 방법은 잘못된 것과 관련된 특별한 지식을 사용하여 직접 수정하는 것이다. 예를 들면, 제안된 풀이가 부적합한 이유가 작용자 중의 하나를 수행하려 했지만 이것의 선결 조건이 만족되어 있지 않아 이 작용자를 적용할 수 없었다고 가정하자. 이것은 만약 작용자가 두 개의 선결 조건을 가지고 있고, 두번째 선결 조건을 참으로 하는 일련의 작용이 첫번째 선결 조건을 발생하지 않은 것처럼 할 때 발생한다. 이러한 경우, 작용자의 수행 순서를 바꾸면, 이러한 문제가 해결되는 수도 있다.
불완전한 풀이를 수정하는 또 하나의 효과적인 방법은 풀이를 수정하지 않고, 대신 가능한 한 많은 정보를 이용할 수 있게 될 때까지 풀이를 불완전하게 규정한 채로 남겨 두는 것이다. 정보를 충분히 이용할 수 있게 되었을 때, 어떤 충돌도 발생시키지 않는 방법을 사용하여 풀이를 완전히 규정한다. 이 방법을 최소 실행 방법 (least commitment strategy) 으로 생각할 수 있다. 다양한 방법으로 이것을 적용할 수 있다. 한 가지 방법은 연산 작용의 수행 순서에 대한 결정을 뒤로 미루는 것이다. 앞의 예에서 선결 조건의 집합을 만족시키는 순서를 임의로 선택하는 대신 순서를 규정하지 않은 채로 두는 것이다. 부분적인 풀이 간에 존재하는 의존도를 결정하기 위해 부분적인 각 풀이의 효과를 조사한다. 이때 순서를 선택한다.
상호 작용을 하는 여러 목표들을 풀기 위해 개발된 초기 기법 중의 한 가지는 목표 스택을 사용하는 것으로, STRIPS 에서 이용되었다. 이 방법에서는 문제를 풀기 위해, 목표 및 이 목표를 만족시키기 위해 제안된 작용자를 모두 포함하고 있는 한 개의 스택이 사용된다. 문제 풀이 과정은 현재의 상황 및 PRECONDITION, ADD 그리고 DELETE 리스트로 나타내진 작용자들의 집합을 기술하고 있는 데이터 베이스에 의해 좌우된다.
|
|
|
|
start : ON (C, A) ∧ |
goal : ON (A, B) ∧ |
그림 4
이 문제를 풀기 위해 두 개의 부분 목표로 나누어 얻어진 계획은 다음과 같다.
|
1. UNSTACK (C, A) 2. PUTDOWN (C) 3. PICKUP (A) 4. STACK (A, B) 5. UNSTACK (A, B) |
6. PUTDOWN (A) 7. PICKUP (B) 8. STACK (B, C) 9. PICKUP (A) 10. STACK (A, B) |
이다.
비록 이 계획에 의해, 원하는 목표를 얻을 수 있지만, 매우 비효율적이다. 만약 반대순서로 두 개의 부분적인 목표를 조사한다면, 유사한 상황이 발생하게 될 것이다. 지금까지 사용하고 있는 기법으로는 이 문제를 효과적으로 풀 수 있는 계획을 찾을 수가 없다.
앞으로 소개할 두 가지 방법을 사용하여 적절한 계획을 찾을 수가 있다. 한 가지 방법은 이미 얻어진 계획을 수정하여, 더욱 효율적인 것으로 만드는 방법을 찾는 것이다. 계획에 따라 작용을 수행하다, 이것을 마치 수행하지 않은 것처럼 하는 장소를 찾을 수 있다. 이런 장소를 찾았다면, 계획에서 이 단계를 제거한다. 앞의 계획에 이 규칙을 작용하면, 단계 4 와 단계 5 를 없앨 수 있다. 그리고 단계 3 과 단계 6 이 다시 제거된다. 이로부터 얻어지는 결과는 다음과 같은데, 이것이 이 문제를 위한 최적 계획이다.
|
1. UNSTACK (C, A) 2. PUTDOWN (C) 3. PICKUP (B) |
4. STACK (B, C) 5. PICKUP (A) 6. STACK (A, B) |
그러나 이보다 복잡한 문제의 경우, 계획내에서 상호 작용하는 것들이 서로 멀리 떨어져 있기 때문에, 이를 알아 내기는 어렵다. 뿐만 아니라 나중에는 제거될 단계들을 만들기 위해서도 많은 노력이 소모된다. 만약 효과적인 계획을 직접 만들 수 있는 과정이 있다면, 이것이 더욱 적합할 것이다. 다음 절에서 그러한 알고리즘이 소개된다.
앞 절에서는 목표 스택에 의한 계획 방법을 사용하여 여러 구성 요소 목표들로 이루어진 원래 목표를 얻을 때까지, 구성 요소 목표들을 하나씩 해결하면서, 목표를 찾았다. 이 방법에 의해 얻어진 계획들은 모두 각각의 구성 목표를 달성하기 위해 사용되는 일련의 작용자들을 포함하고 있다. 이 계획에서는 구성 요소가 되는 한 목표를 얻고자 할 때, 다른 구성 요소 목표에 사용되는 일련의 작용자중 일부를 불러, 이 목표를 위한 작용자의 일부로 사용하는 것이 불가능하다. 그러나, 때때로 서로 뒤얽힌 계획을 필요로 하는 문제도 있다. 완전한 부분적인 계획을 선형적으로 연결하여 원래 문제에 대한 계획으로 사용하는 것이 아니기 때문에, 이러한 계획을 비선형 계획이라 부른다.
그림 4 에 소개된 문제를 사용하여, 비선형 계획이 필요한 예를 살펴 보자. 이 문제를 푸는 적절한 계획은 다음과 같다.
1. A 위에 아무 것도 없게 하고, 탁자 위에 블럭 C 를 놓음으로써, 목표 ON (A, B) 에 대한 작업을 시작하라.
2. 블럭 C 위에 블럭 B 를 놓아 목표 ON (B, C) 를 이루어라.
3. 블럭 B 위에 블럭 A 를 놓아 목표 ON (A, B) 를 완성하라.
이런 계획을 찾는 한 가지 방법은 원하는 목표의 묶음을, 제일 위에 있는 원소만을 들어 낼 수 있는 스택이 아니라, 어떤 원소라도 다음에 선택할 수 있는 집합으로 간주하는 것이다. 이것은 목표 상태에서 초기 상태로 후진 수행해 가는 탐색 과정으로써 어떤 적용자도 실제로 적용되는 것은 아니다. 이 과정의 개념은 먼저 최종적인 풀이에 마지막으로 적용될 작용자를 찾는 것이다. 하나의 구성 요소 목표만을 제외하고, 나머지 모든 구성 요소가 되는 목표들이 이미 만족되었다고 가정하고, 마지막 구성 요소 목표를 만족시킬 모든 작용자를 찾는다. 물론 이들 각각이, 적용에 앞서 만족되어 있어야 할 선결 조건을 가지고 있기 때문에, 원래 목표뿐만 아니라 성분으로 새로이 구성된 목표들도 이 선결 조건을 포함하고 있어야 한다. 주어진 목표를 만족시키는 방법 뿐만 아니라, 구성 요소 목표들의 가능한 순열을 모두 조사해야 하기 때문에, 이 과정을 사용하면, 상당히 복잡한 탐색 트리가 만들어 진다. 그러나 다행히 이 경로중의 대부분은 빨리 제거할 수 있다.
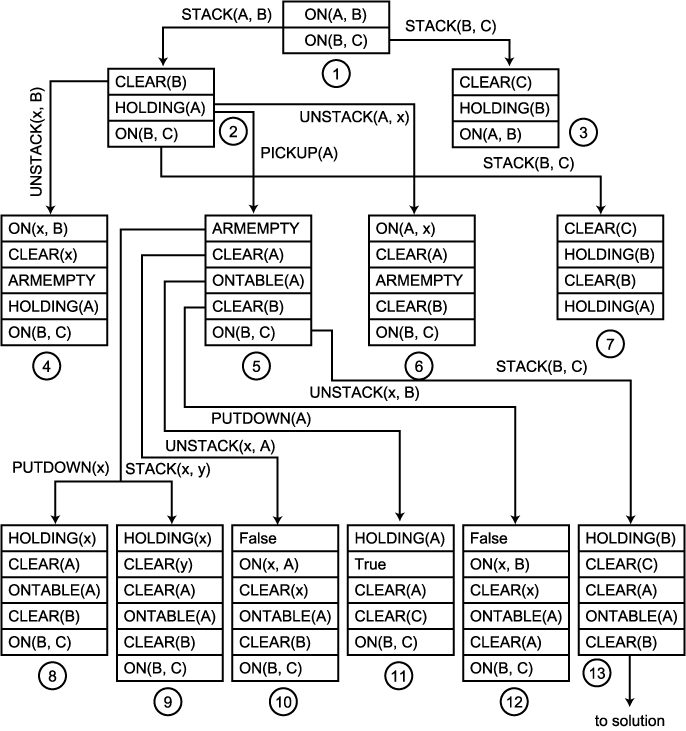
그림 5
그림 4 의 문제에 이 후진 추론 방법을 적용해 보자. 그림 5 에 이 후진 추론 과정으로부터 얻어지는 탐색 트리의 일부분이 소개되었다. 첫번째 레벨에서는, 수행될 마지막 작용자의 후보 두 가지를 살펴 보고 있다. 마지막으로 행해질 일은 블럭 B 위에 블럭 A 를 놓거나, 블럭 C 위에 블럭 B 를 올려 놓는 것이다. 만약 마지막으로 행해질 일이 블럭 C 위에 블럭 B 를 올려 놓는 것이라면, 수행에 앞서 술어를 포함한 명제 ON (A, B) 뿐만 아니라, 이 작용의 선결 조건 또한 모두 참이어야 함을 주목하라. 그러나 기술된 블럭 세계에서는 로보트 팔이 한 번에 하나의 블럭만을 가질 수 있기 때문에, 만약 블럭 A 가 블럭 B 위에 있다면, 로보트 팔이 블럭 B 를 집는 것은 불가능하다. 이러한 불일치는 블럭 세계를 정의하는 공리의 집합에 비교 흡수 방법을 적용함으로써 알아 낼 수 있다. 이 불일치 경로를 제거하면, STACK (A, B) 가 마지막 작용의 후보로 남아 있다.
이 경로를 따라 가면, 세 개의 목표가 발견되는데, 이 중의 하나는 STACK 을 수행하기에 앞서 만족시켜야 되는 것이다. CLEAR (B) 를 선택한다고 가정하자. 이 목표를 달성할 수 있는 유일한 방법은 UNSTACK 을 수행하여, 블럭 B 위에 있는 것을 들어 내는 것이다. 그러나 UNSTACK 을 성공적으로 수행시키기 위해 만족시켜야 할 목표의 집합은 로보트 팔이 블럭 A 를 가지고 있는 동시에 아무 것도 가지고 있지 않아야 하기 때문에 이것은 서로 모순이다. 따라서 이 경로에 대한 탐색을 중단한다. 만약 마지막으로 수행될 작용으로 HOLDING (A) 를 선택한다면, PICKUP (A) 와 UNSTACK (A, x) 를 적용할 수 있다.
PICKUP (A) 에 의해 어떤 모순도 포함되어 있지 않는 노드 5 를 얻어 이 경로를 따라간다. UNSTACK (A, x) 에 의해 노드 6 이 만들어 진다. 블럭 x 가 블럭 C 와 같다고 가정하자. 그러면, ON (A, C), 와 ON (B, C) 간에 모순이 있다. 반면, 블럭 x 와 블럭 B 와 같다면, 초기 목표 집합을 포함하고 있는 목표 집합을 얻을 수 있다. 따라서 어떤 진행도 일어나지 않기 때문에, 이 경로의 탐색을 중단한다. 블럭 x 에 대입할 어떤 다른 블럭도 없기 때문에 이 분기의 탐색을 중단한다. 만약 마지막으로 만족시켜야 할 목표로 ON (B, C) 가 선택된다면, 적용할 수 있는 유일한 작용자는 STACK (B, C) 이다. 이것은 노드 7 에 나타나 있다. 그러나 로보트 팔이 블럭 A 와 블럭 B 를 동시에 가질 수 없기 때문에 여기에도 모순이 있다. 따라서 이 분기에 대한 탐색을 중단한다. 노드 5 만이 탐색을 위해 남아 있다.
노드 5 의 후계 노드를 탐색하기에 앞서, 수행중 발생한 문제점에 대해 논의할 필요가 있다. 지금까지, 다음에 수행될 목표와, 이 목표를 만족시킬 작용자를 선택할 때 부모 노드로부터 선택되지 않은 많은 모든 목표를 복사하고 제안된 작용자의 선결 조건을 첨가함으로써, 만들어진 새로운 노드에 대한 목표의 기술을 계산하였다. 그러나 이것이 반드시 옳은 것은 아니다. 선택된 적용자를 선택하기에 앞서, 선택되지 않은 목표가 모두 참이라고 가정하였다. 그러나 만약 작용자에 의해 목표 중의 하나가 간섭을 받아 거짓이 된다면 어떤 일이 발생할까? 이를 조사하여 보자. 선택되지 않은 목표를 직접 새로운 목표 집합에 다시 기록하는 것이 아니라, 대신 회귀 (regression) 라 불리는 과정을 이 선택되지 않은 목표에 적용한다.
회귀 (regression) 는 후진하면서 작용자를 적용하는 방법이다. 작용자를 사용하여 목표로 되돌아갈 때, 원하는 목표를 얻기 위해, 적용될 작용자를 수행하기에 앞서 참으로 되어야만 할 것을 결정해야 한다. 대부분의 경우, 원하는 목표 자체만 참이면 된다. 왜냐하면 대부분의 작용자는 적용하려는 목표에만 영향을 미치기 때문이다. 다음과 같은 예를 살펴 보자.
REGRESSION (ON (A, B), PICKUP (C)) = ON (A, B)
작용자를 적용하여 얻고자 하는 목표의 경우, 작용자를 적용시키기 전에 특별히 참으로 되어야 할 다른 어떤 사항도 필요로 하지 않는다. 사실상, 작용자의 선결 조건은 참이어야 하지만, 다른 방법을 사용하여 이들을 처리할 수 있다. 따라서, 예를 들면
REGRESSION (ON (A, B), STACK (A, B)) = True
이다. 다른 목표들이 참으로 회귀되는 경우도 있는데, 이것은 어떤 한 목표를 얻기 위해 선택되었던 작용자로 인해 우연히 다른 어떤 목표를 얻게 될 때 발생한다. 예를 들면, STACK (B, D) 는 로보트 팔에 아무 것도 없게 하기 위해서 사용되었지만, 그러나 만약 목표 ON (B, D) 가 또한 목표 집합의 원소라면, 이것은 참으로 회귀될 것이다. 어떤 목표가 참으로 회귀되면 언제든지 목표 집합으로부터 이것을 제거할 수 있다. 작용자를 적용하기에 앞서, 참인 사항들과는 관계없이 이 목표가 참으로 되기 때문에, 이것을 문제 삼을 필요는 없다.
목표에 어떤 영향도 미치지 못하는 작용자도 있으며, 수행된 후 즉시 목표를 참으로 만들 수 있는 작용자도 없다. 예를 들어
REGERESSION (ARMEMPTY, PICKUP (A)) = False
를 살펴 보자. 목표 집합에 False 가 포함되어 있으며, 그 목표 집합은 결코 얻을 수 없기 때문에, 이것으로부터 시작되는 분기를 곧 제거한다.
때때로, 회귀과정은 노드 자체나 True 혹은 False 가 아닌, 시스템이 얻고자 하는 다른 어떤 목표를 생성할 수도 있다. 이러한 상황은 앞에서 다룬 블럭 세계에서는 발생하지 않지만, 다른 문제에서는 발생할 수 있다. 예를 들어
REGRESSION (HAVE ($100), BUY (RADIO))
= HAVE ($100 + PRICE (RADIO)))
를 살펴보자. 만약 라디오를 구입한 후에도 100 달러를 가지고 있기를 원한다면, 라디오를 사기 전에, 라이오의 가격뿐만 아니라, 100 달러를 더 가지고 있어야 한다.
앞에서 다루었던 문제로 다시 돌아와, 이 문제에 회귀가 어떻게 사용되는지, 그 사용 방법에 대해 알아 보자. 조사할 첫번째 부분 목표는 ARMEMPTY 이다. PUTDOWN (노드 8) 이나 STACK (노드 9) 을 사용하여, 이 목표를 얻을 수 있다. PUTDOWN 이나 STACK 에는 내려 놓을 블럭이나, 다른 상자 위에 올려 놓을 블럭을 나타내는 변수들이 포함되어 있다. 이 연산 작용을 수행하기 위해서는, 변수에 어떤 특정한 블럭을 대입해야 한다. PUTDOWN 과 STACK 을 수행하기에 앞서, 가져야 할 선결 조건은 로보트 팔이 블럭을 가지고 있어야 한다는 것이다. 그러나 목표 집합 내에 있는 다른 목표들은 로보트 팔이 가지고 있는 블럭이 아닌 다른 이용 가능한 세 개의 블럭 중의 하나를 요구한다. 블럭 A 는 탁자 위에 있어야 하고, 블럭 B 는 블럭 C 위에 있어야 한다. 그러므로 변수 x 에 블럭을 대입하고자 할 경우 모순이 발생한다. 따라서 이 두 경로를 모두 제거할 수 있다.
만족된 목표를 찾는 탐색의 중단 시기를 결정하기 위해, 이 과정에서 알아야 할 한가지 사항을 살펴 보자. ARMEMPTY 가 노드 5 와 관계된 목표 집합의 일부로서 나타났지만, 이것은 초기 상태의 기술에서 이미 만족된 것이다. 이미 만족된 목표를 다시 만족시킬 방법을 찾아야 하는 이유는 후진 하면서, 먼저 마지막 작용자를 찾기 때문에 탐색을 수행하기 위해 주어진 특정한 점에서 이미 적용된 작용자와 이것의 적용으로 인한 영향 - 작용자들의 적용으로 목표 집합 내의 한 목표를 제외한 모든 목표들이 만족되었음을 알 수 있다 - 은 알 수 없다. 이러한 이유 때문에, 어떤 목표도 그것이 True 로 회귀되지 않는다면, 목표의 집합으로부터 이것을 제거할 수 없다. 초기 상태에서 만족되었던 모든 원소들을 가지고 있는 목표 집합이 발견될 때까지 탐색 과정을 계속 수행해야 한다. 이러한 목표 집합을 찾으면, 지금까지 발견된 일련의 작용자들을 적용하기 전에는 어떤 작용자도 수행할 필요가 없음을 알 수 있다. 따라서 전체 초기 상태는 여전히 모두 참이라고 가정할 수 있다. 물론, 초기 상태에 관한 지식을 탐색 과정의 독학적 지식으로 사용할 수 있다. ARMEMPTY 가 많은 작용자에 의해 변경되기 때문에 초기 상태에서 이것이 참이었는 지의 여부는 후에 수행될 연산 작용에 거의 영향을 끼치지 못한다. 그러나 다른 조건들은 거의 변경되지 않는다. 만약 초기 상태에서 참이었던 목표 중의 하나가 목표 집합에 포함되어 있을 때, 효과적인 경험적 방법이라면, 이 목표에 즉시 작용하지 않고, 대신 집합 내의 다른 원소에 적용하여, 이미 만족된 목표를 다시 만족시키려고 하는 불필요한 일을 함이 없이 풀이를 찾을 수 있을 지 조사할 것이다. ONTABLE (A) 가 초기 상태에서 참이었기 때문에 노드 11 로 가는 경로는 조사할 필요가 없다.
선택될 수 있는 다음 목표는 CLEAR (A) 이다. 만약 이것이 선택된다면, 이용이 가능한 작용자는 UNSTACK (x, A) 뿐이다. 이와 관련된 목표 집합이 노드 10 에 나타나 있다. 여기서도 회귀의 중요성을 알 수 있다. 노드 5 에는 목표 ARMEMPTY 가 포함되어 있다. 그러나 UNSTACK 을 통해 ARMEMPTY 로 회귀할 때, ARMEMPTY 가 UNSTACK 의 DELETE 리스트에 포함되어 있기 때문에 False 가 얻어 진다. 목표 False 는 결코 만족될 수 없는 목표이기 때문에, 이 분기는 제거한다.
CLEAR (B) 를 만족시키기 위해 사용될 수 있는 유일한 작용자는 UNSTACK (x, B) 이다. 그러나 이것의 결과로 얻어진 목표 집합 - 노드 12 가 이 목표 집합을 나타낸다 - 에는 만족시킬 수 없는 목표 False 가 포함되어 있다. 따라서 이 경로도 역시 제거할 수 있다.
지금까지, 노드 5 의 가능한 후계 노드 여섯 개중 다섯 노드를 제거하였다. 결국 이로부터 모순이 없는 일관된 목표 집합을 얻을 수 있다. 이 예로 부터, 이 과정에 의해 얼마나 복잡한 탐색 트리가 만들어지는 지 알 수 있고, 또한 실제 탐색 과정을 효과적으로 수행하기 위해, 탐색 트리에 존재하는 불필요한 분기를 제거하는 방법을 알 수 있다.
만약, 이 방법에 의해 수행을 계속한다면, 원하는 풀이를 얻을 수 있다. 초기 상태에서 만족되었던 원소들을 모두 포함하고 있는 목표 집합이 만들어 진다. 이 알고리즘에서는 목표 리스트를 스택이 아닌 집합으로 간주하여, 목표들의 가능한 순서를 모두 살펴 보았다. 이러한 이유 때문에 이 알고리즘의 실행은 연습 문제로 남긴다.
그러나, 대형 문제, 특히 부분적인 목표들이 전혀 상호 작용을 하지 않는 문제에 이 방법을 적용하는 것은 부적합하다. 만약 부분적인 목표들이 상호 작용을 하지 않는다면 작용자의 수행 순서는 중요하지 않다. 즉, 가능한 어떤 순서로 작용해도 무관하다. 따라서 매우 큰 탐색 트리가 만들어지는데, 이를 처리할 수 있는 방법이 또한 필요하다.
중요한 목표와 중요하지 않는 목표를 구별할 수 있는 방법이 없기 때문에, 최적 경로를 찾는 계획의 세부적인 사항에 많은 시간이 소모된다. 이 문제를 풀기 위해서는, 먼저 목표의 중요한 부분을 만족시키기 위한 계획을 계략적으로 세운 후, 필요에 따라 목표의 세부 사항을 채워나가는 계획 과정이 필요하다.
어려운 문제가 주어 졌을 때 문제 풀이 과정은 이 문제를 풀기 위해 상당히 긴 계획을 작성해야 할 경우도 있다. 이를 효과적으로 하기 위해 중요한 결과를 이끄는 풀이가 발견될 때까지, 문제중 일부 세부 사항을 제거할 필요가 있다. 세부 사항은 이후에 다시 채워질 수 있다. 이를 위해, 작은 작용자로부터 큰 작용자를 만드는 매크로 명령 (macrocommand) 을 사용한다. 그러나 이 방법에서, 어떤 세부 사항도 작용자에 대한 실제 기술로부터 제거할 수 없다. ABSTRIPS 시스템에서는 이보다 좋은 방법이 사용되었는데, 실제로 낮은 레벨에서는 선결 조건이 무시되는 개념 공간 (abstraction space) 의 계층 구조로 계획되었다.
문제 풀이에 대한 ABSTRIPS 방법은 간단하다. 임계값 (criticality value) 이 가장 높은 선결 조건만을 고려하여 문제를 푼다. 임계값은 선결 조건을 만족시킬 때 예상되는 난이도를 반영한다. 가장 높은 임계값보다 낮은 값을 가진 선결 조건은 무시하면서, STRIPS 가 했던 일들을 정확하게 수행한다. 일단 이것이 수행되면, 이렇게 만들어진 계획을 완전한 계획의 윤곽으로 사용하고 아래에 있는 다음 임계 레벨의 선결 조건을 조사한다. 이 선결 조건을 만족시키는 작용자들을 계획에 첨가한다. 다시 작용자를 선택할 때, 현재 조사되고 있는 레벨보다 낮은 임계값을 가진 선결 조건은 무시한다. 원래 주어진 규칙의 선결 조건이 모두 조사될 때까지 이 과정을 계속 반복 수행한다. 이 과정은 낮은 레벨이 있는 계획들을 조사하기 전에, 이 레벨보다 위에 있는 레벨의 목표를 모두 탐색해야 하기 때문에, 길이 우선 탐색 (length-first-search) 이라 한다.
적절한 임계값의 배정은 계층 계획 방법의 성공에 매우 결정적인 역할을 한다. 어떤 작용자도 만족시킬 수 없는 선결 조건은 가장 중요한 역할을 한다. 예를 들어, 만약 집안에서 움직이는 로보트에 관한 문제를 풀고자 할 때, 작용자 PUSHTHROUGHDOOR 를 적용시키려 한다면, 로보트가 드나들 수 있을 만큼 충분히 큰 문이 존재한다는 선결 조건은 계획 과정의 성공에 중요한 요인이다. 왜냐하면, 만약 그러한 문이 존재하지 않는다면, 일반적인 상황에서는 어떤 일도 할 수 없기 대문이다. 그러나 OPENDOOR 라는 작용자가 있을 때, 문이 열려 있다라는 선결 조건은 이 보다 덜 중요하다. STRIPS 와 같은 규칙을 사용하여 계층적 계획 시스템을 수행하기 위해서는 규칙뿐만 아니라, 선결 조건에 나타난 각 항에 대해 적정한 임계값을 또한 알아야 한다. 주어진 임계값에 대해 기본적인 과정은 비 계층 구조가 작용하는 방법과 같은 방법에 따라 잘 적용한다. 그러나 문제의 풀이를 이끌어 내지 못하는 계획의 세부 사항을 채우는 불필요한 작업은 제거된다. 다음 절에서는 계층적 계획의 예를 자세히 소개한다.
일련의 작용자에 대한 모든 순열을 조사하지 않고도 비선형 계획을 찾을 수 있는 한가지 방법은 최소 실행 방법을 작용자의 수행 순서 선택 문제에 적용하는 것이다. 수행될 작용간의 순시 뿐만 아니라, 필요한 작용을 발견하는 계획 과정도 필요하다 (예를 들어, 작용자의 실행에 앞서, 주어진 작용자의 선결 조건을 설정하는 과정을 수행해야 한다). 이러한 과정을 수행한 후, 요구된 모든 제한 조건을 만족시키는 작용자들의 순서를 결정하는 과정을 수행한다. 문제풀이 시스템 NOAH [Sacerdoti, 1975 : Sacerdoti, 1977a] 는 선택된 작용자들 간의 순서를 기록하기 위해 격자 구조를 사용한다. 또한 NOAH 는 먼저 계획의 대략적인 골조를 만든 후, 단계적으로 세부 사항을 채워 나가는 계층적인 방법에 따라 적용한다.
NOAH 에서 작용의 수행 순서에 대한 결정을 뒤로 미루기 위해 사용되었던 최소 실행 방법은 더욱 복잡한 계획 시스템에서 발생하는 많은 결정을 처리하는데 또한 사용될 수 있다. 지금까지 논의된 간단한 블럭 세계에 대한 계획에서 내려야 할 중요한 결정은 사용될 작용자와 이것의 수행 순서이다. 그러나 계획에는 작용 뿐만 아니라, 물체도 포함된다. 블럭 세계에서도 이러한 경우가 있다. 예를 들어, 만약 블럭 A 를 그 물체로부터 들어내야 한다. 따라서 작용자 UNSTACK (A, x) 가 사용된다. 원칙적으로 x 에 어떤 블럭이라고 대답할 수 있다. 그러나 만약 블럭 A 가 이미 특정한 어떤 상자위에 놓여 있지 않다면, UNSTACK 의 작용은 로보트 팔이 블럭 A 를 집도록 하는데 부적합하다. 따라서 x 에 대입될 블럭을 실제로 결정할 필요는 없다.
그러나 좀 더 복잡한 문제 분야에서, 물체의 결정은 계획 과정에 핵심이 되는 중요한 역할을 한다. 분자의 유전적 특질에 대한 실험을 계획하는 MOLGEN 은 그러한 문제 분야에서 작용하는 계획 시스템의 예이다. 이 시스템에서는 물체에 대한 결정을 비록 이 결정들이 서로 상호 작용을 하더라도, 가능한 한 오랫동안 지연되도록 하기 위해, 제한 조건의 배치 (constraint posing) 라는 기법을 사용한다. 분자의 유전적 특질보다 간단한 문제를 사용하여 이 기법의 작용 방법을 알아 보자.
여러 분이 어떤 조직체의 지명 위원회의 구성원이라고 가정하자. 이때 한 명의 회장 후보와 다른 한 명의 총무 후보를 선출하고자 한다. 각 위치에 적합한 후보를 선택하기 위해 여러 가지 사항들을 고려해야 한다. 사람들의 가능한 모든 쌍을 고려할 필요는 없다. 대신 이 문제를 두 개의 독립적인 부분적인 문제로 나누어 풀어 간다. 사실상 이 두 개의 부분적인 문제는 독립적이지 않다. 제한 조건의 배치 기법을 사용하여 이 상호 작용을 쉽게 처리할 수 있어 다음 두 개의 독립적인 목표를 설정한다.
ASSIGN (PRESIDENT = x) ASSIGN (TREASURER = y)
그리고, 전역적인 제한 조건 리스트에 다음 두 개의 필요 조건을 첨가한다 :
COMPATIBLE (x, y)
NOTEQUAL (x, y)
이제, 두 개의 부분적인 목표를 서로 완전히 독립적인 것으로 간주하여, 계획 과정을 수행할 수 있다. 계획 과정이 수행됨에 따라 이 리스트에 새로운 제한 조건이 첨가될 수 있다. 계획 과정이 수행되는 동안, 소개된 변수에 대입할 값을 결정해야 할 곳이 여러군데 발생한다. 이 경우 고려중인 변수와 이에 관련된 모든 제한 조건을 참조해야 하는데, 이를 위해 제한 조건의 만족 과정을 사용할 수 있다.
만약 계획 과정의 수행이 끝났는데도, 변수가 여전히 작용자에 존재한다면, 문제의 모든 제한 조건을 만족시키는 특정한 값을 찾을 수 있다. 이것은 값의 선택에 대한 후진이 불필요하다는 것을 보장한다.
논의되지는 않았지만, 그러나 여러 시스템에서 유용한 것으로 판명된 계획 기법들이 존재한다. 여기에는 다음과 같은 기법들이 포함되어 있다.
지금까지, 인공 지능 프로그램의 작성에 유용한 많은 여러 기법들이 소개되었으며, 지식을 표기하는 방법과 이 지식을 처리하는 알고리즘이 논의되었다. 그러나 이러한 방법 중 어느 것도 대부분의 인공 지능 문제를 풀기에 충분한 것은 없다. 어려운 문제를 풀기 위해서는 많은 과정들과 지식의 조화가 필요하다. 이러한 조화를 용이하게 하는 기법들을 알아 보자.
다른 여러 지식의 출처를 하나의 시스템으로 결합할 수 있는 가장 쉬운 방법은 모든 지식을 포함하는 규칙을 작성하여, 주어진 상황으로부터 목표 상태로 가는 경로를 찾기 위해 시스템으로 하여금 이 모든 규칙을 사용하도록 하는 것이다. 그러나 이 방법에는 다음과 같은 몇 가지 중요한 결함이 내재되어 있다.
이러한 이유 때문에 커다란 시스템을 이루는 지식을 상당히 독립적인 모듈로 분리하는 것이 효과적이다. 이러한 견해는 어떤 큰 시스템을 고안할 때 더욱 많이 강조되는 모듈화의 중요성과 일치한다. 그러나 현재, 주어진 문제를 풀 때 개개의 모듈이 서로 어떻게 조화를 이루는지, 그 조화의 방법이 문제로 남아 있다. 다음 세 개의 절에서 조화를 이루는데 사용되는 세 가지 기법이 소개된다.
수행 가능한 작업을 기록한 비망록을 사용하여 최적 우선 탐색 기법을 구현하는 방법에 대해 앞에서 논의한 바 있다. 커다란 시스템의 조직이라는 차원에서 볼 때, 비망록 기법의 중요성은 특정한 작업의 선택에 대한 지지나 반대를 위한 증거를 그 작업의 정당화 리스트에 첨가함으로써, 독립적인 모듈간에 서로 정보를 주고 받을 수 있다는 점이다. 이렇게 하여 작업을 지지하기 위한 여러 증거 가운데 시스템은 지지도가 가장 높은 작업을 선택할 수 있다. 그러나 모듈들이 여러 가지 작업의 수행 결과를 공유한다 하더라도, 하나의 모듈은 다른 모듈들이 여러 가지 작업의 수행 결과를 공유한다 하더라도, 하나의 모듈은 다른 모듈들이 어떠한 일을 하는지 혹은 다른 모듈들이 어떠한 지식을 포함하고 있는 지에 대해 전혀 알 필요가 없다. 결과적으로 대규모의 시스템에서는 모듈화에 의해 별다른 단점없이 이에 대한 모든 장점이 얻어질 수 있다.
또한 모듈들 간에 공통되는 비망록을 공유하여 사용하는 것은 시스템이 동일한 비망록 작성을 위한 일을 반복하지 않음으로써, 가장 유용한 작업을 하는 모듈에 시스템의 노력이 집중될 수 있다. 시스템의 노력이 집중되는 이러한 모듈은 주어진 문제의 풀이 과정 중 변할 수 있다.
커다란 인공 지능 프로그램을 구성하는 방법인 흑판 기법은 HEARSAY-II 음성 이해 프로젝트에서 처음 개발되었다. 이 흑판 기법의 개념은 간단하다. 전체 시스템은 주어진 문제 분야와 관련된 특정한 지식을 포함하고 있는 지식의 출처 (knowledge source : KS) 라 불리우는 독립적인 모듈과 모든 KS 가 공유하여 사용할 수 있는 데이터 구조인 흑판 구조로 구성되어 있다. HEARSAY-II 에서, 이 KS 들은 음성, 언어 그리고 논의될 작업에 대한 지식의 레벨과 대응한다.
HEARSAY-II 에서 사용된 제어 구조에 존재하는 한 가지 문제점은 한 KS 에 의해 만들어진 평가 등급을 다른 KS 에 의해 만들어진 평가 등급과 비교해야 한다는 것이다. 이것은 다음에 수행될 가장 유망한 부분을 선택하는데 필수적이다. 그러나 KS 들이 서로에 대한 어떤 정보도 가지고 있지 않다고 가정했기 때문에 이러한 비교는 어렵다. KS 들간의 서로에 대한 정보가 없을 때, 평가 등급의 의미에 모순이 없이 일관성이 있는지에 대해 알아 보자. 아래에 소개된 Δ-Min 탐색 과정을 사용하여 이러한 문제를 처리할 수 있다.
한 번에 하나씩 일련의 입력을 받아 들여, 이 입력들을 순차적으로 처리하여 일관성있게 하나로 번역하는 문제를 살펴 보자. 이러한 문제는 음성인지 혹은 자연 언어의 이해와 같은 문제의 분야에서 발생한다. 이 문제들의 풀이를 위한 Δ-Min 기법은 각 KS 가 적합하게 될 때면 언제든지 이것을 실행시켜, 가능성이 높다고 추측되는 가설을 모두 생성하고, 각 가설에 평가 등급을 지정한다. 이렇게 얻어진 평가 등급으로부터 한 가설의 평가 등급과 가장 유망한 가설에 주어진 평가 등급 간의 차이를 나타내는 Δ 값을 계산할 수 있다. 이제 가장 유망한 가설을 조사한다. 그러나 만약 그 가설이 모순을 유도한다면 유망한 가설중의 하나를 조사한다. 후진이 필요하다면, Δ 값을 사용하여 가장 유망한 가설을 선택할 수 있다.
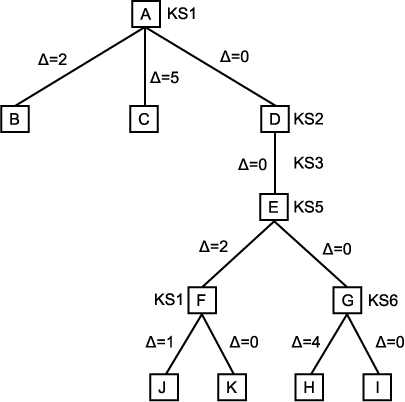
그림 6
그림 6 은 이 과정의 적용 방법을 설명한다. 노드 A 는 KS 가 활성화되기 전의 초기 상태를 나타낸다. 첫번째 입력이 읽혀지면, KS1 은 활성화되어, 노드 B, C 그리고 D 로 표시된 가설을 만든다. 노드 D 는 가장 유망한 노드이며, 이것의 Δ 값은 0 이다. 노드 D 의 평가 등급과 노드 B 의 평가 등급간의 차이는 2 이고, 노드 C 의 평가 등급간의 차이는 5 이며, 이것은 이 두 노드의 Δ 평가 등급에 반영된다. 노드 D 로 표기된 상태만이 다른 KS 에 의해 더 탐색된다. KS2 가 활성화되지만 이것은 아무 일도 수행하지 못한다. KS3 가 활성화되어, 노드 E 로 표기된 하나의 가설을 만든다. KS5 가 활성화되고, 노드 F 와 G 로 표기된 두 개의 가설이 생성된다. 노드 G 가 가장 유망한 노드이기 때문에, KS6 를 사용하여 더 조사된다. 이것으로부터 노드 H 와 I 로 표기된 두 개의 가설이 만들어 지는데, 노드 I 가 가장 유망한 것으로 보여 진다. 지금까지 깊이 우선 탐색 과정을 설명해 왔다. 그러나 KS6 에 이용할 수 없는 정보가 노드 I 의 가설에 모순을 초래한다고 가정하자. 이 정보는 전체 시스템의 제한 조건이나 다른 독립적인 KS 로부터 얻어질 수 있다. 이 경우 후진이 필요하다.
이제 Δ 값의 역할에 대해 살펴 보자. 탐색 과정이 어느 노드로 복귀하는 지에 대해 알아 보자. 가장 직접적인 대답은 4 라는 Δ 값을 가지고 있는 노드 H 이다. 다시 말하면, 마지막 결정을 내렸던 곳으로 되돌아 가는 것이다. 그러나 만약, 트리의 위쪽을 조사한다면, 노드 E 에서의 KS5 는 다음 최적으로 생각되는 노드 F 가 2 라는 Δ 값을 가지고 있기 때문에, 이것의 최적 가설인 노드 G 가 가장 유망한 것임을 확실히 하지 못함을 알 수 있다. 이것은 노드 F 를 탐색하는 것이 최상의 방법임을 의미한다. Δ-Min 탐색 과정을 사용하여 후진 과정은 전체적으로 다음의 가장 유망한 것으로 보이는 노드로 돌아 같다.
이 예에서 KS1 에 의해 두 개의 가설 노드 J 와 K 가 만들어 짐을 알 수 있다. 노드 K 가 KS1 에게 가장 유망한 노드로 보이지만 다시 노드 K 를 제거하는 외부적인 제한 조건이 존재한다고 가정하자. 이때 다시 후진 과정이 필요하다. 이 경우 가장 작은 Δ 값은 노드 J 의 Δ 값이다. 이때 다시 후진 과정이 필요하다. 이 경우 가장 작은 Δ 값은 노드 J 의 Δ 값이다. 그러나 노드 J 는 노드 F 의 후계 노드이며, 노드 F 자체가 또 다른 하나의 선택이 될 수 있음을 주목하라. 노드의 타당성에 대한 불확실성은 노드 J 자체의 불확실성과 이것의 선임 노드들의 불확실성에 기인한 것이다. 이로 인해 Δ 값 2 를 가진 노드 B 가 만들어 지며, 이것이 가장 유망한 노드로 보여져, 다음에 조사된다.
이 제어 과정에 대해 다음과 같은 사항들을 지적할 수 있다.
시스템의 성분들을 조합시키기 위한 방법으로 비망록 기법, 흑판 기법, 그리고 Δ-Min 기법을 사용할 때, 이들 기법에서의 정보 교환은 공유된 대상을 통해서 이루어짐을 알 수 있다. 물론 정보 교환은 항상 공유된 대상에 의해 이루어지지만, 흔히 이 대상들은 한 과정에서 다른 과정으로 전달되는 동안만 존재하고 곧 사라져 버리는 일시적인 메시지이다. 그러나, 위 기법에서의 정보 교환 대상은 상당히 오랫 동안 존재한다. 비망록 기법에서의 정보 교환 대상은 수행될 작업을 나타낸다. 이러한 작업은 수행되어야 할 증거가 나타날 때까지 혹은, 수행되지 말아야 할 증거가 오랜 시간동안 나타나지 않게 될 때까지 비망록에 남아 있게 된다. 가설은 이것이 옳지 않다고 증명될 때까지 존재하고, 활성화 레코드는 수행을 위해 선택될 때까지 존재한다. Δ-Min 시스템의 경우 대상은 입력에 대한 현재 가설의 집합을 나타내는 문제 상태이다. 이러한 세 종류의 시스템에서 개개 과정은 정보 교환은 정보 교환을 위한 대상을 만들 수 있고, 또한 다른 과정에 의해 만들어진 대상에 의견을 첨가한다.
다양한 종류의 의견이 부가된 대상이 존재하는 시스템의 일반적인 모형은 인공 지능 시스템의 여러 분야에서 유용하게 사용된다. 지금가지 논의한 시스템뿐만 아니라, 또 마이신이라는 시스템이 있는데, 이 마이신의 경우 대상은 발견된 증거의 양에 대한 가설이다. DENDRAL 에서의 대상은 제한 조건으로써, 규칙으로 구성된 한 집합에 만들어지며 다른 집합에 의해 사용된다. 다음 장에서는 유사한 정보 교환 대상들에 대하여 깊이 살펴 본다.
지금까지 논의된 대다수의 프로그램은 누구든지 쉽게 수행할 수 있는 상식적인 추론 작업을 수행하기 위해 작성되었다. 그러나 대부분의 사람들이 가지고 있지 않는 전문화된 많은 지식을 필요로 하는 흥미있는 작업들이 있다. 이 작업들은 필요한 지식을 수집했던 전문가들에 의해 수행된다. 의학 진단, 회로 고안, 그리고 과학적인 분석들이 이 작업에 포함된다. 이 작업들을 수행하는 프로그램은, 대체로 이 작업들에 대한 전문가들이 부족하기 때문에 매우 유용하게 사용된다. 이러한 종류의 작업중 일부를 수행하는 프로그램은 이미 작성되었다. 이 프로그램은 대화식 전문 시스템이라 불리며, 이 프로그램의 작성을 지식 공학 (knowledge engineering) 이라 한다.
대화식 전문 시스템의 가장 중요한 특징은 이 시스템이 지식의 거대한 데이터 베이스에 의존한다는 것이다. 많은 양의 지식이 대화식 전문 시스템의 성공에 중요한 역할을 하기 때문에 이 지식의 표기 방법 또한 시스템의 고안에 중요한 역할을 한다.
다양하고 수학적인 작업을 수행했던 가장 초기 대화식 전문 시스템의 하나인, MAC.SYMA 는 상당히 비 구조적인 LISP 언어가 제공하는 기능들로 구성되었다. 현재의 대화식 전문 시스템에는 거대한 양의 지식이 사용되기 때문에 구조화의 중요성은 더욱 깊게 인식된다. 뿐만 아니라, 크기의 변화가 필연적인 데이터 베이스를 변화가 거의 없는 프로그램과 구별하는 것 또한 중요하다. 결과적으로, 대화식 전문 시스템의 지식을 표기하기 위해 가장 널리 사용되는 방법은 생성 규칙의 집합을 사용하는 것이다. 이 시스템의 작용은 간단한 프로시쥬어에 의해 조절되는데, 이 프로시쥬어의 정확한 구조는 사용되는 지식의 성질에 의해 좌우된다.
|
MYCIN If : the
stain of the organism is gram-positive, and R1 If : the
most current active context is distributing massbus devices, and PROSPECTOR If : magnetite
or pyrite in disseminated or veinlet form is present |
그림 7
그림 7 은 다음과 같은 대화식 전문 시스템에서 사용되는 규칙들을 영문으로 번역한 것이다 :
이 규칙들 간의 차이는 대화식 전문 시스템의 작용 방법에 대한 중요한 차이 중의 일부를 나타낸다.
<확률적 추론 (probalistic reasoning)>
이러한 차이를 발생시키는 중요한 원인 중의 하나는 확률적인 지식을 처리하는 방법이다. 그림 7 의 세 규칙은 이러한 정보를 표기하여 사용하는 문제에 대해 각기 다른 세 가지 방법으로 접근한 것을 나타낸다. 마이신의 접근 방법은 규칙에 포함된 추론의 확실성을 의미하는 0 과 1 사이의 값을 각 규칙에 연결시키는 것이다. 이 숫자는 확률은 아니지만 확률과 유사한 것이다. 이 숫자들이 사용되는 자세한 방법은 6-3-3 절에서 이미 소개되었다. 여기서 기억해야 할 중요한 사항은 이 숫자들을 바탕으로 하여 마이신은 불확실한 정보를 결합하여 거의 확정적인 결론을 형성할 수 있다는 점이다.
확률적인 접근 방법의 다른 하나는 PROSPECTOR 에서 사용된 것이다. PROSPECTOR 에서, 신뢰도의 측정은 확률로 정확히 표기되고, 베이스의 규칙이 추론 과정의 기본으로 사용된다. 확률적인 접근 방법의 또 다른 하나는 R1 에서 사용된 방법이다. R1 에 의해 처리되는 작업에서는 주위 환경에 대한 특별한 각 집합에, 수행될 일을 정확히 기재할 수 있다. 따라서 이 경우는 확률적인 정보가 불필요하다. 이와 같이 추론이 확실한 경우에 이런 규칙들이 사용된다. 그러나 의학과 같은 일부 분야에서는 이러한 규칙이 존재하지 않기 때문에 1 보다 작은 신뢰도를 가진 규칙을 사용해야만 한다. 이러한 시스템에서는 6-3-3 절에서 기술된 것과 같은 기법을 사용하여 전체적인 규칙을 형성하기 위해 이 규칙들을 결합한다.
위에서 언급한 것처럼 규칙을 토대로 한 추론 시스템에서 확률적인 정보를 처리할 수 있는 방법에는 여러 가지가 존재한다. PROSPECTOR 와 MYCIN 에서는 사용된 추론 규칙의 차이뿐만 아니라 특정한 증거가 부족할 때 이를 처리하는 방법에도 차이가 있다. MYCIN 의 경우, 만약 증거의 부족이 시스템의 작용에 중요한 영향을 미친다면, 선결 조건의 하나로 이 부족한 증거를 가지고 있는 규칙을 규칙의 데이터 베이스에 첨가해야 한다. 그림 8 은 그러한 규칙의 예이다.
|
If : the
identity of the organism is not known, and then : (.3) the category of the organism is enterobacteriaceae. |
그림 8
반면 PROSPECTOR 에서는 각 규칙에 두 개의 신뢰도 추정값이 포함되어 있다. 첫번째 신뢰도 추정값은 규칙의 조건 부분에 기술된 증거의 존재가 규칙의 결론에 의해 암시되는 타당성의 범위를 알려 준다. 위에 보여진 PROSPECTOR 규칙에서 2 라는 숫자는 증거의 존재를 약하게 뒷받침한다. 두번째 신뢰도 추정값은 증거가 결론의 타당성을 위해 얼마나 필요한 지, 그 필요한 범위를 나타낸다. 다시 말하면 증거가 부족할 때, 이로 인해 결론이 부당한 범위를 나타낸다. 위에 보여진 규칙에서 -4 라는 숫자는 증거가 부족할 때, 결론을 거의 뒷받침할 수 없음을 의미한다.
<직접 추론과 탐색>
다른 인공 지능 프로그램에서처럼 대화식 전문 시스템에서도 탐색은 다른 기법들을 이용할 수 없을 때 사용하는 방법이다. 탐색 기법에만 의존하는 대화식 전문 시스템은 지금까지 논의한 대화식 전문 시스템과는 상당히 많은 차이를 가지고 있다. 이러한 차이에 영향을 끼치는 중요한 요인을 살펴 보면 다음과 같다 :
MYCIN 과 R1 은 탐색을 이용한 분야의 시스템이다. MYCIN 은 치료되어야 할 발병 유기체가 존재하는 지를 결정하는 목표로 부터 후진 추론한다. 일단 이것이 수행되면, 치료법을 선택하는 과정이 호출되고, 적합한 치료 계획서가 출력된다. 현재 목표와 일치하는 우측면을 가진 규칙이 여러 개 존재할 수 있으며, 이 경우 만족되는 모든 규칙을 고려해야 한다. 그러나 R1 은 완전한 배치 구조가 만들어질 때까지 점점 커지는 부분적인 배치 구조를 만들어 가면서 전진 추론해 간다. 이를 위해 사용되는 규칙은 잘 규정된 좌측면 (선결 조건) 을 가지고 있으며, 이 좌측면은, 매 단계마다 적절한 규칙을 선택하기 위해 수행되어야 하는 작업을 처리하기 위해 일치 과정에 의해 사용된다. 이때, 일치 과정은 현재 만족되는 선결 조건을 가진 규칙들을 결정하게 된다. 따라서, 탐색은 거의 불필요하다.
위에서 언급된 두번째 문제, 즉 하나의 풀이로 충분한 지의 문제에 대한 답 또한 MYCIN 과 R1 에서 서로 다르다. MYCIN 은 처리하는 분야의 특성 때문에, 환자의 증세를 설명할 수 있는 가능한 병을 모두 찾아야 한다. 만약 환자가 실제로 가지고 있는 병이 탐지되지 않아 치료되지 않은 채 남아 있게 된다면 환자는 사망하게 될 것이다. 따라서 가능한 병을 모두 찾는다는 것은 중요한 역할을 한다. 그러나 R1 의 경우, 하나의 적절한 시스템 배치 구조를 찾는 것으로 충분하며, 다른 가능성은 고려할 필요가 없다. 제 2 장에서, 이것을 문제에 대한 중요한 특성중의 하나로 설명한 바 있다. 만약 오직 하나의 풀이만이 필요하고, 또한 적당한 경험적 정보가 이용 가능하다면, 프로그램의 수행을 풀이를 얻을 수 있는 경로로 유도하여 탐색을 제한할 수 있다. 그러나 모든 문제 풀이가 필요하다면, 모든 경로를 전부 조사해야 하기 때문에 경험적 지식의 유용성에는 상당한 한계가 있고, 따라서 더 많은 탐색이 수행되어야 한다. 이로부터 MYCIN 이 R1 보다 훨씬 더 탐색에 의존해야 하는 또 하나의 이유를 알 수 있다.
대화식 전문 시스템이 작성된 분야의 수가 매우 제한되어 있기 때문에, R1 의 결정적인 기법이 수행되는 분야와 MYCIN 의 확률적이고 탐색을 기초로 하는 기법이 필요한 분야를 정확히 특성지울 수 있는 방법은 없다.
그러나 한 가지 방법은 MYCIN 처럼 주어진 자료에 대한 분석이 요구되는 분야와 R1 처럼 주어진 조건을 만족해야 하는 종합적인 고안이 필요한 분야로 나눌 수 있다. 이 질문에 대한 확실한 대답을 하기 위해서는 더욱 많은 연구가 필요하다.
대화식 전문 시스템이 효과적인 도구로 사용되기 위해서는, 인간이 이것과 서로 쉽게 상호 작용할 수 있어야 한다. 이러한 상호 작용을 쉽게 하기 위해, 대화식 시스템은 기본적으로 수행하는 작업뿐만 아니라, 다음과 같은 두 개의 능력을 가지고 있어야 한다 :
MYCIN 의 처음과 끝에 사용되는 TEIRESIAS 에 의해 이 두 능력이 모두 제공된다. 이 유용한 상호 작용을 쉽게 하기 위해 대화식 전문 시스템의 지식을 표기하기 위한 생성 규칙이 어떻게 사용되는지, 그 방법에 대해 알아 보자. TEIRESIAS 가 사용자의 질문에 대한 응답에 MYCIN 의 행동에 관한 설명을 만들어 내는 방법부터 알아 보자. 사용자와 TEIRESIAS/MYCIN 간의 대화중 일부가 그림 9 에 나타나 있다. 프로그램은 추론을 계속 수행하기 위해 필요한 정보를 요구한다. 의사는 프로그램이 정보를 요구하는 이유를 알고자 한다. 후에, 의사는 또한 프로그램이 어떻게 결과를 만들었는지, 그 방법에 대해서도 알고자 한다.
TEIRESIAS 에서 사용된 설명에 대한 기법의 중요한 전제는 프로그램의 실행 과정을 언급함으로써 간단히 프로그램의 행동을 설명하는 것이다. 만들어질 수 있는 설명의 종류에 제한을 가하기 위해, 이 가정을 사용하는 방법이 여러 가지 있으나 이 가정은 설명을 만들 때 관계되는 총 경비를 최소화한다. TEIRESIAS 가 MYCIN 의 행동에 대한 설명을 만드는 방법을 이해하기 위해, 그 행동이 어떻게 구조화되는 가를 알아야 할 필요가 있다.
MYCIN 은, 환자의 병에 대한 원인을 찾음으로써 목표인 특정한 환자에 대한 치료법을 찾고자 한다. MYCIN 은 목표로부터 임상 관찰로 후진 추론하기 위해 생성 규칙을 사용한다. 진단 목표를 위해 MYCIN 은 우측면이 병을 나타내는 규칙을 찾는다. 규칙들을 계속 불러낼 수 있는 부 목표 (subgoal) 를 설정하기 위해, 찾은 규칙의 좌측면, 선결 조건 1 을 사용한다. 이 과정을 계속 반복 수행한다. 선결 조건이 특정한 임상 증거를 기술할 때마다, MYCIN 은 이 증거가 이미 제공되어 있다면, 이것을 사용하고 그렇지 않다면 정보를 제공 받을 수 있는 지를 사용자에게 묻는다. 정보에 대한 MYCIN 의 요구가 사용자에게 일관성이 있는 것으로 인정된다면, MYCIN 이 설정한 실제 목표는 개개 규칙의 선결 조건을 만족시키기 위해 필요한 것보다 훨씬 일반성을 띤다. 예를 들어 만약 선결 조건이 유기체의 이름이 x 라는 것을 규정하는 것이라면, MYCIN 은 "infer identity (이름을 추론하라)" 라는 목표를 설정할 것이다. 이러한 방법은 또한, 만약 또 다른 규칙이 유기체의 이름을 언급한다면, 이름이 알려질 것이기 때문에, 더 이상의 작업이 불필요하다는 것을 의미한다.
|
Is the patient's illness with ORGANISM-1 a hospital-acquired infection? ** WHY [i. e., WHY is it important to determine whether or not the infection with ORGANISM-1 was acquired while the patient was hospitalized?] [2.0] This will aid in determining the category of ORGANISM-1. It has already been established that [2.1] the gram stain of ORGANISM-1 is gramneg, and [2.2] the morphology of ORGANISM-1 is rod, and [2.3] the aerobicity of ORGANISM-1 is facultative Therefore, if [2.4] the infection with ORGANISM-1 was not acquired while the patient was hospitalized, then there is strongly suggestive evidence (.8) that the category of ORGANISM-1 is enterobacteriaceae [ALSO : there is weakly suggestive evidence (.1) that the identity of ORGANISM-1 is pseudomonas-aeruginosa] [ALSO : there is weakly suggestive evidence (.1) that the identity of ORGANISM-1 is pseudomonas-aeruginosa' [RULE037] ** HOW [2.3] [i. e., HOW was it established that the aerobicity of ORGANISM-1 is facultative?] The following were used : [3.1] RULE027 indicated there is strongly suggestive evidence (.8) that the aerobicity of ORGANISM-1 is facultative. [3.2] RULE033 indicated there is weakly suggestive evidence (.2) that the aerobicity of ORGANISM-1 is not facultative. Since this gave a cumulative CF of (.6) for facultative, the evidence indicates that the aerobictiy of ORGANISM-1 is facultative. |
그림 9
그림 9 에 보여진 TEIRESIAS/MYCIN 의 행동 과정을 살펴 보자. 사용자의 첫번째 질문은 "Why do you need to know that? (왜 그 정보를 알고자 하는가?)" 라는 의미가 내포되어 있는 "WHY" 이다. 특별히 많은 비용을 필요로 하거나 위험한 임상 실험의 경우, 실험을 수행하기에 앞서 정보가 실제로 필요하다는 것을 의사가 납득해야 한다. MYCIN 이 후진 추론하기 때문에, 목표 트리를 조사하여 질문에 대한 답을 쉽게 할 수 있다. 이렇게 함으로써 다음과 같은 두 종류의 정보가 얻어진다 :
TEIRESIAS 로부터 이중 첫번째 질문에 대한 답을 얻으면, 사용자는 만족하거나 혹은 후진 추론을 더 수행하기를 원할 수도 있다. 사용자는 "WHY" 라는 질문을 더 함으로써, 이를 할 수 있다.
TEIRESIAS 가 이 중 두번째 질문에 대한 답을 마련하여 사용자에게 알려주면 사용자는 이 답이 무엇을 바탕으로 하여 얻어진 것인지 알고자 할 것이다. 사용자가 "HOW" 를 사용하여 이 답에 대해 질문하면 TEIRESIAS 는 "HOW" 라는 것을 "How did you know?" (이를 어떻게 알았는가?) 로 번역할 것이다. 목표 트리를 찾아 기술된 사실로부터 이 사실을 결정한 규칙을 활성화시킨 증거로 후진 추론하면서 이 질문에 대해 답할 수 있다. 따라서 문제의 목표로부터 후진추론하고, 이 과정동안 탐색되는 전체 트리를 기억함으로써, TEIRESIAS/MYCIN 은 사용자에게 시스템의 추론 과정을 적절하게 정당화할 수 있다.
대화식 전문 시스템의 행동을 설명하는 문제에 대한 또 다른 방법은 주어진 전문 시스템에 대해 하나의 프로그램으로 만들어서 프로그램 전체에 대한 질문에 답하기 위하여 프로그램의 각 부분이 하는 일에 관한 지식을 사용한다.
60 년대 중반 이후, 대화식 전문 시스템의 프로그램은 많은 진보와 함께 개발되었다. 이로부터 다음과 같은 결론을 얻을 수 있다.
제 3 장에서는 매우 단순한 문제나 혹은 거대한 문제를 구성하는 각각의 작은 문제에 적절히 사용되는 간단한 문제 풀이 기법에 대해 많이 논의했다. 본 장에서는 상당히 어려운 문제가 주어졌을 때, 이 문제를 작고 처리 가능한 작은 문제들로 나누어 이 작은 문제들을 각각 풀어 답을 구한 후, 이들을 결합하여 원래 문제에 대한 풀이를 찾는 방법에 대해 논의하였다.
이 장의 핵심은 문제 풀이가 어느 정도까지 어려운가 하는 것이다. 이 장에서 보여준 기법은 의학 진단과 같은 명백히 어려운 문제뿐만 아니라 1 절에서 광범위하게 다루어진 3-블럭 문제와 같이 표면상으로는 간단한 문제를 푸는데도 중요하다.
1. 다음과 같은 작용자의 집합이 주어진 STRIPS 형의 시스템을 살펴 보자.
|
SKIP-EXAM : |
P & D A |
: Equal (grade, x) : Sleep-late ∧ Equal (grade, x-10) |
|
WRITE-PAPER : |
P D A |
: Equal (grade, x) Equal (grade, x) ∧ Sleep-late : Equal (grade, x+50) |
또한 이 시스템에는 다음과 같은 공리가 주어졌다.
GE (grade, 80) → ABLE-TO-GRADUATE
LT (grade, 80) → NOT (ABLE-TO-GRADUATE)
이 시스템이 초기 조건으로 GRADE = 70 이 주어졌을 때 다음과 같은 목표를 만족시키려고 한다고 가정하자.
SLEEP-LATE & ABLE-TO-GRADUATE
목표
집합 기법 (goal set approach) 를 사용하여 이를 수행하는 방법을 설명하라.
회귀
(regression) 가 이 과정에 어떻게 영향을 미치나를 명확하게 설명하라.
2. 부엌 청소를 위한 계획을 세우는 문제를 살펴보자.
a. 사용될 STRIPS 형 작용자의 집합을 기술하라. 작용자가 기술할 때 다음과 같은 상황을 고려하라.
b. 부엌 청소가 필요한 경우의 초기 상태를 기술하라. 또한 좀처럼 얻기 어려울지도 모르는 바람직한 목표 상태를 기술하라.
c. 목표 스택을 사용하는 계획 기법이 이 문제를 풀기 위해 어떻게 이용되나?
d. 목표 집합을 사용하는 계획 기법이 이 문제를 풀기 위해 어떻게 이용되나?
3. 원래의 목표로 되돌아가는 탐색 경로가 더 이상 조사되지 않도록 하는 상황의 예가 앞의 1-3 절에서 나와있다. 프로그램이 이러한 상황을 발견할 수 있는 기법을 만들어 보아라.
4. 그림 5 은 비선형 계획을 위한 후진추론에 의해 만들어진 탐색 트리의 시작을 보여준다. 완전한 풀이가 발견될 때까지 이 트리를 확장하라. 불필요한 경로는 가능한 한 조기에 자르고 그 이유를 설명하라.
5. STPIPS 가 복합 목표를 분해할 때, 복합 목표와 함께 그 구성 요소들도 목표 스택에 들어가게 된다. 이는 구성 요소들을 만족한 후에도 처음의 복합 목표가 만족된다는 것을 확실히 하기 위해 매우 중요하다. 이와는 반대로 NOAH 에서는 복합 목표가 구성 요소들로 분해되고 난 후에는 더 이상 이 복합 목표를 고려하지 않는다. STRIPS 가 구성 요소들이 만족된 후에 원래의 복합 목표로 되돌아가 다시 확인하는 과정을 NOAH 에서는 어떻게 처리하는지 설명하라.
6. 레지스터 A 와 B 의 내용을 교환하는 문제에 대해 생각해 보자. 작용자 ASSIGN 이 다음과 같이 이용 가능하다고 하자.
ASSIGN (x, v, lv, ov) {lv 에 있는 값 v 를 x 에 수록한다. 이 경우 x 의 이전 값은 ov 이다}
P
: CONTAINS (lv, v) ∧ CONTAINS (x, ov)
D : CONTAINS
(x, ov)
A : CONTAINS (x, v)
이때, 또 다른 레지스터 C 가 이용 가능하다고 가정하자.
a. STRIPS 는 이 문제를 풀기 위해 어떠한 일을 한다고 생각되나?
b. NOAH 는 이 문제를 풀기 위해 어떠한 일을 한다고 생각되나?
c. 이 문제를 풀기 위한 프로그램을 어떻게 작성할 것인가?
7. 규칙을 토대로한 시스템의 경우에 따라서 왼쪽면에 여러 개의 조건을 나타내는 규칙을 포함한다.
a. 왜 MYCIN 에서 이것이 사실인가?
b. 왜 R1 에서 이것이 사실인가?
8. 대화식 전문 시스템을 위하여 비교흡수 방법이 적당한 추론 기법인가? 3-2 절에서 제기된 문제점들을 명심하여 답하라.