학습
(Learning)
인공지능 이론 및 실제 : Thomas Dean. James Allen. John Aloimonos 공저, 김진형.박승수.백은옥. 서정연.이일병 공역, 사이텍미디어, 1998 (원서 : Artificial Intelligence: Theory and Practice, 1995), Page 187~264
청소로봇은 사무실 문에 붙어있는 이름에 카메라의 초점을 맞추고 있다. 이 로봇은 내일 있을 쓰레기 수거에 대비해서 재활용품을 미리 모으기 위하여 재활용 상자를 찾아다니고 있다. 로봇의 문자인식 시스템은 이 방이 한 교수의 사무실이라는 것을 알아낸다. 로봇이 바로 전에 들어갔던 5 층에 있는 세 개의 교수 사무실에는 재활용 상자가 있었고, 지금 쳐다보고 있는 이 교수실은 4 층에 있다. 문 앞에 서서 로봇은 내장된 분류 시스템을 수행시켜 그 결과를 참조한다. 분류 시스템은 그 사무실에는 재활용 상자가 없는 것 같다고 결론을 내리고 있으나 로봇은 이와 같은 결론에 확신을 가질만한 충분한 자료가 없기 때문에 일단 사무실로 들어가서 상자가 있는지 찾아보기로 한다. 분류 시스템의 결론과는 달리 그 사무실에서 한 개의 재활용 상자를 찾게 되고, 4 층에 있는 교수 사무실에도 재활용 상자가 있다는 사실이 반영되도록 분류 시스템을 재조정한다.
로봇은 각 사무실에 대해서 재활용 상자가 있다거나 또는 없다고 분류한다. 로봇이 그의 분류 시스템에 대해서 취한 조정 작업이 바로 학습 의 한 가지 형태인 것이다. 학습이란 어떤 작업에 대하여 성능을 향상시키기 위해 시스템의 지식 내용이나 혹은 지식 구조를 변화시키는 것을 말한다 [Simon, 1981]. 즉, 학습은 시스템이 환경으로부터 새로운 지식을 습득하거나 또는 기존 지식의 더 나은 사용을 위하여 현재의 지식을 재구성할 때 발생한다.
3 장 표상과 논리에서는 자동추론 시스템의 성능을 향상시키기 위하여 연역적 추론방법 (deductive inference) 을 사용하는 설명 기반 일반화 (explanation-based generalization) 라는 방법을 고려했다. 이 장에서는 귀납적 추론 (inductive inference) 을 사용하는 학습 방법에 대하여 설명한다. 귀납적 추론이란 특별한 예를 실험하여 일반적인 결론에 도달하는 추론 방법이다. 예를 들어 청소로봇이 들어간 교수 사무실마다 재활용 상자가 있었다면 로봇은 어느 정도 착신을 가지고 "모든 교수들의 방에는 재활용 상자가 있다" 고 결론을 내릴 수 있을 것이다.
이 장에서 우리는 다양한 귀납적 학습 방법에 대해서 설명할 것이다. 어떤 방법은 통계적 의사결정방법에서 사용하는 기술을 이용하고, 어떤 것들은 귀납적 추론을 위하여 생물학적 시스템의 아이디어를 이용한다. 먼저 귀납적 학습 문제에는 어떤 것들이 있는지 그 문제들을 분류하고, 그 다음에 귀납적 추론 기술에 관련된 기초 이론에 대해서 설명하기로 하자. 이 장의 나머지 부분에서는 특정 학습 방법에 대한 구현과 실험에 대해서 설명한다. 독자들은 이 장에 묘사된 실험의 결과를 재구현해 보고 각자 실제 응용에 실험해 보기를 권한다. 학습은 이론과 실제가 통합되어 과학을 어떻게 발전시킬 수 있는가를 보여주는 훌륭한 예가 될 것이다.
귀납적 추론에 기반한 학습은 교사학습 (supervised learning) 과 비교사학습 (unsupervised learning) 으로 나뉠 수 있다. 귀납적 추론에 관련된 학습에서 학습 프로그램은 특정한 입력과 출력간의 관계를 추론하려 한다. 교사학습이란 입력과 그 입력에 대한 올바른 출력이 학습 프로그램에 주어지는 것을 의미한다. 교사학습이 아닌 경우에는 프로그램에게 입력만 보여주고 그 입력에 대한 출력은 제공되지 않는다. 즉, 비교사학습에서는 학습 프로그램이 올바르게 학습되었는지 판단하기 위해 출력 외에 다른 종류의 근거에 의존해야 한다. 예를 들면, 복도를 돌아다니는 로봇의 학습에서는 벽에 부딪치는 것이 이 로봇의 항법에 조정이 필요하다는 근거를 제공해 준다. 이와 같은 근거는 어떤 입력에 대한 출력의 형태가 아니므로 이런 학습은 비교사학습이라 할 수 있다.
교사학습
교사학습에서는 학습 프로그램에 (xi, yi) 와 같이 입출력의 쌍의 형태로 입력이 주어지며, 이때 xi 가 입력이고 yi 는 xi 와 연관된 출력을 나타낸다. 입출력의 쌍은 예제 (example) 라고 불리며, 이러한 예제는 아직 알려지지 않은 어떤 함수의 결과라고 가정한다. 학습 프로그램은 모든 i 에 대해 f (xi) = yi 로 나타나는 학습 예제들을 설명할 수 있는 함수 f 를 학습해내는 것을 말하며, 이 학습이 성공적이 되면 임의의 입력에 대한 출력을 추측할 수 있게 된다. 입력이 어떤 객체들에 대한 설명일 수도 있고, 그 경우 출력은 그 객체가 속하는 부류에 대한 정의가 될 것이다. 다른 예로서 어떤 상황에 대한 설명이 입력으로 주어지면, 이때의 출력은 그 상황에서의 적절한 행동이나 또는 그 상황에 대한 어떤 예측이 될 것이다. 예를 들어 입력은 사무실이 몇 층에 있고, 교수 사무실인지 아닌지와 같은 사무실에 대한 묘사가 될 수 있고 이때의 출력은 그 사무실에 재활용 상자가 있느냐 없느냐에 대한 것이 될 수 있다.
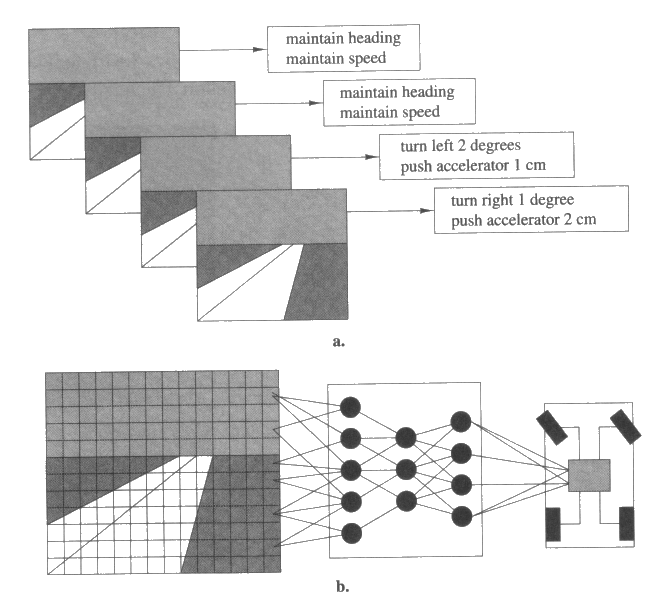
교사학습에 대한 예로 한 로봇에게 사람이 운전하는 예를 보여주고, 그 예로부터 운전하는 것을 배우도록 한다고 가정하자. 이때의 입력은 자동차 안에 장착된 카메라로부터 얻어진 운전자의 화상과 운전자가 길에서 보는 것에 대응하는 바깥의 화상으로 간주할 수 있다. 출력은 자동차를 조종하거나 그것의 속도를 조정하는 운전자로부터 획득한 행동이다. 그림 1a 는 이런 과제에 대한 학습 프로그램에게 제공하는 예제의 형태를 보여준다. 이런 예제들을 입력으로 사용하여 학습 프로그램이 각 화상에 대해 적절한 운전행동을 사상시키는 함수를 학습하게 될 것이다. 이렇게 학습된 함수는 예제에서 보지 못한 상황도 해결할 수 있도록 하기 위해 일반화되어야만 한다. 이 학습된 함수는 그림 1b 에서 보인 것처럼 자동차를 조정하기 위한 프로그램으로 구현될 것이다.

그림 1 : 학습 프로그램은 전문 운전자의 행동을 관찰하면서 운전을 학습할 수 있다. 위쪽에 있는 그림은 차에 부착된 카메라에 의해 들어온 화면과 각 화면에 나타난 상황에서 운전자가 취한 가속과 조향행위를 일련의 입출력쌍의 형태로 표기한 것이다. 아래쪽의 그림은 화상으로 들어온 입력을 받아 그 때 취해야 되는 조작행위를 결정짓는 학습된 결과를 망구조로 표현한 것이다.
분류와 개념 학습
함수가 이산 (discrete) 값을 가지게 되면 그 출력은 부류 (class) 라 불리며, 이러한 함수를 학습하는 것을 분류 (classification) 라고 한다. 고속도로 통행량을 조사하기 위해 고안된 시스템은 운송 수단을 승용차, 소형트럭과 밴, 중형트럭과 버스 그리고 대형트럭의 4 가지 부류로 분류하도록 학습할 수도 있을 것이다. 가능한 출력이 2 개만 있다면 그 학습된 함수는 개념 (concept) 이라고 불린다. 이 경우 각 입력이 그 개념을 만족시키는지 아닌지 판단하는 함수를 학습하는 것이다. 이런 학습은 개념학습 (concept learning) 이라고 불린다. 예를 들어 로봇은 움직일 수 있는 객체에 대한 개념을 학습할 수 있다. 모든 객체는 움직일 수 있거나 그럴 수 없는 두 가지 경우에 해당된다. 이러한 개념을 이용하여 로봇은 움직일 수 있는 객체를 실제로 움직여보지 않고도 인식할 수 있다.
비교사학습
비교사학습인 경우 학습 프로그램에 입력과 출력 둘 다 주어지지 않는다. 강제학습 (reinforcement learning) 이라 불리는 비교사학습의 한 형태는 학습 프로그램이 제대로 학습했는지 판단할 수 있는 피드백 신호를 사용한다. 체스를 학습하는 것은 강제학습의 한 예이며, 여기서 피드백 신호는 게임의 승패를 나타내는 함수로 볼 수 있다. 체스 학습을 포함한 많은 응용에서 시스템은 상황과 행동을 연계시키는 것을 배운다. 피드백은 특정한 상황에서 수행될 수 있는 여러 단계의 행동을 수행한 결과 얻게 되는 보상의 형태로 되어 있다. 이런 유형의 강제학습의 목표는 보상의 기대값을 최대화하는 데에 있다.
다른 형태의 비교사학습에서는 학습의 목표가 문제별로 서로 달라질 수 있다. 패턴인식과 같은 응용에서는 군집화 (clustering) 라는 비교사학습을 사용한다. 군집화 알고리즘이란 주어진 입력들을 비슷한 성질을 가진 것들끼리 묶어서 지정된 숫자만큼의 집단을 만드는 것이다. 이때 한 입력은 반드시 한 집단에 속해야 한다. 도로지도 학습 의 경우에는 운행을 쉽게 할 수 있는 공간의 표상을 학습하는 것이 목표가 될 것이고, 발견 (discovery) 학습에서는 자료들 사이에 새로운 관계를 발견하는 것이 학습의 목표가 된다. 로봇은 "문" 이라는 개념이 "어떤 장소로 들어가기 위해서 꼭 사용해야 하는 객체" 를 지칭한다는 것을 발견할 수 있을 것이다.
온라인학습과 일괄학습 방법
몇몇 응용에서는 학습 프로그램에 많은 예제들이 주어지며 그것들을 한번에 처리하도록 할 수 있다. 이러한 학습 시스템을 일괄 (batch) 학습 방법이라고 한다. 또 다른 응용에서는 학습 프로그램은 모든 예제들을 다 저장할 필요가 없이 한 번에 하나의 예제를 처리하도록 되어 있다. 이러한 학습 시스템을 온라인 (online) 학습 방법이라 한다. 이 장에서는 이 두 가지 방법에 대해서도 다룬다. 어떤 특정한 방법에 대하여 알아보기 전에 귀납적 추론의 본질에 대한 통찰력을 제공하기 위한 이론적 문제들에 대해 고려해 본다.
이 절에서는 귀납적 추론에 관련한 기본적인 이론 결과들에 대해 알아본다. 여기서 개념 학습에 초점을 맞추어서 설명하지만 많은 내용들이 다른 형태의 학습에 대해서도 같이 적용되는 것들이다. 집합 X 를 학습에 사용될 모든 예제들의 집합이라고 하자. 보다 정형화시켜 표현하면, 개념이란 부분집합 C ⊂ X 로서, 그 개념에 해당하는 예제들의 집합이다. 개념학습에서 학습 프로그램은 X 로부터 훈련 예제 (training example) 를 입력으로 받는다. 이 훈련예제들은 각각 학습하고자 하는 개념에 속하는 예제인지 아닌지 미리 표시가 되어있다. 학습의 목적은 X 로부터 나온 모든 예제를 그 개념에 속하는지 올바르게 결정하는 규칙을 학습하는 것이다.
이 학습 프로그램에 주어진 예제의 형태는 <x, y> 인데, 여기서 x ∈ X
이고,
y 의 값은 만일 x ∈ C 이면 1, 그렇지 않으면 0 값을 갖는다. 이 프로그램이 학습해야
할 함수 f 는 x ∈ C일 때 f (x) = 1, 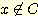 일 때 f (x) = 0 이 되는 함수이다. 이 함수 f 는 규칙의
집합으로도 표현될 수도 있고 절차적인 형태나 또는 뇌신경을 모델링한 계산 요소의
망과 같은 여러 형태로 표현될 수 있다.
일 때 f (x) = 0 이 되는 함수이다. 이 함수 f 는 규칙의
집합으로도 표현될 수도 있고 절차적인 형태나 또는 뇌신경을 모델링한 계산 요소의
망과 같은 여러 형태로 표현될 수 있다.
귀납 편중의 역할
지금까지 설명한 학습 문제는 충분하게 잘 정의되지 않아서 그 문제에 대한 해답을 정밀하게 정규화할 수 없다. 그래서 우리는 함수 f 를 어떤 함수들의 집합에서 골라야 할지 그 함수들의 집합을 지정해야 할 필요가 있고, 또한 여러 함수들 중에서 어떤 함수를 선택해야 할지 기준을 설정할 필요가 있다. 우선 간단한 방법으로 주어진 훈련예제로부터 그 예제를 설명하는 함수는 쉽게 만들 수 있다. 그것은 각 예제에 대한 예상된 출력을 지정하는 테이블로써 표현한 것이다. 그러나 이러한 테이블은 이미 보여진 예제들에 대해서는 정확하게 설명하나 보여지지 않은 예제의 경우에는 아무런 지침을 주지 못한다. 함수 f 에 대해 더 이상의 제약조건이 없다면 테이블이야말로 가장 정확하게 훈련예제들을 설명하는 표상이 될 것이다.
앞으로 우리는 함수 f 를 가능한 가설로부터 찾아낸다고 하고, 가설공간 (hypothesis space) 은 H 로 표기하기로 하자. 개념학습을 잘 정의하기 위해서 우리는 H 에 대한 제약조건을 소개할 필요가 있다. 이러한 제약조건을 귀납적 편중 (inductive bias) 또는 편중 (bias) 이라고 부른다. 편중은 학습 프로그램으로 하여금 함수 f 에 대한 모든 가능한 표상 중에서 하나를 선택할 수 있는 기본을 제공한다. 완전히 비편중된 학습 프로그램은 훈련예제 외의 것을 예상하는 정당한 함수를 얻을 수 없다. 특정 편중에 의해 유도되면 학습 프로그램은 나름대로의 정당성을 가지고 관찰된 훈련예제 외의 것까지 설명할 수 있는 일반화된 함수를 선정할 수 있다.
초등학교 학생이 수학 숙제를 풀 때 교과서에서 문제를 푸는 방법을 발견할 것이다. 그 책이 바로 학생으로 하여금 해법을 찾아내야 하는 범위를 제한하는 편중을 제공하는 것이다. 학생은 숙제에 대한 해법을 발견하기 위하여 상급 과정의 책을 볼 필요는 없다. 귀납적 편중은 학습에서 관찰된 예제 외의 것까지 일반화시키는 함수를 선택할 때 지침을 주는 것과 비슷한 역할을 한다.
제한된 가설공간 편중
우리가 고려할 첫번째 형태의 편중은 가능한 가설의 집합 H 를 제한함으로써 가설의 선택을 유도하는 것이다. 이러한 편중을 제한된 가설공간 편중 (restricted hypothesis space biases) 이라 한다. 만약 훈련예제들이 정확하게 포함된 테이블이 H 에 없다면 학습 프로그램은 이러한 테이블을 선택하지 못한다. 가설공간에 제한이 없어서 학습에 필요한 계산이 매우 복잡해지는 경우에는 H 를 제한하는 것이 학습을 쉽게 만든다. 그러나 H 를 제한하는 것이 올바른 가설을 제외시킬 수 있기 때문에 제한을 할 때에는 조심해야 한다.
n 개의 변수에 정의된 불리언함수공간 {x1, x2, ..., xn} 을 고려하자. 청소로봇의 예제에서 우리는 사무실이 교수에게 속하는지 속하지 않는지를 나타내는 변수 x1 과 사무실이 5 층에 있는지 아닌지를 나타내는 변수 x2 를 가질 수 있다. 훈련예제는 이 변수들에 대하여 참값과 거짓값을 할당할 수 있다. 가설 f 는 1 ≤ i ≤ k 에서 f (xi) = yi 인 경우에 훈련예제 {<xi, yi> | 1 ≤ I ≤ k) 와 일치한다 고 할 수 있다. 훈련예제의 집합과 일치하는 임의의 불리언함수를 찾는 것은 쉽다. 이 경우에 모든 긍정예제를 참으로, 모든 부정예제를 거짓으로 사상하는 모든 함수가 훈련예제와 일관성이 있게 된다.
이제 불리언함수의 제한된 공간을 생각해 보자. 우리는 불리언식으로 어떤 불리언함수도 표현할 수 있다. 예를 들어 (x1 ∨ (¬ x2 ∧ x3)) 로 표현되는 함수는 x1 이 참이거나 x2 가 거짓이고 x3 이 참인 경우에 참이 된다. 모든 불리언함수들의 공간을 제한시키는 방법 중의 하나는 긍정 리터럴의 논리곱의 형태인 불리언함수로만 이루어진 공간으로 제한하는 것이다. 예를 들어 {x1, x2, (x1 ∧ x2)} 는 두 개의 변수들에 대한 모든 긍정 리터럴들의 논리곱으로 이루어진 집합이다. 가설공간을 긍정 리터럴의 논리곱의 형태로만 한정한다면, 변수들의 개수에 대해서 다항식 시간 안에 일관성있는 가설을 찾을 수 있다. 한 걸음 더 나가서 불리언함수의 공간을 k-DNF 또는 k-CNF 식의 공간으로 제한하여도 같은 효과를 볼 수 있다. k-DNF 식이란 임의의 개수만큼 논리합 인자를 가질 수 있으나 각 논리곱에서 기껏해야 k 개의 논리곱 인자들만 가질 수 있는 논리합 정규형태 (disjunctive normal form) 의 불리언식을 말한다. k-CNF 는 k-DNF 의 정의에서 논리합과 논리곱을 바꾸면 된다.
H 에 대한 어떤 제한들은 계산 복잡도를 충분히 낮출 수 없을 정도로 충분하지 않다. 불리언식이 기껏해야 k 개의 논리합 인자만을 가질 수 있는 논리합 정규형태를 k-term-DNF 라고 한다. 흥미롭게도 k-DNF 형태의 불리언함수들의 부분집합인 k-term-DNF 로 제한이 강화된 가설공간에서 일관성있는 가설들을 찾는 문제는 NP-hard 이다.
뒤에서 설명할 신경망 모델에서도 비슷한 결과를 얻을 수 있다. 신경망들은 종종 포함하고 있는 신경과 같은 계산 요소의 층이 몇 단계로 이루어져 있는지에 따라서 분류된다. 일관성있는 3 단계층의 신경망을 찾는 것은 NP-hard 인 반면 2 단계층 신경망에서는 망의 크기에 대해 다항식 시간 내에서 가능하다.
선호 편중
두번째 형태의 편중은 선호 편중 (preference bias) 이라 하는데, 이것은 H 내에 있어서의 어느 것이 더 선호되는지에 대한 선호 관계들간의 순서나 선호도 측정 기준을 가진 학습 프로그램을 제공한다. 종종 우리는 Occam 의 면도칼 (Occam's razor) 에 의하여 짧고 간결한 설명을 선호한다. Occam 의 면도칼은 과학과 철학에서 자주 적용되는 휴리스틱으로 14 세기 영국의 Occam 지역출신 철학자 William 이 처음 제안한 것이다. Occam 의 면도칼이란 관찰된 자료를 설명하는 이론들 중에서 가장 간결한 것을 선호하라는 것으로서, 알려지지 않은 현상을 설명할 때 불필요한 개념이나 용어를 장황하게 사용하는 것은 옳지 않다고 하는 의미로 사용되는 것이다.
선호 편중들에 대해서 계산적인 면은 매우 복잡하다. 주어진 일반적인 선호에 대해 가장 선호되는 가설을 찾아내는 효율적인 알고리즘은 아직 알려져 있지 않다. 예를 들어, 훈련예제들과 일관성 있는 가장 적은 논리곱의 식을 구한다던가, 또는 3 단계로 이루어진 신경망을 찾는 다항식 시간 알고리즘들은 아직 알려지지 않고 있다. 가장 간결한 최적의 가설을 찾는 것은 어려울지 모르나 어느 정도 제약조건을 만족할 정도로 간단한 가설을 찾는 것은 가능하다. 여기서 어느 정도 만족할 정도란 학습 문제의 영역이 되는 신경망의 크기나 불리언 변수들의 개수에 대해 다항식으로 표현될 수 있는 수만큼의 범위를 만족할 정도로 간결한 가설을 찾는 것은 가능하다. 이러한 가장 간결한 가설에 대한 개략적인 접근은 긍정 리터럴들의 논리곱인 경우에 다항식 시간 내에 계산될 수 있으나 유한 상태기계 (finite state machine) 들로 제한된 가설의 경우에는 그렇지 않다.
주어진 제한된 가설 편중에 대해서 훈련예제와 일관성 있는 가설을 찾는 문제와 주어진 선호 편중에 대해서 간결한 가설을 찾는 문제는 편중들을 구현하는 문제로 귀착된다. 이것을 위해서는 어떤 것을 올바르게 학습했다고 하는 것의 의미가 무엇인지 정의해야 할 필요가 있다. 그렇지 않으면 훈련예제들의 수를 조절할 수 있다고 가정할 때 우리는 어느 순간에 추가 예제들을 입력시키는 것을 멈추고 그때까지 학습된 것을 옳다고 받아들여야 하는지 알 수가 없다. Valiant [1984] 는 추가 예제들을 입력시키는 것을 언제 멈추는가 하는 문제에 대한 이론적 해답을 제공한다.
Valiant 는 특정한 편중에 대해 학습이 제대로 이루어지기 위해 얼마나 많은 수의 훈련예제가 필요한지를 보여주는 훈련예제의 수에 대한 표본 복잡도 (sample complexity) 라고 하는 것을 제안했다. 기본적인 아이디어는 가설공간이 작으면 훈련예제와 일관성 있는 모든 가설이 다 정착할 가능성이 높다는 것이다. 즉, 이것은 훈련예제들의 집합이 모든 예제의 집합을 대표한다고 가정하는 것이다.
확률적으로 근사하게 정확한 학습
X 로부터 확률분포 Pr (X) 에 의해서 훈련예제들이 선택되어 진다고 가정하자. 주어진 가설 f 와 개념 C 에 대한 오류값을 다음과 같이 정의한다.
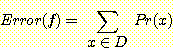
여기서 D 는 가설 f 를 적용했을 때 개념 C 와 일치되지 않은 예제들의 집합을 가리킨다.

학습에서는 오류값이 최소가 되는 가설을 발견하는 것이 목표가 된다. Error (f) ≤ ε 일 때 가설 f 가 정확도 ε 를 가지면서 거의 정확 (approximately correct) 하다고 정의한다. 모든 학습 프로그램이 오류를 가질 수 있다는 불가피함을 인정하고 이 오류를 줄이려고 한다.
학습의 결과가 허용되는 오류의 경계를 약간 벗어날 확률을 어느 정도 허용함으로써 학습에서 이론적으로 요구되는 조건을 느슨하게 약화시킬 수 있다. 즉, 분포 Pr 에 의하여 뽑혀진 훈련예제들의 집합이 주어졌을 때 학습 프로그램이 Pr (Error (f) > ε) < δ 인 가설 f 를 출력하면 이 학습 프로그램은 확률 δ 과 정확도 ε 이 확률적으로 근사하게 정확하다 (probably approximately correct : PAC) 라고 한다. 공정하게 하기 위해 훈련예제를 선택하는 확률분포는 성능을 측정하는 데 사용하는 분포와 동일해야 한다. 만일 기말시험에 숙제로 나온 연습문제나 교과서와 상관없는 곳에서 문제들이 출제된다면 학생들은 놀랄 것이다.
어떤 경우에는 훈련예제와 일관성 있는 가설을 찾는 알고리즘을 사용하여 PAC 인 학습 프로그램을 만들 수 있다. 가설공간이 한정적이라고 가정하자. 가설공간이 작으면 PAC 하지 않는 가설을 제거하기 위하여 많은 훈련예제를 가질 필요는 없다. 좀더 정확히 말하면 훈련예제와 일관성 있는 가설을 출력하는 프로그램이 되기 위해서는 훈련예제의 크기가 1n (δ / |H|) / 1n (1 - ε) 보다 크면 PAC 하다. |H| 는 H 에서의 가설들의 수이다. 이렇게 되는 것을 보기 위하여 다음 설명을 고려해 보자.
f 가 근사하게 정확하지 않다면 Error (f) 는 ε 보다 크고 모든 m 개의 예제들에 대해 가설 f 가 정확하게 적용될 확률은 (1 - ε)m 보다 작다. 제한된 가설공간에는 |H| 개의 가설이 있으므로 H 내에 m 개의 예제들을 정확하게 분류면서도 근사하게 정확하지 않은 가설들이 있을 확률은 |H| (1 - ε)m 보다 클 수 없다. 부등식 |H| (1 - ε)m < δ 을 m 에 대해서 풀면 1n (δ / |H|) / 1n (1 - ε) 를 구하게 된다. 이 결과는 훈련예제를 선택하는 특정 확률분포와 오류의 측정과는 독립적이라는 것을 유의하라. 이런 이유로 PAC 학습 결과는 분포자유 학습 (distribution-free learning) 결과 라 불린다.
효율성의 측면에서 훈련예제의 수가 증가함에 따라 얼마나 빨리 ε 와 δ 가 줄어드는지 또는 얼마나 빨리 1 / ε 와 1 / δ 가 증가하는지를 알아볼 필요가 있다. 1 / ε 와 1 / δ 의 증가함수로서 1n (δ / |H|) / 1n (1 - ε) 는 상대적으로 느리게 증가한다. 100 개의 가설에 대하여 확률 0.9 를 가지고 에러를 0.1 이하로 감소시키기 위해서 약 70 개의 훈련예제가 필요하다. 1000 개의 가설에 대해서는 약 90 개면 충분하고, 10000 개에 대해서는 110 개면 충분하다. 확률 0.99 를 가지고 에러를 0.01 이하로 하기 위해서는 위의 예제 개수에 10 을 곱하면 되고 0.999 의 확률과 0.001 이하의 에러를 위해서는 100 을 곱하면 된다.
PAC 학습가능한 개념의 부류
우리는 상대적으로 학습목표가 빠르면서도 작은 수의 예제만으로 높은 확률의 정확도를 가지는 학습 프로그램을 원한다. 입력의 크기와 예제의 수와 같은 여러 가지 관련된 변수에 대해 다항식 시간 내에 돌아가는 학습 프로그램의 개발이 목표인 것이다. 이런 요구를 다 통합시키면 가설공간이 주어졌을 때 한 개념 부류가 PAC 학습가능하다 라는 것이 무엇을 의미하는지 정의할 수 있다.
![]() 를 개념의 한 부류로써 모든 C ∈
를 개념의 한 부류로써 모든 C ∈ ![]() 에 대해서 C
⊂ X 라고 하자. 훈련예제를 저장하고
읽는 데 필요한 시간을 고려하기 위해서 주어진 훈련예제의 집합 X 의 한 원소를 처리하는
데 요구되는 시간이 작은 상수 시간을 넘지 않는다고 가정하자. A 가 다항식 시간
알고리즘이고 모든 C ∈
에 대해서 C
⊂ X 라고 하자. 훈련예제를 저장하고
읽는 데 필요한 시간을 고려하기 위해서 주어진 훈련예제의 집합 X 의 한 원소를 처리하는
데 요구되는 시간이 작은 상수 시간을 넘지 않는다고 가정하자. A 가 다항식 시간
알고리즘이고 모든 C ∈ ![]() 와 모든 분포 Pr
(X) 그리고 ε > 0, 0 ≤ δ < 1 을 만족하는
알고리즘 A 에게 확률분포에 의해 적어도 p (1 / ε, 1 / δ) 훈련예제가 입력으로 주어졌을
때 A 가 1 - δ 의 정확도를 가지고 Error (f) ≤ ε 인 가설 f 를 출력하면 δ
는 가설공간
H에 의해서 PAC 학습가능한 개념 (PAC learnable by a hypothesis space H) 이라고
말한다. k-DNF 와 k-CNF 개념들은 학습하려는 개념의 부류와 가설공간이 같을 경우
PAC 학습가능하다.
와 모든 분포 Pr
(X) 그리고 ε > 0, 0 ≤ δ < 1 을 만족하는
알고리즘 A 에게 확률분포에 의해 적어도 p (1 / ε, 1 / δ) 훈련예제가 입력으로 주어졌을
때 A 가 1 - δ 의 정확도를 가지고 Error (f) ≤ ε 인 가설 f 를 출력하면 δ
는 가설공간
H에 의해서 PAC 학습가능한 개념 (PAC learnable by a hypothesis space H) 이라고
말한다. k-DNF 와 k-CNF 개념들은 학습하려는 개념의 부류와 가설공간이 같을 경우
PAC 학습가능하다.
이런 PAC 학습 결과들은 최악의 경우이므로 일반적으로 매우 비관적으로 보인다. 실제적으로 많은 개념들이 PAC 학습 결과보다 훨씬 쉽게 배울 수 있다. 그렇다고 그런 현상이 PAC 결과들에 대하여 모순되지는 않는다. 다만 여러 가지 실제 문제들이 존재하는 PAC 결과에서 고려되지 않은 구조를 가지고 있고 그 구조가 학습을 활성화시키는 데 사용된다고 제안한다. 지금까지 우리는 귀납적 편중이 학습에 있어서 어떻게 역할을 하는가를 알아보았고, 유용한 편중들을 구현하기 위한 실제적인 방법들을 논의하였다.
일관성 있는 가설 찾기
학습 이론에 의하면 몇몇 경우에 효과적인 학습을 위해서 훈련예제와 일관성 있는 가설을 찾는 수준의 학습만으로도 충분하다고 한다. 그러나 이런 가설을 찾는 데에 시간이 많이 걸린다. 특정한 편중을 구현하는 학습 시스템을 만드는 연구자들에게는 계산 복잡도 문제를 해결하기가 쉽지 않게 된다.
뒤에 나올 두 절은 두 개의 귀납적 편중들을 구현하는 방법을 설명한다. 버전공간방법 (version-space method) 이라 불리는 첫번째 방법은 모든 개념의 집합 내에서 훈련예제들의 집합과 일관성 있는 개념들의 집합을 구분하는 경계를 유지하기 위해서 제한된 가설공간의 구조를 사용하는 방법이다. 이 방법은 한 번에 하나의 훈련예제를 처리하면서 진행되며 긍정 리터럴의 논리곱으로 구성된 제한된 가설공간에 대해서는 점근적으로 최적 (asymptotically optimal) 이다.
결정트리 방법 (decision-tree method) 이라 불리는 두번째 방법은 상당히 일반적인 가설공간을 사용하고 선호 편중과 지금까지 보지 못한 예제들에 대해서도 일반적으로 설명할 수 있는 간결하고 일관성 있는 가설을 찾기 위한 휴리스틱을 도입했다. 이 방법은 일괄처리 방법의 한 예이다.
개념 C1 은 예제들의 집합으로서 만일 C1 ⊂ C2 이면 C1 은 C2 의 특수화 (specialization) 라 부른다. C1 이 C2 의 특수화이면 C2 는 C1 의 일반화 (generalization) 이다. 예를 들어 "5 층에 있는 사무실" 이란 개념은 "5 층에 있는 조교수의 사무실" 이란 개념보다 더 일반적이다. 일반화와 특수화는 개념간의 전이 관계 (transitive relation) 이다. 우리는 C2 의 특수화이고 동시에 C1 의 일반화가 되는 다른 개념이 없을 때 C1 은 C2 의 직접 특수화 (immediate specialization) 라 말한다.
하나의 버전공간 은 하나의 그래프로써 표현되고, 그 그래프의 노도는 개념을 나타내고, 그래프의 선은 하나의 개념이 다른 개념의 직접 특수화인 관계를 나타낸다. 이 절에서 설명하는 방법은 버전공간을 사용하여 지금까지 보여진 예제들과 일관성 있는 모든 개념 집합의 표상을 간결하게 유지한다. 이 표상은 특수화 관계에 의해 유도된 순서를 이용하여 일관성 있는 가설들의 집합에 대한 일반화 경계와 특수화경계를 유지할 수 있도록 한다. 버전공간 방법은 긍정 리터럴의 논리곱에 대해서는 최적의 방법이 되는데, 이것은 어떤 방법도 이 문제에 대한 편중을 구현하는 데 더 빠른 방법을 제공하지 못한다는 뜻이다. 기본적으로 이 방법은 다른 가설공간에 대해서도 잘 작동되지만 계산적인 복잡도가 너무 높다.
좀더 구체적으로 설명하기 위해서 3 개 층을 돌아다니면서 쓰레기를 줍고 재활용품을 찾는 청소로봇 문제로 돌아가자. 로봇은 어느 사무실에 재활용 상자가 있는지를 학습하려고 한다. 각 사무실에 대해서 로봇은 다음의 정보를 미리 안다. 즉, 각 사무실이 교수사무실인지, 직원용인지, 아니면 학생용인지 또한 사무실이 3, 4, 5 층 중 몇 층에 위치해 있는지, 사무실이 전산과에 속해 있는지 또는 전자과에 속해 있는지 그리고 방의 크기가 큰지, 중간인지, 작은지를 알고 있다. 이 정보의 조합으로 로봇은 가능한 모든 예제공간의 구조를 정의할 수 있게 되고, 이것을 이용하여 학습을 하게 된다.
속성, 특징 그리고 차원
속성 (attribute) 은 가능한 훈련예제들의 공간인 X 에 속하는 객체들을 묘사하는 데 사용되는 변수이다. x 가 X 의 원소라고 주어졌을 때, x 의 각 속성은 가능한 값들 중에서 오직 하나의 값만을 가진다. x 의 모든 속성들과 그 속성에 가능한 모든 값을 X 의 차원 (dimension) 이라고 부른다. 한 속성과 그 속성에 할당된 값의 쌍을 특징 (feature) 이라고 한다. 로봇 예제에서는 4 개의 차원이 있는데, 다음과 같이 표기할 수 있다 (status, {faculty, staff, student}), (floor, {three, four, five}), (dept, {ee, cs}), (size, {large, medium, small}).
각 개념들을 그 개념에 대한 속성들의 불리언 조합으로써 표현할 수 있다. 이 책에서 사용되는 예제에서는 모든 속성들이 서로 다른 종류의 값을 갖는다고 가정하므로 특징을 표현할 때 종종 그 특징에 해당하는 속성의 이름은 생략하고 그 값만으로 줄여서 표기한다. 다른 제한된 가설공간에서의 개념들에 대한 예제들을 살펴보자. 긍정 리터럴의 논리곱을 이용해서 5 층에 있는 전산과 교수사무실에 대응하는 개념을 다음과 같이 표현한다.
faculty ∧ cs ∧ fifth
다음에 나타난 논리합으로 표현된 것은 큰 사무실이거나 학생들의 사무실이라는 개념을 나타낸 것이다.
large ∨ student
마지막으로 각 논리곱마다 최대한 2 개까지의 불리언 변수를 갖는 CNF 를 이용해서 표현된 다음의 표현 예는 학생들의 사무실이거나 전산학과 교수사무실이라는 개념을 나타낸 것이다.
student ∨ (faculty ∧ cs)
개념의 특수화와 일반화
다음의 3 차원적으로 생성되는 예제들의 공간을 긍정 리터럴의 논리곱으로 표현한 버전공간을 고려해 보자 (status, {faculty, staff}), (floor, {four, five}), (dept, {ee, cs}). 가장 일반적인 개념은 True 로 표현되거나 논리곱 인자가 없이 단순히 논리곱 연산자인 ∧ 로 표현된다. 즉, ∧ 라는 표현은 가장 일반적인 개념이라는 의미로 청소로봇의 예에서는 모든 사무실을 가리킨다. ∧ 의 직접 특수화된 개념은 단일 리터럴에 대응하는 개념이다. 즉, ee 나 faculty 는 ∧ 보다 한 단계 특수한 개념으로써 각각 전자과에 속하는 사무실 그리고 교수사무실에 해당된다. 2 개의 속성 리터럴이 논리곱으로 결합된 것은 단일 리터럴의 직접특수화 (immediate specialization) 이고, 3 개의 속성 리터럴의 논리곱으로 결합된 것은 2 개의 개념의 논리곱에 대해 직접특수화이다. 이 예제에서 사용되는 제한된 표현언어에서는 3 개 리터럴의 논리곱은 실제 예제인 각 사무실에 해당된다.
그림 2 는 예제들의 3 차원 공간과 리터럴의 논리곱에 대한 제한을 고려한 로봇예제의 버전공간을 나타낸 것이다. 이 절의 나머지 부분에서는 일반적 경계 (general boundary) 와 특수적 경계 (special boundary) 를 수정해 가는 실시간 알고리즘에 대해 설명한다. 초기에 일반적 경계는 그림의 가장 상위에 위치한 ∧ 으로 특수적 경계는 그림의 가장 하위에 위치한 모든 3 개 리터럴의 논리곱 집합으로 되어 있다. 그림 2 에는 지면 관계상 모든 가능한 2-논리곱과 3-논리곱 중에 몇 개가 생략되었다.
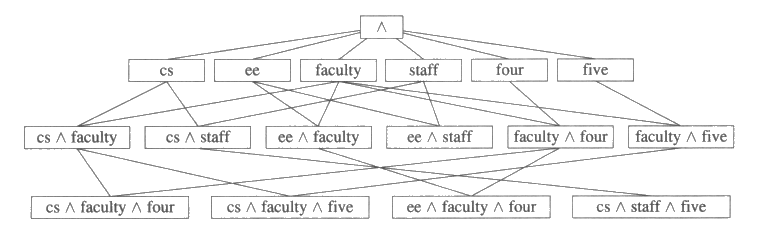
그림 2 : 청소로봇 영역에서의 간단한 버전공간의 예. 긍정리터럴의 논리곱을 포함하고 있는 직사각형 상자들은 각각 하나의 개념을 표기한다. 두 상자간의 선은 아래쪽에 연결된 상자의 개념이 위쪽에 연결된 상자의 개념에 대한 직접특수화인 관계를 나타낸다.
훈련예제들이 주어질 때마다 경계는 수정된다. 만일 훈련예제가 긍정예제 (general boundary) 이면 특수적 경계 내에 있는 각 개념들을 예제와 일관성이 있을 때까지 일반화한다. 개념이 긍정 리터럴 논리곱으로 표현된 경우에는 일반화란 논리곱인자를 없애는 작업이다. 예를 들어 특수한 경계 내에 "purple and smooth" 라는 개념이 있고 "purple and rough" 라는 긍정 훈련예제가 들어왔다면 "purple and smooth" 를 "purple" 로 일반화시킬 수 있다. 좀더 풍부한 표현이 가능한 가설공간에서는 논리합을 도입하거나 상수에 관련된 개념을 한정식 (quantified formula) 으로 표현함으로써 일반화시킬 수 있다.
만일 훈련예제가 부정예제 (negative example) 이면 학습된 개념이 부정 예제와 일관성이 없도록 하기 위해 일반적 경계 내에 있는 각 개념을 특수화시킨다. 한정된 가설공간에서의 특수화는 논리곱인자를 추가시키는 작업으로 구성되어 있다. 좀더 풍부한 표현을 사용하는 가설공간에서 논리합인자를 없애거나 전체한정식 (Universally quantified formula) 을 사례화 (instantiate) 함으로써 특수화를 할 수 있다.
만일 이와 같은 규칙에 의해 특수적 경계와 일반적 경계가 유지되었을 때 두 경계사이에 위치하는 개념은 모든 긍정예제를 포함하고 모든 부정예제를 제외한다는 것을 보증한다. 정확히 말해서 개념 C 에 대해서 다음과 같이 정의된 C' 과 C" 이 존재한다면 C 는 모든 긍정예제를 포함하고 모든 부정예제를 제외한다고 보증한다.
1. C' 은 일반적 경계 안에 있다.
2. C 는 C' 와 같거나 C' 보다 특수하다.
3. C" 는 특수적 경계 안에 있다.
4. C 는 C" 와 같거나 C" 보다 일반적이다.
5. C' 은 C" 와 같거나 C" 보다 일반적이다.
버전공간 경계의 유지
우리가 하나의 개념으로 수렴하는 경계를 원한다면 경계로부터 개념들을 제거하기 위해 좀더 작업을 해야 한다. 경계를 유지하기 위한 완전한 알고리즘을 여기에 소개한다. 이 알고리즘은 모든 훈련예제와 일관된 개념이 하나만 존재할 경우 그 개념으로 수렴하는 것을 보증하는 알고리즘이다.
① 예제가 긍정이면 다음의 과정을 수행하라.
a) 예제와 일관성이 없는 일반적 경계 안에 있는 모든 개념들을 제거하라.
b) 예제와 일관성이 있을 때까지 특수한 경계 안에 있는 모든 개념들을 최소한으로 일반화시키고 다음의 두 요구조건을 만족시키지 못하는 것들을 제거하라.
i. 각 개념은 일반적 경계 안에 있는 어떤 개념의 특수화이다.
ii. 각 개념은 특수적 경계 안에 있는 어떤 다른 개념의 일반화가 아니다.
② 예제가 부정이면 다음의 과정을 수행하라.
a) 예제와 일관성이 있는 특수적 경계 안에 있는 모든 개념들을 제거하라.
b) 예제와 일관성이 없을 때까지 일반적 경계 안에 있는 모든 개념들을 최소한으로 특수화시키고 다음의 두 요구조건을 만족시키지 못하는 것들을 제거하라.
i. 각 개념은 특수적 경계 안에 있는 어떤 개념의 일반화이다.
ii. 각 개념은 일반적 경계 안에 있는 어떤 다른 개념의 특수화가 아니다.
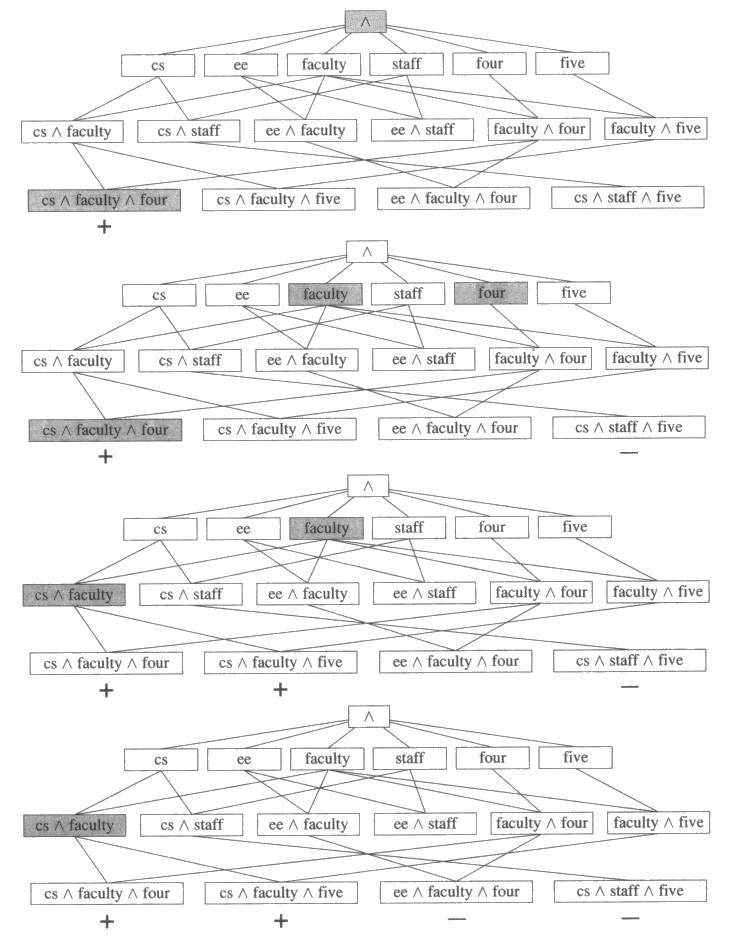
그림 3 : 버전공간에서 경계들의 수렴과정. '+' 표시가 된 예제는 긍정예제, '-' 표시는 부정예제를 가리킨다. 어둡게 칠해진 상자는 주어진 훈련예제를 반영해서 수정된 두 경계를 표시하고 있다. 마지막 그림에서는 두 경계가 하나의 상자로 수렴한 것을 볼 수 있다.
그림 3 은 각 긍정과 부정 예제들의 입력에 따라 버전공간과 경계들이 변화해가는 모습을 보여준다. 간단히 하기 위해서 예제들은 3 개의 논리곱인자들의 논리곱 형태로 표현되며 +, - 는 각각 긍정과 부정을 나타낸다. 맨 위의 그림에서는 긍정예제가 하나 입력되었으며, 이때의 특수적 경계는 바로 그 예제에 대응되고 일반적 경계는 가장 일반적인 개념인 ∧ 에 대응된다. 두번째 그림에서는 CS ∧ staff ∧ five 가 부정 훈련예제로 제시되고 ∧ 로만 구성되었던 일반적인 경계는 faculty 와 four 로 특수화된다. 세번째 그림에서 CS ∧ faculty ∧ five 가 긍정예제로 제시되고, 이에 따라 각 경계는 변한다. 마지막 그림에서는 부정예제가 하나 더 추가되면서 경계가 하나의 개념으로 수렴하였다. 즉, 4 개의 훈련예제로부터 전산학과 교수사무실에만 재활용상자가 있다는 것을 학습하게 된 것이다.
학습을 위한 자료구조
이 장에서는 몇 개의 알고리즘을 Lisp 로 구현한 것을 제공한다. 다른 인공지능분야와 마찬가지로 학습에서의 이론적 연구는 경험적 연구를 대신하지는 못한다. 학습 알고리즘의 한계에 대하여 유용한 통찰력을 얻는 것은 종종 실험을 통해서 이루어진다. Lisp 에서 학습 알고리즘을 구현하기 위해서 다음의 몇 가지 추상적 자료타입을 소개한다. FEATURE 는 하나의 속성과 그 속성의 값을 나타낸다.
(defun make-FEATURE (attribute value) (list attribute value))
(defun FEATURE-attribute (feature) (first feature))
(defun FEATURE-value (feature) (second feature))
DIMENSION 은 하나의 속성과 그 속성의 모든 가능한 값들의 집합을 나타낸다.
(defun make-DIMENSION (attribute values) (list attribute values))
(defun DIMENSION-attribute (dimension) (first dimension))
(defun DIMENSION-value (dimension) (second dimension))
EXAMPLE 은 예제의 고유이름과 그 예제를 묘사하는 특징들의 집합과 그리고 어느 부류에 속하는지에 대한 표현으로 나타난다. 이 책의 예제에서 표현되는 부류는 yes 와 no 두 개뿐이다.
(defun make-EXAMPLE (id features class) (list id features class))
(defun EXAMPLE-id (example) (first example))
(defun EXAMPLE-features (example) (second example))
(defun EXAMPLE-class (example) (third example))
Dimension 은 인자가 없는 함수로서 주어진 문제와 연관된 차원의 리스트를 출력한다. Classes 도 인자가 없는 함수로서 주어진 분류문제 영역의 모든 부류를 대표하는 기호의 리스트를 반환한다. Dimension 과 Classes 는 전역 변수를 사용하기 때문에 바람직하지 않은 프로그램 방법이다. 이 방법은 좋은 프로그램 스타일이 아니지만 교육적 목적을 위해서 간단한 프로그램을 위해 허용한다. 이 함수에서는 차원과 부류를 매개변수로 전달하지 않기 때문에 프로그램이 매우 간단하다.
버전공간 방법의 구현
이 장의 마지막에서 버전공간 방법의 Lisp 프로그램을 제공한다. 다음의 차원과 부류가 존재한다고 가정하고 yes 와 no 는 사무실에 재활용 상자가 있는가 없는가를 나타낸다고 가정하자.
(defun dimensions ()
(list (make-DIMENSION 'status '(faculty staff)
(make-DIMENSION 'floor '(four five))
(make-DIMENSION 'dept '(cs ee))))
(defun classes () '(yes no))
훈련예제는 특징 (features) 의 리스트로 표현된다. 우리의 제한된 가설공간을 위해서 개념 역시 특징의 리스트로 표현된다. 그림 3 의 초기 경계와 4 개의 훈련예제에 대한 Lisp 표현은 그림 4 에 나타나 있다. 훈련예제들의 속성에 대응하는 모든 개념들을 포함하도록 특수적 경계를 지정한다. 일반적 경계는 단지 공백 리스트로 표현되는 인자가 없는 논리곱이다.

그림 4 : 훈련예제와 초기 경계 설정에 대한 Lisp 표현
그림 5 는 그림 4 에 있는 초기 경계와 훈련예제를 가지고 버전공간 방법으로 구현한 결과를 보여준다. 최종 훈련예제에 의하여 일반적 경계와 특수적 경계가 하나의 개념으로 수렴하는 것을 주목해라.

그림 5 : 버전공간의 경계 조정과정
긍정 리터럴의 논리곱을 위한 최적의 방법
버전공간 방법은 긍정 리터럴의 논리곱으로 표현되는 제한된 가설공간에 대해서는 근사적으로 최적의 방법이다. 이 방법은 다른 가설공간에서도 사용될 수 있지만 다른 몇몇의 경우에는 가능한 개념의 수가 너무 많아서 실용적이 되지 못한다. 모든 가능한 불리언 공식으로 이루어진 가설공간에서 개개의 개념은 상당히 커질 수 있고, 또 어떤 개념에 대해서는 버전공간 방법에서의 경계들을 명백히 표현하기 힘들 경우도 있다. 이런 경우에 훈련예제와 일관성 있는 모든 가설을 표현하겠다는 목표를 버리고, 훈련예제와 일관성이 있는 가설 중에 상대적으로 작고 표현하기 쉬운 것을 찾는 데 만족해야 한다. 다음 절에서는 이렇게 하기 위한 휴리스틱 방법에 대해서 논의한다.
학습의 가장 단순한 형태인 기계적 암기학습은 단순히 경험한 모든 것을 기억하는 것을 말한다. 이 방법은 개념학습의 경우 모든 예제와 그것의 긍정, 부정을 기억하는 것을 요구한다. 그러나 이 기계적 암기학습은 새로운 예제에 대해서 적용하기가 어렵다. 즉, 기존의 예제에서 볼 수 없었던 것까지 설명할 수 있도록 일반화 시켜야지만 새로운 예제를 올바르게 분류할 수 있게 된다. 그러나 모든 예제의 특징을 기억하는 대신에 부정예제와 긍정예제를 구분하는 역할을 하는 특징이 뚜렷한 예제만을 기억한다고 가정하면 매우 일반적인 방법으로 발전할 수 있다. 예를 들어 그림 2 의 버전공간에서 전자계산학과에 속하는 사무실은 긍정이고, 그렇지 않은 사무실은 부정이고, 나머지 특징들은 분류에 중요한 요소가 아니다.
4 장 탐색에서 정보의 저장과 효과적인 검색을 위해 결정트리 (decision tree : discrimination tree 라고도 함) 들의 사용을 고려했다. 이 장에서는 분류를 위한 방법으로 사용되는 특수 목적 메모리를 설계하기 위해서 결정트리를 소개하려고 한다. 결정트리의 각 비단말 노드 (nonterminal node) 에는 트리의 단말 노드에 저장된 개체들에 관한 질문이 들어있다. 질문에 대한 대답에 의해서 그 질문이 소속된 노드의 자식 노드로 연결된 가지를 따라 밑으로 내려가면서 트리의 어느 위치에 새로운 개체를 저장할 것인지 결정하게 된다. 결정트리의 뿌리 (root) 로부터 다른 노드로의 경로는 일련의 질문과 해답에 대응이 된다. 단말 노드에 저장이 된 개체들은 모두 다 뿌리로부터 각 노드로 가는 경로 위에 있는 질문과 해답들과 일치하는 개체들이다. 이 장에서 질문은 속성에 해당되고 해답은 그 속성의 값에 해당된다. 뿌리로부터 노드의 경로에 있는 질문들과 해답들은 모든 가능한 예제들의 집합의 어떤 부분 집합을 정의하는 특징들의 논리곱 형태로 표현된다.
표 1 : 청소로봇 문제를 위한 훈련예제들 |
|||||
|
# |
status |
floor |
department |
size |
recycling bin? |
|
307 309 408 415 509 517 316 420 |
faculty staff faculty student staff faculty student staff |
three three four four five five three four |
ee ee cs ee cs cs ee cs |
large small medium large medium large small medium |
no no yes yes no yes yes no |
분류 목적을 위해서 한 개의 단말 노드에 같은 부류에 속하는 개체들을 숫자에 관계없이 포함시킬 수 있다. 표 1 은 변형된 청소로봇 문제를 위한 몇 개의 훈련예제들을 보여준다. 마지막 열은 재활용 상자가 사무실에 있는지 (yes), 없는지 (no) 를 나타낸다. 그림 6 은 표 1 에 있는 예제들을 위한 결정트리를 보여준다. 어둡게 칠해진 항목들은 재활용 상자가 있는 사무실을 나타낸다. 509 와 420 은 같은 단말 노드에 저장되어 있다는 것을 명심해라.

그림 6 : 청소로봇 문제를 위한 결정트리이다. 비단말 노드들은 속성에 관한 정보가 표시되어 있다. 선에는 그 속성에 대한 값이 붙여져 있다. 단말 노드들은 원으로 표현되었고, 단말 노드들의 밑에는 그 노드에 속한 훈련예제들이 사무실 번호로서 표현되었다. 검게 칠해진 사각형은 재활용 상자가 있는 사무실을 의미한다.
작은 결정트리를 위한 선호 구현
그림 6 에 있는 결정트리가 가진 문제점은 새로운 예제에 대한 일반성이 떨어진다는 것이다. 예를 들어 그 결정트리는 전자공학과 학생들이 사용하는 중간 크기의 사무실에 대하여 아무 정보도 줄 수 없다. 그림 7 의 결정트리는 부류에 따라 예제들을 분별할 수 있는데, 그림 6 의 트리보다는 훨씬 더 간단하게 표현되었다. 이 트리로부터는 전자공학 학생들이 사용하는 중간 크기의 사무실은 재활용 상자를 가지고 있다고 결론을 내릴 수 있다. 실제로 이 결정트리는 모든 학생 사무실이 재활용 상자를 가지고 있다고 나타내고 있는데, 이것은 주어진 자료에 의하면 합리적 가설이다. 이 두 개의 결정트리는 각각 목표 분류함수에 대하여 나름대로의 합리적인 가설을 표현하고 있는데, Occam 의 면도칼에 의하면 둘 중에서 더 작은 것을 선택해야 한다. 다음에 우리는 어떻게 이러한 선호 편중을 구현하는가를 설명한다.
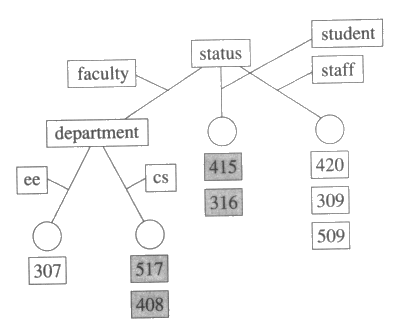
그림 7 : 청소로봇 문제를 위한 간단한 결정트리
선호 편중은 일반적으로 매우 어려운 문제로 알려진 최적화 문제를 야기한다. 훈련예제와 일관성이 있으면서 가장 작은 결정트리를 선택하는 것은 계산적으로 매우 어렵다. 효율적이고 정확한 해답 대신에 어느 정도 근접한 해답을 제공하는 휴리스틱을 찾아야 한다. 다음에 설명되는 결정트리를 만드는 방법은 최적의 결정트리를 찾는다고 보장하지는 못한다. 그러나 이 방법이 실제적으로 어느 정도 잘 동작하는 것이 싫증되어 왔다.
결정트리를 구현하기 위해 트리의 노드에 대한 추상적 자료 타입을 정의해야 한다. 결정트리는 속성, 예제들의 리스트, 자식 노드의 리스트로 구성되어 있다.
(defun make-NODE (examples) (list nil examples nil))
(defun NODE-attribute (node) (first node))
(defun NODE-examples (node) (second node))
(defun NODE-children (node) (third node))
(defun set-NODE-attribute (node attribute)
(setf (first node) attribute))
(defun set-NODE-children (node children)
(setf (third node) children))
테이블 1 의 예제들에 의하면, 가능한 예제들의 공간은 4 차원이고 이 문제는 예제들을 2 개의 부류로 분류하는 문제이다.
(defun dimensions ()
(list (make-DIMENSION 'status '(faculty staff student))
(make-DIMENSION 'floor '(three four five))
(make-DIMENSION 'dept '(cs ee))
(make-DIMENSION 'size '(large medium small))))
(defun classes () '(yes no))
결정트리를 찾아내는 방법은 루트로부터 아래로 결정트리를 만들어 가는 것이다. 루트는 항상 모든 훈련예제들의 집합을 포함하고 있다. 다른 모든 노드들은 루트로부터 노드로의 경로에 의해 결정된 예제들의 부분집합을 포함하고 있다. 한 노드에 속한 모든 예제가 하나의 부류로 결정되면 그 노드는 단말 노드가 된다. 단말 노드의 경우에는 분류를 위하여 더 이상 식별을 할 필요가 없다.
Lisp 구현에 관해 설명한 절에서 우리는 결정트리를 만드는 buildtree 라는 함수를 구현하였다. buildtree 는 처음 시작에 모든 훈련예제를 포함하지만 어떤 지정된 속성이나 자식을 가지지 않는 하나의 노드를 가지고 호출되는 재귀함수이다. buildtree 의 알고리즘은 다음과 같다.
① 만일 노드에 있는 모든 예제들이 같은 부류에 속하면 중지하라.
② 만일 한 노드에 있는 모든 예제들이 같은 부류에 속하지 않으면 다음의 과정을 수행하라.
a) 몇 개의 속성을 선택하고 그것을 노드의 속성으로 지정하라.
b) 선택된 속성의 값에 의해서 예제들을 분할하여라.
c) 적어도 한 개 이상의 예제를 갖는 각 분할에 대해서 한 개의 새로운 노드들을 생성하라.
d) (c) 에서 생성된 새로운 노드들의 리스트를 위 노드의 자식으로 지정하라.
e) 각 새로운 노드들에 대해 Buildtree 를 재귀적으로 적용하라.
알고리즘에서 유일하게 어려운 부분은 어떤 속성을 선택하는가 하는 것이다. 모든 예제들을 갈라놓지 못하고 하나의 부분집합에 속하도록 하는 속성은 훈련예제를 분류하는 능력의 개선이 없이 결정트리만 커지게 만드는 것이다. 다음에 실제적으로 결정트리를 작게 만들 수 있는 속성을 선택하기 위한 규칙적인 접근방법에 대하여 설명한다.
무질서와 정보 이론
S 를 모든 훈련예제들의 집합으로 할 때 이 S 의 모든 원소를 잎 (leaves) 노드로 갖는 결정트리를 고려해보자. 새 예제를 분류함에 있어서 가능한 한 적은 수의 질문을 하면서 그 예제를 포함한 잎 노드를 찾을 수 있기를 원한다. 그러기 위해서 우리는 가능한 한 결정트리가 작아지기를 원하는 것이다. 가장 작은 결정트리를 찾는 것은 계산적으로 어렵기 때문에 트리를 루트로부터 아래로 휴리스틱을 사용하여 질문을 포함한 노드의 하부트리에서 무질서 (disorder) 의 정도가 최소화되는 속성에 대한 질문을 선택하면서 결정트리를 만든다.
정보 이론 (information theory) 은 무질서와 정보의 개념을 연결시킨다. 집합이 무질서할수록 그 집합의 원소를 추측하는 데 더 많은 정보가 요구된다. 예를 들어 한사람이 수의 집합에서 하나의 숫자를 선택한 후 그 숫자를 추측하라고 질문할 수 있다. 주어진 임의의 유한 집합에서 그 숫자를 맞추기 위한 가장 좋은 방법은 반복적으로 그 집합을 반으로 나누고 그 중에서 숫자가 어디에 속하는지를 묻고 다시 그 답에 대하여 나누고 묻는 작업을 반복적으로 하면 된다. 이 방법을 사용하면 집합 S 의 원소를 맞추는 데 요구되는 질문의 수는 log2 |S| 이다. 이 수를 맞는 원소를 추측하는 데 사용되는 시간이라는 개념으로 보지 말고 x 라 불리기 위한 정보의 값으로 생각하자.
U 를 S 의 부분집합이라 하자. x ∈ U 인지를 알아낸 후에 x 라 불리기 위한 정보의 값은 다음과 같다.

Pr (x ∈ U) 는 |U| / |S| 의 식으로 표현되는 비율이고 Pr (x ![]() U) 는 1-
Pr (x ∈ U) = |S - U| / |S| 이다. 집합 U 와 S - U 는 S 의 분할이 된다. P U N
= S 일 때, 분할 {P, N} 을 위한 식을 다시 쓰면 x ∈ P 인지 x ∈ N 인지를 알고 난 다음에는 x
라 불리기 위한
정보의 값을 다음과 같이 얻을 수 있다.
U) 는 1-
Pr (x ∈ U) = |S - U| / |S| 이다. 집합 U 와 S - U 는 S 의 분할이 된다. P U N
= S 일 때, 분할 {P, N} 을 위한 식을 다시 쓰면 x ∈ P 인지 x ∈ N 인지를 알고 난 다음에는 x
라 불리기 위한
정보의 값을 다음과 같이 얻을 수 있다.

결정트리의 노드와 관련된 속성은 그 속성의 가능한 값에 의하여 그 노드에 속한 예제들을 분할하는 역할을 한다. 속성 분할의 모든 가능한 부분 집합들은 그 자체가 가능한 부류들로 분할된다.
부류 분할과 속성 분할의 차이점을 이해하기 위하여 S = {307, 309, 316, 408, 415, 420, 509, 517} 을 숫자로 분별되는 표 1 에 있는 예제들의 집합으로 놓자. {{316, 517, 415, 408}, {420, 509, 309, 307}} 은 S 의 부류 분할이다. {{517, 408, 307}, {420, 509, 309}, {316, 415}} 는 status 라는 속성에 의하여 만들어진 S 의 속성 분할이다. 3 개의 집합 {{408, 517}, {307}}, {{ }, {309, 509, 420}} 과 {{416, 316}, { }} 은 S 의 속성 분할의 3 개 부분 집합을 status 속성에 따라서 분류한 부류 분할들이다.
여기서 우리는 무질서를 최소화하는 노드의 속성을 선택하는 것이 중요하다. 속성을 선택하는 이 방법은 최소 크기의 결정트리를 찾는다는 보장은 없으나 (연습문제 8 참고) 실제적으로는 그런대로 잘 작동한다 {Si | 1 ≤ i ≤ n} 을 특정한 속성에 의해서 생성된 S 의 분할로 놓자. 간단히 하기 위해서 2 개의 부류와 관련된 개념 학습의 경우로 하고 P (Si) 를 Si 에서의 긍정 예제의 집합으로 놓고 N (Si) 를 부정 예제의 집합으로 놓자. 이 속성 분할과 연관된 정보의 값 (또는 무질서) 은 부류 분할 {P (Si), N (Si)} 의 정보 값을 모든 Si 에 대하여 가중값을 두어 더한 확률이다.
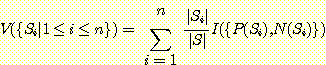
테이블 2 는 테이블 1 의 예제들을 포함한 노드를 위한 4 개 속성과 연관된 무질서와 부류 분할의 결과를 나타낸다. 테이블 2 는 이 노드에 status 라는 속성이 할당되어야 한다는 것을 보여주고 있다.
표 2 : 무질서와 다양한 속성들을 위한 분류 결과 |
||
|
속성 |
무질서 |
분류결과 |
|
status floor department size |
0.34 0.94 1.00 0.94 |
{{408,517},{307}} {{},{309,509,420}} {{415,316},{}} {{316},{307,309}} {{408,415},{420}} {{517},{509}} {{408,517},{509,420}} {{415,316},{307,309}} {{415,517},{307}} {{408},{509,420}} {{316},{309}} |
임의의 부류 분할 {X | 1 ≤ i ≤ n} 에 대해서 일반화하기 위하여 찾으려는 원소를 포함한 분할의 부분집합을 아는 것의 값은 다음과 같다. X = X1 U X2 ... Xn 이라고 할 때
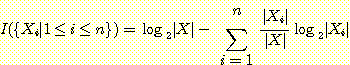
노드에 속한 예제들을 분할하는 속성을 선택할 때, 이러한 무질서의 척도를 사용한다. 이 척도는 실제적으로 잘 적용된다. 그러나 다른 척도들도 비슷한 성능을 보인다. 성능의 척도는 예제들이 각 부류에 동일한 숫자만큼 나누어진 경우에 최대가 되며 모든 예제들이 하나의 부류에 속하면 최소가 된다.

그림 8 : 훈련예제 집합의 Lisp 표현
그림 8 은 표 1 에서 보여진 훈련예제들을 Lisp 표현으로 나타낸 것이다. 그림 9 는 표 1 로부터의 훈련예제의 집합에 대한 Buildtree 의 작동을 보여준다. Buildtree 가 그림 7 에 있는 결정트리와 다른 트리를 생성하나 그것의 크기는 서로 같다는 것을 살펴보기 바란다.

그림 9 : buildtree 에 의해서 결정트리가 만들어지는 과정. 두번째 줄부터 각각 buildtree 가 적용되고 있는 노드에 속하는 예제들의 집합을 두 부류로 나누었을 때 각 부류에 속한 예제들의 수를 리스트로 표시하였다. 또한 그 노드가 단말 노드인지, 아니라면 그 노드에 대해서 어떤 속성에 이용하여 분류를 했는지에 대한 정보를 보여주고 있다.
실제 응용에서의 결정트리
결정트리를 현실 세계의 응용에 적용하기 위해서는 고려해야 할 것들이 굉장히 많다. 연속적인 값의 속성결정, 이산적인 값들의 매우 큰 집합, 또는 학습 예제에 속성값이 없는 경우 등 이런 문제들을 다루기 위해 여러 가지 기법들이 제안되었다. 잡음 (noise) 예제는 실제로 빈번히 발생하는 또 하나의 문제이다 (연습문제 6 참고). 청소로봇의 경우 때때로 그 로봇이 전자공학과 사무실을 전산과 사무실로 착각한다고 가정해보자. 다양한 통계적인 조사는 실험을 이용해 잘못된 예제들을 고려하지 않도록 해야 한다. 그러나 이러한 실험을 이용하기 위해서는 확률값을 알아내기 위해 더 많은 학습예제들이 필요하다. 다른 예로, 사무실에서 불이 켜지고 꺼지는 것을 학습의 문제에서 한 차원의 속성으로 고려한다고 가정하자. 물론 재활용 상자가 있는 사무실을 분류하는 경우에 우리는 이러한 차원을 무시하고자 할 것이다. 그러나 만일 그것이 문제와 관련이 있다고 가정하면 시간에 따라 변하는 그런 속성이 그 문제를 해결하기 어렵게 할 수도 있다. 기본적인 결정트리 방법은 가장 널리 사용되고 성공적인 학습 방법이다. 그리고 실제 응용에 대해 도움이 되는 좋은 문헌들이 매우 많이 있다 (예로 Ouinlan [1986] 또는 Breiman et. aI [1984] 을 참고).
이번 절과 앞으로 전개될 세 절에서는 병렬망 계산 모형 (network parallel computing model) (역자주 : 보통 신경회로망 (neural network), 인공신경망 (artificial neural network), 연결주의 모형 (connectionist model) 이나 병렬분산처리 (parallel distributed processing : PDP) 모형 등으로 불리우나 여기서는 원자의 어휘에 충실한다는 의미에서 병렬망 계산 모형 (network parallel computing model) 이라고 번역한다.) 에 관해 논의할 것이다. 병렬망 계산 모형은 계산 요소 (unit) 들로 구성되어 있는데, 이 계산 요소는 간단한 함수 (function) 를 계산한다. 이런 계산 요소들은 더욱 복잡한 함수를 계산하기 위해 서로 연결되어 있다. 계산 요소들은 각각의 요소의 입력에서 출력으로 값 (value) 을 전파시킴으로써 계산을 수행하는데, 각각의 요소들에 해당되는 계산을 병렬적으로 특정 모형에 따라 동시에 수행되기도 하고 비동시적으로 수행하기도 한다.

그림 10 : 망 계산 모형의 기본적인 요소들. 제일 위에 있는 요소는 합 요소 (summation unit) 로서 n 개의 입력을 가지며, 이들의 합을 계산해낸다. 중간에 있는 요소는 곱 요소 (multiplication unit) 로서 하나의 입력값을 상수 w 와 곱한다. 가장 밑에 있는 요소는 임계요소 (thresholding unit) 로서 하나의 입력값이 0 보다 크면 1 을 출력하고, 그렇지 않은 경우에는 0 을 출력한다.
그림 10 은 망 계산 모형에서 가장 많이 사용하는
3 가지 요소들을 나타내고 있다. 합 요소 (summation unit) 는 n 개의 입력을 가지고
있으며, 이것은 입력으로 들어오는 값을 모두 합하며 수식으로는 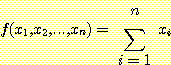 으로 나타낸다. 곱 요소 (multiplication unit) 는 하나의 입력값을 상수인 w
와
곱하는 것으로 수식으로는 f (x) = wx 로 나타낸다. 마지막으로 임계요소
(thresholding unit) 는 하나의 입력값이 0 보다 크면 1 을 출력하고 그렇지 않은 경우에는 0
을 출력한다.
으로 나타낸다. 곱 요소 (multiplication unit) 는 하나의 입력값을 상수인 w
와
곱하는 것으로 수식으로는 f (x) = wx 로 나타낸다. 마지막으로 임계요소
(thresholding unit) 는 하나의 입력값이 0 보다 크면 1 을 출력하고 그렇지 않은 경우에는 0
을 출력한다.
|
f (x) = |
|
1 |
if x > 0 |
|
0 |
otherwise |
이 3 가지 요소들은 그림 11 과 같은 이른바 선형 임계요소 (linear threshold unit) 로 결합된다.
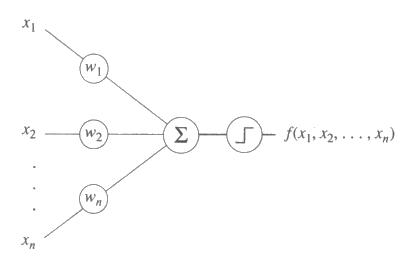
그림 11 : n 개의 입력값에 대한 가중값의 합이 0 보다 크면 1 을 출력하고, 그렇지 않은 경우에는 0 을 출력하는 선형 임계요소
생물 시스템에서의 계산모형
신경세포 (neuron) 는 생물 시스템이 정보처리를 하는 가장 기본적인 요소이다. 선형 임계요소는 이런 신경세포들을 위한 모형으로 사용되어져 왔다. 이 모형은 일반적으로 McCulloch-Pitts 신경세포라 한다. 실제 신경세포는 McCulloch-Pitts 신경세포와는 달리 매우 복잡하다. 예를 들면, 실제 신경세포는 입력값들을 합하는 계산을 선형적이라기 보다는 비선형적으로 수행하고, 출력이 (0 과 1 만의 값을 가지는) 이진화된 값이 아니라 연속적인 값이다. 생물 모형으로서의 장점이 어떻든 간에 선형 임계요소와 이와 관련된 요소 단위 (component unit) 들이 어떻게 병렬적으로 계산을 하고, 학습을 하는지에 대한 큰 관심이 있다. 이제부터는 망 계산 모형에 관련된 생물 모형의 관한 많은 부분을 무시하고 넘어갈 것이다.
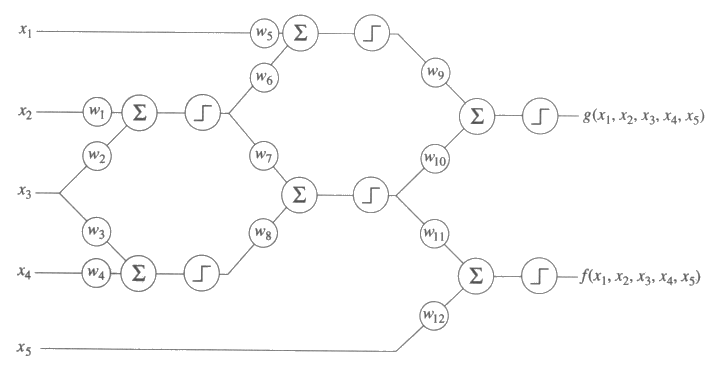
그림 12 : 신경조직과 유사한 (neural-like) 계산 요소 망
단 하나의 선형 임계요소는 계산 장치로서 한계가 있지만, 그림 12 와 같이 선형임계요소를 망으로 구성하면 임의의 부울 (Boolean) 함수를 계산하는 데 사용되어질 수 있다. 이런 망을 인공 신경회로망 (artificial neural network) 이라고도 부른다. 망 모형은 연속적인 함수를 계산하는 데 사용되어질 수 있다.
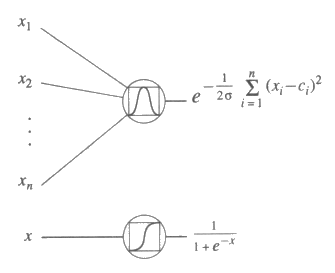
그림 13 : 망 계산 모형의 부가적인 요소들. 제일 위에 있는 요소는 n 개의 입력을 가지고 있는 여러 개의 입력 가우스 (Gaussian) 함수이고, 아래에 있는 요소는 시그모이드 (sigmoid) 함수로 임계요소를 연속적인 것으로 바꾼 것이다.
연속적인 함수를 나타내는 망에 전형적으로 사용되어지는 2 개의 함수가 그림 13 에 나타나 있다. 이 두 개의 함수는 가우스 (Gaussian) 함수와 시그모이드 (Sigmoid 혹은 logistic) 함수인데, 이 중 가우스함수는 f (x1, x2, ..., xn) = e 로서, σ 와 ci 은 상수이고, 시그모이드함수는 f (x) = 1 / (1 + ex) 이다. 가우스함수와 시그모이드함수의 예가 그림 14 에 나타나 있다.
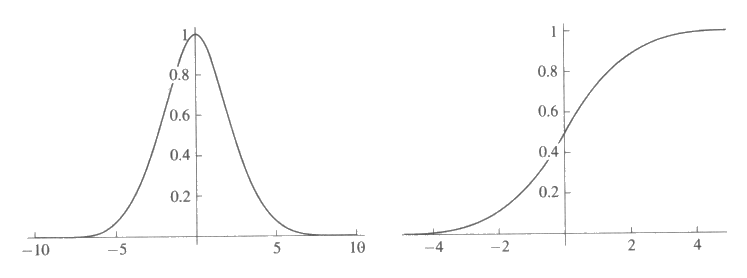
그림 14 : 연속적인 함수를 나타내는 두 개의 계산 요소들의 그래프. 왼쪽에 있는 그래프는 중심이 0 이고 폭이 5 인 가우스함수를 나타내고, 오른쪽에 있는 그래프는 시그모이드함수를 나타낸다.
가우스함수의 출력은 n 차원 입력공간에서의 가우스함수의 중앙 (center) 값인 <c1, c2, ..., cn> 까지의 거리에 의해 결정된다. 중심에서부터의 거리가 폭 (width) σ 의 2 배 이상이 되면 그 입력에 대한 출력값은 무시되어도 좋을 정도로 작다. 이런 지역적인 종류의 출력은 생물 시스템에서 발견되는 신경구조에서 흔히 볼 수 있으며, 신경망 모형을 연구하는 학자들에게 널리 알려져 있는 사실이다. 또한 함수는 분석을 간편하게 해 주는 여러 수학적인 특성을 가지고 있다. 나중에 가우스함수가 어떻게 다른 함수를 근사하는 데 사용되어지는지에 대하여 설명할 것이다.
시그모이드함수는 임계요소 (thresholding unit) 의 대안으로 사용되는데, 이 함수는 연속적이고도 미분가능하다. 그림 12 에 나타난 망을 시그모이드함수로 바꾸면 이 망은 연속적이고도 미분가능한 함수들을 나타내게 되고, 수학적으로 좀더 쉽게 다룰 수 있게 된다. 임계요소가 시그모이드함수로 바꿔 선형 임계요소를 시그모이드 요소 (sigmoid unit) 라 한다.
조정가능 가중값과 제한된 가설공간
지금까지 설명되었던 것과 같이 망 모형은 단지 계산장치일 뿐이다. 이런 망은 학습 프로그램 중 망 요소들을 기술하는 약간의 매개변수를 수정함으로써 학습에 사용될 수 있다. 이렇게 수정될 수 있는 매개변수들을 조정가능 가중값 (adjustable weight 또는 weight) 이라 한다. 이 조정가능 가중값은 매개변수 공간 (parameter space) 을 정의하는데, 이 매개변수공간의 차원은 조정가능 가중값의 수에 의해 결정된다. 예를 들어 상수값을 곱하는 요소에서 상수값은 조정가능 가중값으로 취급된다. 마찬가지로 가우스 요소의 폭 (width) 과 중심 (center) 을 조정할 수 있다. 조정할 수 있는 임계값은 표준적인 0-임계요소를 사용하고, 조정가능 가중값이 0 이 아닌 수로 할당되고 고정된 입력을 가진 부가적인 곱 요소를 추가한다면 선형적인 임계요소에서 구현될 수 있다.
조정가능 가중값들의 집합이 있는 망 모형은 함수부류에 대응되는 제한된 가설공간을
정의한다. 예를 들면 n 개의 입력이 n 개의 조정가능 가중값들과 곱해지는 합요소는
n 차원 매개변수 공간과 다음과 같은 함수 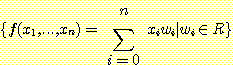 을
정의한다. 지금까지 망 모형을 사용하여 귀납적인 편중 (inductive biases) 을 나타내는
방법에 대하여 알아보았다. 다음의 세 절에서는 이런 편중을 어떻게 구현하는지 그
방법에 대하여 알아보도록 하겠다.
을
정의한다. 지금까지 망 모형을 사용하여 귀납적인 편중 (inductive biases) 을 나타내는
방법에 대하여 알아보았다. 다음의 세 절에서는 이런 편중을 어떻게 구현하는지 그
방법에 대하여 알아보도록 하겠다.
이번 절에서는 조정가능 가중값을 가지는 망 모형인 제한된 가설공간에서부터 일관된 가설을 찾는 것에 대해 살펴볼 것이다. 가설 f 에 관한 수행능력을 평방 오차의 평균 (Mean Squared Error : MSE) 을 사용하여 측정한다.
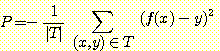
이때 T 는 훈련예제들의 집합이고 P 는 성능함수 (performance function) 라고 한다.
우리는 성능함수를 최대화하는 가장 좋은 가설을 찾아야 한다. 일반적으로 이런 가설을 찾기 위해서는 가설공간을 탐색해야 한다. 가설공간이 조정가능 가중값을 가진 연속적이고도, 미분가능한 함수에 대응되는 계산 요소로 구성된 망으로 정의되었다고 하자. 표기를 단순히 하기 위하여 가설공간이 스칼라 (scalar) 함수로 구성되어있다고 하자. 그러면 가설 f 는 함수 f (x) = F (w, x) 로 나타낼 수 있다. 여기서 w 는 조정가능 가중값들의 벡터를 의미한다. P 도 역시 연속적이고도 미분가능하다는 것과 성능함수 P 가 w 의 함수임을 주목하라.
몇몇 간단한 경우에서는 성능함수의 기울기를 0 으로 놓고 가중값에 대한 방정식의 해를 구함으로써 우리가 찾고자 하는 가장 좋은 가설을 찾아낼 수 있다. 또는 탐색을 하기 위해 기울기를 사용할 수도 있다. 기울기를 통해서 우리는 가중값을 어떻게 조정할 것인지를 알 수 있게 되고, 평방 오차가 줄어든다. 만일 기울기가 지시한 방향에서 가중값을 아주 작게 여러 번 조정한다면, 결국 가중값이 어떤 방향으로 조정되더라도 성능이 더 이상 개선되지 않는 가중값을 얻게 될 것이다. 이 경우를 성능함수의 지역 최대값이라 한다. 만일 운이 좋다면 지역 최대값이 전역 최대값이 될 수도 있고, 평방 오차의 평균을 가장 최소화하는 가설을 찾을 수도 있는 것이다.
다음의 제한된 가설공간을 생각해 보자.
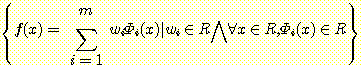
이때는 Φi 는 서로 다른 실수함수이다. 성능함수의 기울기 ▽P 는 미분가능한 가중값들에 대해 편미분한 벡터이다.
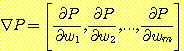
이때
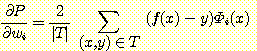
이다. ∇P 는 P 를 wi 에 대하여 편미분하여 얻어진 값으로 j ≠ i 인 wj 를 모두 가지고 있다.
기울기 방법은 대개 학습률을 가지고 있는데, 이 학습률은 기울기에 의해 지시된 방향으로 가중값들이 얼마나 조정되느냐를 결정한다. i 번째 가중값을 기울기 방법에 의하여 조정하는 규칙은 다음과 같다.
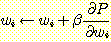
이때 β 는 학습률이고, ← 은 화살표 오른쪽에 있는 식의 결과값이 화살표 왼쪽에 있는 식에 할당된다는 것을 뜻한다.
가중값을 조정하는 이 규칙은 모든 훈련예제 (training examples) 들을 사용한다. Widrow 와 Hoff [1960] 에 의한 다음과 같은 규칙은 시간 <x, y> 에 단 하나의 훈련예제를 사용하는 예전의 규칙에의 온라인 근사를 나타낸다.

선형함수 공간에서의 탐색
예전에 기술했던 제한된 가설공간은 공간에 있는 각 함수가 {Φi} 의 선형적인 결합이기 때문에 선형함수 공간 (linear function space) 이라고 한다. {Φi} 는 함수공간에서 기저함수 (basis function) 이다. 기저함수는 입력공간에서의 특징 이라고 말하기도 하고, 이것이 선형적일 필요는 없다. 선형함수공간의 경우에는 성능함수는 가중값이 2 차로 되어 있다. 2 차 함수는 하나의 최대값을 가지는 볼록 (convex) 함수의 특별한 경우이다. 만일 가설공간이 선형적 함수공간이고 학습되어지는 함수가 가설공간에 있다면 기울기가 지시한 방향에 따라 가중값을 아주 작게 충분히 여러 번 조정한다면 평방오차의 평균이 아주 작은 가설을 찾아낼 수 있다.
예를 들어 제한된 가설 공간이 {f (x) = w0 + w1x + w2x2 + w3x3 | wi ∈ R} 이고, 그림 15의 검은 곡선과 같은 2 차 다항식을 학습한다고 하자. 훈련예제들의 집합은 40 개의 입력 / 출력쌍으로 되어 있고, 입력값은 {x | -1 ≤ x ≤ 1} 사이의 임의의 수를 선택하였다. 그림 16a 는 가중값을 조정하는 규칙을 수행시킨 결과를 나타낸 것으로, 이 규칙은 기울기를 계산하기 위해서 모든 예제들을 사용하고 β 값이 0.1 이다. 100 번의 조정을 한 후의 가설은 그림 15 의 짧은 선으로 만들어진 곡선에 나타나 있다. 그림 16b 는 가중값을 조정하는 규칙을 수행시킨 결과를 나타낸 것으로 이 규칙은, 조정을 하기 위해 많은 예제들 중에 하나를 임의적으로 선택한 단 하나의 표본을 사용하고, β 값이 0.1 이다 (기울기를 알아내기 위하여 하나만의 예를 사용하면 약간의 복잡성이 일어난다. 만일 주어진 입력의 특징이 크기 (예로 x 와 x3) 에 있어서 상당히 틀리다면 어떤 형태로든 이를 정규화시켜서 가중값을 변화시키는 데 있어서의 불균형을 제거해야 한다. 2 차 다항식을 학습시키는 예에서, 가중값을 조정하는데 다음과 같은 규칙을 사용하였다.
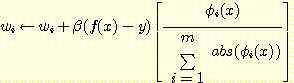
이때
|
abs (x) = |
|
x |
if x > 0 |
|
- x |
otherwise |
이다. 정확한 기울기를 계산했을 때 행해졌던 것과 마찬가지로 모든 예들을 평균하여 이와 같은 문제점을 제거할 수 있다.). 100 번의 조정을 한 후의 가설은 그림 15 의 점으로 된 곡선에 나타나 있다. 임의적으로 고른 하나의 예제를 사용한 조정 규칙은 조정을 하기 위해 주어진 정보가 거의 없음을 감안할 때 상당히 좋은 결과를 보였다.
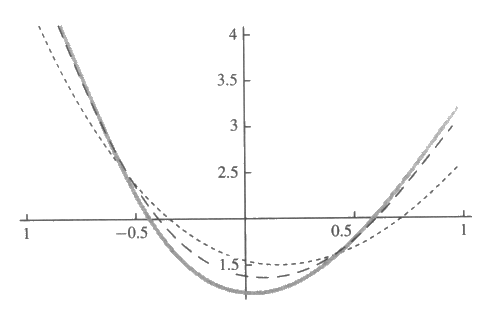
그림 15 : 기울기 방법의 예로 든 2차 다항식. 검은 곡선은 우리가 학습시키려고 하는 함수이고, 짧은 선으로 만들어진 곡선은 기울기를 계산하기 위하여 40개의 모든 훈련예제를 사용하여 100번의 조정을 한 후에 학습된 함수이다.
실험을 통한 타당성 조사
우리들의 학습 프로그램에 대한 신뢰는 경험 때문에 생긴 것이다. 이제 우리는 학습프로그램을 어떻게 경험적으로 평가할 것인가에 대하여 간단히 살펴볼 것이다. 그림 16 에서는 2 개의 기울기 방법의 성능을 평가하는 데 훈련예제들의 집합을 사용하였다. 실제로 평가를 목적으로 훈련예제들을 사용하는 것은 가능하다면 피해야 한다.
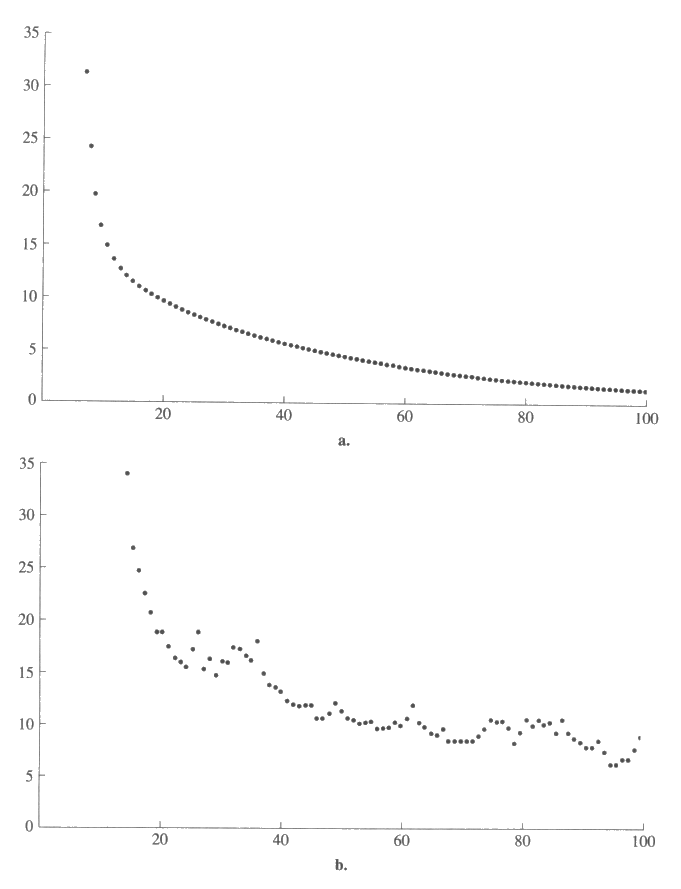
그림 16 : 2 개의 기울기 방법의 성능을 보여주는 그래프. 각 그래프는 40 개의 예제들에 대한 평방오차들의 평균을 보여주는 것으로 이것은 조정되는 수에 대한 함수로 나타난다. (a) 에서는 각각의 조정에 모든 40 개의 예제들을 다 사용했고, (b) 에서는 각각의 조정에 임의적으로 선택된 하나의 예제만 사용했다.
우리가 어떤 특정 학습 프로그램을 평가하고자 하려면 먼저 예제가 필요하다. 이상적인 경우에는 우리가 원하는 만큼의 많은 예제들을 만들 수 있는 생성기가 있겠다. 그러나 대부분의 경우에 있어서는 우리가 원하는 최상의 것은 고정된 크기를 가지는 하나의 예제 집합이 된다.
우리는 학습 프로그램에 모든 예제들을 집어 넣고, 가설을 만들게 하여 예제들에 대한 오차의 합을 계산함으로써 성능을 평가할 수 있다. 간단히 예제들을 표에 저장함으로써 그 예제들에 대해서는 프로그램이 절대 오류를 범하지 않게 될 것이다. 하지만 훈련에 사용되어진 예제들의 집합 외의 예제들에 대해서는 이 현상이 일반화되지 않는다.
만일 훈련예제의 집합 T 가 작다면 T 의 부분집합만을 훈련에 사용하면
학습 프로그램의 효과가 떨어진다. 교차 확인 (cross validation) 은 모든 훈련예제를
사용할 수 있게 하고, 주어진 학습 프로그램의 성능에 대하여 믿을 만한 추정을 얻게
한다. 교차확인을 하기 위해서 T 를 가능한 동일한 크기의 V 개의 부분집합 T1,
T2, ..., TV 로 나눈다. 각 v = 1, 2, ..., V 에 대하여 T
- Tv 를 훈련예제들의 집합으로
사용하여 학습프로그램에 적용시키고, Pv 를 훈련에 사용되어지지 않은 예제들의 부분집합인
Tv 를 사용하여 측정된 결과 가설의 성능으로 한다. 모든 T 를 사용한 학습 프로그램에
의해 생성된 가설에 대한 v 겹 교차 확인 추정 (v-fold cross-validation
estimate) 은 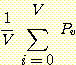 로 정의된다. 교차 확인은 비교적 많지 않은 예제들이 훈련에 사용된 경우에
학습 프로그램의 성능을 평가하는 데 추천될 만하다.
로 정의된다. 교차 확인은 비교적 많지 않은 예제들이 훈련에 사용된 경우에
학습 프로그램의 성능을 평가하는 데 추천될 만하다.
비선형적 함수공간과 인공 신경회로망
비선형적인 함수공간에 대응되는 가설공간에서는 기울기 유도 탐색을 사용할 수 있지만, 이런 공간에서는 기울기 방법이 전역 극대값을 꼭 찾는다는 것을 보장하지는 못한다. 비선형적인 함수공간에서의 탐색전략은 지역 극대값에 빠지지 않기 위해서 때때로 가중값 조정 폭을 크게 하는 것이다. 기울기에 의해 지시된 방향으로 조정의 폭을 크게 하여 가중값을 조정하면 평방 오차가 작아지는 것을 보장할 수 없다. 예로 학습에 관한 문헌에서 발견되는 전형적인 인공신경회로망 부류의 가설공간을 생각해 볼 수 있다.
우리가 여기에서 고려하는 인공신경회로망들은 시그모이드 요소로 되어 있고, 층으로 차례차례 나열되어 있다. 각 층은 시그모이드 요소로의 입력 또는 시그모이드 요소로부터의 출력과 연관되어 있다. 하나의 층과 연관되어 있는 시그모이드 요소로의 입력은 앞에 있는 층에서 나온 결과이다. 모든 망은 전체 망의 입력에 대응되는 입력층 (input layer) 과 출력에 대응되는 출력층 (output layer) 을 가지고 있다. 입력층을 제외한 모든 층은 시그모이드 요소의 출력과 연관되어 있다. 입력층과 출력층 외의 층을 은닉층 (hidden layer) 이라 한다.
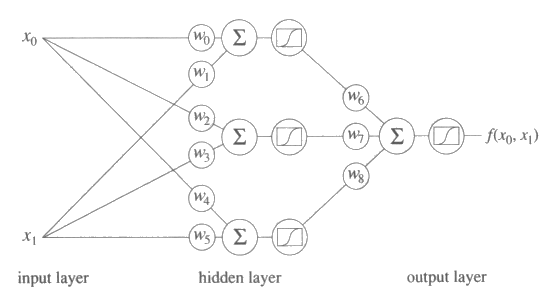
그림 17 : 3 개의 층을 가진 인공신경회로망. 입력층은 입력들의 집합으로 되어 있다. 은닉층과 출력층은 시그모이드 요소와 이와 연관된 출력들로 되어 있다.
그림 17 에 보여진 인공신경회로망은 3 개의 층으로 된 망이다. 입력층은 w 개의 입력으로 되어 있고, 은닉층은 3 개의 시그모이드 요소로부터의 출력으로 되어 있고, 출력층은 하나의 시그모이드 요소 (인공신경망에 관한 문헌을 읽을 때 주의하라. 몇몇 연구자들은 입력을 층으로 간주하지 않고, 그렇기 때문에 이들의 관점에서 보면 그림 17 에 보여진 망은 2 개의 층으로 이루어졌다.) 로부터의 출력으로 되어 있다. 은닉층에 충분한 수의 요소를 가지고 있는 망은 어떤 함수도 나타낼 수 있다. 하지만 불행히 이런 결과는 얼마나 많은 요소를 특정 함수를 학습시키는 데 망에 추가시켜야 하는지 결정하는 데 도움을 주지 못하며, 불필요한 요소를 추가시켜서 학습의 속도를 느려지게 할 수도 있다. 이제부터 우리에게 신경망이 주어졌고, 특정함수를 학습하기 위해서 이를 이용하고자 한다고 가정해보자.
다층 신경망에서의 기울기 유도
우리는 인공신경회로망의 가중값을 조정하기 위해서 기울기 방법을 사용한다. 다층 인공신경회로망의 기울기를 유도하는 것으로부터 시작하자. 수학적으로 증명하기 위해서 하나의 입력층과 각 은닉층과 출력층에 연관된 한 개의 입력을 가진 시그모이드 요소로 구성된 간단한 3 개의 층을 가진 망을 선택한다. 이에 대응되는 함수는 σ (wσ (w'x)) 로 σ (u) = 1 / (1 + e-u) 이다. 평방 오차의 평균으로 성능을 정의하는데, 단 하나의 훈련예제 <x, y> 만을 고려한다.
P = - (F (w, w') - y)2
이때 F (w, w') = σ (wσ (w'x)) 이다. 하나의 훈련예제를 사용할 경우의 기울기는 P 를 w 와 w' 에 대하여 편미분한 벡터이다.
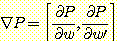
필요로 하는 편미분을 결정하기 위해서 연쇄 규칙 (chain rule) 을 사용한다. 주어진 f, g, u 가 함수이고 g 와 u 는 미분가능할 때, 만일 f (x) = g [u (x)] 이면 df(x) / dx = dg (u (x)) / du (x) • du (x) / dx 이다. 연쇄 규칙은 편미분에도 적용될 수 있다. 시그모이드 함수를 미분하면 dσ(x) / dx = σ(x)[1 - σ(x)] 이다.
w 에 대한 성능의 편미분은 연쇄 규칙을 적용시켜서 다음을 얻어낸다.
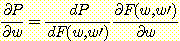
성능함수의 정의로부터 첫번째 항을 풀면

을 얻는다. 두번째 항을 풀기 위해서는 연쇄 규칙을 다르게 응용해야 한다.
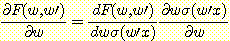
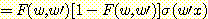
w' 에 대한 성능의 편미분도 위와 같은 형식으로 얻는다.
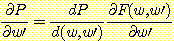
첫번째 항은 앞에서 미분했던 결과와 동일하다. 두번째 항은 연쇄규칙을 여러 번 적용하여 얻어낸다.
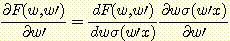
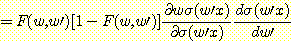
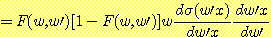
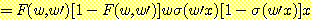

오류 역전파 학습법
앞서 행해졌던 분석은 간단한 다층 망의 기울기를 계산하게 해준다. 이 분석을 일반화시키면 기울기 방법을 가지고 인공신경회로망의 가중값을 조정하는 오류 역전파 (error backpropergation) 라 일컫는 학습법을 얻을 수 있다. 관례대로 가장 우측에 있는 층 또는 출력층을 첫번째 층으로 명하자. 이제 중간의 출력을 거론하고자 한다. i 번째 층에서 나온 출력은 i 번째 층 또는 i 가 입력층이라면 입력층에서의 시그모이드 요소의 출력이다. wi→j 를 i 번째 층에서 j 번째 층으로의 가중값이라 하자. j 가 i + 1 이 될 필요는 없다. wi→j 에서의 oi 는 i 번째 층에서의 출력으로 wi→j 와 곱해진 것이고, oj 는 j 번째 층에서의 출력으로 oi 와 wi→j 의 결과이다. 그림 18 은 이런 관계를 나타낸 것이다. 각 가중값은 정확히 하나의 시그모이드 요소에 입력되어서 주어진 특정 출력 oi 와 가중값 wi→j, 출력 oj 이 유일한 것이 되도록 가정하자.
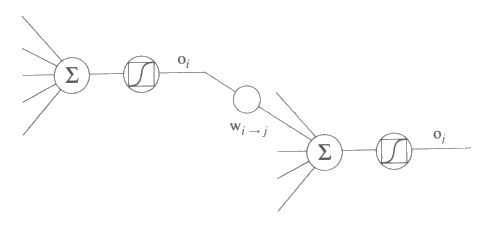
그림 18 : 특정 가중치 wi→j 에 연관된 망의 요소들에 대해서 본문에서 언급한 내용에 대한 연결도
W 가 주어진 망에서 조정가능 가중값의 벡터라고 하고, T 를 훈련예제들의 집합이라고 하자 성능함수는 다음과 같이 정의된다.
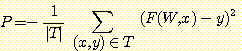
이때 F (W, x) 는 주어진 입력 x 와 가중값 W 에 대한 망의 출력이다. 성능함수의
기울기는 각 훈련예제들의 기울기들의 합이다. P<x, y> = (F (W,
x) - y)2 이라
하자. 그러면 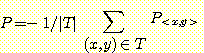 이 된다. 앞서 기술되었던 분석을 확장할 때, 시그모이드 요소가 있는 임의의 망에서 ∂
P<x, y> / ∂ wi→j 을 계산하기 위해 다음과 같이 한다.
이 된다. 앞서 기술되었던 분석을 확장할 때, 시그모이드 요소가 있는 임의의 망에서 ∂
P<x, y> / ∂ wi→j 을 계산하기 위해 다음과 같이 한다.
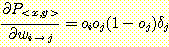
이때 δ1 = - (F (W, x) - y) 이고 j > 1 에 대하여 δj = wi→j ok (1- ok) δk 이다. 기울기 방법을 반복할 때마다 β 가 학습률일 때 망의 가중값을 다음과 같이 조정한다.
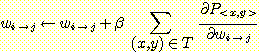
앞에서도 말했듯이 은닉층에 충분히 많은 요소를 가지고 있는 3 개의 층으로 된 망은 적어도 이론상으로는 어떤 함수라도 표현할 수 있다. 그러나 실제로는 가중값을 조정하기 위한 적절한 망과 전략을 세우는 것은 생각만큼 간단한 일이 아니다. 학습은 조정가능 가중값에 의해 정의된 크고도 여러 차원의 공간에서의 탐색을 포함하고, 기울기 방법은 단지 지역 극대값을 어떻게 찾을 수 있는지에 대해서만 알려준다.
만일 고정된 학습률을 사용한다면 이 학습률은 최적이 아닌 지역 극대값에서 빠져나올 만큼 충분히 크고, 전역 극대값을 찾았을 때 이 값을 유지하고 있기에 충분히 작은 것이어야 한다. 일반적으로 이런 필요조건을 만족할 만한 고정된 학습률을 찾는다는 것은 불가능하다. 따라서 고정된 학습률을 사용하는 대신, 몇몇 학습 시스템은 모의 담금질 (simulated annealing; 4 장 참고) 을 사용하여 시간이 지남에 따라 학습률을 조정한다. 다음 절에서는 인공신경회로망을 Lisp 로 구현해볼 것이며, 오류역전파를 사용함으로써 생기는 복잡성과 2 개의 입력을 가진 부울함수를 학습하기 위한 기울기 방법에 관하여 살펴볼 것이다.
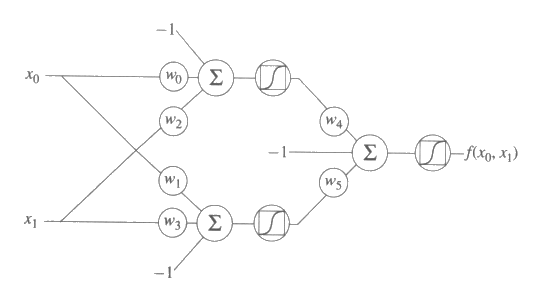
그림 19 : 2 개의 은닉층과 고정된 임계값을 가지고 있는 3 개의 층으로 된 망
인공 신경회로망의 Lisp 구현
그림 19 에서 보인 우리가 고려할 첫번째 망은 2 개의 은닉요소를 가진 3 개의 층으로 된 망이다. 부울함수를 학습시키기 위해서는 임계값 0 에 근사하는 시그모이드 요소를 사용할 수 없다. 실제 많이 쓰이는 대로 각 시그모이드 요소의 입력에서 1 을 빼서 구현한 0 이 아닌 고정된 임계값을 사용함으로써 이 문제점을 극복하였다.
(defun simoid(x) (/ 1 (+ 1 (exp (- 1 x)))))

그림 20 : 2 개의 은닉요소와 고정된 임계값을 가지고 있는 망의 Lisp 구현
그림 20 은 함수 net 을 정의한 것으로, 이는 그림 19 에서 보여준 망을 구현한 것이다. net 은 2 개의 입력으로 된 부울함수의 입력에 대한 리스트와 6 개의 가중값들에 대한 리스트에 해당하는 변수 2 개를 가지고 있다. 여기서는 목표 부울함수를 입력과 이에 대응하는 출력의 쌍으로 된 리스트로 표현하였다. ((1 0) 1) 은 입력이 1 과 0 일 때 함수의 출력이 1 임을 나타낸다. 아래에 부울함수의 or, and, xor 함수에 대한 표현이 있다.
(setq or '(((0 0) 0) ((1 0) 1) ((0 1) 1) ((1 1) 1))
and '(((0 0) 0) ((1 0) 0) ((0 1) 0) ((1 1) 1))
xor '(((0 0) 0) ((1 0) 1) ((0 1) 1) ((1 1) 0)))
주어진 부울함수를 학습하기 위하여 오류 역전파와 기울기 방법을 사용하여 가중값을 조정하였다. 그림 21 은 가중값에 의해 지정된 매개변수 공간 안의 점에서의 성능함수에 대한 평방 오차 평균의 기울기를 계산하기 위한 코드를 열거한 것이다. Gradient 는 훈련예제들의 집합과 가중값들의 집합을 취하여 가중값에 의해 지정된 점에서의 기울기를 반환한다. v 와 w 가 벡터를 나타내는 수의 리스트일 때 식 (mapcar #' + v w) 은 벡터의 합을 의미한다. 특정 훈련예제에 대한 기울기는 함수 delta 에 의해 앞서 제시되었던 일반적인 오류 역전파 학습법에 따라 계산된다.
Train 은 2 개의 입력을 가진 부울함수와 그림 19 에서 보여준 망의 가중값들의 집합을 취한다. 만일 가중값이 목표함수를 성공적으로 이행하면 train 이 존재하게 되어 가중값을 출력한다. 그렇지 않으면 train 이 성능함수의 기울기를 결정하고, 기울기를 예전의 가중값에 더함으로써 새로운 가중값들의 집합을 계산해낸 후 새로운 가중값 집합에서 자기자신을 재귀적으로 호출한다. train 은 학습률을 1 로 가정한다. 만일 다른 학습률을 사용하려면 gradient 에서 반환되는 숫자들의 각 리스트를 사용하고자 하는 원하는 학습률에 곱한다. 앞으로 나오는 구현에는 훈련예제들의 집합이 전체 입력공간을 포함하고 있다는 것에 유념하라. 좀더 큰 입력공간에서는 이것이 올바르지 않게 될 수도 있다.
(defun train (target weights)
(if (successp target weights) (princ weights)
(train target (mapcar #' + weights (gradient target weighs)))))
주어진 입력에 대해서 망의 출력에 해당되는 시그모이드함수는 0 과 1 의 값을 낸다. 주어진 가중값들의 집합은 실제 출력과 원하고자 하는 출력간의 차이가 0.4 미만일 때 목표함수를 성공적으로 수행한다. 또한 그 차이가 꼭 0.5 미만이어서 반올림된 출력이 원하는 출력과 동일해야만 한다. abs 함수는 일반적인 Lisp 로 짜여져 있고 하나의 변수에 대한 절대값을 반환한다.
(defun successp (target weights)
(every #'(lambda (x)
(< (abs (- (second x)
(net (first x) weights))) 0.4))
target))

그림 21 : 2 개의 은닉요소와 고정된 임계값을 갖는 망의 기울기의 계산
가중값의 초기값을 선택하는 것은 다층 망에서 학습시킬 때 중요한 점이다. 일반적으로 모든 가중값의 초기값을 모두 같은 값으로 설정하는 것은 별로 좋은 방법이 아니다. 여기서는 임의의 가중값을 0 에서 2 사이의 벡터값으로 설정하였다.
(defun init( )
(mapcar #'random '(2.0 2.0 2.0 2.0 2.0 2.0)))
여기서 기술한 방법으로는 몇몇 가중값들의 초기값 집합을 가지고는 단지 and, or, xor 함수만을 학습할 수 있다. 다른 가중값들의 초기값 집합에 대해서는 train 이 해를 찾지 못하고 무한정 학습한다. 이것은 train 이 전역 극대값이 아닌 지역 극대값에 빠졌기 때문이다. 또한 학습률을 증가시킨다고 해서 train 이 모두 지역 극대값에서 빠져 나올 수 있는 것은 아니다. 여기에 xor 함수를 학습할 때 결정된 가중값들의 예를 보인다.
> (train xor (init))
(5.67 1.80 6.84 1.27 4.49 -4.39)
이제 2 개의 입력을 가진 부울함수를 학습하는 또 다른 망을 소개하고, 2 개의 망의 성능을 비교해 볼 것이다. 먼저 성능에 영향을 미치는 몇몇 요인들에 대하여 살펴볼 것이다.
표상적인 문제점과 계산적인 문제점
다층 망에서 부울함수를 학습시키면 그 성능속도가 특별히 빠르지 않다. train 은 가중값을 몇 백번 조정을 한 후에야 성공적으로 학습한다. 그러나 3 개의 층으로 된 망에 해당되는 편중을 구현하는 것은 어려운 일이다. 3 개의 층으로 된 망에서 훈련표본들의 집합들과 서로 양립하도록 가중값을 찾는 것은 NP-hard 한 일이다. 어떤 경우에서는 좀더 큰 학습률을 사용하면 처리가 빨라질 수 있으나, 학습률이 너무나 크게 되면 원하지 않은 일이 생길 수 있다.
xor 함수를 수행하는 그림 19 와 같은 망의 가중값은 쉽게 만들어낼 수 있다. 예를 들어 제일 위에 있는 은닉요소의 가중값이 2 와 -2, 맨 밑에 있는 은닉요소의 가중값이 -2 와 2, 출력요소의 가중값이 2 와 2 라 하자. 이 가중값과 임계값 1 로 제일 위에 있는 은닉요소는 x0 이 1 이고 x1 이 0 일 때에만 1 을 출력하는 함수에 해당하고, 맨 밑에 있는 은닉요소는 x0 이 0 이고 x1 이 1 일 때에만 1 을 출력하는 함수에 해당한다. 출력요소는 or 함수에 근사한다. 이 3 가지 함수는 전체적으로 부울 xor 함수를 수행한다.
다른 가중값을 설정하여 xor 문제를 구현할 수도 있다. 예를 들어 제일 위에 있는 은닉요소의 가중값이 5.7 과 6.8, 맨 아래에 있는 은닉요소의 가중값이 1.8 과 1.3, 출력요소의 가중값이 2.5 와 -4.4 라 하자. 이 경우에는 맨 위에 있는 은닉요소는 두개의 입력이 모두 0 이 아닐 때 항상 1 을 출력하는 함수에 해당하고, 맨 아래에 있는 은닉요소는 두 개의 입력이 모두 1 이 아닐 때 항상 0 을 출력하는 함수에 해당한다. 그리고 출력요소는 맨 위에 있는 은닉요소의 출력이 1 이고 맨 아래에 있는 은닉요소의 출력이 0 일 때만 1 을 출력하는 함수에 해당한다. 따라서 이 3 가지 함수는 전체적으로 부울 xor 함수인 ((x0 ∨ x1) ∧ ¬ (x0 ∧ x1)) 을 수행한다.
문제를 해결하는 데 있어서 내부 표상 (internal representation) 은 문제와 연관된 입력 또는 출력을 기술함에 있어서 명시적으로 언급되지 않은 표상을 말한다. 체스에서 입력은 체스판에 나열되어 있는 조각들로 기술되고, 출력은 움직임으로 기술된다. 체스 게임을 할 때 내부 표상은 조각들을 중요한 연산에 사용할 수 있는 요소로 기술해야 한다. 인공신경회로망에 있어서의 은닉요소에는 내부 표상이 있다. 은닉요소의 가중값을 설정함으로써 우리는 부분적으로 목표함수에 대한 표상을 결정한다. 아직 알지 못한 채 내버려진 매개변수는 은닉요소를 결합하는 가중값이다. 우리에게 만일 은닉요소의 옳은 가중값 집합이 주어졌다면 출력요소의 가중값은 기울기 방법을 사용하여 쉽게 결정할 수 있다. 만일 은닉요소의 가중값이 고정되어 있는 값이라면 은닉요소를 기저함수로 하는 선형적인 함수공간에서 볼록 성능함수를 가지고 탐색한다.
다층 망에서 학습을 하면 가능한 모든 내부 표상으로 이루어진 큰 공간에서 탐색해야 한다. 이것이 오류 역전파와 기울기 방법이 문제를 해결하는 데 매우 느린 이유이다. 사실 내부 표상공간은 우리가 일반적으로 생각하는 것보다 훨씬 크다. 다음절에서는 2 개의 입력을 가진 부울함수를 학습하기 위한 서로 다른 망에 대해 살펴볼 것이다.
조정가능한 임계값을 가지는 망
지금부터는 하나의 은닉층을 가진 3 개의 층으로 된 망을 고려해 보고자 한다. 그림 22 에 나타나 있는 이 망은 어떤 주어진 층에 있는 모든 요소들이 출력층에 근접한 각 층에 있는 모든 요소로 연결되어 있기 때문에 '완전히 연결되어 있다 (fully connected)' 라고 한다. 그림 22 의 망은 고정된 임계값이 아닌 조정할 수 있는 임계값을 가지고 있다. 그림 23 은 7 개의 가중값을 가진 망을 Lisp 로 구현한 것이다. 수정해야 할 유일한 함수는 delta 함수이며 특정한 훈련예제들과 가중값을 집합의 기울기에 대한 기여로 계산해 낸다. 그림 22 에 있는 망을 delta 함수로 구현해 놓은 것이 그림 24 이다.
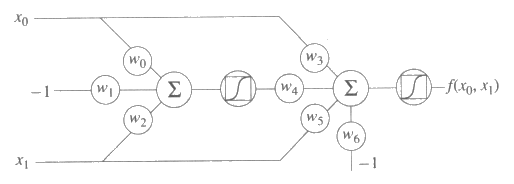
그림 22 : 하나의 은닉요소와 조정할 수 있는 임계값을 가지는 3개의 층으로 되어 있는 망

그림 23 : 하나의 은닉요소와 조정할 수 있는 임계값을 가지는 망의 Lisp 구현

그림 24 : 하나의 은닉요소와 조정할 수 있는 임계값을 가지는 망의 기울기를 계산하는 코드
그림 22 에 있는 망을 사용하여 xor 함수를 학습시킬 때 결정되는 가중값들의 예가 다음과 같다.
> (train xor (init))
(-5.75 -1.71 -4.95 -4.02 -6.53 -3.02 -4.64)
그림 22 에 있는 망은 3 개의 입력으로 된 부울함수에 뒤따르는 2 개의 입력으로 된 부울함수이다. 은닉요소는 입력이 모두 0 일 경우에만 1 을 출력하는 부울함수이다. 은닉층은 입력이 모두 0 일 경우에만 1 을 출력하는 부울함수에 해당한다. 출력층은 2 개의 입력 중의 하나가 1 이고, 은닉요소의 출력이 0 또는 은닉요소의 입력과 출력이 모두 0 일 경우에 1 을 출력하는 부울함수에 해당한다.
다른 망들과의 성능 비교
그림 22 의 망은 그림 19 에 있는 망보다 하나 더 많은 가중값을 가지고 있기 때문에 학습하기 위해 좀더 많은 가중값을 탐색하는 데 더 많은 시간이 걸릴 것이라는 생각이 들지도 모른다. 실제로는 그렇지 않다. 표 3 은 서로 다른 망과 학습률, 부울함수에 대한 자료를 보여준다. 2 개의 은닉요소를 가지는 그림 19 의 망은 2HU 라 명시하였고, 하나의 은닉요소를 가지는 그림 22 에 있는 망은 1HU 라 명시하였다. 또한 학습률도 1.0 과 2.0 의 2 개를 사용하였다. 각 망과 학습률 목표함수를 결합하여 10 개의 가중값들의 초기값 집합에 대하여 학습시켰다. 각각 가중값을 1000 번 정도 조정할 수 있도록 하였다. 표 3 에 나와있는 통계자료를 보면 k (h / 10) 의 형태로 되어 있는데, k 는 성공적으로 목표함수를 학습할 때의 평균 조정수를 나타내고, h 는 프로시저가 10 번 중에서 성공적으로 수행된 수를 나타낸다. 모든 경우에서 1HU 가 2HU 보다 더 좋은 수행을 보여주지만, 1HU 와 2HU 모두 xor 함수를 학습하는 것은 어렵다는 것을 알 수 있다.
표 3 : 서로 다른 두 망에서의 평균 조정 수 |
||||
|
|
|
목표 함수 |
||
|
네트워크 |
비율 |
Or |
And |
Xor |
|
2HU |
1.0 |
297 (3 / 10) |
301 (3 / 10) |
394 (3 / 10) |
|
2HU |
1.0 |
345 (5 / 10) |
152 (6 / 10) |
199 (6 / 10) |
|
1HU |
1.0 |
5 (10 / 10) |
12 (10 / 10) |
264 (9 / 10) |
|
1HU |
1.0 |
5 (10 / 10) |
6 (10 / 10) |
145 (10 / 10) |
이번 절에서는 퍼셉트론 (perceptron) 이라 불리우는 특별한 망 모형에 대하여 간단히 알아보겠다. 퍼셉트론은 부울함수의 제한된 가설공간을 사용한다.
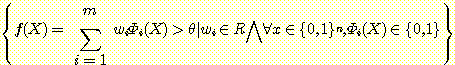
x = <x1, ..., xn> 이고, 기저함수인 {Φi} 는 임의의 부울함수이고, θ 는 고정된 임계값이다. 그림 25 는 망 계산 모형으로서의 퍼셉트론을 나타낸다. 임계에 의해 나온 결과를 보지 않고도, 이 함수공간은 기저함수 (basis function) 들이 선형적으로 결합한 함수들로 구성되어 있으므로 이런 편중에 대해서는 학습이 매우 쉬울 것이라고 짐작할 수 있을 것이다. 이 짐작은 이 절 뒷부분에 정의하게 될 선형 분리가능 (linearly separable) 이라고 하는 중요한 개념에 의해서 맞다는 것을 확인할 수 있다. 물론 기저함수와 임계 (thresholding) 가 모두 불연속적이고 미분가능하지 않은 함수를 만들어내기 때문에 기울기 방법 (gradient method) 을 사용할 수 없다. 그러나 선형적인 분리 개념에 잘 수행되도록 보장된 아주 간단한 가중값 조정 (weight-adjustment) 법칙이 존재한다.
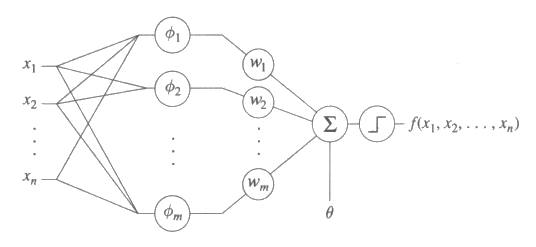
그림 25 : 망 계산 모형으로 묘사된 퍼셉트론. 기저함수 Φ1, Φ2, ..., Φm 는 임의의 부울함수를 나타내고, θ 는 고정된 임계값을 나타낸다.
그림 26 은 2 개의 입력을 가진 부울함수를 학습하는 간단한 퍼셉트론을 보여준다. 이것은 입력이 곧장 가중값에 연결되어 있기 때문에 곧장 연결된 임계 논리요소 (straight-through logic-threshold unit) 라 한다. 곧장 연결된 임계 논리요소에서는 기본함수가 아주 간단하다: {Φi <x1, ..., xn> = xi}. 가중값 조정 법칙은 다음과 같은 직관적인 통찰에 의해 동작된다. 퍼셉트론이 특정 입력에 대하여 원하는 출력을 만들면 우리는 가중값을 그냥 놔두어야 한다. 그러나 만일 퍼셉트론이 1 을 출력해야 하는데, 0 을 출력했다고 가정해보자. 이 오류를 조정하기 위해서 1 을 출력하는 기저함수 (곧장 연결된 임계 논리요소의 경우 입력) 들의 가중값을 증가시킨다. 마찬가지로 만일 퍼셉트론이 0 을 출력해야 하는데, 1 을 출력했다면 1 을 출력하는 기저함수들의 가중값을 감소시킨다. 0 을 출력하는 기본함수들의 가중값은 특정 입력에 대해서 결과에 영향을 미치지 않는 가중값이므로 이 가중값은 조정할 필요가 없다.
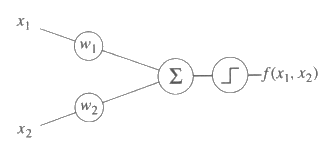
그림 26 : 2 개의 입력을 가진 부울함수를 학습하는 퍼셉트론
퍼셉트론 학습 규칙
우리는 위와 같은 직관적인 통찰을 퍼셉트론 학습 규칙이라 불리우는 가중값 조정 전략으로 요약할 수 있다.
1. 만일 퍼셉트론이 틀린 결과를 만들어냈다면
a) 만일 퍼셉트론이 0 을 출력해야 하는데, 1 을 출력했다면 결과에 대응되는 기저함수들의 가중값을 감소시킨다.
b) 만일 퍼셉트론이 1 을 출력해야 하는데, 0 을 출력했다면 결과에 대응되는 기저함수들의 가중값을 증가시킨다.
2. 그렇지 않다면 가중값을 변화시키지 않는다.
다음은 Lisp 로 구현한 것이다. 먼저, 고정된 임계값 1 을 가지며, 임의의 길이의 입력과 가중값 벡터가 곧장 연결된 임계 논리요소를 구현한 것이다.
(defun ltu (input weights)
(if (< 1 (apply #' + (mapcar #' * input weights))) 1 0))
다음은 퍼셉트론 학습 규칙을 구현한 것이다.
(defun adjust (input output weights)
(cond ((= (Itu input weights) output) weights)
((= (Itu input weights) 0) (mapcar #' + weights input))
(t (mapcar #' - weights input))))
퍼셉트론은 모든 입력에 대하여 퍼셉트론의 출력이 목표출력과 동일할 때 주어진 목표함수를 성공적으로 학습한다.
(defun successp (target weights)
(every #' (lambda (x) (= (Itu (first x) weights) (second x))) target))
실험에서 학습은 임의의 입출력쌍을 목표로부터 선택하고 퍼셉트론 학습 규칙에 따라 가중값을 목표가 성공적으로 학습될 때까지 조정함으로써 수행된다.
(defun train (target weights)
(if successp target weights) nil
(let ((pair (nth (random (length target)) target)))
(train target (adjust (first pair) (second pair) weights)))))
or 함수를 사용하여 목표를 학습 프로그램으로 20 번 학습시켰더니 이 함수를 학습하는데 적으면 3 번, 많으면 18 번, 평균 8 번의 조정이 필요하였다. 아래에 train 을 변경하여 프로그램이 수행되는 과정을 보여주고 요약 통계를 보여주는 출력의 예가 있다.
> (test or '(0 0))
Training example: ((1 1) 1) Adjusted weights: (1 1)
Training example: ((0 1) 1) Adjusted weights: (1 2)
Training example: ((0 1) 1) Adjusted weights: (1 2)
Training example: ((1 0) 1) Adjusted weights: (2 2)
Number of adjustments: 4
이번 수행에서 모든 가능한 입력에 대해 학습 알고리즘이 제시되지 않았음에도 불구하고 함수를 학습했다. 가중값의 초기값을 어떻게 설정해주느냐가 퍼셉트론이 학습하는 데 얼마나 빠르게 할 수 있는가에 중요한 역할을 한다. 그러나 이 방법은 가중값의 초기값이 무엇이든 간에 옳은 가중값들의 집합을 잘 찾아낸다. 퍼셉트론은 앞 절에서 언급한 다중 망보다 훨씬 빠르게 동작한다. 하지만 불행히도 그림 26 의 퍼셉트론은 2 개의 입력을 가진 모든 부울함수를 학습하지는 못한다.
선형 분리함수
입력들의 집합인 x1, ..., xn 은 n 차원 공간을 규정짓는다. 만일 어떤 부울함수가 입력을 받아 결과로서 1 또는 0 을 만들 경우, 결과를 달리 내는 입력을 분리해 주는 초평면 (hyperplane) 이 입력 공간상에 존재할 때 선형 분리적 이라고 한다. 곧장 연결된 임계 논리요소에 적용되는 퍼셉트론 규칙은 선형 분리가능 (퍼셉트론 학습 법칙을 사용하여 선형 분리가능한 부울함수를 학습하기 위해서는 예전에 했던 것과 같이 0 이 아닌 고정된 입력에 연결된 여분의 조정할 수 있는 가중값을 제공하여 조정할 수 있는 임계값을 추가해야 한다.) 이라는 개념하에서만 잘 수행된다. 그림 27 은 선형 분리가능이 존재하는 부울함수에 대한 예와 선형분리가능을 가지지 않는 부울함수에 대한 예를 보여준다. 입력이 2 차원 공간이면이곳에 존재하는 초평면은 하나의 직선이다. 다층의 망을 골치 아프게 했던 xor 함수는 선형 비분리적임에 주의하라.
이 때문에 퍼셉트론은 빠르지만 제한적이다. 그러나 개념을 기저함수 중 하나의 것으로 만듦으로써 선형 분리적인 것으로 만들 수 있다. 이것은 앞 절에서도 말했듯이 좋은 내부 표상을 결정하는 문제를 제시한다. 옳은 표상을 가지고 시작하면 학습은 쉽게 된다. 다음 절에서는 망 학습 모형에 대한 좋은 내부 표상을 찾는 문제에 대하여 살펴볼 것이다.
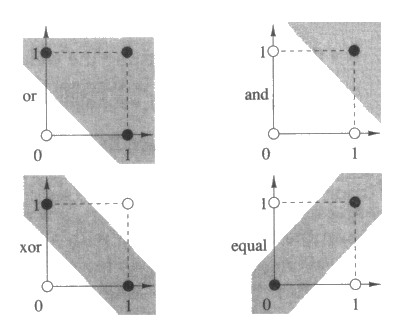
그림 27 : 부울함수와 선형 분리성. OR 과 AND 함수는 선형 분리적이다. 이 두 함수는 초평면이 결과로 1 을 만들어내는 입력과 0 을 만들어내는 입력을 입력공간의 테두리에 있는 동그란 영역을 검게 칠하고 칠하지 않음으로써 분리해낸다. XOR 와 EQUAL 함수는 선형 비분리적이다. 이 두 함수는 결과로서 1 과 0 을 만들어내는 입력쌍을 분리해 주는 초평면이 존재하지 않는다.
선형함수공간은 2 가지의 중요한 이유로 인하여 흥미를 끌고 있다. 첫번째는 기울기 탐색 기술 (gradient search technique) 이 이 공간에서 전역 극대값을 잘 찾는다는 것이다. 두번째는 옳게 주어진 기저함수들이 있다면 어떤 함수도 학습할 수 있다는 것이다. 물론 두번째 이유는 우리가 항상 목표함수를 기저함수 중의 하나로 선택하므로 크게 중요한 사실은 아니지만 방사 기저함수 (Radial Basis Function : RBF) 라고 하는 함수부류를 사용하여 매우 다양한 문제를 해결할 수 있음이 밝혀졌다. 이번 절에는 함수를 근사함으로써 학습을 하는 것에 초점을 맞추고 이에 대하여 살펴 볼 것이다. 함수를 근사함으로써 학습을 하는 목적은 최소 평균 평방 오차를 가지는 가설을 찾기 위해서이다.
앞에서, 우리는 다항식을 기저함수로 사용한 학습함수를 고려하였다. 집합 {1, x, x2, x3} 에 있는 다항식 기저함수 (polynomial basis function) 의 경우에는 각 기저함수는 입력공간 전체에 걸쳐서 망의 출력에 무시하지 못할 영향을 끼친다. 만일 w0 = w1 = w2 = w3 이라면 기저함수인 x2 은 x 가 0 에 근접할 경우만 제외하고는 w0 + w1x + w2x2 + w3x3 의 결과에 큰 영향을 미칠 것이다. 이번 절에서는 미치는 영향이 보다 지역적인 기저함수에 대해서 살펴볼 것이다.
방사 기저함수 는 출력이 입력 공간상에서 고정된 점 또는 중심과 대칭을 이루고, 폭에 의해 정해진 범위 밖에서는 그 출력의 중요도가 무시할 수 있는 출력을 만들어낸다. 그림 28 은 약간의 간단한 방사 기저함수를 나타낸 것으로, 폭은 계속 변하며 중심은 0 이다. 함수를 근사하는 데 있어서 방사 기저함수의 중심은 좀처럼 같은 점에 위치하기가 힘들며, 입력 공간 전반에 걸쳐서 널리 펴져 있다.

그림 28 : 연속적이고 불연속적인 방사 기저함수. (a) 와 (b) 각각은 1 (실선), 5 (짧은 선), 10 (점선) 의 폭을 가지고 있는 가우스함수와 계단 방사 기저함수를 나타낸다. (c) 와 (d) 는 각각은 폭 5 를 가지는 가우스함수와 계단 방사 기저함수로 1.0 (실선), 0.6 (짧은 선), 0.3 (점선) 로 함수의 크기가 감소되었을 때 어떻게 되는지 나타낸다.
가우스함수 결합에 의한 함수 근사
목표함수가 가우스함수의 선형적 결합 형태라면 기저함수가 가우스인 선형함수공간을 사용하여 학습을 하면 된다. 하지만 만일 가설공간이 개념공간과 다르다면 어떻겠는가? 예를 들어 만일 우리가 3 차 다항식을 학습하려고 한다고 하자. 이 경우에서도 가우스 기저함수가 도움이 되겠는가? 대답은 그렇다는 것이다. 적절한 중심과 폭을 가지고 있는 충분한 가우스함수를 사용하면 어떤 함수라도 원하는 정밀도에 근사시킬 수 있다. 이것은 우리가 다층 망에 대해 주장하는 것과 같은 것이다. 하지만 방사 기저함수의 경우에서는 이렇게 할 수 있는 이유를 직관적으로 좀더 쉽게 이해할 수 있을 것이다.
그림 28 의 계단함수를 가우스함수에 구분적 상수함수로 근사한다고 생각해보고, 계단함수의 기본원리를 고려해 보라. 각 계단함수는 중심과 폭에 의해 결정되는 입력공간의 어떤 한 영역에서 0 이 아니다. 우리가 중심이 -0.75, -0.25, 0.25 와 0.75 이고 폭이 0.5 인 4 개의 구분적 상수함수를 사용한다고 하자.
|
h1 (x) = |
|
1 |
if -1 ≤ x ≤ -0.5 |
|
0 |
otherwise |
||
|
h2 (x) = |
|
1 |
if -0.5 ≤ x ≤ 0 |
|
0 |
otherwise |
||
|
h3 (x) = |
|
1 |
if 0 ≤ x ≤ 0.5 |
|
0 |
otherwise |
||
|
h4 (x) = |
|
1 |
if 0.5 ≤ x ≤ 1 |
|
0 |
otherwise |
대응되는 제한된 가설공간은 {w1h1 + w2h2 +w3h3 +w4h4 | wi ∈ R} 로 정의된다. 4 개의 각 가중값에 값을 할당하면 그림 29 와 같이 3 차 다항식에 대한 구분적 상수 근사를 얻게 된다. 근사된 결과는 표로 나타나는데, 기저함수로 정의된 0 이 아닌 각 영역에 대한 목록이 있다. 목록은 주어진 계단함수와는 가중값으로 연관되어 있고, 0 이 아닌 영역에 대하여 목표함수의 출력의 평균으로 할당되어 있다. 충분히 작은 영역을 사용하여 어떤 함수라도 원하는 정확도로 근사시킬 수 있다.
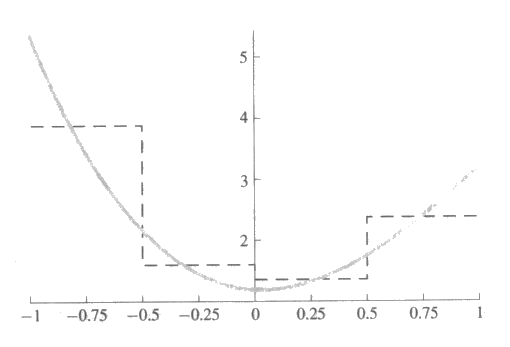
그림 29 : 다항식의 구분적 상수함수로의 근사. 실선은 우리가 학습시키려고 하는 3 차원 다항식을 가리킨다. 짧은 선은 다항식을 구분적 상수함수로 근사시킨 것이다.
방사 기저함수의 중심과 폭에 의해 결정된 입력 공간의 영역을 수용야 (receptive field) 라고 한다. 가우스 기저함수를 사용했을 때에 수용야는 어떤 범위에 걸쳐 중복된다. 이 경우 특정 입력에 대응되는 출력에 몇몇 기저함수가 중대한 역할을 한다. 겹쳐지는 수용야에서는 목표함수에 부드럽게 근사한다. 우리는 평활화 정도를 기저함수의 폭을 변형함으로써 제어할 수 있다. 만일 예로 조금만 학습시킨다면 결과함수는 예전 2 개의 입력함수 값 사이의 값을 할당하기 위하여 평활화된 함수를 사용하여 새로운 입력에 대한 값을 계산한다.
그림 30 은 가우스 기저함수의 선형적인 결합 형태를 나타내는 망의 전반적인 그림 구조를 나타낸다. 우리는 가중값 wi 를 망의 다른 매개변수들인 방사 기저함수의 폭과 중심과 구별하여 망의 계수 (coefficient) 라 규정지음으로써 구별을 한다. 망과 연관된 매개변수 공간은 망의 계수와 방사 기저함수의 폭과 중심에 의해 정의된다. 이런 망을 사용하여 학습을 할 때 수행함수에 대한 전체적인 최대값을 위한 매개변수 공간을 찾기 위하여 기울기 방법을 사용할 수 있다. 그러나 이것은 다층 망에 적용된 같은 방법에 비해 아마도 크게 나은 방법은 아닐 것이다.
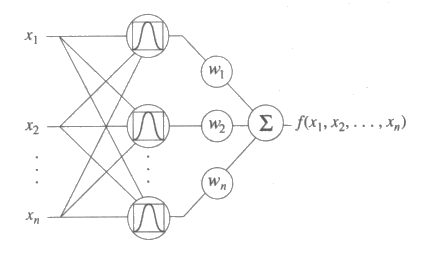
그림 30 : 함수들을 근사하는 망
가중값을 조정하기 위한 두 단계 전략
모든 가중값을 동시에 조정하는 대신, 학습 문제를 두 단계로 나눌 수 있다. 첫번째로 방사 기저함수를 입력공간 영역에 할당함으로써 목표함수에 거친 표상을 만든다. 이 단계에서는 방사 기저함수의 폭과 중심을 고정시킨다. 많은 좁은 폭의 기저함수를 입력 공간상에서 중요한 곳이나 목표함수가 급격히 변하는 입력공간의 부분에 할당시킬 수도 있다. 오류를 막기 위해서 객체의 한 부분을 추정하도록 학습하는데 있어서 로봇은 먼 곳에서는 객체에 대한 정착한 추정을 필요로 하지 않는다. 학습 프로그램은 대부분의 방사 기저함수를 로봇 가까이에 있는 물리적인 공간의 부분에 대응되는 입력 공간의 영역에 할당한다. 두번째 단계에서는 각 수용야가 얼마나 학습된 함수의 출력에 공헌을 했느냐를 결정함으로써 표상을 정련한다. 이 단계에서는 망의 계수를 결정한다.
각 단계는 약간의 경험이 필요하다. 사실, 목표함수의 구조에 대해 좀더 알고자 한다면 이 두 단계에 대하여 실험을 해야만 한다. 이 두 단계를 특정 문제에 어떻게 적용시킬 수 있는지 생각해 보자.
우리가 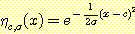 인 {η c1,σ1, η c2,σ2, η c3,σ3,
η c4,σ4} 의 방사 기저함수의 집합을 사용하여 그림 29 에서 본
것과 같은 3 차 다항식을 근사한다고 하자. 중심과 폭을 다른 값들로 고정시키고, 40
개의
입출력 쌍을 사용하며 [-1, 1] 사이의 무작위 수를 입력값으로 한다. 각 시간마다
기울기를 계산하기 위하여 모든 40 개의 예제를 사용한 기울기 방법을 500 번 적용시킨다
(더 많이 적용시킨다고 해서 우리가 감지할 수 있을 만큼 수행에 큰 영향을 미치지
않는다.).
표 4 는 40 개의 예제에 대하여 평방 오차의 평균에 입각하여 계산된 폭과 중심값으로 선택된 값을 보여준다.
그림 31 은 목표함수와 2 개의 대표적인 근사함수를 보여준다.
인 {η c1,σ1, η c2,σ2, η c3,σ3,
η c4,σ4} 의 방사 기저함수의 집합을 사용하여 그림 29 에서 본
것과 같은 3 차 다항식을 근사한다고 하자. 중심과 폭을 다른 값들로 고정시키고, 40
개의
입출력 쌍을 사용하며 [-1, 1] 사이의 무작위 수를 입력값으로 한다. 각 시간마다
기울기를 계산하기 위하여 모든 40 개의 예제를 사용한 기울기 방법을 500 번 적용시킨다
(더 많이 적용시킨다고 해서 우리가 감지할 수 있을 만큼 수행에 큰 영향을 미치지
않는다.).
표 4 는 40 개의 예제에 대하여 평방 오차의 평균에 입각하여 계산된 폭과 중심값으로 선택된 값을 보여준다.
그림 31 은 목표함수와 2 개의 대표적인 근사함수를 보여준다.
표 4 : 기저함수의 서로 다른 중심과 폭에 대한 오류 |
|||||
|
중심 (Centers) |
폭 (Width) |
오류 (Error) |
|||
|
-0.75 |
-0.375 |
0.0 |
0.50 |
1.0 |
48.10 |
|
-0.75 |
-0.375 |
0.0 |
0.50 |
0.5 |
9.45 |
|
-0.75 |
-0.25 |
0.25 |
0.75 |
1.0 |
38.19 |
|
-0.75 |
-0.25 |
0.25 |
0.75 |
0.5 |
5.22 |
|
-1.00 |
-0.500 |
0.0 |
1.00 |
1.0 |
16.51 |
|
-1.00 |
-0.500 |
0.0 |
1.00 |
0.5 |
2.64 |
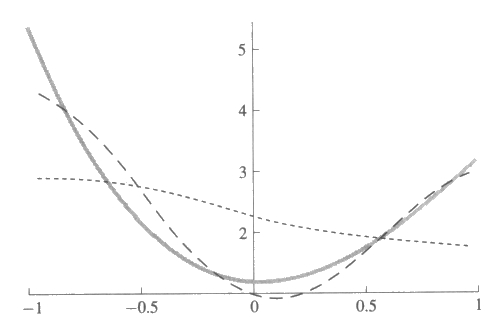
그림 31 : 가우스 기저함수를 사용한 3 차 다항식의 근사. 검은 곡선은 목표함수이고, 짧은 선으로 된 곡선은 폭을 0.5, 중심을 -1.0, -0.5, 0.0, 1.0 으로 하여 근사한 것이다. 점으로 된 곡선은 폭을 1.0, 중심을 -0.75, -0.25, 0.25, 0.75 로 하여 근사한 것이다.
폭과 중심의 변화는 근사되는 정도에 많은 영향을 끼친다. 어떻게 적절한 폭과 중심을 찾을 수 있을까? 이 물음에 대하여서는 쉬운 대답이 없다. 실제 종종 사용하고 있는 한 가지 전략에 대해 살펴보겠다. 작은 훈련 집단이 주어졌다고 하자. 우리는 각 표본이 입력공간 가까이에 있는 전형적인 예제이었으면 하고 바라지만 이 사실을 확신할 수는 없다. 우리는 이 훈련예제들을 가우스 기저함수의 중심과 폭의 값을 정하는 데 사용하고자 한다.
우리가 <xi, yi> 의 형태를 지닌 4 개의 훈련예제를 선택한다고 하자. x1 = -0.8, x2 = -0.2, x3 = 0.3, x4 = 0.9 그리고 목표함수 g (x) = 1.20 - 0.20x + 3.10x2 - 0.90x3 인 yi = g (xi) 라 하자. xi 를 가우스함수의 중심으로 하고 xi 가 0.5 만큼 떨어져 있으므로 폭을 0.5 로 한다. 그렇다면 σ 가 0.5 일 때 결과함수 f 는 다음과 같이 정의된다.

1 ≤ i ≤ 4 에 대하여 f (xi) = yi 이므로 다음과 같은 다항식을 사용하여 wi 를 구할 수 있다.
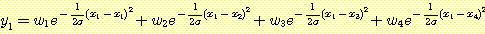
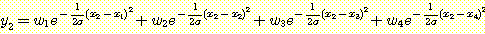
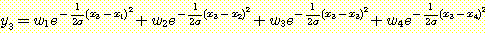
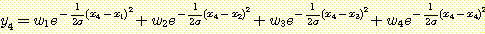
근사된 결과는 그림 32 에 있다. 이렇게 맨 처음으로 근사된 결과를 기울기 방법과 wi 를 잘 조정하도록 부가적인 예제를 사용하여 정련할 수 있으나 단지 4 개의 예제들만 가지고도 이미 목표함수에 잘 근사하였다. 이런 두 단계 방법은 목표함수에 대한 좋은 표상을 생각해내는 문제를 풀지는 못한다. 그러나 수용야 측면에서 방사기저함수를 고려해 보면 기저함수를 선택하는 데 종종 도움이 된다.

그림 32 : 3 차 다항식의 근사, 검은 곡선은 목표함수이고, 짧은 선으로 된 곡선은 폭을 0.5, 중심을 -0.8, -0.2, 0.3, 0.9 로 하여 근사한 것이다. 중심에 정확하게 근사한 것을 검은 점으로 표시하였다.
다차원 입력공간에서의 함수
모든 망 모형에서 알아두어야 할 중요한 또 하나의 사실이 있다. 이것은 방사 기저함수에서는 이미 명백히 드러났던 사실이다. 이 문제는 크기가 서로 다르게 책정되어진 몇 개의 차원으로 되어 있는 함수와 관련되어 있다. 물리적인 단어 문제를 해결하려면 측정의 단위가 무엇인지를 먼저 알아야 하는데, 거리를 측정하기 위해서 '미터' 대신 '피트' 를 사용하거나, 온도를 측정하기 위해서 '섭씨' 대신 '화씨' 를 사용할 때 틀려진다.
다차원 입력공간의 함수를 근사하기 위해 가우스함수를 사용하려면, 다변수 가우스함수를 사용한다.
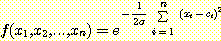
이때 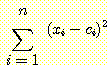 은 거리에 대한 척도이고, 벡터형식으로는 x = <x1, ..., xn>,
c = <c1, ..., cn> 일 때 ∥x - c∥이라고 표시한다. 여기서 c
는 n 차원 입력공간의
가우스함수의 중심이다. 이런 척도를 유클리드 거리 척도라고 한다 (L2
미터법이라고
거론되는 것을 들어보았을 것이다).
은 거리에 대한 척도이고, 벡터형식으로는 x = <x1, ..., xn>,
c = <c1, ..., cn> 일 때 ∥x - c∥이라고 표시한다. 여기서 c
는 n 차원 입력공간의
가우스함수의 중심이다. 이런 척도를 유클리드 거리 척도라고 한다 (L2
미터법이라고
거론되는 것을 들어보았을 것이다).
만일 각 입력의 크기 단위가 서로 다르면서 유클리드 척도를 사용하면 거리를 잘못 측정하게 된다. 예를 들면 2 차원 공간에서 x1 을 밀리미터로, x2 를 킬로미터로 측정하였다면 <0, 0> 은 <1, 0> 에 근접하게 될 것이나, <O, 1> 과는 멀어지게 될 것이다. 이런 크기 효과 (scaling effect) 를 조정하기 위해서 가중값을 둔 거리 척도를 사용한다.
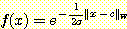
단, w = <w1, ..., wn> 일 때
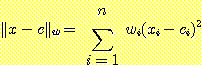
이것은 크기 효과 문제를 해결하지만, n 개의 조정할 수 있는 매개변수를 학습 프로그램에 추가해야 하고, 그만큼 탐색 문제를 더 어렵게 만든다.
편중 형태의 사전 지식이 없다면 많은 학습 프로그램들이 실제적으로 학습하는 것이 불가능하게 된다. 우리는 망 모형으로서 많은 수의 학습 프로그램을 지정할 수 있지만, 가중값에 만족할 만한 값을 찾으려면 굉장한 많은 시간이 필요하다. 일반적인 경험법칙은 다음과 같다: 더 많은 수의 매개변수가 있는 학습방법일수록 실제 적용하기는 더 어렵다.
이 장에서는 교사학습과 귀납적 추론에 대해 살펴본다. 연습문제에서 유전자 알고리즘이 학습에 적용되는 방법에 대해 잠깐 언급하고, 다른 장에서는 학습 속도를 높이기 위한 설명기반 (explanation-based) 일반화에 대해서도 설명한다. 그러나 이러한 주제들로 기계 학습이 모두 설명되었다고 보기는 어렵다. 따라서 여기서는 시스템 이동적 환경하에서 학습하는 방법을 중심으로 하여 비교사학습과 관련된 문제들에 대해 간략히 설명한다. 여기서 동적 환경 이란 시간에 따른 환경의 변화를 지배하는 물리적 법칙이나 상태들의 집합으로 정의된다.
강화학습
동적 환경 하에서 보상값 (reward) 의 형태로 궤환신호 (feedback) 를 받는 어떤 시스템이 장기간 동안 축적된 보상값을 극대화하는 방향으로 환경에 대해 반응을 하도록 학습하는 방법에 대해 알아보자. 어린아이들은 부모로부터의 궤환신호를 바탕으로 하여 그들이 받는 관심을 극대화하는 행동 방법을 배운다. 이때 사용되는 궤환신호는 어떤 행동들은 강화하고, 다른 행동들은 억제시키기도 한다. 따라서 이러한 형태의 학습을 강화학습 (reinforcement learning) 이라고 한다.
임의의 동적환경하에 있는 시스템을 모형화하기 위해 먼저 동적환경을 3 가지 집합, 즉 상태 집합, 행동 들의 집합, 상태전이함수 의 집합을 이용하여 정의한다. 상태전이함수는 주어진 동적환경을 제어하는 물리적 규칙을 나타내고, 초기상태와 시스템이 취할 행동이 주어졌을 때 다음 상태를 결정한다. 여기서 고려하는 방법들은 매우 일반적이고, 따라서 게임이나 컴퓨터 네트워크의 최적화 문제 등 매우 다양한 분야에 적용될 수 있다. 그러나 여기서는 직관적인 이해를 돕기 위해 사무실 환경에서 동작하는 배달 로봇을 예로 들겠다.
배달로봇 문제에 있어서 상태는 사무실들을 말하고, 행동은 한 사무실에서 다른 사무실로 옮겨가는 것을 말한다. 그림 33 에 간단한 사무실 환경이 그래프로 나타나 있는데, 이와 같은 것을 상태전이도 라고 한다. 상태전이도에서 상태는 노드 (node) 로, 상태전이는 아크 (arc) 로 나타내고 각 아크에는 행동의 이름을 붙인다. 그림 33 의 상태전이도에는 모두 4 개의 상태가 있고 각각 0, 1, 2, 3 으로 사무실 이름이 붙여져 있다. 각 사무실들은 하나의 원으로 연결되어 있고, 로봇은 3 가지 행동을 취할 수 있는데, 시계방향 이동 (+), 반시계방향 이동 (-), 제자리지키기 (@) 의 3 가지이다.
먼저 시간을 제어하는 시계가 있다고 가정하고, 시계바늘이 움직일 때마다 로봇이 한 가지 행동을 취한다고 하자. 다음 번에 로봇이 어떤 상태에 있게 되는가는 현재의 상태와 로봇이 취하는 행동에 의해 결정된다. 어떤 환경하에서 초기상태와 행동이 정해졌을 때 다음 상태가 될 수 있는 것은 오직 하나로 결정된다. 그러한 환경은 결정적 (deterministic) 이라고 한다. 따라서 그림 33 의 환경은 결정적이라고 볼 수 있다. 또 당분간 이 로봇은 항상 현재의 상태가 무엇인지 알 수 있다고 가정하고 설명을 계속한다.
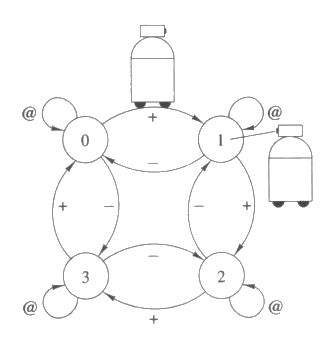
그림 33 : 결정적 환경에 대한 상태전이도. 노드들은 상태 (0, 1, 2, 3 으로 이름 붙여짐) 들을 나타내고, 아크는 3 가지 행동으로 이름이 붙여져 있다. 로봇은 현재상태가 무엇인지 파악하고, 하나의 아크에 해당하는 행동을 취함으로써 다음상태로 간다.
로봇은 하나의 행동을 취할 때마다 어떤 보상을 받게 되는데, 그 보상은 로봇이 새로 도달하게 되는 상태에 의해 결정된다. 그림 33 의 환경에서 만약 로봇이 상태 3 에 도달하면 10 의 보상을 받고, 그 외 다른 상태에 도달하면 0 의 보상을 받는다고 가정한다. 보상의 값이 로봇이 취한 행동과 시작한 상태에 따라서도 달라지는 경우도 많지만, 여기서는 간단한 경우만 고려하기로 하자.
이제 로봇이 하나의 주어진 상태에서 시작하여 일련의 행동을 수행하면서 보상값을 받는다고 하자. 예를 들어서, 상태 0 에서 시작하여 행위 + 를 4 번 수행하면 총 10 의 보상을 받고, 행동 + 를 8 번 수행하면 20 의 보상을 받는다.
이때 로봇이 취하는 행동들은 각 상태에 대해 각각 하나의 행동을 대응시키는 간단한 프로그램으로 결정될 수 있는데, 이 프로그램을 정책 (policy) 이라고 부른다. 즉, 정책이란 어떤 상태에서 어떤 행동을 취해야 할지를 로봇에게 말해주는 것이다. 결정적 환경하에서는 정책과 상태전이함수가 정해지면, 임의의 초기상태로부터 시작하여 여러 번의 전이를 통해 생성될 수 있는 상태의 열이 오직 하나로 결정되게 된다. 따라서, 하나의 정책을 계속 따른다고 가정하면, 그 정책에 대한 각 상태들의 값을 결정할 수 있게 된다.
첫번째 예로, 각 상태에 행동 @ 를 대응하는 정책을 사용하게 되면, 로봇은 상태 0 에서 시작하면 결코 상태 3 으로 갈 수 없고, 따라서 상태 0 의 값은 0 이 된다. 두번째로, 각 상태에 대해 행동 + 를 대응시키는 정책을 사용하면 상태 0 의 값은 무한대가 된다. 세번째로, 상태 3 에 대해서는 행위 @ 를, 다른 상태들에 대해서는 행위 + 를 대응시키는 정책의 경우도 두번째와 마찬가지로 상태 0 의 값은 무한 대가 된다. 여기서 두번째 방법을 정책 0 으로, 세번째 방법을 정책 1 로 정의하고 두 정책의 차이점에 대해 두 가지 관점에서 살펴보자.
첫번째, 각 단계에서의 보상값들을 합하는 대신에 평균값을 취할 수 있다. 이렇게 하면 정책 0 에 대한 평균 보상값의 극한값은 10 / 4 이 되고, 정책 1 의 경우는 10 이 된다. 두번째는 먼저 행한 행동에 대한 보상값은 높은 값으로 정하고, 같은 행동에 대해서도 시간이 흐름에 따라 그 보상값을 감소시키는 것을 생각할 수 있다. 이러한 정책은 감소율 (discount rate) 로 규정지을 수 있다. 즉, 감소율이 γ 라면 어떤 행동이 n 번째 단계에 행해졌을 때의 보상값은 초기 보상값에 γn 을 곱한 값이 된다. 예를 들어 그림 33 의 환경에서 γ 가 0.5 라면, 정책 0 의 경우 상태 0 에 대한 감소 누적 보상값 은 1.33 이 되고, 정책 1 의 경우는 2.5 가 된다.
그러면, 이 감소 누적 보상값은 어떻게 계산되었는가? 여기서는 동적 프로그래밍에 기반한 반복법을 사용하였다. 동적 프로그램에서는 하나의 문제를 순환적으로 보다 작은 문제들로 나눈 다음, 작은 문제들로부터 큰 문제 쪽으로 진행하면서 해결해 나간다. 이때 작은 문제의 해가 보다 큰 문제를 푸는 데 사용될 수 있다. 어떤 주어진 정책하에서 감소 누적 보상값을 계산하기 위해서는, 먼저 오직 한 단계에 그 정책을 적용하였을 때의 값을 계산한다. 즉, n 번째 단계에 대한 계산 결과가 주어지면, n + 1 번째 단계의 보상값을 계산할 수 있다.
보상값들이 행동에 의존하지 않는다고 가정하고 R (j) 를 상태 j 에서의 보상값으로 정한다. 또 특정한 정책을 π 라고 하면, 이 정책을 사용할 때 상태 j 에서 취해야 하는 행동은 π (j) 로 쓸 수 있다. 또한 f (j, α) 는 상태 j 에서 행동 α 를 취했을 때 도달하게 되는 새로운 상태이고, Viπ(j) 는 정책 π 를 써서 동적 프로그래밍을 i 번 반복수행하였을 때, 상태 j 에 대한 값이라고 하자. 이때 그 추정값을 구하는 동적 프로그래밍 알고리즘은 다음과 같다.
① 모든 j 에 대해, 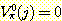
② i ← 0
③ 모든 j 에 대해, 
④ i ← i + 1
⑤ 만약 i 가 최대
반복 횟수보다 크면, ![]() 값을 내고, 그렇지 않으면 3
번 단계로 간다.
값을 내고, 그렇지 않으면 3
번 단계로 간다.
정책 π 에 대한 가치함수 (value function) 는
Vπ 로 표시되며 i → ∞ 일 때 ![]() 로 정의된다. 동적 프로그래밍을 통하거나 적은 수의 반복을 통해서도 비교적 좋은
추정값을 얻을 수 있다.
로 정의된다. 동적 프로그래밍을 통하거나 적은 수의 반복을 통해서도 비교적 좋은
추정값을 얻을 수 있다.

그림 34 : 감소 누적 보상값을 계산하는 함수
그림 34 는 각 상태에 보상값을 대응시키는 보상함수와 정책 0 과 정책 1 각각에 대한 상태전이함수들과 동적 프로그램을 LISP 언어로 구현한 것이다. 감소율이 0.5 인 경우에 각 정책을 사용하였을 때 4 가지 상태에 대한 값을 계산하면 다음과 같다.
> (dynamic #'deterministic-transition-0 0.5 100)
(1.33 2.66 5.33 10.66)
> (dynamic #'deterministic-transition-1 0.5 100)
(2.5 5.0 10.0 20.0)
우리가 제시한 동적 프로그램은 기계 학습에 있어서 하나의 중요한 문제에 대한 해결책을 제공하고 있다. 그 문제는 시간적 기여도 할당문제 (temporal credit assignment problem) 로, 일련의 행동들이 모두 끝난 후에야 궤환신호를 얻을 수 있는 상황에서 그때까지 수행된 일련의 행동들 중 어떤 행동에 기여도 (credit) 를 주고 또 어떤 행동에 벌점 (blame) 을 줄 것인지 결정하는 것을 말한다. 예를 들어 당신이 체스를 두어 졌을 경우에, 지게 된 원인이 반드시 마지막 수나 바로 그 전 수에 있다고 말할 수는 없다. 당신은 몇 가지 실수들을 저질렀을 수 있고 또한 그 실수를 수정했을 수도 있다. 또 그런 실수들이 일련의 행동들의 일부가 되었다 하더라도 그것이 당신이 최종적으로 게임을 지게 한 원인이 되지 않았을 수도 있다. 이때 어떤 수가 패배의 원인이 되었는지를 알아내는 것이 시간적 기여도 할당 문제라고 볼 수 있다. 동적 프로그래밍에서는, 어떤 정책에 의해 결정되는 일련의 행동들 중에서 먼저 행해진 상태쪽으로 보상값을 역전파 시킴으로써 시간적 기여도 할당 문제를 해결한다. 이 방법을 이용하면, 어떤 정책하에서 상태들의 값을 추정하는 방법이 주어졌을 때 최적의 정책이 무엇인지 찾아 낼 수 있다.
최적의 정책을 찾는 방법
이제 우리는 주어진 정책에 대해 각 상태들의 값을 구할 수 있는 프로그램을 가지고 있다. 많은 방법들이 감소 누적 보상값을 최대화하는 정책을 찾기 위해 이 알고리즘을 사용한다. 여기서는 그 중 정책 반복 (policy iteration) 방법에 대해 설명하겠다.
어떤 정책 π 에 대해, Vπ' (j) > Vπ (j) 이고 k ≠ j 인 모든 k 에 대해서는 Vπ' (k) ≥ Vπ (k) 인 조건을 만족하는 정책 π' 와 상태 j 가 존재하지 않는다면, 이때 정책 π 를 최적 정책 (optimal policy) 이라고 한다. 다음 알고리즘을 사용하면 유한한 단계 내에서 최적 정책을 찾을 수 있다.
① π0 를 임의의 정책으로 놓는다.
② i ← 0
③ 모든 j 에 대해, 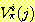 를 계산한다.
를 계산한다.
④ π i+1 가 R (j) + γ V π i (f (j, α)) 를 최대화하는 행동 α 가 되도록 정책 π i+1 을 계산한다.
⑤ 만약 π i+1 = π i 이면 π i 를 결과로 내고, 그렇지 않으면 i ← i + 1 로 하고 3 단계로 간다.

그림 35 : 정책모의 및 상태값의 수정에 관한 함수
여기까지 우리는 어떤 정책 하에서 상태들의 값을 계산하는 것이 최적 정책을 찾는 데 어떻게 도움이 되는지를 보여주었다. 다음 단락에서는 상태들의 값을 계산하는 함수인 가치함수를 학습하는 것과 관련된 다른 주제들에 대해 논의하겠다.
가치함수를 학습하는 온라인 방법
앞서 설명한 동적 프로그래밍 알고리즘은 주어진 환경에 대해 보상함수와 상태전이함수를 알고 있다고 가정하였지만, 이런 정보들을 로봇에게 알려주지 않는 경우도 많이 있다. 그러나 이런 경우에도 로봇들은 환경과의 상호 작용을 통해 이러한 함수들을 학습할 수 있다. 다음에서 우리는 가치함수를 학습하는 온라인 방법을 제시하고자 한다. 이 방법은 상태전이함수나 보상함수와 같은 정보들을 알고 있지 않아도 학습이 가능하다.
그림 35 에는 일반적인 환경 모의실험에 대한 코드가 나타나 있다. simulate 라는 함수는 모두 4 가지의 매개변수를 받는데, 특정 정책에 대한 상태전이함수, 가치함수를 수정한 함수 (각 상태에 대한 값들을 원소로 갖는 벡터로 표현됨), 감소율, 모의실험해야 할 단계수가 그것이다. deterministic-update 라는 함수는 주어진 상태하에서 얻을 수 있는 정보, 즉 현재 상태, 다음 상태, 현재 추정된 가치함수 그리고 감소율 등을 매개변수 값으로 받아들인 다음, 이 정보를 이용하여 가치함수값을 새롭게 추정한다. deterministic-update 함수는 한번 수행할 때마다 하나의 상태에 대한 가치함수값을 수정하는데, 이것은 앞서 설명한 동적 프로그램이 한번 수행시 모든 상태에 대한 수정을 가하는 것과는 다른 점이다. 그러나 이 방법 역시, 상태전이 회수가 무한대일 때 어떤 상태를 무한번 방문하게 되면, 그 상태에 대해서는 이전의 동적 프로그래밍 방법과 같은 값으로 수렴함을 보장한다.
> (simulate #'deterministic-transition-0
#'deterministic-update 0.5 100)
(1.33 2.66 5.33 10.66)
> (simulate #'deterministic-transition-1
#'deterministic-update 0.5 100
(0.0 0.0 0.0 20.0)
위 결과에서 볼 때 정책 1 에 대한 결과는 이전의 값과는 다르다는 것을 알 수 있다. 이것은 정책 1 에서는 상태 3 에 일단 도달하게 되면 상태 0, 1, 2 는 더 이상 방문할 수 없게 되어 방문회수가 무한대가 될 수 없기 때문이다.
지금까지 우리는 환경이 결정적이라고 가정한 상태에서 설명해왔다. 추정통계적 (stochastic) 환경에서는 초기상태와 행동이 정해져 있을 때 다음상태는 상태 집합에 대한 확률 분포에 의해 결정된다. 그림 36 은 그림 33 의 사무실 환경의 추정통계적 변화에 대한 전이 확률을 보여주고 있다. 그림 36 에 의하면, 상태 0 에서 행동 + 를 취할 때, 로봇이 상태 1 에 도달하게 될 확률은 70 %, 상태 0 에 머무르게 될 확률은 30 % 가 된다. 그림 37 에는 앞서 제시한 두 개의 전략에 대한 추정통계적인 상태전이함수를 각각 보여주고 있다. 그림 37 의 코드에서 각 상태는 (state probability-of-most-likely-next-state most-likely-next-state next-most-likely-next-state) 형태로 확률 분포와 함께 표시되는데, 이때 각 상태에서 옮겨갈 수 있는 다음 상태는 최대 2 개로 제한한다. 예를 들어 (2 0.7 3 2) 라는 코드가 의미하는 바는, 상태 2 에 있는 로봇이 상태 3 으로 옮겨갈 확률이 70 % 이고 그렇지 않은 경우에는 상태 2 에 그대로 남아있게 된다는 것이다.
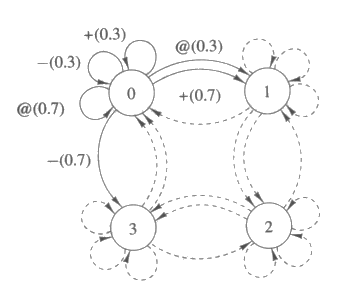
그림 36 : 추정통계적 환경에 대한 상태전이도. 상태 0 에 대한 전이 확률만이 나타나 있고 다른 상태들에 대한 전이 확률은 모두 이와 같다.
그림 34 에 나타난 결정적 수정 (update) 전략은 추정통계적 환경하에서는 잘 동작하지 않는다. 따라서 상태의 기대값 (expected value of a state) 이라는 새로운 개념을 도입한다. 이것은 추정통계적 환경을 제어하는 확률 분포에 의해 결정되는 일련의 상태전이 과정에서 얻어지는 감소 누적 보상값의 평균을 말한다. 여기서 관심있는 것은 상태의 기대값을 결정하는 것인데, 결정적인 수정 전략을 사용하여 계산된 가치함수들은 엉뚱한 값으로 변할 수 있기 때문에 어떤 경우에는 앞서의 경우와 같이 두 가지 정책을 비교할 수 없다.
> (simulate #'stochastic-transition-0
#'deterministic-update 0.5 100)
(1.33 2.65 5.33 10.66)
> (simulate #'stochastic-transition-1
#'deterministic-update 0.5 100)
(1.33 2.65 5.33 10.66)

그림 37 : 두 개의 고정된 정책에 대한 추정통계적 상태전이함수
따라서, 추정통계적 환경하에서 상태의 기대값은 그 상태의 보상값과 가능한 다음 상태들의 기대값에 확률을 곱해서 합한 확률-가중합과의 총합으로 결정된다. 각 상태에 대해 모두 행동 + 를 대응시키는 정책에서의 상태 0 의 값은, 상태 0 의 보상값과 상태 1 의 값에 0.7 을 곱한 값 그리고 상태 0 의 값에 0.3 을 곱한 값을 모두 더한 것이 된다. 이때 필요한 계산, 즉 가능한 다음 상태들과 각각의 확률값을 곱해서 가중합을 구하는 계산을 동적 프로그래밍 알고리즘이 수행할 수 있도록 고치는 것은 어렵지 않다. 즉, 어떤 정책을 따라 움직이는 로봇이 방문하게 되는 상태들은 추정통계적 환경을 제어하는 확률 분포에 의해 결정된다는 사실을 이용하면 온라인수정 (online update) 알고리즘을 사용하여 추정값을 계산할 수 있다. 전이가 일어날 때마다 로봇은 전이를 일으키기 전의 상태에 대한 추정값을 조금씩 조정한다. 이렇게 여러 번의 전이가 일어난 후, 우리는 그 상태에 대한 보상값과 가능한 다음상태들에 대한 확률가중합과의 총합을 얻을 수 있게 된다. 조정률 β (0 ≤ β ≤ 1) 와 감소율 γ 를 사용한 온라인 알고리즘이 아래에 있다.
① 모든 i 에 대해, Vπ (i) ← 0
② j 를 초기상태로 둠
③ r 을 상태 j 에서 받은 보상값으로 둠
④ π (j) 를 수행하고, 그 결과 상태를 k 로 둠
⑤ Vπ (j) + Vπ (j) + β [r + γ Vπ (k) - Vπ (j)]
⑥ j ← k 그리고 3 번 단계로 간다.
이 알고리즘은 실제 기대값으로 수렴하지는 않지만, 여러 번의 전이가 일어난 후에 기대값 주변의 작은 구간 내의 값을 추정값으로 출력하는 안정상태에 도달하게 된다. 이때 그 구간의 크기는 조정률 (β) 에 의해 좌우된다. 만약 조정률 값이 1 에 가까우면 구간의 크기는 커지지만 안정상태로 도달하는 데 필요한 전이 횟수는 줄어든다. 반대로 조정률이 작아질수록 구간은 작아지고 필요한 전이 횟수는 많아지게 된다. 연습문제 16 에서 여러 가지 조정률로 시험해 보는 기회가 주어질 것이다. 그림 38 은 알고리즘을 구현한 코드이다.

그림 38 : 추정통계적 환경하에서 상태의 값을 수정하는 함수
탐험에 의한 학습
여기서는 시스템이 어떻게 환경과 상호작용하고 환경에 대해 학습하는가에 대해 생각하고자 한다. 앞서 논의된 기술들에서 로봇은 주어진 정책에 따라 환경을 탐험함으로써 환경에 대해 학습하게 된다. 로봇이 어떤 상태에 도달했을 때 받게 될 보상이 무엇이며, 주어진 행동을 취했을 때 어떤 상태에 도달하게 될 것인지를 모른다고 가정하자. 앞서 제시한 온라인 알고리즘에서는 보상이나 상태전이함수에 대한 학습은 고려하지 않았다. 그러나 만약 이런 함수들을 학습한다면 정책들도 빠르게 학습할 수 있을 것이다.
이제 환경에 대한 상태전이함수의 학습에 대해 고려해 보자. 만약 상태들을 물리적인 위치에 연관시키고 행동들을 그 사이를 움직이는 전략에 연관시켜서 생각한다면, 상태전이함수에 대한 학습은 그 환경의 지도를 학습하는 것과 유사하다 그림 33 의 환경에서 로봇이 현재 어떤 상태에 있는지 알 수 있다고 가정하면, 상태전이함수를 학습하는 것은 간단하다.
상태전이함수의 학습은 불확실성으로 인해 복잡해 질 수 있다. 다음에서 우리는 행동과 관찰에 대한 불확실성을 고려하고자 한다. 그림 36 에서 보여지는 추정통계적인 환경에서는 행동에 대한 불확실성은 존재하지만, 관찰에 대한 불확실성은 없다. 즉, 로봇이 어떤 행동을 수행할 때 다음상태가 무엇이 될지는 확신할 수 없다. 그렇지만 추정통계적 방법을 사용하면 그림 36 에 대한 확률적 상태전이함수의 학습은 비교적 쉽게 해결할 수 있다.
한편, 관찰에 있어서의 불확실성은 결정적 환경하에서도 일어날 수 있다. 즉, 당신이 어떤 상태에 있는지 정확히 알 수 없는 경우가 많이 있다. 예를 들어, 당신이 염력과 같은 방법에 의해 맥도날드 식당으로 이동되었다고 하자. 그때 당신은 자신이 맥도날드에 와있다는 것은 알 수 있게 되겠지만, 비슷한 인테리어를 가진 여러 개의 식당 중 정확히 어떤 맥도날드 식당에 와 있는지는 확신할 수 없다. 이것은 다시 말하면, 모든 상태들이 이름 붙여져 있는데, 그 중 몇 가지들은 같은 이름을 갖고 있는 경우와 같은 것으로 생각할 수 있다.
이밖에 추정통계적인 환경에서는 관찰에 있어서의 불확실성을 유발하는 또 다른 경우가 있을 수 있다. 당신의 시각 시스템이 추정통계적 프로세서에 의해 제어된다고 가정해 보라. 당신이 맥도날드 식당에 있는 동안, 대부분의 경우는 그것이 맥도날드 식당으로 보일 것이다. 그렇지만 어떤 경우에는 버거킹 식당처럼 보일 수 있다. 이런 경우는 다시 말하면, 당신이 어떤 상태에 있을 때, 그 상태가 무엇인지를 관찰하는 것을 제어하는 확률 분포가 존재하는 것이 된다.
이제 추정통계적 환경을 고려하지 말고 결정적 환경에 대해 논하되, 인식 프로세서가 추정통계적이라고 가정하자. 즉, 우리는 실제로는 맥도날드에 있으면서 버거킹에 있는 것처럼 인식할 수 있고, 로봇이 실제로는 시계방향으로 움직이면서 자신이 반시계방향으로 움직이고 있는 것처럼 인식할 수 있다고 가정하는 것이다. 그림 39 는 같은 이름을 가진 상태들이 있을 때 로봇이 직면하게 되는 상황을 보여주고 있다. 로봇은 상태의 이름을 인식하고 어떤 변환을 수행해야 할 지를 결정하는 데 오류를 범할 수도 있게 된다.
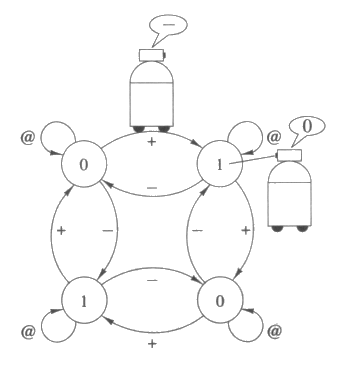
그림 39 : 결정적 상황하에서의 인식의 오류
그림 39 에서, 비록 인식의 오류는 없다고 가정한다 해도 이런 종류의 환경에서 임의의 상태전이도를 학습한다는 것은 어려운 일이고 심지어 불가능할 수도 있다. 예를 들어, 상태 0 과 상태 1 을 각각 하나 씩만 가진, 두 상태로 구성된 환경을 그림 39 의 환경과 구분하는 것은 불가능하다. 이러한 복잡한 문제를 무시한다고 하더라도, 일반적으로 환경을 학습하는 것은 어렵다. 어떤 환경이 로봇에 의해 관찰되는 상태와 행동으로 구성되고, 그 크기 또한 실제 환경의 일부분으로 제한되어 있는 경우에는 그 환경을 유추하는 것은 다루기 힘든 문제이다.
학습에 관한 문헌에서는 그림 33 과 그림 39 에 있는 것과 같은 종류의 환경은 유한상태 오토마타로 표현된다. 유한상태 오토마타의 학습에 대한 연구들은 PAC 학습가능한 오토마타 부류를 발견하는 것과 관련되어 있다. 예를 들어, 많은 실제환경에서, 로봇은 정해진 순서로 행동들을 수행하면서 관찰을 통해 얻은 일련의 상태들을 바탕으로 하여 임의의 두 상태를 구분한다. 로봇이 그러한 상태열을 찾을 수 있는 환경은 PAC 학습가능한 것이다. 유한상태 오토마타를 학습하는 알고리즘을 개발하는 것은 기계학습과 관련된 많은 연구 분야 중 하나이다.
학습이란 어떤 시스템이 주어진 일을 수행하는 성능을 향상시키기 위하여 시스템이 가지고 있는 지식의 내용이나 구조를 변화시키는 것과 관계된 것이다. 이 장에서 우리는 많은 예시들을 통해 결론에 도달하는 방식을 취하는 귀납적 추론이라고 불리는 특별한 형태의 학습에 대해 논하였다. 가장 먼저 시스템이 학습할 때 입력값과 원하는 출력값으로 이루어진 예시들이 학습 집합으로 주어지는 교사학습에 대해 살펴보았다. 이때 시스템은 학습을 수행함으로써 학습쌍들에 부합되는 결과를 냄과 동시에 학습되지 않은 다른 입출력쌍에 대해서도 의미 있는 출력을 내는 일반화 능력을 보여주었다.
그런데 만약, 가설공간에 어떠한 제약도 주어지지 않는다면 학습되지 않은 예시에 대해 시스템이 찾아낸 일반화된 함수는 우리가 원하는 것이 아닌 엉뚱한 것이 될지도 모른다. 따라서 시스템이 학습을 통해 함수를 찾아낼 때 그 탐색 범위 대상이 되는 가설공간을 제한할 필요가 있는데, 이것이 바로 시스템의 학습이 우리가 원하는쪽으로 진행되도록 하기 위한 편중 (bias) 이 된다. 예를 들어서 만약 시스템이 어떤 논리함수를 학습해야 한다면, 그 대상은 양의 리터럴 (positive literals) 의 논리곱이어야 한다거나, 될수록 작은 논리함수이어야 한다는 등의 제약이 편중으로 사용될 수 있다.
학습에 있어서 오차란 반드시 존재하는 것이다. PAC 학습이란 오차의 허용값을 설정 (근사 부분) 하고, 그 허용값이 때때로 만족되지 않을 수 있음 (확률적 부분) 을 인정하는 학습의 계산적 모델이다. 만약 어떤 함수의 집합에 대해, 임의의 허용값과 집합 내의 함수 집합이 주어졌을 때, 다항수 (polynomial number) 의 패턴을 학습쌍으로 사용하여 주어진 허용값을 만족하는 대응 관계를 찾아내는 다항시간 (polynomial-time) 알고리즘이 존재한다면, 그 함수 집합은 어떤 가설공간에 대해 PAC 학습가능하다고 할 수 있다. 만약 충분한 수의 학습 예시가 주어지기만 한다면, PAC 학습을 통해 학습 예시들에 부합되는 대응 관계를 찾아 수 있는 경우가 많이 존재한다.
귀납적 편중을 구현하기 위해서는 그 편중을 만족하면서 학습 예제들에 부합되는 가설을 찾아내야 한다. 이때 어떤 편중들은 때로 다른 것들에 비해 비교적 구현하기 쉬운 것도 있다. 예를 들어, 단순명제들의 논리합이라는 가설공간에서 적절한 가설을 찾는 것은 다항시간 내에 해결될 수 있다. 그러나 최대 k 개의 논리합 인자 (disjunct) 를 가진 논리합 기본형 (disjunctive normal form) 을 가지는 가설공간에서 적절한 가설을 찾아내는 것은 NP-hard 한 문제이다.
버전공간 (version-space) 방법이란 이제까지 관찰된 학습쌍들에 부합되는 모든 가설들로 이루어진 집합으로 그 탐색 범위를 제한해가면서 학습을 진행하는 온라인방법이다. 이 방법은 단일명제들의 논리합이라는 가설공간에 대해서는 최선의 방법이 될 수 있다. 결정트리 (decision-tree) 방법은 일괄처리 방법으로, 학습쌍들로 이루어진 집합을 하나 취하고, 경험규칙을 이용하여 그 예시들을 분류할 수 있는 작은 결정트리를 찾는 방법이다. 이때 사용되는 경험규칙은 정보이론의 무질서 양에 기반하는 것이다. 이 결정트리 방법은 품질 제어 시스템에서 불량품 인식문제에서부터 주식시장의 투자 예측에 이르기까지 매우 다양한 분야에 적용되고 있다.
간단한 계산 요소로 구성된 회로망은 넓은 범위의 계산 기기를 구현하는 데 사용될 수 있다. 그러한 회로망들은 또한 조정가능한 가중값의 개념을 추가함으로써 가설 관계 공간을 나타내는 데 사용될 수 있다. 이때 가중값은 그 회로망이 나타내는 함수의 집합을 정의하게 된다. 또 학습쌍들에 대한 오차를 최소화하는 가설을 찾기 위해 가중값을 조정하는 방법으로 기울기 (gradient) 방법이 사용될 수 있다. 선형함수공간을 나타내는 회로망에 대해서는 이 기울기 감소 방법을 사용함으로써 오차를 최소화하는 해로 수렴해 감이 보장된다. 비선형 함수공간을 나타내는 회로망에 대해서는 그러한 보장을 할 수는 없지만, 이 경우에도 기울기 감소 방법이 사용될 수 있으며 실제 문제에서 좋은 결과를 내는 경우가 많이 있다. 퍼셉트론이라고 불리는 비교적 간단한 회로망은 선형 분리가능한 함수 집합에 대해 오차를 최소화할 수 있는 가설로 수렴함이 보장되는 가중값 조정 규칙을 가지고 있다.
일반적으로 하나의 회로망을 구성하고 특정한 함수를 학습하기 위해 그 가중값을 조정하는 방법을 찾아서 적용하는 문제는 대단히 복잡하며 많은 시행착오를 요구한다. 가우스함수의 합을 계산하는 회로망은 메모리의 각 부분에 입력공간의 특정 범위에 대한 출력값을 근사하도록 일을 할당하고 그것들을 학습하는 방법을 제공한다. 이 회로망은 학습을 두 단계로 구분해 두고 있다. 첫번째 단계는 기억장치의 각 부분에 입력 공간들을 각각 할당하는 것이고, 두번째 단계는 각 범위에 대해 함수를 근사할 수 있도록 하는 것이다.
강화학습이란 비교사학습의 하나로, 학습 과정에서 시스템은 그것이 가정하고 있는 대응관계가 맞는지 틀린지를 말해주는 궤환신호를 받게 된다. 강화학습에서 일어날 수 있는 시간적 기여도 (temporal credit) 할당 문제는 모든 행동들이 끝났을 때에야 궤환신호를 받을 수 있는 경우에 그때까지 수행한 일련의 행동들 중 어떤 것에 기여도나 벌점을 줄 것인지를 결정하는 것이다. 동적 프로그래밍은 이러한 시간적 기여도 할당 문제를 해결하는 방법이다. 어떤 강화학습 방법은 그것이 학습하고 있는 환경의 모형이 없이도 학습을 수행할 수 있다. 또 다른 비교사학습 방법은 환경을 탐험함으로써 그 환경의 모형을 추론한다. 환경을 유추하게 되면 강화학습이 촉진될 수 있다.
학습이 AI 의 모든 어려운 문제에 대한 만병통치약이 될 수는 없다. 오히려 효율적인 학습 방법의 경우에는 시스템에 귀납적 편중을 줌으로써 대응 관계에 대한 가정을 탐색함에 있어서 그 시야를 좁혀야 하는 것일 수도 있다. 탐색이라는 관점에서 학습을 볼 때 가장 중요한 계산적 역할을 하는 것은 표상이다. 가정에 대한 표상을 선택하는 것은 궁극적으로 시스템이 학습해야 하는 것과 학습 속도를 결정하는 귀납적 편중과 직접적으로 관련되기 때문이다.
기계학습에 대한 일반적인 내용에 대해 알고 싶다면 Dietterich [1990] 를 읽도록 권한다. Michalski et. al [1983] 과 Shavlik 와 Dietterich [1990] 은 기계학습과 관련된 많은 문헌을 읽기 위한 좋은 첫걸음이 될만한 논문들의 모음집이다.
Mitchell [1977] 은 학습에 있어서 귀납적 편중이 필요한 경우를 제시하고 있다. 학습의PAC 모델은 Valiant [1984] 에서 도입되었으며, 이것은 기계학습에 있어서 이론적 연구를 촉진 시켰다. 본 저서에서 설명한 PAC 학습의 분석은 Blumer et. al [1987] 을 참조하였다.
변형공간은 MitchelI [1982] 에서 좋은 일반화 해를 찾는 전략의 일환으로 개발되었다. 결정트리는 추정통계적 분석과 학습의 분야에서 긴 역사를 갖고 있다. 이 장에서 논의된 결정트리 내용은 Ouinlan [1986] 을 참조하였고 Breiman et. al [1984] 에 다른 관점이 제시되고 있다. 이 장에서 제시한 의학적 응용 예는 Breiman et. al [1984] 에 설명되어 있다. 결정트리에 기반한 학습은 Lin 과 Vitter [1992] 에서 제시하는 자료 압축 방법과도 밀접한 관련이 있다.
계산 신경회로망 모형에 관한 대부분의 연구는 McCulloch 와 Pitts [1943] 에 의해 개발된 신경 시스템 모형에 기반을 두고 있다. 특히 이 모형의 일반화된 형태가 선형 임계값 모형이다. 선형 임계값 모형의 특별한 예인 퍼셉트론은 Rosenblatt [1961] 에 의해 개발되었다. 퍼셉트론 학습의 수렴성이나 퍼셉트론이 가지는 제한점 등의 상세한 토의에 대해서는 Nilsson [1965] 나 Minsky 와 Papert [1969] 에 논의되어 있다.
다층 신경회로망에서의 기울기 방법은 Werbos [1974] 에서 소개되었다. 이장에서 소개된 방법은 역전파 방법으로 불리는 것으로, Rumelhart et. aI [1986] 에서 제시된 것이다. 함수근사 문제를 풀기 위해 방사 기저함수 (radial basis function) 를 사용하는 신경망은 Poggio 와 Girosi [1989] 에 자세히 설명되어 있다. Hertz et. al [1991] 에서는 인공 신경회로망에 대한 기초 이론을 소개하고 있다.
Pomerleau [1991] 에서는 ALVINN 을 설명하고 인공신경망을 차량 운행 시스템에 응용한 예를 제시하고 있다. Sejnowski 와 Rosenberg [1987] 에서는 영어 문장을 발음하는 인공 신경망인 NETtalk 에 대해서 설명하고 있다. Tesauro 와 Sejnowski [1957] 과 Tesauro [1992] 에서는 벡게몬 (backgammon) 놀이를 학습하는 프로그램을 제안하고 있다.
Barto et. al [1990] 은 강화 학습 방법에 대한 관련 논문들에 대한 조사 논문이며, Sutton [1988] 에서는 시간적 기여도 할당 문제를 해결하는 일반적인 방법들을 제시하고 있다. Tesauro [1992] 에서는 강화학습을 토너먼트식 주사위 놀이를 학습하는 데 적용한 예를 보이고 있다. 유한 오토마타를 이용하여 환경을 나타내는 방법은 Moore [1956] 에서 제안되었으며, 학습하는 오토마타에서의 이론적 결과를 제시하고 있는 논문으로는 Angluin [1987], Rivest 와 Schapire [1987], Basye et. al [1995] 이 있다. 유전자 알고리즘을 이용한 분류 시스템에 대한 연습문제는 Holland [1975] 에 기반한 것이다.
Lisp 로 작성된 학습 알고리즘
이 장에서는 변형공간과 결정트리에 기반한 학습 알고리즘을 구현한 코드를 제공한다. 이 알고리즘들에 대한 코드를 나열하기 전에 두 알고리즘 모두에 사용되는 두 개의 유틸리티를 설명한다.
findall 이라는 함수는 하나의 리스트와 하나의 함수를 받아서 그 리스트 안에 있는 모든 항목들을 결과로 내어 그 함수가 해당 항목에 적용되면 non-nil 이라는 결과를 낼 수 있도록 한다.
(defun findall (list test)
(do ((items list (rest items)) (results nil))
((null items) results)
(if (funcall test (first items))
(setq results (adjoin (first items) results
:test #'equal)))))
문제의 차원에 따라 모든 특징 집합의 각 경우를 언급할 필요가 있다. features 는 dimension 을 사용하여 주어진 문제의 모든 특징 리스트를 생성한다.
(defun features ()
(mapcan #'(lambda (dim)
(mapcar #'(lambda (value)
(list (DIMENSION-attribute dim)
value))
(DIMENSION-values dim)))
(dimensions)))
변형공간에서 경계 다듬기
다음은 새로운 학습 예가 주어진 경우 변형공간의 한계를 수정하는 코드를 나타낸다. 제공된 코드는 유일한 개념에 수렴한다는 것을 보장하지 못한다. 연습문제 4 에서 교재에서 주어진 완전한 알고리즘을 구현하기 위해 코드를 어떻게 수정해야 하는가를 알아보았다.
refine 은 하나의 학습 예시와 일반적인 경계와 특정한 경계를 나타내는 두 개의 개념 리스트를 입력받는다. 논리곱 (conjunction) 개념은 특징리스트로서 표상된다. refine 은 학습 예가 yes 인지 no 인지를 결정한 후 각각 특정 한계 내의 개념으로 일반화 또는 일반 한계의 개념으로 특정화하는 처리를 한다.
(defun refine (example general specific)
(if (eq (EXAMPLE-class example) 'yes)
(list general (generalize-specific example specific))
(list (specialize-general example general) specific)))
특정 한계를 일반화하는 것은 한계 내에 있는 각 개념들을 학습 예와 부합될 때까지 계속적으로 일반화하는 것이다.
(defun generalize-specific (example boundary)
(mapcan #'(lambda (concept)
(aux-generalize-specific example concept))
boundary))
(defun aux-generalize-specific (example concept)
(if (consistent (EXAMPLE-features example) concept)
(list concept)
(generalize-specific example (generalize concept))))
일반 한계를 특정화하는 것은 한계 내에 있는 각 개념들을 학습 예와 부합되지 않을 때까지 계속적으로 특정화하는 것을 의미한다.
(defun specialize-general (example boundary)
(mapcan #'(lambda (concept)
aux-specialize-general example concept))
boundary))
(defun aux-specialize-general (example concept)
(if (not (consistent (EXAMPLE-features example) concept))
(list concept)
(specialize-general example (specialize concept))))
하나의 개념이 어떤 예시에 부합되기 위해서는 다음 두 가지 조건 중 하나를 만족하면 된다. 즉, 그 개념에 있는 각 특징에 대해 그 속성값이 예제를 설명하는 리스트에 언급되어있지 않거나, 언급되더라도 대응되는 특징이 같은 속성값을 가지면 그 개념은 예제에 부합된다고 본다. 예를 들어, 하나의 예제가 3 층 사무실에 해당한다면 이 예시와 부합되는 개념은 층에 대해 언급되지 않았거나 3 층을 의미하는 것이다.
(defun consistent (features concept)
(every #'(lambda (f)
(or (not (assq (FEATURE-attribute f) features))
(member f features :test #'equal)))
concept))
단일 명제로 구성되어 있는 제한된 가설공간에 대해서, 일반화라는 것은 특징 리스트로 표현된 개념에서 특징을 제거하는 것이다.
(defun generalize (concept)
(mapcar #'(lambda (feature)
(remove feature concept :test #'equal))
concept))
특정화라는 것은 개념에 부합되는 특징을 추가하는 것이다. specialize 와 generalize 는 각각 함수의 인자로 제공된 개념보다 최소한 좀더 특정화된 개념과 최소한 좀더 일반화된 개념을 결과값으로 리턴한다.
(defun specialize (concept)
(mapcar #'(lambda feature) (cons feature concept))
(findall (features)
#'(lambda (feature)
(and (consistent (list feature) concept)
(not (member feature concept
:test #'equal)))))))
versions 는 학습예제들의 집합과 초기 한계쌍을 입력으로 받아 각 학습예제를 교대로 처리함으로써 한계를 다듬는다.
(defun versions (example boundaries)
(mapcar #'(lambda (example)
(setq boundaries (refine example
(first boundaries)
(second boundaries)))
(format t "Example: ~A~%General: ~A~%Specific: ~A~%"
example (first boundaries) (second boundaries)))
examples))
결정트리의 구축
주어진 예의 집합에 대해서 classify 는 예제들을 부류 (class) 로 분할한다.
(defun classify (examples)
(mapcar #'(lambda (class)
(findall examples #'(lambda (s)
eq class (EXAMPLE-class s)))))
(classes)))
partition 은 예시의 집합을 입력으로 받아 속성값에 따라서 차원의 속성을 분할한다.
(defun partition (examples dimension)
(let ((attribute (DIMENSION-attribute dimension)))
(mapcar #'(lambda (value)
(findall examples
#'(lambda (example)
(member (list attribute value)
(EXAMPLE-features example)
:test #'(equal))))
(DIMENSION-values dimension))))
buildtree 는 결정트리를 구축하기 위해 간단한 재귀적 함수로 구현되었다.
(defun buildtree (node)
(format t "Class distribution" ~A~%"
(mapcar #'length (classify (NODE-example node))))
(if (< 1 (length (findall (classify (NODE-examples node))
#'(lambda (s) (not (null s))))))
(let ((dim (splitter node)))
(format t "Dimension chosen: ~A~%" dim)
(set-NODE-attribute node (DIMENSION-attribute node))
(set-NODE-children node
(mapcar #'make-NODE
(partition (NODE-examples node) dim)))
(mapc #'buildtree (NODE-children node)))
(format t "Terminal node. ~A~%")))
splitter 는 evaluate 에 의해 구현된 특별한 평가함수를 극소화시키는 속성을 찾는다.
(defun splitter (node)
(do* ((dims (rest (dimensions)) (rest dims))
(value (evaluate node (first (dimension))))
(splitter (first (dimensions))) (min value))
((null dims) splitter)
(setq value (evaluate node (first dims)))
(if (< value min)
(setq splitter (first dims) min value))))
속성 분할이 주어지면, 함수 evaluate 는 모든 부류 부분에 대한 무질서의 가중합을 계산한다.
(defun evaluate (node dimension)
(let ((total (length (NODE-examples node))))
(apply #'+
(mapcar #'(lambda (subset)
(* (/ (length subset) total)
(disorder (classify subset))))
(partition (NODE-examples node) dimension)))))
disorder 는 결정트리 절에서 언급된 식에 따라서 특별한 부류와 연관된 정보간 (무질서, disorder) 을 계산한다.
(defun disorder (partition)
(let* ((sizes (mapcar #'length partition))
(total (apply #'+ sizes)))
(if (= total 0) 0
(- (log total 2)
(apply #'+ (mapcar #'(lambda (s)
(if (= s 0) 0
(* (/ s total) (log s 2))))
sizes))))))