표상과 논리

(Representation and logic)

 

인공지능 이론 및 실제 : Thomas Dean. James Allen. John Aloimonos 공저, 김진형.박승수.백은옥. 서정연.이일병 공역, 사이텍미디어, 1998  (원서 : Artificial Intelligence: Theory and Practice, 1995), Page 75~136

 

1. 명제논리

2.  의 형식 체계

3. 의 자동 정리 증명

4. 술어논리

5.  의 형식체계

6. 에서의 자동 정리 증명

7. 비단조 논리

8. 연역검색 시스템

요약

배경

Lisp 구현

 

 

발전기 냉각수 펌프가 제대로만 작동하고 있다면 발전기의 외부 덮개가 뜨겁지 않을 것이라고 발전소의 기술자가 일러주었다. 방금 당신이 외부 덮개에 손을 데었다면 냉각수 펌프가 어떤 상태라고 결론 지을 수 있을까? 그 기술자가 당신에게 전한 지식을 어떻게 표현할 것인가? 그리고 원하는 추론을 위하여 그 지식을 어떻게 활용할 것인가?

전문가 시스템 (expert system) 의 경우 주로 전문가들이 하는 작업을 수행하기 위하여 규칙 형태로 코드화된 지식을 사용한다. 예를 들면, MYCIN 이라는 전문가 시스템은 세균성 감염을 진단하고 처방을 써내는데, 거기에서는 다음과 같은 규칙들을 사용한다.

위의 규칙은 환자의 병력과 실험실 검사에서 나타난 징후들을 근거로 감염의 원인을 결정한다. 또 XCON 이라는 전문가 시스템은 Digital Equipment Corporation 의 고객을 대상으로 디스크 드라이브나 프로세서 같은 컴퓨터 구성요소의 구성환경을 설계한다. MYCIN 과 XCON 은 모두 해당 전문 분야의 전문가들 이상으로 훌륭하게 작업을 수행한다.

대부분의 전문가 시스템은 코드화된 지식을 이용하여 결론을 도출하는 과정에서 몇 가지 종류의 논리적 추론에 의존하고 있다. 이 장에서는 명제논리 (propositional logic) 와 술어논리 (predicate logic) 를 기초로 한 지식 표현에 대하여 생각해 보기로 하자. 우선 이들 논리의 구문 (syntax) 과 의미 (semantics) 를 설명하고 그것을 사용하여 표현할 수 있는 것들의 예를 보일 것이다. 또, 논리를 사용하여 실세계 지식을 코드화하고 그 지식으로부터 선택적으로 결론을 이끌어내는 과정에서 발생하는 몇 가지 계산적 이슈들을 자세히 살펴볼 것이다. 마지막으로, 규칙으로 코드화한 지식에 관련된 추론을 실제로 수행하는 전략들을 고찰하려 한다 우선, 약간 단순하긴 하지만 대단히 유용한 논리에서부터 논의를 시작해보자.

1. 명제논리

대략적으로 말하면 논리란 기호 표현식 (symbolic expression) 을 구성하고 조작하기 위한 수학적 도구이다. 명제논리는 기호 표현식을 다루는데, 명제 (예를 들면 "불이 켜져 있다" 혹은 "문이 닫혀 있다") 를 나타내는 기호와 이들 명제를 서로 결합시키는 방법 (예를 들면 "불이 켜져 있고, 문이 닫혀 있다" 에서와 같은 두 명제의 접속) 을 표현하는 기호들로 구성된다.

논리를 하나의 언어 개념으로 특징 지어 볼 수 있다. 이 언어는 엄격한 구문론적 규정을 따른다는 점에서 컴퓨터 언어와 유사하다. 논리언어는 근본적으로 "어떻게" 보다는 "무엇" 을 설명하는 데 치중하며 이러한 이유에서 지시적이고 절차적인 컴퓨터언어와는 대조적으로 선언적이라고 볼 수 있다. 논리언어를 영어와 같은 구어 (spoken language) 의 제한된 형태로 보고 앞으로 우리가 특정 논리언어를 연구해 나갈 때 이러한 제한된 언어의 표현할 수 있는 것이 구어에 비해 얼마나 한정되어 있는가를 생각해 보기 바란다.

식 (formula) 이란 기호 표현식을 의미한다. 정형식 (well-formed formula 혹은 wff) 은 적절히 형식화되기 위한 특정 기준을 따르는 식을 말하며 wff 의 집합이란 동일 기준을 따르는 정형식들의 집합이다. 형식언어 (formal language) 는 정형식의 집합으로 정의한다. 형식논리의 중요한 점은 그 어떠한 의미 해석을 언급하지 않고도 이를 정의할 수 있다는 것이다. 이 절에서는 특정한 형식언어인 명제언어 에 대하여 살펴보려 한다. 명제라는 용어는 에 있는 하나의 정형식을 의미한다. 이 절에서는 의 정형식을 결정하는 구문과 이들 식의 뜻을 결정하는 의미를 정의하는 데 주로 초점을 맞추고자 한다.

명제변수 (propositional variable) 란 더 이상 나눌 수 없어 보이는 명제를 표현하는 기호이다. 예를 들면 "불이 켜 있다" 를 명제변수를 사용하여 표현할 수는 있지만 "불이 켜있고 문이 닫혀있다" 를 하나의 명제변수로 표현하지는 않을 것이다. 진리함수 접속기호 는 명제를 결합시키는 방식을 표현하는 데 사용되는 심볼이다. 구문적으로 의 식들은 명제변수의 집합과 다음과 같은 진리함수 접속자들, 즉 ∧ (논리곱), ∨ (논리합), ￢ (부정), ⊃ (함언), ≡ (동등) 등을 포함하는 집합으로부터 구성된 기호 표현식에 해당한다. 이 접속기호들은 대략 영어로 "and", "or", "not", "implies", "if and only if" 에 해당한다.

다른 책에서는 명제변수가 구문적으로 나뉘어질 수 없다는 점에서 명제 아톰 (propositional atom) 이라는 용어를 사용하기도 하는데 여기에서는 의미상 이들이 True 나 False 인 진리값 을 취한다는 사실을 강조하여 "명제변수" 를 택하기로 한다. 명제변수에 지정되는 진리값과 상관없이 항상 참인 식을 논리적 참 (logical truth) 이라 부른다. 명제 논리는 바로 명제변수와 진리 함수적 접속으로 표현되는 논리적 참에 관한 이론이다.

실제에 있어서는 흔히 복합적인 기호 표현식을 사용하여 명제변수를 나타내기도 한다. 예를 들면 어떤 전자장치의 출력이 고압이라는 명제를 표현할 때 단순히 high45 보다는 (status (output device45) high) 를 사용할 수도 있다. 그러나 이러한 표면의 내부 구조는 논리식을 읽기 쉽게 하기 위함일 뿐이다. 짧은 식보다 긴 것을 사용하는 것은 마치 훌륭한 프로그램 작성에 있어서 기억하기 쉽도록 연상 용이한 변수이름을 쓰는 것과 같은 이유이다. 명제변수의 형태가 (status (output device45)) 이든 high45 이든 식들의 형식적인 의미는 동일하다.

 의 구문

형식 언어에 있어서 구문 (syntax) 은 정형식 (wff) 의 집합을 정의해 준다. 언어 의 구문은 다음과 같이 기술한다.

논리곱 (conjunction) 과 논리합 (disjunction) 은 각각 A1 ∧ A2 ∧ … ∧ An. 과 A1 ∨ A2 ∨ … ∨ An 형태의 식을 지칭하며, 논리곱 인자 (conjunct) 와 논리합 인자 (disjunct) 는 이들의 각 부분인 Ai 를 지칭한다.

괄호는 보통 수학 기호와 마찬가지로 논리적 결합의 선행 관계를 나타낸다. 괄호를 사용함으로써 ((PI ∧ P2) ⊃ P3), 즉 if P1 and P2 then P3 와 (P1 ∧ (P2 ⊃ P3)), 즉 P1 and if P2 then P3 를 구분할 수 있다.

P 가 명제변수라면 P 와 ￢ P 는 명제 P 에 부여된 리터럴 (literal : 즉치 자료) 이다. ￢ 이 없는 변수들은 긍정 리터럴 (positive literal) 이라 하며, ￢ 이 붙은 변수들은 부정 리터럴 (negative literal) 이라 한다. 앞에서 우리는 전문가 시스템이 규칙 형태로 이루어진 지식을 사용한다고 언급한 바 있다. 다른 말이 없을 때, 규칙 은 A ⊃ B 의 형태이며 이때 A 와 B 는 긍정 리터럴이거나, 긍정 리터럴의 논리곱이다. 발전소의 기술자가 말한 지식은 다음의 규칙을 사용하여 표현이 가능하다.

이 때의 심볼,

와

는 명제변수이다. 앞의 규칙을 Lisp 형태의 함수기호를 써서 다음과 같이 기술할 수 있다.

이 때는

와

가 명제변수이다. 이러한 또 다른 표현식은 이 장의 뒷부분에서 논의될 술어논리에서도 찾아볼 수 있다. 술어논리에서 (pump generator17), (housing generator17), normal, 50 등은 객체를 표시하며, status 와 < 는 객체들간의 관계를 표시한다. 명제논리에서는 이러한 기호식들에 아무런 의미가 없다. 그것은 의 식에서 명제변수는 인식 가능한 그 어떤 구조도 가질 수 없기 때문이다 그러나 편의상 어떤 표현이라도 명제변수로 사용할 수 있다.

의 의미론

의미론은 주어진 표현에 대한 정형식의 의미를 결정해 준다. 의미라는 것은 언어의 기호와 특정한 관심 영역의 구성 요소를 연관시키는 여러 가지 다양한 방법들에 대한 정의이다. 이러한 가능한 연관을 해석 (interpretation) 이라고 한다.

형식상으로 보면 언어 에 대한 해석은 각 명제변수에 True 나 False 을 지정하고 명제 접속자에 "통상적인" 진리 함수적 의미를 지정하는 것이다. 그림 1 은 표준접속자 ∨, ∧, ⊃, ￢ 에 대한 진리 함수적 의미를 진리표 라는 도표형식으로 보여주고 있다. A 와 B 는 wff 를 표시하기 때문에, 명제변수 모두에 진리값을 지정하고 그림 1 의 진리표를 이용하면 의 모든 식에 대한 진리값을 결정할 수 있다. 예를 들어, P 에 False 를 지정하고 Q 에 True 를 지정한다면, ￢ P ∧ (P ∨ Q) 에는 ￢ P 와 (P ∨ Q) 에 True 가 지정되므로 True 가 지정된다.

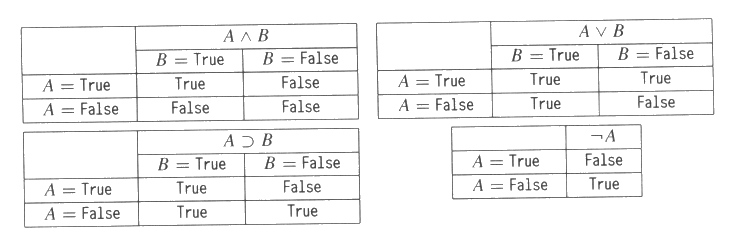
그림 1 : 표준 접속자들에 대한 진리값 함수

일반적으로 논리에서 어떤 해석 I 가 논리식 집합의 모든 식에 대하여 True 를 지정한다면 그 해석 I 를 논리식 집합에 대한 모형 (model) 이라고 한다. 어떤 논리식이 모형을 갖는다면 그것이 만족가능 (satisfiable) 하다고 한다. 어떤 식의 부정이 만족가능하지 않을 때 이를 정당 (valid) 하다고 말한다. 명제논리에서 이론 (theory) 이란 단순히 논리식의 집합을 말한다. 어떤 논리식 A 가 이론 T 의 모든 모형에서 True 라면, 식 A 는 이론 T 에 대하여 정당하다 고 말한다. 이론 (혹은 논리식) 이 모형을 가질 수 없을 때 그것이 모형이론적으로 비일관적 (model theoretically inconsistent) 이라고 말한다. 어떤 논리식 A 가 정당하다는 것을 판정하려면 그 대신 그것의 부정을 이론 T 에 더한 결과가 (모형이론적으로) 비일관적인가를 살펴봄으로써 이를 판정할 수도 있다. 만약 그러하고 T 와 A 가 각각은 일관적이라면 A 는 T 에 대해 정당할 수밖에 없다.

P 의 식들 중 그것의 구성 부분에 지정된 진리값에 상관없이 참의 값을 갖는 식을 항진명제 (tautology) 라 한다 (여기에서 논리적 참 (logical truth) 은 명제변수들에 지정된 진리값과 무관하게 참인 식이라고 편의상 정의하였다. 기술적으로 보자면, 논리적 참은 항진명제 (tautology) 이지만, 모든 항진명제가 논리적 참은 아니다. 수식 ￢ A ∨ A (A 는 임의의 wff 를 나타내는 변수) 는 항진명제이지만 논리적 참은 아니다. 그러나 ￢ A ∨ A 에서 A 를 wff 로 대체함으로써 만들어지는 모든 문장은 논리적 참이다.). 식 (A ∨ ￢ A) 는 항진명제의 예이다. A ≡ B 가 항진명제라면 A 는 B 와 논리적으로 동등 (logically equivalent) 하다고 한다. 구성부분에 지정된 진리값에 상관없이 거짓인 식은 모순 (contradiction) 이라고 부른다. 식 (A ∧ ￢ A) 는 모순의 한 예이다.

논리식의 집합으로 표시된 어떤 이론에 대하여 우리는 가끔 추가된 식이 그 이론에 대해 정당한지를 판정하고 싶을 때가 있다. 논리의 가장 중요한 특성 중 하나는 단순히 구문적 조작만을 통하여 정당한 명제들을 도출할 수 있다는 것이다. 인공지능 분야의 사람들 중에는 인간 지식의 많은 부분이 형식논리의 명제로서 표현될 수 있고 기호 조작을 통하여 추론 능력을 흉내 낼 수 있다고 믿는 사람들이 많이 있다. 다음 절에서는 그러한 조작을 수행하기 위한 기계를 소개한다.

2.  의 형식 체계

이제 우리는 논리식 형태의 지식 표현을 위한 언어를 갖게 되었다. 그러한 지식을 이용하여 정당한 결론들을 도출해내고자 한다. 예를 들어, "불이 꺼져 있다" 와 "불이 꺼져 있으면 사무실은 비어있다" 라는 사실을 안다면 "사무실은 비어있다" 라고 결론 지을 수 있다. 이 절에서는 언어 로 표현된 지식으로부터 결론에 이르는 형식 기계 (formal machinery) 를 설명하려 한다.

공리 (axiom) 란 지식을 구성하는 하나의 정형식 (wff) 이다. 총리는 앞 절에서 정의한 것과 같은 규칙의 형태이거나 좀더 복잡한 형태일 수도 있다. 공리 스키마 (axiom schema) 란 적정 형태화된 정형식은 아니지만 수많은 거의 무한한 공리집합을 정의할 수 있게 하는 식을 말한다. 공리 스키마에서 스키마 변수 (schema variable) 라 불리는 기호는 스키마식 내에 명세화된 식을 써넣을 수 있는 자리를 표시하는 데 사용한다. 예를 들면, A ⊃ A 는 공리 스키마이고 여기에서 A 는 스키마 변수로서 그 자리에 임의의 wff 를 대입할 수 있다. 논리식 P ⊃ P는 A ⊃ A 의 스키마 변수 A 대신 P 를 대입한 결과로써 얻어지는 공리이다.

발전기 냉각 펌프에 대한 규칙도 일종의 공리로서 고유영역 공리 (proper axiom) 라고 한다. 고유영역 공리는 실세계를 기술하는 특정 이론에 한정된 것이다. 예를 들면, 발전기 설비의 작동에 대한 이론을 이루는 공리의 집합이 있을 수 있다. 고유영역 공리들로 구성된 집합을 영역 이론 (domain theory) 혹은 단순히 이론 (theory) 이라 부른다. 영역 이론의 공리들은 우주를 지배하는 물리 법칙과도 유사하다.

추론 규칙 (rule of inference) 은 여러 식의 집합으로부터 또 다른 식을 추론할 수 있도록 해준다. 추론 규칙은 앞서 논의된 다른 규칙들과는 성격이 다르다. 추론 규칙은 이전의 식에서 새로운 식을 생성해 주는 프로시저와 유사한 것이다. 형식 체계 (formal system) 는 형식 언어와 더불어 공리 집합 그리고 추론 규칙의 집합으로 구성된다.

의 논리적 공리

실세계에 대한 지식을 부호화하려 할 때에는 주로 고유영역 공리를 작성하는 데 관심을 기울인다. 그러나 로 표현된 모든 이론에 적용되는 논리적 공리 (logical axiom) 라는 것도 있다. 논리적 공리는 대개 공리 스키마의 집합 형태로 명기된다. 다음 스키마는 의 논리적 공리를 기술하고 있다.

이때 A 와 B 는 스키마 변수로서 임의의 wff 를 대입할 수 있다. AS1 에 따르면 "만일 논리가 쉽다면, 만일 돼지가 날 수 있다면 논리는 쉽다." 는 문장도 공리이다. AS1 은 그다지 쓸모있게 보이지는 않지만 이 형식체계가 의 모든 논리적 참인 문장을 도출할 수 있으려면 AS1 을 빼놓을 수 없다. 다른 스키마들은 이보다 더 유용해 보인다. 예를 들어, 다음의 식은 공리 스키마 AS3 의 일례이다.

공리 AS1-3 은 부정 (negation) 과 함언 (implication) 만을 포함하도록 한정시킨 언어 에 속하는 모든 논리적 참을 도출해내기에 충분하다. 다른 논리 접속자를 수반하는 논리적 참을 도출하기 위해서는 다른 접속자들을 부정기호와 함언기호를 이용하여 정의해야만 한다. 다음의 공리 스키마는 이에 필요한 정의를 제공한다.

공리 스키마는 고유영역 공리의 집합을 기술하는 데에도 사용할 수 있다. 예를 들면, generator17 에 대한 규칙을 여러 발전기와 그에 해당하는 냉각펌프에 적용시킬 수 있을 것이다. generator17 대신 스키마 변수로 대체하여,

로 기술하고 g 가 집합 {generator17, generator45, generator9} 의 원소라고 명시함으로써 이전보다 표현가능한 것이 증가하지는 않지만 영역 이론을 더 간결하게 명시할 수 있다.

정규헝태

때때로 동일한 논리 문장을 여러 가지 형태로 표현할 수 있다. 예를 들어, P ⊃ Q, ￢ P ∨ Q 그리고 ￢ (P ∧ ￢ Q) 는 논리적으로 동등하다. 식을 표현하는 데 어떤 규약을 정할 수만 있다면 논리식을 처리하는 컴퓨터 프로그램의 작성이 더욱 간단해질 수 있다. 그러한 규약은 표준 (canonical) 혹은 정규 (normal) 형태라고 하며 지식의 표현을 표준화하는 데 사용한다. 논리식의 집합을 데이터베이스로 생각해 볼 수 있다. 정규형태는 마치 인사기록을 표준화된 포맷으로 만들면 인사 데이터베이스의 정보검색이 훨씬 간단해지는 것처럼 자동 추론을 훨씬 단순화시킨다.

매우 유용한 정규형태 중 하나로 논리곱 정규형태 (conjunctive normal form : CNF) 가 있다. 논리식으로 이루어진 데이터베이스가 리터럴 (literal) 들의 논리합의 논리곱으로 표현된다면 그것은 논리곱 정규형태이다. 임의의 명제식 데이터베이스에 대하여 이와 동일한 CNF 형태의 데이터베이스가 생성가능하다. 예를 들자면, P ⊃ Q, ￢ (￢ S ∧ ￢ T) 그리고 R 로 구성된 데이터베이스를 (￢ P ∨ Q) ∧ (S ∨ T) ∧ R 와 같이 표현할 수 있다. 또, 논리합 정규형태 (disjunctive normal form : DNF) 도 있는데, 이것은 리터럴의 논리곱들로 이루어진 논리합의 형태이다. 의 모든 식에 대하여 그와 동등한 DNF 식이 존재한다.

그 외에도 다음과 같은 논리적으로 동등한 식들의 예가 있는데 동등 기호의 우변항은 논리곱 정규형태이다.

실제의 경우 데이터베이스는 종종 다음과 같은 형태인 규칙들의 논리곱으로 표시되기도 한다. (P1 ∧ … ∧ Pn) ⊃ Q 단, Q 와 Pi 는 명제변수, Pi 는 규칙의 선행항 (antecedents) 그리고 Q 는 규칙의 결과항 (consequent) 이라 불린다. (P1 ∧ … ∧ Pn) ⊃ Q 가 (￢ P1 ∨ … ∨ Pn ∨ Q) 와 동등함을 감안한다면 이 데이터베이스 표현은 CNF 의 특수한 예로서 각 논리합이 정확히 하나의 긍정 리터럴만을 갖는 것이다. 문헌들에서 한 개의 긍정 리터럴을 동반한 논리합을 호온절 (Horn Clause) 이라고 부르는 경우가 있는데, 이는 동명의 논리학자 이름에서 따온 것이다. 모든 식이 호온절의 논리합으로 표현 가능한 것은 아니다.

추론 규칙

결론을 이끌어내자면 형식 체계의 공리뿐만 아니라 추론 규칙 (rule of inference) 도 필요하다. 사람들은 항상 무의식적으로 추론 규칙을 사용하고 있다. 예를 들어, 친구의 차가 집 앞의 차도에 있으며, 그의 차가 집 앞의 차도에 있을 때면 언제나 그가 집에 있다는 사실로부터 그 친구가 집에 있다고 결론지었다면 바로 추론 규칙을 적용한 것이다.

 추론 규칙은 두 부분으로 구성되어 있는데 하나는 조건들의 집합이고 또 하나는 그 조건들이 주어질 때 확정되는 결론 부분이다. 예를 들어, 모두스 포넨스 (modus ponens) 라 불리는 추론 규칙은 임의의 wff 인 A 와 B 에 대하여 A 와 A ⊃ B 가 주어지면 B 를 결론지을 수 있다. 논리곱 (conjunction) 이라고 불리는 추론 규칙은 wff A1 에서부터 An 까지 주어질 때, (A1 ∧ A2 ∧ … ∧ An) 이라는 결론을 도출할 수 있음을 말한다.

증명과 정리

고유공리 P 와 P ⊃ Q 가 주어진다면 모두스 포넨스를 사용하여 Q 라는 결론을 얻을 수 있다. 이 문장은 P 와 P ⊃ Q 로부터 Q 의 증명 (proof) 을 기술하고 있다. 더 일반적으로 말하면 증명이란 와 같이 적절한 언어로 된 일련의 문장 (statement) 들로서 각 문장은 단순히 공리이거나 아니면 몇 가지 추론 규칙과 몇 개의 선행 문장들의 직접적 결과인 경우를 말한다.

증명은 흔히 각각에 번호가 붙여진 여러 줄로 이루어진 형태인데 각 줄에 하나의 문장이 등장하게 된다. 각 문장 다음에는 그 문장에 대한 근거 (justification) 를 명시하는데 그것이 공리이거나 아니면 거기에 사용된 추론 규칙 그리고 그 규칙의 조건에 대응되는 이전 문장의 번호를 명시해 준다. 증명에 근거를 기술할 때 모두스 포넨스와 논리곱 추론이라는 용어 대신 각각 MP 와 CONJ 라는 약어를 쓰기로 한다. 이들 두 규칙은 그림 2 의 증명에 예로서 나타나 있다.

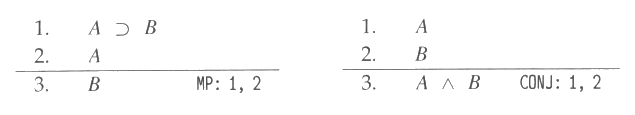
그림 2 : 모두스 포넨스와 논리곱 추론 규칙이 사용된 예

그림 3 은 (P ∧ Q) ⊃ R, (S ∧ T) ⊃ Q, S, T, P 로 구성된 고유영역 공리의 집합과 두 개의 추론 규칙 모두스 포넨스와 논리곱 법칙이 주어졌을 때 R 의 증명을 명기한 것이다. 증명의 각 라인을 그 형식 체계에 대한 정리 (theorem) 라고 한다.

그림 3 : 명제논리에서의 간단한 증명

모두스 포넨스와 논리곱 법칙만으로는 고유영역 공리의 집합으로부터 나올 수 있는 모든 결론을 도출할 수 없다. 예를 들어, 선희가 사무실과 회의실 중 한 곳에 있으며, 두 방 모두 비디오 터미널을 갖추고 있다는 사실을 우리가 안다면, 선희는 비디오 터미널이 있는 방에 있다고 결론 내릴 수 있을 것이다. 식으로 쓴다면, office ∨ conference, office ⊃ video 그리고 conference ⊃ video 로부터 video 라는 결론을 내리고자 한다. 약간의 인내심이 있다면 공리 스키마 AS1-8 로부터 생성된 논리적 공리들을 사용하여 이것을 증명할 수 있다. 그러나, 정리 증명을 위한 또 다른 체계에서는 논리합이 관여된 그러한 증명이 쉽게 수행될 수 있다. 예를 들어, 어떤 체계에서는 만약 office 를 가정함으로써 video 가 결정되고, 또 conference 를 가정함으로써 video 가 결정된다면 office ∨ conference 가 주어지는 경우 video 라는 결론이 가능하다.

추론 규칙들을 모으거나 논리적 공리들을 추가함으로써 논리식의 데이터베이스로부터 나올 수 있는 모든 정리들의 도출을 보장할 수 있다. 그러나, 추론 규칙과 공리들을 추가함으로써 정리 증명이 어려워질 수도 있다. 다행스럽게도 우리가 원하는 모든 추론이 가능한 단일 추론 규칙이 존재한다.

논리융합 추론 규칙

그림 4 에 주어진 추론 규칙을 생각해보자. 논리융합 (resolution) 이라고 알려진 이 규칙이 의미상 타당하다는 것을 다음과 같이 설명할 수 있다. 그림 4 의 1 항에서, A1, …, Ai, ￢ C, Ai+1, …, Am 중 하나는 반드시 참이 된다. 2 항 B1, …, Bj, C, Bj+1, …, Bn 의 한 원소도 반드시 참이다. 중간배제 법칙 (the law of excluded middle)에 의하면 모든 명제는 반드시 참이거나 거짓이어야 한다. 그러므로 C 또는 ￢ C 둘 중의 하나는 이 법칙에 의해 반드시 참이어야 한다. 만약 C 가 참이라면 ￢ C 는 거짓이고  따라서 A1, …, Am 중의 최소 한 개는 참이어야 한다. 역으로, ￢ C 가 참이라면 C 는 거짓이 되며 B1, …, Bn 에서 하나는 참이어야만 한다. 결론적으로 C 또는 ￢ C 가 반드시 참이므로, A1, …, Am, B1, …, Bn 중의 하나는 반드시 참이 된다.

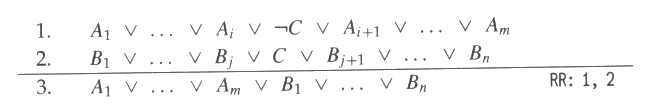
그림 4 : 논리융합 규칙

모두스 포넨스는 논리융합 규칙의 특수한 경우이다. n = 0 이고 m = 1 인 경우를 생각해 보면 된다. 논리융합 규칙을 이용하는 명제 정리의 증명기 (prover) 는 축소명령집합 컴퓨터 (reduced-instruction-set computer : RISC) 에 비유될 수 있는데, 여기에서 명령집합이 추론 규칙으로 구성되어 있는 것이다. 단일 추론 규칙만을 이용한다면 또 다른 추론 규칙을 적용하기 위한 작업을 제거할 수 있기 때문에 자동화 추론이 간소화될 수 있다.

완전성, 무결성, 결정성

어떤 형식 체계 S 에서 만약 S 의 공리에 대하여 모든 정당 (valid) 한 식이 S 의 정리가 된다면 S 는 완전 (complete) 하다고 한다 (여러 문헌에서 이것은 의미론적 완전성 (semantic completeness) 으로 불린다 [Hunter, 1973]. 다른 한편, 모든 식 A 에 대하여 A 혹은 ￢ A 중 하나가 항상 정리인 경우 그 형식 체계는 구문적으로 완전 (syntactically complete) 하다 [Mendelson, 1979]. 우리가 종종 편의상 P 와 ￢ P 가 모두 아닌 이론을 다루어야 된다는 것을 감안한다면 구문적 완전성이 특별히 유용하다고는 볼 수 없다.). 형식 체계의 모든 정리가 정당하다면 그 체계는 무결 (sound) 하다고 한다. 우리는 형식 체계가 무결하고 완전한 것을 선호한다. 어떤 체계가 무결하고 동시에 완전하다면, 정당한 식들의 집합과 정리의 집합이 동일해지기 때문이다.

정의에 의하면 항진명제 (tautology) 는 정당하고 따라서 논리융합 규칙만을 사용하는 형식 체계는 완전하지 못하다. 논리융합 규칙만을 이용하면 (P ∨ ￢ P) 를 증명할 수 없기 때문이다. 그런데 또 다른 개념의 완전성이 존재한다. 즉, 개개의 공리가 리터럴의 논리합으로 이루어진 공리 집합이 있을 때 만약 이들이 만족불가능 (unsatisfiable) 한 경우 주어진 추론 규칙 집합만을 이용하여 어떤 명제변수 P 에 대하여 두개의 식 P 와 ￢ P 로 이루어진 형태의 모순을 도출할 수 있다면 그 추론 규칙 집합은 반박 완전 (refutation complete) 하다고 한다. 개개의 공리가 리터럴의 논리합으로 주어지는 공리집합은 상당히 일반적이라는 사실을 주지하기 바란다. 왜냐하면 어떤 식 혹은 논리곱 형태의 식이건 간에 이들을 논리곱 정규 형태로 변형시킬 수 있기 때문이다. 논리융합 규칙만으로 구성된 집합은 반박 완전하다. 이러한 관찰을 이용하면 정리를 증명하기 위한 한 가지 프로시저를 제시할 수 있다. P 가 정리인가를 결정하려면 ￢ P 를 공리 집합에 더하고 논리융합 규칙을 이용하여 모순을 이끌어내면 된다.

어떤 문제의 해를 구하기 위한 프로시저 (혹은, 방법) 가 있을 때 만약 그 프로시저의 유한 단계를 거쳐 주어진 물음에 정확한 답을 구할 수 있다면 그 프로시저는 효과적 (effective) 이라고 한다. 어떤 형식 체계의 모든 식에 대하여 그 식이 정리인가 아닌가를 묻는 물음에 답할 수 있는 효과적인 프로시저가 존재할 때 그 형식 체계를 결정적 (decidable) 이라고 한다. 가 AS1-8 의 공리와 논리융합 규칙을 포함한다면 그것은 결정적인 특성을 갖게 되는데 이것은 단지 그림의 일부에 지나지 않는다. 어떤 것이 계산가능하다는 사실만으로는 충분하지 못하다. 이를 효율적으로 계산할 수 있어야 하기 때문이다. 불행하게도 계산적으로 복잡한 문제들이 와 연관되어 있다.

계산 복잡도

무결성 (soundness) 과 완전성 (completeness) 을 갖춘 형식 체계에서 정당성 (validity) 과 만족가능성 (satisfiability) 과 관련된 복잡도 문제는 주어진 식이 정리인지의 여부를 파악하는 것이 얼마나 어려운가를 잘 말해주고 있다. 에서 임의의 식이 만족가능한지를 결정하는 것은 NP-complete 문제군에 속한다. 이것은 만족가능성이 식의 길이에 대하여 다항식 시간 내에 결정될 가능성이 거의 없음을 의미한다. 이는 각각의 논리합이 세 개의 리터럴을 갖는 CNF 의 식에 대하여도 동일하게 적용된다. 그러나 만약 개개의 논리합이 최대 투 개의 리터럴만을 갖는다면 만족가능성은 다항식 시간 내에 결정될 수 있다. 논리합의 경우 최소 하나의 논리합 인자가 만족될 수만 있다면 그 식이 만족됨을 기억하기 바란다. 각각의 논리합 인자가 단순히 리터럴의 논리곱으로 이루어져 있고, 리터럴의 논리곱에 대한 만족가능성을 다항식 시간내에 검사할 수 있으므로 DNF 식의 만족가능성은 다항식 시간 내에 검사할 수 있다. 이와 같은 관찰을 통해 임의의 식을 DNF 로 전환하는 것이 아주 어렵거나 아니면 지수비례의 긴 식을 산출한다는 사실을 알 수 있다. 그렇지 않다면, 임의의 식을 DNF 로 변환하고 그 DNF 식이 만족가능한지를 결정함으로써 임의의 식이 만족가능한지를 다항식 시간 내에 결정할 수 있을 것이다.

만족가능성을 결정하는 것이 어렵다면 당연히 정당성을 결정하는 것도 어렵다는 것을 알 수 있다. 왜냐하면 A 가 정당하다는 것은 필요충분적으로 ￢ A 가 만족가능하지 않음을 의미하기 때문이다. 만족가능성 여부의 검사가 어렵다는 사실을 받아들이고 또 우리가 관심을 갖는 이론이 무결성과 완전성을 만족한다고 가정한다면, 임의의 식이 정리인지 여부를 결정하는 것도 당연히 어려울 것이다. 이러한 사실들은 다소 비관적인 결론처럼 보일지 모르지만, 이러한 결과는 최악의 경우까지 고려한 분석에 기반한 것이다. 실제에 있어서는 우리가 의도하는 결과를 쉽게 도출하는 경우도 종종 있다.

논리에 의한 문제 해결

명제논리는 여러 종류의 문제들을 표현하고 해결하는 데 이용될 수 있다. 예를 들면, 제약 산업에서 커다란 분자의 원자 구조를 통제하는 조건 (constraint) 을 표현하는데 논리식이 이용될 수 있다. 그리고 이러한 식은 특정 구조를 가진 분자를 만드는 것이 가능한지의 여부를 추론하는 데 사용될 수도 있다. 논리가 어떻게 문제 해결에 이용될 수 있는가를 보기 위해 다소 쉬운 문제들을 생각해 보자.

어떤 학생이 기숙사방 선택의 우선권을 가질 것인가를 결정하기 위하여 대학의 기숙사 관리자들은 때때로 추첨을 사용한다. 다음 예에서 네 명의 학생 Bob, Lisa, Jim, Mary 가 추첨으로 어떻게 순위가 결정되는지 살펴보자. 네 명의 학생에 대하여 우리가 아는 것은 다음 제약에 의해 정리되어 있다.

퍼즐에 능통한 사람은 Mary 가 1 순위, Bob 이 2 순위, Jim 이 3 순위, Lisa 가 4 순위라고 결론내릴 수 있을 것이다. 논리를 사용하면 같은 결론에 도달할 수 있다.

위 문장을 논리식으로 전환하기 전에 두 가지 명제 타입을 도입하기로 하자. X-ahead-of-Y 는 X 가 Y 바로 앞 순위에 있음을 일컬으며, X-bio-major 는 X 가 생물학 전공자임을 말한다. 이러한 명제 타입을 이용하여 다음과 같이 표현한다. Lisa 가 Bob 의 바로 옆에 있지 않다.

Jim 은 생물학 전공자 바로 앞에 위치한다.

여학생 중 한 명은 생물학 전공자이다.

Bob 은 Jim 의 바로 앞에 위치한다.

마지막으로, Mary 또는 Lisa 가 1 순위라는 사실을 모든 가능한 순위를 표현하는 논리합을 이용하여 표현한다.

순위를 결정하는 방법은 이 식에서 한 개의 논리합 인자가 남을 때까지 논리합 인자를 제거해 나가는 것이다. 논리합 인자를 제거하기 위해서는 문제의 표현이 보완되어야 한다.

문장의 논리 변환뿐만 아니라 상식적으로 통용화된 사실, 즉 학생은 기껏해야 한명의 다른 학생 바로 앞에 위치할 수 있다는 것 그리고 X 가 Y 의 바로 앞에 위치한다는 것은 곧 Y 가 X 의 앞에 위치하지 못한다는 것을 표현하는 식이 필요하다. 그러한 상식적인 사실을 표현하는 예는 다음과 같다.

이제, Bob-ahead-of-Jim 이 주어진다면 우리는 ￢ Bob-ahead-of-Lisa 를 증명할 수 있으며,이 식을 이용하여 다음의 결론에 도달할 수 있다.

이러한 방법으로, 'Bob 이 Jim 의 앞에 위치하지 않는다' 가 포함되는 모든 논리합 인자를 제거할 수 있으며, 네 개의 가능한 순위에 관한 하나의 논리합을 얻을 수 있다.

비슷한 방법으로, 'Lisa 는 Bob 의 다음에 위치한다' 가 포함되는 논리합들을 제거시킬 수 있다.

정확한 해를 얻기 위해서는 두 개의 논리합 중에서 두번째의 항을 소거시켜야만 한다. 이 마지막 소거는 좀 까다로운데 이를 위해서는 표현에 약간의 수정이 필요하다. 연습문제 5 에서 우리는 이와 같은 수정에 대하여 자세히 살펴볼 것이다. 앞의 예에서 지식의 표현과 정리 증명 모두가 꽤 복잡해질 수 있음을 알았을 것이다. 정확한 모든 제약을 코드화하는 완전한 표현 (식의 집합) 을 만들기는 매우 어렵다. 그리고 일단 완전한 표현을 구한다 해도 정확한 결론 도출이 어려울 수도 있다. 다음 절에서 우리는 컴퓨터가 어떻게 정확한 결론을 이끌어내는 지를 살펴보게 된다.

3. 의 자동 정리 증명

이 절에서는 간단한 명제 정리 증명기에 대하여 기술한다. 여기에서는 시스템의 고유영역 정리가 (P1 ∧ … ∧ Pn) ⊃ Q 형태로서 이때 Q 와 Pi 는 명제변수라는 형태의 규칙을 가정한다. 선행항 (antecedent) 이 없는 규칙 fact (사실) 라는 용어를 사용한다. 사실이란 단지 명제변수에 불과하다.

에서의 목표 단순화

목표 단순화 (goal reduction) 는 앞에서 설명했던 것들과 같은 규칙의 형태로 공리가 주어졌을 때 명제변수의 논리곱을 증명하기 위한 기법이다. 논리곱의 논리곱 인자들이 바로 목표 (goal) 이다. 목표 Q 와 규칙 (P1 ∧ … ∧ Pn) ⊃ Q 이 있다고 가정하자. (P1 ∧ … ∧ Pn) 를 증명할 수 있다면 Q 를 증명할 수 있다. 이 경우 Q 를 증명하는 것은 (P1 ∧ … ∧ Pn) 를 증명하는 것으로 단순화된다.

다음은 목표 단순화를 위한 비결정적 (nondeterministic) 인 알고리즘이다. 이 알고리즘은 어떤 선택을 할 때 그 방법이 규정되어 있지 않기 때문에 비결정적이다. (P1 ∧ … ∧ Pn) 에 대한 증명은 다음과 같이 진행된다.

조금만 노력하면 이 알고리즘을 Lisp 으로 구현된 결정적 알고리즘으로 변형할 수 있다.

규칙은 Lisp 에서 리스트로 표현되는데, 그 첫번째 요소가 결론항 (consequent) 이고 뒤따라 if 와 선행항 (antecedent) 들이 나온다. 예를 들어, 규칙 (P ∧ Q) ⊃ R 은 (R if P Q) 와 같이 표현된다. 사실 (fact) 은 한 개의 요소를 가지는 리스트로서 그 요소는 바로 명제변수에 해당한다. 예를 들어, P 는 (P) 와 같이 표현한다. 이러한 방법을 아래의 자료 추상화 (data abstraction) 로 코드화할 수 있다.

두번째 정의는 nil 의 rest 는 nil 이라는 사실을 이용하여 (antecedents  ′ (P)) 는 nil 임을 표시한다.

그림 5 : 명제논리의 정리 증명기

그림 5 의 코드는 기재된 비결정적 알고리즘의 결정적 버전에 따른 간단한 정리 증명기를 함수로 정의한 것이다. 비결정적 선택을 하는 대신에 함수 theorem 은 모든 규칙들을 차례로 적용해 본다. 그림 5 의 코드는 논리곱 인자의 리스트, 리스트의 첫번째 논리곱 인자에 아직 적용하지 못한 규칙들의 리스트 그리고 모든 규칙들의 리스트가 주어졌을 때 다음의 재귀 알고리즘을 구현하고 있다.

다음에, theorem 함수가 그림 3 의 예에 대하여 수행되는 과정을 볼 수 있다.

Theorem 함수는 몇 가지 잠재적인 문제를 안고 있다. Q 에 추가적으로 두 개의 규칙 (P if Q) 와 (Q if P) 로 표현된 P ≡ Q 형태의 공리가 있고, P 를 증명하려 한다고 가정해 보자. 여기에 theorem 이 어떻게 응답할지 나타나 있다.

일반적으로 STACK OVERFLOW 와 같은 메시지를 받을 때는, 코드나 알고리즘상에 심각한 문제가 있다는 의미이다. 이 경우, theorem 은 처음에 규칙 (P if Q) 그 다음에 (Q if P) 그 다음 (P if Q) 이런 식으로 계속적으로 자신을 재귀호출할 뿐이다. 결국, 재귀호출은 매번 새 환경 구성이 필요하므로 Lisp 에 메모리 부족 상태가 발생한다.

이 장의 마지막 부분의 연습 6 은 theorem 의 이 문제를 수정하는 것에 대한 것이다. 그러한 수정을 하면 theorem 이 앞서 기술한 제한적 형태의 공리로부터 나오는 긍정 리터럴의 논리곱 형태의 그 어떤 정리라도 증명할 수 있음을 보일 수 있다.

모순에 의한 증명

theorem 함수는 의미적으로 다음과 같이 그 정당성을 설명할 수 있다. T 가 여기에서의 규칙 리스트에 해당하는 이론이라 하고, A 는 여기에서 중명하고자 하는 논리곱이라고 가정하자. T 와 A 는 모두 일관성이 있다고 가정한다. ￢ A 와 합쳐진 T 가 비일관적 (inconsistent) 이라면, ￢ A 는 T 의 모든 모형에서 False 로 지정된다. 그러므로, A 는 T 의 모든 모형에서 True 로 지정되고 A 는 T 에 관하여 정당 (valid) 하다. 모순명제에 대응되는 모형은 없기 때문에 어떤 이론에서 모순을 이끌어낼 수 있다면 그 이론은 비일관적이다.

theorem 함수는 규칙과 첫번째 인자인 논리곱의 부정으로부터 모순 유도를 시도한다.

4. 술어논리

이 절에서는 술어논리 (predicate calculus : ) 라고 불리는 좀더 표현력이 강한 형식 언어에 대해 살펴보기로 하자. 술어 (predicate) 란 임의의 객체 (object) 의 특성과 관계를 기술한다는 뜻이다. 는 객체를 나타내거나 객체의 특성 그리고 객체들 사이의 관계를 나타낼 수 있다. 예를 들어, 장난감 블록을 bock17 로 그리고 테이블을 table45 라는 항 (term) 으로 표현한다. 특정 블록이 빨간색이라는 특성을 red (block17) 로 표현하고, 블록이 테이블 위에 있다는 관계를 on (block17, table45) 라고 표현한다.

한정 서술문 (quantified statement) 이라는 것은 객체의 부류 (class) 전체에 적용이 되는 문장 (statement) 이다. 는 임의의 객체 부류들에 대하여 한정 서술문 (quantified statement) 을 허용한다. 예를 들어, 다음 문장은 특정 테이블 위의 모든 것이 빨간색이라는 것을 나타낸다.

여기에서 ∀ 기호는 한정자 (quantifier) 이고 x 는 변수 (variable) 이며 table45 는 상수 (constant) 이다. 위의 식은 "모든 x 에 대해서 만약 x 가 table45 위에 있다면 그 x 는빨간색이다" 라고 읽는다. ∀ 과 ∃ 는 각각 전체 (universal)와 존재 (existential) 한정자라고 불린다. 위의 식과 on (block17, table45) 로부터 block17 이 table 위에 있기 때문에 빨갛다라고 말할 수 있다.

만일 유한 집합에 속한 객체들에만 관심이 있다면 는 객체와 그들 사이의 관계에 대한 구문론적 편리성을 제외한다면 명제논리에 비하여 표현력이 더 좋다고 말할 수는 없을 것이다. 그러나 유한 집합의 객체들에 대해서도 는 지식 표현의 간결한 형태를 제공하고 그러한 지식을 다루기 위한 강력한 계산법 (calculus) 도 제공하고 있다.

의 구문

에서 대상 영역 (domain) 내의 객체는 항 (term) 이라 불리는 표현식을 사용해서 나타낸다. 항은 함수, 상수 그리고 변수로 이루어지며, 정형식 (wff) 은 항과 술어 (predicate) 그리고 한정자 (quantifier) 로 이루어져 있다. 각 함수와 술어는 여러 개의 인자를 갖는다. 이 인자의 개수를 함수 또는 술어의 인자수 (arity) 라고 부른다. 기술적으로 보자면 상수란 인자수가 0 인 함수에 불과하지만 상수는 함수와는 달리 취급된다. 다음과 같은 요소들로써 의 구문을 기술할 수 있다.

이 요소들로부터 모든 항 (term) 의 집합을 귀납적으로 다음과 같이 정의할 수 있다.

p 가 인자수 n 인 술어이고 ti 가 항일 때 p (t1, t2, ..., tn) 은 단위문 (atomic sentence) 이라고 한다. 의 정형식 (wff) 은 다음과 같이 정의된다.

어떤 식 안에서 한정자가 적용되는 부분을 한정자의 영역 (scope) 이라고 한다. 그리고 한정자의 영역은 Lisp 에서 지역변수 영역이 결정되는 것처럼 괄호에 의해 결정된다. ((∀x, p(x)) ∧ (∀x, q(x))) 에서 처음 나온 ∀x 의 영역은 p(x) 이고 두번째 것의 영역은 q(x) 이다. 어떤 변수가 한정자 영역에 있지 않은 경우 그 변수는 자유 (free) 변수 라고 한다. 자유변수를 갖지 않는 wff 를 폐쇄식 (closed wff) 이라 한다. 기초항 (ground term) 이나 기초식 (ground wff) 은 전혀 변수를 지니지 않은 항과 wff 를 뜻한다.

표현 방법을 설계하는 데 있어서 수많은 선택이 필요하다. 술어 (predicate) 는 특성과 관계를 표현하는 데 사용된다. 예를 들면 어떤 사람이 덩치 크다, 무겁다, 빠르다, 혹은 키 크다 라고 말할 수 있다. 여기에서 덩치가 크다, 무겁다, 빠르다, 키 크다 등은 모두 사람의 특성이다. 또한 부모나 친구처럼 사람들 사이의 관계들도 있을 수 있다. 객체를 표현할 때에는 그 객체의 이름이나 함수에 기초한 항 (term) 을 이용한다.

예를 들어 Fred 와 그의 아파트를 Fred 와 apartment102 라는 상수로 표시할 수 있다. 또 이를 함수적으로 apartment (Fred) 라는 항을 이용해 표현할 수도 있다.

에서는 어떤 것을 표현하는 데 한 가지 이상의 방법이 있을 수 있다. "누구나 그의 엄마를 사랑한다" 라는 문장을 ∀x, y, mother (y, x) ⊃ loves (x, y) 또는 ∀x, loyes (x, month (x)) 로 표현할 수 있는데, 첫번째 경우의 mother 는 술어로 두번째의 경우는 함수로 사용되고 있다. 그렇다면 어떤 것이 옳은가? 둘 다 옳지만 경우에 따라 더 편리한 쪽이 있을 수 있다.

일반 문장에서 논리로의 변환

인간지식의 대부분 자연어 형태의 문장으로 코드화되어 있다. AI 시스템을 구축하려면 이러한 지식을 컴퓨터가 다루기 쉬운 표현법으로 번역할 필요가 종종 있다. 이것이 어떻게 수행되는가를 보기 위해 버섯에 관한 문장들을 mushroom(x), purple(x) 그리고 poisonous(x) 등의 술어를 이용하여 술어논리로 번역하는 것을 살펴보기로 하자.

한정화

한정화 (qualification) 를 이용하여 객체들의 집합에 대한 내용을 나타낼 수 있다. 전체 한정자 ∀ 는 무한개까지의 논리곱 인자 (conjunct) 를 논리곱하는 것과도 같다. 만일 정의역이 Fred 와 Lynn 만으로 이루어져 있다면 우리는 ∀x, loves (x, x)를 loves (Fred, Fred) ∧ loves (Lynn, Lynn) 로 나타낼 수 있다. 그러나 이러한 간단한 기교는 ∀x, integer (x) ⊃ (odd (x) ∨ even (x)) 과도 같은 문장에는 적용되지 않는다. 존재 한정자 ∃ 는 무한개까지의 논리합 인자 (disjunct) 들의 논리합과도 같다. Fred 와 Lynn 이라는 유한개의 정의역을 가정할 때 ∃x, happy (x) 는 happy (Fred) ∨ happy (Lynn) 을 나타낸다. 한정화는 항상 정의역의 객체들에 대한 한정이지 술어나 함수에 대해 행해지는 것은 아니다. 만약 이 제약을 완화시키면 2 차 논리 (second-order logic) 또는 고차 논리 (higher-order logic) 라 불리는 식을 만들 수 있다.

아래의 동치성을 이용하면 존재 한정자를 포함한 식들은 전체 한정자를 사용한 문장으로 바꿀 수 있고 그 역도 성립한다.

이 동치성이 옳다는 것을 확인하기 위하여 유한 집합에 대한 한정화를 논리합과 논리곱으로 생각해 보기 바란다. 이 동치성을 이용하여 다음의 다섯 가지의 식들이 논리적으로 서로서로 동일함을 알 수 있다.

의 의미론

어떤 언어의 의미론 (semantics) 은 그 언어의 기호들과 특정 관심 영역 내의 원소들을 연결 시켜주는 해석 (interpretation) 들의 집합을 정의한다. 일단 해석의 집합이 주어지면 식들을 만족시키는 해석에 대한 조건을 명세화시킬 수 있다. 다음에서 우리는 술어논리의 의미론이 술어와 상수기호, 한정자 그리고 변수를 다루는 방법에 대하여 잠시 살펴보겠다. 우선 술어기호가 전체 그림을 얼마나 복잡하게 만드느냐에 대하여 고려해 보자.

몇 개의 탱크 안에 있는 액체의 높이를 추론하는 데 사용될 수 있는 간단한 언어에 대한 구문을 살펴보자. 이 언어는 한 개의 술어기호인 overflow 와 두 개의 상수 tank45, tank17 로서 구성된다. 이 언어에서 만들 수 있는 정형식은 다음의 세 개뿐이라고 가정해 보자.

각 해석 (interpretation) 은 의미론에서 설명하고자 하는 원소들의 집합에 해당하는 영역과 연관이 된다. 만약 우리가 마음속에 세 개의 탱크 1, 2, 3 이 있는 세계를 생각하고 있다면 영역 D 는 {1,2, 3} 이 된다. 각각의 해석은 언어의 각 항을 영역의 원소와 매핑시켜야 한다. 해석에 있어서 항들을 영역 원소에 매핑시키는 함수를 M1 으로 표시하기로 하자. 이 경우 M1 은 {tank45, tank17} 을 {1, 2, 3} 에 매핑한다. 좀더 정확히 말하자면, M1 은 tank45 를 1 로, tank17 을 2 로 매핑하는데, 이는 이 해석상에서 tank45가 Tank 1 에 그리고 tank17 은 Tank 2 에 대응됨을 의미한다.

각 술어기호는 영역의 원소들간의 관계 (relation) 를 나타내고 있으므로 각 해석은 술어기호와 관계를 매핑시켜야만 한다. 해석에서 술어기호와 관계들 사이를 매핑시키는 함수를 M2 로 나타내기로 한다. 한 변수에 대한 관계는 단순히 {1, 2, 3} 의 부분집합이므로 M2 는 {overflow} 라는 술어기호를 2 {1, 2, 3} 으로 매핑시킨다. 여기에서 2 {1, 2, 3} 은 {1, 2, 3} 의 멱집합 (power set, 모든 부분집합들의 집합) 을 나타낸다. 만약 어떤 해석에서 M2 가 overflow 를 {1, 3} 으로 매핑한다면 이는 Tank 1 과 3 이 overflow 된다는 것을 가리킨다. 이 단순한 언어에서 D, M1 그리고 M2 가 함께 한 가지의 가능한 해석을 형성한다.

이제 어떤 정형식이 해석 (D, M1, M2) 를 만족한다는 것이 무슨 의미인가에 대하여 살펴보자. 위의 해석은 M1 (tank45) 가 M2 (overflow) 의 한 원소이므로 overflow (tank45) 를 만족한다. 그 해석은 ￢ overflow (tank17) 도 만족하는데 그 이유는 M1 (tank17) 이 M2 (overflow) 의 원소가 아니기 때문이다. 마지막으로 이 해석은 overflow (tank45) ∧ overflow (tank17) 을 만족시키지는 못하는데 그 이유는 {M1 (tank17), M1 (tank45)} 가 M2 (overflow) 의 부분집합이 아니기 때문이다.

일반적으로 말하면 일단 논리접속자를 갖지 않는 식에 대하여 어떤 해석이 그 식을 만족한다는 것이 어떤 뜻인지를 간단한 집합 연산을 사용하여 정의하고, 그 다음에 논리접속자를 갖는 식에 대하여 어떤 해석이 그 식을 만족한다는 것이 무엇인가를 귀납적으로 정의한다. 술어기호의 해석은 다중체 (tuple) 들의 집합에 의해 정의되는 관계이다. 예를 들어, 만일 p 가 인자수 3 인 술어기호라면 p 의 해석은 D x D x D 의 부분집합으로서 각각이 어떤 관계로 맺어진 삼중체 (triple) 들의 집합이 된다. 만일 (M1 (t1), M1 (t2), M1 (t3)) 가 p 의 해석에 해당하는 삼중체들 집합의 한 원소라면 단위식 p (tl, t2, t3) 는 이러한 p 의 해석에 의해 만족된다.

해석에 대한 이러한 조건사항을 다음과 같이 형식화할 수 있다. 해석 I 는 삼중체 (D, M1, M2) 로서 M1 은 항들을 D 에 매핑시키고 M2 는 항수 n 인 각각의 술어기호를 n-중체들의 집합으로 매핑시킨다. 다음의 조건을 만족할 때 I 는 wff φ 의 모형 (model) 이라고 한다 (이것을 I φ 라고 쓴다).

I  φ 라는 표현은 I 가 φ 의 모형이 아니라 는 것을 나타낸다.

한정식의 해석은 영역의 원소들을 한정변수에 대입함으로써 해결된다. 만약 어떤 해석이 한정변수에 임의의 영역 원소를 대입하더라도 그 식의 모형이 된다면 그 해석은 전체 한정식 (universally quantified formula) 의 모형이 된다. 어떤 해석이 있을 때 만약 어떤 영역 원소가 존재하여 그 원소를 한정변수에 대입한 식에 대하여 그 해석이 모형이 된다면 그 해석은 존재 한정식 (existentially quantified formula) 의 모형이 된다. 만족가능성 (satisfiability), 정당성 (validity) 그리고 모형이론적 비일관성 (model-theoretic inconsistency) 등의 개념은 명제논리로부터 그대로 가져올 수 있다.

5.  의 형식체계

에서 증명을 하기 위해서는 공리들과 추론 규칙들로 이루어진 형식 체계가 필요하다. 이 절에서 논의되는 의 형식 체계는 명제논리의 추론 규칙들을 포함하며 한 가지 부가적인 규칙을 덧붙였다. UI (Universal Instantiation, 전체 사례화) 라는 것은 전체 한정변수가 등장하는 모든 장소에 어떤 항 (term) 을 대입하는 추론 규칙이다. 그림 6 은 이 추론 규칙을 보여준다.

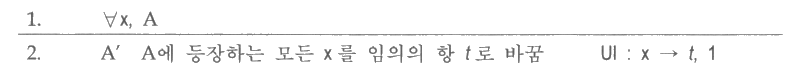
그림 6 : UI (전체 사례화) 추론 규칙

'Fred 가 사람이다' 라는 문장은 person (Fred) 로 그리고 'Fred 가 로비에 있다' 는 사실은 location (Fred, lobby) 로 나타낼 수 있다. 건물 관리 로봇이 로비를 청소하려는데, 만약 로비에 사람이 있다면 청소를 하지 못한다고 가정해 보자. 그 상황에 대하여 우리가 알고 있는 사실이 모두 주어졌을 때 그 로비에 사람이 있다는 것을 증명할 수 있을까? 그림 7 은 person (Fred) 와 location (Fred, lobby) 가 주어진 상태에서 그 로비에 사람이 있다는 사실을 증명하는 단계를 보여주고 있다. 만일 'Fred 가 로비에 있다' 는 사실 대신 '모든 사람이 로비에 있다', 즉 ∀x, person (x) ⊃ location (x, lobby) 라는 것이 주어지더라도 몇 개의 단계만 더 거치면 똑같은 결론에 다다를 수 있을 것이다.

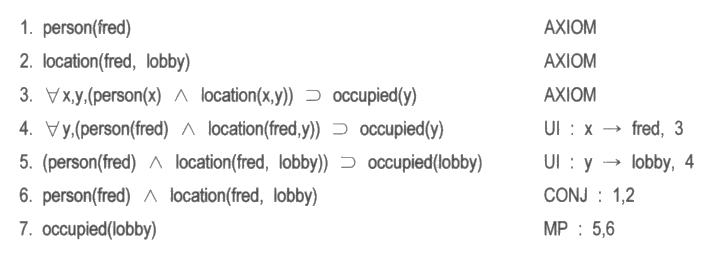
그림 7 : 술어논리에서의 간단한 증명

2개의 항 (term) 이 어떤 의미에서건 동등 (equivalent) 한지의 여부를 추론할 수 있는 것이 유용할 때가 많이 있다. 예를 들어, "학생들 중 2 명만이 합격했다" 라는 문장을 ∃x, y, passed (x) ∧ passed (y) ∧ ￢ equal (x, y) 로 표현할 수 있다. equal 이라는 관계를 추론키 위하여 동등 관계 (equivalence relation) 의 세 가지 특성, 즉 반사 (reflexive), 대칭 (symmetric) 그리고 전이 (transitive) 특성을 나타내는 다음의 3 가지 공리들을 추가할 수 있다.

특정 영역 이론에는 몇 가지 동등 관계가 있을 수 있다. 예를 들어, Lisp 의 추론에서는 메모리 주소에 대한 동등성과 리스트 구조에 대한 동등성을 구분하고 있다.

Prolog 에 의한 프로그램 작성

위에서 설명한 동등 관계를 이용하여 Lisp 에서 볼 수 있는 리스트 처리 계산들을 나타낼 수 있다. 예를 들어, 어떤 것이 리스트의 첫번째 원소와 같거나 혹은 그 리스트 나머지의 일원이면 그 리스트의 일원이다. 이 선언적 내용은 다음과 같은 공리들로 나타낼 수 있다.

위와 같은 공리들을 이용하여 어떤 항목이 리스트의 일원인지에 대한 정리를 증명할 수 있다. 실제로 리스트에 대한 그 어떤 임의의 연산이라도 이를 기술하는 공리들을 만들 수 있다. 논리 프로그래밍 언어인 프롤로그 (Prolog) 는 그러한 공리의 형태로 프로그램을 작성할 수 있도록 해 준다. 이 장의 마지막에 나오는 연습문제에서는 목표 단순화 (goal reduction) 정리 증명기를 이용하여 수행가능한 논리 프로그램의 예가 나와 있다. 이러한 프로그램들의 순차적 세부사항은 Prolog 가 정리를 중명하는 방법 속에 함축되어 있다. Prolog 는 논리와 계산 사이의 밀접한 연관성을 보여준다는 점에서 매우 흥미있는 언어이다.

한정자의 제거

컴퓨터가 기호식들을 쉽게 다룰 수 있도록 하기 위하여 학자들은 표상에 대한 표준형태 (canonical form) 를 만들고자 노력했다. 이미 우리는 논리곱 정규형태 (conjunctive normal form : CNF) 와 논리합 정규형태 (disjunctive normal form : DNF) 의 표준형태들에 대해서 살펴보았다. 한정자 (quantifier) 는 표준형태의 설계를 복잡하게 만들 수 있다. 그런데 한 종류의 한정자, 즉 전체한정자만 있고 모든 식을 다음과 같은 형식으로 바꿀 수 있다고 가정해 보자.

여기에서 φ (x1, x2, ..., xn) 는 변수 x1, x2, ..., xn 을 포함하며 한정자를 포함하지 않는 임의의 식이다. 이 경우, 변수들과 다른 항 (term) 을 구분할 수 있다고 가정한다면 한정자를 완전히 제거하고 φ (x1, x2, ..., xn) 을 논리곱 정규형태로 변형시킬 수 있다. 다음 단락에서는 존재한정자를 제거시킴으로써 임의의 한정식 (quantified formula) 을 이러한 형태로 변형시킬 수 있음을 보이겠다.

먼저 ∃x, happy (x) 는 ￢ (∀x, ￢ happy (x)) 와 동일하다는 사실을 주의하기 바란다. 이동일성은 적절히 일반화시키면 존재한정자를 제거할 수 있도록 해 주지만 이것만으로는 임의의 식을 위에서 말한 형식으로 변환시키기에는 충분하지 않다. 존재 한정자를 제거시키는 또 하나의 방법은 새로운 함수를 만들어 존재하는 물체를 나타내는 방법이다. 예를 들어, ∃x, happy (x) 는 새로운 상수 (인자수 0 인 함수) the-happy-one 을 이용해 happy (the-happy-one) 으로 바꿀 수 있다. 다른 한정자가 섞인 경우는 이보다 복잡해진다. 예를 들어 ∀x, ∃y, loves (x, y) 는 ∀x, loves (x, the-loves-of (x)) 로 바뀔 수 있다. 새로운 함수 the-love-of 는 전체 한정변수 x 하나의 인자만을 취하고, 그 의미는 각각의 가능한 x 에 대하여 특정한 서로 다를 수 있는 애인을 나타낸다.

함수 the-happy-one 과 the-love-of 는 논리학자의 이름을 따서 스콜렘 (Skolem) 함수라고 불린다. 일반적으로 말하면, 다음과 같은 형식의 표현이 있다고 하자.

여기에서 φ (x1, x2, ..., xn) 이 변수 x1, x2, ..., xn 을 포함한 임의의 식이라면 이 식의 스콜렘화 (Skolemization) 라는 것을 다음과 같이 정의할 수 있다.

여기에서 skm 은 처음 등장하는 새로운 함수이다. 때때로 스콜렘 함수는 정리 증명기에 의해 자동 생성되며 sk421 과 같은 새로운 이름이 붙여진다. 다음에서는 몇 가지의 예제 식에서 어떻게 존재 한정자를 제거하는지에 관하여 살펴보기로 하자.

∀x, ∃y, location (y, x) 라는 식이 있다면 우선 그 존재 한정변수를 스콜렘화시켜서 ∀x, location (sk37 (x), x) 라는 식을 만든다. 그 다음 남아있는 한정자를 마저 제거함으로써 location (sk37 (x), x) 라는 식을 얻게 된다.

좀더 복잡한 식에서는 서로 다른 위치에서 나타나는 같은 이름의 변수들의 출현을 구분하기 위하여 어떤 변수에 새 이름을 줄 수도 있다. 이 재명명 (rename) 과정을 변수 구분의 표준화 (standardizing the variable apart) 라고 부르고 이 과정은 (∀x, black(x)) ∨ (∀x, white (x)) 처럼 같은 변수가 2 개 이상의 한정자를 통해 나타날 때 필요하다. 상수와 변수를 구분하기 위한 방법도 필요하다는 사실에 주목하기 바란다.

약간 복잡한 예로서 ∀x, human (x) ⊃ (∃y, parent (x, y)) 가 있다고 하자. 먼저 한정자를 될 수 있는 한 왼쪽으로 옮겨서 ∀x, (∃y human (x) ⊃ parent (x, y)) 을 만든다. 다음에는 스콜렘화시키고 함언기호를 논리합으로 바꿔 ∀x, ￢ human (x) ∨ parent (x, sh42 (x)) 라는 식으로 바꾼다. 마지막으로 남아있는 한정자를 없애고 변수 구분의 표준화를 통하여 ￢ human (x64) ∨ parent (x64, sk42 (x64)) 라는 식을 얻는다. 연습문제 11 에서는 한정자를 제거하는 일반적 알고리즘을 살펴볼 것이다. 이 알고리즘에서 유일하게 복잡한 부분은 스콜렘화 과정이 적용될 수 있도록 부정기호를 모든 한정자의 안으로 옮기는 것이다.

학습과 연역적 추론

5 장 학습에서는 귀납적 추론 (inductive inference) 에 중점을 둔 학습에 관하여 배우게 될 것이다. 귀납적 추론에서는 특정한 예들에 기반하여 일반적인 결론을 도출한다. 예를 들어, 지금까지 보아온 .lisp 라는 확장자를 가진 모든 파일은 Lisp 함수의 정의를 포함했다고 가정해 보자. 이러한 관찰로부터 .lisp 라는 확장자를 가진 모든 파일은 Lisp 함수 정의를 포함한다는 결론을 내릴 수 있을 것이다.

이 장에서는 주로 연역적 추론 (deductive inference) 에 관심을 두려고 한다. 연역적 추론에서는 결론이 반드시 공리들과 지정된 추론 규칙으로부터 나와야 한다. 다음 단락에서는 연역적 추론이 어떻게 학습도 지원하게 되는 지를 살펴보려 한다.

그림 8 : 소프트봇이 어떤 파일을 지울 수 있다는 것의 증명

UNIX 시스템의 모든 파일을 지우는 작업을 맡은 소프트봇 (softbot - 소프트웨어 로봇) 이 있다고 생각해 보자. 소프트봇은 super 사용자의 경우 어떠한 파일이라도 지울 수 있다는 사실과 그 자체가 super 사용자임을 안다.

위의 공리들을 이용해 소프트봇은 자신이 어떤 파일이라도 지울 수 있다는 것을 쉽사리 증명할 수 있다. 그림 8 에서 보듯이 증명은 단지 다섯 줄에 불과하지만 전체 파일 시스템을 지우는 과정에서 소프트봇은 이러한 일련의 추론 과정을 여러 번 반복해야만 할 것이다. 이 특정 소프트봇은 꽤 영리하였다. 그 증명이 임의의 파일에 대해서도 성공하리라는 것을 알아차리고 다음의 일반적인 식을 증명한다.

소프트봇은 이 식을 공리 집합에 추가하여 다음 번에 파일을 지우고 싶을 때에는 새로운 공리에 UI (전체 사례화) 를 적용하여 단 두 줄만으로 파일을 지울 수 있다는 사실을 증명할 수 있다. 이 새로운 공리를 이용하여 소프트봇은 이전에 증명될 수 없었던 그 어떤 것도 증명하지는 못한다. 그러나 어떤 것들은 훨씬 쉽게 증명할 수 있다. 소프트봇은 결국 정리 증명을 가속화하는 방법을 깨달은 것이다. 그러므로 이런 종류의 학습을 가속학습 (speedup learning) 이라고 부른다.

이 소프트봇이 수행한 학습 형태의 또 다른 이름은 설명기반 일반화 (explanation-based generalization) 이다. 그림 8 의 증명은 소프트봇이 왜 특정 파일을 제거할 수 있는가에 대한 설명이다. 설명기반 일반화에서는 설명이 검토된 후 적절한 상수를 전체 한정 변수로 바꿈으로써 일반화시키는 것이다.

어떤 소프트봇이 컴퓨터 네트워크상의 파일 서버에 저장되어 있는 학술 논문 개요를 검색하는 역할을 맡았다고 가정하자. 소프트봇이 파일 서버와 개요에 대해 추론할 수 있도록 다음과 같은 공리들이 주어졌다고 가정하자. 첫번째 공리는 만일 개요가 어떤 파일 서버에 있고 그 서버에 접근 가능하면 그 학술 논문의 개요가 표준 네트워크 파일전송규약 (FTP) 을 이용하여 네트워크로 가져올 수 있다는 것이다.

어떤 논문이 IEEE 에서 발행한 잡지에 실렸다면 그 개요는 JOSIAH 파일 서버상에 있다.

만일 서버가 무계정 (anonymous) FTP 서비스를 제공한다면 그 서버는 접속 가능하다.

마지막으로 Josiah 는 무계정 FTP 서비스를 제공한다.

만약 소프트봇에게 개요 MCD83 을 검색하라고 요청하였다고 가정해 보자. 소프트봇은 MCD83 이 IEEE 에서 출판되었고 PAMI 라는 애칭으로 알려져 있는, IEEE 패턴분석과 기계 지능에 대한 보고서 (Transactions on Pattern Analysis and Machine Intelligence) 라는 논문집에 실려 있다는 것을 알고 있다고 가정하자.

그림 9 : 소프트봇은 네트워크로 파일에 접속할 수 있음을 증명할 수 있다.

그림 9 는 소프트봇이 개요 MCD83 을 FTP 할 수 있다는 증명을 보여주고 있다. 설명기반 일반화 방법으로 그 증명을 분석하고 유용한 일반화를 유도할 수 있는가를 살펴보기로 하자. 만약 증명에서 MCD83 을 전체 한정변수로 대체한다고 가정해보자. ∀a, ftp(a) 라는 것을 증명할 수 있을까? 대답은 "아니오" 이다. 왜냐하면 그 증명은 개요가 파일 서버인 JOSIAH 상에 있다는 사실에 기반을 두었기 때문이다. 만약 모든 개요가 JOSIAH 서버상에 존재한다면 ∀a, ftp (a) 라는 것을 증명할 수도 있다. 실제로 다음의 식은 정당한 (valid) 일반화이다.

좀더 나은 방법으로 할 수도 있다. 다음의 일반화도 정당하며 훨씬 짧은 증명을 얻을 수 있다.

설명기반 일반화를 이용하는 시스템은 일종의 연역적 추론을 이용하여 문제를 해결한다. 이들은 각 단계들을 분석하여 이후 추론의 속도를 높이는 데 사용될 수 있는 식을 유도한다. 7 장 계획수립에서는 설명기반 일반화를 이용하여 계획수립 (planning) 시스템의 성능을 향상시키는 방법에 대하여 살펴볼 것이다.

결정가능성

술어논리는 일반적으로 결정적이 아니다. 이 말은 주어진 식이 정리인지 아닌지를 결정하는 효율적 방법이 없다는 것을 의미한다. 그러나 결정적인 몇 가지 특수 이론이 존재한다. 예를 들어, 유한 개의 항 (term) 을 가진 이론은 모두 결정적이다. 유한개의 항을 갖는 경우 전체 한정자는 논리곱으로, 존재한정자는 논리합으로 바꿀 수 있어 술어논리 이론을 명제논리 이론으로 변환할 수 있기 때문이다. 다음 절에서는 효과적인 정리 증명기를 구현할 수 있는 유한 개의 상수와 술어기호를 갖는 특정 이론들에 대해 살펴보겠다.

6. 에서의 자동 정리 증명

다음과 같은 이론을 생각해 보자,

의 추론 규칙을 이용하면 이들 공리로부터 pleasing (block17) 이라는 식을 증명할 수 있다. 명제논리에서 사실 (fact) 과 한정자를 포함하지 않는 규칙 (rule) 을 표현하는 방법에 대해서는 이미 배웠다. 한정변수에 block17 과 block41 을 대입함으로써 각각의 전체 한정식을 명제식 (propositional formula) 들의 논리곱으로 나타낼 수 있다. 그 결과로 얻어지는 명제이론을 앞서 정의한 theorem 함수에 직접 이용할 수 있다. 그러나 이 장에서는 명제이론으로 바꾸지 않고, 특정한 경우의 전체사례화 (universal instantiation) 를 구현하는 방법과 간단한 PC 이론들에 대한 정리를 증명하는 방법에 대해서 고려해 보자.

우리의 데이터베이스가 앞에서 언급한 표준 형태이므로 한정자를 굳이 표시할 필요는 없을 것이다. 그러나 전체 한정변수와 상수를 구분할 필요성은 있다. 이를 위하여 Lisp 의 변수를 위한 추상 데이터형을 소개하고자 한다.

첫 원소가 ? 인 모든 리스트는 한정 범위가 자신이 포함된 표현식 전체인 전체 한정 변수로 해석된다. 이 공리들을 Lisp 에서는 다음과 같은 사실과 규칙들로 표현했는데, 충돌을 피하기 위해 변수들을 구분되게 표준화한 것에 주의하라.

정합과 UI

UI 는 어떤 식 내에서 전체 한정변수의 모든 출현 (occurrence) 들에 대하여 이를 임의의 항으로 치환 (substitute) 할 수 있도록 허용한다. 만일 두 개의 식이 구문적으로 동일하게끔 만드는 변수들에 대한 치환을 찾을 수 있는 경우 두 식은 정합 (match) 되었다고 한다. 우선 (pleasing block17) 과 같은 기초식 (ground formula) 에 대응되는 상수와, (pleasing (? x)) 와 같은 한정식에 대응되는 패턴이 정합되는지를 알아내는 Lisp 함수를 정의해 보자. 만약 이들이 정합된다면 그 함수는 변수들을 항으로 대응시키는 이른바 변수결합 (binding) 이라 불리는 치환들의 집합을 반환한다. 상수는 다른 상수와 equal 인 경우 정합된다. 미결합 (unbound) 변수 (현재 변수결합 안된 변수) 는 어느 식에라도 정합된다. 결합된 (bound) 변수는 그 변수에 묶인 값과 상수가 equal 일 때 그 상수에 정합된다.

다음 알고리즘은 앞에서의 정의에 따라 하나의 패턴과 하나의 상수가 정합되는지를 결정하는 데 사용될 수 있다. 실패한 정합과 성공적이지만 변수결합이 없는 정합을 구분하기 위하여 변수결합의 초기 리스트가 nil 이 아니라고 가정하자.

그림 10 : 상수와 패턴 표현식의 정합을 위한 코드

그림 10 은 이 알고리즘을 실행하는 match 라는 재귀함수의 Lisp 코드를 나타낸 것이다. 2 장에서 Lisp 함수 assoc 가 2 개의 인자, 즉 하나의 표현식 그리고 리스트들의 리스트를 가지며, 이들 리스트들의 리스트 중에서 첫 원소가 첫 인자의 값과 eq 인 첫번째 리스트를 반환함을 기억하기 바란다. match 함수에서 assoc 를 사용할 때 우리는 :test 라는 선택적 키워드 인자를 사용하여 기본 검사 방법인 eq 대신 equal 로 대치하였다.

match 가 성공했을 때의 예를 몇 가지 살펴보기로 하자.

다음은 match 가 실패했을 때의 예이다.

에서의 목표 단순화

이제 theorem 함수를 약간 변형하여 (pleasing block17) 을 증명할 수 있다. 먼저 규칙의 결과항과 증명하려는 논리곱 인자가 정합되는지의 여부를 결정하는 데 eq 대신에 match 를 사용한다. 두번째로 규칙의 선행항을 증명하려는 논리곱 인자들의 리스트에 추가한 다음 그 리스트의 모든 논리곱 인자들에 대하여 변수결합에 주어진 치환을 수행한다. 이것은 UI (전체 사례화) 와 모두스 포넨스 (modus ponens) 를 연속적으로 적용하는 것과 같은 효과이다.

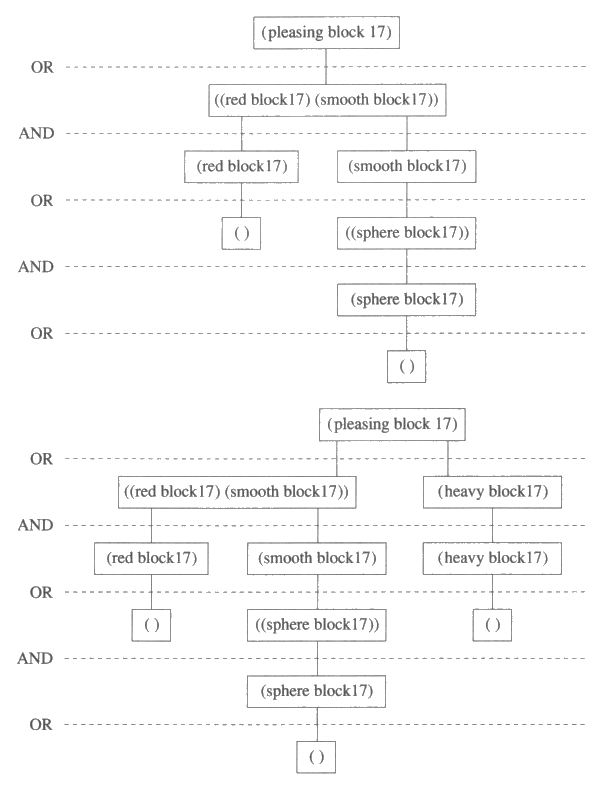
그림 11 : 목표 단순화를 위한 AND / OR 트리의 예

그림 11 의 위의 그림은 AND / OR 트리로 묘사한 증명의 구조이다. AND / OR 트리는 AND 와 OR 층으로 나뉘어져 이들이 번갈아 나타난다. AND 층을 통과하는 에지 (edge) 들은 논리곱의 논리곱 인자들을 연결시켜 준다. OR 층을 통과하는 에지들은 논리곱 인자를 데이터베이스 내의 규칙에 따라 가능한 단순화된 목표로 연결시켜 준다. 만약 어떤 논리곱 인자가 공리스트로 단순화되거나 혹은 그것이 (재귀적으로) 각 논리곱 인자가 AND / OR 트리 내에 증명을 갖는 논리곱으로 단순화되면 그 논리곱 인자는 AND / OR 트리 내에서 증명을 갖는다. AND / OR 트리 내에서 어떤 논리곱 인자의 증명트리 (proof tree) 는 바로 그 논리곱 인자를 루트로 갖는 AND / OR 트리의 부분트리로서 그 논리곱 인자의 모든 논리곱 인자는 정확히 하나의 단순화된 인자를 갖고 그 논리곱 인자가 AND / OR 트리에서 증명을 갖는 것이다. 그림 11 위쪽의 AND / OR 트리는 모든 논리곱 인자에 대하여 가능한 증명이 단지 하나뿐이므로 그다지 흥미롭지 않다. 그러므로 그 트리는 pleasing (block17) 의 증명트리가 된다. 만약 규칙 ((pleasing (? x)) if (heavy (? x))) 과 새로운 사실 heavy (block17) 을 첨가한다면 그림 11 의 아래쪽 그림과 같은 좀더 흥미로운 AND / OR 트리를 얻게 되는데, 그 트리에서는 pleasing (block17) 이 두 개의 증명트리를 갖는다.

pleasing (block17) 에 대한 증명은 특별히 쉬운 케이스에 속하는데, 이는 만약 적당한 치환을 하는 경우 변수를 포함한 논리곱 인자를 추가시키지 않기 때문이다. 이는 어떤 패턴에 대하여 항상 상수만을 정합하는 것을 의미하는데, 이는 바로 match 가 유일하게 할 수 있는 것이기도 하다. 그러나 한정식을 증명하는 것이 유용할 때도 있다. AND / OR 트리 내에서 논리곱 인자에 대응되는 한정식은 존재 서술문 (existential statement) 으로 해석된다. 예를 들어, AND / OR 트리 내의 (pleasing (? x)) 는 ∃x, pleasing (x) 로 해석된다. ∀x, sphere (x) ⊃ smooth (x) 가 주어진 상태에서 ∃x, smooth (x) 를 증명하려면 ∃x, sphere (x) 를 증명하는 것만으로도 충분하다. (pleasing (? x)) 를 증명하려면 x 에 대입할 수 있는 적당한 값 v 를 찾아 (pleasing v) 가 증명가능하도록 하면 된다. 이러한 작업에서 가장 까다로운 것은 정합시키려는 각각의 식이 모두 변수를 포함하는 경 우이다.

단일화

이번에는 단일화 (unification) 라고 불리는 더욱 일반적인 형태의 정합에 대하여 고려해 보자. 동일화 과정에서 사용되는 치환 (substitution) 은 앞에서 소개되었던 간단한 형태의 정합에서 사용된 치환보다 좀더 복잡하다. 만일 두 개의 변수 x 와 y 에 대하여 ((x fred)(y fred)) 라는 치환을 사용하면 이들이 동일해지지만 이는 우리가 의도한 것보다 너무 특수한 치환이 된다. 두 가지 패턴을 단일화시킬 때 그들 패턴이 구문적으로 동일하게 해 주는 가장 일반적인 치환 (most general substitution) 을 찾아야 한다.

다음의 재귀적 단일화 프로시저는 만약 그러한 치환이 존재하는 경우 두 식의 가장 일반적인 치환을 계산해 낼 수 있다. 단일화 프로시저는 두 식 사이의 불일치 (disagreement) 라는 개념을 이용한다. 트리를 나타내는 표현식 p 와 q 가 있을 때 이 둘 사이의 첫번재 불일치 는 그 트리들에 대하여 나란히 깊이우선 탐색 (depth-first-search) 방식으로 비교해 나갈 때 첫번째 등장하는 서로 다른 부분식을 말한다. 예를 들어 p 가 (loves (mother (? z)) (? z)) 이고 q 가 (loves (? x) (? y)) 이면 첫 일치는 (mother (? z)) 와 (? x) 에 해당된다. 단일화 프로시저는 3 개의 인자를 가지고 호출이 된다. 2 개의 식 p 와 q 그리고 치환의 상태를 추적하기 위하여 변수결합의 집합 σ 를 넘겨준다.

단일화 프로시저가 진행되는 방식을 예를 통해서 살펴보자. p 가 (loves (dog (? z)) (dog fred)) 이고 q 가 (loves (? x) (? x)) 라고 가정해 보자. p 와 q 사이의 첫 불일치는 (dog (? z)) 와 (? x) 이다. p 와 q 에서의 (? x) 를 (dog (? z)) 로 치환시키면 p' 는 (loves (dog (? z)) (dog fred)) 가 되며 q' 는 (loves (dog (? z)) (dog (? z))) 가 된다. p' 와 q' 에서의 첫 불일치는 fred 와 (? z) 인데 p' 와 q' 에서의 (? z) 를 fred 로 치환시키면 2 개의 동일한 식을 얻게 된다. 단일화 프로시저는 (((? x) (dog (? z))) ((? z) fred)) 의 치환을 가지고 성공한다.

다른 예를 들면, 2 개의 식 (loves (mother (? z)) (? z)) 와 (loves (? x) (? y)) 에 대하여 단일화 프로시저는 치환 (((? x) (mother (? z))) ((? y) (? z))) 를 되돌려 주면서 성공한다. (loves (? z)(? z)) 와 (loves (mother (? x)) fred) 와의 단일화 프로시저는 실패한다.

집고 넘어가야 할 것은 위의 단일화 프로시저가 한 가지의 버그를 가지고 있다는 점이다. 이 프로시저는 두 개의 식, (loves (mother (? z)) (? z)) 와 (loves (? x)(? x)) 에 대하여 치환 (((? x) (mother (? z))) ((? z) (mother (? z)))) 를 결과로 내고 성공한다. 이 단일화 프로시저는 변수가 변수결합된 표현식 속에 바로 그 변수가 포함되어 있는지 여부를 확인하지 못한다. Prolog 언어에서 사용되는 단일화 프로시저도 이 버그를 가지고 있다. 그러나 Prolog 에서는 이것이 버그가 아니고 하나의 특성으로 여겨지는데, 그 이유는 이것으로 인하여 몇 가지 아주 유용한 프로그래밍 기법이 가능하게 되고 단일화를 더 빨리 해주기 때문이다.

그림 12 : 가장 일반적인 치환을 구하기 위한 메인 루틴

그림 13 : 가장 일반적인 치환을 구하기 위한 서브루틴

그림 12 과 13 은 정확은 하지만 약간 비효율적인 단일화를 위한 Lisp 코드이다. Unify 함수는 만약 두 개의 인자를 equal 하게 만드는 치환이 존재한다면 가장 일반적인 치환을 되돌려 주고 그렇지 않으면 nil 을 되돌려 준다. 여기에서의 구현은 Prolog 에서 허용되는 일종의 가짜 단일화를 방지하기 위하여 '출현 (occur) 체크과정' 을 추가시켰다.

그림 12 와 13 에서 나타난 단일화의 버전은 Lisp 함수 subst 와 2 개의 식이 처음으로 불일치하는 지점에서의 상응하는 부분식을 계산해 내는 disagreement 라는 함수를 이용해서 반복적으로 치환을 함으로써 수행된다.

다음은 두 개의 한정식에 대한 unify 연산을 설명해 주는 예이다.

이제 (pleasing (? x)) 를 증명하기 위한 theorem 함수를 다시 한번 변형시켜 볼 수 있다. 대체로 match 를 사용할 때와 같은 방법으로 진행되나 치환 계산을 위하여 unify 를 사용한다. 변수를 포함한 논리곱 인자들을 다룰 때 문제가 좀더 복잡해진다. 많은 경우 증명을 하는 과정에서 같은 규칙이 한번 이상 사용될 필요가 있다. 서로 다른 논리곱 인자에 같은 규칙이 적용되면서 변수에 다른 값이 사례화 (instantiation) 되어 발생하는 충돌을 피하기 위해 어떤 규칙이 사용될 때마다 그 규칙의 모든 변수들을 재명명 (rename) 한다.

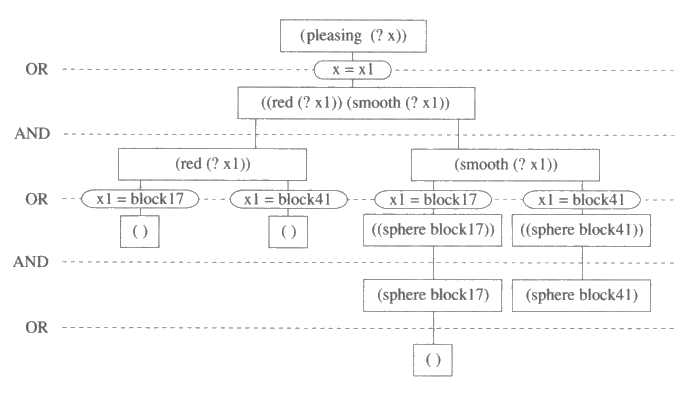
그림 14 : 한정식에 대한 목표 단순화 방법

그림 14 는 (pleasing (? x)) 에 대한 AND / OR 그래프를 보여준다. 이 그림에서는 모든 단순화에 대하여 치환 명칭이 붙여진 것에 주의하기 바란다. 이러한 치환이 부착된 증명트리에서는 앞서 언급했던 조건 이외에도 각 변수가 기껏해야 하나의 변수결합만을 가져야 한다는 조건이 따른다. 각 변수가 최대 하나의 변수결합을 갖는다는 사실을 확인하기 위하여 이전의 논리곱 인자를 증명할 때 만들어진 치환에 해당하는 모든 변수결합의 리스트를 유지하고 그 리스트를 theorem 함수에 재귀호출할 때마다 넘겨주어야만 한다. 하나의 논리곱 인자가 증명되기 전에는 우선 변수결합 리스트를 이용하여 그 식 속에 변수결합된 변수들에 대하여 치환을 해 준다. 이러한 추가 사항이 더해지면 theorem 함수는 논리 프로그래밍 언어인 Prolog 의 간단한 해석기 (interpreter) 역할을 해 줄 수 있다.

개념 기술 언어

술어논리에서 일반적인 정리 증명은 계산적으로 복잡하다. 이러한 이유 때문에 학자들은 어떤 내용의 지식을 나타내기에 충분히 표현력이 있으면서 계산적으로도 타당성이 있는 연산 특성을 갖는 술어논리의 부분집합을 찾으려 애쓴다. 이러한 술어논리의 부분집합은 특수한 언어를 정의하게 된다. 목표단순화 기법에 사용했던 규칙들은 바로 그러한 특수 언어에 해당한다. 목표단순화 규칙만 가지고는 술어논리에서 나타낼 수 있는 모든 것을 나타내지는 못한다. 그러나 목표단순화 규칙들은 상당히 많은 유용한 지식을 나타낼 수 있도록 해 주면서도 그러한 지식을 효율적으로 처리할 수 있는 많은 형태의 추론을 가능하게 해 준다.

여기에서 부류 (class) 는 객체들의 집합이고, 부류의 사례 (instance) 라는 것은 대응하는 집합의 한 일원 (member) 이고, 만일 한 부류가 다른 부류의 부분집합일 때는 전자를 하위부류 (subclass) 라 하며 후자를 상위부류 (superclass) 라고 한다. 개념 기술 언어 (concept description languages) 란 객체들의 부류, 부류의 사례 (instance) 들, 부류들 사이의 하위부류 (subclass) 관계성 그리고 부류와 사례들의 특성 (feature) 등을 기술해 주는 특수 언어이다.

여기서 제시될 간단한 개념 기술 언어는 3 가지의 술어 (predicate), 즉 instance, subclass 그리고 feature 를 포함하고 있다.

는 object 가 class 의 instance (사례) 임을 나타내고

는 class 가 superclass 의 subclass (하위부류) 임을, 그리고

는 class 내의 모든 객체는 value 값을 지닌 속성 (attribute) 을 가지고 있음을 나타낸다.

Ralph 가 로봇들 부류의 사례임을 표현하려면 instance (Ralph, robot) 이라 표현한다. 로봇이 자율시스템의 하위부류임은 subclass (robot, autonomous-system) 이라 표현한다. 모든 로봇은 기계 부품으로 만들어 졌다는 사실은 feature (robot, construction,   mechanical) 로서 나타낼 수 있다.

부류와 사례에 대해서 몇 가지의 일반적인 문장을 만들 수 있다. 만일 어떤 객체가 부류의 사례라면 그 객체는 그 부류의 모든 상위부류의 한 사례이다. subclass 라는 관계성은 전이적 (transitive) 인 특성이 있다. 만일 한 부류가 어떤 특성 (feature) 을 갖는다면 그 부류에 속하는 모든 사례들은 그 특성을 갖는다. 지금까지 말했던 이러한 문장들은 다음과 같은 술어논리식으로 표현된다.

개념 기술 언어로 쓰여진 지식이 주어졌을 때 사례들의 특성을 추론하고자 하는 경우가 많다. 예를 들면 Ralph 가 기계부품으로 만들어졌다는 것을 증명하고 싶다고 하자.

추론을 단순화하기 위하여 개념 기술 언어로 쓰여진 지식을 편리한 도표 형식으로 변환할 수 있다.

의미망

의미망 (semantic net) 이란 유향 그래프 (directed graph) 로서 각 노드는 부류, 사례, 속성의 값들에 해당한다. 의미망에서 표지 (label) 가 붙은 아크는 사례와 하위부류 관계성 그리고 부류를 설명해 주는 속성 등을 표시한다. 다음의 식들을 살펴보자.

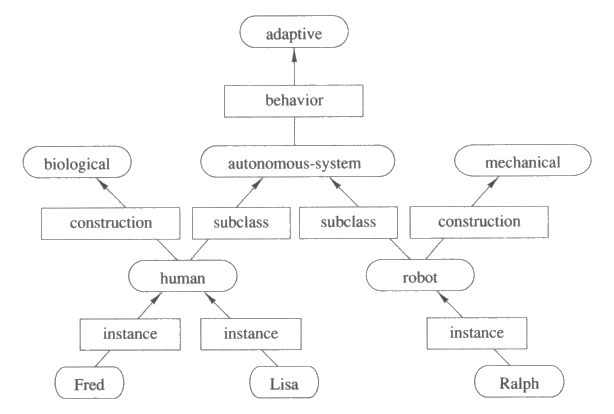
그림 15 : 의미망

이 식들은 그림 15 와 같은 의미망으로 나타낼 수 있다. 각각의 사례, 부류 그리고 속성의 값에 해당하는 하나의 노드가 있음을 주의하기 바란다. 의미망 내에서의 주어진 사례에 대한 속성값을 계산하기 위해서는 그 사례로부터 원하는 속성의 표지가 붙은 아크를 가진 부류 쪽으로 따라 올라가야 한다. 속성간에 대한 질문에 답하는 것은 의미망의 크기에 대해 선형시간 (linear time) 내에 수행될 수 있다.

그림 15 는 가장 간단한 형태의 의미망이다. 더 복잡한 형태에서는 하나의 사례 혹은 부류 노드로부터 하나 이상의 아크가 나올 수도 있다. 예를 들면, 어떤 사람이 인간과 구별할 수 없는 로봇을 만들려 한다고 가정하자. 이 로봇은 사람과 로봇으로 동시에 분류가 되어 혼돈을 불러일으킬 수도 있을 것이다. 특히 이 인간 복제 로봇은 construction 속성에 대하여 두 가지의 값을 가질 수도 있을 것이다.

또한 우리가 나타내고자 하는 사례들 중에는 그것의 부류의 모든 특성을 가지지 않는 것들도 있을 수 있다. 그러한 사례는 그 부류의 전체에 적용되는 일반적인 규칙에 대하여 예외 (exception) 가 된다. 예를 들면 기계적 요소와 생물학적 요소로 구성된 복합 로봇이 있을 수 있다. 그 외의 모든 면에서 그 복합 로봇은 다른 로봇과 같다. 예외는 상위부류의 특성 (feature) 에도 역시 적용될 수 있다. 예를 들면, 자율시스템의 모든 특성을 가지면서도 적응력 있는 행동은 하지 못하는 로봇이 있을 수도 있다.

개념 기술 언어에 예외의 개념이나 그 외의 다른 확장들을 추가시킴으로써 이러한 언어들의 표현력을 중대시킬 수 있다. 때때로 이 증가된 표현력은 추론과 관련된 부가 계산 또한 증가시킨다. 계산적 효율과 표현력을 어떻게 맞바꾸어야 하는가는 표현 방법의 설계시 중요한 고려사항이다.

7. 비단조 논리

지금까지 설명된 논리들은 어떤 식이 특정한 형식 이론에 대하여 정리 (theorem) 이면 그 이론에 새로운 공리들이 추가되어 얻어지는 어떠한 확장된 이론에 대해서도 그 식은 여전히 정리라는 점에서 단조 (monotonic) 논리 이다. 비단조 (nonmonotonic) 논리 에서는 하나의 논리식이 어떤 형식 이론에 대한 정리일 때 그 식은 확장된 이론에 대하여 꼭 정리일 필요는 없다. 대부분의 상식 추론은 새로이 첨가된 정보가 이전의 결론을 철회하는 충분한 근거를 제공할 수 있다는 면에서 비단조적이다. 예를 들어, 당신이 앨리스라는 이름의 여동생이 없다고 믿는다고 하자. 그러나 만약 당신부모님의 이름이 기재되어 있는 앨리스라는 아이의 출생증명서를 발견한다면, 당신은 이전의 믿음을 철회할 수밖에 없을 것이다. 이 절에서는 어떻게 기존의 단조 논리를 확장하여 비단조 형태의 추론을 다룰 수 있는 지를 간단하게 다룬다.

닫힌 세계 가정

만약 어떤 이론에서 모든 (변수와 접속자를 포함하지 않는) 기초 단위식 (ground atomic formula) 에 대해 그 식 자체나 그 식의 부정이 항상 정리이면 그 이론은 단위식 수준에서 구문론적으로 완전하다 (syntactically complete). 만약 어떤 이론이 구문론적으로 완전하지 않다면 거기에는 비록 정리는 아니지만 결론짓기에 타당한 어떤 것들이 있을 것이다. 닫힌 세계 가정 (closed-world assumption) 은 정보의 결핍에 근거하여 어떤 결론을 이끌어내는 작업을 정당화시키기 위해 종종 사용된다. 예를 들어, 인사 담당자인 당신에게 Fred 라는 사람이 당신 회사에 고용되어 있는지 알아보라는 요청을 받았다고 가정해 보자. 당신은 employee (Fred) 가 참인지 결정하고자 한다. 고용자 데이터베이스에는 Fred 에 대한 기록이 없다. 하지만 그렇다고 ￢ employee (Fred) 를 증명할 수는 없다. 이러한 문제를 해결하는 한 가지 방법은 닫힌 세계 가정을 사용하여 정리가 아닌 모든 기초 단위식의 부정을 첨가하여 이론을 완전하게 만드는 것이다.

어떤 이론을 완전하게 한다는 것은 만약 서로 다른 술어기호들이 공리적으로 서로 연관되는 경우 매우 복잡해 질 수 있다. 두 개의 술어 inside 와 outside 가 있고 두 술어를 연관시키는 공리 ∀x, ￢ inside (x) ≡ outside (x) 가 있다고 가정하자. 만약 Fred 가 어디 있는지 모른다고 가정하면 ￢ outside (Fred) 나 ￢ inside (Fred) 를 그 이론에 첨가할 아무런 이유가 없다. 문제는 술어의 선택이 너무 임의적이라는 것이다. Fred 가 밖에 있다는 가정보다 안에 있다는 가정을 선호할 아무런 이유도 없다. 일반적으로 우리는 어떤 술어를 완전화할 것인가에 대하여 통제할 수 있기를 원한다. 다음과 같은 방법은 이러한 통제를 가능하게 한다.

block17 은 우리가 알고 있는 유일한 빨간 물체라고 가정해 보자. 실제로 block17 이외의 다른 물체는 빨간색이 아니라고 결론 지을 용의도 있다고 하자. block17 이외의 모든 x 에 대해 일일이 ￢ red(x) 를 첨가하는 방법말고 이것을 어떻게 표현할 수 있을까? 한 가지 답은 술어 red 를 다음과 같은 완전화 공식 (completion formula) 을 사용하여 완전하게 하는 것이다.

이 완전화 공식과 (구문적으로) 다른 두 개의 항은 동일하지 않다는 가정을 통하여 ￢ red (block41) 을 쉽게 증명할 수 있다. 나중에 또 다른 예를 들어 block32 가 빨간색이라는 것을 알게 되면 완전화 공식의 우변만 다음과 같이 변형시키면 된다.

만약 완전화하려는 술어가 어떤 다른 식에 함언 (implicate) 되어 있다면 문제는 좀더 복잡해진다. 예를 들어, block17 이 빨간색이라는 것을 알고 ∀x, on (x, table32) ⊃ red (x) 라는 것을 안다고 가정해 보자. 이제는 다음과 같은 완전화 공식이 생성된다 :

비단조 논리에 관한 문헌에는 닫힌 세계 가정의 특수한 경우가 종종 나타난다. 첫번째는 영역 닫힘 가정 (domain-closure assumption) 이라 불리며, 이 가정에 따르면 영역 내에 존재하는 유일한 객체들은 바로 이론에서 명시된 상수와 함수들로 이름 붙일 수 있는 것들뿐이라는 것이다. 두번째는 고유 명칭 가정 (unique-names assumption) 이라 불리는데 이는 두 개의 기초항 (ground term) 이 동일하다고 증명될 수 없으면 그 둘은 다른 것으로 가정한다는 것이다. 이러한 가정들은 우리가 사용하는 프로그램에서도 종종 암묵적으로 나타난다.

역추론과 디폴트 추론

특수 목적의 추론 규칙들을 첨가함으로써 허용될 수 있는 다양한 형태의 비단조 결론들에 대하여 우리의 영역을 넓혀보기로 하자. 이러한 추론 규칙들을 명시하기 위해 일관적 (consistent) 임을 의미하는 특수 기호 C 를 도입하려 한다. 직관적으로 말하면, 모든 wff α 에 대하여 만약 α 를 공리로서 첨가하였을 때 모순을 일으키지 않는다면 C (α) 가 성립한다. 이때 C 는 형식 언어의 일부가 아니기 때문에 의사술어 (pseudo-predicate) 라 부른다. 즉, C (α) 형태의 정리는 증명할 수 없다. 그림 16 은 두 가지 특수 목적 추론 규칙에 대한 일반 형태를 나열하고 있는데 이들 일반 형태에 등장하는 α 와 β 는 특정 wff 에 대응된다. 그림 16 의 형태들은 그림 2 나 4 에서 보았던 그런 스키마 (schema) 가 아니라는 것에 주의하기 바란다. α 와 β 는 아무 wff 로 그냥 치환할 수는 없다.

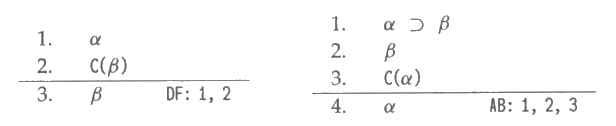
그림 16 : 비단조 추론 규칙에 대한 두 가지 일반 형태

그림 16 에 나타난 규칙의 첫번째 형태는 디폴트 추론규칙 (default rule of inference) 이라 한다. 그 의미는 어떤 필요 조건 α 를 증명할 수 있고, β 가 이론과 모순을 일으키지 않으면 β 라는 결론을 내릴 수 있다는 것이다 (의사술어 C 때문에 디폴트 추론 규칙을 사용하는 논리에 있어서 구문론적인 증명 (proof) 의 개념과 의미론 모두 복잡해지게 된다. C 로 인하여 증명에 대한 전통적 개념에 순환적 문제가 발생하는 것이다. 증명과정에서 C 를 이용한 추론 규칙을 사용해야 할텐데 이는 다시 모순을 증명할 수 있는가 여부를 밝혀야 하기 때문이다.). α 와 β 에 아무 치환이나 허용하지는 않지만, 그 이론에 첨가할 수 있는 그림 16 의 일반 형태에 대한 하나의 사례를 보일 수 있다.

디폴트 규칙 PR 에 따르면, 엔지니어는 실용적 (practical) 이라고 믿는 것이 일관적인 한 엔지니어는 실용적이라는 것이다.

그 자체만 보면, PR 과 같은 규칙은 아무런 문제가 없는 듯 보일 수 있다. 그러나 디폴트 규칙들이 서로 경쟁을 하게 될 수도 있다. 예를 들어, 다음과 같은 규칙을 추가했다고 가정해 보자.

그리고 어떤 사람이 실용적이면서 동시에 이론적 (theoretical) 일 수 없다는 (그릇된) 믿음, ∀x, theoretical (x) ≡ ￢ practical (x) 와 Lynn 은 과학자이면서 엔지니어라고 가정해 보자. 이제 이론에 모순이 발생하지 않도록 하려면 theoretical (Lynn) 또는 practical (Lynn) 중의 하나만을 첨가할 수 있다. 이는 PR 과 TH 두 규칙 중 하나만을 적용할 수 있다는 것을 의미한다. 단조 논리에서는 추론 규칙의 적용 순서가 어떤 정리를 이끌어낼 수 있는가 여부에 영향을 미치지 않는다. 그러나 비단조 논리의 경우 그 순서에 따라 차이가 생길 수도 있다.

그림 16 의 비단조 추론 규칙에서 두번째 형태는 역추론 (abductive rule of inference) 규칙이라 불린다. 역추론은 만약 그것이 모순적이지 않다면 함언의 결과항 (consequent) 이 주어질 때 그 선행항 (antecedent) 을 결론지을 수 있도록 해 준다. 그러한 규칙은 진단 형태의 추론에서 종종 발생한다. 예를 들어, 차에 기름이 없다면 차의 시동이 걸리지 않을 것이다. 역추론을 사용하여 차가 시동이 걸리지 않는다면 달리 믿을 이유 (방금 전에 연료를 채웠다거나) 가 없다는 가정하에서 기름이 없는 것으로 결론내릴 수 있을 것이다. 다음의 추론 규칙은 이러한 진단 전략을 표현하고 있다.

역추론과 불완전하고 확실하지 않은 정보에 근거한 추론들에 대해서는 8장 불확실성에서 다시 다루기로 한다.

최소 모형

비단조 논리에 대한 또 하나의 접근방법은 최소 모형 (minimal model) 개념에 근거하고 있다. 이를 설명하기 위해 다음과 같은 규칙을 생각해 보자.

bird (Ralph) 가 주어진다면, 만약 Ralph 가 정상적 (normal) 이라고 증명할 수만 있다면 flies (Ralph) 를 증명할 수 있다. 어쩌면 ￢ abnormal (x) 를 증명할 수 없을지도 모른다. 그러나 일반적으로 정상적이지 않다는 것을 증명할 수 없는 한 정상적인 것으로 기꺼이 결론내릴 수 있다고 가정한다. 명제논리의 정당성 (validity) 에 대한 정의에 따르면 abnormal (Ralph) 가 참인 해석 (interpretation) 도 존재하고 거짓인 해석도 존재한다면 그러한 결론은 정당하지 않을 것이다. 다음에서는 최소로 비정상 (minimally abnormal) 인 해석, 즉 최대한 정상 (maximally normal) 인 해석에만 적용되는 또 다른 형태의 정당성 개념에 대하여 살펴보기로 한다.

최소로 비정상인 해석에 대한 개념을 정의하기 위하여 해석에 대하여 정의되는 선호 관계 (preference relation) 라는 것을 우선 소개하려 한다. 다음과 같은 조건이 만족될 때 해석 I2 보다 I1 을 선호한다고 말한다 (기호로는 I1 ≫ I2).

다시 말해서, 하나의 해석이 다른 해석과 같으면서 단지 abnormal 의 해석에 있어서만 처음 해석이 두번째 해석의 진부분 집합을 만족시킨다면 전자는 후자보다 선호된다는 것이다. I′ ≫ I 인 다른 해석 I′ 가 존재하지 않을 때 해석 I 는 최소 비정상이라 말한다.

만약 정당성의 개념이 모든 최소 비정상인 해석에서의 만족성 (satisfiability) 에 상응하는 것이라고 의미를 약화시킨다면, bird (Ralph) 와 ∀x, (bird (x) ∧ ￢ abnormal (x)) ⊃ flies (x) 로 구성된 이론에서 모든 최소로 비정상인 해석에 대해 ￢ abnormal (Ralph) 는 참이 될 것이고 따라서 flies (Ralph) 도 참이 된다.

최소로 비정상인 해석을 사용하는 이러한 접근 방법에서 PC 의 구문 (syntax) 은 그대로 유지되었지만 의미 (semantic) 에 있어서는 변화를 주었다. 불행하게도, P 와 PC 의 형식 체계는 이러한 또 다른 형태의 의미론적 이론을 위한 무결 (sound) 하고 완전한 (complete) 이론을 생성하기에는 부족하다. 그러나 비단조 논리에 대한 문헌을 보면 이 장의 앞에서 설명한 형식 체계에 자연스럽게 구축되는 여러 가지 증명기법들이 나와 있다.

비단조 추론의 일반적 사항 혹은 특정 비단조 논리와 관련된 이슈들은 인공지능에서 중요한 세부 분야를 형성하고 있다. 이들에 대한 기술적인 문제들을 자세히 다루는 것은 이 책의 범위를 벗어나지만, 뒤에서 우리는 비단조 추론과 관련된 몇 가지 이슈들에 대해서 살펴볼 것이다.

8. 연역검색 시스템

논리적 추론은 단순히 정리를 증명하는 것에만 사용되는 것이 아니다. 연역검색 시스템 (deductive retrieval system) 은 지식을 규칙의 형태로 저장하고 지식으로부터 결론을 이끌어 내는 프로시저를 구현하는 시스템을 말한다. 연역검색 시스템은 어떤 면에서 정리 증명 (theorem proving) 과 비슷하지만, 일반적으로 특정한 형태의 문제해결에 적합하게 맞추어져 있다. 대부분의 전문가 시스템은 연역검색 시스템으로 특징 지어질 수 있다.

연역검색 시스템과 정리 증명기가 공통적으로 갖고 있는 한 가지 특성은 지식을 기호적으로 (symbolically) 그리고 선언적 (declarative) 으로 표현한다는 것이다. 전형적인 연역검색 시스템은 사실과 규칙들의 데이터베이스와 그 데이터베이스상에서 작동하는 프로시저들의 집합으로 구성된다. 그 프로시저들은 질의에 답하고, 언제 어떤 결론이 보장되는지 예측하며, 새로운 자료가 첨가될 때마다 사실과 규칙을 확장하고 자료가 철회될 때 그것을 정리하는 등의 역할을 한다. 이 절에서는 이러한 구성 프로시저들에 대해 살펴보겠다.

대부분의 연역검색 시스템에서 데이터베이스는 사실과 규칙의 피동적인 저장소 이상의 것이다. 많은 경우 데이터베이스에 하나의 항목을 첨가하거나 제거할 때면 복잡한 일련의 과정을 수행해야만 한다. 그 중 몇몇 과정은 보다 손쉬운 자료 검색을 위해 데이터베이스를 재구성하는 것일 수도 있다. 어떤 데이터베이스에서는 검색속도를 높이기 위해 술어논리식들이 구분트리 (discrimination tree) 라는 구조로 저장되어 있다. 4 장 탐색에서는 구분트리에 대해 자세히 다룰 것이다.

때때로 데이터베이스에 저장되는 정보는 정리될 뿐만 아니라 보강되기도 한다. 예를 들어, 데이터베이스에 술어논리식 (precedes a b) 와 (precedes b c) 가 있다고 가정해보자. 선행 (precedes) 관계는 일반적으로 전이적 관계 (transitive relation) 로 나타내어진다. 원소쌍들 사이의 선행관계를 나타내는 식의 집합이 주어질 때 그 집합의 전이 닫힘 (transitive closure) 은 원래의 식에 전이성 (transitivity) 을 적용하여 얻어지는 식들을 모두 포함하는 집합이다. (precedes a b) 와 (precedes b c) 가 주어질 때 연역 검색시스템은 (precedes a c) 를 첨가하여 두 식의 전이 닫힘을 완성한다. 그 결과를 데이터베이스에 저장함으로써 시스템이 같은 정보를 반복적으로 이끌어내지 않도록 할 수 있다. 데이터베이스는 단순히 단조적으로 증가하지 않는다.

데이터베이스로부터 정보가 제거될 수도 있다. 그러므로 만약 어떤 자료에 의해 유도되는 결론들로 데이터베이스의 정보를 자동적으로 확장시킨다면, 그 자료가 제거될 때에는 그 자료에 의존하고 있는 결과들도 철회되어야 한다. 이 절의 후반부에서 자료 의존성 (data dependency) 을 다루는 방법에 대하여 고려해 보려고 한다.

전향 연결과 후향 연결

연역검색 시스템에서의 추론은 정보를 더하고 빼거나 질의어를 입력함으로써 시작한다. 전향 (forward) 과 후향 연결 (backward chaining) 은 연역검색 시스템에서 추론을 수행하는 기본 방식이다. 전형적인 전향 연결 규칙은 행동부 (action part) 와 조건부 (conditional part) 로 구성된다.

여기에서 Pi 는 행동 A 를 수행하기 전에 데이터베이스 내에 존재해야 하는 명제에 해당한다. 전향 연결 규칙에서 행동은 데이터베이스에 무엇인가를 첨가하거나 삭제하는 것 또는 Lisp 프로그램을 실행시키는 것까지도 해당한다.

후향 연결 규칙은 이미 소개된 바 있다. 목표 단순화 (goal reduction) 추론을 설명하는데 소개되었던 규칙들이 바로 후향 연결 규칙의 형태이다. 후향 연결에서 규칙

은 'Q 를 증명하려면 P1 ∧ … ∧ Pn 을 증명하면 된다' 와 같이 절차적으로 해석된다. 전향 추론에서는 똑같은 규칙을 '만약 P1 에서 Pn 까지를 데이터베이스에 추가하면 Q 도 데이터베이스에 추가하여야 한다' 와 같이 절차적으로 해석할 수 있다.

전향 연결과 후향 연결 규칙에 대하여 변수들을 사례화 (instantiate) 하기 위하여 단일화 (unification) 과정을 수행하게 된다. 연역검색 시스템은 연역이라는 이름으로 가장된 복잡한 계산들을 수행하는 데 사용된다. 가장 자주 수행되는 계산은 논리식 형태의 질문에 답하는 것 그리고 데이터베이스에 어떤 식을 첨가함으로써 유도되는 특정 결과들을 이끌어내는 것 등이다. 전자는 이 장의 앞에서 설명한 것과 같이 후향 연결의 형태로 다루어진다. 후자는 패턴지향 추론 (pattern-directed inference) 이라 하며 주로 전향 연결이 사용된다.

패턴지향 추론 시스템 (생성 [production] 시스템 또는 게시판 [blackboard] 시스템이라고도 함) 은 전향 연결에 의한 계산을 수행한다. 여기에서 계산은 데이터베이스에 하나의 식을 첨가함으로써 시작된다. 이 식은 데이터베이스에 있는 전향 연결 규칙의 선행항 (antecedent) 과 정합되고 데이터베이스의 다른 식들이 나머지 선행항과 정합될 때 새로운 결론들을 이끌어내게 된다.

예를 들어, 데이터베이스에 사실 (precedes b c) 와 규칙 ((precedes (? x) (? z)) if (precedes (? x) (? y)) (precedes (? y) (? z))) 가 있고 사용자가 (precedes a b) 를 주장 (assert) 하였다고 가정해보자. 이때 패턴지향 추론 시스템이 그러한 질의에 어떻게 대응할 것인지를 단계적으로 설명하겠다. 우선, 시스템은 (precedes a b) 를 규칙들의 선행항과 정합을 시도한다. 특히 이 시스템은 그 규칙의 첫번째 선행항에 대하여 다음과 같은 정합 결과를 얻어낸다.

이 결과인 치환값을 사용하여 규칙을 사례화한다. 그 사례화는 varsubst 함수에 의해 수행되는데, 그 결과 한정식 (quantified formula) 에 일련의 치환이 이루어진다. varsubst 함수는 이 장의 끝에서 연습문제로 주어진다.

그 다음에 시스템은 두번째 선행항에 대해 정합을 실시하여 그 규칙의 결과항을 결론으로 얻는다.

(precedes a b) 를 가지고 데이터베이스 내의 모든 규칙들에 대해 비교를 시도한 후 시스템은 마치 사용자가 하는 것처럼 모든 결론들을 하나씩 차례로 주장하게 된다. 시스템은 더 이상 새로운 주장이 생성되지 않을 때까지 이것을 반복한다. 패턴지향 추론 시스템에 대한 문헌을 살펴보면 이러한 과정을 신속하게 하기 위한 복잡한 기법들이 많이 소개되어 있다. 하나의 주장이 데이터베이스에 추가되면 일반적으로 수 많은 다른 주장들이 재귀적으로 추가되게 된다. 데이터베이스로부터 어떤 사실을 제거하는 일은 이보다 더 복잡하다.

논거유지 시스템

P 와 P ⊃ Q 가 데이터베이스에 있다는 사실에 근거하여 명제 Q 를 데이터베이스에 첨가한다고 가정해보자. 그렇다면 P 가 제거될 경우 Q 도 자동적으로 제거되는 방법이 있다면 매우 유용할 것이다.

좀더 일반적으로 말하면, 어떤 사실이나 규칙이 데이터베이스에 존재할 때 (또는 존재하지 않을 때) 어떤 식은 반드시 데이터베이스에 존재해야 한다는 것을 필수화할 수 있기를 바라는 것이다. 예를 들어, 로봇 프로그래밍에서 프로그래머는 모든 감각기기가 5 미터 이내에 아무 물체도 없다고 보고한다면 로봇은 최고 속도를 유지해야 한다고 명시할 수 있다. 논거유지 시스템 (reason maintenance system) 은 어떤 특정 사실과 규칙에 변화가 있을 때 이를 깨닫는 것에 대한 계산을 수행한다. 다음에서 간단한 논거유지 시스템에 대하여 설명하겠다.

의존 그래프 (dependency graph) 는 데이터베이스에 저장되는 항목들이 어떻게 서로 의존하고 있는지를 보여준다. 의존 그래프는 어떤 항목들이 데이터베이스에 실제로 저장되어 있는지를 추적하는 데 사용된다. 이를 효과적으로 하기 위하여 때로는 삭제되었거나 데이터베이스에 첨가된 적이 없었던 항목들도 참조해야 한다 예를 들어, 의존 그래프는 P 와 P ⊃ Q 가 데이터베이스에 있으면 Q 가 데이터베이스에 있어야 한다는 사실을 표현할 수 있다. IN 은 항목이 데이터베이스에 있음을 나타내고 OUT 은 데이터베이스에 없음을 나타낸다. 의존 그래프는 IN 이나 OUT 으로 표시된 노드들과 justification 이라 불리는 노드 사이의 연결로써 구성된다. justification 은 justifier 라고 하는 노드들의 집합을 justificand 는 하나의 노드에 연결시킨다.

그림 17 에는 justification 의 기본 형태가 나와 있다. 여기에서 노드는 사각형으로, justification 은 원으로 표시하고 있다. 전제 (premise) 는 justifier 를 갖지 않는 justification 의 노드이다 (그림 17a). 대부분의 justification 에는 하나 혹은 그 이상의 justifier 가 있으며 (그림 17b), 노드들은 종종 하나 이상의 justification 을 갖는다 (그림 17c). 

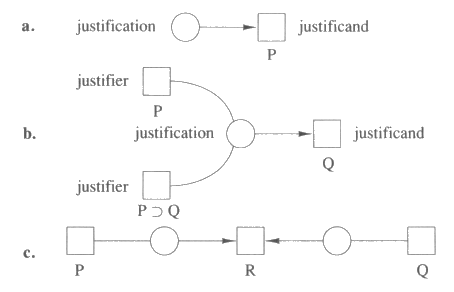
그림 17 : 전제와 justification

의존 그래프를 유지하기 위해 항목이 데이터베이스에 첨삭될 때마다 그래프의 노드에 정확히 표지 지정 (label assignment) 을 해 주어야 한다. 각 justification 에 대하여, 그 justification 의 모든 justifier 가 IN 일 때 그 justification 의 justificand 의 표지가 IN 이 되면 노드에 대한 표지 지정이 일관성있다 (consistent) 라고 한다. IN 으로 되어있는 모든 노드에 대하여, 그 노드를 justificand 로 하고 justifier 가 모두 IN 인 justification 이 최소 하나 존재한다면 그러한 표지 지정은 잘 갖추어졌다 (well-founded) 고 한다. 우리가 원하는 것은 의존 그래프의 모든 노드에 대하여 일관성 있고 잘 갖추어진 표지 지정을 계산할 수 있는 것이다.

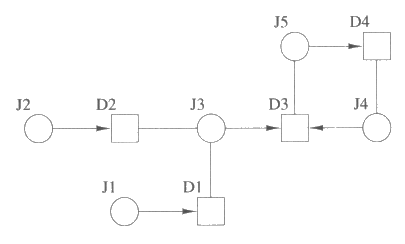
그림 18 : 순환적 자료 의존

순환적 (circular) 자료 의존성이 존재할 수 있다는 것을 주의하기 바란다. 예를 들어, 그림 18 과 같은 의존 그래프에서 모든 노드를 IN 으로 지정하면 일관성 있고 잘 갖추어진 지정이 된다. 여기서 justification J1 을 제거한다면 그 결과로 일관성있고 잘 갖추어진 표지 지정은 D2 에 IN 을 지정하고 다른 모든 노드에 OUT 을 지정하는 것이다.

의존 그래프의 일반적인 연산은 노드에 justification 을 첨가하고 삭제하는 것이다. 각각의 첨삭 후에는 일관성있고 잘 갖추어진 표지 지정을 계산하여 그래프를 변경시킨다. 의존 그래프의 변경은 두 개의 패스를 거치면서 이루어진다. 첫번째 패스에서는 이전의 표지가 모두 지워지고 그 노드를 방문했다는 표시를 한다. 두번째 패스에서는 새로운 표지가 지정되고 이러한 지정은 justification 을 따라 justifier 에서 justificand 로 확산된다.

의존 그래프가 각각의 첨삭 후에 변경된다고 가정하면 모든 노드를 변경할 것이 아니라 justification 을 따라 justifier 에서 justificand 로 의존 그래프를 거슬러 올라가면서 도달가능한 노드들만 변경시키면 된다. 다음의 알고리즘은 두 단계의 프로시저를 기술한다. 방금 노드 n 에서 justification 을 첨가하거나 삭제했다고 가정해보자.

비단조 자료 의존

앞에서 기술한 방법에 대하여 비단조적인 확장이 가능한데, 그 방법에서는 justification 의 justifier 가 IN justifier 와 OUT justifier 로 나뉘어진다. justification 의 justificand 가 IN 이 되기 위해서는 그 justification 의 모든 IN justifier 는 반드시 IN 이어야 하고 모든 OUT justifier 는 OUT 이어야 한다.

예를 들어, 모든 기술자들은 그가 특별히 이론적인 사람이라고 알려지지 않은 한 대체로 실용적인 성향을 갖는 것으로 여겨진다고 가정해 보자. 특정한 사람 p 에 대해 이 규칙은 그림 19a 와 같이 표현된다. 여기에서 + 로 표시된 노드는 IN justifier 이고 - 로 표시된 노드는 OUT justifier 이다. 그림 19a 는 engineer (p) 가 데이터베이스에 있고 theoretical (p) 가 데이터베이스에 없을 때 practical (p) 가 데이터베이스에 존재해야 한다는 사실을 명시하고 있다.

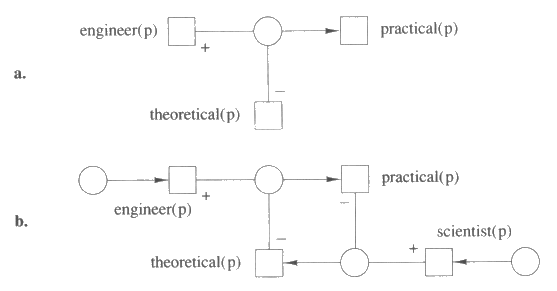
그림 19 : 비단조 자료 의존

비단조 자료 의존은 비단조 논리에서 발생하는 것과 똑같은 문제를 갖는다. 만약 당신이 모든 과학자들은 그가 특별히 실용적이라고 알려져 있지 않는 한 이론적인 성향을 갖는다고 믿고, p 는 기술자인 동시에 과학자라고 가정해 보자. 이 경우 비단조 논리의 디폴트 규칙에 대한 논의에서 발생했던 것과 같은 문제에 직면하게 된다. 그림 19b 의 의존 그래프는 그 노드들에 대하여 두 가지의 일관성 있고 잘 갖추어진 표지 지정이 있을 수 있다.

논거유지 시스템에는 여러 가지의 형태가 있고 그 각각은 저마다 특정 영역의 작업에 적합하도록 되어 있다. 여기에서는 그 기술과 이슈들에 대해 맛만 보았을 뿐이다. 논거유지 시스템은 사실과 규칙들로부터 유도되는 결론을 추적하여 이들 사실과 규칙에 변화가 생겨 더 이상 보장되지 않는 결론들을 자동적으로 철회한다. 어떤 경우에는 논거유지 시스템을 이용하여 연역검색 시스템이 똑같은 결론을 반복적으로 이끌어 내지 않도록 함으로써 검색 시스템의 성능을 향상시킬 수도 있다. 그러나 연역검색 시스템을 설계할 때 의존 그래프의 변경에 걸리는 시간 때문에 실제로 성능이 떨어지는 결과를 낳지 않도록 유의해야 한다.

▼ 요약

이 장은 실세계에 대한 지식을 표현하기 위해 논리를 어떻게 이용할 것인가에 대한 내용을 다루고 있다. 전문가 시스템에서 지식은 주로 인간 전문가에 의해 행해지는 작업을 수행하기 위해 사용되는 규칙의 형태로 표현된다. 대부분의 전문가 시스템은 그 기본 연산을 정당화하는 데 있어서 여러 가지 논리적 연산에 의존하고 있다.

명제논리는 명제변수와 명제논리 접속자들에 의해 표현될 수 있는 논리적 참에 대한 이론이다. 정규형태 (normal form) 는 데이터베이스에 지식을 명시함에 있어서 논리의 구문을 제한하는 하나의 약속으로 사용된다. 형식 체계 (formal system) 는 증명 구축을 위한 공리와 모두스 포넨스 (modus ponens) 와 같은 추론 규칙들을 제공한다. 증명 (proof) 이란 형식 체계의 공리와 추론 규칙을 따르는 일련의 추론 단계들을 말한다. 정리 (theorem) 는 증명 과정에서 한 단계의 결과를 말한다.

명제논리에 대한 의미론은 각 식에 대하여 참과 거짓을 지정하는 형태의 해석 (interpretation) 을 통하여 이루어진다. 어떤 식을 True 로 지정하는 해석이 존재하는 경우 그 식은 만족가능 (satisfiable) 하다. 하나의 명제가 만족가능한지 결정하는 것은 계산상으로 어려운 문제이다. 이러한 복잡성 때문에 논리에 근거한 표상을 설계할 때에는 양면성을 고려해야 한다.

직관적으로 말하면, 어떤 형식 체계가 증명할 수 있어야 하는 모든 것을 증명할 수 있으면 완전하다 (complete) 고 하고, 증명해선 안되는 것이 증명될 수 없을 때 이를 무결 (sound) 하다고 하며, 또 유한 개의 단계에서 어떤 식이 정리인지 아닌지를 결정할 수 있으면 결정가능하다 (decidable) 고 한다. 이론적으로는 어떤 형식 체계가 무결하고 완전하며 결정가능하기를 바라지만 실제에 있어서는 실세계에 대한지식 표현에 있어서 구문을 제한할 수밖에 없다.

술어논리는 명제논리에 함수, 변수, 한정자 (quantifier) 를 첨가하여 얻어진다. 술어논리에서는 무한정의 영역을 한정할 수 있도록 허용하고 유한의 영역에 대해서도 간결한 표상을 제공한다. 명제논리의 추론 규칙에 전체 사례화 (universal instantiation) 규칙을 첨가하여 한정식 (quantified formula) 이 포함된 정리를 증명할 수 있다. 정합 (matching) 과 단일화 (unification) 를 이용하여 한정식을 포함한 논리식의 자동 정리 증명에 필요한 전체 사례화를 수행할 수 있다.

설명기반 일반화 (explanation-based generalization) 란 연역적 추론에 근거한 자동학습 방법으로서 자동추론 시스템의 성능을 향상시키는 데 사용될 수 있다. 설명기반 일반화를 사용하는 시스템은 문제를 푼 뒤, 문제를 푸는 과정을 분석하고 이후의 문제 해결을 가속화시키는 표현방법을 이끌어낸다.

개념 기술 언어 (concept description language) 는 객체, 부류 그리고 객체와 부류의 속성에 대한 표현을 가능하게 한다. 의미망에서 작동하는 그래프 탐색 알고리즘은 개념 기술 언어에 적용되는 자동 정리 증명의 특수한 예이다. 술어논리의 진부분 집합만을 표현함으로써 개념 기술 언어는 표현력을 희생하는 대신 추론의 효율성을 얻는다.

단조 논리에서는 공리를 추가하게 되면 정리의 집합은 증가하기만 한다. 비단조 논리에서는 공리를 추가함으로써 이전에 인정되던 사실을 철회해야 할 수도 있다. 닫힌 세계 가정 (closed-worId assumption) 은 정보의 부재로부터 결론을 이끌어낼 수 있도록 하는 특정한 형태의 비단조 추론을 허용한다. 디폴트 추론과 진단 추론등을 포함하는 비단조 추론을 위하여 특수 형태의 추론 규칙이 사용되기도 한다.

연역검색 시스템은 논리 추론의 실용적인 방법에 대한 것이다. 이러한 시스템은 논리식 형태의 질문에 신속하게 답하기 위해 전향 연결, 후향 연결과 같은 전략을 사용한다. 연역검색 시스템에서는 때때로 데이터베이스에 정보를 첨삭하는 데 근거 (justification) 를 유지하기 위하여 논거유지 시스템을 사용한다.

2 장에서 Lisp 는 람다 계산법 (lambda calculus) 이라고 불리는 논리 (그리고 형식 체계) 에 근거하고 있다고 언급한 바 있다. 람다 계산법에 사용되는 두 개의 추론 규칙은 베타 단순화 (beta reduction) 과 람다 추상화 (lambda abstraction) 이다. 베타 단순화는 하나의 표현 식을 더 간단하게 축소시킨다. 예를 들면, 베타 단순화에 의해 (+ 2 3) 으로부터 5 를 얻는다. 람다 추상화는 어떤 부분식을 변수로 대신하는 람다함수를 생성함으로써 특정한 표현식으로부터 일반적인 프로시저를 추출한다. 예로서, (+ 2 3) 으로부터 람다 추상화를 통하여 (lambda (x) (+ x 3)) 을 얻을 수 있다. 부수 효과 (setq 와 defun 의 결과로 발생) 를 무시한다면 Lisp 해석기 (evaluator) 는 바로 추론 규칙을 적용하여 Lisp 표현식의 값을 결정하는 것으로 볼 수 있다. 이 장에서는 정리 증명을 통하여 어떻게 계산이 가능한가를 보임으로써 논리와 계산 사이의 밀접한 관계를 설명하고 있다.

● 배경

일반적인 전문가 시스템의 자세한 사항은 Jackson [1990] 을 참조하고 특히 MYCIN 전문가 시스템에 대해 더 알고 싶으면 Shortliffe [1976] 를 참조하기 바란다. MYCIN 은 주된 추론 방법으로 후향 연결을 사용한다. Davis [1982] 는 MYCIN 규칙의 방대한 데이터베이스를 취합하고 관리하는 자동화된 방법을 기술하고 있다. XCON 은 McDermott [1982] 에서 설명된다. Backer 와 O'Conner [1989] 는 XCON 의 효율성에 대해 흥미로운 산업 전망을 밝히고 있다. XCON 의 주된 추론 방법은 전향 연결이다. American Express 회사의 전문가 시스템의 자세한 사항은 Dzierzanowsk et. al [1992] 에 나와있다. 제조에서의 전문가 시스템의 응용은 Schorr 와 Rappaport [1989] 를 참조하기 바란다.

형식논리에 대한 일반적인 소개는 Mendelson [1979] 에 잘 나와 있다. 일관성, 완전성, 결정가능성 등 1 차 논리의 메타 이론에 대한 자세한 사항은 Hunter [1973] 를 참조하기 바란다. Manna 와 Waldinger [1983] 는 전산학도를 위한 매우 훌륭한 논리 입문서이다. Schagrin et. al [1985] 은 자동 정리 증명을 위한 프로그램과 함께 명제논리와 술어논리를 설명하고 있다.

논리융합 (resolution) 추론 규칙은 Robinson [1965] 에 의해 개발되었는데, 실용적인 자동정리 증명 시스템을 개발하는 데 있어서 핵심적인 역할을 하였다. 자동 정리 증명이 프로그램 분석과 합성에 응용되는 것에 대한 자세한 사항은 Chang 과 Lee [1973] 를 참조하기 바란다. Wos et. al [1984] 은 회로의 검사, 실시간 제어, 전문가 시스템 등에서 응용되는 자동 정리 증명 기법을 설명하고 있다. 설명기반 일반화 기법에 대한 소개는 Shavlik 과 Dictterich [1990] 의 4, 5 장에 나와 있다.

Prolog 에 대한 소개는 Bratko [1986], Clocksin 와 Mellish [1987], Sterling 과 Shapiro [1986] 에 나와 있다. Shoham [1994] 은 논거유지 시스템과 패턴지향 추론 (pattern-directed inference) 과 같은 Prolog 의 좀더 고급에 속하는 AI 프로그래밍 기술을 다룬다. Kowalski [1979] 는 자동화된 문제 해결에 논리를 이용하는 통찰력을 제공하고 있다. Brachman [1985] 에서는 의미망과 개념 기술 언어에 대한 이슈와 지식 표상과 관련된 쟁점들에 대한 개괄적인 내용을 다루고 있다. Minsky [1975] 는 개개의 객체에 대한 모든 지식을 모아 캡슐화 (encapsulate) 함으로써 표상을 구축하는 아이디어를 처음으로 제시하였고 그러한 표상이 계산적인 면에서도 이점이 있다는 사실을 인식한 것으로 인정받고 있다. Schank 와 Abelson [1977] 은 그러한 표상이 고수준의 인지능력을 설명하고 모의실험하는 데 있어서 어떻게 사용될 수 있는지를 제시하였다.

비단조 추론에 대하여 기본 기법의 개괄적인 설명은 Genesereth 와 Nilsson [1987] 이나Davis [1990] 에 잘 나와있다. 이 책에서 다룬 디폴트 추론 규칙은 Reiter [1980] 의 이론에 근거한 것이며 해석들 사이의 선호도 (preference) 는 Shoham 의 선호 의미론 (preferential semantics) [1986] 에 근거하고 있다. 이 분야의 초석이라 할 수 있는 초기의 논문들, 특히 McCarthy 의 circumscription 이론 [1980], McDermott 과 Doyle 의 비단조 양상논리 [1980] 등을 읽는 것도 많은 도움이 될 것이다.

Charniak et al [1987] 은 여러 형태의 연역 추론 시스템과 논거유지 시스템 (이 문헌에서는 진리 유지 시스템 [truth maintenance system] 이라 함) 을 Lisp 로 구현하는 방법을 기술하고 있다. Forbus 와 Kleer [1994] 는 연역 추론 시스템에 대하여 심도있게 다루고 있는데, 특히 논거유지 시스템에 대하여 자세히 기술하고 있다. Waterman 과 Hayes-Roth [1978] 전향 연결을 사용하는 패턴지향 추론에 대한 논문들을 한데 모아 편집하였다.

▶ Lisp 구현

자료 의존

이 장에서는 자료 의존 그래프를 생성하고 변경하는 Lisp 프로그램을 설계해 보겠다. 우선 자료 의존 그래프를 나타내기 위한 자료구조를 살펴보자.

추상 자료형 node 는 name, label (IN 혹은 OUT, justification 리스트 그리고 그 노드가justify 하는 노드들의 리스트로 구성된다.

node 애서 name 을 제외한 모든 요소는 지정가능 (settable) 한데 name 은 node 의 사례가 생성될 때 명시된다.

기존 의존 노드에 justification 을 첨가한다.

기존의 의존 노드로부터 justification 을 제거한다. remove 함수와 :test 인자의 선택 사양에서 equal 함수를 이용한 검색을 실시하여 justification 들의 리스트에서 justification 을, justificand 들의 리스트에서 justificand 를 제거한다. 이 간단한 방법은 몇 가지 제한 사항이 있는데 이 장의 연습문제에서는 이를 극복하는 방법에 대하여 묻고 있다.

의존 그래프를 node 로부터 시작하여 두 패스를 거치며 변경한다. 첫번째 패스에서는 모든 도달 가능한 노드에 대하여 기존의 명칭을 지우고 이들을 visited 라고 새로운 명칭을 붙인다. 두번째 패스에서는 모든 도달 가능한 노드들에 대하여 새로운 명칭을 지정한다.

node 로부터 시작하여 justifier 에서 justificand 방향으로 justification 을 탐색해 나가며 node 로부터 도달가능한 모든 노드에 대하여 visited 라는 명칭을 붙인다.

node 로부터 시작하여 justifier 에서 justificand 방향으로 justification 을 탐색해 나가며 명칭을 확산시켜 나간다. 만약 node 의 명칭이 바뀌어질 필요가 없을 때 명칭의 확산을 멈춘다.

만약 어떤 노드가 그 justifier 가 모두 IN 으로 명칭된 justification 을 가질 때 그 노드는 IN 으로 명칭되어야만 일관성을 갖는다. 만약 그렇지 않은 경우에는 OUT 으로 되어야 한다. 2 장에서 설명한 바와 같이 every 와 some 은 그 형태나 연산에서 mapcar 함수와 유사하다. (every test args) 를 부르게 되면, 만약 args 모두에 대하여 test 를 적용한 것이 non-nil 일 때 t 가 되고 그렇지 않으면 nil 을 되돌려 보낸다. (some test args) 를 부르게 되면, 만약 args 의 어떤 것들에 대하여 test 를 적용한 것이 최소 하나가 non-nil 일 때 t 가 되고 그렇지 않으면 nil 을 되돌려 보낸다.

justification 의 모든 justifier 가 IN 인가를 확인하는 함수는 다음과 같다.

이 코드들을 이용하여 그림 18 의 의존 그래프를 만들 수 있고 또 본문에 주어진 예를 이용하여 검증해 볼 수 있다.