
논리 와 정리 증명
(Logic and Theorem Proving)
인공지능 : Patrick Henry Winston 저서, 황종선.정태충 공역, 생능출판사, 1990 (원서 : Artificial Intelligence, 2nd ed, Addison Wesley, 1987, 참고 : Artificial Intelligence 3rd ed), Page 245~294
(3) 해석 (Interpretation) 은 논리 기호를 세계와 연관시킨다.
(2) 레졸루션을 사용하려면 공리들을 절의 형태 (clause form) 로 바꾸어야 한다.
(4) 레졸루션은 단일화 (Unification) 를 요구한다.
(5) 전통적인 논리는 단조적 (monotonic) 이다.
(6) 정리 증명은 모든 것에는 아니지만 어떤 문제들에 대하여 적당하다.
(1) 연산자 순서를 발견하기 위해서는 상황 변수를 필요로 한다.
(2) 프레임 (frame) 공리는 프레임 문제를 다룬다.
4. 제한 조건 전파 (constraint propagation) 에 의한 증명
(2) 진리값 전파는 정당성 (justification) 을 발견할 수 있다.
논리는 하나의 강력한 문제 해결 모범 예 (paradigm) 라 할 수 있다. 다른 방법들처럼 논리는 매혹적인 장점들과 지루한 단점들도 모두 갖고 있다.
긍정적인 면에서는 수세기 동안 성숙되어온 논리에 대한 사상은 라틴어처럼 간결하고 (concise) 일반적으로 이해된다. 더욱이 최근까지 논리 학자들은 우리가 지식으로 할 수 있는 모든 것에 관한 것들을 증명하는데 촛점을 맞춰 왔다. 따라서 문제의 범위가 수학의 어떤 것들처럼 논리에 의해 성공적으로 공략이 가능할 때, 우리에게 허락되는 것으로서 우리가 해결할 수 있는 것에 대한 한계들을 알 수 있으므로, 우리는 운이 좋다.
부정적인 면에서는 논리가 억지로 규범에 맞추려는 것 (procrustean bed) 일 수 있는데, 이는 논리에 집중하다 보면 수학적 분석과 틀리지만 가치있는 문제해결 기법을 간과하게 되 는 것이다.
이런 문제점들을 보다 잘 이해하기 위해서,이 장에서는 표기법 (notation) 과 증명에 대한 방법과 추론 규칙 (rules of inference) 즉 기존의 표현들 (expressions) 로부터 새로운 표현을 만들 수 있도록 해주는 모더스 포넨스 (modus ponens), 모더스 톨렌스 (modus tolens) 와 레졸루션 (resolution) 을 소개한다. 그리고 레졸루션을 이용해서 반박에 의한 증명 (proof by refutation) 과 레졸루션 정리 증명을 설명한다.
다음으로 논리에 연산자를 소개함으로써 논리기반 계획 (logic based planning) 을 가능하게 하지만 어려움도 만들게 된다. 어려움의 예로서 다양한 연산자가 적용되어도 유지되는 표현을 구분하는 방법이 있어야 한다. 이것을 후레임 (frame) 문제라 한다.
마지막으로, 레졸루션 정리 증명은 강력한 반면에 제한 조건 전파를 이용한 증명 (proof using constraint propagation) 은 때때로 더 나은 방법일 수 있다. 제한 조건 전파는 여전히 참 (True) 인 산술식을 없애 버리지 않고 단순히 상관되는 가정들 (assumptions) 을 철회할 수 있게 하므로 정당성 (justification) 을 쉽게 유지할 수 있도록 해 준다. 이것은 3 장에서 처음 보았던 종속성을 이용한 (dependency-directed), 비연대기적 백트랙킹 (non-chronological backtracking) 을 회상하게 한다.
초보자들에게 논리란 어려운 것인데 이는 새로운 개념의 갑작스런 출현 때문이다. 이것이 논리 용어로서 표현하는 것들이 보다 더 엄밀함에도 불구하고 다른 장들에서 논리의 용어로 표현하기를 회피한 이유이다. 어려운 개념들을 결합하면 이해에 방해가 된다.
똑같은 이유로 이 장에서는 사람들이 충분히 자신의 직관으로도 이해되도록 하기 위해서 매우 간단한 예제들을 가지고 논리의 중심 개념들이 설명된다. 예제들은 어떤 관계가 다른 관계들 (relations) 로부터 어떻게 추론되고, 목표를 달성하기 위해 일련의 연산들이 어떻게 유도되는가를 보여줄 수 있는 블럭 세계 (block world) 에 한정한다.
어떤 대상이 깃털을 가지거나 날고 알을 낳는다면 그것이 새라는 것을 안다. 이들 사실들은 6 장에서의 전제 귀결 규칙 (antecedent-consequent rules) 의 형태로 다음과 같이 표현된다.
|
|
I3 |
If |
동물이 깃털을 가지면 |
|
|
|
then |
그것은 새다 |
|
|
I4 |
If |
동물이 날고 |
|
|
|
then |
그것은 새다 |
이러한 전제 귀결 규칙을 이용하는 것이 단지 논리를 이용하는 특별한 경우에 불과함을 알 것이다.
논리에 있어서 깃털과 새에 관계되는 전제 귀결 규칙의 의미를 표시하기 위하여, 우리는 어떤 것이 깃털을 갖고 어떤 것이 새라는 관념을 표현할 방법을 가져야 한다. 이것은 술어 (predicate) 를 이용함으로써 가능한데, 왜냐하면 술어는 대상 인수들 (arguments) 을 참 또는 거짓의 값으로 사상시키는 함수이기 때문이다.
예를 들어서 Albatross 라는 대상과 Feathers 와 Bird 라는 술어를 해석해주는 정상적인 방법을 가지면 비공식적으로 다음의 표현이 참임을 말할 수 있다.
Feathers (Albatross)
Bird (Albatross)
또한 다음의 표현이 참이다 라고 할 때 의미하는 것을 생각해 보자.
Feathers (Squigs)
명백히 Squigs 는 Feathers 라는 술어를 만족하므로, 깃털을 갖는 어떤 것을 표시하는 상징이다. 따라서 Squigs 가 지칭할 수 있는 것에 제한 사항을 갖는다. Flies 와 Lay-eggs 와 같은 다른 술어들로 또 다른 제한 사항을 표시할 수 있다. 실제로 다음과 같은 두개의 식이 참이라고 말함으로써 두 개의 술어 모두를 만족하는 것들에 대해서만 Squigs 라고 지칭할 수 있게 제한할 수 있다.
Flies (Squigs)
Lays-eggs (Squigs)
그렇지만 그 관념을 표현하는 보다 전통적인 방법이 있다. 단순히 첫째식과 둘째식을 결합해서 그 조합이 다음과 같이 참이라고 말한다.
Flies (Squigs) and Lays-eggs (Squigs)
물론 두 술어 중 하나를 만족하는 어떤 것의 이름으로 Squigs 를 해석해야 한다고 말할 수 있다. 이것은 다음과 다음 조합을 사용함으로써 가능하다.
Flies (Squigs) or Lays-eggs (Squigs)
그러나 논리학자들은 명확히 다른 표기법을 선호한다. 그들은 & 로서 and 를 ∨ 로서 or 를 기록하기를 좋아한다.
이제 우리는 다음과 같이 논리학자들이 사용하는 것과 유사한 것으로 표시할 수 있다.
Flies (Squigs) & Lays-eggs (Squigs)
Flies (Squigs) ∨ Lays-eggs (Squigs)
식들이 & 로 결합될 때 논리곱 (conjunction) 을 형성하고 각 부분은 논리곱 요소 (conjunct) 라 부른다. 이와 유사하게 식이 ∨ 로 결합될 때 논리합 (disjunction) 을 형성하고 각 부분을 논리합 요소 (disjunct) 라 부른다.
& 와 ∨ 를 논리적 연결자 (logical connectives) 라 부르는데 이는 참과 거짓의 조합을 참과 거짓으로 사상 (mapping) 시키기 때문이다.
& 와 ∨ 에 부가해서 두 개의 보조적인 필수 연결자가 있는데 하나는 ¬ 로 표기하는 부정 (not) 이고 다른 하나는 ⇒ 로 표기하는 의미 함축 (implies) 이다. 다음을 보자.
¬ Feathers (Suzie)
이 식이 참이므로 Suzie 는 Feathers (Suzie) 가 참이 아닌 어떤 것을 표시해야 한다. 즉 Suzie 는 Feathers 술어를 만족시키지 못하는 (not satisfied) 어떤 것임에 분명하다.
관심을 ⇒ 사용법으로 옮겨 보자. 전제 귀결 규칙과 닮은 하나의 표현을 쓸 수 있다. 즉,
Feathers (Suzie) ⇒ Bird (Suzie)
이 식의 값이 참이라 함은 Suzie 가 표시할 수 있는 것을 제한한다. 허용될 수 있는 한 가지 가능성은 Suzie 가 Feathers (Suzie) 와 Bird (Suzie) 라는 두 식 모두가 참이게 하는 어떤 것이다. 본래 ⇒ 의 정의는 또한 Feathers (Suzie) 와 Bird (Suzie) 두 식이 거짓인 것도 허용한다. 기묘하게도 ⇒ 의 정의로서 허용되는 다른 가능성은 Feathers (Suzie) 가 거짓이나 Bird (Suzie) 가 참일 때이다. 그러나 만일 Feathers (Suzie) 가 참이고 Bird (Suzie) 가 거짓이면 식 Feathers (Suzie) ⇒ Bird (Suzie) 는 거짓이다.
아마도 더 늦기 전에 연결자들인 ⇒, &, ∨ 그리고 ¬ 에 대해 보다 엄밀한 정의가 필요할 것이다. 함수로서 이들을 고찰해보면 각 변수의 가능한 조합에 대해 승인된 값을 열거해 봄으로써 정의하면 쉽다. 이것은 진리표 (truth table) 를 이용해서 그림 1 에 나타내었다.

그림 1 : 몇 개의 기본적인 연결자에 대한 진리표
연결자들은 공인된 우선 순위 (precedence) 를 갖는다는 것을 명심하라. 일반적인 산술식에서 단항 (unary) 연산자 - 기호는 + 기호보다 높은 우선 순위를 갖고 - a + b 라고 쓰면 이것은 - (a + b) 가 아니라 (- a) + b 를 의미한다. 이와 유사하게 ¬ 는 ∨ 보다 높은 우선 순위를 가지므로 ¬ E1 ∨ E2 라고 쓰면 이것은 ¬ (E1 ∨ E2) 라는 혼란의 가능성없이 (¬ E1) ∨ E2 를 의미한다.
공인된 우선 순위를 보면 "¬" 이 제일 높고 다음이 & 와 ∨ 이고 ⇒ 의 순이다. 명확하게 하기 위해서 괄호를 사용하는 것은 좋은 습관이다.
⇒ 에 대한 진리표의 정의에서 E1 ⇒ E2 의 값이 E1 과 E2 에 대한 값의 모든 조합에 대하여 ¬ E1 ∨ E2 의 값과 똑같다는 것을 명심하라. 따라서, 더욱 중요한 것은 언제든지 ¬ E1 ∨ E2 은 E1 ⇒ E2 로 대체할 수 있고 그 역도 성립한다. 역이 성립 가능한 규칙은 다음과 같이 이중화살표 (⇔) 를 사용해서 표시한다.
E1 ⇒ E2 ⇔ ¬ E1 ∨ E2
진리표는 논리 연결자에 대한 다른 유용한 성질들도 보여준다. 그 성질들은 완벽성을 기하기 위하여,그리고 가끔 사용하기 때문에 여기에 몇 개 열거한다. 첫째로 & 와 ∨ 연결자들은 교환적 (commutative) 이다.
즉, E1 & E2 ⇔ E2 & E1
E1 ∨ E2 ⇔ E2 ∨ E1
둘째로 이들은 배분적 (distributive) 성질을 갖는다.
E1 & (E2 ∨ E3) ⇔ (E1 & E2) ∨ (E1 & E3)
E1 ∨ (E2 & E3) ⇔ (E1 ∨ E2) & (E1 ∨ E3)
덧붙여서 같은 연결자의 경우 이들은 연관적 (associative) 이다.
E1 & (E2 & E3) ⇔ (E1 & E2) & E3
E1 ∨ (E2 ∨ E3) ⇔ (E1 ∨ E2) ∨E3
이들은 드모르강의 법칙 (de Morgan's laws) 을 따른다.
¬ (E1 & E2) ⇔ (¬ E1) ∨ (¬ E2)
¬ (E1 ∨ E2) ⇔ (¬ E1) & (¬ E2)
마지막으로, 두 개의 ¬ 은 각각을 상쇄시킨다.
¬ (¬ E1) ⇔ E1
한정사 (Quantifier) 들은 사물들이 참일 때 (when) 를 결정한다.
우리가 시작한 전제 귀결 규칙이 모든 가능한 것에 대해 참이라 가정하자. 식이 범용적으로 (universally) 참임을 표시하기 위해 가능한 것이 놓일 변수뿐만 아니라 'for all' 을 의미하는 심볼로서 ∀ 를 사용할 필요가 있다. 다음 예에서 식이 참일 때, 이 식은 깃털을 갖는 어떤 것도 새임을 말한다.
∀x [Feathers (x) ⇒ Bird (x)]
다른 식들과 마찬가지로 ∀x [Feathers (x) ⇒ Bird (x)] 는 참이거나 거짓일 수 있다. 참이라면 ∀ 표기는 대괄호 내에 있는 x 에 어떤 것이 대체될지라도 참인 식을 얻을 수 있음을 의미한다. 예를 들어서 식 ∀x [Feathers (x) ⇒ Bird (x)] 가 참이면 확실히 식 Feathers (Squigs) ⇒ Bird (Squigs) 도 참이고 Feathers (Suzie) ⇒ Bird (Suzie) 도 참이다.
하나의 식이 한정사로 연관된 대괄호로 싸여져 있을 때, 그 식은 그 한정사의 영역 (scope)에 놓여 있다고 말한다. 따라서 식 Feathers (X) ⇒ Bird (X) 는 한정사 ∀x [ ] 의 영역에 있다.
∀ 로 시작되는 참인 식은 그들의 영역내에서 그 변수에 대한 모든 가능한 대체물에 대한 것을 말하기 때문에, 그 식들은 범용적으로 한정된다 (universally quantified) 고 말한다. 따라서 ∀ 을 범용 한정사 (universal quantifier) 라고 부른다.
항상 참은 아닌 어떤 식들은 적어도 어떤 것에 대해서는 참이다. 논리는 이들 역시도 포함한다. 이들은 다음과 같이 ∋ 로 쓰여지는 'there exists' 의미를 나타내는 기호를 사용해서 다음과 같이 표시된다.
∃x [Bird(x)]
이 식이 참일 때, 이것은 대괄호 내부의 식을 참으로 만드는 적어도 한가지의 가능한 x 에 대체될 대상이 존재함을 뜻한다. 아마도 Bird (squigs) 가 참이면 Bird (Squigs) 와 같은 식을 만족시키는 어떤 것이 존재하므로 그 식은 참이다.
∃ 를 갖는 식은 존재적으로 한정된다 (existentially quantified) 고 말한다. ∃ 기호를 존재 한정사 (existential quantifier) 라 부른다.
논리의 한 가지 문제점은 정연하게 유지하기 위한 어휘 (vocabulary) 가 상당히 많다는 것이다. 참고로 그림 2 와 다음의 정의에 의해 이제 그 단어의 공통적 원소를 모아 완전하게 해 보자.
• 한 영역의 객체들 (domain's objects) 은 항 (term) 이다.
• 한 영역의 객체들에 범위를 둔 변수들은 항이다.
• 함수들은 항이다. 함수에 대한 인수들 (arguments) 과 반환되는 값들은 대상 (object) 이다.

그림 2 : 논리의 어휘 비공식적으로 말해 예제 정형식 (well-formed formula) 은 다음을 의미한다. 즉, 특정한 객체 A 와 지정되지 않은 객체 X 가 술어 On 을 만족한다면 X 는 함수 support 를 객체 A 에 적용할 때 반환되는 값과 같음을 내포한다 (imply).
항들 (terms) 은 술어 (predicates) 에 대한 인수 (arguments) 로서 나타나는 유일한 것이다.
• 기초 공식 (Atomic formulas) 은 인수들을 갖고 있는 술어 각각을 말한다.
• 리터럴 (literals) 은 기초 공식과 부정된 (negated) 기초 공식이다.
• 약자 WFFS 로 일반적으로 언급되는 정형식 (well-formed formula) 은 자기 호출적으로 (recursively) 정의된다. 즉 리터럴은 WFFS 이고 ¬, &, ∨ 그리고 ⇒ 등으로 연결된 WFFS 는 WFFS 이고 한정자로 둘러싸인 WFFS 는 역시 WFFS 이다.
WFFS 에 대하여 다음과 같은 몇 가지의 특별한 경우가 있다.
• 모든 변수가 대응하는 한정사의 영역 내에 있는 하나의 WFF 는 하나의 문장 (sentence) 이다. 다음은 문장들이다.
∀x [Feathers (x) ⇒ Bird (x)]
Feathers (Albatross) ⇒ Bird (Albatross)
대응하는 한정사는 범위내에 나타나는 x 와 같은 변수들은 한정되어 (bound) 있다고 말한다. 한정되지 않는 변수들은 자유 (free) 변수이다. 다음의 식은 문장이 아닌데 자유변수 y 를 포함하기 때문이다.
∀x [Feathers (x) ∨ ¬ Feathers (y)]
변수들은 단지 객체들만을 표현한다는 것을 절대 명심하라. 특별히 술어를 나타내는 변수를 금지한다. 따라서 일차 술어 논리 (first-order predicate calculus) 라고 하는 종류의 논리를 다루고 있다. 더욱 진보된 주제인 이차 술어 대수 (second-order predicate calculus) 를 나타내는 변수를 취급한다. 덜 진보적인 주제인 명제 대수 (propositional calculus) 는 어떤 종류의 변수도 허용치 않는다.
• 리터럴들의 논리합으로 구성된 WFF 는 절 (clause) 이다.
일반적으로 WFF 란 말 대신에 표현식 (expression) 이란 말을 사용할 것인데, 왜냐하면 WFF 를 많이 사용하다 보면 핵심에 관해서라기 보다는 논리에 대해 생각하기가 더 어렵기 때문이다.
궁극적으로 논리의 요점은 어떤 상상이 가능한 세계에 관한 어떤 것을 말하는 것이다. 따라서 객체와 술어 그리고 함수를 보다 명백한 것에 연관시켜야 한다. 그림 3 의 예가 보여주듯 세 개의 논리 기호 범주가 이 세상 영역과 대응한다. 즉
• 어떤 영역 내의 객체는 논리에 있어서의 객체 기호와 대응한다. 그림 3 의 예에서 보듯이 왼쪽의 객체 기호 A 와 B 는 오른쪽에 나타난 상상이 가능한 세계에 있는 두 개의 객체와 대응한다.
• 어떤 영역 내의 관계는 논리에 있어서의 술어에 대응한다. 관계가 어떤 객체에 관한것을 가질 때마다 대응하는 술어를 대응하는 객체 기호에 적용될 때 그 술어는 참이다. 예에서 객체 기호 B 와 A 에 적용된 논리 세계 술어인 On 은 참인데, 상상의 세계에서 위에 있다 라는 (On) 관계가 두 개의 객체 사이에 유지되기 때문이다.
• 어떤 영역내의 함수는 논리에 있어서의 함수에 대응한다. 영역내의 함수는 영역 객체 (domain object) 에 적용될 때 영역 객체를 반환한다. 논리에서 대응하는 함수는 대응하는 논리 심볼에 적용될 때 논리 심볼을 반환한다. 예에서 논리 세계 함수인 on-logic-function 은 객체 심볼 B 를 객체 심볼 A 에 사상하는데 이는 상상이 가능한 세계의 함수인 on-world-function 이 해당되는 객체 사이에 대응하는 사상을 하기 때문이다.
해석 (interpretation)은 객체와 객체 기호, 관계와 술어, 객체 함수와 객체 기호 함수사이에 대응되는 것을 충분히 설명하는 것이다.
.gif)
그림 3 : 해석 (interpretation) 은 어떻게 객체와 관계 그리고 함수가 객체, 기호, 술어 및 함수에 사상되는가에 대한 계산이다.
이제 증명에 대한 개념을 다룰 때가 되었다. 다음과 같은 두 개의 식이 참이라고 가정해 보자.
Feathers (Squigs)
∀x [Feathers (x) ⇒ Bird (x)]
해석의 개념을 이해했으므로 그런 식이 참이라고 말하는 것이 무엇을 뜻하는지를 이해한다. 즉 그것은 내포된 상상가능한 세계 관계가 갖고 있는 것들에 대한 객체 기호들, 술어들, 그리고 함수의 해석을 제한하고 있다는 것을 의미한다. 식을 참으로 해주는 어떠한 해석도 그 식에 대한 모델 (model) 이라 말한다.
Feathers (Squigs) 와 ∀x [Feathers (x) ⇒ Bird (x)] 가 참이라고 했으므로 이것들을 공리 (axioms) 라고 부른다. 이제 그 공리들을 참으로 하는 모든 해석은 또한 다음의 식을 참으로 만든다는 것을 입증하기를 요구받았다고 가정하자.
Bird (Squigs)
성공한다면 Bird (Squigs) 가 그 공리들의 관점에서 정리 (theorem) 임을 증명했다고 말할 수 있다.
• 간단히 말하면 참인 공리가 참으로 주어지고, 정리가 참임에 틀림없다고 보여 줄 (show) 때 식이 정리임을 증명하는 것이다.
• 가장 공상적인 용어로 말하면 공리에 대한 어떤 모델이 또한 정리에 대한 모델임을보일 때 이 식이 정리임을 증명한 것이다. 그 정리가 공리로부터 논리적으로 따른다 (logically follows) 고 말한다.
정리를 증명하는 방법은 증명 프로시저 (proof procedure) 를 이용하는 것이다. 증명 프로시저는 앞선 표현식을 참으로 하는 모델이 그 식으로부터 유도된 새로운 표현식을 역시 참으로 만든다고 보증하는 유도 방법인 건전한 (sound) 증명 규칙 (rulee of inference) 을 이용한다. 따라서 가장 쉬운 증명 프로시저는 원하는 정리가 나타날 때까지 건전한 추론 규칙을 공리와 적용된 공리의 결과들에 적용하는 것이다.
일반적으로 다른 식들이 참으로 주어질 때 한 표현식인 정리가 참임을 보이기 위하여, 모델에 기초한 방법보다 증명 프로시저를 이용하여 생각할 것이다.
정리를 증명하는 것은 식이 모든 가능한 심볼의 해석에 대해서 참임을 의미하는 유효할 (valid) 을 보이는 것과 똑같지는 않다는 것을 명심하라. 이와 유사하게 정리를 증명하는 것은 식이 심볼의 몇 가지 가능한 해석에 대해 참임을 의미하는 만족가능함 (satisfiable) 을 보이는 것과 똑같지도 않다.
증명 프로시저에 사용되는 가장 직접적인 건전한 추론 규칙은 모더스 포넨스 (modus ponens) 이다. 모더스 포넨스는 다음과 같이 말할 수 있다. 즉 E1 ⇒ E2 란 형태의 공리가 존재하고 E1 이란 형태의 다른 공리가 존재한다면 E2 는 논리적으로 따른다.
만일 E2 가 증명될 정리이면 증명은 이루어진 것이다. 그렇지 않다면 E2 를 공리에 추가하는 것이 좋은데 왜냐하면 나머지 모든 공리들이 참일 때 항상 참이 될 것이기 때문이다. 점증하는 공리 목록에 모더스 포넨스로 계속 적용할 때 결국은 원하는 정리가 참임을 보일 수 있고, 따라서 정리를 증명한 것이다.
앞에서의 Feather-and-bird 예제는 바로 모더스 포넨스의 응용에 적합하다. 그러나 먼저 두번째 식을 특정화 (specialize) 해야 한다. ∀x [Feathers (x) ⇒ Bird (x)] 라는 식이 있다. 그 식은 모든 x 에 대하여 Feathers (x) ⇒ Bird (x) 가 참이므로 x 가 Squigs 인 특별한 경우에 대하여도 참이어야 한다. 따라서 Feathers (Squigs) ⇒ Bird (Squigs) 는 참이어야 한다.
이제 첫째식인 Feathers (Squigs) 와 두번째 식의 특정화된 형식인 Feathers (Squigs) ⇒ Bird (Squigs) 에 모더스 포넨스를 적용하면 E1 대신에 Feathers (Squigs) 및 E2 대신에 Bird (Squigs) 를 대치할 수 있고, 따라서 우리는 Bird (Squigs) 가 참이어야 한다는 결론을 얻는다. 따라서 그 정리는 증명되었다.
아마도 지금이 중요한 어떤 것에 대하여 말할 때가 되었다. 정리를 만들기 위해 증명프로시저를 사용하는 것은 어떤 내재된 식의 의미에 의한 것이 아닌 구문론적인 동작 (syntactic activity) 이다. 실제 세계가 아닌 어쩌면 우스울 수 있는 상상가능한 세계에 대해서 논하고 있다. 공리는 우리들의 진실감과 맞지 않을 수도 있다. 우리의 세계에서 Squigs 는 깃털을 갖지 않을 수 있다. 그리고 새가 아니면서 깃털을 가진 것들이 있다. 이것에 혼란되지 말라. 요점은 공리가 우리가 믿는 것에 대응하는 것이 아니라 정리가 공리들로부터 논리적으로 따른다는 것을 보여주는 것이다.
추론의 가장 중요한 규칙 중의 하나는 레졸루션 (resolution : 도출 연역, 비교 추론) 이다. 레졸루션이란 다음과 같다. E1 ∨ E2 형태의 공리와 ¬ E2 ∨ E3 란 형태의 다른 공리가 존재하면 E1 ∨ E3 는 논리적으로 따른다. 식 E1 ∨ E3 를 E1 ∨ E2 와 ¬ E2 ∨ E3 의 도출절 (resolvent) 이라 부른다.
레졸루션이 믿을만한 것인지 보이기 위해서 다양한 가능성에 대해 고찰해보자. 첫째로 E2 가 참이라고 가정하면 ¬ E2 는 거짓이어야 한다. 그러나 ¬ E2 가 거짓이면 두번째 식으로부터 E3 는 참이어야 한다. 그러나 E3 가 참이면 확실히 E1 ∨ E3 는 참이다. 둘째로 E2 가 거짓이라고 가정해보자. 그러면 첫째식으로부터 E1 은 참이어야 한다. 그러나 E1 이 참이므로 확실히 E1 ∨ E3 는 참이다. 따라서 도출절인 E1 ∨ E3 는 E1 ∨ E2 와 ¬ E2 ∨ E3 가 참인 한 참이어야 한다는 결론을 얻는다.
두 개의 레졸루션되는 식들에 하나 이상의 여러 개의 논리합 요소가 존재할 때의 레졸루션으로 일반화하기란 쉽다. 유일한 요구 사항은 한 레졸루션할 표현식이 다른 레졸루션할 표현식에 있는 논리합 요소 (disjunct) 의 부정인 논리합 요소를 가져야 한다는 것이다. 일단 일반화되면 모더스 포넨스에 의해 도달한 Squigs 에 관한 똑같은 결론에 도달하기 위해서 우리는 레졸루션을 이용할 수 있다.
첫번째 단계는 다시 Squigs 에 정량화된 식을 특정화하는 것이다. 그 다음 단계는 그 식에서 ⇒ 를 얽앤 형태로 다시 쓰면 다음과 같은 식을 생성한다.
Feathers (Squigs)
¬ Feathers (Squigs) ∨ Bird (Squigs)
이렇게 쓰여졌을 때 레졸루션을 적용하면 Feathers (Squigs) 와 ¬ Feathers (Squigs) 는 떨어지고 Bird (Squigs) 가 생성된다.
사실상 이 예는 일반적인 진리를 암시한다. 즉 모더스 포넨스는 레졸루션의 특별한 경우로 관찰될 수 있는데 이는 모더스 포넨스로 얻은 어떤 결론도 마찬가지로 레졸루션으로 결론을 얻을 수 있기 때문이다. 그 이유를 보기 위해서 한 식을 E1, 다른 식을 E1 ⇒ E2 라 하자. 모더스 포넨스에 따라서 E2 는 참이어야 한다. 그러나 우리는 E1 ⇒ E2 는 ¬ E1 ⇒ E2 로 다시 쓸 수 있다는 것을 알고 있다. 그래서 다시 쓰면 레졸루션이 적용되고 E1 과 ¬ E1 이 제거되어 E2 가 생성되는데 이것은 모더스 포넨스를 이용해서 얻은 결과와 똑같다.
이와 유사하게 리졸루션은 명백히 모딕스 톨렌스라고 하는 추론의 또 다른 규칙을 포함한다. 모더스 톨렌스는 다음과 같이 말할 수 있다. 즉 E1 ⇒ E2 라는 형태의 공리와 ¬ E2 란 형태의 또 다른 공리가 존재하면 ¬ E1 은 논리적으로 따른다.
정리 (theorem) 를 증명하기 위한 명백한 전략은 결국 정리를 우연히 도출하기를 희망하며 건전한 추론 규칙을 공리들에 적용하여 찾아내는 것이다. 레졸루션 정리 중명에 사용되는 것으로서의 또 다른 전략은 정리의 부정이 참이될 수 없음을 입증하는 것이다.
즉,
• 정리의 부정이 참이라고 가정한다.
• 공리와 그 정리의 가정된 부정이 모두 참이 될 수 없음을 보인다.
• 그 정리의 가정된 부정이 모순 (contradiction) 을 유도하므로 참이 될 수 없다는 결론을 내린다.
• 그 정리의 가정된 부정이 참이 될 수 없으므로 그 정리는 참이 되어야 한다는 결론을 내린다.
정리의 부정이 참이 될 수 없음을 입증함으로서 그 정리를 증명하는 것을 반박 (refutation) 에 의한 증명이라 부른다.
다시 Squigs 예를 고려해 보자. 다음과 같은 공리들로부터 알 수 있음을 상기하자.
¬ Feathers (Squigs) ∨ Bird (Squigs)
Feathers (Squigs)
증명될 것의 부정을 추가함으로써 다음과 같은 리스트를 얻을 수 있다.
¬ Feathers (Squigs) ∨ Bird (Squigs)
Feathers (Squigs)
¬ Bird (Squigs)
첫째와 둘째식을 레졸루션함으로써 다음과 같이 위의 리스트에 새로운 식을 추가할 수 있다.
¬ Feathers (Squigs) ∨ Bird (Squigs)
Feathers (Squigs)
¬ Bird (Squigs)
Bird (Squigs)
그러나 이제 모순이 발생한다. 리스트에 있는 식 모두가 참이 된다고 가정된다. 그러나 Bird (Squigs) 와 ¬ Bird (Squigs) 가 모두 참일 수는 없다. 따라서 이 모순을 이끌어낸 가정은 거짓이어야 한다. 즉 그 정리의 부정인 ¬ Bird (Squigs) 는 거짓이어야 한다. 그러므로 Bird (Squigs) 란 정리는 참이어야 하고 이것은 전에 입증한 것과 같다. 정리가 증명되었다는 것을 인식하기 위한 전통적인 방법은 레졸루션이 리터럴과 그것의 모순되는 부정이 발견될 때까지 기다리는 것이다. 결과는 식에 아무 것도 포함하지 않는 모순식 (empty expression) 인데, 이것은 통상 Nil 로 표시된다. 레졸루션이 Nil 을 생성하면 레졸루션이 이미 명백한 모순식을 생성했다고 보장된다. 따라서 Nil 을 생성하는 것은 레졸루션이 정리를 증명했다는 신호이다.
대개 정리들의 모순식을 생성하는 과정에서 어떻게 레졸루션이 되는지를 기록하기 위해 트리 형태의 도표를 사용해서 밝히고 있다. 그림 4 는 우리가 입증했던 간단한 증명에 대한 트리이다.
.gif)
그림 4 : Bird (Squigs) 를 증명하는데 필요한 레졸루션을 기록한 트리
레졸루션에 의한 증명이 어떻게 동작되는지에 대한 일반적인 감각을 얻었으므로, 보다 어려운 증명을 가능하게 하는 상당히 많은 조작 (manipulations) 을 이해할 때가 되었다. 기본적으로 이들 조작의 요점은 임의의 식을 레졸루션이 가능한 형태로 변형하는 것이다. 특히 주어진 공리를 리터럴들이 모두 논리합 (disjunction) 으로 연결된 등가의 새로운 공리로 변형하는 방법을 원한다. 다른 방법으로 말하자면, 새로운 공리가 절의 형태 (clausal form) 를 원한다.
다시 시작해 보자. 조작의 예를 보이기 위해서 블럭을 포함하는 공리를 이용하자. 모든 변경 단계를 연습하기 위해 공리가 조금은 인공적인 반면에 공리의 메세지는 단순하다. 명백히 벽돌은 다음과 같은 3 가지를 포함한다. 첫째, 벽돌은 피라미드가 아닌 어떤 것 위에 있다. 둘째, 그 벽돌 아래의 벽돌이 동시에 위에 있을수 없다. 셋째, 벽돌이 아니면 벽돌과 같은 것은 아무 것도 없다.
∀x [Brick(x) ⇒ (∃y [On(x, y) & ¬ Pyramid(y)]
& ¬ ∃y [On(x, y) & On(y, x)]
& ∀y [¬ Brick(y) ⇒ ¬ Equal(x, y)])]
그러나 공리가 주어질 때 절 (clause) 형태에 있지 않으므로 도출절을 생성하는데 사용될 수 없다. 그러나 다음은 절 형태로 쓰여진 등가의 공리들이다.
¬ Brick(x) ∨ On (x, Support(x))
¬ Brick(w) ∨ ¬ Pyramid (Support(w))
¬ Brick(u) ∨ ¬ On (u, y) ∨ ¬ On (y, u)
¬ Brick(v) ∨ Brick(z) ∨ ¬ Equal (v, z)
다음으로 임의의 논리식을 절 형태로 변환시키는데 필요한 단계들을 고려해 보자. 일단 설명하고 난후 그 단계들을 프로시저에 요약될 것이다.
• 의미 함축 (implication) 을 제거한다.
첫번째 해야할 일은 모든 의미 함축 (implication) 을 제거하는 것이다. 이것은 쉬운데 필요로 하는 작업은 E1 ⇒ E2 를 ¬ E1 ∨ E2 로 대치만 하면 되기 때문이다. 아래의 예에서 두 개의 그러한 대치 작업을 해야 한다.
∀x [¬ Brick(x) ∨ (∃y [On(x, y) & ¬ Pyramid(y)]
& ¬ ∃y [On(x, y) & On(y, x)]
& ∀y [¬ (¬ Brick(y) ⇒ ¬ Equal(x, y)])]
• 부논리 (negation) 를 기초 공식 (atomic formula) 앞으로 옮긴다.
이것은 몇가지 변환 법칙들을 요구하는데, & 표현식의 부논리를 다루기 위한 것 하나와, ∨ 식을 위한 하나, ¬ 식을 위한 하나 그리고 ∀ 와 ∃ 에 대해서 각각 하나씩이다. 즉
¬ (E1 & E2) ⇒ (¬ E1) ∨ (¬ E2)
¬ (E1 ∨ E2) ⇒ (¬ E1) & (¬ E2)
¬ (¬ E1) ⇒ E1
¬ ∀x [E1(x)] ⇒ ∃x [¬ E1(x)]
¬ ∃x [E1(x)] ⇒ ∀x [¬ E1(x)]
다음의 예에서 겹치는 ¬ 를 제거하는 세번째 변환 법칙이 필요하다.
• 그리고 ∃ 를 제거해서 다른 ∀ 를 도입하기 위한 것 등이며 따라서 다음식이 유도된다.
∀x [¬ Brick(x) ∨ (∃y [On(x, y) & ¬ Pyramid(y)]
& ∀y [¬ On(x, y) ∨ ¬ On(y, x)]
& ∀y [Brick(y) ∨ ¬ Equal(x, y)]
• 존재 한정사를 제거한다.
불행하게도 존재 한정사를 제거하기 위한 프로시저는 조금은 불분명하고, 모든 것을 이해하기 위해서는 보다 오랜 공부를 해야 한다. 다음과 같이 ∋ 를 포함하는 공리의 일부를 면밀히 고찰해 보자.
∃y [On(x, y) & ¬ Pyramid(y)]
이제 잠깐동안 이것이 의미하는 바를 잘 생각해 보자. 명백히 누군가가 만일 어떤 특정한 객체 x 를 제공하면 그 식을 참을 만드는 y 에 대한 객체를 명명할 수 있을 것이다. 다른 방법으로 말하자면 인수 x 를 취해서 적당한 y 를 반환하는 함수가 존재한다. 어떻게 함수가 동작한다는가 또는 그것이 어떻게 보인다던가 하는 것을 반드시 알 필요는 없지만 그런 함수는 존재해야 한다. 당분간 그 함수를 Magic(x) 라 부르자.
이제 이 새로운 함수를 이용하면 더 이상 y 가 존재한다고 말할 필요가 없는데, 어떤 환경에서 적당한 y 를 생성하는 방법이 있기 때문이다. 따라서 식을 다음과 같이 다시쓸 수 있다.
On(x, Magic(x)) & ¬ Pyramid(Magic(x))
존재 한정사에 대한 필요를 없애주는 함수를 Skolem 함수라 부른다. Skolem 함수 Magic(x) 는 x 에 종속되어야 함을 명심하라. 그렇지 않으면 특정한 x 에 종속인 y 를 생성할 수 없기 때문이다. 범용 (universal) 한정사가 Skolem 함수 인자를 결정한다는 것이 일반적인 규칙이다. 존재 한정 변수에 대치되는 Skolem 함수에는 존재 한정 변수를 포함하는 범위 (scope) 를 갖는 각각의 범용 한정 변수가 각각 인수로 존재해야만 한다.
다음은 존재 한정사 ∃ 를 제거하고 Support 란 함수라 불리는 Skolem 함수를 소개하기 위해 전개된 공리이다.
∀x [¬ Brick(x) ∨ ((On(x, Support(x)) & ¬ Pyramid(Support(x))
& ∀y [¬ On(x, y) ∨ ¬ On(y, x)]
& ∀y [Brick(y) ∨ ¬ Equal(x, y)])]
• 어떤 두 개의 변수가 같지 않도록 하기 위해 필요한 만큼 변수를 재명명 (rename) 하라.
한정사는 그들의 변수 이름이 무엇이건 개의치 않는다. 각 한정사가 유일한 이름을 갖도록 각 식 내의 어떤 중복도 재명명하라.
이것은 다음 단계에서 모든 범용 한정사를 각 식의 왼쪽으로 옮기고자 하기 때문이다. 대치하면 다음과 같다.
∀x [¬ Brick(x) ∨ ((On(x, Support(x)) & ¬ Pyramid(Support(x)))
& ∀y [¬ On(x, y) ∨ ¬ On(y, x)]
& ∀z [Brick(z) ∨ ¬ Equal(x, z)])]
• 범용 한정사를 왼쪽으로 옮겨라.
이 작업은 각 한정사가 왼쪽으로의 이동에도 어떤 혼란한 결과를 초래하지 않도록 각 한정사가 유일한 변수명을 사용하기 때문에 가능하다.
예에서 다음에 그 결과가 열거되어 있다.
∀x∀y∀x [¬ Brick(x) ∨ ((On(x, Support(x)) & ¬ Pyramid(Support(x)))
& ¬ On(x, y) ∨ ¬ On(y, x)
& Brick(z) ∨ ¬ Equal(x, z)
• 논리합 (disjunction) 을 리터럴 쪽으로 옮겨라.
이것은 & 들 안으로 ∨ 를 옮기는 것이므로, 단지 분배 법칙 중의 단지 하나만 필요하다.
E1 ∨ (E2 & E3) ⇒ (E1 ∨ E2) & (E1 ∨ E3)
다음의 예에서 두 단계에서 작업을 해보자.
∀x∀y∀z [(¬ Brick(x) ∨ (On(x, Support(x)) & ¬ Pyramid(Support(x))))
& (¬ Brick(x) ∨ ¬ On(x, y) ∨ ¬ On(y, x)
& (¬ Brick(x) ∨ Brick(z) ∨ ¬ Equal(x, z))]
∀x∀y∀z [(¬ Brick(x) ∨ On(x, Support(x)))
& (¬ Brick(x) ∨ ¬ Pyramid(Support(x)))
& (¬ Brick(x) ∨¬ On(x, y) ∨ ¬ On(y, x)
& (¬ Brick(x) ∨ Brick(z) ∨ ¬ Equal(x, z))]
• 논리곱 (conjunction) 을 생략하라.
실제로 이것들을 정말 제거하지 않는다. 대신에 단순히 논리곱의 각 부분이 마치 분리된 공리인 것처럼 각 부분을 기술했다. 모든 논리곱이 (conjunction) 이 참이면 논리곱의 각 부분이 참이므로 의미가 있다. 다음은 그 결과이다.
∀x [¬ Brick(x) ∨ On(x, Support(x))]
∀x [¬ Brick(x) ∨ ¬ Pyramid(Support(x))]
∀x∀y [¬ Brick(x) ∨ ¬ On(x, y) ∨ ¬ On(y, x)
∀x∀z [¬ Brick(x) ∨ Brick(z) ∨ ¬ Equal(x, z)]
• 두 개의 어떤 변수도 같지 않도록 필요한 대로 모든 변수들을 재명명하라.
이 단계에서 변수들을 제명명하는 데에는 아무런 문제도 없는데, 이는 단지 논리곱의 각 부분 안에 있는 범용 한정화된 변수를 재명명하고 있기 때문이다. 어떤 변수 값에 대해서 결합된 각각의 부분이 참이어야 하므로, 변수들이 각 부분에 대해 다른 이름을 갖는다 해도 문제될 것이 없다. 다음은 예제의 결과이다.
∀x [¬ Brick(x) ∨ On(x, Support(x))]
∀w [¬ Brick(w) ∨ ¬ Pyramid(Support(w))]
∀u∀y [¬ Brick(u) ∨ ¬ On(u, y) ∨ ¬ On(y, u)]
∀u∀z [¬ Brick(v) ∨ Brick(z) ∨ ¬ Equal(v, z)]
• 범용 한정사를 제거하라.
실제로는 정말로 한정사를 제거하지 않았다. 단지 이 시점에서 모든 변수들이 범용 한정화된다고 가정하는 관습을 택할 것일 뿐이다. 예제는 다음과 같다.
¬ Brick(x) ∨ On(x, Support(x))
¬ Brick(w) ∨ ¬ Pyramid(Support(w))
¬ Brick(u) ∨ ¬ On(u, y) ∨ ¬ On(y, u)
¬ Brick(v) ∨ Brick(z) ∨ ¬ Equal(v, z)
위 결과는 레졸루션을 사용하는데 필요한 정도의 절 형식이 되었다. 각 절은 리터럴의 논리합으로 구성되었다. 절의 모든 집합을 취하면 최상위 레벨에 내포된 &, 최하위 레벨에 리터럴 그리고 이들 사이에 ∨ 를 갖는다. 각 절의 변수들은 다르고 모든 변수들은 묵시적으로 (implicitly) 범용 한정화되었다. 요약해 보기 위해서 우리가 행한 작업을 열거해보자.
|
공리들 (axioms) 을 절 (clause) 형식으로 변형하기 : 1. 의미 함축 (implication) 을 제거한다. 2. negation (부논리) 를 기초 공식 (atomic formula) 쪽으로 옮긴다. 3. 존재 한정사를 제거한다. 4. 필요하다면 변수들을 재명명한다. 5. 범용 한정사를 왼쪽으로 옮긴다. 6. 논리합을 리터럴 쪽으로 옮긴다. 7. 논리곱을 제거한다. 8. 필요하다면 변수들을 재명명한다. 9. 범용 한정사를 제거한다. |
절 형태로 변환하기 위한 프로시저로 다음과 같은 레졸루션 증명을 위한 프로시저를 쓸 수 있다.
|
레졸루션을 이용하여 정리를 증명하기 : 1. 증명될 정리를 부정하여 공리의 리스트에 추가한다. 2. 공리의 목록을 절의 형태로 바꾼다. 3. 비어 있는 절인 Nil 이 생성되거나 어떤 레졸루션 가능한 한쌍의 절도 없을 때까지, 레졸루션 가능한 절들을 찾고, 그들을 레졸루션하고 결과를 절의 목록에 추가한다. 4. 빈 절이 생성되면 그 정리가 참이라고 보고한다. 만일 어떤 레졸루션 가능한 절도 없으면 정리는 거짓이라고 보고한다. |
논술했듯이 이 프로시저는 어떤 주어진 점에서 연역도출할 많은 절들의 쌍의 어떤 것에 대해서도 언급이 없다. 어떻게 탐색 (search) 이 진행되는가를 특정화하는 방법을 곧 언급할 것이다.

그림 5 : 증명을 위한 어떤 자료
그러나 첫째로 한 예를 들 때가 되었다. 다음의 공리는 그림 5 에 보이는 블럭 관계에 대한 설명이다.
On(B, A)
On(A, Table)
물론 이들은 이미 절의 형태에 있다. 이것들을 B 가 책상 위에 있다는 것을 보이는데 이용하자.
Above(B, Table)
이것을 보이기 위해서 두 개의 범용 한정화된 표현식의 절 형태가 필요하다. 첫째로 언급할 것은 객체 위에 (on) 존재하는 것은 그 객체 위쪽 (above) 에 존재한다는 것이다. 두번째로 언급한 것은 한 객체는 사이에 객체가 존재하면 다른 객체 위쪽 (above) 에 있다는 것이다.
∀x∀y [On(x, y) ⇒ Above(x, y)]
∀x∀y∀z [Above(x, y) & Above(y, z) ⇒ Above(x, z)]
절의 형태로 감축하기 위한 프로시저를 진행한 후에 이 공리들은 다음과 같이 보인다.
¬ On(u, v) ∨ Above(u, v)
¬ Above(x, y) ∨ ¬ Above(y, z) ∨ Above(x, z)
보여야 할 것은 Above(B, Table) 임을 상기하라. 부정 (negation) 시킨 다음에는 어떤 변환도 필요치 않다.
¬ Above(B, Table)
다음에는 정연하게 유지하기 위해 모든 절에 숫자가 필요하다.
|
|
¬ On(u, v) ∨ Above(u, v) ¬ Above(x, y) ∨ ¬ Above(y, z) ∨ Above(x, z) On(B, A) On(A, Table) ¬ Above(B, Table) |
(1) (2) (3) (4) (5) |
이제 시작할 수 있다. 실제 블럭의 배열을 지정하는 공리들에 대한 레졸루션을 가능하게 하는 On 관계로 Above 관계를 대체하는 것이 전략이다. 먼저 다음과 같이 (2) 마지막 부분이 정확히 (5) 에 있는 부정된 것과 똑같이 보이기 위하여 x 를 B 로 그리고 z 를 Table 로 특정화함으로써 (2) 와 (5) 를 레졸루션한다.
|
|
¬ Above(B, y) ∨ ¬ Above(y, Table) ∨ Above(B, Table) ¬ Above(B, Table) ¬ Above(B, y) ∨ ¬ Above(y, Table) |
(2) (5) (6) |
이제 우리는 u 를 y 로 교체하고 v 를 Table 로 특정화함으로써 (6) 과 (1) 을 레졸루션할 수 있다.
|
|
¬ On(y, Table) ∨ Above(y, Table) ¬ Above(B, y) ∨ ¬ Above(y, Table) ¬ Above(y, Table) ∨ ¬ Above(B, y) |
(1) (6) (7) |
이상하지만 u 를 B 로 특정화하고 v 를 y 로 대체함으로써 (1) 을 다시 (7) 과 사용한다.
|
|
¬ On(B, y) ∨ Above(B, y) ¬ On(y, Table) ∨ ¬ Above(B, y) ¬ On(B, y) ∨ ¬ On(y, Table) |
(1) (7) (8) |
이제 y 를 A 로 특정화하여 (3) 과 (8) 을 이용해 보자.
|
|
On(B, A) ¬ On(B, A) ∨ ¬ On(A, Table) ¬ On(A, Table) |
(3) (8) (9) |
이제 (4) 와 (9) 를 비어있는 절인 NIL 로 레졸루션하라.
|
|
On(A, Table) ¬ On(A, Table) Nil |
(4) (9) (10) |
여기서 종료해야 한다. 모순에 도달했으므로 정리의 부정인 ¬ Above(B, Table) 은 거짓이어야 한다. 따라서 정리 Above(B, Table) 은 참이어야 한다.
레졸루션을 하기에 적절한 절들을 선택하기 위해서 얼마나 고민해야 하는가는 커다란 문제이다. 그 해답은 전혀 그렇게 고민하지 않았다는 것인데, 다음과 같은 2 가지 사항을 이용하기 때문이다.
• 첫째, 우리는 자신들이 유일한 부정된 정리 (negated theorem) 나 직접 또는 간접적으로 부정된 정리를 이용해서 새로 유도된 절을 레졸루션하는 것으로 제한했다.
• 둘째, 우리는 우리가 어디에 위치했다는 것을 알고, 우리가 갔던 곳을 알고, 우리는차이점을 주목하고, 우리는 직관을 사용했다. 이미 우리의 머리로 문제에 대한 해답을 발견했으므로, 우리는 우리가 on 이 아닌 above 가 있는 절이, B 를 중간에 있는 A 와 함께 탁자와 묶어 사용하여 증명하는데, 필요로 했다는 것을 쉽게 알고 있다. 일단 그것이 성취되면 우리는 우리가 실제로 On 을 만족하는 대상을 연결하는 Above 를 포함하는 식을 가졌음을 알고 있다. 따라서 우리는 above-because-or 절을 동작으로 취할 필요가 있음은 명백하다.
불행히도 순수 논리에서 수학적으로 매력적인 개념들에 우리 자신을 제한하면, 표현할 수 있는 것에도 제한이 따른다. 예를 들어 순수 논리는 방법 목적 분석 (means-ends-analysis) 또는 경험적 거리 (heuristic distance) 등 최적 우선 (best-first) 탐색 등에서 요구되는 것과 같은 차이 (difference) 같은 것들을 표현하도록 허용하지 않는다. 정리 증명기 (theorem prover) 들은 그런 개념들을 사용하지만, 문제 풀이 부담 (problem solving burden) 의 많은 부분은 논리적으로 표현된 이미 알려지고 이미 이루어진 문장 (statement) 밖의 지식에 달려 있다.
그러나 어떤 탐색 전략은 순수 논리로부터 우리 자신들을 상당히 분리하도록 요구하지만, 다른 탐색 전략들은 그렇지 않다. 그러한 전략 중의 하나로 단위절 우선 전략 (unit preference strategy) 은 최소의 리터럴 (literal) 로 구성된 절을 포함하는데 레졸루션에 우선권을 부여한다. 지원 집합 (set-of-support) 전략은 단지 직접적이건 간접적이건 부정된 정리를 이용해서 유도된 새로운 절 또는 부정된 정리를 포함하는 레졸루션만 허용한다. 넓이 우선 (breadth-first) 전략은 처음에 초기의 절의 모든 가능한 쌍들을 레졸루션하고 나서 레벨 단위로 초기의 집합들과 함께 결과의 집합과 모든 가능한 쌍을 레졸루션한다. 이 모든 전략들은 완전 (complete) 하다고 말하는데, 그 이유는 어떤 정리가 공리로부터 논리적으로 따른다면 증명을 발견한다는 것을 보증하기 때문이다. 불행히도 거기에는 다음과 같은 단점이 있다.
• 모든 레졸루션 탐색 전략은 지수적 폭발 문제(combinatorial explosion problem)를 갖고 있는데, 그 이유는 관여된 탐색 트리가 엄청나게 자라나서 긴 추론의 사슬을 요구하는 증명에 대한 성공을 방해하기 때문이다.
• 모든 레졸루션 탐색 전략은 멈추는 (halting) 문제의 부류를 갖고 있는데, 그 이유는 탐색이 실제로 증명이 존재하지 않으면 종료를 보장받지 못하기 때문이다.
사실 일차 술어 논리 (first-order predicate calculus) 에 대한 모든 완전한 (complete) 증명 프로시저는 멈춘는 문제를 갖고 있다. 완전한 증명 프로시저는 반결정적이다 (semidecidable) 라고 하는데, 이는 단지 식이 실제로 정리이면 우리에게 식이 정리인지 여부를 말해주는 것이 보증되기 때문이다.
두 개의 리터럴을 레졸루션하기 위해서는 하나가 부정되어 있다는 점을 제외하고는 두 개의 리터럴이 정확히 일치 (match) 되어야 한다. 종종 리터럴들은 그들 자체로 정확히 일치한다. 그러나 때로는 리터럴들은 적당한 대체물 (substitution) 을 적용함으로써 일치될 수 있다.
이제까지의 레졸루션의 일치화 (matching) 부분은 쉬웠다. 즉 같은 위치에 나타나는 같은 상수는 명확히 매치한다. 또는 해당되는 상수로 즉시 일치화될 수 있는 범용 한정화된 변수가 놓인 위치에 상수가 나타났었다. 다른 말로 같은 상수들을 일치시키거나 변수를 특정화했다. 다음의 예를 위해 대체물 (substitution) 을 유지하기 위한 보다 좋은 방법이 필요하고, 대체물을 만들 규칙이 필요하다. 먼저, 다음과 같이 대체물을 표시하도록 하자.
{v1 ⇒ C; v2 ⇒ v3; v4 ⇒ f(…)}
이것은 변수 v1 이 상수 C 로 대치되고, 변수 v2 가 변수 v3 로 대치되며, 변수 v4 가 인수가 있는 함수 f 로 대체됨을 의미한다. 다른 저자들은 쓰기는 쉽지만 유지하기가 힘든 표시법 인 {C / v1, v2 / v3, f(…) / v4) 를 사용한다. 이런 대치에 대한 규칙은 한 변수를 그 변수를 포함하지 않는 임의의 항 (term) 으로 대치할 수 있음을 말한다.
• 변수는 상수로 대치될 수 있다. 즉 우리는 대체물 {v1 ⇒ C} 를 얻을 수 있다.
• 변수는 변수로 대치될 수 있다. 즉 우리는 대체물 {v2 ⇒ v3} 를 얻을 수 있다.
• 변수는 함수식이 그 변수를 포함하지 않는 한 함수식으로 대치될 수 있다. 즉 우리는 대체물 {v4 ⇒ f(…)} 를 얻을 수 있다.
두 개의 절을 레졸루션 가능하게 하는 대체물을 단일자 (unifier) 라 부른다. 그리고 그런 대체물을 발견하는 과정을 단일화 (unification) 라 부른다. 단일화에 대한 많은 프로시저들이 있다. 그러나 예를 위해서는 조사만 될 것이다.
어떤 식 (expression) 이 어떤 공리 (axioms) 의 집합에 대하여 정리 (theorem) 라고 가정하자. 어떤 새로운 공리를 추가한 후에도 그 식이 여전히 정리일까? 확실히 그렇게 되어야 한다. 왜냐하면 증명은 그 새로운 공리를 무시한 후 예전 공리만을 이용해서 이루어질 수 있기 때문이다.
새로운 공리는 단지 증명가능한 정리의 리스트에 추가되지 결코 다른 것을 취소시키지 않으므로, 전통적 논리는 단조적 (monotonic) 이라고 말한다.
그러나 단조적 술어는 몇몇 자연적인 사고 방식과는 맞지 않는다. 모든 새는 난다는 말을 듣고 그것으로부터 어떤 특정한 새가 난다는 것을 아는 한 완전히 타당한 결론을 제시했다고 가정하자. 그러면 누군가가 펭귄은 날지도 않고 또 죽은 새도 아니라고 지적한다. 이런 새로운 사실들을 추가함은 이미 내려진 결론과 위배될 수 있으나 정리 증명기를 중단할 수는 없다. 단지 최초의 공리를 수정할 수 있을 뿐이다.
이런 종류의 문제를 다루는 것은 새로운 논리의 방식을 요구하며, 비단조적 (nonmonotonic) 이라는 논리학 (logics) 으로 이끈다. 이러한 논리를 다루는 것은 여기에서는 다소 어긋나는데, 그것은 아직도 많은 논란과 다듬어지지 않은 이론에 둘러싸인 채 남아있기 때문이다. 그러나 12 장에서는 다른 전제 귀결 규칙을 위배하는 전제 귀결 규칙의 도입으로써 비단조성에 대한 논의를 추가로 할 것이다.
논리는 어떤 작업에 대해서는 훌륭하지만 다른 작업에서는 그렇게 좋지 못하다. 그러나 논리는 그것의 원래 목적 분야에 대해서는 제일이므로 매력적이다. 사람들은 논리가 어울리는 것들에만이 아닌 모든 어려운 문제에 대해 논리를 사용하려고 한다. 그러나 이것은 망치가 걸쇠 (fastener) 의 한 종류를 다루는 데에는 좋다고 나사를 돌리기 위해 망치를 사용하는 것과 같다.
따라서 논리와 정리 증명기를 사용하는 것이 분명히 옳아보일 때 다음의 경고 사항들을 다시 검토해 보자.
• 정리 증명기는 너무 긴 시간을 요구할 경우가 있다.
완전한 정리 증명기는 검색을 요구하고 검색은 원초적으로 지수적 (exponential) 이다. 지원 집합 (set-on-support) 레졸루션 같은 빠른 검색 방법들은 탐색에 대한 지수의 크기를 감소시키지만 지수적의 성격을 변화시키지는 않는다.
• 정리 증명기는 일시적일지라도 많은 도움이 되지 못할 수 있다.
몇몇 지식은 구체적 표현을 공리로 하기 힘들다. 논리로서 형식화된 문제를 푸는 것이 상당한 노력을 요구할 수도 있는 반면에 다른 방법으로 형식화된 문제를 푸는 것이 간단할 수 있다.
• 논리는 어떤 종류의 지식에 대한 표현으로는 빈약하다.
순수 논리의 표기법은 경험적인 거리 (heuristic distance), 또는 상태 차이 (state difference) 또는 어떤 특정한 접근 방법이 특별히 빠른 그런 개념들을 표시하는 데에는 곤란하다. 정리 증명기는 그런 지식을 사용할 수 있지만 그 지식은 순수 논리의 개념들이 아닌 다른 개념들을 이용해서 표현되어야 한다.
논리는 주어진 것의 결과로서 무엇이 참인지를 보여주지만 논리는 또한 어떤 것들을 변화시키는 연산자 (operator) 들을 사용함으로써 어떻게 참이 되는지를 입증할 순 있다.
그림 6a 에서 보여주듯이 블럭 B 는 A 의 위에 그리고 A 는 탁자 위에 있는 블럭 세계 상황을 가정해 보자.그림 6b 처럼 탁자 위에 B 를 놓는 방법을 발견하는 것이 문제라 하자. 논리적 표기법을 이용하면 문제는 다음 식이 참이 되도록 배열하는 것이다.
On(B, Table)
명백히 윗 식은 초기의 문제 세계의 상황에서는 참이 아니지만 다른 블럭 배열을 갖는 다른 상황에서는 참일 수 있다. 따라서 어떤 식이 참이라고 말하는 것은 불완전하다. 즉 어떤 식이 참이 되기 위해서 그 식이 참인 상황을 지정해야 한다.

그림 6 : 블럭을 포함하는 단순한 초기와 마지막 상황. 문제는 초기 상황을 마지막 상황으로 변형시키는 연산자 (operator) 의 순서를 발견하는 것이다.
필요한 부기 (book keeping) 는 다음과 같은 다양한 상황에서 참이라고 알려진 식들을 가리 킴으로써 이루어질 수 있다.
|
|
초기 상황 : On(B, A) & On(A, Table) |
마지막 상황 : On(B, Table) & On(A, Table) |
그러나 목적을 위하여 보다 좋은 대안은 술어에 상황 인수 (situation argument) 를 추가하는 것이다. 초기 상황 S 에서 B 가 A 위에 있고 A 가 탁자 위에 있음을 말하기 위해서 다음과 같이 여분의 인수의 값으로서 S 를 삽입한다.
On(B, A, S) & On(A, Table, S)
S 는 알려진 상수 상황 (constant situation) 을 표시하지 알려지지 않은 상황인 변수 상황이 아니므로 대문자를 사용한다.
원하는 것은 B 가 탁자 위에 있는 마지막 상황 sf 이다.
∃sf [On(B, Table, sf)]
sf 는 알려지지 않은 변수 상황이지 알려져 있지 않은 상수 상황이 아님을 명심하라. 따라서 소문자를 사용한다. 이제 탁자 상에 물체를 놓음으로써 상황을 변화시키는 동작인 PutonTable 을 상상해 보자. 대개 이것은 PutonTable(x, s) 가 다음과 같은 작동을 한다는 것이다.
• PutonTable 은 어떤 상황 S 에서 블럭 x 를 발견한다.
• PutonTable 은 x 가 탁자 위에 있는 새로운 상황을 생성한다.
내부에서 볼 때 만일 그것이 서로 간섭하는 (interfering) 물체를 취급한다면 PutonTable 은 꽤 복잡하겠지만 외부에서 관찰할 땐 PutonTable 은 그것의 값으로서 한 상황을 뒤로 넘겨주는 블랙 박스 (black box) 이다. 물체 x 와 상황 s 가 주어질 때 PutonTable 의 값은 On(x, Table) 가 참인 새로운 상황이다. PutonTable 의 값이 참 또는 거짓이라기 보다는 상황이므로 PutonTable 은 분명히 술어가 아님을 주의하라. PutonTable 의 값이 상황임을 알았으므로 PutonTable 은 나타나리라고 기대하는 상황으로써 On 의 인수가 될 수 있다. 사실 PutonTable 은 다음과 같은 방법으로 정의될 수 있다.
∀s∀x [¬ On(x, Table, s) ⇒ On(x, Table, PutonTable(x, s)]
위 식을 이용하기 위하여 탁자 위에 어떤 것도 없을 때 알기 위한 방법이 필요하다. 명백히 어떤 것이 탁자가 아닌 어떤 것 위에 있으면 탁자 위에 있지 않다. 이것은 다음과 같이 말할 수 있다.
∀s∀y∀z [On(y, z, s) & ¬ Equal](z, Table) ⇒ ¬ On(y, Table, s)]
이제 탁자 위에 블럭 B 를 갖기 위한 어떤 방법이 존재한다는 것을 입증하기 위해서 알고 있는 것을 이용할 수 있다. 단순히 PutonTable 의 정의와 공리의 리스트에 탁자 위에 있지 않은 식을 취해서 레졸루션을 사용한다. 초기 공리는 다음과 같다.
On(B, A, S) & On(A, Table, S)
∀s∀x [¬ On(x, Table, s) ⇒ On(x, Table, PutonTable(x, s))]
∀s∀y∀z [On(y, z, s) & ¬ Equal(z, Table) ⇒ ¬ On(y, Table, s)]
원하는 정리인 식은 다음과 같다.
∃sf [dOn(B, Table, sf)]
이제 원하는 식을 부정하면 다음을 얻는다.
¬ ∃sf [On(B, Table, sf)]
¬ 를 기초 공식 (atomic formula) 쪽으로 옮기면 다음을 얻는다.
¬ ∀sf [¬ On(B, Table, sf)]
위식을 골라 라스트에 더하고 객체 간의 등식에 관한 몇 개의 표현식들로 윤색하고, 절 형태로 모든 것을 놓고, 각 절에 유일한 변수들을 사용하도록 하면 다음을 얻는다.
|
|
On(B, A, S) On(A, Table, S) On(x, Table, s3) ∨ On(x, Table, PutonTable(x, s3)) ¬ On(y, z, s4) ∨ Equal(x, Table) ∨ ¬ On(y, Table, s4) ¬ Equal(B, A) ¬ Equal(B, Table) ¬ Equal(A, Table) ¬ On(B, Table, sf) |
(1) (2) (3) (4) (5) (6) (7) (8) |
새로운 문자로 싫증나게 하는 것보다는 s3 와 같이 첨자화된 문자가 사용됨을 주의하라. 이것은 이들 변수들이 모두 상황을 표현한다는 것을 기억시키기를 원하기 때문이다. 우연한 첨자의 중복을 피하기 위하여 철자는 절 번호에 대응한다.
이제부터 증명은 쉬워진다. 그림 7 을 조사해 보라. {x ⇒ B; sf ⇒ PutonTable (x, s3)} 를 이용해서 (3) 과 (8) 을 레졸루션할 수 있고 변수들을 재명명한 후에 다음을 얻을 수 있다.
|
|
On(B, Table, s9) |
(9) |
이제 {y ⇒ B; s4 ⇒ s9} 를 이용해서 (9) 와 (4) 를 작업하고 나서 변수를 재명명하면
|
|
¬ On(B, w, s10) ∨ Equal(w, Table) |
(10) |
{w ⇒ A} 를 이용해서 (7) 로 (10) 을 레졸루션하고 재명명하면 다음을 얻는다.
|
|
¬ On(B, A, s11) ∨ ¬ On(A, Table, PutonTable(B, s11)) |
(11) |
{s11 ⇒ S} 를 이용해서 (1) 로 (11) 을 레졸루션함으로서 끝내면 Nil 을 얻는다 :
|
|
Nil |
(12) |

그림 7 : 연산자 PutonTable 을 포함하는 증명
그러나 단지 B 가 탁자 위에 있다는 상황이 가능하다는 결론을 얻었다. 어떻게 그 상황에 도달하는지를 모른다. 그러나 원하는 곳을 어떻게 도달하는가에 대한 지식은 모든 단일화 과정에 내재 (implicit) 된다. 우리가 했던 것을 되돌아 볼 때 다음과 같은 일련의 대치를 알 수 있다.
sf ⇒ PutonTable(B, s3)
s3 ⇒ s9
s9 ⇒ s10
s10 ⇒ s11
s11 ⇒ S
모든 대치들을 통해 명백히 원하는 상황인 sf 는 초기 상황 S 에서 B 에서 PutonTable 연산자를 적용함으로서 얻을 수 있는 상황이다.
상황의 과정을 추적하는 것은 많은 연산자들이 관여된 관계의 경우 지루하고 오류를 유발하는 일이다. 따라서 그린의 기법 (Green's trick) 이라고 하는 것을 사용하는 것이 일상적인 관례이다. 그 기본적 개념은 원하는 결과의 식에 하나의 항 (term) 을 첨가하는 것이다. Answer 항이라고 불리는 이것은 상황 정보를 추적 유지하기 위한 일반적인 단일화 장치이다. ¬ On(B, Table, sf) 대신에 ¬ On(B, Table, sf) ∨ Answer(sf) 라고 기록한다. 그리고 증명하는 데에 그 단계를 반복하자.
|
|
¬ On(B, Table, sf) ∨ Answer(sf) On(B, Table, s9) ∨ (Answer(PutonTable)(B, s9) ¬ On(B, w, s10) ∨ Equal(w, Table) ∨ Answer(PutonTable)(B, s10)) ¬ On(B, A, s11) ∨ Answer(PutonTable(B, s11)) Answer(PutonTable(B, S)) |
(8) (9) (10) (11) (12) |
Answer 는 단지 한번만 공리에 삽입됨을 주의하라. 따라서 Answer 는 결코 레졸루션의 대상이 될 수 없다. 반면에 그것은 일련의 레졸루션을 통해서 원하는 상황에 역으로 추적될 수 있는 모든 절들을 동반한다. 더욱이 답의 인수는 항상 일련의 레졸루션에 관련된 상황 변화에 대한 기록이다.
물론 Nil 일 때 종료하는 대신에 이제 Answer 만을 포함하는 절을 가질 때 종료하자. 레졸루션 단계는 그림 8 에 도시되어 있다. 개정된 레졸루션 프로시저는 다음과 같다.
|
Green's trick 을 갖는 레졸루션을 이용하여 존재 한정화된 단일 리터럴 정리를 증명하기 : 1. 정리를 부정하고 그것을 절 형태로 변환하고 Answer 항을 추가한다. 2. 공리의 리스트를 절 형태로 변환한다. 정리와 Answer 항으로부터 유도된 절을 추가한다. 3. 유일한 Answer 항을 가진 절이 생성되거나 어떤 레졸루션 가능한 절의 생성이 존재하지 않을 때까지 레졸루션 가능 절을 구하고 그들을 레졸루션해서 절의 리스트에 결과를 추가한다. 4. 만일 유일한 Answer 항을 갖는 절이 생성되면 Answer 항 내의 일련의 동작들이 요구된 결과임을 보고한다. 만일 어떤 레졸루션 가능한 절도 없으면 요구된 동작은 이루어지지 않았음을 보고한다. |
이 프로시저는 여러 개의 리터럴들과 범용 한정사를 갖는 정리들에 대한 증명을 하는 데에 일반화될 수 있다. 그러나 이 프로시저 자체로 만족할 것이다.
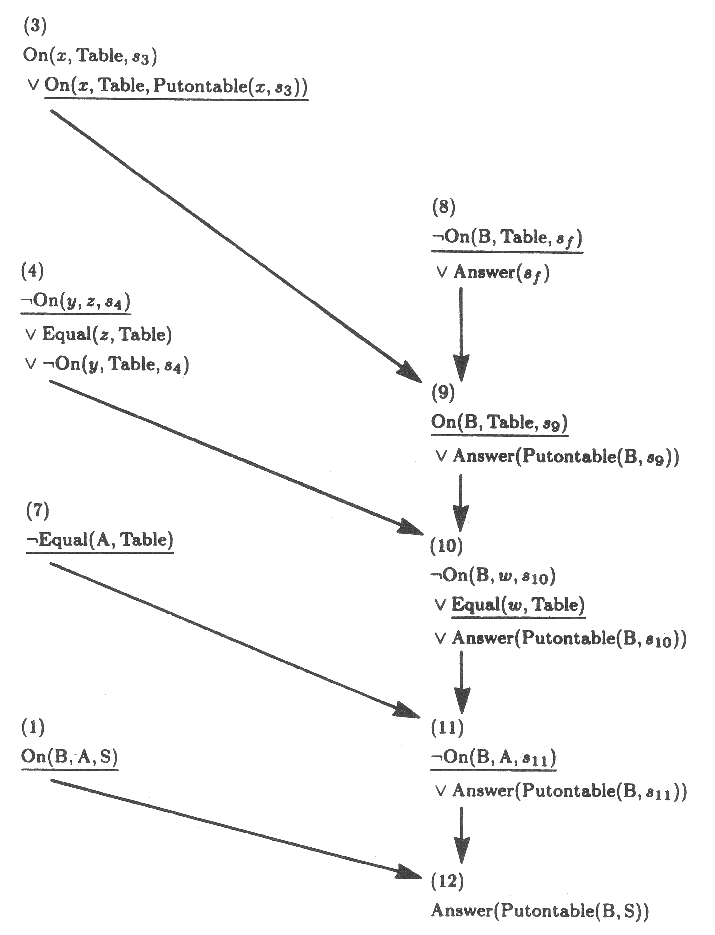
그림 8 : 목표식에 Answer(sf) 를 추가하는 것은 표준 단일화 장치를 이용하는 상황 변화 연산을 추적 유지하기 위해서이다. 그림 7 의 증명이 Answer(sf) 를 이용해서 반복된다. 그 결과는 탁자 위에 블럭 B 를 놓기 위해 한 연산만 필요가 있음을 알려 준다.
이제 B와 A 양쪽 모두가 마지막 상황에서 탁자 위에 있도록 요구되는 전번 문제와 유사한 문제를 추구한다고 가정하자. 즉 목표는 다음과 같다.
∃sf[On(B, Table, sf) & On(A, Table, sf)]
탁자 위에 B 를 놓는 똑같은 동작이면 충분함을 안다. A 는 이미 탁자 위에 있다. 먼저 다음 단계와 같이 부정하고 절 형태로 변환하자.
¬ ∃sf[On(B, Table, sf) & On(A, Table, sf)]
∀sf[¬ (On(B, Table, sf) & On(A, Table, sf))]
∀sf[¬ On(B, Table, sf) ∨ ¬ On(A, Table, sf)]
¬ On(B, Table, sf) ∨ ¬ On(A, Table, sf)
마지막 표현식은 번호를 붙일 식이며 그 공리들에 추가된다.
|
|
¬ On(B, Table, sf) ∨ ¬ On(A, Table, sf) |
(8) |
이전의 증명에서와 같이 {x ⇒ B; sf ⇒ PutonTable(x, s3)} 를 이용하고 재명명해서 (3) 과 (8) 을 레졸루션해서 (9) 를 생성한다.
|
|
On(B, Table, s9) ∨ ¬ On(A, Table, PutonTable(B, s9)) |
(9) |
대체물 {y ⇒ B; s4 ⇒ s9} 과 재명명으로 (9) 와 (4) 를 이용해서
|
|
¬ On(B, w, s10) ∨ Equal(w, Table) ∨ ¬ On(A, Table, PutonTable(B, s10) |
(10) |
{w ⇒ A} 와 재명명을 이용해서 (7) 과 (10) 을 레졸루션하면 일상적으로 다음을 얻는다.
|
|
¬ On(B, A, s11) ∨ ¬ On(A, Table, PutonTable(B, s11) |
(11) |
{s11 ⇒ S} 를 이용해서 (1) 로 (11) 을 레졸루션함으로서 종료하면 다음을 얻는다.
|
|
¬ On(A, Table, PutonTable(B, S)) |
(12) |
이 시점에서 (2) 식 On(A, Table, S) 로 (12) 를 레졸루션 해보자. 그러나 이것은 심한 장애물일 수 있는데 이를 두 개로 레졸루션하는 것은 대체물 {s ⇒ PutonTable(B, S)} 를 요구하기 때문이다. 그러나 S 는 변수가 아닌 상황이므로 그러한 어떤 치환이 가능하지 않다.
처음에는 이러한 것이 이상하게 보일 수도 있는데 초기 상황에서 A 가 탁자에 있으면 확실히 A 는 B 가 역시 탁자 위에 놓여진 후에도 탁자 위에 남아 있다. 우리는 A 가 놓였다는 것을 알지만 우리의 지식은 논리적이지 못하다. PutonTable 공리는 움직여진 물체에 무엇이 일어나는가를 설명하지만 다른 물체에 발생한 것들을 설명하지 않는다. 더 이상 알지 못하면 어떤 술어의 값이 한 상황에서 다른 상황으로 진행되는 중에 변화되지 않는지를 논리 기반 추론 기관은 추론할 아무런 방법도 없다. 결국 일부만 변한다. 이 딜레마는 프레임 문제로 알려져 있다.
결론적으로 탁자 위에서 B 와 A 모두를 얻기 위하여, 불변하는 관계들에 관한 레졸루션 정리 증명기를 알릴 필요가 있다. 이렇게 하기 위한 한가지 보편적인 방법은 프레임 공리를 도입하는 것이다. 프레임 공리란 어떻게 술어가 연산에도 불변하는지에 관한 문장이다. 여기에 어떻게 On 이 PutonTable 에도 살아남는지에 대한 한가지 설명이 있다.
∀s∀x∀y∀z[On(x, y, s) & ¬ Equal(x, z) ⇒ On(x, y, PutonTable(z, s))]
영어로 이것은 PutonTable 연산 이전에 x 가 y 위에 있으면, x 가 탁자 위에 놓인 물체가 아닌 한 연산 이후에도 y 위에 남아 있다는 것을 설명한다.
이제 프레임 공리를 절 형태로 변환하고, 필요한 만큼 변수 이름을 바꾸면, 다음과 같은 프레임 공리를 얻는다.
|
|
¬ On(p, q, so) ∨ Equal(p, r) ∨ On(p, q, PutonTable(r, so)) |
(0) |
다음과 같은 곳에서 증명이 멈췄음을 기억하라.
|
|
¬ On(A, Table, PutonTable(B, S)) |
(12) |
그러나 이제 더 이상 멈추어 있을 필요가 없는데, 이것은 새로운 프레임 공리가 해결해 주기 때문이다. {p ⇒ A : q ⇒ Table : r ⇒ B : so ⇒ S} 로 대치하고 (0) 으로 (12) 를 레졸루션하면 다음을 얻는다.
|
|
¬ On(A, Table, S) ∨ Equal(A, B) |
(13) |
재빨리 (5) 로 (13) 을 그리고 (2) 로서 결과인 (14) 를 레졸루션함으로서 증명을 완결짓는 Nil 을 얻을 수 있다.
|
|
¬ On(A, Table, S) Nil |
(14) (15) |
우리가 원한다면 원하는 일련의 연산자를 생성하는 그린의 기법을 이용해서 반복할 수 있다.
이 시점에서 탁자 위의 두 개의 블럭을 얻을 수 있었지만 그것은 작은 일이었다. 일반적으로 설명된 방법은 같지 않다는 공리 (not-equal axioms) 와 프레임 공리의 집합을 요구한다. 같지 않은 대상들의 각 쌍에 대해 하나의 같지 않다는 공리를 필요로 하고, 대부분의 술어 연산자 쌍에 대해 하나의 프레임 공리를 필요로 한다. 다행스럽게도 프레임 문제를 해결하는 데에는 다른 방식이 있지만 우리가 가야할 너무 많은 방향들을 갖고 있기 때문에 그것들에 관한 논의는 동떨어진 것일 수 있다.
이제까지 논리적 연결자들인 &, ∨, ¬, 그리고 ⇒ 에 대하여 생각해 왔다. 만약 그들이 함수라면 인수를 받아들이고 참 (True), 혹은 거짓 (False) 을 되돌려 줄 것이다. 이제 제한 조건이 전파되는 노드들의 망을 구성하는데 논리적 표현을 사용하는 방법에 대하여 살펴보기로 하자. 이렇게 하는 것은 몇 가지 이유가 있다.
첫째로, 논리 위주의 제한조건 망 (logic-oriented constraint net) 은 정리 증명이 제한조건을 해결하는 방법으로서 보여질 수 있다는 사실을 강조한다. 둘째로, 제한 조건망은 가정들이 만들어지거나 혹은 취소가 될 때, 무엇이 참이고 거짓인지에 관한 추적을 쉽게 할 수 있다. 이것은 제한 조건망이 진리값 유지 (truth maintenance) 개념과 연상되는 이유이다. 셋째로, 제한 조건 망은 가정이 서로 맞지 않을 때 일어나는 모순을 바로잡기 위하여 종속성을 이용한 (dependency-directed), 비연대기적 (nonchronological) 백트랙킹 (backtracking) 이 어떻게 도움을 줄 수 있는가를 쉽게 보여 준다. 그러나 종속성을 이용한 백트랙킹은 제한 조건 망에 관여하는 것이 아닌 어떤 다른 증명 프로시저와 함께 동작한다는 사실에 유의해야 한다.
또한 기술될 제한 조건의 전파 프로시저가 한계가 있다는 사실에도 유의해야 한다. 하나는 그 프로시저가 완전한 (complete) 증명 프로시저가 아니라는 것이다. 왜냐하면 프로시저가 TRUE 라고 증명할 수 없는 TRUE 인 표현식이 존재하기 때문이다. 다른 한계점으로는 한정되어진 (quantified) 표현식이 없어야만 하거나, 혹은 한정사가 있는 표현식일지라도 유한한 수의 한정사가 없는 공리들로 변환시켜주기 위한 전처리 (preprocess) 방법이 존재해야만 한다. 따라서 이 프로시저는 단지 명제 논리 (propositional calculus) 만 다룬다.
논리적 표현식을 망에서의 노드들로 생각해 보자. 만약 한 노드와 연관된 표현식이 다른 노드와 연관된 표현식의 일부라면, 두 노드는 연결된다. 예를 들어 다음 표현식을 생각해 보자.
Happy(A) ⇒ Happy(B)
자! 그림 9a 에서 보이는 바와 같이 이 표현식과 Happy(A) 과 Happy(B) 인 두 개의 부표현식에 대한 노드들을 만들었다. 더 나아가 큰 표현식이 TRUE 라고 가정하면 연관된 노드에 TRUE 라고 레이블을 붙인다. 다른 두 노드들에 대해서는 가정이 없으므로 그들에 대해서는 UNKNOWN 이라고 레 이블을 붙인다.
그러나 만약 더 나아가 A 가 행복하다면 Happy(A) 는 TRUE 이고 따라서 Happy(B) 역시 TRUE 이다. 3 장에서 소개된 제한 조건 전파에 대한 용어로 생각할 때 Happy(A) 와 연관된 노드에 대하여 TRUE 값을 가정하고 Happy(A) ⇒ Happy(B) 와 함께 연관된 노드도 TRUE 인 것이 그림 9b 에서처럼 Happy(B) 도 역시 TRUE 값을 가지게 만들 것을 원한다.
분명히 한 표현식에 대한 값이 다른 것들에 대한 값을 결정하는데 도움을 줄 수 있도록 다양한 종류의 노드들을 통하여 전파가 가능하도록 하는 어떠한 규칙들을 필요로 한다.
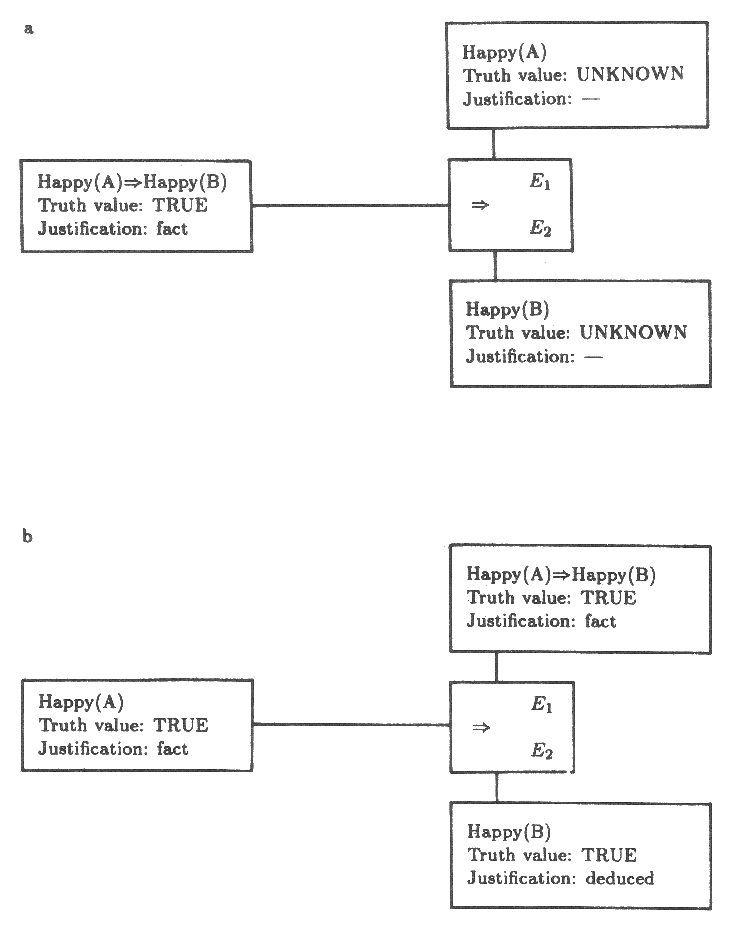
그림 9 : 논리적 표현식들을 제약조건 전파망에서 노드들로 볼 수 있다. 부분 a 에서 ⇒ 표현식에 해당되는 노드는 그것의 부분 표현식에 연결되어 있다. b 에서 한 부분 표현식의 값이 참이라면 전파가 ⇒ 노드를 통해 일어나 다른 노드가 참이어야 함을 요구한다.
이제 잠시 후에 E1 ⇒ E2 의 정의가 다음의 논리적 결과들 (logical consequences) 을 갖는다 (즉, E1 ⇒ E2 가 참이면 다음 식들도 참이다) 는 것을 볼 것이다.
¬ E1 ∨ E2 ∨ ¬ (E1 ⇒ E2)
E1 ∨ (E1 ⇒ E2)
¬ E2 ∨ (E1 ⇒ E2)
각 줄에 있어서 리터럴들 중에 적어도 하나의 값은 TRUE 가 되어야만 함을 주의하라. 강조하기 위해 이 표현식을 구문적으로 세련된 (syntactically sugared) 형태로 다음과 같이 바꾸어 써 보자.
E1 이 거짓이거나 E2 가 참이거나 혹은 (E1 ⇒ E2) 가 거짓임을 요구한다.
E1 이 참이거나 (E1 ⇒ E2) 가 참임을 요구한다.
E2 가 거짓이거나 (E1 ⇒ E2) 가 참임을 요구한다.
이러한 방법으로 쓰면 각 줄에 있어서 부표현식들 중의 적어도 하나는 명기된 TRUE 혹은 FALSE 값과 매치되어야 함이 명백하다. 그러므로 만약 하나를 제외한 모든 부표현식이 매 치가 되지 않는다면, 그 나머지 부표현식은 매치가 되도록 요구되어진다. 그러므로 각 줄은 그 줄에 표시되어 있는 표현식들의 값에 대한 제한조건이 된다. 결론적으로 그러한 것들을 제한 조건 표현식 (constraint expressions) 이라고 부르자. 그러면 진리값을 전파하기 위하여 다음의 프로시저를 사용한다.
|
진리값 전파하기 : 1. 모든 노드에 대하여 1.a 각 제한 조건 표현식에 대하여 1.a.a 만약에 하나를 제외한 모든 부표현식들의 주어진 TRUE, 혹은 FALSE 값으로 매치가 되지 않는다면 그 한 부표현식 값은 매치되어야만 한다. 1.a.b 그렇지 않으면 아무일도 하지 않는다. |
이제 잊기 전에 제한조건이 어디로부터 나오게 되는지를 살펴봐야 한다. 나머지 절에서는 다소 지루한 작업이 될 것이므로, 지루한 독자들은 다음 절로 그냥 넘어가기 바란다.
먼저 E1, E2, 그리고 E1 ⇒ E2 에 대해 어떤 TRUE 와 FALSE 조합이 ⇒ 의 정의에 의하여 배제되어지는가를 보여 줘야만 한다. 그 다음으로 ⇒ 에 연관된 제한 조건 표현식들을 사용하는 것이 배제된 조합이 일어나지 않도록 보장하기 위한 것과 같다 라는 것을 보인다.
⇒ 의 진리값 표 정의로부터 E1 ⇒ E2 는 다음과 같은 조합들만을 허용한다는 것을 알 수 있다.
|
|
E1 |
E2 |
E1 ⇒ E2 에 의해 강요되는 값 |
|
|
TRUE FALSE FALSE TRUE |
FALSE FALSE TRUE TRUE |
FALSE TRUE TRUE TRUE |
그러나 세 개의 TRUE-FALSE 값들의 여덟 개의 가능한 조합이 존재한다. 따라서 네 개의 나머지 조합은 금지되어야만 한다.
|
|
E1 |
E2 |
E1 ⇒ E2 에 의해 강요되는 값 |
|
|
TRUE FALSE FALSE TRUE |
FALSE FALSE TRUE TRUE |
TRUE FALSE FALSE FALSE |
이것을 다른 방법으로 말하면 각 줄 (line) 이 네 개의 금지된 조합을 배제한 것이므로 다음 식은 반드시 TRUE 가 되어야만 한다.
¬ (E1 & ¬ E2 & (E1 ⇒ E2))
& ¬ (¬ E1 & ¬ E2 & ¬ (E1 ⇒ E2))
& ¬ (¬ E1 & E2 & ¬ (E1 ⇒ E2))
& ¬ (E1 & E2 & ¬ (E1 ⇒ E2))
바깥쪽 부정을 안쪽으로 집어 넣어서 표현식을 다음과 같이 다시 쓴다.
(¬ E1 ∨ E2 ∨ ¬ (E1 ⇒ E2))
& (E1 ∨ E2 ∨ (E1 ⇒ E2))
& (E1 ∨ ¬ E2 ∨ (E1 ⇒ E2))
& (¬ E1 ∨ ¬ E2 ∨ (E1 ⇒ E2))
이제 두번째 줄과 세번째 줄을 합치고 세번째와 네번째 줄을 합치면 다음과 같은 동치 표현식을 얻을 수 있다.
(¬ E1 ∨ E2 ∨ ¬ (E1 ⇒ E2))
& (E1 ∨ (E1 ⇒ E2))
& (¬ E2 ∨ (E1 ⇒ E2))
바로 이것이 이전에 가정했던 ⇒ 의 논리적 귀결 (consequences) 이다. &, ∨, 그리고 ¬ 에 대해 지루하게 반복할 수 있다. 요약 결과에 만족하자.
⇒ 노드들에 대하여 우리는 다음의 각각의 제한 조건 표현식을 얻을 수 있다.
E1 이 FALSE 이거나 E2 이 TRUE 이거나 (E1 ⇒ E2) 이 FALSE 임을 요구한다.
E1 이 TRUE 이거나 (E1 ⇒ E2) 이 TRUE 임을 요구한다.
E1 이 FALSE 이거나 (E1 ⇒ E2) 이 TRUE 임을 요구한다.
& 노드들에 대하여 다음의 각각의 제한 조건 표현식을 얻을 수 있다.
E1 이 FALSE 이거나 E2 이 FALSE 이거나 (E1 & E2) 이 TRUE 임을 요구한다.
E1 이 TRUE 이거나 (E1 & E2) 이 FALSE 임을 요구한다.
E2 이 TRUE 이거나 (E1 & E2) 이 FALSE 임을 요구한다.
∨ 노드들에 대하여 다음의 각각의 제한 조건 표현식을 얻을 수 있다.
E1 이 TRUE 이거나 E2 이 TRUE 이거나 (E1 ∨ E2) 이 FALSE 임을 요구한다.
E1 이 FALSE 이거나 (E1 ∨ E2) 이 TRUE 임을 요구한다.
E2 이 FALSE 이거나 (E1 ∨ E2) 이 TRUE 임을 요구한다.
¬ 노드들에 대하여 다음의 각각의 제한 조건 표현식을 얻을 수 있다.
E1 이 TRUE 이거나 ¬ E1 이 TRUE 임을 요구한다.
E1 이 FALSE 이거나 ¬ E1 이 FALSE 임을 요구한다.
이러한 제한 조건 표현식들로 무장했으므로 문제를 공략할 수 있다. 네 명의 사람들 A, B, C 와 D 로부터 시작하기로 하자. A 는 B 를 알고, B 는 C 를 알고, C 는 D 를 안다. 서로를 알고 있는 사람만이 서로의 행복에 영향을 줄 수 있다고 가정하자. 따라서 한 사람의 행복이 다른 사람의 행복의 원인이 됨을 말하는데 24 가지의 가능한 표현식이 존재한다. 그것들 중에서 신뢰할 만한 사실들이라 여길 수 있는 다음의 표현들을 가정해 보자.
Happy(A) ⇒ Happy(B)
Happy(B) ⇒ Happy(C)
또한 A 와 D 는 확실히 행복하다고 가정하자.
Happy(A)
Happy(D)
이러한 가정된 표현은 그림 10 에서 보여지는 망에 부합된다. 이런 것들은 두 가지의 제한 조건 표현식들의 집합이다. 한 개는 Happy(B) 에 영향을 준 Happy(A) 를 반영한 것이다.
Happy(A) 가 FALSE
이거나 Happy(B) 가 TRUE
이거나 (Happy(A) ⇒ Happy(B)) 가 FALSE
임이 요구된다.
Happy(A) 가 TRUE 이거나 (Happy(A) ⇒ Happy(B)) 가 TRUE
임이 요구된다.
Happy(B) 가 FALISE이거나 (Happy(A) ⇒ Happy(B)) 가 TRUE
임이 요구된다.
Happy(B) 와 Happy(C) 사이의 제한 조건을 다루는 유사한 집합은
Happy(B) 가 FALSE
이거나 Happy(C) 가 TRUE
이거나 (Happy(B) ⇒ Happy(C)) 가 FALSE
임이 요구된다.
Happy(B) 가 TRUE 이거나 (Happy(B) ⇒ Happy(C)) 가 TRUE
임이 요구된다.
Happy(C) 가 FALSE 이거나 (Happy(B) ⇒ Happy(C)) 가 TRUE
임이 요구된다.
⇒ 에 대한 제한 조건 표현식들과 A 는 행복하다는 사실을 사용함으로서 Happy(B) 와 Happy(C) 둘 모두가 참이라는 사실을 쉽게 끌어낼 수 있다. 이제 잠정적으로는 D 는 C 의 기분에 부정적인 영향을 줄 수 있다고 가정해 보자.
Happy(D) ⇒ ¬ Happy(C)
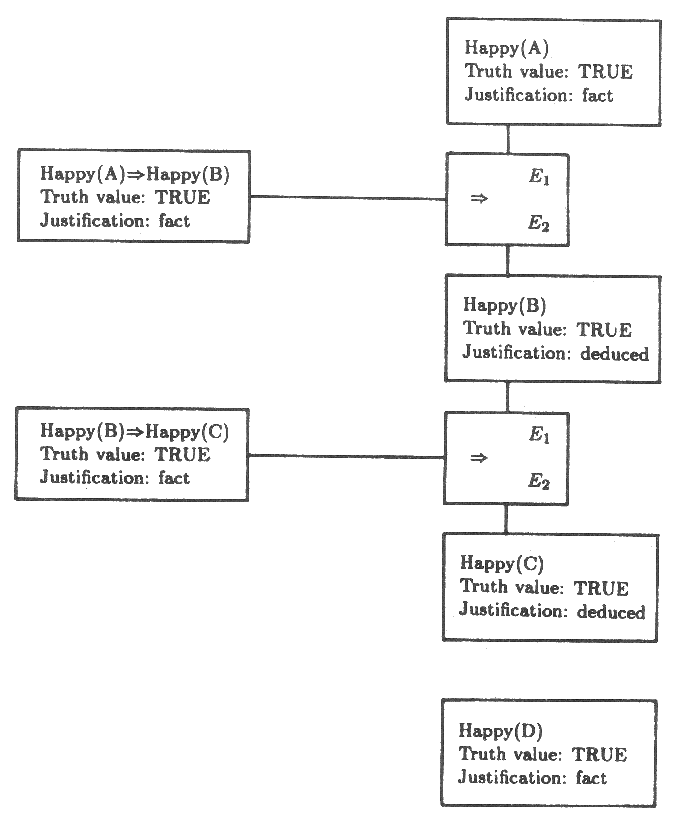
그림 10 : 제한 조건 전파 망. 제한 조건 표현식은 진리값의 전파를 지배한다.
이 표현식은 그림 11 에서 보여지듯이 부가적인 망 구조를 만들어 내며 두 가지의 제한 조건 표현식들의 집합을 갖는다. 그 중 ⇒ 와 ¬ 에 대한 것으로는
Happy(D) 가 FALSE
이거나 ¬ Happy(C) 가 TRUE
이거나 (Happy(D) ⇒ Happy(C)) 가 FALSE
임이 요구된다.
Happy(D) 가 TRUE 이거나 (Happy(D) ⇒ ¬ Happy(C) 가 TRUE
임이 요구된다.
¬ Happy(C) 가 FALSE 이거나 (Happy(D) ⇒ ¬ Happy(C)) 가 TRUE
임이 요구된다.
Happy(C) 가 TRUE 이거나 ¬ Happy(C) 가 TRUE
임이 요구된다.
Happy(C) 가 FALSE 이거나 ¬ Happy(C) 가 FALSE
임이 요구된다.
이것들은 모순 (contradiction) 을 만들어 낸다. 첫번째 ⇒ 의 제한조건 표현식 집합은 ¬ Happy(C) 로 하여금 참이 되게 한다. 왜냐하면 Happy(D) 는 FALSE 가 아닌 TRUE 이고 또한 (Happy(D) ⇒ ¬ Happy(C)) 가 TRUE 로 가정되었기 때문이다. 그러나 ¬ Happy (C) 가 TRUE 라면 두번째 ¬ 제한 조건 표현식의 집합은 Happy(C) 를 FALSE 로 만드므로 Happy(C) 는 참이라는 앞의 결론과 모순된다. 뭔가 잘못되었다.
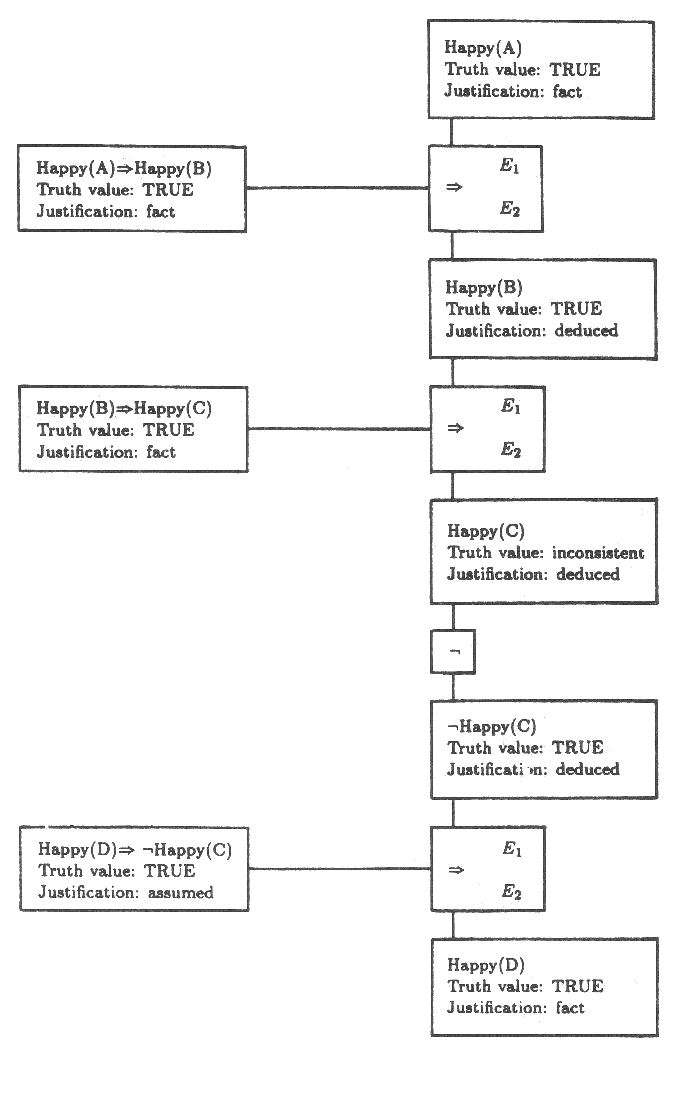
그림 11 : 진리값들은 Happy(D) 로부터 ⇒ 와 ㄱ 노드를 통해 진리 유지망을 거쳐 이동되어 Happy(C) 를 모순되게 한다.
제한조건 전파가 일어날 때 진리값들이 어떻게 결정되었는가에 대한 기록을 유지하는 것은 쉽다. 기록은 단지 유추된 단정 (assertion) 으로부터 그것이 나오게 된 곳 까지를 가리키는 정당성 링크 (justification link) 를 포함하기만 하면 된다.
행복에 대한 예제에서 정당성 링크는 Happy(C) 에 대한 참 값으로부터 사실들과 A, D 및 ㅎ행, 분행에 영향을 주는 것들에 대한 가정들로 거꾸로 추적하는 것을 쉽게 해 준다.
따라서, 어떤 것이 잘못되었을 때, 만약에 한 방향의 추론이 TRUE 라 하는데 다른 것은 FALSE 라고 말한다면 모순을 유발한 가정들을 추적하는 것은 가능하다. 다른 말로 하면 정당성 링크는 우리에게 종속성을 이용한 백트랙킹을 사용 가능하게 함으로써 호환적인 가정들을 발견해낼 수 있게 하는 것이다.
앞 예제에서 C 에 대한 TRUE 값으로부터 뒤로 추적하여 다음과 같은 확실한 것 (solid facts) 으로 주어진 표현식을 얻을 수 있다.
Happy(A) ⇒ Happy(B)
Happy(B) ⇒ Happy(C)
Happy(A)
C 에 대한 FALSE 값의 추적은 다음과 같은 확실한 것으로 주어진 표현식을 가져다 준다.
Happy(D)
FALSE 값은 또한 잠정적인 가정으로 주어진 한 표현식을 가져다 준다.
Happy(D) ⇒ ¬ Happy(C)
모순을 초래한 모든 것을 거꾸로 추적함으로써 무엇을 해야 할까를 고려해야 할 때가 되었다. 서술한 바와 같이 명백한 것은 확실한 것은 남겨 두고 잠정적으로 주어진 단순한 가정을 철회하는 것이다. 따라서 D 의 행복이 C 를 불행하게 한다는 가정을 더 이상 가정할 필요는 없다.
마찬가지로, 만일 가정이 철회된다면 철회된 가정에 의존한 결과들 (consequences) 도 추적하기 쉬워진다. 물론 때때로 한 개 이상의 인자가 결론을 지원할 때 그들 중 하나가 취소되어도 결론은 달라지지 않는 경우도 있다.
예를 들면 Happy(A) 가 TRUE 라는 가정을 철회함으로써 Happy(C) 는 TRUE 라는 결론을 철회하도록 만든다. 그러나 다음과 같이 확실한 사실로서 다섯번째 E 라는 사람은 행복하고 그의 행복은 C 의 행복을 초래한다고 가정하자.
Happy(E)
Happy(E) ⇒ Happy(C)
이제 그림 12 에서 보는 바와 같이 Happy(C) 는 TRUE 라는 것을 보일 두번째 독립적인 방법을 갖고 있다. Happy(E) 가 가정되자마자 새로운 ⇒ 에 대한 제한 조건 표현식의 집합을 다시 사용함으로써 Happy(C) 가 TRUE 라고 결론을 내릴 수 있다. Happy(A) 가 TRUE 라는 가정을 철회해도 Happy(C) 는 TRUE 이다.
.gif)
그림 12 : Happy(C) 를 지원하는 두번째 경로가 주어진다면 Happy(C) 는 첫번째 경로가 철회된 후에도 TRUE 로 남게 된다.
1. 논리는 공리 (axioms) 로부터 새로운 표현식을 유도해낸다. 하나의 과목으로서 논리는 지식을 엄격하고 아마도 올바른 방법으로 사용하는데 중점을 둔다. 다른 문제 해결 모범예들 (problem solving paradigms) 은 지식 그 자체에 집중한다.
2. 논리는 implies, and, or, not 들에 대한 전통적인 표기법인 ⇒, &, ∨, ¬ 을 갖고 있다.
3. ∨ 가 TRUE 일 때 그 영역 (scope) 내에서 그 표현식은 한정된 변수의 모든 값들에 대해 TRUE 임을 규정한다. ∃ 가 TRUE 일 때 그 영역 내에서의 그 표현식은 최소한 한 개의 값에 대하여 TRUE 이다.
4. 만약에 건전한 (sound) 추론 규칙을 사용하여 정리가 공리들로 연결되는 일련의 단계들이 존재한다면 그 정리는 가정된 공리로부터 논리적으로 따른다 (logically follows).
5. 가장 명백한 추론 규칙은 모더스 포넨스 (modus ponens) 이다. 그보다 더 일반적인 추론 규칙은 레졸루션 (resolution) 이다.
6. 레졸루션 정리 증명 방법은 추론 규칙으로서 레졸루션을 사용하고 전략 (strategy) 으로서 반박 (refutation) 을 사용한다. 레졸루션은 공리들과 부정된 정리를 절 (clause) 형식으로 변환시킬 것을 필요로 한다.
7. 레졸루션은 또한 단일화 (unification) 라 불리는 변수 치환 (variable substitution) 과정을 필요로 한다.
8. 지원 집합 (set-of-support) 전략은 레졸루션을 사용할 때 최소한 한 개는 증명되기 위하여 부정된 정리로부터 나온 도출절을 사용한다는 것이다.
9. 논리는 종종 깨끗이 동작되므로 매력적이다. 그러나 논리는 많은 도구들 중의 하나일 뿐이다.
10. 논리를 사용하여 일련의 연산자 (operator sequences) 를 찾으려면 상황들을 추적 기록할 수 있는 어떤 기법이 요구된다. 보통 방법은 상황을 나타내는 인수들 (situation-indicating arguments) 을 갖는 술어 (predicates) 에 표시하는 것이다.
11. 상황을 나타내는 인수들이 소개되었으므로, 연산자가 적용되어도 그 값이 불변하는 술어들을 추적 보관할 수 있는 어떤 기법이 있어야만 한다. 프레임 공리를 사용하는 것은 하나의 방법이다.
12. 논리에 제한 조건의 전파 방법을 사용할 때, 논리적 표현식에 의하여 제공된 제한 조건을 사용하는 노드들을 통하여 진리값들이 전파된다.
13. 제한 조건의 전파를 사용하면, 모든 결론들에 대하여 정당성의 추적 기록을 쉽게 할 수 있다. 이런 정당성은 철회된 가정을 쉽게 다루게 해 준다.
정리 증명을 위한 레졸루션의 개발은 비록 다른 사람들도 중요한 공헌을 했지만 J. A. Robinson [1965, 1968] 이 일반적으로 명성을 얻고 있다. 특별히 C. Crodell Green 은 그의 영향력 있는 논문에서 상황 변수와 Green 의 기법을 논리로 끌어들여 일련의 연산자들의 유도를 가능하게 하였다 [1969]. Green 의 논문은 또한 논리 프로그래밍의 아이디어를 소개 했다.
Robert Kowalski 는 논리 프로그래밍을 대중화시키는데 공헌하였다. 그의 책 "문제 해결을 위한 논리 [1979]" 는 고전이다. 오늘날 논리 프로그래밍은 항상 Alain Colmerauer 와 그의 동료 [Colmerauer, H. Kanoui, R. Pasero, 그리고 P. Roussel 1973 ; Colmerauer 1982] 에 의하여 개발되어진 PROLOG 프로그래밍 언어로 하게 된다. 좋은 논문들을 만나 보려면 Keith L. Clark 그리고 StenAke Tarnlund 에 의하여 편집된 "논리 프로그래밍 [1982]" 을 보면 된다. 좋은 교재로서는 William F. Clocksin 과 Christopher S. Mellish 가 저술한 "Programming in PROLOG" 를 보라.
많은 관점에서 PROLOG 는 Gerald J. Sussman, Terry Winograd, 그리고 Eugene Charniak [1971] 에 의하여 개발된 MICROPLANNER 언어와 닮았다. 그것은 Carl E. Hewitt [1969] 에 의하여 제안되어진 PLANNER 언어에 기본을 두고 있다. Hewitt 는 지금 다른 방향으로 연구를 하고 있다. [William A. Kornfeld 와 Hewitt 1981].
프레임 공리의 사용의 대안으로 연산자들에게 연산자를 적용할 때 공리들 집합에 추가될 표현식 및 삭제될 표현식 리스트들을 부여하는 것이다. 이러한 연산자들은 프레임 공리들이 필요없이 정확하게 술어값을 유지한다. STRIPS 는 Richard E. Fikes, Nils J. Nilsson, 그리고 Peter Hart 에 의하여 개발되어진 문제 해결기로서 그러한 연산자들을 방법 목적 분석 (means-ends analysis) 과 결합하여 일반적 문제 해결기 (General Problem Solver), GPS [Fikes 와 Nilsson 1971] 를 만들었다.
진리값 유지 (Truth-maintenance) 에 대한 아이디어는 Gerald J. Sussman 과 Richard M. Stallman [1975] 에 의하여 전자 회로 분석의 연구로부터 출현하였다. 이 장의 표현식들은 David A. McAllester [1980] 의 연구에 기초를 두어 표현하였다. Drew McDermott 와 Jon Doyle [1980] 의 연구는 또한 관계가 있다.
인공 지능에서의 논리의 역할을 훌륭히 다룬 것을 보려면 Patrick J. Hayes [1977] 을 보라. 또한 Nils Nilsson 의 교재인 "Principles of Artificial Intelligence [1980]"을 보라. Nilsson 은 인공 지능이 응용된 논리라는 논쟁적 관점을 갖고 있다.