계획수립
(Planning)
인공지능 이론 및 실제 : Thomas Dean. James Allen. John Aloimonos 공저, 김진형.박승수.백은옥. 서정연.이일병 공역, 사이텍미디어, 1998 (원서 : Artificial Intelligence: Theory and Practice, 1995), Page 309~369
로봇 지게차가 대형 트레일러에서 엔진 블록을 내리고 있는데, 공장으로부터 부품이 부족하여 주 생산라인이 중단되었다는 연락이 왔다 (그림 1). 로봇은 들고 있던 엔진 블록을 내려놓으면서 동시에 생산을 계속하기 위해 필요한 부품이 무엇인지를 알아본다. 생산라인의 부품조립부에서 특정한 가스켓이 다 떨어졌다는 것을 알게 된 로봇은 우선 창고에 그 부품이 있는 위치로 가서 필요한 가스켓을 싣고, 공장의 부품조립부에 가져다 준 후에 엔진 블록을 내려놓는 일을 계속한다.
그림 1 : 자동화된 공장과 통신 중인 로봇 지게차가 공장에서 생산중단의 원인이 된 가스켓을 실어 나르는 계획을 한다.
이 시나리오에서 로봇 지게차는 공장에서의 생산을 계속되게 해야 한다는 목적을 갖고 있다. 생산이 중단되었다는 정보를 들은 로봇은 생산을 재개하기 위한 계획을 수립한다. 이 계획은 다음과 같은 단계로 이루어진다 : 1) 현재 들고 있는 엔진 블록을 내려놓는다. 2) 필요한 부품이 무엇인지, 그 부품이 창고 안 어느 위치에 있는지를 알아본다. 3) 창고의 그 위치로 간다, 4) 필요한 부품을 싣는다, 5) 공장 내의 알맞은 위치로 간다, 6) 부품조립부에서 사용할 수 있도록 부품을 내려놓는다.
어떤 목적을 달성하기 위해 일정한 행동 순서열을 계획해야 할 필요는 여러 응용에서 많이 찾아볼 수 있다. 다음의 예들을 보면 계획을 필요로 하는 응용이 얼마나 다양한가를 알 수 있을 것이다.
• 과학실험 일정관리 - 우주 셔틀이나 허블 (Hubble) 망원경과 같은 값비싼 미항공 우주국 (NASA) 의 장비들은 이를 사용하고자 하는 과학자의 수가 많아서 이 장비들을 요하는 실험의 일정을 관리하기 위한 계획 시스템이 개발되었다.
• 맥주제조 과정에서 부족한 자원의 관리 - 발효를 위한 양조통은 양조업에서는 귀한 자원이다. 주문 양조장에서 여러 종류의 맥주를 조금씩 생산할 때 사용할 수 있는 양조통을 배분하는 데에 계획 시스템이 사용된다.
• 해상운송업계의 순서 정하기 - 항구에서는 선박에 적재된 컨테이너 화물을 싣고 부리기 위해 대규모의 기중기가 사용된다. 계획 시스템을 사용하여 어떤 순서로 선박의 화물을 처리할 것인지와 이를 위해 기중기를 어떻게 배정할 것인지를 결정한다.
이 장의 뒷부분에서 알 수 있듯이 계획수립은 탐색과 공통점이 많다. 그리고 실질적인 이익을 얻을 만한 문제는 대부분 계산적 복잡성이라는 문제를 야기하는 조합적 폭증의 성질을 갖고 있다.
계획수립이란 무엇인가?
직관적으로 계획이란 행동하기 위한 전략이다. 계획을 한다는 것은 여러 가지 계획들을 고려하고, 이들이 가져 올 결과에 대해 추론하는 것을 내포한다. 간단한 경우를 생각해 보자. 어떤 로봇이 대여섯 가지 행동 중에서 딱 한 가지만을 수행할 수 있으며, 일단 한 행동을 수행하고 나면 다른 어떤 행동도 할 수 없다고 하자. 또한, 로봇은 자신이 하는 행동의 결과를 예측할 수 있으며, 각 행동은 서로 다른 결과를 낳게 된다고 할 때 행동을 선택하는 것은 곧 미래를 선택하는 것이 된다.
로봇이 여러 가지 행동 중에서 하나를 선택하기 위해, 즉 여러 가지 미래 중에서 하나를 선택하기 위해 사용할 수 있는 여러 기준을 생각해 볼 수 있다. 예를 들어, 어떤 명제가 (스스로 부유해지는 것) 어떤 미래 상황에서 참이 된다면 그 명제가 거짓이 되는 미래 상황보다 더 바람직한 미래를 가져오는 경우를 생각해 볼 수 있다. 그러한 명제를 목적 (goal) 이라 부른다. 어떤 행동을 선택함으로써 미래에 특정한 목적이 참이 되게 하는 에이전트를 만족화한다 (satisficing) 라고 한다. 행동을 선택하기 위한 다른 전략으로서 에이전트는 가능한 미래에 대해 각각 어떤 값을 설정할 수 있다고 하고 이 값이 크면 클수록 어떤 의미에서 더 나은 미래라 하자. 행동을 선택할 때 그 행동이 가져 올 미래의 값이 최대가 되도록 하는 에이전트를 최적화한다 (optimizing) 라고 한다.
4 장 탐색에서 우리는 이미 만족화하며 최적화하는 알고리즘을 살펴보았다. 계획을 한다는 것은 탐색의 특정한 경우로 바람직한 미래를 가져 올 계획을 찾기 위한 탐색을 하는 것이다.
탐색으로서의 계획수립
계획수립을 탐색의 일종으로 설명하는 방법에서는 탐색공간을 다루고자 하는 세계의 모든 가능한 상태 (state) 의 집합으로 본다. 이때, 연산자는 한 상태를 다른 상태로 변환하는 행동에 해당하며 초기상태를 변환하여 주어진 목적을 만족시키는 상태로 이르게 하는 연산자들의 모든 순서열이 성공적인 계획에 해당한다. 이런 이유로 해서 계획을 일종의 상태공간 (state-space) 에서의 탐색으로 여기는 방법론을 상태공간 탐색 (state-space search) 이라 부른다.
계획수립을 탐색의 일종으로 설명하는 또 다른 방법에서는 모든 가능한 계획들로 이루어진 탐색공간을 생각하는데 이 경우 연산자는 하나의 계획을 다른 계획으로 변환하며 이는 행동에 해당하는 계획 단계 (plan step) 를 추가하거나 이들의 순서를 조정하여 이루어진다. 이 방법론의 장점은 하나의 계획을 단순히 하나의 행동 순서열 이외의 다른 것으로 생각할 수 있다는 것이다. 예를 들어, 계획을 행동의 부분순서 집합으로 표현함으로써 행동들 사이의 순서가 의미없을 때에는 이에 대한 결정을 피할 수 있다.
다른 에이전트나 프로세스와의 조정이 가능하도록 계획하는 것은 훨씬 복잡한 문제이다. 한 에이전트가 취할 수 있는 행동이 단 하나로 제한되어 있다 하더라도 그 에이전트는 다른 에이전트나 프로세스들이 자신의 행동이 가져 올 결과를 바꿀 수 있는 수 많은 가능성에 대하여 고려해야만 하기 때문이다. 한 에이전트가 일련의 행동을 고려하고 있다면, 다른 에이전트와 프로세스들이 만들어 내는 효과들에 대응할 방법을 고려해야만 한다.
다른 에이전트나 프로세스는 없지만 자신의 행동의 결과에 어떤 불확정성이 있을 때에는 고정된 행동 순서열이 최선의 계획이 아닐 수도 있다. 에이전트가 자신의 행동의 즉각적인 결과를 관찰할 수 있다고 하면 조건부 계획 (conditional plan) 을 수립하여 계획의 각 단계에 대하여 그 이전 단계의 결과를 관찰한 뒤에 취해야 할 올바른 행동을 명시할 수 있다. 예를 들어, 밤늦게 우유 한잔을 사 마시기 위한 계획은 동네의 가게에 가서, 그 가게가 열려 있으면 (이는 그 가게에 가면 관찰할 수 있는 것이다) 거기에서 우유를 사고, 그렇지 않으면 24 시간 편의점까지 차를 타고 가서 사는 것일 수 있다.
어떤 경우에는 미래가 불확실할 뿐더러 아무리 관찰을 많이 하더라도 행동을 취하기 전에 그 불확실성을 해결할 수 없을 수도 있다. 예를 들어, 휴가를 잘 보내려면 날씨가 좋아야 하는 것이 중요할 터인데 불행히도 장기 일기예보는 정확하지 않고 그럼에도 불구하고 여러 가지 이유로 해서 휴가계획은 충분한 시간을 두고 미리미리 세워야 하는 것이다. 이런 경우에는 불확실한 결과의 확률값을 고려하는 것이 유용하다. 예를 들어, 휴가를 가려고 하는 장소가 8 월 중에는 날씨가 좋을 가능성이 70 % 이고, 12 월 중에는 30 % 밖에 되지 않는다는 것을 알아볼 수 있을 것이고, 이런 확률값과 두 가지 가능한 시기에 휴가를 잘 보내는 데 필요한 비용을 감안하여 기대값을 최대화하는 행동 순서열을 선택할 수 있다.
이 장에서는 확률적 모델링에 관련된 문제를 다루지 않으나, 8 장 불확실성에서는 불확실성 하에서의 계획에 관하여 언급할 것이다. 이 장에서는 계획을 실행하는 것보다는 계획을 수립하는 것에 중점을 두겠지만 실제로는 계획의 수립과 실행이 흔히 서로 맞물려 있다. 많은 경우 우리가 처한 세계와의 상호작용을 통해 계획을 잘 수립하거나 정확히 미래를 예측할 필요없이 우리의 목적하는 바를 이룰 수 있다. 계획수립과 실행에 관련된 문헌에서는 일어나는 사건에 직접적으로 반응하는 것을 흔히 상황에 처한 활동 (situated activity) 이라 부른다.
급박하게 진행되는 비디오 게임에서 높은 점수를 얻는 것이 목적인 경우에는 매번 어떻게 할 것인지를 미리 잘 계획하려는 것이 오히려 방해가 될 수가 있다. 높은 점수를 얻으려면 일어나는 사건들을 재빨리 관찰하고 상황에 맞게 대처해야 한다. 2 장 기호 프로그래밍에서 설명된 규칙기반 반응 시스템은 상황에 처한 활동을 위해 간단히 설계된 예이다. 상황에 처한 활동에 관련된 문제들 중 지각과 상관있는 것들은 9 장 영상 이해에서 살펴볼 것이다.
이 장에서는 계획 수립을 위한 몇 가지 방법론을 살펴본다. 우선 계획수립을 상태공간에서의 탐색으로서 묘사하고 나서 여기서 사용된 기본적인 행동표현을 확장하여 좀더 일반적인 계획표현을 개발하고 이와 같은 계획 공간에서의 탐색을 어떻게 할 것인가를 고려해 보겠다. 또한 계획 수립 문제를 여러 추상 수준에서 표현하고 가장 추상적 수준에서 시작하여 일련의 정련 (refinement) 을 통해 가장 덜 추상적인 수준에 도달하게 함으로써 계획 수립을 빠르게 할 수 있는 방법론에 대해서도 설명하겠다. 계획 수립을 빠르게 할 수 있는 또 다른 방법론은 과거의 해법을 기억하고 있다가 현 상황에 맞게 그것을 고쳐 사용하는 것이다. 계획 수립에 대한 이와 같은 적응방법론은 일종의 학습에 해당한다. 또한 우리는 불완전 정보 하에서의 계획 수립 방법론에 대하여도 고려해 보며, 마지막으로는 행동을 더욱 표현력 있게 나타냄으로써 계획 수립과 관련된 몇 가지 문제에 대하여 논의해 보겠다.
탐색문제의 표현과 해결
이 절에서는 탐색문제를 계획수립으로서 표현하고 해결하는 방법론을 소개한다. 탐색에 대한 이 방법론이 계획수립에 관한 장에서 첫번째 절로 나오는 이유는 계획수립과 탐색 사이의 밀접한 연결을 강조하기 위해서다.
앞으로 탐색공간에서의 노드는 상태 라 부르고, 탐색공간 과 상태공간 은 혼용하겠다. 이 장에서 서술된 명제논리판 계획수립에서는 모든 상태의 집합을 명제적 상태변수 (propositional state variable) 의 집합 P = {P1, ..., Pn} 로 정한다. 예를 들어, 명제적 상태변수 "불이 켜져 있다" 와 "문이 닫혀 있다" 가 있다고 할 때, 특정한 상태란 진리값의 할당 σ : P → {True, False} 에 해당한다. 즉, "불이 켜져 있다" 는 True 로, "문이 닫혀있다" 는 False 로 할당되는 것이 한 상태가 되는 것이다.
하나의 목적이란 부분할당 γ : Q → {True, False}, Q ⊆ P 이다. 예를 들어, 우리는 상태변수 "문이 닫혀 있다" 가 True 로 할당되기를 원하지만, "불이 켜져 있다" 의 진리값에는 무관심할 수 있다. 하나의 목적 γ 가 주어졌을 때, 상태공간에서의 탐색의 목표는 초기상태 σ 를 σ' 으로 변환하는 것인데, 이때 σ' 은 γ 를 함언 (imply) 해야 한다.
상태 변환은 주어진 연산자의 집합에서 선택된 연산자들의 순서열을 적용함으로써 이루어진다. 각 연산자는 하나의 규칙으로 표현될 수 있는데, 이 규칙은 연산자가 어떤 조건하에서 한 상태에 적용될 수 있는지를 결정하고, 적용의 결과가 되는 상태를 서술한다. 예를 들어, 불이 켜 있고 문이 열려 있을 때에만 적용될 수 있는 그리고 결과적으로 문이 닫히게 하는 문닫기 연산자를 생각해 볼 수 있다. 진리값의 할당으로 생각해보면 이 연산자는 "불이 켜져 있다" 가 True, "문이 닫혀 있다" 가 False 로 할당되어 있는 경우에 적용되어 문 닫는 연산자를 적용한 결과로 "문이 닫혀 있다" 는 True 로 할당되고 나머지 진리값은 적용 이전과 같게 되는 것으로 표현될 수 있다.
많은 경우에 상태와 목적 그리고 연산자를 집합론적 용어로 표현하는 것이 편리한데, 그럴 경우 조건은 상태변수나 그 부정에 해당하고, 상태는 True 가 할당된 조건들의 집합이 된다. 임의의 상태변수 P 와 상태 S 에 대해 P ∈ S 이거나 ￢ P ∈ S 이며 둘 다 성립하지는 않는다. 상태 S 가 목표 G 에 대해 G ⊆ S 이면 S 가 G 를 만족시킨다 (satisfy) 라고 한다.
상태 S 에서는 절대로 P 와 ￢ P 가 동시에 허용되지 않지만 모든 상태변수 P 에 대하여 P ∈ S 또는 ￢ P ∈ S 둘 중의 하나는 성립해야 한다는 조건을 완화하는 것은 편리할 것이다. 즉 예를 들어, 하나의 상태에 어떤 물체가 빨강색이라는 조건이 포함되어 있을 때 그 물체가 파랑색이 아니고, 초록색도 아니고 등등을 나타내는 조건들도 모두 포함되어 있기를 원하지 않을 것이다. 이와 같이 상태변수에 진리값을 내포적으로 할당하는 방법은 일종의 닫힌 세계 가정인데, 이는 3 장 표상과 논리의 비단조추론에 관한 절에서 논의된 바 있다.
집합론적 용어로 말하면, 연산자는 (P, A, D) 세 부분으로 이루어지며 각각은 조건들의 집합이다 : P 는 연산자가 적용되는 상태에서 참이어야 하는 전제조건 (preconditions) 의 집합, A 는 연산자를 적용한 결과가 되는 상태에서 참이어야 하는 추가조건 (additions) 의 집합, D 는 연산자를 적용한 결과 상태에서 거짓이어야 하는 삭제조건 (deletions) 의 집합이다.
상태 전진
전방향 (forward) 으로 연산자를 적용하는 것 (하나의 상태를 다른 상태로 변환하는 것) 을 상태 전진 (state progression) 이라 부른다. 연산자 α = (P, A, D) 는 어떤 상태 S 가 P 를 포함하면 S 에 전방향으로 적용될 수 있는데 이때 결과가 되는 상태는
fα (S) = A U (S - D)
이고 U 과 - 는 각각 합집합과 차집합을 나타낸다.
함수 fα 는 최강의 증명가능한 사후조건 (strongest provable postcondition) 을 계산한다고 하는데 이는 연산자의 적용으로 인해 결과상태에서 참이어야만 하는 것들을 고려할 때 전진된 상태가 원래의 상태에서 최대한 많은 것들을 유지하기 때문이다. 원래 상태에서 참이었던 것들 중 연산자의 삭제조건에 명시되어 있지 않은 것은 모두 전진된 상태에서도 참인 것으로 가정한다.
목적 회귀
연산자를 후방향 (backward) 으로 적용하는 것 (하나의 목적을 다른 목적으로 변환하는 것) 을 목적 회귀 (goal regression) 라 부른다. 연산자 α = (P, A, D) 는 어떤 목적 G 가 D 와 공통된 것이 없을 때 G 에 후방향으로 적용될 수 있는데, 이때 결과가 되는 목적은 아래와 같이 정의된다.
bα (G) = P ∪ (G-A)
함수 bα 는 최약의 증명가능한 전제조건 (weakest provable precondition) 을 계산한다고 하는데, 이는 회귀된 목적이 연산자의 적용 이전에 만족될 경우 연산자를 적용한 이후에도 여전히 원래의 목적이 만족되어야만 한다는 것을 보장하면서 원래의 목적에서 최소한의 것만을 유지하기 때문이다. 예를 들어, "문이 닫혀 있다" 라는 목적과 앞에서 본 문닫기 연산자가 주어졌을 때 문닫기 연산자를 사용하여 얻어진 회귀목적은 "불이 켜져 있다" 와 "문이 열려 있다" 로 이루어진다.
상태전진을 이용하면 초기상태에서 시작하여 주어진 목적을 만족시키는 전진된 상태를 찾아 전방향으로의 탐색을 해 나갈 수 있고 목적회귀를 사용하면 주어진 목적에서 시작하여 초기상태에서 만족되는 회귀된 목적을 찾아 후방향으로 탐색을 해나갈 수 있으며 또한 전방향과 후방향 탐색을 동시에 하는 탐색 전략도 가능하다.
목표와 수단 분석
목적 G 와 상태 S 사이의 차집합 G - S 는 흔히 하나의 상태가 어떤 목적에서 얼마나 떨어져 있는지를 측정하는, 약하지만 유용한 잣대가 된다. 차이 (difference) 는 목적에서는 참이지만 현 상태에서 거짓인 것들을 말하고, 목표와 수단 분석 (means / ends analysis) 은 현 상태와 목표 사이의 차이의 개수를 줄이는 연산자들을 선호하여 적용하는 휴리스틱 전략을 말한다.
예를 들어, 우리가 문이 열려 있고 불이 켜있는 상태에 있고 우리의 목적이 문이 닫히도록 하는 것이라고 하면 우리는 문닫기 연산자를 불끄기 연산자보다 선호할 것이다. 그러나 목표와 수단 분석이 해 주는 충고에 어긋나게 연산자를 선택해야 할 때도 있을 것이다. 우리에게 세 개의 연산자가 있다 하자. 하나는 불이 켜 있고 문이 열려 있어야만 문을 닫는 것, 두번째는 불이 꺼져 있을 때 켜는 것, 세번째는 불이 켜 있을 때 끄는 것이라 하자. 지금 우리가 문이 열려 있고 불이 꺼져 있는 상태에 있고 우리의 목적이 불을 끄고 문을 닫는 것이라면 이 목적을 달성하기 위해서는 우선 불을 켜고 문을 닫은 다음에 불을 꺼야 할 것이지만, 첫 단계인 불을 켜는 행동은 차이를 줄이기보다는 늘이게 된다.
우리는 간단한 형태의 상태공간에서의 탐색을 상태전진에 근거하여 비교적 쉽게 구현할 수 있다. 먼저 연산자들에 대한 자료 추상화로부터 시작해 보자.
(defun make-OPERATOR (preconditions additions deletions)
(list preconditions additions deletions))
(defun preconditions (operator) (first operator))
(defun additions (operator) (second operator))
(detun deletions (operator) (third operator))
그림 2 는 연산자의 집합과 상태가 주어졌을 때 주어진 상태에서 전제조건이 참인 모든 연산자들을 적용하여 얻어진 결과 상태들의 리스트를 리턴한다. Apply-operators 의 구현은 리스트로 표현된 집합을 처리하는 Common Lisp 루틴을 사용한다. Subsetp, union 그리고 set-difference 는 집합에 대한 포함관계, 합집합, 차집합 연산을 한다. 이들은 각각 집합의 원소들 사이의 동등성을 검사하기 위하여 사용되는 함수에 해당하는 것을 선택적 키워드 인자 (argument) 로 취하는데, 임의의 표현을 조건으로 허용하는 것이 편리하므로 동등성 검사에 equal 을 사용하겠다. Apply-operators 를 사용하면 4 장 탐색에서 정의된 일반적 탐색 루틴으로 상태공간에서의 탐색을 구현할 수 있다.
그림 2 : 상태공간에서의 탐색에서 다음 상태의 생성
그림 3 은 두 종류의 상태공간에서의 탐색을 나열하고 있다. 첫번의 sss 는 일반적인 너비우선 탐색 루틴을 사용하였는데, 목적함수는 Common Lisp 의 subsetp 루틴을 사용하여 구현되었고, 한 노드의 자식들을 생성하는 데 필요한 함수는 apply-operators 를 사용하여 구현되었다. 두번째의 mea 는 수단 / 목표 분석을 도입하였는데, 이는 한 상태와 목표간의 차이에 근거한 거리 측정을 가지고 최상우선 탐색을 적용함으로써 이루어졌다. 너비우선 방법은 컴퓨터의 메모리가 모자라지 않는다고 가정할 때, 해가 존재한다면 언제나 해를 찾을 것이다.
그림 3 : 상태공간 탐색의 두 가지 구현 예
기계조립 예
위의 상태공간 탐색을 설명하는 간단한 예를 살펴보자. 세 개의 부품으로 이루어진 기계를 조립하는 방법을 알아내려고 하는 로봇이 있다고 하자. 처음에는 조립된 부품이 하나도 없으며 세 개를 모두 조립하는 것이 로봇의 목적이라 하자.
네 개의 연산자가 있는데 이들은 부품이 조립되어야 하는 순서와 관련된 상호작용을 나타내고 있다. 한 연산자는 첫째 부품이 아직 조립되어 있지 않을 때 이를 조립한다. 다른 연산자는 앞의 두 부품이 조립되었을 때에만 세번째 부품을 조립한다. 두번째 부품의 조립을 결정하는 연산자는 둘인데 하나는 첫째 부품이 조립되어 있을 경우에 적용되고, 다른 하나는 첫째 부품이 조립되어 있지 않을 때 적용된다. 첫째 부품이 이미 조립되어 있는 상태에서 둘째 부품을 조립하게 되면 첫째 부품은 떼어내지는 결과를 초래한다. 그림 4 는 초기상태, 목적 그리고 연산자를 Lisp 로 구현한 것을 보여 준다.
그림 4 : 기계조립 예에 대한 초기상태와 연산자와 목적
두 형태의 상태공간 탐색 모두 이 간단한 문제에 대한 해를 쉽게 찾는데, 수단 / 목표 분석을 사용하는 경우에 해를 찾는 데 걸리는 시간이 다른 경우의 절반 정도이다. 수행 시간의 차이는 기저의 탐색공간을 조사해 보면 그 이유가 명백하다.
그림 5 는 기계조립 예에 대한 상태공간을 묘사하고 있는데 네 가지 연산자는
a, b, c, d 로 표기되었다. 그림 5 의 윗부분에서 각 연산자는 여러 부분으로 나뉘어진
네모로 표기되어 있는데, 네모의 왼쪽은 전제조건을, 오른쪽 위는 추가조건을, 오른쪽
아래는 삭제조건을 지칭한다. 그림 5 의 아랫부분은 탐색공간을 보여 주는데 숫자
1 에서 3 까지를 세 부품을 지칭하는 데 사용하였다. 숫자 위에 막대를 그은 것은
해당하는
부품이 조립되지 않았음을 나타내고, 막대가 없는 것은 부품이 조립되었음을 나타낸다.
상태는 집합으로 표현되는데 예를 들어,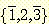 
은, 부품 2 는 조립되어 있고 부품
1 과 3 은 조립되어 있지 않은 상태를 나타낸다.
그림 5 에서 점선으로 된 화살표는 차이의 개수를 감소시키는 변환에 해당하는데, 이 경우 수단 / 목표 분석은 탐색 방향이 거의 직접 해답에 이르도록 해 준다. 이 절에서 이미 언급한 바와 같이 수단 / 목표 분석이 늘 유용한 길로 인도하는 것은 아닌데 이는 해를 찾기 위해 차이의 개수를 증가시킬 필요가 있는 때도 있기 때문이다.
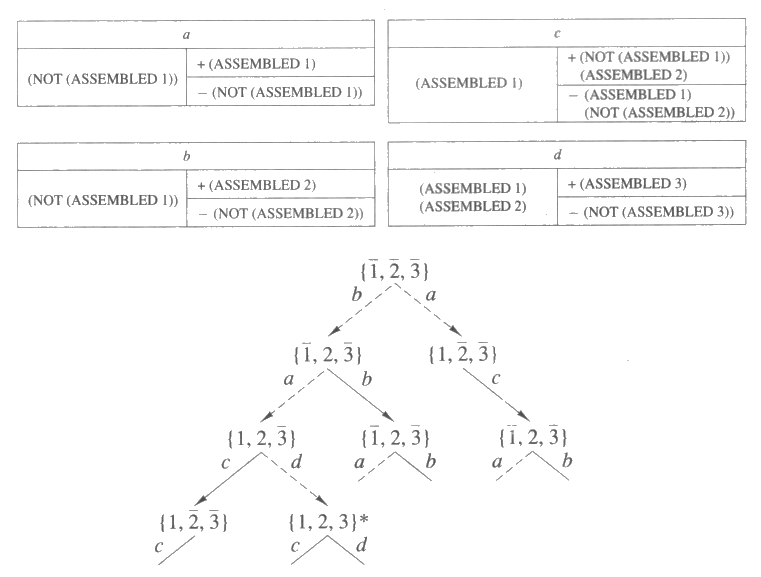
그림 5 : 기계조립 예의 상태공간 탐색. 네 개의 연산자 a, b, c, d 는
위에 여러 부분으로 나뉜 네모로 나와 있는데, 왼쪽에는 전제조건, 오른쪽에는
추가조건 (+) 과 삭제조건 (-) 이 표시되어 있다. 탐색공간은 아래쪽에 나와 이는데,
각 상태는 집합으로, 에지는 연산자로 표시되어 있다. 예를 들어 
는 연산자 c
가 첫째 부품만 조립되어 있는 상태를 둘째 부품만 조림되어
있는 상태로 변환함을 나타낸다. 점선으로 된 에지는 차이를 줄이는 변환을 나타내고,
목적상태는 별표로 표시되어 있다.
연산자 스키마
우리가 사용하는 종류의 연산자가 여러 다른 대상에 적용되는 것이라면, 연산자를 일일이 명시하는 것이 귀찮은 일이 될 수 있다. 예를 들어, 여러분의 바로 앞에 움직일 공간이 있을 때에 앞으로 일보 전진할 수 있는 연산자를 갖고 있다고 해보자. 모든 가능한 위치에 대해 일일이 새로운 연산자를 적어 내려가는 대신 연산자 스키마 (operator schema) 를 사용하여 이 모든 움직임 연산자의 집합을 간결하게 표현할 수 있다.
상태공간 탐색에서의 연산자 스키마는 명제논리에서 정리증명을 할 때 공리 스키마가 하는 것과 거의 비슷한 역할을 한다. 3 장 표상과 논리에서 소개한 정합 (matching) 과 변수대입 기술을 사용하여 Lisp 에서 연산자 스키마를 구현하는데, 특별히 (? x) 와 같은 형태를 사용하여 주어진 도메인의 모든 객체를 그 값으로 가질 수 있는 스키마 변수 (schema variable) 를 표현한다. 이 장의 연습문제에는 3 장에서 정의한 함수 match 와 varsubst 를 이용하여 apply-operators 를 연산자 스키마에 대해서도 동작할 수 있도록 고치는 문제가 있다.
볼록쌓기 문제
연산자 스키마의 사용에 관해 설명하기 위해 블록쌓기 문제라 불리우는 종류의 문제들을 소개하겠다. 이 책에서 특별히 살펴 볼 블록쌓기 문제에서는 하나의 탁자와 여러 개의 블록이 사용되는데, 각 블록 위에는 아무 것도 없거나 단 하나의 다른 블록이 있을 수 있다. 연산자를 적용함으로써 변화되는 조건들은 (on (? x) (? y)) 나 (clear (? x)) 의 형태로 되어 있는 것들이다. 또한, (not (equal (? x) (? y))) 의 형태로 표현된 정적 조건 (static condition) 들의 집합이 있는데, 이들은 어떤 블록과 타자를 또 서로 다른 블록들을 구분하는 데 쓰인다.
(not (on (? x) (? y))) 형태의 조건은 상태 안에서 직접 명시되지는 않고, (on x y) 가 상태에 포함되어 있으면 y ≠ z 인 모든 z 에 대해 (not (on x z)) 가 암시적으로 포함된 것이 된다. 마찬가지로 (on x y) 가 상태에 들어 있고 y 가 탁자가 아니라 블록이면, x ≠ z 인 모든 z 에 대해 (not (on z y)) 가 그 상태에 암시적으로 포함된다. 다음은 현재 다른 블록 위에 있는 블록을 탁자로 내려놓는 연산자의 일례이다.
;; 블록 (? x) 를 블록 (? y) 위에서 탁자로 내려놓는다.
(make-OPERATOR ;; 전제조건
'((on (? x) (? y)) (clear (? x))
(not (equal (? y) table)))
;; 추가조건
'((on (? x) table) (clear (? y)))
;; 삭제조건
'((on (? x) (? y))))
이 연산자 스키마에 따르면 (? x) 위에 아무 것도 없고 (? x) 가 (? y) 위에 있으면, (? x) 와 (? y) 가 특정 블록에 결합된 상태에서 그 스키마의 사례 (instance) 를 적용할 수 있다는 것이다. 한 상태에서 전제조건이 만족되면 결과가 되는 상태에서는 (? y) 위에는 아무 것도 없게 되고 (? x) 는 (? y) 위가 아니라 탁자 위에 있게 된다. 다음은 주어진 연산자 스키마에서 (? x) 가 a 로, (? y) 는 b 로 결합된 경우에 해당한다.
;; 블록 a 를 블록 b 위에서 탁자로 내려놓는다.
(make-OPERATOR ;; 전제조건
'((on a b) (clear a)
(not (equal b table)))
;; 추가조건
'((on a table) (clear b))
;; 삭제조건
'((on a b)))
이 연산자 스키마에서 (not (equal (? y) table)) 은 (? x) 가 이미 탁자 위에 있을 때는 연산자가 적용되지 않도록 하기 위해 필요한 조건임에 주의하라. 또한 각 블록 a 에 대해 모든 상태에는 (not (equal a table)) 이, 그리고 a 와 b 에 대해 모든 상태에는 (not (equal a b)) 가 포함되어야 한다는 것에도 주의하라. 다음 절에서는 이런 정적 조건을 일일이 상태에 포함시키지 않고 처리하는 좀더 나은 방법에 대해 살펴 볼 것이다.
앞 절에서 서술된 상태공간 탐색방법에 따르면 초기상태에서 시작하여 전방향으로 진행하거나 목적으로부터 후방향으로 진행하는 연산자들의 순서열이 만들어지고, 이 연산자들의 순서열이 바로 하나의 계획이 된다. 목적을 만족시키는 연산자들의 순서열을 찾는 문제는 일반적으로 계산적 복잡성 (4 장 탐색에서 정의된 종류의, 주어진 상태를 변환하여 주어진 목적을 만족시키는 상태로 바꾸는 일정한 순서열의 연산자들을 찾는 문제는 PSPACE 완전 문제의 부류에 속한다. 어떤 문제가 PSPACE 부류에 속한다는 것은 그 문제의 공간수요가 어떤 다항식에 의해 제한된다는 것이다. NP (비결정적 다항 시간) 부류는 PSPACE 부류에 포함되며, PSPACE 완전과 PSPACE 사이의 관계는 NP 완전과 NP 사이의 관계와 같다.) 을 지니며, 따라서 해를 구하기 위해 탐색방법을 사용하게 된다.
앞 절에서 설명한 방법에 따르면 어떤 연산자를 별 이유없이 다른 연산자 뒤에 놓게 되는 수가 흔히 있다. 많은 경우, 그 두 연산자는 어느 것이 먼저 적용되는지가 상관이 없고 심지어는 병행하여 적용되어도 된다. 블록 a 는 b 위에, c 는 d 위에 놓여져야 하는 블록쌓기 문제를 해결할 때 앞절의 방법은 두 연산자 사이에 순서가 있을 이유가 있는지 고려하지 않고 무조건 순서를 짓는다.
여러분이 식품점과 야구경기장에 가야한다고 해 보자. 이 두 가지 활동이 한 계획에 포함된 단계라고 생각하자. 처음에는 이 두 단계를 어떤 순서로 실행해도 괜찮다고 생각하지만, 나중에 가서 야구경기가 여러 시간 계속될 수도 있으며 그러면 경기장에 먹을 것을 좀 가져가는 것이 좋겠다고 생각한다. 식품점에 먼저 들르게 되면 야구경기의 전제조건, 즉 경기장에서 먹을 것이 있어야 한다는 것을 만족시킬 수 있다는 것을 깨닫는다. 이 경우, 계획에 포함된 단계들의 순서에 대한 결정을 미룸으로써 계획하는 과정에서 고려해야만 하는 가능한 계획들의 수를 줄여 준다.
이 절에 서술된 방법에서는 두 연산자들 사이에 순서를 정해야 할 근거가 없을 때에는 절대로 순서를 정하지 않는다. 이 방법의 기저에 깔려있는 휴리스틱 전략은연산자들의 순서에 대한 개입을 최소화하는 것이고, 이런 이유로 이 방법을 최소 개입 계획수립 (least commitment planning) 이라 부른다.
부분순서 계획공간에서의 탐색
최소개입 계획수립에서 하나의 계획은 연산자들의 순서열이 모여서 된 집합으로 정의되는데, 이는 연산자들의 부분순서 집합으로 간결하게 표현이 가능하고, 부분순서 계획 (partially-ordered plan) 이라 불리운다. 그림 6 은 1 에서 5 까지 번호가 매겨진 연산자들로 된 하나의 부분순서 계획을 보여 준다. 두 연산자들 사이의 화살표는 화살표가 시작되는 연산자가 화살표가 가리키는 연산자보다 선행해야 함을 나타낸다. 그림 6 의 그래프는 연산자 순서열의 집합 {{1, 2, 3, 4, 5}, {1, 3, 2, 4, 5}, (1, 3, 4, 2, 5}} 를 나타낸다. 연산자들의 부분순서집합은 언제나 연산자 순서열의 집합으로 나타낼 수 있지만 그 역은 성립하지 않음에 주의해야 한다. 최소개입 계획수립은 가능한 상태들의 공간에서 탐색을 하는 대신, 가능한 부분순서 계획들의 공간에서 탐색을 한다. 이런 탐색방법을 사용하면 하나의 계획자가 주어진 계획수립 문제를 해결할 때 더 적은 수의 계획을 고려하는 것이 가능할 때가 많다.
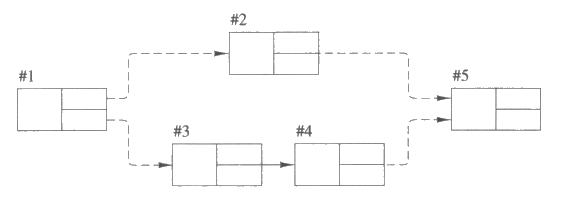
그림 6 : 다섯 단계로 이루어진 부분순서 계획. 점선 화살표는 단계들의 순서에 관한 제약 요건을 표현한다.
다음에 우리는 최소개입 계획수립의 구현에 관해 서술하겠다. 처음에는 한 상태를 다른 상태로 변환하는 연산자들이 변수를 포함하지 않는 경우에 대해 설명하고, 그 다음에 변수가 있는 연산자들의 경우로 확장하여 구현하는 것에 대해 알아본다. 연산자들의 자료 추상화는 앞 절에서와 똑같은 것을 사용하는데, 계획을 표현하기 위한 자료 추상화는 추가되어야 하겠다.
앞으로, 계획의 구성은 연산자에 해당하는 단계 (step) 들의 집합과 이들 단계가 수행되는 순서에 관한 제약요건 (constraint) 과 단계들이 상호 어떤 의존관계를 갖고 있는가에 관한 정보로 이루어진다. 이 의존관계 정보는 세 가지 종류가 있는데, 첫째는 요구사항 (requirements) 이란 레코드 (record) 로 연산자들이 그들이 바라는 효과를 가질 수 있기 위해 요구되는 명제들을 가리킨다. 다음으로는 연결고리 (link) 라 불리우는 레코드로 한 연산자의 효과가 어떻게 다른 연산자의 요구사항을 만족시키는데 사용되는지를 설명한다. 마지막으로 충돌 (conflict) 이라 불리우는 레코드로 연산자들 사이에 있을 수도 있는 바람직하지 않은 상호작용을 나타낸다. 충돌의 예로 한 연산자가 다른 연산자가 추가한 명제를 삭제해 버릴 수도 있는데, 이때 삭제된 명제가 계획이 성공하기 위해서 요구되는 경우를 생각할 수 있다.
(defun make-PLAN (steps constraints conflicts links requirements)
(list steps constraints conflicts links requirements))
(defun PLAN-steps (plan) (first plan))
(defun PLAN-constraints (plan) (second plan))
(defun PLAN-conflicts (plan) (third plan))
(defun PLAN-links (plan) (fourth plan))
(defun PLAN-requirements (plan) (fifth plan))
제약요건은 시작단계와 끝단계를 사용해 표현하는데, 각 단계에는 고유한 숫자가 할당되어서 같은 연산자를 사용하는 서로 다른 단계들을 구별한다.
(let ((n 0)) (defun make-STEP (operator)
(list (setq n (+ n 1)) operator)))
(defun STEP-id (step) (first step))
(defun STEP-operator (step) (second step))
(defun make-CONSTRAINT (begin end) (list begin end))
(defun begin (constraint) (first constraint))
(defun end (constraint) (second constraint))
앞절에서와 마찬가지로 하나의 상태는 조건의 집합으로 나타낸다. 요구사항은 한단계와 그 단계 직전에 참이어야 하는 조건에 해당한다. 요구사항의 조건은 그 단계가 지칭하는 연산자의 전제조건에 해당한다.
(defun make-REQUIREMENT (step condition) (list step condition))
(defun REQUIREMENT-step (req) (first req))
(defun REQUIREMENT-condition (req) (second req))
연결고리는 두 단계와 한 조건을 포함한다. 생산자 (producer) 라 불리우는 단계는 자신의 연산자의 추가조건 리스트에 그 조건을 갖고 있어서 이를 참으로 만든다. 소비자 (consumer) 라 불리우는 단계는 연산자의 전제조건에 이 조건을 갖고 있어 이 조건이 참이 되기를 요구한다. 연결고리는 요구사항을 만족시키기 위해 만들어진다.
(defun make-LINK (producer condition consumer)
(list producer condition consumer))
(defun LINK-producer (link) (first link))
(defun LINK-condition (link) (second link))
(defun LINK-consumer (link) (third link))
하나의 충돌은 한 연결고리와 한 단계로 되어 있다. 이 단계는 훼방꾼 (clobberer) 이라 불리우는데, 그에 연관된 연산자의 삭제조건 리스트에 연결고리의 조건을 갖고 있다. 충돌이 발생하는 것은 한 단계가 계획에 추가되었는데 그 단계가 연결고리의 생산자보다는 나중에 그리고 소비자보다는 먼저 수행될 수 있으면서 연결고리가 도입될 때 만족시키고자 했던 요구사항을 만족시키지 못하게 하는 경우이다. 충돌이 발생할 때 훼방꾼은 연결고리를 위협한다 (threaten) 고 말한다.
(defun make-CONFLICT (link clobberer) (list link clobberer))
(defun CONFLICT-link (conflict) (first conflict))
(defun CONFLICT-clobberer (conflict) (second conflict))
계획수립 문제의 사례 (instance) 는 초기상태와 목적으로서 주어지는데, 초기상태와 목적은 조건들의 리스트로 표현되며 그런 예는 두 단계로 이루어진 계획으로 표현 가능하다. 첫 단계는 의사연산자 (pseudo operator) 로서 초기상태에 해당하는 것을 추가조건의 집합으로 취하며 전제조건과 삭제조건은 갖고 있지 않다. 두번째 단계는 목적상태에 해당하는 것을 전제조건의 집합으로 가지며 추가조건과 삭제조건은 갖고 있지 않다. 이 계획은 첫단계가 두번째 것보다 선행해야 한다는 것을 나타내는 제약요건을 하나 가지며 목적상태에 해당하는 조건들의 목록에 속한 각 조건이 하나의 요구사항이 된다.
부분순서 계획의 실례를 보게 되면 이와 같은 용어들을 이해하는 데 도움이 될 것이다. 앞 절에서 나왔던 기계조립의 예를 다시 살펴보자 그림 7 은 기계조립 예에서 세 부품의 조립에 대한 두 가지 계획을 보여 준다. 그림 7 의 위쪽 계획은 단 두 개의 단계만을 갖고 있는데, 이들은 각각 초기 상태과 목적을 나타내는 두 의사연산자에 해당한다. 이 계획에는 두 단계를 순서 짓는 제약요건이 하나 있으며 세 부품을 각각 조립하는 것에 해당하는 세 개의 요구사항이 있다.
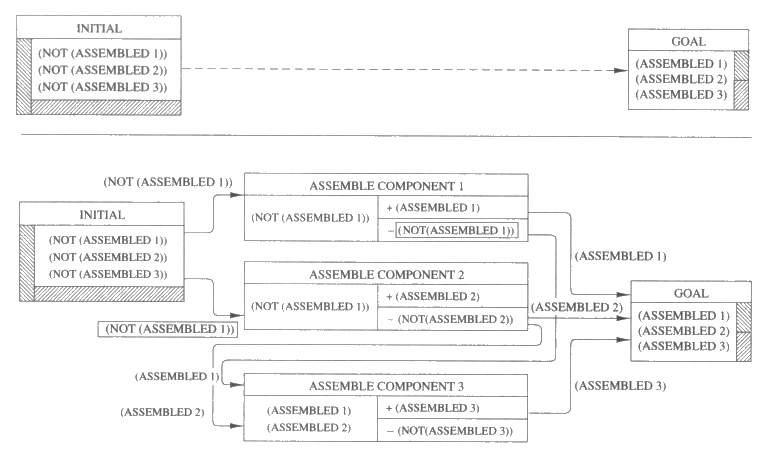
그림 7 : 기계조립 예에 관한 두 개의 부분순서 계획이 계획에서 한 단계에 해당하는 연산자는 각각 하나의 네모로 표현되고 각 네모는 몇 개의 부분으로 나뉘는데 (윗부분) 연산자의 서술, (왼쪽) 전제조건의 집합, (오른쪽 위) 추가조건의 집합, (오른쪽 아래) 삭제조건의 집합을 포함한다. 각 연결고리는 생산자와 소비자 사이에 제약요건이 있음을 내포한다. 점선으로 된 화살표는 연결고리가 아닌 제약요건을 나타낸다. 아래쪽 계획에는 하나의 충돌이 존재하는데 위협을 받는 것은 한 연결고리에 나타난 조건으로 네모표시가 되어 있고 이를 위협하는 단계의 삭제조건에 같은 조건이 네모로 표시되어 있다.
그림 7 의 아래쪽 계획은 두 개의 의사연산자에다가 세 부품의 조립을 위한 세단계가 추가되어 모두 다섯 단계를 갖고 있다. 이들 세 조립 연산자를 추가함으로써 결과적으로 새로운 요구사항을 네 개 더하게 되는데 이 계획에서는 일곱 개의 요구사항이 모두 연결고리에 의해 만족되었다. 그러나 이 계획에는 하나의 충돌이 존재하는데, 이는 한 단계에서는 첫째 부품이 조립되어 있지 않는 것을 요구하는 반면 다른 단계에 의해 첫째 부품이 조립되는 결과가 발생하기 때문이다.
무결한, 완전한 그리고 체계적인 탐색
뒤에 나올 문단에서는 부분순서 계획 공간에서 체계적으로 탐색을 하는 방법에 관해 서술하겠다. 한 탐색 프로시저가 탐색공간에서 절대로 같은 노드를 다시 검사하지 않을 때 이를 체계적 (systematic) 이라 하며, 탐색 프로시저가 어떤 계획을 돌려주었을 때 그 계획의 부분순서와 일치하는 전체순서로 각 단계를 나열하여도 그 순서에 따르면 초기상태에서 시작하여 목적을 만족시키는 상태로 변환 가능할 때 이를 무결하다 (sound) 고 한다. 마지막으로, 탐색 프로시저가 해가 존재할 때는 언제나 해를 찾는다면 이를 완전하다 (complete) 고 한다.
우리에게 부분순서 계획을 위한 표현은 있지만, 이들로 이루어진 탐색공간을 완전히 서술하려면 기존의 계획으로부터 새로운 계획을 생성하는 방법을 명시해야 한다. 한 상태를 다른 상태로 변환하는 데에 쓰인 연산자들로는 하나의 부분순서 계획을 다른 부분순서 계획으로 변환할 수 없다. 이처럼 부분순서 계획을 변환하는 과정을 계획정련 (plan refinement) 이라 부르겠다. 우리는 계획 내의 충돌을 없애기 위해 제약요건을 추가함으로써 계획을 정련하기도 하고, 계획 내의 요구사항을 없애기 위해 기존의 단계에 연결고리를 만들어 줌으로써 정련을 하기도 한다.
• 충돌을 없애는 유일한 방법은 훼방꾼으로 하여금 위협받는 연결고리의 생산자보다 선행하거나 이 연결고리의 소비자보다 후행하도록 제약요건을 더하는 것이다.
• 단계 q 의 조건 r 에 해당하는 요구사항을 없애는 유일한 방법은 r 을 추가해 줄 수 있는 단계 p (이때 p 는 새로운 단계일 수도 있고 계획 안에 이미 존재하는 단계일수도 있다) 가 생산자이고, q 가 소비자이며, r 이 조건이 되는 연결고리 l 을 더하는 것이다.
기존의 계획으로부터 계획정련 과정을 통해 새로운 계획을 생성할 때 다음과 같은 성질들을 새로운 계획이 갖고 있어야 한다.
• 새로운 계획은 그것을 생성하는 데 사용한 이전의 계획이 갖고 있던 모든 단계, 제약요건, 연결고리를 갖고 있어야 한다.
• 한 계획 안에 생산자가 p 이고 소비자는 q 이며 조건이 r 인 연결고리 l 이 있으면, 그에 해당하는 단계 p 와 q 가 계획에 포함되어 있어야 하며 이때 r 은 p 의 추가조건에 또 q 의 전제조건에 들어 있어야 한다.
• 한 계획 안에 생산자가 p 이고 소비자는 q 이며 조건이 r 인 연결고리 l 이 있으며 단계 c 가 있어서 현재의 제약요건 하에서는 p 와 q 사이에 올 수 있을 뿐 아니라 c 가 r 을 삭제할 수 있다면 연결고리 l 과 훼방꾼 c 로 된 충돌이 존재한다.
다음의 알고리즘은 계획과 연산자의 집합을 사용해 다음으로 고려할 계획의 집합을 생성한다 :
① 충돌이 있으면 하나를 선택하여 제약요건을 추가함으로써 해결한다. 이 경우, 생성되는 새 계획이 없을 수도 있고, 하나나 둘이 될 수도 있다. 충돌이 해결될 수 없다면 새 계획이 없다.
② 충돌이 없다면 요구사항을 하나 선택하여 이를 만족시키는 모든 가능한 방법, 즉 주어진 연산자의 집합을 사용하여 형성할 수 있는 새로운 단계와 기존의 단계 모두를 사용하여 새 계획을 생성한다.
Lisp 구현 절에는 위 알고리즘의 예가 나와 있는데, 이에 해당하는 Lisp 함수는 requirements 라 불리우며 두 인자 (argument) 를 취하는데, 하나는 계획이고 나머지는 연산자들의 목록이다.
블록쌓기 예
계획 공간에서의 탐색이라는 방법론을 설명하기 위해 간단한 블록쌓기 문제를 살펴보자. 그림 8 은 특정한 블록쌓기 문제의 초기상태와 목적을 만족시키는 상태를 나타낸다. 그림 9 에서는 초기 계획을 어떻게 구축하는지와 그림 8 에서 본 블록쌓기 문제를 해결하기 위한 연산자들의 집합을 보여주고 있다.
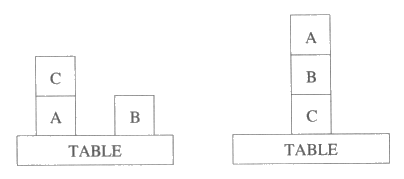
그림 8 : 간단한 블록 쌓기 문제의 초기상태와 목적상태
그림 9 : 블록 쌓기 예의 명세
계획수립의 기본으로는 최상우선 탐색을 사용하므로 목적을 만족시키는지를 검사하는 함수 goalp 와 탐색공간에서의 두 상태를 비교하는 함수 comparep 그리고 기존의 계획으로부터 새 계획을 생성하는 함수 next 를 명세해야 한다.
① 계획 내에 해결되지 않은 충돌이나 요구사항이 없을 때 이 계획은 목적을 달성한 것이다.
(defun goalp (plan)
(and (null (PLAN-conflicts plan)) (null (PLAN-requirements plan))))
② 두 계획을 비교하는 방법은 여러 가지가 있을 수 있는데, 다음에서는 더 적은 수의 요구사항을 가진 계획이 더 좋은 것으로 한다.
(defun comparep (p g)
(< (length (PLAN-requirements p)) (length (PLAN-requirements q))))
③ 명세된 연산자의 집합을 갖고 탐색에서 다음 탐색상태를 생성하는 것을 아래와 같이 정의한다.
(defun next (plan) (refinements plan operators))
다음은 그림 8 의 블록쌓기 문제에 탐색 프로시저를 적용했을 때 얻어진 해를 보여준다. 결과로 얻어진 계획을 보여주기 위한 프린트 루틴을 목적함수에 추가하였다.
> (best (list plan) #'goalp #'next #'comparep)
Steps: (5 (((ON B TABLE) (CLEAR B) (CLEAR C))
((ON B C))
((ON B TABLE) (CLEAR C))))
(4 (((ON C A) (CLEAR C))
((ON C TABLE) (CLEAR A))
((ON C A))))
(3 (((ON A TABLE) (CLEAR A) (CLEAR B))
((ON A B))
((ON A TABLE) (CLEAR B))))
(2 (((ON A B) (ON B C))
NIL
NIL))
(1 (NIL
((ON C A) (CLEAR C) (CLEAR B)
(ON A TABLE) (ON B TABLE))
NIL))
Order: ((1) (4) (5) (3) (2))
부분순서에 관한 정보는 다음과 같이 해석된다. 리스트의 각 원소는 계획 내의 단계에 해당하는데, 이는 그 단계에 할당된 고유한 수에 의해 구분된다. 이들 원소는 계획에서 명시하는 부분순서에 맞게 등급이 매겨진다. 만약 주어진 계획이 완전순서를 가지지 않는다면 이와 같은 등급은 주어진 부분순서와 일치하는 여러 개의 가능한 완전순서 중 하나일 뿐이다. 한 단계가 다른 단계에 대해 순서가 정해지지 않았다면, 후자의 단계들은 전자의 단계에 해당하는 원소의 rest 에 나온다. 위에 나온 계획에서는 단계들이 완전순서를 갖는다.
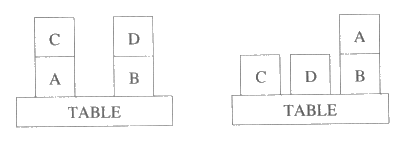
그림 10 : 왼편 상태를 오른편 상태로 변환할 때, c 와 d 를 탁자에 놓는 단계는 어떤 순서로도 수행가능하다.
그림 10 은 부분순서 단계들을 포함하는 해가 가능한 볼록쌓기 문제를 나타낸다. 부분순서 계획 내의 단계들이 순서가 정해지지 않았다는 것은 이들 단계들이 어떤 순서로 수행되어도 괜찮음을 의미한다. 우리의 구현 예가 찾아낸 다음의 해는 c 와 d 를 탁자 위에 놓는 단계들이 임의의 순서로 수행될 수 있음을 나타낸다.
Steps: (5 (((ON D B) (CLEAR D))
((ON D TABLE) (CLEAR B))
((ON D B))))
(4 (((ON C A) (CLEAR C))
((ON C TABLE) (CLEAR A))
((ON C A))))
(3 (((ON A TABLE) (CLEAR A) (CLEAR B))
((ON A B))
((ON A TABLE) (CLEAR B))))
(2 (((ON A B))
NIL
NIL))
(1 (NIL
((ON C A) (ON D B) (ON A TABLE)
(ON B TABLE) (CLEAR C) (CLEAR D))
NIL))
Order ((1) (5 4) (4 5) (3) (2))
충돌의 인식과 해결
그림 11 과 12 는 계획수립 중에 어떻게 연결고리가 형성되는지 그리고 충돌이 어떻게 인식되고 해결되는지를 설명한다. 이 두 그림에는 네 개의 부분순서 계획이 묘사되어 있는데, 이들은 그림 8 에 나온 문제를 해결하는 과정에서 만들어진 것들이다. 그림 11 의 위쪽 계획은 초기계획을 나타낸다. 그림 11 의 아래쪽 계획에서는 (on a b) 라는 요구사항이 a 를 b 위에 올려놓는 단계를 추가함으로써 제거되었다. 이로 인해 세 개의 요구사항이 추가되었는데, 그들 중 두 요구사항은 초기조건에 해당하는 단계와의 연결고리에 의해 해결되었다.
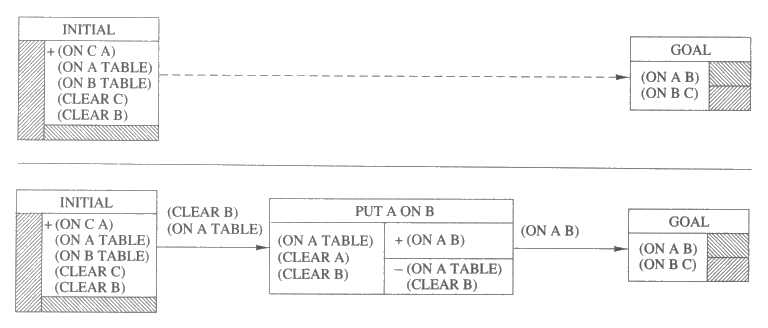
그림 11 : 간단한 블록쌓기 문제를 해결하는 과정에서 만들어지는 연결고리를 설명하는 두개의 부분순서 계획. 부분순서 계획의 한 단계에 해당하는 각 연산자는 네모로 표시되어 있으며 각 네모는 다시 몇 개의 부분으로 나뉘는데 각 부분은 (위) 연산자 설명, (왼쪽) 전제조건 집합, (오른쪽 위) 추가조건 집합, (오른쪽 아래) 삭제조건 집합을 포함한다. 각 연결고리는 생산자 단계로부터 소비자 단계로의 실선 화살표로 표시되며 화살표에는 관련된 조건이 적혀있다. 생산자 / 소비자 쌍이 하나 이상의 연결고리를 포함하면 화살표는 하나만 표시하고 거기에 관련된 조건들을 모두 적는다.
그림 12 의 위쪽 계획에서는 (on b c) 라는 요구사항을 없애기 위해 또 다른 새로운 단계가 추가되었다. 이 경우에는 새로이 도입된 단계에 의해 생긴 세 개의 요구사항이 모두 초기조건에 의해 만족되었다. 그러나, 여기에는 충돌이 존재하는데 이는 b 를 c 위에 올려놓는 연산자가 (clear b) 를 전제조건으로 갖고 있는데 a 를 b 위에 놓는 연산자는 (clear b) 를 삭제하기 때문이다. 이 충돌은 b 를 c 위에 놓는 것을 a 를 b 위에 놓는 것 보다 먼저 하도록 함으로써만 해결될 수 있다.
그림 12 의 아래쪽 계획에서는 마지막 남은 요구조건을 c 를 table 에 놓는 단계를 추가함으로써 해결한다. 이 단계는 (clear c) 를 요구하며 이는 b 를 c 위에 놓는 단계가 (clear c) 를 삭제하기 때문에 충돌을 일으킨다. 이 충돌은 c 를 table 위에 놓는 것을 b 를 c 위에 놓는 것 보다 먼저 하도록 함으로써 해결된다.
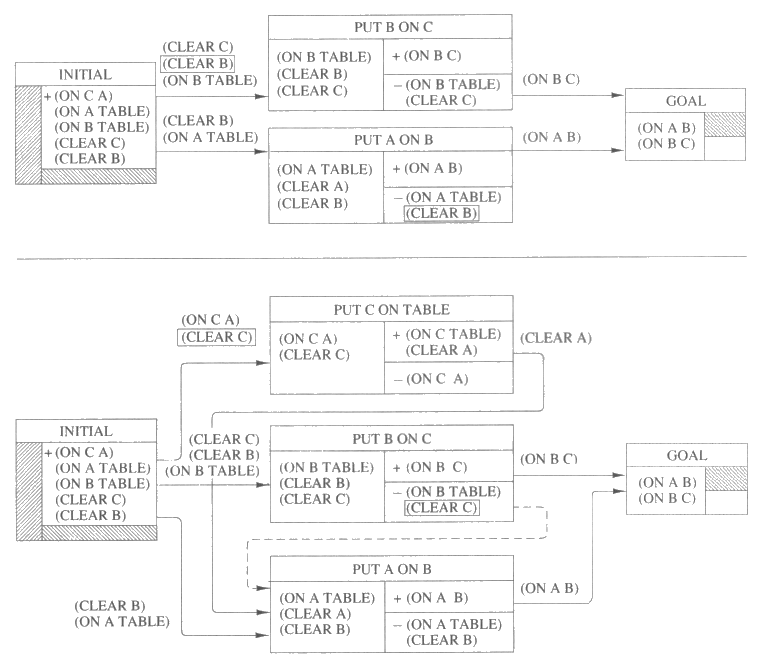
그림 12 : 간단한 블록쌓기 문제를 해결하는 과정에서 생성되는 충돌을 설명하는 두 개의 부분순서 계획. 충돌을 일으키는 조건에 네모를 침으로써 충돌을 표시하는데 위협을 받는 연결고리에도 충돌조건이 나오며 또한 위협을 하는 단계의 삭제조건에도 나온다. 아래쪽 계획에는 점선으로 된 화살표가 나와 있는데 이는 위쪽 계획에서 발견된 충돌을 해결하기 위해 추가된 제약요건을 표시한다.
우리가 계획을 수립하는 과정에서 늘 우리의 목표를 향해 진전을 할 수 있다면 매우 좋겠지만, 불행히도 일반적으로 그렇게 되기는 어렵다. 그림 13 은 목표에 맞는 완전한 탑을 쌓기 위해 부분적으로 이루어진 탑을 우선 허물어야만 하는 블록쌓기 문제를 보여주고 있다. 앞서의 구현에 따르면 (on a b) 요구조건을 만족시키기 위하여 목적에 해당하는 단계가 초기조건에 해당하는 단계와 연결고리로 이어진 계획이 생성될 것이고, 이 계획은 해에 이르도록 확장될 수 없다. 이 경우에는 생성된 계획이 제대로 된 것이 아님을 판단하기가 쉽지만, 전혀 희망이 없는데도 그것을 인식하는 일이 어려운 경우도 있다.
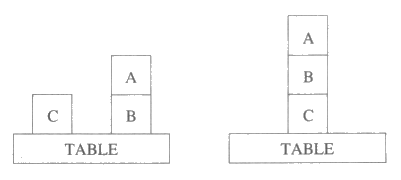
그림 13 : 왼쪽 상태를 오른쪽 상태로 변환하기 위해서는 부분적인 해로 보이는 것을 무너뜨려야 한다.
그림 14 : 블록 쌓기를 위한 연산자 스키마
부분순서 계획에서의 변수
앞서의 구현을 변수가 포함된 연산자 스키마도 다룰 수 있도록 확장하는 것은 비교적 간단한 일이며 그럼으로써 충돌을 해결할 수 있는 또 다른 방법을 도입할 수 있다. 연산자 스키마를 다룰 수 있도록 확장하기 위해서 적절한 연산자를 찾아내고 사례화 (instantiate) 하며 연결고리를 만들거나 충돌을 찾아내는 데에 equal 대신에 3 장 표상과 논리에서 소개한 단일화 (unify) 와 변수치환 (varsubst) 루틴을 사용한다. 최소개입 계획수립을 할 때 연산자 스키마를 사용하는 데에는 몇 가지 미묘한 어려움이 있다.
최소개입 계획수립을 하는 데에 사용되는 연산자 스키마는 일반적으로 전제조건, 추가조건, 삭제조건 집합 외에 다른 부분을 갖고 있는데, 이 추가적인 부분은 변수들이 어떻게 결합될 것인가에 관한 제약요건들로 이루어진다. 이들 제약요건들은 두가지 목적으로 쓰이는데 첫째는 이를 이용하면 앞절에서처럼 많은 수의 정적조건들을 일일이 나열하지 않더라도 연산자의 적용에 관한 정적조건들을 명세할 수 있다는 것이고 둘째로는, 부분순서 계획에서 충돌을 해결하는 새로운 수단을 제공해 준다는 것이다.
그림 14 는 블록쌓기 문제를 해결하기 위한 연산자 스키마들을 보여준다. 두 가지 기본적인 스키마가 나와 있는데 한 가지는 하나의 블록을 블록 위에서 탁자로 옮기기 위한 것이고 또 한 가지는 하나의 블록을 블록에서 블록으로 옮기기 위한 것이다. 탁자에 놓을 수 있는 블록의 수에는 제한이 없으며 적어도 하나의 블록은 늘 탁자 위에 있다고 가정하겠다. 두번째 가정에 따르면 탁자 위는 언제고 깨끗이 치워져 있을 수 없다. 연산자 스키마의 마지막 부분에 해당하는 제약조건들의 리스트는 연산자들이 부적합하게 쓰이지 않도록 한다. 예를 들어, 한 블록을 바로 그 블록 위에 올려놓을 수 없으며 탁자 위를 깨끗이 치울 수 없고, 탁자를 블록 위에 올려놓을 수 없다는 것을 이들 제약요건들이 명령하는 셈이다. 한 블록을 탁자에서 다른 블록으로 옮기는 경우를 다루기 위해 또 다른 연산자 스키마가 필요하다는 것에 주의하라.
(not (equal ? y)) 와 같은 형태의 제약요건은 변수 x 와 y 가 결합하지 않으면 만족된다. 조건 (on a b) 로 이루어진 요구사항을 만족시키는 연산자를 찾는 한 가지 방법은 다음과 같다. (on a b) 를 모든 연산자의 모든 추가조건과 단일화가 되는지 시도해 본다 (실제로는 좀더 효율적인 색인방법을 사용할 것이다). 이런 시도는 두번째 연산자의첫째 추가조건에서 성공하게 되는데, 단일화에 의해 얻어진 변수결합을 사용해 변수들을 치환하면 다음과 같이 모든 제약요건이 만족되고 변수들이 일부 사례화된 연산자를 얻을 것이다.
(;; 전제조건
((on a (? z)) (clear a) (clear b))
;; 추가조건
((on a b) (clear (? z)))
;; 삭제조건
((on a (? z)) (clear b))
;; 제약요건
((not (equal a b)) (not (equal a (? z))) (not (equal b (? z)))
(not (equal a table)) (not (equal b table))))
실제 구현에서는 모든 변수들의 이름을 바꿀 것이고, 위의 부분적으로 사례화된 연산자는 하나의 단계로 계획에 더해질 것이다. 주목할 것은 부분적으로 사례화된 연산자들로 된 계획 단계들이 있기 때문에 부분순서 계획의 변수들을 다루는 데 간단한 match 대신에 unify 가 필요하다는 것이다.
이 연산자는 (on a (? z)) 라는 조건을 삭제한다. 계획수립 도중 계획 내에 (on a d) 라는 조건을 가진 연결고리가 있다고 가정해보자. 두 조건 (on a (? z)) 와 (on a d) 는 단일화할 수 있으며 단일화를 하여도 모든 제약요건들이 여전히 만족된다. 이는 충돌이 있을 가능성이 있다는 것을 의미하며 이 충돌은 훼방꾼을 생산자 앞에 오도록 하거나 소비자 뒤에 오도록 함으로써 해결할 수 있었는데, 이제는 (not (equal (? z) d)) 라는 제약요건을 추가함으로써도 충돌을 해결할 수 있다. 어떤 단계를 이루는 연산자와 관련된 제약요건들을 충돌을 해결하는 데 사용하는 경우에는 그 제약요건 리스트의 크기가 증가할 것이다.
어떤 단계에 연관된 요구사항을 만족시키기 위해 다른 단계를 사용하려면 해당하는 연산자들의 조건들을 단일화해야 하며 (이때 전자는 소비자, 후자는 생산자의 역할을 한다), 제약요건들의 만족여부를 알아보는 검사를 해야 한다. 만족될 경우, 두 연산자에 적절한 치환을 하고 나서 변수가 없는 경우일 때와 마찬가지로 진행한다.
제약요건을 추가함으로써 동작하는 계획자는 문헌에서 흔히 제약요건 게시 계획자 (constraint-posting planner) 라 부른다. 제약요건의 게시와 개입을 연기하는 것을 조합하면 많은 계획자의 기본이 된다. 많은 경우, 효율성 때문에 탐색의 방향을 제시하는 다른 기법도 사용하는데 다음에서는 그러한 기법 중 하나를 살펴보겠다.
지금 우리가 커다란 사무실 건물을 건축하려고 계획하고 있다고 가정해 보자. 계획수립을 하려면 건물의 여러 방면을 책임지는 많은 계약자들이 하는 일을 조정해야 한다. 예를 들어, 주 계약자는 기초를 다지고, 벽돌담을 세우고, 목수일과 배관 및 배선을 하고, 또 회벽을 바르는 일을 책임 맡은 하청업자들의 일을 조정해야 한다. 계획수립 문제를 좀더 다루기 쉽게 하려면 전체 문제의 세부사항을 무시하는 좀더 작은 탐색공간을 살펴봄으로써 문제를 추상화한다. 실제로 우리는 가장 추상적인 탐색공간에서부터 가장 구체적인 탐색공간에까지 이르는 위계구조를 고려한다.
예를 들어, 처음에는 기초를 다지고 기본적인 골격을 세우는 것을 책임진 하청업자만을 고려할 것이다. 이런 추상적인 공간에서 하나의 해를 찾고 나서 건축의 다른 측면을 고려함으로써 그 해를 좀더 자세히 만들어 나갈 수 있을 것이다. 예를 들어, 기본적인 구조에 대한 계획이 주어지면 이 계획에 배관과 배선을 더하여 정련된 계획으로 만들 수 있다. 이는 탐색을 좀더 구체적이고 덜 추상적인 탐색공간 내에서 계속해 나가는 것에 해당한다. 마지막으로, 기본 구조와 배관 및 배선을 고려한 후에 도벽공사와 마무리 작업을 책임 맡은 다른 하청업자까지 통합할 수 있을 것이다. 이상적인 경우에는 어떤 추상화 레벨에서 이루어진 일이 그보다 덜 추상적인 레벨에서 일을 세분화하는 데에 방해가 되지 않을 것이다.
여러 추상화 레벨에서의 계획수립에 관한 분석
어떤 공간에서 탐색을 할 때, 항상 길이가 l 인 계획을 길이가 l + 1 인 계획보다 먼저 검사한다고 가정해보자. 가장 짧은 해의 길이가 l 이고 분기계수 (branching factor) 가 b 인 문제에 대해 그러한 해를 찾는 일의 최악 복잡도는 O (bl) 이다.
이제 n 개의 추상화 레벨을 도입하였고 레벨 i 에서의 해의 길이가 레벨 i - 1 에서의 해의 길이보다 k 배 길다고 가정하자. 단, 이때 k 는 1 보다 큰 상수이다. 여러 추상화 레벨을 도입하면 특정 추상화 레벨에서 계획수립을 할 때 전체 조건 중 일부에만 초점을 맞출 수 있다. 현재 고려되는 조건의 집합에 속하지 않는 조건은 계획수립 과정에서 무시된다. 가장 덜 추상적인, 즉 가장 구체적인 추상화 레벨에서만 모든 조건들이 고려된다. 이상적인 경우에는, 레벨 i 에서의 해로부터 레벨 i + 1 에서 풀어야 할 l / kn i 개의 같은 크기의 하부문제 (subproblem) 들이 만들어지며, 이때 각 하부문제는 그 해에 나오는 조건에 해당하지만 이전 레벨에서는 무시된 것이다. n = logk l 이라 가정하고, 주어진 추상화 레벨에서 구해진 각 하부문제에 대한 해는 서로 간섭이 없어서 독립적으로 해결될 수 있다고 가정하자. 조금은 강한 듯한 이런 가정을 하면 위계구조적 추상화 공간에서의 계획수립의 복잡도는
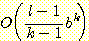
임을 보일 수 있다 (역자 주 : 위의 이론적 결과를 본문의 내용만으로는
쉽게 이해할 수 없을 것 같다. 가장 간단한 경우, 즉 추상화 레벨이 둘 뿐인 경우를
우선 살펴보자. 두 레벨을 각각 "구체적 레벨" 과 "추상적 레벨"
이라
부르기로 한다. 이때 k 는 구체적 레벨에서 구해진 해의 길이와 추상적 레벨에서 구해진
해의 길이 사이의 비율이다. 또한 l 은 구체적 레벨에서 구할 수 있는 가장 짧은 해의
길이이며, b 는 구체적 레벨에서의 분기계수이다. 이로부터 추상적 레벨에서 구해진
해의 길이는 l / k 이며, 따라서 추상적 레벨에서의 탐색트리의 크기는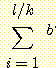 
임을 쉽게 알 수 있다. 이 경우 우리가 원하는 해를 얻기 위한 전체 탐색공간의
크기는 각 레벨에서의 탐색공간의 크기의 합, 즉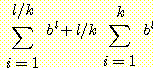 
이 된다. 물론 여기서도 본문에서 가정한 것들이
성립한다는 가정이 들어 있다. 이제, n 개의 추상화 레벨이 있는 경우를 살펴보자.
각 레벨 사이에서 해의 길이 간의 비율이 k 로 일정하다는 가정을 이용하여 위에서와
같은 방법으로 생각하면, 전체 탐색공간의 크기는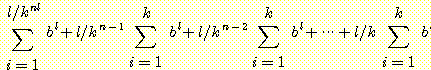 
가 된다. 또한 n = logk l 일 때, 앞의 식은 
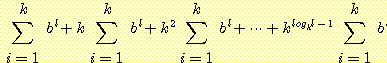이므로, 근사적으로 계산하면 
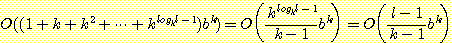이 된다.). 또 b 와 k 를 고정하면 O (l) 임을
보일 수 있다 [Knoblock,1991].
일반적으로는 여기서 도입한 가정들을 만족시키는 것이 불가능하다. 그러나 이런 가정들을 만족하는 문제 부류가 있으며, 그런 문제에 대해서는 위에 설명한 근사적인 지수적 (exponential) 가속효과를 얻을 수 있다. 다음에서 그러한 부류에 속한, 하노이탑 (towers-of-Hanoi) 문제라 불리우는 문제를 고려해 본다.
하노이탑 문제
하노이탑 예에는 막대의 집합과 여러 가지 크기의 원판의 집합이 사용된다. 각 원판은 가운데 구멍이 나 있어서 어떤 막대에도 꽂아 놓을 수 있다. 모든 원판은 막대에 꽂혀 있어야 하며 하나의 막대에 여러 원판이 동시에 꽂힐 수 있지만 어느 원판도 자신보다 더 작은 원판 위에 있어서는 안 된다. 원판 위에 아무 것도 없을 때에는 그 원판을 한 막대에서 다른 막대로 옮겨 꽃을 수 있는데 물론 옮겨질 곳에 이미 있는 원판들이 그 원판보다 커야 한다. 일반적으로는 막대와 원판의 개수에 제한이 없으며, 원판의 초기 배치와 목적이 되는 배치 형태에도 제한이 없다. 그러나 앞으로 하노이탑 문제의 예에 관해 말할 때에는 원판과 막대가 모두 n 개이고, 초기에는 모든 원판이 하나의 막대에 꽂혀 있고 이들 원판을 모두 다른 막대로 옮기는 것이 목적인 경우만을 생각한다. 그림 15 는 n = 3 인 경우의 초기와 목적상태를 나타낸다.
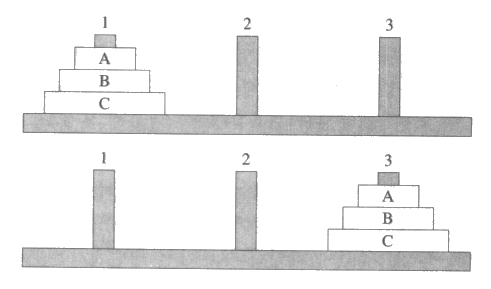
그림 15 : 하노이탑 문제의 일례에 대한 초기상태와 목적상태
그림 15 에서 사용된 표현은 블록쌓기 문제에 사용되었던 것과 유사하다. 여기서는 원판을 블록처럼 막대를 탁자처럼 다루는데, 원판들이 어떻게 배치되는 것이 가능한지는 원판의 크기와 이들이 어떤 순서로 쌓여 있는지에 의해 결정된다. 막대를 생각할 때 움직일 수 있는 어느 원판보다도 더 큰, 움직이지 못하는 원판으로 생각하여도 된다. 움직일 수 있는 원판은 어느 것이든 다른 원판 위에 놓여져야 하며,각 원판에는 자신 (바로) 위에 최대 하나의 원판만이 놓일 수 있다.
그림 16 : 하노이탑 문제에 대한 비위계구조적 표현
그림 16 은 하노이탑 문제에 대한 탐색공간을 나타낸다. 이 경우에는 원판을 한 막대에서 다른 막대로 옮기는 연산자 하나만이 있다. n 개의 원판 문제에 대해서는 가장 짧은 해의 길이가 2n - 1 이다. 이 문제에 해당하는 탐색공간에서 맹목 탐색을 하게 되면 적은 수의 원판만을 포함한다 하더라도 계산량이 엄청나게 많을 수 있다.
탐색의 양을 줄이기 위해 추상화 공간들의 위계구조를 도입한다. 여기서 추상화 공간은 연산자의 집합과 상태공간을 결정하는 조건들의 집합에 의해 정의된 탐색공간일 뿐이다. 우리에게 주어진 것은 연산자의 집합과 가장 덜 추상적인, 즉 기본 (ground) 공간을 결정하는 조건들의 집합이다. 이들 연산자와 조건들로부터 위계구조적 공간을 다음과 같이 구축한다. 조건집합을 분할하여 추상화 레벨들의 순서집합을 정의하는데 각 추상화 레벨은 조건집합의 부분집합에 해당한다. 각 레벨이 정의하는 추상화공간에서 우리는 그 레벨이나 그보다 상위 레벨에 속하는 조건에만 유의한다. 그보다 하위인 모든 레벨에 대하여는 마치 그 조건이 존재하지 않는 것처럼 생각한다.
계획수립은 다음과 같이 진행된다. 초기조건과 목적이 주어졌을 때 가장 높은 추상화 레벨에 명시된 조건만을 사용하여 해를 구한다. 이 레벨에서 해를 구한 후에 그 다음 레벨, 즉 좀더 구체적인 추상화 레벨에서 해를 정련한다. 가장 구체적 레벨에서 계획을 구할 때까지 한 레벨씩 이렇게 계획을 정련해 나간다.
그림 17 은 하노이탑 문제를 위한 다른 탐색공간 표현을 보여준다. 이 표현에서는 이전의 방법론과 달리 주어진 막대 위에 한 개 이상의 원판이 있을 수 있다는 것을 표현하였다. 큰 원판을 작은 원판 위에 놓지 못하게 하는 제약요건은 추상화의 위계구조를 도입함으로써 이루어졌다. n = 3 인 경우에 대한 연산자를 제공하였는데, 임의의 n 에 대하여는 n 개의 각 원판마다 하나의 연산자 스키마가 있어야 하므로 n 개의 연산자 스키마가 있게 된다. 그림 17 에는 세 개의 연산자가 있는데, 각각을 (move_c (? p) (? q)), (move_b (? p) (? q)), (move_a (? p) (? q)) 로 표기하며, 이때 (? p) 와(? q) 는 막대를 변수값으로 취한다. 연산자에 표현된 조건의 종류는 세 가지인데, (on_c (? p)), (on_b (? p)), (on_a (? p)) 이며 이들 조건에 추상화 레벨을 다음과 같이 할당한다. 조건 (on_c (? p)) 는 레벨 2, (on_b (? p)) 는 레벨 1, (on_a (? p)) 는 레벨 0 이 할당된다.
그림 17 : 하노이탑 문제에 대한 위계구조적 표현
하노이탑 문제를 이와 같이 위계구조로 분해하는 것은, 앞서 나열한 가정들을 만족시킨다. 기본공간에서의 가장 짧은 해의 길이는 l = 2n - 1 이며, 추상화 레벨의 수는 O (log2 l), 레벨간의 해의 길이의 비율은 2, 그리고 주어진 레벨에서의 하부문제들은 서로 독립이다.
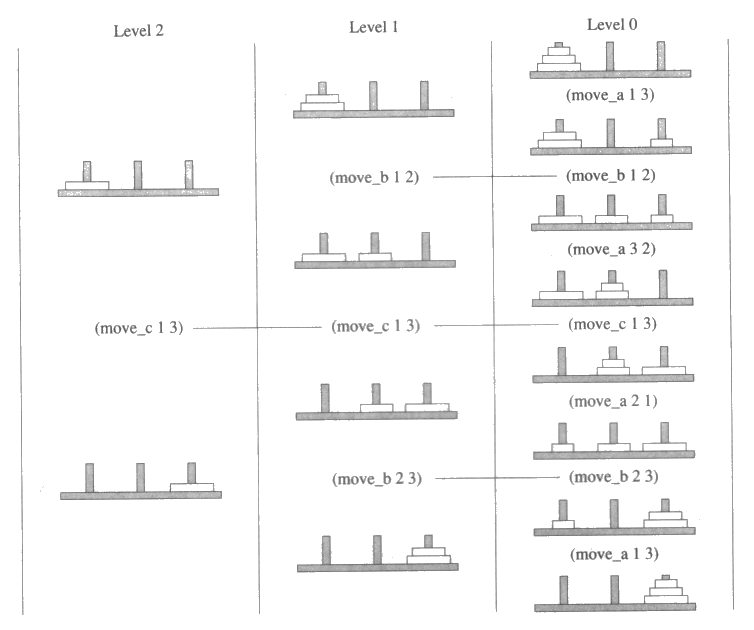
그림 18 : 하노이탑 문제의 일례에 대한 위계구조적 해. 단계들의 순서열은 위에서 아래로 진행된다.
그림 18 은 그림 15 에서 보여준 하노이탑 문제의 예에 대한 해를 나타낸다. 각 추상화 레벨에서 생성된 계획이 그 이전 레벨에서 생성된 계획의 정련임을 유의해서 보라.
실제에서는 하노이탑 문제에서와 같은 종류의 성능향상을 실현하는 일이 어렵지만, 추상화의 위계구조를 적절히 정하면 효율성을 증대하는 것이 가능할 때가 많이 있다. 어떤 경우에는 연산자들의 전제조건과 사후조건에 의해 결정되는 의존관계를 분석함으로써 추상화 위계구조를 자동적으로 만들어 낼 수도 있다. 그와 같은 추상화 위계구조를 생성한다는 것은 조합적 문제에 내재하는 고유한 구조를 찾아내는 일에 해당하며, 탐색을 줄이는 매우 강력한 방법론이다.
작업축소 계획수립
추상화는 계획수립을 위한 여러 가지 방법론에서 그 역할을 한다. 계획수립을 위한 중요한 실용적인 방법론 중에는 작업 (task) 이라는 개념을 가지고 구성된 것이 있는데 작업이란 계획자가 수행하려는 추상적인 작용이다. 작업이 추상적이란 것은 세부적인 것을 자세히 명시할 필요없이 어떤 작용을 성취하려고 하는지에 관한 일반적인 성질을 정한다는 의미이다. 예를 들어, 건축계약자는 2 층짜리 집을 지어야 한다는 작업을 가지고 있을 수 있지만 그 작업을 성취하기 이전에 충분한 세부사항을 제공해야만 목수나 전기공, 배관공 그리고 다른 기술자들이 일을 할 수 있다.
세부사항을 증대하는 방법 중 하나는 추상적인 작업을 하나의 또는 여러 구체적인 작업으로 대치하는 것이다. 이처럼 추상화 레벨을 정련해 나가는 과정을 작업축소 (task reduction) 라 부른다. 추상적인 작업을 축소함으로써 계획자는 좀더 구체적인 작업을 수행하기로 하는 것이다. 예를 들어, 건축계약자는 2 층짜리 집을 짓는 작업을 축소하여 네 개의 좀더 구체적인 작업으로 만들 수 있다 : 즉 기초공사, 일층 건축, 이층 건축 그리고 지붕공사. 축소과정은 모든 작업이 충분히 자세하게 명세될 때까지 계속된다.
각 추상화 레벨은 이 장에서 우리가 행동을 표현하기 위해 사용했던 연산자와 얼추 상응한다. 작업축소에 의한 계획수립의 대부분은 작업을 축소하기 위한 여러 전략을 시도해 보고 나서 각 레벨에서 작업들을 조정하여 최소개입 계획수립에서 보았던 것과 같은 충돌을 피하도록 노력하는 것이다. 추상적 작업을 축소하는 전략들은 문제를 쪼개어 더 간단한 것들로 나누는 일반적인 방법에 해당하는데, 이와 관련된 아이디어 중에는 기존의 계획을 적절히 변화시켜 새로운 문제의 해결에 사용하는 경우도 있다.
여러분이 한 도시에서 다른 도시로 가기 위한 계획을 만들어 냈다고 가정해 보자. 만약에 이 두 도시간을 다시 다녀가게 된다고 하면 지금 만들어 낸 계획을 재활용하는 것에 대해 적어도 고려는 해 볼 것이다.
심지어는 여러분의 계획을 일반화하여 다른 두 도시에 대해서도 쓸 수 있도록 만드는 것을 생각해 볼지도 모르겠다. 예를 들어, 서울에서 제주도 서귀포시로 가려고 한다고 가정해 보자. 서울에서 공항버스를 타고 김포공항까지 간 다음 비행기로 김포에서 제주까지 그리고는 제주에서 서귀포까지 버스를 탈 수 있다. 서울에서 서귀포까지 가는 이 계획으로부터 일반적으로 가장 가까운 공항까지 육상수단을 이용하고, 목적지에 가장 가까운 공항까지 항공편을 이용한 다음, 마지막 목적지까지 다시 육상수단을 이용하는 계획을 만들 수 있을 것이다.
많은 계획수립 시스템은 기존의 계획들을 모아 놓은 라이브러리 (library) 를 이용한다. 어떤 경우에는 계획수립 시스템이 스스로 이전에 만들어 낸 계획들을 한데 모아놓기도 하고 또 다른 경우에는 그 응용분야에 전문가인 사람에 의해 제공된 것들을 모아 놓을 수도 있다. 그런 계획수립 시스템이 새로운 문제를 만나면 라이브러리에 이미 있는 계획을 찾아서 그것을 응용하여 새로운 문제를 해결한다. 어떤 때에는 이 계획자가 주어진 문제를 해결하는 과정에서 발생하는 여러 하부문제를 해결하기 위해 여러 개의 라이브러리 계획을 사용하기도 한다. 다음에서는 이전에 생성된 계획을 응용하는 한 가지 방법론에 관해 살펴보기로 한다.
계획의 색인, 검색, 응용
이 절의 나머지 부분에서는 다음 세 가지 기본적인 문제를 생각해 보기로 하자.
1. 어떤 문제를 해결하는 계획이 주어졌을 때, 어떻게 색인을 만들어 놓아야 나중에 비슷한 문제를 해결하기 위해 검색될 수 있겠는가?
2. 해결해야 할 문제가 주어졌을 때, 그 문제를 해결하는 데 응용할 수 있는 예전의 계획을 계획 라이브러리에서 어떻게 검색할 것인가?
3. 과거의 계획을 갖고, 어떻게 새로운 문제를 해결할 수 있게 응용할 것인가?
우선 한 문제에 대한 해를 어떻게 저장해야 나중에 이것을 응용해서 다른 문제를 해결할 수 있겠는가에 대하여 생각해 보자.
그림 19 : 블록쌓기 문제에 대한 해
그림 19 는 그림 8 에 나온 블록쌓기 문제에 대한 해를 보여 주는데, 이 계획은 어떤 세 블록이 주어지더라도 초기와 목적상태에 해당하는 배열이 같으면 사용될 수 있음을 주지하라. 이런 관찰로부터 세 블록의 초기 배열과 목적 배열이 이와 같은 문제에는 언제나 적용할 수 있는 계획 스키마를 만들고자 한다. 추후에 색인하는 일을 쉽게 하기 위해 초기상태와 계획이 해결하는 목적상태의 일반적인 형태를 명백히 해야 한다.
그림 20 : 세 블록을 쌓기 위한 라이브러리 계획
그림 20 은 그림 8 의 문제에 대한 해를 일반화한 계획 스키마를 나타내는데, 계획 라이브러리 내에서 이 계획을 색인하기 위하여 사용되는 초기조건과 목적도 함께 나와 있다. 계획을 일반화하는 과정은 3 장 표상과 논리에서 살펴 본 설명기반 학습의 형태를 갖는다. 또한 연결고리의 형태로 된 의존관계 정보가 그림 20 에는 그려져 있지 않지만 계획의 일부라고 가정한다.
앞에서는 논의하지 않았지만 중요한 문제가 있는데, 이를 여기서 언급하는 이유는 여러분이 혹 계획들의 라이브러리를 구축하는 일이 쉬운 것이라고 잘못 생각할 우려가 있기 때문이다. 예를 들어, 계획의 초기상태나 단계에 있는 어떤 조건들은 계획의 성공 여부와는 무관할 수 있는데 이들이 무엇인지 알아내서 라이브러리 계획에서 삭제하면 좋을 것이다. 또 다른 문제로는 계획 라이브러리의 크기를 고려하지 않았다는 것인데, 라이브러리에 더 많은 계획이 저장될수록 계획수립 중에 고려되어야 할 계획이 더 많다는 것이고 따라서 응용가능성이 있는 라이브러리 계획을 검색하는 일이 더 어려워진다는 것이다. 앞으로는 적절한 크기와 형태를 가진 계획 라이브러리를 가지고 있다고 가정하겠다.
다음으로는 계획 라이브러리에서 계획을 검색한 후에 어떻게 그들을 맞춤 (fit) 하여 앞으로 정련하는 데 사용할 수 있는 계획으로 만드느냐 하는 문제를 살펴보자. 맞춤은 라이브러리 계획을 가지고 수정하여 현재 우리가 해결하고자 하는 문제에 해당하는 초기조건과 목적을 갖도록 만드는 일을 말한다. 정련과정은 최소개입 계획수립에 관한 절에서 소개한 알고리즘을 약간 수정한 버전 (version) 을 이용하며 응용은 맞춤과 정련을 모두 사용하게 된다.
만약 우리가 풀어야 할 새로운 문제가 초기조건의 집합과 목적에 해당하는 것으로 주어졌다 하자. 응용은 다음과 같이 진행된다. 각 라이브러리 계획에 대하여 그 라이브러리 계획의 목적을 새로운 목적에 정합시켜 본다. 예를 들어, 라이브러리 계획은 P 와 Q 를 성취하여야 한다는 목적을 가지고 있으며, 새로운 목적은 Q 만을 성취하면 되는 것일 수 있다. 또한 부분적인 정합도 허용되는데 예를 들어, 라이브러리 계획은 P 만을 성취하는 반면, 새로운 목적은 P 와 Q 를 요구할 수도 있다. 다음에서 우리가 서술할 방법은 어떤 라이브러리 계획을 선택하는 경우에도 올바른 계획을 생성할 것인데 (올바른 계획이 존재한다는 가정하에서), 새로운 목적과 초기조건에 잘 정합하는 라이브러리 계획을 가지고 시작하면 탐색을 적게 할 것이다. 여러 개의 정합 (match) 이 가능한 경우에는 여러 계획 중에서 그 초기조건이 새로운 초기조건에 얼마나 잘 정합하느냐에 따라 선택한다. 구체적으로는 맞춤 동안에 얼마나 많은 수의 새로운 요구사항을 계획에 추가해야 할 것인가를 고려한다.
라이브러리 계획 중에서 그 목적이 새로운 목적에 정합하는 것이 주어졌을 때, 다음과 같이 그 계획을 새로운 문제에 맞춤한다 :
① 정합 중에 얻어진 변수치환을 사용하여 라이브러리 계획을 사례화한다.
② 라이브러리 계획의 목적을 새로운 목적으로 대치한다.
③ 새로운 목적에는 있지만 라이브러리 계획에는 나오지 않는 조건 각각에 대하여 요구사항을 추가한다.
④ 라이브러리 계획의 초기조건을 새로운 초기조건으로 대치한다.
⑤ 예전의 초기조건에 의해서는 만족되었지만 새로운 초기조건에 의해서는 만족되지 않는 조건을 가진 연결고리를 모두 삭제한다. 그렇게 삭제된 각 연결고리에 대하여 그 연결고리의 조건과 소비자로 이루어진 요구사항을 추가한다.
⑥ 예전의 목적에는 있었지만 새로운 목적에는 없는 조건을 만족시키기 위한 연결고리를 모두 삭제한다.
그림 21 은 맞춤 과정을 설명해준다. 그림 21 의 위쪽 계획은 라이브러리 계획을 나타내고, 가운데 계획은 새로운 목적과 초기조건을 보여준다. 그림 21 의 위쪽계획과 가운데 계획의 목적들은 부분적으로만 정합될 뿐임을 주의하라. 그림 21 의 아래 계획은 라이브러리 계획을 새로운 목적과 초기조건에 맞춘 결과를 보여준다. 맞춤된 계획은 #8 로 표지된 단계의 T 와 #2' 으로 표지된 단계의 S 를 성취하여야 한다는 두 요구사항을 갖게 된다. 여러분은 조건 P 를 가진, #5' 에서 #8 로의 연결고리를 없애는 것이 왜 중요한지 의문을 가질 것이다. 또한 이제 U 가 초기조건에 있으므로 #2' 가 필요없을 것 같다는 것도 주의하자. 물론, #3' 과 #5' 으로 표지된 단계에 대해서도 마찬가지 이야기를 할 수 있을 것이다. 여러분들이 어떻게 그런 단계들을 삭제하여 더 잘 맞춤된 계획을 생성할 수 있을지 한번 고려해 볼 수 있을 것이다.
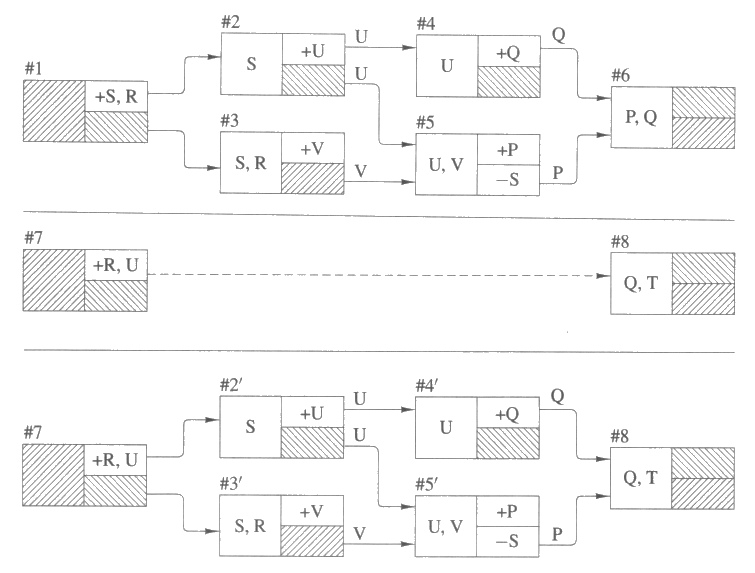
그림 21 : 기존의 계획을 새로운 목적과 초기조건에 맞춤. 위쪽 계획은 라이브러리 계획을 나타낸다. 가운데 계획은 새로운 목적과 초기조건에 대한 초기계획을 나타낸다. 아래쪽 계획은 라이브러리 계획을 새로운 목적과 초기조건에 맞춤한 결과이다. 맞춤된 계획에서는 연결고리들이 삭제되기도 하고 간단한 순서제약으로 대치되기도 했다는 것을 주지하라.
이제 우리는 새로운 문제에 대한 해를 얻기 위하여 정련을 시도해 볼 수 있는 계획을 하나 또는 그 이상 갖고 있을 것이다. 이전에 계획정련을 하던 방법은 계획 응용 (plan adaptation) 에는 맞지 않을텐데, 그 이유는 라이브러리 계획으로부터 맞춤에 의해 얻어진 계획을 가지고 시작해서는 해에 도달할 수 없을지도 모르기 때문이다. 해에 이르기 위해서는 다시 맞춤한 (refitted) 라이브러리 계획에서 단계나 연결고리 또는 순서에 관한 제약요건을 철회해야 할 수도 있다는 것이다.
탐색의 관점에서 이것이 갖는 의미는 탐색트리를 따라 내려가기만 하는 것이 아니라 올라가야 할 수도 있다는 것이다. 다시 맞춤한 계획 (refitted plan) 을 정련할 때 가능한 대안은 그림 22 에 설명되어 있는데, 다시 맞춤한 계획은 굵은 동그라미로 표시되고 에지 (edge) 는 회색 화살표로 표시되며, 에지는 다시 맞춤한 계획에서 단계나 제약요건 등을 철회하는 정련과정에 해당한다. 계획공간을 체계적으로 탐색하기 위하여 어떤 에지도 두 번 지나가지 않도록 주의해야 한다. 최소개입 계획수립을 위한 알고리즘의 경우에는 이것이 문제가 되지 않았는데, 이는 탐색공간이 트리구조라는 가정이 있었고 알고리즘이 늘 트리의 아래쪽으로만 진행하였기 때문이다.
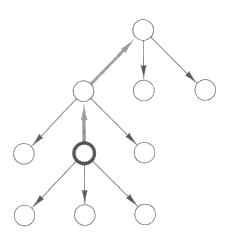
그림 22 : 정련과정 중 계획의 확장과 수정
체계성을 얻기 위하여 우리는 탐색상태에 해당하는 각 계획을 ↑ 또는 ↓ 로 표시한다. 계획수립 동안에 그런 계획들의 큐 (queue) 를 유지하는데, 이들은 다음 번에 살펴 볼 계획들이다. 어떤 계획을 정련할 때 그 계획이 ↓ 로 표시되어 있으면 refinements 를 적용하고, 결과로 얻어지는 계획들을 각각 ↓ 표시를 한 후 모두 큐에 넣는다. 어떤 계획 π 가 ↑ 표시가 되어 있으면, 앞서 π 에 대해 정련한 것을 딱 하나만 철회하여 하나의 새로운 계획 π' 을 만들고 이를 ↑ 표시하여 큐에 넣는다. 그리고 난 후, π' 에 refinements 를 적용하여 계획 집합을 얻는데, 그 중 하나는 원래의 π 가 될 것이다. π 를 제외한 각 정련결과는 ↓ 로 표시하여 큐에 넣는다. 이 전략은 탐색공간에서 각 상태 (계획) 를 최대 한번 방문하게 됨을 보장한다.
응용 계획수립의 분석
기존의 계획을 다시 맞춤하는 방법론은 계획수립 동안에 일을 더 적게 하게 된다는 보장을 해 주지 않는다는 것에 주의하라. 아주 형편없는 계획을 갖고 시작하게 되면 심지어 일을 더 많이 하게 될 수도 있다. 이전에 생성된 계획을 응용하는 것이 언제 좋을지에 대해 알아보려면, Hanks 와 Weld [1992] 의 분석을 단순화한 다음의 분석을 살펴보자.
우선, 계획을 응용하는 데 있어서 앞에서 소개한 최소개입 계획수립 방법론에서 보다 정확히 하나의 대안이 더 있을 뿐임을 명심하자. 탐색공간에 해당하는 트리에서 아래로 내려갈 수 있을 뿐 아니라 위로도 올라갈 수 있다는 것이다. 최소개입 탐색의 분기계수가 b 라 하고, 주어진 문제에 대한 최단 계획의 길이가 n 이라 하자. 최소개입 계획수립을 너비우선 탐색으로 구현하면 bn 의 시간을 필요로 할 것이다.
이제는 우리의 응용 계획자에게 다시 맞춤한 계획이 처음에 주어졌고 이로부터 목적을 성취하는 계획을 생성할 수 있으며, 그 과정에서 철회와 정련에 해당하는 k 번의 응용을 사용한다고 가정하자. 이 경우에,
(b + 1)k < bn
일 때에는 언제나 응용을 사용하는 것이 시간을 덜 요구하게 된다. 이 부등식은 k / n < logb+1 b 일 때 성립한다. 대부분의 실용적 계획수립 문제에서는 b 가 적어도 3 이 되는데 log4 3 = 0.79 라는 것을 생각하면, 검색과 다시 맞춤 루틴이 돌려주는 계획이 필요로 하는 응용의 수가 기본적인 최소개입 전략이 요구하는 정련의 수의 80 % 를 넘지 않는다면 응용을 사용하는 것이 더 나을 것이라고 결론지을 수 있다. 실험연구결과에 따르면 응용 전략은 실제 문제에 있어서 많은 경우 좋은 결과를 낸다고 알려져 있다.
앞에서 서술한 종류의 계획수립에 있어서는 어떤 주어진 시점에서의 세계가 어떤 상태인지 완전히 알 필요가 없었다. 그러나 연산자를 적용하기 위해서는 연산자의 전제조건에 명시된 조건들이 참인지를 알아야 한다.
일반적으로 계획자가 어떤 계획수립 문제에 연관된 모든 조건을 알 수 있을 것으로 기대해서는 안 된다. 대부분의 상태에서는 계획자가 전혀 알지 못하는 조건들이 있으며 과거에는 알았던 적도 있었지만 현 상태에서는 확실히 알지 못하는 조건들도 있다. 이 절에서는 각 조건에 대해서 계획자가 그 조건이 True 임을 알고 있거나 (안다는 것의 의미를 정당성을 갖는 참된 믿음으로 생각할 때 (역자 주 : 언어철학에서 흔히 쓰이는 정의로서 "안다는 것 (knowledge)" 을 "정당화된 참된 믿음 (justified true belief)" 으로 정의하는 것을 말한다.)), False 임을 알고 있거나 또는 그 어느 쪽도 알지 못하는 경우를 생각해 본다. 마지막 경우는 고전적인 2 가 논리 (two-valued logic) 에서 말하는 배제된 중간 (excluded middle) 에 해당하는 것이며 Unknown 으로 지칭된다.
그림 23 : 로봇이 복사기의 종이 서랍에 종이를 넣거나 프린트 카트리지를 교체하거나 기계를 재고정함으로써 복사기를 고치려면, 무엇이 잘못되었는지를 알아내야 한다.
이제는 한 상태에서 각 조건에 True, False, Unknown 중의 한 값을 할당하기 때문에 한 상태를 참이 되는 조건들의 목록으로만 표현할 수가 없게 되었고 한 상태가 각 조건에 대해 값을 일일이 할당해야 된다. 예를 들어, 계획자가 a 가 b 위에 있고 b 가 a 위에 있지 않다는 것은 알고 있으나 b 가 c 위에 있는지 그렇지 않은지는 알지 못하는 상태는 (((on a b) True) ((on b a) False) ((on b c) Unknown)) 으로 표현된다. 연산자들을 명세할 때 추가조건과 삭제조건을 합하여 하나의 사후조건 (postcondition) 의 집합으로 나타내며, 전제조건과 사후조건 모두 조건에 대한 값의 할당으로 명세된다.
복사기 수리 문제
이제 우리가 알지 못하는 것이 무엇인지를 표현할 수 있는데, 이와 같이 증강된 표현 능력을 어디에 사용할 것인가? 다음의 문제를 생각해 보자. 사무실 건물에 있는 복사기가 동작을 안 하는데 ((working copier) False), 로봇에게 그 복사기를 고치라는 목적이 주어졌다 ((working copier) True). 복사기가 고장날 수 있는 이유는 (1) 종이 서랍이 비어 있거나, (2) 카트리지를 교체해야 하거나, (3) 일시적인 하드웨어나 소프트웨어 문제로 인해 재고정 (reset) 을 해야 하는 경우뿐이라고 가정하자 (그림 23). 이 문제를 복사기 수리 문제 라고 부르겠다.
그림 24 : 복사기 수리 문제에 관한 연산자
이 복사기를 수리하는 표준 절차는 종이 서랍이 비었으면 서랍을 채우고, 필요하다면 카트리지를 교체하고 나서 기계를 재고정하는 것이다. 종이 서랍을 채우려면 서랍이 비어 있어야 하고 로봇이 복사기가 있는 곳에 와 있어야 하며 로봇이 종이를 가지고 있어야 한다. 카트리지를 교체하려면 카트리지가 다 닳았어야 하고 로봇이 복사기가 있는 곳에 있어야 하며 로봇이 교체한 카트리지를 가지고 있어야 한다. 기계를 재고정하려면 종이 서랍이 비어 있으면 안 되고 카트리지가 다 닳았어도 안된다. 이에 해당하는 세 연산자들이 그림 24 에 나와 있다.
그러나, 만약 로봇이 카트리지나 종이 서랍의 상태에 대해 알지 못하고 있으며 복사기를 조사해 보지 않고서는 그 상태를 알아낼 수 없다고, 즉 ((empty_paper copier) Unknown) 이고 ((spent_cartridge copier) Unknown) 이라고 가정해 보자. 또한, 현재 로봇이 있는 위치가 복사기가 있는 곳과는 좀 떨어진 곳에 있는 실험실이라고 하자.
복사기를 수리하기 위한 한 가지 계획은 복사기가 있는 방으로 가서, 문제가 무엇인지를 진단한 다음, 그 문제를 바로잡기 위해 필요한 조치를 취하는 것이다. 그러한 계획을 만들어 내기 위해서는 로봇으로 하여금 현재는 Unknown 인 조건들의 상태가 True 나 False 중 어떤 것인지를 결정하는 데 쓰이는 연산자들을 표현할 필요가 있다.
그림 25 : 정보 획득을 위한 연산자
그림 25 는 카트리지가 과연 교체될 필요가 있는지 그리고 종이 서랍이 비어 있는지를 결정하기 위한 연산자들을 보여준다. 각 경우에, 어떤 조건이 Unknown 이어야 한다는 전제조건이 있으며 연산자가 적용되고 난 후에는 그 조건이 True 인 것으로 알려지거나 False 인 것으로 알려질 것임을 나타내는 논리합 (disjunction) 에 해당하는 사후조건이 있다.
로봇이 복사기에 종이가 다 떨어졌는지를 알아보는 것에 대한 전제조건으로서 로봇이 그것에 대하여 알지 못해야 한다는 것이 좀 이상하게 보일 것이다. 물론 그처럼 무엇을 몰라야 하는 전제조건은 로봇이 종이가 다 떨어졌는지 알아보기 위해 복사기가 있는 곳에 있어야 한다는 전제조건과는 매우 다른 것이다. 좀더 표현력이 강한 연산자 언어에서는 루울렛 판을 돌리는 것과 같이 불확실성을 야기하는 행동과 루울렛 판이 멈추었을 때 결과를 관찰하는 것과 같이 불확실성을 해결하는 행동을 구분할 수 있을 것이다 [Etzioni et. al., 1992]. 그러나, 다음에서는 그와 같은 구분을 하지 않겠다.
사후조건에 나오는 논리합은 이전에 소개한 상태공간 탐색 방법을 사용해서는 다룰 수 없지만 (한 조건이 True, False 또는 Unknown 의 값을 가질 수 있을 때 추가조건에 나온 논리합은 항진명제 (tautology) 가 아님에 주의하라.), 사후조건에 나오는 논리합을 정리증명에서 흔히 사용하는 전략을 사용하여 처리할 수 있다. 만약 p 가 주어질 때 r 을 증명할 수 있고, q 가 주어질 때도 r 을 증명할 수 있다면, p ∨ q 가 주어질 때에도 r 을 증명할 수 있다. 이런 증명 전략을 흔히 경우에 따른 추론 (reasoning by cases) 이라 일컫는다. 복사기를 수리하기 위한 계획을 수립할 때 이와 매우 비슷한 일을 한다.
우선, 복사기가 무엇이 잘못 되었는지를 알아보는 계획을 세운다. 이를 계획의 무조건적인 (unconditional) 부분이라 부른다. 이 계획은 로봇이 복사실에 가서 종이 서랍과 교체 카트리지를 검사하는 것을 수반한다. 이런 검사를 하고 나면 네 가지 경우 중 하나로 결정이 될 것이다. 종이는 있는데 카트리지를 교환해야 한다 ; 종이는 없지만 카트리지는 괜찮다. 종이와 카트리지 모두 손을 보아야 한다 ; 종이나 카트리지 모두 문제가 없는데 일시적으로 하드웨어나 소프트웨어에 문제가 있었던 것같다. 실제 상태가 이들 네 가지 경우 중 어느 것에 해당하는지를 로봇이 알게 되려면 실행 시간이 되어야만 한다.
조건부 계획의 생성
계획의 무조건적인 부분 외에 우리는 네 가지 경우 각각을 위한 네 개의 예비 계획을 만들어 낸다. 실행시간에는 이 네 가지 경우 중 어느 것이 실제에 해당하는지를 알아보기 위한 무조건적인 부분을 실행하고 나서 그 다음에 실제 상태에 해당하는 예비 계획을 실행한다. 전체 계획은 조건부 계획 (conditional plan) 이라 불리운다. 조건부 계획에서는 계획의 실행 중에 어떤 조건들의 상태가 True 로 결정되는지 False 로 결정되는지에 따라 로봇이 어떤 단계를 수행하느냐 마느냐가 정해진다.
불완전성은 계획수립에 있어서 선택의 여지를 추가로 도입하게 한다. 예를 들어, 어떤 요구사항을 만족시키는 방법은 그것을 True 로 만드는 단계를 수행하는 것일수도 있고, 그것이 True 임을 관찰하는 것일 수도 있다. 많은 경우에 연산자의 전제조건이 관찰에 의해서만도 성취될 수 있다면 이를 구체적으로 표시하는 것이 유용하다. 문이 초록색인 사무실을 찾는 방법 중에는 아무 사무실이나 골라서 그 사무실문을 초록색 페인트로 칠하는 것도 있을 수 있다. 그러나 아마도 우리의 로봇이 그런 해를 받아들이지 않기를 바랄 것이다.
앞서의 연산자를 사용하면 종이 서랍이 비어 있는지 또는 카트리지가 다 닳았는지를 알지 못하는 경우 빈 종이서랍이나 다 닳아버린 교체 카트리지 때문에 고장난 복사기를 수리할 수가 언다. 그러나, 실제에서는 어떤 부품에 문제가 있는지 없는지를 알지 못하더라도 기계를 수리하려고 하는 과정에서 그 부품을 교체하는 일이 흔히 있다. 이는 어떤 부품이 고장인지 아닌지를 결정하는 일이 무조건 새 것으로 교체하는 것 보다 더 비용이 많이 들기 때문이다.
이 방법론에서는 필요한 정보를 모으는 계획을 수립하고, 그 계획을 실행하여 필요한 정보를 알아 본 후에 정보획득의 결과로 정해진 구체적인 상태에 맞는 계획을 수립하는 순서로 일을 함으로써 계획수립에 따르는 노력을 절감할 수 있다. 그러나 이렇게 하는 것이 어느 정도 계산을 절감할 수는 있으나 실행하기에는 값비싼 계획을 만들어 낼 수도 있다.
예를 들어 로봇이 처음 위치해 있던 실험실에 종이와 교체 카트리지들이 쌓여 있다고 하자. 똑똑한 로봇이라면 복사기에 무슨 문제가 있는지 모르지만 준비하는 셈치고 새 카트리지와 종이 한 권을 가지고 갈 것이다. 많은 경우, 여러 가능한 관찰결과를 예측하여 로봇이 행동을 취하는 계획을 만들어 내도록 노력할 필요가 있다.
물론, 어떤 문제를 예상하는 것과 그에 대비하는 것은 전혀 다른 문제이다. 어쩌면 로봇은 교체 카트리지와 한 권의 종이를 함께 가지고 갈 수는 없을지도 모르고 이런 경우, 로봇은 둘 중 어느 것이 복사기 고장의 원인이 될 가능성이 더 높은가에 대한 통계에 근거하여 둘 중 하나를 선택해야 한다. 불완전 정보하에서의 계획수립에는 여러 가능한 미래들에 대처하는 계획들을 조합하는 일이 수반된다.
다음에서는 불완전 정보하에서의 계획수립을 위한 알고리즘을 서술한다. 논의를 단순화하기 위하여 각 연산자는 최대 하나의 사후조건을 가지며 이 사후조건은 논리합으로서 (or (condition True) (condition False)) 의 형태라고 가정한다. 계획에 나오는 연산자의 이런 논리합 중의 한 논리합인자 (disjunct) 를 관찰 (observation) 이라 부른다.
문맥은 가능한 관찰의 집합을 표현
알려지지 않은 조건들에 해당하는 여러 가능한 경우를 추적하기 위하여 문맥 (context) 이라는 개념을 도입한다. 문맥은 조건의 집합에 True 또는 False 를 할당하는데, 각 문맥은 관찰의 집합에 해당한다 (어떤 응용에 있어서는 조건들이 결과적으로 Unknown 이 되는 연산자들을 표현하는 것이 유용할 수도 있을 것이다. 예를 들어, 로봇이 방에서 나가면 이제는 그 방에 누가 있는지에 대하여 확실히 알지 못할 것이다. 이는 문맥이란 개념을 복잡하게 만드는데, 그렇게 되면 조건들이 여러 번 알려졌다가 모르게 되었다가 하는 것이 반복적으로 되풀이될 수 있기 때문이다. 이 절에서는 일단 한 조건의 진리같이 True 나 False 로 되면 또 다시 Unknown 이 되는 일은 절대로 없다고 가정하겠다. 그러나 우리의 방법론을 확장하여 Unknown 과 True 나 False 사이를 왔다갔다하는 조건들도 다루게 할 수 있는데, 이는 같은 조건에 관한 관찰의 서로 다른 사례를 구별함으로써 가능하다.). 각 문맥이 값을 할당하는 모든 조건에 대해 일치할 때 두 문맥을 서로 호환적 (compatible) 이라고 한다. 예를 들어, 문맥 ((condition1 True) (condition2 True)) 는 ( ) 이나 ((condition1 True) (condition3 False)) 와는 호환적이나 ((condition2 False)) 와는 호환적이지 않다.
앞 절에서는 두 단계로 이루어진 계획을 가지고 탐색 알고리즘을 시작하였다 : 한단계는 사후조건이 초기조건에 해당하는 의사연산자이고 또 한 단계는 전제조건이 목적조건에 해당하는 의사연산자였다. 불완전 정보하에서의 계획수립에서는 완전정보의 경우와 마찬가지로 시작하지만, 이 단계들이 의존하는 관찰들을 추적하기 위하여 각 단계에 문맥을 표지하여 놓는다. 우리가 바라는 바는 실행시간에 어떤 관찰을 하게 되더라도 성공하는 계획을 만드는 것이지만 관찰되지 않은 조건들에 의존하는 단계들을 수행할 필요는 없는 것이다.
단계에 대한 유도문맥 (derived context) 이 어떤 관찰을 포함하는 것은 그 단계가 어떤 연결고리의 소비자이면서 그 연결고리의 조건이 유도문맥에 포함되는 관찰이거나 연결고리의 생산자가 갖는 문맥이 그 관찰을 포함하는 경우로 정의된다. 목적이 아닌 단계에 대한 문맥은 유도문맥이 된다. 불완전 정보하에서의 계획수립에서는 서로 다른 비호환적인 문맥에 해당하는 목적단계를 여러 개 만드는 것이 보통이다. 목적단계에 대한 초기문맥 (initial context) 은 그 단계가 생성될 때 정해진다. 목적단계에 대한 문맥은 그 단계의 초기문맥과 유도문맥의 합집합이 된다. 목적단계만이 초기문맥을 갖는다.
계획수립은 다음과 같이 진행된다. 초기계획은 완전 정보의 경우와 마찬가지로 생성한다. 목적단계에 공 문맥 (empty context) 을 초기문맥으로 할당한다. 완전 정보의 경우와 마찬가지로 진행하되 다음 두 가지 중요한 차이점을 갖는다. 첫째, 한 단계와 다른 단계 사이에 연결고리를 만들 때는 두 단계가 호환적인 문맥을 가져야만 하며 연결고리를 만든 후에는 소비자의 문맥이 생산자의 문맥을 논리적으로 함언해야 (entail) 한다. 둘째, 한 단계가 연결고리와 충돌하는 것은 연결고리 소비자의 문맥이 그 단계의 문맥과 호환적인 경우뿐이다.
불완전 정보하에서 올바른 계획의 기준은 다음과 같다. 첫째, 완전 정보의 경우와 마찬가지로 계획 안에 요구사항이나 충돌이 없어야 한다. 둘째, 목적단계의 문맥이 True 와 False 만을 갖는 2 가 논리에서의 항진명제에 해당해야 한다. 이 두번째 요건은 어떤 가능한 실제 관찰의 경우에도 그와 호환적인 문맥을 가진 목적단계가 있음을 보장한다. 계획수립 중에 요구사항이나 충돌은 없지만 목적단계의 문맥이 항진명제가 되지 못하면 기존의 목적단계의 모든 문맥과 비호환적인 문맥을 가진 새로운 목적단계를 생성하여 계획수립을 계속한다.
계획수립 알고리즘을 설명하기 위해 복사기 수리 문제의 간단한 경우를 살펴보겠다. 우선 조건들의 집합을 정의한다. working, 복사기가 정상적으로 작동한다, atlab, 로봇이 실험실에 있다; atcopier, 로봇이 복사실에 있다; empty, 복사기의 종이 서랍이 비어 있다; spent, 복사기의 교체 카트리지를 교체해야 한다; cart, 로봇이 교체할 카트리지를 가지고 있다; paper, 로봇이 복사기에 채울 종이를 갖고 있다. 조건 c 에 대한 세 가지 가능한 값 True, False, Unknown 의 할당을 각각 c, ￢ c, ?c 로 표현한다. 표 1 은 복사기 수리 문제를 풀기 위해 사용되는 연산자의 집합에 대한 전제조건과 사후조건을 나열해 보인다.
|
연산자 |
전제조건 |
사후조건 |
|
goal |
working |
|
|
initial |
|
atlab ￢paper ￢cart |
|
getcart |
atlab |
cart |
|
getpaper |
atlab |
paper |
|
gocopier |
atlab |
atcopier |
|
checkcart |
atcopier ?spent |
(or spent ￢spent) |
|
checkpaper |
atcopier ?empty |
(or empty ￢empty) |
|
changecart |
atcopier cart spent |
￢spent |
|
addpaper |
atcopier empty paper |
￢empty |
|
reset |
atcopier ￢spent ￢empty |
working |
표 1 : 복사기 수리 문제를 위한 연산자
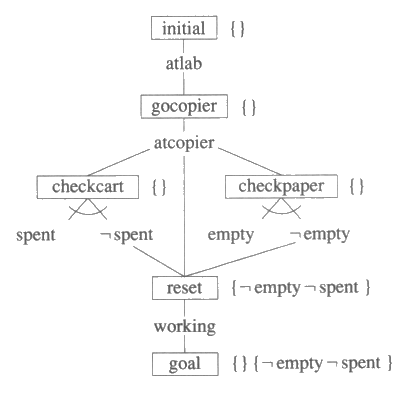
그림 26 : 한 가지 가능한 문맥에서 복사기 수리 문제에 대한 해
목적단계를 공 문맥으로 초기화한다. 그림 26 은 카트리지를 교체할 필요가
없고 종이 서랍도 비어있지 않은 문맥에서 복사기 수리 문제를 해결하기 위한 계획을
보여 준다. 각 단계는 연산자에 해당하는 표현에 네모 표시가 되어 있고, 전제조건과
사후조건은
네모 표시를 하지 않은 것들이다. 목적 단계에는 초기문맥과 그 오른편에 유도문맥이
표지되어 있다. 관찰의 논리합은 
과 같이 그림에서 표시된다.
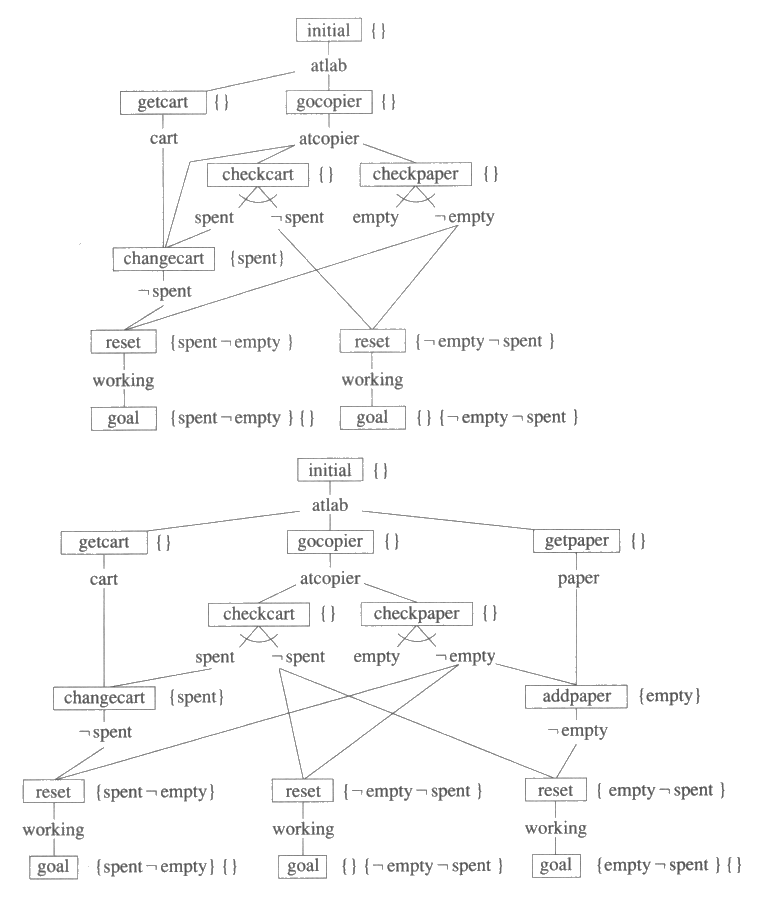
그림 27 : 문맥이 추가됨에 따른 복사기 수리 문제에 대한 해. 그림이 너무 복잡해지는 것 위해 reset 이 atcopier 를 전제조건으로 요구한다는 것을 표시하지 않았다.
그림 27 은 두 개의 계획을 더 보여 주고 있는데, 위쪽 계획은 종이 서랍이 비어있지만 않으면 카트리지를 교체해야 하는지 아닌지와 상관없이 동작하는 계획이고 아래쪽 계획은 카트리지도 교체해야 하고 종이 서랍도 비어 있는 경우만 아니면 동작하는 계획이다. 초기문맥이 {spent empty} 인 목적단계를 추가하면 실행시간에 어떤 관찰을 하게 되더라도 작동하는 계획을 생성할 수 있다.
복사기 수리 문제에 있어서 실행시간에 어떤 조건들이 관찰되더라도 동작하는 계획을 만들기 위해 모든 가능한 문맥을 고려해야 했다. 일반적으로, 이제까지 서술된 모델에서는 2n 개의 관찰이 있다고 할 때 2n 개의 문맥이 있게 된다. 계획수립은 완전 정보의 경우에도 이미 어려운 문제인데 불완전 정보는 계산상의 문제를 더 악화시킬 뿐이다. 더욱 곤란한 것은 해가 존재하지 않는 문맥도 있을 수 있다는 것이다. 예를 들어, reset 에 또 다른 전제조건이 있는데 이는 로봇이 제어할 수 있는 것이 아니라 하자. 최선의 경우로 우리는 무결하고 완전한 계획자를 바랄 수 있지만 게다가 종료를 보장하기를 요구하는 것은 너무 많이 바라는 것일지 모른다. 실용적인 계획수립에 있어서는 도메인에 관련된 좋은 휴리스틱들이 필요한데 어려운 문제의 해결을 위한 노력을 언제 포기할 것인지 또 어떻게 실패로부터 회복할 것인지를 알 필요가 있다.
여태까지 우리가 살펴 본 기법들은 모두 매우 간단한 행동모델에 근거하고 있다. 다음 절에서는 행동과 시간에 따른 변화를 좀더 정교하게 표현해 볼 경우 얻게 될 결과에 대하여 살펴보겠다.
앞 절의 계획수립 방법에서는 한 상태를 다른 상태로 변환하는 연산자를 사용하여 행동을 표현하였다. 각 연산자는 전제조건과 사후조건으로 명세되고, 어떤 상태에서 전제조건이 만족되지 않으면 연산자가 그 상태에서 적용될 수 없다. 이 계획수립 방법은 어떤 연산자 직전의 상태에서는 그 연산자의 전제조건이 만족되며 그 직후의 상태에서는 사후조건들이 참이 되는 것을 보장한다.
지금까지 살펴 본 여러 연산자 표현방법들은 일종의 표현의 한계를 가지고 있는데, 이 절에서는 이 한계를 넘어서는 방법들을 살펴보겠다. 특별히 연산자 직후의 상태가 연산자 직전의 상태에 의해 결정되는 조건부 효과 (conditional effect) 와 사물의 집합에 대해 성립하는 전체 한정 효과 (universally quantified effect) 에 대하여 살펴보겠다. 앞 절에서는 상태, 연산자, 전제조건 그리고 사후조건을 나타내기 위하여 명제논리를 사용하였는데, 다음에서는 표현의 편이를 위하여 전체 한정사를 도입한다. 또 유한 영역 (domain) 을 가정하여 전체 한정 문장을 논리곱으로 변환할 수 있게 하고 전적으로 명제논리 내에 머물러 있을 수 있게 한다.
많은 경우, 표현력의 증가는 계산적 부대비용 (overhead) 의 증가를 가져온다. 우리는 이미 연산자를 확장하는 한 가지 방법을 살펴보았는데, 이 경우에도 계산적 부대비용이 추가되었다. 연산자의 효과에 있어서의 불확실성을 표현하기 위해 사후조건을 논리합으로 표현하는 것은 탐색공간의 크기를 지수적으로 증가시킬 수 있는데, 이때 지수가 되는 것은 논리합으로 된 사후조건의 개수이다. 이 절에서 우리는 한가지 확장 방법에 초점을 맞출 것인데 이로 인한 계산 부대비용의 증가는 비교적 온건할 것이다.
이 절에서는 연산자를 코드화하기 위해 다시 한번 연산자 스키마에 대한 우리의 표기법을 바꾼다. 이 절의 나머지 부분에서 연산자는 두 개의 공식으로 이루어진다. 하나는 연산자의 전제조건을, 또 하나는 사후조건을 서술한다. 이 표기법을 사용하면 블록 (? x) 를 다른 블록 (? y) 에서 탁자 위로 옮기는 연산자를 다음과 같이 표현할 수 있다.
(make-OPERATOR ;; 전제조건
' (and (on (? x) (? y))
(clear (? x))
(not (equal (? y) table)))
;; 사후조건
' (and (on (? x) table)
(clear (? y))
(not (on (? x) (? y)))))
연산자의 사후조건 공식에 추가조건과 삭제조건이 모두 나오는데, 삭제조건은 연산자 직후의 상태에서 참이 아님을 나타내기 위해 부정되어 있다.
조건부 효과
상태공간 탐색에 관한 절에서 기계조립 예에 대하여 논할 때 두번째 부품을 조립하는 행동을 모델하기 위해 두 개의 연산자를 사용할 필요가 있었음을 상기하자. 두번째 부품을 조립하려 할 때 첫째 부품이 이미 조립되어 있으면 둘째 부품을 조립하는 과정에서 첫째 부품이 해체되어야만 했다. 한 연산자는 둘째 부품의 조립을 시도하기 이전에 첫째 부품이 조립되어 있는 경우를 다루었고, 다른 연산자는 둘째 부품의 조립을 시도하기 전에 첫째 부품이 조립되어 있지 않은 경우를 다루었다.
첫째 부품이 결과적으로 어떤 상태가 되는지, 조립이 되는지 안 되는지를 둘째 부품을 조립하는 행동의 조건부 효과 (conditional effect) 라 말한다. 조건부 효과에 관해 추론하기 위하여 연산자 직전의 상태에서 선행조건 (antecedent) 이 참인 때는 언제나 연산자 직후의 상태에서 후행조건 (consequent) 이 참이 됨을 나타내는 데에 (when antecedent consequent) 와 같은 표기를 사용한다.
그림 28 : 기계조립 예에 관한 수정된 연산자 집합
그림 28 은 기계조립 예에 관한 수정된 연산자를 보여 준다. 다음의 예는 최소개입 계획수립에서 조건부 효과가 어떻게 처리되는지를 설명해 준다.
초기상태에서는 세 부품 모두가 조립되어 있지 않으며 목적은 세 부품을 조립하는 것이라 하자. 계획수립의 시작은 세 개의 요구사항, 즉 각 부품이 조립되어야 한다는 것으로부터 이루어진다. 이들 요구사항을 만족시키기 위해 세 개의 연산자를 모두 추가하게 되고 따라서 두 개의 요구사항, 즉 셋째 부품보다 먼저 첫째와 둘째부품이 조립되어야 한다는 것이 추가된다. 이 두 개의 새로운 요구사항을 만족시키기 위해서 순서에 관한 제약요건이 추가되고, 이제 계획은 첫째와 둘째 부품을 어떤 순서로든 조립하고 나서 셋째 부품을 조립하는 것으로 이루어진다.
우리는 둘째 부품이 첫째 부품보다 먼저 조립되어야 한다는 것을 알고 있다. 최소개입 계획자가 조건부 효과를 사용하여 어떻게 이와 같은 결론에 도달하게 되는지 살펴보자. 계획자는 첫째 부품을 조립하는 단계와 목적단계 사이의 연결고리의 조건인 (assembled 1) 과, 둘째 부품을 조립하는 연산자의 조건부 효과의 결과부분인 (not (assembled 1)) 이 서로 상충되는 것을 알아차리게 된다. 조건부 효과의 결과부분이 실현되지 않게 하기 위하여 둘째 부품을 조립하는 단계 직전에 조건부 효과의 조건부분의 부정이 참이어야 한다는 요구사항을 계획자가 추가한다.
이 새로운 요구사항이 도입하는 충돌은 단 한 가지 방법으로만 해결될 수 있는데, 그것은 둘째 부품을 첫째 부품보다 먼저 조립하는 것이다. 지금 간략히 살펴본 바와 같이 조건부 효과를 다루는 전략을 최소개입 계획수립 알고리즘에 추가하는 것은 약간의 계산을 더 함으로써 쉽게 이루어질 수 있다.
논리합 전제조건
불완전 정보하에서의 계획수립에 관한 절에서는 불확실성을 표현하기 위하여 논리합으로 된 사후조건을 사용하였다. 전제조건에도 논리합을 쓸 수 있는데, 그 경우에는 계산적 부대비용이 사후조건의 경우보다 더 온건하다.
어떤 의미에서는 전제조건의 논리합이 불필요한데 이는 논리합을 전제조건을 가진 연산자를 각 논리합 인자에 해당하는 연산자들로 나누어 전개할 수 있기 때문이다. 그러나, 논리합을 명시적으로 표현하는 것이 좀더 자연스러울 때가 많으며 어떤 경우에는 그렇게 하는 것이 연산자의 적용범위를 명백히 해 준다. 전제조건 내의 논리합은 흔히 연산자가 적절한 문맥에서 적용되는 것을 확실히 하기 위해 사용된다.
논리합 전제조건의 논리합 인자는 정적조건들을 사용하는 경우가 많다. 앞서 우리는 (not (equal x y)) 형태의 정적 조건을 본 바 있는데, 정적조건들은 객체의 유형 (type) 을 명세하기 위해서도 종종 사용된다. 예를 들어, 정적조건 (bloch a) 는 a 라는 객체가 블록 유형임을 나타낸다.
우리는 객체들의 집합과 그들의 유형에 관한 지정은 정적인 것으로 가정하는데, 그 의미는, 행동의 결과로서 객체를 생성하거나 소멸시킬 수 없으며 또한 객체의 유형을 바꿀 수도 없음을 말한다. 예를 들면, (not (block b)) 와 같은 사후조건을 가진 연산자를 쓸 수 없다.
그림 29 는 논리합 전제조건과 조건부 효과를 사용하여 블록을 옮기기를 표현한 연산자 스키마를 제시하고 있다. 이 하나의 연산자로 한 블록을 블록에서 블록으로, 블록에서 탁자로 또 탁자에서 블록으로 옮기는 경우를 모두 처리한다.
그림 29 : 블록쌓기를 위한 일반적인 연산자 스키마
최소개입 계획수립에서 논리합 전제조건을 처리하기 위하여 각 논리합 인자에 대해 요구사항을 추가하고 그 요구사항이 만족되었을 때는 나머지 논리합 인자들을 삭제하는 기제가 필요하다. 논리합 전제조건은 탐색공간의 크기를 증가시키지만 절도있게 사용할 경우에는 편리할 때가 많다.
전체 한정 효과
전제조건과 사후조건을 서술할 때 어떤 객체들의 부류 전체에 관한 서술을 하는 것이 유용할 때가 있다. 그러한 전제조건이나 사후조건은 전체 한정된 공식을 사용하여 표현가능하다.
예를 들어, clear 술어 (predicate) 를 따로 사용하는 대신에 다음과 같이 한정된 공식을 사용하여 (clear (? y)) 를 표현할 수 있는데, 이때 유형 정보를 명시함으로써 한정사의 범위 (scope) 를 제한한다 :
(forall (block (? x))
(not (on (? x) (? y))))
이와 같이 전체 한정 문장을 표현하는 데에는 어떤 추가적인 기제도 필요하지 않다. 유형 정보가 정적이며 영역 (domain) 이 유한하다는 사실을 이용하여 전체 한정문장을 논리곱으로 변환할 수 있는데 예를 들어, 세 개의 블록 a, b, c 만이 있다면,위의 한정 공식은 다음의 논리곱으로 표현될 수 있다 :
(and (not (on a (? y))) (not (on b (? y))) (not (on c (? y))))
실제에서는 전체 한정 전제조건은 그와 동치인 논리곱으로 직접 확장되며, 전체 한정 사후조건은 적당한 요구사항이나 잠재적인 충돌에 대응해야 할 필요가 있을 때 확장된다.
방랑하는 서류가방 예
조건부 효과와 한정된 사후조건의 유용성을 설명하기 위해서 여러분의 서류가방이 집에 있는데 그 안에 여러분의 월급봉투가 있으며 여러분의 목적이 서류가방은 사무실에, 월급봉투는 집에 두는 것이라고 가정해 보자. 그림 30 은 두 연산자를 나열하고 있다. 하나는 서류가방과 그 안의 내용물을 한 곳에서 다른 곳으로 옮기는 것이고, 다른 하나는 서류가방에서 어떤 물체를 꺼내는 것이다.
그림 30 : 서류가방에 관해 추론하는 데 쓰이는 연산자
b 가 서류가방이고 c 가 월급봉투라 할 때, 처음에는 (at b home), (in c b), (at c home) 이 성립하고, 우리의 목적은 (at b office), (at c home) 이 된다. 초기상태에서 (at c home) 은 이미 성립하므로, (at c home) 을 조건으로 갖는 연결고리를 초기단계와 목적단계 사이에 만든다. (at b office) 를 성취하기 위해, b 를 home 에서 office 로 옮기는 연산자를 사례화하는데, 이때 연산자는 아래의 조건부 효과 (이는 한정된 사후조건의 사례이다) 의 결과가 (at c home) 을 조건으로 갖는 연결고리와 상충됨을 알아차린다.
when (in c b) (and (at c office) (not (at c home))))
월급봉투가 서류가방에 그냥 남아 있으면 서류가방과 함께 사무실로 옮겨져 월급봉투가 집에 있어야 한다는 요구사항을 만족시키지 못한다. 이러한 조건부 효과가 실현되지 않게 하기 위하여 서류가방을 사무실로 옮기는 연산자 직전에 조건부 효과의 조건부분이 참이 아니어야 한다는 요구사항을 설치한다. 이 요구사항을 만족시키기 위하여 서류가방을 사무실로 옮기기 전에 월급봉투를 꺼내는 연산자를 더하게 되고, 따라서 목적을 달성하는 완전한 계획을 형성하게 된다.
한 가지 덧붙일 말은 이 장에서 우리는 어떤 목적들을 성취하는 것에만 관심을 가졌다는 것이다. 실제적인 계획수립 시스템에서는 목적들이 지속 (maintenance) 되게 하는 것도 중요하다. 지속목적의 예로는 집 열쇠를 늘 여벌로 하나 서류가방에 넣어가지고 있어서 위급한 상황에 열쇠를 쓸 수 있도록 하는 것을 들 수 있다. 최소개입 계획수립에서는 어떤 목적이 지속되게 하는 것은 비교적 간단히 구현할 수 있다.
계획자의 제어가 불가능한 프로세스
이 절에서 서술한 계획 방법들은 실용적으로 매우 유용한 것들이나 그 표현력에 있어서는 여전히 제한이 많다. 예를 들어, 이 방법을 확장하여 임의의 수만큼 중첩된 용기 (역자 주 : 가방 안에 월급봉투가 들어 있으므로 가방을 하나의 용기로 볼 수 있다. 만약 가방의 서류봉투 안에 들어 있는 수첩 갈피 안에 월급봉투가 들어 있다면, 월급봉투는 세 개의 용기에 중첩되어 있다고 볼 수 있다.) 를 다룰 수 있도록 하는 것은 쉬운 일이 아니다. 포함관계는 보통 전이적 (transitive), 비반사적 (irreflexive), 비대칭적 (antisymmetric) 관계로 표현된다. 우리가 서류가방을 여행가방 안에 넣고 여행가방을 옮기면 서류가방 안의 내용물들은 어떻게 될까?
계획자가 제어할 수 없는 사건들도 다루려고 한다면 계획에 관하여 추론하는 것은 더욱 복잡해진다. 가장 간단한 도메인에서도 계획자는 시간의 흐름을 제어할 수없다. 만약 계획자가 제어할 수 없는 다른 에이전트 (agent) 나 프로세스들을 고려한다면 문제는 더욱 복잡해진다. 다른 에이전트들의 행동에 관해 알고 있으면 그 행동의 결과를 표현하는 것이 가능할 때도 많다. 문제는 계획수립 중에 그와 같은 결과에 관해 고려할 여유가 있는가 하는 것이다.
6 장 고급 지식 표현에서는 행동의 결과에 관하여 추론할 때 적용될 수 있는 인과관계에 관한 추론에 대하여 몇 가지 아이디어를 제공하고 있다. 문헌에서는 시간적 추론과 계획수립이 늘상 매우 밀접하게 연관되어 있다. 이 두 가지 소분야에서 중요한 쟁점은 표현력과 계산적 복잡성을 균형있게 다루는 표현방법을 만들어내는 데 있다.
계획수립이란 우리가 바라는 결과를 가져오는 행동을 선택할 수 있도록 행동의 결과에 대하여 추론하는 것을 수반한다. 이 장에서는 계획수립을 탐색의 특별한 경우로서 생각하였다. 다른 탐색문제의 경우와 마찬가지로 탐색공간을 어떻게 표현하느냐 하는 것은 계획 시스템의 성능에 중요한 영향을 미칠 수 있다.
상태공간 탐색에 의하면 계획수립은 이 세계가 처할 수 있는 가능한 상태들의 공간에서 탐색을 하는 것이 된다. 계획수립 문제는 초기상태와 목적이 되는 상태들의 집합으로 명세되고, 연산자들은 한 상태를 다른 상태로 변환하며 계획수립 문제에 대한 해는 초기상태를 목적상태로 변환하는 연산자의 순서열에 해당한다.
이 세계의 가능한 상태공간에서 탐색을 하는 대신에 가능한 계획들의 공간에서 탐색을 할 수 있다. 최소개입 계획수립은 계획을 연산자들의 부분순서집합으로 표현하고, 이들로 이루어진 탐색공간을 사용한다. 각 부분순서집합은 하나 이상의 연산자 순서열을 표현할 수 있다. 우리는 최소개입 계획수립을 위한 탐색 절차를 제공하였는데, 이는 무결하고 (이 절차가 어떤 것이 해라고 하면 그것이 실제로 해가 된다), 완전하며 (주어진 문제에 대한 해가 존재하면 이 절차가 해를 찾아낸다), 체계적이다 (이 절차는 탐색공간 내에서 절대로 같은 노드를 두 번 검사하는 법이 없다).
계획수립은 계산적으로 복잡한데 추상화는 복잡성을 줄이는 한 방법론을 제공한다. 추상화 공간은 탐색을 촉진시키기 위해 어떤 세부사항들을 무시하는 탐색공간을 말한다. 위계구조에 따라 점점 더 추상적인 추상화 공간들을 정의함으로써 계획수립의 속도를 여실히 올릴 수 있다.
계획수립의 속도를 높이는 또 다른 방법론으로는 이전에 생성된 계획을 계획 라이브러리에 저장하는 것을 들 수 있다. 새로운 문제를 맞닥뜨렸을 때 계획자는 라이브러리에서 비슷한 문제를 푸는 데 사용했던 계획을 찾아내어 그것을 새 문제에 맞게 응용한다. 이와 같은 응용 방법은 계획을 저장하고 검색하는 데 드는 비용을 여러 번의 응용과 상각하려 하는 것이다.
대부분의 실용문제에서 계획자는 이 세계의 상태에 대한 완전한 정보를 갖고 있지 못한다. 그런 실용문제에 맞는 계획수립을 하려면 정보가 없을 때 어떻게 할지를 알아내야 한다. 어떤 때는 필요한 정보를 획득하기 위한 계획을 세울 수 있고 어떤 때는 정보가 없더라도 사용가능한 정보는 무엇이든 쓰면서 진행해야 할 때도 있다. 불완전 정보를 극복하는 것은 계획수립에 있어서 새로운 차원의 계산적 복잡성을 추가한다.
이 장에서는 대부분 상태공간 탐색에 관한 절에서 개발된 단순한 형태의 행동표현을 사용하였다. 이 표현은 비교적 단순한 일상생활의 행동이나 프로세스들의 결과를 처리할 수 있을 만큼도 표현력이 충분치 않다. 그러나 조건부 효과나 객체들의 유한집합에 대한 한정 (quantification) 을 처리할 수 있도록 우리의 표현을 확장하는 것은 비교적 쉬운 것으로 밝혀졌다. 논리합과 시간을 처리할 수 있도록 하는 확장은 난해한 표현 상의 문제를 제기한다. 연속적인 수량에 관하여 추론하거나 계획자가 제어할 수 없는 프로세스에 관해 추론하는 것은 더욱 어려운 문제를 제기한다. 이러한 어려움은 그와 같은 결과를 어떻게 형식적으로 표현할 것인가 하는 문제 때문에 생긴다고 하기보다는 계산을 가능하게 하는 효율적인 표현을 어떻게 제공할 것인가 하는 문제에서 발생한다. 실제 세계의 프로세스에 관하여 효율적으로 추론하는 방법을 개발하는 것은 자동 계획수립의 중요한 연구분야이다.
상태공간 탐색에 관한 내용은 Ernst, Newell 과 Simon [1969] 의 연구에서 끌어 온 것인데, 이들의 연구는 일반적 문제 해결자 (General Problem Solver, GPS) 라는 것으로서, 문제를 해결하는 데 있어서의 인간의 수행방법을 모델하기 위한 프로그램을 개발하는 것이었다. GPS 는 그 영향력이 엄청났으며, GPS 의 많은 아이디어들이 현대의 계획수립과 탐색 시스템에 도입되었다. 우리가 자세히 살펴 본 상태공간 탐색 방법은 STRIPS [Fikes 와 Nilsson, 1971] 에 의해 사용된 표현방법에 근거하고 있다. 행동에 대한 STRIPS 의 표현방식은 많은 계획수립 시스템의 표현방법의 근간을 이루고 있다.
최소개입 계획수립에 관한 절은 Sacerdoti [1977] 와 Tate [1977] 의 부분순서 계획에 관련된 연구와 Sussman [1975] 의 충돌의 인식과 해결에 관한 연구 그리고 Stefik [1981] 의 제약요건 게시 계획자에 관한 연구에서부터 비롯된 것이다. Chapman [1987] 은 부분순서 계획의 수립에 관한 기존의 연구를 좀더 엄밀하게 재구축하였으며, McAllester 와 Rosenblitt [1991] 은 이 아이디어들을 더욱 상세히 정련하여 이 장에서 서술된 방법론을 개발하였다.
위계구조를 이루는 추상화 공간에서의 계획수립에 관한 최초의 연구는 Sacerdoti [1974] 의 연구인데 여기서 우리가 다룬 내용은 Knoblock [1991] 의 내용을 따랐으며 계획수립을 탐색의 일종으로 분석한 Korf [1987] 의 연구와도 관련이 있다.
계획응용에 관한 연구는 일종의 학습에 해당하는데, 이와 관련된 연구는 문헌에서 계획 재활용 (plan reuse), 고속화 학습 (speedup learning), 응용 계획수립 (adaptive planning), 계획 수정 (plan debugging), 케이스기반 계획수립 (case-based planning) 등의 용어로 나와 있는 것을 찾아 볼 수 있다 [Fikes et. al, 1972; Schank 와 Abelson, 1977; Minton, 1988; Simmons 와 Davis, 1987, Hammond, 1989, Kambhampati 와 Hendler, 1992]. 특히 이 장에서 다룬 내용은 Hanks 와 Weld [1992] 의 연구에 의거한 것이다.
실행시간에 융통성 있게 대처할 수 있도록 하기 위하여 조건부 계획을 생성하는 계획자에 관한 많은 연구가 이루어져 왔다 [Warren, 1974; Dean, 1985; Schoppers, 1987; Collins와 Pryor, 1992 ; Peot 와 Smith,1992 ; Etzioni et. al,1992]. 더욱 신축성 있는 계획을 제공하기 위해 연구자들은 계획수립과 실행을 동시에 하는 시스템을 개발하여 왔다 [McDermott, 1978; Georgeff 와 Lansky, 1987; Firby, 1987; Krebsbach et. al, 1992]. 만약 이 세계가 매우 빨리, 또는 예측할 수 없이 변화한다면 계획수립을 전혀 하지 않고, 그 대신 변화하는 환경에 반응하면서 앞일을 예측하거나 계획을 세우기 위해 복잡하지만 쓸모없을지도 모르는 계산을 하지 않는 것이 더 합리적일 것이다 [Agre 와 Chapman, 1987; Brooks, 1956; Rosenschein 과 Kaelbling, 1986].
좀더 표현력있는 행동표현을 처리하기 위해 확장된 방법은 Green [1969], Pednault [1988], Dean et. al [1988], Penberthy 와 Weld [1992] 등에서 다루고 있다. 여기서 우리가 행동표현을 강화하는 방법에 관해 논의한 것은 Weld [1994] 의 연구에서 빌어 온 것이다. 이 장에서 소개된 아이디어들이 실제에 어떻게 적용될 수 있는가에 관하여는 Wilkins [1988] 의 저서에 흥미롭게 논의되어 있다. 우주 응용을 위한 계획수립과 일정관리 시스템에 관하여 알아보려면 Aarup et. al [1987] 의 연구를 참조하라.
부분순서 계획의 정렬
다음에는 refinements 를 Lisp 로 구현한 것이 나와 있다. 계획이 목적을 만족시키지 않는 경우에는, 충돌이 있거나 요구사항이 남아있는 경우임을 상기하자.
(defun refinements (plan operator)
(if (PLAN-conflicts plan)
(resolve-conflict (first (PLAN-conflicts plan)) plan)
(append (resolve-req-new-step (first (PLAN-requirements plan)) operators plan)
(resolve-req-existing-step (first (PLAN-requirements plan)) plan))))
충돌은 훼방꾼을 충돌과 연관된 연결고리의 생산자보다 앞에 오도록 하거나 그 연결고리의 소비자보다 뒤에 오도록 하는 제약요건을 가하여 해결된다.
(defun resolve-conflict (conflict plan)
(let ((link (CONFLICT-link conflict))
(step (CONFLICT-clobberer conflict)))
(append (constrain step (LINK-producer link) plan)
(constrain (LINK-consumer link) step plan))))
한 단계를 다른 단계보다 앞에 나오도록 하면 새로운 계획이 생성되는데 이는 이들 두 단계가 이 순서와 반대로 순서가 정해져 있지 않을 때에만 가능하다.
(defun constrain (step1 step2 plan)
(if (precedes step2 step1 (PLAN-constraints plan)) nil
(list (make-PLAN (PLAN-steps plan)
(adjoin (make-CONSTRAINT step1 step2)
(PLAN-constraints plan)
:test #'equal)
(rest (PLAN-conflicts plan))
(PLAN-links plan)
(PLAN-requirements plan)))))
Precedes 는 제약요건의 집합이 주어졌을 때 한 단계가 다른 단계보다 먼저 나오는지를 결정한다.
(defun precedes (step1 step2 constraints)
(or (equal step1 step2)
(some #' '(lambda (c) (and (equal step1 (begin c)) (precedes (end c) step2 constraints)))
constraints)))
새로운 단계를 추가함으로써 어떤 요구사항을 제거하기 위해 적용가능한 각 연산자에 해당하는 새로울 계획을 생성한다.
(defun resolve-req-new-step (req operators plan)
(mapcan #'(lambda (p) (applicable p req plan)) operators))
연산자가 적용가능한 것은 어떤 요구사항의 조건이 그 연산자에 의해 추가될 때만이다. 적용가능하다면 기존의 계획에 새로운 단계를 추가하여 새 계획을 생성하는데 이때 새로 추가되는 단계는 해결되는 요구사항의 단계보다 선행해야 한다는 제약이 있어야 하고, 이 요구사항은 삭제되어야 하며 새로 추가되는 단계를 생산자로 가지면서 그 요구사항을 해결하는 연결고리가 추가되어야 하고 이 연산자의 전제조건에 해당하는 새로운 요구사항의 집합이 추가되어야 하며 충돌의 집합도 적절히 갱신되어야 한다. 새로이 추가되는 단계의 삭제조건들이 기존의 연결고리들을 위협하거나, 기존의 단계들이 새로 추가되는 연결고리를 위협할 때 충돌이 발생할 수 있다.
(defun applicablep (operator req plan)
(if (not (member (REQUIREMENT-condition req)
(additions operator) :test #'equal)) nil
(let* ((step (make-STEP operator))
(constraint (make-CONSTRAINT step (REQUIREMENT-step req)))
(link (make-LINK step (REQUIREMENT-condition req)
(REQUIREMENT-step req))))
(list (make-PLAN (cons step (PLAN-steps plan))
(adjoin constraint (PLAN-constraints plan) :test #'equal)
(append (LINK-conflicts link plan)
(STEP-conflicts step plan)
(PLAN-conflicts plan))
(cons link (PLAN-links plan))
(append (generate-requirements operator step)
(rest (PLAN-requirements plan))))))))
연결고리가 추가될 때, 그것과 충돌이 일어날 수 있는 모든 단계를 찾는다. 이 함수는 LINK 유형의 객체에 대한 자료 추상화를 확장한다.
(defun LINK-conflicts (link plan)
(mapcan #'(lambda (step) (conflictp link step)) (PLAN-steps plan)))
한 단계가 추가될 때 그와 충돌이 일어날 수 있는 모든 연결고리를 찾는다. 이 함수는 STEP 유형의 객체에 대한 자료 추상화를 확장한다.
(defun STEP-conflicts (step plan)
(mapcan #'(lambda (link) (conflictp link step)) (PLAN-links plan)))
한 단계가 어떤 연결고리의 소비자가 아닌 경우, 그 단계의 연산자가 연결고리의 조건을 삭제할 때는 언제나 둘 사이에 충돌이 있다.
(defun conflictp (link step)
(if (and (not (equal step (LINK-consumer link)))
(member (LINK-condition link) (deletions (STEP-operator step)) :test #'equal))
(list (make-CONFLICT link step)) nil))
어떤 단계의 연산자에는 그 연산자의 각 전제조건에 대해 하나의 요구사항이 연관되어 있다.
(defun generate-requirements (operator step)
(mapcar #'(lambda (p) (make-REQUIREMENT step p)) (preconditions operator)))
계획 안에 이미 존재하는 단계를 사용하여 요구사항을 제거하기 위해서는 요구사항을 만족시키도록 연결고리를 걸 수 있는 기존의 단계 각각에 대하여 새로운 계획을 생성한다.
(defun resolve-req-existing-step (req plan)
(mapcan #'(lambda (s) (linkablep s req plan)) (PLAN-steps plan)))
한 요구사항을 만족시키기 위해 기존의 단계에 연결고리를 걸 수 있는 것은 그에 연관된 연산자가 그 요구사항의 조건을 추가조건으로 갖고 있고 기존의 단계가 요구사항의 단계보다 나중에 나와야 한다는 제약요건이 없을 때뿐이다. 이 기준이 충족되면 기존의 계획으로부터 새 계획을 생성하는데 이때 기존의 단계가 해결되는 요구사항의 단계보다 앞서 나와야 하며, 이 요구사항은 삭제되고, 기존의 단계를 생산자로 갖는 연결고리가 요구사항을 해결하기 위해 추가되어야 하며 충돌 집합도 갱신되어야 한다.
(defun linkablep (step req plan)
(if (or (not (member (REQUIREMENT-condition req)
(additions (STEP-operator step)) :test #'equal))
(precedes (REQUIREMENT-step req) step
(PLAN-constraints plan))) nil
(let ((link (make-LINK step
(REQUIREMENT-condition req)
(REQUIREMENT-step req)))
(constraint (list step (REQUIREMENT-step req))))
(list (make-PLAN (PLAN-steps plan)
(adjoin constraint (PLAN-constraints plan) :test #'equal)
(append (LINK-conflicts link plan) (PLAN-conflicts plan))
(cons link (PLAN-links plan))
(rest (PLAN-requirements plan)))))))
위의 구현에 약간의 수정을 가하면 체계적인 계획시스템을 얻을 수 있다. 이에 필요한 수정에서는 충돌의 기준을 약간 확장하여 한 연결고리의 조건이 어떤 단계의 연산자에 의해 추가되거나 또는 삭제될 때 그 단계와 연결고리 사이에 충돌이 있다고 한다. 실제로는 이와 같은 수정 내용을 보통 구현하지 않는데, 그럼에도 이 분야의 종사자들에 의해 이에 따르는 해로운 결과가 보고 된 바 없다.
또한 여기에 구현된 것은 무결하고 완전하다. 이 외에도 시스템의 종료를 보장하는 여러 수정방법들이 있으나 이들은 모두 상당한 계산적 부대비용을 요구하는데 이는 단계들의 어떤 순서열에 따르면 같은 상태에 여러 번 도달하게 되는 사이클 (cycle) 이 있는지를 검사해야 하기 때문이다.