
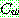 : 해집단 내에서 가장 나쁜 해의 비용
: 해집단 내에서 가장 나쁜 해의 비용
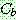 : 해집단 내에서 가장 좋은 해의 비용
: 해집단 내에서 가장 좋은 해의 비용
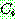 : 해 i 의 비용
: 해 i 의 비용
유전 알고리즘의 연산자들
유전알고리즘 : 문병로, 두양사, 2003, Page 39~68
PMX (Partially Matched Crossover)
산술적 교차 (Arithmatical Crossover)
교차에 쓰이는 두 개의 부모해를 고르기 위한 연산자이다. 다양한 선택 연산자들이 있으나 공통된 원칙은 우수한 해가 선택될 확률이 높아야 한다는 것이다. 우수한 해들과 열등한 해들 사이의 적합도 차이를 조절함으로써 선택 확률을 조절할 수 있는데, 이 차이의 정도를 선택압 (selection pressure) 이라 한다. 선택압이 높을수록 수렴은 빠르나 설익은 수렴 (premature convergence) 의 가능성이 높아진다. 반면 선택압이 너무 낮으면 해집단의 평균 품질이 좋아지지 않을 가능성이 많다. 선택압은 프로그래머가 조절할 수 있는 파라미터이다. 아래에 몇 가지 대표적인 선택 연산자들과 선택을 위한 염색체의 적합도 계산 방법을 소개한다.
가장 대표적인 선택 방법이다. 각 해의 품질을 평가한 다음 가장 좋은 해의 적합도가 가장 나쁜 해의 적합도보다 k 배가 되도록 조절한다. 임의의 비용 최소화 문제를 예로 들어 설명해 보자. 해집단 내의 해 i 의 적합도는 다음과 같이 계산된다.

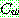 : 해집단 내에서 가장 나쁜 해의 비용
: 해집단 내에서 가장 나쁜 해의 비용
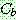 : 해집단 내에서 가장 좋은 해의 비용
: 해집단 내에서 가장 좋은 해의 비용
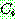 : 해 i 의 비용
: 해 i 의 비용
여기서 k 값을 높이면 선택압이 높아진다. 일반적으로 가장 흔히 쓰는 k 값은 3~4 이다. 이 적합도 값을 기준으로 룰렛휠 선택을 하게 된다.
위와 같이 계산한 각 염색체의 적합도를 모두 합한 값 만큼의 크기를 가진 룰렛휠을 가정한다. 각 염색체는 이 룰렛휠 상에 자신의 적합도 만큼의 공간을 배정받는다. 그림 3.1 은 8 개의 염색체가 적합도에 비례해서 룰렛휠 상의 공간을 배정받은 모양의 예를 보인다. 여기에 활을 쏘면 각 염색체의 선택 확률은 배정된 공간의 크기에 비례하게 된다. 룰렛휠 선택은 다음과 같이 간단히 구현할 수 있다.

그림 3.1 룰렛휠 공간 배정의 예
point = random (0, SumOfFitnesses) ;
sum = 0 ;
for i = 0 to n-1 {
sum
= sum + 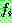 ;
;
if (point < sum) return i ;
}
여기서 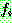 는 염색체의 i 의 적합도이고, SumOfFitnesses 는 모든 염색체들의 적합도 값을
더한 수치이다. random (0, SumOfFitnesses) 은 [0, SumOfFitnesses) 구간에서의
임의의 값을 의미한다.
는 염색체의 i 의 적합도이고, SumOfFitnesses 는 모든 염색체들의 적합도 값을
더한 수치이다. random (0, SumOfFitnesses) 은 [0, SumOfFitnesses) 구간에서의
임의의 값을 의미한다.
초보자들이 유전 알고리즘을 처음 구현하면서 흔히 범하는 실수는 위와 같이 k 를 사용해서 적합도를 조정하지 않고 주어진 문제에서의 해의 품질을 그대로 적합도로 사용하는 것이다. 이렇게 하면 대부분의 경우 해집단에서 가장 좋은 해와 가장 나쁜 해의 품질이 너무 차이가 나서, 적합도에 비례해서 선택 기회를 갖게 되면 나쁜 해들은 거의 선택될 기회를 잃게 된다. 결과적으로 엄청나게 큰 선택압을 주어 해의 다양성을 급속히 떨어뜨리는 결과를 부르게 된다.
가장 간단한 토너먼트 선택은 두 개의 염색체를
임의로 선택하여 [0, 1) 범위의 난수를 발생시킨 다음 이것이 t 보다 적으면 두 염색체
중 품질이 좋은 것을 선택하고 그렇지 않으면 품질이 나쁜 것을 선택하는 것이다.
여기서 t 는 파라미터화 할 수 있는 것으로 t 값이 높을수록 선택압이 높아진다.
t 가 0.5 근처이거나 이보다 작은 것은 비합리적이다. 두 개의 염색체를 선택하는
대신  개의 염색체를 선택한 다음 이들을 (위와 같은 난수 발생에 의해) 토너먼트 형식으로
비교하여 마지막으로 남은 것을 선택하는 방법도 있다. 여기서도
개의 염색체를 선택한 다음 이들을 (위와 같은 난수 발생에 의해) 토너먼트 형식으로
비교하여 마지막으로 남은 것을 선택하는 방법도 있다. 여기서도 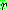 값이 클수록, 즉 토너먼트에 참가하는 염색체가 많을수록 선택압이 높아진다.
토너먼트 선택은 대체로 수행에 필요한 시간이 매우 짧다는 매력이 있다.
값이 클수록, 즉 토너먼트에 참가하는 염색체가 많을수록 선택압이 높아진다.
토너먼트 선택은 대체로 수행에 필요한 시간이 매우 짧다는 매력이 있다.
품질 비례 선택에서 k 값을 조정함으로써 좋은 품질의 해와 나쁜 품질의 해가 지나치게 적합도의 차이를 갖게 되는 것은 막을 수 있다. 그러나 해들의 적합도의 분포는 조절할 수 없다. 순위 기반 선택은 해집단 내의 해들을 품질 순으로 '순위' 를 매긴 다음 가장 좋은 해부터 일차 함수적으로 적합도를 배정하는 방법이다. 그림 3.2 는 순위 기반 선택의 적합도 배정 함수를 그림으로 보여 준다. n 개의 염색체 중 i 번째 순위를 가진 염색체의 적합도는 다음과 같은 식으로 계산할 수 있다.
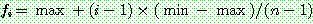
이 식에서 max 와 min 값의 차이를 바꿈으로써 선택압을 조절할 수 있다. 해들의 적합도는 max 와 min 사이에서 균일한 간격으로 분포하게 된다.

그림 3.2 순위 기반 선택의 적합도 배정 함수
공유는 해집단의 다양성을 보다 오래 유지하고자 하는 목적에서 고안되었다. 공유는 먼저 품질 비례 선택이나 순위 기반 선택에서 쓰는 적합도 값을 구한다. 여기에 해당 염색체가 해집단 내의 나머지 염색체들과 유사한 (특징을 '공유' 하는) 정도가 높을수록 나누어 적합도를 조정한다. 공유를 감안한 적합도는 아래와 같이 계산된다.
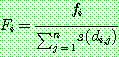
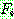 : 공유를 고려한 염색체 i 의 적합도
: 공유를 고려한 염색체 i 의 적합도
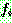 : 일반 적합도
: 일반 적합도
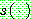 : 공유 함수
: 공유 함수
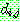 : 염색체 i 와 염색체 j 의 차이
: 염색체 i 와 염색체 j 의 차이
위의 공유 함수  는 두 염색체의 차이가 적을수록 큰 값을 가져야 한다. 전형적인 공유 함수의
모양은 그림 3.3 과 같이 일차 함수로 나타낼 수 있다. 그림에서
는 두 염색체의 차이가 적을수록 큰 값을 가져야 한다. 전형적인 공유 함수의
모양은 그림 3.3 과 같이 일차 함수로 나타낼 수 있다. 그림에서 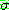 는 해집단에서 가장 차이가 많이 나는 두 해의 차이로 잡는 것이 합리적이다.
공유 함수는 그림과 같은 일차 함수를 쓰지 않고 다양한 변형이 가능하다. 예를 들어
는 해집단에서 가장 차이가 많이 나는 두 해의 차이로 잡는 것이 합리적이다.
공유 함수는 그림과 같은 일차 함수를 쓰지 않고 다양한 변형이 가능하다. 예를 들어
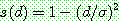 과 같이 잡으면 [Goldberg & Richardson, 1987] 염색체간의 유사성에 불이익을
더욱 많이 주게 된다.
과 같이 잡으면 [Goldberg & Richardson, 1987] 염색체간의 유사성에 불이익을
더욱 많이 주게 된다.
공유는 해집단 내의 해들을 문제 공간상에서 지리적으로 분산되게 도와 주는 효과가 있다. 이는 몇 개의 부분 해집단을 각각 독립적으로 운영하며 가끔 교류시키는 섬식 방법 (island method) 과 유사한 동기를 갖고 있다.

그림 3.3 간단한 공유 함수
공유는 두 해의 차이를 계산하는 기준을 잡는 방법에
따라 유전자형 공유와 표현형 공유로 나눌 수 있다. 유전자형 공유는 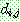 를 위해 염색체의 모양 그 자체가 다른 정도를 사용하는 것이고 (예를 들면 해밍
거리 (Hamming distance)), 표현형 공유는 표현형의 차이를 계산 기준으로 삼는 것이다.
예를 들어, 각 해가 100 개의 십진수를 파라미터로 갖는 문제의 경우, 이진 표현에서
염색체는 400 비트의 이진 스트링으로 표현할 수 있다. 유전자형 공유의 경우 두
염색체간의 해밍 거리, 즉 400 비트 중 서로 다른 비트의 총 수를 사용하며, 표현형
공유의 경우 400 비트로부터 100 개의 십진수를 추출하여 두 염색체에서 각 십진수간의
크기의 차이를 사용할 수 있다. Goldberg 와 Richardson (1987) 에 의해 제안된 이후
공유를 이용한 많은 연구 결과들이 발표되어 있다 [Darwen & Yao, 1997 ; Sareni
& Krahenbuhl, 1998].
를 위해 염색체의 모양 그 자체가 다른 정도를 사용하는 것이고 (예를 들면 해밍
거리 (Hamming distance)), 표현형 공유는 표현형의 차이를 계산 기준으로 삼는 것이다.
예를 들어, 각 해가 100 개의 십진수를 파라미터로 갖는 문제의 경우, 이진 표현에서
염색체는 400 비트의 이진 스트링으로 표현할 수 있다. 유전자형 공유의 경우 두
염색체간의 해밍 거리, 즉 400 비트 중 서로 다른 비트의 총 수를 사용하며, 표현형
공유의 경우 400 비트로부터 100 개의 십진수를 추출하여 두 염색체에서 각 십진수간의
크기의 차이를 사용할 수 있다. Goldberg 와 Richardson (1987) 에 의해 제안된 이후
공유를 이용한 많은 연구 결과들이 발표되어 있다 [Darwen & Yao, 1997 ; Sareni
& Krahenbuhl, 1998].
교차 연산은 유전 알고리즘의 대표 연산자이다. 연산자들 중 가장 다양한 대안이 존재한다. 본 장에서는 대표적인 몇 가지 교차 연산자들을 소개한다. 여기서 소개되는 교차 연산들을 여러분이 응용하고자 하는 문제에 선택하여 사용하거나, 이들로부터 새로운 교차 연산자를 만드는 실마리를 얻을 수 있을 것이다.
일점 교차는 1.7 절에서 소개한 바 있는 대표적인 교차 연산이다. 초기의 유전자 알고리즘들은 대부분 일점 교차를 사용하였고, 요즘도 가장 많이 사용되는 교차연산이다. 길이가 n 인 일차원 문자열로 된 염색체 상에서 일점 교차로 자르는 방법의 총 수는 n-1 가지이다.

1.7 절에서 다점 교차의 한 예인 3 점 교차를 소개한
바 있다. 다점 교차는 일반적으로 일점 교차보다 자르는 방법의 수가 훨씬 많다.
염색체의 길이가 n 일 때 k 점 교차로 자르는 방법의 총 수는 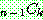 가지이다. 만일 맨오른쪽 유전자의 오른쪽에도 자름선이 올 수 있도록 하면 위의
방법의 총 수는
가지이다. 만일 맨오른쪽 유전자의 오른쪽에도 자름선이 올 수 있도록 하면 위의
방법의 총 수는 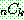 가 된다. 전통적인 유전 알고리즘은 위의
가 된다. 전통적인 유전 알고리즘은 위의 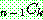 방식을 쓰고 있으나 사실은
방식을 쓰고 있으나 사실은 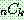 방식이 더 합리적이다. 4.2 절에 이 이유를 알 수 있는 내용이 있다. 다점 교차는
일점 교차보다 교란 (perturbation) 의 정도가 크다. 따라서 보다 넓은 탐색 공간을
탐색할 수 있다. 반면에 교란이 강하면 수렴성이 떨어져 주어진 시간 예산내에 제대로
수렴하지 않을 가능성이 있다.
방식이 더 합리적이다. 4.2 절에 이 이유를 알 수 있는 내용이 있다. 다점 교차는
일점 교차보다 교란 (perturbation) 의 정도가 크다. 따라서 보다 넓은 탐색 공간을
탐색할 수 있다. 반면에 교란이 강하면 수렴성이 떨어져 주어진 시간 예산내에 제대로
수렴하지 않을 가능성이 있다.
교란이 강하다는 것은 스키마가 파손될 확률이 높다는 것이다. 대신 새로운 스키마의 생성은 더 다양하게 할 수 있다. 따라서 항상 최적인 교란의 정도란 있을 수 없다. 일반적으로 다점 교차는 순수 유전 알고리즘보다 혼합형 유전 알고리즘에 더 어울린다. 왜냐하면 혼합형 유전 알고리즘에는 다소의 지역 최적화 기능이 있으므로 순수 유전 알고리즘보다 교란에 대한 회복력이 강하다. 혼합형 유전 알고리즘의 경우, 교란의 정도가 너무 미약하면 후반부에 부모해와 같은 자식해가 만들어질 확률이 높아져 탐색 시간의 낭비가 커진다. 혼합형 유전 알고리즘은 5 장에서 소개되는데 여기서는 지역 최적화 알고리즘과 유전 알고리즘을 결합한 것 정도로 알아두자.
교차 연산에서 스키마의 파손 확률은 자름선의 개수에 영향을 많이 받는다. 일점 교차는 스키마의 길이가 결정적인 영향을 미치고, 다점 교차는 이의 영향을 덜 받는다. 4 장에서 스키마의 생존 확률에 대해 깊이 있게 다룬다. 자름선의 개수가 짝수이면 염색체의 첫번째 유전자와 마지막 유전자가 인접한 것 같은 효과가 있어 사실상 염색체가 고리 모양을 하고 있는 셈이다.
일점 교차와 다점 교차가 자름선을 이용하여 이루어지는
데 반해 균등 교차는 자름선을 이용하지 않는다. 균등 교차는 먼저 임계 확률 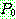 를 설정한다. 가장 일반적인 임계 확률은 0.5 이다. 두 부모해를
를 설정한다. 가장 일반적인 임계 확률은 0.5 이다. 두 부모해를 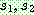 라 하자. 각각의 유전자 위치에 대하여 난수를 발생한 다음 이 값이
라 하자. 각각의 유전자 위치에 대하여 난수를 발생한 다음 이 값이 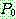 이상이면
이상이면 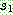 의 같은 위치로부터 유전자를 복사해오고, 그렇지 않으면
의 같은 위치로부터 유전자를 복사해오고, 그렇지 않으면 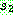 의 같은 위치로부터 복사를 한다. 아래는
의 같은 위치로부터 복사를 한다. 아래는 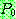 = 0.6 인 균등 교차의 한 예를 보인다.
= 0.6 인 균등 교차의 한 예를 보인다.
|
난수 :
자식해 : |
|
|
균등 교차는 자름선을 이용하지 않으므로 일점 교차나 다점 교차에 비해 스키마의 결합 형태가 다양하다. 스키마내의 특정 기호의 위치가 영향을 미치지 않는다. 대신 일반적으로 교란의 정도가 크므로 수렴 시간이 오래 걸린다. Syswerda (1989) 에 의해 제안된 이후 많은 주목을 받았고 폭넓게 이용되고 있는 교차 연산이다.
싸이클 교차 [Oliver 등, 1987] 는 TSP 의 예에서와
같이 염색체가 순열로 표현되는 경우에 적용 가능한 교차 연산이다. 아래와 같은
두 부모해 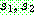 로부터 싸이클 교차를 한다고 하자.
로부터 싸이클 교차를 한다고 하자.
|
|
8 |
7 |
1 |
0 |
6 |
3 |
4 |
9 |
5 |
2 |
|
|
0 |
2 |
4 |
3 |
1 |
5 |
6 |
7 |
8 |
9 |
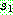 의 첫 번째 유전자 (8) 로부터 복사를 시작한다. 방금 복사한 위치에 대응되는
의 첫 번째 유전자 (8) 로부터 복사를 시작한다. 방금 복사한 위치에 대응되는
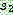 유전자는 0 이므로
유전자는 0 이므로 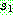 상에서 0 이 있는 위치를 찾아 자식해의 같은 위치에 0 을 복사한다. 같은 원리로
상에서 0 이 있는 위치를 찾아 자식해의 같은 위치에 0 을 복사한다. 같은 원리로
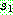 상에서 3 이 있는 위치를 찾아 자식해의 같은 위치에 복사한다. 마찬가지로 5
가 복사된다. 이제 5 와 같은 위치에는 8 이 있는데 8 은 이미 복사가 되었으므로
더 이상 진행 할 수가 없다. 이 과정을 아래 그림처럼 화살표를 따라 표시해 보면
하나의 싸이클이 만들어진다는 데에서 싸이클 교차란 이름이 붙게 되었다.
상에서 3 이 있는 위치를 찾아 자식해의 같은 위치에 복사한다. 마찬가지로 5
가 복사된다. 이제 5 와 같은 위치에는 8 이 있는데 8 은 이미 복사가 되었으므로
더 이상 진행 할 수가 없다. 이 과정을 아래 그림처럼 화살표를 따라 표시해 보면
하나의 싸이클이 만들어진다는 데에서 싸이클 교차란 이름이 붙게 되었다.

다음은 자식해의 유전자 값이 아직 결정되지 않은
위치들 중 가장 왼쪽의 위치로부터 시작하는데 이번에는 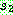 로부터 시작한다. 2, 7, 9 순으로 복사하면서 아래 그림처럼 다시 싸이클이 만들어진다.
이렇게
로부터 시작한다. 2, 7, 9 순으로 복사하면서 아래 그림처럼 다시 싸이클이 만들어진다.
이렇게 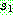 과
과 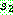 를 번갈아 시작해 가면서 더 이상 결정되지 않은 유전자가 없을 때까지 계속하면
최종적인 자식해는 8210634789 가 된다.
를 번갈아 시작해 가면서 더 이상 결정되지 않은 유전자가 없을 때까지 계속하면
최종적인 자식해는 8210634789 가 된다.

순서 교차 [Davis, 1985] 역시 염색체가 순열로
표시되는 경우를 위하여 고안된 교차 연산자이다. 마찬가지로 두 부모해 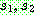 를 사용하여 설명한다. 먼저 임의로 두 개의 자름선을 정한 다음 두 자름선 사이에
있는 부분을
를 사용하여 설명한다. 먼저 임의로 두 개의 자름선을 정한 다음 두 자름선 사이에
있는 부분을 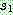 으로부터 복사한다 (063). 나머지 위치는
으로부터 복사한다 (063). 나머지 위치는 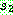 로부터 복사하되, 두 번째 자름선 바로 다음 위치부터 시작하여 사용되지 않은
기호들 중
로부터 복사하되, 두 번째 자름선 바로 다음 위치부터 시작하여 사용되지 않은
기호들 중 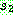 에서 나타난 순서대로 (2415789) 복사한다.
에서 나타난 순서대로 (2415789) 복사한다.

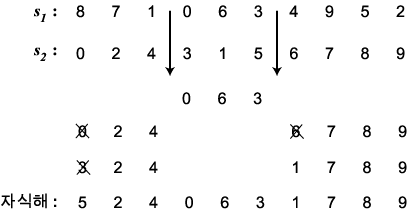
PMX [Goldberg & Lingle, 185] 역시 염색체가
순열로 표시되는 경우를 위하여 고안된 교차 연산자이다. 두 부모해 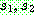 에 임의로 두 개의 자름선을 정한 다음 두 자름선 사이에 있는 부분을
에 임의로 두 개의 자름선을 정한 다음 두 자름선 사이에 있는 부분을 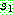 으로부터 복사한다 (063). 나머지 위치는
으로부터 복사한다 (063). 나머지 위치는  로부터 복사하되 만일 해당 값이 이미 사용되었으면 같은 값을 가진
로부터 복사하되 만일 해당 값이 이미 사용되었으면 같은 값을 가진  의 위치를 찾아 같은 위치의
의 위치를 찾아 같은 위치의  로부터 복사한다 (아래 그림의 자식해의 0 과 6). 이 값은 아직 사용되지 않았을
수도 있고 (예, 1), 이미 사용되었을 수도 있다 (예, 중간 과정의 × 표시된
3). 마지막으로 이미 사용되어 중복이 일어난 유전자는 고쳐준다.
로부터 복사한다 (아래 그림의 자식해의 0 과 6). 이 값은 아직 사용되지 않았을
수도 있고 (예, 1), 이미 사용되었을 수도 있다 (예, 중간 과정의 × 표시된
3). 마지막으로 이미 사용되어 중복이 일어난 유전자는 고쳐준다.
산술적 교차 [Michelewicz, 1992, pp.104-5] 는 실수 염색체를 사용하는 경우에 사용할 수 있는 교차 연산이다. 염색체의 각 위치에 대해 두 부모 염색체의 두 유전자의 값의 평균을 내어 자식해의 해당 위치의 값으로 배정한다. 아래는 간단한 산술적 교차의 한 예를 보인다.
|
|
1.98 |
3.31 |
20.43 |
12.01 |
-2.34 |
8.34 |
98.86 |
|
|
11.28 |
2.21 |
12.39 |
1.44 |
2.45 |
3.55 |
87.44 |
|
|
|
|
|
|
|
|
|
|
자식해 : |
6.63 |
2.76 |
16.41 |
6.73 |
0.06 |
5.95 |
93.15 |
산술적 교차는 수의 '크기' 라는 개념을 교차 행위에 사용하는 점에 큰 매력이 있다. 그렇지만 수들의 산술 평균을 지향하므로 매우 빠른 수렴을 보인다. 변이 등을 적절히 조절하여 설익은 수렴이 되지 않도록 주의해야 한다.
지금까지 소개한 교차 연산들은 부모해의 유전자만을 바탕으로 자식해의 유전자를 결정하는 것이었다. 교차 연산 중에는 부모해의 유전자 정보에 더하여 문제에 대한 지식을 이용하는 교차들이 있는데 이들은 다소간 지역 최적화의 특성을 띤다. 다음에 소개할 간선 재결합도 약한 휴리스틱 교차라 할 수 있다. TSP 를 위한 교차로서 강한 지역 최적화 경향을 지닌 간선 조합 교차 (edge assembly crossover)[Nagata & Kobayashi, 1997] 도 휴리스틱 교차의 한 예이다.
간선 재결합 [Starkweather 등, 1991] 은 TSP 를 위해 개발되었다. TSP 의 두 부모해를 분석, 각 도시에 연결된 인접 도시 목록을 만든다. 한 도시는 최대 4 개까지의 인접 도시를 가질 수 있고 (중복이 없을 경우), 최소 2 개는 가진다. 먼저 시작 도시를 정한다. 시작 도시는 부모해 중 하나의 시작 도시가 될 수도 있고, 인접 도시수가 가장 적은 도시가 될 수도 있다. 현재 도시의 인접 도시 리스트에 있는 도시 중 가장 인접 도시수가 적은 도시를 고른다. 후보 도시가 둘 이상이면 그 중 하나를 임의로 선택한다. 이렇게 부모해의 특징을 분석하여 휴리스틱하게 구성하는 방식은 다른 문제에도 응용할 수 있을 것이다.
|
|
||
|
Edge table: |
city |
links |
|
|
0 1 2 3 4 5 6 7 8 9 |
9, 1, 5 0, 2, 6, 4 1, 3, 4, 5 2, 4, 7, 8 3, 5, 1, 2 4, 6, 2, 0 5, 8, 1 8, 9, 3 6, 7, 3 7, 0 |
|
자식해 : 0 9 7 8 6 1 2 4 3 5 |
||
지금까지 소개한 교차 연산자들은 일차원의 염색체를
대상으로 했다. 이차원 이상의 표현 방법을 쓴 염색체들에 대한 연산자들도 있다.
Cohoon 과 Paris (1987) 는 VLSI 회로 배치 문제를 위해 이차원의 염색체를 사용하였고
이를 위한 교차 연산을 제안하였다. 이들은 한 부모해에서 정사각형을 잘라낸 다음
다른 부모해의 해당 부분으로 보충해 넣는 방식으로 교차를 하였다. 그림 3.4 는
이의 예를 보인다. 그림의 한 부모해  에서 3 × 3 의 사각형을 선택하여 이를
에서 3 × 3 의 사각형을 선택하여 이를  의 같은 자리에 놓는다. 그러면
의 같은 자리에 놓는다. 그러면  에서 심볼 B, D, E, G 는 중복이 되므로 이들을 제거하고
에서 심볼 B, D, E, G 는 중복이 되므로 이들을 제거하고  의 사각형에 들어 있던 V, X, Y, Z 를 대치해 넣는다.
의 사각형에 들어 있던 V, X, Y, Z 를 대치해 넣는다.
Anderson 등 (1991) 은 염색체를  블록으로 분할한 다음 각 블록에 대해 난수를 발생시켜 0 또는 1 의 값을 얻은
다음 0 이면
블록으로 분할한 다음 각 블록에 대해 난수를 발생시켜 0 또는 1 의 값을 얻은
다음 0 이면 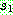 으로부터 1 이면
으로부터 1 이면 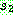 로부터 복사하는 블록 균등 교차 (block uniform crossover) 를 제안하였다.
그림 3.5 는 이의 예를 보인다.
로부터 복사하는 블록 균등 교차 (block uniform crossover) 를 제안하였다.
그림 3.5 는 이의 예를 보인다.
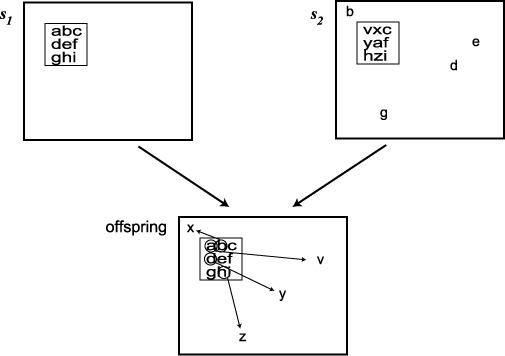
그림 3.4 Cohoon 과 Paris 의 교차 연산자의 예
Bui 와 Moon (1995) 은 이를 일반적인 N 차원으로 확장하였다. 또한 다차원의 교차 연산에서 직선만을 사용하여 염색체를 분할하는 방법은 일차원 상의 교차 연산들에 비해 다소 다양성이 떨어져 새 스키마의 생성 능력은 오히려 떨어지므로 직선의 제약을 없앤 다차원 지오그래픽 (geographic) 교차 연산자가 제안되었다 [Kahng & Moon, 1995]. 그림 3.6 은 이의 예를 보인다.

그림 3.5 블록 균등 교차의 두 예

그림 3.6 직선의 제약을 없앤 이차원 지오그래픽 교차의 두 예
이차원 염색체를 사용하더라도 행렬과 같은 모양으로 각 유전자를 위치시키는 방법은 일차원 표현보다는 유전자들간의 지리적 인접성을 잘 반영하지만 문제 자체에 깃든 유전자들간의 지리적 정보를 얼마간 잃어버리는 것은 피할 수 없다. 앞에서 소개한 다차원 교차들은 모두 행렬 형태의 정형적인 염색체를 사용하였다. 이에 착안하여 Jung 과 Moon (2000, 2002) 은 TSP 를 위한 이차원 교차인 내추럴 교차를 제안하였다. 내추럴 교차는 이차원 지도상의 도시들의 분포와 투어의 모양 그 자체를 염색체로 삼는다. 이렇게 하면 염색체 표현 과정에서 도시들의 인접성 정보는 전혀 손실이 없다. 교차는 이 그림 위에서 자연스런 손의 궤적을 따라 긋는 선들에 의해 이루어진다. 내추럴 교차는 다음과 같은 과정으로 이루어진다.
1. 이차원상에서 도시들의 위치가 표시된 그래픽 이미지 상에서 자연스런 손의 궤적을 따라 k 개의 자름선을 긋는다.
2. 이로 인해 모든 도시들은 두 개의 그룹으로 나뉜다. 이를 각각 클래스 1, 클래스 2 라 하자.
3. 부모해 1 에 속한 간선들 중 두 끝점이 모두 클래스 1 에 속한 간선들을 자식해에 포함시킨다. 마찬가지로 부모해 2 에 속한 간선들 중 두 끝점이 모두 클래스 2 에 속한 간선들을 자식해에 포함시킨다.
4. 위 스텝 3 의 결과로 나온 부분적 투어들에 간선들을 보충하여 유효한 투어를 만든다.
위 스텝 2 의 '그룹' 은 동형 클래스 (equivalence class) 를 직관적으로 표현한 말인데, 이에 대한 이론적인 증명은 [Jung & Moon, 2000, 2002] 에 제시되어 있다. 앞에서 설명한 다른 교차 연산자들에 비해 구현하기가 다소 까다로운 교차 연산자이다. 위 스텝 1 에서 자연스런 손의 궤적을 따라 긋는 선을 구현하여 실험한 결과는 아직 없다. 대신 [Jung & Moon, 2000, 2002] 에서는 직선, 원, 삼각형, 사각형 등의 도형을 사용하였다. 내추럴 교차는 지오그래픽 교차에서 더욱 발전한 형태로, 다차원 표현의 이점은 극대화하되 이의 약점이 될 수 있는 새 스키마의 생성 능력을 효율적으로 보완한 연산자이다. 그림 3.7 은 내추럴 교차 연산자의 예를 보인다.

그림 3.7 내추럴 교차의 예
어떤 경우에는 한 개의 해를 표현하기 위한 염색체가 여러 개인 경우가 있다. 즉, 하나의 표현형에 대해 여러 개의 유전자형이 대응되는 경우가 있다. 이런 경우, 교차 연산은 심각한 혼란을 겪는다. 1.5 절에서 소개한 그래프 이등분 문제를 예로 들어보자. 염색체 0000111101 과 1111000100 을 부모로 삼아 다음과 같이 일점 교차를 해보자.

사실 염색체 0000111101 과 1111000100 은 모양은 많이 다르지만 실제로는 유사한 점을 많이 갖고 있다. 1~4 번, 5, 6, 7, 10 번 노드들이 각각 이등분의 양쪽에 그룹지어져 있는 것은 매우 유사한 특성이다. 그러나 위의 교차의 결과로 만들어진 염색체는 두 부모해가 갖고 있던 특성을 제대로 물려받지 못한 밋밋한 해가 되어 버렸다. (이 해는 정확한 그래프 이등분을 못 만들므로 수선 (repair) 을 해서 이등분으로 고쳐주는 것이 좋지만 여기서는 논점을 벗어난 주제이므로 다루지 않는다.) 위의 교차는 두 해의 특성을 부분 결합하는 교차의 본래 목적과는 달리 아주 심한 변이 효과를 낸다. 이러한 일이 발생하는 이유는 한 해에 대해 두 개의 염색체가 존재하기 때문이다. 여기서 1111000100 을 똑같은 해를 나타내는 0000111011 로 바꾸어보자. 그러면 아래와 같이 염색체 0000111101 과 0000111011 사이에 교차가 일어난다. 이 결과는 앞의 교차 결과보다 훨씬 부모해의 특징들을 잘 반영하고 있다.

그래프 분할의 정도가 커지면 위 문제는 더욱 심각해진다. 그래프 32 등분 문제의 경우에는 동일한 한 해에 32! 개의 서로 다른 염색체가 존재한다.
위와 같이 동일한 해에 대해 복수 개의 염색체가 존재할 때, 두 부모 염색체 중 하나의 염색체를 바꾸어서 부모해의 특성을 보다 잘 반영하도록 하는 것을 정규화라 한다. 정규화의 필요성은 다양한 문제들에 대해서 발생하는데 그래프 분할 [von Laszewski, 1991; Bui & Moon, 1993, 1996; Kang & Moon, 2000], 정렬 네트웍의 최적화 [Choi & Moon, 2002], 뉴럴 네트웍 최적화, 지수귀문도 최적화 등이 정규화의 필요성이 확인된 주제들이다. 한 해를 서로 다른 염색체로 표현할 수 있을 때 일단 정규화에 대해 생각해볼 필요가 있다.
변이 연산은 부모해에 없는 속성을 도입하여 탐색 공간을 넓히려는 목적을 가진 연산이다. 전형적인 형태의 변이 연산자는 1.8 절에 소개된 바와 같이, 각각의 유전자에 대하여 [0, 1) 범위의 난수를 생성하여 미리 정한 임의의 임계값 미만의 수가 나오면 해당 유전자를 임의로 변형시키고 그 이상의 수가 나오면 그냥 둔다. 전형적인 임계값으로는 0.0015 등을 들 수 있는데 이것은 문제와 유전 알고리즘의 타입에 따라 상당한 폭으로 변할 수 있다. 변이 연산이 임의로 일어나므로 절대적인 비율로 변이는 해의 품질을 저하시킨다. 변이의 결과로 잘못 만들어진 유전자는 시간이 흐르면서 사라지고 가끔 발생하는 성공적 변이는 집단의 품질을 향상시키는 데 기여를 하게 된다.
유전 알고리즘의 초기에는 해들의 품질이 좋지
않은 것이 보통이고 시간이 지남에 따라 점점 품질이 좋아져 간다. 따라서 초반에는
변이의 정도가 다소 강해도 품질 향상이 일어날 가능성이 있지만, 해가 상당한 수준에
이른 후반에는 변이가 강하면 거의 품질 향상이 일어나기 힘들다. 이에 착안하여
유전 알고리즘이 진행됨에 따라 점점 변이의 강도를 줄여가는 비균등 변이 (non-uniform
mutation) 연산자가 제안되었다 [Michalewicz, 1992, pp.103-4]. 임의의 실수 유전자
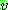 에 대한 비균등 변이는 이진 난수
에 대한 비균등 변이는 이진 난수 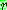 을 발생시킨 다음 아래와 같이 이루어진다.
을 발생시킨 다음 아래와 같이 이루어진다.
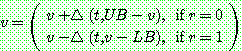
여기서 UB 와 LB 는 유전자 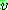 가 가질 수 있는 상한값과 하한값이다.
가 가질 수 있는 상한값과 하한값이다. 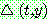 는 0 과
는 0 과 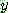 사이의 값을 갖는데 t 가 증가함에 따라 점점 0 으로 근접하는 특성을 갖는다.
사이의 값을 갖는데 t 가 증가함에 따라 점점 0 으로 근접하는 특성을 갖는다.
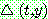 를 위해 아래와 같은 식을 사용할 수 있다.
를 위해 아래와 같은 식을 사용할 수 있다.
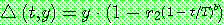
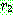 : [0, 1] 범위의 난수
: [0, 1] 범위의 난수
T : 최대 세대수 (끝나는 시간)
b : 시간에 따른 의존도를 조절하기 위한 파라미터
시뮬레이티드 어닐링 (simulated annealing) 에서도 시간이 지남에 따라 교란의 정도를 감소시켜 가는데 비균등 변이도 비슷한 동기를 가진 변이 연산이다.
교차와 변이 연산의 결과로 생긴 해는 적격해 (feasible solution) 가 아닌 경우가 많다. 앞에서 예를 든 그래프 이등분 문제의 경우 임의의 염색체에는 1 을 값으로 가진 유전자 수와 0 을 값으로 가진 유전자 수가 같아야 한다. (설명의 편의상 유전자의 총수가 짝수라 가정한다. [총 유전자의 수가 홀수이면 하나 차이가 나야 한다.]) 임의의 두 부모해로부터 교차와 변이를 수행하면 대부분 1 의 수와 0 의 수가 일치하지 않는다. 이를 해결하기 위한 간단한 방법을 한 가지 소개한다. 먼저 1 의 개수와 0 의 개수의 차이를 계산한다. 이 차이를 d 라 하자. 그래프 이등분 문제의 경우 이 d 는 항상 짝수이다. 염색체 상에서 임의의 위치를 지정한다. 여기서 시작하여 오른쪽으로 움직이면서 맨처음 나타나는 d/2 개의 1 을 모두 0 으로 (또는 0 을 모두 1 로) 바꾼다. 이 결과로 생긴 염색체는 1 의 개수와 0 의 개수가 일치하는 해가 된다.
순회 세일즈맨 문제의 경우에는 도시들이 중복 방문되는 경우가 생길 수 있다. 중복 방문이 있으면 방문되지 않은 도시가 있기 마련이므로 중복 방문된 도시들을 적당한 방법으로 제거하고 방문되지 않은 도시들을 포함시키면 된다. 위치기반 표현을 사용하는 경우에는 하나의 사이클 대신 여러 개의 부분 사이클로 나누어져 버리는 경우가 자주 발생한다. 부분 사이클 문제는 각 사이클에서 적어도 하나의 간선을 제거하고 전체가 하나의 사이클을 이루도록 만들어주면 된다. 이 과정에서 어떠한 간선들을 사용하여 적법한 사이클을 만드느냐 하는 것은 선택의 문제이다. 임의의 간선들을 더할 수도 있고 (random repair), 지역최적화 관점에서 가장 매력적인 간선을 더할 수도 있다 (greedy repair).
교차와 변이가 모두 해의 적법성을 깰 수 있으므로 대부분 수선은 변이까지 수행한 후에 행하게 된다. 수선 자체도 일종의 변이 효과를 초래한다. 수선이 초래하는 변이를 즐기고 싶으면 교차와 변이 후에 각각 해주어도 상관은 없다.
k 개의 연속된 유전자를 취하여 값을 뒤집는 방법을 쓰기도 하고 [Colorni 등, 1991], 일련의 연속된 유전자를 마구 뒤섞는 방법을 쓰기도 한다 [Davis, 1991]. 임의의 두 유전자 값을 서로 치환하는 변이도 있다 [von Laszewski, 1991]. TSP 를 위한 유전 알고리즘 중에서는 경로에서 간선 두 개를 제거하고 다른 두개로 수선을 하는 더블브리지 (double-bridge) 변이라는 특수한 형태의 변이를 쓰기도 한다 [Merz & Freisleben, 1997]. 이외에도 다양한 변이 연산들이 있는데 문제의 특성에 따라 합리적인 변이 연산자는 다를 수 있다. 앞에서 소개한 비균등 변이는 합리적인 방법이기는 하나 유전 알고리즘에 지역최적화 알고리즘이 결합되는 혼합형 유전 알고리즘의 경우는 조심스러울 필요가 있다 (혼합형 유전 알고리즘은 5 장 참조). 지역최적화 알고리즘은 임의의 해를 주변의 지역최적점으로 당기는 효과가 있다. 유전 알고리즘의 후반부에는 해집단이 수렴하여 대부분의 (또는 많은) 해들의 같거나 유사한 해를 갖게 되는데 이러한 두 해를 부모해로 삼아 교차를 수행하면 만들어진 자식해는 부모해와 매우 유사할 확률이 높다. 즉, 교차가 아주 미약한 교란을 초래하게 되는 것이다. 이럴 때 지역최적화 알고리즘의 성능이 충분히 강하다면 자식해는 두 부모해 중의 하나로 돌아가 버릴 가능성이 높다. 따라서 비균등 변이는 혼합형 유전 알고리즘에서는 그리 매력적인 대안은 아니다. 오히려 혼합형 유전 알고리즘의 경우, 후반부에 변이의 정도를 높여주는 것이 더 좋다는 본 연구실의 초기 실험 결과가 있다. 변이는 유전 알고리즘에만 국한되지 않고 시뮬레이티드 어닐링, 큰 스텝 마르코프 체인 (large-step Markov chain) 등에서도 연구되고 있는 주제이다.
1.9 절에서 언급한 바와 같이 세대형 유전 알고리즘의 경우는 해집단 내의 대부분의 염색체가 대치되므로 대치 연산이 비교적 간단하다. 안정 상태 유전 알고리즘은 한 개 또는 소수의 해가 생기는 즉시 해집단 내의 해 (들) 와 대치하게 되므로 대치될 대상을 고르는 작업이 매우 중요한 영향을 미친다. 이미 언급한 바와 같이 대치 연산자는 문제의 난이도, 교차, 변이 연산자의 교란 강도와 연관되어서 결정되어야 한다.
편의상 자식해가 생기는대로 즉시 해집단 내의 해 하나와 대치를 하는 가장 강한 안정 상태 유전 알고리즘을 대상으로 설명을 하자. 가장 손쉬운 방법은 해집단 내에서 가장 품질이 낮은 해를 대치하는 것이다 [Whitley, 1988]. 이는 새로 만들어진 해가 즉각적으로 해집단의 진화에 영향을 미침으로써 강한 수렴성을 갖는다. 반면, 설익은 수렴을 하지 않도록 주의를 기울여야 한다. 해집단에서 가장 우수한 해는 대치되어 없어지지 않도록 하는 것을 엘리티즘 (elitism) [DeJong, 1975] 이라 한다. 엘리티즘은 세대형 유전 알고리즘이나 안정 상태 유전 알고리즘에 다 적용될 수 있다. Cavicchio (1970) 는 두 부모해 중 품질이 나쁜 해와 대치하는 preselection 을 제안하였다. 이는 해집단에서 자신과 닮았을 가능성이 가장 높은 해가 부모해들이므로 다른 해들보다 부모해 중의 하나를 제거함으로써 해집단의 다양성을 오래 유지시키는데 도움이 된다. 부모해 중의 하나보다 품질이 좋을 경우에는 부모해와 대치하고 그렇지 못하면 해집단에서 가장 나쁜 해를 대치하는 방법도 있다. 부모해 중의 하나보다 좋을 때만 대치하고 그렇지 않은 경우에는 대치를 포기하는 방법도 해집단의 다양성을 유지하는 데는 강력한 방법이나 수렴성이 너무 떨어져 '아주' 충분한 시간 예산이 없으면 시도하기 조심스러운 방법이다. 해집단 전체를 비교하여 자신과 가장 가까운 해를 대치하는 방법을 쓰기도 한다. 이에 대한 실용적 변형으로써 DeJong (1975) 은 해집단에서 임의로 몇 개의 해를 선택하여 그 중 새로 만든 해와 가장 닮은 해를 제거하는 군집대치 (crowding) 를 제안하였다. 유전 알고리즘의 초반에는 해집단 내의 해들이 서로 많이 다르므로 군집대치는 크게 임의로 하나를 대치해 버리는 방식과 큰 차이가 없으나, 유전 알고리즘이 진행되면서 점점 유사한 해들이 많이 발생하여 수렴하려는 경향이 있으므로 유전 알고리즘의 후반에 해집단의 다양성을 높이는 데 기여를 한다. 군집대치에서 비교를 위해 고려하는 후보해의 개수를 늘릴수록 해집단의 수렴은 늦추어진다. 3.1 절에서 소개된 공유 (sharing) 기법과 유사한 동기를 갖고 있다.