인공지능의 이해
백 은 옥 : 전 서울대 컴퓨터공학과 강사, 전 LG 선임연구원
인지 과학 : 김영정, 김재권, 조인래, 김정오, 조명한, 이정민, 김영주, 김영택, 장병탁, 김형주, 백은옥, 강봉균, 서유헌, 이경민, 최재천 공저, 태학사, 2000. Page 273~378
1.2.2. 자연언어 처리 (natural Language Processing)
1.2.3 데이터베이스 응용 (Application of Database)
1.2.6 문제풀이 및 계획수립 (Problem solving and Planning)
1.2.8 자동화 프로그래밍 (Automatic Programming)
3.1.2 폭 우선 (Breadth first) 탐색법
5. 자동화 추론 (Automated reasoning)
5.2 비교흡수 부정 시스템 (Resolution refutation system)
5.2.2 비교흡수 부정 (Resolution refutation)
5.3 규칙에 기초한 추론 (Rule-based deduction)
5.3.1.1 AND/OR 형태의 사실 (fact) 표현
5.3.1.2 사실 표현을 나타내기 위한 AND/OR 그래프의 이용
5.3.1.3 규칙 적용에 의한 AND/OR 그래프의 변환
5.3.2.2 후향 시스템에서의 규칙 (B-규칙) 적용
6.2.2 과정회복 불가능 (irrevocable) 한 제어
6.4.3 규칙 형태의 자연성 (naturalness)
6.5 생성 시스템을 설계하는데 있어서의 고려해야 할 점
7.6 전문가 시스템의 예 (의료 전문가 시스템 : MYCIN)
인공지능이란 지능을 가진 컴퓨터 시스템을 설계, 구현하는 전산과학의 한 분야를 말하는 것이다 다시 말하자면, 인간의 많은 행동 중 지능을 요구하는 행동ㅡ언어의 이해, 학습 (learning), 논리적 추론 (reasoning), 문제 풀이 (problem solving), 컴퓨터 프로그램의 작성,수학 문제의 해석, 상식적인 사고 행위, 자동차의 운전 등ㅡ과 관련된 컴퓨터 시스템을 만드는 대부분의 작업이 인공지능이라 불리우는 분야에서 행해지고 있다.
과거 몇십년 동안, 이들 행위를 수행할 수 있도록 여러 컴퓨터 시스템이 만들어져 산업 전선에서 상업적인 관심과 흥미를 끌고 있다. 이러한 시스템 중에는 화학이나 생물학, 지질학, 공학, 의학분야에서 전문가들이 다룰 수 있는 어려운 문제 (예를 들면, 환자의 병 진단, 복잡한 유기화합 물질 합성 계획, 수식 형태의 복잡한 미분 방정식 풀이, 전기회로 분석 등) 를 풀거나, 인간의 음성을 제한된 범위 내에서 인식하거나, 혹은 인간의 언어 즉 자연언어 (natural language) 를 이해하고 간단한 물음에 답할 수 있는 시스템들이 있다. 이와 같은 시스템은 어느 정도의 인공지능을 보유하고 있다고 할 수 있다.
이런 종류의 시스템을 만드는 작업은 주로 경험적이고 공학적인 측면을 가진 반면, 구조적이지 못하다는 단점이 있으나, 널리 확장되는 연산 방법에서 추출되었기 때문에 인공지능 시스템은 개발되고, 실험이 진행되고, 또한 개선되어 가고 있다. 이와 같은 과정을 통해 여러 응용분야에 있어서 몇 가지 일반적인 인공지능의 원칙이 만들어지고 다듬어지게 되었다.
이 책은 인공지능에서 다루고 있는 핵심적인 아이디어들과 중요한 원칙들에 관하여 서술하고 있다. 우리는 또한 몇 가지 예를 통해 이들이 어떻게 응용되는지를 보인다.
본 장의 나머지 절에서는 현재 연구가 진행중인 여러 인공지능 분야에 대해 소개하고, 각 분야의 현재 기술 상태를 서술함으로써 인공지능에 대한 이해를 돕고자 한다.
인공지능 분야에서 첫 번째로 거둔 큰 "성공" 은 바로 퍼즐을 풀거나 체스와 같은 게임을 할 수 있는 프로그램을 만들어 낸 일이었다. 체스나 바둑 같은 게임에서 몇 수 앞을 내다보는 것이나, 어려운 큰 문제를 여러 개의 작은 문제로 나누어 생각하는 기술 등은 인공지능의 기본적인 기술인 "탐색 (searching)" 이나 "문제 축소 (problem reduction)" 의 분야로 발전하게 되었다. 현재의 프로그램의 상태를 보면 체커 (체스와 같은 게임의 일종) 나 백개먼 (서양 주사위판 놀이의 일종) 과 같은 게임에서는 벌써 세계 챔피언의 수준에 올라와 있는 상태이고, 체스는 아직 세계 챔피언의 자리에는 올라서지는 못했으나 거의 도달해 있는 실정이다.
그러나 이러한 분야에서 현재 부딪치고 있는 문제점은, 컴퓨터 시스템과는 달리 사람들은 게임을 할 때, 명료하게 설명해 낼 수 없는 어떠한 능력을 발휘한다는 점이다. 즉 예를 들자면 체스를 잘 두는 사람들은 말판에 놓여 있는 말들의 형태를 보면서 자신 나름대로의 의미는 형상으로 말판을 해석하는 능력을 가지고 있는데, 이러한 지식은 명료한 설명이 불가능한 것이므로 이를 해석하여 컴퓨터 시스템에 옮겨 놓을 수는 없는 것이다.
또 다른 하나의 문제점은 인공지능의 분야에서 "문제 표현의 선택 (the choice of problem representation)" 이라고 불려지는 것이다. 즉, 해결하고자 하는 문제를 어떻게 표현하여야 컴퓨터가 작업하는 영역과 시간 (time and space product) 을 최소화시킬 수 있느냐 하는 것이다.
앞으로 인공지능의 게임 (game playing) 분야는 위의 문제를 어떻게 해결해 나가는가에 그 성쇠가 달려 있다고 볼 수 있다.
사람들은 언어를 사용하여 서로 대화를 할 때, 별 어려움 없이 아주 복잡하면서도 이해하기 어려운 처리과정을 사용하여 의사소통을 한다. 그러나, 컴퓨터 시스템을 영어와 같은 자연언어 (natural language) 의 단편이라도 이해하거나 만들어낼 수 있는 정도에 이르게 하는 것은 대단히 어려운 작업으로 인식되어 오고 있다. 인공지능에 대해 연구를 하는 사람들은 언어 이해 능력을 컴퓨터 시스템에 이식시키기 위해 벌써부터 연구를 진행시켜 왔으며, 현재까지도 이 분야는 미완의 작업으로 연구원들의 흥미를 끌고 있다. 현재 몇몇의 프로그램들은 컴퓨터에 타이핑을 해서 명령어를 입력받지 않고, 마이크로폰을 이용하여 사람의 목소리를 입력받아 해석하여 명령을 처리하는 수준정도의 제한적인 성공을 가져온 것들도 있다. 물론 이러한 시스템의 언어 이해 정도는 사람에 비교될 수 있는 정도는 아니나, 이를 이용하는 응용 분야가 생겨나고 있는 것도 사실이다.
자연언어를 컴퓨터가 이해하도록 만드는데 생겨나는 문제점은 바로, 한 문장을 입력받았을 때 이들을 단지 단어의 나열로 생각하고, 각 단어의 품사를 생각하고, 문장 구조를 이해하여, 사전을 찾아 나열하는 단순한 작업만으로는 문장을 정확히 해석해 낼 수 없다는 점에 있는 것이다. 각 단어의 사전상의 뜻만 해도 여러 개가 될 것이며, 또한 이 단어가 숙어나 관용어의 일부분이 되었을 경우에는 다른 해석을 취해야 하며, 상식이 뒷받침되지 않았을 경우에는 해석이 이상해지는 문장이 많이 존재하기 때문이다.
그래서,간단한 질문들에 대답할 수 있는 시스템들을 만드는 데에는 성공했으나, 기계 번역 (machine translation) 과 같은 거대한 작업에서 실패한 연구원들은 현재의 언어이해에 대한 인공지능의 개발 방향을 바꾸기 시작했다. 단지 사전적인 지식만을 사용하는 한계를 극복하기 위해, 의사소통의 상황에 근거한 추측 (expectation) 의 역할과 상식 (worldwide commonsense) 의 중요성 등을 언어이해 연구분야의 주요한 테마로 설정하게 된 것이다.
언어는 기본적으로 인간들의 각 두뇌가 크고, 매우 흡사한 여러 정신적 구조들을 지니고 있는 상황에서, 이들 정신적 구조들의 한 부분만을 한 두뇌로부터 다른 두뇌로 이전하는 것이다. 더욱이 이러한 흡사하며 공통적인 정신적 구조들의 일부는 각 참여자들로 하여금 다른 사람들도 이와 같은 공통의 구조를 소유하고, 통신과정에서 이 구조를 사용하여 어떤 수행을 할 수 있게 끔 한다.
자연언어의 메시지를 이해할 수 있는 컴퓨터 시스템은 구분적인 지식과 추론할 수 있는 과정을 갖춘 일종의 메시지 생성기로 생각되어질 수 있다. 구어나 문어의 단편을 이해하는 이런 종류의 컴퓨터 시스템에 대한 개발은 점차적으로 진전되어 오고 있다. 이런 종류의 시스템에 대한 개발의 근본은 구문적인 지식을 표현하고, 지식으로부터 유추할 수 있는 기술에 대한 인공지능의 원칙들에 있다. 이 책에서는 언어처리 문제는 다루지 않지만, 지식의 표현에 중요한 몇 가지 방법을 기술하고, 언어처리 시스템의 몇 가지 응용의 예를 찾기 위한 작업을 기술한다.
데이터베이스 (database) 시스템은, 주어진 주제에 대한 사용장의 질문에 답을 하기 위해 몇 가지 주제에 대한 많은 양의 사실을 저장하고 있는 컴퓨터 시스템이다. 예를 들어, 대기업에 근무하는 직원들의 정보들에 관해 생각해 보자. 이들로 구축된 데이터베이스 내의 내용들은 "최불암은 총무부에서 일한다.", "최불암은 1990년 8월 8일에 고용되었다.", "총무부에는 17명의 직원들이 있다.", "최진실은 총무부의 부장이다." 등이다.
데이터베이스 시스템의 설계 (design) 는 컴퓨터 공학 (computer engineering) 의 특별한 부분으로, 이 부분에서는 효과적인 자료의 표현이나 저장 및 많은 양의 정보 검색을 가능하게 하는 기술들이 이미 많이 개발되었다. 인공지능의 분야에서 관심을 가지고 있는 것은 데이터베이스내의 저장된 사실들을 이용해 연역적인 추론으로 답을 얻어 낼 수 있는 시스템의 설계에 있는 것이다.
이와 같은 지적인 정보 유도 시스템의 설계에는 몇 가지 문제점이 대두되게 된다. 첫째, 위의 자연언어 처리 부분에서도 언급했듯이 영어와 같은 자연언어 (natural language) 로 기술된 질문을 이해할 수 있는 시스템의 구축이 상당히 어렵다는 점이다. 둘째, 비록 언어 이해에 따른 문제를 공식적이며, 기계가 이해할 수 있는 질문 언어를 사용함으로써 해결할 수 있다 하더라도 저장된 정보로부터 어떻게 원하는 답을 유도할 수 있는가에 대한 문제가 남게 된다. 마지막으로 질문을 이해하고 답을 추론하기 위하여는 데이터베이스내에 저장된 정보 이상을 요구하게 되는 경우가 있다. 왜냐하면, 대부분의 경우 주어진 데이터베이스에는 상식적인 지식이 저장되어 있지 않기 때문이다.
예를 들어, 개인 신상의 정보에서 인공지능 데이터베이스 시스템은 "최불암의 상관은 누구인가?" 라는 질문에 "최진실" 이라는 대답을 유도할 수 있어야 한다. 이런 시스템에서 그 부서에서 일하는 사람의 장을 "상관" 이라고 한다는 상식을 알아야만 한다. 이런 상식을 어떻게 표현하고 사용하는가에 대한 방법에 관해서 인공 지능의 방법론을 채택하게 된다.
인공지능은 자동적인 전문가 시스템 (expert system) 의 개발에도 도입되었다. 이들 시스템은 사용자에게 특별한 주제에 대한 전문가들의 의견을 제공하는 역할을 수행하기 때문에 "지식 기반 시스템 (knowledge based system)" 이 라고 불리기도 한다. 이 시스템들은 병의 진단, 광물의 매장량 평가, 복잡한 유기물의 구조 분석, 다른 컴퓨터 시스템의 사용에 대한 조언 등, 사회에서 전문적인 역할을 수행하는 사람들의 일을 대치시키기 위해 개발된 것이다.
많은 사람들은, 전문가에게 맡기면 되는 일을 왜, 인간에게 거부감을 줄 수도 있는 기계에게 수행시키는가에 대한 의문을 제기하기도 한다. 물론 옳은 말이기는 하다. 하지만 다음의 이유들로 인하여 인공지능 연구자들은 전문가 시스템을 구축하게 된 것이다. 먼저 인간 전문가의 수명은 한정이 되어 있기 때문에, 과거에 사용되던 많은 유용한 전문적인 기술들이 현재까지 전승되어 오지 않게 된다. 또한 전승이 된다 할지라도, 전문가의 지식을 전수 받는 과정은 시간이 오래 걸리는 매우 힘든 작업이다. 그러나 전문가의 모든 시작을 일단 추출하여 전문가 시스템을 구축했을 때는 거의 영구적으로 이 기술을 간직할 수 있으며, 전문적인 지식의 전수 또한 단지 시스템의 데이터 베이스를 복사하기만 하면 되는 쉬운 일이 된다. 또 다른 문제는 인간 전문가의 경우에는 그 때의 상황에 따라 다른 결론을 내리게 되는 경우가 발생할 수도 있으나, 전문가 시스템은 어떤 상황에 영향을 받지 않는다. 마지막으로 가장 중요한 문제 중의 하나가 바로 인간 전문가를 이용하기 위해서는 그 비용이 많이 든다는 점이다. 위와 같은 이유로 인공지능 연구자들은 전문가 시스템을 개발하게 되었고, 현재까지의 인공지능 연구에서 볼 때 가장 많은 성공을 야기시킨 분야가 된 것이다. 물론, 전문가 시스템이 인간 전문가에 비해 장점만을 가진 것은 아니다. 창조적이지 못하고, 적응성이 없으며, 넓은 분야에의 상식이 부족하다는 단점도 지니고 있다.
전문가 시스템의 개발에 가장 중요한 문제는 이들 각각의 주제에서 전문가가 보유하거나 사용하는 지식을 어떻게 추출하여, 어떠한 방법으로 표현하고, 시스템에 이식시켜 사용하는가에 있다. 특히 이 문제는 여러 많은 부분에서 전문가의 지식이 불명확하고 부정확하며 경험적인 면이 많이 있기 때문에 더욱 어려워진다. (물론 이러한 지식이 전문가 자신에게는 유용한 결론을 내는데 충분할 수 있다.)
많은 전문가 시스템은 규칙을 기초로 해 추론을 하는 인공지능 기술을 택하고 있다. 이런 시스템에서 전문가 지식은 많은 양의 간단한 규칙들로 표현된다. 이들 규칙들은 시스템간의 대화를 유도하는데 사용되고 결론을 유도하는데 이용된다. 규칙을 기초로 하는 추론은 이 책에서 중요한 주제로 다루고 있기 때문에 다시 언급하겠다.
수학에서 추측으로 만들어진 정리를 증명 (또는 반증) 하는 일은 지적인 작업이다. 가설로부터 추론을 하는 것뿐 아니라, 주어진 정리를 증명하기 위해 어떤 보조정리 (lemma) 를 먼저 증명해야 될지의 여부에 대해 직관적인 사고력이 요구된다.
뛰어난 수학자는 많은 익숙한 지식을 기초로 무엇을 결정할 것인가의 판단을 내리기 위해 관련된 주제에서 이미 증명된 정리를 이용하여 원래의 정리를 여러 부분의 소정리로 나누어 증명한다. 몇 가지 자동 정리 증명 프로그램들은 한정된 부분이지만 같은 기술을 이용하는 방법으로 개발되었다.
인공지능 방법의 개발에는 이와 같은 정리 증명에 대한 연구가 매우 중요시 되어왔다. 연역적인 처리를 서술 논리언어를 이용하여 공식화한 방법은 추론 방법을 이해하는 데 많은 도움을 준다. 많은 비공식화 된 방법ㅡ 의학적인 진단, 정보 검색 등ㅡ을 정리 문제로 공식화할 수 있다. 이런 이유에서, 정리 증명은 인공지능 기술 연구에 매우 중요한 주제인다.
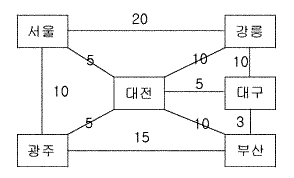
많은 흥미로운 문제들이 최적의 계획 또는 배열 등과 관련되어진다. 이들 문제들의 대부분은 이 책에서 거론되는 방법으로 해결이 가능하다. 이에 대한 고전적인 예는 판매사원 여행문제이다. 이 문제는 특정도시에서 시작해서 나머지 모든 도시를 각각 한번씩 방문한 후 다시 처음에 출발한 도시로 되돌아오고자 할 때, 이를 위한 가장 짧은 거리를 찾고자 하는 것이다. 이 문제는 [그림 1.1] 과 같이 n 개의 노드를 갖는 그래프에서 각 노드를 한번씩 방문한 뒤 되돌아오는 경로의 최소값을 구하는 일반적인 문제로 간주될 수 있다. 많은 퍼즐 문제들이 이와 같은 일반적인 성질을 가지고 있다.

[그림 1.1] 판매사원 여행문제

[그림 1.2] 8 queen problem
또 다른 예는 "8 여왕 문제 (8 queen problem)" 로 8개의 여왕 말을 표준 체스판에 배열하는데 어떤 한 여왕 말이 다른 여왕 말을 잡을 수 없도록 하게 하는 것이다 ([그림 1.2]). 즉, 이를 위해서는 같은 행이나 열 혹은 대각에 있어서 두 개 이상의 여왕 말이 놓여져서는 안 된다. 이런 종류의 대부분의 문제들에서는 문제의 답을 구하기 위해 생각되어져야만 하는 가능한 배열 또는 순서들이 매우 많다. 이러한 문제들을 단순하고 평범한 방법들을 통해 풀려고 한다면 언청난 수의 배열, 순서들로 인해 아무리 용량이 크고 빠른 컴퓨터를 가지고서도 풀 수가 없는 것이다.
"판매사원 여행문제"를 포함하는 이러한 종류의 문제들 중 몇 가지는 연산이론가들에 의해 NP-complete 문제로 불리어진다. 연산이론가들은 문제해결의 어려움을 가장 잘 개발된 방법으로 해결할 때 최악의 경우에는 걸리는 시간이 문제의 크기에 대해 어떻게 변화하는가를 가지고 평가한다. 그러므로, 문제의 어려움은 문제의 크기에 따라 선형적, 다항식적 또는 기하급수적으로 증가될 수 있다.
NP-complete 문제를 현재까지 알려진 최선의 방법으로 푸는데 걸리는 시간은 문제의 크기에 따라 기하급수적으로 증가한다. 좀 더 빠른 방법이 존재하는지는 아직 미지수이나 만일 어떠한 특정 NP-complete 문제에 대해 그러한 방법이 존재한다면 이를 나머지 모든 NP -complete 문제들에 적용시킬 수 있다는 것은 이미 증명이 되어졌다. 그때까지는 기하급수적으로 증가하는 방법을 가지고 생각해야 한다.
인공지능 연구가들은 여러 종류의 배열문제들을 해결하는 방법에 대해 노력을 기울여 왔다. 그들의 노력은 비록 시간이 기하급수적인 증가를 하여야 만 할 때에도, 가능한 한 문제의 크기와 시간 사이의 관계가 완만한 증가를 하게끔 하는 데에 있었다. 몇 가지 방법들이 필연적인 배열 문제의 어려움을 완화시키고, 지연시키는 데 중점을 두고 개발되었다. 다시 말하지만 문제의 영역 (domain) 에 관한 지식은 보다 효과적인 해결방법의 중요한 요소가 된다.배열 문제들을 다루기 위해 개발된 방법들 중 많은 것들은 보다 덜 어려운 다른 배열 문제를 해결하는 데에도 또한 유용하다.
(각 노드는 도시 이름이고 노드를 이은 선분들은 갈 수 있는 길들을 나타내며, 그 위의 숫자들은 거리를 나타낸다. 서울에서 출발하여 다른 5개의 도시를 거쳐 다시 서울로 돌아오기 위한 가장 짧은 노선은 어떻게 될까?)
문제풀이 (problem solving) 분야에서의 성공에도 불구하고 '학습 (machine learning)' 분야는 아직도 인공지능에서 구현하기 어려운 분야로 남겨져 있다.특히 학습의 능력은 인간의 지능적인 행위 중 가장 중요한 부분 중의 하나이기 때문에 인공지능의 분야에서 반드시 해결해야 하는 문제로 남아 있는 것이다.
사람들은 보통의 경우 여러 개의 비슷한 문제들을 반복해서 풀게 되면, 문제를 풀면서 습득한 지식을 이용하여 다음 문제를 풀 때에서 좀 더 간편하며 쉬운 계산방법을 이용하여 문제를 풀게 된다. 그러나 컴퓨터 전문가 시스템은 어떤 한 문제를 풀면서 엄청나게 많은 계산과정을 수행하면서도 학습의 능력이 없기 때문에, 똑같은 문제 혹은 비슷한 문제를 다시 풀 게 했을 때에도 역시 똑같은 계산과정을 반복하여 수행하게 된다. 이와 같은 문제점을 극복하기 위해 컴퓨터 시스템에 학습의 능력을 부여하려 하는 것이다.
'학습 (machine learning)' 이 연구하기에 힘든 분야임은 틀림없으나, 현재 제작된 몇 가지 시스템들을 보면, 이것이 불가능한 목표만은 아님을 알 수 있다.
수학의 여러 가지 정리들을 찾아내기 위해 설계된 AM (Automatic Mathematician) 이라는 시스템이 아마도 현재의 시스템 중 가장 놀라운 학습능력을 보여주는 시스템일 것이다. 이 시스템에 초기값으로 집합이론의 공리와 개념만을 제공해 주었더니, AM은 cardinality, 정수 연산, 수 이론의 여러 가지 정리들을 이끌어 낼 수 있었다. AM 은 자신이 가지고 있는 지식 베이스를 변환하고, 여러 가지 가능한 대안들 중 가장 '흥미로운' 방법을 찾기 위한 휴리스틱을 사용하여 새로운 정리들을 추론해 내었다.
AM과 같은 여러 '학습 (machine learning)'에 관련된 프로그램들이 선보여지게 됨으로써 '학습'에 대한 여러 이론들이 정립되어 가고 있고, 이로 인한 앞으로의 '학습'의 발전 또한 컴퓨터 분야에 새로운 바람을 몰고 올 것이다.
컴퓨터의 프로그램을 작성하는 작업은 정리 증명 (theorem proving) 이나 로봇 (robotics) 분야와 연관되어진다. 자동화 프로그래밍에서 기본적인 연구의 대부분은 정리증명이나 로봇 문제 해결에 관한 연구와 겹치게 된다. 어떤 면으로는 기존의 컴파일러 (compiler) 가 자동 프로그램의 한 예일 수 있다. 컴파일러는 완전한 입력 언어ㅡ즉,모든 문법이 정의되어 있는, 프로그램을 위한 언어ㅡ의 프로그램을 기계언어 (machine language) 로 변환시킨다. 그러나 여기에서 우리가 뜻하는 자동화 프로그래밍은 "슈퍼 컴파일러 (super compiler) " 의 개념으로, 수행하고자 하는 작업에 대해 매우 높은 차원의 표현으로 쓰여진 프로그램일 경우, 이를 받아들여 기계언어로 변환시켜 줄 수 있는 프로그램을 의미한다. 매우 높은 차원의 표현이란 서술 논리문과 같은 형식적인 언어로 표현된 문장일 수도 있고, 또는 시스템과 사용자간에 모호성을 해결하기 위해 더 많은 대화를 요구하게 되는 영어와 같은 융통성 있는 표현일 수도 있다.
즉, 예를 들어 설명하자면, 컴퓨터로 하여금 "테트리스" 와 같은 오락을 만들 게 하려면 보통의 프로그램 언어로는 모든 데이터 구조와 알고리즘, 그래픽 기능 등을 프로그래머가 일일이 손수 제작하는 과정을 거쳐야 한다. 그러나 만일 이런 오락 프로그램을 자동적으로 생성해 주는 "슈퍼 컴파일러" 가 있다면, 우리는 아마 이런 식의 설명만을 컴퓨터에 입력시킴으로써 "테트리스" 를 얻어 낼 수 있을 것이다.
"정사각형 4개를 이어서 만들 수 있는 모든 모형을 랜덤 하게 발생시키도록 하라. 블록의 색은 빨간색, 녹색, 파란색, 노란색, 흰색의 5가지 색이 번갈아 가며 나오도록 한다. 이러한 블록은 일정한 시간 (0.5초) 이 경과될 때마다 한 칸씩 아래로 이동한다. 이동하는 도중 키보드의 오른쪽 화살표를 누르면 오른쪽으로 한 칸씩, 왼쪽 화살표를 누르면 왼쪽으로 한 칸씩 블록을 이동시킨다. 또한 5번 키를 누르면 블록의 모양을 오른쪽으로 90도씩 회전시킨다. ...."
어떠한 결과를 얻기 위한 프로그램을 자동적으로 만들어내는 작업은 주어진 프로그램으로 이 결과를 얻을 수 있다는 것을 증명하는 작업과 밀접한 관계가 있다. 이것을 우리는 프로그램 검증 (verification) 이라 부른다. 대부분의 자동화 프로그래밍 시스템은 프로그램의 검증결과를 부산물로 제공하게 된다.
자동화 프로그램의 연구에 있어서 가장 큰 기여를 한 부분 중의 하나는 문제 해결 방법으로서의 오류수정 (debugging) 개념이었다. 프로그래밍이나 로봇 제어문제에서, 처음부터 완벽한 프로그램의 작성보다는 비용이 많이 들지는 않으나 에러를 유발할 가능성이 있는 프로그램을 우선 작성한 후, 이를 수정해 나가는 것이 훨씬 효과적이라는 것이 주지되어 왔다.
현 단계의 자동화 프로그래밍 역시 인공지능에서 시작 단계에 불과한 분야이다. 이 분야 역시 자연언어 처리, 정리 증명, 로보트 공학 등의 인공지능 분야들의 발전과 더불어 계속 개발되어 나갈 것이다.
요즘 들어 주목을 받고 있는 인공지능 연구 분야 중의 하나가 바로 로보트를 다루는 프로그램을 만드는 로봇 공학 (robotics) 분야이다.
어린아이들도 그들의 주위를 잘 돌아다닐 수 있고, 물건을 다루고, 스위치나 장난감의 동작 혹은 젖꼭지 빠는 일 등을 할 수 있다. 이와 같이 이들 행위는 인간에게는 무의식적으로 수행될 수 있지만, 기계가 수행하려면 많은 지식이 동원되어야 한다.
로봇에 대한 연구도 많은 인공지능의 도움을 얻고 있다. 실제상의 한 상태를 모델화하는 여러 기술들이 개발되었고, 하나의 상태에서 다른 상태로의 전환을 표현하는 기술도 많이 개발되어졌다 그리하여 행동의 순서에 대한 계획을 어떻게 생성할 것인가에 대한, 보다 나은 이해를 할 수 있게 되었다.
복잡한 로봇 제어 문제는, 처음에 세부적인 사항을 무시한 가장 높은 단계에서의 계획을 수립하고, 점차로 세부적인 사항을 생각하며 낮은 단계의 계획을 세우는 방향으로 해결한다. 이 책에서 이에 대한 중요한 아이디어들이 로봇 문제 해결의 예를 통해 보여진다.
또 다른 하나의 인공지능의 분야로, 컴퓨터 시스템에 TV 카메라를 부착하여 주위를 볼 수 있게 하거나, 마이크로폰을 부착하여 주변의 말하는 소리를 들을 수 있게 끔 하는 노력이 행해져 오고 있다. 이러한 시험을 통해 복잡한 입력 데이터를 효율적으로 처리하는 데는 "이해 (understanding)" 가 필요하며, 이 '이해' 라는 것은 사물을 식별하는데 대한 많은 지식을 요한다는 것이 알려졌다.
인공지능에서 연구되는 식별의 과정은 대개 일련의 단계들이 수행되는 것을 요하게 된다. 예를 들어 시각적인 장면은 감지기 (sensor) 에 의해 부호화 (encode) 되어서 명암 (intensity) 값들의 행렬로 표현된다. 이들은 기초적인 그림의 구성요소를 탐색하는 검사기에 의해 선분, 간단한 곡선, 또는 모서리 같은 것으로 처리된다.
다음에 이들의 장면은 3차원적인 특성에 관한 정보를 추출하기 위해 표면과 형태로서 처리된다. 마지막으로 이 장면이 적절한 모델로 표현되는 것이다. 이 모델은 아마 "풀을 먹는 소가 있고, 꼭대기에 나무 한그루가 있는 언덕" 이라는 높은 차원의 묘사가 될지도 모른다. 식별의 전 과정에 있어 핵심은 무한히 거대하고 자연 그대로의 데이터를 대체할 수 있는 함축된 데이터를 생성해내는 것이다. 최종적인 표현의 본질과 특성은 식별 시스템의 목적에 좌우되는 것이 분명하다.
색깔이 중요하다면 색깔에 유의하여야만 하고, 공간적인 관계와 크기가 중요하다면 정확하게 측정되어야만 한다. 각 시스템마다 지니는 목적은 다를지라도 각 시스템이 입력에서의 거대한 양의 지각 가능한 데이터를, 처리 가능하고 의미 있는 표현으로 줄여야만 하는 것은 공통적이다.
장면을 식별하는데 있어 가장 큰 어려움은 그 시스템이 만들어낼 수 있는 가능한 표현이 수없이 많다는 것이다. 그렇지 않다면, 아마 한 장면의 범주를 결정하는 검사기를 상당히 많이 만들어 낼 수 있을 것이고 그 장면의 범주는 이의 표현으로서 제공될 수 있을 것이다. 예를 들면, 어떤 장면이 "풀을 먹는 소가 있으며, 꼭대기에 나무 한 그루가 있는 언덕" 의 범주에 속할 수 있는가를 알기 위해 그 장면을 검사할 수 있는 검사기가 아마도 만들어질 수 있을 것이다. 그러나 왜 사용될 수 있는 수많은 다른 것들 대신에 이런 검사기가 선택되어야만 하는가?
여러 단계의 표현에 대한 가설을 설정하고 이 가설을 검토하는 방법이 이 문제에 대한 접근 방법을 제시하는 듯하다. 장면 구성요소에 대한 장면의 적절한 표현을 처리하는 가설을 발전시키기 위해 시스템이 구성되어 오고 있다. 이러한 가설들은 해당되는 요소들에 대한 표현을 전문적으로 검사할 수 있는 검사기들에 의해 테스트 되어지고, 이러한 테스트의 결과는 보다 나은 가설을 발전시키는 데에 이용되어진다.
이러한 가설과 테스트 (hypothesize and test) 의 방식은 식별과정의 많은 단계에 적용된다. 여러 선분들을 한 방향으로 연결시킨다면 한 직선이 암시되어지고, 이것을 테스트하는데는 선에 대한 검사기가 이용되어질 수 있다. 인접한 사각형으로부터 간단한 각이 진 물체의 한 표현이 암시되고 물체에 대한 검시기가 이 사실을 테스트하는데 이용되어질 수 있다.
가설 설정의 과정은 예상된 장면에 대한 많은 지식을 필요로 한다. 몇몇 인공지능 연구자들은 이러한 지식이 틀 (frame) 혹은 스키마 (schemas) 라고 불리우는 특수한 구조 내에서 형성된다고 주장해 오고 있다. 예를 들면, 로보트가 현관을 통해 방으로 들어올 때, 방에 대한 스키마를 활성화하여, 빈 기억 공간에 다음에 나타날 것에 대한 많은 예상되는 정보를 담아두게 된다. 로봇가 직사각형을 식별했다고 가정하자. 방의 스키마로부터 이 형태는 창문임을 인식할 것이다. 창문의 스키마는 창문이란 마루바닥에 닿지 않는 것이란 지식을 지닐 것이다. 이 장면에 적용되는 특수한 검사장치는 이 예상을 확신시킬 것이며, 따라서 창문이란 가설에 신뢰성을 부여하게 된다. 우리는 이 책에서 틀 (frame) 구조의 표현이나 추론과정의 기초가 되는 여러 개념에 대한 거론을 하겠다.
인공지능 분야의 연구자들은 오랜 동안 컴퓨터에 인공지능의 여러 가지 응용분야를 구현하고자 노력하여 왔다. 그러나 기존의 프로그래밍 언어로는 이를 구현하는데 어려움이 많다는 것을 인식하게 되었고, 그리하여 인공지능을 컴퓨터에 이식시키는데 좀더 적합한 언어를 개발하기 시작하였다. 그 결과로 각 응용 분야에 적합한 많은 프로그래밍 언어들이 탄생하게 되었다. 그 중 현재까지 보편적으로 사용되고 있는 언어들로는, 객체 지향 프로그래밍을 위한 Smalltalk, Flavors, Common Objects 등이 있고, 리스트의 처리를 위한 LISP, 서술 논리식을 이용한 PROLOG, 그 외에 전문가 시스템을 구축하기 위한 여러 언어들이 있다. 이 장에서는 이런 언어들 중 대표적인 언어로 PROLOG 와 LISP를 소개하려 한다.
PROLOG 프로그램은 1970년대 프랑스의 Marseille에 의해 자연언어처리를 위해 처음으로 사용되었다. PROLOG (PROgramming in LOGic) 는 그 이름에서 알 수 있듯이, 논리 프로그래밍 언어로 1차 서술 논리식 (first order predicate calculus)을 사용하고 있다. 1차 서술 논리식을 이용하게 되면 명확하고 간결한 문법 (syntax), 잘 정의된 의미 (semantics) 로 언어를 표현할 수 있다는 장점이 있다. PROLOG는 주로 다음과 같은 프로그램을 개발하는데 사용되었다.
1) 계획 형성 프로그램 (Plan formation program).
2) 기하학의 정리 증명, 대수 방정식 풀이.
3) 컴파일러 (compiler) 작성 프로그램.
4) 자연 언어 처리.
LISP 언어는 1950년대에 John McCarthy 에 의해 제안되었으며 재귀적 함수 (recursive function) 이론에 기초를 두고 있다. LISP 는 LISt Processing 의 약어로 다음과 같은 목적을 두고 개발되었다.
1) 재귀적 함수 이론에 기초를 둔 계산 모델의 구현.
2) 프로그래밍 언어의 문법 (syntax) 과 의미 (semantics) 에 대한 명확한 정의의 제공.
3) 숫자의 계산이 아닌 심볼처리를 위한 언어의 생성.
위에서 인공지능분야의 대표적인 두 가지 언어를 잠시 소개하였고, 앞으로의 절에서는 두 언어의 프로그램 구조 예를 들어, 여러분의 인공지능 언어에 대한 이해를 돕고자 한다.
PROLOG 프로그램은 다음의 3가지 부분으로 이루어져 있다.
- 객체 (object) 와 객체들 간의 관계 (relationship) 에 관련된 사실 (fact) 의 선언.
- 객체 (object) 와 객체들 간의 관계 (relationship) 에 관련된 규칙 (rule) 의 정의.
- 객체 (object) 와 객체들 간의 관계 (relationship) 에 관련된 질문들 (questions).
이제부터 위에서 언급한 3가지 부분에 관한 설명을 해 나가도록 하자.
먼저 사실 (fact) 의 선언은 PROLOG 프로그램을 통하여 컴퓨터에게 알려주고자 하는 사실들을 PROLOG 프로그램의 문법에 맞게 표현해 주는 것을 뜻한다. 예를 들어 "John likes Mary." 라는 사실이 있다면 PROLOG 프로그램에서는 이를 객체 (object) 와 객체의 관계 (relation) 로 바꾸어 "likes (john, mary)."와 같이 표현해야 한다. 물론 객체들간의 관계를 표현할 때 객체들의 순서는 프로그래머의 재량에 따라 "likes (mary, john)."과 같이 나타낼 수도 있으나, PROLOG 프로그램의 전통에 따라 전자와 같이 주어와 목적어의 순으로 배열하는 것이 사용하기 편리하다. 이러한 사실 (fact) 들을 표현할 때 지켜야 할 몇 가지 규칙들은 다음과 같다.
- 모든 객체들과 객체들간의 관계를 나타내는 단어는 'likes','mary', john' 과 같이 알파벳 소문자로 시작하여야 한다.
- 객체들간의 관계 (relationship)를 나타내는 단어가 가장 앞에 쓰여져야 하고, 객체들은 괄호로 묶여 관계 (relationship) 뒤에 쓰여지며, 괄호 안의 객체들은 ',' 로 분리된다.
- 모든 사실 (fact) 들은 ',' 로 끝나야 한다.
이러한 규칙을 지켜서 몇가지 영어 문장들을 사실 (fact) 들로 바꾸어 표현하면 다음과 같다.
cho likes tennis → likes (cho, tennis).
Jane is female. → female (jane).
Gold is valuable. → valuable (gold).
John owns gold. → owns (john,gold).
John is the father of Mary. → father (john, mary).
John gives the book to Mary. → gives (john, book, mary).
PROLOG 프로그램에 의해 위와 같은 사실들을 컴퓨터로 하여금 인식하도록 했다면, 위의 사실들과 관련된 질문을 컴퓨터에게 할 수 있다. PROLOG 프로그래머는 "?-' 의 기호를 사용함으로써 컴퓨터에게 질문을 할 수 있게 되는데 "Does Cho like tennis?" 라는 질문은
?- likes (cho, tennis).
와 같이 할 수 있고, 이 질문에 대해 컴퓨터는 자신이 알고 있는 사실이라면 (즉, 사용자가 선언해 준 사실이라면) 'yes'라는 출력을 보여주게 되고, 컴퓨터에게 선언해주지 않은 사실에 관련된 질문이나 선언된 사실과 다른 질문을 하게 되면 'no' 라는 출력을 보여주게 된다. 다음과 같은 예를 생각해 보자.
human (socrates).
human (aristotle).
athenian (socrates).
위의 내용을 fact 로 입력하고 다음의 질문을 하면,
?- athenian (socrates).
yes
?- athenian (aristole).
no
?- greek (socrates).
no
역사적으로 볼 때 aristotle은 athenian이 맞으나 컴퓨터는 자신이 알고 있는 데이터베이스에는 이런 사실이 없으므로, 질문에 대하여 'no' 라는 답변을 하게 되는 것이다. 또한 athenian 이면 greek 이라는 규칙도 컴퓨터는 모르기 때문에 이에 관련된 규칙 (rule) 을 넣어주지 않는 한 컴퓨터는 이 질문에 대해서도 'no'라는 답변을 하게 되는 것이다.
LISP 언어는 리스트를 처리하기 위한 언어이다. LISP 언어를 사용하기 위해서는 아톰 (atom) 과 리스트 (list), 표현 (expression) 을 먼저 이해해야 한다. 먼저 아톰은 LISP에서 사용하는 원소들 중 가장 기본이 되는 것으로서, 심볼이나 숫자, 알파벳 단어 같은 객체 (object) 를 뜻하며ㅡ예)27, 3.14 , FOO , B27 , HYPHENATED-SYMBOL ,'a , 'fly 등ㅡ리스트를 구성하는 원소가 된다.리스트는 아톰, 또는 리스트들의 집합을 괄호 ' ( ' , ' ) ' 로 묶어 놓은 것으로 하나의 문장과 같은 구조로 구성되어 있다. 그리고 표현 (expression) 은 이러한 아톰들과 리스트들의 의미 있는 연속을 뜻하는 것이다.
LISP언어는 이러한 리스트들을 다루기 위한 기본적인 명령어 (primitives) 들로 구성이 되어 있다. 명령어들은 모두'(명령어 파라미터들)' 의 형태를 따르고 있다. 예를 들면 '1+2'의 연산을 수행하기 위해서는 '(+ 1 2)'의 형태 (prefix form) 로 명령어를 수행해야 하는 것이다. 이러한 명령어들과 제어문, 재귀적인 함수 (recursive function) 들을 이용하여 심볼들로 이루어진 리스트들 표현을 다루기 편리하게 만들어 놓은 언어가 바로 LIPS인 것이다.
다음 단원에서는 인공지능의 대표적인 탐색 방식들을 살펴보아서, 지능의 일반적인 형태의 구현 방법에 대해 살펴보기로 하겠다.
일반적인 인공지능 (AI) 에 있어서의 문제 해결 방식은 초기의 어떠한 문제 상태로부터 가능한 작용소 (operation) 를 통하여 상태가 변환되고 이 상태로부터 새로운 작용을 통하여 또 하나의 가능한 상태가 만들어지며 이러한 계속적인 일련의 작용으로 탐색 상태들이 하나의 트리 (tree) 구조를 가지게 된다. 따라서 문제 해결은 탐색 트리에서 초기상태로부터 목표상태로 순회 (traverse) 하는 과정을 의미한다.
AI에서 문제를 기술한다고 함은 그 문제의 처음 상태, 다시 말해 초기상태와 목표상태를 기술해야 한다. 그리고 이러한 트리구조를 하나의 그래프로 나타내면 이러한 그래프의 탐색에는 가능한 상태를 순서대로 순회하는 맹목적인 탐색법과 사전에 지식을 적용해서 탐색할 상태를 결정하여 탐색효율을 높이는 발견적 (heuristic) 탐색법이 있다. 어떠한 지식을 어떻게 적용하면 효율적인 탐색, 즉 발견적 탐색이 될 수 있을 것인지를 결정하는 것을 제어전략 (control strategy) 이라고 한다.
이러한 탐색 과정은 하나의 초기 상태와 하나 이상의 종결상태를 연결하는 경로 (path) 를 찾아내야 한다. 일반적으로 탐색 트리에서 어떤 초기상태에서부터 도달할 수 있는 모든 상태들을 순회하는 것은 많은 불필요한 탐색이 포함되므로 내면적으로는 전체 트리를 상상하지만 외면적으로는 이 전체 트리에서 선택적으로 상태에 대한 탐색을 수행한다. 이러한 탐색 과정은 초기 상태에서 종결 상태로 나아가는 전향 탐색과 종결 상태에서부터 초기 상태로 나아가는 후향 탐색이 있다. 그리고 이러한 탐색 트리의 순회에서 새로 탐색되어지는 새로운 상태가 이전에 탐색되어진 상태와 일치할 경우 순환 경로 (closed loop) 를 갖는 그래프 형태의 탐색이 된다.
복잡한 인간의 추론사고도 로봇의 동작에 대한 문제해결도 최종적으로는 상태공간의 트리형 그래프에 관한 탐색의 문제로 바뀐다는 것을 이해할 수 있다. 이 탐색을 효율적으로 행하기 위해서는 발견적 탐색법이 있으나 컴퓨터가 자동적으로 목표상태를 탐색하여 문제를 해결하기 위한 짜임새를 이해하기 위하여 여기서는 맹목적인 깊이 우선 (depth first) 과 폭 우선 (width first) 의 탐색법에 관한 알고리즘 작성법을 설명한다. 이것은 보다 효율적인 탐색법에 관한 알고리즘을 만들 경우의 기초가 되기도 한다.
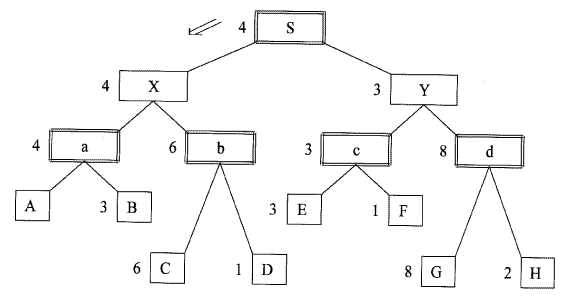
가장 간단한 문제로서 [그림 3.1]에 보이는 IDBR이라나 4문자의 인접문자를 치환하여 BIRD라는 문자열로 만드는 문제를 고려하자. 이 경우의 작용소 (operation) 는 그림에서 보이는 바와 같이 좌, 중, 우의 3가지로 되고, 이것이 적용된 뒤의 문자열을 기입해 두고 있다. [그림 3.1]에서와 같이 노드 n 에 작용소가 적용되어,n1 , n2, n3 인 노드를 생성해 내는 것을 "노드 n을 전개 (expansion) 한다." 라고 표현한다. 상태공간은 초기상태의 노드를 전개한 있을 수 있는 상태 모두의 집합이다. 문제의 상태가 이 상태공간 속을 이동해 가는 것이지, 트리형의 그래프가 되어 있는 것은 아니다. 그래프는 우리가 이해하기 쉽도록 표현해 주고 있는 것이다. 그러면 컴퓨터는 자동적으로 어떻게 하여 목표점을 탐색하는 것 인지 알아보자.
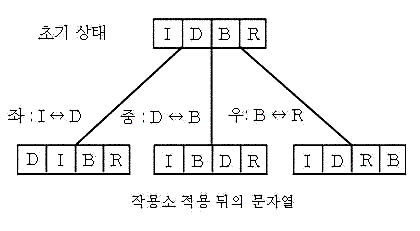
[그림 3.1] 문자의 치환에 대한 작용소의 정의
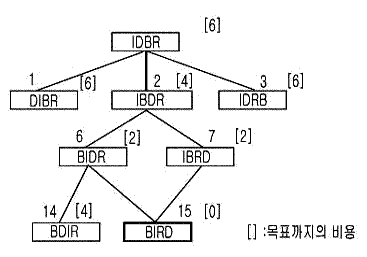
[그림 3.2]은 이 문자의 치환 퍼즐에 대한 상태공간의 그래프이다. 탐색의 깊이 3인 레벨에서 목표 노드가 나타나고 있다. 그림의 가지 부분에는 이에 적용시킨 작용소가 표시되어 있다. 그리고 전개된 노드에는 숫자가 표시되어 있는데. 이 순서에 따라 탐색하는 것이 폭 우선 탐색이며, 15번째에 목표상태인 BIRD 가 나타난다.
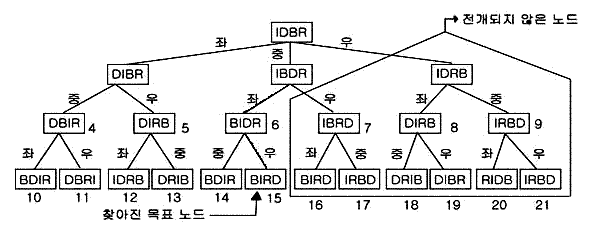
[그림 3.2] "BIRD" 의 문자열 탐색
이것은 그림에 굵은 선으로 나타낸 바와 같이 초기상태로부터 2→6→15의 순으로 목표 노드까지의 최단 경로를 찾아내게 된다. 그러나 깊이가 목표노드 보다 얕은 노드 모두를 전개하지 않으면 목표 노드를 찾아 낼 수 없게 된다.
만약 초기상태의 문자수가 많을 경우, 예를 들면 DANGER→GARDEN과 같은 6문자의 치환 퍼즐인 경우는 깊이 8의 탐색이 필요하게 되며, 탐색 노드들의 기하급수적인 (exponential) 증대현상에 의해 목표 노드가 얻어질 때까지 약 5만개의 노드를 생성하여 조사하지 않으면 안되며 이것은 계산시간을 길어지게 하고, 컴퓨터의 기억용량이 큰 것을 필요로 하게 된다.
깊이 우선 탐색법의 경우는 처음 생성된 노드로부터 차례차례로 다음 노드를 전개해 가는 방법이다. 이 방법은 그 가지에 목표 노드가 없는 경우는 무한히 탐색을 계속하므로, 처음 그 탐색의 깊이를 결정해 두고서, 그 이상의 깊이에서는 탐색을 않게끔 하여, 옆의 노드로 이동되도록 한다.
[그림 3.2]로 깊이 우선 탐색을 한다면, 1→4→10→11→5→12→13로 탐색을 하여도 그 가지에 목표 노드가 없으므로 옆의 가지로 이동해서, 2→6→14→15로 탐색을 하여 목표를 찾아낸다.
이 방법을 쓰게 되면, 우측의 점선으로 둘러 싼 부분의 탐색은 필요가 없고, 또 폭 우선 탐색은 15번째에 목표상태를 찾아내는데 비해, 깊이 우선 탐색에서 11번째에 탐색이 끝난다. 꽤 탐색 효율이 좋아지는 것을 알 수 있다.
그러나 그래프 구조에 따라서는 역핵 (backtracking) 이 많아지고, 탐색에 시간이 걸리는 수도 있다. 일반적으로 목표 노드가 탐색 트리의 깊은 곳에 있으면 깊이 우선 탐색이 알맞고, 얕은 곳에 있으면 폭 우선 탐색이 좋다.
가장 간단한 탐색은 시행착오에 의해 작용소를 선택하게 되는 것인데, 반드시 목표 노드에 도달된다고 하는 보증은 없다. 반드시 해를 구하고 싶은 경우는 계통적으로 상태 공간을 탐색해야 한다.
탐색 비용 (cost) 이 최소인 해를 구하는 방법, 혹은 목표 노드까지의 비용이 예측 가능한 경우의 탐색방법 등, 여러 가지 탐색의 알고리즘이 고려되고 있는데, [그림 3.3]에 가장 간단한 탐색의 알고리즘을 보인다. 이 방법은 초기 상태가 목표 상태에 도달할 뿐, 경로는 기억하고 있지 않으므로, 다시 뒤에 그 상태 변화에 관한 과정을 더듬어 볼 수가 없다. 이를 위해, 다음 3.2 절에서 보일 비용의 개념을 이해해야 할 것이다.
|
procedure search 1 state 를 초기 상태로 한다. 2 while state ≠ 목표 노드 do 3 begin 4 state 에 적용가능한 작용소를 선택하여 그것을 operator 로 한다. 5 state : = operator (state) 6 end ※
state : = operator (state) |
[그림 3.3] 가장 간단한 탐색의 알고리즘
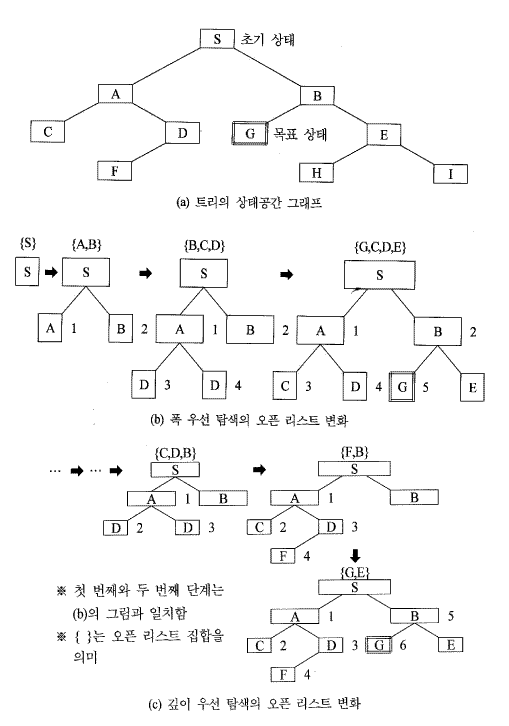
[그림 3.4] 기본적인 탐색 방법
[그림 3.4]에 트리형의 상태 공간 그래프의 일부를 보인다. 이와 같은 그래프는 처음부터 되어 있는 것은 아니다. 탐색의 전략에 바탕을 두고서, 폭 우선 탐색에 의해 모든 노드를 맹목적으로 조사해 간다고 한다면, 같은 그림 (b) 에서와 같이, 초기상태 ⓢ 에 있는 작용소를 적용시키면, ⓐ 와ⓑ 를 조사하여, 목표 노드가 아니면, 다음 ⓐ 상태에 작용소를 적용시킴으로 해서, 트리형의 그래프가 커져 가고, 이어서 목표 상태의 목표 노드를 찾아내게 된다. 그림의 (c) 에 보이는 깊이 우선 탐색도 이와 같다. 이 경우, 예를 들면 그림의 (b) 에서 ⓢ 에 작용소를 적용시킨 경우, 노드 ⓐ, ⓑ가 생성되고, 이 순으로 탐색해야만 하는 것을 컴퓨터가 기억해 두고 있어야 한다.
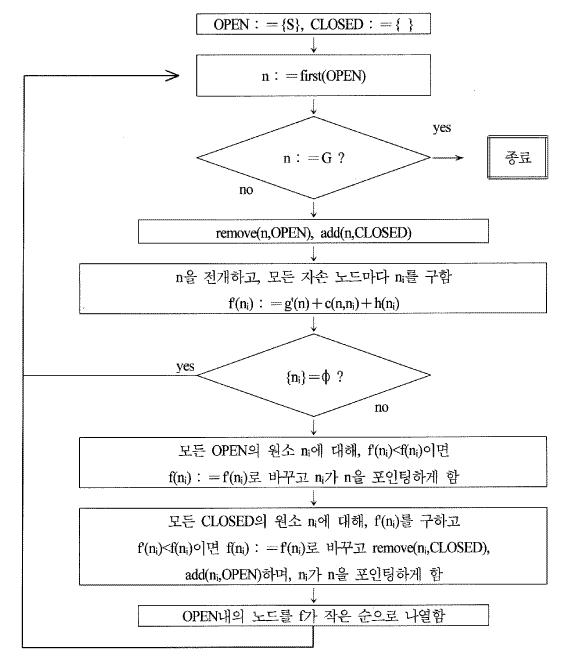
다음,ⓑ 를 조사하여, 노드 ⓢ 에 작용소가 적용되어 생성된 ⓒ,ⓓ 를 조사해야 한다고 함을 기억해 둔다. 그림의 (b) 위에 나타낸 (s),(a,b), (b,c,d),(g,c,d,e)는 오픈 리스트 (open list) 라고 하는 것으로, 이와 같은 리스트에 의해 차례 차례로 폭 우선 탐색의 결과가 기억된다.
또 하나 중요한 것이 있는데, 그것은 탐색을 하여 목표 노드가 아닌 경우, 부모 (parent) 노드로 역행 (backtracking)을 해서, 다음의 자손 노드를 조사하게 된다. 또 목표 노드가 발견된 경우에, 초기 상태 ⓢ로 되돌아 갈 경로를 기억해 둘 필요가 있다. 이를 위해 탐색이 끝난 경우에, 그림의 (b),(c)에 점선으로 나타낸 포인터 (pointer) 를 부모 노드의 방향으로 붙여 둔다.
[그림 3.4] 에 기본적인 탐색 방법인 폭 우선 탐색과 깊이 우선 탐색을 보였다. 이 중, 깊이 우선 탐색의 알고리즘을 [그림 3.5]에서 보인다. 이 탐색 순서를 문자와 흐름도로 나타내고 있다.
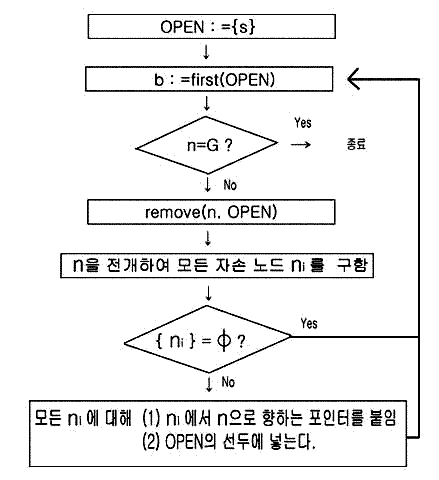
[그림3.5] 깊이 우선 탐색 알고리즘
출발 노드 S로 [그림 3.1] 문자의 치환에 대한 작용소의 정의부터 출발하여 목표 노드 G를 찾을 때까지 전개해서 얻게 되는 자손 노드 중에서 하나를 선택하고, 다음에 이것을 전개하여 탐색을 진행시켜 가는데, 이것은 깊이 우선 탐색에서 탐색할 자손 노드가 없어서 이 이상 나아가지 못할 때, 가장 가까운 부모 노드로 역행하고, 그때까지 탐색 못한 별도의 자손 노드를 선택하여 다시 탐색을 시작한다.
이와 같은 탐색에서의 역행을 잘 제어하기 위하여 OPEN 이란 명칭의 리스트를 준비하여, 전개에 의해 얻게 된 자손 노드에서 아직 전개되어 있지 않은 것은 이 리스트에 집어 넣어 둔다.
또 목표 노드를 찾은 뒤, 출발 노드가 목표 노드에 이르는 경로, 즉 해를 얻기 위해 전개하여 자손 노드가 얻어졌다면, 그때마다 부모 노드로 향하는 포인터를 붙여 둔다. 마찬가지로 폭 우선 탐색에 대한 알고리즘을 [그림 3.6]에 보인다. 이 설명은 ALGOL계의 언어를 쓰고 있으나,깊이 우선의 그것과 마찬가지로 생각할 수 있다. 깊이 우선 탐색과의 차이점은 어떤 깊이의 노드를 전개하여 그 자손 노드의 깊이로 탐색을 진행해 가기 전에 같은 깊이에 있는 그 외의 모든 노드를 전개하여 목표 노드가 있는지의 여부를 조사한다. 따라서 깊이 우선 탐색과의 틀린 점은 새로이 생성된 자손 노드는 OPEN 리스트의 선두가 아닌 맨 끝에 넣는다.
|
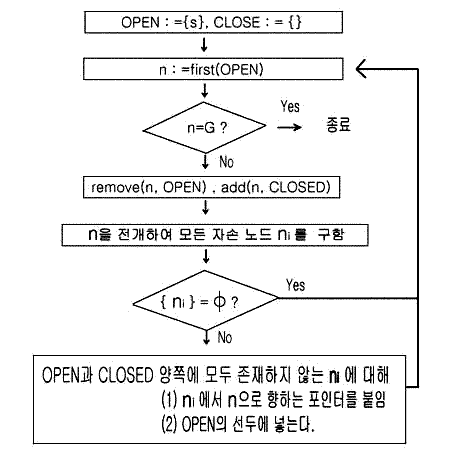
1 시작 노드 S 를 OPEN 에 넣는다 2 LOOP : if OPEN = φ then exit (failure) 3 n : = first (OPEN) 4 if goal (n) then exit (success) 5 reove (n, OPEN) 6 add (n, CLOSED) 7 n 을 전개하고 모든 자손 노드 ni 를 OPEN 의 맨 끝에 넣는다 (ni = goal 이라면 선두에 넣는다) 8 go to LOOP |
[그림 3.6] 폭 우선 탐색의 알고리즘
[그림 3.7] 순환 경로를 갖는 상태 공간 그래프
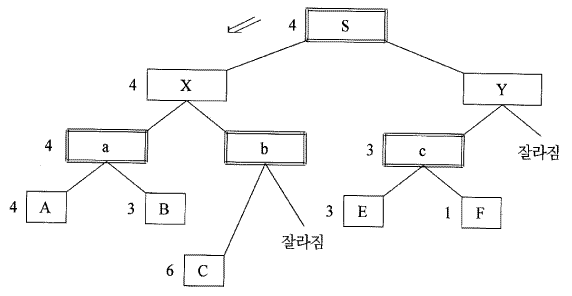
이제 [그림 3.7]에 보이는 것과 같은 순환 경로 (closed loop) 를 갖는 그래프인 경우의 알고리즘에 대해서 생각해보자. 물론 이때에는 순환 경로를 만들고 있는 노드들의 반복 탐색을 피하는 방법에 대한 궁리가 되어 있어야 하는 것이다. 기본적인 생각은 깊이 우선 탐색과 같으나, 그래프 상에서 순환 경로를 만드는 것과 같은 것을 피하기 위해, 전개하여 얻게 된 자손 노드 중에 이미 생성된 노드가 있으면, 그것을 OPEN 리스트에 넣지 않고 CLOSED LIST 라고 하는 별도의 리스트를 준비해서, 여기에 넣어 둔다. [그림 3.8]는 이 알고리즘을 보인다.
일반적으로 목표 노드가 탐색 트리의 깊은 곳에 있으면 깊이 우선 탐색이 적당하고 얕은 깊이에 있으면 폭 우선 탐색이 알맞다. 그러나 그래프 구조에 따라서는 깊이 우선 탐색은 그 탐색의 깊이를 정해 두지 않으면 역행 (backtracking) 에 시간이 걸리며, 탐색 효율이 나빠지는 수가 있다.
[그림 3.8] 그래프에서의 깊이 우선 탐색 알고리즘
인공지능의 연구에 있어서 문제의 이해뿐 만 아니라 문제의 해결에도, 그 문제에 관한 지식을 이용하는 의의는 매우 크다. 문제의 해결은 상태공간 표현 혹은 문제 분할 표현의 그래프 탐색 문제로 바뀐다는 사실을 이해할 수 있을 것이다. 따라서 AI (인공지능) 에 의한 문제의 해결은 그래프의 목표 노드를 탐색하는 알고리즘을 만드는 것이다. 이에 대해서 맹목적 탐색법을 사용하면 복잡한 문제가 되면 될수록 탐색 노드의 폭발적인 증가 현상에 의해 문제 해결을 위한 시간과 컴퓨터의 기억용량 등에 있어서 실용적이 못된다. 그러므로 탐색 효율을 올리기 위해 문제에 관한 지식을 이용하여야 할 것이다. 이 경우 이용할 지식을 휴리스틱 (heuristic : 발견적) 지식이라 부르며, 이와 같은 지식을 이용한 탐색을 휴리스틱 탐색이라 한다.
<3.1.2>에서 폭 우선 탐색법을 서술할 때, [그림 3.1]에서 BIRD라는 인접문자의 치환 퍼즐의 탐색도를 보였다. 초기 상태 IDBR → 목표상태 BIRD와 같이 변환하는 문제이다. 폭 우선 탐색에서는 15번째의 노드전개에 의해 탐색에 성공한다. 여기서 IDBR의 각 분자 I, D, B, R이 목표상태 BIRD에 대하여 각각 1, 2, 2, 1 문자식 떨어져 있는 이 문제 특유의 지식을 이용한다.
여기서 목표까지의 비용으로서, (1+2+2+1)=6을 이용한다. 이것을 [그림 3.1]의 각 탐색노드에 있는 문자마다 계산하면, [그림 3.9]과 같이 되고, 이 비용이 최소인 경로를 찾아감으로 해서 최단경로의 탐색이 가능해진다. 2 →6 →15, 또는 2 →7 →15인 두 경로가 있는데, 어느 쪽도 3회의 노드 생성으로 목표의 탐색에 성공한다. 폭 우선 탐색이 15회의 노드 탐색이 필요했던 것에 비하면 발견적 탐색법이 얼마나 효율적인 탐색인가를 이해할 수 있다.
[그림 3.9] 목표까지의 비용을 사용한 탐색의 효율화
앞에서 설명한 문자 치환 퍼즐의 출발 노드 문자열과 목표 노드 문자열 사이에서 위치의 차에 대한 총합, 다시 말해 "목표까지의 비용 예측치"는 그 노드의 평가 함수에 대한 일종으로 발견적 함수 (heuristic function) 라 부른다.
● n이란 노드의 평가 함수는 보통 f(n)으로 나타낸다.
● n이란 노드의 발견적 함수는 보통 f(n)으로 나타낸다.
● 출발 노드로부터의 비용 즉 거리를 나타내는 함수는 g(n)으로 한다.
노드의 평가 함수 f(n)으로서 출발 노드로부터의 비용 혹은 거리 즉, 거리 함수 g(n)만을 사용하는 탐색법을 최적 해 탐색이라고 하고 노드에서 목표노드까지의 비용 예측치 h(n)만을 사용한 탐색법을 등산법 (hill climbing) 이라고 한다. 그리고 평가 함수 f(n) 으로 g(n)+h(n)을 사용하여 탐색을 할 때 이것으로 A* 알고리즘이 있다. 이 탐색법들 중에서 최적 해 탐색은 문제에 대한 지식을 이용하여 탐색의 효율을 높이기는 하지만 출발 노드로부터 목표 노드까지의 거리가 상당히 먼 경우에는 효율이 떨어지게 된다. 그리고 등산법은 항상 h(n) 이 작아지는 쪽으로만 탐색을 행하므로 반드시 목표 노드를 찾게 된다고 할 수는 없다.
문제에 관한 지식을 사용하면 할수록 그래프 탐색의 효율이 올라간다. 여기서 서술할 A 알고리즘 탐색법은 노드 n의 평가함수로써 거리 함수 g(n)과 휴리스틱 함수 h(n)의 합계를 사용한다. 물론 모든 노드에서의 h(n)=0 이라면 최적 해 탐색이 되고 반대로 g(n)=0 이라면 등산법과 같다는 것은 쉽게 이해할 수 있을 것이다. 이 A 알고리즘을 [그림 3.10]에서 보인다.
[그림 3.10] A 알고리즘
그러나 여기서 설명한 A 알고리즘은 반드시 최적경로가 얻어지는 보장은 없다. 그것은 발견적 함수 h(n)은 예측치 이므로 실제의 목표까지의 거리 함수 h*(n) 보다 크면 f(n)이 과대하게 평가되어 그 노드가 전개되지 않고서 탐색이 끝날 수도 있기 때문이다. 이 간단한 예를 [그림 3.11]에서 보인다. 노드 n에 대한 h(n)은 노드 옆의 괄호 내에 표시한다. S를 전개하여 자손 노드 A,B가 얻어지고 그 평가 함수를 계산하면 f(A)=4, f(B)=6으로 되어 그림 (b)에 보이는 바와 같이 OPEN 리스트는 (A,B)로 된다. 다음에 A를 OPEN에서 집어내어서 전개하여 G를 얻는다. 이와 같이 하여 그림 (b)와 같이 되어,해는 S→A→G인 경로가 된다. 그러나 이 경로의 비용은 분명히 최소는 아니다. S→B→G라는 최적인 경로를 못 찾았던 이유는f(B)가 f*(B)보다 컸기 때문에 OPEN 리스트의 선두에 오지 않았기 때문이다.
따라서 h(n) 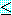 h*(n) 라는 조건을 만족하고 있는 평가 함수를 사용한 탐색은 반드시 최적 경로를
얻는다. 이와 같은 관계를 만족하고 있는 평가함수를 사용한 탐색을 A* 알고리즘에
의한 탐색이라고 하며 문제에 대한 정보를 잘 이용하여 탐색 효율을 높일 수 있는
탐색법이다. 이때 효율성의 관건을 평가 함수를 어떻게 잘 정의하느냐 하는 것이
된다.
h*(n) 라는 조건을 만족하고 있는 평가 함수를 사용한 탐색은 반드시 최적 경로를
얻는다. 이와 같은 관계를 만족하고 있는 평가함수를 사용한 탐색을 A* 알고리즘에
의한 탐색이라고 하며 문제에 대한 정보를 잘 이용하여 탐색 효율을 높일 수 있는
탐색법이다. 이때 효율성의 관건을 평가 함수를 어떻게 잘 정의하느냐 하는 것이
된다.
[그림 3.11] A 알고리즘으로 최적 경로가 얻어지지 않는 예
일반적으로 게임들은 두 경기자가 게임에 관한 완전한 정보를 갖고서 번갈아 가면서 행하는 것으로 두 경기자는 서로가 다른 편이 무엇을 했고, 또 할 수 있는지를 완전히 알 수 있다는 가정하에 시작한다. 게임의 결과는 둘 중의 하나가 이기거나, 지거나,또는 비기는 경우가 된다고 본다. 이러한 게임의 예는 장기, 삼목놀이 (tic-tac-toe), 서양장기, 바둑 등을 생각할 수 있다.
이러한 게임의 상황에 대해서 둘 수 있는 모든 경우를 나열하고 다시 여기서 나열되어진 각각의 경우에 대해서도 둘 수 있는 모든 경우를 나열하는 과정을 반복해 나가면 각 경우가 노드가 되는 트리 (tree) 형태가 되며 삼목놀이에 대한 게임 트리를 [그림 3.12] 에서 나타내고 있다.
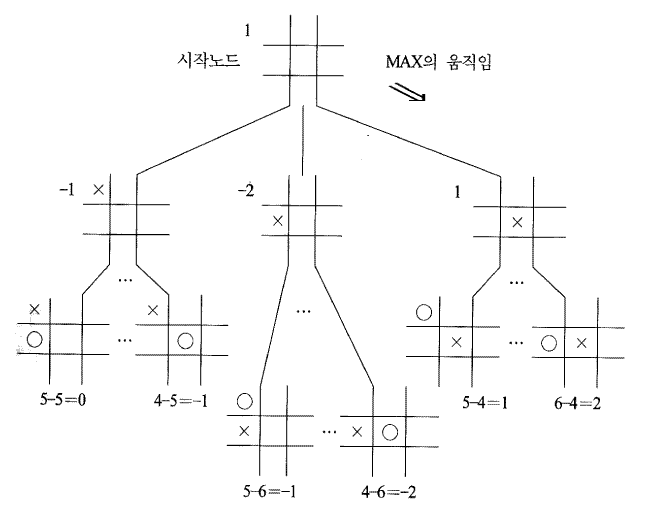
[그림 3.12] 삼목놀이에서의 게임 트리
복잡한 게임인 경우 앞에서 서술한 방식대로 트리를 만들어 나가면 노드들의 갯수가 폭발적으로 증가하게 되어 모든 가지를 탐색하는 것은 사실상 불가능하다. 그러므로 어떤 한 게임 중의 한 상황이 어느 정도 자신에게 유리한가를 나타내는 평가 함수를 사용하여 일정한 깊이 까지만 탐색을 하여 가장 자신에게 유리하고 상대방에게 불리한 쪽을 선택하게 된다. [그림 3.12]에서는 깊이 2까지 탐색하여 유도된 게임 트리 중 일부를 보이며 각 노드 왼쪽 위의 숫자는 자신에 유리한 정도를 나타낸 평가함수 값이다. 여기서는 (자신이 이길 가능성을 가지는 행이나 열 혹은 대각의 수)-(상대방이 이길 가능성을 가지는 행이나 열 혹은 대각의 수)를 평가함수로 사용한다. 맨 아래 노드들의 평가 함수 값에서 상대방은 평가함수의 값이 가장 작은 노드를 선택할 것이라고 간주하고 자신은 평가함수의 값이 가장 큰 노드를 선택하면서,선택된 평가 함수 값을 부모 노드로 역행 시켜 준다. 그리하여 맨 위의 노드에서 선택되어진 평가함수 값을 가지는 노드가 있는 경로를 선택하여 게임을 수행해 나가는 것이다.
단순 min-max 과정을 사용하면 깊이를 깊게 할수록 생성 노드 수가 급속히 증가한다. alpha-beta cut 과정은 생성될 필요가 없는 노드들을 생성하지 않고, 즉 게임 트리에서 가지를 잘라내어 가면서 탐색을 진행시켜 가는 절차이다.
[beta-cut]
[그림 3.13]에서,
① 노드 A, B를 생성하면 A의 값이 올라가 a는 4점인 수로 된다.
② C를 생성한 시점에서, b의 평가치는 a의 평가치보다 높아지고, 상대 입장에서 b는 a보다 불리하다.
③ 상대는 b의 수를 둘 필요가 없다.
④ 따라서 이미 D의 노드는 생성하여 조사할 필요도 없게 된다. H도 마찬가지이다.
[alpha-cut]
① 상대의 수인 a, b, c, d 에는 각각 4, 6, 3, 8점이 주어져 있다. X, Y를 선정하는 데에는 상대의 점수가 최소가 되도록, 즉 상대 입장에서 유리하게 되는 수를 상대가 두어 올 것이라는 전제 하에 있는 것이다.
② 이 전제 하에서 C의 노드를 생성한 시점에서, 적어도 3이하인 점수밖에 Y에 주어지지 않음을 알 수 있다. 더욱이, 이시점에서 자기 입장에서는 d를 생성할 필요가 없게 된다. 이를 alpha-cut이라고 한다.
[그림 3.13]과[그림3.14]를 비교해 보면 전자가 14개의 노드를 만든 것에 비해 후자는 10개의 노드를 생성하고 있음을 알 수 있을 것이다.
[그림 3.13] 게임 트리(노드 위의 숫자는 평가함수 값)
[그림 3.14] alpha-beta cut 과정에 의한 게임의 트리
인공지능의 연구는 말하는 것, 계획하는 것, 장기를 두는 것, 분자구조를 분석하는 것 등 여러 가지 일을 하는 시스템을 개발하는 과정을 포함한다. 이런 일을 사람이 한다고 했을 때는 그들이 이런 일을 할 수 있기 위해 반드시 알고 있어야 할 지식에 대해 언급하지 않을 수 없다. 다시 말해서 어떤 사람의 능력을 설명할 때는 그가 가지고 있는 지식으로 설명할 수밖에 없다는 의미이다. 이와 마찬가지로 우리는 "이 컴퓨터 프로그램은 카드 놀이하는 방법을 안다"는 식으로 말할 수 있을 것이다. 따라서 우리는 어떤 문제의 특성을 관찰한 후 다른 사람에게 그 문제의 해결에 필요한 지식을 설명해주는 것처럼 프로그램에도 미리 지시를 해야 한다.
지식과 지능 (intelligence) 의 특성에 대해서는 철학자, 언어학자, 교육자, 심리학자, 사회학자 등 여러 분야에서 연구해 왔다. 인공지능의 연구는 지능적인 행동을 하는 프로그램을 설계하는 분야를 포함하고 있기 대문에 인공지능의 연구자들을 그들의 프로그램의 성능을 향상시키는 데 초점을 맞추어 지식이라는 주제에 대한 다소 실용적인 접근을 해왔다. 인공지능에서는 "지식 표현" 은 어떤 자료구조 (data structure) 와 그 자료 구조에 가해지는 이해 가능한 프로시쥬어 (procedure) 의 복합체이며 이것이 프로그램 내에서 올바르게 사용된다면 지식을 가진 것처럼 행동할 수 있게 된다. 이런 의미에서 볼 때 인공지능 분야에서 지식 표현과 관련하여 수행하는 연구는 컴퓨터 프로그램에 정보를 저장하도록 하는 여러 종류의 자료구조를 설계하는 일과 이 자료구조를 이용하여 추론을 할 수 있도록 하는 프로시쥬어를 개발하는 일을 포함한다.
지식 표현에 관한 이론과 기술은 지난 수년간 매우 빠른 변화와 발전을 겪어 왔다. 이 장에서는 지금까지 연구되어 온 지식 표현 기법을 살펴보고 각각의 표현 형식과 추론에 이용되는 예, 그리고 장단점을 분석한다.
논리에 의한 지식 표현은 수학이나 논리학에서 사용되었던 논리를 이용한다. 대표적으로 사용되는 논리는 명제 논리 (propositional logic) 와 서술 논리 (predicate calculus) 이다. 명제 (statement) 란 참, 거짓을 판별할 수 있는 문장으로서, and, or, not, implies, equivalent 등과 같은 연결자 (connective) 에 의해 연결될 수 있다. 이러한 문장을 복합문 (compound statement) 이라 한다. 복합문의 참 거짓을 판명하기 위해서는 주어진 법칙을 따른다. 예를 들어 명제 X가 참이고, 명제 Y가 거짓이라면, "X and Y" 는 거짓이고, "X or Y" 는 참이다. 또한 명제 X가 참이고 "X implies Y" 가 참이면 Y는 참이 된다. 서술 논리는 명제 논리를 확장한 것이다. 서술 논리의 단위는 하나의 객체 (object) 이다. 이 객체에 대한 문장을 프레디킷 (predicate) 이라 한다. 예를 들어 "canary is a bird" 는 (is-a canary bird) 라고 표현한다. 서술되는 canary나 bird와 같은 대상물을 인자 (argument) 라고 한다. 프레디킷은 참이나 거짓 값을 갖는다. 서술 논리에서는 프레디킷 안의 대상에 대한 정량자 (quantifier) 로서 forall이나 exists 등을 사용할 수 있도록 한다. 예를 들어 "If x is a bird then x has wings" 이라는 법칙은 (forall (x) (if(is-a bird) (has x wings)) 로 나타내어진다.
논리의 전형적인 추론 방법은 p, p→q에서 q를 도출하는 연역 (deduction) 이다. 논리로 표현된 지식에 대한 추론은 일어나는 시기에 따라서 전향 추론과 후향 추론으로 나눌 수 있다. 전자는 p, p→q에서 q를 도출할 때 p가 데이터 베이스에 추가될 때까지 기다렸다가 q를 이끌어내고 후자는 q가 대답되어질 대가지 q를 부목표로써 찾게 된다. 이 두 방법은 논리에 있어서는 해결 법칙 (resolution principle) 으로 일반화될 수 있다.논리 표현은 개념을 자연스럽게 표현할 수 있으므로 지식을 정형화할 필요가 있는 영역에 적합하다. 또한, 데이터베이스 내의 가정 (assertion) 들이 독립적 (modular) 이므로 쉽게 첨가 삭제되며 단순하다는 장점이 있다. 반면, 절차적, 결정적 지식의 표현이 어렵고 지식 베이스를 구성하는 사실의 구성 법칙이 부족하므로 실세계의 복잡한 구조를 표현하기 어렵다는 단점이 있다.
인공지능 연구 분야에서 현재까지 개발된 많은 시스템은 의미망이라고 불리우는 지식표현 방식들을 사용했다. 이들이 의미망이라는 이름으로 분류되는 이유는 노드와 노드를 연결하는 아크라는 용어를 공통적으로 사용하고 있기 때문인데 이 노드와 아크들에 의해 망 (net work) 의 형태를 띠게 된다. 이 노드와 아크는 각각이 이름을 가질 수가 있으며 노드는 어떤 객체 (object) 나 개념 또는 사건 (event) 을 나타내고 아크는 이런 노드들 사이의 관계를 나타내고 있다.
하지만 여러 의미망 시스템들이 지니는 공통성은 이러한 용어에 있어서의 피상적인 유사성뿐이다. 예를 들자면 Quillian(1968), Norman and Rumelhart(1975), Anderson and Bower(1973)같은 심리학자들은 인간의 기억에 대한 심리학적 모델로서 의미망을 개발했다. 반면 전산 과학 (computer science) 분야의 연구자들은 의미망에 대해서 그들의 시스템에서 필요로 하는 다양한 종류의 지식에 대한 기능적인 표현 (functional representation) 으로서 관심을 가져왔다. 이러한 목적의 상이성 때문에 모든 의미망 시스템에 걸쳐 적용될 수 있는 간단한 원리들의 집합은 존재하지 않는다. 아래에서는 어떤 식으로 간단한 개념들이 의미망으로 표현될 수 있는지에 대해 알아본다.
예를 들어 "All canarys are birds."라는 간단한 사실을 의미망을 사용하며 표현해보자. 우리는 이를 위해 다음과 같이 canary 와 bird를 나타내는 두 개의 노드를 만들고 이를 아크로써 연결할 것이다.
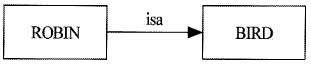
[그림 4.1] 의미망의 예1
그리고 Clyde라는 특별한 개체가 canary의 일종이라는 사실을 추가하고 싶다면 다음과 같이 Clyde를 위한 노드와 아크를 추가할 수 있다.

[그림 4.2] 의미망의 예2
위의 예에서는 우리가 초기에 표현하려고 했던 두 가지 사실 이외에도 매우 쉽게 "Clyde is also bird" 라는 세 번째 사실을 연역해 낼 수 있게 되었다. 이 연역의 과정은 단순히 ISA link를 따라감으로써 이루어 진다. Clyde는 카나리아이다. 카나리아는 새다. 따라서 Clyde는 새이다. 이와 같은 계승 계층구조 (inheritance hierarchy) 를 이용한 추론을 쉽게 할 수 있다는 점 때문에 의미망은 지식표현의 방법으로서 널리 사용되고 있다. 추론의 많은 부분이 복잡한 분류 (taxonomy) 에 근거하여 이루어지는 영역에서는 이 의미망이 가장 자연스러운 지식표현 방법이다.
이러한 분류 문제 이외에도 어떤 사물의 특성에 대한 지식을 표현할 필요가 있을 때에도 사용할 수가 있다. 예를 들어 새는 날개를 가지고 있다는 사실을 의미망에서 표현하고자 할 때는 아래와 같이 노드와 아크를 첨가하면 된다.
이 예에서 보는 바와 같이 이 표현 방법은 카나리아가 날개를 가지고 있고 Clyde도 날개를 가지고 있다는 추론을 가능하게 하는 프로시쥬어를 쉽게 만들 수 있게 한다. 즉 이 프로시쥬어에서는 계층구조의 윗 노드에서 가정된 사실은 아래 노드에서도 가정된 사실로 생각된다는 가정을 가지고 있으면 새로운 사실을 다시 표현할 필요 없이 ISA-hierarchy를 따라가기만 하면 된다. 인공지능분야의 용어로는 이러한 종류의 추론을 속성 계승 (property inheritance ) 이라 한다. 그리고 ISA link는 속성 계승 링크 (property inheritance link) 라 부른다.

[그림 4.3] 의미망의 예 3
이제 좀더 복잡한 문제로 넘어가 보자. Clyde가 둥지를 가지고 있다는 사실을 표현하는 문제를 생각해보자. 간단하게 생각하면 소유관계를 나타내는 아크로써 Clyde의 둥지를 표현하는 노드를 Clyde와 연결하면 된다.
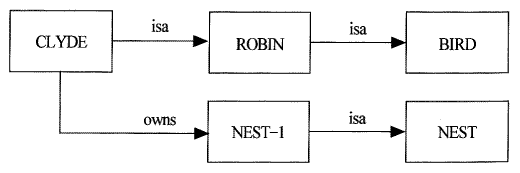
[그림 4.4] 의미망의 예 4
위의 예에서는 NEST-1은 Clyde가 소유한 둥지이며 NEST의 한 인스턴스 (instance) 이다. 즉 NEST 노드는 어떤 객체들의 부류 (class) 를 나타내고 NEST-1은 그 한 예를 나타낸다. 위와 같은 표현 방법은 어떤 예에서는 적당한 표현 방법이 될 수도 있지만 그 나름대로 약점을 지니고 있다. Clyde 가 NEST-1을 봄에서부터 가을까지만 가지고 있다는 사실을 표현한다고 생각해보자.이것은 표현하기가 불가능하다. 왜냐하면 위의 의미망에서는 소유관계가 아크로 표시되어 있는데 아크는 그 특성상 두 개의 노드사이의 관계만을 나타낼 수 있기 때문이다. 하지만 위의 사실은 4가지의 노드사이의 관계를 필요로 한다. 즉 소유자와 소유되는 객체 이외에도 시작 시간과 끝 시간도 필요하기 때문이다. 이러한 문제를 해결하기 위해서는 다자간의 관계를 의미망 내에서 표현하는 방법을 생각해야 한다.
Simmons와 Slocum(1972)은 객체들과 객체들의 집합뿐만 아니라 상황 (situation) 과 행동 (action) 을 표현하는 노드까지 포괄할 수 있는 해답을 제시하였는데 이는 그 후 많은 의미만 시스템에서 받아들여졌다. 각 상황 노드 (situation node) 는 상황 묘사를 위한 여러 인자를 묘사하는 case frame이라 불리우는 외향 (outgoing) 아크들을 가지고 있다. 예를 들어 case 아크를 사용하여 Clyde가 봄부터 가을까지만 둥지를 가지고 있다는 사실을 표현해보자
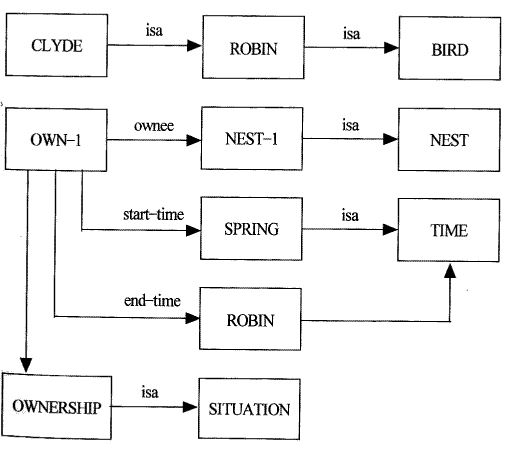
[그림 4.5] 의미망의 예 5
노드 NEST-1은 Clyde의 둥지를 표현한다. 노드 OWN-1은 OWNERSHIP의 한 인스턴스이며 Clyde가 둥지를 가지고 있다는 것을 표현한다. OWN-1 은 OWNERSHIP의 case아크를 계승하여 OWNEE, START-TIME, END-TIME, OWNER등의 아크를 계승하였다. 이 case- frame 구조를 사용하는 데 있어서 중요한 점은 OWN-1 같은 인스턴스 노드가 어떤 애트리뷰트에 대한 기대값 (expectations) 이나 지정값 (default value)을 계승할 수 있다는 사실이다.
이상에서 본 바와 같이 의미망은 지식표현에 있어서 매우 좋은 수단이 됨을 알 수 있다. 위 예에서는 특히 isa 아크와 has-part 아크를 사용한 것을 볼 수 있는데 이들은 매우 자주 사용되는 아크이다. isa는 두 노드 사이의 추상화 단계를 나타내는데 사용되고 has-part는 포함관계를 나타내는데 사용된다.
이제 마지막으로 의미망이 일반적인 언어를 표현하는데 사용된 예를 보도록 한다. 어떤 한 문장에는 기본적으로 객체에 해당되는 부분과 이들 사이의 관계를 표현하는 부분으로 나눌 수 있는데 고찰을 바탕으로 의미망을 통해서 표현할 수 있다.
"Bill gives Judy a gift."
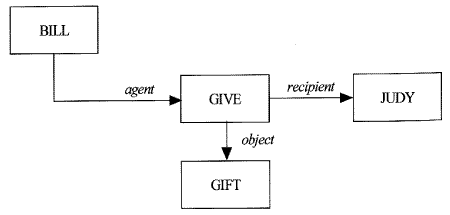
[그림 4.6] 임의의 아크를 사용한 의미망
의미망은 주로 영어로 된 복합문을 표현하기 위한 자연언어 처리 분야에서 성공적으로 쓰여 왔다.
의미망에서의 두 가지 추론, 상향 추론 (upward inference) 과 하향추론 (downward inference) 은 다음과 같다. 상향 추론에 의하면 "P is-a Q" 일 때 만약 Q가 성질 a를 가지면 P도 성질 a를 가진다. 하향 추론에 의하면 "a is-a b" 일 때 만약 P가 성질 a를 가지면 P는 성질 b도 갖는다. 처음 상향 추론이 실패하면 하향추론이 반복적으로 시도된다. 아래에서는 이 추론 과정의 예를 들어 보인다.
Canary is a bird.
A bird has wings.
Banney is a canary.
Banney owns a nest.
Wings is a organ.
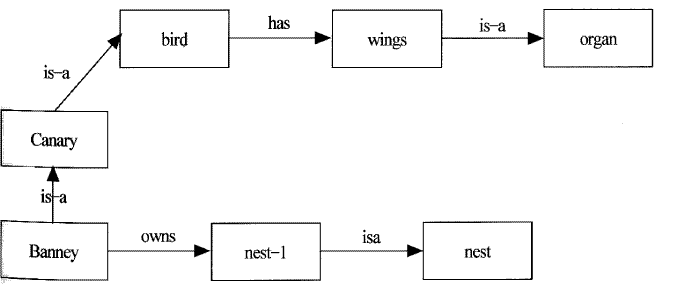
[그림 4.7] 카나리아
위와 같은 의미망이 있을 경우 다음을 추론하여 보자.
(a) ? — (Banney is-a canary) ⇒yes
(b) ? — (X is-a Y) ⇒ X=banney, Y=canary
(c) ? — (canary has wings) ⇒ yes
(c) ? — (bird has organ) ⇒ yes
(a)와 (b)는 매칭에 의해서 쉽게 추출된다. (c)의 경우는 (canary has wings) 라는 사실이 존재하지 않으므로 먼저 상향 추론을 시도하여 좀 더 일반적인 (canary is-a X) 의 매칭을 행한다. 여기서 (canary is-a bird) 와 (bird has wings) 라는 사실을 알 수 있다. canary 가 bird 이고 bird가 갖는 성질은 canary가 가질 수 있으므로 (canary has wings) 는 참이 된다. (d)의 경우는 상향 추론이 실패하고 하향추론이 시도된다. (X is-a organ) 을 매칭하기 위하여 화살표의 반대 방향으로 움직여 (wings is a organ) 과 (bird has wings) 를 찾을 수 있고, (bird has wings) 라는 사실을 알 게 된다. 따라서, 추론의 결과는 참이 된다.
의미망은 매우 복잡한 분류나 인과 관계를 갖는 추론에 자연스러운 표현이 가능하다. 그러나, 지식 베이스의 크기가 커지면 너무 복잡해지므로 다루기 힘들다는 단점이 있다.
프레임은 기본적으로 의미망의 일종으로 그 기본적인 형태는 보다 추상화된 개념이 상위에 위치하고 구체적인 개념이 하위에 위치하는 계층관계를 가지는 노드와 그들의 관계를 나타내는 아크들로 구성되어 있다. 각각의 노드가 가지는 개념은 애트리뷰트의 모임으로 정의될 수 있는데 이 애트리뷰트를 슬롯이라는 용어로 표현한다.
이 각각의 슬롯은 정보를 데이터 (data) 의 형태로 가지고 있고 각각의 슬롯마다 여러 가지 프로시쥬어를 가지게 되는데 데이터가 변하게 되면 해당되는 프로시쥬어가 수행되게 된다. 이러한 프로시쥬어 중 매우 유용하면서 자주 쓰이는 종류로는 If-added Procedure, If-deleted Procedure, If-needed Procedure가 있다. 프로시쥬어가 수행되는 시기는 각각 다음과 같다. If-added Procedure는 data에 정보가 추가될 때 수행되며 If-deleted Procedure는 정보가 제거될 때 수행되고 If-needed Procedure는 슬롯의 정보가 필요한데 그 슬롯이 비어있는 경우에 수행된다.
프레임을 이용한 지식 표현은 대체적으로 다음과 같은 모양을 띠게 된다. 우선 각 노드의 형태는 아래 [그림 4.8]과 같고 이러한 노드들이 아크로 연결되어 전체적으로 하나의 의미를 표현하는 의미망을 이룬다.
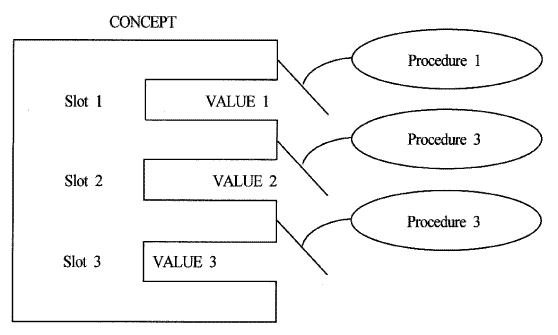
[그림 4.8] 프레임 시스템의 한 노드
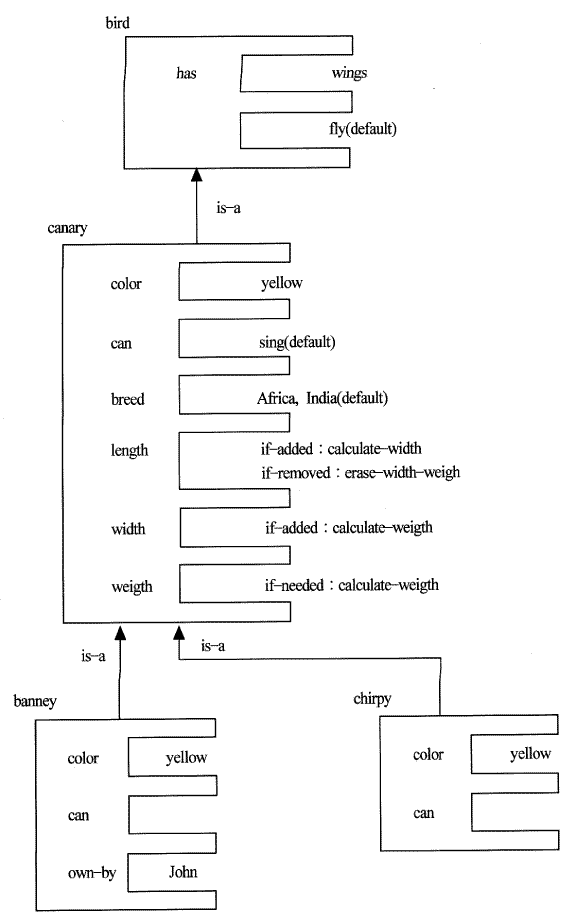
프레임은 의미망의 한 종류로서 프레임이라고 하는 객체의 구조와 슬롯 (slot) 이라고 하는 객체의 애트리뷰트 (attribute) 의 묘사에 중점을 둔 지식 표현 방법이다. 프레임은 데이터 (data) 와 프로시쥬어 (procedure) 를 하나의 구조로 묶는다. 프레임은 계층 (hierarchy) 으로 구성되며, 상위 단계는 고정되어 있고, 상황에 항상 옳은 사물을 표시한다. 하위 단계는 특정한 인스턴스나 데이터에 의하여 채워져야 하는 슬롯을 가지고 있다. 슬롯은 지정값 (default value), 다른 프레임을 가리키는 포인터, 규칙, 프로시쥬어로 이루어진다. 프로시쥬어는 슬롯의 값이 요구되거나, 변하거나, 제거될 때 자동적으로 작동되는 데몬 (daemon) 이다. 프레임은 내부적으로 슬롯이 여러 가지의 값을 가질 수 있도록 각 슬롯에 패싯 (facet) 이라는 키 (key) 를 갖고 있다. 프레임은 "<프레임 이름>, <슬롯이름>,<패싯이름>,<값>"으로 표현된다. 다음은 canary프레임의 한 예이다.
(FRAME canary
(is-a(value bird))
(color(value yellow))
(can(default sing))
(breed(range Africa India))
(length(if-added calculate-width)
(if-removed erase-width-weight))
(width(if-added calculate-weight))
(weight(if-needed calculate-weight))
is-a슬롯은 성질계승을 위한 슬롯으로서, 이를 통하여 상위 프레임을 명시한다. 슬롯이 갖고 있는 각 패싯의 의미는 다음과 같다. range 패싯은 슬롯의 예상될 수 있는 값들을 나타낸다 default 패싯은 반대되는 사실이 발견되지 않을 경우 제시될 수 있는 값을 갖는다. if-added패싯은 슬롯의 값이 주어졌을 때 수행될 필요가 있는 프로시쥬어를 수행시키는 것으로calculate-width나 calculate-weight는 프로시쥬어 이름이 된다. if-needed 패싯은 슬롯의 값이 필요하지만 그 값이 없는 경우, 그 값을 얻을 수 있는 프로시쥬어를 수행시킨다. If-deleted 패싯은 슬롯의 값이 제거될 경우 해당하는 프로시쥬어를 수행시킨다.
프레임은 추론이 진행됨에 따라 현재의 상황을 묘사하는 특정한 인스턴스를 만들기 위해서는 프레임을 초기화 (instantiate) 시켜야 한다. 한 프레임에서 실패하면 그 프레임에서 얻은 사실을 이용하여 다른 프레임을 초기화하게 된다. 어떤 프레임 기반 시스템에서는 부착 프로시쥬어가 추론과정을 지시하기 위한 중요한 방법이 된다. 추론과정을 예시하기 위해 다음과 같은 몇가지 함수를 가정한다.
[그림 4.9] 프레임
(PUT <프레임 이름>,<슬롯이름>,<패싯이름>,<값.)
: 특정한 프레임의 슬롯에 정보를 준다.
(REMOVE <프레임 이름>,<슬롯이름>)
: 특정한 프레임의 정보를 제거한다.
(GET <프레임 이름>,<슬롯이름>,<값>)
: 특정한 프레임의 슬롯의 정보를 얻는다.
[그림 4.9]와 같이 프레임이 형성되어 있다고 가정하면 위의 함수를 다음과 같이 적용할 수 있다.
(a) (GET banney can X) ⇒ sing
: banney는 프레임에서 can 슬롯을 찾지만 값이
없기 때문에 is-a 계승을 쫓아 canary 프레임으로
가서 can 슬롯의 지정값인 sing를 얻는다.
(b) (GET banney has wings) ⇒ yes
: banney 프레임에서 has 슬롯 발견에 실패하고
is-a 계승을 쫓아 canary 프레임에 가지만
또다시 실패한다. 다시 is-a계승을 쫓아 bird 프레임으로 가서 has 슬롯에 wings
를 발견한다.
(c) (GET chirpy weight X) ⇒ weight-value
: chirpy 프레임에서 weight 슬롯 값을 찾지만
실패하고 is-a계승을 쫓아 canary 프레임에서
weight 슬롯 값을 찾지만 역시 실패한다. 그러나 if-needed에 의해 현재의 정보로부터 weight를 계산하도록 calculate-weight
프로시쥬어가 작동하여 값을 구한다.
(d) (PUT canary length value 15cm) ⇒ yes
: canary 프레임의 length 슬롯에 값을 주게 되면
값이 채워지고 if-added calculate- width
프로시쥬어를 작동시켜 length로부터 width를 계산하여 width 슬롯에도 값을 채워준다.
또 width 슬롯에서도 if-added 프로시쥬어가 length와 width로부터 weight를 계산할
수 있는 프로시쥬어를 작동하여 그 계산 값을 weight 슬롯에 채워 준다.
(e) (REMOVE canary length) ⇒ yes
: canary 프레임에서 length 슬롯에서 값을 지운다.
이때 if-needed 프로시쥬어가 erase-width
프로시쥬어를 작동시켜 width와 weight 슬롯의 값도 같이 지운다.
(f) (PUT canary color value red) ⇒ yes
: canary 프레임의 color 슬롯의 값 yellow를 red로
바꾼다. 이 때 canary 프레임의 인스턴스인
banney와 chirpy의 color 슬롯의 값도 red로 바꾼다.
프레임은 지식을 표현함에 있어서 보다 일반적이고 자연스러우며 강력한 방법을 제공해 준다. 그러나 복잡하므로 지식 작성이 어렵다는 단점을 가지고 있다.
규칙은 가정과 결론의 문장으로 표현되는 지식으로 결정을 내리는 상황이 요구될 때 유용하게 사용된다. 규칙기반 시스템 (rule-based system) 에서 문제영역에 대한 지식은 규칙으로 나타내어지며, 규칙의 가정에 해당하는 조건부를 사실과 비교하여 만족된 경우 결론부를 수행하게 된다. 규칙의 결론부는 입출력이나 프로그램 제어를 위한 내용이 될 수 있으며, 또는 새로운 사실을 지식 베이스에 추가하거나, 지식 베이스에 이미 존재하는 사실을 변경시키는 내용일 수 있다.
규칙의 장점은 다음과 같다. 첫째 독립성 (modularity) 이다. 규칙은 서로 독립적으로 추가, 삭제, 변경될 수 있다. 둘째 지식 표현 방법에 대한 정해진 구조가 제공된다. 셋째, 결정을 필요로 하는 지식표현에 적합하다. 단점으로는 문제풀이에 있어서 많은 시간을 요구하며, 제어를 따라가기 어렵다는 문제가 있다.
규칙의 표현 형태는 일반적으로
A → B 와 같다.
이 규칙은 주어진 사실이 조건 A를 만족시키면 B라는 행위를 수행한다는 의미이다. 예를 들어보자
A flammable liquid was spilled →
then call the fire department.
The PH of the spill is less than 6 →
then spill material is an acid.
규칙을 이용한 지식 표현 방법을 시용하는 시스템을 보통 생성 시스템 (Production System) 이라 한다. 이에 대해서는 6장에서 자세히 보기로 한다.
지식의 선언적 표현법 (declarative) 과 프로시쥬어에 의한 표현법 (procedural representatI on) 과의 차이는 인공지능의 생각들이 발전해오는데 지대한 역할을 했다.선언적 표현법은 지식표현의 정적인 측면을 강조했다. 즉 객체, 사건, 또한 그들 사이의 관계 등에 대한 사실이나 세계의 상태 등에 대한 사실을 중점적으로 표현해 왔다. 그러나 프로시쥬어에 의한 표현법의 주장자들은 인공지능 시스템은 그들의 지식을 이용하는 방법―적당한 사실을 골라내고, 추론을 진행하는 등의 방법―을 알아야 하며 지식을 수반하는 행동의 특성은 프로시쥬어에 의해서 가장 잘 포착될 수 있다는 점을 지적해 왔다.
지식을 프로시쥬어로 표현한다는 것이 무슨 의미인지를 설명하기 위해 간단한 예를 들겠다. 알파벳 순서대로 정렬하는 시스템은 그가 하는 일에 애해 무엇을 알고 있는지를 생각해 보자. "A는 B 앞에 나온다"는 지식은 정렬하는 프로시쥬어 속에 암시적으로 포함되어 있는데 그것은 실제로 A와 B를 나타내는 컴퓨터 코드의 정수값을 비교함으로써 행해진다. 모든 컴퓨터 프로그램은 이런 종류의 프로시쥬어를 포함하고 있다. 여기서 주장하는 가장 중요한 점은 알파벳의 순서에 관한 지식을 그 시스템에 암묵적으로 저장되어 있지만 어떤 식으로 정렬을 할 것인가에 관한 지식은 명시적으로 표현되어 있어야 한다는 점이다. 그러나 선언적 표현법을 사용하는 시스템에서는 알파벳의 순서에 관한 지식은 명시적으로 표현되어 있다. 즉 "A는 B의 앞에오고 B는 C의 앞에 온다" 는 지식을 명시적으로 표현하다. 그리고 어떤 식으로 정렬을 해야할 것인가에 대해서는 위의 사실을 다루는 과정에서 얻어질 수 있도록 암묵적으로 표현한다. 예를 들면 정리증명이나 생성시스템의 경우가 이에 해당된다.
이 프로시쥬어에 의한 표현법이 제안되기 전에는 인공지능 분야의 연구자들은 어떤 종류의 지식이 논리나 의미망에 적합하게 표현되는지에 관심을 가지고 연구했다. 그리고 다음으로 관심을 가진 점은 데이터베이스가 커짐에 따라 이를 효율적으로 다루기 위해서 어떤 식의 자료구조를 도입해야 하는 가였다. 즉 지식과 그것을 다루기 위한 프로시쥬어를 분리하여 사고 하였다. 그러나 프로시쥬어에 의한 표기법을 제안한 연구자들은 어떤 영역에 대한 유용한 지식은 그것이 어떻게 이용될 것인가에 관한 지식과 본질적으로 연관되어 있다고 주장하였다. 아래에서는 이 프로시쥬어에 의한 지식 표현 법을 살펴본다.
초기 프로시쥬어 시스템의 가장 큰 장점은 문제를 해결하는 과정에서 부적절한 자료를 이용하지 않고 자연스럽지 않은 추론과정을 따르지 않는다는 데 있었다. 선언적 시스템에서는 모든 문제를 그들이 알고 있는 문제 해결 방식을 적용하여 해결하려고 한다. 이는 매우 비효율적인 행위이며 프로시쥬어 시스템에서는 특별한 추론 프로시쥬어를 사용하여 이를 제거하였다. 그러나 이 방법도 그 나름의 문제점을 가지고 있다. 즉 프로시쥬어를 사용함으로써 지식이 복잡해지고 따라서 다른 사람들이 이해하거나 수정하기가 어려워졌다.
이러한 이유로 1960년대 초반 이 두 가지 지식 표현 방식을 통합하려는 시도가 나타났다. 선언적 시스템의 수정의 편리성 (특히 논리) 과 프로시쥬어 시스템의 추론의 방향성 (directedness) 을 동시에 추구하게 되었다. 이러한 접근 방법의 본질은 보통 논리에 의해 표현된 선언적 지식을 그 사용 방법과 함께 표현하는 것이다. 이후의 프로시쥬어에 의한 지식표현의 많은 연구는 이러한 제어를 더욱 잘 표현할 수 있는 방법을 찾는데 있었다.
어떤 한 지식을 사용하는 데 대한 정보는 수행과정에 대한 여러 측면을 다루고 있다. 제어의 한 형태는 암시 (implication) 가 사용될 수 있는 방향을 지시하는 것이다. 예를 들어 어떤 것이 난다 (fly) 는 것을 증명하기 위해서는 그러한 결론이 나올 수 있도록 그것이 새라는 것을 증명하고자 할 것이다. 이러한 생각을 표현하기 위해서는 다음과 같은 형식을 사용할 수 있을 것이다.
(IF-NEEDED FLIES(X)
TRY-SHOWING BIRD(X))
이렇게 함으로써 만약 우리가 Clyde가 난다는 것을 보이려고 한다면 우리는 위의 휴리스틱을 사용하여 Clyde가 새라는 것을 증명하면 된다. 그러나 주의해야 할 점은 위에 나와 있는 "모든 새는 날 수 있다" 라는 지식은 반대 방향으로는 사용할 수 없다는 점이다. 즉 예를 들어 Fred가 날 수 있다고 해서 바로 Fred가 새라는 결론에 도달할 수는 없는 것이다.
프로시쥬어 지식의 또 다른 유용성은 어떤 특정한 목표를 달성하는 데 어떠한 지식이 적절한 지를 표현할 수 있다는 점이다. 예를 들면 만약 어떤 것이 새라는 것을 증명하고 싶고 THEOREM1 과 THEOREM2가 이사실을 증명하는데 유용하다고 할 때 이를 다음과 같이 표현할 수 있을 것이다.
(GOAL BIRD (TRY-USING THEOREM1 THEOREM2))
본질적으로 지금까지 했던 논의는 논리에 기반한 표현방식의 문제해결 방식에서 제공하는 직접적인 연역방법을 좀 더 장식한 것에 불과하다. 여기서의 추론은 제어된다. : 우리는 시스템에 언제 어떻게 그 시스템이 가지고 있는 지식을 사용할 수 있는 지를 지시한다.
아래에서는 이러한 제어지식을 표현하는 데 사용되는 방법 세 가지에 대해서 설명하도록 하겠다.
1. 제어지식을 사실을 표현하는 방법과 같이 표현한다. 이것은 위의 예에서 사용했던 방법이며 아래에서 설명할 PLANER의 방법이기도 하다.
2. 지식 표현 언어를 하위레벨에서 사용한다. 이렇게 함으로써 사용자는 추론 과정을 묘사하는 기계 내부의 과정에 대한 참조 권한을 가질 수 있다.
3. 지식을 표현하는 데 사용되는 언어 이외에 제어를 나타내기 위한 언어를 새로 정의한다.
이 세 가지 방법 중에서 PLANER를 사용하는 방법이 가장 널리 사용되고 계속적으로 설명할 프로시쥬어 표현언어의 기본이 된다.
PLANER : 유도된 추론, 확장된 논리
PLANER는 지식과 그것의 제어를 한꺼번에 표현하기 위해 만들어진 인공지능 언어의 일종이다. PLANER 연구의 기본적인 관심은 논리적으로 이미 가능한 추론 일반을 용이하게 하기 위한 것이 아니라 실제로 사용하리라 예상되는 추론을 촉진시키고자 함이다. 이 방법도 또한 그 나름대로의 문제점이 있다. 즉 PLANER로서는 풀 수 없으나 논리적으로는 매우 간단한 추론들이 있다.
PLANER의 특징들 중에는 어떤 정리들이 전방향 (forward) 또는 후뱡향 (backward) 으로 사용될 것인지를 지정할 수 있고 또 위의 예에서 설명한 것처럼 어떤 상황에서는 어떤 정리를 사용하도록 추천하는 기능도 있다. 사실 PLANER의 추천 기능은 위의 예보다 더 일반적인 의미를 지니고 있다. 그 정리의 이름으로 추천을 하는 것 이외에 그 정리가 속하는 계층 (class) 에 해한 추천을 필터 (filter) 라는 개념을 이용하여 표현할 수 있다. 예를 들면 아래의 PLANER 표현은 어떤 것이 새라는 것을 증명하기 위해서 동물학에 관한 정리를 이용할 것을 권하는 것이다.
(GOLA BIRD (FILTER ABOUT-ZOOLOGY))
위 표현은 모든 새 X에 대해서 X 가 타조 (ostrich) 가 아니면 날 수 있다는 가정을 한다는 의미이다.
이 THNOT기능은 지식의 여러 측면이 완전한 (complete) 경우에만 올바르게 수행될 수 있다. 위의 예에서는 OSTRICH(X) 라는 표현의 참 거짓을 판별할 수 있어야 한다는 것이다. 따라서 모든 X에 대해서 이를 나타내는 사실이 있거나 또는 추론을 통해서 판별할 수 있는 방법이 있어야 한다. 만약 이러한 의미로서 완전하지 않다면 시스템은 부정확한 추론을 하게 된다.
THNOT를 비롯하여 비슷한 여러 기능들은 논리의 단조성 (monotonicity) 을 깨뜨리기 때문에 논리의 영역을 초월한다. 단조성이란 어떤 사실의 집합에서 하나의 결론이 나왔다면 그 집합을 포함하는 더 많은 사실이 있을 경우도 같은 결론이 나와야 된다는 점이다. 이러한 논리를 확장된 논리 (extended logic) 이라 한다.
지금까지 여러 지식 표현 방법에 대해 알아보았다. 우선 논리는 기본적으로 선언적 수학이나 논리학에서 이미 사용하였던 것을 인공지능 분야에서 이용한 것으로서 추론의 기능도 잘 정립되어 있지만 실세계를 표현하기에는 너무 복잡한 점이 있다. 의미망이나 프레임은 지식을 그래픽의 형태로 표현 함으로써 알아보기 쉽다는 점이 중요하다. 사실간의 계층관계가 잘 표현된다. 그 외 규칙을 이용하는 방법과 프로시쥬어에 의한 표현을 알아보았다. 이들 표현 방법연구의 목적은 실세계를 잘 표현하고 이 표현된 지식을 바탕으로 추론을 용이하게 할 수 있는 표현방법을 찾는데 있다. 앞으로도 많은 연구가 진행될 것이다.
수학에서 추측으로 만들어진 정리를 증명 (반증) 하는 일은 지적인 작업이다. 가설로부터 추론을 하는 것 뿐 아니라, 주어진 정리를 증명하기 위해 어떤 보조정리 (lemma) 를 먼저 증명해야 될지의 여부에 대해 직관적인 사고력이 요구된다.
뛰어난 수학자는 많은 익숙한 지식을 기초로 무엇을 결정할 것인가의 판단을 내리기 위해 관련된 주제에서 이미 증명된 정리를 이용하여 원래의 정리를 여러 부분의 소정리로 나누어서 증명한다. 몇 가지 자동 정리 증명 프로그램들은 한정된 부분이지만 같은 기술을 이용하는 방법으로 개발되었다.
인공지능 방법의 개발에는 이와 같은 정리 증명 (theorem proving) 에 대한 연구가 매우 중요시되어 왔다. 연역적인 처리를 서술 논리언어를 이용하여 공식화한 방법은 추론 방법을 이해하는 데 많은 도움을 준다. 많은 비공식화 된 작업(의학적인 진단, 정보검색 등)을 정리 증명 문제로 공식화할 수 있다. 이런 이유에서, 정리 증명은 인공지능 기술의 연구에 매우 중요한 주제이다.
이 장에서는 정리 증명을 위해 이용되는 두 개의 시스템, 즉 비교흡수 부정 (resolution refutation) 시스템과 규칙에 기초한 연역 (rule-based deduction) 시스템에 대해 고찰한다.
비교흡수 부정 시스템은 어떤 목표문장이, 주어진 문자들의 집합으로부터 논리적으로 뒤따르고 있는지를 증명하기 위해 이 목표문장을 먼저 부정한 후 주어진 문장들과 합하여 새로운 집합을 만들고, 그 다음에 비교흡수(5.2절에서 언급)과정을 이용해서 모순을 유도하는 시스템이다. 비교흡수 부정 시스템의 중심적인 주제는 비교흡수 방법을 명확히 이해하는데서 비롯된다. 비교흡수에 사용되는 문장들은 우선 적용가능한 표현형태(절(clause)이라 하며 5.2.1절에서 변환절차를 언급)로 변환되어야 한다. 더욱이 어떤 문자를 선택하여 비교흡수과정을 수행할 것인가 하는 제어방법은 시스템의 효율성을 증가시키는데 기여를 하게 된다.
인공지능 시스템에 의해 사용되는 지식의 대부분은 암시기호(⇒)를 사용해서 표현이 가능하다. 비교흡수 부정 시스템에서는 이러한 표현을 우선 절들의 표현으로 변환하여 사용한다. 그러나 이러한 변환과정에서는 암시적 표현에서 주어지는 어떤 유용한 제어정보를 잃어 버릴 수 있다. 예를 들어 절의 표현 (A ∨ B ∨ C)는 암시적 표현 (~A∧ ~B) ⇒C, (~A∧ ~C) ⇒B, (~B∧ ~C) ⇒A, ~A⇒(B∨C), ~B⇒(A∨C), ~C⇒(A∨B) 등과 논리적으로는 같지만, 이러한 암시적 표현들에는 절의 표현에 나타나지 못하는 각기 다른 제어정보를 가진다. 비교흡수 부정 시스템과는 달리 규칙을 기초로 한 연역 시스템 (rule-based deduction system) 이란 암시적 표현 그 자체를 규칙으로 사용하는 시스템이다.
규칙을 기초로 한 연역 시스템에는 이와 같이 일반적 지식을 표현한 규칙 (rule) 들과 전체 데이터베이스 (global database) 를 이루는 특정한 지식을 표현한 사실들(규칙들이 적용됨에 따라 전체 데이터베이스의 내용이 변해 감)로부터 목표 wff를 증명한다. 이러한 연역 시스템은 전향 (forward) 시스템과 후향 (backward) 시스템으로 분류된다.
전향 시스템이란, 전체 데이터베이스가 목표 wff를 포함하게 될 때까지 전체 데이터베이스에 규칙(Fㅡ규칙이라 함)들을 적용시키는 것이며 후향 시스템이란, 목표 wff로 된 전체 데이터베이스에 규칙(Bㅡ규칙이하 함)들을 적용시켜 원래 주어진 사실들로 이루어진 전체 데이터베이스를 유도하는 시스템이다.
제4장에서 논리기호를 이용한 지식 표기방법에 대해 살펴보았다. 지식 표현인 잘 구성된 공식 (wff) 의 한 종류로 절 (clause) 이 있는데, 절이란 문자들의 논리합으로 구성된 wff로 정의된다. 여기서 논할 비교흡수방법이란 이러한 절들에 적용되는 하나의 중요한 추론규칙이다. 비교흡수방법을 설명하기에 앞서 먼저 아래의 서술형 명제 wff을 절들의 집합으로 변환시키는 과정을 살펴보자.
(∀ x({P(x)⇒{(∀y[P(y)⇒P(f(x,y))]∧ ~(∀y)[Q(x,y)⇒P(y)]}}
(1) ⇒을 제거한다 : 이것은 X1 ⇒ X2와 ~X1∨X2이 동치라는 사실을 이용한다. 위의 주어진 wff을 변환 시키면
(∀x){~P(x)∨{(∀y)[~P(y)∨P(f(x,y))]∧ ~(∀y)[~Q(x,y)∨P(y)]}}
(2) ~의 영역을 축소한다 : 이것은 ~(~P)=P, ~(A∧B)=~A∨ ~B, ~(A∨B)= ~A∧ ~B, ~( ∀x)Px=(∃x)~p(X),~(∃x)P(x)=(∀x)~P(x)등에 의해 이루어진다. 단계 1로부터의 wff를 변환시키면
(∀x){~P(x)∨{(∀y)[~P(y)∨P(f(x,y))]∧(∃y)[Q(x,y)∧~P(y)]}}
(3) 변수들을 표준화한다 : 변수는 가상이름이고 wff의 진리값에는 영향을 미치지
않으므로 각 한정사는 고유한 가상변수를 가질 수
있다.즉 ( x)[P(x) ⇒(∃x)Q(x)]는 (
x)[P(x) ⇒(∃x)Q(x)]는 ( x)[P(x) ⇒(∃y)Q(y))]로 변형되어 변수 표준화를 이룬다. 단계 2로부터의 wff를 변화시키면
x)[P(x) ⇒(∃y)Q(y))]로 변형되어 변수 표준화를 이룬다. 단계 2로부터의 wff를 변화시키면
(∀x){~P(x)∨{((∀y)[~P(y)∨P(f(x,y))]∧(∃w)[Q(x,w)∧~P(w)]}}
(4) 존재한정기호 (existential quantifier) 를 제거한다. : (∀y)[(∃x)P(x,y)]라는 wff를 우리말 로 하면 '모든 y에 대해 P(x,y)를 만족시키는 y에 종속되는 x가 존재한다' 로 된다.여기서 y 에 종속되어 결정되는 x를 y에 대한 어떤 함수로 표현해 g(y)로 표현할 수 있다. 이와 같은 함수 g를 스콜렘 함수(Skolem function)라 하며, 더욱이 어떤 매개변수도 가지지 않는 스콜렘 함수를 스콜렘 상수 (Skolem constant) 라 한다. 단계 3으로부터의 wff 에 이를 적용시키면
(∀x){~P(x)∨{((∀y)[~P(y)∨P(f(x,y))]∧[Q(x,g(x))∧~P(g(x))]}}
(5) 프리닉스 형 (prenex form) 으로 변환한다: 단계 4를 행한 후의 wff는 한정사 (quantifier) 로 전체한정기호 (universal quantifier) 들만 남고 이들 변수들은 이미 표준화되었으므로 이것들을 wff의 제일 앞에 놓아 진리값에 영향을 줌이 없이 각 한정사의 영역을 wff 전체에 미치도록 할 수 있다. 이와 같이 하여 변환된 wff를 프리닉스 형으로 표기되었다 한다. 또한 프리닉스 형의 wff에서 한정사들로만 된 앞부분을 접두사 (prefix) 라 하고 나머지 뒷부분을 매트릭스 (matrix) 라 한다. 단계4로부터의 변환된 프리닉스 형은
(∀x)(∀y){~P(x)∨{[~P(y)∨P(f(x,y))]∧[Q(x,g(x))∧~P(g(x))]}}
(6) 매트릭스를 논리곱의 정규형 (conjunctive normal form) 으로 변환한다. : 논리곱의 정규 형이란 문자 (literal) 들의 논리합으로 이루어진 유한집합에 대한 논리곱을 말한다. 단계 (5) 에서의 매트릭스는 분배규칙을 연속적으로 적용, (X1∨(X2∧X3))는 (X1∨X2)∧(X1∨X3)로 함에 의해 다음과 같이 된다.
(∀x)(∀y){~P(x)∨~P(y)∨P(f(x,y))]∧[~P(x)∨Q(x,g(x))∧[~P(x)∨~P(g(x))]}
(7) 접두사를 생략한다 : 단계 6에서 구한 wff에서 접두사를 제거하고 공식에 나타나는 모든 변수는 전체 한정기호로 한정된 변수로써 가정한다.
(8) ∧를 없앤다 : 즉 X1∧X2는 {X1,X2} 로 표현된다. 이와 같이 나타나는 각각의 독립된 인자를 절 (clause) 이라 부른다. 그러므로 단계(7)의 공식은 다음과 같은 절들의 집합으로 변환된다.
~P(x)∨~P(y)∨P(f(x,y))
~P(x)∨Q(x,g(x))
~P(x)∨~P(g(x))
(9) 변수들을 조정한다 : 이것은 단계 (8)에서 구한 어떠한 두 개의 절도 같은 이름의 변수가 나타나지 않도록 하기 위해서다. 그러므로 다음과 같이 변수 조정을 할 수 있다.
~P(x1)∨ ~P(y)∨P(f(x1,y))
~P(x2)∨Q(x2,g(x2))
~P(x3)∨ ~P(g(x3))
위의 9가지 단계를 거쳐 wff는 절들의 집합으로 변환이 된다. 만일 wff X가 wff들의 집합 S에 논리적으로 뒤따르는 (logically follow) 것이라면 집합 S에 있는 모든 wff들을 절의 형태로 변환시킨 집합에 wff X는 논리적으로 뒤따르는 것을 보일 수 있다. 그러므로 절의 표현만을 취급하는 비교흡수방법은 정리증명 시스템에서의 한 추론규칙으로 이용이 될 수 있음이 정당화된다.
만일 변수를 가지지 않는 항이 절의 변수에 대치되어질 때 나타나는 표현을 본래절의 기초예시 (ground instance) 라 한다. 예로서 일종의 단순한 절인 Q(A,f(B))는 Q(x,y)의 한 기초예시이다. 비교흡수방법을 쉽게 이해하는 방법은 이러한 기초절들에 어떻게 비교흡수방법이 적용되는가 살펴보는 것이 편리하다. 두 개의 기초절, P1 ∨ P2 ∨···PN 과 ~ P1 ∨ Q2 ···∨QM 이 있다고 하자. Pi와 Qi 모두 서로 다른 것이라고 가정한다. 이 두 개의 부모절 (par ent clause) 로부터 비교흡수절 (resolvent) 이라는 새로운 절을 논리적으로 유도할 수 있다. 이 비교흡수절은 두 개의 절에 대해 논리합을 취하면 P1 ∨ ~ P1 ∨ P2 ∨···∨ PN ∨ Q2 ∨···∨ QM 이 되며 여기서 보수쌍 (complementary pair) 인 P1 ∨ ~ P1 을 제거함에 의해 구해진다. 비교흡수방법의 흥미롭고 특수한 경우가 [표 5.1]에 있다. 다음에는 이런 단순한 규칙이 변수를 지닌 절들에는 어떻게 확장되는지 살펴보자.
[표 5.1]
|
부모 절들 |
비교흡수절 |
설명 |
|
P, ~P∨Q(즉 P⇒Q) |
Q |
모더스 포넨스 (modus ponens) |
|
P∨∨, ~P∨~Q |
Q |
이 비교흡수절을 합병 (merge) 이라 함 |
|
P∨Q, ~P∨~Q |
Q∨~Q, P∨~P |
두 개의 비교흡수절이 가능하며 이들은 모두 항상 만족되는 동치명제 (tautology) 들임 |
|
~P, P |
NIL |
모순 (contradiction)을 나타냄 |
|
~P∨Q(즉 P⇒Q), ~Q∨R(즉Q⇒R) |
~P∨R(즉 P⇒R) |
연결성 (chaining) |
변수를 지닌 절에 대한 비교흡수방법은 제4장의 단일화 과정에서 언급한 치환방법을 두 개의 부모절에 적용하여 이들이 보수문자 (complementary) 들을 서로 가지도록 함으로써 이루어진다. 공식화된 표현을 위해서 먼저 부모절을 문자들의 집합으로 표현한다면, 두 개의 부모절은 각기 {li}와 {mi} 는 각각 {Li}, {Mi}의 부분집합으로 {li}와 {~mi}의 합에 대한 가장 일반적 단일화 (이를 s라 하겠음)가 존재한다고 하자. 그러면 이제 두 개의 절 {Li}와{Mi}는 비교흡수되어 다음과 같은 비교흡수절이 유도되어진다.
{{Li} ㅡ {li}}s ∪ {{Mi} ㅡ {mi}}s
예로서 다음의 두 절에 대한 몇 개의 비교흡수절을 구해 보자
P[x,f(A)]∨P[x,f(y)]∨Q(y)
~P[z,f(A)]∨~Q(z)
여기서 {li} = {P[x,f(A)]}, {mi} = {~P[z,f(A)]}라 하면, 이의 비교흡수 절은 P[z,f(y)]∨ ~Q(z)∨Q(y)이 된다.
또한 {li} = {P[x,f(A)], P[x,f(y)]}, {mi} = {~P[z,f(A)]}라 하면 이의 비교흡수 절은 Q(A)∨ ~Q(z)이 된다.
두 개의 부모절로부터 유도되어진 비교흡수절은 또한 이 부모절에 논리적으로 뒤따르고 있음을 쉽게 보일 수 있다. 이를 기반으로 wff들의 집합 S에 논리적으로 뒤따르고 있는 모든 wff들은 이 wff집합 S에 비교흡수 부정방법을 적용해서 유도되어진다. 그러므로 정리 증명 시스템의 한 종류인 완전성을 지닌 비교흡수방법을 사용하는 비교흡수 부정 시스템의 이해는 이보다 더 효율적인 여러 정리 증명 시스템을 이해하는데 근본적인 기초를 제공하게 된다.
wff의 집합 S에 어떤 wff X가 논리적으로 뒤따른다는 것을 증명하기 위해 비교흡수를 이용하는 비교흡수 부정방법은 먼저 집합 S에 X의 부정인 ~X를 첨가하여 집합 P = S∪{~X}을 형성한다. 이제 이 새로운 집합 P로부터 비교흡수과정을 통해 유도되는 새로운 비교흡수절 Ri을 유도하고, 집합 P에 Ri를 추가하여 나오는 새로운 집합에 대해 다시 비교흡수를 행하는 과정을 반복한다. 이때 과정이 종결되는 시기는 새로이 유도되는 비교흡수절이 모순 (NIL로 표기함)을 나타내는 경우이며, 이로부터 wff X는 집합 S에 논리적으로 뒤따른다고 한다. 이와 같은 비교흡수 부정방법에 의해 정리 증명이 정당화되는 이유는 다음과 같은 논리로 설명된다.
wff들로 구성된 집합 S에 논리적으로 뒤따르는 wff X가 있다고 가정하자. 그러면, 가정에 의해 S을 만족하는 모든 해석 (interpretation) 은 또한 X을 만족한다. 이것은 S을 만족하는 어떠한 해석도 ~X을 만족하지 못한다는 사실과 같다. 그러므로 위의 언급한 모든 해석들은 S 와 {~X}를 동시에 만족시키지 못한다(여기서 어떤 해석에 의해서도 만족되지 않는 wff의 집합을 불만족 (unsatisfiable) 하다고 한다.).
실제적으로 X가 S에 논리적으로 뒤따른 wff라면 S∪ {~X}는 불만족하다. 만일 비교흡수과정이 불만족한 집합에 반복적으로 적용이 되면 결국에는 모순 (NIL) 이 유도되는 것을 보일 수 있다. 그러므로 만일 X가 S에 논리적으로 뒤따르면 비교흡수과정에 의한 S∪ {~X}의 집합으로부터 NIL절을 결국에는 유도하게 될 것이다. 역으로, 만일 NIL이 집합 S∪ {~X}로부터 유도된다면 X는 S로부터 논리적으로 뒤따른다는 것을 보일 수 있다.
비교흡수 부정방법을 하나의 예를 통해 살펴보자. 먼저 wff의 집합 S가 다음과 같다고 할 때, I(z)∧ ~R(z)이 S에 논리적으로 뒤따르는지를 증명하고 자 한다.
(1) ~R(x)∨L(x)
(2) ~D(y)∨L(y)
(3a) D(A)
(3b) I(A)
먼저 목표 wff인 I(z)∧ ~R(z)을 부정하여 아래의 형태와 같은 절을 구한다.
(4) ~I(Z)∧R(z)
(1)~(4)로 이루어진 집합으로부터 NIL의 유도에 이르는 동안의 비교흡수 과정을 나타내면 [그림 5.1]과 같은 트리 형태가 된다.
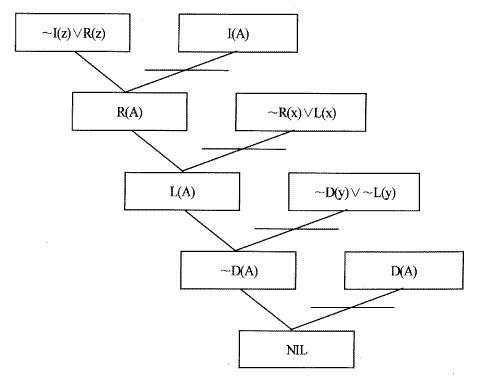
[그림 5.1] 비교흡수 부정 트리
많은 서술 논리 정리 증명 시스템에는 존재를 나타내는 변수가 결국 무엇으로 예시되는지 알고자 하는 경우가 있다. 예로서 기초집합 S에 논리적으로 뒤따르는 (∃x)W(x)가 있다면 x가 무엇으로 예시되는가 하는 것이다. 이를 해결하기 위한 과정을 예를 들어 살펴보자.
"JOHN이 가는 장소면 FIDO도 반드시 그 장소에 간다."는 사실이 주어졌을 때 "JOHN이 학교에 가면 FIDO는 어디에 가는가?"라는 질문이 있다고 하자.
이것은 다음과 같이 표현된다.
(∀x)[AT(JOHN,x)⇒AT(FIDO,x)], AT(JOHN, SCHOOL), (∃x)AT(FIDO,x)
여기서 증명하고자 하는 것은 목표 wff (∃x)AT(FIDO,x)에서 x가 무엇인가 하는 것이다. 이를 구하기 위해 (∃x)AT(FIDO,x)의 부정인 (∃x)~AT(FIDO,x)를 첨가하여 다음과 같은 기초집합이 형성된다.
~AT(JOHN,x)∨AT(FIDO,x), AT(JOHN, SCHOOL), ~AT(FIDO,x)
이 기초집합을 이용해 NIL을 유도하는 비교흡수 부정 트리는 [그림 5.2]와 같다.
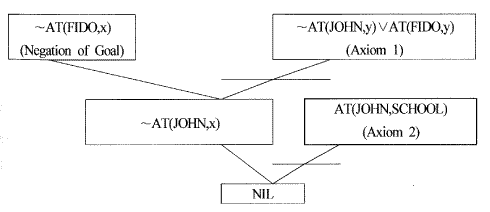
[그림 5.2] 비교흡수 부정 트리
그러나 (∃x)AT(FIDO,x)에서 x를 구하기 위해서는 ~AT(FIDO,x)를 다시 한번 부정한 AT(FID O,x)를 추가하여 논리합을 시킨다. 그러면 다음과 같은 기초집합이 되며 이로부터 위에서와 같은 절차를 거쳐 비교흡수를 행하며, 결국에는 NIL이 아닌 대답을 지닌 문장이 유도된다.
~AT(JOHN,x)∨AT(FIDO,x), AT(JOHN, SCHOOL),
~AT(FIDO,x)∨AT(FIDO,x)
위의 과정을 거친 대답 유도를 위한 트리는 [그림 5.3]과 같으며 AT(FIDO,SCHOOL)은 원하는 해답이 된다.
[그림 5.3] 수정된 증명 트리
전향 시스템은 사실의 집합으로 이루어진 초기의 전체 데이터베이스를 가진다. 이 사실들은 AND/OR형태라 불리어지는 암시적 표현 (⇒) 이 없는 서술 논리문 (predicate calculus) 으로 나타내어 진다. 예로서 어떤 wff를 AND/OR 형태로 전환하는 방법은 다음과 같다 :
(∃u)(∀v){Q(v,u)∧ ~[[R(v)∨P(v)]∧S(u,v)]}
위와 같은 wff에서 존재를 나타내는 존재한정기호 (∃) 는 스콜렘 함수에 의해 제거하고 전체한정기호 (∀) 는 생략하고 부정 심볼 (~) 은 이것의영역이 한 개의 문자에 이를 때까지 드모르강 법칙을 이용하여 바꾸면, 다음과 같은 표현으로 변한다.
Q(v,A)∧{[~R(v)∧ ~P(v)]∨~S(A,v)]}
여기서 사실 표현이 다음 AND결합에 같은 변수가 있지 않기 위해서 변수들을 표준화하면 다음과 같은 표현이 된다.
Q(w,A)∧{[~R(v)∧~P(v)]∨~S(A,V)}
AND/OR 형태의 표현은 ∧와 ∨ 심볼에 의해 연결된 문자들의 부표현 (subexpression) 들로 구성되어진다.
AND/OR 그래프는 AND/OR형태로 된 사실표현을 나타내기 위해 이용이 될 수 있다. 예를 들면, [그림 5.4]는 앞에서 만든 AND/OR 형태의 사실 표현을 나타내고 있다. OR결합에 관계된 부표현 (E₁∨ ∙∙∙∨Ek) 은 각 자식 노드들이 그들의 부모노드에 k-연결자로 연결이 되어져 표현이 되고 AND 결합에 관련된 부표현 (E₁∨ ∙∙∙∨En) 은 각 자식 노드가 그의 부모 노드에 1-연결자에 연결이 되어서 표현되어진다. 이리하면 AND/OR 그래프의 잎 (leaf) 노드는 사실표현 내에 존재하는 해당문자 (literal) 로 주어진다.
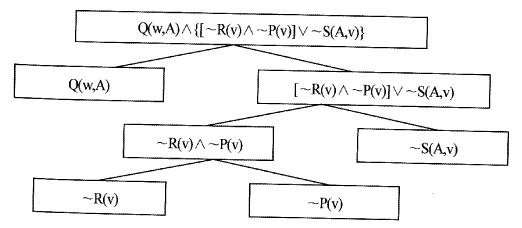
[그림 5.4] 사실 표현의 AND/OR 그래프의 변환
전방향 생성 시스템에 사용되는 규칙은 문제영역에 대한 일반적인 지식을 암시적인 wff로 표현한 것이다. 이러한 wff를 다음과 같이 제한된 형태로 구성하였다 하자. 즉,
L⇒W,
여기서 L은 한 개의 문자이고, W는 어떤 임의의 wff이다. 이러한 형태의 wff는 한정변수의 종류에 관계없이 암시적 심볼의 왼쪽에 국한된 한정변수를 먼저 "역"으로 하고, 그 다음에 모든 존재한정변수들은 스콜렘하여 한정변수의 영역이 전 범위에 걸치도록 하는 형태로 바꿀 수 있다. 예를 들면, 다음과 같은 wff는 이러한 단계를 거쳐 변환이 된다.
(∀x){[(∃y)(∀z)P[(x,y,z)]⇒(∀u)Q(x,u)}
(1) (일시적으로) 암시적 심볼 "⇒"을 없앤다.
(∀x){~[(∃y)(∀z)P[(x,y,z)]∨(∀u)Q(x,u)}
(2) 부정 심볼 "~"을 진행시켜 첫 번째 OR결합에 있는 첫 번째 문자에 관련된 한정 변수들을 "역" 으로 변환시킨다.
(∀x){(∀y)(∃z)[~P[(x,y,z)]∨(∀u)Q(x,u)}
(3) 존재한정변수를 스콜렘시킨다.
(∀x){(∀y)[~P(x,y,f(x,y))]∨(∀u)Q(x,u)}
(4) 모든 전체한정변수를 없앤다
~P(x,y,f(x,y))∨Q(x,u)}
(5) 암시적 심볼을 다시 나타낸다
P(x,y,f(x,y))⇒Q(x,u)
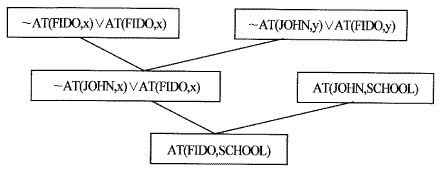
이러한 암시적 심볼을 가진 규칙이 여기서 어떻게 AND/OR 그래프에 적용이 되는지 살펴보자. 먼저 변수를 가지지 않는 서술식의 경우를 생각하면,L⇒W의 규칙이 있다고 할 때 사실 표현 F(L)을 나타내는 AND/OR 그래프에 L⇒W를 적용하여 새로운 사실 표현 F(W)로부터 생성되는 절 (clauses) 들을 나타나게 된다. 예를 들어 아래와 같은 규칙과 [그림 5.5]에 주어진 변수가 없는 AND/OR 그래프를 생각해 보자
[그림 5.5] 변수를 가지지 않는 AND/OR 그래프
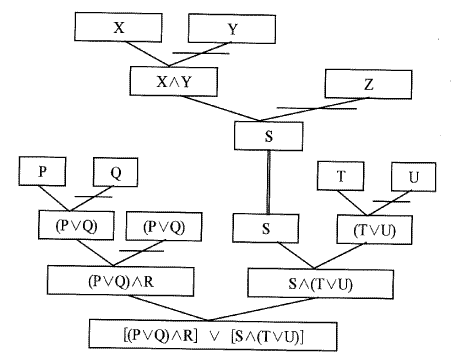
[그림 5.6] 규칙 적용 후의 AND/OR 그래프
[그림 5.5] 에 S로 명칭이 붙여진 노드는 S⇒(X∧Y)∨Z에 의해 새로운 형태의 AND/OR 그래프가 [그림 5.6]처럼 나타나게 된다. 이 때 S에 연결된 선을 비교선택 아크 (match arc) 라 한다.
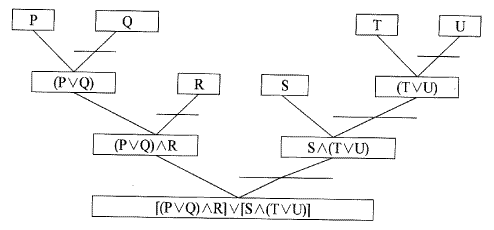
규칙 S⇒[(X∧Y)∨Z]은 다음과 같은 2개의 절 (clause) 로 생각될 수 있다.
~S∨X∨Z, ~S∨Y∨Z
주어진 사실 표현 [(P∨Q)∧R]∨[S∧(T∨U)]로부터 생성되는 절 (clause) 둘중에 S를 포함하는 절들은 다음과 같다.
P∨Q∨S, R∨S
이들과 위의 규칙에서 생성되는 절들을 비교흡수 (resolution) 하면 다음과 같은 네 가지 절들이 유도된다.
X∨Z∨P∨Q, Y∨Z∨P∨Q, R∨Y∨Z, R∨X∨Z
위의 모든 절들은 [그림 5.6]의 그래프의 잎 노드들로 구성되는 해결 그래프들로 나타내어진다.
이와 같이 AND/OR 그래프는 원래의 사실과 규칙이 적용된 후의 유도되는 사실들을 알아내는데 매우 유용한 도구로써 사용될 수 있다.
전방향 시스템의 목적은 주어진 사실과 규칙들로부터 어떤 목표 wff를 증명하는 것이다. 이 때의 목표 wff는 문자들의 OR결합 형태로만 제한되어진다. 이러한 제한은 나중에 설명되는 역방향 시스템과 복합되 시스템에서는 존재하지 않는다. 규칙 적용시와 마찬가지로 목표 문자는 AND/OR 그래프의 자손 노드로 첨가되어진다. 전방향 시스템은 목표 노드들로 이루어지는 해결 그래프를 포함하는 AND/OR 그래프가 생성될 때 성공적으로 끝난다.
후향 시스템은 목표 표현으로 아무런 제한도 받지 않는다. 전향 추론 시스템에서의 사실 표현의 전환과 유사하게 목표 표현의 wff를 AND/OR 형태로 먼저 전환시킨다. 즉, 먼저 ⇒심볼을 제거하고 부정 심볼을 움직이며, 전체 한정변수를 스콜렘 시키고, 존재한정변수를 삭제한다(한정변수의 변환이 전향 추론 시스템의 사실 표현의 경우와는 역이 되는 것을 유의할 것).
예를 들어 다음과 같은 목표 표현,
(∃y)(∀x){P(x)⇒[Q(x,y)∧ ~[R(x)∧S(y)]]}
은 아래처럼 전환이 된다.
~P(f(y))∨{Q(f(y),y)∧[~R(f(y))∨~S(y)]}}
변수를 표준화시키면 다음과 같다.
~P(f(z))∨{Q(f(y),y)∧[~R(f(y))∨~S(y)]}}
AND/OR 형태의 목표 wff들은 AND/OR 그래프로서 표현이 되어진다. 그러나 목표표현을 가진 k-연결자는 AND결합으로 연관된 부표현들을 분리하는데 이용이 된다. 위의 보기의 AND/OR그래프는 [그림 5.7]과 같다.
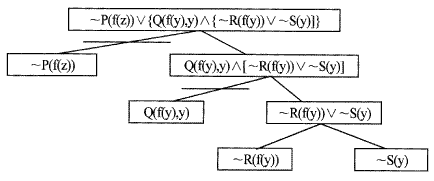
[그림 5.7] 목표 wff의 AND/OR 그래프의 표현
이 그래프의 잎 노드들은 목표 표현의 문자들에 의해 이름이 붙여져 있다. AND/OR 그래프에서, 루트 (root) 노드의 자손을 부목표 (subgoal) 노드라고 한다. 이 목표 wff로부터 생성되는 절들은 잎 노드에서 종결되는 해결 그래프를 따라가면서 유도할 수 있다. 즉,
~P(f(z)),
Q(f(y),y)∧~R(f(y)),
Q(f(y),y)∧~S(y).
목표절들은 문자들의 AND 결합이며 이 절들의 OR결합이 목표 wff를 나타낸다.
B-규칙의 형태는 다음과 같이 제한이 된다.
W⇒L,
여기서 W는 어떤 임의의 wff (AND/OR 형태에 있다고 가정함) 이고, L은 하나의 문자이다. 목표 wff를 나타내고 있는 AND/OR 그래프에 L과 단일화될 수 있는 L'로 이름이 붙은 문자 노드가 존재하면 위의 B-규칙을 적용할 수 있다. 이 규칙의 적용 후 나타나는 그래프는 L'노드로부터 비교선택 아크로 이어지는 새로운 자손 노드 L을 첨가한 형태가 되며, 이 새로운 노드는 u가 L과 L'의 가장 일반적 단일화 (mgu) 라 할 때 Wu에 대한 AND/OR 그래프의 루트 노드가 된다. 위의 설명은 앞에서 설명한 전향 시스템에서의 F-규칙의 적용시와 비교해 볼 때 반대 (duality) 의 성질을 지니고 있다.
후향 시스템에 의해 사용되는 사실 표현들은 문자들의 AND결합의 형태에 한정된다. 후향 시스템에서의 종결조건은 AND/OR 그래프가 사실 노드에서 끝나는 일치된 (consistent) 해결 그래프를 포함하는 것이다. 여기서 일치된 해결 그래프는 비교선택 아크의 치환들이 단일화 결합을 행하는 경우에 생긴다. 예를 들어 다음과 같은 사실과 규칙들이 있다고 하자.
F1: DOG(FIDO)
F2: ~BARKS(FIDO)
F3: WAGSㅡTAIL(FIDO)
F4: MEOWS(MYRTLE)
R1: [WAGSㅡTAIL(x1)∧DOG(x1)]⇒FRIENDLY(x1)
R2: [FRIENDLY(x2)∧ ~BARKS(x2)]⇒~AFRAID(y2,x2)
R3: DOG(x3)⇒ANIMAL(x3)
R4: CAT(x4)⇒ANIMAL(x4)
R5: MEOWS(x5)⇒CAT(x5)
이로부터 다음과 같은 목표 표현을 증명하고자 한다.
(∃x)(∃y)[CAT(x)∧DOG(y)∧ ~AFRAID(x,y)]
이 문제에서 일치되는 해결 그래프가 [그림 5.8]에 나타나 있다. 이 해결 그래프의 일치성을 보이기 위해 해결 그래프에 있는 비교선택 아크에 붙여진 모든 치환들로부터 단일화 결합을 시도한다.[그림 5.8]에서 ({x/c5}, {MYRTLE/x} , {FIDO/y}, {x/y2,y.x2}, {FIDO/y}, {FIDO/y}, {FIDO/y})의 단일화 결합을 해야 한다. 그 결과는 {MYRTLE/x5, MYRTLE/x, FIDO/y, MYRTLE/y2, FIDO/x2, FIDO/x1} 이 된다. 이 단일화 결합을 목표 표현에 적용시키면 다음과 같은 해답을 얻게 된다.
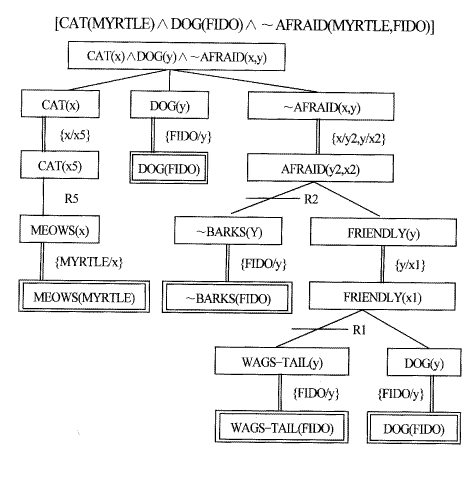
[그림 5.8] 후향 시스템의 일치되는 해결 그래프
전향과 후향의 규칙을 기초로 하나 추론 시스템 각각이 저마다의 한계를 가진다. 후향 시스템의 경우, 어떠한 임의의 형태의 목표 표현도 가질 수 있는 반면에 사실 표현은 문자의 AND결합이어야 한다. 전향 시스템의 경우, 어떠한 임의의 형태의 사실 표현도 가능하지만 목표 표현은 문자들의 OR결합이어야 한다. 그러면 위에서 말한 전향과 후향 시스템에서 나타나는 장점만을 가지는 시스템을 생각해 볼 필요가 있다.
둘을 결합한 시스템의 전체 데이터 베이스는 두 개의 AND/OR 그래프 구조를 가지며, 하나는 목표를, 하나는 사실을 나타낸다. 이 구조들은 앞에서 언급했듯이 Bㅡ규칙과, Fㅡ규칙에 의해 각각 수정이 되어진다. 이 결합된 시스템은 종결조건이 복잡하게 되는데. 종결이 되는 순간은 그래프에서 비교선택되는 모든 문자 노드들이 단일화되어지는 순간이다. 두 그래프 사이의 모든 가능한 비교선택이 이루어진 후, 목표 그래프의 루트 노드에 있는 표현이 사실 그래프의 루트 노드에 있는 표현과 규칙으로부터 증명이 되는지를 결정해야 한다. 이것이 증명될 때 결합된 시스템은 종결이 된다. 이 종결조건은 사실 노드와 목표 노드가 CANCEL될 때 이루어진다. CANCEL은 다음과 같이 순환적으로 정의된다.
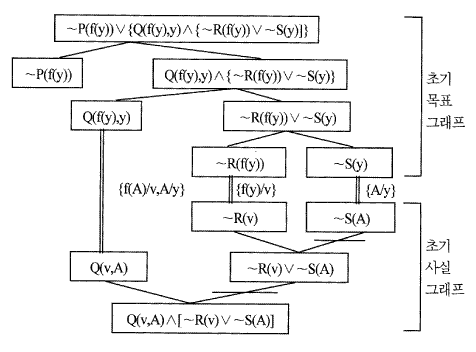
[그림 5.9] CANCEL 그래프의 예
1. n이 사실 노드이고 m이 목표 노드일 때 두 개의 노드 n과 m은 CANCEL 될 수 있다.
2. n 과 m이 단일화되는 문자들에 의해 주어졌거나 또는 n이 그의 자식들의 노드 {si}에 k-연결자를 가지고 연결되어 있을 때 각각의 si노드가 m과 CANCEL될 수 있다면 두 개의 노드n과 m은 CANCEL될 수 있다.
예로서 [그림 5.9]의 굵은 선은 사실 노드와 목표 노드가 CANCEL되는 과정을 보여준다.
생성 시스템은 처음 Post(1943)에 의해서 제안되었지만 그 동안 이론적인 측면에서나 응용시스템에서나 많은 발전을 해왔기 때문에 현재의 생성 시스템은 Post의 제안과 비교해서 공통적인 점이 거의 없다. 의미망이 노드와 아크라는 개념에 기반을 둔 많은 서로 다른 지식 표현 기법을 의미하듯이 생성 시스템이라는 용어도 생성규칙 (production rules or productions) 이라 불리우는 조건ㅡ행동 쌍 (conditionㅡaction pair) 이라는 용어에 기반을 둔 서로 다른 많은 시스템을 지칭하는데 사용한다. 이 장에서는 간단한 예를 통해 생성 시스템을 설명하고 생성 시스템의 제어 방법과 생성시스템의 구조에 영향을 미치는 여러가지 설계 결정 문제 (design decision problem) 를 다루어 본다.
생성시스템은 세 부분으로 구성되어 있다. (a) 생성규칙을 구성하는 규칙 베이스 (rule base),(b) 버퍼형태를 띤 자료구조: 맥락 (contest) 또는 작업 메모리 (working memory) 라고 한다. (c) 번역기 (interpreter): 시스템의 작동을 제어한다. 보통 추론 엔진 (inference engine) 이라 불린다. 이 세 부분을 간략히 설명한 후 예를 하나 살펴보도록 한다.
생성 규칙은 대체로 다음과 같은 형태를 띤 문장이 된다. "IF 조건 만족, THEN을 키워드로 사용하여 하나의 규칙을 표현한다. 예를 들어 다음과 같은 규칙을 생성규칙의 표현 형태를 따라 표현해보자.
규칙:
"Always punt of fourth down with long yardage required"
생성규칙:
"IF it is fourth down AND long yardage is required THEN punt"
여기서 IF부분은 조건부 (condition part) 또는 Left Hand Side (LHS) 라고 불리는데 그 생성 규칙이 실행되기 위해서는 반드시 존재해야 하는 조건을 의미한다. 그리고 THEN 부분은 실행부 (action part) 또는 Right Hand Side(RHS) 라 불리는데 IF 부분이 만족되었을 때 실행할 행동을 나타낸다. 생성 시스템이 수행되는 도중에 조건부가 만족되는 생성 규칙은 번역기에 의해서 실행될 수가 있다. 물론 반드시 실행되는 것은 아니다. 왜냐하면 여러 개의 생성규칙이 동시에 조건부를 만족시킬 수 있기 때문이다. 나중에 설명할 예는 매우 간단하기 때문에 생성 규칙이 몇 개 되지 않지만 대부분의 큰 시스템의 경우는 수백 개의 생성 규칙을 포함하고 있다.
작업 메모리는 생성 규칙의 조건부를 만족시킬 정보를 저장하고 있는 부분이다. 즉 생성 규칙이 실행되기 위해서는 이 생성 규칙의 조건부가 작업메모리에 있는 내용과 일치해야 한다. 예를 들면 위에서 제시한 생성 규칙의 예에서는 "It is fourth down and yardage is required." 라는 내용이 작업 메모리에 존재하면 그 규칙이 실행된다. 생성 규칙의 실행부는 작업메모리의 요소를 변화시킬 수 있다. 그렇게 함으로써 다른 생성 규칙의 조건부가 만족될 수 있도록 한다. 이 작업 메모리는 간단한 array로 이루어질 수도 있고 그 내부에 특별한 자료 구조를 가질 수도 있다.
마지막으로 번역기에 대해 설명한다. 이 번역기는 다른 시스템에서의 번역기와 마찬가지로 다음에 해야 할 일을 선택하는 역할을 한다. 또한 여러 개의 생성규칙이 동시에 조건부를 만족하고 있는 경우 그들 중 하나를 선택하는 역할도 한다.
위의 설명을 바탕으로 생성시스템의 한 예를 들어보자. 스무 고개 놀이에서와 같은 방식으로 질문을 던진 후 주어진 대답을 바탕으로 음식물의 종류를 알아내는 시스템을 생각해보자. 여기서의 작업 메모리는 단순한 심볼의 list 이다. 이를 CL(context list) 라 부르자. 그리고 "OnㅡCL X" 는 "작업 메모리에 현재 X가 존재한다" 라는 의미로 사용한다. 이 시스템은 다음과 같은 규칙베이스와 번역기를 가지고 있다.
생성 규칙:
P1. IF OnㅡCL green THEN PutㅡOnㅡCL produce
P2. IF OnㅡCL packed in small container THEN PutㅡOnㅡCL delicacy
P3. IF OnㅡCL refrigerated OR OnㅡCL produce THEN PutㅡOnㅡCL perishable.
P4. IF OnㅡCL weighs 15 lbs AND OnㅡCL inexpensive AND NOT OnㅡCL perishable THEN PutㅡOnㅡCL staple
P5. IF OnㅡCL perishable AND OnㅡCL weighs 15lbs THEN PutㅡOnㅡCL turkey
P6. IF OnㅡCL weighs 15 lbs AND OnㅡCL produce THEN PutㅡOnㅡCL watermelon
번역기 :
S1. 조건부가 참이 되는 모든 생성 규칙을 찾고 이를 적용할 수 있는 상태라고 표시한다.
S2. 만약 하나 이상의 생성 규칙을 적용할 수 있으면 CL에 중복되는 심볼을 생성하여 넣는 규칙은 적용가능한 생성 규칙에서 제외시킨다.
S3. 적용가능한 생성 규칙들 중 번호가 가장 작은 생성 규칙의 실행부를 실행시킨다.
S4. 모든 생성 규칙의 적용가능 상태를 취소시키고 다시 S1으로 되돌아 간다.
여기에서 조건부는 스무 고개의 질문에 해당하고 실행부는 질문에 대한 답을 토대로 새로이 생성된 지식에 해당한다.
생성시스템은 위의 번역기의 예에서 보이듯이 계속적인 순환의 과정 속에서 자신의 역할을 수행해 나간다. 매 순환 과정에서 번역기는 생성 규칙을 조사하여 적용가능한 것을 골라내고 이런 생성 규칙이 하나 이상이 발견될 경우 그 중 하나를 선택한다. 그리고 마지막으로 선택한 규칙을 실행시킨다. 이 순환에서의 세 가지 단계를 각각 비교 (matching), 충돌 해결 (conflict resolution, select), 실행 (action, execute) 이라 한다. 참고로 이 추론 수행 과정을 그림으로 표현하면 [그림 6.1]과 같다.
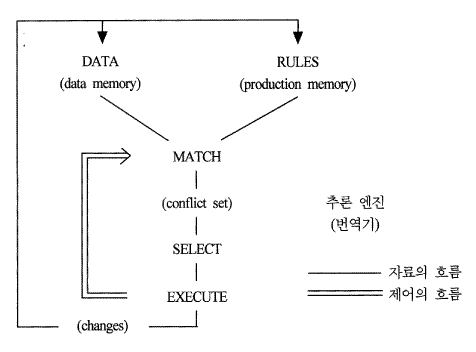
[그림 6.1] Rete 추론 기관
이제 실제 데이터를 가지고 위 생성 시스템의 추론이 어떤 식으로 수행되는지를 알아보자. 우선 문제의 음식물에 대한 초기 정보가 음식물의 색깔이 녹색 (green) 이며 무게는 15파운드 (15 lbs) 라고 하자. 즉 첫 번째 순환에 들어가기 전에 작업 메모리 리스트에 존재하는 값들이 다음과 같다는 의미이다.
CL={green, weighs 15 lbs}
첫 번째 순환은 우선 번역기 알고리즘의 step 1을 수행하는 것에서부터 시작한다. 즉 조건부가 다 만족되는 모든 생성 규칙을 찾아낸다. 현재의 CL에 존재하는 정보에 만족되는 것을 P1뿐이다. 따라서 여러 개의 생성 규칙 중에서 하나를 선택하는 step 2는 불필요하다. 이제 step 3에서는 P1의 실행부가 실행되도록 한다. 이 생성 규칙은 CL에 "produce" 라는 심볼을 첨가한다. 이 심볼은 문제의 음식물에 대한 새로운 사실을 의미한다.
CL={produce, green, weighs 15 lbs}
step 4는 첫 번째 순환을 끝내고 제어를 step 1으로 돌려준다. 여기에서는 다시 적용가능한 모든 생성 규칙을 찾아낸다. 두 번째 순환에서는 생성 규칙 P1, P3, P6가 적용가능하다. 여러 개의 생성 규칙이 적용가능하므로 step 2에서는 이 중 CL에 중복되는 심볼을 첨가하게 되는 생성 규칙을 찾아내어 제외시킨다. 따라서 P1이 제외된다. 다음 step 3에서 적용가능한 생성 규칙들 중 번호가 가장 작은 P3를 선택하여 실행시킨다. 생성 규칙 P3의 수행 결과로서 CL 은 다음과 같다.
CL={turkey, perishable, produce, green, weighs 15 lbs}
세 번째 순환에서는 적용가능한 생성 규칙이 P1, P3, P5, P6 이다. 이 중 step 2에서 제외되는 생성 규칙은 P1, P3이다. 그리고 step 3에서 선택되는 생성 규칙은 P5이다.
CL={trukey, perishable, produce, green, weighs 15 lbs}
이 과정에서 turkey 라는 심볼이 생성되었는데 이는 CL상에서 일종의 오류를 나타내고 있다. 즉 우리는 규칙 베이스를 만들 때 우리가 알고 있는 녹색 (green) 인 어떤 음식이 turkey를 생성 (produce) 한다는 의미를 의도하지는 않았기 때문이다. 이 후 두 번의 순환으로 이 시스템의 수행은 종결되는데 그 과정에서 watermelon 이라는 심볼이 CL에 첨가된다. 그리고 step 3에 까지 남아 있는 생성 규칙이 존재하지 않기 때문에 수행이 종결된다.
CL={watermelon, turkey, perishable, produce, green, weighs 15 lbs}
만약 우리가 결론으로 선택할 심볼을 CL상에서 맨 처음 나온 심볼로 정하면 중간에 오류를 발생했던 turkey와는 상관이 없이 watermelon이 결론으로 선택된다. 이때 독자나 또는 이 시스템 개발자는 규칙 베이스를 수정하여 이 오류를 고칠 수 있는 방법을 생각해 볼 수 있다. 즉 새로운 규칙을 첨가하거나 규칙의 순서를 바꿀 수도 있고, P5의 조건부에 새로운 조건은 더 첨가할 수도 있다. 이런 식으로 규칙베이스를 유지관리하는 편리성 때문에 다른 지식 표현방법을 이용하는 시스템보다 생성 시스템이 널리 사용되고 있다.
위에서 제시한 번역기의 알고리즘은 다소 특수한 것이라고 할 수 있다. 충돌 해결 (conflict resolution) 방법이나 이후 결론을 선택하는 방법이 어떤 특수한 영역에서만 적용될 수 있다는 의미이다. 이제는 생성 시스템이 수행되는 좀 더 일반적인 절차에 대해 살펴보자.
프로시쥬어 PRODUCITON
1. DATA ← 초기 데이터베이스
2. DATA가 종결 조건을 만족할 때가지 단계 3 ~단계 6을 반복 수행한다.
3. begin
4. DATA에 적용가능한 규칙들 중에서 한 규칙 R을 선택한다.
5. DATA ← (DATA에 규칙 R을 적용한 결과)
6. end
위의 프로시쥬어는 단계 4에서 적용할 규칙을 어떻게 선택할 것인지에 대해 명확히 언급되어 있지 않다. 생성 시스템에서 제어방법의 형성이란 규칙을 선택하고 동시에 수행과정에서 여태까지 적용되어온 일련의 규칙과 이것들에 의해 유도된 데이터베이스를 유지함을 말한다.대부분의 인공지능 응용에 있어, 제어방법을 위한 정보는 충분한 것이 아니어서 위의 프로시쥬어에서 단계 4를 매번 수행할 때, 여러 규칙들 가운데 어느 규칙이 가장 적절한 규칙인가를 완벽히 결정하지 못한다. 그러므로 인공지능 생성 시스템의 수행과정은 종결 조건을 만족하는 데이터베이스를 유도하는 일련의 규칙들이 발견될 때까지 규칙을 적용해 가는 탐색과정 (search process) 이라 할 수 있다.
제어 방법은 크게 두 가지 종류로 분류된다 : 과정 회복 불가능한 (irrevocable) 제어 방법과 과정 회복 가능한 (tentative) 제어 방법을 들 수가 있다. 과정회복 불가능한 제어 방법에서는 적용할 규칙이 일단 선택되어 적용이 되어 버리면 나중에 이 상황으로 다시 올 수 없다. 과정 회복 가능한 제어방법에서는, 규칙이 선택되어(무작위이거나 어떤 이유로 인해서나 간에) 적용이 되어도 나중에 이 상황으로 다시 되돌아와서 다른 규칙의 적용이 가능하다.
과정회복 가능한 제어방법은 두 가지 형태의 역행 (backtracking) 방법과 그래프 탐색 (graph search) 방법이 있다. 역행 방법에서는 한 규칙이 선택될 때 역행점 (backtracking point) 이 설정된다. 그래서 차후 계산에서 해결책 유도의 어려움이 발견되면 이 역행점으로 계산상태를 되돌려 다른 규칙을 적용함에 의해 과정을 진행시킨다. 그래프 탐색방법에서는 여러 개의 규칙들에 의한 효과를 동시에 추적할 수 있도록 되어 있으며 이들이 다루어지는 제약에 따라 여러 구조의 그래프들과 그래프 탐색 방법이 있게 된다.
이러한 제어 방법을 설명하기 위해 인공지능 생성시스템의 예로서, 간단한 퍼즐 (puzzle) 문제를 해결하는 방법을 살펴보기로 한다.
여러 인공지능 응용 시스템들은 일련의 동작들을 요구하게 된다. 로봇의 동작 조정과 자동 프로개밍이 이러한 예들이다. 이런 종류의 간단하고 낯익은 문제로써 기본적인 개념을 잘 나타내는 8-퍼즐 문제가 있다. 8-퍼즐 문제는 3행과 3열로 이루어진 (3 x 3) 틀에 이동이 가능한 8개의 숫자타일들로 구성되어 진다.
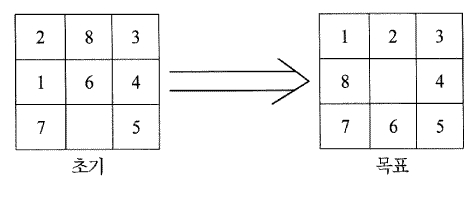
[그림 6.2] 8-퍼즐의 초기 및 목표 배열 형태
틀 내의 한 부분은 항상 비어 있어서 바꾸어 말하면 공백 타일과 인접된 어느 숫자 타일과의 자리교환이 가능하다. 이와 같은 퍼즐은 [그림 6.2]에서 두 가지 배열 형태로 주어져 있다. 초기 배열 형태를 목표 배열형태로 변환시키기 위한 문제의 해결책은 타일 6을 아래로 내리고 타일 8을 아래로 내리며 그 다음에 타일 2를 오른쪽으로 이동시키고, 그 다음에 타일 1을 위로 옮기며 마지막으로 타일 8을 왼쪽으로 옮김에 의해 이루어진다.
이 문제를 생성 시스템을 사용해서 해결하기 위해서는 전체 데이터베이스와 규칙들 그리고 제어 방법을 명시해야 한다. 어떤 주어진 문제 설명을 생성시스템의 이러한 세 가지 요소로 전환하는 것을 인공지능에서는 표현문제 (representation problem) 라 흔히 부른다. 문제를 표현하는 데는 여러 방법이 있을 수 있다. 그러나 좋은 표현방법을 설정하는 것은 실제 문제에 인공지능 기법을 적용하는데 있어서 고려해야 할 중요한 작업 중의 하나이다.
8ㅡ퍼즐을 포함하는 특정부류의 문제들에 대해서는, 이 세 가지 요소들과 대응되는 문제의 요소들을 쉽게 유도할 수 있다. 이들 요소란 문제 상태 (state), 이동 (move), 목표 (goal) 이다. 8ㅡ퍼즐 문제에서 각 타일들의 배열된 정체 형태가 문제 상태이다.
이러한 모든 가능한 배열 형태들로 이루어진 집합은 이 문제의 문제 공간 (problem space) 이 된다. 관심이 되는 대부분의 문제는 매우 큰 문제공간을 가지고 있다. 그러나 8-퍼즐 문제는 비교적 작은 문제공간을 가진다. (단지 362,880=9! 개의 상태가 존재함 : 이 공간은 각각 9!/2상태들의 공간인 두 개의 겹치지 않는 부공간 (subspace) 으로 분할되어 질 수 있다.).
일단 문제 상태들이 개념적으로 확인되면 이들을 컴퓨터 표현으로 구성해야 한다. 이 표현은 생성 시스템의 전체 데이터베이스(작업메모리라고 할 수 있다)로 이용되며, 8-퍼즐에서는 3 X 3 행렬로 주어질 수 있다. 초기 전체 데이터베이스는 초기 문제상태에 대한 이러한 표현이다. 상태를 표현하기 위해서는 문자열 (string), 벡터 (vector), 집합 (set), 트리 (tree), 리스트 (list),등 어떠한 데이터 구조도 사용될 수 있다. 8-퍼즐에서처럼, 데이터 구조의 형태가 해결하고자 하는 문제의 외형과 매우 유사한 경우도 있다.
이동 (move) 은 한 문제 상태에서 다른 문제상태로 변형시키는데, 8-퍼즐의 경우는 빈 공간 (공백 타일)을 상, 하,좌, 우의 네 가지 이동을 갖는 것으로 해석된다. 이들 이동들은 주어진 상태 표현 상에서 운용되는 생성규칙들로 적절히 정형화되어 진다. 생성규칙들 각각이 상태표현에 적용가능하기 위해서 만족해야만 하는 전제조건을 가지고 있다. 따라서 빈 공간을 위로 옮기라는 규칙에 대한 전제조건은 빈 공간이 문제상태에서 가장 윗줄에 있어서는 안 된다는 요구조건에서 유도되어진다.
8-퍼즐 문제에서는 하나의 특정한 문제상채(목표 상태)를 명시하게 된다. 어떤 문제에서는 여러 개의 목표 상태들을 명시하고 이들 가운데 하나를 해결하는 것을 목표로 하는 경우도 있다. 좀더 일반화하여 상태에 관한 참 거짓 조건을 목표 조건 (goal condition)(종결 조건 (termination condition) 이라고도 함)으로 명시할 수 있다. 그러면 문제 목표란, 이 종결 조건을 만족하는 어떠한 상태에 이르는 것이 된다. 이러한 종결 조건은 암시적으로 목표 상태들로 이루어지는 집합을 정의하게 된다. 이제까지 설명한 상태, 이동 그리고 목표라는 개념에 의해 문제 해결의 정의를 초기상태에서 목표 상태로 변환시키는 일련의 이동을 유도하는 것이라 할 수 있다.
제어 시스템은 목표 상태 표현이 유도될 때까지 상태표현에 규칙들을 계속 적용하며 동시에 적용되어 온 규칙들을 유지하고 있음으로 해서 나중에 수행 종결이 이루어진 후 문제해결에 이르기까지의 적용되어온 규칙순서를 알게끔 한다.
어떤 문제에 대해서는 해결에 이른 결과가 여분의 어떤 제약조건을 가져야만 하는 경우도 있다. 예를 들어, 8-퍼즐 문제에서 이용횟수를 최소화하는 해결책을 원할 수도 있다. 일반적으로 각 이동에는 이동 적용에 대한 비용 (cost) 이 주어지며, 문제 해결경로로서 최소비용의 해결경로를 요구하는 문제도 있다.
과정회복 불가능한 제어방법은 탐색에 의한 문제를 해결하려는 생성 시스템에는 부적합한 것으로 보일 수도 있다. 예를 들어 퍼즐 문제를 해결하는 데는 시행착오적 (trial-and-error) 방법이 적격일 수 있다. 또한 생성 시스템의 제어방법이 각 상태표현에 적용할 규칙을 아주 완벽히 선택할 만큼 충분한 지식을 제공받는다면, 퍼즐 문제는 이미 해결되어져 있다 해도 무방하다 할 수도 있다. 그러나 이러한 주장은 어떤 상태에서 목표 상태로 어떻게 수행이 진행되어야 하는가에 대한 명확히 나타난 국부적 (local) 지식과 위에서 말한 완전한 해결의 암시된 전체 지식과의 차이를 인식하지 못한데서 비롯된다. 확실한 국부적 지식의 사용이 가능하다면 과정회복 불가능한 생성 시스템은 이것을 사용해서 해결의 명확한 전체 지식을 형성할 수 있게 된다.
전체해결을 형성하기 위해 국부적 지식을 이용하는 가장 흔한 예의 하나로 함수의 극대값을 구하는 언덕-오르기 (hill-climbing) 과정을 들 수 있다. 수행과정의 어느 지점에서도 가장 가파른 각도의 방향으로 수행이 진행되게 된다. 언덕-오르기 과정이 과정회복 불가능한 생성 시스템에 직접 적용되기 위해서는 단지 전체 데이터베이스에 어떤 실수값 함수만 설정하면 된다. 제어방법은 규칙을 선택하는데 이 함수를 사용한다. 즉 함수의 값을 가장 크게 증가시켜 주는 데이터베이스를 생성하는 적용가능한 규칙이 선택(회복 불가능하게)된다. 여기서 언덕-오르기 함수는 종결조건을 만족하는 데이터베이스에 대해 극대값을 갖는 것이어야 한다.
[그림 6.3] 8-퍼즐 문제에서의 상태들의 함수 값
|
목표 상태 |
|
초기 상태 |
||||
|
1 |
2 |
3 |
|
1 |
2 |
5 |
|
|
7 |
4 |
← |
|
7 |
4 |
|
8 |
6 |
5 |
|
8 |
6 |
3 |
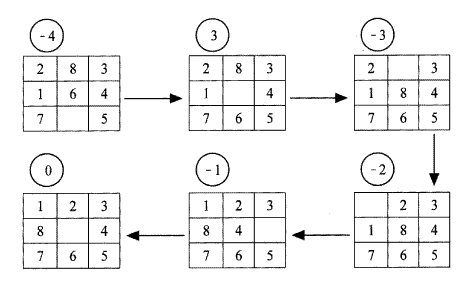
언덕-오르기 과정을 8-퍼즐 문제에 적용하고자 할 때, 상태표현의 함수로 이 상태와 목표 상태를 비교해서 놓인 위치가 일치하지 않는 타일의 갯수에 음수기호(-)를 붙인 것으로 정할 수 있다. 예를 들어,[그림 6.3]의 초기 상대에서 함수값은 -4이고 목표 상태에서는 0이되며, 그 외 어떤 한 상태에서도 이 함수값을 쉽게 계산할 수 있다.
초기 상태로부터 다음 단계에서 가장 증가된 값을 얻기 위해서는 공백 타일을 위로 이동시킴에 의해 이루어진다.[그림 6.3]에서 이러한 과정 반복이 목표 상태에 이를 때까지(이 때는 함수 값이 최고값이 된다) 계속된다.[그림 6.3]에서 보듯이 어떤 단계에서는 함수값이 증가되지 않았다. 적용가능한 어떠한 규칙도 함수값을 증가시키지 않을 경우에는 함수값을 감소시키지 않는 규칙을 선택한다. 만일 이러한 규칙이 없다면 언덕-오르기 과정은 멈추게 된다.
[그림 6.3]의 8-퍼즐 문제에서 보듯이, 언덕-오르기 제어방법의 사용은 목표 상태에 이르는 경로를 구하게 한다. 그러나 일반적으로 언덕-오르기 함수들은 다수의 국부적 극대값을 가질 수 있으므로 언덕-오르기 과정이 실패로 멈추는 수도 있다. 예를 들어 목표 상태와 초기 상태가 다음과 같다고 가정 하자.
이 경우에 초기상태에 어떠한 규칙이 적용되어도 언덕-오르기 함수값은 감소된다. 이러한 현상은 초기상태의 함수값이 국부적 극대값(전체의 극대값 아님)을 가지고 있음을 의미한다.
언덕-오르기 과정이 실패할 수도 있는 또 다른 이유가 있다. 함수값이 평원 (plateau) 혹은 산등성이 (ridge) 에 도착했을 때이다. 이러한 난점은 더 효과적인 언덕-오르기 함수, 예를 들어, 단 하나의 전체 극대값만 가지며 평원이 존재하지 않도록 하는 함수를 고안해 낸다면 해결될 수 있다. 인공지능에 관계되는 문제들에서 쉽게 계산될 수 있는 함수들은 대개 위에서 언급한 몇 가지 난점들을 가지고 있다. 그러므로 과정 회복 불가능한 생성 시스템에서 규칙 선택을 결정하기 위해 언덕-오르기 방법의 사용은 아주 제한된 문제에 한하게 된다.
그러나 비록 제어방법에 의해서 각 단계에서 항상 가장 유망한 규칙이 선택되기는 불가능할지라도 과정 회복 불가능한 제어방법이 적절한 경우가 있다. 부적절한 규칙으로 판명된 규칙을 적용해 버렸다고 해서 차후 적절한 규칙들이 적용되는데 방해를 주지 않는다면, 과정회복 불가능한 규칙 적용을 하는데 아무런 (과다한 규칙적용이 아닌) 위험부담이 없다.
많은 종류의 문제에서 부적절한 규칙이 적용되면 성공적인 종결이 안되거나 또는 상당한 지연을 가져오게 된다. 이러한 경우에는 규칙 적용을 시도해봐서 나중에 이 규칙 적용이 적절한 것이 아니었다고 판명되면 원래 위치에 되돌아 와서 다른 규칙을 재시도 해볼 수 있도록 하는 제어방법이 필요하다.
역행 방법은 과정 회복 가능한 제어 방법의 한 종류로써, 어떤 규칙이 선택되어 이 규칙이 해결점에 이르지 못하면 지금까지 시행단계를 무시하고 다시 이 지점으로 되돌아와서 다른 규칙을 선택하여 시도하게 된다. 역행 방법은 규칙 선택을 위해 정보로 제공받는 양에 관계없이 이용될 수 있다. 만일 아무런 정보도 제공받지 않을 경우 규칙선태근 무작위 (random) 로 이루어 진다. 그러나 결국에는, 합당한 규칙이 선택될 때까지 제어가 역행을 반복하게 될 것이다. 적절한 규칙 선택에 도움을 줄 수 있는 정보를 제공받은 제어는 훨씬 적은 역행이 이루어진다. 따라서 전체 수행과정은 더 효율적이 된다. 예를 들어 8-퍼즐 문제에서, 규칙 선택을 위한 수단으로 언덕-오르기 함수를 사용할 수 있다. 과정 회복 불가능한 제어에서는 국부 극대값에 봉착하는 수도 있지만, 역행 제어에서는 역행에 의해 다시 다른 경로를 추적해 갈 수 있다.
그러나 역행제어를 사용하는데는 기억용량에 대한 문제점이 있다. 즉 역행점이 설정될 때마다 그 순간의 작업메모리의 상태를 저장해야 하기 때문이다 또한 연속적으로 역행점이 설정되어 동시에 저장해야 할 작업메모리의 양이 증가할 경우는 더욱 큰 문제가 발생한다. 이를 해결하기 위해서는 작업메모리를 전부 저장하는 것이 아니라 규칙 적용 전 후의 변화된 상황만을 저장하는 방법을 사용할 수 있다. 그러나 어쨌든 하나의 작업메모리만을 사용하는 데 비해서는 많은 기억장소를 필요로 한다.
생성 시스템을 구성하기 위한 또 하나의 조건이 종결 조건을 결정하는 것이다. 앞에서 제시한 두 가지 예(음식물 이름 맞추기와 8-퍼즐 문제)에서는 서로 다른 종결 조건을 가지고 시스템이 수행된다는 것을 눈치 빠른 독자는 아시리라 생각된다. 즉 첫 번째 경우는 더 이상 적용할 규칙이 없는 경우 종결이 되는 것이 되고, 두 번째 경우는 더 이상 적용할 규칙이 없거나 또는 목표에 도달했을 경우이다. 또 하나의 종결조건으로 생각할 수 있는 것은 어떤 특정한 규칙이 실행될 경우로서 이 경우는 보통 그 규칙이 추론의 결과를 출력하는 것으로 끝난다. 이러한 종결 조건의 차이는 여러 원인에 의해 발생한다. 원하는 결과가 어떤 종류인가에 따라 달라지거나 또는 문제 표현이 다름에 따라 같은 결과를 원하는 시스템이라 할지라도 다른 종결 조건을 가질 수 있다. 이에 아래에서는 문제 표현에 대해 설명한다.
효율적인 문제 풀이는 효율적인 제어방법뿐만 아니라 문제 상태, 규칙, 종결 조건 등이 어떻게 표현되어지는 가에도 영향을 받는다. 어떤 문제 표현은 그 문제의 해결에 필요한 노력에 매우 중대한 영향을 미친다. 분명히 작은 상태 공간을 지닌 표현이 바람직하다. 외면상으로는 어려운 문제인 것 같지만 적절히 표현한다면 매우 작은 상태공간을 지닌 문제가 되는 예가 많다. 흔히 어떤 규칙은 제거 가능하고 또 어떤 규칙들은 서로 결합하여 질 수 있다는 사실을 인식할 수 있다면 주어진 상태공간이 축소될 수도 있다. 또한 이러한 간단한 변형이 이루어질 수 없는 경우라 하더라도, 문제를 완전히 재구성함으로써(예를 들어 상태라는 개념자체를 변경시킴) 보다 작은 상태곡간을 이루게 할 수 있는 경우도 있다.
처음에 문제를 표현하고 이 표현을 향상된 표현으로 전환시켜가는 과정에 대해 따라야 하는 분명한 기준은 아직 정해져 있지 않다. 문제 표현에 있어서의 바람직한 전환은 아마도 주어진 표현으로 문제를 해결하려는 노력에서 얻어지는 경험에 좌우된다 할 수 있다. 이러한 경험은 예를 들어 대칭성 또는 연속적으로 자주 적용되는 일련의 규칙들의 매크로 (macro) 규칙 형성 등을 인식함에 의해 개념들의 단순화를 이루게 한다. 예를 들어 8-퍼즐 문제의 처음 표현은 다음과 같은 32개의 규칙을 명시할지도 모른다.: 1번 타일을 왼쪽으로 이동, 1번 타일을 오른쪽으로 이동, 1번 타일을 위로 이동, 1번 타일을 아래로 이동, 2번 타일을 왼쪽으로 이동 등이다. 물론 이들 규칙들 중의 대부분은 어떠한 주어진 상태표현에 결코 적용되지 않는다. 그러므로 이러한 사실이 인식된다면 좀 더 나은 표현방식으로 (예를 들어 공백 타일(빈 공간)의 이동) 전환될 수 있다.
생성 시스템은 의료 진단이나 언어 이해 또는 광물 탐사 같은 실세계의 일에 대한 지식을 표현하는데 쓰여져 왔다. 특히 심리학에서는 생성 시스템을 자극과 반응 (stimulus and response) 이라는 생성 규칙의 특성을 이용하여 인간 행동을 모델화라는 유용한 도구로서 사용해 왔다 (Aderson and Bower, 1973). 이러한 생성 규칙을 이용하는 인공지능 시스템은 매우 다양한 범위에 걸쳐 존재한다. 그러나 일반화시킬 수 있는 여러 장점과 단점 등 그 특성을 알아보자.
생성 시스템의 매우 분명한 장점중의 하나는 지식 베이스 내의 개개의 생성 규칙들이 서로 독립적으로 첨가되고 제거되고 수정될 수 있다는 점이다. 즉 그 규칙들은 서로 독립적인 지식의 한 조각처럼 존재한다는 의미이다. 하나의 생성 규칙을 변화시키는 것은 비록 그것이 시스템 전체의 성능을 변화 시킨다 할지라도 다른 생성 규칙에 직접적으로 영향을 끼치지는 않는다. 왜나하면 규칙들 사이의 상호작용은 작업메모리에 저장되어 있는 정보를 통해서 다른 생성 규칙들을 적용 가능하게 만들거나 그렇지 않게 만들 뿐이지 함수 호출 (function call) 처럼 직접 호출하지는 않기 때문이다. 이러한 상대적인 독립성은 현재의 인공지능 시스템내의 대규모의 지식 베이스를 구성하는 데 있어서 매우 중요한 역할을 한다. 즉 제시된 생성 규칙이 어떠한 상황에서 사용되더라도 그 생성 규칙이 어떠한 의미를 지니는 지만 알고 있으면 지식 베이스를 구성하는 것이 매우 쉬운 일이 된다. 그러나 시스템의 크기가 커질수록 생성 규칙의 독립성은 보장하기가 어렵게 되고 비록 독립성이 보장된다고 하더라도 독립성 보장으로 인한 규칙들간의 상호작용의 제한은 시스템의 비효율성으로 나타날 수 있다.
생성 시스템은 규칙베이스의 지식이 매우 단일한 형태의 자료 구조로 유지된다. 모든 지식은 생성 규칙이라는 다소 엄격한 형태의 구조 속에 맞게 형성되어야 한다. 이러한 구조는 다소 자유로운 형태를 띠고 있는 의미망이나 프레임에 비해서 다른 사람이 이해하기 쉽고 또 시스템의 다른 부분에서 사용하기 편리하다. 특히 이러한 특성을 이용하여 시스템 자체적으로 규칙베이스를 검사하여 오류를 수정할 수 있는 방법까지 연구되고 있다.
생성 규칙의 형태는 여러 가지 중요한 지식을 매우 쉽게 표현할 수 있다. 특히 어떠한 상황 하에서 어떤 일을 할 것인가 하는 종류의 지식은 매우 자연스럽게 생성 규칙으로 표현할 수 있다. 그리고 이런 방식은 인간 전문가가 다른 사람에게 자신이 하는 일을 설명할 때 사용하는 방법이기도 하다.
위에서는 많은 장점을 언급했지만 생성 시스템의 지식 표현 방법은 본질적으로 내재되어 있는 단점이 있다. 그 중 하나는 프로그램 수행의 비효율성이다. 강한 독립성과 표현의 단일성은 문제 풀이 (problem solving) 에서 생성 시스템을 사용하는 데 매우 큰 부담을 주고 있다. 한가지 예를 들면 생성 시스템은 matchㅡaction 순환을 통해 모든 행동을 실행하고 작업 메모리를 통해서만 정보를 전달하므로 미리 정해진 단계를 거쳐 수행되는 특별한 상황에 대해서는 잘 반응하지 못하고 다른 상황과 똑같은 식으로 매우 긴 수행과정을 밟는다.
생성 시스템의 두 번째 문제점은 문제 해결과정의 제어 흐름을 따라가기가 곤란하다는 점이다. 즉 일반적인 프로그래밍 언어로 구현된 시스템보다 구현된 알고리즘 자체가 잘 드러나 보이지 않는다. 다시 말하면 어떤 주어진 상황에 대한 행동을 나타내는 지식은 잘 표현되지만 미리 문제해결의 알고리즘이 주어진 지식의 경우는 제대로 표현하기가 곤란하다. 이러한 문제를 유발시킨 두 가지 요인은 생성 규칙들의 상호 분리와 크기의 단일성이다. 즉 생성 규칙이 상호 분리독립적으로 유지되기 때문에 서로를 호출할 수가 없고 크기가 단일하므로 부 생성 규칙 (sub productions) 이라는 개념이 존재하지 않는다. 즉 한 생성 규칙 내에 여러 개의 부 생성 규칙이 존재하지 않는다는 것이다. 함수 호출의 기능은 일반적인 모든 프로그래밍 언어에서 사용되는데 이를 사용하면 제어의 흐름을 따라가기가 쉬워진다.
생성 시스템의 크기와 복잡도가 증가함에 따라 규칙베이스의 생성 규칙의 실행부와 조건부의 구조가 점점 복잡해져 왔다. 그에 따라 현재의 많은 생성 시스템에서는 조건부가 LISP 함수로 구성되어 임의의 복잡한 조건문도 그 참 거짓을 평가할 수 있게 되었다. 그런데 어떤 시스템에서는 생성규칙의 조건부를 검사하는 과정이 부작용 (side effect) 을 발생시켜서 그 생성규칙이 적용되지 않고서도 작업메모리의 내용을 변화시키거나 제어의 흐름을 바꾸는 수가 있다. 이와 비슷하게 실행부의 형태도 변화하여 변수를 포함할 수가 있게 되었는데 이 변수는 조건부를 검사하는 도중에 값이 결정된다. 그리고 단지 작업 메모리의 내용만을 변화시키는데 그치지 않고 임의의 프로그램을 실행시키는 기능도 가지게 되었다. 이러한 프로그램들은 그 영역에 맞는 여러 가지 일을 하게 된다. 특히 어떤 시스템의 경우는 이 프로그램들이 다른 생성규칙이 선택되는 것을 가능하게 하기도 하고 불가능하게 하기도 한다. 이런 경우는 초기의 생성 시스템의 표현 형태를 크게 벗어나는 것이다.
생성시스템의 순환과정은 앞에서 언급했듯이 세 가지 단계를 가진다. ㅡ matching, conflict resolution, action ㅡ 이 세 단계 중 가장 많은 계산 시간을 차지하는 과정은 matching과정이다. 생성 시스템이 커지고 복잡해짐에 따라 효율성의 문제가 대두되고 이는 규칙베이스와 작업메모리를 복잡하게 만들어야 하는 필요성을 가중시켰다. 예를 들어 주어진 상황에서 규칙베이스 전체를 검사하지 않고서도 어떤 생성 규칙이 적용가능한지를 빠르게 결정하기 위해서 생성 규칙들은 그들을 적용가능하게 하는 조건들에 의해 분할 (partition) 되거나 인덱싱 (indexing) 된다. 또한 작업메모리의 구조도 보다 효율적으로 구성하며 복잡한 지식도 표현가능하도록 그 내부적인 복잡도가 증가하였다. 복잡한 작업메모리의 예는 MYCIN의 context tree, HEARSAY의 blackboard, PROSPECTOR 의 의미망 등이 있다.
실제적으로 상당한 규모의 생성 시스템은 한번의 순환에 있어서 적용가능한 생성 규칙은 하나 이상이 있게 마련이다. 따라서 그 시스템은 그 중 하나의 생성 규칙을 선택해야 한다. 이들 적용가능한 생성 규칙의 집합을 충돌 집합 (conflict set) 이라 한다. 일례로 앞의 음식이름 맞추는 시스템에서는 생성규칙의 일련번호가 가장 작은 것을 선택했다. 이 충돌 해결단계에서 제어방법에 따라 서로 다른 방식을 사용하게 되는 것이다. 충돌 해결을 여러 방법 중 중요한 몇 가지를 아래에 나열한다.
1. 조건부가 만족되는 "첫 번째" 생성 규칙을 선택한다. 여기에서 첫 번째라는 의미는 규칙 베이스가 생성 규칙을 저장하고 있는 순서에서의 첫 번째라는 뜻이다.
2. "우선 순위"가 가장 높은 생성 규칙을 선택한다. 우선 순위는 프로그래머가 주어진 문제영역의 필요성이나 특성에 따라 지정한다.
3. 가장 "구체적인" 생성 규칙을 선택한다. 이는 조건부의 갯수가 가장 많은 생성 규칙을 의미한다.
4. 가장 "최근에" 작업메모리에 첨가된 작업메모리 요소를 참조하는 생성 규칙을 선택한다.
5. "새로운" 규칙, 즉 이전에 한 번도 선택되지 않았던 규칙을 선택한다.
6. "임의로" 선택한다.
7. 하나를 선택하지 않고 모든 적용가능한 생성 규칙을 동시에 수행시킨다. (MYCIN에서 사용된 방식이다.)
생성 시스템에서는 이런 단순한 충돌 해결 방법의 조합해서 사용한다. 이러한 충돌 해결 규칙의 선택은 생성 시스템의 중요한 두 가지 요소인 민감성 (sensitivity) 과 안정성 (stability) 에 많은 영향을 끼친다. 민감성은 작업메모리의 내용의 변화에 빨리 반응하는 성질을 의미하며, 안정성은 어떤 긴 과정의 action들을 수행하는 능력이다. 그러나 어떠한 충돌 해결 규칙도 만족할 만한 성능을 가지고 있지는 못하다.
연역적 추론에 관한 연구는 인간이 추론하는데 있어서 두 가지의 본질적인 추론 방식이 있음을 인식하였다. 한 예로 이미 주어진 정보를 가지고 우리가 원하는 목표에 적합한 결론을 끌어내는 방식으로 추론을 하는 경우가 있다. 이를 생성 시스템에서는 전방향 추론 (forward chaining) 이라 한다. 반대로 미리 생각하는 목표에서부터 시작하여 이를 뒷받침하는 증거를 찾는 방식으로 추론을 진행해 나갈 수도 있다. 생성 시스템에서는 이를 후방향 추론 (backward chaining) 이라 하는데 그 이유는 우선 목표를 만들어 내는 실행부를 가진 생성규칙을 찾아낸 후 이 생성 규칙의 조건부가 만족되는지를 검사하고 만족되지 않는 조건이 있으면 다시 이를 만족시키는 생성 규칙을 찾는 식으로 추론을 수행하기 때문이다.
이제까지 생성 시스템의 예와 그 수행 과정에 대해서 논하였다. 생성 시스템은 규칙 베이스와 작업 메모리 그리고 추론 엔진으로 구성되었음을 보았다. 그리고 각각의 기능에 대해서도 알아보았다. 그 중 추론 엔진은 제어 방법에 의해 그 기능이 결정되는데 제어 방법은 크게 과정 회복 가능한 제어 방법과 과정 회복 불가능한 제어 방법으로 구분된다. 어떤 제어방법을 사용할 지는 해당 영역의 특성에 달려있다. 생성 시스템의 장점은 그 규칙들이 서로 독립적이고 규칙 표현의 형태가 단일하며 인간의 생각과 매우 비슷하여 자연스럽게 표현할 수가 있다. 하지만 매우 비효율적이고 원하는 결과가 무엇인지에 대해 매우 모호하다는 점이 단점으로 지적될 수 있다. 생성 시스템을 설계하기 위해서는 몇 가지 고려햐야 할 사항들이 있다. 조건부와 실행부의 복잡도, 규칙베이스와 작업 메모리의 구조, 충돌해결 방식, 추론의 방향 등을 고려해야 한다.
일반적인 문제의 풀이 기법과는 달리 특정 응용 분야의 지식 및 능력을 체계적으로 잘 조직하여 컴퓨터 시스템에 입력시켜서, 이렇게 구축된 지식들을 이용하여 어떤 상황에 대한 문제를 해결해 나가는 시스템을 지식 기반 시스템이라고 한다. 물론 이러한 지식 기반 시스템은 하나의 프로그램으로 구현되며 일반적인 프로그램과는 다른 특별한 구조를 갖는다. 일반적인 프로그램에서는 문제 그 자체에 대한 지식과 문제 풀이를 위한 제어 그리고 사용자와의 상호 작용 방법 등이 하나의 프로그램 안에 혼합된 형태로 존재한다. 그러나 지식 기반 시스템에서는 문제 그 자체에 대한 지식을 나머지들과 분리된 형태로 유지시키며 이때 문제 영역 자체에 대한 지식들을 지식 베이스 (Knowledge base) 라고 하고 그 지식으로 어떤 영역에 대한 문제 풀이를 위한 제어를 맡고 사용자와의 입출력에 관한 기능 등을 수행하는 부분을 추론 엔진 (inference engine) 이라고 한다.
이것은 새로운 지식의 갱신과 기존 지식의 수정 등을 지식 베이스만을 변경함으로써 가능하게 해주며 전문가 시스템의 유지, 관리를 효율적으로 하게 해준다. 지식 기반 시스템에서의 지식 베이스는 어떠한 문제를 표현하기 위한 지식으로서 규칙 (rule), 의미망 (semantic net), 프레임 (frame) 등을 사용할 수 있고 추론 엔진은 지식을 어떻게 해석하여 적용할 것인가를 결정하는 해석기 (interpreter) 와 지식을 어떠한 순서로 적용할 것인지를 결정하는 스케줄러 (scheduler) 를 포함한다. 이러한 지식 기반 시스템의 일반적인 구조를 [그림 7.1]에서 보여주고 있다.
|
사용자 |
|
|
↕ |
|
|
사용자 인터페이스 |
|
|
↕ |
|
|
추론 엔진 |
작업 메모리 |
|
지식 베이스 |
|
[그림 7.1] 지식 기반 시스템의 구조
[그림 7.1]에서 주어진 지식 기반 시스템의 각 구성 요소들을 성명하면 다음과 같다. 사용자 (user) 는 지식 기반 시스템을 사용하는 일반인으로서, 적용분야에 대해서 지식이 부족하여 컴퓨터 시스템을 이용하여 특정의 문제를 해결하려고 하는 사람이나, 어느 정도 지식이 있으나 자신이 문제를 해결하는데 조언을 필요로 하는 사람이 될 수 있다. 사용자 인터페이스 (user interface) 는 지식 기반 시스템과 사용자가 실제로 접촉하는 부분으로서 지식 기반 시스템이 얼마나 사용하기 쉽고 편리한가를 결정하는 부분이다. 작업메모리 (working memory) 는 전문 지식이 저장된 지식 베이스를 컴퓨터내의 주기억 장치에 적절한 자료 구조로 변환하여 저장하고 있는 부분으로서, 지식 기반 시스템이 실제로 추론을 수행하는 동안에 처리하는 지식을 저장한다. 추론 기관 (inference engine) 은 작업 메모리내의 지식을 이용하여, 삼단 논법 등의 추론 기법을 이용하여 결론을 이끌어 내는 부분이다. 문제 영역의 특징이나 지식 표현 방법에 따라서 서로 다른 추론 기법을 사용할 수 있다. 일반적으로 추론 기관이 수행하는 추론 기법에는 전향 추론 (forward inference), 후향 추론 (backward inference), 혼합 추론 (mixed inference) 등이 있다. 지식 베이스 (knowledge base) 는 전문가의 전문 지식이 특정의 지식 표현 기법에 따라 조직되어 저장되는 곳으로 지식 기반 시스템이 주어진 문제를 해결하는데 필요한 지식들을 가지고 있다.
지식 기반 시스템에는 다음과 같은 기본 기능이 요구된다.
(1) 지식의 표현과 저장, 관리
(2) 지식의 이용 및 그 지원
(3) 지식의 획득 및 그 지원
종래의 데이터 베이스가 대상으로 하는 데이터는 비교적 낮은 레벨의 정보였으나, 지식 기반 시스템의 취급 지식은 구조화된 데이터 군(群)을 단위로 하는 데이터이며, 대상 세계를 기술하는 능력이 높을 것을 요구한다. 그러나 그 구조가 복잡하고 이해하기 어려우면 취급상 어려운 시스템이 되어 버린다. 따라서 위의(1)의 지식 표현법에 요구되는 것은
(1.1) 표현 능력이 높을 것
(1.2) 지식이 쓰기 (writing) 쉬울 것
(1.3) 이해하기 쉬운 표현일 것
이다. 또 지식 베이스 시스템이 실용에 공급될 때에는 다종다량의 지식을 효율 좋게 취급할 필요가 있게 된다. 즉,
(1.4) 대량의 지식의 효율적인 축적
(1.5) 대량의 지식의 고속 탐색, 갱신
이 요구된다. 이와 같은 기능에 관하여는 종래형의 데이터 베이스 시스템의 힘을 빌리는 방식도 생각되고 있다.
한편, 위의 (2)에 관해서는
(2.1) 추론 기능
(2.2) 유연한 지식 조작 기능
(2.3) 고도의 사람ㅡ기계간의 인터페이스 (interface) 기능
이 요구된다. 이들 중에서도 추론 기능은 중심적인 기능이다. 또 지식 베이스 시스템의 이용자는 인간-기계 인터페이스를 중개로 하여 지식 조작을 하거나 추론의 결과를 이용한다. 그를 위해 (2.2)와 (2.3)이 필요한다.
또, 지식 베이스 시스템을 실용에 쓰기 위해서는 전문가의 지식을 지식베이스에 축적시킬 필요가 있으나, 이것은 현 상태로는 지식 공학자가 전문가로부터 지식을 채취하여, 지식 기술(記述)을 하는 수가 많다. 이 지식 기술(記述)은 지식 획득 도구에 의해, 지식 공학자를 중개로 하지 않고 전문가로부터 직접 수행되는 것이 바람직하다. 지식 획득 도구에 요구되는 기능으로 서는
(3.1) 모순되는 또는 틀린 지식의 검출, 제거
(3.2) 부족되어 있는 지식의 검출, 요구
(3.3) 애매모호한 지식의 검출
(3.4) 주어진 지식 또는 보유 지식으로부터 필요한 지식을 추출하고, 획득하는 능력
이 있다. (3.1)~(3.3)은 지식의 일관성이란 입장에서 지식의 부가, 변경시, 요구되는 기본 기능이다. 일관성이 없는 지식 베이스는 사용자의 불신을 초래하게 되고, 존재의 의의를 잃어 버리게 될 것이다.
지식 기반 시스템이 어떤 전문적인 분야의 지식을 획득하여 지식 베이스를 구축하고 인간 전문가를 대신하는 역할을 하게 될 때 이러한 지식 기반 시스템을 특별히 전문가 시스템이라고 한다. 물론 전문가 시스템은 지식 기반 시스템의 하나이며 중요한 응용분야로서 활발한 연구가 진행되어져 왔고 이 책에서는 지식 기반 시스템을 전문가 시스템을 중심으로 설명한다.
전문가 시스템은 인간 전문가의 문제에 대한 해결 방법을 본따서 만들어 지게 되는 것이 일반적이다. 인간 전문가는 여러 가지 경우에 과거 경험한 노하우 (know-how) 나 연구한 지식을 떠올려서 정확한 답을 추론하여 판단을 내린다. 문제가 발생한 경우에 정확한 판단을 내린다는 것은 문제로부터 얻어진 사실, 즉 데이터를 바탕으로 하여, 인간의 지식 베이스에 있는 정보를 이용하여 추론을 행하고, 정확한 답을 내고 있음에 주목해야 하겠다.
현재의 컴퓨터에는 많은 정보를 기억시킬 수가 있고, 이 기억 정보는 필요에 따라 실시간으로 불러 낼 수도 있게 되어 있다. 따라서 전문가가 갖고 있는 지식을 어떻게 기억시켜 둘 것인가라는 지식 베이스 속에 지식의 표현 방법과, 이것을 어떻게 이용할 것인가라는 지식의 추론기구가 만들어져 있으면, 전문가가 생각하여 판단하는 기능을 대행하는 "생각하는 기계", 즉 전문가 시스템이 실현된다.
전문가가 갖고 있는 전문지식을 이용하고자 하는 시도로 맨 처음 성공한 것은 미국의 스탠포드 대학에 있는 E. A. Feigenbaum 교수에 의해서 였다. 그가 DENDRAL 이라는 것에 화학 분자식과 질량 스펙트럼을 입력시키면, 그 물질의 가장 가능성이 높은 화학구조식을 추정하여 출력하는 컴퓨터 프로그램을 만든 것은 1971년이었다.
이에 자극되어 1976년 이후로 의료 진단을 위한 전문가 시스템 MYCIN이 개발되었고 광물자원 탐사를 위한 전문가 시스템 PROSPECTOR와 주식 예측 시스템 등을 개발했다.
또한 경영, 관리는 가장 경험과 직감을 요하는 분야이며, 전문가 시스템 도입이 크게 업적을 좌우하게 될 것이다. 지금까지 컴퓨터를 사용하여 OA 시스템의 구축에 성공하고 있는 기업일수록 인공지능을 사용한 OA를 지향하고 잇는 것이 세계적인 추세이다.
지식 베이스의 구축과 관련하여 전문가의 전문 지식을 지식 베이스로 구성하는 작업을 지식 공학 (knowledge engineering) 또는 지식 획득 (knowledge acquisition) 이라고 하며 이와 같은 작업을 수행하는 사람을 지식 공학자 (knowledge engineer) 라고 한다.
최근에는 이러한 지식 공학 과정에 대한 연구도 활발히 진행되고 있으며 성공적인 연구 결과들을 낳고 있다.
전문가 시스템은 경험과 전문성을 요구하는 문제들을 아주 효율적으로 풀 수 있는 진보된 프로그램이다. 특정 문제 영역의 전문가 시스템을 구축하기 위해서는 일반적으로 다음 세 가지 단계가 요구된다. 첫째 단계는 특정 문제 영역의 전문가로부터 지식을 수집하는 것이고, 둘째 단계는 수집된 지식을 특정의 지식 표현 기법에 따라 지식 베이스를 형성하는 단계이다. 마지막 단계는 형성된 지식 베이스가 오류를 가지지 않도록 지식 베이스를 검증하는 단계이다.
특정 문제 영역의 전문가 시스템을 구축하기 위해서는 지식 공학자가 문제 영역의 전문가로부터 전문 지식들을 습득하여 지식 베이스를 구축하여야 한다. 최근의 인공 지능 분야에서는 전문가 시스템 구축 과정을 쉽고 빠르게 해주는 시스템이 많이 개발되고 있는데, 이와 같은 시스템을 전문가 시스템 구축 언어라고 한다. 전문가 시스템 구축 언어는 전문가 시스템을 개발하고 실행시키며 유지 관리하는 기능들을 지원해주는 소프트웨어 시스템들의 집합이다.
전문가 시스템 구축 언어는 전문가 시스템을 개발하고 관리하는 기능들을 제공하는 소프트웨어 시스템으로서 인공 지능 분야에서 상업 시장을 넓게 차지하고 있다.
일반적으로 전문가 시스템 구축 언어는 특정 문제 영역의 지식들을 추가하는 즉시 그 영역의 전문가 시스템이 구축될 수 있도록 지식 표현 기법 (knowledge representation), 다양한 추론 엔진 (inference engine), 그래픽 사용자 인터페이스 (graphic user interface), 지식 베이스의 디버깅 (debugging) 및 검증 (verification) 기능들을 제공하고 있다.
최근에 개발된 많은 전문가 시스템 구축 언어들은 전문가 시스템을 개발하는 과정에서 여러 가지의 지식 표현 기법과 추론 기법, 가설에 의한 추론 (hypothetical reasoning), 진리 유지 기법 (truth maintenance), 객체 지향적 프로그래밍 (object-oriented programming), 그리고 풍부한 디버깅 기능들과 그래픽 인터페이스들을 이용할 수 있도록 함으로써 상업적인 상품들로 생산되게 되었다. 따라서, 최근에 상업 시장에서 선보이는 이러한 기능들을 가지는 전문가 시스템 구축 언어들은 제 3세대 지식 공학 환경 (knowledge engineering environment) 으로 일컬어지고 있다. 제 1세대 전문가 시스템 구축 언어는 LISP 와 같은 논리 프로그래밍 언어 (logic programming language) 를 이용하여 지식과 제어 구조를 잘 연결하여 전문가 시스템을 구축하였다. 제 2세대 전문가 시스템 구축 언어는 특정 문제 영역의 지식과 쉘 (shell) 의 분리의 유용성을 이용하여 추론 기능과 지식 베이스를 분리하는 개념을 사용하였다.
전문가 시스템 구축 언어의 효율성을 결정하는 요인으로는 전문가의 전문 지식 분야 및 특성에 적합한 지식 표현 기법의 제공, 사용한 지식 표현 기법 및 응용 분야 및 특성에 적합한 지식 표현 기법의 제공, 사용한 지식 표현 기법 및 응용 분야에 따른 알맞는 추론 기법의 제공, 전문가 시스템의 구축을 편리하고 빠르게 할 수 있도록 하는 개발 환경으로써 여러 가지 유용한 인터페이스의 제공 등이 있다.
초기의 전문가 시스템들은 주로 C, Pascal, Lisp, Prolog 등의 고급 프로그래밍 언어를 사용하여 구축되었다. 그러나, C나 Pascal 은 인간이 지닌 사고나 개념과 같은 복잡한 지식을 표현하는 기초 처리 과정에 있어서 그 기능이 부족하고, 새로운 지식을 추가시키는데 기존 시스템의 내용을 많이 수정할 필요가 있고, 또한 Lisp나 Prolog는 그 개발 기간이 길고 지식 표현에 불편함이 많기 때문에 이러한 전문가 시스템 구축 언어를 이용하여 전문가 시스템이 많이 개발되고 있다.
전문가 시스템의 개발에서는 문제 영역으로부터 지식을 획득하는 것이 효율적인 시스템 구현을 위한 필수적인 과정이므로 이러한 시스템을 개발하는 데는 지식 획득과정이 아주 중요한 과정으로서 존재한다. 그리고 획득되어진 지식을 컴퓨터가 수행할 수 있는 형태로 입력시켜 지식 베이스를 구축하고 전체적인 전문가 시스템을 만드는 구현 과정이 뒤따르게 된다. 따라서 전문가 시스템 개발 과정은 크게 지식 획득과 구현이라는 두 가지 부분으로 나누어지게 된다.
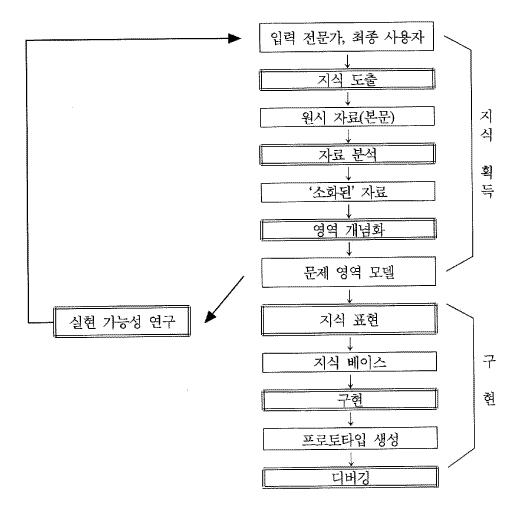
[그림 7.2] 전문가 시스템 개발 과정의 기능적 모델
[그림 7.2]은 전문가 시스템 개발 과정의 기능적 모델을 나타내는데 겹사각형은 각 단계의 활동을 의미하고 직사각형은 그 활동의 입력과 출력을 나타낸다. 처음으로부터 3개의 겹사각형(지식도출, 자료분석, 영역 개념화)은 지식 획득의 단계를 의미하며 나머지 겹사각형은 구현의 단계들이다. 화살표는 서로 다른 부분 작업간의 순서 관계를 표시한다. 예를 들어 지식 도출은 원시자료를 만들어내고 이것은 자료분석 작업의 입력이 되는 것이다. 다양한 작업간의 상호작용은 전혀 예상할 수 없는 형태일 수 있으므로 지식 고학자는 새로운 지식을 모으거나 존재하는 자료를 변형하거나 오류를 찾아내기 위해 그전의 단계로 거슬러 올라갈 수도 있다. 겹사각형으로부터 나와 위로 향한 화살표는 이러한 모든 활동들을 반복하는 특성을 표시한다.
이러한 모델은 지식을 영역 전문가로부터 도출하고 지식 표현 형태로 정형화된 개념적 모델을 만들며 이것을 실제 코드로 구현하는 과정으로 구성된 지식공학을 잘 표현한다. 물론 디버깅은 지식 공학 과정의 각 단계에서 만들어지는 모델들에 대해서 평가하고 증명하는 과정으로 이 그림에서 나타내어지는 각 단계의 활동에 대해 가해지는 과정으로 존재한다.
일반적으로 지식획득은 전체적인 작업 구조 (문제에 대한 모델) 와 영역전문가의 지적인 행위 그리고 영역을 정의하는 개체들의 현상에 대한 개념적인 표현을 만들어 나가는 과정이다. 대개의 경우 지식공학자는 영역에 대한 지시뿐만 아니라 최종 사용자로부터 시스템의 예상되는 양식에 대한 지식도 획득하여야 한다. 이 그림에서 "실행 가능성 연구"의 겹사각형으로부터 나오는 화살표는 지식공학자가 지식의 실행가능성을 연구하기 위해 지식획득의 이전단계들을 사용함을 의미한다. 이러한 반복적인 과정의 중요한 점의 하나는 이전의 지식 획득 과정을 통해서 얻어진 모델이 다른 지식 획득과정에도 사용되어질 수 있다는 것이다.
이와 같이 이미 존재하는 개념적 모델을 이용한 기법을 하향식 (top-down) 기법이라 하고 이용하지 않은 기법을 상향식 (bottom-up) 기법이라 하여 구분한다.
전문가 시스템의 개발 과정 중에서 구현의 각 단계는 어떤 전문가 시스템 도구를 사용하여 구현하느냐 또는 어떤 하드웨어를 사용하느냐에 크게 영향을 받으므로 아래에서는 전문가 시스템의 개발 과정 중에서 지식 획득의 각 단계에 대해 설명하겠다.
영역 전문가로부터 지식을 도출하는 초보적인 단계에는 일반적으로 구조화되지 않고 해석되기 어려우며 혼란스럽고 신뢰도가 떨어지는 자료를 낳게 된다. 이때의 자료는 사용되어지는 특정한 기법에 크게 의존한다. 인터뷰와 같이 기법이 일반적인 것일수록 도출되어지는 자료는 더 구조화되지 못하게 되며 이때의 자료를 원시 자료라고 한다.
지식도출 단계의 가장 중요한 면은 명백히 사용되어지는 기법과 도출되어지는 원시 자료의 형태이다. 대부분의 지식 도출 기법은 심리학적인 데 그 기초를 두고 있고 중요한 쟁점은 정형화된 기법과 비정형화된 기법 (formal vs informal), 직접적인 방법과 간접적인 방법 (direct vs indirect), 강한 기법과 약한 기법 (strong vs weak) 에 관한 문제이다. 일반적으로 지식 공학자는 인터뷰와 같은 비정형화된, 직접적인 기법을 사용한다. 이러한 지식 도출 기법은 산업체 환경에 적합하며 또한 특정한 기법이나 표현 양식에 얽매이게 하지 않음으로 해서 영역 전문가에게 최대한의 정보를 표현할 수 있게 하는 이점을 가지고 있다. 그 반면 거의 구조화되어 있지 않은 원시 자료를 낳게 됨으로 인해 지식공학자에게 그 자료를 분석하고 개념화하는데 많은 노력을 요구한다. 또 하나의 문제점은 영역 전문가의 개성에 따라 인터뷰에 의해 도출되어 지는 자료에 영향을 끼친다는 것이다.
일단 자료가 도출되어져 나오면 지식 공학자는 원시자료로부터 적당하지 않은 정보와 불필요한 자료를 제거하기 위해 자료 분석단계를 거치게 된다. 이 자료 분석 단계에서는 개념, 명제, 정의나 관계들의 형태로부터 핵심이 되는 지식의 조각을 확인하고 추출해내는 과정을 주로 한다. 자료분석이 행해지는 방법은 지식 획득 기법에 크게 의존하므로 정형적인 기법이 사용될 때에는 이 과정은 간단한 것일 수 있다. 그러나 원시 자료가 특별히 구조화되지 않은 것일 때에는 복잡한 과정이 되어진다. 예를 들어 원시 자료의 본문에서 주요어와 개념들을 확인하고 찾아내어 부분영역으로 문제를 나누어 나가는 기법이 있다. 이 단계에서의 지식 표현은 피상적이며 개념적인 틀로 통합되지 않은 수준에 머무른다. 물론 다른 영역 전문가의 같은 지식들일 경우 서로 다른 용어를 사용하고 다른 구조를 가지므로 다르게 표현되어져야 함이 마땅할 것이다. 따라서 자료 분석 단계의 전형적인 결과는 '소화된 자료' (digested data) 라고 나타내어지며 주요 어휘들과 각 지식들의 대략적인 범주화가 된다. 이때 범주화는 반드시 문제 영역수준에 관한 것이어야 할 필요는 없으며 메타수준 (meta-level) 개념의 범주화일 수도 있다. 이러한 범주화의 목적은 과학적인 연역을 추상적인 모델화하는데 필요한 개념들을 끄집어 내는데 있다. 여기서 자료 분석에 의해 나오는 소위 '소화된 자료'는 문제영역이나 작업의 전체적인 모델에 의해 통합되어지지 않았으므로 부분적인 의미만을 갖고 있다. 사실상 이 과정에서는 전문가는 인식할 수 있지만 문제 영역의 전체적인 모델을 제공하지는 않는 고립되어진 지식의 조각을 만들게 된다. 이러한 과정을 이해하는 가장 좋은 방법은 지식들에 대한 백과사전을 만드는 것으로 보는 것이다. 이러한 비유는 어휘들을 만들어 내는 것과 대략적인 범주화는 자료 분석 과정의 단지 한 부분일 뿐이다라는 사실에 의해 다음과 같이 실증되어 진다. 자료분석의 이 수준에서 개념들이 확인되어지고 자료 본문의 한 부분들과 연관되어지며 이러한 본문의 한 부분은 그에 연관되는 개념을 백과사전의 내용과 같이 묘사하고 설명하는 역할을 한다.
영역 개념화 단계에서는 지식공학자가 문제에 대한 추상적인 모델을 만들기 위해 지금까지 골라진 자료들에 전체적인 구조를 부여한다. 이때의 자료들은 계층구조, 의미망구조, 관계표, 흐름도 등으로 나타내어질 수 있다. 이 단계에서 만들어지는 지식은 반드시 수행가능한 형태인 것은 아니며 단지 작업의 구조를 정형화된 형태로 나타내는 것이다. 영역 개념화 단계는 모델이 준구조화된 특성을 갖기 때문에 자동적으로 탐지되기는 힘들지만 지식들의 불일치나 지식집합의 구멍 (hole) 이 나타나느냐 단계이다. 그러므로 이 단계는 매우 복잡하고도 세심한 작업을 필요로 하는 지식공학의 과정이다. 개념화 단계에서 부딪히게 되는 문제중의 하나는 하향식 기법으로 돌출된 자료와 개념화된 모델사이에 존재할 수 있는 불일치이며 이것은 지식 도출 단계에서 발생할 수 있는 문제점과 유사하다. 영역전문가가 문제 풀이 방법에 대해서 완전히 알고 있지 못할 때 문제는 더 복잡해진다. 그러므로 도출되어진 자료를 지원할 수 있는 상식이나 타당한 이성을 발견하고 적용해 내는 것은 지식공학자가 해야 하는 몫이다. 영역 전문가의 행위나 선택을 모델화한 지식으로부터 지식 공학자는 연역적으로 추론을 해 나가는 기법을 사용할 수도 있는 것이다.
MYCIN은 감염증의 진단과 치료에 관한 조언을 행하는 것을 목적으로 설계되었다. 이러한 조언은 특히 입원 중의 감염, 가령 심장병 환자의 심장 수술 뒤의 감염증의 경우에, 주치의가 감염증의 전문의가 아닌 까닭에, 입원 환자에 대해 자주 필요로 된다. 시간적 문제에 대한 배려가 이 문제를 한층 복잡하게 한다. 환자로부터의 검사 (혈액, 오줌 등) 는 경우에 따라서는 12시간 이내라고 해도 무언가의 세균 증식의 징후를 보일 경우도 있는데, 일반적으로 균종류의 판별이 가능하게 되기까지 24~48시간 이상을 필요로 한다. 이 때문에 의사는 자꾸 필요로 하는 모든 정보를 입수하지 못한 상황 하에서, 치료를 해야 할 것인지의 여부, 하면 어떠한 약제를 쓸 것인지를 결정해야 한다. 이들은 어느 쪽도 어려운 문제이다.
다음에 보일 MYCIN의 실용 예는 의사와 시스템간의 대화에 대한 맨 처음과 마지막 부분을 보이고 있다. 요컨대, MYCIN은 의사에 대해 환자에 관한 질문을 하고, 진단을 내리거나 적절한 치료를 선택하는 등의 추론 기초로 되는 정보를 수집한다. 의사의 응답은 2개의 별표시 다음에 이어진다.
ㅡ 환자 1 ㅡ
1) 환자의 이름은 : (성명)
* * 홍길동
2) 환자의 성별은 :
* * 남성
3) 환자의 나이는 :
* * 55세
4) 홍길동의 감염 부위로부터의 검사 배양물에서, 균이 검출된 것이 있는가?
* * 있다.
ㅡ 감염증 1 ㅡ
5) 감염증은 무엇인가?
* * 원발성 균혈증 (原發性 菌血症)
6) 원발성 균형증 (감염증 1) 의 증상 또는 징후가 최초로 나타난 대략적인 일시를 넣어 주시오(년/월/일) :
* *1980년 5월 5일
.......
46) 0~4의 범위에서 큰 수치일수록 높은 중증도 (重症度) 를 나타낼 때 홍길동의 중증도는?
* * 3
47) 홍길동은 임상 상 중요한 알레르기 반응을 항균제에 대해 보이는가?
* * 보이지 않는다.
48) 홍길동의 체중은 kg 단위로 :
* * 70
[처방]
항목 <1, 2, 3, 5, 6>을 커버하기 위해 :
투여약제 :겐타미신 (gentamicon)
용 량 :1일량 119mg을 8시간 간격으로 10일간 정맥주사(또는 근육주사)
주 의 : 신 (腎) 기능 장애가 있을 때에는 용량을 조정할 것
항목 <4>를 커버하기 위해 :
투여약제 : 크린다마이신 (clindamycin)
용 량 : 1일량 595mg을 6시간 간격으로 14일간 정맥주사 (또는 근육주사)
주 의 : 설사나 그 외 소화관 증상이 나타났을 경우에는 위막성 (僞膜性) 대장염의 병발을 고려한다.