의도적인 합리적 행동

통합인지이론 : Allen Newell 저, 차경호 옮김, 아카넷, 2002 (원서 : Unified Theories of Cognition, Harvard Univ. Press, 1990), Page 489~575

1. 암호숫자산술

     1.1 암호숫자산술에서의 소어

2. 삼단논법

     2.1 명제와 모형

     2.2 주석이 달린 모형

     2.3 소어와 심성 모형

     2.4 삼단논법에서의 소어

3. 문장 검증

     3.1 문장검증에서의 소어

     3.2 과제 획득에서의 소어

4. 요약

이 장에서 우리는 인간들이 그들의 목표들을 어떻게 얻게 되는지 —— 그들이 합리적인 것이기 위해 어떤 지향을 하는지 intend —— 를 탐구할 것이다. 그것을 합리성 rationality 의 작은 언덕을 탐구하는 것으로 생각하자. 이상적으로, 충분한 시간이 주어진다면 지능적 시스템은 지식수준을 향해 이동하는데, 지식수준에서는 생각하기 위한 내부적인 노력의 표시들은 사라지고, 단지 과제환경에 대한 적응적인 반응만 남는다. 이 지점에서 그 시스템은 합리성의 절정에 이르렀다고 말해질 수 있다. 그러나 그 곳에 도달하는 것은 몇 가지 것들이 수행되어질 것을 요구한다. 사실상, 전영역이 먼저 통과되어야만 한다. 특히 시스템이 생각하고 문제 - 해결할 정도의 적당한 시간만을 갖고 있을 때, 그것의 행동은 그것의 기본적인 인지 능력 (5 장과 6 장에서의 초점) 들, 과제환경의 구조, 그리고 그것의 부분적이고 불완전한 표상과 접근할 구조에 침투하기 위해 사용할 수 있는 지식체계의 상호작용을 반영해야만 한다.

이러한 모든 영역을 이 한 장에서 모두 포함할 수는 없다. 그 대신, 나는 여러 가지 점들을 주장할 수 있을 만한 3 개의 특정한 과제들을 선택할 것이다. 우리는 암호숫자산술 cryptarithmetic, 삼단논법 syllogisms, 그리고 마지막으로 단순한 문장검증 sentence verification 을 살펴볼 것이다. 그 과제들은 5 장에서 검토된 즉시적 - 반응 행동이나 6 장에서의 기초 학습 상황들처럼 간단하지는 않지만, 모두 다 매우 단순한 것들이다. 내가 주장하고 싶은 점은 소어가 어떻게 이러한 과제들을 수행하는지 —— 우리가 정보처리와 AI 에 관해 알고 있는 것들이 주어진다면, 그것들은 이의가 없을 정도로 매우 간단하다 —— 가 아니라 의도적인 합리성의 본질과 합리성이 어떻게 제기되는지에 대한 것이다.

이 장에서 논의하고 싶은 나의 부가적인 주제는 모의실험과 다른 사용법이다. 내가 주장했듯이, 통합인지이론은 구성으로서 제시될 수 있다. 그것은 유기체가 직면하는 모든 과제들에서의 행동들을 함께 묶어 주는 공유성의 주요한 근거이다. 그러므로 가정된 구성으로부터 크던 작던 간에, 인간 행동에 대한 구성의 결과들을 어떻게 추출할 것인가라는 질문이 제기된다.

기본적인 답은 고릴라와 레슬링하는 것과 유사할 것이 틀림없다 —— 당신은 어떤 방법이나 수단을 써서라도 할 수 있다. 사실 우리는 구성으로부터 추리해가는 매우 다양한 방법들을 이미 보여주었다. 우리는 구성의 일반적 특성으로부터 인간 인지의 형태를 주장해왔다 (4 장). 우리는 산출들의 조건들의 상세사항으로부터 기능적으로 필수적인 연산자들의 계산 accounting 을 추출해왔다 (5 장). 우리는 상세한 모의실험을 만들어서 그것으로부터 학습곡선들을 도표화할 수 있었다 (6 장). 그러나 모든 종류의 이론들이 표면화되는 것은 아니었다. 우리는 어떤 강력한 수학적 이론들을 생성해 낸 것도 아니고 구성에 대한 어떤 정리들을 증명하지도 못했다. 그 일반적인 원인은 구성이 매우 복잡하다는 데에서 기인한다. 단지 연산자 - 계산 방법들 (5 장) 에서나 청킹에 의한 매우 추상적이고 일반적인 학습이론에서처럼 강력한 단순화가 이루어질 때에만, 수학이 유용할 정도로 충분히 설득력을 갖게 된다.

모의실험은 분명히 복잡한 시스템들에 대한 중요한 기법이지만, 모의실험을 사용하는 많은 방법들이 있고, 그것이 모든 통합인지이론에 대한 주요 분석기법이 될 것이기 때문에, 그것들의 다양성을 예시하는 것은 유용하다. 나의 경험으로는, 심리학자들은 일반적으로 그들의 모의실험들을 매우 조심스럽게 취급한다. 그들은 그것들을 무대밖에 유지시키며, 그것들을 주로 그들의 이론이 연산적인지를 확증하는 데 사용하는 경향이 있다. 인지과학에서의 고전적 연구들로부터 두 개의 예들이 인용될 수 있는데, 그것들의 긍정적 영향은 의심할 여지가 없다. 앤더슨 Anderson 과 바워 Bower 의 『 인간 연합 기억 Human Associative Memory 』(1973) 과 코스린 Kosslyn 의 『 심상과 마음 Image and Mind 』(1980) 에서, 모의실험 모형들은 모형들의 기능성에 대해 보증적인 역할을 하지만, 그것들은 그 주장을 지지하기 위해서 단지 짧은 출현만이 허용되었다. 그것들의 상세사항들에 대해서는 아무 말이 없고, 그것들은 그 모형에 관한 연역, 추론, 또는 실증하는 데 결코 개입하지 않는다. 그러나 단순히 보증서를 제공하는 것 이외에도 모의실험에 대한 여러 가지 많은 사용법들이 있다.

의도적인 합리적 행동은 시스템이 지식수준으로 접근함을 함의한다. 다시 살펴보면 (2 장으로부터), 지식-수준 시스템은 목표, 행위, 그리고 시스템이 그것들 두 가지를 관련시켜야만 한다는 지식들 —— 물론 외부적 제약의 범위 안에서 작동하는 —— 로부터 완전하게 결정된다. 시스템이 지식수준으로 이동함에 따라, 행동은 더욱더 과제환경의 함수가 되며 더 이상은 내부적 제약들의 함수가 아니다. 점진적으로 인지적 시간대를 떠나 합리적 시간대로 올라간다 (그림 3 - 3 에서의 인간의 시간척도를 회상하라). 그 이동은 점진적인데, 이는 그것이 각각의, 그리고 모든 구체적인 사례에서 제약들을 극복하는 유기체의 능력들에 의존하기 때문이다. 그러므로 구성은 행동에서 뚜렷하게 남아 있으며 적절한 행동에 이르게 되는 기호적 처리 역시 그렇다.

지능은 시스템이 지식 - 수준 시스템에 어느 정도 접근했는가 하는 것이다. 아마 거의 모든 것들에 대해 더 많은 시간이 가용적으로 될수록 지능은 향상된다. 소어는 이러한 특성들을 갖고 있는 시스템의 모형이다.우리는 절 4. 6 에서 소어의 기제들이 지식 - 수준 시스템의 좋은 추정이 되는 데 얼마나 기여하는지를 알아보기 위하여, 그것들을 검토하는 데 시간을 보냈었다. 그러나 지능은 내적 체제화의 많은 측면들에 의해 영향은 받는데, 이것은 고정된 기간 동안에 어떤 시스템들은 다른 시스템들보다 더 지능적임을 의미한다. 우리는 지능이 어떤 방식으로 변화할 수 있는지, 또는 어떤 것들이 그 방식에 관여하는지에 대해서는 거의 탐구하지 않았다. 인간의 행동을 관찰할 때, 많은 의문들이 제기된다. 어떻게 시스템이 합리적인 것으로 접근하는가? 얼마나 빨리 접근하는가? 시간적 제한 이외에 다른 한계들이 존재할 수 있는가? 이것이 바로 이 장에서 다루게 될 개념적 영역이다.

1. 암호숫자산술

암호숫자산술부터 시작해 보자. 이 과제는 바틀렛 (Bartlett, 1958) 에 의해 처음으로 분석되었고 나중에는 허브 사이먼과 나 (Newell & Simon, 1972) 에 의해 분석되었다. 그것은 인지심리학의 출현에 중요한 역할을 한다 —— 적어도 내게 있어서, 그리고 아마 다른 이들에게도 그럴 것이다. 그것은 발견법 탐색의 AI 이론이 말하는 것처럼, 인간들이 정말로 문제공간들을 사용하고 그것들 안에서 탐색한다는 것을 가장 강력하게 확신시켜주는 것이었다.

그림 1 암호숫자산술 과제

암호숫자산술 과제는 단지 작은 산술적 퍼즐이다 (그림 1 을 보아라). 단어들인 DONALD, GERALD, 그리고 ROBERT 는 6 자리의 숫자 3 개를 나타낸다. 각 낱자들은 각기 다른 숫자들로 교체된다 (즉, D 와 T 는 각각 숫자여야 하며, 예컨대 D = 5, 그리고 T = 0, 그러나 그것들이 동일한 숫자일 수는 없다). 이러한 교체가 올바른 합, 즉 DONALD + GERALD = ROBERT 를 만들어야만 한다. 수학적으로 보면, 그 문제는 상등, 부등, 그리고 비상등 unequality 을 포함하는 다중 정수 제약들을 만족시키는 것 중의 하나이다.

그림 2  DONALD + GERALD = ROBERT 에서의 피험자 S3 의 문제행동 도표

사람들은 암호숫자산수 과제를 풀도록 시켜질 수 있고, 프로토콜 protocols 은 그들이 문제를 풀면서 말로 표현한 것의 사본으로부터 얻어질 수 있다 (Newell & Simon, 1972). 그 분석은 사람들이 문제공간에서 탐색함으로써 과제를 해결함과 그 탐색이 명시적으로 도식화될 수 있음을 보여준다. (주석 : 모든 사람들이 동일한 문제공간을 사용하는 것은 아니다 (Newell & Simon, 1972, 7 장).) 그림 2 는 DONALD + GERALD = ROBERT 문제에서 S3 의 행동을 보여준다. (주석 : 1960 년에 이 프로토콜이 얻어졌을 때 젊은 대학생이었던 S3 이 지금은 50 대라는 것을 깨닫는 것은 충격적인 일로 보인다. 내가 말했듯이, 인지 혁명도 그 정도로 오래 되었다.) 그 도표는 문제행동 도표 problem-behavior graph (PBG) 라고 부른다. 그것은 단지 탐색이 검토될 수 있도록 탐색을 펼쳐놓는 하나의 방법이다 (그림 1 - 4 는 체스에 대한 PBG 를 보여주었다). S3 은 상단 왼편 점 (상태) 에서 시작하며 탐색은 수평선을 따라 이동한다. 각 마디는 그 공간에서의 연산자 적용을 나타내며, 각 적용은 새로운 상태를 생성한다. 그림에서는 연산자와의 이러한 연결들을 명명하기 위한 공간이 없다. 탐색선이 수평선의 오른쪽에서 종결될 때, S3 은 더 깊이 탐색하기를 중단하고 그가 이미 생성했던 어떤 사전의 상태로 되돌아간다. 이것은 수직선에 의해 표시된다 (수직적으로 연결된 모든 점들은 연속적인 귀환들 returns 에서의 동일한 상태를 나타낸다). 그 다음의 또 하나의 수평선은 연속적으로 더 깊은 상태들의 또 하나의 연쇄를 나타낸다. 이중선은 그곳에서 S3 이 앞에서 이미 적용했던 연산자를 적용함을 표시하는데, 달리 말하면, 그 곳 공간에서의 동일한 경로가 다시 취해짐을 표시한다 (명칭들 없이는 어떠한 사전 경로가 반복되는지를 말하는 것이 항상 가능한 것은 아니지만).

S3 은 약 30 분, 즉 ~2,000 초 동안 공간을 배회한다. 이것을 ~2 초인 즉시적-반응 행동보다 계수단위 (10) 의 3 배 정도 더 길다. 그러므로 30 분은 인간들이 작동하는 다른 시간 척도들에 비하면 여전히 짧지만, 이것은 확장된 행동이다. 각 상태에서의 평균거주시간은 ~7 초인데, 그것은 특정한 과제를 위해 구성된 연산자들에 대해, 여기서는 암호숫자산술 - 공간 연산자들에 대해 우리가 사용하는 ~10 초와 거의 같다.

그림 2 는 진정한 인지적 행동을 나타낸다. 그러므로 소어는 그것을 모형화해야 한다. 그것은 간단하다. 통합인지이론이란 그러한 모든 과제들에 대해 사용되는 그런 이론이어야 한다. A 과제에 대해서는 A 이론, 그리고 B 과제에 대해서는 B 이론이 아니다. 그러므로 소어로 하여금 이 프로토콜의 자세한 모의실험을 생성하도록 만드는 데에 어느 정도의 노력이 기울여졌다. (주석 : 이것은 올린 시버스 Olin Shivers 의 연구이다.) 이것은 이상한 것을 하는 것처럼 보일 수도 있다. 어쨌든, 바로 이 프로토콜은 20 년 전에 대부분의 심리학자들이 흥미롭게 또는 아마 가능하다고 생각하는 것보다도 더 자세히 분석되었다 (Newell, 1967 ; Newell & Simon, 1972). 모의실험은 산출 시스템으로부터 생성되었고, 전체 시스템은 수작업에 의한 것이었지만 (산출 시스템들이 실제 프로그래밍 시스템들로서 존재하기 전에 이것은 있었다), 그 문제를 또다시 분석한다는 것은 여전히 이상하게 보인다. 사실, 또다시 분석하는 일에 대한 두 가지의 좋은 이유가 존재하는데, 그 하나는 작은 이유이고 다른 것은 큰 이유이다.

작은 이유를 먼저 살펴보자. 통합인지이론으로서의 소어는 궁극적으로 모든 인지행동을 포함해야만 한다 —— 축적된 모든 현상들에 대한 설명들 또는 (경우에 따라) 예측들이 제공되어야 한다. 연구된 분석들을 포함하여, 그러한 현상들이 상당히 많이 축적되어 있다. 소어가 올바른 종류의 이론이라고 여겨질 수 있을지라도, 소어가 적용되지 않았던 현상들의 덩어리들을 소어가 포함한다는 것은 믿음에만 기초해서 받아들여질 수 없다는 것은 분명하다. 그러므로 우리는 모든 인지 영역에서 나온 예전의 결과들을 취해서, 그것들에 소어를 적용시킴으로써 소어 (또는 다른 어떠한 통합인지이론이라도) 를 지속적으로 검사해야만 한다. 우리는 이것의 일부를 자극 - 반응 호환성, 사본 타이핑, 그리고 이팸에 대한 연구에서 이미 그렇게 했다. 여기서 우리는 우리의 검사를, 『 인간문제 해결 Human Problem Solving 』에서 암호숫자산술과 과제의 분석에 의해 나타나는 것처럼, 문제 - 해결 수준까지 확장시킨다.

큰 이유는 인지에서의 근본적 문제에 대한 반응이다. 인간이 인지 구성을 갖고 있다는 것은 실제로 마음의 기계가 있다는 것과 같다. 원리적으로, 특정한 과제의 언덕을 덮고 있는 사실들의 숲을 통해서 지그재그로 움직이며 길을 가는 마음의 실제 궤적을 추적하는 것이 가능해야 한다. 마음과 마음이 거주하는 상황들은 매우 복잡하고 접근하기 힘들기 때문에 사실 그러한 궤적을 계산하는 것이 거의 불가능하다는 것을 우리 모두는 이해하고 있다. 인지 이론은 단순히 일종의 편리한 추상적 가설로서 보려는 유혹은 너무나도 용이하다. 어떤 전체적 현상을 계산하는 데는 유용하지만 분자적인 지그재그식 움직임을 추적할 수는 없다. 이러한 견해는 널리 퍼져 있는 카오스 chaos 이론 (Gleick, 1988) 에 대한 관심에 의해 쉽게 이해된다. 카오스 이론은 매우 단순한 비선형적 동적 시스템들이 근본적으로는 예측될 수 없다는 것을 보여준다. 그러나 인간 인지는 분명히 비선형적이지만, 개인의 목표를 달성하기 위해 행동을 적응시키도록 강력하게 형성된다. 충분히 발전된 인지이론은 과제 환경과 개인의 목표들과 지식이 충분히 알려진다면, 개인의 의도적이고 합리적 움직임을 추적할 수 있어야만 한다.

그러므로 인지 이론이 행동의 긴 기간을 예측할 수 있는 사례들을 찾는 것은 아주 중요하다 —— 긴 기간은 비교적 비제약적이며, 그 기간동안에 인간은 자유롭게 생각한다고 가정될 수 있다. 그러한 실례의 하나 또는 둘조차도 우리에게 인지이론이 근본적으로 옳다는 것을 확신시키는 데 크게 기여할 것이다. 암호숫자산술은 항상 이러한 종류의 결정적인 증거에 대한 주요한 후보자였다. (주석 : 다른 후보자들도 있다. 하나의 좋은 예는 어린 아동들에 의한 다중숫자 빼기의 수행과 학습이다 (Brown & Burton, 1978 ; burton, 1982 ; Brown & Vanlehn, 1980 ; Vanlehn, 1983 ; Vanlehn & Garlick, 1987). 흥미롭게도, 빼기 영역은 암호숫자산술과 분리되어 있지는 않은데, 이는 암호숫자산술이 산술적 추리를 사용하기 때문이다. 또 하나의 후보자는 숙달된 기억 skilled memory 의 영역이다. 체이스 Chase 와 에릭슨 Ericsson (1981) 은 초당 하나씩 제시되는 87 개의 숫자들을 회상하도록 한 대학생을 훈련시켰고, 그 기술의 인지적 구조를 밝히는 훌륭한 일련의 연구들을 수행했다. 추가적인 연구는 그 묘사를 확증했으며 (Ericsson & Staszewski, 1989), 이제 그것은 인지의 현대적 견해의 효율성에 대한 자세하고 우아한 실증을 제공한다.)

지난 30 년 동안 심리학의 중심 무대를 차지해온 방법론적 패러다임을 생각하면, 이것은 심리학에서 폭넓은 호소력을 갖는 것처럼 보이는 연구계획은 아니다. 위에서 암시한 것처럼, 기술적 어려움들의 평가이외에, 카오스적 이유 때문이 아닌, 자유의지 대 결정론의 문제 때문에, 그것은 진정한 기계적 심리학의 가능성에 대한 뿌리 깊은 불신에 부딪친다. 그럼에도 불구하고, 그 연구계획이 나에게 있어서는 절대적으로 중요하다. 그러므로 우리는 예전의 과제와 예전의 자료로 되돌아갔는데, 이는 그것이 비교적 안전한 출발점이기 때문이다. 목표는 궁극적으로 소어가 수십 분에 걸쳐서, 행동의 자세한 순간순간의 모의실험들을 수행하도록 만드는 것이다.

암호숫자산술 과제는, 실험실에서 행해지지만 모든 사람들의 정의에 따르면 퍼즐이며, 모든 일반적 기준에서 자유롭고 비제약적인 것이다. S3 은 단순히 탁자 앞에 앉아서 30 분 동안 이 문제를 푼다 —— 그 퍼즐을 해결하는 방법을 찾으려고 한다. 그의 머릿속에서 진행되고 있는 것은 그가 만들어내고 심사숙고하는 과제의 순간적인 상태들에 전적으로 통제된다. 그것은 심리학 실험실에 있다는 사실 —— 아마 약간의 추가적 압박의 분위기 또는 자기 노출의 느낌 —— 에 의해서는 단지 간접적으로만 통제된다. 그러나 이러한 느낌과 고려사항들은 매초 피험자가 그 퍼즐을 해결하기위해 이러한 낱자들과 숫자들에 대해 생각해야만 하는 상황의 주변에서 단지 표류한다. 외부 맥락에 대한 지식이 결정의 많은 부분 영향을 주는 데 사용될 수 있는 방법은 없다.

1.1 암호숫자산술에서의 소어

소어는 그림 2 에 표시되어 있듯이, 약 100 초 동안 지속되는 프로토콜의 두 부분을 모의실험한다. 처음 부분에서의 행동은 매우 명확하지만 두 번째에서는 매우 복잡하다. 처음, 우리의 목적은 소어로 하여금 문제공간에서 S3 이 수행하는 탐색에 대한 자세한 모의실험 —— 달리 말하면, 기술 —— 을 제공하게 만드는 것이다. 그러므로 그 모의실험은 시스템의 하위수준 행동, 즉 기본적 공간의 연산자들을 가정한다. 중요한 질문들은 이러한 연산자들이, 특히 더 복잡한 연산자들이 어떻게 수행되는가에 대해 물어질 수 있지만, 여기서의 연구 방략은 나누어서 정복하는 것이다. 처음 단계는 연산자들을 가정하고, 그림 2 의 문제 행동도표를 결정하는 탐색 통제를 연구하는 것이다.이러한 방략의 구현은 흥미로운 모의실험의 형태를 포함한다. 소어가 연산자를 구현할 때는 언제나, 그것은 현인 (연구자 또는 내부적 일람표) 앞에 나타나서, 입력과 그 상황을 진술하고 출력을 요구한다. 그 현인은 실제적인 실험적 자료로부터 이 정보를 제공하므로, 그 시점에서 모의실험된 연산자가 프로토콜과 일치하는 시점에 피험자가 수행했던 것을 정확하게 전달함을 보증한다. 물어오는 질문은, 만약 연산자가 피험자의 연산자들이 전달하는 것을 정확히 전달한다면, 그 시스템은 무엇을 할 것인가 또는 탐색 - 통제 지식의 역할을 무엇인가 하는 것이다.

그림 3 숫자암호산술에서의 소어 (Newell & Simon, 1972 에 따름)

그림 3 은 공간에서의 연산자들을 보여준다. 상단에 있는 4 개의 새로운 지식을 얻는 것들이다. 첫 번째 것은, PC, 행 처리하기 processes a column 는 자극판의 한 행을 처리해서 산술적 지식과 행에서의 낱자들과 올림수에 대해 알려진 것으로부터 새로운 지식을 도출한다. 두 번째 것인, AV, 할당 assign 은 낱자에게 숫자를 할당한다. 즉 그것은 하나의 할당을 가정한다. 이것은 다른 자료로부터 도출되었다는 의미에서 새로운 지식은 아니지만,그것은 그 때부터 피험자가 그 할당이 옳은 것처럼 —— 그 주장을 무효화하는 어떤 증거가 제시되기 전 까지는 —— 행동하는 상황을 생성한다. 세 번째 것인, GN, 생성 generate 은 주어진 낱자에 대해 수용 가능한 할당들을 만드는데, 모든 낱자는 합산되는 여러 행들에 참여하기 때문에 다중의 제약들에 의해 제한된다. 그러므로 어떤 시점에서 그것은 단지 숫자들의 전체집합 (0, 1, …, 9) 의 하나의 부분집합만을 취할 수 있다. GN 은 이 집합을 생성한다. 네 번째이며 마지막 연산자인, TD (검사 test) 는 만약 다른 낱자들에 대한 숫자들의 할당에 의해 제외된 값들이 주어진다면, 한 낱자에 한 숫자의 할당이 허용되는지를 검사한다. 문제 공간에 대한 하나의 강력한 주장이 여기서 만들어진다 —— 30 분 동안의 문제해결의 시간 동안에 과제에 대한 새로운 지식을 얻기 위하여, 이러한 그리고 단지 이같은 연산자들만이 수행된다.

그러나 다른 연산자들도 역시 요구된다. 그것들은 주의를 집중시키는 focusing 연산자들처럼 생각될 수 있다. 그것들의 필요성은 지식 - 습득 연산자들을 실례화 시킬 필요성으로부터 나온다. 이러한 4 개의 연산자들은 추상적이다. PC 는 어떤 행에 그것이 적용될 것인지를 명세하지 않는다. AV 는 어떤 변수에 값이 할당될 것인지 또는 변수에 어떤 값이 할당될 것인지 명세하지 않는다. GN 도 어떤 낱자가 생성된 값들을 가질 것인지 명세하지 않는다. TD 도 어떤 할당 (낱자, 그리고 숫자) 이 검사될 것인지 명세하지 않는다. 그러므로 문제의 현재 상태의 고정된 맥락 안에서 주의의 초점들 —— 낱자, 행, 값 —— 안의 공간에서 각 낱자에 대한 가능한 숫자들에 대해 알려진 것들을 연산할 추가적인 연산자들이 필요하게 된다.

찾기-행 Find-column 이란 연산자가 있는데, 그것은 현 상태와 주의 초점을 입력으로 취하여 PC 를 위한 행을 생성한다. 이것은 그 초점의 목적을 그것의 일부로 갖고 있다 —— 즉 결과로 나온 행은 처리될 것이고, 그러므로 어떤 새로운 지식을 생성할 행이 발견되어야 한다. 찾기-낱자 Find-letter 연산자는 변수의 상위수준의 선택이고, 전체과제는 이것을 가지고 진행되고, 그러므로 현재 초점의 제약들에 의해 축소되지 않지만, 이 연산자에 대해서도 마찬가지이다. 생성-행 Generate-columns 는 합산이 옳은지를 검토하기 위해 오른쪽에서 왼쪽으로의 다음 행을 체계적으로 획득하는 데 요구된다. 그것은 다중숫자 multidigit 덧셈을 위한 기본적인 행위일람표의 일부이다. 마지막 두 개의 초점 연산자들인, 찾기-선행사 Find-antecedent 와 찾기-산출 Find-production 은 앞선 상태들에의 접근을 허락한다. 그것들은 여기서 모의실험된 행동 단편에는 개입하지 않지만 나는 어쨌든 그들의 이름들을 목록에 적어넣었다. 그것들 두 가지 모두 기억과 접근에 대한 흥미로운 문제들을 제기하며, 소어는 산출들 그 자체에 접근하지 못하기 때문에 소어에서는 원래의 시스템에서와는 조금 다르게 실현된다.

마지막으로, 소어는 몇 개의 목표 연산자 goal - operators 들 —— 특수한 유형의 정보가 요구됨을 확립하는 연산자들 —— 을 갖고 있다. 이것들은 뉴웰과 사이먼 (1972) 에서 명세된 원래의 구성에서의 목표들이었다. 그러나 소어는 막다른 상태로부터 그것 자신의 하위목표를 만든다. 그러므로 원래의 목표들은 원하는 정보를 만드는 소어 연산자들의 역할을 하며, 소어가 숙고적으로 적용을 결정하는 다른 연산자들과 다르지 않다.

이 과제에서의 S3 의 수행의 탐색통제는 초점 연산자들의 공간에 존재한다. 이러한 연산자들의 결과는 다음번에 PC, AV, GN, 그리고 TD 의 주 연산자들 중 무엇이 적용될 것인지를, 특히 어떠한 실례화가 적용될 것인지를 결정한다. 이 선택공간은 자극판과 특정한 할당들, 그리고 변수들 (낱자들과 올림수들) 에 대해서 알려진 제약들을 주어진 것으로 받아들인다. 그것은 이 표상에 통제 결정을 하는 지식을 부호화하는 통제 속성 control attributes 들의 작은 집합을 덧붙인다. 이것들은 단순한 상태의 속성들이다. 결과가 새로운 new 것인지, 모순 contradiction 이 생성되었는지, 어떤 것이 불확실 unclear 한지, 그리고 어떤 것이 알려져야 함이 요구되는 상황에서 모르는 unknown 것인지. 그것들의 의미들은 그러한 용어들로 정의된 발견법에 의해서 주어진다. 예를 들면, 새로운 것이라고 명명된 결과의 의미는 그것의 함축들이 발견되야 한다는 것을 의미한다. 이것은 제약전파의 약한 방법인데, 여기에서 제약으로부터 얻어진 새로운 정보 (행 또는 할당) 는 시스템이 그 정보를 포함한 다른 제약들을 처리하도록 한다. 불확실한 또는 모르는 것이라고 명명된 항목의 의미는 그 항목에 대해서 조사하라는 것이다.

여러 개의 과학적 질문들이 탐색통제를 둘러싸고 있다. 어떠한 탐색 발견법들이 개인의 행동을 특성화하는가? 그것들이 행동을 얼마나 많이 통제하는가? 그러한 발견법들의 작은 집합이 긴 기간동안의 행동을 통제하는가? 또는 지식체계 (여기서는 탐색 - 통제 지식) 는 시간에 따라 계속해서 증가하는가?

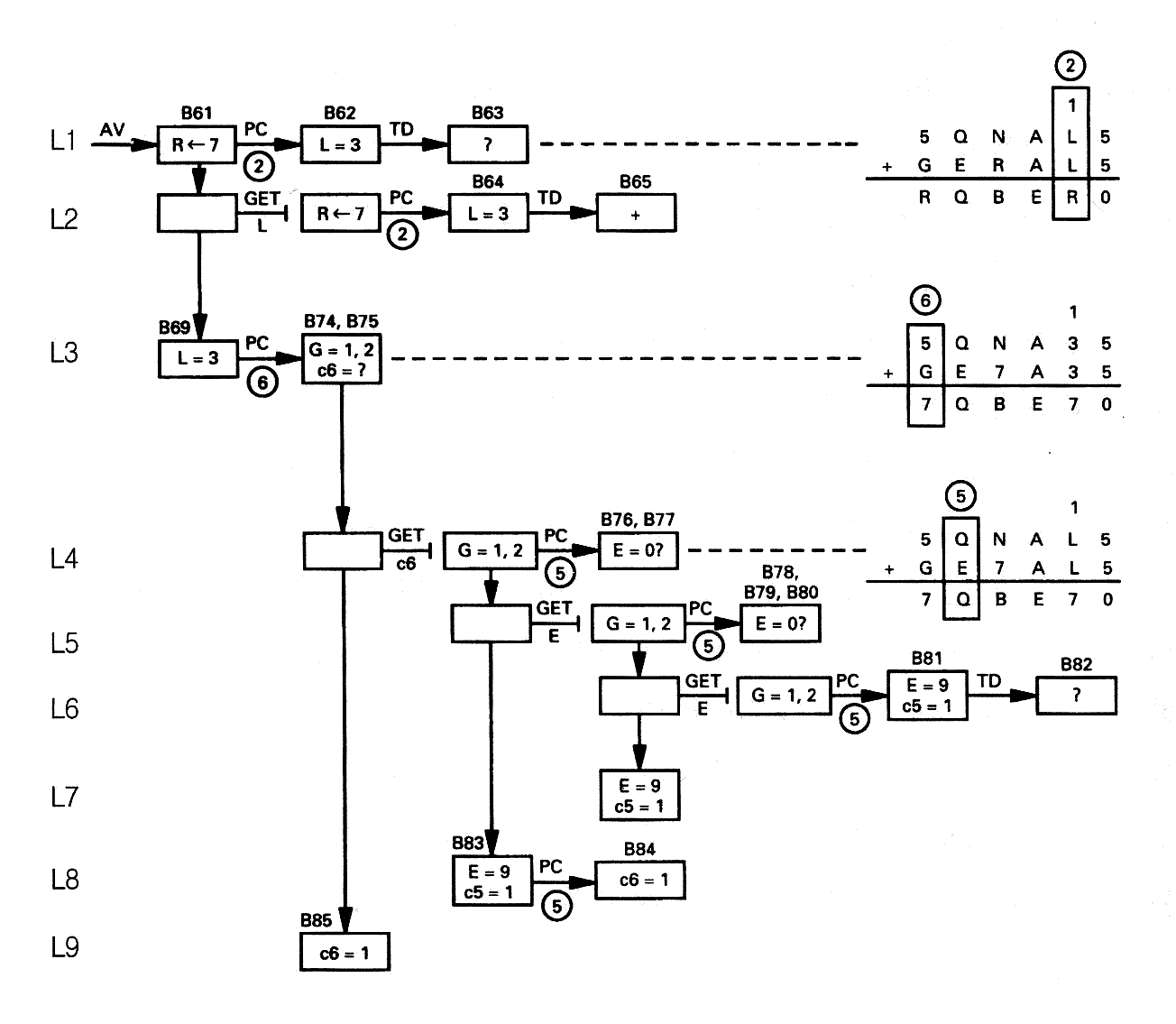
그림 4  숫자암호산술에서 하나의 복잡한 상황 동안의 문제행동 도표

그림 4 는 그림 2 의 열 8 과 열 12 사이의 프로토콜 모의실험의 짧은 단편을 보여준다. 그 행위는 다른 행들도 포함하지만, 다섯 번째행인, O + E = O 에 집중되어 있다. S3 이 그 행에서 어려움을 겪는다는 것은 전체 문제 - 행동도표로부터 분명하게 알 수 있다. 그는 열 9 에서 29 까지 그것에 대하여 계속적으로 약 10 분 동안 작업하며, 그 다음에 또다시 열 35 에서 45 까지 약 7 분 동안 작업한다. 그 어려움의 근원은 매우 분명하다. O + E = O 에서, O 의 값은 차이를 만들지 않는다 (만약 그 행이 제약방정식처럼 생각된다면, O 는 생략된다). 사실상, 이것은 E 의 값을 들어오는 올림수, 그리고 나가는 올림수에 의존하게 만든다. Cin + E = 10 Cout. 그러나 만약 올림수들이 항상 고려되지 않는다면, 혼란스러워지고 불확실해지기 쉽다. 그러므로 올림수를 완전히 무시하면 E = 0 이라는 결론에 이르게 되며, 이것은 T = 0 이라는 이미 견고하게 결정된 사실과 모순된다. 만약 그 결론이 Cin = 0 그리고 Cout = 0 임을 명확히 가정하는 데 기초했다면, 둘 중 하나를 C = 1 로 변경시키는 것을 고려하기는 쉬울 것이다. 그러나 만약 올림수들이 무시되었다면, 진행할 곳이 없는 것처럼 보인다. 어쨌든, 이것이 바로 S3 이 빠진 어려움이다.

그림 5 하나의 복잡한 상황 동안의 프로토콜의 단편

그러므로, 개인이 혼란스러워지고 그의 능력의 한계에서 어떤 것을 추리해 내고자 할 때, 그가 무엇을 할 것인지에 대한 좋은 예를 우리는 갖게 된다. 그림 5 는 이 기간동안의 프로토콜 자료를 보여준다. S3 이 진짜로 그 상황에 대해 의문을 갖고 있다는 것에 대한 명확한 표시가 있다 (B62 - 65 그리고 B80 - 82). 우리에게 —— 통합인지이론인 소어 —— 에게 있어서의 의문은 그러한 행동적 동요에 대한 통제가 기술될 수 있는가이다. 그림 4 의 문제-행동 도표는 소어의 것이며, 그것을 확립시키는 프로토콜 자료의 한계 안에서 그것은 S3 의 문제-행동 도표와 구별이 되지 않는다. 소어의 PBG 상태 상자 위의 B-숫자는 프로토콜의 해당하는 부분을 표시한다.

그 부분을 살펴보자. 그것은 열 L1 에서 시작하는데, 그곳에서 S3 은 R 에 7 을 (AV 를 통해서) 할당하고 행 3 에 초점을 집중한다. 이 단계의 사전 역사는 D → 5, 그리고 T = 0 이고, 행 2 로 올림수 1 을 갖고 있지만 그것의 상세사항들은 완전히 무시될 수 있다. 그 다음 S3 은 행 3 을 처리하고 (PC), L = 3 으로 만들고, 그 다음 이 할당을 검사한다. 이 연쇄는 밀접하게 결합되어 있다. 탐색 통제는 만약 새로운 결과가 발생하면 (R → 7), 그것이 어느 곳에 이르게 되는지 보라고 (행 3 에서의 PC 와 L = 3 에 이르게 된다) 먼저 말한다. 그 다음 그것은 만약 낱자에 대해 새로운 값이 있으면 (L = 3), 그것이 올바른지 검토하라 (L = 3 에 대한 TD) 고 말한다. PC 다음 TD 의 연쇄는 이러한 두 개의 탐색 - 통제 지식의 적용에 의해서 프로토콜 내내 반복해서 발생한다. TD 의 결과는 불확실하다 (?) 이다. 이 탐색 - 통제 - 수준 모의실험의 관점에서 보면, 이 결과는 연산자 (TD) 의 실행으로부터 단순히 출현하며, 우리는 그것에 대해 의문을 가질 필요가 없다. TD 안에서 그 효과를 갖는다는 불확실성의 사실상 기초는 만약 R 이 7 이 아니라면 L = 7 또한 가능하다는 것이다. 그러므로 7 을 포함한 두 개의 관계들의, 그 중 하나 (R → 7) 는 도출된 것이 아니라 가정되어진, 추가적인 상호작용이 있으며, 그러므로 그것은 변화될 수 있다. 이것은 불확실함을 이끌어내기에 충분히 명확하다. 그것을 탐구하기 위해 AV, PC, 그리고 TD 에서의 인지행동에 대한 모형들이 요구된다.

TD 의 결과가 불확실하다고 결정했기 때문에, S3 은 (즉 S3 에 대한 우리의 소어 모의실험은) 되돌아가서 (열 L2), 연산자 GET L 을 실행한다. 이 연산자는 시스템을 그것의 구현공간에 이르게 하며 (일반적인 방법인 무변화에 의한 막다른 상태를 통하여) 동일한 경로를 또다시 진행한다 —— 처리를 반복한다. 두 번 처리한 후에, S3 은 이제 L = 3 에 대해서 분명해진다. (또 다시, 우리의 모의실험은 이것을 단순히 TD 의 결과로 본다). S3 은 R 에 대해 확증된 값 7 을 갖고 막다른 상태로부터 출력한다 (B66). 이것과 새로운 항목 (L = 3) 은 그로 하여금 행 6 에 이르게 한다 (열 L3). PBG 는 초점 연산자들의 연산, 즉 FC 는 L 을 포함한 행들을 찾으려 하나, 하나도 발견하지 못했음을 보여주지 않지만, 프로토콜은 그것을 명백히 한다 (B72 - 73). 그러므로 앞에서도 사용되었던 것을 우리가 살펴보았던, 이 탐색 - 통제 발견법은 아무것도 생성하지 않는다. R 도 역시 여전히 새로운 것이고, 그래서 R 에 적용되는 이와 동일한 탐색 - 통제 발견법은 R 이 행 2, 4, 그리고 6 에서 발생함을 발견한다. 행 6 은 행 4 (그것은 D = 5 를 갖고 있고, 왼쪽 끝에 있으며, 올림수를 결정한다), 그러므로 행 6 이 선택되고 처리된다 (행 6 에 대한 PC). 그 결과는 행 6 에 올라오는 올림수는 모르고 (?), G 는 1 또는 2 라는 것이다.

이 결과는 분명한 것이 아니므로, TD 는 선택되지 않는다. 그 대신, 행 6 에 올라오는 올림수 c6 을 모른다는 것은 c6 에 대한 GET 연산자를 선택한다. 이것은 또다시 구현 하위목표에 이르고, 그것은 S3 으로 하여금 c6 의 근원, 즉 행 5 로 되돌아가게 하여 행 5 를 처리하게 한다 (PC). 이 탐색 통제는 제약 - 전파 발견법의 단순한 거슬러올라가는 upstream 변형판, 즉 어떤 것을 발견하기 위해 그것에 대한 지식을 갖고 있는 근원으로 가는 것이다. 행 5 를 처리하려는 첫 번째 시도는 잘 작동하지 않는다. S3 은 E = 0 을 생성했지만 그것을 불확실하다 (?) 고 명명했다. 우리가 위에서 지적했듯이, 모의실험의 관점에서 보면 0 + E = 0 은 단지 주어진 것이지만, 피험자가 0 + E = 0 에 관하여 불확실하다는 것은 놀랄 일이 아니다. E 에 관하여 불확실하기 때문에, S3 은 GET E 연산자를 적용한다 (열 L5). 그가 처음에 행 5 를 처리할 때, 그가 E 를 얻으려 하지 않았음을 주목하라. 그는 c6 을 얻으려 시도했었다. E 를 얻는 연산자는 또다시 구현 공간에 이르며 (이 단편의 처음에 행 3 에서 PC 의 반복과 마찬가지로) 그 행에서 PC 의 반복에 이른다.

또 다시 S3 은 E = 0 을 얻었지만 그는 여전히 불확실한 채로 남아있다 (또 하나가 모의실험에 주어진다). 이것은 그로 하여금 GET E 를 두 번째로 적용시키게 하며 (열 L6), 또 하나의 구현공간으로 내려가게 한다. 이번에 그는 앞의 행에서 올라올 올림수 (c5) 가 1 일 수 있음을 고려한다. 그러므로 행 5 를 처리하려는 시도는 E = 9 를 생성한다. 이것은 정확한 결과이므로, 그는 E = 9 에 (앞에서 행 2 에 대한 TD 의 적용과 같이) TD 를 적용해서 긍정적 출력을 얻는다. 이 확증된 결과는 그가 처음의 GET E 의 결과를 갖고 있음 (열 L7) 을 깨닫고 c6 을 얻는 것으로 출력하도록 하는데, 이제는 c6 은 행 5 에 대한 PC 에 의해서 c6 = 1 로 생성될 수 있다. 이것은 결국 그를 행 6 의 원래의 PC 로 되돌아가게 한다 (열 9).

그림 4 에서의 소어에 의한 행동들의 연쇄는 S3 이 진행하는 연쇄들과 매우 흡사하지만, 그것은 행 5 에 대한 그의 반복적인 시도의 단지 초반만을 보여주므로 (그림 2 를 보라), 해결해야 할 많은 것들이 있다. 좀더 일반적으로 말하면, 통합인지이론을 예시하기 위해 소어를 사용할 목적으로 이루어진 이 같은 처음의 노력은 여전히 많은 것들이 이루어지지 않은 채로 남겨둔다. 생략과 행함에 관하여 (항상 그런 것 같이) 소어와 S3 간의 어느 정도의 불일치가 남아 있다. 예를 들면, 모의실험은 S3 은 R 이 발생하는 3 개의 행 각각을 명백하게 검토하는 방법을 보여주지는 않는다 (B66 - B68). 더 중요하게, 궁극적으로 소어는 말하면서 생각하는 동시적인 과제를 수행해야만 한다. 이것은 S3 이 수행하는 과제의 일부일 뿐 아니라, 그것 없이는 인간에 의해 생성된 자료와 모의실험에 의해 생성된 자료 사이에 좁힐 수 없는 격차가 존재한다. 예를 들어, 처음의 GET E 로 출력하는 열 L7 에 해당하는 것이 프로토콜에는 존재하지 않는다. 이 단계가 어떠한 언어 행동도 생성하지 않았을 가능성도 있지만, 그것은 이론에 의해서 설명될 필요가 있다. 더 나아가, 소리내어 생각하기 thinking aloud 에 대한 이론은 에릭슨과 사이먼 (1984) 에 의해서 프로토콜을 자료로서 사용하는 것에 대한 그들의 연구에서 이미 발전되었다. 그러므로 이것은 통합이론으로부터 기대하는 자연스러운 확장이다.

우리는 여기서 모의실험의 다른 사용법을 가지고 있다. 정상적인 형식은 시스템의 행동의 흔적들을 생성하거나 매개변수들을 수치적으로 추정하기 위해서, 전체 시스템을 프로그램으로 작성해 한 번 또는 여러 번에 걸쳐서 그것을 실행하는 것이다. 우리의 암호숫자산술의 예에서, 시스템의 전체적인 기저수준 bottom - level 은 정의되지 않은 채로 남아 있다. 이것은 우리가 낮은 수준들 없이 상위수준들을 검사할 수 있도록, 즉 전체 모의실험 기록으로부터의 분석에 의해서가 아니라 사전의 설계에 의해 낮은 수준들의 영향들을 제거하는 개념적 장점을 허용한다. 또한 하위수준의 모의실험을 만들지 않는 것은 연구 효율성에 있어서도 역시 중요한 이득이 있다. 현 사례는 이것이 얼마나 중요할 수 있는지를 보여준다. 만약 하위 수준이 포함되어진다면, 그것은 매우 정밀해야만 하며, 그렇지 않으면 그것은 상위 수준을 이해하려는 모든 시도들을 오염시킬 거이다. (말하자면) PC 에서의 하나의 오류는 모의실험이 사람의 행동과 영원히 달라지게 만들 것이다. (주석 : 만약 이것에 관하여 어떠한 의문이라도 있다면, 힌트로서 하나의 오류를 생각해 보아라 ; 예를 들어, S3 이 E = 9 가 옳다고 말했다고 가정하라.) 그러나 하위수준 단위들 몇 가지들은 특히 PC 는 그것 자체만으로도 과학적 퍼즐들이다. 그러므로 회피되는 것은 연산자들을 프로그램화하는 노력이 아니라 주요한 과학적 물음, 즉 복잡한 문제 해결에서의 탐색 통제의 본질이라는 주요한 과학적 물음에 이르는 결정적인 경로에 다른 하나의 과학적 물음을 부과하는 것이다.

물론, 연산자들과 그것들의 문제 공간들에 관한 의문을 잠시 동안 적절하게 우회하는 것이 유용할지라도, 그러한 의문 역시 과학적으로 똑같이 중요하다. 통합인지이론의 주요한 특징은 수직적인 통합이다. 소어는 PC, AV, GN, 그리고 TD 에 대한 이론을 제공할 수 있어야만 한다. 그러나 그것이 소어가 제공하는 모든 것은 아니다. PC 는 산술, 추론, 그리고 어떤 결과를 획득할 것인지에 대한 선택의 혼합을 포함한다. 이런 모든 요소들은 올림수를 모를 때 (행 5 에서), G = 1 또는 2 를 도출하는 데 존재한다.

PC 가 달성되어가는 맥락은 두 개의 다중숫자 수들을 합하기 위한 산술절차들의 집합이다. 여기서 개인의 행동은 다중숫자 빼기나 (VanLehn, 1983), 단일 - 숫자 덧셈이나 뺄셈 (Sielger, 987) 과 같은 다른 과제에서처럼 그의 행동과 일치한다.

이러한 후자의 과정들은 5 장에서 논의된, 자극-반응 호환성과 선택-반응 시간들의 수준에서 작동한다. 수직적 통합은 문제해결과 즉시적 인지행동을 연결시킨다. 불행히도, 이러한 단계들은 암호숫자산술에 대해 소어에서 아직 이루어지지 않았기 때문에 우리는 이러한 통합을 예시하기 위해 그것을 사용할 수는 없다.

이 탐색 - 통제 시스템의 흥미로운 특질은 새로운, 모순된, 모르는, 불확실한과 같은 통제 기호들이 작고, 고정된 집합을 사용한다는 것이다. 이러한 기호들은 행동을 통제하기 위해서 문제해결에 대한 지식의 순간적인 상태를 서술적 형태로 부호화한다.

4 개의 구별되는 기호들의 집합은 매우 인공적인 방식처럼 보이는데, 이는 사람이 평가와 통제에 대해 더욱 더 명확하고 자세한 인식을 갖고 있다고 우리가 기대하기 때문이다.

이것은 그 사람의 실제적인 행동이 단순한 통제방식에 의해서 결정되어진다고 보여질 수 있는 정도 만큼은 틀린 것으로 나타난다. 하나의 흥미로운 가능성은, 사람은 특정한 상황에 대해서 통제 신호들의 집합을 만들어내고, 이러한 기호들은 단지 수중의 과제를 위해 필요한 정도로만 정교화된다는 것이다.

2. 삼단논법

삼단논법은 아마 대부분의 독자들에게 친숙할 것이다 —— 이에 대한 논의는 아리스토텔레스까지 거슬러올라가며, 많은 세기 동안 논리학 관심의 중심에 있었기 때문이다. 그림 6 은 몇 가지의 예들과 사물의 범주에 대한 연역인 범주적 삼단논법 categorical syllogisms 의 영역을 정의한다. 왼편의 예는 모든 배우들은 볼러들이다 all actors are bowlers, 모든 볼러들은 요리사들이다 all bowlers are chefs. 그러므로 필연적으로, 모든 배우들은 요리사들이다 therefore, necessarily, all actors are chefs 라고 읽혀진다. 이것은 구체적인 용어로 구성된 명백한 예이다. 오른편의 것 —— 어떤 B 는 A 가 아니다, 모든 B 는 C 이다 Some B are not A, all B are C —— 에서는, 전제들이 추상적이며 결론이 생략되어 있으므로, 당신은 스스로 결론을 도출할 수 있다. 필연적으로 무엇이 뒤따를까? 이것은 그렇게 쉬운 일은 아니다.

그림 6 범주 삼단논법들

삼단논법은 대전제 major premise, (A, B) 와 소전제 minor premise, (B, C) 에서 연결되어진 세 개의 항 terms 들 —— A, B, 그리고 C —— 을 포함하는 기본적인 추론 방식이다. 각 전제는 속성의 부정 negation 또는 긍정 affirmative 의 결합사 (또는 부호 sign 라고 불리는) 와 함께 양화사인, 모든 all 또는 어떤 some 으로 구성되어 있다. 어떤 A 도 B 가 아니다 No A are B 는 모든 A 는 B 가 아니다 All A are not B 와 동일하다. 그러므로 4 개의 가능한 전제 형식들 forms (또는 고전적 논리학의 용어를 이용하면 논식들 moods) 이 있고, 그것들은 그림 6 의 왼쪽에 제시되어 있다. 그것들의 약자 —— A, I, E, O —— 는 중세의 학자들로부터 시작된다. 삼단논법에서의 항들은 4 개의 다른 방법으로 배열될 수 있는데, 그것은 그림 6 의 중간에 제시된 것처럼 4 개의 격 figures 으로 불린다. 모든 변형들을 취하면, 첫 번째 전체에 대해 4 개의 형식 곱하기 두 번째 전제에 대해 4 개의 형식 곱하기 4 개의 격이 있다. 이것은 모두 64 개의 다른 삼단논법을 생성한다. 삼단논법의 결론은 말항 end terms 인, A 와 C 를 관련시키는 4 개의 형식들 중 하나로 표현되는 하나의 타당한 추론이다. 주어진 삼단논법에 대하여 9 개의 다른 결론들이, 즉 4 개의 다른 형식 곱하기 두 개의 다른 순서 (AC 또는 CA), 그리고 타당한 결론이 없는 경우 no valid conclusion (NVC) 가 가능하다. 그림 7 - 6 의 오른편에 제시된 것처럼, 하나의 삼단논법에 대해서 타당한 결론들의 수는 0 에서 4 개까지 변할 수 있다. NVC 반응은 대부분의 경우 올바른 것이고 (37 / 64), 단지 사례들의 27 / 64 만이 타당한 결론을 갖고 있다.

삼단논법 과제는 의도적인 합리적 행동의 영역의 아주 초기에 위치한다. 삼단논법 추리에 친숙한 사람 —— 예를 들어, 실험의 과정에서 그러한 삼단논법을 많이 수행한 사람 —— 은 인지 시간대의 최상층이지만 거의 확장된 과제가 아닌, ~10 초를 소요할 것이다. 과제가 친숙하지 않을 때 그 시간은 상당히 더 길어질 것이지만, 노력의 많은 부분은 그 과제를 이해하는 것과 관련되어 있다.

삼단논법과 관련된 중심적인 심리학적 현상들은 그것들이 어렵다는 것과 특정한 삼단논법의 함수로서 어려움에서의 강한 변이가 있다는 것이다. 많은 사람들, 교육을 받은 사람들조차도, 올바른 결과를 얻지 못한다. 그림에서의 두 가지 예들을 고려해 보자. 20 명씩 4 집단이 64 개의 모든 다른 삼단논법들을 해나가는 과정에서 이 두 개의 삼단논법을 시도했다 (Johnson-Laird, 1983, Johnson-Laird & Bara, 1984). 거의 모든 사람들이, 각 집단에서 19/20 가 쉬운 (왼편의) 예를 풀었다. 그러나 오른편의 삼단논법은 전혀 달랐다. 4 집단에서 9/20, 2/20, 12/20, 그리고 14/20 만이 그 예를 풀었다. (주석 : 두 삼단논법 모두 (오른편의 예처럼) 추상적 용어가 (왼편의 예처럼) 구체적 용어로 진술되었다.) 앞의 두 집단은 입학이 자유로운 이탈리아의 시립대학에서의 집단이고, 뒤의 두 집단은 미국의 비교적 일류 사립대학에서의 집단이므로, 이 둘은 모두 대학생들의 집단이지만 두 전집의 일반적 지적 수준에 차이가 있다. 이러한 중심적인 결과들은 반복적으로 검증되었기 때문에 어떤 삼단논법들은 정말로 어렵다는 것은 의심할 여지가 없다.

삼단논법이 주류를 차지했다고 기술될 수는 없지만, 삼단논법 추리에 관한 연구는 오랫동안의 활발한 역사를 갖고 있다 (Evans, 1982 ; Falmagne, 1975 ; Johnson-Laird, 1983 ; Revlin & Mayer, 1978 ; Woodworth & Sells, 1935). 그러한 활기에 대한 이유를 찾기는 어렵지 않다. 그것은 서구 문명에서의 이성과 감정 —— 머리와 가슴 —— 사이의 긴장이다. 사람들은 합리적이고 논리적일 수 있는가? 아니면 그들은 감정의 노예인가? 이성 reason 의 우월성에 대한 필수적인 조건은 사람들이 논리정연하게 생각할 수 있다는 것처럼 보인다. 논리적 추론을 한다는 것보다 논리정연한 생각을 한다는 점을 더 잘 나타내주는 것으로 무엇이 있을 수 있을까? 아리스토텔레스 이래로, 논리적 추리의 전형인 삼단논법은 그 문제를 탐구하는 사람들의 자연스러운 주의의 초점이었다. 그것들이 지금 우리에게는 다소 신비스럽지만, 배경으로의 삼단논법의 쇠퇴는 현재 기호적 논리학의 출현과 함께 발생했다.

만약 (자주 제안되었던 것처럼) 대부분의 초보적이고 특정한 형식의 추리 (삼단논법들) 가 사실상 어렵다면, 아마도 사람들은 전혀 논리적이지 않고, 합리적이지 않고, 또는 그들의 논리력에 심각한 한계들을 갖고 있을 수도 있다. 아마도 사람들은 일종의 심리논리학 psychologic 을 따를 수도 있다는 개념 —— 그들의 추리가 결함이 있는 것이 아니라 그들 자체의 법칙들을 따른다 —— 이 제시되었다. 대부분의 그러한 논의들은 공적 또는 철학적 토론회들에서 행해졌지만, 그렇다 하더라도 그것들은 실험 심리학 연구의 지속적인 흐름에 자극을 주었다.

우리에게도 마찬가지로, 삼단논법들이 어렵다는 것은 그것을 흥미롭게 만든다 (그러나 우리가 보게 되겠지만, 이것은 단지 하나의 이유이다). 인지이론은 인간을 지식수준에 점진적으로 접근하는 것으로 본다. 지식수준에서, 삼단논법은 수행 가능한 것으로 보인다 (그렇지 않은가?). 언어를 이해하는 데 물론 어려움이 있을 수 있다 —— 모든 다람쥐들은 보존된다 또는 어떤 나비들은 정원사가 아니다 또는 무엇이 필연적으로 뒤따르는가? 라는 지시문의 의미에 대해. 그러나 그러한 난관을 극복하고, 우리들은 앞을 향해 분명한 항해를 해야 한다. 만약 시간이 짧다면 어려움이 있을 수 있다 —— 시간 척도는 언제나 결정적이다. 그러나 무한정의 시간을 갖고, 성공적일 때는 단지 몇 초만을 소요하는 과제에 대해서는 어려움이 주된 요인이 아님은 틀림없다. 그러므로 사람들이 삼단논법을 풀 때 실제적인 어려움들이 출현하고 지속된다면, 그 과제는 인간이 의도적인 합리적 수준에 어떻게 접근하고 추정하는지를 탐구하는 데 유용한 사례를 제공한다. 아마도 우리는 시간적인 것 이외에 합리성에 대한 다른 유형의 한계들도 발견할 수 있을 것이다.

그림 7 삼단논법 추리의 규칙성들

과제에 과학적인 매력을 주는 어려움에 주의를 집중하는 것 이외에, 우리는 삼단논법 추리에서 인간이 어떠한 규칙성들을 보여주는지를 살펴보는 것도 역시 원한다. 5 장에서, 심리학에서 이미 알려진 규칙성들이 얼마나 많은지를 관찰하는 것을 나는 강조했었다. 삼단논법에 대하여, 심리학이 비교적 적은 현상들을 발견해온 것 같다 —— 나의 중심적인 견해와는 다소 반대되지만 —— 고 나는 인정해야만 한다. 어려움에 관한 주요한 질문들이 지배적인 것 같은데, 이는 그것에 대해서 만족스러운 답변이 이루어지지 않았기 때문이다. 그림 7 은 발견된 몇 개의 규칙성들을 보여주지만, 나는 30 개를 생성하도록 강력하게 강요되었을 것이다.

처음의 3 개의 규칙성들은 중심적인 수수께끼를 그것의 독립적인 구성요소들로 분해한다. (1) 각각의 전제들은 쉽게 이해되며 그 과제는 쉽게 진술된다. 그러나 삼단논법은 매우 어려울 수 있다. (2) 난이도의 정도는 특정한 삼단논법에 강력하게 의존한다. 우리의 두 개의 예들은 양극단을 보여주었다. 그러므로 삼단논법 추리과제 그 자체가 놀라울 정도로 어려운 것은 아니다. (3) 난이도는 지적 능력에 따라 변화한다. 왼편의 삼단논법은 쉬워서 모든 사람이 그것을 푼다. 오른편 삼단논법은 어려웠지만, 처음의 두 검사 집단에게는 매우 어려웠고 두 번째 두 집단에서는 반수가 그것을 해결했다.

(4) 가정 초기에 발견된 규칙성들 중의 하나는 분위기 효과 atmosphere effect (Woodworth & Sells, 1935) 이다. 만약 둘 중 하나의 전제라도 특칭 particular (어떤) 이면, 전칭 universal (모든) 결론들은 거의 발생하지 않는다 (이것은 물론 타당한 추리와 일치한다). 그러나 만약 두 개의 전제 모두가 전칭이면, 타당한 결론이 특칭인 경우에도, 결론들은 전칭으로 되는 경향이 있다. 사람들이 단지 전제들의 양화사들에 기초해서 결론의 양화사 (모든 또는 어떤) 에 대해 결정을 하는 것처럼 보인다. 유사한 상황이 긍정적, 그리고 부정적 부호들에 대해서도 존재한다. 부정 전제들은 부정 결론들로 귀결되는 경향이 있다. 많은 오류들은 전제들의 분위기와 일치한다.

(5) 전환 효과 conversion effect (Chapman & Chapman, 1959) 는 전제들이 뒤바뀌는 경향성이다 ; 모든 A 는 B 이다는 모든 B 는 A 이다를 의미하는 것으로도 역시 해석된다. 즉 (분위기 효과에서와 마찬가지로) 상당수의 오류들은 삼단논법의 명세화들에서의 그러한 변화를 가정함으로써 설명될 수 있다. 이 효과는 부호화 단계에서 발생하는 것으로 해석되어졌다. 추리 그 자체는 오류의 근원으로 여겨지지 않는다 (Henle, 1962). 전환 효과는 언어이해의 효과들과 추리의 효과들 자체를 구분하기 어렵다는 추리검사들에서의 일반적인 문제점을 반영한다.

(6) 격 효과 figural effect 는 여러 개의 타당한 삼단논법들 중 무엇을 사람이 생성할 것인가와 관련이 있다 (Johnson-Laird, 1983). 그림 6 이 지적하듯이, 많은 삼단논법들은 다중의 해결들을 갖고 있다. 이것들의 많은 것들은 동일한 형식의 쌍들로 이루어지지만 그것들의 항들은 다른 순서로 되어 있다. 예를 들면, 어떤 A 는 C 이다, 그리고 어떤 C 는 A 이다는 언제나 두 가지 모두 타당하거나 또는 타당하지 않다. 그림 7 에서 보이듯이, 격 효과는 어떤 순서가 생성될 것인지를 예측한다. 그 법칙은 격들의 두 가지의 경우 (AB, BC, 그리고 BA, CB) 에는 적용되지만, 다른 두 가지 경우 (AB, CB, 그리고 BA, BC) 에 대해서는 언급이 없다. 추리는 전제들을 통과하는 연쇄를 구성하는 것처럼 보인다. AB, BC 의 경우에서 연쇄는 A 에서 B, 그리고 C 로 움직이므로 A 에서 C 로 연결시킨다. BA, CB 의 경우에서 연쇄는 C 에서 B, 그리고 A 로 움직이므로 C 에서 B 로 연결시킨다.

(7) 삼단논법이 구체적 (모든 배우는 볼러들이다) 또는 추상적 (모든 A 는 B 이다) 인지는 뚜렷한 효과를 가지고 있는 것처럼 보인다 (Willkins, 1928 ; D'Andrade, 1989). 그러나 그 상황은 어려움에서의 단순한 차이 이상으로 더욱 복잡하다 (추상적 삼단논법들이 더 어렵다). 삼단논법의 내용은 (단지 그것의 구체성이 아니고) 효과를 갖고 있다. 만약 삼단논법이 그 내용과 일치한다면, 그것은 해결하기가 더욱 쉬워진다. 그러나 만약 삼단논법이 그 내용과 일치하지 않는다면, 그것은 해결하기가 더욱 어렵다. 그러므로 자연 상황들에서 제기되는 구체적 삼단논법들은 내용의 추상성이 도움을 제공하지 못하는 추상적 삼단논법들보다 비교적 더 쉬운 경향이 있다. 그러나 심리학 실험에서 발생할 수 있는 것과 마찬가지로 사실과는 다른 구체적 삼단논법들은 더욱 어려울 것이라고 기대될 것이다 (그러한 실험들이 실행된 것처럼 보이지는 않지만).

이제 우리는 통합인지이론으로서의 소어가 삼단논법 추리에 어떻게 적용되는지를 검토할 준비가 된 것 같다. 그 기초에는 통합이론이 인지 행동의 모든 영역들에 확장되어야 한다는, 그러므로 삼단논법 추리에도 확장되어야 한다는 생각이 있다. 그 전면에는 그 영역에서의 중심적인 질문, 즉 인간 합리성의 본질에 대한 물음이 있다. 그러나 삼단논법 추리에 대해 심리학이 제안한 이론들은 우리에게 그 영역을 고려해야 하는 또 하나의 이유를 제공한다. 인간들이 명제들 propositions 또는 심성 모형들 mental models 에 기초해 생각하는지에 대한 문제. 이러한 두 개념들, 특히 심성 모형은 인지과학의 다른 영역들에서 강력한 역할을 한다 (Gentner & Stevens, 1983). 이와 같은 개념들은 모두 앞의 세 장들에서 기술된 소어의 부분은 아니다. 그러므로 추가적인 물음은 인지과학에서 강력한 역할을 하지만 소어에서는 생소한 주요 개념들에 소어가 어떻게 대처해야 하는가이다.

2.1 명제와 모형

우리는 인간들이 명제보다는 심성모형을 사용하여 추리한다는 가설에 주의를 집중하려고 한다. 이것은 필립 존슨-레어드 Philip Johnson-Laird (Johnson-Laird, 1983, 1988b) 에 의해서 가장 명확하게 형식화되었다. (주석 : 존슨 - 레어드 오랫동안 삼단논법과 다른 형태의 논리적 추리에 관한 심리학적 연구에서 가장 활동적이었던 연구자들 중 한 사람이다 (Wason & Johnson-Laird, 1972). 그와 그의 동료들은 동일한 사람들의 집단에 의한 모든 가능한 삼단논법에서의 자료를 글로 제공한 유일한 연구자이고, 그러므로 우리가 했던 것처럼, 다른 연구자들도 그들 자신의 이론들을 위해 그 자료를 사용할 수 있다. 좋은 자료집합들을 가용적으로 만드는 것을 통합이론들의 사업을 위해 중요하다.) 그 가설은 매우 일반적으로 취급되어지지만, 우리는 삼단논법 추리에 초점을 유지할 것이며, 삼단논법 추리는 또한 존슨 - 레어드가 아주 자세하게 탐구한 과제이다.

그림 8 심성모형들에 의한 삼단논법 추리 (Johnson-Laird, 1983 을 따름)

그림 8 은 삼단논법에 대한 존슨 - 레어드의 심성 모형의 예를 보여준다. 한 사람이 삼단논법을, 예컨대, 어떤 B 는 A 가 아니다, 그리고 모든 B 는 C 이다를 읽을 때, 그는 전제들이 주장하는 구체적인 상황에 대한 내적 모형을 구성한다. 예를 들어, 그림에서의 모형 0 은 전제 P1 에 대해 구성될 수 있다. 각 열은 특수한 특성들 (A, B, C, . . .) 을 갖고 있는 한 개인을 나타내며, 여기서 앞에 붙어있는 o 는 임의선택적 optional 임을 의미한다. 그러므로 A 일 수 있는 한 사람이 있고, A 이면서 B 일 수도 있는 또 한 사람이 있고, B 인 세 번째 사람이 있다. 모형에서의 경계선은 마지막 사람은 분명히 A 가 될 수 없음을 표시한다. 이것이 바로 모형에서 부정 negation 이 부호화되는 방법이다.

두 번째 전제가 읽혀질 때, 그 상황의 단일한 모형을 만들기 위해, 그것은 원래의 모형에 추가된다. 이것이 모형 1 이고, 원래 모형에서의 B였던 사람들은 이제 모두 C 이다. 그러나 추가적으로 또 하나의 개인이 만들어지는데, 그는 임의선택적으로 단지 C 이다. 즉 그는 C 일 수도 있다. 등호부호 (=) 는 연결된 특성들이 틀림없이 함께 움직이는 것을 표시한다. 그러므로 그 사람은 구체적 상황에 대한 기호적 모형을 만들어낸다. 각 유형에서 단지 한 사람만이 제시되었지만, 물론 유형들에 대해 어떠한 수도 가능하다 —— 그것은 부호화 과정에 의존한다.

새로운 사실들은, 단순히 그 모형을 검토함으로써 발견될 수 있다 —— 그것들은 단순히 판독된다 read off. 삼단논법 추론의 목적은 A 와 C 를 포함하는 어떠한 사실 —— 즉 소위 말항이라고 불리는 이들 둘을 연결시키는 사실 —— 을 찾는 것이다. 예를 들어, 세 번째 개인은 C 이지만 A 는 아니다 (경계선). C 이면서 A 인 또 다른 개인 (두 번째) 이 존재하기 때문에, 참 true 인 것은 모든 C 는 A 가 아니다 (어떤 C 도  A 가 아니다와 동일함) 가 아니고 어떤 C 는 A 가 아니다 이다. 어쨌든, 이 두 번째 개인의 존재는 또 다른 결론으로 귀결되지 않는데, 이는 그가 임의선택적 (o) 이며 그러므로 그 모형에서 필연적으로 발생할 필요는 없다.

검토에 의해 얻어진 결론은 단지 이 특정한 모형에서만 유지되지만 이것이 필연적으로 존재들과 일치되도록 만들어질 수 있는 유일한 모형은 아니다. 사실상, 표준적인 모형-이론적 견해 (Addison, Henkin, Tarski, 1972) 에 따르면, 하나의 결론은 단지 그것이 모든 가능한 모형들에서 참일 때만이 필연적으로 참이다. 존슨 - 레어드 이론은 인간들은 이러한 견해의 논리를 인식하며 처음의 결론 (즉, 어떤 C 는 A 가 아니다) 에 대한 검사들을 제공하는 대안적인 모형들을 생성하려고 시도함을 가정한다. 예를 들어, 모형 2 도 역시 전제들과 일치하는데, 여기에서는 세 명의 개인이 있고 그 중 한 사람은 C 이면서 A 이지만, 단지 C 인 개인은 존재하지 않는다. 이 모형에서도 마찬가지로 어떤 C 는 A 가 아닌 것으로 밝혀지고, 그러므로 그 결론은 유지된다. 이러한 두 모형들은 가능성들을 완전히 다 검토하는데, 이것은 그 결론이 필연적으로 뒤따르며 최종결론으로 생성될 수 있다는 것을 의미한다.

심성모형에 기초한 삼단논법 이론은 사람이 어떻게 다중의 모형을 생성하는가 그리고 어떻게 그는 충분한 (모든 것을 포함하는) 집합이 생성되었음을 아는지를 기술해야만 한다. 삼단논법들의 단순성 때문에, 단지 몇 개의 모형들만이, 빈번하게는 하나의 모형만이 요구되어진다는 것이 밝혀졌다. (주석 : 일반적인 양화 표현의 타당도를 확증하기 위해 모형들의 무한한 집합이 필요하지만.) 어려움에 대한 존슨 - 레어드의 이론은 모형의 수에 기초한다. 사람들이 생성할 초기 모형은 각 전제 형식에 대한 명시적인 부호화 규칙을 제시함으로써 기술될 수 있다. 이러한 하나의 초기 모형으로 충분한 삼단논법의 집합을 결정하는 것은 매우 쉽다. 이것들은 쉬운 문제들이다. 그 이론은 하나 이상의 모형이 요구될 때 추가적 모형의 생성을 기술하지 못한다. 이것은 내적 표상에 대한 많은 문제들, 사람이 사용하는 심리적 연산들의 유형들, 그리고 그것들이 어떻게 사용되는지에 달려 있다. 그러나 하나의 모형 또는 다중 모형들의 사이를 분리하는 것이 그 이론에 많은 설득력을 제공하기에 충분하다는 것이 밝혀졌다. (주석 : 존슨-레어드 (1983) 는 2-모형과 3-모형 삼단논법들 간을 구별하는 좀더 강력한 형태의 이론을 제시한다. 그러나 그가 그 당시 생각했던 것보다 문제들이 더욱 복잡하다는 것이 그 중간단계의 시기 동안에 명확해졌다.)

모형 - 이론적 추리는 명제들과 새로운 명제들을 도출하기 위해 추론 규칙들을 적용하는 작업과 동일하지는 않다. 요구되는 명제적 추론은 양화사들을 포함하므로 완전히 명확하지는 않다. 그림 9 는 무엇이 포함되는가를 보여준다. 첫째, 우리는 전제들과 원하는 결론을 일차술어계산법 first-order predicate calculus 에서의 표현들로 전환시킨다. 범주 A, B, 그리고 C 는 술어 A (x), B (x), 그리고 C (x) 가 된다. 예를 들어, 만약 x 가 범주 A 의 구성원이라면 A (x) 는 참이고 그렇지 않으면 거짓이다. 그러므로 어떤 B 는 A 가 아니다는 B (x) 이고 A (x) 가 아닌 x 가 존재한다고 전환된다. 달리 말하면, B (x) 는 참이고 A (x) 는 거짓인 한 개인이 존재한다. 유사하게, 모든 B 는 C 이다는 모든 x 에 대해, 만약 B (x) 가 참이면, 그러면 C (x) 는 참이다로 전환된다. 이러한 두 전제들이 주어진다면, 과제는 P3 에 해당하는 명제, C (x) 이며 A (x) 가 아닌 x 가 존재한다가 뒤따르는지를 증명하는 것이다.

그림 9 명제적 추론에 의한 삼단논법 추리

추론 규칙, 공리, 증명의 유형이 다른 많은 다양한 (그러나 동등한) 형태의 술어계산법들이 존재한다. 우리는 에빙하우스 Ebbinghaus, 플룸 Flum, 그리고 토머스 Thomas (1984) 를 따를 것인데, 이 방법은 공리를 사용하지는 않지만 추론 규칙들에서 모든 것을 구체화하고 추가적인 파생된 규칙들의 사용을 허용한다. 그것의 형식은 가정을 하고, 주어진 이러한 가정들에 의해서 추리하고, 그 다음 그 가정들을 제거한다. 그러므로 그림 9 에서의 한 증명은 가정된 것들에 대한 행, 결론 내려진 것에 대한 행, 그리고 오른편에 그 단계를 정당화하는 추론 규칙을 표시하는 행을 갖고 있다. 무엇이 요구되는지에 대한 느낌을 제공하기 위해, 단순히 그 증명을 따라가며 설명해 보자.

(1) 전제 P1 은 하나의 결론으로서 도입된다. (2) 어떠한 가정이라도 만들어질 수 있는데, 이는 결론으로 나올 수 있는 것은 그 가정에 조건적으로 남아 있을 것이기 때문이다. 물론 증명을 찾는 용이성은 유용한 선택들을 하는데 의존한다. 이것은 x 의 영역으로부터 임의적인 개체 (a) 을 갖고 있는 전제 P1 의 실례이다. (3, 4) 하나의 가정된 연언으로부터 그것의 각 부분들은 결정될 수 있다. 그러므로 결론 행으로 이전된다. 그것들의 타당성은 그 가정에 조건적으로 남아 있다. (5) 이제 전제 P2 가 도입된다. (6) 보편 양화 quantification 는 어느 실례화라도 결론이 되는 것을 허용한다. 그러므로 P2 는 개체, a 에 대해 특수화될 수 있다. (7) 추론 규칙들은 단지 결론들과 동일한 가정들을 결합시킨다. 임의적 가정들이 추가된다 (물론 가정들이 임의적으로 생략될 수는 없다). 그러므로 단계 6 에서의 표현은 다른 곳에서 사용된 가정들에 의해 참이라고 선언된다. (8) 이제 단계 3 과 7 은 C (a) 를 얻기 위해 전건긍정 modus ponens (A, 그리고 A ⊃ B 로부터 B 를 추론) 에 의해 결합될 수 있다. (9) 그 다음, 이 결론은 단계 4 에 결합되어질 수 있는데, 이는 만약 두 개의 표현들이 결론들이라면, 그것들의 연언도 마찬가지이다. (10) 특수한 개체 a 에 대하여 단계 8 에서 C (x) ∧ ¬A (x) 가 결론으로 내려진다. 그러므로 C (x) ∧ ¬A (x) 를 참으로 만드는 x 가 존재한다는 약한 결론을 내리는 것이 가능하다. (11) B (a) ∧ ¬A (a) 의 가정아래 추론이 진행된다. 이제는 무조건적인 unconditional 결론이 만들어지는 것이 필요하다. 첫 번째 단계는 특수한 변항 a 로부터 가정을 제거해내는 것이다. 만약 B (a) ∧ ¬A (a) 의 가정 아래서 그 결론이 유지된다면, B (x) ∧ ¬A (x) 를 참으로 만드는 x 가 존재한다는 가정 아래서 그 결론이 유지될 것이다 (그러한 x, 즉 a 가 존재하기 때문에). 이러한 가정의 변경은 단지 단계 10 에서의 결론인 a 에 의존하지 않을 때에만 타당하다. 그러나 단계 9 는 그 표현에서 a 의 제거를 정확히 성취했다. (12) 최종적으로, 단계 11 의 가정이 타당한 것으로 알려졌기 때문에 (단계 1), 그것의 결론은 절대적이다. 이 규칙은 긍정논법의 또 하나의 형식, 즉 A, 그리고 A ⊃ B 에서부터 B 로 결론짓는 것이다. 단계 12 는 원하는 결론인 P3 이다.

명제적인 방법들을 기초로 인간 삼단논법적 추리에 대한 이론을 고려하는 것은 가능하다. 그림 9 에서의 단계들의 연쇄는 쉽지 않아보이고 인간이 실시간으로 이것들을 따라갈 것이라고 기대하지는 못할 것이다. 사실, 이것이 과정 이론으로서 사용되는 것은 기대되지 않을 것이며, 오히려 어려움을 나타내는 표시로 사용될 것이 기대된다. 이 특정한 형식화에서, 쉬운 삼단논법이나 어려운 삼단논법의 증명들은 대략 같은 수의 단계들을 취하지만, 다른 형식화는 더 좋을 수도 있다. 그러나 명제에 기초한 이론들에 대해서는 추가적인 요건들이 있다. 증명은 발견되어야 하는 것이지, 완전히 만들어지는 것은 아니다. 그림 9 에서의 증명은 상당한 창조력을 요구한다. 또한 증명은 단지 검증절차이다. 시도되는 결론은 생성되어야만 한다. 이러한 것들은 일반적인 명제적 이론의 형식화에 어려움을 추가시킨다. 그러나 우리 과제는 그것을 하는 것이 아니고, 단지 명제적 추리의 본질을 예시하는 것이다.

수중에 있는 모형-기반적 그리고 명제-기반적 추리에 대한 이러한 예들을 갖고, 모형들과 명제들의 본질을 좀더 면밀히 검토해 보자. 그러 주제에 대하여 쓰인 것들의 양을 생각했을 때, 우리는 비교적 피상적인 검토에 만족해야만 한다. 그러나 본질적인 것들은 분명해질 수 있다. 그렇다 하더라도, 우리의 주목적은 그러한 논의의 중심에 자주 있는 것은 아닐 것이다.

모형이나 명제는 둘 다 표상들이다. 우리가 2 장에서 보았듯이, 시스템이 대상을 부호화할 수 있고 그것의 변형을 어떤 내적 대상과 활동으로 부호화할 수 있을 때 (이것들은 적절한 표상이다), 시스템의 외부 세계에 존재하는 어떤 대상에 대한 표상을 갖는다. 그리고 그 다음 부호화된 변형들을 부호화된 대상에 적용시켜서 부호화된 결과를 생성한다, 그리고 마지막으로 외부적 변형과 일치되게, 이 결과를 외부세계에서의 어떤 측면으로 번역한다. (현재의 목적을 위하여) 두 경로들이 동일한 점에서 종결될 때, 내적 경로는 표상법칙을 만족시킨다. 이런 의미에서 명제들과 모형들 두 가지 모두는 표상들이다. 둘 다 외부 세계를 표상하는데 사용될 수 있다. 더 나아가, 명제나 모형 모두 기호적 구조들일 수 있으며, 둘 다 광범위한 표상 법칙들을 만족시키기 위하여 구성될 수도 있다 (그러나 모형들은 2 장에서 논의된 유사 analogue 표상에서와 같은 기호구조들일 필요는 없다).

표상들은 2 가지 차원들에 따라 특성화될 수 있다 —— 그것들의 적용범위 scope (그것이 표상할 수 있는 것) 와 그것들의 처리비용 processing cost (그것들을 사용하는 데 요구되는 처리가 어려운 정도). 명제와 모형은 두 차원에서 모두 차이가 있다. 이것은 그것들의 표상형식, 그리고 그것들의 형식과 외부 대상 간의 대응에 있어서의 차이를 반영한다. 우리는 형식부터 시작할 수 있다. 형식에서의 구별은 범주적이고 중심적인 것 —— 명제는 한 형식을 갖고 모형은 다른 형식을 갖는다 —— 이어야만 하는 것 같지만, 본질적인 구별은 처리의 구별이다. 결과적으로, 명제와 모형의 개념들은 원형 prototypes 과 더욱 유사하며 그것들의 형식들은 범주적으로 구별될 수는 없다.

그림 9 는 여러 개의 작은, 그러나 일차 술어 계산법에서의 원형적인 명제들을 보여주었다. 그것들은 여러 가지 장치들 —— 논항들, 논리적 연결사 (그리고 and, 또는 or, …), 술어와 양화사 (또는 예에서는 나타나지 않은 함수들) —— 의 사용에 의하여 주장들을 형성한다. 핵심은 연결사의 반복적 특성으로부터 제기되는 구절의 구조화 phrase structuring 인데, 여기에서 연결사의 논항들은 참의 값을 갖고 그 연결사들은 차례로 참 값들을 생성하는 명제들을 생성한다. 명제와 외부세계 사이의 중심적인 대응은 참 truth 이다 —— 각 명제는 논항들, 술어, 함수들의 대응 아래서 명제가 표상하는 세계에 대하여 참이어야만 한다. 어떻게 그러한 전체 표상 루프가 존재하는지를 보기는 용이하다.

명제 표상은, 범위에서는 보편적 universal 일 수 있고 요구되는 처리에서는 어려울 hard 수 있다. 표상적 측면에서 본질적으로 표상될 수 없는 것은 아무것도 없다. 이것은 일차술어 계산법에서 집합이론과 수학의 모든 것들을 형식화할 수 있는 능력에 반영되어 있다. 이에 대응하여, 그러한 표상들을 사용하는 처리는 매우 어려울 수 있다. 예를 들어, 술어계산법에서 두 개의 명제들, 즉 하나의 대상을 독특하게 특성화하는 두 개의 명제들을 고려해 보자. 그 두 대상들이 사실상 동일한 대상인지를 결정하는 것은 일반적으로 임의적으로 어려워질 수 있는 정리 - 증명 문제이다. 마찬가지로, 한 대상의 내적인 명제적 특성화에서 그것을 구성하는 것과 같이, 그것의 어떤 외적 표현으로 이동하는 것 역시 도출 또는 정리 - 증명 문제이다. 이것은 놀라운 것이 아니다. 명제적 표상은 임의적 지식체계들의 표현을 허용하고, 그러므로 그러한 지식을 처리하는데 제기되는 문제들은 틀림없이 그 문제들만큼 어려울 것이다.

모형 표상은 범위에서 한계가 있지만 처리하기는 쉽다. 모형은 구조-대응 원리 structure-correspondence principle 에 충실하기 때문에 단순성이 얻어진다. 모형 표상 (즉, 내적 자료구조) 은 요소들 parts 과 관계들 relations 을 갖고 있다. 이들은 각각 그 모형이 표상하는 외부세계에 있는 것의 요소와 관계에 일치한다. 그러므로 내적 모형의 각 개별적 요소와 관계는 어떤 것인지를 표상한다. 완전성 completeness 또는 망라성 exhaustiveness 은 함의되지 않는다. 외부세계는 많은 다른 요소들, 관계들, 그리고 여러 가지 것들을 갖고 있을 수 있다 —— 세계는 항상 어떠한 모형에 비교해 봐도 제한할 수 없을 만큼 풍부하다. 이것이 모든 표상들이 작동하는 방식이라고 생각될 수도 있지만, 그림 9 의 술어계산법 표현들을 살펴보면 그렇지 않다는 것을 볼 수 있을 것이다. 예를 들어, P2 에서 그 표현 (표상인 자료구조) 의 요소들에 해당하는 외부세계의 것들은 아무것도 없다. 즉 (y), B (y), ⊃, 또는 나머지 것들에 해당되는 것이 없다. B (y) 가 무엇인가와 일치해야만 한다고 생각할 수도 있지만, 그것은 그 함의의 선행한 antecedent 측면에서 발생한다 —— 만약 B (y) 가 유지되면 C (y) 도 역시 유지되지만, B (y) 가 유지하고 있는 것이 거기 있을 필요가 없다. P2 가 하는 것은 외부 세계에 대하여 진실을 표현하는 것이다. 그것이 바로 명제 표상력의 많은 부분의 근원이다. 물론, 모형의 모든 측면 (자료 구조) 이 표상하는 것은 아니다. 모형은 물리적 대상이며, 그러므로 그것 자신의 무한정한 측면들과 특성들의 집합을 포함한다. 그러므로 그 원리는 자료 구조로서의 모형의 어떤 특성화를 그것 자신의 독특한 요소들과 관계들에 의해 주어진 것으로 취급한다. 그리고 이러한 것들 때문에, 각각은 지시물에 해당되는 것들을 갖고 있어야만 한다.

이 원리의 중요한 결과는 대응-같은, 그리고 계산 counting 과정들이 그 모형을 갖고 작업하는 데 충분하다는 것이다. 대응과 계산은 근본적으로 비용이 저렴한 과정들이다. 두 표상들이 동일한 대상을 표상하는가를 검사하는 것은 단지 그것들의 요소들이 일치되게 만든 다음 동일함을 검사하는 것만을 요구하는데, 그것 자체가 대응과정이다. 만약 대응에서 불완전성이 발생하면, 그것은 곧바로 명확해진다. 만약 대응에서 실패가 발생하면, 더 이상의 처리가 결과를 뒤집을 수 없다는 것이 알려진다. 대상은 표상의 명세 사항들로 구성하는 것은 만약 모형이 형판 template 처럼 사용된다면 가능하다 —— 또 다시 대응-같은 과정, 그러므로 처리는 비용이 저렴할 뿐 아니라, 그것은 강력한 방식으로 제한되어 있다.

저렴한 처리에 대한 대가로 무엇인가 지불되어야만 한다. 그것은 바로 표상 범위이다. 모든 것들이 모형에서 표상될 수 있는 것은 아니다. 표상되기 어려운 것 그리고 모형이 그것의 한계점을 보여주는 것은 환경에 관한 불완전한 지식의 다양한 형식들이다. 특히, 부정 negation, 선언 disjunction (대안들 alternatives), 임의선택성 optionality, 조건문 conditionals, 제약들 constraints, 교환 trade-offs, 불확실성 uncertainty, 등을 포함하는 지식을 모형에서 표상하기는 어렵다.

그 상황은 이 점을 생각해보는 것으로 좀더 분명해질 수 있다. 어느 사람이 어떤 질문에 대한 답을 얻기 위해서 당신의 집으로 올 것이라고 알려졌다고 생각해 보자. 그것에 대한 모형, 출입구에 대한 모형과 그 사람에 대한 모형을 갖고 있는 모형을 구성하는 것은 쉽다. 그러나 그 사람이나 또는 그의 하인이 도착할 수도 있다는 것을 상상해 보아라. 이제는 두 개의 다른 상황이 있다. 그러나 그 사람과 그의 하인은 매우 유사하기 때문에, 그리고 단지 그들의 출현과 정보 수령자로서의 그들의 기능만이 관련이 있기 때문에, 문 앞에 있는 추상적인 사람을 갖고 있는 하나의 모형을 구성하는 것은 여전히 가능하다. 그러나 그가 도착할 수도 있고 또는 그가 전화를 걸 수도 있음을 상상해 봐라. 또한 그가 도착할 수 있지만 만약 그가 8 시 전까지 도착하지 않는다면 당신은 그의 집으로 가야만 하는가? 어느 시점에선가 그러한 대안들을 하나의 복합적 모형에서 결합시킬 방법이 없게 된다 (중요한 모든 것들을 제거하지 않는다면). 모형에서 결과적으로 발생한 실제적인 상황을 표상하는 것은 비교적 분명해 보인다. 어려움을 만들어 내는 것은 이러한 다양한 상황들에 관한 지식 상태에서의 변산이다.

단일한 모형이 실패할 때 (그리고 명제들에 의존하지 않으려고 할 때), 일반적인 탈출구가 있다 —— 하나의 모형이 대안들 중 하나에 해당하도록, 모형들의 집합을 하나하나 열거하는 것이다. 이제 처리는 별개의 모형들에 대하여 반복함으로써 진행되어야만 하며, 그러므로 더욱 비용이 많이 들게 된다. 만약 변이에 대해서 단 하나의 차원만 있다면, 처리의 증가는 단지 선형적이다. 그러나 다중의 임의선택적 그리고 조건적 상황들이 제기될 때는, 그 증가는 쉽게 조합적 combinatorial 이 된다. 그러므로 열거의 사용 가능성에서의 핵심적 문제는 요구되어지는 처리이다.

명제적, 그리고 모형적 표상들은 또 하나의 중요한 방식에서 차이가 있다. 명제들은 참조틀 문제 frame problem 를 갖고 있지만, 모형은 그렇지 않다. 참조틀 문제 (Mccarthy & Hayes, 1969 ; Pylyshyn, 1987) 는 어떤 행위가 취해질 때, 어떠한 배경지식 (참조틀) 이 타당하게 남아 있는가와 관련이 있다. 탐색 공간에서 새로운 상태 (이것은 표상에 대한 행위이다) 를 생성하기 위해 한 상태에 연산자를 적용할 때, 그 문제가 제기된다. 그 상태들이 명제적으로, 즉 외부 상황에 대해 연언적으로 참을 유지하는 주장들의 집합에 의해 표상된다고 하자. 연산자의 적용이 외부 상황에서의 실제적인 변화를 표상한다고 하자. 즉 새로운 상황은 예전 것과는 다르다 ; 행위자가 원래의 상황에 관해 추가적 지식을 간단하게 얻는 것은 아니다. 연산자에 의해서 직접적 directly 으로 영향을 받는 결과적인 상황의 새롭고, 변화된 측면들 (즉, 그것의 주장들에서 명명되어지는) 을 진술하는 새로운 주장들의 집합과 그 연산자를 연합시키는 것은 언제나 쉽다. 그러나 간접적 indirect 인 결과들은 무엇인가? 특히 원래 상황에서 적용된 다른 모든 주장들에 대해서는 어떤가? 그것들 중 어느 것이 참이고 또 어느 것이 거짓인가, 그리고 어떤 다른 주장들이 이제 유지되는가? 참조틀 문제는 결과적인 표상을 어떻게 계산하는가이다. 그리고 근본적인 어려움은 일차술어 계산의 계산력이 있는 명제적 표상을 갖고서는 연산자 적용의 결과들을 포함할 방법이 없다. 참조틀의 물음에 일반적으로 답하는 것은 임의적인 정리를 증명하는 것과 똑같다. 이것은 처리가 어려운 명제적 표상의 하나의 예이다.

다른 한편, 모형에서는 참조틀 문제가 없다. 좀더 정확히 말하면, 참조틀 문제에 대한 직접적이고 만족스런 해결책을 갖고 있다. 모형에서 허용되는 연산자들은 모형의 적절한 측면들을 수정함으로써 새로운 상황을 간단하게 만들어낸다. 수정되지 않은 상황의 측면들은 단순히 수정되지 않은 채로 있다. 물론 단순히 내적 연산자들이 외적인 연산자들을 표상하고, 그러므로 그것들의 효과들을 표상하기 때문에, 이것이 효과가 있다. 참조틀 문제의 회피는 부분적으로 (지식의) 복잡한 상황을 표상하는 능력이 없기 때문이며, 그러므로 그것은 제한적인 범위를 반영한다. 그와 더불어 내적-모형 연산자에서 포착되지 않는 외적-세계 변환의 숨겨진 효과들이 분명히 있을 수 있다. 이것은 특정한 표상의 실패로서 취급되어지며, 어떤 특수한 갱신하는 updating 어려움 (참조틀 문제) 의 반영으로서는 취급되지 않는다. 표상적 오류는 어떤 종류의 표상에서도 언제나 존재하는 일상적 가능성이다. 여기에 마술은 없다. 단지 한계점들을 수용하는 결과만 있을 뿐이다.

2.2 주석이 달린 모형

모형으로부터 외부 상황으로의 구조-일치 대응에 의해 정의되는 모형들은 이론적으로 명쾌하며, 모형이론이라 불리는 논리학의 한 분야에서 확고한 기초를 갖고 있다. (주석 : 그러나 모형이론에서는 용어가 뒤집혀진다. 사람에게 하나의 명제적 시스템이 주어지고, 그것의 의미를 하나의 모형에서 실현한다. 그러므로 그 모형은 외부세계의 역할을 한다 (모형이론은 그 모형의 일부로서 의미 영역으로의 대응을 포함하는 경향이 있다). 우리의 고려사항들에서, 그 모형은 밖에 있는 외부세계의 하나의 표상이며, 그 표상은 정상적인 분석에서 또 하나의 표상을 갖지 않는다.) 그러나 실세계에 적응하려고 하는 행위자의 목적들에 대해서 모형들은 너무 제한적이다. 그것들은 표상의 범위의 관점에서 너무 많은 것들을 잃는다. 좀더 풍부한 표상을 고려하지 않을 이유는 없다. 그것들이 사용될 수 있는지에 대한 궁극적인 준거는 행위자가 직면하는 실시간 제약들을 행위자가 만족시킬 수 있는 충분한 한계 안에서 그것들의 처리가 유지될 수 있느냐의 여부이다. (주석 : 표상의 실제적 또는 기대되는 처리비용은 선험적으로 확정된 처리 한계들과는 분명히 다르다. 후자의 것이 좀더 중요한 것 같다.)

모형들이 여전히 대응-같은 처리의 본질적인 것들을 유지하면서 명제를 갖고 모형을 증대시키는 것은 가능하다. 그러한 첨가물 augmentations 을 갖고 있는 모형은 주석이 달린 모형들 annotated models 로 불려질 것이다. 필요한 곳에서는, 우리는 구조-일치 원리를 엄격하게 만족시키는 표상들은 순수 모형들 pure models 이라고 부를 것이다. 주석의 좋은 예는 존슨-레어드 모형 표상 (그림 8) 에서 볼 수 있다. 그것은 모형의 주어진 요소가 임의선택적이라는 꼬리표 tag 를 허용한다. 그 꼬리표는 그 모형에서 그것이 적용되는 개인 앞에 붙여진다. 그 꼬리표는 두 개의 순수 모형들, 즉 하나는 개인이 존재하는 것과 다른 하나는 개인이 존재하지 않는 모형을 회피하는 한 가지 방법이다. 이것들은 임의선택성 주석 optionality annotation 을 갖고 있는 단일한 모형에 설치되어질 수 있는데, 이는 임의선택을 다루는 처리가 그 모형의 일부분으로 좁혀지기 때문이다. 만약 다중의 임의선택들이 한 모형에 존재한다면, 각각은 독립적이다. 그러므로 각각 두 개의 임의선택들을 갖고 있는 그림 8 의 예에서 보듯이, 모형으로 생각되는 많은 표상들은 순수한 모형들이 아니며 (즉, 그것들은 일치 원리를 엄격하게 따르지 않는다), 이런 저런 종류의 주석을 덧붙임으로 해서 표상 범위를 증가시킨다. 임의선택 optional 이외에, 모형에서의 한 대상에 존재하지 않음 not-exist 이라는 꼬리표가 붙여질 수도 있다. 즉, 모형은 특정한 대상이 없는 외부 구조를 표상한다. 이것은 분명히 일치 원리를 위반하지만, 그것은 여전히 그 모형이 그 요소의 부재에 관한 국소적 검토와 일 대 일 대응을 하도록 허용하는 방식으로 있다. 또 하나의 주석은 많다 many 인데, 여기에서 그 모형의 대상은 많은 일치되는 외부 대상들과 대응된다. 또 하나는 쌍 pair 인데, 이것은 대응들의 정확한 숫자를 명세화한다.

주석이 모형의 한 가지 요소에 첨가되고 그 요소에 적용되는 한, 주석을 일종의 명제로 생각하는 것은 유용하다. 주석의 본질은 그것이 단지 그것의 요소가 포함되었을 때에만 처리를 요구한다는 것인데, 그러므로 그것의 처리는 국소적이다. 모든 주석들을 자세히 살펴볼 필요가 없고, 그리고 그것들이 제약들의 임의적 집합인 것처럼 그것들을 취급할 필요도 없다. 주석의 가장 단순한 형식들은 임의선택 또는 많다와 같이 그것들이 부착된 대상을 단순히 지칭하는 명제들이다. 그러나 주석들의 범위는 그것들이 주석의 지점과 상대적으로 정의된 모형의 다른 요소들을 지칭하도록 함으로써 증가될 수도 있다. 예를 들어, 왼쪽 (의자) left (chair) 이라는 주석은 부착된 요소와 관련해서 다른 요소를 검토할 것을 요구한다. 그것은 또한 모든 요소들의 처리에 있어서 다른 요소들에 부착된 주석들의 가능성이 고려되어야 한다는 것을 의미한다 (그러나 처리는 여전히 비교적 국소적 탐색들로 제한될 수 있으며, 그러므로 그것은 통제아래에서 유지될 수 있다). 주석들의 범위가 증가함에 따라, 그것들은 완전한 명제 표상들과 차이가 없게 된다. 그러므로 표상의 처리는 그것의 대응-같은 성격을 잃는다. 다중의 주장들의 결과들과 함의들이 그 처리를 많이 지배할수록, 단순한 대응, 주사 scanning, 그리고 계산이 점점 더 부족해진다. 주석이 달린 모형들의 주요한 요점은 증가되는 처리의 대가로 순수모형의 엄격한 범위 요건들을 완화시킬 수 있는 가능성이지, 주석이 달린 모형들과 완전한 명제 표상들 사이에 분명한 경계선이 있다는 것이 아니다. (주석 : 명제적 형태의 한계점들에 대하여 만들어진 구분들은 변수들과 양화사들의 숫자와 유형을 포함한다. 예를 들어, 그것들은 표상이 (box A) 또는 box (A) 와 같은 표시법을 사용함으로써 명제같이 보는가 하는 문제의 여부를 포함하지는 않는다. 논리적 표현들의 형태에 대한 제한들을 가정함으로써 모형들의 문제들을 전적으로, 그 표현들의 순수 모형들과 동질이형인 술어 논리학 안에서 연구하는 것은 매우 가능하다. 레벡 Levesque (1986) 의 생생한 표상들을 보아라.)

2.3 소어와 심성 모형

이제 우리는 시작할 때 갖고 있었던 질문들의 하나에 대하여 답할 준비가 되었다. 인지과학에서의 중요한 구성개념 construct 으로 출현한 심성 모형이 소어에 어떻게 설치될 수 있는가? 이 질문은 어느 통합인지이론이라도 반복적으로 답변할 필요가 있는 질문의 실례이다. 도식은 어떻게 설치되는가? 활성화는 어떻게 설치되는가? 문법, 변형적인 것, 어휘-기능적인 것, 그리고 다른 것들은 어떻게 설치되는가? 정리해서 요약하자면 인지과학에서 강력한 설명력을 갖고 있다고 증명된, 그러나 소어이론의 직접적 일부가 아닌 모든 구성개념들이 어떻게 소어에 설치될 수 있는가?

그러한 질문들을 심각하게 취급한다는 것이 쿤 Kuhn (1962) 의 개념에서의 패러다임들에 의해 함의되는 입장, 즉 새로운 패러다임은 옛 패러다임에 의해 제기되지 않은 새로운 질문들을 가지며 옛 질문들은 무시한다는 입장과는 대조를 이루는 것처럼 보일 수도 있다. 그와는 반대로, 이것은 통합인지이론이 새로운 패러다임과 같은 것이 아니라는 점을 강조하는 데 도움이 된다. 통합이론의 기능은 기존의 패러다임 안에 있는 기존의 지식들을 통합하고 합성하는 것이지 새로운 질문과 극단적으로 다른 답들을 제공하는 것은 아니다. 또한 만약 인지심리학이 아직도 패러다임 과학이 아니라고 생각한다면 —— 아마 너무 단편적인 것들로 보여진다면 —— 통합이론의 기능은 현존하는 경험적 결과들의 풍부한 해결과 성공적인 초소형 이론들로부터 패러다임을 촉진시키고, 만들어내는 것이다.

그 질문에 대한 답은 분명하다. 심성 모형은 문제를 해결하는 데 연산되는 것으로서 발전되었다. 그러므로 그것들은 문제공간에서의 상태의 표상이어야만 한다. 그것들은 소어에서의 현재의 실체에 어떤 실체를 새롭게 추가하지는 않는다. 그러나 그것들은 상태 표상의 본질을 특수화시킨다 —— 즉 그것은 명제적 표상이나 어떤 다른 종류의 표상이라기보다는 주석이 달린 모형일 것이다. 이러한 제한과 함께 문제 공간에서 이에 일치되는 연산자들의 명세화들은 그러한 표상들의 의미론 semantics 을 고려하게 된다.

흥미롭게도, 이것은 심성 - 모형 분야에서의 견해는 아니었는데, 그 분야에서는 심성 모형들이 문제 공간에 대한 하나의 대안으로 고려되었다. 사실상, 심성 모형들에 대한 문헌들이 보여주는 것은 문제 공간들과 발견법 탐색은 단순히 존재하지 않는다는 것이다 (Gentner & Stevens, 1983 ; Johnson-Laird, 1983). 방금 기술된 심성 모형과 문제 공간 사이의 밀접한 관련성을 생각할 때, 이것은 약간 놀라운 일이다. AI —— 문제 공간의 개념의 출처 —— 에서 발견법 탐색에서의 많은 기초적인 연구들은 상태 표상들을 위해 항상 모형들을 사용해 왔다 —— 작은 과제들 (선교사와 식인종, 하노이 탑), 체스 프로그램, 공간 배치 프로그램 (Pfefferkorn, 1971) 등. 그것들은 거의 모두 주석이 달린 모형들을 사용하는데, 그것들은 표상적 범위를 확장하고 처리를 통제하기 위해서 기본적인 순수 - 모형 구조에 여러 가지 플래그 flags 나 꼬리표를 첨가시킨다.

왜 심성 모형이 문제 공간에 대해서 개념적으로 별개의 것으로 보여질 수 있는지에 대해서 가능성있는 두 가지 이유가 있다. 하나는 AI 에서 문제 공간에 대한 논리의 사용을 포함하여 표상 언어로서의 논리의 사용의 증가이다 (Fikes & Nilsson, 1971 ; Sacerdoti, 1974, 1977 ; Nilsson, 1980). 사실상, 지금은 논리주의자 logicists (Genesereth & Nilsson, 1987) 라고 불리는 AI 에서의 움직임은 모든 시스템들은 논리적인 형식으로 기술되어야 한다는 것을 공리적인 것으로 받아들인다. 그러므로 반대되는 많은 연구들에도 불구하고, 심성 모형과 명제 표상간의 대조는 심성 모형과 문제 공간간의 대조인 것처럼 쉽게 취급될 수도 있다. 다른 하나의 이유는 심성 모형에서의 초기 AI 연구들에서 경사에서 굴러 내리는 공에 관한 추리 (Bobrow, 1985) 와 같은 동적인 물리적 시스템들에 주의가 집중되었기 때문이다. 이와 반대로, 문제 공간에 대한 초기 연구는 정적인 것이었다. 모든 변화는 문제해결자의 생각 (또는 행위) 에 의한 것이었다. 이러한 것은 두 경우를 매우 다르게 보이도록 했는데, 특히 동적 상황에 대한 연구는 문제 공간의 다른 유형들의 연산자들을 매우 무시하면서 단지 질적으로 정의된 (상상된) 심적 실행 모형들의 문제들에만 집중했기 때문이다. 심성 모형들은 곧 전등 스위치나 온도 변경에 관한 추리를 포함하도록 확장되었지만, 아마도 그 때에 이러한 구분이 매우 확실하게 굳어졌던 것 같다.

2.4 삼단논법에서의 소어

사람들이 내적 표상으로 주석이 달린 모형들을 사용한다고 가정하자. 이것은 4 장에서 기술된 소어 구성을 넘어서는 추가적인 가설이다. 속성과 값을 가지고 있는 대상의 기초적인 표상 매체는 명제적 또는 모형 표상의 사용에 대해서 또는 내적 구조가 외부세계와 일치되는 방식에 대한 가정에 있어서는 중립적이다. 우리는 이러한 제약에 대해 제기되는 문제를 무시한다. 그것은 정말로 구성적인 것일 수도 있고, 또는 부호화가 발전되는 방식 때문에, 예컨대 실시간으로 작동해야 하기 때문일 수도 있다. 아무튼. 여기서의 강조점은 가설 그 자체에 있는 것이 아니라 그것을 소어에 통합시키는 것을 탐구하는 데 있다.

그러므로 소어가 주석이 달린 모형을 사용할 때, 소어가 삼단논법을 어떻게 해결하는지를 보기 위해, 우리는 이제 삼단논법으로 되돌아갈 수 있다. (주석 : 이것은 타드 폴크 Thad Polk 의 연구이다. 여기서 기술된 특정한 시스템은 Syl-소어/S88 이다 (Polk & Newell, 1988). 그 후 이 시스템은 즉시적 추리를 다루기 위해서 좀더 일반적인 형식화로 이동한다 (Polk, Newell, & Lewis, 1989).) 소어는 통합인지이론의 본보기이기 때문에, 그것은 인간이 삼단논법을 어떻게 해결하는지에 대한 이론일 것이다. 소어안에서 삼단논법을 수행하는 분명한 방법이 무엇인지를 물음으로써 (평상시처럼) 진행하자. 우리는 삼단논법 과제, 그 자체에 의해서 부여되는 제약들로부터 시작해 그 다음은 주석이 달린 모형에 의한 제약, 끝으로는 소어 구성에 의한 제약들을 살펴볼 것이다.

최소한 그 과제는 전제들을 읽기, 그리고 그것들에 대한 어떤 유형의 내적 표상을 구성하기, 그런 후 참이라고 믿어지는 방식으로 전제들의 말항들을 관련시키는 결론을 구성하고 말하기를 포함한다. 이러한 기술은 어떻게 전제들이 표상되어지며, 결론이 어떻게 추론되고 구성되는지를 결정하지 않은 상태로 남겨놓는다. 주석 달린 모형의 사용은 이러한 요건들을 충족시키는 방향으로 움직인다. 전제들은 상황모형 situation model —— 전제에서 기술된 상황의 주석 달린 모형 —— 에서 표상된다. 하나의 모형으로서 이 표상의 구조는 기술된 상황의 구조와 (주석에 의해 표시되는 대안적인 해석이 있는 곳은 제외하고) 직접적으로 일치한다. 그러므로 그것은 사람들과 일치하는 기호들을 가질 것이고 전제에서 진술된 특성들과 일치하는 속성들 —— 볼러이면서 카누 타는 사람이기도 한 사람 —— 을 갖고 있을 것이다.

이런 배열에는 잠재적인 어려움이 있는데, 이는 특성을 갖고 있는 사람들에 대한 단일한 주석 달린 모형에서 직접적으로 포착될 수 있는 상황을 전제들이 기술하지 않을 수도 있기 때문이다. 전제들은 애매할 수 있고, 그러므로 하나의 단일한 주석 달린 모형을 구성하는 어떤 처리라도 단 하나의 모형으로 종결될 것이다. 아마도 그러한 애매성은 탐지될 것이지만, 이 단계에서 보여질 수는 없다. 물론 이러한 어려움은 정확히 주석 달린 모형의 범위의 제한들 때문에 제기된다.

다른 한편, 범위에서의 이러한 제한은 효율적인 대응-같은 처리를 허용한다. 상황모형이 주어진다면, 모형에서의 사람의 특성들, 또는 어떤 특성을 갖고 있는 사람이 있는지 없는지는 모형을 조사함으로써 간단하게 판독될 수 있다. 물론 그 결론은 특정한 관계, 꼭 특정한 특성을 갖고 있는 사람 (즉, 전제들의 말항에 의해 주어진 것들) 에 대해 질문한다. 만약 이러한 것들이 모형에 있다면, 그것들은 판독될 수 있지만 그것들이 모형에 없을 수도 있다. 그러한 실패는 조사에 의해 분명하게 알 수 있을 것이다. 그럴 때에는 결론이 구성될 수 있기 전에 초기 모형을 증대시키거나 수정하는 것이 필요하다. 이것을 하기 위한 지식의 출처는 전제들이며, 그러므로 그것들은 또다시 참조될 필요가 있다. 만약 전제들이 더 이상 지각적으로 가용적이지 않다면, 전제들에 대한 어떤 표상이 내적 표상에 가용적으로 남아 있어야만 한다. 그러므로 기술된 상황에 대한 모형 이외에, 전제들에 대한 모형 (발화모형 utterance model) 역시 갖고 있을 필요가 있다.

과제와 주석이 달린 모형의 이러한 제약들은 삼단논법 추리의 질적인 특질들을 지배한다. 전제들을 읽는 것은 그것들이 기술하는 상황 (상황모형) 과 전제들 (발화모형) 모두에 대한 모형들의 구성으로 귀결된다. 모형들이 필요한 표상적 범위가 부족하거나 또는 이해 과정들이 가용적인 모든 정보를 추출하는데 실패하기 때문에, 상황 모형은 전제들에서 가용적인 모든 정보를 완전하게 포착하지는 못할 것이다. 만약 하나의 결론이 모형의 직접적인 조사에 의해 구성될 수 없다면, 결론이 판독될 수 있을 때까지 더 많은 정보가 전제들로부터 추출된다.

이것은 제약의 세 번째 출처 —— 소어 —— 와 연결되기 때문에 충분한 구조이다. 심성 모형들은 단지 문제 공간에서의 상태들이고, 그러므로 그것들은 그러한 문제 공간에서의 연산자들에 의해서 구성되고 연산된다. 그러나 우리는 더 이상 진전할 수 없다. 지식의 부족은 막다른 상태로 귀결되고 그러므로 막다른 상태를 해결하기 위한 반복적인 문제 해결로 귀결된다. 전제에 대한 불완전한 모형은 분명히 지식이 부족한 상황이다. 결론이 직접적으로 구성될 수 없을 때는 언제나 소어는 막다른 상태에 도달할 것이고, 그 막다른 상태를 해결하려는 시도로 또 하나의 문제 공간에서의 문제해결에 의존할 것이다. 이 하위공간에서, 소어는 전제들로 되돌아가야 하며, 상황모형을 증대시키는 데 사용될 수 있는 정보를 추출하려고 시도해야 한다.

이러한 제약들로부터 우리는 삼단논법 추리를 수행하는데 필요한 문제 공간들의 유형들을 결정할 수 있다. 입력되어지는 전제들을 처리할 수 있고, 그것들의 언어적 구조에 대한, 그리고 그것들이 기술하는 것에 대한 주석 달린 모형 표상들을 구성할 수 있는 문제 공간이 존재해야만 한다. 상황에 대한 모형에 기초해서 상황에 관한 결론을 구성할 수 있는 문제 공간이 존재해야만 한다. 전제들로 되돌아가서 더 많은 정보를 추출하고 상황모형을 정교화시킬 수 있는 문제공간이 존재해야만 한다.

이러한 문제 공간들은 과제 - 관련 처리가 진행될 수 있는 무대를 제공한다. 이러한 공간들 사이의 이동은 발생한 막다른 상태에 의존한다. 이러한 공간들 각각에서 발생하여 처리되는 일은 가용적인 탐색 - 통제 지식에 의존한다. 그러한 지식의 일부는 말항들에 대한 상황모형들을 조사하는 것과 같은 과제 정의로부터 직접적으로 도출된다. 그러나 다른 선택들도 발생할 수 있고, 여기서는 가능한 것들 중 어느것을 해야 할지 명확하지 않을 것이다. 특히 결과를 부분 조합하는 것을 피할 방법이 없다. 상황모형은 전제와 같아야 하기 때문에, 부분들은 주어, 목적어, 부호, 그리고 양화사를 갖는 것으로 알려진다. 그러나 어떤 요소가 먼저 획득되어야 하는가? 아마도 그것이 별다른 차이를 만들지 않을 수도 있는데, 이 경우 선택은 문제가 되지 않는다. 그러나 그것이 차이를 만들 수도 있다. 그 효과는 단순히 올바른 선택을 찾아내는 데 소요되는 시간의 길이일 것이다. 예를 들어, 어떤 요소들 (예컨대, 부호) 은 다른 것들 (예컨대, 목적어) 전에 결정될 수 없으며, 그러므로 틀린 것을 선택하는 것은 막다른 상태를 발생시킨다. 그러나 특정한 요소가 옳은지 또는 틀린 것인지를 구별하는 지식이 존재하지 않기 때문에, 그 효과는 오류일 수도 있다 (결국, 이것은 타당한 결론을 결정하는 과정이다. 그것은 결론이 옳은 것인지를 검토하기 위하여 타당한 결론을 획득했는지에 대한 지식을 사용할 수 없다).

이러한 효과들은 선택하기의 결과들이다. 추리자가 직면한 상황은 선택을 위한 지식이 없이 여러 가지의 선택들 중에 하나를 선택하는 것이다. 이것은 소어의 동점에 의한 막다른 상태를 함의하지만, 막다른 상태는 단지 지식을 찾을 기회만을 제공한다. 그 지식이 실제적으로 가용적이지 않다면, 추리자는 또 다른 상황으로 안내되지만 여전히 선택을 할 만한 적당한 지식이 부족하다. 그 상황은 4 장에서의 블록세계의 예와는 차이가 있음을 주목하라. 미리 앞서서 살펴봄 (룩어헤드) 으로써 동점에 의한 막다른 상태에 반응하는 것은 소어가 원하는 상황에 대해 어떤 확고한 지식에 접촉하는 것을 허용한다. 여기서 룩어헤드는 분명히 발생 가능하지만 추리자에게 그러한 지식이 존재하지 않기 때문에 지식의 확실한 출처와의 접촉 (타당한 추론) 이 이루어지지 않는다. 물음은 여러 선택들이 도착할 때 여러 선택들 중에서 아무것이나 선택하는 것보다는 지식에 접근하는 것이 더 좋다는 지식이 추리자에게 가용적일 수 있느냐이다. 사실상, 하나의 그럴 듯한 발견법이 있다. 그 결론은 전제들로부터 제기되므로, 그것은 어떤 일반적인 방식으로 전제들의 본질에 의해서 결정되어야만 한다. 그러므로 이미 조합된 것들과 유사한 것들에 주의를 제한하는 것이 더 좋다. 그러므로 다음에 어떤 것에 주의를 줄 것인지를 결정하기 위해서 연합적으로 작동하는 이러한 공간에서의 주의 연산자들이 있다.

우리는 삼단논법 추리를 위해서 특정한 소어 시스템에 의해서 기술되어진 구조를 구현했다. 이러한 시스템은 6 개의 문제 공간들을 사용한다. 그것들 중 3 개인 이해 comprehend, 삼단논법 syllogism, 그리고 형성-결론 build-conclusion 은 제시된 전제들과 반응 간의 최상 수준의 경로를 형성된다. 그것들을 형성하기 위한 지식은 과제의 정의와, 읽기와 쓰기에서의 일반적 기술들로부터 나온다. 이해 공간은 자연언어를 다루는 능력을 구체화한다. 그러나 전제들이 현실에서 매우 제한되어 있기 때문에, 우리는 이러한 일반적인 능력은 실험에서 사용되는 전제들의 단순한 단일-단어 문제에 적합화 된 특수한 부호화 연산자들로 교체할 수 있다. 이러한 부호화 연산자들은 특성들 properties 을 갖고 있는 대상들 objects 과 주석인 아니다 not 를 기초로 초기 (아마도 불완전한) 상황모형을 구성한다 ; 그것들은 역시 부산물로서, 각 전제를 주어 Subject, 목적어 object, 그리고 부호 Sign (이것은 술어를 형성한다), 그리고 양화사의 부분들을 갖고 있는 명제로서의 각 전제에 대한 모형 (발화 모형) 을 남긴다. 다른 3 개의 문제공간인, 명제-명제 prop-to-prop, 모형-명제 model-to-prop, 그리고 명제-모형 prop-to-model 들은 상황모형과 명제모형들을 정교화하고 주의를 안내하는 데 요구되는 기초적 연산자들을 갖고 있다. 그것들은 (전제인든 또는 상황 모형이든) 표상의 요소들로부터 정보를 추출하고, 그 표상의 다른 요소들을 정교화하기 위해 그 정보를 사용한다. 단지 정적인 상황을 이해하는 것만을 포함하는 삼단논법의 과제에 대해서는 모형-모형 model-to-model 공간은 요구되지 않는다.

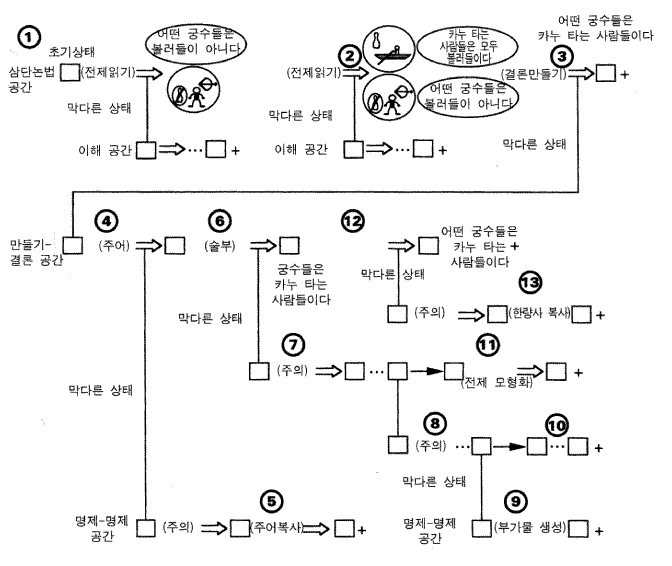
그림 10  어떤 궁수들은 볼러들이 아니다, 모든 카누 타는 사람들 소어의 행동

그림 10 은 어떤 궁수들은 볼러들이 아니다, 모든 카누 타는 사람들은 볼러들이다 에서의 시스템의 행동을 예시한다 (이 삼단논법은 그림 6 에서의 것과는 다르다. 그것을 해결하는 것이 더 쉽지는 않지만). 단계들은 그림에 표시되어 있다. (1) 그것은 첫 번째 전제에 대해서 그 다음은 두 번째 전제에 대해서, 삼단논법 문제공간에서 시작해서, 이해 공간에서 구현된 읽기-전제 read-premise 연산자를 적용한다. (2) 이것은 초기 모형과 두 개의 내적 명제들 (발화모형) 로 귀결된다. 이 부호화는 단지 전제의 주어에 관한 정보만을 추출한다, (3) 전체적 과제는 결론을 생성하는 것이기 때문에, 형성 - 결론 연산자가 적용된다. 그것의 공간 (형성 - 결론) 은 합법적인 명제들을 조합한다. 두 말항들 간에 필연적으로 뒤따르는 것을 생성하는 과제에 대한 지식은 그 공간에서 탐색 통제의 형식으로 존재한다. 그 과제는 결론의 주어, 술어, 그리고 양화사 —— 결론의 구성요소들 —— 로 분해된다. 그 과제 지식은 다른 요소들이 명세화되지 않은 채, 어떤 요소들을 결정하는 것을 허용한다. 불완전하거나 틀린 지식은 타당하지 않은 결론을 구성하는 것으로 귀결된다. (4) 주어를 생성하는 것이 처음으로 시도되었고, 이것은 명제 - 명제 공간을 사용하는데 이는 주어와 목적어를 구분하는 것이 모형이 아니라 명제들이기 때문이다. (5) 주의-명제 attend-to-prop 는 첫 번째 명제를 선택하고, 복사-주어 copy-subject 는 결론의 주어 (궁수) 를 생성한다. (6) 다음에, 생성-술어 generate-predicate 가 선택된다. 이것은 모형-명제 공간에서 발생하는데, 이는 명제들이 아마 술어에 대한 유용한 정보를 포함하고 있지 않기 때문이다. (7) 주의-목적어 attend-to-object 연산자는 적용되지만 다른 것들은 적용되지 않는데, 이는 모형이 불완전하기 때문이다. 이 연산자의 사용은 명제 - 모형 공간에서 그 모형의 증대로 귀결된다. (8) 더 많은 정보를 추출하기 위하여 주의 - 명제는 전제들을 선택하지만, 어떠한 전제도 아무것도 생성하지 않는다. (9) 생성-보조자 create-auxiliary 연산자는 명제-명제 공간에서 새로운 명제를 생성한다. 그것은 두 번째 전제에 주의를 주고 그것을 전환시키는 연산자들을 적용해서, 새로운 전제인, 모든 볼러들은 카누 타는 사람들이다 를 생성한다. (10) 이제 소어는 새로운 명제에 주의를 집중하고 모형을 증대시키기 위하여 그 모형을 사용하기 때문에, 그 새로운 명제는 명제 - 모형 공간에서 문제해결이 다시 시작되는 것을 허용한다. (11) 이제 모형은 술어를 제안하며, 그러므로 해결은 결론을 위한 술어 (카누 타는 사람들이다) 를 획득하기 위하여 모형 - 명제 공간에서 계속될 수 있다. (12) 형성 - 결론 공간에서 수행되어야 할 것으로 남아 있는 모든 것은 양화사를 생성하는 것이다, 그 모형은 양화사에 관한 지식을 포함하지 않는데, 이는 이것이 단일한 상황모형에서는 표상되어질 수 없는 것이기 때문이다. 그러므로 명제 - 명제 공간이 다시 사용된다. (13) 소어는 첫 번째 명제에 주의를 주어서 그것의 양화사 (어떤) 를 복사해서, 최종적으로 어떤 궁수들은 카누 타는 사람들이다 를 획득한다. 이것은 틀린 것이지만 많은 사람들도 마찬가지로 이 삼단논법에서 실패한다. 타당한 결론을 얻는 것은, 소어가 상황 모형과 전제들을 왕복하며 조사할 때 많은 국소적 선택점들에서 가용적이 되는 적절한 지식에 의존한다.

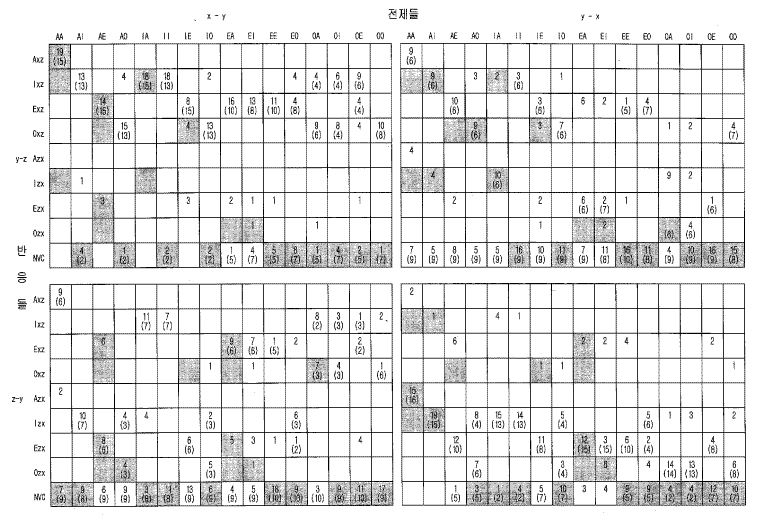
그림 11  삼단논법들에서의 인간과 소어 수행에 관한 자료

이제 우리는 삼단논법 과제, 주석 달린 모형들의 사용, 소어 구성, 그리고 가용적인 것이 될 것 같은 발견법적 지식의 제약들을 직접적으로 반영하는 삼단논법을 수행하기 위한 소어 시스템을 갖게 되었다. 인간 자료를 고려하여, 이 이론이 인간 수행을 얼마나 잘 설명하는지를 살펴보자. 밀란 대학의 학생 20 명이 64 개의 모든 삼단논법을 수행한 (무제한적인 시간으로) 존슨-레어드와 바라 Bara (1984) 의 자료와 소어의 자료들이 그림 11 에 제시되어 있다. 도표의 4 개의 부분들은 4 개의 격들에 해당한다. 각 열은 9 개의 합법적인 반응들 각각에 해당한다. 각 셀에서의 상단 숫자는 특정한 삼단논법에 대하여 그 반응을 한 사람들의 숫자를 나타낸다, 어떤 궁수들은 볼러들이 아니다 와 모든 카누 타는 사람들은 볼러들이다 의 약자는 각각 Oxy, Azy 이며, 이것은 왼쪽 하단의 사분면에서 발생하고, 여기서 8 명이 Ixz (어떤 궁수들은 카누 타는 사람들이다) 로, 7 명이 Oxz (어떤 궁수들은 카누 타는 사람들이 아니다) 로, 3 명은 NVC (타당한 결론이 없다) 로 반응했다. 다른 반응을 한 사람은 없다는 것을 우리는 알 수 있다. 타당한 반응들은 음영이 들어가 있다. 평균적으로 단지 38 % 가 정확했고, 7 개의 삼단논법들은 아무도 해결하지 못했다.

개개의 인간들은 서로 다르게 행동하고, 또 다른 경우들에서 그들은 다르게 행동한다. 그들의 지식에서, 어떤, 필연적, 뒤따르다와 같은 용어들에 대한 그들의 이해에서, 그리고 그들이 직면했던 초소형 - 상황들에 의존하는 그들의 학습을 통해 개인마다 차이가 생긴다. 이러한 상황은 그림 11 에서 동일한 삼단논법에 대하여 여러 가지의 반응들이 존재함에 의해서 밝혀진다. 9 개의 가능성들 중에서 몇 개의 반응들로 반응들이 군집화되는 것은 개인차가 존재한다는 것과 과제 상황의 특질들에 의하여 개인차의 형태가 강력하게 영향을 받고 있다는 사실을 모두 보여준다.

소어 삼단논법 시스템을 결정하기 위해 우리가 고려했던 사항들은 독특한 시스템으로 귀결되지는 않았는데, 이것은 여러 가지의 소어 시스템들이 동일한 일반적인 구조 안에 존재할 수 있음을 의미한다. 우리는 3 개, 2 개, 그리고 2 개의 가능한 값들을 각각 갖고 있는 세 개의 매개변수들을 포함하는 12 개의 소어 변형들의 집단을 구성했다 (3 × 2 × 2 가능성들은 12 개의 변형을 이룬다). 첫 번째 매개변수는 어떻게 전제들이 아니다 주석들을 갖고 있는 대상들을 증대시키는지와 관련이 있다 (3 개의 값). 둘째, 어떤 대상들을 지칭하는 전제들이 그 상황에서 동일한 특성을 갖고 있는 대상을 증대시키는지의 여부 (2 개의 값). 셋째, 내적 명제들이 생성될 것인가의 여부 (2 개의 값). 첫 번째와 두 번째 매개변수들은 부정과 존재의 수량이 어떻게 해석되는지를 반영한다. 세 번째 것은 사람이 정말로 내적 추리를 수행하는지 또는 단순히 주어진 명제들에 머무를 것인가 (사람이 내적인 룩어헤드 탐색을 수행할 것인가와 유사하게) 의 표시로 여겨질 수 있다. 이러한 세 개의 매개변수들 이외의 다른 변수들은 기본적인 이론의 범위 안에서 개별적 변형을 규정하는 것으로 정의될 수 있는데, 그러한 변형은 과제, 주석 달린 모형표상, 그리고 소어 구성의 제약들을 만족시킨다. 이들 세 개를 선택하는 것은 자료 적합화 data fitting 의 한 형태로 해석될 수 있다. 아무튼, 필요한 것은, 그 이론이 개인차의 어떤 범위를 포함하므로 그것이 모든 개인이 동일한 방식으로 행동하지 않는다는 자료의 특질을 예측할 수 있다는 것이다.

이 작은 집단은 하나 또는 그 이상의 반응들을 포함하는 193 개의 셀들 중 131 개의 셀을 포함으로써 (Oyx, Ayz = Izx 의 한 경우를 제외하고 6 명 이상을 갖고 있는 모든 셀들이 예측된다), 관찰된 합법적인 반응들의 1, 154 개 중 980 개 (85%) 를 설명한다. (주석 : 총 20 × 64 = 1, 280 반응들 중, 126 개의 반응은 허용되지 않는 반응들이거나 기록의 실패들이었고 자료에 포함되지 않았다. 그러므로 총 1, 154 개가 남는다. 허용되지 않는 반응들은 중간 항 (B) 에 관한 결론들과 같은 것들이었다.) 한 사람도 반응하지 않은 반응은 단 한 가지만 예측된다. (Oyx, Ayz = Ozx). 그림 11 의 괄호 안에 제시된 적합화를 생성하기 위해 빈도들이 그 집단의 다른 구성원들에게 할당되었다 (10 % 의 기록되지 않은 반응들을 포함해서 25 % 의 반응들이 예측되어지지 않았기 때문에, 사람들의 15/20 가 그 집단에 있는 것으로 가정되었다). 가장 많은 사람의 반응과 가장 적은 사람의 반응을 포함한 셀들이 가장 많은 프로그램의 반응과 가장 적은 프로그램의 반응을 역시 포함한다는 것을 주목하라. 소어 이론이 그 자료와 일치하는 방식의 많은 추가적인 초소형 - 특질들이 주어질 수 있다. 그러나 보여진 것은 그 이론이 매우 효과적이라는 것을 입증하는 데 충분하다. (주석 : 20 명 각각으로부터 64 개의 반응에 대한 자료를 얻는 것이 선호되는 것이었다. 그러나 출판된 자료는 이렇게 조합된 형태로 주어진다.)

소어 이론이 사람들의 한 집단이 합성된 반응들을 설명하는 것을 보았으므로, 이제는 그림 7 에 제시된 주요 규칙성들을 그것이 어떻게 설명하는지에 대해 생각해 보자. 그것이 규칙성들의 대부분을 예측하는 정도는 그림 11 에 함축되어 있다 —— 그것은 단지 반응들과 삼단논법들을 범주화시키는 것과 각 규칙성을 찬성하거나 반대하는 전체적인 것들을 보는 것에 대한 물음이다.

첫째, 해결하기 위해서 전제에서의 애매성의 이해를 요구하는 삼단논법은 그렇지 않은 것보다 더욱 어려워야 한다. 이것은 주석 달린 모형에서 애매성을 표상하기가 어렵다는 점으로부터 직접적으로 도출된다. 더 나아가 삼단논법들이 난이도의 차이가 있어야 하는데, 이는 어떤 것들은 애매하지만, 다른 것들은 그렇지 않기 때문이다. 단지 하나의 예로서 모든 x 는 y 이다, 어떤 y 는 z 이다 를 생각해 보자. (이것은 그림 11 의 xy - yz 사분면에서 AI 행으로 나타난다.) 이러한 전제들에 대한 가능한 모형은 z 인 x 을 갖지만 (만일 z 이면서 y 인 것들 중에 x 인 것이 없다면) 그런 것이 없는 경우도 (다른 모형에서) 생각해 볼 수 있다. 올바른 답 (타당한 결론이 없다는 것) 을 얻는 것은 두 모형 모두 올바를 수 있고, 그러므로 어떤 x 는 z 이다 는 필연적으로 참이 아니라는 것을 인식할 것을 요구한다. 그러므로 우리는 이 삼단논법이 비교적 어렵다고 기대할 것이다. 우리는 또한 어떤 x 는 z 이다 가 매우 일반적인 반응일 것이라고 역시 기대할 것이다. 그림 11 에서의 자료는 이러한 두 예측 모두를 지지한다. 단지 4 명의 피험자만이 (그리고 두 개의 소어 변형들만이) 올바른 반응 (NVC) 을 했으며, 13 명의 피험자들은 (13 개의 소어 변형들은) 예측된 오류 (Ixz) 를 범했다. 다른 삼단논법들에 대한 유사한 예측들도 역시 정확하다 (좀더 자세한 설명을 위해, Johnson-Laird & Bara, 1984 를 보아라).

우리는 또한 특정한 차원들에 따라 그 이론을 변화시킴으로써 개인차를 설명하기 위하여 그 이론이 어떻게 만들어지는지 역시 보았다. 이 설명의 정확성은 그림 11 에서 역시 보여질 수 있다. 사람의 반응들을 포함한 (상단에 숫자를 갖고 있는) 셀들은 역시 소어의 반응들 (하단의 괄호 안의 숫자) 을 포함하는 경향이 있다. 또한 사람들이 하지 않은 (상단에 숫자가 없는) 반응들은 어떠한 소어의 변형들에 의해서도 거의 이루어지지 않았다 (하단에 숫자가 없다). 우리는 각 소어 변형의 수를 변화시킴으로써 반응들의 빈도를 일치시킬 수도 있었다. 그러므로 각 셀에서 사람의 반응들의 수 (상단의 수) 와 소어 변형의 반응들의 수 (하단의 수) 사이의 높은 상관이 있다.

이론은 분위기 그리고 격 효과들도 역시 생성한다. 분위기 효과를 보기 위하여, 그림 11 의 어떤 전제들을 갖고 있는 삼단논법들 (행위 머리말이 I 나 O 를 포함한 것) 을 고려해 보자. 이러한 삼단논법들에 대한 가장 일반적인 반응들은 (피험자와 소어 변형 모두에서) 어떤 결론들 (Ixz, Oxz, Izx, 그리고 Ozx) 인 경향이 있다. 반면에, 어떤 전제를 갖고 있지 않은 삼단논법들은 전칭 결론들 (Axz, Exz, Azx, Ezx) 인 경향이 있다. 유사하게, 부정 전제를 포함한 삼단논법들 (행의 머리말이 E 또는 O) 은 부정결론 (Exz, Oxz, Ozx) 으로 귀결되는 경향이 있지만, 반면 단지 긍정 전제들만을 갖고 있는 삼단논법들은 긍정결론 (Axz, Ixz, Azx, Izx) 으로 귀결되는 경향이 있다. 격 효과는 그림 11 의 xy - yz, 그리고 yx-zy 격들 (상단-왼편 사분면, 그리고 하단-오른편 사분면) 에서 나타난다. xy-yz 격 (상단 왼편) 에서, 결론들은 주어로서 z 보다는 x 를 갖는 경향이 있으므로, 그 사분면의 하단의 4 개의 열들 (Azx-Ozx) 에 비하여 그 사분면의 상단의 4 개 열들 (Axz-Oxz) 에서 매우 많은 반응들이 있다 (사람과 소어 변형들에서 모두에서). yx-zy 격 (하단 오른편) 에서, 그 효과는 역전된다. 반응들은 하단의 4 개의 열들 (Azx-Ozx) 에 비해 상단의 4 개 열들 (Axz-Oxz) 에서 상당히 적다. 이 이론에서 선택적 주의가 전제들과 유사한 결론으로 결론의 구성을 치우치게 하기 때문에, 격 효과가 발생한다. 그러므로 주어가 전제들의 주어와 일치하는 결론이 다른 것보다 먼저 시도되기 때문에 격 효과가 나타난다. 이러한 효과들 모두는 NVC 반응의 빈도에 대해서는 어떤 언급도 하지 않는다.

전환 효과는 대부분의 반응들이 (오류들조차도) 두 전제들과 그것들의 전환된 것들이 참이라는 가정하에서는 타당하다고 말한다. 어떤 x 는 y 이다 와 어떠한 x 도 y 는 아니다 는 그것들의 전환 형태를 함의하지만, 다른 두 전제들에 대하여 그것은 참이 아니다. 예를 들면, 모든 x 는 y 이다, 모든 z 는 y 이다 (Axy, Azy) 는 타당한 결론을 가지고 있지 않다. 그러나 만약 두 번째 전제의 전환 형태가 참이라면 (모든 y 는 z 이다), 모든 x 는 z 이다 가 타당한 결론이 될 것이다. 그리고 자료는 9 명의 사람과 6 개의 변형들이 이 반응을 했음을 보여준다. 이 효과는 아마 사람들이 전제들을 해석하는 방식 때문일 것이다. 전제의 해석이 필연적으로 그것의 전환 형태를 함의하는가의 여부에 해당하는 첫 번째 매개변수의 값을 변화시킴으로써 이 이론은 그 효과를 직접적으로 생성한다.

구체성 효과는 그림 11 의 자료에 나타난 있지 않은데, 이는 그 실험이 단지 구체적 형태의 삼단논법만을 포함하고 있었기 때문이다. 더구나, 기술된 시스템에서 구체화된 이론은 구체성 효과에 대해서도 설명하지 않는다. 그러나 그렇게 하는 방법은 상당히 명백하다. 그러한 효과의 위치는 구성되어진 모형이다. 그러므로 전제가 빵 굽는 사람인 궁수들 또는 B 인 A 를 부호화하는 데 있어서 어디에선가 차이를 만들어낼 필요가 있다. 더 나아가, 만약 궁수, 빵 굽는 사람, 그리고 그들의 관계성에 대해 알려진 다른 사실들이 있다면, 어떤 조건 아래에서는 이러한 것들이 인출되고 상황모형을 부호화하는 데 개입할 것이다. 이러한 효과들은 이론의 언어 - 이해 구성요소들에 국한되며, 그 이론이 더욱더 발전될 때까지는 접근될 수가 없다.

이제 삼단논법에서의 이 긴 여행으로부터 교훈을 얻어내 보자. 첫째, 인지과학에서 사용되는 용어로서의 심성 모형 (Johnson-Laird, 1983 ; Gentner & Stevens, 1983) 은 바로 문제 공간이고 좀더 정확히 말하면, 문제 공간의 상태 표상이다. 우리는 문제 공간들에서 수행되어지는 심성 - 모형 추리의 명확한 실증을 제공했고, 그것으로부터 심성 모형이 상태 표상임이 분명해진다. 그것은 모형인데, 이는 그것이 바로 표상의 본질이기 때문이다. 소어의 관점에서 보면, 그 상황은 완벽하게 표준적인 것이다.

그렇다면 시스템이 주석 달린 모형들을 사용한다는 가정 아래에서 명제적 표상에 대해서는 어떤 일이 일어날까? 상태들이 명제적 표상이고 연산자들이 논리적 추론 규칙들인 문제 공간들을 만드는 것은 분명히 가능하다. 이러한 것들은 단지 심성 모형만을 사용하는 유기체에 있어서 단순히 금지되어 있는 것인가? 그에 대한 답은 매우 놀랍다. 그러한 표상들도 사용될 수 있다. 그것들이 사용될 때, 유기체가 갖고 있는 것은 명제에 대한 심성 모형이다 (이것은 본질적으로 삼단 논법에서의 발화 모형의 본질이다). 유기체가 추론 규칙을 사용하여 그 모형을 연산할 때, 유기체는 명제들의 한 집합에 대한 모형으로부터 다른 집합에 대한 모형으로 이동한다. 그러나 물론 명제들의 집합에 대한 모형은 그러한 명제들이 의미하는 것에 대한 모형은 아니다. 모형 - 표상 시스템이 명제적 표상을 직접적으로 사용한다는 것은 그것이 그러한 명제들이 표상하는 세상에 대해서는 간접적으로 작용한다는 것을 의미한다. 사람이 명제들을 사용할 때, 이 같은 부분에 있어서는 항상 고려되지 않는 것처럼 보인다. (주석 : 주석들은 명제들이지만, 그 상태에 대한 명제적 표상들의 사용은 모형에서의 주석들의 사용과는 다르다. 주석들은 모형 그 자체의 대응과 같은 처리의 일부로서 처리된다. 명제들은 추론 연산자들에 의해 처리된다. 결과적으로, 명제 - 같은 연산들의 두 형태들은 인간 인지에서 진행될 수 있고, 그러므로 명제 - 같은 표상의 확인은 약간의 주의를 요구한다.)

둘째, 삼단 논법이 어려운 주요한 이유는 표상의 부적절성, 즉 (주석달린) 모형의 사용이 부적절하기 때문이다. 모형들은 많은 목적들에, 특히 지각되어진 세상을 다루는 데 적합하다. 그러므로 왜 사람들이 일상적으로 모형을 사용하는지에 대한 좋은 이유들이 있다. 그러나 양화사를 갖고 있는 범주적 삼단논법은 인간들에게 가용적인 종류의 주석들을 갖고 단일한 모형에 의해 표상되기에는 너무 복잡하다.

표상적 부적절성이 어려움에 대한 유일한 이유는 아니다. 사용되어지는 언어에 대한, 특히 어떤, 그리고 모든에 대한 해석의 문제들이 가능하다. 더 중요한 것은, 어떠한 교정적 피드백이 발생해서 사람들이 올바로 추리하는 방법을 찾아낼 수 있는 과제 상황이 아니라는 것이다. 그러므로 인간 인지의 주요한 특질인 학습하는 능력이 근본적으로 배제된다. 실험에서 64 개 삼단논법을 수행할 때 어떠한 학습이 발생하는지에 대해서 출판된 연구들은 없는 것 같지만, 여기서 논의되었던 연구의 원자료에 대한 검토는 수행에서 거의 변화가 없음을 보여준다. 실증된 것처럼, 이러한 삼단논법 과제에서 소어는 학습을 하지만, 그것은 단지 속도의 면에서이지, 정확성에서는 아니다. 피드백 부재의 효과는 탐색이 검증에 대한 기회가 없이 약한 연합적인 발견법에 의존한다는 것에서 명백하다. 또한 의미적 해석의 오류들은 학습에 의해 어느 정도는 교정이 가능해 보인다. 아마도 덜 명확한 것은 피드백의 부재가 올바른 방법을 찾아내는 가능성에 영향을 주는가이다. 모형에 의한 추리는 만약 결론이 포함하는 집합의 모든 모형들에서 검증된다면 타당한 결과들을 얻어낼 수 있다. 이것은 좀더 복잡한 방법이지만, 이것이 이러한 실험들에서 많은 사람들의 능력을 벗어나는 것은 아니다. 그러나 좀더 단순한 방법들이 부적합하다는 것을 학습하고 좀더 복잡한 방법들을 발견하고 결함을 제거할 수 있는 기회가 존재하지 않는다. 수많은 시행들은 있으나 결과들에 대한 지식은 없다.

셋째, 우리가 개인차의 방향으로 선회한 것은 좀더 일반적인 주장을 하는데 사용될 수 있다. 통합인지이론은 개인차를 신중한 방식으로 다루어야만 한다. 다른 사람들은 다른 표상들, 그리고 다른 방법들을 사용하며, 동일한 사람도 역시 다른 경우들에서는 다르게 행동한다. 다양한 방법들이 고려되지 않는다면, 자세한 결과들의 면밀한 설명이 기대될 수 없다.

심리학 전반에 만연한 단일 - 방법 접근법은 그 분야에서 적절한 이론을 획득하는 데에 있어서의 단지 초기의 반복적인 것 iteration 으로 여겨질 수 있다. 삼단논법에 대해 여기서 우리가 한 것은 단지 간단하고 부적절한 단계였다.

예를 들어, 적어도 하나의 극단적으로 다른 방법, 즉 많은 사람들이 (특히 기술적으로 훈련된 사람들이) 사용하는 벤다이어그램 Venn diagrams 이 있다는 것을 우리는 알고 있다. 이것은 개별적인 것이기보다는 관련된 집합들에 대한 모형 표상이다. 삼단논법 추리의 완전한 이론은 이것을 포함해야 한다.

마지막으로, 모의실험에 관한 작은 방법론적인 설명이 있다. 여기서의 모의실험의 주요 사용법은 고전적인 것이다. 우리는 64 개의 모든 삼단논법들에서 12 개의 모의인간들의 모든 변형들을 모의실험했고, 기본적인 수행자료들의 표를 축적했고 (그림 11), 그것으로부터 우리는 기본적인 인간 자료들과 여러 가지 규칙성들에 대한 적합성을 판독했다. 그러나 모의실험은 또 하나의 다른 역할도 수행한다. 우리는 처음에 모형들의 조사에 의해서 삼단논법들이 수행된다는 (존슨 - 레어드와 일치하는) 견해에 직접적으로 기초해서 소어에서 삼단논법 추리의 상위수준의 수정판을 만들어냈다.

우리가 작성한 산출들에 의해서 직접적인 재인을 수행하는 모의실험 시스템을 우리는 얻었다. 그러므로 우리는 이러한 산출들이 어떤 곳에서부터 나와야만 한다는 것을 심사숙고 했다. 그래서 우리는 이러한 산출들을 청크들로 생성해 내는 공간을 창안해냈다. 이것이 바로 모형을 정교화시키기 위해 전제들로 되돌아가서 더 많은 정보를 추출하는 공간들을 우리가 획득한 방법이다. 모의실험으로부터 시작하고, 그리고 경험으로부터의 학습에 의해 즉시적 반응의 모든 것을 획득해야만 하는 시스템에서 그것의 기원이 무엇인가를 물음으로써, 우리는 소어에서 이론의 부분들을 생성하기 위하여 모의실험을 사용했다.

이론 구성을 도와주는 모의실험의 이러한 사용법은 예측하는 곳에서의 사용법보다는 덜 일반적이지만, 이것은 모의실험이 도움을 줄 수 있는 다양한 방식들을 보여준다.

3. 문장 검증

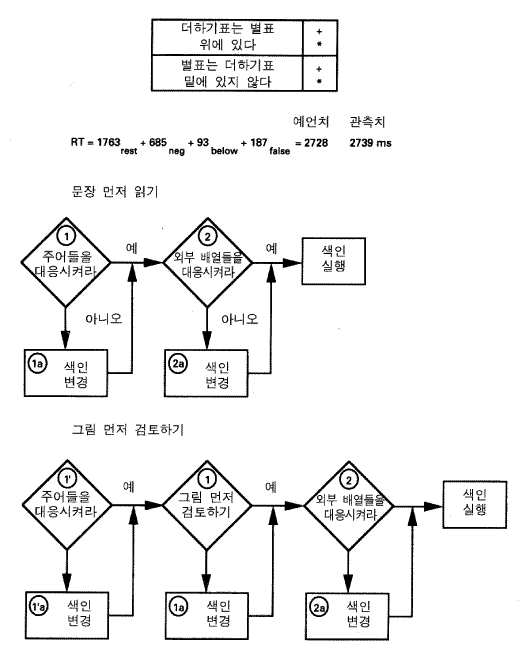
그림 12  초보적인 문장 검증 (Chase & Clark, 1972 에서 인용)

우리는 합리성의 언덕에 있는 우리의 세 번째 과제 —— 초보적인 문장검증 —— 에 도달했다. 검증에 대한 패러다임은 1970 년대 초기에 그 뿌리를 둔다. 사람들은 더하기표는 별표 위에 있다 plus is above star 와 같은 단순한 문장들을 읽는다 (그림 12). 그 다음 그들은 단순한 그림들을 보고 그 문장이 그림에 대해서 참인지 아니면 거짓인지 둘 중 하나의 단추를 누름으로써 간단히 표시해야 한다. 모든 과정은 2 - 3 초를 소요한다. 그 과제는 초보적이지만, 언어가 자연스럽고 직접적인 방식으로 사용되는 맥락에서 언어를 이해하는 완전하고도 매우 자연스런 행위를 구성한다. 이러한 과제들에 대한 연구는 인지심리학의 낱자에서 단어, 문장, 그리고 구절에까지 이르는, 점진적으로 복잡한 언어 기능을 탐구하기 위해 선택한 긴 경로에서의 한 걸음이었다.

문장이 어떻게 이해되는지를 이해하기 위해서, 연구자들은 그 과제들을 체계적인 방식으로 변화시켰다. 예를 들어, 문장들은 우리의 예에서 거짓 문장인, 별표는 더하기표 밑에 있지 않다 star isn't below plus 와 같이 복잡할 수도 있다. 기본적인 결과는 그러한 과제를 수행하는데 사람들이 소요하는 시간은 매우 규칙적인 방식으로 변화한다는 것이다 (그렇게 단순한 과제들에 대해서는 본질적으로 오류들이 없다). 그림은 전형적인 결과를 보여준다 (Chase & Clark, 1972). 반응시간은 다음과 같이 분해된다. 기본시간 (1, 763 ms) 은 변화하지 않는 것들 모두 (그림을 지각하기, 문장 읽기, 반응 운동하기) 를 포함한다. 문장이 부정문일 때 추가되는 시간 (685 ms). 문장이 위 above 가 아니라 아래 below 가 사용될 때 추가되는 시간 (93 ms). 문장이 그림에 대하여 거짓일 때 추가되는 시간 (187 ms). (기본시간 위의) 이러한 세 가지 요소들은 긍정/부정, 위/아래, 그리고 참/거짓의 모두 8 가지의 조합을 매우 정확하게 (평균들 간의 변량의 95 ~ 97 %) 설명한다. 그림에서의 두 번째 문장과 같은 복잡한 경우에 대하여, 모형은 2, 728 ms 를 예측하며 관찰치는 2, 739 ms 이다. 평균들은 개별적 변이의 많은 부분을 숨기지만 그것들은 규칙적인 처리의 존재를 분명하게 보여준다.

이러한 실험들 —— 1970 년대에 그것들을 생성해내는 연구사업이 있었다 (Clark & Clark, 1977) —— 은 인간들이 진정한 인지 과제들에서 매우 규칙적으로 행동한다는 증거들의 증가에 중요한 일부분을 제공했다. 1960 년대에 시간측정적 혁명 chronometric revolution 을 시작시킨 과제들은 단순한 지각적, 그리고 기억 - 탐색 과제들이었다 (Neisser, 1967). 우리는 5 장에서 이러한 것들 중의 하나인, 스턴버그 패러다임 (Sternberg, 1966) 을 검토했다. 문장 - 검증 과제들은 과제 복잡성에서 (~1 초에서 ~2-3 초로의 이동에서 보일 수 있는 것처럼) 한 단계 더 높아진 것이다. 더욱 중요하게, 그것들은 상위 심적 과정들에 대한 우리의 개념에서 특수한 역할을 차지하고 있는 언어적 행동을 포함시켰다. 그러므로 그 패러다임은 1970 년대 초기에 인간이 계산적 시스템임을 확증시키는 규칙성들의 커다란 집합을 형성하는데 중요한 역할을 했다. 그것은 우리의 ~ ~3, 000 개의 규칙성들에 자신의 몫을 기여했다.

이러한 과제들에서 정보처리에 관한 이론화의 형식은 흐름도 flowcharts (그림에 제시된 것 같은) 를 사용한 것이었다. 어떤 심리학자들이라도 인지에 대한 모든 문헌에서 그러한 흐름도가 언제나 나타난다는 것을 증언할 수 있다. 그것들은 실험에서 연산되는 특정한 측면들의 분석과 논의를 위한 기본틀을 제공한다. 상단의 흐름도의 해석은 다음과 같다. 첫째 (흐름도에 적절히 들어가기 전에) 사람은 문장을 읽고 그것을 명제로서 내적으로 부호화한다. 그 다음 그 사람은 그림을 검토하고 그것으로부터의 정보를 또 하나의 내적 명제로서 부호화한다. (문장으로부터 그리고 그림으로부터) 지식의 두 항목들은 비교되기 위해서 어떤 공통적인 표상양식으로 만들어져야만 한다. 여기에서 코드들은 문장에 대하여 (더하기표 (위 별표) (plus (above start)), 그리고 그림에 대하여 (더하기표 (위 별표) (plus (above start)) 로 표상될 수 있다. 실제적인 비교가 시작되기 전에, 기대되는 답에 대한 색인 index 이 설정된다 (여기서, 기정 표준 값은 문장이 참이기 때문에, 반응은 참일 것이다). 이러한 설정이 주어지면, 그림의 흐름도는 비교가 진행되는 방식을 보여준다. 첫째, 두 코드들의 주어가 비교된다. 만약 그것들이 대응되면, 처리는 단순히 진행된다. 그러나 그것들이 대응에 실패하면, 반응 색인은 변경된다 (참에서 거짓으로), 그 다음 <외부 열들> 이 비교되는데, 이것은 원래의 논문에서 관계 (위 또는 아래) 를 지칭하는 방법이다. 또 다시, 만약 비교가 유지되면 처리는 단순히 진행된다. 그러나 비교가 실패하면, 그 색인은 또 다시 변경된다 (참에서 거짓으로 또는 반대로). 마지막에, 반응은 그 색인에 따라 만들어진다. 이 흐름도는 단지 그 과제를 수행하는 방법만이 아니라 인간들이 과제를 수행하는 방법도 표상한다. 예측 방정식에서의 요인들은 흐름도의 여러 가지 구성요소들의 과정들에 의해서 소요되는 시간에 일치하며, 시간들 사이의 독립성은 흐름도에서 나타난 구조적 독립성으로부터 제기된다.

클라크 Clark 와 체이스 Chase 는 우리가 예시로서 사용한 특정한 문장 - 검증 과제를 설명하기 위해 이 흐름도를 제안했고, 그 과제에서는 문장이 먼저 읽혀지고 그 다음 그림이 검토된다. 그리고 그들은 또한 두 번째 과제, 즉 그림이 먼저 검토되고 그 다음 문장들이 읽혀지는 과제도 역시 검토했다. 그들은 이 두 번째 과제에서의 처리를 그림 7 - 12 의 두 번째 흐름도로 기술했다. 약간의 검토는 그것이 첫 번째 것과 밀접하게 관련되어 있다는 것을 알려주지만, 그것은 그림을 먼저 검토하는 과제의 구조를 반영한다. 특히 사람이 문장을 읽을 때, 그림은 문장이 말하는 것에 따라 검토될 수 있다. 만약 그것이 별표에 대한 것이라면, 주의는 그림의 별표로 향해질 수 있다. 만약 그것이 더하기 표에 관한 것이라면, 주의는 더하기표로 향해질 수 있다. 그러나 사람이 그림을 먼저 검사할 때는, 그림에서 무엇이 보이는지에 의해서 문장이 다르게 읽혀질 수는 없다. 언어적 표현은 그것들이 제시된 것처럼 읽혀질 것을 요구한다. 그렇지 않다면, 그것들의 의미는 드러날 수 없다. 그러므로 부호화가 또 하나의 방식으로 차이가 있을 수 있기 때문에, 그림이 먼저 제시되는 경우에는 하나의 추가적인 단계가 생긴다. 이론적 처리의 기본틀을 구체화하는 흐름도의 이 같은 사용법은 인지심리학에서 전형적으로 사용하는 방법이다. 그들 자료의 아름다움, 그들 연구의 역사적 중요성, 그리고 이러한 과제들에서 진행되는 정보처리의 분석에서 그들이 흐름도를 단순히 하나의 요소로 정교하게 사용했다는 점에서 그 예는 긍정적인 본보기이다.

3.1 문장검증에서의 소어

흐름도는 어디에서 나오는가? 만약 이 질문이 곧바로 마음 속에서 떠오르지 않는다면, 그렇게 될 수 있도록 해야만 한다. (주석 : 그 문제는 얼마 전에 내 마음에 떠올랐다 (Newell, 1980c). 이것은 이 문제에 답하려는 나의 두 번째 시도이다. 그 답은 변하지 않았지만, 소어는 그것을 실증하는 더 좋은 방법을 제공한다.) 그것들이 심리학 문헌에 나타났을 때, 흐름도는 실험자의 합리적인 과제 분석으로부터 나온다. 그러므로 중요한 매개변수가 없을지라도, 그것들은 이론을 위한 자유도를 구성한다. 그것들은 매우 명백해서 일반적으로 의문의 여지가 없다. 그것들은 과제를 수행하는 그럴 듯하고 합리적인 방법을 표상한다. 사실, 그것들은 과제의 요구에 대한 사람의 반응에 대하여 무엇인가를 밝혀낸다. 그렇기 때문에 흐름도는 통합인지이론으로부터 출현되어야 한다. 만약 우리가 흐름도는 의도적인 합리적 행동을 검토하는 이번 장의 시각에서 본다면, 어떻게 인간들이 그런 흐름도에 따라 행동하기 위해서 자신들을 체제화하는지에 대하여, 우리는 자연스럽게 질문할 것이다. 다시 말해서 그 물음은 흐름도가 어디에서부터 오느냐 하는 것이다. 소어가 흐름도의 기원에 대한 이론을 제공한다는 것이 당신을 놀라게 하지는 않을 것이다. 통합인지이론의 본보기는 그 정도는 할 수 있다.

소어의 이론은 흐름도가 단지 문제공간을 통과하여 흘러가는 것의 합성된, 정적인 이미지들이라는 것이다. 사람은 문제공간에서 작업함으로써 과제를 달성한다 —— 소어에 따르면, 이것은 일반적인 상황이다. 만약 사람이 그 과제의 변형들을 수행한다면, 공간에서의 경로들은 과제의 상세한 요구들과 가용적인 지식에 의존해서 변화할 것이다. 취해질 수 있는 모든 다른 경로들을 통합하는 것이 흐름도를 생성한다. 물론 이러한 통합은 많은 상황들에서 사람들이 어떻게 행동할 것인지를 표상하기 위하여 과학자들에 의해서 만들어진다.

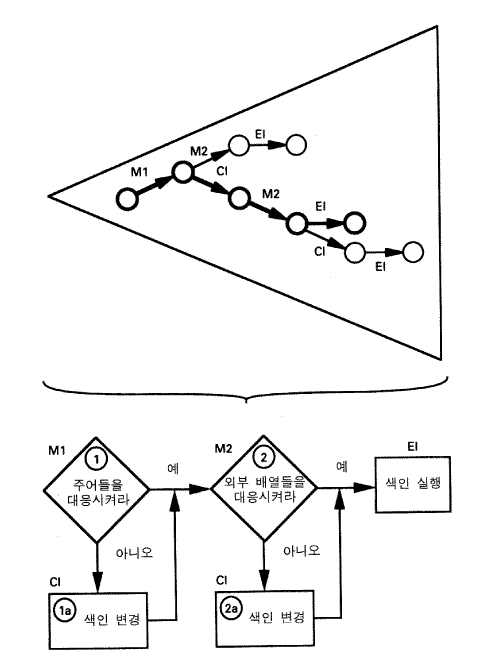
그림 13  흐름도에 관한 소어 이론

그림 13 은 이러한 통합을 예시한다. 문제 공간에서의 두꺼운 선은 사람이 취하는 실제경로이다. M1 은 첫 번째 대응에 해당하며, C1 는 색인을 변경시키는 것에 해당하며, M2 는 두 번째 대응에 해당하며, 그리고 EI 는 색인을 실행하는 것에 해당한다. 문제공간에서 다른 가능성을 경로들은 가는 선들에 의해 표시되었다. 각 과제 변형에 대한 문제공간에서 이동할 때, 사람은 각 경로를 동적으로 생성한다. 그림들은 주요경로 이외의 다른 탐색을 보여주지는 않는데, 흐름도에 의해서 특징화될 수 있을 정도로 행동이 일상화되어 있을 때에는 오류들이 거의 발생하지 않기 때문이다.

사람 안에는 해석자 interpreter 와 계획 구현자 plan implementor 에서처럼, 따라가야 하는 흐름도인 자료구조가 존재하지 않는다. 사람이 학습해감에 따라 그 경로는 매우 신뢰를 받게 되는데, 이는 탐색통제가 제시된 것처럼 동일한 상황에서 동일한 것을 하라고 항상 말할 것이기 때문이다. 그러나 흐름도는 구조로서의 실체를 갖고 있지는 않다 —— 그것은 행동에 대한 과학자의 외부적 표상이다. 이것은 사람이 계획에 따라 해석적으로 절대 작동할 수 없음 (사람들은 분명히 이렇게 할 수 있다) 을 의미하는 것이 아니라, 단지 이렇게 숙달된 상황들 속에서는 그런 방법을 통해 진행되는 것이 아니라는 것을 의미한다.

그림 14 문장에 관한 소어의 이해

소어가 문장을 이해하고 검증하는 과제를 어떻게 수행하는지를 살펴봄으로써, 이 예에 살을 좀더 붙여보자. (주석 : 이것은 그레그 요스트  Gregg Yost 의 연구이다.) 소어의 방법적 주요한 특질들은 그림 14 에 제시되어 있다. 또다시, 우리의 과제는 소어가 그 과제 —— 즉 문장을 이해하는 과제 —— 를 수행하는 자연스런 방법이 무엇인가를 소어에게 단순히 물어보는 것이다. 그 기초에 우리는 지각, 부호화, 그리고 자극판 위의 문장에 주의 주기와 같은 연산들을 가지고 있다. 우리는 이같은 연산들이, 문장을 단어들의 연쇄로서 순서대로 전달하는 것으로 취급할 수 있다. 만약 소어가 문장을 이해하기를 원한다면, 그렇게 되기 위하여 자연스럽게 그 문장에 대하여 이해 연산자 comprehension operator 를 실행하는 것이다. 소어는 문장을 단어 단위로 획득하기 때문에, 자연스럽게 단어가 도착할 때마다 각 단어에 대하여 이해 연산자를 실행하는 것이다. 이것은 곧 저스트 Just 와 카펜터 carpenter (1987) 의 해석의 즉시성 원리 immediacy of interpretation principle 의 수정판이다.

자연스러운 natural 이란 용어의 사용은 중요한 점을 숨긴다. 소어가 문장의 이해를 구현하거나 다른 어떤 과제를 수행하는 방법은 많이 있다. 사실, 사람이 과제를 수행하는 방법도 많이 있다. 하나의 자연스러운 방법이란 추가적인 지식이나 계산적 장치, 그리고 우회적 방법을 거의 포함하지 않는 방법이다. 그것은 명백하기 때문에 일반적으로 효율적이기는 하지만 가장 효율적인 방법이라고 볼 수는 없는데, 이는 어떤 복잡한 알고리듬이 더 효율적일 수 있기 때문이다 —— 때때로 매우 효율적이다. 자연스러운 방법은 분석을 시작하는 지점이지 분석이 종결되는 지점은 아니다. 그것의 발견법적 본질은 인식되어야만 하며, 어느 시점에선가는 대안적인 것들이 검토되어야만 한다. 궁극적으로 그러한 개념은 과제를 수행하는 방법들이 경험과 함께 어떻게 학습되고 향상되거나 변경되는지에 대한 이론들에 의해 교체될 것이다 —— 이것이 바로 소어의 청킹이 제공하기로 되어 있는 것이다. 구성은 올바로 만드는 것의 중요성은 시간 척도가 증가함에 따라 감소하는 것으로 보이지만, 이에 대한 일반적 찬성론의 하나는 구성 안에서 자연스러운 것을 수행하는 것이 바로 사람들이 실제적으로 과제를 수행하는 방법일 것이라는 것이다.

단어 - 이해 연산자를 실행하는 것은 단어의 전체 맥락에서 (그 사람에 대한) 그 단어의 중요성을 결정하려는 시도이다. 그것은 필연적으로 기대 - 기반적인 방식인데, 언어란 단어의 중요성이 나중에 들어올 단어들에 자주 의존하는 것이기 때문이다. 그러므로 단어 - 이해 연산자의 행동은 나중에 들어올 단어들이 제공할 지식을 (그것들은 아직 도착하지 않았기 때문에) 고려할 수는 없다. 그러므로 연산자는 나중의 단어들이 도착할 때 그것들에 의해 (즉, 그것들의 이해연산자들에 의해) 사용될 자료구조를 만들어야 한다. 기능적으로, 이러한 자료구조들은 기대들 expectations 이다. 이해연산자는 그 이상의 기대들을 언제나 만들 필요는 없다. 때때로 그것은 들어오는 발화의 의미의 부분을 생성하기 위해 필요한 모든 지식을 가질 것이다 —— 사실상, 궁극적으로 어떤 이해 연산자들은 그렇게 할 수 있어야만 하며, 그렇지 않다면 문장은 절대로 이해되지 않을 것이다.

이러한 방식은 통사적 지식과 의미적 지식을 고려하는 이해의 전 과제를 수행한다. 그러므로 이 방식은 단순한 분석 시스템이 아니라, 그것의 계산적 구조는 기대 - 기반적 분석 시스템과 유사하다. 이러한 사례는 통합인지이론 (여기서는 소어) 은 그것이 포함하려고 하는 현상들에 대하여 극단적인 새로운 이론들을 일차적으로 제안하는 것이 아니라는 개념을 확실히 하는 또 하나의 기회를 제공한다. 소어는 문장 이해에 대한 극단적으로 새로운 이론을 제공하지는 않는다. 기대-기반적 분석 expectation-based parsing 은 잘 탐구된 경로이며 사례-기반적 도식들 case-based shemes 과 밀접하게 관련되어 있다. 소어의 기본적 특성들의 많은 것들은 이러한 연구들에 친숙한 것들이다. 사실, 기본개념에서, 그 방식은 예일 대학의 로저 샹크 Roger Schank 와 그의 동료들과 학생들 (Schank & Reisbeck, 1981) 에 의해 발전된 언어 분석에 대한 접근방법으로부터 발전된 스티브 스몰 Steve Small (1979) 의 단어 전문가 시스템 Word Expert system 과 매우 유사하다. 소어 시스템은 기존의 시스템이 갖고 있는 몇 가지 문제들을 해결하고, 중요한 방식으로 확장을 허용하는 것 (예를 들어, 학습) 으로 나타나는 어떤 (중요한) 묘안들을 갖고 있다. 그러나 소어는 이러한 기제들의 새로움에 대하여 함축적인 주장을 하는 것은 아니다. 그것은 언어기제들이 다른 모든 인지를 위하여 사용되는 기제들과 관련될 수 있고, 그리고 이러한 모든 기제들에서 서로간에 상호 제약을 가하는 전체 인지 시스템안에서 이러한 기제들을 소어가 실현한다는 것을 주장한다 —— 이 주장은 가볍거나 사소한 주장이 아니다.

각 이해 연산자가 무엇을 할 것인지를 정의하기 위해, 문장의 단어들을 자세히 검토해 보자. 우리는 단지 최소의 지식만이 이 특수한 이해를 수행하는 데 필요하다는 점을 지적했었다. 단어 plus 는 이름이 <plus> 인 대상을 생성한다. 단어 is 는 전-대상 pre-object (문제의 단어전에 발생한 단어들에 의해 결정되는 것) 에 대한 기대를 생성한다. 이것들은 의미적 표상에서의 대상들에 대한 기대들이지, 들어오는 발화에서의 단어들에 대한 것들은 아니다. 만약 이러한 기대들이 만족되면 연산자는 술어 —— 대상이 그 특성을 갖는다는 것 —— 를 생성할 것이다. 단어 above 는 후-대상에 대한 기대들을 생성한다. 만약 이 기대가 만족되어지면, 연산자는 대상 위에 존재한다는 특성을 생성한다. 마지막으로 단어 star 는, plus 와 유사하게, 이름이 <star> 인 대상은 생성한다.

우리는 이러한 단어들에 대해 어떠한 대안적인 의미들을 포함하지 않았다. 그것은 설명적이거나 분석적인 단순성의 질문으로 생각되어질 수 있다. 사실, 단순한 문장 검증의 실험실 과제 맥락은 사람들이 그 과제에 익숙해진 후에 그 과제를 반복적으로 수행하는 맥락이다. 결과적으로, plus 가 덧셈을 의미하는 것 같은 모든 언어적 모호성들은 사라진다. 물론, 과제 자체에서 어느 모호성도 찾지 않도록 사람이 어떻게 특수화되는가에 대한 의문은 남아 있다. 분명히, 소어는 그것에 대한 이론도 마찬가지로 제공할 것이라 기대되어야 한다. 그러나 이 과제에 대해서 (그리고 그 예에 대해서) 이러한 문제들은 분명하지 않다.

이 과제를 위해 세 개의 문제 공간들이 요구된다. 최상-수준 과제가 이루어지게 될 과제 공간이 있다. 그것은 정보를 획득 acquire 하는, 표상들을 비교 compare 하는, 단추를 누름으로써 반응 respond 하는, 그리고 과제가 완료 done 되었을 때를 인식하는 연산자들을 갖고 있다. 이러한 연산자들의 일부는 그것들 자신의 공간들에서 구현되어야만 한다. 이해 공간 comprehension space 은 우리가 기술했듯이 이해 연산자들로 가득 채워져 있는 공간이다. 그것은 또한 환경으로부터 다음의 단어를 획득하는 읽기-단어 read-word 연산자를 갖고 있다. 이 공간은 때때로 문장과 그림에 적용될 것이다. 이해는 단지 언어에 대해서만 아니라 좀더 광범위하게 요구된다. 그것은 외부 세계와의 어떠한 종류의 접촉에 대해서도 요구되는 기능이다. 비교 공간 compare space 은 기록 recode 연산자, 변경-색인 change-index 연산자, 그리고 그것 자신의 완료 done 연산자를 가지고 있다. 연산자들의 몇몇 (기록 연산자) 과 그것들의 탐색 통제가 언어의 지식 —— 예를 들어, 더하기표는 별표 위에 있다라고 말하는 것이 무엇을 의미하는가 —— 으로부터 나온다는 점에서, 이 공간이 부분적으로는 언어적이다.

그림 15 문장-검증 과제에서의 소어

이것은 단순한 과제에서 작동하는 소어의 흔적을 보여주기에 적당한 예이다 (그림 15). 소어는 검증과제의 수행의 외부에 있는 특정한 시행 - 특수적 지시문의 맥락에서 시작한다. 그 지시문은 다음과 같다. 첫째, 경고 불빛이 발생할 것이다, 그 다음 문장과 그림이 자극판의 두 개의 구분된 칸에 동시에 도착할 것이다, 그 다음 문장이 읽혀진다, 그 다음에는 그림이 뒤따른다, 마지막으로 적합한 단추가 눌러진다. 그림에서의 각 열은 연속해서 번호가 매겨진 결정주기 (dc) 이고, 그 다음 행은 수행된 결정의 내용인, p (문제공간), s (상태), o (연산자), 또는 g (목표) 가 뒤따르고, 그 뒤에 대상의 내적 확인자 (p194) 가 뒤따르고, 그 다음 기술적인 이름 (이해 문제공간에 대하여 이해와 같이) 이 뒤따른다. 막다른 상태의 발생은 오른쪽을 향하는 이중화살표에 의해 표시되고 (dc 9 에서처럼), 그 흔적은 막다른 상태가 해결될 때까지 열이 안쪽으로 들어가서 시작되며 막다른 상태가 해결될 때, 열이 다시 밖으로 나와서 시작된다 (dc 43 처럼).

소어는 기본 공간에서 시작하는데, 그것도 역시 이해 문제공간이다. 이것이 바로 소어가 읽기 - 단어 연산자를 반복적으로 실행함으로써 단어를 읽어들이는 장소이다. 첫 번째 단어는 경고 불빛이며 (dc 3 에서), 그것은 입력된 것에 접근할 수 있도록 입력을 현재 상태에 연결시키는 설치-마디 install-node 연산자를 적용해야만 한다. 소어는 무엇이 들어 왔는지를 이해할 필요가 있기 때문에, 그것에 대하여 이해 연산자를 실행한다 (dc 6). 이것은 임박한 과제 (do-c&c-sf), 즉 문장을 먼저 보고 나서 그림을 보는 것을 포함하는 채이스와 클라크의 과제를 시도하라고 말하는 의도 연산자를 소어가 실행하도록 한다. 이 연산자는 무변화에 의한 막다른 상태에 도달하며, 이것은 의도를 구현하는 하위목표로 귀결된다 (dc 9 에서의 g222). 그것에 대한 문제공간은 do-c&c 이고 초기상태는 s224 이다.

적용되는 첫 번째 연산자는 문장 채널에 대한 획득-입력 get-input 연산자인데, 이는 그 문장을 먼저 읽어야 한다는 것을 소어가 알고 있기 때문이다. 중앙인지와 지각적 구성요소들 사이의 모든 상호작용 (지각과 부호화) 은 이 연산자 안에 숨겨져 있고, 소어가 이해공간으로 다시 들어가도록 한다. 그곳에서 소어는 문장 채널에 주의를 줄 수 있으며 (dc 16), 읽기 - 단어 연산자를 사용해서 단어들의 연쇄를 이해하기 시작한다.

처음에 읽혀진 단어는 plus 로 이것은 그 상태에 설치되며 (dc 18), 그 다음 이해 연산자가 그것에 적용된다. 이런 패턴 —— 읽기, 단어, 새로운 상태에 설치 - 마디, 그리고 그 다음 이해 —— 은 계속해서 반복될 것이다. 그러므로 우리는 plus (dc 20), is (cd 25), above (dc 30), star (dc 35) 의 이해의 위치를 찾아낼 수 있다. 그 흔적에서는 아무것도 나타나 있지 않지만, 다양한 기대들이 설정되어지고 다양한 대상들이 만들어진다. 우리는 above 에 대한 이해 연산자가 또 다시 점화됨 (dc 37) 과 그 다음 is 에 대한 이해연산자가 점화되는 것 (dc 41) 을 본다. 이것들 둘 모두 결국 나타날 단어 star 의 이해에 의해서 만족되는 기대들을 채워넣는다. 그러므로 어떤 종결-문장 end-of-sentence 처리가 존재한다. 이것은 문장 채널로부터의 정보의 획득을 완성시키기 때문에 소어는 기본 공간으로 되돌아간다.

그 다음 소어는 그림 채널로부터 입력을 받으며, 이것은 또 다시 적절한 채널을 선택하는 주의 연산자를 요구한다 (dc 48). 소어는 그림으로부터의 각각 세 개의 정보에 대하여 읽기-단어, 설치-마디, 그리고 이해 루프를 통과한다. 그림 자극판이 뚜렷하게 구별되고 간단해서 더욱 정교한 지각적 모형이 요구되지 않기 때문에, 그것이 또 하나의 문장인 plus/star 인 것처럼 우리는 해석한다. 기하학적 관계(/) 에 대한 이해 연산자는 다시 실행되는데 (dc 66), 이는 그것의 기대들이 만족되기 때문이다.

마지막으로, 비교 연산자가 실행될 수 있다 (dc 69 그리고 기본공간으로 돌아와서). 그것은 이러한 두 개의 표현들이 동일한 상황을 나타내는지를 검토할 것이다. 비교는 막다른 상태에 이르게 된다 (dc 70). 이 특정한 사례에서, 표현들이 동일한 구조들이므로 실제적으로 하다-비교 do-compare 를 실행하고 비교과 완료되는 것, 비교-완료 compare-done (dc 73) 를 보는 것을 제외하고는 설명할 처리가 없다. 비교 - 완료 연산자는 속성, 참을 생성하고, 반응 연산자는 이것을 외부 반응으로 전환시킨다 (dc 74).

우리는 소어가 단순한 문장을 읽고, 단순한 그림을 읽고, 그것들을 비교하고 그리고 반응하는 행동의 작은 부분을 살펴보았다. 이 특정한 행동은 흐름도를 통과하는 하나의 경로, 즉 그림 13 에서의 두꺼운 선을 생성한다. 만약 우리가 소어에게 다른 문장들을 준다면, 소어는 그 공간의 다른 부분들을 통과하는 흔적들을 만들 것이고, 그것들 전부는 채이스와 클락에 의해 주어진 흐름도에 추가될 것이다. 그러므로 우리는 매우 간단하지만 실제적인 하나의 사례에 대한 흐름도를 생성했다.

3.2 과제 획득에서의 소어

그림 16 과제 획득하기

위의 실증은 흐름도가 문제공간으로부터 나왔음을 보여주지만, 다음의 질문은 답변되지 않은 채로 남겨둔다. 문제 공간은 어디에서 나오는가? 뒤로 돌아가서 좀더 큰 실험상황을 고려해 보자 (그림 16). 경고 불빛이 켜지고, 자극판이 나타나고, 사람이 문장을 읽고, 그림을 검토하고, 단추를 누를 때, 그 실험은 발생한다. 단지 그 사람이 어떤 지식, 우리가 사전적 시행-특수 지시문 prior trial-specific instructions 이라고 부를 수 있는 지식을 갖고 있어야 그것은 발생할 수 있다. 문장을 읽고, 그림을 검토하고, 만약 문장이 그림에 대하여 참이면 참-단추를 누르고, 만약 문장이 그림에 대하여 거짓이면 거짓-단추를 누르고, 그 다음 그 과제는 완성된다. 물론, 그 지식 자체만으로는 그 과제를 수행하는 일이 충분하지 않다. 그것은 어떤 다른 지식, 우리가 사전적 일반 지시문 prior general instructions 이라 부를 수 있는 지식을 요구한다. 어떤 시기에 불이 켜질 것이고, 불이 켜진 후에 자극판이 나타날 것이고, 자극판의 왼편에는 문장이 나타나고 등. 그것도 역시 충분치는 않은데, 이는 이것이 소개 지시문 introductory instructions 이라고 불릴 수 있는 것을 미리 가정하기 때문이다. 안녕하세요, 오늘 아침 우리는 실험을 실행할 것입니다 … 어떤 시점에 이르러 외부 맥락은 사람이 이미 알고 있는 것에 의해, 그리고 장비와 함께 실험실 바에 위치됨으로써 해야 할 것이 무엇인지 해석할 수 있을 정도로 충분해진다.

그림 17 사전 시행 - 특수 지시문들

적지만 개략적으로, 이것은 그 질문에 대한 답을 제공하기에 충분한 정보이다. 문제공간들은 사람들로 하여금 그 과제에 착수하게 하는 것들로부터 —— 우리는 이것을 지시문 instructions 이라 부른다 —— 나온다. 그림에서 보듯이, 외부 맥락의 동심원적 계층들의 연속이 존재한다 (이것은 궁극적으로 초기 지식의 기능에 따라 종결된다). 바로 다음의 계층인, 그림 16 에서의 사전적 시행-특수 지시문을 살펴보자. 그림 17 은 소어가 이 과제를 어떻게 수행하는지를 보여준다. (주석 : 이것은 그렉 요스트의 연구이다. 이것은 루이스 Lewis, 뉴웰 Newell, 그리고 폴크 Polk (1989) 에 의해 계속되고 확장된다.) 그것의 가정은 그림 16 에서의 더 아래의 지시문들에 있는 유형의 지식을 포함한다. 특히, 소어는 시행 - 특수 지시문들을 읽음으로 인해 새로운 과제를 획득할 것이란 것을 이해한다. (실제적으로, 여기 그 과제에 대한 지시문들이 있다 와 같은 또 하나의 문장을 추가시키는 것은 이것을 가정하는 것을 피할 것이다.)

소어는 (그림 15 에 보인 것처럼) 그 과제에 있는 문장을 읽는 것과 정확히 같은 방법으로, 시행 - 특수 지시문에 있는 문장들을 읽는다. 단 이 시기에서만, 소어는 새로운 연산자인 하다-과제 do-task 연산자와 그것을 구현하는 새로운 문제 공간을 함께 생성하게 되며, 그 다음 지시문으로부터 그것의 연산자들을 구성하기 위하여 이 새로운 구현 공간의 맥락에서 이해하게 된다. 지시 문장들은 매우 간단하며, 그것들의 이해는 실제적인 어려움을 만들지 않는다. 각 문장은 하나의 연산자에 대한 지시를 제공한다. 이것을 하기 위한 지식은 단어들의 의미론에 전적으로 포함되어 있다 —— 즉 read, the, sentence, then, examine … done 에 대한 이해 연산자들 안에. 소어가 이러한 지시문들로부터 생성하는 새로운 공간은 문장 - 검증 과제를 수행하는 원래의 능력을 소어에게 제공하기 위해 손으로 작성되었던 공간과 동일하다.

소어는 그림 17 에서의 문장 지시문을 이해하는 것 이상의 일을 해야만 한다. 그것은 그 과제를 수행하기 위해 그 자신을 체제화해야만 한다. 그것을 하기 위해, 소어는 산출들의 적절한 조합 ensemble —— 적절한 막다른 상태에서 문제공간을 선택하는 조합, 목표들을 위한 연산자들을 선택하는 조합, 그리고 연산자들을 구현하는 조합 —— 을 만들어야만 한다. 이것은 소어가 지시문장들로부터 적절한 산출들로 이동해야 한다는 것을 의미한다. 새로운 산출들을 얻어내기 위하여 소어가 갖고 있는 유일한 기제는 청킹이다. 그러므로 소어는 청킹에 의해서 적절한 산출들을 생성한다. 그러나 이것은 6 장에서의 자료 청킹의 사례에서 보았던 것처럼, 소어가 올바른 청크들로 귀결되는 과제들을 수행해야만 한다는 것을 의미한다.

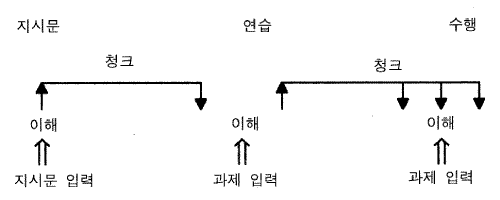
그림 18  과제 획득의 단계들

그림 18 은 무엇이 진행되는가를 개략적으로 보여준다. 소어는 언어적 형태로 입력된 지시문들로부터 시작하는데, 지시문은 우리가 살펴보았던 과정에 의해서 이해된다. 그 결과는 작업기업에서의 자료구조의 집합이며 이것은 이해를 구성한다. 이러한 자료구조들은 나중의 사용을 위하여 장기기억에 저장된다. 저장은 청킹에 의하여 자연스럽게 이루어지는데, 이는 그것이 바로 장기기억이 의미하는 것이기 때문이다. 저장을 달성하는 과제는 자료 청킹의 수정판이다 —— 어떠한 생성되어질 산출들의 행위들로서 나타날 필요가 있는 자료구조가 있는데, 그것은 나중에 그 당시 가용적인 어느 단서들의 기능으로서 회상되어질 수 있어야만 한다. 그러나 이 자료구조 자체는 이러한 산출들의 조건들의 부분이어서는 절대로 안 되는데, 그렇지 않다면 그 산출들은 결코 점화될 수가 없다 (좀더 정확하게 말하면, 단지 자료구조가 이미 작업기억에 존재할 때에만 그것들은 점화될 수 있다). 그리고 사실 이 청킹을 하는 데 사용되는 기제들은 본질적으로 자료 청킹에서 사용되는 것들과 동일하다.

새로운 과제 —— 여기서는, 문장-검증 과제 —— 를 수행하기 위한 첫 번째 설계가 제기될 때 소어에게 가용적인 것은 이러한 자료 청크들이다. 점화되었을 때, 청크들은 작업기억에 자료구조의 재구성된 수정판을 생성한다. 그러나 그 과제를 처음으로 수행하기 위해서, 소어는 이러한 자료구조들을 해석해야만 한다 —— 연산자들을 갖고 있는 문제공간들의 사용에 의해서 (어떤 다른 방법으로 그것이 이루어질 수 있겠는가?). 결과적으로, 해석이 성공할 때, 이 과제를 수행하는 새로운 청크들이 만들어진다. 문장 - 검증 과제의 후속적인 수행에서는, 이 같은 산출들이 직접적으로 문제공간과 연산자들을 구현한다. 그러므로 소어는 해석의 단계를 통과함으로써 그 과제를 획득하기 위해 움직인다. 여기서 사용된 문장 - 검증 과제와 같이 단순한 사례들에서, 소어는 단 한번의 통과로 그 과제를 수행하기 위해 손으로 작성된 산출들을 정확하게 획득한다. (주석 : 사실상, 그 실행들은 모든 수준들에서 청킹을 통해 이루어졌다. 만약 상향적 청킹이 사용되었다면, 이러한 모든 산출들을 학습하기 위하여 여러 번의 실행들이 취해져야 했을 것이다.) 그러나 좀더 복잡한 과제들에서는 한 번의 경험은 단지 과제수행의 가능성들을 통과하는 한 부분만을 제공하므로, 나중의 수행들은 청크화된 행동과 해석된 행동들의 혼합일 것이다. 이러한 기본적인 방식은, 현재 구체화된 소어에서는, TAQ 라고 불리는 문제공간들의 집합들에서 작동한다 (Yost, 1988).

해석에 의해 서술적 구조로부터 산출로 이동하는 이런 형태의 기술 획득은 기술 획득에 대한 액트스타 이론 (Anderson, 1981, 1983) 의 중심적인 견해이다. 그러므로 소어는 액트스타가 사용하는 동일한 획득방식을 이용한다. 물론 소어는 전적으로 청킹 기제와 문제 공간들에 의해서 그렇게 하며, 이 방법은 그것을 소어의 나머지 부분에 통합시킨다. 그러므로 또 다시 통합인지이론에서 제기되는 것은 기제들의 수렴이다. 액트스타를 또 하나의 인지의 보편적 이론의 후보자라고 생각하면, 나는 이러한 수렴을 소어에 대해서도 마찬가지로 긍정적인 증거라 취급한다.

이 예는 또한 학습과 문제해결이 함께 섞여지는 방식을 강조한다. 개념적으로 그것들을 구분하는 것은 더 이상 큰 의미가 없다. 문제공간, 막다른 상태, 청킹의 기본적인 구성개념들은 잘 정의되는데, 이는 그것들이 소어 구성에서 확인이 가능한 기제들이기 때문이다. 그러나 문제해결과 구분되는 것으로의 학습과 같은 —— 그리고 생각할 수 있듯이, 지각과 구분되는 것으로의 인지와 같은 —— 행동의 더 큰 범주화는 원리에서조차 명확히 정의되지 않을 것이다.

그러므로, 소어는 그림 13 에 제시된 이론, 즉 흐름도들은 단지 문제공간들을 반영한 것임을 정말로 구체화한다. 문제 공간들은 지시문들에 대한 반응으로 동적으로 만들어지기 때문에 그것들은 새롭게 만들어진 인지 구조들이다. 소어는 이러한 문제 공간들을 생성하라는 지시문들을 제공하는 정보를 받아들일 수 있고, 그 시점에서 그것은 과제를 이해하고 적절한 형식으로 행동한다. 소어는 이러한 과제 지시문들이 어떻게 수행되어지는가에 대한 진정한 이론을 제공한다. 더 나아가, 이 이론은 그 과제가 어떤 방법으로 수행되는지에 대한 이론과 함께 하며, 이것은 분명히 통합인지이론에서 기대되는 것이다.

4. 요약

작은 시간적 공간 안에서 인간들이 작동할 때, 인간이 그들의 목표들을 어떻게 달성하게 되는지에 대한 우리의 탐구를 요약해 보자. 비교적 긴 시간에 걸친 (~100 초) 문제해결에서의 탐색 통제에 대한 단서들을 찾기 위해 우리는 암호숫자산술을 먼저 살펴보았다. 만약 소어가 통합인지이론으로서의 충분한 범위를 갖는다면, 우리는 이 수준에서 적절하게 행동을 모형화하는 것이 중요하다. 그러나 우리는 통합이론이 허용해야 하는 수직적 통합의 예를 제공할 수 있을 정도로는 아직 소어를 발전시키지 못했다. 인지이론이 근본적으로 올바른 확신을 만들기 위해서 복잡한 행동, 특히 비교적 제약받지 않는 자연적인 행동의 큰 범위에 대한 자세한 모의실험을 고안하는 것이 중요하다는 것을 우리는 주장했다. 암호숫자산술에서의 모의실험의 사용은, 복잡성이 하위수준의 연산자들을 수작업으로 제공함으로써 통제될 수 있었으며, 그러므로 우리는 상위수준의 통제문제들에 직접적으로 주의를 집중할 수 있었음을 예시했다. 만약 우리가 암호숫자산술의 연산자들을 만들어내는 데 몰두하게 되었더라면, 우리가 탐색 - 통제 행동을 모의실험하기까지는 긴 시간이 필요했을 것이다.

합리성에 대하여 시간 이외의 한계들이 있는지를 묻기 위해서 우리는 삼단논법을 사용했다. 삼단논법들은 비교적 간단하고 짧은 과제들이지만, 어떤 실례들은 지능적인 사람들에게조차도 매우 어려운 것으로 밝혀졌기 때문에, 삼단논법은 이 물음에 대한 좋은 검사를 제공한다. 일반적으로 그 답은 어려움이 과제의 형식화에 있다는 것이다. 이것은 본질적으로 부호화 규칙들에 대한 질문이 아니다 (개별적인 자료가 보여주듯이 그러한 효과가 존재하지만). 그것은 처리의 속도를 위해서 표상적 계산력을 포기한 표상 (모형들) 의 사용으로부터 나온다. 양화사들이 사용되는 범주적 삼단논법들은 그 한계점을 보여준다. 그렇다 하더라도 적절한 수행을 허용하는 처리 방략들이 존재한다. 그러나 이러한 것들 (다중의 모형을 생성하고 검토하기) 은 복잡하며, 중요한 것은 피드백이나 올바른 수행이 발견되도록 허용하는 다른 지시문들 없이 그 과제들이 제시된다는 것이다. 모의실험의 관점에서 삼단논법의 흥미로운 측면은 그 이론을 실제적으로 급하게 만들어야 했다는 것이었다. 산출들에 의해 직접적으로 만들어졌다는 의미에서 이미 직접적인 수정판을 모의실험함으로써 우리는 본질적으로 우리의 이론으로 되돌아갔다. 그리고 그 다음 우리의 경험을 통해 청크화된 공간을 생성할 숙고적인 공간들로 되돌아갔다. 청크화된 공간은 흥미로운 구조를 가지고 있는 것으로 밝혀진 것이었다.

문장-검증 과제에서, 우리는 실행적-수준의 흐름도가 어디서부터 나왔는지를 설명하려고 시도했다. 우리는 직접적인 심리학적 타당도를 갖고 있는 구조로서의 흐름도를 제거하고, 그것들을 문제 공간에서 동적으로 생성된 행동의 정적이고 합성된 투사물 projections 로서 보여주는 이론을 제시했다. 궁극적인 —— 사실 훨씬 더 중요한 —— 요점은 지시문과 과제 수행이 하나의 이론 안에서 합쳐질 필요가 있다는 것이다. 그것은 통합인지이론의 의무인 동시에 그것을 위한 기회이기도 하다. 우리는 소어가 이러한 능력에 접근할 수 있음을 예시할 수 있었다. 모의실험의 관점에서 보면, 여기서의 교훈은 복잡성에 대처하려는 일반적인 것과는 반대된다. 문장 검증에 의해 보이는 상황들은 매우 단순하다. 결과적으로, 문제는 결론들이 이론에 의해서 생성되는 것이지 분석가의 직관적인 합리성에 의한 것은 아니라는 것을 어떻게 명백하게 하는냐 하는 것이다. 우리의 심리학 전공 서적을 채우고 있는 흐름도들은 과학자의 암묵적인 합리성에 몰래 들어가기 위한 전형적인 기회로서 그 효과를 유지할 수 있다. 여기서 모의실험은 이같은 단순한 상황들에서 이론화를 통제하기 위해서 사용된다.

그림 19 통합인지이론으로서 소어의 지금까지의 적용범위

마지막으로, 이러한 세 개의 주제들은 통합인지이론으로서의 소어의 범위에 대한 우리의 계속 진행 중인 점수판에 기여한다. 확장된 목록이 그림 19 에 제시되어 있다. 우리의 추가사항은 통합인지이론은 광범위한 시간적 범위에 걸쳐 작용한다는 요건을 나타낸다.