
계획과 산출
(Plans and productions)
컴퓨터와 마음 : Philip N. Johnson-Laird 지음, 이정모. 조혜자 옮김, 민음사, 1991, Page 187~205 (원서 : The Computer and the Mind: An Introduction to Cognitive Science, Harvard Univ. Press, 1988)
학습과 기억, 그리고 그 외 모든 고등정신과정들은 마음을 지배하는 동일한 일반원리들이 각기 다르게 나타난 것일 수가 있다. 그렇다면, 현명한 연구기법은 그러한 심적 <구조 (architecture)> 에 대한 이론을 발전시키고, 그리고서 이 구조에 근거하여 특정 프로그램들이 심적 과정들을 모형화하도록 작성할 수 있는 그러한 프로그래밍 언어를 구현하는 것이다. 마음의 구조에 대해서는 두 가지 주요 입장이 있다 : 그 하나는 <산출체계> 에 기초한 것이고, 다른 하나는 <병렬분산처리 (parallel distributed processing)> 에 기초한 것이다. 이 둘은 모두 학습과, 기억에서의 정보 인출에 대해 중요한 것들을 말해 준다. 나는 이 장에서 먼저 산출체계를 기술하고, 다음 장에서 병렬분산처리를 기술하려 한다.
심리학자들이 행동은 외적 사건들에 의해 조절된다고 믿었던 때가 있었다. 래슐리 (Karl Lashley) 는 이런 가정으로는 내적인 조직화를 요구하는 기술들이 빨리 수행되는 것을 설명할 수 없다고 지적했다. 1960 년에 밀러 (George Miller) 와 갈란터 (Eugene Galanter), 프리브램 (Karl Pribram) 은 『 계획과 행동의 구조 (Plans and the structure of Behavior) 』를 출판함으로써 행동주의를 관 속에 집어 넣고 봉해 버렸다. 그들은 계획이란 <일련의 조작이 수행되는 순서를 조절할 수 있는 유기체 내의 위계적인 과정> 이라고 정의하고, 계획하는 것이 인지의 중요한 부분임을 제시하였다. 산출체계는 그 뿌리를 <계획하기> 에 두었으며, 심적 과정의 계산모형의 선구자인 뉴월 (A. Newell) 과 사이먼 (H. Simon) 의 연구에 근거하고 있다. 계획에 대한 연구의 근원을 고려함으로써 산출에 대한 설명을 시작해 보자.
뉴월과 사이먼의 논의에 따르면, 여러분은 계획을 발전시킬 때 마음속에 초기상태 (initial state) 와 목표 (goal) 를 지니게 된다. 여러분의 과제는 전자에서 후자로 가게 할 일련의 조작들 (operations) 을 고안하는 것이다. 여러분의 과제가 기하학의 한 정리 (theorem) 를 입증하는 것이라고 가정해보자. 초기상태는 종종 도표로 요약되는 조건들의 집합이며, 목표는 결론이고, 조작들은 여러 공리들 (axioms) 과 사용 가능한 추론규칙들로 이루어진다. 이러한 조작들의 가능한 배열은 방대하다. 그리고 여러분이 이러한 가설적인 <문제 공간> 에서 발견해야 하는 것은 초기상태에서 목표까지의 공간을 통과하는 통로이다 :
초기상태 → 상태 2 → 상태 3 → …… → 목표
여기에서 각 화살표는 허용된 조작들 중의 하나를 상징한다.
여러분이 문제공간을 통과하는 통로를 탐색할 수 있는 데는 여러 다른 방식들이 있고, 많은 방식들이 컴퓨터 프로그램들로 구현되어 왔다. 여러분은 초기상태에서 시작하여, 모든 가능한 조작들을 초기상태에 적용시켜 가능한 대안적인 두 번째 상태들을 산출하고, 그리고서 마찬가지로 이들 상태들 각각에 조작들을 적용하여 다음 상태로 갈 수 있다. 문제가 본질적으로 해결될 수 없는 것이거나, 여러분이 모든 핵심적인 조작들을 알고 있지 못한다면, 여러분의 노력은 수포로 돌아갈 것이다. 그렇지 않다면 이런 식의 소위 <넓이 우선적 (breadth - first)> 탐색은 빠르든 늦든 간에 목표에 도달할 것이다. 문제는 탐색되어야 할 통로의 수가 지수 함수적으로 증가한다는 것이다 : 즉 각 지점에서 적용될 수 있는 가능한 조작이 두 개뿐인 경우에도 각 단계마다에서 통로의 수는 배로 증가하는 것이다. 따라서 모든 통로들을 탐색한다는 것은 곧 불가능해진다 ─ 여러분이 우주만큼이나 용량이 크고 빛의 속도만큼 빠른 컴퓨터를 가지고 있을지라도 그러하다. 탐색의 문제는 다루기가 힘들다. 제 12 장에서 보겠지만, 더군다나 어떤 영역들에서는 어떤 탐색절차이건 간에 성공적으로 통과할 통로가 없다는 사실을 발견하는 데 실패할 수도 있음이 입증되어 왔다 : 사실상 그 경우에 탐색절차는 문제 공간으로 들어가, 길을 잃어 버리고, 결코 답을 가지고 나오지 못한다. 따라서 어떤 절차가 사용되었건 간에 다룰 수 있는 크기로 탐색을 유지하기 위해서는 제약조건이 요구된다. 다시 강조하자면 제약조건들은 심적 과정에서 결정적 역할을 담당한다.
또 다른 유목의 탐색절차들은 한 번에 하나의 통로씩 <깊이 우선적 (depth - first)> 으로 탐색하는 것이다. 이는 마치 여러분이 미로를 통과하는 하나의 길을 발견하려고 노력할 때 행하는 것과 유사하다. 여러분이 통로들 중 하나를 선택하게 될 때에는 어떤 것이든 여러분이 현재 쓸 수 있는 방법들에 기초해서 하나를 선택한다. 문제를 해결하려고 노력할 때 여러분은 대안들 각각의 잠재적인 가치를 평가하여 선택할런지도 모른다. 물론 여러분이 절대적으로 자신하는 측정방법을 가지고 있다면 어려움은 없다. 여러분은 각 지점에서 최선의 선택을 하고, 따라서 어떤 막다른 골목으로 찾아 들어가는 일 없이 목표에 도달할 것이다.
많은 계획하기 문제들은 햄턴 왕궁 (Hampton Court) 의 미로와 같다. 여러분은 어떤 대안의 가치에 대해 불확실한 정보 아래 선택하지 않으면 안되게 될 수 있고, 이런 식으로 목표 지점이나, 막다른 곳에 도달할 때까지 진행을 하게 된다. 만약에 여러분이 막다른 곳에 도달한다면, 여러분은 이전의 선택점으로 물러서서 다른 대안을 시도해 볼 수 있다. 여러분이 이 지점에서 가능한 모든 선택을 다 해보았으나 소용이 없다면, 여러분은 한 걸음 더 뒤로 물러설 수 있다. 또한 거기에서도 마찬가지면 다시 뒤로 물러설 수 있다. 드디어 여러분이 모든 선택점에서 모든 가능성들을 검토했으나 목표에 도달하지 못했다면, 그 문제는 해결할 수 없는 것이다. 이런 식으로 선택점들을 되돌아가 작업하는 절차는 <후진추적 (backtracking)> 이라 불린다. 그것을 사용하기 위해서는 여러분은 아리아드네 (Ariadne) 의 실뭉치를 풀며 미노토 (Minotaur) 의 미궁을 더듬어 나갔던 테세우스 (Theseus) 만큼 신중해야만 한다. 즉 여러분은 자신이 만든 각 선택에 대해 기록을 해야만 한다. 로봇의 여행 체계처럼 (제 3 장 참조) 프로그램들은 더미를 이런 목적을 위한 기억으로 사용한다.
<역사를 모르는 사람은 실수를 반복하도록 운명지어져 있다> 는 말이 있다. 특정 선택이 실패한 이유 (reason) 를 고려하지 않는 단순한 후진추적도 마찬가지이다. 만약 여러분이 달군 부지깽이를 한 손으로 집어들었을 때, 단순한 후진추적은 여러분으로 하여금 다른 손으로 시도해 보도록 할 것이다.
여러분이 반드시 문제 <공간> 내의 초기상태에서 시작하여 목표에 이르는 길을 찾아 맹목적으로 전진적 탐색을 해야 할 필요는 없다. 뉴월과 사이먼은 수학자인 폴리아 (George Polya, 그의 입장은 플라톤이 예견했다) 의 생각에 기초를 둔 프로그램을 고안했다. 그 프로그램은 목표와 초기상태 사이의 차이를 줄이는 조작을 찾는 것이다. 따라서, 만약 여러분이 자신의 물통에 난 구멍을 수선할 계획을 발견하려고 하고 있다면, 목표와 초기상태 간의 차이를 줄이는 적절한 조작은 구멍 안에 마개를 막는 것이다. 그러나 그러한 조작을 수행하는 것은 전제조건들 중의 어떤 하나를 충족시킬 수가 없기 때문에, 예를 들어 마개를 발견할 수 없기 때문에 불가능할 수도 있다. 이러한 시점에서 뉴월과 사이먼은 근사한 생각을 도입했다. 여러분은 마개를 발견할 새로운 하위목표를 만들고, 이 하위목표를 여러분의 주 목표의 더미 위에 올려놓는 것이다. 이제 여러분은 이 하위목표를 달성하기 위해 동일한 절차를 사용한다. 즉 여러분은 하위목표와 초기상태 간의 차이를 줄이는 데 적합한 조작을 탐색한다. 만약 여러분이 마개를 발견하는 데 성공한다면, 여러분은 그 하위목표가 달성되었기 때문에 더미에서 그 하위목표를 제거한다. 이러한 제거로 인해 주 목표는 더미의 맨 위로 옮겨져 회복되고, 여러분은 일시적 목표 전환을 야기시켰던 그 원래 조작을 수행해 낼 수 있다. 즉 예를 들어 여러분은 마개를 여러분의 물통의 구멍에 넣는다. 하위목표의 해결을 위한 탐색은 또다시 하 - 하위목표를 만들 수가 있고, 따라서 하위목표들은 더미 속에 상당한 높이로 층층이 쌓여질 수가 있다. 물론 그러한 하위목표들의 생성이 언제까지나 하위목표 그 자체의 해결의 일부로서 동일한 하위목표로 되돌아가는 식이어서는 안된다. 여러분은 구멍난 물통을 수선하기 위해 물통을 가져오는 하위목표에 도달하기를 원하지는 않을 것이다.
GPS (일반문제 해결자, <general problem solver>) 로 알려진 뉴월과 사이먼의 프로그램에는, 특정 영역의 어떤 문제를 해결하는 것과 관련된 모든 조작들에 대한 지식과, 그것들이 유용하게 될 것 같은 상황에 대한 제약조건들이 장치되어야 한다. 그것은 일반 탐색절차를 사용하여 문제 해결 행위의 과정을 계획한다. 앞에서 설명하였듯이 그 탐색절차는 프로그램의 하위 부분들을 해결하는 데도 사용된다. 그러한 설계는 <순환 (recursion)> 의 또 다른 예로서, 그것은 여기에서 한 문제를 해결하기 위한 위계적인 계획을 구성하게 한다.
사람들이 계획을 할 때에는 관련 조작들에 대한 지식을 기억해 내야한다. 그러나 어떤 프로그램이 장기기억으로부터의 지식 인출을 조절하며, 또 지식은 장기기억에 어떤 형태로 저장되어 있는가? 보다 최근 이론에서 뉴월과 사이먼은 지식이 다음의 형태를 띤 조건규칙들의 방대한 집합으로 표상된다고 제안하였다.
조건 → 행위
<물통에 구멍이 있고, 여러분이 마개를 가지고 있다면, 그 마개를 구멍 안에 넣어라> 와 같은 조건규칙들은 일반지식에 대한 빈약한 표상같이 보일 수가 있다. 그러나 사실상 그것들은 보편 튜링기계의 성능과 등가적일 수 있는 문법을 구상한다. 실제로 미국의 논리학자 포스트 (Emil Post) 는 무엇이 계산될 수 있는지를 규정하기 위해 산출규칙들을 고안하였다. 그것들은 특수한 인지이론들을 구성할 수 있도록 하는 심리학 지향적인 계산이론이다.
제3장에서 언급했던 것처럼 문법은 아무것도 행할 수가 없다. 문법은 문법을 사용해 주는 프로그램을 필요로 한다. 마찬가지로, 산출규칙들도 어떤 것을 행할 수 있기 위해서는 하나의 프로그램에 의존해야만 한다. 뉴월과 사이먼은 산출규칙들은 장기기억 내에 저장되어 있고, 그것들을 인출하고 사용하기 위한 프로그램은 작업기억 내에서 행해진다고 가정하였다. 어떤 규칙의 <조건> 으로 기술된 사건들의 상태가 작업기억 내에서 발생할 때마다 그 규칙은 촉발되고 <행위> 가 수행되게 된다. 따라서 하나의 규칙을 촉발시키기 위해 작업기억의 현재 내용들은 장기기억 내의 모든 규칙들의 <조건> 들에 대한 비교 부합 테스크를 거치게 된다. 이러한 비교 부합 과정은 인간에게서는 단 하나의 병렬적인 단계에서 이루어진다고 추측된다. 규칙의 작용 (<행위>) 은 신체적인 반응으로 나올 수 있지만, 그것은 또한 작업기억의 내용들을 변화시킬 수 있고, 이런 식으로 어떤 규칙이 다음번에 촉발될 것인지를 통제할 수도 있다. 따라서 하나의 규칙이 어떻게 다른 규칙을 따라 일어나는가를 결정하는 원리들이 규칙들 자체에 내장되어 있다. 그 체계는 내가 앞 장의 마지막 부분에서 언급했던 문제를 해결한다 : 즉 그것은 한 과제의 수행을 통제한다. 이러한 추상적 처방은 처음에는 이해하기 힘들지만 예를 보면 더 분명해질 것이다.
산출체계의 작용을 묘사하기 위하여 나는 나의 동료인 영 (Richard Young) 이 고안했던 모델을 개관해 보려 한다. 그것은 단순 과제를 주었을 때의 아동들의 수행을 모형화한 것이다. 아동들은 나무막대들을 길이 순서대로 놓아야 했다. 피아제 (Jean Piaget) 와 그 동료들이 관찰했던 것처럼, 아동들이 그 과제를 수행하는 능력은 몇 단계를 거쳐야 했다. 4 살 난 아동들은 이따금 두 막대를 올바른 순서로 맞추는 데 성공했다. 이런 제한된 능력에는 단순한 몇 개의 산출규칙만이 요구된다. 나는 그것을 언어로 의역해 보겠다. 그것들은 목표들이 놓여져 있다가 성취되면 제거되는 더미형태의 작업기억에 의존적이다.
초기단계는 주 목표를 (서열화된 순서를 만드는) 더미 위에 놓는 것이다. 나머지 수행은 규칙들에 의해서 좌우된다. 첫 번째 막대가 제자리에 놓여지는 것을 보장하는 규칙들이 있다 :
1. 현재의 목표 (예 : 더미의 맨 위에 있는 것) 가 막대를 하나로 배열하는 것이고 어떤 막대도 제 위치에 있지 않다면, 첫 번째 막대를 제 위치에 놓는다는 목표를 더미에 첨가하라.
2. 현재의 목표가 첫 번째 막대를 제 위치에 놓는 것이라면 큰 막대를 집어 들라.
3. 현재의 목표가 첫 번째 막대를 제 위치에 놓는 것이고, 큰 막대가 집어 들어졌다면, 그것을 가장 왼쪽에 내려놓고 더미의 맨 위에 있는 목표를 제거하라 (그것은 성취되었기 때문이다).
이 마지막 단계는 그 배열을 시작하기 위해 첫 번째 막대를 놓는 목표를 만족시킨다. 그러나 하나의 서열을 형성하라는 주 목표는 더미의 맨 위에 아직도 남아 있다. 두 번째 규칙 집합은 막대들을 순환적으로 계속 배치하게 한다 :
4. 현재의 목표가 막대를 하나로 배열하는 것이고 적어도 하나의 막대가 제 위치에 놓여져 있다면, 그 다음 막대를 제 위치에 놓는다는 다음의 목표를 그 더미에 첨가하라.
5. 현재의 목표가 그 다음 막대를 제 위치에 놓는 것이라면, 가장 가까운 막대를 집어 들라.
6. 현재의 목표가 그 다음 막대를 제 위치에 놓는 것이고 하나의 막대가 바로 집어 들어졌다면, 그것을 서열의 오른편에 놓고 더미에서 그 목표를 제거하라.
7. 현재의 목표가 하나의 서열을 형성하는 것이고 적어도 하나의 막대가 제 위치에 놓여져 있고 더 놓여야 할 막대가 남아 있지 않다면, 그 목표를 더미에서 제거하고 멈추어라.
이러한 일곱 규칙들을 갖는 프로그램은 처음에는 큰 막대 하나 ─ 아마도 가장 큰 것 ─ 를 집어들 것이고, 그리고서 그 서열에 막대들을 멋대로 첨가할 것이다. 이는 마치 피아제가 관찰했던 가장 어린 아동들의 수행과 유사하다.
영은 새로운 규칙들을 첨가함으로써 아동 발달의 한 단계에서 다음 단계로의 전이가 어떻게 모형화될 수 있는지를 보여주었다. 그래서 다음과 같은 후속 규칙들의 첨가는 새롭게 형성된 근접 막대 쌍이 잘못된 순서로 있을 때 그것들의 위치를 바꿈으로써 수행을 개선시킨다 :
8. 현재의 목표가 그 다음 막대를 제 위치에 놓는 것이고 막대들의 새로운 배치가 형성되어졌다면, 새로운 위치에 있는 막대가 그 서열내의 인접 막대보다 더 큰지를 검토하라.
9. 현재의 목표가 그 다음 막대를 놓는 것이고 새로운 위치에 있는 막대가 인접 막대보다 작다면, 그 목표를 더미에서 제거하라.
10. 현재의 목표가 그 다음 막대응 제 위치에 놓는 것이고 세 위치에 있는 막대가 인접 막대보다 더 크다면, 두 막대의 위치를 바꾸어라.
이 마지막 규칙의 효과는 전체 막대의 배열에 적용된다. 이 규칙은 다음과 같은 배열처럼 배열에 첨가된 막대가 서열 내의 인접 막대보다 더 클 때 촉발된다 :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
위의 마지막 규칙은 새로운 배열을 산출하도록 작용한다 :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
이러한 배열은 새로운 위치에 있는 막대가 왼쪽에 근접해 있는 막대보다 클 때를 지적한 규칙 8 을 촉발하고, 이 사실은 또다시 규칙 10을 촉발한다. 그것의 결과는 다음과 같다 :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
이러한 새로운 배열은 규칙 8, 즉 새 막대가 그것의 왼편에 있는 것보다 더 작은 것을 기록하는 규칙을 촉발하고, 이러한 사실은 규칙 9, 즉 그 막대를 제자리에 놓는 목표를 더미에서 제거하라는 규칙을 촉발한다.
결국 이 규칙체계는 막대들을 올바른 서열로 배열한다. 이는 대여섯 살난 아동들이 이 과제를 수행할 수는 있지만 막대들을 올바른 서열로 끊임없이 재배열함으로써 비로소 가능한 경우와 아주 유사하다. 여덟 살난 아동들은 보통 실수 없이 막대들을 올바른 서열로 놓을 수 있으며, 첨가된 막대를 올바른 위치에 끼어놓기까지 할 수 있다. 영은 이 단계를 그 이상의 규칙들에 의해 모형화하였다. 즉 막대의 크기에 의존하여 막대들이 집어 들어지는 순서가 지켜지는 규칙이다.
그 프로그램은 목표들을 위계적인 더미로 쌓는 것이고, 과제는 다음과 같이 더 이상 첨가될 막대가 없을 때까지, 막대를 제자리에 놓는 목표가 계속되는 구조를 갖는다.

따라서 여기서는 계획이란 하나의 목표가 두 개의 하위목표들을 지배하는 단순 위계이다. 원칙적으로 계획들은 계속 하위의 목표들로 분할되는 위계를 지닌다. 목표가 하위목표를, 하위목표가 하 - 하위목표를, 하 - 하위목표는 하 - 하 - 하위목표를 지배하는 이러한 분할은 무한히 계속 도는 것은 아니고, 낮은 수준의 목표들을 달성하는 기본행위들 집합에 이를 때까지 계속될 수 있다.
산출체계란 바로 이런 위계적인 계획들을 생성하고 실행하는 한 방식이다. 이런 체계들 내에 가장 자연스럽게 구조화되어 있는 이론들은 뚜렷한 패턴을 기초로 작용한다. 규칙 조건들은 예를 들어 각기 다른 많은 막대들을 지시할 수 있는 <막대> 와 같은 변수들을 내포한다. 따라서 규칙을 촉발시키는 것은 작업기억의 특정한 내용이라기보다는 작업기억 내의 정보의 패턴이다.
원래 뉴월과 사이먼은 논리나 체스, 그 외의 영역들에서 어떻게 사람들이 문제를 해결하는지에 대한 이론을 만들기 위해 산출체계를 사용하였다. 그 이래로 다양한 프로그래밍 언어들이 산출체계에 근거해 왔다. 산출체계들은 전문가의 지식 (제 12 장에서 논의할 소위 <전문가 체계 expert system>) 을 구현하는 실제적인 프로그램을 발전시키는데 사용되어 왔다. 그것들은 또한 많은 심리학적 이론들을 구성하는데도 사용되어 왔다. 이러한 이론들간의 주된 차이는 산출 규칙들과 관련된 것이 아니라 그것들을 조작하는 프로그램과 관련된 것이다. 작업기억이 집적적인 더미인지 아닌지에 대해서는 의견이 분분하다. 왜냐하면 더미식의 기억에서는 별문제가 없을 것 같은 과제들에서, 예를 들어 아주 삽입적인 문장글을 이해하는 과제에서 사람들이 어려움을 겪기 때문이다. 따라서 어떤 프로그램들은 루프나 <완충기 (buffer)> 처럼 작용하는 작업기억을 사용한다. 거기에서 항목들은 기억에 들어가는 순서에 따라 접근되어 첫 번째 들어온 것은 첫 번째로 나간다.
이론들간에 있는 또 다른 차이는 독자를 궁금하게 만들어 왔을지도 모르는 어떤 문제, 즉 하나 이상의 산출규칙이 기억의 내용들과 부합될 때에는 무슨일이 일어나는가 하는 문제와 관련된다. 영의 체계는 가장 상세하게 기억의 내용들과 부합되는 규칙을 촉발시킨다. 규칙들은 프로그래머에 의해 우선순위가 정해질 수도 있다. 따라서 갈등이 발생할 때에는 가장 우선적인 규칙이 선택된다. 아니면 얼마나 빈번하게 하나의 규칙이 사용되어 왔는가, 또는 얼마나 최근에 그것이 촉발되었는가가 고려되어 갈등 해결이 결정될 수 있다.
앤더슨 (John Anderson) 은 산출체계에 기초하여 기억과 학습에 대한 포괄적인 이론을 발전시켰다. 그가 ACT 라고 부른 이 이론은 계속 발전되는 일련의 컴퓨터 시뮬레이션으로 구현화되어 왔다. 최근의 이론은 ACT 로서 그림 9.1 에 요약되어 있다. 이 이론은 두 가지 유형의 장기기억을 구별한다 : 즉 사실과 경험에 대한 기억과. 기술 (skill) 에 대한 기억이다. 여러분은 경험을 기억할 때는 마음에 떠올리고 아마도 다시 그것을 음미하는 식으로 기억할 것이다. 그러나 기술들에 대해서는 잘 기억하지를 못하거나, 아니면 다시 해 보일 수조차 없다 : 여러분은 상황에 맞는 방식으로 기술을 수행한다. 이전 장에서 보았듯이 뇌손상은 경험에 대한 기억을 손상시키지만 기술에 대한기억은 거의 본래의 상태대로 남겨둔다. 튤빙 (Endel Tulving) 과 같은 몇몇 심리학자들은 기억이 특정한 자서전적인 일화적 경험들에 대한 기억과, 단어의 의미와 같은 일반지식의 항목들에 대한 기억으로 더 구분될 수 있다고 논의한다. 그러나 앤더슨은 세 가지 기억의 요소들을 가정한다. 순간순간 용량에 변화가 오는 작업기억과, 기술에 대한 장기기억 (산출기억) 과, 명제와 심상, 사건의 순서표상에 대한 장기기억 (서술기억) 이 그것이다.
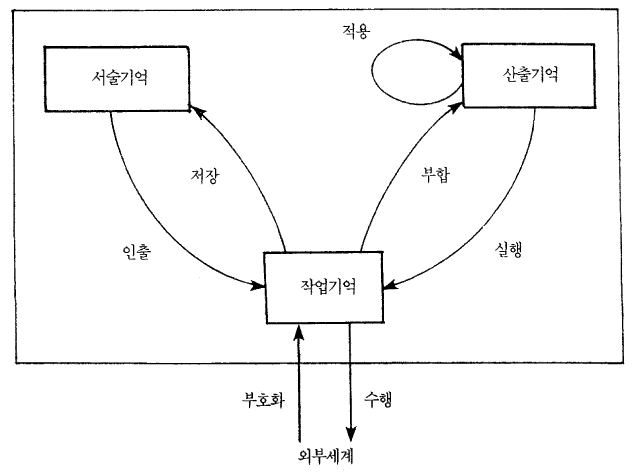
그림 9.1 : 앤더슨이 제안한 ACT 기억이론의 주요 구성요소. (From J. R. Anderson, The Architecture of Cognition. Cambridge, Mass : Harvard University Press, 1983, p.19)
이 이론은 여러 복잡한 문제를 산출체계의 구조에 도입한다. 세 기억들 모두에 있는 항목들은 각기 <활동> 정도가 다를 수 있다 (이는 무선점 양안시에 대한 마(Marr)와 포지오 (Poggio)의 처리기들과 유사하다). 작업기억의 내용이 산출기억 내에서 하나 이상의 규칙과 부합한다면 가장 활동적인 규칙은 그것이 무엇이건 간에 촉발된다. 더욱이 하나의 패턴이 활성화되면 그것은 그 패턴의 보다 특수한 변형들을 흥분시키고, 대안적인 패턴은 억제한다. 이와 같이 ACT는 정상적인 <상향 (bottom - up)>적 패턴 부합 처리 양식과, 이에 따르는 <하향 (top - down)>처리, 즉 활성화된 상위 수준의 구조에서부터 하위 수준의 세부 사항들을 예견하도록 하는 하향처리를 조합한다. 하향처리는 작업기억의 내용과 완전히 부합되지 않는 규칙을 촉발시킬 수도 있다 - 이는 유용할 수도 있지만 그러나 또한 사람들이 일으키는 오류와 유사한 수행상의 오류를 일으킬 수도 있는 절차이다.
앤더슨 이론의 핵심적인 가정은 모든 지식이 초기에는 명제적이지만 그것이 절차로 변형될 수 있다는 것이다. 예를 들어 여러분은 운전을 배울 때 어떤 사실들을 들음으로써 시작을 하고, 들은 것을 행위의 지표로 아주 느리게 해석해 낼 수 있다. 연습의 결과로 이러한 지식은, 빨리 그리고 자동적으로 실행되는 산출체계 내의 절차로 전환된다. 이러한 생각은 학습의 문제와, 특히 어떻게 그것이 산출체계 내에서 이루어질 수 있는가 하는 문제를 다시 불러일으킨다.
복잡한 기술의 학습, 특히 계획하기와 같은 지적인 기술의 학습은 오랜 시간이 소요된다. 사이먼은 아동들이 학교 갈 준비가 되기까지는 5 ~ 6 년이 걸리고, 유능한 의사나 과학자, 또는 전문가가 되려면 그 이후 20년의 교육이 더 필요하다는 점을 지적하였다. 과연 이런 느린 현상이 필연적인 것인지, 그리고 이 현상이 사실들을 수집하고 지식 사용에 숙련되는 과정 동안 일어나는 마음의 어떠한 면을 반영하는 것인지 궁금하다.
하나의 단서는 학습의 <멱 (power)> 법칙으로서, 하나의 과제를 수행하는데 걸리는 시간은 그 과제가 얼마나 많이 연습되어져 왔는가와 관련된다는 것이다. 분명히 연습은 완전함을 낳고, 연습하면 할수록 더 빠른 수행이 가능하다. 그러나 뉴월과 로젠블룸 (Paul Rosenbloom) 은 많은 학습 연구들 - 공장에서 담배 만드는 일에서부터 실험실에서 거꾸로 제시된 텍스트 읽는 것에 이르기까지 -을 검토한 결과, 도처에서 양적인 법칙이 존재함을 발견했다 : 즉 여러분이 어떤 과제를 수행해 온 횟수의 대수값과 관련하여 그 과제를 수행하는 데 걸린 시간을 대수적으로 그려 본다면 결과는 직선으로 나타난다. 그림 9.2 는 그러한 전형적인 예를 보여준다. 이 법칙의 주 제약조건은 사람들이 오류 없이 즉시 수행할 수 있는 과제여야 한다는 것이다. 어떤 과제가 얼마나 빨리 최고로 수행될 수 있는가 하는 데에는 물리적인 장애가 있다. 그것이 이 법칙상의 또 하나의 제한이다.
이 법칙은 무엇을 의미하는가? 가령 한 과제를 수행하는 데 걸리는 시간이 그 과제의 분리된 요소들 각각을 수행하는 데 걸리는 시간들의 합에 근거한다고 하자. 만약에 연습으로 인해 이들 요소들 각각이 똑같이 일정한 비율로 더 빨리 수행된다면, 현재 그 과제를 수행하는 데 걸리는 시간에 정비례하여 절약 (학습효과) 이 일어날 것이다. 이 원칙은 지나치게 효율적이다 : 그것은 소위 <지수 (exponential)> 법칙이라는 것이 된다. 그러나 멱 법칙이 보여주는 것은 학습진도가 항상적이지 않고 점차 느려진다는 것이다. 그것은 마치 연습이 계속되면 (학습수행) 개선의 가능성은 점점 소진되는 것과 같다. 그러나 이런 가능성들은 대체 무엇일까?
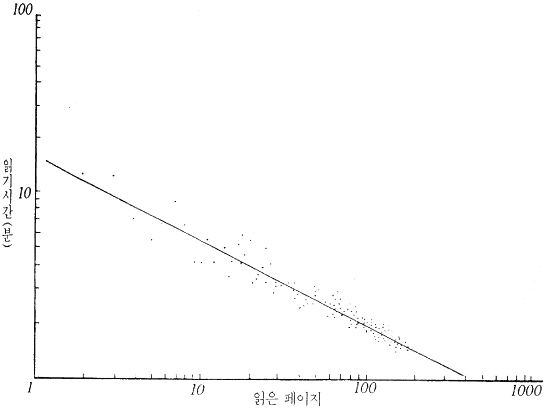
그림 9.2 : 학습의 <멱 (power)> 법칙의 한 예 : 거꾸로 된 텍스트
한 페이지를 읽는 데 걸리는 시간의 대수값이 그 사람이 이미 읽은 페이지 수와 대수함수로
그려져 있다. 이 자료는 원래 콜러스에 의해 보고되었다.
(From A. Newell and P.S. Rosenbloom, Mechanisms of skill acquisition and
the law of practice. In J.R. Anderson, ed., Cognitive Skills and their Acquisition.
Hillsdale, NJ : Lawrence Erlbaum, 1981, p. 7. The data were originally reported
in P.A. Kolers, Memorial consequences of automatized encoding. Journal of Experimental
Psychology : Human Learning and Memory, 1, 1975)
이전 장에서 보았던 조지 밀러의 생각은 연습이 학습자로 하여금 한 과제의 요소들을 점점 더 큰 단위나 <청크> 로 조직하도록 할 수 있다는 것이다. 예를 들어 장기 초보자들에게 장기판을 몇 초 동안만 보도록 하면 그들은 장기판의 세부적인 위치를 기억하기가 어렵다. 그러나 장기 고수들은 똑같이 짧은 순간 장기판을 보더라도 각 장기알의 위치를 기억한다. 그들은 장기 위치에 대해 방대한 기억능력을 발전시켰고, 이러한 위치들은 장기알들을 의미있는 관계로 묶은 <묶음 (청크)> 으로 저장되어 있다. 사이먼의 측정에 따르면, 그들은 여러 해 경험의 결과로 50,000 여 청크를 형성해 지니고 있다. 청크의 범위가 크면 클수록 ─ 즉 청크가 포함하는 장기알이 많을수록 ─ 게임에서 그러한 청크가 발생할 기회는 더 적어진다. 크기가 더 큰 새로운 청크는 그 구성성분들을 이루고 있는 형태들이 발생되어야만 형성될 수 있다. 뉴월과 로젠블룸은 청크가 커지는 것을 모사하기 위해 산출체계를 사용한다. 그들이 지적했듯이 청크가 커지면 커질수록 그것을 학습하는 경우는 더 드물어진다. 학습의 속도가 필연적으로 느려지는 것은 멱 법칙을 설명하는 것일 수도 있다.
우리는 이제 다시 원점으로 되돌아와서 학습을 새로운 프로그램들을 구성하는 하나의 프로그램으로 다루는 입장을 보기로 하자. 단 결과로 나타나는 프로그램들이 산출체계의 형태를 취해야 한다는 단서를 가지고 보기로 하자. 산출체계는 규칙들의 집합이고, 따라서 학습은 기존의 집합에 단지 새로운 규칙을 첨가함으로써만 일어날 수 있다. 그러한 규칙들을 구성하는 많은 기제들이 가능하다. 새로운 규칙들을 구성하거나, 새로운 규칙들을 첨가하거나, 아니면 루이스 (Claytoin Lewis)가 제안했었던 것처럼 각기 다른 기존의 규칙들을 하나로 통합하는 능력을 갖는 특수한 규칙들이 있을 수 있다.
또 다른 산출의 원천은 사실들에서 비롯된다. 예를 들어 여러분의 장기기억 내에 있는 사실들 가운데 학교에서 배웠던 통상적인 덧셈표가 있다고 하자. 이는,
3 + 5 = 8
이라는 사실을 포함할 것이다. 이러한 사실들은 3 + 5 의 합을 찾거나, 아니면 8 을 얻기 위해서는 어떤 수가 3 에 더해져야 하는가를 알아내는 등, 여러 가지 일들을 하는 데 사용할 수 있는 이점을 가진다. 그러나 물론 사실들을 사용하기 위해서는 그것들을 해석할 절차들이 필요로 되고, 이러한 해석에는 시간이 소요된다. 만약 여러분이 덧셈표와 그것을 해석하기 위한 절차들만을 가지고 있다면, 여러분의 수행은 비교적 느릴 것이다. 적어도 앤더슨에 있어서는, 초기의 머뭇거리는 기술 수행에서부터 고도로 연습된 수행으로의 전환은 사실들의 집합이 산출규칙들의 집합으로 변형되는 것에 해당한다. 산출은 그것들이 즉시 수행될 수 있다는 이점을 가진다. 따라서 여러분이 덧셈표의 사실을 산출로 전환할 수 있다면 여러분은 보다 빨리 수행할 수 있을 것이다. 다음의 예는 일상 언어로 의역된 특수한 산출규칙의 한 예로서, 위와 같은 덧셈에서 여러분이 필요로 하는 종류의 산출을 만들 것이다 :
덧셈표가 A + B + C 형태의 사실을 내포한다면, <A
와 B 를 더하는 ![]() >
를
<C 를
>
를
<C 를 ![]() >
를
>
를 ![]() 로 하는 새로운 규칙을 형성하라.
로 하는 새로운 규칙을 형성하라.
이러한 규칙은 다음과 같은 새로운 규칙을 구성할 수 있다 :
목표가 3 과 5 를 더하는 것이라면, 그 답은 8 이다.
이러한 기제가 어떤 형태의 학습에는 가공할 만큼 좋다는 것은 당연하다.
앤더슨은 또한 대안적인 학습방법도 제안하였다. 그는 사실들을 규칙으로 변형하는 특수한 기제를 도입하였다. 이러한 변형은 상위 수준의 프로그래밍 언어로 쓰여진 어떤 프로그램을 컴퓨터를 직접 제어하는 기계어로 <번역하는 것 (compilation)> 과 유사하다. 다른 부호로의 번역이 그것을 수행하는 특수한 프로그램에 의존적인 것과 같이, 명제들이 절차적인 규칙으로 전환되는 데는 산출체계의 구조에 내장된 특수한 기제가 필요하다. 앤더슨이 지적했던 바와 같이, 이러한 설명의 멋있는 특징들 중 하나는 그것이 연습의 부정적인 측면들 중 얼마를 설명한다는 것이다. 어떤 기술이 자동화되면 지금까지는 중간단계였던 단계들 중 어떤 것을 생각하거나 의식적으로 접근하지 않고도 그 기술이 수행될 수 있다. 그 결과는 때때로 바보 같은 것이다. 여러분이 어떤 공식적인 행동 방식을 학습해 왔다면, 여러분은 새로운 상황에서 일어나는 분명한 지름길을 간과해 버릴지도 모른다. 여러분의 수행은 다음의 아동용 수수께끼가 보여주는 것처럼 오류를 만들도록 이끌어갈 수도 있다. 여러분은 <M>, <A>, <C>, <H>, <A >, <M>, <I>, <S>, <H> 를 어떻게 발음하는가? <M>, <A>, <C>, <H>, <E>, <N>, <R >, <Y>는 어떻게 발음하는가? <M>, <A>, <C>, <H>, <I>, <N>, <E>, <R>, <Y> 는 어떻게 발음하는가?
산출체계란 학습과 표상, 지식의 인출에 대해 하나의 이론을 구성하는 세련되고 일률적인 방식이다. ACT 와 같은 특수한 이론은 분명히 잘못되었다는 것이 보여질 수 있다. 그러나 원칙적으로 산출체계는 보편 튜링 기계가 갖는 무제한적인 능력을 갖는다. 따라서 마음의 구조에 대한 가설로서의 산출체계는 어떤 경험적인 증거에 의해서도 반박될 수 있는 것 같지 않다. 산출체계는 어떤 일관성 있는 형태의 결과들도 다 설명할 수 있는 것이다. 따라서 산출체계는 경험적으로 검증 가능한 이론이라기보다는 프로그래밍 언어와 보다 유사하다.
산출체계를 구성했던 이론가들에게 공통점이 있다면 그것은 무엇인가? 답변은 세 가지 주 원리들인 것 같다. 첫째, 이론가들은 단일한 심적 구조를 신봉한다. 둘째, 그들은 심적 과제의 수행을 지배하는 통제 과정들이 비교적 단순해야 한다고 논의한다 : 즉 본질적으로 작업기억의 내용들은 장기기억 내에 저장된 절차들을 촉발하고, 한편 그 절차들은 교대로 그것이 작업기억에 영향을 미치는 방식에 따라 다음에 선택되는 것을 지배할 수 있다는 것이다. 셋째, 그들은 학습과 기억을 지배하는 과정들은 상징적인 규칙들에 의존한다고 가정한다. 산출체계 내의 특정 상징의 의미는 그것이 일어나는 규칙들에 전적으로 의존하고, 이 규칙들은 그 체계 내에서 분명한 구조로 명시되어야 한다. 여러분은 언어로 그렇게 쉽게 의역되는 그런 규칙들이 여러분의 심적 생활의 기저에 놓여 있다는 것이 오히려 이상하다고 생각할지도 모른다. 여러분이 마음의 뚜껑을 벗기고 자세히 들여다볼 수 있다면, 의회 조례 (Act of Parliament) 처럼 진열된 원칙들의 집합을 과연 실제로 발견하며, 그런 원칙들이 우발적인 모든 것들까지 포괄할 수 있는 것일까? 아마도 그렇지 않을 것이다. 이러한 의심은 부분적으로는 다음 장에서 기술할 심적 구조에 대한 대안적인 생각의 배후에도 놓여 있다.
읽을거리
뉴월 (1973) 은 심리학적 관점에서 산출체계에 대한 설명을 하고, 사이먼 (1981, 제 4 장) 은 기억과 학습에 대한 자극적인 논술을 제시하며, 윈스턴 (Winston, 1984, 제 6 장) 은 프로그래밍 절차를 개관한다. 학습과 아동발달을 모형화하는데 산출체계를 사용하는 것에 대한 최근의 논문집이 클라 (Klahr), 랭글리 (Langley), 니취스 (Neches) (1986) 에 의해 편집되었다. 아동의 서열과제 수행에 대한 연구들은 피아제 (1952), 인헬더 (Inhelder) 와 피아제(1964) 에 기술되어 있다.