신경회로망

1. 서론

이 장에서는 인공지능을 구현하는 또 다른 방법인 신경회로망 (Neural Networks) 에 대해 설명한다. 신경회로망은 생물학적 뇌의 작동원리를 그대로 모방하여 새로운 형태의 컴퓨터를 만들려는 노력으로 신경회로망과 대비하여 앞장들에서 설명된 인공지능기법들을 '부호추론에 의한 인공지능' (Symbolic AI) 이라고 구별하여 부른다.이 장에서는 신경회로망컴퓨터가 필요해진 동기 및 간단한 역사를 살펴본 후 이해를 돕기 위해 먼저 간단한 응용사례를 들어 신경회로망의 성격, 구성요소 및 이용방법들을 간단히 설명하고 신경회로망의 구성요소, 학습방법 및 신경회로망 모형분류에 대해 구체적으로 설명한다. 또 대표적인 신경회로망 모형들의 소개 및 전문가시스템과 신경회로망의 결합에 대해 설명한 후 각 분야별 신경회로망의 응용사례들을 간략히 소개한다.

인간두뇌에 대한 연구는 상당히 오래 전부터 계속되어 왔으며 정보처리기술의 발달과 더불어 인간과 같이 사고하고 판단하며, 사물을  인삭할 수 있는 인공지능을 실현시키기 위해 많은 노력이 있어왔고, 덕택에 우리는 특정 분야의 전문가가 가진 전문지식을 컴퓨터에 옮기고 이를 자유로이 이용할 수 있는 단계에까지 이르렀다. 현재 제한된 범위 내에서라는 전제만 한다면 인간보다 더 빠르고 정확하게 사고하고 판단하는 인공지능컴퓨터의 구현은 어려운 일이 아니다. 하지만 사물의 인식, 특히 시각적 패턴인식의 측면에서는 아직도 큰 진전이 없었다. 다시 말해, 한두 살짜리 어린아이의 얼굴인식능력이나 연상 능력은 현재 가장 우수하다는 수퍼컴퓨터를 여러 대 동원해도 따라가기 힘든 실정이다. 따라서 이와 같은 현상을 설명하기 위해서는 기존의 컴퓨터 작동원리와 두뇌의 작동원리간에 어떤 차이가 있는가를 이해할 필요가 있다.

컴퓨터 하드웨어의 급속한 발전에도 불구하고, 인공지능분야에서는 아직도 컴퓨터의 더 많은 계산능력이 요구되는 응용분야들을 우리는 쉽게 발견할 수 있으며, 이러한 요구에 대처하기에는 현재의 컴퓨터 구조로는 다음과 같은 한계가 있다. 첫째는 물리적인 한계로 아인슈타인 애로 (Einstein Bottleneck) 라고도 불리는데 한 기계내에서 신호의 전달속도는 빛의 2/3이상의 속도를 가질 수 없다는 것이다. 이느 중앙처리장치 (CPU) 의 크기가 1입방피트일 경우 처리속도는 최대 567MHz를 넘어설 수 없다는 것이다. 둘째는 구조적 한계로써 바배지 및 폰 노이만 애로 (Babbage/Von Neumann Bottleneck) 인데, 이는 기존 컴퓨터의 구조가 연산장치와 주기억장치가 분리되어 있고 순차처리만이 가능한 통제구조를 가지고 있어 자원의 낭비가 심하고 처리능력을 향상시키는데 제약이 많다는 것이다. 셋째는 지식획득의 한계 또는 화이겐 바움 애로 (Feigenbaum Bottleneck) 라고 하는데 이는 궁극적으로 기계학습과 관련된 문제이다. 다시 말해 지식획득 과정 및 획득된 지식의 컴퓨터 내에의 표현을 전적으로 지식공학자의 손에만 의존할 경우 너무 많은 시간와 노력이 필요하다는 것이다. 이와 같은 한계들은 현재 다중처리기를 이용한 병렬처리시스템의 개발과 다양한 기계학습방법의 개발을 통해 극복해 나가고 있는 과정에 있다.

이에 반해 신경회로망은 아주 다른 개념의 컴퓨터라고 생각할 수 있다. 즉, 기존의 컴퓨터 구조로부터 과감하게 벗어나 생물학적 두뇌의 작동원리를 그대로 모방하여 새로운 형태의 계산도구를 만들고자 하는 것이다. 계산에 관한한 컴퓨터는 인간보다 훨씬 빠르고 정확하다. 현재 컴퓨터의 단위연산 처리 속도는 피코 초 (pico) 단위로 측정될 정도로 빠르지만 인간의 두뇌는 밀리 초단위로 측정할 수 있을 만큼 느리다. 하지만 물체를 인삭하고 인식된 물체들간의 관계를 파악하여 기억장치로부터 주어진 상황에 적절한 정보를 끄집어 내어 이용하는 능력에 있어서는 인간이 훨씬 뛰어나다.이러한 현상은 인간의 두뇌가 대단위 병렬처리시스템 (Massively Parallel Processing System) 이라는 사실에 의해 설명될 수 있다.

뇌를 구성하는 가장 기본적인 단위는 뉴론 (Neuron) 이라고 불리우는 세포로 뉴론의 기본구조는 <그림 14-1> 과 같다. 뇌는 수많은 뉴런들이 서로 연결된 하나의 망이라고 볼 수 있으며, 각 뉴런들은 다른 뉴런들과 연결돼 있는 수상돌기를 통하여 입력신호를 받아들인 후 간단한 변환과정을 수행한 후 축색을 활성화시켜 변환된 신호를 타 뉴런들에 전달하게 된다. 뉴런간의 정보전달과정에서 시냅스는 전달되는 신호의 강도를 조절하는 역할을 한다. 이와 같은 뉴런들간의 정보전달속도는 매우 느리지만 동시에 수많은 뉴런들이 정보처리과정에 참여함으로써 빠른 정보처리를 가능하게 한다. 인간의 두뇌에는 10¹⁰개의 뉴런이 있고, 뉴런들간의 연결 (Connection) 은 10¹⁴개에 이르는 것으로 추정된다. 반면에 하등동물에 속하는 지렁이의 경우는 10³개, 파리는 10⁷개 바퀴벌레는 10⁸개 벌은 10⁹개 정도의 뉴런들간의 연결을 가지고 있다. 현재의 슈퍼 컴퓨터를 이용하여 신경회로망을 시뮬레이션 할 경우 최대 10⁶CPS (Connections Per Second) 정도를 구현할 수 있어 곤충 이하의 지능을 실현할 수있는 정도 이다. 한편 기존의 컴퓨터 이용방식은 사람이 이미 학습한 결과를 정리하여 프로그램의 형식을 빌려서 컴퓨터 내의 특정 장소에 보관하였다가 이용하는 것임에 반하여 생물들은 스스로 다양한 학습기능을 수행하여 주어진 상황에 적응해가며 그 과정에서 얻어진 경험이나 지식들을 뇌 속에 축적하고 필요시 자유자재로 끄집어 내어 사용한다. 뇌에 이어 학습된 내용의 기억 및 재생에 시냅스에 의해 강도가 조절되는 뉴런들간의 연결이 중요한 역할을 하는 것으로 알려져 있다.

<그림 14-1> 뉴론의 기본구조

따라서 생물학적 두뇌의 작동원리를 모방한 인공신경회로망 (Artifical Neural Networks) 의 특징은 다음과 같이 정리할 수 있다. 첫째, 신경회로망은 초병렬분산처리 시스템 (Parallel Distributed Processing System) 으로서 정보의 저장, 처리 및 전달을 신경회로망 내의 특정 부위들이 분담하는 것이 아니라 항상 신경회로망 전체로 그 기능을 수행한다. 둘째, 신경회로망은 자기조직화시스템 (Self-Organization System) 이다. 즉, 신경회로망은 새로운 이미지나 패턴 또는 사례가 주어졌을 경우 이를 기억하기 위해 자동적으로 자신의 내부상태를 바꾸지만, 이용자의 입장에서 볼 때 신경회로망의 내부상태는 블랙박스 (Black Box) 로 존재한다. 하지만 신경회로망은 학습된 이미지나 패턴의 일부 또는 손상된 정보로부터 완전하고도 정확한 정보를 재생해낼 수 있는 능력이 있다. 이와 같은 기능은 연상기억 (Associative Memory) 또는 내용주소기억장치 (Content Addressable Memory) 라고 불리운다. 셋째, 신경회로망에서 학습된 지식은 뉴런들간의 연결강도 (Connection Strength) 에 의해 분산저장된다. 학습은 신경회로망에 있어 가장 중요하고도 기본적인 요소로서 신경회로망을 이용자가 원하는 상황에 적응하도록 훈련시킬 수 있음을 의미한다. 신경회로망 학습방법의 근간을 이루는 대표적인 학습방법으로 헤비안 학습 (Hebbian Learning) 방법을 들 수 있는데, 이 학습방법은 주어진 사례에 대해 신경회로망이 정답을 내도록 기여한 뉴런들간의 연결은 강화시키고, 반대의 경우는 연결을 약화시키는 과정을 반복하는 것이다. 이 과정에서 획득된 지식들은 뉴런들간의 연결 사이로 스며들어 분산 저장되게 된다. 이와 같은 분산저장방법은 학습된 신경회로망의 일부가 손상되어도 본래의 기능을 수행함에 큰 지장을 받지 않게 되는 오류허용 (Fault Tolerance) 기능을 갖게 한다. 넷째, 신경회로망은 이용자의 측면에서 볼 때 기존의 컴퓨터처럼 복잡합 프로그래밍 과정을 요구하지 않는다. 이용자는 신경회로망의 구조 및 학습방법을 지정함으로써 간단히 원하는 결과를 얻을 수 있으며, 신경회로망 내부의 처리절차도 매우 간단하게 이루어진다. 마지막으로 신경회로망은 패턴의 분류나 인식에 있어 강력한 힘을 발휘하며, 우리가 부딪치는 많은 문제들은 패턴분류문제로 볼 수 있기 때문에 신경회로망의 응용범위가 매우 넓다는 것이다.

2. 신경회로망의 역사

신경회로망 관련연구의 역사는 1940년대까지 거슬러 올라간다. 1943년 McClloch와 Pitts에 의해 뉴런의 모형화가 최초로 시도되었으며, 1949년 캐나다의 심리학자인 헵 (Hebb, D.) 은 그의 유명한 저서인 "The Organization of Behavior" 에서 헵의 시냅스라고 알려진 연결강도조정을 위한 학습규칙을 최초로 기술하였다. 또 헵은 connectionism 이라는 단어를 그의 저서에서 사용했는데 신경회로망을 지칭하는 또 다른 용어로 아직도 사용되고 있다. 최초의 신경회로망 모형은 1957년 Rosenblatt에 의해 개발된 퍼셉트론 (Perceptron) 이다. 퍼셉트론은 학습이 가능한 기계모형을 제시했고 여러 종류의 분류작업에 적용될 수 있다는 기대감에 많은 사람의 관심을 모았다. 또 1960년 스탠포드 대학의  Widraw & Hoff 는 최소자승오차 (Least Mean Squared Error) 알고리즘에 근거한 델타 학습규칙 (Delta Learning Rule) 을 사용하는 Adaline이라는 신경회로망 모형을 발표하여 신경회로망에 대한 세인의 관심을 고조시켰다. 하지만 1969년 Minsky와 Papert에 의해 단일계층 퍼셉트론으로는 exclusive OR문제를 해결할 수 없음이 밝혀진 후 신경회로망으로는 복잡한 분류문제들을 해결할 수  없다고 생각하여 이후 20년 가까이 신경회로망 연구를 암흑기를 맞게 되었다. 이 암흑기 동안 보스톤 대학의 Grossberg, 헬싱키 대학의 Kohonen 및 일본의 Amari, Fukusima 등 소수의 학자들에 의해 신경회로망 연구의 명맥을 이어가게 되었다.

80년대 들어 신경회로망 연구의 암흑기를 벗어나게하는 중요한 사건 두가지가 일어났다. 첫 번째는 1982년 캘리포니아 공대 물리학과 교수인 Hofield가 에너지 개념을 이용하여 신경회로망의 행위를 분석하고 학습시키는 것이 가능하다는 것을 보인 것으로, 이 Hofield 네트워크느 연상기억장치로 사용되거나 최적화문제를 푸는데 이용될 수 있다. 두 번째는 Rosenblatt의 퍼셉트론과는 달리 여러 계층을 사용하는 다계층 퍼셉트론을 학습시킬 수 있는 백프로파게이션 (Backpropagation) 알고리즘이 Werbos 등에 의해 발견된 것이다. 이 학습방법은  Rumelhart, Hinton 및 Sejnowski 등의 PDP그룹에 의해 널리 알려짐으로써 신경회로망에 대한 연구가 활발히 진행되어 많은 모형들이 새로이 제시되었고 신경회로망의 응용분야도 패턴분류나 연상기억장치의 범주에서 벗어나 최적화, 로봇 제어, 문자인식, 음성인식, 신호처리, 머신비전 등으로 확대되었으며 최근에는 경영분야에도 많이 응용되고 있다. <표 14-1> 은 대표적인 신경회로망 모형 및 응용분야를 정리한 것이다.

<표 2-1> 대표적인 신경회로망 모델

 3. 신경회로망을 이용한 문자인식 예제

신경회로망을 이용하여 0에서부터 9가지 열 개의 필기체 숫자드을 인식하는 문제를 생각해 본다. <그림 14-2> 는 이 문제를 해결할 수 있는 신경회로망의 한 모형을 나타낸 것이다. 그림에서 노드들은 뇌의 뉴런에 해당하는 것으로 처리요소 (Processing Element) 라고 부르며, 노드와 노드를 연결하는 아크는 뉴런들간의 연결 (Connection) 에 해당한다. 또 노드들이 모여서 하나의 층 (Layer 혹은 Slab) 을 이루게 되는데 입력층, 출력층 및 입출력층 사이에 존재하는 은닉층이 있다.

<그림 14-2> 신경회로망을 이용한 숫자인식

<그림 14-3> 필기체 숫자

주어진 문제가 열 개의 필기체 숫자를 인식하는 것이므로 출력층 처리요소들이 각기 하나의 숫자를 나타낸다고 생각하면, 출력층은 열 개의 처리요소를 갖게 된다. 이 경우 학습된 신경회로망의 출력층 처리요소들은 주어진 입력에 대응되는 처리요소만이 활성화되고 나머지들은 모두 비활성화되어야 한다. 만약 처리요소가 활성화되면 1, 비활성화되면 0을 출력값으로 한다면, '5'가 입력된 경우의 출력값들은 [0,0,0,0,0,1,0,0,0,0]의 형태가 되는 것이 가장 바람직할 것이다. 한편 입력은 디지타이저나 화상기록장치를 통하여 이미지 형태로 들어오며 10 X 8행렬의 픽셀들에 의해 표현되는데, 각 픽셀들은 "on" 이면 1, "off" 면 0의 값을 가진다고 생각하자. 그러면 입력층에는 80개의 처리요소들이 필요하게 되며 입력값들은 그림에서와 같이 0과 1을 값으로하는 10 X  8행렬의 형태가 될 것이다. 이제 남은 문제는 신경회로망의 구조를 확정하기 위해서 은닉층 처리요소의 수를 정하고 사례로써 주어진 입출력자료들을 사용하여 처리요소들간의 연결강도 (Connection Weights)를 조절하여 신경회로망을 학습시키는 것이다. 신경회로망의 학습절차는 앞으로 설명하겠지만 한 가지 지적할 중요한 사실은 모든 신경회로망의 학습은 사례에 의한 학습 (Learning by Examples) 이라는 사실을 명심해야 한다. 즉, 신경회로망 응용의 성패를 좌우하는 가장 중요한 요인은 신경회로망의 학습에 사용된 사례들이 주어진 문제를 얼마나 잘 대표할 수 있는가이다. 신경회로망은 단지 주어진 학습자료에만 근거하여 주어진 문제에 대한 해결책을 스스로 찾아간다는 사실을 잊어서는 안된다.

<그림 14-3> 은 학습이 끝난 신경회로망에 의해 인식된 숫자와 인식되지 못한 숫자들의 예를 나타낸 것이다. 이 숫자들은 신경회로망의 학습자료에 포함되어 있지 않았다. 즉, <그림 14-3(b)>와 같이 심하게 변형된 입력이 아니면 신경회로망은 비록 훈련받지 않은 입력에 대해서도 원하는 출력값을 정확히 산출해낼 수  있는 능력을 가졋는데 이를 신경회로망의 일반화 능력 (Generalization Power) 이라고 한다. 우리는 신경회로망이 <그림 14-3(b)> 의 숫자들도 인식할 수 있도록 하기 위해서는 좀더 많은 사람들로부터 손으로 쓴 숫자들의 사례를 얻어 기존 학습자료에 추가하고 신경회로망을 재학습시켜 일반화능력을 제고시키는 것이 필요하다. 이상의 논의에서 우리는 신경회로망의 이용은 두 단계로 이루어짐을 알 수 있다. 즉, 학습자료에 의한 신경회로망의 훈련과 학습된 신경회로망을 실제 이용하는 두 단계가 있는데 신경회로망의 훈련과정은 학습자료에 내재 된 문제해결에 필요한 정보들을 추출하여 신경회로망 내에 축적하는 과정으로 대부분의 경우 많은 시간이 소요된다. 반면에 학습된 신경회로망의 이용시에는 어떤 문제해결 방법보다도 빠른 시간 안에 해결책을 얻는 것이 가능하다.

4. 신경회로망의 구성요소

현재 다양한 신경회로망 모형들이 개발되어 사용되고 있지만, 이들은 모두 뇌의 뉴런을 모형화한 처리요소들을 기본구성단위로 하고 있더. 따라서 신경회로망 모형을 이해하기 위해서는 처리요소들의 수, 처리요소의 조직방법 및 처리요소들 사이의 연결형태 등 신경회로망의 구조를 파악한 후, 신경회로망의 행위를 결정짓는 중요한 요소인 학습방법에 대해 알아야 한다. 이 절에서는 이와 같은 신경회로망의 구성요소들에 대해 구체적으로 살펴본다.

4.1 처리요소

신경회로망 내의 처리요소는 매우 간단한 형태의 계산만을 수행하는데 이를 도식화한 것이 <그림 14-4> 이다. 처리요소는 여러 다른 처리요소들로부터 입력을 받아들이지만 자신은 x_i라고 표기된 단 하나의 출력값만을 생성하고, 이를 연결된 처리요소들에게 전달한다. i 번째 처리요소가 j번째 처리요소로부터 전달받는 입력값을 x_j 라고 표기하는데 x_j 는 j 번째 처리요소의 출력값이다. 생물학적 뉴런들간의 정보전달에 있어 시냅스가 중요한 역할을 담당하고 있듯이, 처리요소들간의 연결강도를 반영하기 위해 신경회로망에서는 연결가중치 (Connection Weight), 혹은 단순히 가중치 (Weight) 를 사용하는데 I 와 j 번째 처리요소 사이의 연결가중치를 W_ij 로 표기한다. 각 처리요소들은 전달받은 입력값들과 연결가중치를 사용하여(식 14-1) 과 같이 먼저 순 입력값 (net_i) 를 계산 한 후, 이를 (식 14-2)를 이용하여 출력값을 결정한다.

x_i = ƒ_i (net_i)...........................................(식 14-2)

이때 순입력값을 출력값으로 변환시키는 함수 ƒ_i 를 전이함수 (Transfer Function) 또는 활성함수 (Activation Function) 라고 부른다. 신경회로망의 설계시 어떤 전이함수를 사용할 것인가도 중요한 결정사항 중의 하나인데 <그림 14-5> 는 전이함수의 형태들을 나타낸 것이다. 최근 신경회로망의 전이함수로는 비선형함수들이 사용되고 있으며 특히 시그모이드 (Sigmoid) 함수가 많이 사용되고 있다.

<그림 14-4> 처리요소의 기본구조

<그림 14-5> 여러 형태의 전이함수들

4.2 연결형태

신경회로망에서는 처리요소들을 모아 층을 구성하게 되는데 각 층을 구성하는 처리요소들은 모두 같은 타입인 경우가 일반적이며 이들은 <그림 14-6> 과 같이 다른 층에 있는 처리요소들과 연결되어진다. 두 층간의 연결형태를 구분하면 다음과 같다.

① 전부연결

첫 번째 층의 각 처리요소는 두 번째 층의 모든 처리요소들과 연결된다.

② 일부연결

층간의 처리요소들의 연결이 일부만 이루어지는 것으로 임의의 처리요소들과 선택적으로 연결 (Random Connection) 하는 경우와 가장 가까운 이웃들만 연결 (Nearest-Neightbor Connection) 하는 두 가지 형태가 있다.

③ 전방향 연결

첫 번째 층의 처리요소의 출력값이 두 번째 층의 처리요소에 일방적으로 전달되기만 한다.

<그림 14-6> 처리요소의 층간 연결형태

④ 양방향 연결

전방향 연결과 동시에 두 번재 층의 출력값이 다시 첫 번째 층의 처리요소들에 전달되는 피드백 연결을 갖는다.

이와 같은 층간 연결 외외에 좀더 복잡한 구조를 갖는 신경회로망에서는 같은 층내의 처리요소들 사이에도 연결을 갖게 되는데 다음의 두 가지 형태가 있다.

① 리커런트 (Recurrent) 연결

한 층내의 처리요소들간에 서로의 출력값이 교환될 수 있도록 전부 또는 일부만 연결이 된다. 이 경우 처리요소의 출력값이 안정될 때까지 타 층으로의 정보전달이 유보된다. 홉필드 네트워크이나 다계층 퍼셉트론의 변형된 형태에서 이와 같은 연결이 사용되고 있다.

② 온센터/오프서라운드 (On-center Off-surround) 연결

특정 처리요소를 기준으로 할 때 자신과 이웃하는 처리요소들과는 활성화를 자극하는 연결 (Excitatory Connections) 을 갖고, 그 외의 처리요소들과는 활성화를 억제하는 연결 (Inhibitory Connections) 을 갖는다. 이와 같은 층내 연결형태는 경쟁학습을 사용하는 코호넨의 형상지도 (Feature Map) 이나 Grossberg의 ART (Adaptive Resonance Theory) 모형에서 사용되고 있다.

<그림 14-7> 층내 연결형태

4.3 학습방법

(식 14-1)과 (식14-2)로부터 주어진 입력에 대해 처리요소의 출력값을 결정하는 가장 중요한 요소가 연결가중치임을 쉽게 알 수 있으며, 각 처리요소들의 출력값들은 결국 신경회로망의 출력결과를 결정하게 되므로 신경회로망을 이용하여 원하는 출력값을 얻기 위해서는 연결가중치를 조정하여야 한다. 모든 신경회로망은 주어진 사례들을 이용하여 처리요소들 사이의 연결가중치를 스스로 조정하게 되는데 이 과정을 학습이라고 부른다. 신경회로망 모형마다 각자 특유의 학습방법을 갖고 있는데, 학습방법은 신경회로망을 구별하는 중요한 요인으로서 일반적인 관점에서 학습방법들을 분류하여 설명한다.

학습방법의 가장 기본적인 분류는 지도학습 (Supervised Learning) 과 자율학습 (Unsupervised Learning) 이다. 지도학습은 신경회로망 이용자가 각 입력자료에 대해 원하는 목표출력값 (Target Output) 을 대응시켜 학습자료를 구성하는 것이다. 따라서 신경회로망은 학습자료 내에 각 입력자료들에 대응되는 목표출력값을 생성할 수 있을 때까지 연결가중치들을 조정하게 된다 이에 반해 자율학습은 목표출력값이 학습자료에 주어지지 않는 것으로 주어진 입력패턴 자체를 기억시키거나, 유사한 패턴들을 군집화 (Clustering) 시키는데 많이 이용된다.

신경회로망을 의사결정수단으로 사용하기 위해서는 연결가중치를 조정하는 학습기간을 반드시 거쳐야 하므로 신경회로망의 이용은 학습상태와 운영상태의 두 단계로 이루어진다. 이와 관련하여 학습방법을 오프라인 학습과 온라인 학습의 두 가지로 분류하는데 오프라인 학습은 신경회로망의 학습이 끝나 운영상태로 넘어가면 연결가중치들은 더 이상 수정되지 않는다. 이에 반해 온라인 학습에서는 신경회로망이 운영상태에 있더라도 학습시 보지 못했던 새로운 형태의 입력패턴이 나타나면 이를 기억하기 위해 연결가중치를 즉시 조절하게 된다. 현재는 Grossberg 의 ART모형만이 온라인 학습이 가능하다고 알려져 있다.

신경회로망 내의 연결가중치 조절방법은 곧 신경회로망의 학습방법을 결정한다고 해도 과언은 아니다. 이미 수많은 학습방법들이 개발되어 있지만 이들은 모두 헤비안 학습규칙, 델타 학습규칙, 일반화 델타 학습규칙 및 코호넨 학습규칙 중의 하나에 속한다고 볼 수 있다. 이 네가지 학습규칙을 수식으로 표현하기 위해 <그림 14-4> 에서의 기호들을 그대로 사용하고, 변경되기 전후의 연결가중치를 W_ij^old,  W_ij^new 로 각각 표기하며, △W_ij 는 연결가중치의 변화량이라고 하면 변화된 가중치 W_ij^new 는 다음과 같이 표현된다.

W_ij^new = W_ij^old  + △W_ij  ............................................(식 14-3)

각 학습규칙에서 △W_ij 의 계산방법은 다음과 같으며 t_i는 목표출력값, error_i 는 (t_i - x_i), ƒ ' 은 전이함수의 미분값을 각각 나타낸다.

① 헤비안 학습규칙  :  △W_ij = α • x_j • x_i .............................(식 14-4)

② 델타 학습규칙 : △W_ij = α • x_j • error_i .............................(식 14-5)

③ 일반화 델타 학습규칙 : △W_ij = α • error_i •  ƒ(net_i) .............................(식 14-6)

④ 코호넨 학습규칙 : △W_ij = α (x_j  ㅡ  W_ij^old) .............................(식 14-6)

각 학습규칙에 사용된  α 는 학습계수로서 학습속도를 조절하는 역할을 하며, 코호넨 학습규칙은 여타의 학습규칙과 달리 경쟁학습방법을 사용하므로 경쟁에서 이긴 처리요소만이 출력값을 갖고 이 처리요소에 연결된 가중치들만이 조정된다. 이를 승자독점 (Winner-takes-all) 원칙이라고 한다.

5. 신경회로망 모형들

신경회로망의 구성요소들, 즉 처리요소 및 처리요소들 사이의 연결방법, 학습방법들이 결합되어 이루어지는 신경회로망 모형들 중 대표적인 네 가지 모형에 대해 살표보기로 한다.

5.1 다층 퍼셉트론 (Multilayer Perceptron)

Rosenblatt의 퍼셉트론은 학습가능한 층이 하나만 존재하기 때문에 단층퍼셉트론이라고도 불리우며, 선형분리가능 (Linear Separable) 한 문제에만 적용가능하므로 <그림 14-8> 에서와 같은 Exclusive-OR문제를 해결할 수 없다는 한계가 있다. 이러한 한계를 벗어나는 방법은 입출력층 사이에 은닉층을 사용하여 신경회로망을 계층구조를 갖도록 하는 것이나, 은닉층에 연결된 가중치들을 조정할 수 있는 학습방법의 개발에 어려움이 있었다. 1980년대 중반 PDP그룹에 의해 다층퍼셉트론은 백프로파게이션 (Backpropagation) 알고리즘에 의해 학습시킬 수 있음이 알려진 후 다층퍼셉트론은 가장 널리 사용되는 신경회로망 모형이 되었다.

<그림 14-8> 단층 퍼셉트론과 Exclusive-OR

다층 퍼셉트론은 <그림 14-2>에서 이미 보았던 바와 같이 하나 이상의 은닉층을 사용하며, 처리요소들 사이의 층간연결은 전부 전방향 (Fully-connected Feedforward) 연결형태이며 층내 연결은 없다. 지도학습의 대표적인 예인 백프로파게이션 알고리즘은 일반화 된 델타 학습규칙으로 볼 수 있는데 이 학습규칙은 (식 14-5)에서와 같이 전이함수의 미분값을 요구하므로 Rosenblatt 의 퍼셉트론에서 많이 사용된 계단형 (Hard-limiting) 함수 대신 미분이 가능한 비선형 함수인 시그모이드 함수를 처리요소 내의 전이함수로 많이 사용한다.

백프로파게이션 알고리즘은 목표출력값과 신경회로망의 출력값 사이의 오차들의 제곱합을 최소로 하기 위해 최급하강법 (Gradient-descent Method) 을 사용하고 있으며 전방향 계산과 역방향 계산의 두 단계로 이루어진다. 전방향 계산은 주어진 입력값에 대해 신경회로망의 출력값을 계산하는 과정이며, 역방향 계산은 전방향 계산에 의해 얻어진 출력값과 목표출력값의 차이, 즉 오류를 출력층으로부터 입력층으로 역전파시켜가며 연결가중치들을 저장하는 과정으로 백프로파게이션이라는 이름이 붙여진 이유도 여기에 있다. 백프로파게이션 알고리즘에 의한 훈련과정은 다음과 같다.

<백프로파게이션 알고리즘에 의한 학습절차>

백프로파게이션 알고리즘은 다층구조를 갖는 신경회로망을 학습시킬 수 있는 매우 유용한 학습방법이지만 몇 가지 문제점을 가지고 있다. 가장 큰 문제점으로 지적되고 있는 것은 지역최소점에 관한 것이다. 연결가중치들에 의해 구성되는 다차원 공간을 상정할 때 오차함수, 즉 ∑(t_i - x_i)²는 매우 복잡합 형상을 가지게 된다. 이 오차함수를 특정 연결가중치의 하나의 함수로 나타내면 <그림 14-9> 와 같이 되며 여러 개의 지역최소점을 가짐을 볼 수 있다. 최급하강법에 의한 최소점 찾기는 바로 지역최소점에 빠졌을 경우 이로부터 탈출할 방법이 없다는 것이다. 이는 다층 퍼셉트론이 원하는 목표값을 얻지 못한 상태에서 더 이상의 학습이 이루어지지 못함을 의미한다.

또 백프로파게이션 알고리즘은 많은 수의 반복학습을 필요로 해 학습에 많은 시간이 요구되며, 학습완료시점을 예측할 수 없으며, 추가학습이 요구될 때는 전체적인 재학습을 해야 한다는 문제점들이 지적되고 있다.

<그림 14-9> 연결가중치와 오차함수

하지만 지역최소화문제는 학습과정에서 가중치의 초기값들을 바꾸어가며 여러번 학습을 반복 시행할 경우 현실문제에의 적용에 큰 문제점이 되지 않으며, 연결가중치의 조절시 누적학습방법을 사용하거나 관성향 (Moment Term) 의 도입이나 학습계수의 최적화를 통해 백프로파게이션 알고리즘의 학습속도를 개선할 수 있다. 또 학습된 신경회로망의 일반화 능력을 재고시키기 위해 오차함수에 신경회로망의 복잡도 (Complexity) 를 반영하여 추가시켜 학습시킴으로써 영향력이 없는 연결가중치들의 값이 0 에 가깝도록 만들거나, 학습종료 후 영향력이 적은 연결가중치나 처리요소들을 제어하는 방법들이 제안되고 있다. 이와 같은 백프로파게이션 알고리즘의 개선은 여러 문제점에도 불구하고 다층퍼셉트론을 가장 폭넓은 응용분야를 갖는 신경회로망 모형이 되게 했으며, 최근에는 리커런트 모형으로의 확장도 이루어졌다.

5.2 홉필드 네트워크

1982년 미국 캘리포니아 공과대학의 저명한 물리학자였던 John Hopfield는 물리학의 스핀글라스 모델과 신경회로망을 비교하고 신경회로망의 행위분석에 에너지개념을 도입하여 에너지 함수를 최소화하면 신경회로망을 안정상태에 도달시킬 수 있다는 것을 보였다. 홉필드 네트워크는 <그림 14-10>에서와 같이 단일계층으로 이루어지며 층내모든 처리요소들은 양방향으로 상호연결되어 있으나 자기자신으로의 피드백 연결은 갖지 않는다. 이 신경회로망이 정상적으로 작동하여 안정상태에 도달하기 위해서는 첫째 두 처리요소 사이의 연결가중치들은 대칭적, 즉 W_ij = W_ji 이어야 하며, 둘째 각 처리요소들은 완전히 비동기적 (Asynchronously) 으로 동작하여야 한다는 제약이 있다.

<그림 14-10> 홉필드 네트워크의 구조

초창기 홉필드 네트워크는 입출력으로 이진수, 전이함수로 계단함수를 사용하고 신경회로망 내에서 학습이 이루어지지 않는다는 특징이 있었으나, 최근에는 아날로그값을 입출력에 사용하고 델타 학습규칙이나 헤비안 학습규칙을 이용해 학습이 가능하도록 하는 모형의 확장이 이루어지고 있다. 홉피드 네트워크는 연상기억장치로서 효과적으로 작동할 뿐만 아니라, 순회판매원문제 (Traveling Salesman Problem) 와 같은 최적화문제를 해결하는데 있어 많은 수의 비동기적이고 국소적인 계산을 통하여 전역적 최적화를 이룰 수  있다는 사실 때문에 많은 관심을 모았다.

사람들은 한번 보았거나 기억하고 있는 패턴에 대해 불완전한 패턴이나 왜곡된 패턴이 주어질 경우에는, 본래의 완전한 형태를 유추해내는 능력을 가지고 있다. 이와 같은 기능을 연상기억기능이라고 하며 이를 신경회로망을 통해 구현할 수 있다. 연상기억장치는 내용주소기억장치 (Cabinet Addressible Memory) 라고도 하는데 <그림 14-11> 은 홉필드 네트워크의 연상기억장치로서의 예를 보인 것이다.

<그림 14-11> 연상기억장치로서의 홉필드 네트워크

연상기억장치에 대한 이해를 돕기 위해 선형 연상기억장치를 간단히 설명하면 다음과 같다. 즉 입력벡터 X로부터 출력벡터 Y를 계산할 수 있는 변환 행렬 T가 (식 14-8)을 만족한다면 M, N을 각각 입출력벡터의 크기로 갖는 P개의 입출력벡터 쌍에 대한 변환행렬 T는 (식 14-9)와 같이 나타낼 수 있다.

Y = TX.................................(식 14-8)

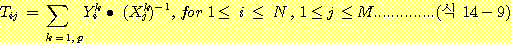
(식 14-9)를 이용하여 주어진 입력벡터 X^q에 대한 출력 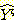을 계산하면 (식 14-10)과 같다.

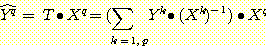
재현된 패턴 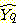는 (식 14-10)의 마지막 식의 두 번째 항만큼 본래 패턴 Y^q와 차이가 생기게 된는데 만약 변환행렬 T 를 구할 때 주어진 입력패턴들이 상호직교 (Orthogonal) 한다면 (X^k)^-1X^q = 0이 되므로 완전한 패턴을 재현할 수 있다.

홉필드 네트워크는 비선형 전이함수와 피드백 연결을 통하여 연산기억기능을 향상시킨 것이지만, 입력패턴들이 상호직교해야만 좋은 결과를 얻을 수 있다는 사실을 잊지 말아야 한다. 다음은 홉필드 네트워크가 자기연상기억장치 (Auto-associative Memory) 로 사용될 경우의 동작알고리즘을 기술한 것이다.

<홉필드 네트워크의 동작 알고리즘>

홉필드 네트워크는 Hopfield 와 Tank에 의해 순회판매원문제에 적용되어 좋은 결과를 보임으로써 최적화문제를 해결하기 위한 새로운 수단으로 인식되었다. 순회판매원문제란 판매원이 방문해야 할 도시와 도시들 사이의 거리가 주어졌을 경우, 모든 도시를 반드시 한번만 거쳐서 출발도시로 되돌아오는데 총여행거리를 최소화하는 것이다. 만약 10개 도시의 경우에는 9!/2=181,440가지의 경로를 검사하여야 하며, 30개의 도시일 경우에는 무려 4 X 10³⁰에 달하는 경로가 있게 되어 이 문제는 NP-Complete 라고 알려져 있다.

순회판매원문제를 풀기 위해 Hopfield와 Tank는 새로운 에너지함수를 개발하였는데, 10개 도시의 경우를 예로 들어 설명하면, <그림 14-12>는 순회판매원문제를 행렬의 형태로 나타낸 것으로, 각 열은 도시에 해당되고 각 행은 해당 도시의 방문순서를 나타낸다. 따라서 <그림 14-12>에 표현된 여행경로는 D→ H →I→ F→ G→ E→ A→ J→ C→ B 이다.

<그림 14-12> 순회판매원문제 행렬

에너지함수를 구성하기 위해 순회판매원문제의 제약조건들을 세분화해보면 다음과 같다.

① 각 도시는 반드시 한번만 방문하여야 한다.

② 동시에 두 도시를 방문할 수 없다.

③ 반드시 모든 도시(즉 m개)를 방문해야 한다.

④ 총여행거리가 최소화되어야 한다.

에너지함수 내의 각 항들을 위의 네 조건이 열거된 순서에 맞추어 적으면 (식 14-11)과 같이 된다.

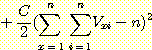
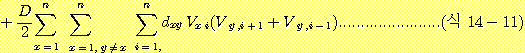
(식 14-11)에서 x, y는 도시를 i, j는 여행순서를, d_xy는 두 도시 사이의 거리를 나타낸다. V_xi는 X도시를 i 번째 방문하면 1이고 아니면 0이다. A, B, C, D는 상수항이다. (식 14-11)의 앞의 세항들은 열거한 조건에 부합될 때만 0의 값을 가지게 됨을 유의해야 한다. 따라서 이 에너지함수를 이용하여 홉필드 네트워크의 연결가중치들을 결정할 수 있다. 홉필드 네트워크의 수렴과정을 힌톤 도표 (Hinton Diagram) 에 의해 표시하면 <그림 14-13>과 같다. 네 번째 힌톤 도표에서 수렴된 여행경로를 확인해 보면 D→ H →I→ F→ G→ E→ A→ J→ C→ B 가 됨을 알 수 있다.

<그림 14-13> 힌톤 도표에 의한 홉필드 네트워크의 수렴과정 : (a)는 임의값들로 초기화된 것이며, (b) 와 (c) 는 중간과정을 나타내고 (d)는 수렴된 홉필드 네트워크의 출력값들을 나타낸 것이다.

홉필드 네트워크는 연상기억장치로 사용되건, 최적화수단으로 사용되건 간에 신경회로망이 최소의 에너지를 가질 때, 즉 신경회로망이 안정상태에 도달했을 경우 응용문제가 해결된 것으로 간주한다. 이러한 접근방법은 제안당시 새로운 아이디어로써 많은 주목을 받았지만, 연상기억장치로 사용할 경우에는 기억용량의 제한이 있으며, 최적화문제에 있어서는 신경회로망칩 등의 하드웨어를 이용하지 않을 경우 문제해결에 상당히 오랜 시간이 요구된다는 한계가 있다.

5.3 코호넨 네트워크

코호넨 네트워크는 자기조직화 형상지도 (Self-Organizing Feature Map) 라고도 불린다. 다층 퍼셉트론이나 홉필드 네트워크가 생물학적 신경시스템과는 거리가 먼 모형임에 반해, 자율학습 (Unsupervised Learning) 방법을 채택하고 있는 코호넨 네트워크는 그 구조 및 작동원리가 생체신경시스템에 상당히 가깝게 모형화된 것이다. 갓 태어난 아기는 눈에 보이는 자극과 물체들을 서로 연관시키는 것을 시간이 지남에 따라 스스로 배우게 된다. 하지만 갓 태어난 아기에게 시각적 자극을 보고 이해하도록 가르칠 수 있는 방안은 없다. 즉, 생물계에서는 각자 주어진 환경에 적응해 나가는 과정에서 자율학습이 매우 중요한 역할을 하는 것이다. 따라서 신경회로망 연구에 있어서도 자율학습방법을 사용하는 신경회로망 모형의 의미는 상당히 크다고 할 수 있다.

코호넨 네트워크는 두 계층으로 이루어지는데 첫 번째 층은 입력층으로 단순히 입력값들을 전달하는 버퍼역할을 수행하며, 두 번째 층은 흔히 코호넨 층 (Kohonen Layer) 이라 불리우며 처리요소들간에 출력을 내기 위한 경쟁이 이루어진다. 층간 연결은 완전 전방향 연결이며, 코호넨 층내의 처리요소들은 통상 2차원 격자형태로 많이 묘사되며, 처리요소들간에도 서로 완전히 연결되어 있다. 다차원공간 내에서 어떤 입력패턴이 어느 클래스에 속하느지 파악하는 것보다는 이를 2차원 공간에 투영하여, 어느 클래스에 속하는지 파악하는 것이 쉽고, 또 해당 클래스가 여타의 클래스와 얼마나 차이가 나는지도 쉽게 파악 할 수 있다. 코호넨 네트워크는 바로 이와 같은 역할을 수행하기 때문에 위상 보존지도 (Topological-Preserving Map) 라고도 불린다.

코호넨 층내의 처리요소들의 활성화는 (식 14-12)에 의해 이루어진다.

r_i(x_i) 는 손실항의 일반적인 표기이고, net_i는 통상적인 신경회로망에서와 같이 i번째 처리요소 내의 순입력값으로 입력값과 연결가중치들의 곱의 합을 나타낸다. 마지막 항은 코호넨 처리요소들간의 상호작용을 나타내는 것으로 <그림 14-14 (a)> 와 같은 멕시코 모자함수 (Maxican-hat or Sombrero Function) 가 많이 언급되는데, 이 경우 i번째 처리요소에 가까이 근접해 있는 이웃처리 요소들은 양의 피드백값을 전달받게 되고 (Excitating Input이라고도 함), 멀리 떨어져 있는 처리요소들은 부의 피드백값을 전달받게 되는 (Inhibitory Input) 효과가 있다. 이와 같이 코호넨 층에서는 측면제어 (Lateral Inhibition) 방식을 사용하여 처리요소들간에 경쟁이 일어나게 되며, 경쟁에서 이긴 하나의 처리요소만이 출력을 내게 되고, 학습과정에서도 이 처리요소와 이웃하는 소수의 처리요소들만이 연결가중치를 조정할 수 있는 권리를 갖는 승자독점 (Winner-take-all) 의 원칙이 적용된다. 승자처리요소가 결정되고 나면 코호넨 학습규칙에 의해 연결가중치를 조정하게 된다.

W^new_ij = W^old_ij + α(x_j - W^old_ij )...........................................(식 14-13)

<그림 14-14>

(식 14-13)에서 i는 코호넨 층에서의 승자 및 이웃처리요소를 나타내며 j는 이들에 연결된 입력층의 처리요소들이다. 학습의 초기에는 이웃의 범위를 넓게 잡지만 학습이 진행됨에 따라 이웃의 범위를 점차 좁혀나가는데 이를 표현한 것이 <그림 14-15>이다.

이상의 설명에 의하면 코호넨 네트워크의 학습방법이 매우 복잡해 보이지만 사실은 승자처리요소는 입력벡터와 가중치벡터의 차이를 구하여 쉽게 구할 수 있다. 이를 정리하면 다음과 같다.

<그림 14-15> 코호넨 네트워크의 구조와 학습과정에서의 이웃의 범위

<코호넨 네트워크의 학습알고리즘>

<그림 14-16>은 0과 1사이의 균등분포 (Uniform Distribution) 로부터 임의의 추출된 2차원 벡터들을 학습패턴으로 사용하여 코호넨 네트워크가 안정상태에 이르는 과정을 묘사한 것이다.<그림 14-16 (a), (b), (c), (d)>는 연결가중치들을 나타낸 것인데, 처음에는 초기화에의해 가중치들이 지도의 중앙에 모여 있었으나 학습에 의해 연결가중치들이 균등하게 확산되어감을 알 수 있다.

<그림 14-16> 코호넨 네트워크의 학습과정

코호넨 네트워크는 연상기억장치로 많이 사용되고 있으며, Teuvo Kohonen 자신에 의해 신경회로망 음성타자기를 개발하는데 이용되었는데 이 장치는 음성을 실시간 내에 문자로 변환시킬 수 있는 능력을 가졌으며 정확도는 92~97%정도를 보였다.

5.4 ART

미국 보스턴 대학의 Grossberg와Carpenter는 경쟁학습의 약점인 안정성을 보강하기 위해 ART (Adaptive Resonance Theory) 를 제안했다. 사람은 새로운 지식을 배워도 과거에 배웠던 지식을 재학습할 필요가 없다. 하지만 앞서의 신경회로망 모형들은 이 경우 재학습을 요구한다. ART는 이와 같이 기존의 학습내용이 새로운 학습에 의하여 지워지지 않도록 새로운 지식을 기존의 지식과 적절히 통합시킬 수 있는 능력이 있다. 즉, 새로운 정보가 기존의 학습 내용과 유사하다면 이를 새로운 지식으로 간주하지 않고 단지 기존의 지식을 정제하는데만 사용하며, 새로운 정보가 완전히 다른 유형의 지식이라면 이를 새로운 지식으로 추가저장하게 되는데,이는 저장용량이 소모될 때까지 지속된다. 초기모형인 ART Ⅰ은 이진값만을 입력으로 사용하였으나 그 후 아날로그 입력도 사용할 수 있는 ART Ⅱ가 개발 사용되고 있다. 이 ART모형은 지금까지 개발된 신경회로망 모형들 중에서는 가장 복잡한 모형이므로 여기에서는 간단히 구조와 특성만을 기술한다.

ART모형은 입력층(FI층이라고 함)과 경쟁층(F2층이라고 함)의 두 계층으로 구성된 신경회로망인데, 학습과 학습된 패턴의 재현과정에서 두 계층이 서로 상호작용하기 때문에 ART라는 이름을 얻었으며, 이를 위해 F2층으로부터 F1층으로 하향연결이 존재한다는 점이 코호넨 네트워크와 크게 다른 점이며, ART모형의 작동을 제어하기 위하여 <그림 14-17>에서 볼 수 있듯이 주의 서브시스템 (Attentional Subsystem) 과 적응 서브시스템 (Orienting Subsystem) 으로 구성된다.

<그림 14-17> ART모형 구조

ART에서는 패턴 매칭 개념을 사용하여 새로이 입력된 패턴이 기존에 이미 학습한 패턴인가 아닌가를 검증하는 단계를 주의 서브시스템과 적응 서브시스템의 상호작용을 통하여 해결하였다. 즉, F1층에 제시된 입력패턴은 상향연결을 통해 F2층에 전달되고 F2층은 입력패턴에 대응되는 기대패턴을 선정하게 된다. 이때 입력패턴과 기대패턴 사이의 불일치를 조사하여 입력패턴이 새로운 유형의 패턴이라고 판정되면 적응 서브시스템은 F2에 리셑신호를 보내 기대패턴에 대응되는 처리요소의 출력을 억제하고 학습이 이루어지도록 한다. 이때 입력패턴과 기대패턴 사이의 불일치 정도를 허용하기 위해 경계변수 (Vigilance Parameter) 를 사용한다. <그림 14-17>에서 보면 새로운 입력패턴이 제시되면 이 신호는 F1, 이득제어 및 리셑시스템의 세군데로 전달된다. F1층은 비활성적이므로 입력신호가 리셑시스템에 도달되면 리셑시스템은 F2에 신호를 보내 F2층에 활성화되어있는 처리요소들의 활동들을 정지시켜 새로운 입력패턴에 준비하게 한다. 한편 활동이 억제된 F2는 G1이득제어에 대한 통제력을 상실하게 되고, 이득제어는 F1층에 신호를 보내 F1층을 활성화시킨다. 이와 같이 F1층의 활성화를 위해서는 F1층에 신호를 전달하는 외부입력패턴, 이득제어 및 F2층으로부터의 세 신호 중 반드시 두 가지 이상의 신호를 전달받아야만 한다는 '2/3규칙' 이 ART모형의 동작에 있어 매우 중요한 역할을 한다.

<그림 14-18>ART에 의한 영문자 인식

<그림 14-18> 은 ART모형을 이용한 영문자 인식의 예를 나타낸 것으로 새로운 문자를 기억시키기 위해 이미 학습된 문자들을 재학습시킬 필요성이 없음을 보여 주고 있다. 이와같이 ART모형은 온라인 학습이 가능하다는 장점을 가지고 있지만 안정성-성형성 딜레마의 해결을 궁극적으로 경계변수에 의존하고 있으며, 학습 가능한 패턴의 총수가 출력층 처리요소의 수라는 저장공간의 비효율성이 문제점으로 지적되고 있다.

5.5 신경회로망 모형의 분류

앞에서 설명한 대표적인 네 가지 신경회로망 모형 외에도 14.2 절의 <표 14-1>에서 보았듯이 많은 신경회로망 모형들이 이미 개발되어 사용되고 있다. 이들 모형들을 분류하는 기준은 여러 가지가 있을 수 있는데 Lippman에 의한 신경회로망 모형의 분류를 소개한다. Lippman은 신경회로망의 주된 기능을 패던분류 (Pattern Classfication) 로 보고 신경회로망 모형들을 나누었는데, 신경회로망의 입력값으로 이진수만을 사용하는가 또는 실수값을 허용하는가 여부와 학습방법, 즉 지도학습 또는 자율학습을 사용하는가에 따라 신경회로망 모형들을 분류한 후, 각 신경회로망 모형들을 전통적으로 사용되어 오던 패턴분류 알고리즘과 대비시켰다. <표 14-2>에서 볼 수 있듯이 신경회로망은 패턴분류기로서 사용될 때는 연상기억장치 (Auto-assocation Memory), 패턴분류 (Pattern Classifier) 및 패턴군집화 (Pattern Clustering) 의 세 가지 기능을 수행할 수 있다. 신경회로망의 연상기억기능은 홉필드 네트워크나 코호넨 네트워크에서 이미 설명하였으며, 패턴분류와 패턴군집화의 가장 큰 차이는 목표출력값이 사전에 주어지는가의 여부이다.

<표 14-2> 신경회로망 모형의 분류

6. 신경회로망의 응용

6.1 서론

생체의 신경시스템이 여러 학문의 대상이 되고 있듯이 생체의 신경시스템을 기본모델로 한 지능시스템인 인공신경회로망도 Teuvo Kohonen의 지적처럼 학문적 배경이 다른 연구자들이 각기 다른 목적과 관점을 가지고 접근할 수 있는 연구대상이다. 이와 같이 신경회로망에 대해 다양한 관점이 존재할 수 있다는 사실은 바로 신경회로망이 광범위한 응용분야를 가질 수 있을을 암시하는 것이다. 과거, 부호적 추론에만 의존하던 인공지능 (Symbolic AI) 분야에서 해결하기 어려웠던 문제로 인식되어 온 문자인식, 음성인식, 영상처리 및 로봇제어 등의 공학적 응용분야에 대해 신경회로망은 새로운 접근방법으로써 각광받고 있을 뿐 아니라, 최근 기업의 경영관리 수단으로써 응용하려는 노력이 시도되어 경영문제의 거의 전 분야에서 성공적인 사례들이 많이 보고 되고 있다. 따라서, 경영문제의 해결을 위한 신경회로망의 응용기법 및 사례들을 정리하고자 한다.

<그림 14-19> 패턴분류 작업

인류가 가진 지식의 대부분은 어떤 현상을 간단한 형태로 모형화하거나 많은 관련 자료를 수집하고 정리하는 분류작업의 소산이므로 인류는 많은 분석방법론들을 개발하여 사용해 왔다. 이러한 분류작업을 위해 신경회로망이 어떻게 사용 될 수 있는가를 통계학의 판별분석 방법과 대비시킨 것이<그림 14-19> 이다.

경영관리분야에서 통계학은 중요한 분석수단의 하나로 자리잡고 있지만 최근 통계학이 갖는 여러 한계들을 극복하기 위해 인공지능의 여러 기법들을 응용하고자 하는 연구들이 많이 시도되고 있으며, 그 중에서도 신경회로망이 가장 유력한 수단으로 주목받고 있다. <그림 14-20>은 신경회로망, 부호적 추론에 의한 인공지능 및 통계학의 여러 모형들과 이들이 수행할 수 있는 기능들을 정리한 것이다.

<그림 14-20> 신경회로망과 경쟁 분석수단들

신경회로망은 여타의 분석방법론들에 비해 훨씬 다양한 기능을 갖고 있을 뿐만 아니라 경영문제를 분석함에 있어서도 타 분석방법론들이 갖지 못한 장점을 가지고 있다. 경영문제의 분석시 가장 유의해야 할 사항은 첫째, 기업이 처해 있는 환경은 계속 변화하며 대부분의 분석자료들이 많은 잡음을 가지고 있다는 점과, 둘째 주어진 문제에 대해 고려해야 할 변수들이 너무 많고, 그 중에는 정성적 변수들이 포함되는 경우가 일반적이라는 사실이다. 이와 같은 경영문제의 특성에 대해 통계학적 분석방법론을 이용할 경우 변화에 대한 적응이 힘들고, 분석자료가 갖는 분표에 대한 엄격한 가정이 요구되며, 계량적 변수와 정성적 변수가 혼합된 경우 성과가 좋지 못하다는 어려움이 있다. 따라서, 대규모 병렬성 및 학습을 통한 적응성 등의 특징을 갖는 신경회로망은 통계학이 갖는 한계를 극복시켜 줄 수 있는 유력한 분석수단일 뿐만 아니라 전문가시스템의 구축에 있어 최대 장애가 되고 있는 지식획득 작업을 위한 수단도 될 수 있어 앞으로 경영문제의 해결에 있어 강력한 방법론이 될 것으로 생각된다.

신경회로망이 예측, 제조 및 운용관리와 재무 및 회계분야 등 경영문제에 어떻게 응용될 수 있는가를 보이기 앞서 신경회로망을 이용한 시스템 개발 방법론에 대해 설명하기로 한다. <그림 14-21> 은 전통적인 시스템 개발 방법론 및 전문가시스템 개발시에 많이 사용되는 프로토타이핑 접근방법과 신경회로망을 이용한 시스템 개발 방법론을 대비시킨 것이다. 신경회로망의 경우 가장 중요한 것은 학습자료의 준비과정으로서 학습자료가 목표로 하고 있는 문제를 잘 반영하지 못하는 경우에는 실패할 가능성이 매우 높다. 하지만 학습자료만 잘 준비된다면 매우 빠른 시간 안에 원하는 시스템을 개발할 수 있다는 장점이 있다. 또 선택된 신경회로망을 훈련시키기 위해서는 필요에따라 학습자료들을 사전에 전처리과정을 거쳐 사용하거나 또는 신경회로망의 출력값들의 해석을 보다 원활히 하기 위해 후처리과정을 필요로 하는 경우가 있다.

<그림 14-21> 시스템 개발 방법들간의 비교

6.2 예측분야에의 이용

(1) 시계열 분석

시계열 분석이란 일정한 시간간격을 두고 모아진 자료, 즉 시계열 자료 그 자체에만 의존하여 예측을 행하는 것으로<그림 14-22>의 시계열 생성과정을 블랙박스로 취급하고, 단지 데이터패턴의 변동에만 의존하여 이를 수학적 관계식으로 표현하고자 하는 것이다. 시계열 분석에서 중요시 되는 데이터 패턴은 임의변동 • 추세 • 계절성 및 순환주기 등으로, 이들을 파악하는데 가장 많이 이용되는 수단은 자기상관계수 (Autocorrelation), 즉 일정한 Time-lag상에 위치하는 자료들간의 상호의존관계를 나타내는 척도 이다. 따라서, 신경회로망의 뛰어난 패턴인식능력을 주어진 자료에 내재하는 상호의존관계를 찾아내는 수단으로 사용하려는 노력은 당연한 것이다.

<그림 14-22> 시계열 생성관계

신겨회로망을 시계열 예측에 처음 이용한 학자는 신호처리 분야의 Lapedes & Farber 로서, 시계열 [Z_t, t ∈ T} 에 대해 <그림 14-23> 과 같은 다계층퍼셉트론을 백프로파게이션 알고리즘에 의해 학습시킨 결과, 기 관측지에의 fitting은 물론 예측에 있어서도 신경회로망이 기존의 계량적 기법들보다 우수함을 보였으며, 이러한 연구에 자극을 받아 많은 학자들이 신경회로망을 자료분석에 이용하고자 연구한 결과, 다계층 퍼셉트론은 비선형 회귀분석을 하는 것과 마찬가지 효과가 있으며 Universal Approximator라는 주장이 나올 만큼 다계층 퍼셉트론의 주어진 자료에의 적합능력이 뛰어남을 입증하였다.<그림 14-23>은 신경회로망이 주어진 시계열에 대해 비선형 자기회귀분석 (Nonlinear Autoregression) 을 하는 것으로 볼 수있는데, 만약 입력을 Z_t가 아닌 다른 변수들로 대체한다면 인과관계분석에 많이 사용되는 다중회귀분석 (Multiple Regression) 의 형태로 신경회로망을 이용하는 것이 된다. 통상 시계열 분석은 1년 이하의 단기예측에, 인과관계분석은 장기예측에 많이 사용되고 있다.

<그림 14-23> 다계층 퍼셉트론을 이용한 시계열 분석

하지만, 신경회로망이 실세계의 시계열에 대해서도 유용하게 사용될 수 있기 위해서는 아직도 해결되어야 할 많은 과제가 남아 있다. Lapedes & Farber의 연구는 이미 잘 알려진 함수를 이용하여 컴퓨터로 많은 수의 관측치를 생성시킨 후, 신경회로망과 기존의 예측기법들의 예측성과를 비교한 것이다. 하지만 사회경제적 시스템의 경우 그와 같이 많은 관측치를 얻기란 거의 불가능하며 또한 많은 잡음을 내포하고 있다는 사실이 중요하다. 특히, 다계층 퍼셉트론의 적합능력이 뛰어나므로 불필요한 임의변동까지도 학습할 위험이 크므로 과잉적합문제의 해결이 더욱 중요한 문제가된다. 과잉적합을 방지하여 예측력을 높이기 위해 Weigand et al은 가중치제거기법을 사용하였고, 지원철과 이재규[92]는 Recurrent Network를 도입한 결과를 발표하였다.

Weigand et al은 시계열 예측에 있어 벤치마크 데이터로 많이 사용되는 태양흑점수 자료 및 외화환율예측에 다계층 퍼셉트론을 이용하였는데 overfitting문제의 심각성을 파악하고 가중치제거라는 기법을 사용하여 학습된 신경회로망의 크기를 최소화하려고 했다. 흑점수자료에 대해서는 자기회귀형태로, 환율예측에 있어서는 다중회귀분석의 형태로 각각 신경회로망을 이용하였다. Werbos는 장기에너지 수요예측에, Hoptroff는 영국의 경기변동예측에 신경회로망을 사용한 사례를 보고했다.

6.3 제조 및 운영관리에의 이용

(1) 최적화

Hopfield & Tank[90]에 의해 신경회로망에 의한 판매원여행문제를 해결할 수 있는 알고리즘이 발견된 후, 컴퓨터의 작업처리계획, 위성통신일정계획 및 승무원탑승계획 등과 같이 최적화기법이 요구되는 분야에 많은 응용이 이루어져 왔다. Hopfield & Tank의 접근방법은 항상 최적해를 보장하지 못하는 단점이 있는데, 이를 위해 볼츠만 머신과 시뮬레이티드 어닐링기법을 함께 상용하거나, 코호넨 네트워크 등을 사용하려는 노력이 있었다. 하지만 신경회로망에 의한 해가 전통적 알고리즘인 Branch and Bound 기법을 사용했을 때 보다 더 좋은 해를 구한다는 보장은 아직 없으므로 이 분야에 대한 많은 연구가 앞으로 요구된다.

이러한 신경회로망의 한계를 인식하고 다른 각도에서 최적화문제에 응용하려는 연구가 이재규[91] 등에 의해 발표되었는데, 신경회로망을 최적화 모형에 대한 민감도분석 (Sensitivity Analysis) 수단으로 사용하는 것이다. 이들은 정유공장의 제품생산계획을 세움에 있어 해당 정유공장의 특수사정에 의해 원유배합 (Charge plan) 문제가 매우 복잡한 비선형계획문제가되며, 일일공장가동계획을 세우기 위해서는 대형 컴퓨터로도 10시간 이상 걸린다는 것을 발견했다. 이러한 어려움을 해결하기 위해 신경회로망을 이용한 것이다. 즉, 제품수요와 그에 따른 원유배합 사례들을 사전에 최적화 모형을 이용하여 구한 다음, 그 결과를 신경회로망에 훈련시켜 주어진 제품수요에 최적인 원유배합을 찾도록 함으로써, 오랜 시간을 요하는 비선형계획문제를 매일풀지 않아도 되도록 하였다. 이와 같은 접근방법은 아직 신경회로망 컴퓨터가 실용화되지 못한 시점에서 시간적 제약이 많은 최적화문제에 대해 좋은 대안을 제시한 것으로 볼 수 있다.

(2) 일정 계획

주문식 생산체제에 있어서 일정계획문제는 NP-Complete문제의 전형적인 예일 뿐만 아니라 실제의 상황도 매우 복잡하고 동적이다. 이 문제에 대해 순회판매원 기법을 응용하려는 노력이 있었으나,이는 m개의 기계와 n개의 작접이 확정되어 있는 상황에서만 유효하다는 한계가 있다. 최근 Rabelo et al[90]은 유연생산체제의 일정계획을 수립하기 위해 신경회로망, 전문가시스템 및 휴리스틱을 혼합한 시스템을 연구했다. 즉, 이 시스템이서 신경회로망의 역할은 주어진 상황에 가장 적절한 일정계획 휴리스틱을 산정하고, 해당 휴리스틱이 작동하기 위해 필요한 계수값들을 제공하는 역할만을 수행하며 시스템의 전체적인 통제에는 전문가시스템을 채용함으로써 좋은 결과를 얻었다.

좋은 일정계획이란 실제 생산현장의 상황을 잘 반영한 것이라야 한다. 하지만, 실제 생산현장에서는 현장여건이나 작업자의 숙련도 등에 의해 작업시간 (Manhours or Processing Time, 공수) 이 많은 영향을 받는다. 이는 아무리 좋은 일정계획을 수립했다 해도 무용지물화할 수 있음을 의미한다. 이와 같은 문제를 해결하기 위해 작업공수예측에 신경회로망을 이용한 결과, 일정계획수립의 전문가들에 비해 작업공수의 계획대비 실행오차를 50% 가까이 줄임으로써 수립된 일정계획의 신뢰성을 크게 높였다.

(3) 품질관리

현재 신경회로망은 복잡한 무늬를 갖는 직물이나 가공된 목재의 표면검사, 소다수병이나 유리의 결점발견 등과 같이 생산된 제품이나 부품의 이상유무를 확인하는 검사업무의 자동화에 많이 이용되고 있으며 특히, Nestor Learning Company는 복잡한 형상을 갖는 부품들을 검사하는 신경회로망 시스템을 상용화하였다.

하지만, 아직 검사의 결과를 종합하여 생산공정상의 문제점을 파악하여 전체적인 생산성을 향상시키는 품질관리의 수단으로써 신경회로망을 응용한 연구가 없는 실정이다. 전통적으로 통계적 품질관리에서 관리도 (Control Chart )를 사용해 왔는데, 통계적 기법의 대체나 관리도들을 종합적으로 통제하는 수단으로서 신경회로망의 응용가능성은 매우 크다고 할 수 있다.

(4) 물류관리

대표적 예로는 차량수송문제 (Vihicle Routing Problem) 를 들 수 있는데, 이 문제는 복수대의 차량이 존재하고 각 차량에 적재할 화물의 종류와 양을 결정해야 하므로 순회판매원문제의 확장된 문제로 볼 수 있다. Matsuyama는 자기 조직화 네트워크를 사용하여 얻은 해의 질은 Branch and Bound기법을 사용했을 때보다 약간 못하지만 계산시간은 반으로 줄이는 결과를 얻었다. Bigus and Goolsbey는 차량에 짐을 적재하는 문제는 전문가시스템으로 해결한 후, 최적 배달경로의 결정에는 신경회로망을 사용함으로써 좋은 결과를 얻었다. 이 물류관리는 앞으로 최적화기법의 연구와 함께 상당한 연구결과가 기대되는 분야이다.

6.4 재무 및 회계분야에의 응용

(1) 주식시장의 분석

주식시장 만큼 많은 분석방법이 사용되고 있는 곳도 드물 것이다. 많은 학자들은 주식시장에 대해 집중적인 통계분석을 해 왔으며, 투자자들도 더 높은 수익률을 얻기 위해 상상할 수 있는 모든 분석방법을 동원하고 있다. 최근에는 주식투자의 전문가시스템을 개발 사용하려는 노력도 보편화되고 있다. 그러나 투자 관련지식의 다양한 원천 및 자료의 방대함, 주식시장에 내재하는 근원적인 불확실성 등으로 인해 통계적 분석은 한계가 있게 마련이며 전문가의 시스템의 개발에 있어서도 지식획득 작업이 큰 애로가 되고 있는 실정이다. 최근 신경회로망을 주식시장분석에 활용하려는 시도가 매우 활발한데 다음과 같이 세 가지 형태의 연구로 요약할 수 있다.

첫 번째는 신경회로망을 이용한 주가예측이 가능한가에 대한 연구이다. White는 IBM주식에 대해 일일 주가수익률의 예측이 가능한가를 검증하기 위하여 은닉층이 하나인 다층퍼셉트론을 사용하였다. 입력으로 예측시점 직전 5일간의 주가수익률을 사용했는데 불행히도 연구결과는 실망적인 것이었다. 하지만 어떤 측면에서는 이미 예견된 결과이기도 한데 그 이유는 다음과 같다. 첫째, 분석대상이 되었던 IBM주식은 랜덤워크 이론을 입증하는 좋은 자료로 많이 이용되었던 것이며, 둘째 신경회로망의 능력이 아무리 뛰어나더라도 아무 정보를 갖고 있지 않은 자료로부터 유용한 자료를 창출해 낼 수는 없기 때문이다.  비록 이 연구결과는 실망적이지만 그 방법론을 확장시킨다면 현재주식시장 분석의 이론적 근간을 이루고 있는 효율적 시장가설에 대한 새로운 검증 방법론으로 신경회로망은 유용하게 이용될 수 있을 것이다.

두 번째는 주식매매 시점의 포착을 위해 신경회로망을 이용하려는 노력이다. 일본 후지쯔와니코증권에 의해 개발된 TOPIX 예측시스템은 모듈접근방법을 사용하고 있다.<그림 14-24>에서 볼 수 있듯이 벡터커브, 회전율, 이자율, 외화환율, 뉴욕증시의 다우존스지수 등을 입력으로 사용하는 여러 개의 작은 신경회로 망을 사용하여 얻은 결과들을 사후처리를 통해 최종적인 판단이 내려지도록 시스템을 구성하였다. 이 TOPIX 예측시스템은 훈련용 학습자료에대해 99%정도의 정확성을 보였으며, 실제 주가변동의 예측에 있어서도 6%의 향상이 있었다고 보고 되었다. NEC는 아직 실험중인 단계에 있지만 일본에서 많이 사용되는 candlestick chart를 분석할 수  있는 신경회로망을 개발하였다. 훈련된 신경회로망은 전문가들에 의해 준비된 검증패턴들에 대해 93.8%라는 정확도를 보였다. 이는 신경회로망이 여러 가지 형태의 차트분석에 의존하는 주식시장의 기술적분석 (Technical Analysis) 에 효과적으로 활용될 수 있음을 입증한 것이다. 한편 미국의 Neural Trading Company는 신경회로망과 전문가시스템을 결합한 하이브리드 시스템을 개발하여 높은 수익률을 올리고 있다. 이 시스템은 신경회로망의 패턴인식능력을 이용하여 주식의 매매시점을 포착한 후, 전문가시스템을 이용하여 자금운영에 대한 최종 의사결정을 내리도록 되어 있는데, 주식투자시스템의 개발에 있어 바람직한 접근방법을 제시한 것으로 생각된다.

<그림 14-24> TOPIX 시스템의 구조

(2) 재무위험 분석

보험, 대출심사, 기업신용평가 등과같이 재무위험에 대한 분석을 필요로 하는 분야들에서도 신경회로망은 기존의 통계적 방법론을 대체해 나갈 것으로 예상되는데, 대표적인 응용사례는 다음과 같다.

Nestor Learning System 이 RCE네트워크를 이용해 개발한 시스템은 저당설정전문가들의 판단을 학습했는데 실제업무에 적용한 결과 부실담보를 12% 줄일 수 있었다고 한다. Hecht-Nielson Company는 연간소득, 주택보유여부, 주거기간 등을 입력으로 사용하는 개인대출심사를 위한 평점모형을 개발했는데 기존의 평점모형들보다 연간 수익률을 최고 27%나 향상시킬 수 있었다고 보고했으며, 이를 담보물의 1차 screening에도 활용하고 있다. 이와 같은 신경회로망의 이용은 개인신용카드의 발급여부를 결정하는데에 이용될 수 있을 것이다.

Odom은 5개의 재무비율을 사용하여 기업도산여부를 예측하였는데, 사용된 신경회로망은 은닉층이 하나인 다계층 퍼셉트론이었다. 특히 이 연구는 학습자료 속에 포함된 도산기업의 수를 변화시켜가면서 신경회로망을 훈련시켰는데, 그 결과가 <표 14-3>에 정리되어 있다. 전체적으로 신경회로망이 판별분석 (Discriminant Analysis) 에 비해 월등한 예측력을 보여 주고 있으며, 도산기업의 사례가 적게 포함된 경우에도 효과적인 학습이 가능하므로 통계적 분석이 갖는 한계를 극복할 수 있다는 것을 명확히 보여 주었다. 또, Dutta & Shekha[88]는 Value Line Index 사와 S & P사의 채권등급자료와 10개의 재무비율을 상용하여 채권등급을 예측하는 신경회로망을 설계했는데 검정자료에 대해 선형회귀분석은 64.7%, 신경회로망은 82.4%의 정확도를 각각 보였다. 지원철[89]도 한국신용평가의 CP등급에 대해 판별분석과 비교분석한 결과, 유사한 결론을 얻어 신경회로망의 우수한 예측력을 확인한 바 있다.

<표 14-3> 기업도산의 예측 사례

(3) 회계분야

Coakley & Brown 는 신경회로망이 회계감사에 이용될 수 있는 가능성을 제시하였다. 회계감사에 있어 추가적 조사가 필요한 항목의 결정을 위해 신경회로망, 재무비율분석 및 회귀분석의 세 방법론을 비교했다. 이들은 외상매출금, 매출액, 매출원가, 재고상품 등 15개의 계정과목에 대해 42개의 입력, 15개의 처리기를 갖는 하나의 은닉층 및 15개의 출력처리기를 갖는  다계층 퍼셉트론을 설계했는데 회귀분석이나 재무비율분석보다 훨씬 더 좋은 결과를얻었다. 특징적인 것은 신경회로망을 이용할 경우, 추가적 조사가 필요한 항목을 조사하지 않을 위험은 크게 줄어든 대신 별로 중요하지 않은 항목에 대해서도 조사 필요성을 지적하는 경우가 있다는 것이다. 이는 감사의 신뢰성을 크게 높일 수 있는 반면, 감사의 효율성을 저하시킨다는 것으로 이 연구에 사용된 신경회로망기법이 아직 단순함에도 불구하고 신경회로망의 뛰어난 패턴인식능력을 입증해주는 결과라 할 수 있다. 앞으로 각 계정과목 내의 작은 변동은 무시할 수 있도록 신경회로망을 훈련시키는 방법을 개발한다면 신경회로망의 회계감사의 자동화 및 신뢰성을 높이는 데 크게 기여할 수 있을 것이다.

6.5 신경회로망의 응용방향

현재 신경회로망은 기업 내 하위수준의 의사결정문제로부터 경영전략에 이르는 최고경영자의 의사결정문제에 이르기까지 폭넓은 응용이 시도되고 있으며 좋은 결과들이 많이 보고 되고 있다. 이러한 응용사례들을 검토해 볼 때 바람직한 신경회로망의 응용방향이나 요구 사항들을 정리하면 다음과 같다.

첫째, 복잡한 문제에 대해서는 소규모의 신경회로망을 여러 개 계층적으로 조직하여 사용하는 것이 바람직하다.

둘째, 학습된 신경회로망의 일반화 능력 (Generalization Power) 을 높일 수 있는 방법이 강구되어야 한다.

셋째, 통계분석 등을 통하여 신경회로망의 성과분석을 철저히 하는 검증과정이 반드시 필요하다.

경영문제해결에 있어 고려해야 할 사항들은 주어진 문제에 대해 여러 개의 해결책이 존재하고 그 선악도 불분명하며, 하나의 문제해결 방법으로는 완전한 해결책을 얻기 어려운 경우가 많다. 또 경영자들은 자신이 이해하지 못한 해결책은 채택하지 않으려 하는 경향이 있는데 신경회로망은 설명기능이 없다는 약점을 갖고 있다. 따라서 현재로서는 <그림 14-25(a) >와 같이 주어진 문제를 적절히 분해한 후 신경회로망, 전문가시스템 및 전통적 알고리즘들을 적당한 부분에 각기 적용하는 하이브리드 시스템의 구축이 매우 바람직할 것이다. 하지만 앞으로 <그림 14-25(d)>와 같이 전문가시스템과 신경회로망과의 관계에 대한 연구가 진전된다면 하나의 체계하에서 양 기술을 효과적으로 사용할 수 있는 시대가 올 것으로 예상된다.

<그림 14-25> 신경회로망과 전문가시스템의 결합

현재 신경회로망과 타 인공지능방법론과 연계함으로써 보다 현신적인 문제들은 해결하고자 하는 연구가 많이 진행되고 있으며, Schreinemaker과 Touretzsky는 그러한 가능성을 보여 주고 있다. 이렇게 신경회로망기법과 타 인공지능 기법간의 결합연계개발이 가능하려면 이들 두 기법간의 상호 내부구조를 이해 할 수 있어야 하며, 이러한 형태의 결합을 가능케 하는 구조로서 한국과학기술원 경영정보공학과에서 개발된 UNIK-NEURO 신경회로망개발도구가 있다. UNIK-NEURO는 UNIK 인공지능시스템 개발 환경하에서 UNIK-BWD(후방향 규칙기반추론기관 및 개발도구)이나 UNIK-FWD(정방향 규칙기반추론기관 및 개발도구)와 UNIK-OBJECT라는 범용객체지향 지식표현도구를 이용해 상호 이해가능하도록 구성되어 있으며, 특히 UNIK-OBJECT를 이용해서 개발된 모든 휴리스틱이나 방법론과도 상호 결합가능한 구조를 제공하고 있다.

<그림 14-26>UNIK-NEURO와 타 인공지능기법과의 결합형태

UNIK-NEURO는 <그림 14-26>에서 도시한 바와 같이 UNIK-FWD, UNIK-BWD 및 UNIK-OBJECT와의 동등한 수준에서의 연결구조를 제공함으로써 앞의 <그림 14-25>에서 제시한 "느슨한 결합형태" 에서의 "문제의 분해" 구조와 "완전 결합형태" 에서의 "내재된 신경회로망" 구조의 복합형 시스템의 개발을 지원하고 있으며, "전문가시스템을 위한 지식획득 수단" 으로서도 개발을 용이하게 해주고 있다. UNIK-NEURO를 이용하여 개발된 신경회로망과 규칙기반시스템의 결합 예를 든다면 아래에서는 정유회사에서의 일정계획문제를 해결하기 위해 규칙기반시스템과 신경회로망시스템이 상호 연계하여 문제를 해결하는 과정에 해당하는 예제 규칙을 보여 주고 있다.

(RULE diesel_product_sulfur-under_qualification

          IF

                         (FINAL_PRODUCT

                                        ^product_type         'DIESEL

                                        ^quality                   ^MAXSUL               (max-sulfur>)

                          (GP_SOLUTION

                                       ^production              ( > <> 0 )

                                       ^SUL                       ( >  <> <max-sulfur> )

                                       ^frame-name           <product_name>)

         THEN

                          (new-value <product_name> 'SUL <max-sulfur>)

                          (call 'Adaptive_Optimal_Control_Neural_Network

                                  (get-value 'GP_SOLUTION 'GP_NAME)))

위의 예제규칙은 최종제품의 황함유율이 정해진 최대치를 초과하는 경우는 자동적으로 최대치를 초과하지 않도록 선행공정을 통제할 수 있도록 학습된 신경회로망이 규칙기반추론기관에 의해 불리워지는 상황을 예시하고 있다. 이러한 형태로 신경회로망과 기타 인공지능기법들은 상호 협력적인 관계로 하나의 복합구조로서 시스템화 될 가능성을 가지고 있으며 앞으로 이러한 형태로서 많은 시스템들이 여러 분야에서 구축되어 신경회로망과 인공지능기법간의 시너지효과를 보게 될 것으로 기대된다.