불확실성의 표현과 처리

 전문가 시스템 원리와 개발 : 이재규, 최형림, 김현수, 서민수, 주석진, 지원철 공저, 법영사, 1996, Page 294~337

1.서론

실제로 지식이 확실하여 애매함이 없이 정확한 경우는 오히려 드물어 지식에는 거의 필연적으로 불확실성 (Uncertainty) 이 내포되어 있다. 따라서 수학적 논리와 같이 오직 참이냐 거짓이냐만을 다루는 결정적 (Deterministic) 인 방법으로는 실제로 발생하는 불확실성을 제대로 나타낼 수는 없다. 불확실성이란 "판단이나 의사결정에 필요한 적절한 정보의 부족" 이라 할 수 있다. 불완전한 정보나 애매한 정보, 잘못된 정보 등은 판단이나 의사결정에 있어서 불확실성을 증대시킨다. 우리는 지금까지 모든 지식에 불확실성이 없는 경우만 가정하여 오직 논리적 추론으로써 명제나 사실의 참, 거짓을 명확하게 결정지을 수 있는 경우만 생각했다. 이러한 상황에서 일어나는 추론을 정확한 추론 (Exact Reasoning) 이라 한다. 그러나 실제로는 어떠한 사실이나 지식에 대한 확실성이 100%라고 하는  경우는 극히 드물다. 따라서 불가피하게 제기되는 불확실성을 표현하고 처리할 수 있는 기능이 전문가 시스템에는 포함되어 있지 않으면 그 전문가시스템이 처리 할 수 있는 영역은 매우 한정될 수 밖에 없을 것이다. 그렇다면 불확실성이 야기되는 이유는 무엇인가.

첫째, 지식의 불완전성 (Incompletness), 즉 전문가로부터 얻은 지식자체의 완전성의 결여이다. 즉, 있어야 될 정보의 결여로 말미암아 정확한 결론을 내릴 수 없는 상황일 때 발생한다. 이를 다시 설명하면 규칙 형태의 조건부와 결론부 사이의 상호관계가 확실히 설정되지 않은 경우이다. 즉, IF A THEN B 라는 형태에서 A라는 조건부가 성립되었다고 해서 B가 성립된다는 것이 확실히 보장되지 않는 것이다. 이는 대상에 대한 전문지식의 부족이나 부실한 지식획득으로써 야기될 수도 있고, 문제 영역자체가 이미 불확실성을 내포하고 있는 경우일 수도 있다. 전자의 경우는 병에 대한 진단영역에서 전문적인 의사의 자문없이 지식을 만든 경우가 해당되며, 후자의 경우는 내년의 부동산 경기예측이나 10일 후의 주가예측처럼 문제자체가 알려지지 않은 수많은 요인에 의해 결정되기 때문에 완전한 지식을 구축하는 것이 불가능한 경우이다.

둘째, 지식 표현의 애매성 (Vagueness) 또는 모호함 (Ambiguity) 이다. 지식의 표현이 자연어로 표현될 경우 인간인 사용하는 애매한 용어가 포함될 수밖에 없으며 이렇게 될 경우 표현의 애매함으로 인해 내용이 여러 가지로 해석될 가능성이 있다. 예를 들어 다음과 같은 지식 표현을 보자.

"키가 어느 정도 크고 안정된 직장을 가진 20대 후반의 남자는 A타입의 배우자를 원한다."

여기서 "어느 정도," "안정된," "후반" 등의 표현은 해석하는 사람에 따라 구체적으로 다른 값을 가질 수 있다. 이러한 애매성을 일으키는 단어로는 많다. 적다, 작다, 길다, 잛다와 같이 양을 나타내는 형용사와 매우, 약간, 어느 정도, 거의 등 양을 나타내는 부사가 있다. 이러한 표현들은 실제로 해당 되는 측정 수치로써 대응되어야 한다. 예를 들어, 170㎝ 이상을 "키가 크다" 라고 본다든지, 180㎝ 이상을 "매우 크다" 라고 보는 것이다. 또한 28세부터 29세를 "20대 후반" 이라고 하는 것이다. 보다 자세한 내용은 퍼지집합이론에서 설명하도록 한다. 또한 이외에도 안정된, 아름다운, 웅장한, 빼어난 등의 주관적 판단을 나타내는 형용사가 지식에 포함될 경우 그 해석에 있어서 더욱 애매함이 증대될 수 있다. 따라서 안정된 직장이라는 범위를 국영기업체나 상장회사 중 3년 이상 근무 중인 직장과 같이 구체적으로 대응될 수 있어야 한다.

셋째, 지식의 오류 (Incorrectness) 이다. 논리적 오류나 전문지식의 부족 등으로 말미암아 잘못된 지식을 생성한 경우이다. 예를 들어, 지금까지 A라는 기계가 고장이 나지 않았기 때문에 A라는 기계는 앞으로도 고장이 나지 않는다라고 추론한다면 오류가 된다.

넷째, 측정의 오류 (Errors of Measurement) 이다. 지식자체는 아무런 불확실성이 없는 것처럼 보이나 실제로 이것을 특정한 대상에 적용시킬 때, 규칙의 조건과 실제 대상과의 연계에서 오류가 발생할 수 있다. 즉 "IF A THEN B" 라는 규칙에서 A라는 조건을 실제사실이나 대상과 결부시킬 때 생기는 측정이나 적용에서의 오류이다. 예를 들어, 2억 이상인 부동산 담보를 제공할 수 있는 자에게 대출을 하라고 했을 때, 부동산을 시가로 평가할 것인지 공시시가로 할 것이지에 따라 해당 지식의 적용여부가 달라질 것이다. 또 다른 예로서 주가의 패턴이 "head & shoulder" 의 형태가 발생하면 주가가 떨어진다라는 지식이 있을 때, 주가의 패턴인식에서 사람의 주관적 경험이 반영되어 사람마다 현재의 패턴에 대한 판단이 다를 수가 있다. 또한 소음인이면 성격이 꼼꼼하다라고 한다면 누가 소음인인지에 대한 판단이 각자 다르다면 이 규칙의 적용에 오류가 발생할 수 있다.

이상에서 살펴보았듯이 불확실성은 여러 가지 원인으로 발생되는데 본 장에서는 이러한 불확실성을 어떻게 표현하고 처리하는지에 대한 문제를 다루고자 한다.

2. 확률적 접근법

확률적 표현으로 지식의 불확실성을 나타내는 경우는, 예를 들어 내일 비올 확률이 80%라든지 이 병에 걸리면 5명 중 1명꼴로 사망한다라는 것이다. 확률은 불확실성을 수량적으로 표현이 가능하게 한다. 확률의 고전적 정의는 다음과 같다.

사건(event) H가 발생될 확률 P(H)는

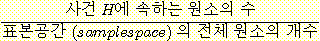
단, 표본공간의 원소는 모두 발생될 가능성이 다 같아야 한다. 이러한 확률은 다음과 같은 공리로써 정의할 수  있다.

• 확률 P(H)는 0과 1사이의 값이다.    0≤P(H)≤1

• 모든 발생가능한 사건들의 확률의 합은 1이다.    ∑P(H_i)=1 ∀_i

• 상호 배타적인 (Mutually exclusive) k개의 사건이 일어날 확률은 각각의 발생확률의 합이다.

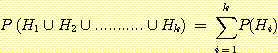
그리고 전문가시스템에서 중요한 확률의 특성은 어떤 사건(또는 가설)과 그 사건의 여집합 (complement) 이 발생활 확률의 합은 1이다라는 것이다.

 P(H) +  P(_ㄱH) = 1

그리고 확률값을 측정하는 데에는 다음과 같은 방법이 사용될 수 있다.

첫째, 모든 발생가능한 사건들을 알고 있고 또한 모든 사건들이 동일한 발생 가능성을 갖고 있다면, 전통적인 확률정의대로 사건 H가 발생할 확률  P(H)는 n/N, 즉 사건 H에 속하는 원소의 수 N으로 나눔으로써 사전적으로 계산될 수 있다. 즉, 주사위 눈이 1이 나올 확률 1/6은 그 주사위가 정육면체라면 주사위를 던져 보지 않고서도 계산될 수 있다.

둘째, 사전적인 계산이 불가능할 경우 실험이나 경험적인 데이터를 통하여 사후적으로 확률을 추정할 수 있다. 즉,  P(H)는

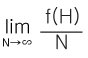
으로 계산된다. 여기서 f(H) 는 N번의 실험(관찰)에서 사건 H가 발생한 횟수를 나타낸다. 물론 실제적으로 실험 또는 관찰의 횟수를 무한 대로 할 수는 없기 때문에 P(H) 의 근사값으로 측정될 것이다.

셋째, 첫째와 둘째의 경우와 달리 관심 있는 사건에 대해 실험이 불가능하거나 과거에 그런 사건이 반복적으로 나타난 사례가 없는 경우, 예를 들어 새로운 장소에 유전을 개발할 경우 유전이 발견될 확률을 계산하는 경우에는 주관적인 확률값을 산정한다. 즉, 전문가의 경험이나 판단, 의견 또는 믿음을 확률의 값으로 나타내는 것이다. 즉, P(H) 는 사건 H가 일어나리라고 믿는 정도 (Degree of Belief) 를 나타내는 것으로 이는 전통적인 의미의 확률이 아니다. 그러나 이러한 주관적 확률은 전문가시스템에서 매우 유용하다. 왜냐하면 전문가시스템이 주로 전문가의 주관적 판단을 기초로 지식을 구성하기 때문이다.

이제 규칙과 결부하여 확률적 불확실성을 나타내 보자. 어떤 규칙의 조건부를 증거 (Evidence) 그리고 결론부를 가설 (Hypothesis) 이라고 해석할 경우,

IF < 증거 > THEN  < 가설 >

로 나타내지면 여기에 불확실성을 확률로써 나타내면,

IF <  증거  > THEN <  가설  > WITH 확률 P

라는 형태로 나타낼 수 있다. 이는 규칙의 조건부에 있는 증거가 참으로 관찰되면 가설 H도 참일 정도는 확률 P 라고 할 수 있다는 것이다. 이러한 확률의 개념을 이용한 불확실성의 처리방법 중 가장 대표적인 것이 베이지안 (Bayesian) 확률이론인데 다음은 베이지안 확률이론에 대해 살펴보기로 하자.

임의의 증거 E가 주어졌을 경우 가설 H가 참인 확률은 조건부확률 (Conditional Probability) P(H|E) 로써 나타낼 수 있다. 조건부 확률은 정의에 비해,

이며, 여기서 P (H∩E) 는 H와 E가 동시에 발생할 확률이다. 그런데 확률의 곱셈법칙에 따라

P(E ∩ H) = P(H|E)P(E) = P(E|H)P(H)...............(식 11-2)

이므로 (식 11-1) 은 다음과 같이 쓸 수 있다.

또한, 확률의 분할법칙을 따르면

P(E) = P(E ∩ H) + P(E ∩_ㄱH)

       = P(E|H)P(H) + P(E |_ㄱH)P(_ㄱH).....................................(식 11-4)

이다. 여기서 _ㄱH는 H의 여사건(H가 아닌 사건)을 가르킨다. (식 11-4)를 (식 11-3)에 대입하면 (식 11-3)은,

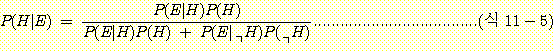
이 된다. (식 11-4)는 베이즈 정리 (Bayes Theorem) 의 특수한 경우이다. 만약 상호 배타적 (Mutual Exclusive) 인 가설 H₁, H₂, ...., H_n 이 있다면(식 11-4)를 확장하여

이고 E가 주어졌을 때 i번째 가설 H_i의 조건부확률 P(H_i|E)는 다음과 같다.

(식 11-7)을 베이즈정리라 한다.

베이지안 확률론에서는 P(H_i)를 사전 확률 (Prior Probability), P(H_i|E)를 사후확률 (Posterior Probability) 이라 한다. 사전확률은 증거 E를 관찰하기 전의 가설 가 참일 확률이고 사후확률은 증거 E를 관찰하고나서의 H_i가 참일 확률이다. (식 11-7)을 이용하여  P(H_i)와 P(E|H_i) 의 확률이 주어진다면 사후확률 P(H_i|E)를 얻을 수 있다. 이제 베이즈정리를 이용하여 사후확률을 구해보는 예를 살펴보겠다.

특정 지역에 유전이 있을 확률을 P(H₁)라고 하고, 유전이 없을 확률을 P(H₂)라 할 때 이들 사전 확률이 다음과 같이 주었다고 하자.

P(H₁) = 0.6     P(H₂) = 0.4

유전발견의 중요한 도구 중 하나는 폭발물을 이용한 인공지진에 의한 탐사(지진탐사)이다. 이 폭발음이 울리는 소리를 여러 지점에서 포착하여 전파속도, 음파의 변형도 등을 토대로 해당 지역의 지질구조가 유전이 있을 구조로 되어 있는지를 파악하게 된다. 그러나 이 방법이 100% 적중되는 것은 아니다. 그러나 과거 이 지진탐사방법을 사용해 본 결과 다음과 같은 조건부확률 (Conditional Probability) 을 갖는다고 가정하자. E는 지진탐사결과 유전이 있다는 반응을 나타내는 기호이다.

P(E|H₁) = 0.8 : 유전이 있는 지역에서 지진탐사를 한 결과 유전이 있다는 반응을 보일 확률

P(E|H₂) = 0.1 : 유전이 없는 지역에서 지진탐사를 한 결과 유전이 있다는 반응을 보일 확률

이때,  과  P(H₂|E)는 다음과 같이 계산된다.

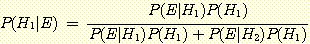
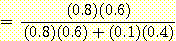
= 12/13 = 0.923

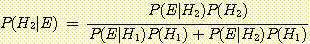
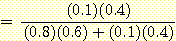
= 1/13 = 0.077

여기서 지진탐사의 실험정보가 유전이 있다는 반응을 보인 증거가 유전이 있을 확률을 사전확률 값 0.6에서 사후확률 값 0.923로 높여주었고 유전이 없을 확률은 0.4에서 0.077로 낮아진 것을 볼 수 있다. 이는 지진탐사라는 증거가 결론에 대한 불확실성을 낮게 한 것이라 할 수 있다.

또한 Odds와 Likelyhood ratio를 이용하여 사후확률을 계산할 수도 있다. 이는 사후확률에 대한 의미가 주관적인 믿음의 정도를 나타낼 때 유용하다.  Odds란 내기에서 건 돈의 비율과 같은 뜻으로, A라는 자동차가 시동이 걸릴 것인가에 대해서 걸린다는 쪽의 확률이 90%, 안 걸린다는 쪽의 확률이 10% 라면 9:1의 비율로 시동이 걸린다는 쪽으로 돈을 건다는 것이다. 다시 말하면, 누가 1000원을 내고 시동이 안 걸린다는 쪽으로 내기르 했다면 우리는 9000원을 내고서라도 시동이 걸린다는 쪽으로 내기를 할 수 있다는 것이다. 이를 식으로 표현하면 다음과 같다.

그리고 이것이 특정 사건 H와 연관되어 H가 발생하면 이긴다고 할 때,

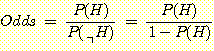
또한 Odds를 먼저 안다고 했을 때, 위 식으로부터

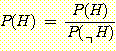
증거 E가 주어졌을 때 H에 대한 사후 Odds 는,

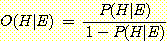
이므로

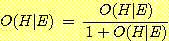
라고 할 수 있다. 따라서 사후 Odds를 측정할 수 있으면 사후확률이 계산된다. 이는 사전확률 P(H) 나 P(E|H)를 미리 추정하지 않더라도 사후확률을 계산할 수 있게 하므로 보다 실용성이 있다. 위의 유전문제에 적용시키면 지진탐사의 실험정보가 유전이 있다는 반응을 보였을 경우 유전이 있으리라는 것과 없으리라는 것의 Odds값이 12로 주어진다면, 즉 다시 말하면 유전이 있다는 것에 없다는 것보다 12배의 돈을 걸 수 있다면 유전이 있다는 사후확률은 12/12이 되는 것이다. 또한 사후 Odds는 likelyhood ratio를 이용하여 다음과 같이 구할 수 있다.

간단한 베이즈 이론으로부터

이고,

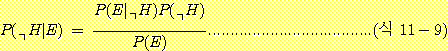
인데 (식 11-8)을 (식 11-9)로 나누면,

likelihood ratio  LR(H|E)를 다음과 같이 정의하면,

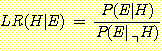
(식 11-10)은 다음과 같이 표현될 수 있다.

O(H|E) = LR(H|E)O(H).......................................(식 11-11)

이는 사후 Odds를 추정하기 힘든 경우 사전 Odds 와 likelihood ratio를 이용하여 사후 Odds를 추정할 수 있다. 앞의 석유탐사 예에서는,

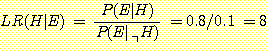
즉, 유전이 있는 지역에서 지진탐사 실험결과 유전이 있다는 반응을 보일 것에 유전이 없는 지역에서 지진탐사 실험결과 유전이 있다는 반응을 보인다는 것보다 8배의 돈을 걸 수 있다는 것이다. 또한 해당 지역에서 유전이 있다는 것과 없다는 것에 3:2의 비중을 둘 수 있으므로,

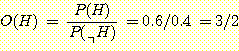
이 두 값으로써 사후 Odds는

O(H|E) = 8x(3/2) = 12

이고, 따라서 지진탐사반응 결과 유전이 있다고 나왔을 때 유전이 있을 사후확률은,

P(H|E) = 12/(1 + 12) = 12/13

로 계산된다.

이제 또 다른 예로서 투자의사결정과 관련하여 적용된 예를 들어보겠다. 먼저 다음과 같은 데이터가 있다고 하자.

위의 2차원 평면의 빈도수 표는 200개의 주식으로부터 얻은 데이터이다. 이제 각 가설 H, H'와 증거 E, E'가 다음과 같다고 하자.

가설 H = 수익률이 높다

가설 H' = 수익률이 낮다

증거 E =전자산업이다

증거 E' = 전자산업이 아니다

만약에 개별 주식에 대한 아무런 정보가 없다면 어떤 주식을 선택했을 때 기대되는 수익률에 대한 확률은 다음과 같이 사전확률로써 얻어진다.

P(높다) = 90/200 = 0.45

P(낮다) = 1 -P(높다) = 0.55.

만약 주식이 속한 산업을 안다면 (식 11-11)을 이용할 수 있다. 먼저 사전 Odds는 다음과 같이 계산된다.

O(높다) = P(높다)/[ 1- P(높다)]

            = (90/200)/[ 1-90/200]

            =0.8181.

likelyhood ratio 는,

LR(높다/전자산업) = P(전자산업|높다)/P(전자산업|낮다)

                          =(40/90)/(10/110)

                          = 4.888

따라서 (식 11-11)에 의해,

O(높다|전자산업) = LR((높다/전자산업)O(높다)

                         = (4.888)(0.8181)

                         = 3.996

이를 사후확률로 전환하면,

P(높다|전자산업) = 3.996/(1 + 3.996)

                         = 0.8006.

그러므로 어떤 주식이 전자산업에 속한다는 사실로 인해 수익률이 높을 확률은 0.45에서 0.08으로 30% 이상 증가하였다.

또한 기업이 수출위주의 기업이냐 내수위주의 기업이냐에 대한 추가적인 정보가 있고 그에 대한 빈도수 표가 다음과 같다고 하자.

앞에서와 같은 방법으로 사후확률은 다음과 같이 계산된다.

LR(높다|수출) = P(수출|높다)/P(수출|낮다)

                    = (50/90)/(30/110)

                    = 2.037

그러므로,

O(높다|전자산업,수출)

=LR(높다|수출)LR(높다|전자산업)O(높다)

=LR(높다|수출)O(높다|전자산업)

= (2.037)(3.996)

= 8.14.

그리고

P(높다|전자산업, 수출) = 0.8907

이제 수출위주와 전자산업이란 두 가지 정보를 알았을 때의 높은 수익률이 발생될 사후확률은 0.45에서 0.8907로 늘어났다.

이제 하나의 증거 E가 아닌 여러 개의 증거들로 규칙의 조건부가 이루어 졌을 경우를 생각해 보자. 이때의 사후확률은 다음과 같다.

P(H_i|E₁ ∩ E₂ .....∩ E_k)

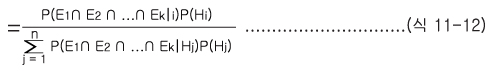
여기서P(E₁ ∩ E₂ ∩........∩ E_k|H_j)를 추정하여야 하는데, 바로 추정이 불가능 하다면 (식 11-2)에서 나온 확률의 곱셈법칙을 확장하면 다음을 얻을 수 있다.

P(H_i|E₁ ∩ E₂ ∩.....∩ E_k)

=P(E₁|E₂ ∩ .....∩ E_k ∩ H_j)P(E₂|E₃ ∩ ...∩ E_k ∩  H_j)...

P(E_k|H_j).......................................................(식 11-13)

그러나 위의 식을 이용하려면 증거들과 가설간의 조건부확률들을 다시 추정해야 한다. 이것은 상당히 복잡한 문제이다. 만약 증거 E_i를 간에 조건부독립 (Conditionally Imdependent) 관계가 유지된다면(식 11-13)은 다음과 같이 보다 간단하게 표현될 수 있다.

P(E₁ ∩ E₂ ∩.....∩ E_k |H_j)

=P(E₁|H_j)P(E₂|H_j)...P(E_k|H_j)...........................(식 11-14)

조건부독립이라는 것은 H_j를 알고 있는 상황에서 어떤 증거들을 관찰할 것이 그와 다른 증거의 관측에 아무런 영향을 미치지 못한다는 것을 의미한다. 그러나 조건부독립이라는 가정이 어느 분야에나 늘 해당되지는 않기 때문에 적용에 제한이 있다. 또한 조건부독립이라는 가정하에서도 하나의 새로운 증거 E_i가 추가되면P(E_i|H₁), ..... , P(E_i|Hn) 을 추가로 추정해야 한다. 따라서 규칙이 많다면 이에 포함된 증거와 가설의 수도 많다는 것이고 이에 따라 추정해야 할 요소들은 더욱 많아지게 된다.

이상과 같은 베이지안 접근법은 이론적으로는 잘 정리되어 있으나 실제로 적용할 경우 사전확률 P(H_i)와 조건부 확률 P(E_i|H_j)을 알고 있어야 하며, 각 증거들이 조건부독립을 만족하거나 또는 각 증거들 사이의 조건부확률을 알아야 한다. 따라서 이 접근법은 확률적 추정이 용이하거나 복잡하지 않은 영역의 문제해결에만 유용하게 사용될 수 있다.

3. 확신도 (Certainty Factor)

3.1 확률적 접근의 한계

IF E THEN H 라는 규칙에서 E라는 증거가 있음에도 H라는 결과가 100%나오지 않을 경우, 앞에서 확률적 방법론을 이용하여 이를 P(H|E) 라는 조건부확률로 표현할 수 있다고 하였다. 또한 이 조건부확률은 베이즈정리를 이용하여 다음과 같이 구할 수 있다.

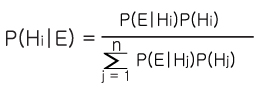
그러나 이러한 베이지안 접근법은 이론적으로는 매우 명확하나 실제 문제에 적용함에 있어 여러 가지 문제점이 발생될 수 있다.

첫째, 조건부확률 P(H_i|E) 를 알기 위해 사전확률 P(H_j)와, 조건부 확률 P(E|H_j)를 알아야 한다. 예를 들어, E가 환자의 몸에 나타나는 증상이고 H_i가 질병이라 하자. 어떤 증상 E가 있을 때 어떤 병 H_i일 확률 P(H_i|E) 를 알기 위해서는, 각 질병들의 사전확률  P(H_j) 와 질병 H_j임을 알고 있을 때 증상 E 가 나타날 확률 P(E|H_j)가 주어져야 하나 현실적으로 이들에 대한 데이터가 부족한 경우가 많다.

둘째, 위의 식에서 각 질병들 H_i 는 서로 배타적인, 즉 P(H_i∩H_j) =0 이어야 하나 어떤 환자의 경우두 세 가지의 질병이 동시에 나타날 수 있기 때문에 이러한 상호 배타적이어야 한다는 가정이 만족되지 않을 수 있다.

셋째, 새로운 증상들이 추가될 때  P(H_i|E₁ ∩ E₂ ∩....∩ E_n)을 구하기 위해서는 더욱 복잡한 증상들간의 조건부확률들이 주어져야 한다. 그리고 이를 간단히 하기 위한 증상들간의 조건부독립이라는 가정, 즉 P(E_i|E_j ∩ H_k) = P(E_i|H_k) 이 적용되지 않을 수 도 있다.

넷째, 확률의 정의상 ∑P(H_i) = 1 이어야 하는데, 새로운 질병이 추가된다면 이들 사전확률값과 또 이러한 새로운 질병과 관련된 각 증상들의 조건부확률값을 새로이 추가시켜야 하며, 따라서 기존의 규칙들과 관련된 조건부확률 값을 새로이 수정해야 하는 복잡한 과정을 거쳐야 한다.

다섯째, 확률값의 추정에 있어서 부족한 데이터 등으로 인해 사전적인 계산이나 사후적인 실험으로 여러 확률값을 구할 수 없는 경우 주관적 확률값을 추정할 수 있다. 이때 확률값은 전문가의 확신의 정도를 나타내게 된다. 그러나 이 경우에는 다음과 같은 문제가 발생할 수 있다. 세 가지 증상 E_{1 ,} E_{2 ,} E₃ 가 모두 사실일 때  H라는 질병이라는 것을 0.7 의 정도로 가능성이 있다고 어느 전문가가 제시했다고 하자. 이는 조건부확률로 표현하면 다음과 같다.

P(H|E1 ∩ E2 ∩ E3) = 0.7

여기서 0.7은 주관적 확률값이다. 그러나 그렇다고 해서 아래의 식과 같이 3가지 증상 모두 사실일 때 질병 H가 아닐 가능성에 대한 확신이 0.3이라고 이야기 할 수 있는 것은 아니다.

P(_ㄱH|E1 ∩ E2 ∩ E3) = 0.3

0.3이라는 것은 확률의 공리상 P(H|E) + P(_ㄱH|E) = 1이기 때문에 계산된 것이다. 따라서 이것이 성립되지 않는다는 것은 0.7이라는 값이 확률값이 아니라는 것을 의미한다. 위와 같은 공리가 성립되지 않는 이유는 0,7이라는 부분에 대해선 질병 H라고 확신하나 그렇다고 0.3만큼 질병 H가 아니라고 확신한다는 것은 아니기 떄문이다. 이것은 확신과 불신이 따로 취급되어야 함을 의미한다. 0.3 은 단지 모르는 (Unknown) 부분이다. "모른다"  또는 "무시한다" 는 것과 적극적으로 "부정 (Refute) 한다" 는 것은 다른 개념이다. 확률의 공리를 따른다면 0.7만큼 질병 H라고 확신해야 하고, 또 동시에 0.3만큼 질병 H가 아니라고 확신해야 한다. 만약 이렇게 확신과 불신이 동시에 존재한다면 차라리 확신의 강도를 낮추어 표현해야 될 것이다. 즉, 0.4만큼으로 확신을 줄여야 할 것이다. 만약 0.7로서 그대로 둔다면 나머지 0.3은 불신이 아니라 단지 생각할 수  없는, 또는 모르는 영역일 뿐이다.

3.2 확신도

확신도 (Certainty Factor) 는 앞 절에서 제기된 바와 같은 실제적인 문제를 해결하기 위한 확률적 접근방법의 대체안으로서 MYCIN을 개발하는 과정에서 Shortliffe 와 Buchanan[1975]가 고안한 방법이다. 이들은 엄청난 양의 확률 값 추정과 확률적 공리와 가정을 만족해야만 하는 확률이론이 실제 적용되기 어려운 문제에 있어, 비확률적이며 비정형적인 방법을 채택하였다. 비록 그것이 이론적으로는 떨어진다 해도 해당 영역의 전문가들이 오랫동안 사용해 온 그들의 판단과정을 잘 모형화할 수 있다면 보다 유용하지 않겠느냐는 것이다.

확신도는 확신의 정도 (Degree of Confirmation) 를 나타내며 다음과 같이 확신 (Belief) 과 불확신 (Disbelief) 의 차로써 표현된다.

CF(H,E) = MB(H,E) - MD(H,E)

여기서 CF 는 증거 E가 주어졌을 때 가설 H에 대한 확신도, MB는 E로 인한 H에 대한 증가된 확신의 정도 (Measure of Increased Belief), MD는 E로 인한 H에 대한 증가된 불확신의 정도 (Measure of Increased Disbelief)를 말한다.

확신도는 확신과 불확신을 결합하여 하나의 수로 표현하는 방법이다. 확신의 정도와 불확신의 정도는 다음의 화률형태로 표현될 수 있다.

위 식에서의 MB의 의미는 사전적으로 가설 H가 지지되지 않는 영역 1-P(H)와 증거 E를 통해 증가된 확신과의 비율이다. 또한 MD는 사전적으로 가설 H가 지지되는 영역 P(H) 와 E로 말미암아 줄어든 확신과의 비율이다. 위 식을 다시 쓰면,

가 된다. max[1,0]은 항상 1이고, min[1,0]은 항상 0이다. 위와 같이 쓴 것은 MB와 MD간의 대칭성을 보여 주기 위함이다.

각각의 범위는 다음과 같다.

0 ≤  MB ≤ 1

0 ≤  MD ≤  1

-1 ≤  CF ≤  1

CF는 주어진 어떤 증거로 인한 확신의 순증가도를 의미한다. CF>0이라는 것은 MB-MD>0으로써 주어진 증거는 가설에 대한 확신을 증가시켰고, CF=1이라는 것은 증거로 인해 가설이 명백히 증명되었다는 것이고, CF=0일 때는 두 가지 경우가 있는데 MB=MD=0인 경우, 어느 것도 확신할 수 없는 것이도, MB=MD>0인 경우는 확신이 불확신에 의해 상쇄되었다는 것이다. CF가 음의 값을 가진다는 것은 가설이 부정이라는 확신이 더 크다는 것이다.

CF =0.7이라는 것은 확신이 불확신보다 70%크다는 것이다. 결국 MB와 MD 각각의 값이 중요한 것이 아니라 이 둘의 차가 중요하다.

예를 들어 다음의 경우 모두 같은 CF값을 가진다.

CF = 0.7 = 0.7 - 0.0 = 0.8 - 0.1,......

또한 확신도 (Certainty Factor) 에서는 어떤 증거로 인해 가설을 CF(H,E)만큼 확신한다고 해서 그 가설의 불확신 정도가 1-CF(H,E)를 의미하지 않는다. 즉,

CF(H,E) + CF(_ㄱH,E) ≠ 1

이다. 이는 증거 E가 H에 대해 CF(H,E) 만큼 확신을 증가시켰다고 해서, 1-CF(H,E) 만큼 H가 아니라는 확신을, 즉 불신을 증가시켰다고 보지 않는다. 이것은 확률론에서의 공리와는 다른 면이다.

확신도에서는 다음 식이 성립한다.

CF(H,E) + CF(_ㄱH,E) = 0

위 식의 의미는 어떤 증거로 인해 가설 H의 확신도가 증가된 만큼 H가 부정이라는 것에 대한 확신은 그만큼 줄어든다는 것이다. 예를 들어, 어떤 학생이 학덤 A를 받음으로써 졸업에 대한 확신이 70% 증가하였다면 졸업을 못하리라는 것에세 대한 확신은 70%만큼 줄어든 것으로 생각할 수 있기 때문이다.

CF (H,E) = 0.7                       CF(_ㄱH,E) = -0.7

이제는 MB와 MD에 관한 성질을 알아보겠다.

(1) 절대적 확신과 절대적 불신

① 증거 E+로 인한 MB(H, E+) = 1이면 불신의 증거 E-가 어떠한 정도이든 MD(H,E-)=0이다. 따라서 CF(H,E+)=1이다.

② 증거 E-로 인한 MD(H, E-) = 1이면 확신의 증거 E+가 어떠한 정도이든 MB(H,E+)=0이다. 따라서 CF(H,E-) = -1이다.

③ MB(H,E+) = MD(H,E-) =1인 경우는 모순이고, 따라서 CF는 정의가 안된다.

(2) 연속적으로 추가되는 증거

①    

②

(3) 가설의 논리적(論理積, Conjunction)

MB(H₁ ∧ H₂, E) = min(MB(H₁, E), MB(H₂, E))

MD(H₁ ∧ H₂, E) = max(MD(H₁, E), MD(H₂, E))

(4) 가설의 논리합 (論理合, Disjunction)

MB(H₁ ∨ H₂, E) = max(MB(H₁, E), MB(H₂, E))

MD(H₁ ∨ H₂, E) = min(MD(H₁, E), MD(H₂, E))

지금까지는  E가 확실하다는 가정하의 CF(H,E) 만을 생각했다. 그러나 E에도 불확실성이 존재한다면 다시 말해 만약 E자체에 관한 확실성이 1이 아니라면 규칙 IF E THEN  B 의 확신도 CF(H,E)는 다음과 같이 CF(H,e) 로 대체되어야 한다.

CF(H,e) = CH(H,E)CH(E,e)

CF(E,e) 는 규칙의 조건인 증거 E의 확신도는 또 달리 관측된 전제증거인 e로 표현된다는 것을 보여 준다. 여기서 CF(E,e)=1 이라면 CF(H,E) 만으로 H의 증거 E로 인한 확신도가 표시된다. 위의 식을 다시 쓰면,

CF(H,e) = (MB(H,E) - MD(H,E)) •  max(0,CF(H,e)

여기서 max를 쓴 것은 CF(H,e)<0인 것은 모두 0으로 보겠다는 의미이다. 조건부를 구성하는 증거가 여러 개로 구성되어 있다고 하자. 다음과 같이 조건문이 세 개의 증거의 AND 결합형태인 규칙이 있다면,

IF  E₁  AND  E₂  AND  E₃  THEN  H

이때

CF(H,E) = CF(H,E₁ ∧ E₂ ∧ E₃) = 0.7

MB(E1,e) = 0.5, MD(E1,e) = 0, CF(E1,e) = 0.5

MB(E2,e) = 0.6, MD(E2,e) = 0, CF(E2,e) = 0.6

MB(E3,e) = 0.3, MD(E3,e) = 0, CF(E3,e) = 0.3

이라고 할 때,

CF(E,e) = CF(E1∧ E2 ∧ E3,e)

           =MB(E1∧ E2 ∧ E3,e) - MD(E1∧ E2 ∧ E3,e)

           =min(MB(E1,e), MB(E2,e), MB(E3,e)) -

             max(MD(E1,e), MD(E2,e), MD(E3,e))

          =min[ 0.5, 0.6, 0.3] -0

CF(H,e) = CF(E,e)CF(H,E)

           = 0.3 • 0.7

           = 0.21

또 다른 확신도 결합의 형태는 두 개의 규칙이 동일한 가설을 결론으로 할 때 나타난다. 이 두 개 규칙의 확신도를 각각 CF₁과 CF₂라고 하면 같은 가설을 결론으로 하는 이 두 개 규칙의 결합된 확신도는 다음과 같다.

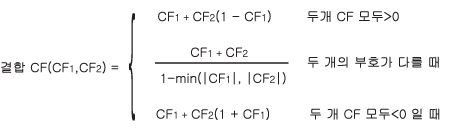
세 개 이상의 CF를 결합할 때는 먼저 두 개를 결합한 후 그 결과에 세 번째 CF를 결합하는 식으로 결합하면 된다. 예를 들어, 두 개의 CF가 각각 CF₁=0.21, CF₂ =0.5일 때 이 둘의 결합은,

결합 CF(CF1,CF2) = 0.21 + 0.5(1-0.21) = 0.605

이다. 또한 세 번재 규칙이 같은 가설을 결론으로 하되 CF₃ = -0.4라면

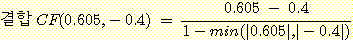
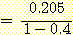
= 0.34

이다.

이제 확신도의 장단점에 대해 논해 보기로 하자, 확신도는 확률이론 (Probabillity Theory) 과 확신이론 (Confirmation Theory) 에 기본을 둔 임의적인 접근방법이다. 계산이 간단하고 쉽게 접근할 수 있어 MYCIN 외에도 여러 전문가시스템에서 채택하고 있다. 그러나 다음과 같은 경우 사후확률과는 상치되는 현상을 야기할 수 있다.

P(H₁) = 0.8                          P(H₂) = 0.2

P(H₁|E) = 0.9                      P(H₂|E) = 0.8

이라고 할 때, CF 의 정의에 의해 CF를 계산하면,

CF(H₁, E) = 0.5          CF(H₂, E) = 0.75

이다. 여기서 사후확률이 높은 쪽이 오히려 확신도는 떨어짐을 볼 수 있다. 이것은 확신도가 확신의 증가율(혹은 감소율)이지 절대적인 확신의 정도를 나타내는 것이 아니기 때문이다.

또한 "IF e THEN i" 와 "IF i THEN H" 라는 연쇄적인 규칙이 있을 때, 각각의 불확실성을 사후확률로 표현하였을 경우 일반적으로 다음과 같은 식이 성립한다.

P(H|e) ≠ P(H|i) • P(i|e)

이 식이 성립하는 것을 다음의 밴다이어그램을 통해 알 수 있다.

<그림 11-1> P(H|e) ≠ P(H|i)  P(i|e)의 밴다이어그림

위의 그림에서 P(H|i) > 0, P(i|e) > 0이나 P(H|e) = 0임을 알 수 있다. 그러나 불확실성을 확신도로 표현하였을 경우,

CF(H,e) = CF(H,i)CF(i,e)

로 계산된다. 이는 불확실성의 전파 (Propagation) 에 대한 계산은 쉬우나 추론의 경로가 긴 경우 최종결론에 대한 확신도의 값은 매우 낮아지는 현상이 발생할 수 있음을 의미한다.

3.3 VP-EXPERT에서의 확신도 계산

이제 제4장에서 다룬 VP-EXPERT에서의 확신도계산을 소개한다. VP-EXPERT에서의 확신도계산은 다음과 같다. 단, VP-EXPERT 는 표기상 백분율 척도를 사용하기 때문에 확신도100%는 1의 확신정도, 80%는 0.8의 확신정도로 해석된다.

① 단일 조건문

다음과 같이 IF문이 하나의 조건만으로 되어 있다고 하자.

RULE 8

IF Travel_Budget = Low

THEN Country = Taiwan CNF 80;

여기서 CNF 80이란 RULE 8의 확신도가 80%란 뜻이다. 확신도를 명시안하면 100%로 간주된다. Travel_Budget 이 Low 일 때 결론인 Country를 Taiwan이라고 선정한데 대한 확신도는 0.8이 된다. 조건문 자체에 대한 확신도는 줄 수 있다. 만약 사용자가 Travel_Budget = Low에 대한 확신도를 50이라고 주었으면 결론에 대한 확신도는 0.5 × 0.8 = 0.40가 된다. 즉, 40이라는 것이 Country가 Taiwan에 대한 확신도인 것이다.

② AND로 연결된 조건문

다음과 같은 규칙이 있다고 하자.

RULE 17

IF          Travel_Budget = High AND

            Mexico = Yes AND

            Preferred Climate = Tropical

THEN    Area = Yucatan CNF 70;

이와 같이 AND로 연결된 경우 조건 중 가장 낮은 (Min) 확신도를 규칙의 확신도와 곱하여 결론의 확신도로 삼는다. 예를 들어, 위 세 개 의 조건들에서 50, 75, 60으로 각각 High, Yes, Tropical에 대한 확신도가 결정되었다면 결론인 Area = Yucatan은 0.50 × 0.70 = 0.35인 확신도를 갖게 된다.

③ OR로 연결된 조건문

OR로 연결된 조건문은 각 조건문별로 분리시켜 결론에 대한 확신도를 구한 후 이를 다시 결합하는 방법으로 계산한다. 예를 들어 다음과 같은 규칙이 있다고 하자.

RULE 27

IF         Country = Japan OR

            Country = Taiwan

THEN    Airline = AsiaAir   CNF  80;

그리고 각 조건이 다음과 같은 확신도라 하자.

 Country = Japan      CNF  80

 Country = Taiwan    CNF   50

Airline=AisaAir에 대한 확신도는 먼저 첫 번째 조건에 의한 확신도 0.8 × 0.8 = 0.64와 두 번째 조건에 관한 확신도 0.50 × 0.80 = 0.40를 다음 공식을 적용한다.

CNF1 + CNF2-(CNF1 xCNF2) = 최종 CNF

이 공식에 의해 Airline=AisaAir에 대한 확신도는 다음과 같이 계산된다.

0.64 + 0.40-(0.64×0.40) = 0.78

4. Demster-Shafer 증거이론 (Theory of Evidence) 

Dempster-Shafer 증거이론 (이하 D-S 이론이라 칭함) 은 1967 년 Arthur Dempster 가 주창하여 1976 년 Glenn Shafer 가 발전시킨 것으로 이 이론에서는 확신의 정도가 구간으로 표현되고, P(H) 와 P(￢H) 는 더하여 반드시 1 이 될 필요가 없다. D-S 이론에서는 먼저, 확률이론에서와 같이 서로 배타적인 가설집합을 설정한다. 이를 환경 (Environment) 이라 한다. 환경은 관심이 되는 대상의 집합이다. 예를 들면 다음과 같이 환경 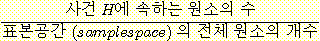를 설정할 수 있다.

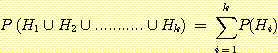= { 빨강, 초록, 파랑, 노랑, 검정 } ………………………… (식 1)

= { 아주 좋음, 좋음, 보통, 나쁨, 아주 나쁨 } ·…………… (식 2)

이들 예에서 볼 수 있는 바와 같이 환경을 구성하는 각 원소들은 서로 배타적이다. 즉, 빨강이 초록이 될 수는 없다. 환경 는 부분집합을 가질 수 있다. 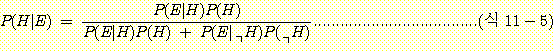가 위의 (식 1) 과 같다면 다음과 같은 것이 모두 부분집합들이다.

= { 아주 좋음, 좋음 }
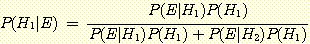= { 아주 좋음 }
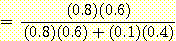= { 좋음, 보통, 나쁨 }
= = {  }
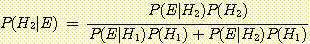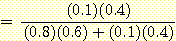= { 아주 좋음, 좋음, 보통, 나쁨, 아주 나쁨 }

각 부분집합은 하나의 질문에 대한 대답으로 해석될 수 있다. 즉, 어떤 사람의 성격이 어떠냐 라는 질문에 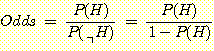과 같이 대답할 수도 있고, 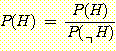와 같이 대답할 수도 있다. 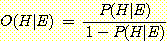와 같이 공집합인 경우는 대답이 없는 경우이다. 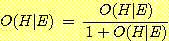의 각 원소가 가능한 대답이 될 수 있고, 오직 하나의 원소만이 대답이 될 수 있을 때 이러한 를 frame of discernment 라 한다. 여기에 discernment (분별) 이란 말을 쓴 것은 하나의 원소가 다른 원소와 분별되어 대답될 수 있다는 것이다. 즉, 어떤 사람의 성격에 대해 "좋음" 인지 "보통" 인지를 구별할 수 있어서 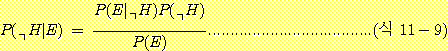이나 와 같은 대답을 하지 않는 것이다.

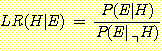가 n 개의 원소로 되어 있을 때, 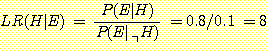의 부분집합은 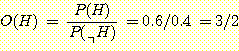와 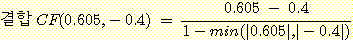자신을 포함하여 모두 2ⁿ 개이다. 이러한 2ⁿ 개의 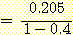의 모든 부분집합으로 구성된 집합을 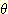의 power set 이라 하고 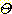라 표시한다. 하나의 증거 (Evidence) 는 이들 power set 의 특정 부분집합에 대한 믿음의 정도에 영향을 미칠 수 있다. 이러한 믿음의 정도를 0 에서 1 사이의 값으로 나타낸다. D-S 이론에서는 이렇게 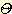의 원소에서 [0, 1] 로 사상시키는 함수를 기본확률배정함수 (Basic Probability Assignment : B.P.A) 라 하고 이를 m 으로 나타내며 다음과 같은 특징을 갖는다.

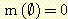
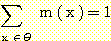
공집합에 대한 m 은 0 이고, 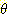의 power set 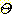의 모든 원소에 대한 m 값의 합은 1 이다. 여기서 m 값이 0 보다 큰 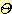의 부분집합을 관심원소 (Focal Element) 라 한다. 관심원소 S 에 대한 믿음 Bel (S) 는 다음과 같이 정의된다.

예를 들어, 어떤 증거를 보고 그 사람의 성격이 "아주 좋음" 과 "좋음" 에 대한 믿음이 생기면 S = { 아주 좋음, 좋음 } 이고, Bel(S) 는 { 아주 좋음 }, { 좋음 }, { 아주 좋음, 좋음 } 의 m 값을 모두 더한 값이 된다. 그런데 D-S 이론에서는 관심원소에 대한 믿음을 단순히 Bel 하나만으로 표현하지 않고 하나의 구간으로 표현하며, 이 구간을 evidential interval 이라 한다. 어떤 증거에 관심원소 S 에 대한 믿음의 구간에서 작은 쪽은 Bel(S) 값이 되고 큰 쪽은 S 의 개연성 (Plausibility) 으로서 Pls(S) 값이 되고 Pls(S) 는 다음과 같이 정의된다.

Pls(S) = 1 - Bel(￢S)

여기서 ￢S 는 S 의 여집합이다. 즉, S = { 좋음 } 이라고 했을 때, Bel(S) = 0.2 이고, Bel(￢S) = 0.3 이면 evidential interval 은 0.2 에서 0.7 이 된다. 여기서 0.2 는 적극적으로 확신하는 부분이고 0.3 은 적극적으로 불신하는 부분이므로, 0.7 은 불신하지는 않는 부분이 됨으로 개연성이 있다고 할 수 있는 정도를 나타낸다. evidential interval 은 구간의 범위에 따라 다음과 같은 의미가 있다.

D-S 이론은 확률이론과는 다르다. 예를 들어, 어떤 사람의 성격이 "좋음" 에 대한 m 값을 0.7 이라고 하자.

m({좋음}) = 0.7

그렇다면 나머지 0.3 은 어떠한 의미를 가지는가? 확률이론이었다면 0.3 은 그 사람이 좋지 않다, 즉 ￢좋다 또는 NOT (좋다) 에 대한 믿음의 정도 (주관적 확률추정에 근거하여) 를 표현한 것이다. 확률이론에서는 이렇게 두 가지 상반된 가설에 대한 믿음이 동시에 존재하는 것으로 보는데 반하여, D-S 이론에서는 특별히 NOT (좋다) 라는 가설이 설정되어 여기에 대한 믿음이 적극적으로 표현되어 있지 않다면, 0.3 이란 부분은 아는 바 없는, 확신도 불신도 아닌 아무런 믿음이 형성되어 있지 않은 영역으로 인식한다. 이렇게 아무런 믿음이 형성되지 않은 영역에 있어서는 다음과 같이 환경 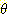에 m 값 0.3 을 할당하는 방식으로 표현된다.

m({ 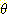}) = 0.3

이외에도 D-S 이론이 확률이론과 다른 점은 m( 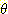) = 1 을 꼭 만족할 필요가 없다는 것이다. 예를 들어, 앞에서 (식 2) 의 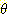에 대해 m({ 아주 좋음, 좋음, 보통, 나쁨, 아주 나쁨 }) = 1 이 될 필요가 없다. 즉, 어떤 사람의 성격에 대해 다섯 가지로 분류하여서 이 중 어디에 속하는지에 대한 믿음의 정도의 합이 꼭 1 이 될 필요가 없다는 것이다. 이는 확률이론에서는 가설집합 {H₁, …, H_n} 이 있을 때, ΣP(H_i) = 1 이 되는 것과는 다른 점이다.

또한 확률이론에서는 가설이 발생할 확률에 대해 아무런 정보가 없을 때, 똑같은 확률값을 부여하게 된다. 예를 들어 이름도, 국적도, 얼굴도 모르는 어떤 외국인 (주어진 정보는 그 어떤 사람이 단지 외국인이라는 것임) 에 대한 성격이 어떨지에 대해선 다음과 같이 확률값을 줄 수밖에 없다.

P(아주 좋음) = 1/5
P(좋음) = 1/5
P(보통) = 1/5
P(나쁨) = 1/5
P(아주 나쁨) = 1/5

이는 1 이라는 전체확률값을 각각의 가설에 동등하게 배분하기 때문이다. 그러나 D-S 이론에서는 믿음이 발생한 곳에만 m 값을 부여하지 나머지에 대해선 m 값을 전혀 부여하지 않아도 된다. 즉, 전혀 아무런 믿음이 생기지 않은 가설에도 1/5 씩이나 m 값을 부여할 필요는 없다는 것이다. 만약 확률의 이론대로 한다면 어떤 지역을 시추할 때, 유전이 존재할지 않할지에 해서 아무런 정보가 없다면, 유전이 존재한다와 존재하지 않는다에 각각 1/2 씩의 확률을 부여할 것이다. 그러나 유전이 존재할 확률이 1/2 정도라면 사실 엄청난 확률이며 충분히 시추작업을 개시할 가치가 있는 확률이다. 이러한 오해는 여기서의 1/2 이라는 값은 서로 반대되는 가설인 "나온다" 와 "안나온다" 에 동등하게 준, 즉 서로 상쇄되어버리는 확률이지 적극적인 의미에서의 1/2 과는 그 의미가 전혀 다르다라는 것이 명확히 드러나지 않았기 때문이다. D-S 이론에서는 믿음이 발생한 가설에 대해서만 적극적인 의미의 m 값을 할당하고 그렇지 않은 부분에 대해선 억지로 값을 할당하지 않는다. 그리고 할당된 값의 합이 1 이 안되면 나머지 부분은 환경 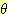에 할당함으로써 아무런 믿음이 없는, 또는 아는바 없는 부분으로 든다.

이상과 같은 확률이론과 D-S 이론의 상이점을 다음표로 정리해 볼 수 있다.

이제는 서로 다른 m 값들을 결합하는 과정에 대해 살펴보겠다. 만약 같은 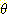에 대해서도 서로 다른 m 값이 형성되어 있다면 이들을 결합할 필요가 있다. 예를 들어, 특정 인물의 성격에 대해 어떤 증거를 통해 값이라는 사람은 다음과 같은 m 값을 주었다고 하자.

m₁({ 아주 좋음, 좋음 }) = 0.70
m₁({ 보통, 나쁨, 아주 나쁨 }) = 0.10
m₁({ 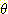}) = 0.20

여기서 m₁({ 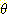}) = 0.20 는 믿음이 형성되지 않은 부분이다. 그런데 또 다른 증거에 의해 을이라는 사람은 다음과 같은 m 값을 주었다.

m₂({ 아주 좋음 }) = 0.80
m₂({ 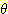}) = 0.20

이들 두 가지 증거들로 인한 믿음의 결합연산 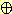은 다음의 공식으로 결정된다.

m₁ 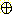m₂ (Z) = Σm₁(X) m₂ (Y)
                   X ∩ Y = Z

여기서 각 X, Y 에 대해 공통된 부분 Z 만이 새로운 믿음의 값을 부여받게 된다. 앞의 예에서의 결합결과는 다음과 같다.

두 개의 집합의 결합에서 아무런 공통원소가 없으면 공집합이 m 값들의 곱의 결과를 받게 된다. 또한 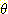와의 교집합은 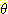와 결합되는 집합자체가 된다. 위의 예로부터 결합된 m 값들을 정리하면 다음과 같다.

m₃ ({ 아주 좋음 }) = m₁ 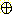m₂ ({ 아주 좋음 }) = 0.56 + 0.16 = 0.72
m₃ ({ 아주 좋음, 좋음 }) = m₁ 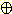m₂ ({ 아주 좋음, 좋음 }) = 0.14
m₃ ({ 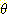}) = m₁ 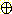m₂ ({ 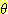}) = 0.04
m₃ ({ 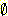}) = m₁ 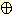m₂ ({ 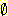}) = 0.08

그런데 여기서 문제가 되는 것은 공집합이 0 이 아닌 m 값을 가지고 있다는 것이다. 이를 해결하기 위해서는 강제로 공집합의 m 값을 0 으로 만들고, 나머지 관심원소의 m 값에 대해서 공집합이 가졌었던 m 값에 비례하여 증폭시키는 의미에서 1 - m ({ 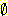}) 으로 나누어 주어야 한다. 이러한 과정을 정규화라고 한다. 다음은 이러한 정규화과정을 거친 후의 결과이다.

m₃ ({ 아주 좋음 }) = 0.72 [ 1 / (1 - 0.08) ] = 0.783
m₃ ({ 아주 좋음, 좋음 }) = 0.14 [ 1 / (1 - 0.08) ] = 0.152
m₃ ({ 보통, 나쁨, 아주 나쁨 }) = 0.02 [ 1 / (1 - 0.08) ] = 0.022
m₃ ({ 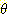}) = m₁ 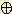m₂ ({ 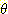}) = 0.04 [ 1 / (1 - 0.08) ] = 0.043

위의 결과로부터 S = { 아주 좋음, 좋음 } 의 evidential interval 을 구해보자. 먼저,

Bel({ 아주 좋음, 좋음 }) = 0.783 + 0.152 = 0.935

또한 Pls 는 다음과 같다.

Pls({ 아주 좋음, 좋음 }) = 1 - Bel(￢{ 아주 좋음, 좋음 }) = 1 - 0.022 = 0.978

따라서 evidential interval 은 [0.935, 0.978] 이 된다.

이제 D-S 이론의 특징과 장단점을 정리해 보자. D-S 이론에서는 환경을 구성하는 n 개의 가설이 상호 배타적이라고 가정하고, 이중 기본확률할당값 m 이 0 보다 큰 것에 해당하는 집단을 관심원소라 하였다. 아는바 없는 영역의 값은 환경에 할당하여 어떤 증거로 인해 가설이 지지되고 남은 값을 굳이 해당 가설의 부정에 대한 지지값으로 할당할 필요가 없게 하였다. 그러나 D-S 이론에서 가장 문제가 되는 것은 m 값들을 정규화하는 방법의 임의적 성격인데 다음 예와 같은 경우 그 결과가 우리의 직관과 위배된다.

먼저 어떤 사람에 대한 성격을 다른 두 사람이 판단하여 다음과 같은 m 값들을 주었다고 하자.

m₁({ 매우 좋다 }) = 0.99
m₁({ 나쁘다 }) = 0.01
m₂({ 좋다 }) = 0.99
m₂({ 나쁘다 }) = 0.01

둘다 나쁘다라는 평가는 극히 미미하고 좋다와 매우 좋다의 비중이 크므로 둘의 의견을 결합하더라도 좋다 쪽이어야 할 것이다. 이 둘의 의견을 결합한 결과는 다음과 같다.

m₃(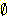) = 0.9999 이므로 정규화를 거치면 m₃({ 나쁘다 }) = 1.0 이 된다. 즉, 이 두 사람의 의견을 합치니 100 % 나쁘다라는 결과가 나왔다. 이같은 결과가 나온 것은 공통집합의 상당부분이 공집합이고 오직 { 나쁘다 } 만이 유일한 공통집합이므로 정규화 이후 이 부분에 매우 높은 m 값이 할당되었기 때문이다. 이것은 가설들의 집합을 어떻게 설정할 것인지가 D-S 이론에서 매우 중요하다는 것을 말해준다.

5. 퍼지 집합과 퍼지 논리

명제논리는 오직 참과 거짓이라는 두 개의 값만을 다룬다. 그러나 실제는 참과 거짓으로 명확히 확정지을 수 없는 경우가 많다. 한편으로는 참이면서도 또한 거짓일 수 가 있다. 예를 들어, 어느 고객의 신용이 좋다라고 했을 때 만약 신용평가에 불확실성이 내재되어 있다면 신용이 좋다 • 아니다라고 단정적으로 말하기 힘들다. 또한 신용평가에 점수제를 도입해 71점에서 100점 만점까지를 신용이 우수하다고 하자. 그렇다면 70점을 맞은 고객은 신용이 우수하지 않다고 할 것인가? 또한 고객평가에서 순자산이 4000만원 이상을 적당하다고 볼 때 3999만 9천원은 적당치 못한 자산규모라고 할 것인가? 그 외에 키가 크다, 날씨가 덥다, 시험이 어렵다 등 자연어의 표현에 그 뜻이 애매한 경우가 많다. 앞의 1절에서 불확실성의 원천에서 언급하였던 지식 표현의 애매성을 해결할 방법이 필요하다. 이러한 문제인식을 토대로 1965년 Zadeh에 의해 퍼지집합에 관한 이론이 처음 제시되어 퍼지명제나 규칙을 다루기 위한 퍼지논리로 발전해 왔다.

5.1 퍼지집합이론

기존의 집합이론에 의하면 집합과 집합과의 구분이나, 어떤 원소가 집합에 속하는지의 여부가 단정적이다. 즉, 속하든지 그렇지 않다면 속하지 않은 것이다. 이것을 소속함수 (Membership Function) 로 표현하면 다음과 같다.

이 소속함수는 전체 집합 X의 원소를 {0, 1}로 대응시킨다. 그러나 퍼지집합에서는 어떤 원소가 집합에 속하는지 속하지 않는지를 단정적으로 다루지 않는다. 대신 원소가 집합에 속하는 정도에 따라 소속함수값 μ_A(x)를 0과 1사이의 임의의 값으로 대응시킨다.

예를 들어 "충분한 수입" 이라는 집합을 생각해 보자. 월 200만원은 "충분한 수입" 이라는 집합에 소속값 1로 속하고 월 160만원은 0.75로 속한다고 할 수 있다. 이를 다음과 같이 소속함수값과 수입액의 쌍으로 된 집합으로 나타낼 수 있다. 우리는 이를 퍼지집합이라 부른다.

충분한 수입 ={ 0/40만원, .125/80만원, .50/120만원, .875/140만원, 1/160만원}

여기서 "/" 표시는 나눗셈표시가 아니라 수입액과 그의 소속함수값을 분리시키는 표시이다.

이것을 그래프로 그리면 다음과 같은 S자형 그래프를 그릴 수 있다.

<그림 11-2> "충분한 수입"이란 퍼지집합의 소속함수

또 다른 예로 성적을 수, 우, 미, 양, 가로 분류한다고 하자. 여기서 "미"라고 하는 퍼지집합을 다음과 같이 표시할 수 있다.

미 = { 0/50점, .25/60점, .75/65점, 1/70점, 1/80점, .75/85점, .25/90점, 0/100점}

그래프로 나타내면 다음과 같은 종 모양이 된다.

<그림 11-3> "미" 라고 하는 퍼지집합의 소속함수

퍼지집합이론에서도 _ㄱ( NOT), ∧(AND), ∨(OR) 등의 논리연산자를 사용할 수 있다. 이들은 각각 퍼지 여집합, 퍼지 교집합, 퍼지 합집합 연산으로 불리우기도 한다. 먼저 A의 여집합에 대한 원소의 소속합수값은 μ_ㄱA(x) = 1 - μ_A(x)로 정의된다.

<그림 11-4> 여집합의 소속함수의 예

다음의 예를 보자.

_ㄱ충분한 수입 = {1/40만원, .875/80만원, .50/120만원, .25/160만원, 0/200만원}

여기서 120만원은 충분한 수입에도 속하고, NOT(충분한 수입)에도 균등히 속할 수 있다는것을 알 수 있다. 이것은 퍼지집합의 독특하면서도 중요한 특성이다. 즉, 서로 반대되는 성격을 동시에 만족하는 영역을 인정하는 것이다. 200만원은 NOT(충분한 수입)에는 속하지 않음을 알 수 있다.

한편 AND 연산자는 두 개의 집합에서 공통된 원소의 소속함수값 중에서 작은 값을 선택한다.

μ_A  ∧  μ_B(x) = [ μ_A(x), μ_B(x)]

만약 낮은 수입의 집합이 다음과 같으면,

낮은 수입 = {1/40만원, .95/80만원 .80/120만원, .30/160만원, .05/200만원 }

_ㄱ충분한 수입 ∧ 낮은 수입 = { 1/40만원, .875/80만원 .50/120만원, .25/160만원, 0/200만원 }

OR 연산자는 두 개의 집합의 모든 원소를 취하고 각 원소의 소속함수값은 두 개의 소속함수값 중 큰 값을 선택한다.

μ_A ∨ μ_B(x) = max[ μ_A(x), μ_B(x)]

_ㄱ충분한 수입 ∨ 낮은 수입 = { 1/40만원, .95/80만원 .80/120만원, .30/160만원, 05/200만원 }

이외에도 다른 특수 연산자들이 있다.

집중화 (Concentration) 연산자 CON은 소속함수값에 제곱을 취함으로써 1이외의 값을 보다 낮추는 효과를 준다. 이는 기존의 집합에서 "매우"라는 수식어를 첨가시킬 때 사용된다.

μ_con(A)(x) = ( μ_A(x) )²

예로써 다음과 같이 "키가 크다" 라는 집합이 있을 때 "키가 매우 크다" 라는 집합은 이들 소속함수값에 제곱을 취한 집중화로써 구할 수 있다.

키가 크다 = { .125/150㎝, .5/160㎝, .875/170㎝, 1/180㎝, 1/190㎝ }

키가 매우 크다 = { .016/150㎝ , .25/160㎝ , .765/170㎝ , 1/180㎝ , 1/190㎝ }

집중화의 반대연산자로 팽창 (Dilation) 이라는 연산자 DIL은 소속함수값에 0.5승(제곱근)을 취함으로써 1이외의 값을 보다 증가시키는 효과를 준다. 이는 기존의 집합에서 "약간" 또는 "어느 정도" 라는 수식어를 첨가시킬 때 사용된다.

μ_DIL(A)(x) = ( μ(x) )^0.5

위에서 살펴본 "키가 크다" 라는 집합으로부터 "키가 약간 크다" 라는 집합을 DIL연산을 사용하여 다음과 같이 도출해 낼 수 있다.

키가 약간 크다 = { .353/150㎝, .707/160㎝ .935/170㎝, 1/180㎝, 1/190㎝ }

5.2  퍼지관계

이제는 두 개 이상의 집합의 원소간의 관계에 대해 살펴보자. 관계라고 하는 것은 집합 A, B가 있을 때 x ∈ A, y ∈ B 이면(x, y) 의 모임으로 볼 수 있다. 예를 들어, 두 학급이 있는데 각 학급은 3명의 학생들로 구성되어 있다고 하자. 즉, A라는 학급에는 {a, b, c} 라는 3명의 학생이 있고, B라는 학급에는 {d, e, f} 라는 학생들로 구성되어 있다고 하자. 이 중 두 학급 구성원간에 친구라는 관계를 만족하는 것은 {(a, d),(c, f)} 라면 이 집합은 친구라는 관계집합이 된다. 물론 A, B라는 두 개의 집합으로 구성된 이항관계 (Binary Relation) 에 반드시 국한시킬 필요는 없다. 세 개 이상의 집합간의 관계가 이루어질 수 있고, 또한 동일한 집합간의 관계일 수도 있다. 위의 예에서 A와 B가 동일한 집합이라면 같은 반에서의 친구관계를 알고 싶을 경우일 것이다. 앞 절에서 일반적인 집합을 소속함수로써 표시할 수 있었듯이 관계 R도 다음과 같은 소속함수 μ_R 로써 나타낼 수 있다.

소속함수  μ_R(x, y) 는 두 개의 집합 A, B로부터 형성되는 곱집합 (Cartisian Product) A × B로부터 {0, 1} 로 대응시킨다. 즉, 위의 예에서 A × B = {(a, b), (a, e), (a, f), (b, d), (b, e), (b, f), (c, d), (c, e), (c, f)} 의 각 원소인 순서쌍이 관계 R = {(a, d), (c, f)}에 속하면 1, 아니면 0인 소속함수값을 갖게 된다. 그런데 퍼지관계에서는 순서쌍 (x, y)가 R에 소속되는 정도를 0에서 1사이의 값으로 표현한다. 즉, 보통의 관계에서의 소속함수는,

  μ_R : A × B → {0,1}

이나 퍼지관계에서의 소속함수는,

  μ_R : A × B → [0,1]

이다. 그리고 특별히 퍼지관계에서의 값은 소속의 정도라기보다는 관계의 강도라고 해석할 수 있다. 위의 예에서  μ_R(a, d) = 1.0, μ_R(c, f) = 0.7이라고 하면 a와 d는 완전한 친구 사이이나 c와 f는 친구이기는 하지만 a, d사이보다는 약한 친구관계이다. 이러한 퍼지관계는 다음과 같은 퍼지관계행렬로 나타 낼 수 있다.

<그림 11-5> 퍼지관계행렬의 예

5.3 퍼지논리

고전논리에서는 논리식 (Logic Formula) 의 값으로 0 또는 1의 값만 취할 수 있다. 그러나 퍼지논리에서는 논리식의 값이 구간 [0,1] 사이의 값을 가질 수 있도록 확장된 퍼지수식 (Fuzzy Expression) 을 다룬다. 퍼지논리는 명제의 진위가 명확히지 않은 경우의 근사추론 (Approximate Reasoning) 에 사용될 수 있다. 퍼지논리에서는 명제의 진리값이 0과 1사이의 값을 갖는다. 명제는 참과 거짓이라 불리우는 집합에 속하는 정도를 나타내는 소속함수값으로 진위를 표현한다.

즉, "갑은 충분한 수입이 있다' 는 명제는 참 집합에의 소속함수 값을 0.8가질 수 있는데, 이를 참값 (Truth Value) 이라고도 한다. 그런데 이 참값을 다른 각도로 다음과 같이 해석할 수도 있다. 즉, "충분한 수입" 이란 퍼지집합의 소속함수가 바로 이 명제의 참값을 결정한다고 할 수 있다. 즉, 퍼지명제의 형태가 "x  is  F" 일 때, x의 성질을 나타내는 F가 퍼지집합이면 이 명제를 퍼지술어 (Fuzzy Predicate) 라 하고, 이 퍼지집합 F의 소속함수값이 μ_F(x) 이면 이는 객체 x가 성질 F를 만족하는 정도라고 해석할 수 있어 이 명제의 참값= μ_F(x)라고 할 수 있다.

예를 들어, 명제 A와 B가 있으며, 이들이 각각 참값  μ(A),  μ(B)를 갖는다고 할 때 다음식이 성립한다.

 μ(_ㄱA) = 1-μ(A)

 μ(A ∧ B) = min[ μ(A),  μ(B) ]

 μ(A ∨ B) = max[ μ(A),  μ(B) ]

 μ(A → B) = μ(_ㄱA ∨ B) = min[1, 1- μ(A)  +  μ(B) ]

고전논리에서는 A ∧ㄱA = 0이고  A ∨ㄱA = 1이나 퍼지논리에서는 이러한 관계가 성립되지 않는다.

A의 참값이 (0, 1) 사이의 값을 갖는 명제라면,

① μ( A ∧_ㄱA) = min( μ(A), μ(_ㄱA) ) = min( μ (A),  1- μ(A) )

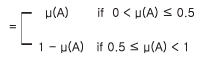
∴ 0 < μ( A ∧_ㄱA) ≤ 0.5

따라서 μ( A ∧_ㄱA) ≠ 0

② μ( A ∨_ㄱA)  = max ( μ(A), μ(_ㄱA) ) =max( μ (A),  1- μ(A) )

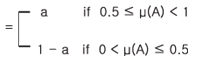
∴ 0.5 ≤ μ( A ∨_ㄱA) < 1

따라서 μ( A ∨_ㄱA) ≠ 1

이제 퍼지논리를 이용한 근사추론의 과정을 살펴보자. 고전논리에 바탕을 둔  modus ponens 에서는 if A then B 라는 규칙이 있으면 이를 수행하기 위해서 반드시 이 규칙의 조건부에있는 명제 A와 완전히 동일한 명제가 사실 (Fact) 로서 존재해야 하며 또한 A 나 B의 진리값은 0이나 1이 되어야 한다. 그러나 이에 반해 Zadeh가 제시한 일반화된 modus ponens 에 의하면 다음과 같은 인간의 인지적 추론 과정에 부합하는 추론을 하고자 한다.

규칙 : 키가 큰 사람은 몸무게가 무겁다.

사실 : 철 수는 키가 약간 크다

새로운 사실 : 철 수는 몸무게가 약간 무겁다.

이는 "키가크다" 와 같은 퍼지술어를 다루고 있는데, 규칙의 조건부와 완전히 동일하지 않은 사실이 주어지더라도 자연스럽게 추론을 가능케 한다. 그러나 이를 위해서는 약간의 복잡한 과정을 거쳐야 한다. 먼저 자연어로 표현된 규칙과 사실로부터 주목변수 (Focal Variable) 의 가능성분포 (Possibility Distribution) 를 구하고, 이를 추론 규칙을 이용해 결론의 가능성 분포를 구한 다음, 이를 다시 언어근사 (Linguistic Approximation) 를 이용해 자연어로 표현된 새로운 사실을 도출해 낸다. 여기서 먼저 주목변수 (Focal Variable) 란 지식베이스에서 주목하고 있는 객체를 말하는데 위의 예에서는 '키' 나 '몸무게'를 말한다. 여기에 주목변수가 취할 수 있는 값인 크다, 무겁다와 같은 언어변수 (Linguistic Variable) 가 결합되어 위의 문자을 형성하고 있다.

따라서 이를 바탕으로 위의 문장을 다시 표현하면 다음과 같다.

키가 큰 사람은 몸무게가 무겁다 → If  X  is  F  then  Y  is  G

여기서

X = 키(사람)

F = 크다

Y = 몸무게(사람)

G = 무겁다

철 수는 키가 약간 크다 → X  is  F^*

여기서

X = 키(철수)

F^* = 약간 크다

철수는 몸무게가 약간 무겁다 → Y  is G^*

여기서

Y = 몸무게 (철수)

G^*= 약간 무겁다

여기서 F, G등은 주목변수에 제약적 역할을 하는 퍼지집합이다. 여기서 제약이라는 것은 주목변수의 분포 중에 퍼지집합 G로 표현된 제약을 만족하는 정도에 따라 위 문장의 참값이 결정된다는 것을 의미한다. 위의 문장을 주목변수와 언어변수를 이용하여 다시 쓰면 다음과 같다.

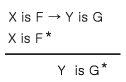
여기서 X가 퍼지집합 F에 속하는 정도인 μ_F(x)의 X에 대한 분포를 가능성분포 (Possibility Distribution) Π_x = F라 하자. 이는 X가 퍼지집합 F를 만족하는 가능성의 정도를 나타낸다. 예를 들어, 키가 180cm 가 '크가' 라는 퍼지집합에 속할 소속합수값이 1이라면, 이는 다시 말해 X = 180cm 일 때 '크다' 라는 퍼지집합이라고 할 가능성이 1이라는 것이다. 즉,

π_x (u) = Poss{X = u} = μ_F(u)

가능성이란 확률과는 다른 개념이다. 예를 들어, "철 수는 아침에 X개의 계란을 먹는다" X = {1,2, ....} 라는 문장이있다. 여기서 철 수가 먹는 계란의 개수 X의 가능성분포 Π_x(u) 와 확률분포 P_x(u)를 다음과 같이 나타낼 수 있다.

가능성분포는 철 수가 쉽게 먹을 수 있는 계란 개수를 표현한 것으로 한 개에서 네 개까지는 쉽게 가능하며, 어떤 경우는 다섯 개까지 가능하나 그 가능 정도(쉬운 정도)는 1보다는 작고, 여덟 개까지도 가능하나 그 가능성, 즉 쉬운 정도 (degree of ease) 는 더욱 작아진다. 반면에 확률분포는 실제로 어느 기간(예를 들어 100일간) 동안 철 수가 아침에 먹은 계란의 개수의 분포를 구한 것으로 실제로 철 수는 네 개 이상 먹은 적은 없다는 것이 위 표에서 나타난다. 위의 표에서 나타나듯이 가능성분포는 확률분포처럼 합이 1일 필요가 없다. 그리고 가능성이 높다고 반드시 확률이 높은 것은 아니나 가능성이 낮으면 확률 또한 낮음을 알 수 있다. 이제 이러한 위의 예에 대한 가능성분포를 구한다. 이를 다음과 같이 나타내자.

X  is 크다  → Π_x = 크다

Y  is 무겁다 → Π_x =무겁다

if  X  is 크다 then Y  is 무겁다  → Π_(Y|X)  = H

여기서  Π_(Y|X)는 X가 주어졌을 때 Y의 조건부 가능성분포 (Conditional Possibility Distribution) 이고 H는 다음과 같이 F와 G로써 정의된다.

 μ_H(u,v) = 1∧ ( 1-  μ_F(u) +  μ_G(v))

여기서 u와 v는 각 X와 Y가 취할 수 있는 값 중의 하나이며,  μ_H : UxV →[0,1]은 H의 소속함수이고 U와 V는 각기 X와 Y가 취할 수 있는 전체집합이다. 또한 μ _F : U → [0,1]과 μ_G : V →[0,1]은 각기 F와 G의 소속함수 값이다. 따라서 다음과 같은 식이 성립한다.

π_(Y|X)(u,v) = Poss{Y = v| X = u}

= 1 ∧( 1- μ_F(u) + μ_G(v))..................................................(식 11-17)

이제 명제 p₁과 p₂를 다음과 같이 정의한다.

p₁ = If  X  if   F  then  Y   is   G

p₂ = X  is  F^*

여기서 F, G, F^*는 모두 퍼지집합이다. 앞에서 보인 가능성분포로 각 명제를 나타내면,

p₁ → Π_(Y|X) = H

p₂ → Π_X = F^*

이러한 사실과 규칙의 결합을 통한 추론의 결과 Y의 가능성분포는 다음과 같이 도출된다.

Π_Y = H • F^*

이를 다시 표현하면 다음과 같다.

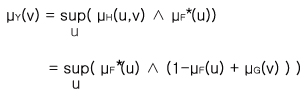
이렇게 하여 결론은 다음과 같이 유도된다.

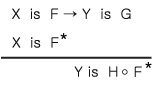
이러한 과정을 일반화된 modus ponens라 한다.

이제 마지막으로 이와 같이 추론된 가능성분포로부터 가장 유사한 표현용어를 찾아내는 언어근사 (Linguistic Approximation)를 통해 결론을 자연어로 표현하게 되면 근사추론이 완성된다.

이제 F(키가 크다)와 G(몸무게가 무겁다)의 가능성분포가 다음과 같다고 하자.

F = { 0.125/150cm, 0.5/160cm, 0.875/170cm, 1.0/180cm, 1.0/190cm }

G = { 0.1/40Kg, 0.3/50Kg, 0.9/70Kg, 1.0/80Kg }

또한 X   is (키가) 크다 →  Y   is (몸무게가) 무겁다라는 규칙이 있다고 하자. 이의 조건부 가능성분포 π_(Y|X)(u,v) = 1 ∧( 1- μ_F(u) + μ_G(v))는 다음과 같다.

여기서 F^* (키가 약간 크다)의 가능성 분포를 위 F의 가능성 분포에 각기 제곱근을 취하여 다음과 같이 산출하였다.

F^* = { 0.353/150cm, 0.707/160cm, 0.935/170cm, 1.0/180cm, 1.0/190cm }

여기서 μ_F^*(u) ∧ (1 - μ_F(u) + μ_G(v))를 구하면 다음과 같다.

 최종적으로 를 구하면 다음과 같다.

G^* = { 0.6/40kg, 0.707/50kg, 0.825/60kg, 0.9/70kg, 1.0/80kg }

6. 맺음말

지금까지 지식의 불확실성을 표현하는 여러 가지 방법을 살펴보았다. 가장 고전적인 방법은 확률적 접근법이다. 확률적 접근법은 사건의 발생이 아주 빈번하여 사전확률이나 조건부확률 등의 값이 충분히 추정되어 있을 경우 유용하게 사용할 수 있다. 그러나 데이터의 부족 때문에 주관적으로 확률값을 추정할 수밖에 없다면 확률적 접근법의 제반 공리와 가정이 지켜지지 않을 수 있다.

이를 보완하기 위해 다소 인위적이지만 보다 현실적인 확신도접근법을 사용할 수 있다. 확신도는 믿음의 정도를 긍정과 부정으로 나누어 이의 합성으로 확신의 정도를 나타낸다. 이는 현재 규칙형태로 표현된 지식의 불확실성 표현에 널리 사용되고 있다.

이러한 확신도방법은 하나의 숫자로서 불확실성을 표현하는데 비해 구간 개념으로 불확실성을 표현하고자 하는 것이 Dempster-Shafer증거이론이다. D-S이론은 확률론의 공리에 제한되지 않고 주관적인 믿음의 정도뿐만 아니라 개연성의 정도까지 포함한 구간으로 불확실성을 나타내고자 한다. 그러나 지식에 사용되는 술어를 모두 독립된 형태로 받아들임으로 인해 술어 중에 정도의 차이만 있지 같은 부류에 속하는 술어(예를 들면 좋다, 약간 좋다, 매우 좋다 등) 조차도 독립적으로 처리하고 있다.

지식의 불완전성으로 인한 불확실성과 지식에 사용되는  술어-크다, 아름답다 등- 자체의 애매함으로 인한 불확실성은 구별되어야 한다. 이를 위해서 퍼지집합이론이 사용될 수 있다. 퍼지집합이론에서는 지식으로 표현되는 각종 술어를 퍼지집합으로 인식하고, 주목변수값이 이 퍼지집합에 속하는 정도를 소속함수로서 나타낸다. 그러나 퍼지집합은 용어상의 애매함을 주목변수가 언어변수에 소속되는 정도의 분포형태로 표현함으로 인해 지식자체의 불확실성을 표현하는 것은 더욱 어렵게 된다. 왜냐하면 지식자체의 불확실성은 두 언어변수의 조건부 가능성분포로써 표현되기 때문이다.

이러한 불확실성의 표현문제는 전문가시스템의구현에 있어 어려운 문제로 사용자들에게 여겨지고 있다. 사용자들에게는 조건부 확률 0.7, 확신도 0.7, evidential interval [0.5, 0.7] 이나 소속함수를 정확히 이해하고 추정하여 사용한다는 것이 매우 부담이 되는 것이다. 사용자들에게 가장 이해되기 쉬운 방법은 자연어로서 지식을 표현하는 것이데, 이런 관점에서 본다면 퍼지집합론적 접근이 이러한 요구에 가장 근접하는 것으로 볼 수 있다. 왜나하면 확률적 접근이나 확신도, D-S이론이 명시적으로 각종 추정치를 숫자로 나타내야 하는데 비해 퍼지집합이론은 이러한 추정치를 분포형태로 나타내고 이러한 분포는 삼각형, 종형, S자 형태 중 우리의 직관에 적합하다고 판단되는 것을 선택하여 사용하면 되기 때문이다.

불확실성의 표현 방법은 결국 문제의 성격에 따라 달리 채택되어야 할 것이다. 즉, 매우 정확성을 요하는 문제의 경우에는 확률론적 표현법을 채택하고, 반면 자연어 형태로 표현되고 그 불확실성의 정도에 대한 정확한 추정이 필요치 않는 경우에는 퍼지집합이론을 이용할 수 있다 하겠다.