퍼지 집합

퍼지 이론 및 응용I : 이광형. 오길록 공저, 홍릉과학출판사, 1991

1. 보통집합

     1.1 집합의 원소

     1.2. 집합 사이의 관계

     1.3. 소속함수와 집합의 크기

2. 보통집합의 연산

     2.1. 여집합

     2.2. 합집합

     2.3. 교집합

     2.4. 집합의 분할

3. 보통집합의 특성

     3.1. 일반적 특성

     3.2. 볼록집합

4. 퍼지집합의 정의

     4.1. 퍼지집합의 표시

     4.2. 퍼지집합의 예

     4.3. 퍼지집합의 확장

     4.4. 전체집합과 퍼지집합과의 관계

5. 퍼지집합 개념의 확장

     5.1. 퍼지집합의 예

     5.2. α-수준집합

     5.3. 볼록 퍼지집합

     5.4. 퍼지숫자

     5.5. 퍼지집합의 크기

     5.6. 퍼지집합 사이의 관계

6. 퍼지집합의 연산

     6.1. 여집합

     6.2. 합집합

     6.3. 교집합

본 절에서는 먼저 보통집합 (crisp set) 의 개념 (concept) 과 기호 (notation) 에 대하여 살펴본 다음 퍼지이론의 기본이 되는 퍼지집합에 대하여 다룬다. 앞의 1 장에서는 개념을 중심으로 퍼지집합 및 이론을 소개하였으나 여기에서는 좀더 정형적 (formal) 으로 소개하기로 한다 [Dubois 1980, Zimmemann 1985, Klir 1988, Novák 1989].

1. 보통집합

1.1 집합의 원소

일반적으로 집합을 나타내는 문자는 대문자로 표시하고, 그것의 원소를 나타낼 때는 소문자를 이용한다. 이 책에서는 어느 주어진 문제에 관련되는 모든 요소 (객체) 를 포함하는 집합을 전체집합 (universal set) 이라 부르고 문자 X 로 표시한다. 또한 전체집합 X 에 포함되어 있는 임의의 집합 A 를 다음과 같이 표시하고

    A ⊆ X

임의의 집합 A 가 X 에 포함되지 않으면 다음과 같이 표시한다.

    A  X

임의의 원소 (element) x 가 집합 A 에 소속되어 있으면 이 관계를 다음과 같이 표시하고, x 가 집합 A 의 한 원소 또는 한 멤버 (member) 라고 말한다.

    x ∈ A

또한 원소 x 가 집합 A 의 원소가 아니면 다음과 같이 표시한다.

    x 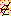A

일반적인 집합의 표시 방법은 각 원소의 이름을 나열하는 방법이다 (원소 나열법). 이 방법은 원소의 개수가 유한 개인 유한집합의 경우에 많이 사용되는데 예를 들어서 원소들의 이름이 이면 이것들로 이루어진 집합 A 는 다음과 같이 표시한다.

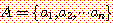
또 다른 집합의 표시방법은 원소의 특성들을 명시하는 방법이다 (조건 제시법). 예를 들어서 어느 집합 B 에 소속된 원소들이 특성 을 만족해야 한다면 집합 B 는 다음과 같이 나타낸다.

    B = {b | b 는 특성 만족}

이때 기호 "|" 는 "~ 와 같은 (such that)" 의 뜻을 내포하고 있다.

N-차원 유클리드 집합 (Euclidean set) 의 크기를 나타내기 위해서 원소의 개수가 이용되고, 이 개수를 cardinality 라 부른다. 이때 집합 A 에 있는 원소의 개수를 |A| 로 표시한다. 이때 |A| 가 유한숫자이면 A 를 유한집합 (finite set) 이라고 하고, |A| 가 무한숫자이면 무한집합이라고 부른다. 일반적으로 전체집합으로 벡터공간 |Rⁿ (n-dimensional Euclidean vector space) 내의 모든 점 (point) 들의 집합을 이용한다.

1.2. 집합 사이의 관계

원소들의 집합으로 이루어진 집합을 집합의 패밀리 (family of sets) 라고 부른다. 예를 들어서 집합 으로 이루어진 집합을

로 표시하고, 이때 i 를 집합 식별자 (set identifier), I 를 식별집합 (identification set) 이라 부른다. 또 색인 (index) i 가 집합 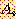를 가리키기 때문에 이 집합의 패밀리를 색인 집합 (indexed set) 이라고도 부른다.

집합 A 의 모든 원소가 집합 B 의 원소일 때, A 를 B 의 부분집합 (subset) 이라고 하고 다음과 같이 표시한다.

    A ⊆ B iff (if and only if)    x ∈ A ⇒ x ∈ B
                                             (implies)

모든 집합은 그 자신의 부분집합이 되고, 모든 집합은 전체집합의 부분집합이 될 수 있다. 만약

    A ⊆ B 와 B ⊆ A

의 관계가 성립되면 A 와 B 는 서로 같은 원소를 포함하고 있다. 이때 A 와 B 는 동일한 집합이고 이를 다음과 같이 표시한다.

    A = B

또한 A 와 B 가 서로 다른 집합일 때는

    A ≠ B

라고 표시한다. 그리고 두 집합 A, B 사이에

    A ⊆ B, A ≠ B

의 관계가 성립되면, B 는 A 에 소속되지 않는 원소를 가지고 있다. 이 관계를 A 가 B 의 진부분집합 (proper subset) 이라 부르고 다음과 같이 표시한다.

    A ⊂ B

집합 중에서 원소를 가지고 있지 않은 집합을 공집합 (empty set) 이라 부르고 φ 로 표시한다. 공집합은 모든 집합의 부분집합이 된다.

1.3. 소속함수와 집합의 크기

전체 집합 X 에 있는 객체 (individual, object) 가 집합 A 에 소속되는가 그렇지 않은가 (또는 A 의 멤버인가 아닌가) 하는 것은 소속함수 (membership, characteristic, discrimination function) 에 의해서 나타낼 수 있다. 예를 들어 집합 A 가 주어졌다면, 소속함수는 원소 x ∈ X 에 다음과 같이 값 μ_A(x) 을 부여한다.

즉, 소속함수는 전체집합의 원소를 집합 {0, 1} 으로 대응 (map) 시킨다고 할 수 있다.

    μ_A : X → {0, 1}

어느 집합 A 에 포함된 원소의 개수 (cardinality) 는 |A| 으로 표시된다. 집합 A 의 모든 부분집합으로 이루어진 집합의 패밀리를 멱집합 (power set) 이라 부르고 P(A) 라 표시한다. 따라서 이 멱집합의 원소 개수는 다음과 같다.

    |P(A)| = 2^|A|

예를 들어서 A = {a, b, c} 일 때에는 |A| = 3 이고

    P(A) = {φ, {a}, {b}, {c}, {a, b}, {b, c}, {c, a}, {a, b, c}}

이 되고

    |P(A)| = 2³ = 8 이 된다.

2. 보통집합의 연산

2.1. 여집합

집합 B 에 대한 집합 A 의 상대 여집합 (relative complement set) 은 B 의 원소 중에서 A 에 속해 있는 원소를 제외한 집합이다. 즉, 다음과 같이 표시한다.

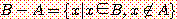
만일 집합 B 가 전체집합 X 이면 이 여집합은 절대 여집합 (absolute complement set) 이 되고, 이것을 A 라 표시한다. 일반적으로 여집합이라고 하면 이 절대 여집합을 가리킨다.

    A = X - A

여집합은 항상 involutive 하다. 즉, 여집합의 여집합은 그 자신이 된다.

     = A

공집합의 절대 여집합은 전체집합이 되고, 전체집합의 여집합은 공집합이 된다.

    φ = X

    X = φ

2.2. 합집합

집합 A 와 B 의 합집합 (union) 은 A 와 B 에 속해 있는 모든 원소를 모아 놓은 집합으로서 다음과 같이 나타낸다.

    A ∪ B = {x | x ∈ A or x ∈ B}

합집합은 여러개의 집합 사이에서도 정의할 수 있다. 예를 들어 패밀리

    {A_i | i ∈ I}

에 있는 집합들의 합집합은 다음과 같이 나타낸다.

어느 집합 A 와 전체집합 X 사이의 합집합은 전체집합이 된다.

    A ∪ X = X

그리고 어느 집합 A 와 공집합 φ 사이의 합집합은 집합 A 가 된다.

    A ∪ φ = A

또한 집합 A 와 그의 여집합 사이의 합집합은 전체집합 X 가 된다.

    A ∪ A = X

2.3. 교집합

집합 A 와 B 의 교집합 (intersection) A ∩ B 는 A 와 B 에 공통으로 포함되어 있는 원소들로 이루어진다.

    A ∩ B = {x | x ∈ A and x ∈ B}

집합의 패밀리 {A_i | i ∈ I} 에 있는 집합 사이의 교집합으로 일반화 (generalization) 하면 다음과 같다.

집합 A 와 전체집합 X 사이의 교집합은 집합 A 가 된다.

    A ∩ X = A

그리고 집합 A 와 공집합 사이의 교집합은 공집합이 된다.

    A ∩ φ = φ

집합 A 와 그의 여집합 사이의 교집합도 항상 공집합이 된다.

    A ∩ A = φ

임의의 집합 A 와 B 가 서로 공유하고 있는 원소가 없을 때는 서로 소 (disjoint) 라고 한다. 즉 A 와 B 의 교집합이 공집합일 때를 말한다.

    A ∩ B = φ

2.4. 집합의 분할

전체집합내에 있는 부분집합들이 서로 소 (교집합이 공집합) 이고 또 이 부분집합들의 합집합이 전체집합을 이루면, 이 부분집합들의 모임을 전체집합의 분할 (partition) 이라고 부른다.

즉, 집합 A 의 분할을 π 라고 표시하면

    π(A) = {A_i | I ∈ i, A_i ⊆ A}

이때, A_i 는 다음 3 가지 조건을 만족한다.

    (1) A_i ≠ φ

    (2) A_i ∩ A_j = φ,    i ≠ j,    i, j ∈ I

    (3)

이와 같이 하면 A 안에 있는 어느 원소는 한 개의 에 소속된다. 그리고 이때 (2) 번의 조건이 없으면 π(A) 를 A 의 포장 (cover, covering) 이라 부른다 (그림 1).

그림 1  분할과 포장

3. 보통집합의 특성

3.1. 일반적 특성

이제 앞에서 간단히 살펴본 합집합, 교집합, 여집합 연산의 특성을 살펴보자. 다음과 같이 합집합과 교집합은 교환법칙 (commutativity) 이 성립된다.

    A ∪ B = B ∪ A

    A ∩ B = B ∩ A

합집합과 교집합의 연산은 적용되는 순서에 상관없이 동일한 결과를 만드는 데, 이 성질을 결합법칙 (associativity) 이라 한다. 즉,

    A ∪ B ∪ C = (A ∪ B) ∪ C = A ∪ (B ∪ C)

    A ∩ B ∩ C = (A ∩ B) ∩ C = A ∩ (B ∩ C)

집합 자신에 대한 합집합과 교집합은 그 집합 자신이 되며, 이 성질을 idempotency 라 한다.

    A ∪ A = A

    A ∩ A = A

또한 합집합과 교집합은 분배법칙 (distributivity) 이 성립한다.

    A ∩ B ∩ C = (A ∩ B) ∩ C = A ∩ (B ∩ C)

    A ∪ B ∪ C = (A ∪ B) ∪ C = A ∪ (B ∪ C)

한편, 드모르강 법칙 (De Morgan's law) 은 두 집합의 교집합에 여집합을 취하면 각 집합에 여집합을 취한 것들의 합집합이 된다는 것을 보이고 있다.

    A ∩ B = A ∪ B

마찬가지로 합집합의 여집합은 각 집합의 여집합에 교집합을 취한 것과 같아진다.

    A ∪ B = A ∩ B

표 1 에서는 일반적인 집합의 특성을 요약하였다 [Klir 1988].

표 1  보통집합 연산의 특성

3.2. 볼록집합

N 차원 유클리드 벡터 (Euclidean vector) 공간 |Rⁿ 에서 정의되는 집합의 성질 중에 볼록 (convex) 이라는 특성이 있다. 집합 A 가 |Rⁿ 내에서 정의될 때 다음 조건을 만족하면 A 가 볼록한다고 한다. 즉,

    1) 집합 A 내의 임의의 두 점 r 과 s 가 다음과 같이 정의되고

        r = (r_i | i ∈ N_n),    s = (s_i | i ∈ N_n)

            (여기서 N 은 양의 정수를 나타내는 집합)

    2) 0 과 1 사이의 임의의 실수 λ 에 대하여 다음과 같이 만들어지는 점 t 가 A 에 소속된다.

        t = (λr_i + (1 - λ) s_i | i ∈ N_n)

좀더 달리 설명하면 |Rⁿ 위에 정의되는 집합 A 내의 두점 r 과 s 를 연결하는 직선 위의 모든 점이 A 내에 존재할 때, A 를 볼록하다고 한다. 볼록집합과 볼록이 아닌 집합이 그림 2 에 비교되어 나타나 있다 [Klir 1988].

그림 2  |R² 에 정의된 볼록집합 A1, A2, A3 과 볼록이 아닌 집합 A4, A5, A6

4. 퍼지집합의 정의

4.1. 퍼지집합의 표시

앞 절에서 어느 원소 x가 보통집합 A에 소속되면 소속함수 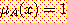, 소속되지 않으면 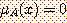이 된다. 즉 보통집합에서는 소속함수의 값이 1 또는 0 이 된다. 한편 소속함수의 값이 1 과 0 뿐 아니라, 1 과 0 사이의 임의의 값을 가질 수 있도록 하는 집합을 퍼지집합 이라 한다.  원소 x가 퍼지집합 의 가능성을 로 표시하고 이 가능성을 0과 1사이의 값이 된다.  

한편 소속함수의 값이 1 과 0 뿐만 아니라, 1 과 0 사이의 임의의 값을 가질 수 있도록 하는 집합을 퍼지집합이라 한다. 원소 x 가 퍼지집합 A 에 소속될 가능성을 로 표시하고 이 가능성은 0 과 1 사이의 값이 된다. 앞에서 보통집합에서의 소속함수 는 전체집합 X의 모든 원소를 집합{0, 1}으로 대응(mapping) 시킨다고 했다.

: X → {0,1}

퍼지집합에서는 소속함수 가 각 원소를 집합 {0, 1}으로 대응시킨다.

: X → [0,1]

이때 [0,1]은 0과 1사이의 모든 실수(0과 1포함)를 나타낸다. 결국 보통집합에 비하여 퍼지집합은 집합의 경계가 애매한 집합이라 생각할 수 있다. 그림 3 은 이 두가지 집합을 소속함수로 표현한 예를 보이고 있다.

[그림 3]  보통집합과 퍼지집합의 표현

예를 들어서 1 장에서 논의한 퍼지집합 "두어" 개를 생각해 보자. 여기에서 전체집합 X 는 양의 정수라 할 수 있다.

    X = {1, 2, 3, 4, 5, 6 ...}

이 모든 양의 정수에 대한 퍼지집합 A = "두어" 개의 소속함수를 나타내면 다음과 같다.

(1) = 0

(2) = 1

(3) = 0.5

(4) = 0

... 

일반적으로 여기서와 같이 원소들이 이산(discrete)일 때는 각 원소별로 소속정보(membership degree, grade)를 다음과 같이 표시할 수 있다.

A={(2, 1.0), (3, 0.5)}

또는

A=1.0 / 2 + 0.5 / 3

여기에서 '+' 표시는 덧셈의 의미가 아니고 합집합의 의미를 가지는 점에 주의하자.  좀더 일반적으로 다음과 같이 나타낸다.

A={ (x, (x)) }

또는

한편 원소들이 연속적일 때는 다음과 같이 나타낼 수 있다.

소속함수를 연속함수로 나타낸 예가 1 장의 그림 3 에 있다. 이 그림에서 25 세가 퍼지집합 Y = "젊은 나이" 에 포함될 가능성을 소속함수를 이용하여 표시하면 다음과 같다.

또한 "매우 젊은 나이" 라는 퍼지집합 Y 에 포함될 가능성은 다음과 같이 나타낸다.

4.2. 퍼지집합의 예

이제 퍼지집합 A = { 0 에 가까운 실수 }를 정의해 보자.   "0 에 가까운 실수" 라는 집합의 경계가 애매하다.  실수 x가 이 집합에 소속될 가능성을 다음과 같은 소속함수(membership function) 로 정의해 보자 [Klir 1988].

이 함수를 그림으로 표시하면 다음 그림과 같이 된다.  이와같이 정의되는 퍼지집합을 다음과 같이 표시할 수 있다.

    또는   

[그림 4]  "0에 가까운 실수라는 퍼지집합"의 소속함수

이 함수에서 정의한 대로라면 실수 1이 집합 A에 속할 가능성은

이다. 또한 2가 집합 A에 포함될 가능성은 0.2이고, 3이 포함될 가능성은 0.1이다.

이제 또 다른 퍼지집합으로  R={0 과 매우 가까운 실수}를 정의하고 이 집합의 소속함수도 다음과 같이 해보자. 

이 함수에 의하면 1이 이 집합에 포함될 가능성은 0.25, 2가 포함될 가능성은 0.01, 그리고 3이 포함될 가능성은 0.01이다 (그림 5).

[그림 5]  "0 에 매우 가까운 실수"의 소속 함수

이상의 소속함수를 이용한다면, 퍼지집합 A={ a 에 가까운 실수 }의 소속함수는 다음과 같이 나타낼 수 있을 것이다.

4.3. 퍼지집합의 확장

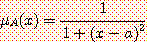
지금까지 살펴 본 퍼지집합의 개념을 다음 3 가지 방법으로 확장할 수 있다. [Zimmermann 1985].

1) 유형-n (type-n) 퍼지집합

어느 퍼지집합이 있을 때 그 집합의 소속함수를 정하는 일은 매우 주관적일 수 있으므로 소속함수의 값은 애매한 값이 될 수가 있다.  이와같이 소속함수의 값이 애매한 값이 될 수 있을 때는, 이 소속함수의 값 자체를 퍼지집합으로 정의할 수 있다.  따라서 소속함수의 값이 애매하지 않을 때는 유형-1(type-1) 퍼지집합이라 부르고, 소속함수의 값 자체가 또 다시 퍼지집합(즉 유형-1 퍼지집합)으로 표시될 때는 유형-2(type-2)퍼지집합이라 부른다(그림 6).

 
[그림 6] 유형-2 퍼지집합

예를 들어서 퍼지집합 "성인"이란 집합을 정의하여 보자.  그리고 이 집합의 소속함수는 모든 사람(어린이 포함)을 "청년","장년","노인"으로 대응시킨다고 하자.  예를 들어서 임의의 사람 x, y, z 에 대하여,

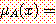"청년"

"장년"

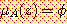
여기에서 소속함수의 값 "청년", "장년" 등이 다시 퍼지집합이라고 한다면, 퍼지집합 "성인"은 유형_2 퍼지집합이 되고, "청년", "장년" 등은 유형-1 퍼지집합이 된다. 마찬가지 방법으로 어느 퍼지집합의 소속함수 값이 다시 유형-2 퍼지집합으로 나타날 때 집합을 유형_3 퍼지집합이라 한다.

2) 레벨-k (level-k) 퍼지집합

이제 퍼지집합의 또다른 확장을 보자.  우리는 앞에서 원소들의 집합으로 이루어진 모임(collection)을 패밀리(family)라 부른다고 했다. 원소들이 퍼지집합인 퍼지집합도 있을 수 있는데 이러한 퍼지집합을 레벨-2(level_2) 퍼지집합이라 부르고, 이에 대응하여 앞에서 정의한 퍼지집합을 레벨-1 퍼지집합이라고 한다(그림 7). 마찬가지 방법으로 확장하면 레벨-k 퍼지집합까지 얻을 수 있다.

레벨-2 퍼지집합의 원소들 A1, A2, A3

[그림 7] 레벨-2 퍼지집합

3) L- 퍼지집합 (L- fuzzy set : lattice fuzzy set)

지금까지의 퍼지집합은 소속함수의 치역 (range) 을 구간 [0, 1] 로 하고 있다. 즉 소속정도 (소속함수 값) 가 전순서 (total ordering) 로 되어 있다. 이것을 일반화하여 이 치역을 부분순서 (partial ordering) 가 되도록 확장한 것이 L-퍼지집합이다. L 은 부분 순서구조를 나타내는 데 이용되는 속 (lattice) 을 표현한다. 따라서 L-퍼지집합에서 소속함수 μ_A 는 다음과 같이 정의된다.

그림 8 은 부분순서를 나타내는 속 L 과 L-퍼지집합을 보이고 있다. 여기에서는 다음과 같은 관계가 있다.

    0 ≤ c ≤ a ≤ 1

    c ≤ b ≤ 1

따라서 원소 x, y, z, w 의 소속함수 사이에 다음의 관계가 성립한다.

    μ_A(z) ≤ μ_A(x) ≤ μ_A(w)

    μ_A(z) ≤ μ_A(y) ≤ μ_A(w)

그러나 a 와 b 사이는 비교할 수 없다. 따라서 μ_A(x) 와 μ_A(y) 사이는 비교할 수 없다.

[그림 8]  속 (lattice) 과 L-퍼지집합

4.4. 전체집합과 퍼지집합과의 관계

보통집합에서와 마찬가지로 퍼지집합 A를 전체집합 X에서 정의한다면, A 는 X 의 부분집합이 된다. 예를 들어서 X = {a, b, c} 라고 정의한다면

A₁ = {(a, 0.5), (b, 1.0), (c, 0.5)}  ,   A₂ = {(a, 1.0), (b, 1.0), (c, 0.5)}

이것은 다음과 같이 표시할 수 있다.

 ,

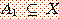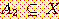
라 표시한다. 이와같은 X의 부분집합(퍼지집합 포함)의 모임을 멱집합(power set) P(X)라 부른다. 

5. 퍼지집합 개념의 확장

5.1. 퍼지집합의 예

이 절에서는 퍼지집합에 관련된 용어들을 정리하면서, 퍼지집합의 개념을 좀더 자세히 정의해 보자. 대부분의 퍼지집합의 개념은 일반집합의 개념을 확장한 것이다.  예를 들어서 설명하기 위하여 다음과 같이 나이를 나타내는 전제집합 X를 고려해 보자. [Klir 1988].

X = {5, 15, 25, 35, 45, 55, 65, 75, 85}

이 전체집합  X위에 4개의 퍼지집합 "유아", "성인", "젊은이", "노인"을 정의해 보자.  이것들은 전체집합 X의 부분집합으로서 X의 부분집합의 모임인 멱집합 P(X)의 원소들이다.

X의 각 원소(나이)가 4개의 퍼지집합에 포함되는 가능성은 다음 표 2 에 있다.

표 2  퍼지집합의 예

원소(나이)	유아	젊은이	성인	노인
5	0	0	0	0
15	0	0.2	0.1	0
25	0	1	0.9	0
35	0	0.8	1	0
45	0	0.4	1	0.1
55	0	0.1	1	0.2
65	0	0	1	0.6
75	0	0	1	1
85	0	0	1	1

전체집합 X내의 원소 중에서 퍼지집합 A에 조금이라도 포함되어 있는 원소들로 이루어진 집합을 A의 지지(support)라고 부른다.

Support(A) = {x ∈ X | μ_A(x) > 0}

예를 들어서 앞의 퍼지집합 "젊은이"의 지지는 다음과 같고, 이것은 보통집합이 된다.

Support(젊은이) = { 15, 25, 35, 45, 55 }

따라서 공집합 "유아"의 지지(support)는 당연히 공집합이다.

퍼지집합의 소속함수 값 중에서 최대값을 이 퍼지집합의 높이라고 할 수 있다. 어느 퍼지집합에서 최대 소속함수 값이 1이 되면 이 퍼지집합을 정규화(normalized) 되었다고 한다. 이때 최대값은 다수가 되어도 무방하며, 퍼지집합의 높이가 1이 되는 집합을 말한다.  앞에서 예로 든 퍼지집합 "젊은이", "성인", "노인"은 정규화되어 있다.

우리는 여기에서 전체집합 나이 X 내에서 퍼지집합 "유아", "젊은이", "성인"등을 정의하였다. 나이라고 하면 0부터 100까지 생각할 수 있다. 이때 보통집합(crisp set)인 "10대"를 생각해 보자.  이 집합은 전체 나이에서 10-19세만을 명확하게 정의한 것이다. 이것은 전체집합에 제약(restriction)을 가하여 10대의 나이로 제한한 집합이다. 이렇게 볼 때 퍼지집합 "젊은이"도 전체집합(나이)에 제약을 가하여 집합을 만들었는데, 이 때는 퍼지제약(fuzzy restriction)을 두어 퍼지집합 "젊은이"가 되었다고 할 수 있다. [Dubois 1980].

[그림 9]  비정규화 퍼지집합과 정규화 퍼지집합

5.2. α-수준집합

퍼지집합에 포함된 원소들 중에서 일정한 가능성(소속함수 값) 이상 포함된 원소들로만 구성된 보통집합을 만들 수 있다.  이것을 α-수준집합 (α-level set 또는 α-cut) 이라고 부르는데, 소속함수의 값이 α 이상인 원소들로 이루어진다.

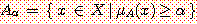
이때 α 는 임의로 선택할 수 있다.  이렇게 만들어진 α-수준집합은 보통집합(crisp set)이 된다. 예를 들어서 앞의 퍼지집합 "젊은이" 에서 α=0.2 로 하여 만든 α-수준집합은 다음과 같고

젊은이_0.2 = { 15, 25, 35, 45 }

이것의 의미는 "0.2 이상의 가능성으로 젊은이라고 할  수 있는 나이" 이다.

만약 α=0.4 로 하면

    젊은이_0.4 = { 25, 35, 45 } 가 되고  

만약 α=0.8 로 하면

    젊은이_0.8 = { 25, 35 } 가 된다.  

가 된다. 한편 α와 α'에 대하여 두 개의 수준집합 와 가 있다고 할 때

    α ≤ α'

의 관계가 있으면

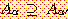
의 관계가 성립한다는 것을 알 수 있다. 예를 들어서 앞의 예에서도

    젊은이_0.2 ⊇ 젊은이_0.4

의 관계가 있다.

여기에서 소속함수의 값을 나타내는 α는 구간 {0,1} 에 포함된 값으로서, α 로 이루어진 집합을 level set 이라 부른다.  즉

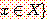    , ,  이다

예를 들어서 앞의 퍼지집합 "젊은이"의 level set 은 다음과 같다.

 A_"젊은이" = { 0, 0.1, 0.2, 0.4, 0.8, 1.0 }

[그림 10]  α-수준집합

5.3. 볼록 퍼지집합

전체집합 X 가 n 차원 유클리드 벡터공간내에서 정의된다고 할 때, 공간내의 한 점은 실수들의 n-tuple 로 표시되고 이 점들이 전체집합 X를 구성한다.  보통집합에서의 볼록집합(convex set) 개념이 퍼지집합에서도 확장될 수 있다. 즉, 어느 퍼지집합의 모든 수준 집합이 볼록집합이면, 그 퍼지집합은 볼록하다. 바꾸어 표현하면

 r, s ∈ |Rⁿ,

 λ ∈ [0, 1]

을 만족하는 퍼지집합 A는 볼록하다고 한다 [Klir 1988].

다음 그림 11 에서는 볼록 퍼지집합을 보이고 있고, 그림 12 에서는 볼록 퍼지집합이 아닌 것을 보이고 있다. 그림에서 알 수 있듯이 레벨집합 내에 있는 모든 α값에 대하여 절단한 집합이 블록이어야 그 퍼지집합이 볼록하다고 한다.

[그림 11]  볼록 퍼지집합

[그림 12]  볼록 퍼지집합이 아닌 경우

5.4. 퍼지숫자

우리는 일상적으로 실수, 양수, 음수라는 용어를 사용한다. 이것은 집합의 관점에서 본다면 실수 |R 위에 정의되는 보통집합을 나타내고 있다. 예를 들어서 "실수" 라고 한다면 모든 실수를 포함하는 집합을 말하고, "양수 (0 포함)" 라고 하면 음수를 제외한 숫자를 나타내는 집합이 된다. 또한 "10 이하의 양수 (0 포함)" 라고 한다면 이것은 0 과 10 구간에 있는 숫자들의 집합을 말한다. 즉

A = "10 이하의 양수 (0 포함)" = {x | 0 ≤ x ≤ 10, x ∈ |R}

또는

    μ_A(x) = 1    if 0 ≤ x ≤ 10,    x ∈ |R

    μ_A(x) = 0    if x < 0    or    x > 10

이것은 보통집합을 나타내기 때문에 소속함수의 값이 1 또는 0 이 된다. 이와 같은 개념을 확장하여 실수 |R 위에서 퍼지숫자를 정의할 수 있다 [Kaufmann 1988].

어느  퍼지집합이 볼록 (convex) 하고 정규화 (normalized) 되어 있으며 실수 |R 에서 정의될 때 그 소속함수가 연속적 (piecewise continuous) 이면, 이 퍼지집합을 퍼지숫자 (fuzzy number) 라고 부른다. 즉 퍼지숫자 (퍼지집합) 는 일정한 구간에 있는 실수들을 말하는데, 각 숫자가 퍼지숫자에 포함되는 가능성이 일정치 않다. 경우에 따라서 정규화되어 있지 않은 (소속함수의 최대값이 1 이 되지 않음) 숫자의 집합도 퍼지숫자라고 부르기도 한다.

[그림 13]  숫자의 구간을 나타내는 집합

5.5. 퍼지집합의 크기

보통집합의 경우와 같이 퍼지집합에서도 원소의 개수를 이용하여 집합의 크기를 나타낼 수 있다. 퍼지집합에서는 cardinality 를 나타내는 방법이 3 가지가 있다.

첫째, 퍼지집합 A 에 있는 각 원소의 소속 가능성 (소속함수의 값) 의 합을 원소의 개수로 하는 방법이 있다. 이것은 스칼라 (scalar) cardinality 라고도 부른다.

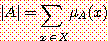
이 방법에 따르면 앞의 표 2 에서 정의한 퍼지집합 "노인" 의 크기는 다음과 같다.

    |노인| = 0.1 + 0.2 + 0.6 + 1 + 1 = 2.9

둘째, 퍼지집합 A 의 크기를 전체집합 X 와 비교하여 나타내는 방법으로서 다음과 같이 나타낼 수 있다.

이것을 상대 (relative) cardinality 라고 부르며 앞의 퍼지집합 "노인" 의 경우에 다음과 같이 계산할 수 있다.

    |노인| = 2.9

    |X| = 9

    ∥노인∥= 2.9 / 9 = 0.32

셋째, 집합의 크기를 퍼지집합 (퍼지숫자) 으로 나타낸 것이다. 이것을 퍼지 cardinality 라 부르는데 이때 |A| 은 퍼지집합으로 표현된다 [Klir 1988].

퍼지집합 A 의 α-수준집합 (crisp set) A_α 를 구해보자. A_α 의 원소의 개수는 |A_α| 가 된다. 바꾸어 말하면 퍼지집합 A 에서 원소의 개수가 |A_α| 가 될 가능성은 α 가 된다. 따라서 우리가 구하고자 하는 퍼지집합 (퍼지 cardinality) |A| 의 소속함수는 다음과 같이 정의될 수 있다.

    μ_|A||A_α| = α,    α ∈ A_α    (레벨집합)

        A_α 는 α-수준집합

이것은 퍼지집합 A 에서 또다른 퍼지집합 |A| 를 확장한 셈이다. 예를 들어서 앞 표 2 의 집합 "노인" 의 크기를 퍼지집합으로 나타내면

    |노인| = {(5, 0.1), (4, 0.2), (3, 0.6), (2, 1)}

와 같이 된다. 우리는 이 집합으로부터 다음과 같은 해석을 할 수 있다. 퍼지집합 "노인" 을 α = 0.1 에서 절단하면 수준집합에서의 원소는 5 개가 되고, α = 0.2 에서 절단하면 원소가 4 개, α = 0.6 에서는 원소가 3 개, α = 1 에서는 2 개가 된다. 좀더 구체적으로 α = 0.1 일 때를 예로 하면 집합 "노인" 을 α = 0.1 에서 절단하면 이때 만들어지는 수준집합은 다음과 같이 된다.

    노인_0.1 = {45, 55, 65, 75, 85}

    |노인_0.1| = 5

5.6. 퍼지집합 사이의 관계

퍼지집합 A, B가 있다고 하자.  모든 원소 x 의 A 와 B 에 소속된 정도가 같을 때는 A 와 B 가 동치라고 한다.  즉

A = B       if       ,       

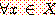
만약 어느 한 개의 원소에 대해서도 이면 A ≠ B 이다.

퍼지집합 A와 B에서 다음 관계가 만족하면 A가 B의 부분집합(subset)이라고 한다.

,       

이때 A ⊆ B라고 표시한다.  또한 다음 관계가 성립하면 A를 B의 진부분집합(proper subset)이라고 한다. 아래 그림은 진부분집합을 나타낸다.

 ,       

이때 A ⊂ B라고 하며, 이 관계는 다음과 같이 나타낼 수 있다.

A ⊂ B         if and only if      A ⊆ B     and     A ≠ B

퍼지집합 "성인"과 "노인"을 비교할 때 노인은 성인의 진부분집합임을 알 수 있다. 

그림 14  부분집합 A ⊂ B 

6. 퍼지집합의 연산

6.1. 여집합

보통집합에서와 마찬가지로 퍼지집합 A의 여집합 (complement) 을 구할 수 있다.  이것은 전체집합 X에 대한 여집합으로서, 로 표시한다.  각 원소의 에 대한 소속정도는 다음과 같이 계산한다.

,    

퍼지집합에서 "성인"의 여집합을 "미성년"이라고 한다면, "미성년"의 원소와 소속 가능성은 다음과 같이 나타낼 수 있다.

"미성년" = { (5,1),(15,0.9),(25,0.1) }

여기에서 우리가 정의한 "미성년"이란 집합이 "젊은이"집합과 일치되지 않는다는 것을 주목하기 바란다. 

6.2. 합집합

퍼지집합 A, B 의 합집합 (union) 은 A ∪ B 로 표시하고 이때 어느 원소 x의 소속함수의 값은 x 가 A 와 B 에 포함될 가능성 중에 최대값 을 취한다.  즉

, ,    

이와같이 하면 당연히 A 와 B 는 A ∪ B 의 부분집합이 되며, 퍼지집합 "젊은이"와 "성인"의 합집합을 구하면 다음과 같다.

"젊은이" ∪ "성인" = { (15,0.2),(25,1),(35,1),(45,1),(55,1),(65,1),(75,1),(85,1) } 

6.3. 교집합

퍼지집합 A, B의 교집합 (intersection) A ∩ B는 소속함수의 값 중에서 최소값을 취하여 정의한다.

, ,    

교집합 A ∩ B는 다음과 같다.

"젊은이" ∩ "성인" = { (15,0.1),(25,0.9),(35,0.8),(45,0.4),(55,1) }

여집합, 합집합, 교집합의 연산은 소속함수의 값이 0 또는 1로 제한되어도(즉, 보통집합) 그대로 적용된다.