A* 알고리즘의 휴우리스틱 유도 방법
인공지능 원론 : 유석인, 교학사, 1988, Page 111~127
2. 문제의 유사성 (similarity) 을 이용하는 방법
복잡한 문제들을 효율적으로 풀기 위해서는 문제 자체에 내포된 정보들을 활용하여 탐색제어를 행하는 것이 유용할 경우가 많다. 이러한 종류의 정보를 휴우리스틱 (heuristic) 정보라고 부른다. 휴우리스틱 정보는 여행에 있어서 안내 가이드와 같은 것이다. 즉, 이것이 관광자에게 만족을 줄 수 있는 올바른 방향을 지정하는 한에서는 좋은 휴우리스틱이 되고 그 반대로 불만족을 줄 수 있는 더 곤경에 헤매는 방향을 지정하는 경우에는 나쁜 휴우리스틱이 된다고 할 수 있다. 휴우리스틱은 여러 가지 성질에 따라 문제 풀이에 영향을 미친다. 어떤 휴우리스틱은 문제 풀이 수행 중에, 고려되어야만 하는 문제에 내포된 제약조건들에 위배되지 않고 탐색과정을 제어하는데 도움을 준다. 그러나 또 다른 휴우리스틱은 시작에서 목표까지 이르는 최적비용의 경로 (path) 을 탐색하는데 도움을 주지 못하는 경우도 있다.
휴우리스틱을 이용하지 않는 경우에는, 대부분의 문제 풀이를 행함에 있어서 계산 시간 (computation time) 이나 탐색공간 (search space) 이 현실적으로는 불가능할 정도로 많은 양이 요구된다. 이 때문에 휴우리스틱을 이용해서 탐색을 제어해 나가는 방법을 택하게 되며 이 밖에도 다음과 같은 이유들로 인해서 휴우리스틱 탐색방법을 이용하게 된다. 첫째, 시작점에서 목표점까지 이르는 경로 (path) 를 구하는 데 있어서 최단거리의 경로를 구하는 것만이 목적이 아닌 문제들이 많다는 것이며 둘째, 비록 휴우리스틱을 사용해서 유도된 경로가 최단거리가 아니라 할지라도 이러한 결과가 전체적인 문제 풀이의 효율성을 오히려 증진시킬 수 있다는 점이다.
휴우리스틱은 여러 종류의 문제영역에 걸쳐 이용되는 일반적인 경우도 있고 특정 문제만을 풀기 위해 그 문제영역에 내포된 지식을 이용하는 특정한 경우도 있다. 이러한 여러 휴우리스틱들은 문제풀이기법의 탐색제어에 영향을 미치기 위한 근거로 이용되어 주어진 문제를 효율적으로 해결하는데 도움을 주게 된다.
이 장에서는 제 4 장에서 설명한 A*-알고리즘에서 이용되는 휴우리스틱으로, 주어진 문제상태로부터 원하는 목표상태에 도달하는 최단거리 경로의 측정값을 구하는 몇 가지 일반적인 방법론들에 관해 논하기로 한다. 이러한 방법론들의 개발은 A*-알고리즘을 실제적인 문제풀이방법으로 이용할 수 있도록 한다는 점에 그 중요성을 가지고 있다.
먼저 Gaschnig 은 문제의 유사성 개념을 이용해 휴우리스틱 유도방법을 제시했으며 [Gaschnig 79], Guida and Somalvico 는 보조문제개념을 이용해 휴우리스틱 유도를 행하고자 했다 [Guida and Somalvico 79]. Pearl 은 문제의 규칙들과 목표를 나타내는 서술문 (predicate) 들 가운데 일부를 삭제하는 것에 의해 본래 문제보다 단순화된 문제를 생성하고 이것을 이용해 휴우리스틱을 구했다 [Pearl 84]. 더욱이 Irani and Yoo 는 문제 상태를 표현하는 기본단위 (elementary unit) 들에 관한 제약조건들을 나타내는 서술문을 완화시키는 것에 의해 보다 간단한 문제를 생성하고 이로부터 휴우리스틱을 유도하였다 [Irani and Yoo 85].
이제 위에서 언급한 여러 가지 휴우리스틱 유도방법들을 각각 설명하고, 이 방법들을 제 3 장에서 소개한 ‘8-퍼즐 문제’ 를 통해 예증해보기로 한다.
2. 문제의 유사성 (similarity) 을 이용하는 방법
이는 문제를 그래프로 표현하고 이로부터 A*-알고리즘의 휴우리스틱을 유도하는데 있어 본 문제와 유사한 그래프를 이용하는 방법이다. 즉, 주어진 문제 P1 에 대하여 직접적으로 휴우리스틱을 구하는 것이 아니고, P1 과 유사성을 지닌 문제로써 P1 보다 더 풀기 쉬운 문제 P2 를 먼저 구하고 (나중에 설명하겠지만 이러한 P2 를 P1 의 “에지 서브그래프 (edge subgraph)” 또는 “에지 수퍼그래프 (edge supergraph)” 라 한다), 그 다음에 문제 P2 에서 경로를 구하는 단순한 알고리즘을 고안하고, 이 알고리즘을 적용하여 구해지는 P2 에서의 경로의 거리를 문제 P1 에서의 대응되는 경로의 최단거리값에 대한 측정값으로 이용하는 법이다. 2-(1) 절에서는 문제의 유사성 (similarity) 에 관한 두 가지 형태인 “에지 서브그래프” 와 “에지 수퍼그래프” 에 대한 개념을 “맨하턴 거리 형태 (Manhattan street pattern)” 그래프와 이것에 변화를 준 형태들과의 비교를 통해 예증하고 이를 통해 휴우리스틱 유도를 위한 기본적인 개념을 설명한다. 2-(2) 절에서는 실제적으로 8-퍼즐 문제의 예를 통해 위의 방법을 적용하고 그 결과를 분석한다.
이 절에서의 설명은 “맨하턴 거리” 의 예를 통해 이루어진다. 그림 1 (a), (b), (c) 에 나타난 그래프인 MSUB44, M44, MSUP44 (Gaschnig 의 용어 표현에 의함) 는 모두 같은 수의 동일한 노드를 가지지만, MSUB44 의 모든 에지 (edge) 는 M44 에 나타나는 에지이며, M44 의 모든 에지는 MSUP44 에 나타난 에지이다. 이러한 의미에서 MSUB44 를 M44 의 “에지 서브그래프” (edge subgraph) 라 하고 MSUP44 를 M44 의 “에지 수퍼그래프” 라 한다.
“에지 서브그래프” 또는 “에지 수퍼그래프” 가 휴우리스틱 유도와 어떻게 연관이 되어지는지를 위의 세 가지 그래프를 통해 설명할 수 있다. M44 를 해결 가능한 문제라 하고 MSUB44 와 MSUP44 를 해결하고자 하는 문제들이라 하자.
문제 M44 에서 풀어지는 것은 현재 노드 s 에서 목표 노드 t 까지의 최단거리
경로라 하겠다 (이 최적비용을 ![]() 로 표현함 : 4 장에서 표현한
로 표현함 : 4 장에서 표현한
![]() 와 같음). 에지의 각 비용이
모두 일정하다 하면
와 같음). 에지의 각 비용이
모두 일정하다 하면 ![]() 는 최적거리라 할 수 있으며,
노드 s, t 의 각 좌표를
는 최적거리라 할 수 있으며,
노드 s, t 의 각 좌표를 ![]() ,
, ![]() 라 할 때
라 할 때 ![]() 로 쉽게 계산이 된다 [
로 쉽게 계산이 된다 [![]() 를 구하는 이 식은 일종의 단순한 알고리즘에 해당된다].
를 구하는 이 식은 일종의 단순한 알고리즘에 해당된다].
MSUB44 를 풀고자 한다 하자. 이 문제는 최적거리인 ![]() 를 M44 의
를 M44 의 ![]() 경우처럼 쉽게 구할 수는 없다.
그러므로 이 문제는
경우처럼 쉽게 구할 수는 없다.
그러므로 이 문제는 ![]() 의 측정값인 휴우리스틱 함수
h(s, t) (제 4 장에서 표현한 h(s) 와 같음) 를 적용한 A*-알고리즘에 의해 해결될 수 있다. MSUB44 의
에지 집합은 M44 의 에지 집합의 부분집합이므로
의 측정값인 휴우리스틱 함수
h(s, t) (제 4 장에서 표현한 h(s) 와 같음) 를 적용한 A*-알고리즘에 의해 해결될 수 있다. MSUB44 의
에지 집합은 M44 의 에지 집합의 부분집합이므로 ![]() 임을 쉽게 보일 수 있다. 그러므로
임을 쉽게 보일 수 있다. 그러므로 ![]() 라 놓고 이를 이용한 A*-알고리즘의
허용성 (admissibility) 로 인해 항상 MSUB44 의 최단거리의 경로를 유도하게 된다.
라 놓고 이를 이용한 A*-알고리즘의
허용성 (admissibility) 로 인해 항상 MSUB44 의 최단거리의 경로를 유도하게 된다.
이제 문제를 바꾸어 MSUP44 를 풀고자한다 하자. 이 때는 ![]() 가 만족되므로
가 만족되므로 ![]() 라 놓은 h(s, t) 는
MSUP44 에서의 s 에서 t 까지의 최단거리를 능가하는 측정값이 된다. 그러므로 이 휴우리스틱 함수 h(s, t) 의 사용은 A*-알고리즘의
휴우리스틱 함수 h(s, t) 로 사용함으로써 MSUP44 에서의 원하는 경로 (비록 이 경로가 최단거리라는 보장은 없을지라도) 를 쉽게 유도할
수 있다.
라 놓은 h(s, t) 는
MSUP44 에서의 s 에서 t 까지의 최단거리를 능가하는 측정값이 된다. 그러므로 이 휴우리스틱 함수 h(s, t) 의 사용은 A*-알고리즘의
휴우리스틱 함수 h(s, t) 로 사용함으로써 MSUP44 에서의 원하는 경로 (비록 이 경로가 최단거리라는 보장은 없을지라도) 를 쉽게 유도할
수 있다.
위에서 예를 들어 설명한 방법을 일반화하면 다음과 같다 : 풀어야 할 문제 그래프
P1 이 주어진 상태에서, ![]() 로써 P2 로부터 계산되는
로써 P2 로부터 계산되는 ![]() 를 사용한다.
를 사용한다.
다음 장에서는 실제적으로 “8-퍼즐 문제” 를 통해 이를 예증해 보이고자 한다.
“8-퍼즐” 에서 판의 배열상태를 간편하게 표기하기 위해 공백 칸을 9 번으로 하여 판의 왼쪽에서 오른쪽으로, 위에서 아래로 배열된 숫자의 번호들을 일렬로 나열하는 표기법을 사용한다 하자.
예를 들어 아래의 배열상태는 398146572 로 표기할 수 있다.
|
3 |
|
8 |
|
1 |
4 |
6 |
|
5 |
7 |
2 |
먼저 “N-swap” 그래프를 다음과 같이 정의한다 : N-swap 그래프는 1,
2, …, N 의 숫자들을 사용해서 이들을 일렬로 나열하는 배열형태 (N! 개가 존재함) 를 한 노드로 표시할 때, 에지는 한 배열형태에서 어느
두 개의 숫자를 서로 교환하여 자리이동을 행함에 의해 생긴다. 여기서 N = 9 라 하면 9 swap 그래프가 된다. 이 9 swap 그래프는
분명 8-퍼즐 그래프의 에지 수퍼그래프가 된다. 더욱이 어느 두 개의 숫자가 교환됨에 의해 에지가 생기는 것이 아니라 가장 큰 수인 N (9
swap 에서는 N = 9) 과 그외 다른 한 숫자 사이의 교환에 의해서만 에지가 생길 수 있다고 제약을 가하면 (이 제약에 의해 생기는 그래프를
N-maxswap 라 함), N = 9 일 때의 그래프인 9-maxswap 은 분명히 9-swap 의 에지 서브그래프가 된다. 그러나 8-퍼즐
그래프의 예지는 숫자 9 와 이것에 인접된 숫자 사이의 교환에 의해서만 생기므로 9 maxswap 그래프는 분명히 8-퍼즐 그래프의 에지 수퍼그래프가
된다. 그러므로 다음과 같은 식이 만족된다 : ![]() 그러므로 8-퍼즐 휴우리스틱으로
그러므로 8-퍼즐 휴우리스틱으로
![]() 또는
또는 ![]() 를 사용할 수 있는데
를 사용할 수 있는데 ![]() 가 더 좋은 휴우리스틱이 된다.
가 더 좋은 휴우리스틱이 된다.
![]() 를 계산하는 간단한 알고리즘으로 다음과 같은 것을 생각할 수 있다 : (여기서 목표 노드 t 의 배열은 123456789
라 가정한다.) 현재상태 s 배열에서 다음 배열로의 전이는 s 배열에서 숫자 9 가 놓인 위치에 올바로 놓여져야 할 숫자와 숫자 9 를 교환하는
에지를 선택함에 의해 이루어진다. 예를 들어 s 배열이 129435678 이 숫자 9 가 놓인 위치가 올바른 위치인 9 이면 배열에서 올바른 위치에
놓여 있지 않은 가장 작은 위치 번호에 놓여 있는 숫자와의 교환이 이루어지는 에지가 선택된다. 예를 들어 s 배열이 124735689 이면 다음의
배열은 129735684 가 된다. 노드 s 에서 목표 노드 t 까지의 경로는 위의 과정에 의해 유도되며 실제적으로 이 유도된 경로거리는
를 계산하는 간단한 알고리즘으로 다음과 같은 것을 생각할 수 있다 : (여기서 목표 노드 t 의 배열은 123456789
라 가정한다.) 현재상태 s 배열에서 다음 배열로의 전이는 s 배열에서 숫자 9 가 놓인 위치에 올바로 놓여져야 할 숫자와 숫자 9 를 교환하는
에지를 선택함에 의해 이루어진다. 예를 들어 s 배열이 129435678 이 숫자 9 가 놓인 위치가 올바른 위치인 9 이면 배열에서 올바른 위치에
놓여 있지 않은 가장 작은 위치 번호에 놓여 있는 숫자와의 교환이 이루어지는 에지가 선택된다. 예를 들어 s 배열이 124735689 이면 다음의
배열은 129735684 가 된다. 노드 s 에서 목표 노드 t 까지의 경로는 위의 과정에 의해 유도되며 실제적으로 이 유도된 경로거리는 ![]() 가 됨을 보일 수 있다. 그러나
허용성을 요구하지 않는 탐색 알고리즘에서는 이러한 방법이 별 효과를 거두지 못한다. 왜냐하면 경로거리를 과대평가하는 휴우리스틱의 사용은 과소평가하는
휴우리스틱의 사용보다 전체적인 문제 풀이의 효율성을 오히려 더 증가시키는 경우가 종종 있기 때문이다. 여기에 대한 자세한 설명은 [Dorank
and Michie 66], [Gaschnig 77] 을 참조할 수 있다.
가 됨을 보일 수 있다. 그러나
허용성을 요구하지 않는 탐색 알고리즘에서는 이러한 방법이 별 효과를 거두지 못한다. 왜냐하면 경로거리를 과대평가하는 휴우리스틱의 사용은 과소평가하는
휴우리스틱의 사용보다 전체적인 문제 풀이의 효율성을 오히려 더 증가시키는 경우가 종종 있기 때문이다. 여기에 대한 자세한 설명은 [Dorank
and Michie 66], [Gaschnig 77] 을 참조할 수 있다.
8-퍼즐의 휴우리스틱 함수 ![]() 로 할 때의 목표 노드 깊이에
대한 확장된 전체 노드 개수의 관계가 그림 2 (a) 에 보여진다. 여기서 세 개의 휴우리스틱 함수에 대해서도 비교가 되어 있는데, h1(s)
란 잘못 놓여진 타일의 각각에 대해 현재 놓여진 위치와 올바른 위치까지의 판에서의 거리에 따라 가중값을 두어 구한 값이며, h3(s)
란 h2(s) 에 다른 정보를 첨가한 형태이다. 그림 2 (a) 에서 보듯이 h(s, t) 는 나비-우선 방식
(breadth-first method) 보다는 훨씬 더 효율적이지만
로 할 때의 목표 노드 깊이에
대한 확장된 전체 노드 개수의 관계가 그림 2 (a) 에 보여진다. 여기서 세 개의 휴우리스틱 함수에 대해서도 비교가 되어 있는데, h1(s)
란 잘못 놓여진 타일의 각각에 대해 현재 놓여진 위치와 올바른 위치까지의 판에서의 거리에 따라 가중값을 두어 구한 값이며, h3(s)
란 h2(s) 에 다른 정보를 첨가한 형태이다. 그림 2 (a) 에서 보듯이 h(s, t) 는 나비-우선 방식
(breadth-first method) 보다는 훨씬 더 효율적이지만 ![]() 보다는 비효율적이다. 더욱이 그림
2 (b) 는 목표 노드까지의 실제거리에 대한 휴우리스틱 측정 값과의 관계를 보여 준다. KMAX(i) 이란 실제거리가 I 인 모든 가능한 노드
상 (s, t) 에 대해 구한 휴우리스틱 측정값의 최대값을 말하며 KMIN(i) 는 최소값을 말한다. 또한 여기서 사용한 휴우리스틱은 위에서 논한
h(s, t) (그림 2 (b) 에서 실선부분) 와 h1(s) (그림 2(b) 에서 점선부분) 이다. 그러므로 이상에서 알
수 있듯이 h(s, t) 는
보다는 비효율적이다. 더욱이 그림
2 (b) 는 목표 노드까지의 실제거리에 대한 휴우리스틱 측정 값과의 관계를 보여 준다. KMAX(i) 이란 실제거리가 I 인 모든 가능한 노드
상 (s, t) 에 대해 구한 휴우리스틱 측정값의 최대값을 말하며 KMIN(i) 는 최소값을 말한다. 또한 여기서 사용한 휴우리스틱은 위에서 논한
h(s, t) (그림 2 (b) 에서 실선부분) 와 h1(s) (그림 2(b) 에서 점선부분) 이다. 그러므로 이상에서 알
수 있듯이 h(s, t) 는 ![]() 의 측정값으로 그렇게 좋은 휴우리스틱은
아니며 (그러나 h(s, t) 의 계산시간이 짧다.), h1 과 비슷한 효율성 (생성된 노드 개수로 평가한) 을 가진다.
의 측정값으로 그렇게 좋은 휴우리스틱은
아니며 (그러나 h(s, t) 의 계산시간이 짧다.), h1 과 비슷한 효율성 (생성된 노드 개수로 평가한) 을 가진다.
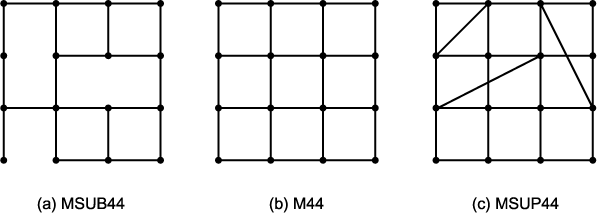
그림 1 맨하탄 거리의 여러 형태
그림 2
문제의 표현 방식을 그래프의 개념을 이용하여 나타낸다. 그래프에서의 노드 (node) 의 개념을 확장하여 휴우리스틱 정보가 이 노드의 내부적 구조에 연관되도록 하는 것이다. 즉, 원래 풀어야 할 문제가 주어졌을 때 이것에 대응되는 그래프는 다음과 같은 표현으로 설명된다 : 그래프 상의 노드는 각 문제상태를 나타내며, 두 노드 간의 아크 (arc) 는 한 문제상태에 적용가능하고 또한 적용시 다른 문제상태를 유도하는 문제규칙을 나타낸다. 더욱이 원래 문제에 대응하는 그래프에 여분의 아크를 첨가함에 의해서 변형된 그래프를 생성할 수 있다. 이렇게 변형되는 그래프에 대응되는 문제를 보조문제 (auxiliary problem) 라 한다. 이 보조문제를 이용해서 현재상태에서 목표상태에 이르는 경로의 최소값을 구하여 이것을 본래 문제의 휴우리스틱 값으로 이용하는 방법이다. 그래프의 개념을 이용해서 표현하는 문제 P 를 Guida and Somalvico 는 “시맨틱 문제 (semantic problem) P” 또는 “S-문제 P” 라고 하였다 [Guida and Somalvico 79]. 시맨틱 문제 P 는 다음과 같이 정의된다 :
P = (A, V, ∏, ∧, i, F)
(1) ![]() 는 주어진 문제 상의 애트리뷰트
(attribute) 인
는 주어진 문제 상의 애트리뷰트
(attribute) 인 ![]() 들로 구성된다.
들로 구성된다.
(2) ![]() 는 애트리뷰트
는 애트리뷰트 ![]() 에 주어질 수 있는 값들로 구성된
집합인
에 주어질 수 있는 값들로 구성된
집합인 ![]() 들로 구성된다.
들로 구성된다.
(3) ∏ 는
유한개의 서술문들로 이루어지며, 문제가 지닌 성질 (property) 을 나타낸다.
(4) ∧ 는
유한개의 서술문들로 이루어지며, 문제에 내포된 합법적 조건 (legal condition) 을 나타낸다. 여기서 그래프의 노드는 ∏ 에 있는 성질들로
명시화될 수 있으며, 아크는 ∧ 에 있는 조건들의 만족에 의해 나타내 질 수 있다.
(5) i 는
초기 시작 노드를 나타낸다.
(6) F 는 종결 노드들로 구성된 집합을 나타낸다.
그러면 8-퍼즐 문제를 이용해서 “시맨틱 문제” 의 정의가 어떻게 적용되고 이에 따라 보조 그래프가 어떻게 유도되어 휴우리스틱이 생성되는지 살펴보자 :
A 는 9 개의 요소 (element) 로 구성된다.
![]()
여기서 ![]() 는 8-퍼즐에서의 빈 공간을 나타내고
(이를 빈 타일로 지칭하겠음),
는 8-퍼즐에서의 빈 공간을 나타내고
(이를 빈 타일로 지칭하겠음), ![]() (i = 1, …, 8) 는 i 번 숫자를 가진 타일을 나타낸다. A 에 속하는 애트리뷰트
(i = 1, …, 8) 는 i 번 숫자를 가진 타일을 나타낸다. A 에 속하는 애트리뷰트 ![]() 가 가질 수 있는 값의 영역
가 가질 수 있는 값의 영역 ![]() 는 i 번 숫자를 가진 타일이
취할 수 자는 판 (board) 에서의 가능한 위치들이다. 예를 들어 판의 열과 행이 각각 1, 2, 3 으로 일련번호가 표시되어 있다고 가정하면,
판에 놓여진 어떤 타일의 위치는 좌표 (x, y) 로 나타낼 수 있으므로
는 i 번 숫자를 가진 타일이
취할 수 자는 판 (board) 에서의 가능한 위치들이다. 예를 들어 판의 열과 행이 각각 1, 2, 3 으로 일련번호가 표시되어 있다고 가정하면,
판에 놓여진 어떤 타일의 위치는 좌표 (x, y) 로 나타낼 수 있으므로 ![]() , i = 0, 1, 2, 3, …, 8 ; 이며
, i = 0, 1, 2, 3, …, 8 ; 이며 ![]() 으로 표현이 된다.
으로 표현이 된다.
8-퍼즐 문제를 수행하는 과정에서 나타나는 유일한 성질 (property) 은
두 개의 타일이 같은 위치에 동시에 놓여질 수 없다는 것이다. 그러므로 성질집합 ∏ 에 속하는 한 성질 ![]() 을 논리적 서술문을 이용해 표현할
수 있다 :
을 논리적 서술문을 이용해 표현할
수 있다 :
![]() , i, j = 0, 1, …, 8,
, i, j = 0, 1, …, 8,
여기서
![]()
이며
![]() , i = 0, i, …, 8.
, i = 0, i, …, 8.
더욱이 현재 노드 상태 ![]() 에서 다음 노드 상태
에서 다음 노드 상태 ![]() 로 합법적 전이가 이루어 진다는
조건들의 집합 ∧ 은 다음과 같은 것들이 있음을 헤아릴 수 있다.
로 합법적 전이가 이루어 진다는
조건들의 집합 ∧ 은 다음과 같은 것들이 있음을 헤아릴 수 있다.
① 매 번 움직여질 때 오직 두 개의 타일만이 동시에 움직여진다 :
![]() , i, j = 0, 1, …, 8
, i, j = 0, 1, …, 8
여기서 (∃!i) 는 “…하는 i 가 오직 하나 존재한다” 는 의미를 나타내며
![]()
![]()
② 매 번 움직여지는 타일 가운데 하나는 빈 타일이다 :
![]()
③ 매 번 움직여 질 때 두 개의 타일의 교환이 이루어지는데, 이 때 이것들은 판에서 같은 열이나 또는 같은 행에 위치해 있는 경우만 가능하다 :
![]() ,
i = 0, 1, …, 8,
,
i = 0, 1, …, 8,
여기서
![]()
이며 각각 판에서의 위치를 나타낸다.
④ 매 번 움직여지는 두 개의 타일은 인접해 있는 경우에 가능하다 :

문제 P 의 보조 시맨틱 문제 P’ 는 위에서 정의한 시맨틱 문제의 표현을 빌리면 다음과 같이 나타나진다 :
P’ = (A’, V’, ∏’, ∧’, i’, F’),
여기서
A’ = A, V’ = V, ∏’ = π, ∧’ ⊆ ∧, i’ = i, F’ = F.
즉, 문제 P 의 보조 시맨틱 문제 P’ 는 합법적 전이조건집합 ∧ 의 부분집합
∧’ 를 취하여 그래프를 형성하게 된다. 이 보조 시맨틱 문제 P’ 를 이용해서 실제적으로 구한 현재 상태 n 에서 목표상태 n’ 이르는 경로의
최소값이 본래 문제 P 에서의 휴우리스틱 값으로 이용한다. 보조문제 P’ 의 그래프에서 현 상태에서 목표상태에 이르는 경로의 최소값은 문제 P
의 그래프에서 구한 최소값보다 항상 작다는 것이 증명되어져 있다 [Guida and Somalvico 79]. 이와 같이 ∧ 의 부분집합 ∧’
을 지닌 보조문제를 이용하여 원래 문제의 휴우리스틱을 구하게 된다. 그러나 보조문제를 유도하기 위해 ∧ 의 원소들 중에서 삭제되는 합법적 전이조건
![]() 들이 어떤 것인지에 따라 휴우리스틱
값의 크기, 탐색기간, 기억공간 등이 영향을 받게 된다. 그러므로 ∧ 의 원소들 중에서 어떤 종류를 얼마 만큼 삭제해야 할 것인지에 대한 구체적인
언급이 필요하다.
들이 어떤 것인지에 따라 휴우리스틱
값의 크기, 탐색기간, 기억공간 등이 영향을 받게 된다. 그러므로 ∧ 의 원소들 중에서 어떤 종류를 얼마 만큼 삭제해야 할 것인지에 대한 구체적인
언급이 필요하다.
4. 서술문을 통한 문제 표기를 이용하는 방법
문제의 규칙과 목표상태의 정의는 서술문 (predicate) 들을 이용해 나타낼 수 있다. 풀고자 하는 문제의 휴우리스틱 유도방법은 이 문제보다 완화된 문제를 이용하게 되는데, 여기서 완화된 문제를 유도하는 방법은 규칙을 정의하는 서술문들의 일부를 세분화 또는 삭제하거나, 문제의 목표상태를 정의하는 서술문들의 일부를 삭제함에 의해 이루어진다.
8-퍼즐의 예에 의해 위에서 말한 완화방법 (relaxation scheme) 을 설명해본다 : 먼저 3 가지 기본적인 서술문이 주어진다 :
ON(x, y) : 타일 x 가 판에서의 y 위치에 놓여 있다.
CLEAR(y) : y 위치에는 타일이 없다. 즉 빈 타일 (또는 빈공간) 이다.
ADJ(y, z) : y 위치는 z 위치와 인접해 있다.
여기서 변수 x 는 타일 ![]() 을 나타내고, 변수 y, z 은
위치값
을 나타내고, 변수 y, z 은
위치값 ![]() 을 나타낼 수 있다. 만일 판에서의
각 위치값을 그림 3(a) 와 같이 정하면 그림 3(b) 에 나타난 상태는 위의 3 가지 기본적인 서술문을 이용해서 표현이 된다 :
을 나타낼 수 있다. 만일 판에서의
각 위치값을 그림 3(a) 와 같이 정하면 그림 3(b) 에 나타난 상태는 위의 3 가지 기본적인 서술문을 이용해서 표현이 된다 :
![]() ,
,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
그림 3
![]()
이며, 판의 위치값들의 관계는 ![]() 이다. 타일 x 가 위치값 y
에서 위치값 z 로의 전이가 되는 규칙은 다음과 같이 표현된다 :
이다. 타일 x 가 위치값 y
에서 위치값 z 로의 전이가 되는 규칙은 다음과 같이 표현된다 :
MOVE(x, y, z) :
전제조건 (P) : ON(x, y), CLEAR(z), ADJ(y, z)
첨가사항 (A) : ON(x, z), CLEAR(y)
삭제사항 (D) : ON(x, y), CLEAR(z)
여기에서 P 는 MOVE(x, y, z) 란 규칙이 적용되기 위하여 문제상태가 지녀야 할 서술문들의 나열이며, A 는 규칙을 적용했을시 유도되는 문제상태를 나타내는 서술문들로부터 삭제되는 서술문들이며, D 는 새로이 첨가되는 서술문들을 나타낸다.
8-퍼즐의 문제 풀이는 초기상태에서 목표상태에 이르는 경로를 규칙 MOVE(x, y, z) 의 연속된 적용의 나열로 구하게 된다. 휴우리스틱을 유도하기 위해 먼저 규칙 MOVE(x, y, z) 을 완화시킨다. 예로서 규칙 MOVE(x, y, z) 의 전제 조건 P 에 나타난 CLEAR(z) 와 ADJ(y, z) 을 삭제함에 의해 완화된 문제를 생각해보자. 그러면 제한조건이 완화된 규칙을 적용하여 현 상태에서 목표상태에 이르는 경로를 유도하는데 필요한 값이 원래 문제의 휴우리스틱 값으로 이용된다. 이와 같이 규칙 MOVE(x, y, z) 를 표현하는 서술문들 중에서 몇 개를 삭제하거나 더 세분화함에 의해서 원래 문제보다 완화된 문제를 유도하게 된다.
그러나 이렇게 하여 유도되는 완화된 문제가 반드시 보다 간단한 문제로 되는 것은 아니다. 그러므로 완화작업을 맹목적으로 행하기 보다는 문제보다 해결하기 쉽고 동시에 아주 다른 형태가 되지 않도록 특정 모델을 구하는 방향으로 진행되어야 한다.
문제의 제약조건을 완화하는 것에 의해 유도되는 문제가 세 분
(decompose) 의 특성을 지니면 대개 간단하며 쉽게 휴우리스틱을 생성하게끔 한다. 여기서 세분 특성이란 문제의 부목표 (subgoal)
들을 서로 독립되게 만족시킬 수 있는 각기 독립된 여러 부속문제 (subproblem) 들이 지니는 특성이다. 예를 들어, 8-퍼즐에서 원하는
위치에 놓여질 수 있다고 한다면 각각의 부목표 조건들인 ![]() 등은 서로 독립적으로 만족되어
질 수 있다. 실제적으로 완전한 세분특성을 지니는 문제는 드물며 적용조건들 중에 많은 부분을 삭제함에 의해 이루어질 수 있다. 그러나 부분-세분
(semi-decomposible) 모델이라 불리는 약한 형태의 독립성에 의해서도 문제의 휴우리스틱을 쉽게 유도할 수 있는데 이에 대하여는 계속
연구가 진행 중이다.
등은 서로 독립적으로 만족되어
질 수 있다. 실제적으로 완전한 세분특성을 지니는 문제는 드물며 적용조건들 중에 많은 부분을 삭제함에 의해 이루어질 수 있다. 그러나 부분-세분
(semi-decomposible) 모델이라 불리는 약한 형태의 독립성에 의해서도 문제의 휴우리스틱을 쉽게 유도할 수 있는데 이에 대하여는 계속
연구가 진행 중이다.
5. 문제의 모델화를 이용하는 방법
휴우리스틱을 문제 성질에 관계없이 독립적으로 구하기 위해 요구되는 단순화된 문제들을 체계적이고 자동적으로 유도하는 기법을 제시한 방법이다. 이 방법은 실제적으로 여러 문제에 대해 이를 적용하여 만족한 결과를 도출했다는 점에서 종래의 방법보다 더 구체적이며, 휴우리스틱을 형식적이고 일반화된 수식으로 표현하였다는데 주목할 필요가 있다.
앞 절에서 언급한 Pearl 의 방법에서는 문제의 규칙을 표현하는 서술문을 완화한 반면에 여기서는 문제의 모델을 설정하고 이 모델 상의 한 요소로 정의되는 문제 내의 기본 단위들에 대한 제약조건들을 완화하는 것에 의해 단순화된 규칙과 부목표를 자동적으로 유도한다. 이와 같은 방식은 Pearl 의 것과는 달리 완화된 문제가 항상 세분의 특성을 만족하게끔 되어 보다 더 단순한 문제가 유도될 수 있다는 점이다.
(1) 문제 모델
문제의 모델화에 사용되는 여러 용어들 중에 핵심이 되는 용어인 기본단위 (elementary unit), 위치값 (position value) 그리고 전이조건공식 (successor condition formula ; 줄여서 scf 라 함) 을 구체적으로 설명하고 나머지 부분은 간략히 언급한다.
기본단위란 문제에 내포된 근본적인 단위로서 이것들로 이루어진 집합을 ![]() 라 하였을 때, 8-퍼즐의 경우
라 하였을 때, 8-퍼즐의 경우
![]() 는 한 타일 또는 공백 (빈 타일이라
하겠음) 을 나타내게 되며, 블록 세계 (block world) 에서의 로보트 계획 (robot planning) 문제인 경우
는 한 타일 또는 공백 (빈 타일이라
하겠음) 을 나타내게 되며, 블록 세계 (block world) 에서의 로보트 계획 (robot planning) 문제인 경우 ![]() 는 한 개의 특정 블록을 나타낸다.
위치값이란 문제상태
는 한 개의 특정 블록을 나타낸다.
위치값이란 문제상태 ![]() 에서 각 기본단위가 취하는 값으로서
에서 각 기본단위가 취하는 값으로서
![]() 를 표현하는데 사용된다. 8-퍼즐의
경우 판의 위치값 설정을 그림 3(a) 와 같이 정한다면 그림 4 의 상태
를 표현하는데 사용된다. 8-퍼즐의
경우 판의 위치값 설정을 그림 3(a) 와 같이 정한다면 그림 4 의 상태 ![]() 에서 1 번 타일의 위치값은
에서 1 번 타일의 위치값은 ![]() 이며, 2 번 타일의 위치 값은
이며, 2 번 타일의 위치 값은
![]() 이 된다. 이것은 위치 함수
pf 를 사용하여
이 된다. 이것은 위치 함수
pf 를 사용하여 ![]() 으로 표현한다. 그림 5 의 로보트
계획에서는 위치값 설정을 지점
으로 표현한다. 그림 5 의 로보트
계획에서는 위치값 설정을 지점 ![]() 에서의 블록 위치와 로보트 손이
블록을 쥐고 있는지 (hold) 의 여부를 사용한다. 그러면 기본단위인 블록 A, B, C 는 각각
에서의 블록 위치와 로보트 손이
블록을 쥐고 있는지 (hold) 의 여부를 사용한다. 그러면 기본단위인 블록 A, B, C 는 각각 ![]() 이 된다.
이 된다.
그림 4 8-퍼즐 문제의 상태들
그림 5 로보트 계획문제의 상태 ey
전이조건공식 (scf) 은 각 문제규칙들의 주어진 문제상태에 대해 이의 적용을 위한 전제조건과 적용하였을시 유도되는 문제상태의 조건을 나타낸다. 8-퍼즐의 경우, scf 를 PROLOG 형태의 언어에 의해 나타내어 보며 다음과 같다. :
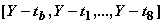
여기서 변수 ![]() 와
와 ![]() , i = 0, 1, …, 8, 는 각각 타일
, i = 0, 1, …, 8, 는 각각 타일 ![]() 가 규칙이 적용가능한 문제상태에서의
취할 수 있는 위치값과 적용했을시 유도되는 문제상태에서 취할 수 있는 위치값을 나타낸다. 부호 ‘;’ 은 논리적 OR 을 나타내며 ‘,’ 은 논리적
AND 를 나타낸다. 또한 각
가 규칙이 적용가능한 문제상태에서의
취할 수 있는 위치값과 적용했을시 유도되는 문제상태에서 취할 수 있는 위치값을 나타낸다. 부호 ‘;’ 은 논리적 OR 을 나타내며 ‘,’ 은 논리적
AND 를 나타낸다. 또한 각 ![]() 에 대해
에 대해 ![]() 는 다음과 같이 표현된다 :
는 다음과 같이 표현된다 :
![]()
여기에서 posv 는 다음과 같다 :

여기서 ![]() 상태에서
상태에서 ![]() 상태로의 전이가 이루어진다는 사실은
규칙들
상태로의 전이가 이루어진다는 사실은
규칙들 ![]() 가운데 적어도 한 개의 규칙이
가운데 적어도 한 개의 규칙이
![]() ,
, ![]() 적용시에 참이 된다는 뜻이다.
규칙
적용시에 참이 된다는 뜻이다.
규칙 ![]() 란 빈 타일
란 빈 타일 ![]() 과 타일
과 타일 ![]() 가 서로 위치를 교환할 때 적용되는
위치값들의 변화를 나타내는 규칙을 말하며, member 란 이의 첫 번째 변수항
가 서로 위치를 교환할 때 적용되는
위치값들의 변화를 나타내는 규칙을 말하며, member 란 이의 첫 번째 변수항 ![]() 이 두번째 상수항
이 두번째 상수항 ![]() 내의 여러 값들 중의 하나를 택할
수 있다는 것을 뜻한다.
내의 여러 값들 중의 하나를 택할
수 있다는 것을 뜻한다.
위의 용어들에 기초한 문제 모델 M 은 다음과 같이 정의된다 :
![]()
EU 는 기본단위들로 이루어진 집합이다.
AT 는 애트리뷰트들로 이루어진 집합이며, 애트리뷰트들의 개수는 기본단위들의 위치값의 표현방식에 따라 결정된다.
S 는 문제의 상태공간이다.
P 는 기본단위가 취할 수 있는 위치값들로 이루어진 집합이다.
Pf 는 위치함수 (position function) pf : EU X S → P 로서 주어진 문제상태에서 기본단위의 위치값을 나타낸다.
R 은 규칙들로 이루어진 집합이다.
SUCCR ⊆ R X S X S 는 두 개의 상태 (예로서 ![]() 라 하자) 와 한 개의 규칙
(예로서
라 하자) 와 한 개의 규칙
(예로서 ![]() 이라 하자) 로 구성된 요소들로서
이루어진 집합으로 각 요소
이라 하자) 로 구성된 요소들로서
이루어진 집합으로 각 요소 ![]() 의 관계는
의 관계는 ![]() 상태에서 규칙
상태에서 규칙 ![]() 가 적용되어
가 적용되어 ![]() 의 상태가 되는 것을 뜻한다.
다시 말하면 전이조건공식
의 상태가 되는 것을 뜻한다.
다시 말하면 전이조건공식 ![]() 가 참이 되는데, 이 때 참이
되는 이유는 규칙
가 참이 되는데, 이 때 참이
되는 이유는 규칙 ![]() 에 대한 조건이 참이 되었기 때문이다.
공식화하여 정의하면,
에 대한 조건이 참이 되었기 때문이다.
공식화하여 정의하면,
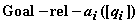
c 는 비용함수 c : SUCCR → R 로서 R 은 실수집합이며 규칙 적용을 위한 비용을 뜻한다.
![]() 는 문제의 초기상태이다.
는 문제의 초기상태이다.
Goal 은 목표조건공식 (goal condition formula) 이다.
(2) 휴우리스틱 유도
휴우리스틱을 구하기 위해 먼저 원래의 전이조건공식 scf 와 목표조건공식
Goal 을 각 기본단위에 대해 완화 (relax) 하는 방법을 생각한다. EU 를 ![]() 에 대한 완화된 공식
에 대한 완화된 공식 ![]() 를 다음을 만족하도록 유도한다
:
를 다음을 만족하도록 유도한다
:
모든
가능한 상수항 ![]() 에 대해 (여기서
에 대해 (여기서 ![]() , i = 1, …, n),
, i = 1, …, n),
만일
![]() = 참이면,
= 참이면,
![]() = 참이다.
= 참이다.
이와 유사하게 Goal 의 완화된 공식 ![]() 를 다음을 만족하도록 유도한다,
를 다음을 만족하도록 유도한다,
모든
가능한 상수항 ![]() 에 대해 (여기서
에 대해 (여기서 ![]() , i = 1, …, n),
, i = 1, …, n),
만일
![]() = 참이면,
= 참이면,
![]() = 참이다.
= 참이다.
(1) 절에서 언급한 바와 같이 전이조건공식 scf 는 규칙들에 관한 제약조건들로써
구성되어 있다. 그러므로 scf 의 기본단위 ![]() 에 대한 완화는 곧 각 규칙들이
이 모든 기본단위들에 대해 만족해야 되는 제약조건들을 단지
에 대한 완화는 곧 각 규칙들이
이 모든 기본단위들에 대해 만족해야 되는 제약조건들을 단지 ![]() 에 대한 제약조건만을 만족하게끔
하여 단순화된 규칙을 유도하게 된다. 그러면 각 기본단위들에 관한 완화된 공식을 이용하여 문제상태
에 대한 제약조건만을 만족하게끔
하여 단순화된 규칙을 유도하게 된다. 그러면 각 기본단위들에 관한 완화된 공식을 이용하여 문제상태 ![]() 에서 완화된 목표공식의 각 부목표에
이르는 경로의 최적값을 구하게 되며 이를 이용하여 휴우리스틱
에서 완화된 목표공식의 각 부목표에
이르는 경로의 최적값을 구하게 되며 이를 이용하여 휴우리스틱 ![]() 값을 유도한다.
값을 유도한다.
실제적으로 단순화된 공식 ![]() 가 어떻게 만들어지는지 8-퍼즐의
경우에 대해 살펴보자. PROLOG 언어에 의해 각
가 어떻게 만들어지는지 8-퍼즐의
경우에 대해 살펴보자. PROLOG 언어에 의해 각 ![]() 에 대한
에 대한 ![]() 는 다음과 같이 표현된다.
는 다음과 같이 표현된다.
![]()
여기서 변수 ‘-’ 은 어떠한 위치값과도 매치 (match) 가 될 수 있음을
나타내는 것이며, 변수 ‘-’ 자체에 값이 지정되는 것은 아니다. 그러므로 위의 표현은 타일 ![]() 가 위치값
가 위치값 ![]() 에서 위치값
에서 위치값 ![]() 로의 전이가 참이 되는가에 대한
검사는 타일
로의 전이가 참이 되는가에 대한
검사는 타일 ![]() 이외의 기본단위들인 타일들의 위치값에
제약을 받지 않는다는 조건하에 이루어진다는 것이다.
이외의 기본단위들인 타일들의 위치값에
제약을 받지 않는다는 조건하에 이루어진다는 것이다.
이제 휴우리스틱 ![]() 을 유도하는 과정을 살펴보자.
먼저 규칙들의 적용비용 w 가 일정하다고 한다. 즉, w = 1. 그러면 문제는 주어진 상태
을 유도하는 과정을 살펴보자.
먼저 규칙들의 적용비용 w 가 일정하다고 한다. 즉, w = 1. 그러면 문제는 주어진 상태 ![]() 에서 목표상태
에서 목표상태 ![]() 에 이르도록 하는데 필요한 최소의
규칙들에 대한 측정값을 유도하는 것이다.
에 이르도록 하는데 필요한 최소의
규칙들에 대한 측정값을 유도하는 것이다. ![]() 를 기본단위
를 기본단위 ![]() 가 목표상태에서 취할 수 있는
위치값들의 집합이라고 하고
가 목표상태에서 취할 수 있는
위치값들의 집합이라고 하고 ![]() 를 현재상태
를 현재상태 ![]() 에서의 위치값이 목표상태에서의
가질 수 있는 위치값과 다른 기본단위들로 이루어진 집합이라 하자.
에서의 위치값이 목표상태에서의
가질 수 있는 위치값과 다른 기본단위들로 이루어진 집합이라 하자.
현재상태 ![]() 에서 목표상태
에서 목표상태 ![]() 에 이르기 위해 요구되는 최소의
규칙들의 적용비용 (4 장에서 언급했듯이
에 이르기 위해 요구되는 최소의
규칙들의 적용비용 (4 장에서 언급했듯이 ![]() 로 표현함) 은 각 기본단위
로 표현함) 은 각 기본단위 ![]() 의 현재 위치값
의 현재 위치값 ![]() 로부터
로부터 ![]() 에 속한 어느 위치값에도 이르기
위해 요구되는 최소의 단순화된 규칙들의 적용비용 (여기서는
에 속한 어느 위치값에도 이르기
위해 요구되는 최소의 단순화된 규칙들의 적용비용 (여기서는 ![]() 로 표현함) 보다 항상 같거나
크다. 그러므로
로 표현함) 보다 항상 같거나
크다. 그러므로 ![]() 을
을
![]()
이라 하였을 때 ![]() 는 허용성
(admissibility) 을 지닌다. 더욱이 집합
는 허용성
(admissibility) 을 지닌다. 더욱이 집합 ![]() 가 하나 이상의 원소를 지니면,
가 하나 이상의 원소를 지니면,
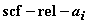 도 허용성을 지니는 휴우리스틱이
된다. 여기서 s 란 한 규칙에 의해 변화되는 위치값을 취할 수 있는 기본단위 개수의 최대값을 뜻한다. 허용성을 지니는 또 다른 휴우리스틱
도 허용성을 지니는 휴우리스틱이
된다. 여기서 s 란 한 규칙에 의해 변화되는 위치값을 취할 수 있는 기본단위 개수의 최대값을 뜻한다. 허용성을 지니는 또 다른 휴우리스틱 ![]() 는 다음과 같이 주어질 수 있다
:
는 다음과 같이 주어질 수 있다
:

여기서 집합 Ω 란 어떠한 규칙에 의해서도 위치값의 변화를 취하는 기본단위로 모여진 집합을 뜻한다. 예를 들어 8-퍼즐에서 ![]() 가 되며 s = 2 가 된다.
가 되며 s = 2 가 된다.
위에서 유도된 3 개의 휴우리스틱의 값들 중 최대값을 지닌 휴우리스틱을 현재상태
![]() 에서의 휴우리스틱
에서의 휴우리스틱 ![]() 로 정한다. 좀더 형식적으로 표현한다면,
로 정한다. 좀더 형식적으로 표현한다면,
![]()
여기서

위 식에서 ![]() 는 기본단위
는 기본단위 ![]() 가 현재 상태
가 현재 상태 ![]() 에서 취하고 있는 위치값
에서 취하고 있는 위치값 ![]() 에서
에서 ![]() 가 목표상태에서 취할 수 있는
위치값들
가 목표상태에서 취할 수 있는
위치값들 ![]() 중의 하나에 이르기 위해 요구되는
단순화된 규칙들의 최소 적용비용이다.
중의 하나에 이르기 위해 요구되는
단순화된 규칙들의 최소 적용비용이다. ![]() 를 구하는 알고리즘은 [Yoo
85] 를 참조할 수 있다. 각 규칙의 적용비용이 일정하지 않는 경우에는
를 구하는 알고리즘은 [Yoo
85] 를 참조할 수 있다. 각 규칙의 적용비용이 일정하지 않는 경우에는 ![]() 에서
에서 ![]() 에 속한 위치값에 도달하기 위해
요구되는 최소의 단순화된 규칙들의 적용비용은
에 속한 위치값에 도달하기 위해
요구되는 최소의 단순화된 규칙들의 적용비용은 ![]() 로 나타낼 수 있으며,
LOCS 를 이용한 휴우리스틱
로 나타낼 수 있으며,
LOCS 를 이용한 휴우리스틱 ![]() 도 위에서 논한 일정비용을 지닌
문제 경우가 유사하게 유도된다. 이에 대한 자세한 설명은 [Yoo 85] 에서 얻을 수 있다.
도 위에서 논한 일정비용을 지닌
문제 경우가 유사하게 유도된다. 이에 대한 자세한 설명은 [Yoo 85] 에서 얻을 수 있다.
그러면 하나의 예로써 8-퍼즐에서 ![]() 가 어떻게 유도되는지 살펴보라.
그림 6.2 에서 보듯이 현재상태
가 어떻게 유도되는지 살펴보라.
그림 6.2 에서 보듯이 현재상태 ![]() 와 목표상태
와 목표상태 ![]() 는 각각
는 각각
![]()
로 표현이 될 수 있다. 상태 ![]() 와 상태
와 상태 ![]() 의 각각 대응되는 위치값 중에
같지 않는 위치 값을 취하는 기본단위들은
의 각각 대응되는 위치값 중에
같지 않는 위치 값을 취하는 기본단위들은 ![]() 에 속하므로
에 속하므로
![]()
이다. 판의 위치값 설정을 그림 1(a) 와 같이 정하고 규칙 적용비용 w 는
1 로 했으므로 단순화된 규칙 적용에 의해 유효되는 ![]() 에 속하는 각각의 기본단위의
Ldist 는 다음과 같게 된다 :
에 속하는 각각의 기본단위의
Ldist 는 다음과 같게 된다 :

8-퍼즐에서는 s = 2 이므로 ![]() 는
는

또한 집합 ![]() 이므로
이므로 ![]() 는
는

그러므로 ![]()
마지막으로 ![]() 값을 구하는데 요구되는 시간이
위의 유도방법을 사용했을시 요구되는 시간보다 좀더 허용된다면 실제값인
값을 구하는데 요구되는 시간이
위의 유도방법을 사용했을시 요구되는 시간보다 좀더 허용된다면 실제값인 ![]() 에 보다 더 접근하는
에 보다 더 접근하는 ![]() 값을 유도할 수 있는 방법이 있다.
위에서 언급한 휴우리스틱 유도방법은 문제 모델에 정의되는 각 기본단위에 대해 완화된 전이조건공식을 유도하고 이를 적용하여 구한 최소 경로값을
값을 유도할 수 있는 방법이 있다.
위에서 언급한 휴우리스틱 유도방법은 문제 모델에 정의되는 각 기본단위에 대해 완화된 전이조건공식을 유도하고 이를 적용하여 구한 최소 경로값을 ![]() 값으로 도출하는데 이용하였다.
그러나 기본단위들로 이루어진 집합 EU 에 분할 (partition) 을 행하여 (분할된 각 요소들을 객체 (object) 라 함), 이때 생기는
각 객체에 대해 완화된 전이조건공식을 유도하고 이를 적용하여 구한 최소경로값을 이용해서
값으로 도출하는데 이용하였다.
그러나 기본단위들로 이루어진 집합 EU 에 분할 (partition) 을 행하여 (분할된 각 요소들을 객체 (object) 라 함), 이때 생기는
각 객체에 대해 완화된 전이조건공식을 유도하고 이를 적용하여 구한 최소경로값을 이용해서 ![]() 값을 유도할 수 있다. 객체는
하나 이상의 기본단위를 포함하므로 각 객체에 속해 있는 기본단위들 사이의 위치값 배정은 제약을 받는다. 그러므로 하나의 기본단위에 대해 유도된
완화된 전이조건공식보다 객체 대해 완화된 전이조건공식은 원래의 전이조건공식 scf 에 좀더 가까운 제약조건을 지니므로 이 공식을 이용해서 구한
휴우리스틱
값을 유도할 수 있다. 객체는
하나 이상의 기본단위를 포함하므로 각 객체에 속해 있는 기본단위들 사이의 위치값 배정은 제약을 받는다. 그러므로 하나의 기본단위에 대해 유도된
완화된 전이조건공식보다 객체 대해 완화된 전이조건공식은 원래의 전이조건공식 scf 에 좀더 가까운 제약조건을 지니므로 이 공식을 이용해서 구한
휴우리스틱 ![]() 값은 위에서 언급한 방법으로 구한
값보다 실제값
값은 위에서 언급한 방법으로 구한
값보다 실제값 ![]() 에 더 접근할 가능성을 지닌다.
에 더 접근할 가능성을 지닌다.
객체에 대해 완화된 전이조건공식 ![]() 을 유도하는 방법은 기본단위에
대해 완화된 공식
을 유도하는 방법은 기본단위에
대해 완화된 공식 ![]() 의 경우와 유사하며
Ldist, LOCS 등도 비슷하게 정의된다. 이에 대한 자세한 설명은 [Yoo 85] 를 참조하기 바란다.
의 경우와 유사하며
Ldist, LOCS 등도 비슷하게 정의된다. 이에 대한 자세한 설명은 [Yoo 85] 를 참조하기 바란다.