
문제 풀이와 계획 수립 (Problem Solving and Planning)
인공지능 원론 : 유석인, 교학사, 1988, Page 129~198
2. 범용 문제 풀이 시스템 (General Problem Solver, GPS)
3. 전향 생성 시스템 (forward production system)
(3) 전향 생성 시스템 (forward production system)
4. 후향 생성 시스템 (backward production system)
(4) 목표들의 상호작용 (interacting goals)
(1) STRIPS 의 제어전략 (control strategy)
8. 계층적 계획 (hierarchical planning)
인공지능에서 문제 풀이란, 추상적으로는 잘 정의된 목표에 도달하기 위한 지적인 행동으로 정의될 수 있다. 좀더 구체적이고 형식적인 정의는 크게 다음의 세 가지로 구별되어진다. 첫째, [Newell & Simon 72] 은 문제 풀이란, 문제의 시작상태에서 원하는 목표상태로 변형시키는 일련의 연속된 규칙들을 구하는 것으로 정의하였다. 여기서 지적 행동이란 문제상태에 여러 가지 종류의 규칙들을 적용함에 의해 생겨나는 여러 상태들에 관한 분석을 통해서 적절한 규칙 순서를 찾는 탐색으로 구성된다. 둘째, [McDermott 67] 와 [Wilensky 83] 는 문제 풀이에 대한 또 다른 정의를 내렸다. 그들에 의하면 문제 풀이란, 계획은 실증화 (instantiation) 시킨다는 것이다. 해결해야 하는 문제에 대한 해답의 윤곽을 위해 여러 종류의 계획이 있게 되는데, 문제 풀이란 이러한 계획들을 명시하고 실증화시키는 것을 말한다. 세째, 문제 풀이란 과거에 해결한 유사한 문제들을 유추 (analogy) 함에 의해 새로운 문제를 풀어가는 것을 말한다. 이것은 풀고자 하는 새로운 문제와 유사성을 지닌 과거 문제들을 찾아서 이것들이 새로운 문제의 해결에 잠재적으로 적용이 될 수 있도록 변형시키는 과정을 수반하게 된다. 이 방법은 [Carbonell 83] 에 의해 주장되고 발전되었다.
문제 풀이 기법들을 분류하는 바람직한 방식은, 요구되는 영역 지식 (domain information) 의 양과 성질에 의해 다음과 같이 열거된다.
① 구조화된 영역 지식이나 유용한 과거 문제 풀이의 경험을 이용하지 않는 경우에는 세분화 방법 (weak method) 이라 불리우는 휴우리스틱 탐색과 방법-목적 분석 과정 (means-ends analysis) 에 근거를 둔 방법이 적용된다.
② 계획, 절차와 같은 형태로 특정한 영역 지식이 영역 지식의 형성되어 있을 때는, 그러한 계획이 직접적으로 실증화되거나 여러 부속문제에 대한 반복적인 적용을 통해 실증화된다.
③ 일반적인 계획이 적용된다면 이 계획을 이용해서 문제를 세분화하여 탐색 공간이 작은 여러 문제들로 유도하여 문제의 복잡성을 줄이게 된다.
④ 특정 계획의 적용은 안되지만 과거에 해결한 유사한 문제가 있다면, 유추에 의한 변형에 의해 새로운 상황의 해결에 도움이 되도록 적용한다.
그림 1 은 위에서 언급한 문제 풀이 기법들을 나타내고 있으며, 이들 각각이 서로 연관되어질 수 있음을 보인다. 문제 풀이의 추론 (inference) 부분은 일반적으로 위의 언급된 여러 가지 기법들을 결합하여 사용하고 있다.

그림 1 문제 풀이를 위한 기법들
(a) 특정 계획의 실증화 (b) 유추를 통한 변형
(c) 문제 복잡성을 줄이기 위해 일반적 계획을
적용 (d) 세분화 방법을 적용
이 장에서는 여러 가지 문제 풀이 기법 가운데 ① 의 방법인 세분화 방법에 대해 살펴보고자 한다. 이 기법의 이용을 위하여는 문제가 도달하고자 하는 목표상태에 대한 지식, 문제 규칙들, 이 규칙들이 적용될 수 있는 전제조건들 그리고 규칙들이 적용되었을 때 나타나는 결과들에 대한 지식 등이 필요하다. ① 의 기법 이외의 다른 기법의 이용을 위한 연구는 앞에서 언급한 관련문헌에서 찾아볼 수 있다.
범용 문제 풀이 시스템은 인공지능 역사에 있어 아마도 가장 널리 알려진 프로그램 중의 하나이다. [Newell, Shaw and Simon 59] 에 의해 최초로 제안된 이것은 그 후 여러 학자들에 의해 다듬어졌다. 범용 문제 풀이 시스템에 대한 최초의 동기는 컴퓨터 과학과 심리학의 흥미로운 혼합이었다. 컴퓨터학의 측면에서 범용 문제 풀이 시스템은 명제 논리학, 평면기하, 적분계산과 같은 특정분야에서의 문제 풀이를 위한 컴퓨터 프로그램 (computer program) 들을 논리적으로 일반화시킨 것이었으며, 심리학 측면에서 범용 문제 풀이 시스템은 지식을 처리하는 인간 두뇌의 성격들에 대한 모델로써 제안되어진 것이었다.
범용 문제 풀이 시스템 (GPS) 은 두 개의 기본원칙은 구현된다. 이는 방법-목적 분석방법 (means-ends analysis) 과 순환적 (recursive) 인 문제 풀이 시스템이다. 방법-목적 분석은 한 연산자 (operator) 가 적용이 된다면 이에 대한 적용의 목적이 있다는 것을 확신하게 만드는 기법이다. 가령 두 개의 목적물 (object) 에 대해 이들을 나타내는 속성들이 정의되어 있다고 하자. 여기서 두 목적물간의 차이는 몇 가지 속성 (atribute) 에서의 값의 불일치로 나타나진다. 이와 같은 차이를 줄이기 위해서는 이 차이를 줄일 수 있는 연산자를 찾아야 한다. 그러나 대부분의 경우, 요구되는 연산자가 현재 목적물 (문제 풀이 시스템에서의 현재 상태라는 개념과 같음) 에 직접 적용될 수 없기 때문에, 이 연산자를 적용시킬 수 있는 상태로 만드는 부속문제 (subproblem) 를 면저 설정하고 이를 해결해야만 한다.
만일 문제 연산자 (문제 풀이에서는 규칙이라는 개념과 같음) 들과 이들이 적용되었을 때 영향을 받는 차이들을 나열함에 의해 연산자-차이표 (operator-difference table) 를 작성한다면, 이 표는 부속문제를 유도해내는 데 이용이 될 것이다. 이와 같이 큰 문제를 해결하기 위해 연산자-차이표를 이용한 방법-목적 분석방법을 순환적으로 적용하게 된다. 연산자-차이표의 작성방법은 다음의 문제로써 예증되어진다.
▷▶▷ 원숭이-바나나 문제 :
"우리 안에 한 마리의 원숭이가 있으며 원숭이 손이 닿지 않는 우리의 중간지점에 바나나가 걸려 있다. 그리고 우리 구석에 상자 하나가 놓여 있다. 이 상황 하에서 원숭이는 어떻게 바나나를 손에 넣을 수 있겠는가?"
주어진 문제로부터 원숭이가 할 수 있는 동작과 이에 따른 여러 목적물의 속성에서의 차이를 설정할 수 있어 표 1 과 같은 연산자-차이표를 작성할 수 있다.
예를 들어 '오른다' 열의 X 표시는 원숭이가 오르는 행위를 함에 의해 전후 상황에 대한 속성의 차이는 원숭이 높이의 값이 변하게 된다는 의미이다. 표 1 은 정의될 수 있는 여러 가지의 연산자-차이표들 중의 하나이다. 그러나 이 연산자-차이표는 문제풀이작업의 환경에 대한 정의의 한 부분으로 프로그램에 주어지는 것이기 때문에 연산자-차이표의 정의는 GPS 자체와는 별개의 개념이다.
표 1 원숭이-바나나 문제의 연산자-차이표
|
연산자 차이 |
오른다 |
걷는다 |
밀친다 |
잡는다 |
|
원숭이 위치 상자 위치 바나나 위치 원숭이 높이 바나나 높이 |
X
|
X
|
X X
|
X
X |
"방법-목적 분석" 은 앞에서 설명한 바와 같이 문제 풀이 시스템을 실행하기 위해 목적들 사이의 차이를 이용한다. "목적물 A 를 목적물 B 로 전환하여라" 는 문제의 분석단계가 그림 2 에 보여준다.

그림 2 방법-목적 분석의 흐름도
(a) A 에서 B 로 전환하는 단계들
(b) 차이 축소를 위한 단계들 (c) 연산자 적용에서의 단계들
첫번째 단계는 목적물 A 와 B 사이의 차이 D 를 구하는 것이다 (만일 차이를 발견하지 못할 경우 문제는 해결된 것으로 간주됨). 일단 차이가 구해지면 이 차이를 줄이기 위해 A 에 연산자들을 적용해야 한다 (물론 A 에 이러한 연산자들의 적용은 D 를 줄이는 새로운 목적물 A' 에 이르게 된다). 이와 같이 D 를 줄이기 위해 연관된 연산자들 (Q1, ..., Qk) 이 연산자-차이표에 의해 구해져서 A 에 적용되는 과정는 그림2 (b) 에 나타나 있다. 그러나 먼저 A 의 형태가 Q 의 적용가능한 형태인지를 먼저 비교해 보아야 한다고 한다. 만일 Q 가 A 에 적용가능하다면, Q 를 A 에 적용하여 A' = Q (A) 의 변환이 이루어지며 제어 프로그램의 올바른 지점 (그림 2 (a) 의 세번째 단계) 에 되돌아가 가게 된다. 그러나 만일 Q 의 적용가능한 형태 C 와 A 가 다르다면, 먼저 A 와 C 사이의 차이 D' 를 구하여 이를 먼저 축소시켜야 한다 (이것은 원래 문제에 대한 부속문제가 됨). 이 부속문제가 해결되어 Q 가 적용가능한 형태 A' 가 형성되면 A' = Q(A") (그림 2(c)) 에 의해 올바른 지점으로 제어가 옮겨진다 (그림 2 (a) 의 세번째 단계).
이와 같이 GPS 에서의 단계들에서 보듯이 프로그램의 수행은 순환적인 성질을 지닌다 (즉, 부속문제의 순환적 해결의 과정을 거쳐 최종에는 원래 문제를 해결하게 되는 과정).

그림 3 GPS 에서의 목표들과 부속문제들
그림 3 은 GPS 의 수행과정을 나타내는 또다른 방법이다. 여기서는 부속문제의 내용 변화에 주의를 기울일 필요가 있다. 그림 3 에서 보듯이 수행되는 단계는 번호순에 따른다.
1) A → B 변환을 뜻하는 목표 G0 을 외부로부터 받는다. A 와 B 사이의 차이를 비교하여 차이 D 를 구한다.
2) 목표 G1 은 목적물 A 에서 D 를 축소시키는 것이다. 이를 위해 연산자-차이표를 살펴 올바른 연산자로써 Q 를 선택한다.
3) 목표 G2 는 Q 를 A 에 적용하고자 한다. 연산자 Q 가 적용가능한 형태 C 를 가진다고 하면 A 와 C 사이의 차이 D' 가 구해진다.
4) 목표 G3 는 A 에서 D' 를 축소시킨다. 이를 위해서 연산자 Q' 를 구한다.
5) Q' 가 적용가능한 형태 C' 를 가지고 A 와 C' 사이에 차이가 없다고 하자 (만일 있다면 그림 3 의 단계 (5) 하단에 노드가 계속 형성되어야 함). 그러면 Q' 가 A 에 적용되어 A' = Q'(A) 가 된다. 이제 제어가 한 단계 위로 올라가서 부속문제들 가운데 하나를 해결한 상태가 된다.
6) Q'(A) 를 A 에 대입함에 의해 차이 D' 가 A 에서 감소된 상태가 된다.
7) D' 가 감소되었으므로 Q 가 A' 에 적용되어 A" = Q(A') 가 된다.
8) A → A" 변환에 의해 차이 D 가 감소된다.
9) 이제 A" 에서 B 로 변환시켜야 하는 문제만 남게 된다. A" 와 B 사이의 차이는 존재하지 않거나, 있다면 그 차이 D* 는 D* ≠ D 가 된다.
10) 만일 D* 가 존재한다면 A" 에서 D* 를 축소시키는 과정을 순환적으로 수행하게 된다.
앞에서 특정의 연역작업들이 가환 생성 시스템 (commutative production system) 에 의해 해결될 수 있음을 보았으나 인공지능의 다른 많은 흥미있는 문제에 대해서는 가장 자연스러운 형식화 과정들은 비가환 시스템 (noncommutative system) 을 포함하고 있다. 전형적인 이런 문제들은 로보트 문제 풀이와 자동 프로그래밍과 같이 목표가 순차적인 행동의 표현이나 프로그램에 의해 성취되는 문제들이다.
로보트 문제는 단순하고 직관적이기 때문에 중요한 개념들을 설명하기 위해 이런 영역의 예들을 사용한다. 로보트 문제를 전형적인 형식화로 하는데 있어서, 충분히 이해가능한 세계에서 수행될 수 있는 기본적인 행동들 (primitive actions) 을 할 수 있는 로보트가 있다고 하자. 예를 들어, 블럭 세계에서 탁자 이에 혹은 다른 블럭 위에 놓여 있는 (장난감 블럭처럼) 몇 개의 명명된 블럭들과 이 블럭들을 집어 올리고 움직일 수 있는 팔을 가진 로보트를 생각해 보자.
로보트 프로그래밍은 로보트 주위의 환경 인식, 행동계획의 형상화, 이런 계획들의 실행을 위한 감시 등을 포함하는 많은 집약적인 기능들을 포함하지만, 여기서는 주로 주어진 초기상태에서 (적절히 실행된다면) 어떤 목표상태를 만족하게 될 일련의 로보트 행동들을 구성하는 문제에 관해 다루겠다.
로보트 문제에 대한 상태 설명과 목표들은 서술식 wff 로 구성될 수 있다. 예를 들어 그림 4 에서 보듯이 로보트 팔과 블럭 배치를 생각해 보자.
공식 CLEAR (B) 는 B 블럭 위에 아무 블럭도 없다는 것을 의미하며 ON 이라는 서술 심볼 (predicate symbol) 은 다른 블럭 위에 (직접) 놓여 있는 블럭들을 표현하는데 사용된다. 이런 상황에서 로보트는 블럭을 움직이는 단순한 팔의 역할로서, 이 움직임에 따라 매순간 다른 상황이 야기된다. HANDEMPTY 라는 서술 심볼은 로보트 팔이 비어있을 때 논리값 T 를 갖는다. 물론, 이 문제의 어떠한 상황도 적절한 서술문들의 AND 결합 (conjuction) 으로 나타내질 수 있다.

그림 4 블럭 구조
목표묘사 (goal description) 도 또한 서술 논리문 (predicate logic formula) 들로 표현될 수 있다. 예를 들어 그림 4 의 로보트 문제의 경우, 만일 C, B, A 의 블럭들을 밑에서부터 쌓기를 원하면 우리는 목표를 다음과 같이 표현하게 될 것이다.
ON(B, C) ∧ ON(A, B)
주어진 상황을 쉽게 표현하기 위해 나타내는 서술문들에 특정 제한을 가할 수 있다. 목표 (혹은 부목표) 상태를 표현하는 데 있어서 각 변수는 존재한정기호 (∃ : existential qualifier) 에 의해 제한되고 모든 서술 심볼들은 AND 결합 (∧ : conjunction) 으로 연결되어진다고 가정할 수 있다.
마찬가지로 시작 혹은 중간 상태 표현에 있어서도 변수를 포함하지 않는 기초 문자 (ground literal) 들이 AND 로 연결된 것을 가정한다. 그림 4 의 공식들은 이런 제약조건을 만족한다. 로보트 행동은 하나 또는 여러 조합의 상태를 다른 상태로 변화시키는데 이런 행동들을 하나의 상태를 다른 상태로 변화시키는 F-규칙들 (전향 생성 시스템의 생성규칙들) 로 규정할 수 있다. 로보트 행동들을 표현하는 간단하면서 상당히 유용한 한 방법은 STRIPS 라 불리는 로보트 문제 풀이 체제를 이용하는 것이다. 이 방법은 7 장에서 논의되는 암시적 규칙들을 생성규칙으로 사용하는 것과 대조적이다. 암시적 규칙이 전체 데이터베이스에 적용되었을 때 추가되는 구조의 확장에 의해 데이터베이스가 변화되지만, 데이터베이스로부터 전혀 제거되는 것이 없으나 로보트 행동 모델에서는 F-규칙들은 반드시 더 이상 참 (true) 이 될 수 없는 서술문들을 제거할 수 있어야만 한다. 예를 들어 그림 4 의 로보트 팔이 블럭 B 를 집어들었다고 생각할 때 분명히 ONTABLE(B) 라는 표현은 더 이상 참이 아니며, 따라서 이는 이러한 행동을 묘사하는 F-규칙에 의해 제거되어야 한다. STRIPS 유형의 F-규칙들은 제거되어지는 표현을 분명히 나열함으로써 어떠한 서술문들이 제거되어지는지를 알려준다.
STRIPS 형 F-규칙들은 세 가지 요소로 구성되어 있는데, 첫째는 전제조건공식 (precondition formula) 이다. 이 요소는 AND 결합규칙의 가정과 같으며 서술문 표현 (predicate calculus expression) 은 반드시 F-규칙이 그 상태에 적용될 수 있도록 상태를 나타내는 묘사에 논리적으로 부합되어야만 한다. 목표를 나타내는 서술문들의 형태에 주어진 제한과 모순이 생기지 않도록 F-규칙의 전제조건들은 표현들의 논리곱들 (conjunction of literals) 로 구성됨을 가정하고 전제조건공식들에 있는 변수들은 존재한정기호를 가진다고 가정한다. 전제조건공식을 나타내는 리터럴들의 논리곱이 주어진 사실을 나타내는 리터럴들의 논리곱과 논리적으로 부합되는지 아닌지 결정은 아주 쉽다. 이것은 전제조건 리터럴들의 각각을 결합 (unify) 하는 사실들의 리터럴들이 존재하고 이들의 mgu 가 일치한다면 당연하다. 그런 비교선택 (matches) 이 있으면 F-규칙의 전제조건은 사실들과 비교선택된다고 말한다. 그 때의 결합요소를 비교 선택치환 (match substitution) 이라 말한다.
이때 F-규칙과 문제상태가 주어지면 많은 비교선택치환이 존재하고 각각의 비교 선택치환은 서로 다르게 적용될 수 있는 F-규칙의 여러 예시들을 유도한다.
F-규칙의 둘째 요소는 제거목록 (delete list) 이라 불리우는 (자유변수를 포함할 수도 있는) 표현의 목록이다. F-규칙이 문제상태에 적용될 때, 비교선택치환은 제거목록의 표현들에 적용되어 얻어진 기초 문자들 (ground literal) 은 새로운 표현을 구성하기 위한 첫번째 단계로서 이전의 상태를 나타내는 표현에서 제거된다. 이 때 제거목록의 자유변수들 모두는 전제조건공식에서 존재한정변수들로 변화되는 것을 가정하는데 이런 제한은 제거목록의 표현들이 결합되면 기초 문자가 된다는 것을 분명하게 해준다.
세번째 요소는 추가공식 (add formula) 이다. 이것은 (자유변수를 포함할 수도 있는) 리터럴들의 논리곱으로 구성되며 함축 F-규칙의 결론과 같다. F-규칙이 문제상태에 적용되었을 때, 비교선택치환이 추가공식에 적용되고 그 결과 생겨난 표현이, 새로운 상태를 나타내는 표현을 구성하는 마지막 단계로서 (제거목록의 표현들이 제거된 뒤에), 이전의 상태를 나타내는 표현에 추가된다. 추가공식의 어떤 결합 표현도 기초 표현의 논리곱이 될 수 있도록 추가공식의 자유변수가 전제 조건공식에서의 변수들로 변환되는 것을 가정하고 F-규칙 요소들에 주어지는 이러한 제한들은 때때로 벗어날 수 있다고 가정한다. F-규칙을 이용하면 표현이 훨씬 쉬워지기 때문에 이를 이용한다.
F-규칙의 예로써, 테이블에서 블럭을 들어올리는 행동을 모델화해 보자. 이 행동의 전제조건은 블럭이 테이블 위에 있고 로보트 팔이 비어 있으며 그 블럭 위에 아무것도 없다는 것이며, 이 행동의 결과는 로보트 팔이 블럭을 쥐고 있는 것이다. 이것은 다음과 같이 표현된다.
pickup(x)
precondition (전제조건) : ONTABLE(x), HADEMPTY, CLEAR(x)
delete list (제거목록) : ONTABLE(x), HANDEMPTY, CLEAR(x)
add formula (추가공식) : HOLDING(x)
앞서 전제조건과 추가공식은 표현의 논리곱이라고 전제하였기 때문에, 우리는 그것들 각각을 표현의 목록이나 집합으로 나타낼 수 있다. 때때로 위의 예처럼 전제조건 공식과 제거목록은 같은 표현들을 포함한다. 위의 예에서 제거목록의 표현들의 부정들을 추가하기보다는 추가공식에 HOLDING(x) 만을 포함시켰다. 우리의 목적을 위해서는 단지 상태를 나타내는 표현에서 그것들을 제거하는 것만으로도 충분하다.
우리는 x 를 B 로 치환함으로써 그림 4 의 상태에 pickup(x) 가 적용될 수 있음을 알 수 있다. 이 경우 새로운 상태표현의 목록은 다음과 같다.
CLEAR(C), ON(C, A), ONTABLE(A), HOLDING(B)
STRIPS 형 F-규칙을 사용한 생성체계는 일반적으로 비가환적이다. 왜냐하면 이러한 규칙들이 상태표현목록에서 어떤 표현들을 제거하기 때문이다. 그러한 F-규칙들은 "함축" 규칙 (implications) 이 적용될 때 단지 원래 상태의 집합을 제한하는 것과는 대조적으로 한 상태의 집합을 다른 상태의 집합으로 변환시킨다.
유추를 쉽게 하기 위하여 한 상태로부터 다른 상태로의 변환은 만화영화에서의 그림의 변환과 비교할 수 있다.
매우 간단한 만화영화에서는 어떤 등장인물들이 고정된 배경에서 구도 내를 움직이고, 좀더 생동감이 넘치는 만화에서는 배경에서도 많은 변화가 일어난다. 간단한 제거목록과 추가목록을 가진 STRIPS 형 F-규칙은 상태표현목록에 있는 대부분의 체계화공식 (wffs) 들이 고정된 배경을 나타낸다고 할 수 있다.
상태목록의 어느 체계화공식 (wffs) 들이 변화되어야 하느냐 혹은 그렇지 않느냐를 정의하는 문제를 인공지능에서의 구조문제라 말한다. 구조문제를 다루는 가장 좋은 방법은 우리가 모델화하는 행동들과 상태들의 종류에 달려 있다. 즉, 상태의 요소들이 서로 밀접하고 불안정하다면 각 행동은 그 상태에 전체적인 영향을 끼칠 것이다. 그런 세계에서는 블럭을 들어올리는 행동이 도미노 게임에서처럼 전체에 큰 변화를 끼쳐 다른 모든 블럭들의 상태가 모두 변하도록 만들 것이며, 따라서 간단한 STRIPS F-규칙은 적절한 행동 모델이 될 수 없다.
전형적으로 상태의 요소들은 우리가 행동의 영향이 국부적 (local) 이라고 가정할 수 있을만큼 충분히 독립적이라는 가정이 성립되면, STRIPS F-규칙은 많은 유형의 행동에 효율적이고 적절한 모델인 것이다.
F-규칙을 상태표현목록에 적용하는 것은 F-규칙으로 표현된 행동을 시뮬레이션 (simulation) 하는 것으로 생각될 수 있는데 시뮬레이션은 규칙들의 행동들을 모델화하는 세부목록과 정확성의 정도에 따라 달라진다. 예를 들어 pickup(x) 라는 F-규칙은 블럭의 무게와 크기 로보트 팔과 블럭간의 마찰력, 주위의 온도 등을 설명하는 시뮬레이션 프로그램 보다 오히려 들어올리는 행동에 더욱 가까운 표현이 된다. 뒤에 좀더 세분화하여 다른 관점에서 행동을 모델화하는 것을 살펴 보도록 한다. 세분화된 모델에서는 높은 차원에서 무시될 수 있는 요소가 서로 관련되어 변화를 일으킬 수 있기 때문에 구조문제는 더욱 어렵게 된다. 구조문제의 또다른 관점은 로보트 팔이 부러지거나, 블럭이 너무 무겁거나 팔에 달린 모터에 결함이 있거나 블럭이 테이블에 아교로 붙어져 있는 경우와 같은 변칙적인 조건을 어떻게 다루냐는 것이다. 물론 F-규칙의 전제조건에 이러한 변칙조건의 부정을 모두 포함함으로써 규칙이 부적절하게 적용되는 것을 방지할 수 있으나 너무 많은 변칙적인 조건이 존재하며, 일반적으로는 비정상적인 조건들이 성립되지 않는다. 그러나 만일 그런 조건이 성립된다면 F-규칙 모델은 부정확하게 된다. 변칙조건의 문제에 대한 몇 가지 접근방식이 제안되었지만 어느 것도 그리 만족할 만하지 않다. 다만 행동 모델의 체계가 사용된다면 그 체계가 자각할 수 있는 모든 조건들을 자동적으로 가장 세부적이고 정확한 시뮬레이션이 고려할 수 있을 것으로 보인다.
로보트 문제풀이 체계의 가장 간단한 유형은, 상태표현을 전체 데이터베이스로 하고 F-규칙을 이용한 로보트 행동 모델을 생성규칙으로 하는 생성 시스템 (production system) 이다. 그러한 체계에서는 목표에 달성될 수 있는 상태표현이 생성될 때까지 적용가능한 F-규칙을 선택할 수 있다. 다음 예에서 그러한 체계가 어떻게 작동되는지 살펴 보자.
STRIPS-형태에서 그림 4 의 로보트 동작의 각각에 대해 다음에 같은 F-규칙으로 생각해 보자.
(1) pickup(x)
P&D : ONTABLE(x), CLEAR(x), HANDEMPY
A
: HOLDING(x)
(2) putdown(x)
P&D : HOLDING(x)
A : ONTABLE(x),
CLEAR(x), HANDEMPTY
(3) stack(x,y)
P&D : HOLDING(x), CLEAR(y)
A
: HANDEMPTY, ON(x, y), CLEAR(x)
(4) unstack(x,
y)
P&D : HANDEMPTY, CLEAR(x), ON(x, y)
A
: HOLDING(x), CLEAR(y)
이러한 규칙들에서 (표현의 나열에 의해 구성된) 전제조건공식과 제거목록이 같게 됨을 주의하라. 첫번째 규칙은 앞에서 언급되었고, 나머지는 테이블 위에 x 블럭은 내려놓고, 블럭 위에 x 블럭을 내려놓고 y 블럭 위에 있는 x 블럭을 들어올리는 행동에 대한 모델들이다.

그림 5 로보트 문제의 목표
우리의 목표가 그림 5 의 상태라고 생각하자. 그림 4 의 초기상태로부터 차례로 전진하기 때문에 pickup(B) 와 unstack(C, A) 만이 적용될 수 있는 F-규칙임을 알 수 있다. 그림 6 은 이 문제에 대한 완전한 상태공간을 보여주고 있고, 진한 검은선은 해결경로를 나타낸다. 초기상태는 SO 로 목표상태는 G 로 표시하였다 (일반적인 것과는 달리 문제에서 대칭성을 보이기 위해 SO 가 제일 위에 있지 않다). 이 예에서 각 F-규칙은 그 역을 가지고 있음을 주의하라.

그림 6 로보트 문제의 상태공간
이러한 간단한 예에서는 (전체 상태공간이 22 개 상태로 구성된) 복잡하지 않은 제어전략 (control strategy) 를 가진 전향 생산체계는 빨리 목표상태로의 경로를 찾아낼 수 있다. 그러나 좀더 복잡한 문제에서는 목표로의 전향탐색 (forward search) 은 더 큰 그래프를 형성하게 되어 잘 정의된 평가함수 (well-informed evaluation function) 와 결합될 때만이 가능하게 된다.
위의 예에서, 목표상태에 이르는 길을 따라 각 선분에 붙여진 F-규칙들을 가지고, 목표를 성취하기 위한 행동의 배열을 구성할 수 있다.
이 배열 (sequence) 은
{unstack(C, A), pickup(B), stack(B, C), pickup(A), stack(A, B)}
이며 이러한 목표를 성취하는 행동배열을 계획이라 부른다. 여러 가지 이유로 해서 추가정보를 포함하여 계획을 나열하는 것이 유용하다. 예를 들어 F-규칙들과 각각이 다른 F-규칙에 제공하는 전제조건들 사이의 관계가 무엇인지 알기를 원할 수 있는데, 그러한 정보는 계획에 포함된 F-규칙들의 전제조건들과 추가목록들을 내용으로 하는 삼각표에 의해 편리하게 제공될 수 있다. 그림 7 은 삼각표 (triangle table) 와 한 예를 나타낸다.
삼각표의 열들은 계획의 F-규칙으로 시작된다. 가장 왼쪽의 열을 0 번째 열이라 하면 j 번째 열은 계획에서 j 번제 F-규칙으로 시작된다. 맨 위의 행을 첫번째 행이라 하고, 만일 계획이 N 개의 F-규칙으로 되어 있다면, 마지막 행은 N + 1 번째 행이 된다. 표의 각 (i, j) 번째 칸은 (j > 0, i < N + 1) j 번째 F-규칙의 실행에 의해 추가되면서 i 번째 F-규칙의 전제조건이 되는 리터럴들이 들어간다. 모든 i < N +1 에 대하여 (i, 0) 번째의 표현들은 초기상태에서 각각 i 번째 F-규칙의 전제조건이 되는 것이다. (N + 1) 번째 행의 표현들은 초기 상태표현의 목록과 F-규칙의 적용에 따라 생기는 추가목록들인데 이는 목표상태를 나타내는 목록 (즉, 모든 계획의 F-규칙이 실행되었을 때 생기는 표현들) 이 된다.
삼각표는 초기상태, 적용한 F-규칙, 목표상태들로부터 쉽게 만들 수 있다. 이 표는 로보트 계획을 위한 간결하고 편리한 표현이다.
i 번째 F-규칙의 왼쪽 행에 들어 있는 표현들은 정확히 이 규칙의 전제조건들이다.
i 번째 F-규칙의 아래 열에 들어 있는 표현들은 정확히 목표상태의 구성요소이거나 또는 다음 F-규칙들이 필요로 하는 이 규칙의 첨가공식 리터럴들이다.
i 번째 핵심 (kernel) 을 i 번째를 포함하는 그 아래부분 모든 행들과의 i 번째 열의 왼쪽에 위치하는 모든 열들의 교집합으로 정의한다. 그림 7 에서 4 번재 핵심은 두줄로 둘러쳐진 부분이 된다. i 번째 핵심에 포함된 표현들은 i 번째 규칙과 그 이후의 F-규칙들이 적용되어 목표를 이룰 수 있기 위한 상태를 표현하는 목록과 동일하여야만 한다. 따라서 첫번째 핵심 즉, 0 번째 열은 목표에 이룰 수 있는 일련의 F-규칙들이 적용가능한 초기상태의 조건을 나타내며, (N + 1) 번째 핵심 (즉 (N + 1) 번째 행) 은 목표상태를 나타내는 조건들을 포함한다. 삼각표의 이러한 성질은 실제 로보트 계획의 실행을 제어하는데 매우 유용하다.

그림 7 삼각표
로보트 계획은 실제 세계에서 어떤 기계장치에 의해 궁극적으로 실행되야 하기 때문에 계획이 실행되고 있는 동안에 기계적 오차에 의하여 원하는 행동을 수행하지 못하고 오류를 범하는 경우가 발생할지 모른다. 행동을 수행하는 동안에 예기치 않은 효과로 인하여 목표에 더 가까워지거나 예정된 경로를 벗어나게 만들지도 모른다. 이런 문제들은 각 실행 이후에 유도되는 새로운 상태목록을 기반으로 새로운 계획을 형성함으로써 해결할 수 있으나 너무 비싼 작업이기 때문에 그 대신 주어진 계획이 실행될 때 지능적으로 제어할 수 있는 방법을 찾는다.
삼각표의 핵심 (kernel) 들은 그런 계획 실행 시스템 (plan execution system) 을 실현시키는데 필요로 하는 정보를 포함한다. 계획 실행이 시작될 때 우리는 계획을 형성할 때 사용되었던 첫번째 핵심의 표현들이 초기상태목록과 일치하기 때문에 전체계획이 적용가능하고 또 목표를 성취하는 데에 적절하다는 것을 알고 있다 (여기서, 로보트의 행동에 의한 것을 제외하고는 일어나지 않는다고 가정한다). 계획의 (i - 1) 번째 행동이 막 실행되었다고 생각해 보자. 그러면 이 행동이 취해진 후 유도되는 상태의 표현과 i 번째 핵심의 표현들을 비교함에 의해 만일 그들이 일치한다면 예정되어진 다음의 i 번째 행동을 적용할 수 있다 (여기에서는 계획을 실행할 때 연속적으로 다음 상태를 정확히 묘사하는 상태표현을 유도할 수 있다고 가정하였다).
실제로 우리는 이러한 작업을 각각의 행동 뒤에 유도되는 상태표현을 단지 연관되는 핵심과 일치하는지를 관찰하는 것 보다는 이와 일치되는 가장 높은 번호의 핵심을 찾는 것에 의해 예정된 행동계획을 좀더 효율적으로 수행할 수 있다. 만일 예기치 못한 결과가 더욱 더 목표에 가까워졌다면, 우리는 그에 맞는 적절한 나머지 행동들만 실행시키면 된다. 그리고 만일 실행오차가 이전의 실행결과를 손상시킨다면 적절한 행동들을 다시 수행하면 된다.
적절하게 일치되는 핵심을 찾기 위하여 우리는 가장 높은 번호의 핵심 (즉, 표의 맨 아래쪽 행)부터 거꾸로 각각을 비교한다. 만일 목표핵심 (표의 마지막 행) 과 일치된다면, 실행은 끝나고, 그렇지 않으면 가장 높은 핵심번호가 i 라 할 때 i 번째 행동이 상태목록에 적용가능하다는 것을 알 수 있다. 이 경우에 체계는 i 번째 F-규칙에 대응되는 행동을 수행한 뒤 위의 작업을 반복한다. 이상적 세계에서는 이러한 과정은 단순히 계획상에 있는 각 행동을 수행하게끔 한다. 실제 세계에서는 이 과정은 필요없는 행동의 실행을 없애고, 적절한 행동의 반복에 의하여 어떤 실패도 극복하기 위한 유연성을 갖는다. 일치되는 핵심이 전혀 없을 때에는 재계획이 시도된다.
이러한 작업이 어떻게 수행되는지에 대한 예로서, 우리의 블럭 쌓기 문제로 돌아가 그림 4 의 삼각표에 의해 표현된 계획을 생각해 보자. 처음 4 개의 F-규칙들에 대응되는 행동들이 실행되고 이러한 행동들의 결과가 계획된 대로 유도되었다고 생각해 보자. 이제 시스템이 A 블럭을 들어올리는 행동을 실행하려고 시도하지만, 이때 실행 프로그램 상의 실수로 A 블럭 대신에 B 블럭을 들어올렸다고 하자 (따라서, 상태목록에는 특히 HOLDING(A) 가 추가되지 않고 HOLDING(B) 가 추가되며, ON(B, C) 가 제거된다). 만일 그런 실수가 없었다면 6 번째 핵심과 일치되겠지만, 실수의 결과 상태목록과 일치되는 가장 높은 핵심번호는 4 이며 따라서 그에 대응되는 행동 stack(B, C) 로 되돌아가 다시 수행되게 된다.
삼각표의 핵심들 (kernels) 이 중복되지 않는다는 사실은 가장 높은 번호의 일치되는 핵심을 효과적으로 찾는데 이용될 수 있다. 맨 밑의 행부터 시작해서 왼쪽부터 오른쪽으로 하나씩 비교하여 현재의 상태목록과 일치되지 않는 부분을 찾는다. 만일 그러한 부분을 찾아내지 못하면 그 상태목록과 목표핵심이 일치되는 것이다. 그렇지 않으면 즉 i 번째 열에서 그러한 부분을 찾아내면 일치되는 핵심의 가장 높은 번호 i 를 넘지 못한다. 이런 경우에 i 번째 열을 경계로 하여 바로 위의 행에 대하여 왼쪽에서 오른쪽으로 하나씩 탐색을 시작한다. 그러나 이 때는 이전의 i 번째 열을 지나지 않을 것이다. 또 일치되지 않는 부분이 발견되면 경계를 다시 바꾸고 행을 하나 위로 올려 놓고서 다시 새로운 탐색 작업을 계속한다. 이렇게 해서 만들어진 최종적인 열의 k 라고 하면 k 번째 행의 탐색이 끝났을 때 k 번째 핵심이 일치되는 가장 높은 번호의 핵심이 되며 이로써 이 과정은 완전히 끝나게 된다.
효율적으로 로보트 계획들을 구성하기 위하여 우리는 때때로 목표상태로부터 초기 상태에 도달하는 역방향의 작업을 필요로 한다. 목표상태의 표현목록 (역시, 표현들의 논리곱) 을 전체 데이터베이스로 하고 부목표의 표현목록 (subgoal descriptions) 을 생성하기 위하여 이 데이터베이스에 B-규칙을 적용하는 체계가 바로 그것이다. 그러한 체계는 부목표목록이 초기상태목록의 사실들과 결합될 때 성공적으로 작업을 끝마치게 된다.
후향 생성 시스템이 제안하는 첫번째 단계는 목표표현들을 부목표표현들로 전환시키는 B-규칙들의 집합을 정의하는 것이다. 하나의 방법은 우리가 이미 논의했던 F-규칙들에 기초를 두고 B-규칙들을 사용하는 것이다. 목표 G 를 부목표 G' 으로 변환시키는 B-규칙은 논리적으로 G' 상태목록에 적용되어 G 상태목록을 생성하는 F-규칙에 기초를 두고 있다.
우리는 어떤 상태목록에의 F-규칙이 적용되면 이 규칙의 추가목록이 첨가되는 새로운 상태목록이 생성된다는 것을 알고 있다. 그러므로 만일 목표표현이 F-규칙의 추가목록상의 어떤 표현과 단일화 (unify) 될 수 있는 표현 L 을 포함한다면, 그 F-규칙의 전제조건의 적절한 표현들과 일치되는 상태목록을 만들기만 하면 F-규칙은 L 과 결합되는 상태목록을 생성하기 위하여 적용되어 질 수 있다. 따라서, F-규칙의 역방향 적용에 의해서 생성되는 부목표표현은 분명히 F-규칙의 전제조건의 표현들을 포함한다. 그러나 목표표현이 (L 이외의) 다른 표현들을 포함한다면 부표현들도 또한 다른 표현들을 포함하고, 이 때의 다른 표현들은 F-규칙의 실행 뒤에 목표표현에서 (L 이외의) 다른 표현이 된다.
자세한 내용은 다음 절에서 설명되어진다.
우리가 표현한 것들을
형식화하기 위하여 [L ∧ G1 ∧ … ∧ GN] 이라는 표현의 논리곱이 목표이고 부목표표현을
생성하기 위하여 어떤 F-규칙을 역방향으로 적용하려 한다고 생각해 보자. 전제조건
P 와 추가공식 A 를 가진 F-규칙이 A 에 L 과 가장 일반적 단일화 (most general
unifier) u 로써 단일화되는 L' 을 포함한다고 생각해 보자. F-규칙의 요소에 u 를
적용하면 F-규칙의 예시가 만들어진다. 분명히 Pu 의 표현들은 우리가 찾는 부목표표현들의
부분집합이다. 우리는 또한 완전한 부목표표현을 위해 G1', ..., GN' 을 포함해야만
한다. 표현 G1', ..., GN' 은 이러한 표현과 일치되는 상태목록들에 F-규칙의 예시가
적용되었을 때 G1, ..., GN 과 일치되는 상태목록이 생성되는 것을 의미한다. 이때
각 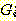 을 F-규칙을 통한
을 F-규칙을 통한 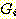 의 역행 (regression) 가 이라고 부르며,
의 역행 (regression) 가 이라고 부르며, 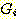 로부터
로부터 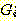 을 얻어내는 과정을 역행이라 부른다.
을 얻어내는 과정을 역행이라 부른다.
간단한 STRIPS 형태에서 정의된 F-규칙들에 대해, 역행과정은 각 규칙의 기초 예시들로 쉽게 설명되어 질 수 있다 (F-규칙의 기초 예시란 이 규칙의 전제조건, 제거목록, 추가공식에 포함되어 있는 모든 문자들이 기초 문자들 (ground literals) 로 되어 있음을 뜻한다). 이제 R[Q : Fu] 를 전제조건 P, 제거목록 D, 추가공식 A 를 가진 F-규칙의 기초 예시 Fu 를 통한 문자 Q 의 역행이라고 하자. 그러면 만일 Qu 가 Au 상에 존재하는 문자이면
R[Q : Fu] = T (참)
이고, 만일 Qu 가 Du 상에 존재자는 문자이면
R[Q : Fu] = F (거짓)
이다. 위의 두 경우에 해당되지 않으면
else, R[Q : Fu] = Qu
이다. 간단히 말해서, F-규칙에 의해 역행되는 Q 는 Q 가 추가목록에 속하면 참, 제거목록에 속하면 거짓, 그밖의 경우에는 그 자신인 Q 가 되는 것이다.
변수를 포함한 F-규칙을 통한 역행과정은 좀더 복잡해진다. 몇 가지 예를 들어 이를 설명해 본다. 앞에서 주어진 unstack 이라는 F-규칙을 살펴 보자. 이 규칙은 다음과 같이 주어진다.
unstack(x, y)
P&D : HANDEMPTY, CLEAR(x), ON(x, y)
A
: HOLDING(x), CLEAR(y).
특히 unstack(B, y) 의 예를 생각해 보자. 아마도 우리의 목표가 HOLDING(B) 를 생성하는 것이라면 이와 같은 규칙 예시가 생각되어질 수 있다. 이 규칙 예시는 변수 u 를 포함하고 있으므로 완전히 예시되었다고 말할 수 없다. 만일 이 F-규칙을 통해 HOLDING(B) 를 역행하면 기대했던 대로 참 (T) 을 얻을 것이다 (표현 HOLDING(B) 는 이 F-규칙이 적용된 후의 상태에서는 항상 참이다). 또 이 F-규칙을 가지고 HANDEMPTY 라는 표현을 역행한다면 우리는 거짓을 얻을 것이다 (표현 HANDEMPTY 는 unstack 이 적용된 상태에서는 결코 참이 될 수는 없다). 만일 ONTABLE(C) 를 역행한다면 ONTABLE(C) 를 얻을 것이다 (ONTABLE(C) 는 이 F-규칙에 전혀 영향을 받지 않는다).
우리가 CLEAR(C) 를 이 완전히 예시되지 않은 F-규칙을 통해 역행하려 한다고 생각해 보자. 만일 y 가 C 이면 CLEAR(C) 는 참 (T) 으로 역행하고 그렇지 않으면 단순히 CLEAR(C) 가 됨을 주의하라. 이 결과를 요약하면 "CLEAR(C) 가 논리합 (y = C) ∨ CLEAR(C) 로 역행된다" 고 말할 수 있다 (unstack(B, y) 가 적용된 뒤에 CLEAR(C) 가 되려면 y 가 C 이어야만 하거나, 아니면 이 F-규칙이 적용되기 이전의 상태에 이미 CLEAR(C) 가 포함되어있어야만 한다). 불행하게도 논리합으로 구성된 부목표를 받아들이는 것은 목표표현에서 허용된 논리곱 형태의 제한에 위배된다. 이런 경우가 생겼을 때는 우리는 선택할 수 있는 두 개의 부목표를 만든다. 앞의 예에서는 하나는 unstack(B, C) 의 전제조건을 포함하고 다른 하나는 ~(y = C) 를 만족하는 unstack(B, y) 의 전제조건을 포함한다.
제거목록의 불완전한 예시표현과 일치되는 문자를 역행할 때도 유사한 일이 발생한다. 예를 들어, unstack(x, B) 를 통해 CLEAR(C) 를 역행하려 한다고 생각해 보자. 만일 x = C 이면 CLEAR(C) 는 거짓 (F) 가 되고 그렇지 않으면 CLEAR(C) 가 될 것이다. 우리는 이 결과를 요약해서 CLEAR(C) 가
[(x = C) → F] ∧ [~(x = C) → CLEAR(C)]
로 역행한다고 말하고, 목표로서 이 표현은 [~(x = C) ∧ CLEAR(C)] 라는 논리곱과 동치이다.
만일 unstack(B, y) 을 통해 CLEAR(B) 를 역행하려 한다면 어떤 결과가 될지 의문이 생긴다. 우리의 예에서, y = B 인 경우에 참 (T) 을 얻게 될 것이다. 그러나 y = B 는 unstack(B, B) 의 표현과 대응되지만 그 전제조건이 ON(B, B) 를 포함해야 하므로 실제로는 불가능하다. 우리는 이 예에서 unstack(x, y) 에 전제조건 ~(x = y) 를 추가함으로써 이 예를 좀더 현실적으로 만들 수 있다.
요약해서 말하자면, 어떤 STRIPS 형 F-규칙은 다음과 같은 방법으로 B-규칙으로서 사용될 수 있다. B-규칙의 적용조건은 목표표현이 F-규칙의 추가목록에 있는 문자들의 하나와 단일화 (unify) 할 수 있는 문자를 포함하는 것이다. 부목표표현은 목표표현에서 (단일화되지 않은) 다른 문자들을 F-규칙을 통해 역행함으로써 생성되는 값과 F-규칙의 전제조건의 단일화된 예시들의 논리곱으로 주어진다.
역행과정을 확실히 하기 위해 몇 가지 예를 좀더 들어 보자. 우리의 목표표현이 [ON(A, B) ∧ ON(B, C)] 라고 생각하자. 앞서의 F-규칙들을 가지고, B-규칙으로서 이 표현에 사용될 수 있는 F-규칙은 stack(x, y) 이며 이에는 두 가지 방법이 있다. 이 두 경우의 mgu 들은 각각 {A/x, B/y} 와 {B/x, C/y} 이다. 첫번째 mgu 를 생각해보자. 부목표목록은 다음과 같이 구성된다.
1) ON(B, C) 를 유도하는 stack(A, B) 를 통해 ON(B, C) 표현 (단일화되지 않은) 을 역행한다.
2) stack(A, B) 의 전제조건인 HOLDING(A), CLEAR(B) 라는 표현들을 추가하여 부목표 [ON(B, C) ∧ HOLDING(A) ∧ CLEAR(B)] 를 구성한다.
또 다른 예는 어떻게 부목표들이 존재한정변수를 가지게 되는지를 보여준다. 우리의 목표가 CLEAR(A) 라고 생각하자. 이때 두 개의 F-규칙이 그들의 추가목록에 CLEAR 를 가지고 있다. unstack(x, y) 의 경우를 보자. B-규칙으로서, mgu 는 {A/y} 이고, 생성된 부목표는 [HANDEMPTY ∧ CLEAR(x) ON(x, A)] 이다. 이 표현에서 변수 x 는 존재한정변수로 제한되어 있다. 즉, 우리가 어떤 블럭이 A 위에 있고, 그 블럭 위에 다른 블럭이 없는 상태를 만들 수 있다면 우리는 목표표현 CLEAR(A) 와 결합되는 상태에 도달하기 위하여 이 상태에 unstack 이라는 F-규칙을 적용할 수 있다.
마지막 예는 어떻게 우리가 불가능한 부목표목록들을 생성하게 되는지를 보여준다. 목표표현 [CLEAR(A) ∧ HANDEMPTY]에 unstack 의 B-규칙화된 것을 적용하려 한다고 생각해 보자. mgu 는 {A/y} 이다. unstack(x, A) 를 통한 HANDEMPTY 의 역행은 거짓 (F) 이다. 거짓을 포함하는 어떤 논리곱도 성취될 수 없으므로 우리는 이러한 B-규칙의 적용이 불가능한 부목표를 생성함을 알 수 있다 (즉, unstack(x, A) 를 어떤 상태에 적용했을 시 CLEAR(A) ∧ HANDEMPTY 를 포함하는 상태를 유도하는 그런 상태는 존재하지 않는다).
불가능한 목표상태는 다른 방법으로 발견될지도 모른다. 일반적으로, 귀납법을 시도하는 정리 증명 시스템을 사용할 수 있다. 만일 목표가 모순이면 그것은 성취될 수 없다. 목표의 모순성을 검사하는 것은 불가능한 목표들을 성취하는 데에 드는 불필요한 노력의 낭비를 피하기 위하여 중요하다.
때때로 목표표현과 F-규칙의 추가목록상의 표현 사이에서 단일화되는 mgu 가 더 이상 F-규칙의 적용을 진전시키지 않는 경우가 있다. 예를 들어 목표 [CLEAR(x) ∧ ONTABLE(x)] 에 적용되는 B-규칙으로서 STPIPS 규칙 unstack(u, C) 을 사용할 경우를 생각해 보자. 이때 mgu 는 {C/x} 이다. 이제 이 치환이 unstack(u, C) 의 적용을 진전시키지 않더라도, 이 치환은 역행과정에 사용된다. ONTABLE(x) 가 unstack(u, C) 를 통하여 역행될 때 우리는 ONTABLE(C) 를 얻는다.
앞서 주어진 STRIPS 규칙을 사용하는 후향 생성 시스템이 어떻게 목표 [ON(A, B) ∧ ON(B, C)] 을 성취하는지 살펴 보자. 이 특별한 예에서, 적용가능한 모든 B-규칙들을 적용해서 생성되는 부목표공간 (subgoal space) 은 F-규칙들을 사용해서 생성된 공간보다 더 크다. 그러나 대부분의 부목표들은 비현실적인 상태이다. 즉, 그러한 목표들은 분명히 거짓이거나 직접 정리 증명에 의해 보일 수 없는 상태이다. 이러한 불가능한 부목표를 제거하는 것은 부목표공간을 크게 감소시킨다.

그림 8 로보트 문제의 후향 탐색 그래프
그림 8 에서, 예로 든 목표에 어떤 B-규칙들을 적용한 결과를 볼 수 있다 (B-규칙 화살의 끝은 규칙의 추가목록의 문자를 유도하는 이 규칙의 전제조건 상의 문자들을 나타낸다). 그림 8 에서, unstack 이 CLEAR(B) 에 적용되었을 때, 이 규칙이 완전히 예시되지 않은 것을 주의하자. 앞에서 논의된 것처럼 가능한 예시가 규칙의 추가목록의 문자를 목표표현 상의 문자와 일치될 수 있다면, 우리는 이것을 이용하여 분리된 부목표 노드 (node) 에서 이 예시를 분명하게 할 수 있다.
그림에서 끝단 노드 중의 하나를 제외한 나머지는 모두 제거될 수 있다. "*" 로 표시된 끝단 노드들은 불가능한 목표를 의미한다. 즉 어떠한 문제상태로 이러한 목표표현으로 주어질 수 없다. 예로서, 이 중의 하나의 경우, 우리는 논리곱 [HOLDING(B) ∧ ON(A, B)] 로 주어지는 목표를 성취해야 하는데, 이는 분명히 불가능하다. 여기에서 우리의 후향 추론 시스템은 성취불가능한 목표들을 탐지하는 어떤 종류의 장치를 가진다고 가정한다.
"**" 로 표시된 끝단 노드는 원래 목표의 좀더 특수한 경우로 볼 수 있다 (즉, 이것은 원래 목표의 모든 표현들에 몇 가지 표현들이 추가되어 있다). 이러한 부목표를 달성하는 것은 아마도 원래의 목표를 달성하는 것보다 더 어려운 작업이기 때문에 이러한 부목표는 제거되거나 또는 이로부터의 확장이 최소화되어야 한다.

그림 9 후향 탐색 그래프 (그림 10 에 계속)
위와 같은 제거작업은 단 하나만의 부목표 노드를 남겨둔다. 이 부목표의 자식 노드들은 그림 9 에서 번호가 붙어 표시되어 있다. 이 그림에서 노드 ① 과 ⑥ 은 변수 x 의 값에 대한 조건을 포함하고 있다 (이러한 조건은 규칙의 제거목록이 역행된 문자와 일치가능한 문자를 포함하고 있을 때 역행과정에 의해 삽입된다). 노드 ① 과 ⑥ 은 둘다 어떤 경우에도 제거될 수 있으며, 그 이유는 이들이 성취될 수 없는 문자 거짓 (F) 을 포함하고 있기 때문이다. 또한 노드 ② 도 HOLDING(B) ∧ ON(B, C) 라는 논리곱 때문에 성취될 수 없다. 노드 ④ 는 조상 노드들 중의 하나와 완전히 일치 된다 (그림 8 에서). 따라서 이것도 제거될 수 있다 (허나 만일 부목표목록이 이의 조상 노드들 중의 하나와 완전히 일치하지 않고 이에 의해 함축 (imply) 된다면 일반적으로 우리는 이러한 부목표를 제거할 수 없다. 부목표 노드들에는 없고 이의 조상 노드들에 속한 문자는 거짓으로 역행되어질 가능성이 있기 때문에 조상 노드에 의해 생성된 어떠한 후계 노드들은 성취가 불가능할지도 모른다).
이러한 제거과정은 우리에게 이제 노드 ⑤ 와 ③ 만을 남겨준다. 잠시 노드 ⑤ 를 살펴 보자. 여기에는 목표목록이 존재한정 변수를 가지고 있다. x 대신에 치환가능한 표현 (즉, B, C) 들은 불가능한 목표상태를 유도하기 때문에, 우리는 또한 이 노드를 제거할 수 있다.

그림 10 후향 탐색 그래프의 최종결과
그림 10 에서, 그림 9 의 유일하게 존재하는 노드 ③ 아래에 목표공간의 부분을 볼 수 있다. 이 부분은 전보다 좀더 가지를 뻗어나갔지만, 우리는 여기에서 곧 해답을 찾을 수 있다 (즉, 초기상태와 일치되는 상태목록을 갖는 부목표가 생성되었다). 이제 검게 표시된 B-규칙의 화살표를 역으로 추적했을 때 루트 노드까지 도달하는 다음의 F-규칙열이 이 문제의 해답이 된다.
{unstack(C, A), putdown(C), pickup(B), stack(B, C), pickup(A), stack(A, B)}
목표상태의 표현목록 상의 몇 문자들이 그의 후손 상태의 표현목록에 존재할 경우 원래 목표상태에 적용 가능했던 B-규칙들 중의 몇 개가 이 후손 상태에 적용되어질 수 있다. 이러한 상황에서는 우리가 원하는 규칙들의 열을 찾기 위하여 모든 가능한 열이 탐색되어야만 한다. 몇 가지 다른 규칙들로 이루어지는 몇 가지 가능한 순서들이 존재하는 경우의 문제에서는 이러한 탐색은 지나칠 정도로 낭비가 심하다.
이러한 효율성 문제가 가분해 시스템 (decomposable system) 의 개념을 유도한다. 서로 다른 부목표들에서 공통되는 목표요소를 달성하는 데에 소요되는 잉여노력을 피하는 방법 중의 하나는 그 목표요소를 따로 떼어내어 독자적으로 해결하는 것이다. 목표상태를 구성하는 여러 요소들 중의 하나를 해결하는 적절한 F-규칙열을 찾은 후 그 다음의 요소를 해결하고, 나머지 요소들도 이러한 과정의 반복을 통해 해결한다. 이 과정은 여러 문자들의 논리곱으로 이루어진 목표를 한 개의 문자를 갖는 부목표로 세분하는 것과 관련이 있으며, 이로부터 가분해 시스템의 사용이 제시되어 진다.

그림 11 복합목표의 분리
만일 우리의 블럭 쌓기 문제의 예를 푸는데 가분해 시스템을 사용하려 한다면, 그림 8 에서처럼, 합해진 목표는 쪼개어 생각할 수 있다. 이 문제의 초기상태는 그림 11 에서와 같고 초기상태는 그림 4 와 같다고 생각하자. 만일 우리가 먼저 ON(B, C) 라는 목표요소에 대하여 작업을 한다면, 우리는 쉽게 해답 {pickup(B), stack(B, C)} 을 찾을 수 있다. 그러나 이 해답을 적용한다면, 그 문제의 상태는 변하고, 따라서 이로부터의 다른 목표요소 ON(A, B) 에 대한 해답은 좀더 어려워질 것이다. 게다가 이 상태로부터 ON(A, B) 로의 어떤 해답도 이미 성취된 ON(B, C) 를 무효화시킨다. 한편, 우리가 ON(A, B) 을 달성하는 작업을 먼저 한다면, 우리는 {unstack(C, A), putdown(C), stack(A, B)} 라는 해답을 얻을 수 있다. 허나 다시금 문제상태는 다른 목표요소 ON(B, C) 가 더욱 해결되기 어렵게 되는 상태로 변화된다. 두 개 이상의 목표요소들로 구성된 상태에서 하나의 목표요소를 선택하여 이를 풀고 이 풀어진 목표요소를 무효화 시키지 않으면서 다른 목표요소를 푸는 방법이 없는 것처럼 보인다.
우리는 이 문제의 목표요소들이 "상호 작용한다 (interact)" 라고 말한다. 하나의 목표를 푸는 것이 독립적으로 해결된 다른 목표를 무효화 시킨다. 일반적으로 전향 생성 시스템이 비가환적일 때, 그에 대응되는 후향 생성 시스템은 분해가능하지 않기 때문에 각 목표요소를 가지고 독립적으로 작업할 수가 없다. F-규칙의 적용에 의한 비가환 결과들에 의해 야기된 상호작용은 각 요소를 독립적으로 성취할 수 있는 해답들이 서로 결합될 수 없도록 한다.
우리의 예에서, 목표요소들은 상호작용의 정도가 상당히 높다. 그러나 좀더 전형적인 문제에서는 상호작용이 때때로 일어나거나 또는 일어나지 않을 수도 있다. 그런 문제에서는, 결합된 목표들의 요소들이 모두 상호작용한다고 가정하는 것보다 상호작용이 일어났을 때 어떤 특별한 방법으로 상호작용을 조정하여 각 요소를 분리하여 풀 수 있다고 가정하는 것이 더 효율적이다. 다음 절에서 이러한 일반적인 방법에 기초한 STRIPS 라고 불리우는 문제 풀이 시스템을 설명한다.
STRIPS 체제는 초기의 로보트 문제 풀이 시스템의 하나이다. STRIPS 는 목표들의 "스택 (stack)" 을 유지하며 스택의 맨 위에 있는 목표에 문제 풀이의 초점을 맞춘다. 초기의 목표 스택은 주목표만을 포함한다. 목표 스택에서 맨 위의 목표가 연속되는 상태목록과 일치될 때마다, 스택에서 제거되고 이 때 선택된 치환은 그 아래 표현들에 적용된다. 그렇지 않고, 만일 맨 위의 내용이 목표요소들의 결합이 이를 임의 순서에 따라 각각의 목표요소를 목표 스택에 추가한다. 기본 개념은 목표 스택에서 나타내는 순서대로 이러한 목표요소의 각각에 대하여 STRIPS 가 작업하는 것이다. 모든 목표요소가 풀렸을 때, 다시 결합된 목표요소들을 생각하여 결합된 목표요소들이 현재의 상태목록에 동시에 일치되지 않는다면 스택의 맨 위에 이 요소들을 재배열하는 것이다. STRIPS 가 이러한 결합ㄷ괸 목표요소들에 대하여 다시 한번 고려해 보는 것은 상호작용하는 목표문제를 안전하게 다루기 위함이다. 만일 한 요소를 푸는 것이 이미 해결된 다른 요소를 무효화시켰다면, 무효화된 요소는 필요에 따라 다시 구성되고 해결되어야만 한다. 목표 스택에 있는 맨 위의 (풀리지 않은) 목표가 하나의 문자로 되어 있을 때 STRIPS 는 그것과 일치될 수 있는 문자를 포함하는 추가목록을 가진 F-규칙을 찾아서, 이 F-규칙의 치환 예시가 스택의 맨 위의 단일 문자의 목표에 대치된다. 이때 F-규칙의 치환예시 위에 그 전제조건 P 의 치환 예시 결과가 추가되고, 만일 P 가 결합된 문자들의 표현이고, 현재의 상태목록과 일치되지 않으면 스택에 그 표현의 각 요소를 임의의 순서에 따라 추가한. 스택의 맨 위에 있는 것이 F-규칙일 때는, 이 F-규칙의 전제 조건이 현재의 상태목록과 일치되어 스택에서 제거된 경우이기 때문이 이 F-규칙을 현재의 상태에 적용하여 새로운 상태목록을 현재의 상태목록에 대치시키고 F-규칙을 제거한다. 이 제거된 F-규칙은 나중에 구성될 일련의 해결규칙들을 위해 시스템 상에서 기억되어진다.
우리는 STRIPS 를 데이터베이스가 현재의 상태목록과 목표 스택의 결합으로 된 생성 시스템으로서 생각할 수 있다. 이 데이터베이스 상의 연산들은 상태목록 또는 목표 스택을 변환시키며, 이 과정은 목표 스택이 빌 때까지 계속된다. 이러한 생성 시스템의 규칙들은 한 데이터베이스를 다른 데이터베이스로 변화시키는 법칙들을 말한다.
이들은 로보트 행동들을 모델화한 STRIPS 규칙들과 혼동되어서는 안된다. 이러한 일종의 상위단계의 규칙들은 상위목록과 목표 스택의 두 가지로 구성된 데이터베이스를 변화시키는 반면, STRIPS 규칙들은 목표 스택에 명기되고 상태목록을 변화시키는데 사용된다.
그래프 탐색 제어방식 (graph-search control regime) 을 가진 STRIPS 체계의 연산은 데이터베이스들은 이루어진 그래프를 만들어 이 그래프의 초기 노드부터 종료 노드에 이르는 경로에 대응되는 해답을 생성한다 (종료 노드 (termination node) 는 빈 목표 스택을 가지고 있는 데이터베이스를 말한다).
이제 STRIPS 가 어떻게 블럭 쌓기 문제를 푸는지 살펴 보자. 목표가 [ON(A, C) and ON(C, B)] 이고 초기상태가 그림 4 와 같다고 한다. 이 목표는 단지 B 위에 C 를 놓고 다시 C 위에 A 를 놓으면 된다. 우리는 앞에서처럼 같은 STRIPS 규칙을 사용한다.
그림 12 는 위 예의 해를 구하는 동안 STRIPS 에 의해 생성될 그래프의 일부분을 보여준다 (이해를 돕기 위하여 각 상태목록과 함께 블럭 상태의 그림도 보여준다). 이 문제는 매우 간단하므로 STRIPS 는 쉽게 해답 {unstack(C, A), stack(C, B), pickup(A), stack(A, C)} 를 얻을 수 있다.

그림 12 STRIPS 에 의한 탐색 그래프
목표가 [ON(B, C) ∧ ON(A, B)] 인 문제에 대해서 STRIPS 는 다소 어려움을 갖게 된다. 이 문제에서는 STRIPS 가 실제 필요한 규칙들보다 더 많은 규칙을 포함하는 {unstack(C, A), putdown(c), pickup(A), stack(A, B), unstack(A, B), putdown(A), pickup(B), stack(B, C), pickup(A), stack(A, B)] 라는 해답을 얻었다. 세번째부터 여섯번째까지의 규칙은 불필요한 우회경로를 표현한다. 이러한 결과는 STRIPS 가 ON(B, C) 를 성취하기 전에 ON(A, B)를 성취하기로 결정하기 때문에 생겨난 경우이다. 이 경우 목표요소들간에 상호작용이 STRIPS 가 ON(B, C) 를 성취할 때 이미 성취된 ON(A, B) 를 무효화하였다.
STRIPS 시스템의 제어요소에 의해 몇 가지 결정이 행해져야 하는데 첫째, 목표 스택에 주어진 내용이 여러 요소들로 결합되어 있을 때, 이 요소들을 어떤 순서로 배열하여야만 하는가를 결정해야 한다. 합리적 접근방식은 먼저 현재의 상태목록과 일치되는 모든 요소를 찾는 것이다 (개념적으로 이들이 우선적으로 스택 위에 놓이고 즉시 제거된다).
다음 단계는 일치되지 않는 요소들을 배열하는 것이다. 각각의 가능한 배열에 대해 새로운 후계 노드를 만들거나, 또는 임의로 그 중의 단 하나 (아마 경험적으로 목표요소가 가장 어려운 것으로 생각되는) 만을 선택하여 오직 이 노드의 후계 노드를 만들 수 있다. 아마도 후자의 방법이 하나의 목표요소가 해결된 뒤, 다시 결합된 목표요소를 가지고 성취되지 않은 다른 요소를 선택할 기회를 가질 수 있기 때문에 적절해 보인다.
(존재한정) 변수가 목표 스택에 있을 때 제어요소는 변수 치환에 따른 몇 가지 가능한 예시들 중에서 하나를 선택해야만 할 경우가 생길 수 있는데, 각각의 가능한 예시에 대하여 다른 후계 노드가 만들어질 수 있음을 알 수 있다. 하나 이상의 STRIPS F-규칙이 목표 스택 맨위의 목표를 성취할 수 있을 때 다시 선택의 문제에 직면하게 되는데, 각각의 적용가능한 규칙이 다른 후계 노드를 생성할 수 있음을 알아야 한다.
그래프 탐색 제어전략은 문제 풀이 그래프에서 적절한 노드를 선택할 수 있어야만 한다. 4 장의 방법들 중 하나가 사용될 수도 있다. 특히, 예를 들어 목표 스택의 길이, 목표 스택에 있는 문제의 어려운 정도, STRIPS F-규칙의 적용 비용과 같은 것을 요인으로 고려하는 경험적 평가함수를 개발할 수도 있다. 만일 그래프 탐색 제어 전략 대신에 역방향 (backtracking) 제어전략을 사용하기로 했다면 STRIPS 의 흥미있는 특별한 경우가 개발될 수 있다. 여기서는 STRIPS 라고 불리우는 스택의 맨위의 목표를 해결하기 위해 자신을 호출하는 순환함수를 생각할 수 있다. 이 경우에 목표 스택의 실제 이용은 순환 STRIPS 가 구현되는 언어 (LISP 와 같은) 의 이미 정의된 기능에 의해 가능할 수 있다.
다음은 순환 STRIPS 에 대한 프로그램이다. 먼저 초기상태목록이 전역변수 (global variable) S 에 놓여지고 STRIPS 가 성취하고자 하는 목표상태 목록을 G 로 주어진다.
순환 프로시쥬어 STRIPS(G)
1 S 와 G 가 일치할 때까지 단계 2 에서 단계 6 까지 반복하라.
2 g ← S 와 일치되지 않는 G 의 요소
3 f ← g 와 일치되는 문자를 포함하는 추가공식을 갖는 F-규칙
4 p ← f 의 전제조건의 치환 예시
5 STRIPS(p) ; p 를 목표상태로 하여 프로시쥬어 STRIPS 를 순환적으로 부른다
6 S ← f 의 치환 예시를 S 에 적용한 결과
STRIPS 는 직접적으로 많은 문제의 해답을 생성하지만, 때때로 필요 이상의 긴 해답을 생성하거나 또는 전혀 풀지 못하는 몇 가지 문제들이 있다. 그중 하나는 컴퓨터에서 두 개의 레지스터의 내용을 교환하기 위한 프로그램을 생성하는 문제이다.
처음의 내용이 각각 A, B 인 두 기억 레지스터 X, Y 를 생각해 보자. 이런 상황을 [CONT(X, A) ∧ CONT(Y, B)] 라는 상태목록으로 나타낼 수 있으며, 여기서 CONT(X, A) 는 X 레지스터가 A 라는 내용을 가지고 있다는 것을 의미한다. STRIPS 에서 목표는 [CONT(X, B) ∧ CONT(Y, A)] 이다. 여기서는 허용되는 유일한 연산은 레지스터의 값을 다른 레지스터로 옮기는 부과문 (assignment statement) 이며 이를 F-규칙으로 표현하면
assign(u, r, t, s)
P : CONT(r, s) ∧ CONT(u, t)
D : CONT(u,
t)
A : CONT(u, s)
이러한 부과문은 현재 t 내용을 가지고 있는 u 레지스터에 현재 s 내용을 가지고 있는 r 레지스터를 부과한다. 이 결과 u 레지스터의 내용은 s 가 되고, r 레지스터의 내용은 그대로 s 가 된다. 이 과정에서 u 의 내용 t 는 없어지게 된다.
CONT 관계가 assign 에 의해 제거되기 때문에, 이러한 F-규칙을 사용하는 생성체계는 비가환적이다. 부과문의 이런 성질 때문에 X 또는 Y 의 내용이 변화하기 전에 그 내용을 세번째 레지스터에 저장해야 한다. 따라서 STRIPS 는 초기상태목록에 CONT(Z, 0) 라는 사실을 추가함으로써 세번째 레지스터를 정하게 된다.

그림 13 STRIPS 가 해결 못하는 문제
그림 13 은 STRIPS 가 문제의 답을 구하는 과정을 보인다. 초기문제가 완전히 대칭적이기 때문에 노드 1 의 초기 결합된 목표요소들을 어떤 순서로 하느냐 하는 데에는 아무런 차이가 없다. 노드 2 에서 STRIPS 는 assign(X, r, t, B) 의 적용을 결정하며 이 연산은 노드 3 를 만든다. 여기서 STRIPS 의 치명적인 약점이 나타난다 :
STRIPS 는 노드 3 의 맨 위의 목표표현이 현재의 상태목록과 mgu {Y/r, A/t} 로서 일치될 수 있다고 즉시 결정한다. 그러나 불행히도 이 결과 A 를 잃어 버려 노드 4 의 맨 위 목표를 풀 수 없게 된다. 더우기 노드 3 의 상태목록을 가지고 노드 3 의 맨위 목표와 일치될 수 있는 mgu 는 위의 것이 유일하다.
이 문제를 해결하는 유일한 방법은 노드 3 의 맨위 목표의 일치과정을 잠시 연기하고 맨 위 목표가 CONT(r, B) 가 되는 후계 노드를 만드는 일이다. 그러면 아마도 언젠가 생성되는 노드에서 Z 는 r 로 대치될 것이다. 그러나 목표 일치과정을 연기하는 이런 방안을 추가하는 것은 STRIPS 를 매우 복잡하게 만든다. 대신에 다음 절에서 STRIPS 보다 좀더 강력한 문제풀이 시스템들을 논의한다.
로보트 문제 자체를 가환적 또는 비가환적으로 말할 수 있는 것은 아니다. 가환성은 전적으로 문제를 푸는데 사용되는 생성체계의 특성에 달려 있다. 예를 들어, 로보트 문제들을 가환생성 시스템에 의해 해결될 수 있도록 이 문제들을 체계화하는 것이 완전히 가능하다. 그러한 가환체계를 얻을 수 있는 한 방법은 로보트 문제를 증명되어지는 정리로 간주하고 여기에 가환연역 시스템을 이용하는 것이다. 로보트 문제를 연역의 문제로 체계화하는 것은 STRIPS 형 규칙을 사용하는 것보다 좀더 어색하고 복잡하지만, 정리-증명 체계화는 상당한 이론적인 관심을 끌고 있으며, 역사적으로 STRIPS 보다 선행되어 왔기 때문에 두 가지 접근방식으로 이를 소개한다.
1) 그린의 체계 (Green's formulation)
로보트 문제를 풀려는 처음 시도는 비교흡수 정리 증명시스템이 해결할 수 있도록 로보트 문제를 체계화한 그린에 의해 이루어졌다.
이 체계화에는 초기상태를 표현하는 서술문들의 집합과 각 상태들에 대한 여러 로보트 동작의 결과를 표현하는 서술문들의 집합이 포함되어 있다. 한 상태에서 어떠한 사실들이 참이 되는지를 추적하기 위해 그린은 각 서술문에 "상태" 또는 "상황" 변수를 포함시켰다. 그러면 목표조건은 존재한정변수들을 가진 공식으로 표현된다. 즉 이 시스템은 어떤 조건이 참이 되는 상태가 존재하는 지를 증명하려고 시도한다. 그러면 구조적인 증명방법이 원하는 상태를 만들기 위한 행동집합을 생성하기 위하여 사용이 된다.
그린의 시스템에서 모든 가정 (그리고 목표조건의 부정) 은 비교흡수 정리 증명 시스템을 사용하기 위해 절 형태 (clause form) 로 변환된다. 물론 다른 연역 시스템도 사용될 수 있다.

그림 14 블럭 구조의 초기상태
예를 들어 이 방법이 어떻게 작동하는지를 정확히 설명한다. 불행히도 이 정리 증명 체계화에 사용되는 표현방식은 약간 복잡하기 때문에 이 때까지 사용한 블럭 쌓기 문제를 약간 단순히 한다.
그림 14 의 상태를 초기상태라 하자. 테이블에는 D, E, F, G 라는 서로 다른 위치들이 있고 A, B, C 세 개의 블럭이 있다. 초기상태를 SO 라 하고, A 가 D 에 있는 것을 ON(A, D, SO) 라 표시한다. 각 상태는 명확한 인자를 갖는 서술 심볼들로 표현된다. 초기상태의 블럭 상황을 표시하면 다음과 같다.
ON(A, D, SO)
ON(B,
E, SO)
ON(C, F, SO)
CLEAR(A, SO)
CLEAR(B, SO)
CLEAR(C, SO)
CLEAR(G,
SO)
이제 어떤 상태에서 여러 로보트 행동의 실행결과를 표현할 수 있는 방법이 필요하게 되는데 정리 증명 체계화에서는 이를 STRIPS 형 규칙보다는 논리적인 함축 (implication) 으로 표현하고 있다. 예를 들어 로보트가 x 블럭을 y 위치에서 z 위치로 옮기는 행동을 생각하고 이를 trans(x, y, z) 라고 표현한다. 여기서 y, z 는 x 가 놓일 블럭 또는 테이블 이름이고 x 와 z 위에는 아무것도 없어야 한다.
어떤 상태에서 하나의 행동이 실행되었을 때 그 결과는 새로운 상태가 되며 이러한 상태간의 변화관계를 표시하기 위해 "do (action, state)" 라는 특별한 함수 표현을 사용한다. 그러므로 만일 s 상태에서 trans(x, y, z) 가 실행되면, 그 결과는 do[trans(x, y, z), s] 에 의해 주어지는 상태이다.
그러면, trans 라고 정의된 행동의 주요 결과 다음과 같이 공식화된다.
[CLEAR(x, s) ∧
CLEAR(z, s) ∧ ON(x, y, s) ∧ DIFF(x, z)]
⇒ [CLEAR(x,
do [trans(x, y, z), s])
∧
CLEAR(y, do [trans(x, y, z), s])
∧
ON(x, z, do [trans(x, y, z), s])
(위 서술문의 모든 변수는 전체한정기호
(universal qualification) 로 간주된다.)
이 공식은 x 와 z 위가 비어있고, s 상태에서 y 위에 x 가 놓여 있고, x 와 z 가 다르면, x 와 y 는 그 위에 아무것도 놓이지 않고 trans(x, y, z) 행동결과 x 는 z 위에 있게 되는 것을 표현한다 (서술 심볼 DIFF 는 그 진위가 상태와 독립되어 있으므로 상태변수를 가질 필요가 없다). 그러나, 이 공식 하나만으로는 그 행동의 결과를 완전하게 표현할 수 없다.
우리는 또한 어떤 관계는 행동에 전혀 영향을 받지 않는다고 명시해야 한다.
STRIPS 유형체계들은 규칙에 명기되지 않는 관계는 불변임을 약속하여 F-규칙을 사용했으나 여기서는 변화되는 부분과 변화되지 않는 부분을 분명하게 표현해야 할 것이다. 불행히도 그린의 공식화에서는 행동에 의해 변화되지 않는 각각의 관계들을 가정으로 가져야 한다. 예를 들어 같은 위치에서 변화되지 않는 블럭들을 표현하기 위하여 다음과 같은 가정이 필요하다.
[ON(u, v, s) ∧ DIFF(u, x)] ⇒ ON(u, v, do [trans(x, y, z), s])
그리고, v 블럭 (u 와 같지 않은) 이 w 블럭 (u 와 같지 않은) 위에 놓여 있을 떼 u 블럭 위에 아무것도 놓여 있지 않았다면, u 블럭은 행동결과 그 위에 여전히 아무것도 가지고 있지 않다는 것을 표현하기 위한 또 하나의 공식이 필요하다. 행동이 실행되는 동안 변하지 않는 블럭들을 나타내는 이런 가정들을 구조 가정 (frame assertion) 이라 부르며, 더 큰 시스템에서는 상태를 표현하기 위한 많은 서술들이 있을 것이다. 그린의 공식화는 각 서술에 대해 분리된 구조 가정을 요구하게 된다. 이런 구조 가정은 고차원논리를 사용하면 다음과 같이 요약될 수 있다.
(∀P)[P(s) ⇒ P[do, (action, s)]
그러나 고차원 논리에서는 그들 고유의 복잡성을 가진다 (이후에 다중 구조 가정이 없는 다른 일차논리를 논한다).
행동에 대한 모든 가정들이 "함축" 규칙에 의해 표현된 뒤에 비로소 실제 로보트 문제를 풀기 위한 준비가 된 셈이다. 블럭 B 위에 블럭 A 가 있는 단순한 목표상태가 있다고 하자. 이 목표는 다음과 같이 표현된다.
(∃s) ON (A, B, s).
문제는 가정들로부터 목표공식의 조립적인 증명을 찾음으로써 해결된다. 이 때 어떤 적절한 정리-증명방식이 사용되도 무관하다.

그림 15 블럭-스택 문제의 결정 그래프
Green 은 부정된 목표와 모든 공식들을 절 형태로 바뀌는 결정 시스템을 사용한다. 그러면 시스템이 모순을 찾고 해답찾기과정은 존재하는 목표상태를 찾는 것이 된다. 일반적으로 이 상태는 목표상태를 생성하는 행동들을 명명하는 do 함수의 합성함수로 표현된다. 그림 15 는 결정 그래프를 보여준다 (DIFF 서술은 다시 풀이되지 않고 유추된다).
그림 15 의 그래프에 해답찾기과정을 적용하면 이 경우 목표 달성에 필요한 단일 행동을 가리키는
s1 = do [trans(A, D, B), SO]
를 얻게 된다.
결정 (resoluion) 대신에 앞에서 규칙을 기초로 하는 연역 시스템을 논의했다. 초기상태를 서술하는 가정은 사실로 사용됐고 행동과 구조 가정은 생성규칙으로 사용될 수 있다.
지금 막 인용한 예는 아주 단순하다. 물론 구조 가정도 사용하지 않았다 (목표가 복합목표 예를 들어 [ON(A, B, s) ∧ ON(B, C, s)] 라면 구조 가정은 꼭 사용되어야 한다. 그 경우에 A 를 B 위에 두는 동안에는 B 가 C 위에 있다는 것을 증명해야 한다.
그러나 약간만 더 복잡한 문제에는 이 공식을 사용하여 로보트 문제를 풀기 위하여 필요로 하는 탐색향을 폭발적으로 증가하여 이 방법은 현실적이 못된다. 이 방법은 구조 가정에 의하여 야기된 어려움과 함께 이 탐색문제 때문에 STRIPS 문제 해결 시스템에 뒤진 주요한 요인이 되었다.
2) 코왈스키 (Kowalski) 의 체계화
코왈스키는 다른 체계를 제안했는데, 구조가정의 문장들을 단순화한다. 그린의 체계에서는 보통의 서술식들이 항 (term) 을 구성한다.
예를 들어 상태 SO 에서 D 위에 A 가 있다는 사실을 나타내기 위해 ON(A, D, SO) 라는 문장 대신에 HOLDS[on(A, D), SO] 를 사용하자. A 는 D 위에 있다는 개념을 나타내는 on(A, D) 항은 새로운 논리계산에서는 개별적인 것으로 취급된다. 일반적으로 개별적인 것으로 관계를 표시하는 것은 일차 공식화에서 높은 차원논리 (high order logic) 의 이점을 얻는 방법이다.
그림 14 의 초기상태는 다음 표현의 집합으로 주어진다.
1 POSS(SO)
2 HOLDS[on(A, D), SO]
3 HOLDS[on(B, E), SO]
4 HOLDS[on(C, F), SO]
5 HOLDS[clear(A), SO]
6 HOLDS[clear(B), SO]
7 HOLDS[clear(C), SO]
8 HOLDS[clear(G), SO]
POSS(SO) 문장은 'SO 상태가 가능하다' 즉 도달될 수 있다는 것을 의미한다. 서술식 POSS 를 도입하는 이유는 나중에 알게 될 것이다. 이제 행동에 의해 참이 되는 각 관계에 대하여 분리된 표현 HOLDS 를 사용하여 행동의 결과 (추가목록) 을 표현한다. 행동이 trans(x, y, z) 인 경우 다음과 같은 표현들을 갖는다.
9 HOLDS[clear(x), do[trans(x, y, z), s]]
10 HOLDS[clear(y), do[trans(x, y, z), s]]
11 HOLDS[on(x, z), do[trans(x, y, z), s]]
(가정에 있는 모든 변수는 전체한정변수들이다)
주어진 상태에서 주어진 행동이 가능하다는 것을 말하기 위해 또다른 서술 PACT 를 사용한다. PACT(a, s) 는 s 상태에서 a 의 행동이 실행가능하다는 것을 나타낸다.
따라서 행동 trans 에 대해 다음 것을 얻는다.
12 {HOLDS[clear(x), s] ∧ HOLDS[clear(z), s]
∧ HOLDS[on(x, y), s] < DIFF(x, z)}
⇒ PACT[trans(x, y, z), s]
다음에 만일 주어진 상태가 가능하고 행동의 전제조건이 만족되면 그 행동의 실행에 의하여 생성된 상태 또한 가능하다.
13 [POSS(s) ∧ PACT(u, s)] ⇒ POSS[do(u, s)]
Kowalki 의 공식화의 주된 장점은 우리는 오직 각 행동에 대하여 하나의 구조가 정만을 필요로 한다는 것이다. 위의 예에서 단일구조가정은 다음과 같다.
14 {HOLDS(v, s) ∧ DIFF[v, clear(z)] ∧ DIFF[v, on(x, y)]}
⇒ HOLDS[v, do[trans(x, y, z), s]]
이 표현은 clear(z) 와 on(x, y) 이외의 다른 모든 행태의 표현들은 trans(x, y, z) 행동의 실행에 의해 생성되는 모든 상태에서도 여전히 유지된다. 시스템의 목표는 보통 존재한정상태변수를 가진 표현으로 주어진다. 만일 C 위에 B 를 B 위에 A 를 놓으려한다면, 목표는 다음과 같이 된다.
(∃s){POSS(s) ∧ HOLDS[on(A, B), s]} ∧ HOLDS (on (A, B)s]}
첨가된 POSS(s) 는 s 가 도달가능한 상태임을 나타내기 위하여 필요하다. 1 ~ 14 까지의 가정들은 문제풀이 시스템에 의해 필요되는 기본 지식을 표현한다. 만일 우리가 이 지식을 사용하여 문제를 푸는데 앞에서 배운 규칙에 기초한 연역 시스템을 사용하려면 1~11 가정은 사실로써 12~14 가정은 규칙으로 사용할 것이다. 그런 시스템의 세부연산은 규칙이 정방향 혹은 역방향으로 사용되는가, 그리고 그 시스템에서 사용된 특정 제어전략에 달려 있다.
예를 들어 규칙을 한 연역 시스템이 STRIPS 형태의 규칙을 사용하는 역방향 생성 시스템에 의하여 수행되도록 흉내내기 (simulate) 위하여 연역 시스템의 제어 전략을 목표에 대조하여 가정 9-11 중에서 하나와 일치되게 한다 (이 단계는 역방향을 작용할 행동을 정하는 것이다).
다음에 가정 12, 13 을 사용하여 전제조건을 설정하고 구조 가정 14 를 이용하여 이 행동으로 다른 목표조건으로 역행하게 하는 것이다. 이런 전 과정은 사실을 나타내는 가정 1-8 과 일치하는 부목표 중의 하나에 모든 부목표가 만들어 질 때까지 되풀이 된다. 물론 다른 제어전략에 의하여 STRIPS 와 더 복잡한 로보트 문제 풀이 시스템도 흉내낼 수 있다. 또 따로 한 제어전략은 PROLOG 언어처럼 사실과 규칙을 순서화하는 것이다.
STRIPS 유형의 시스템과 연역 시스템을 비교하면, 어떤 시스템은 문제를 풀고 다른 것은 못푼다는 식의 주장은 할 수 없다. 사실 적당한 조작방식으로 서로 다른 유형의 시스템에서 문제 풀이 시스템은 필수적으로 동일하게 만들어질 수 있다. 중요한 것은 로보트 문제를 연역 시스템을 사용하여 효과적으로 푸는 것은 STRIPS 유형의 시스템에서 사용된 'built-into" 약속들의 특정화되고 분명한 제어전략을 요구하는 것이다. 그러므로 STRIPS 유형의 로보트 문제 풀이 시스템은 낮은 차원의 프로그래밍 언어와 높은 차원의 프로그래밍 언어의 관계처럼 연역 시스템과 관계된다.
RSTRIPS 는 목표요소들이 상호작용하는 문제를 우회하기 위한 목표 역행방식을 사용하는 STRIPS 의 변형이다. 이 시스템은 계획에서 나중에 적용된 F-규칙 F2 의 전제조건으로 필요로 하는 P 가 이미 성취되어 있을 때, 현재 적용되는 F-규칙 F1 이 이를 무효화한다면 이 F1 을 적용하지 못하게 한다. F1 보다 F2 가 나중에 실행되기 위하여는 F2 적용에 필요한 추가조건이 F1 의 적용에 의해 만들어져야만 한다. F1 을 적용하는 대신에 RSTRIPS 는 P 를 유도하는 F-규칙들을 통해 P' 를 역행함으로써 계획을 재배열한다. 그러면 역행된 P' 를 유도 성취하는 규칙들은 더 이상 P 를 무효화 하지 않는다. RSTRIPS 에 사용된 기법과 체제는 우선 목표요소들이 상호 작용하지 않는 예제를 통해 잘 설명될 수 있다. 이 예제를 설명한 후, 상호작용하는 목표요소들을 가진 경우 RSTRIPS 가 이를 어떻게 해결하는지 상세히 설명한다.
예제 1) 앞서 사용된 단순한 블럭 쌓기문제 중의 하나를 예로 사용하자. 목표는 [ON(C, B) ∧ ON(A, C)] 이고 초기상태는 그림 4 와 같다. 첫째의 F-규칙이 적용될 때까지는 RSTRIPS 는 STRIPS 와 똑같이 작동한다. 그러나 목표 스택에서는 몇 가지 특수한 체제를 사용한다. 특히 스택에서 결합된 목표요소들의 각 요소들을 순서지을 때 RSTRIPS 는 이 요소들을 스택에서 하나의 괄호로 묶어준다. 어떻게 묶는지 간단히 살펴 보자.
첫번째 규칙 unstack(C, A) 가 적용될 때 RSTRIPS 에 의해 만들어진 전역 (global) 데이터베이스의 목표 스택 부분은 다음과 같다.
|
|
[HANDEMPTY ∧ CLEAR(C) ∧ ON(C, y) unstack(C, y) |
|
|
HOLDING(C) CLEAR(B) HOLDING(C) ∧ CLEAR(B) |
|
|
|
|
|
|
|
|
stack(C, B) |
|
|
ON(C, B) ON(A, C) ON(C, B) ∧ ON(A, C) |
|
|
|
|
|
이 목표 스택은 문제 해결 단계에서 STRIPS 에 의해 생성된 것과 같다. 이 예에서는 좀 더 분명히 하기 위해 F-규칙을 적용하여 성취되는 조건을 쓰고 그 위에 그 F-규칙을 목표 스택에 써 넣었다. 직각의 수직괄호는 결합된 목표요소들의 각 목표요소들의 배열을 포함한다.
치환 {A/y} 을 가지고 unstack(C, A) 의 전제조건이 초기상태목록과 일치되기 때문에 STRIPS 는 unstack(C, A) 를 적용할 수 있다. 만족되는 전제조건들과 F-규칙을 목표 스택에서 지우는 대신에 (STRIPS 처럼), RSTRIPS 는 그 F-규칙에 의해서 성취되는 것이 HOLDING(C) 라는 것을 가리키기 위하여 이러한 것들을 그대로 두되 HOLDING(C) 밑에 직선 표시를 해둔다. 시스템이 스택에서 조건들을 시험할 때 시스템은 직선 표시가 여전히 만족될 필요가 있는 다음 조건임을 나타내기 위하여 직선 표시있는 곳으로 조정한다. unstack(C, A) 가 적용된 뒤의 목표 스택은 다음과 같다.
|
|
|
[HANDEMPTY ∧ CLEAR(C) ∧ ON(C, A) unstack(C, A) |
|
|
|
|
*HOLDING(C) |
|
|
|
|
||
|
|
|
CLEAR(B) |
|
|
|
|
HOLDING(C) ∧ CLEAR(B) |
|
|
|
|
||
|
|
|
stack(C, B) |
|
|
|
|
ON(C, B) ON(A, C) ON(C, B) ∧ ON(A, C) |
|
|
|
|
||
|
|
|
(*) 표시 밑에 있는 수평선이 바로 위에서 말한 직선 표시이다. 그 표시 위에 있는 F-규칙들은 모두 적용되었고 그 아래 남아있는 조건, 즉 CLEAR(B) 가 이제 시험되어야 한다 (확실히 하기 위해, 목표 스택에 F-규칙들의 적용에 의해 유도된 상태의 그림을 집어 넣었다).
(위의 목표 스택에서 보는 바와 같이) 이 표시가 수직괄호를 따라 내려갈 때 이 표시를 포함하는 수직괄호의 가장 밑에 있는 결합된 목표요소들 중의 이미 성취된 요소들은 이 표시 위에 존재한다. RSTRIPS 는 이러한 요소들을 주시하여 이들을 보호한다. 이런 보호는 RSTRIPS 가 이 수직괄호 내에서 보호되는 목표요소들을 제거하거나 거짓으로 만드는 F-규칙의 적용을 허용하지 않음을 의미한다. 보호되는 목표들은 목표 스택에서 (*) 에 의해 표시된다.
STRIPS 는 목표 스택에서 F-규칙의 전제조건이 만족될 때마다 새 상태목록을 만들기 위해 현재의 상태목록에 F-규칙을 적용했으나 RSTRIPS 는 이 과정을 수행하지 않고 오히려 직선 표시 위의 목표 스택 부분을 계속 저장하는 것에 의해 지금까지 적용된 F-규칙열을 표시한다. 이 F-규칙열로부터 RSTRIPS 는 항상 이 열이 초기상태에 적용된다면 어떤 상태목록이 만들어지는지 계산할 수 있다. 실제로는 RSTRIPS 에서는 그런 상태목록을 계산할 필요가 없고 기껏해야 어떤 부목표 (subgoal) 가 현재의 상태목록과 일치될 수 있는지 없는지를 계산할 수 있으면 된다.
이 계산은 지금까지 적용된 F-규칙열을 통해 부목표를 역행시킴으로써 행해진다. 예를 들어 위의 목표 스택에서 RSTRIPS 는 CLEAR(B) 가 unstack(C, A) 적용 뒤에 만족되는 상태목록과 일치되는지의 여부를 결정해야만 한다. 이 F-규칙을 통하여 CLEAR(B) 를 역행하면 초기상태목록과 일치되는 CLEAR(B) 가 만들어지고 그러므로 이것은 이 F-규칙의 적용으로 유도되는 상태목록과 일치된다 (만일 CLEAR(B) 가 일치되지 않으면 RSTRIPS 는 그것을 성취하는 F-규칙을 목표 스택에 집어넣어야만 한다).
이 단계에서 RSTRIPS 는 stack(C, B) 의 두 전제조건이 모두 만족되는 것을 인식하고 따라서 (수평선 표시를 아래로 움직임으로써) 이 F-규칙이 적용되고 ON(C, B) 가 보호된다 [복합목표 HOLDING(C) ∧ CLEAR(B) 의 괄호가 완전히 수평선 표시 위에 있으므로 시스템은 HOLDING(C) 를 보호하지 않는다]. 다음에 RSTRIPS 는 ON(A, C) 를 성취하고자 한다. 결과적으로 RSTRIPS 는 다음과 같은 목표 스택을 생성한다.
|
|
|
|
[HANDEMPTY ∧ CLEAR(C) ∧ ON(C, A) unstack(C, A) |
|
|
|
|
|
HOLDING(C) CLEAR(B) HOLDING(C) ∧ CLEAR(B) |
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
stack(C, B) |
|
|
|
|
|
*ON(C, B) |
|
|
|
|
|
||
|
|
|
|
[HANDEMPTY ∧ CLEAR(A) ∧ ONTABLE(A) pickup(A) |
|
|
|
|
|
HOLDING(A) CLEAR(C) HOLDING(A) ∧ CLEAR(C) |
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
stack(A, C) |
|
|
|
|
|
ON(A, C) ON(C, B) ∧ ON(A, C) |
|
|
|
|
|
||
|
|
|
|
pickup(A) 의 전제조건이 지금까지 적용된 F-규칙열 {unstack(C, A), stack(C, B)} 을 통하여 역행함에 의해 알 수 있듯이 이 조건들은 현재의 상태목록과 일치한다 (CLEAR(A) 조건이 초기상태와 일치되지 않지만, 이것은 unstack(C, A) 의 적용에 의하여 현재의 상태에서 참이 된다. 초기상태와 일치되는 HANDEMPTY 조건은 unstack(C, A) 의 적용 뒤에 제거되지만 stack(C, B) 의 적용 뒤에 다시 참이 된다. 역행과정은 이 조건들이 현재에 참이라는 것을 보여준다).
F-규칙, pickup(A) 가 적용될 수 있기 전에 RSTRIPS 는 이것이 어떤 보호되는 부목표를 무효화하지 않는다는 것을 확신해야 한다. 이 단계에서 ON(C, B) 는 보호된다. 무효화하지 않는다는 것을 확신해야 한다. 이 단계에서 ON(C, B) 는 보호된다. 무효화 여부를 검사하는 것은 pickup(A) 를 통하여 ON(C, B) 를 역행함으로써 이루어진다. 보호되는 표현 ON(C, B) 의 무효화는 오직 이것이 거짓으로 역행될 때만 일어난다 (즉, pickup(A) 라는 F-규칙의 적용에 의해서 ON(C, B) 가 제거될 때만이다). 어떤 보호요소도 무효화되지 않기 때문에 F-규칙 pickup(A) 가 적용될 수 있다. 수평선 표시는 HOLDING(A) 밑으로 움직이고 HOLDING(A) 는 보호된다 (ON(C, B) 는 여전히 보호되어야 한다).
stack(A, C) 의 다른 전제조건, 즉 CLEAR(C) 의 F-규칙열을 통한 역행은 이것이 현재의 상태목록과 일치된다는 것을 보여준다. 따라서 stack(A, C) 의 복합된 전제조건이 만족된다. 먼저 해결된 주목표요소 ON(C, B) 의 stack(A, C) 를 통한 역행은 이 보호되는 표현이 무효화되지 않음을 보여주고 따라서 RSTRIPS 는 stack(A, C) 를 적용하여 수평선 표시를 스택의 맨아래 조건 밑으로 옮긴다. 이제 목표 스택의 모든 표현들이 수평선 위에 있으므로 RSTRIPS 는 끝난다. 이 때 목표 스택의 F-규칙들은 해답열 {unstack(C, A), stack(C, B), pickup(A), stack(A, C)} 이 된다.
이 예는 보호방해 (protection violation) 가 없었기 때문에 바로 해결되었다. 그러나 목표요소들이 상호작용할 때에 우리는 보호방해를 갖게 되는데, 이 경우 RSTRIPS 가 어떻게 이러한 것들을 해결하는지를 설명한다.
예제 2) 앞의 그림 4 와 같은 초기상태를 생각하자. 그러나 이번에는 좀 더 복잡한 목표 [ON(A, B) ∧ ON(B, C)] 에 도달하려 한다. 다음 그림에 보여지는 목표 스택에 이르기까지 과정이 순조롭게 진행된다.
|
|
|
|
ONTABLE(A) |
|
|
|
|
|
||
|
|
|
|
[HANDEMPTY ∧ CLEAR(C) ∧ ON(C, A) unstack(C, A) |
|
|
|
|
|
CLEAR(C) HOLDING(C) |
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
putdown(C) |
|
|
|
|
|
HANDEMPTY ONTABLE(A) ∧ CLEAR(A) ∧ HANDEMPTY |
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
pickup(A) |
|
|
|
|
|
HOLDING(A) CLEAR(B) HOLDING(A) ∧ CLEAR(B) |
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
stack(A, B) |
|
|
|
|
|
*ON(A, B) |
|
|
|
|
|
||
|
|
|
|
*ONTABLE(B) |
|
|
|
|
|
[HANDEMPTY ∧ CLEAR(z) ∧ ON(z, B) unstack(z, B) CLEAR(B) HANDEMPTY ONTABLE(B) ∧ CLEAR(B) ∧ HANDEMPTY |
|
|
|
|
|
|
|
|
|
|
|
pickup(B) |
|
|
|
|
|
HOLDING(B) |
|
|
|
|
|
||
|
|
|
|
CLEAR(C) |
|
|
|
|
|
HOLDING(B) ∧ CLEAR(C) |
|
|
|
|
|
||
|
|
|
|
stack(B, C) |
|
|
|
|
|
ON(B, C) ON(A, B) ∧ ON(B, C) |
|
|
|
|
|
초기상태목록에 적용되어진 F-규칙열 {unstack(C, A), putdown(C), pickup(A), stack(A, B)} 은 위의 목표 스택에서 수평선 표시 위에 있다. 또한 부목표 ON(A, B) 와 ONTABLE(B) 은 이 규칙열에 지금 해결되고 보호되어진다. 여기에서 주의할 것은 지금 F-규칙 unstack(A, B) 의 전제조건은 만족되지만 그 적용이 목표 ON(A, B) 의 보호를 방해한다는 것이다. 어떻게 해야 되는가?
RSTRIPS 는 수평선 표시 아래의 F-규칙열의 괄호 안의 것만으로 ON(A, B) 가 재성취되는지의 여부를 조사한다. ON(A, B) 의 참을 요구하는 곳은 오직 괄호의 맨 아랫부분이다. 아마도 괄호 안의 F-규칙들 중의 하나가 이것을 재성취할지도 모른다. 만일 그러하다면 이러한 "일시적인 (temporary)" 방해는 허용될 수 있다. 그러나 위 경우에는 이러한 F-규칙 중의 어느 것도 ON(A, B) 를 재성취하지 못하기 때문에 RSTRIPS 는 보호방해를 피하기 위하여 몇 가지 단계를 수행한다.
RSTRIPS 는 방해받는 목표의 괄호 끝에 있는 복합목표가 ON(A, B) ∧ ON(B, C) 임을 본다. 이 요소 중의 하나, 즉 ON(B, C) 를 풀기 위해 필요한 F-규칙은 이미 성취되어 보호받는 다른 요소를 무효화한다. 이때, 이러한 ON(B, C) 요소를 우리는 '보호방해요소 (protection violating component)' 라고 부른다. RSTRIPS 는 이 방해를 피하기 위하여 이 보호방해요소를 보호되는 부목표를 성취하는 이미 적용된 (직선 표시 위의) F-규칙을 통해 역행한다. 적용된 마지막 F-규칙 stack(A, B) 도 또한 ON(A, B) 를 성취하는 규칙이기 때문에, RSTRIPS 는 stack(A, B) 를 통하여 ON(B, C) 를 역행한다. 이 경우에 부목표는 역행에 의해 변화되지 않고, 이제 RSTRIPS 는 stack(A, B) 의 적용에 앞서서 이 역행된 목표를 성취하고자 시도한다. 이러한 역행과정은 RSTRIPS 가 다음과 같은 목표 스택을 갖도록 해준다.
|
|
|
|
ONTABLE(A) [HANDEMPTY ∧ CLEAR(C) ∧ ON(C, A) unstack(C, A) CLEAR(A) [HOLDING(C) putdown(C) HANDEMPTY ONTABLE(A) ∧ CLEAR(A) ∧ HANDEMPTY |
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
pickup(A) |
|
|
|
|
|
*HOLDING(A) *CLEAR(B) |
|
|
|
|
|
||
|
|
|
|
ON(B, C) HOLDING(A) ∧ CLEAR(B) ∧ ON(B, C) stack(A, B) ON(A, B) ON(A, B) ∧ ON(B, C) |
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
보호방해가 발견된 괄호 끝에 있는 복합목표 ON(A, B) ∧ ON(B, C) 는 여전히 목표 스택에 존재한다. 이전의 목표 스택에서 ON(A, B) 아래의 다른 요소들은 이제 ON(B, C) 를 성취하는 데에 부적절한 계획의 부분이 되므로 스택에서 제거된다. stack(A, B) 를 적용함으로써 ON(A, B) 를 성취하고자 하는 계획은 여전히 타당하므로, 목표 스택에 남겨진다. 여기에서 역행된 목표 ON(B, C) 와 F-규칙 stack(A, B) 바로 위의 복합전제조건이 결합되는 것을 주의하라. 수평선 표시가 괄호 중간을 지나므로, HOLDING(A) 와 CLEAR(B) 의 부목표들은 보호되어야 한다.
RSTRIPS 는 다시 이 목표 스택을 가지고 시작해서 아래의 목표 스택이 생성될 때까지는 어떠한 부수적인 보호방해를 발견하지 못한다.
|
|
|
|
ONTABLE(A) [HANDEMPTY ∧ CLEAR(C) ∧ ON(C, A) unstack(C, A) CLEAR(A) [HOLDING(C) putdown(C) HANDEMPTY ONTABLE(A) ∧ CLEAR(A) ∧ HANDEMPTY |
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
pickup(A) |
|
|
|
|
|
*HOLDING(A) *CLEAR(B) |
|
|
|
|
|
||
|
|
|
|
*ONTABLE(B) *CLEAR(B) |
|
|
|
|
|
||
|
|
|
|
[HOLDING(x) putdown(x) HANDEMPTY ONTABLE(B) ∧ CLEAR(B) ∧ HANDEMPTY |
|
|
|
|
|
|
|
|
|
|
|
pickup(B) |
|
|
|
|
|
HOLDING(B) CLEAR(C) HOLDING(B) ∧ CLEAR(C) |
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
stack(B, C) |
|
|
|
|
|
ON(B, C) HOLDING(A) ∧ CLEAR(B) ∧ ON(B, C) stack(A, B) ON(A, B) ON(A, B) ∧ ON(B, C) |
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
RSTRIPS 는 putdown(A) 의 전제조건이 역행에 의하여 현재의 상태목록과 일치되지만 putdown(A) 의 적용이 HOLDING(A) 의 보호를 방해함을 알게 된다. 이 방해는 일시적인 것이 아니다. 이 방해를 피하기 위하여, RSTRIPS 는 좀더 거슬러 올라가 이번에는 F-규칙 pickup(A) 를 통하여 보호방해요소 ON(B, C) 를 역행한다.
역행 뒤의 목표 스택은 다음과 같다.
|
|
|
|
*ONTABLE(A) [HANDEMPTY ∧ CLEAR(C) ∧ ON(C, A) unstack(C, A) *CLEAR(A) [HOLDING(C) putdown(C) *HANDEMPTY |
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
ON(B, C) ONTABLE(A) ∧ CLEAR(A) ∨ HANDEMPTY ∧ ON(B, C) |
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
pickup(A) |
|
|
|
|
|
HOLDING(A) CLEAR(B) HOLDING(A) ∧ CLEAR(B) |
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
stack(A, B) |
|
|
|
|
|
ON(A, B) ON(A, B) ∧ ON(B, C)
|
|
|
|
|
|
ON(A, B) 를 성취하기 위한 계획은 여전히 남아 있지만 ON(B, C) 를 성취하기 위한 보호방해계획 (protection violating plan) 은 제거된다.
다시 이 목표 스택을 가지고 시작하여 다음과 같은 목표 스택이 생성될 때 RSTRIPS 는 또다른 잠정적인 보호방해를 발견한다.
|
|
|
|
|
*ONTABLE(A) [HANDEMPTY ∧ CLEAR(C) ∧ ON(C, A) unstack(C, A) *CLEAR(A) [HOLDING(C) putdown(C) *HANDEMPTY |
|
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
[ONTABLE(B) ∧ CLEAR(B) ∧ HANDEMPTY pickup(B) |
|
|
|
|
|
|
HOLDING(B) CLEAR(C) HOLDING(B) ∧ CLEAR(C) |
|
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
stack(B, C) |
|
|
|
|
|
|
ON(B, C) ONTABLE(A) ∧ CLEAR(A) ∧ HANDEMPTY ∧ ON(B, C) |
|
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
pickup(A) |
|
|
|
|
|
|
HOLDING(A) CLEAR(B) HOLDING(A) ∧ CLEAR(B) |
|
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
stack(A, B) |
|
|
|
|
|
|
ON(A, B) ON(A, B) ∧ ON(B, C)
|
|
|
|
|
|
|
만일 pickup(B) 가 적용된다면 HANDEMPTY 의 보호가 방해받게 된다. 그러나 이번에는 일시적인 것이다. F-규칙 stack(B, C) (괄호 속에 있는) 는 HANDEMPTY 를 재성취하고, 따라서 우리는 이 방해를 허용하고 따라서 이제 곧바로 해답이 얻어진다.
이 경우에 RSTRIPS 는 STRIPS 가 이 문제에 대하여 찾았던 해답열보다 더 짧은 해답열을 찾아낸다. RSTRIPS 에 의해 찾아진 해답열의 F-규칙들은 마지막 목표 스택에서의 규칙들 즉, {unstack(C, A), putdown(C), stack(B, C), pickup(A), stack(A, B)} 이다.
마지막 예로서 STRIPS 이 풀 수 없었던 두 개의 레지스터 내용을 교환하는 문제를 생각해 보자. 이는 RSTRIPS 의 아래와 같은 역행과정을 통해 {assign(Z, X, O, A), assign(X, Y, A, B), assign(Y, Z, B, A)} 라는 해답을 얻게 된다.
상호작용하는 목표들을 다루는 또다른 시스템으로 DCOMP 가 있다. 이것은 두 가지 단계로 이루어진다. 첫번째 단계에는 상호작용하는 목표가 없는 것으로 가정하여 임시 "해답" 을 구한다. 목표표현은 AND/OR 그래프로 표현되고 초기상태목록과 일치되지 않는 문자에는 B-규칙들이 적용된다. 이 작업은 끝단 노드들이 초기상태목록과 일치되는 모순이 없는 해결 그래프가 생성될 때 끝나게 된다. 이 해결 그래프 (solution graph) 는 문제의 임시 해답으로서 제시된다. 일반적으로 이것은 상호작용을 제거하기 위하여 두번째 단계에 의해 수정되어 진다.
AND/OR 그래프의 해결 그래프는 오직 해답 단계상 부분적 순서 (partial ordering) 만을 제공한다. 만일 상호작용이 없다면, 해결 그래프 상에서 조상과 후계 노드는 관계되어지지 않는 규칙들은 순차적으로 적용되기보다는 병렬로 적용되어질 수 있다. 때때로 로보트는 어떤 행동들을 동시에 수행할 수 있다. 예를 들어, 로보트가 이동하면서 그 팔을 움직일 수도 있다. 여러 행동들이 동시에 가능하도록 확장된 경우에는 로보트 행동열을 행동의 부분적인 순서로서 표현하는 것이 바람직하다. 어떤 특정한 목표를 성취하고자 하는 경우에, 가능한 순서에 따라 가장 적게 움직이는 것이 가장 좋은 것이다. 따라서 AND/OR 그래프의 해결 그래프는 목표를 성취하는 행동들을 표현하는 데에 좋은 표현방법이 된다.
두번째의 단계에서, DCOMP 는 임시 해결 그래프로부터 목표의 상호작용 여부를 검사한다. 예를 들어 어떤 규칙들이 그래프의 다른 가지에 있는 규칙들에서 필요로 하는 전제조건들을 파괴한다. 이러한 상호작용은 규칙 적용의 순서를 정하는데에 제약조건으로 추가되어 진다. 때때로, 우리는 이러한 모든 제약조건을 전부 만족시키는 보다 제한된 부분적인 순서 (아마도 완전한 순차적 순서) 를 찾을 수 있다. 이 경우에 이 두번째 작업의 결과가 곧 문제의 답이 된다. 추가되는 순서조건들이 서로 모순된다면, 직접 답을 구할 수 없고, DCOMP 는 첫번째 단계에서 찾아진 계획에 좀더 철저한 선택을 행해야만 한다.
이러한 개념은 몇 가지 예에 의해 가장 잘 설명될 될 수 있다. 그림 4 에서와 같은 초기상태목록을 가지고, 목표는 [ON(C, B) ∧ ON(A, C)] 이다. 첫번째 작업에서 DCOMP 는 모든 부목표들이 초기상태목록과 일치될 때까지 B-규칙들을 적용한다. DCOMP 는 상호작용이 없음을 가정했으므로 F-규칙을 통하여 조건들을 역행할 필요가 없다.

그림 16 첫 단계 해결
첫단계 작업에 의해 성취될 수도 있는 모순이 없는 해결 그래프가 그림 16 에 주어져 있다 (그림 16 에서, 각 화살표에 표시를 해두었다. 이 예에서 치환의 일치성은 문제가 되지 않는다. 잎 노드 밑에 쓰여진 치환을 통해 이 노드 상의 리터럴이 현재 상태와 일치되어진다).
나중에 F-규칙의 여러가지 성질들을 다루기 위하여, 그래프에서의 B-규칙들은 이들이 유도되는 F-규칙에 의해 표시되어 있다. 그래프에서의 모든 규칙들은 숫자로 표현되어 앞으로의 설명에 사용된다 (여기에서 숫자상의 순서는 아무런 뜻이 없음). 0 으로 표시된 목표 [ON(A, C) ∧ ON(C, B)] 를 두 개의 요소 ON(A, C) 와 ON(C, B) 로 나누는 작업을 주의깊게 살펴 보자. 우리는 이 역방향 분해규칙이 나중에 최종계획 수립을 위해 두 개의 요소를 최종목표로 만들어 줄 가상적인 결합 F-규칙에 근거를 두고 있음을 알 수 있다.
우리는 병렬로 수행될 수 있는 두 개의 F-규칙열 {unstack(C, A), stack(C, B)] 와 {unstack(C, A), pickup(A), stack(A, C)} 로 구성된 해답을 볼 수 있다. 상호작용 때문에, 우리는 분명히 이 두 행동렬을 병행시킬 수 없다. 예를 들어, ⑤ 번 규칙은 ② 번 규칙이 필요로 하는 전제조건 HANDEMPTY 를 없애고, 따라서 ② 번 F-규칙에 바로 앞서 ⑤ 번 규칙을 적용할 수 없다. 게다가, ⑤ 번 규칙은 또한 ④ 번 규칙이 필요로 하는 조건 HANDEMPTY 를 제거한다. 그림 16 의 그래프는 그러한 몇 가지 상호작용을 보여주고 있다.
상호작용하지 않는
부분적 순서를 인식하기 위한 과정에는 해결 그래프에서의 (가상의 결합 (join) 규칙을
포함하여) 모든 F-규칙의 전제조건이 그 규칙이 적용될 때의 상태목록과 일치되는지를
알기 위하여 언급된 모든 규칙들을 조사해야 한다. 그래프에서 j 번째 규칙의 i 번째
전체조건을 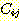 로 표현하자. 그래프에서 각각의
로 표현하자. 그래프에서 각각의 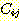 에 대하여 우리는 두 개의 집합 (공집합일 수도 있다) 을 계산한다. 첫번째 집합
에 대하여 우리는 두 개의 집합 (공집합일 수도 있다) 을 계산한다. 첫번째 집합
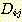 는
는 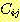 를 제거하는 그래프 상의 F-규칙들 중에서 j 번째 규칙이나 조상 (ancestor)
관계에 있는 규칙들을 제외한 F-규칙들의 집합이다. 이 집합을
를 제거하는 그래프 상의 F-규칙들 중에서 j 번째 규칙이나 조상 (ancestor)
관계에 있는 규칙들을 제외한 F-규칙들의 집합이다. 이 집합을 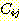 의 제거자 (deleters) 라고 부른다. 어떠한
의 제거자 (deleters) 라고 부른다. 어떠한 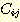 의 제거자도 (F-규칙으로서) j 규칙의 전제조건인
의 제거자도 (F-규칙으로서) j 규칙의 전제조건인 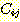 를 없앨 것이다. 따라서 j 규칙에 대한 제거자들의 적용 순서는 중요하다. 만일
그래프에서 제거자가 j 규칙의 후손 (decendant) 이라면, 우리는 특별한 문제점을
갖게 된다 (여기에서 j 규칙 자신이나 이와 조상 관계에 있는 어떠한 F-규칙들이
를 없앨 것이다. 따라서 j 규칙에 대한 제거자들의 적용 순서는 중요하다. 만일
그래프에서 제거자가 j 규칙의 후손 (decendant) 이라면, 우리는 특별한 문제점을
갖게 된다 (여기에서 j 규칙 자신이나 이와 조상 관계에 있는 어떠한 F-규칙들이
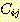 를 제거하는 것은 고려할 필요가 없다).
를 제거하는 것은 고려할 필요가 없다).
두번째 집합  는
는 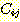 를 추가하는 그래프 상의 F-규칙들 중에서 j 규칙 자신이나 이와 조상 관계에
있는 규칙들을 제외한 F-규칙들의 집합이다. 이 집합을
를 추가하는 그래프 상의 F-규칙들 중에서 j 규칙 자신이나 이와 조상 관계에
있는 규칙들을 제외한 F-규칙들의 집합이다. 이 집합을 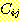 의 추가자 (adders) 라고 부른다. 어떠한
의 추가자 (adders) 라고 부른다. 어떠한 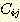 의 추가자도
의 추가자도 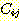 의 제거자의 효과를 감소시킬 수 있도록 j 규칙 앞 또는 뒤에 놓일 수 있기 때문에
이의 역할은 매우 중요하다. 또한 k 라는 어떤 규칙이 원래 해답 그래프에서
의 제거자의 효과를 감소시킬 수 있도록 j 규칙 앞 또는 뒤에 놓일 수 있기 때문에
이의 역할은 매우 중요하다. 또한 k 라는 어떤 규칙이 원래 해답 그래프에서 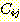 를 성취하기 위해 사용되었다면 k 라는 F-규칙 대신에 j 규칙 앞에 이의 다른
추가자들 중의 하나를 적용함에 의해 k 규칙을 제거할 수 있다 (이때 k 규칙의 후손들도
제거된다).
를 성취하기 위해 사용되었다면 k 라는 F-규칙 대신에 j 규칙 앞에 이의 다른
추가자들 중의 하나를 적용함에 의해 k 규칙을 제거할 수 있다 (이때 k 규칙의 후손들도
제거된다). 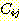 를 추가할지도 모를 j 규칙 자신이나 이 조상들의 규칙들은 이미
를 추가할지도 모를 j 규칙 자신이나 이 조상들의 규칙들은 이미 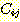 가 필요로 한 후에 적용되기 때문에 이러한 규칙들에 관심을 둘 필요가 없다는
것은 명백하다.
가 필요로 한 후에 적용되기 때문에 이러한 규칙들에 관심을 둘 필요가 없다는
것은 명백하다.

그림 17 추가자와 제거자를 갖는 첫번째 해결 그래프
그림 17 에서, 우리는
그래프에서의 모든 조건들에 대한 추가자와 제거자들을 볼 수 있다. 그래프에서 각
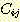 가 다음 두 조건 중의 하나를 갖게 되면 부분적인 순서는 상호작용하지 않는다.
가 다음 두 조건 중의 하나를 갖게 되면 부분적인 순서는 상호작용하지 않는다.
1) F-규칙 j 가
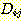 의 모든 요소들 앞에서 수행된다 (이 경우에
의 모든 요소들 앞에서 수행된다 (이 경우에 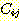 조건은 F-규칙 j 가 적용될 때까지 제거되지 않는다).
조건은 F-규칙 j 가 적용될 때까지 제거되지 않는다).
2)  의 요소인 규칙 k 가 규칙 j 앞에서 수행되고
의 요소인 규칙 k 가 규칙 j 앞에서 수행되고 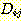 의 어떠한 요소도 k 와 j 사이에 수행되지 않는다.
의 어떠한 요소도 k 와 j 사이에 수행되지 않는다.
위의 기준에 따라서 그림 17 의 해답 그래프는 상호작용이 있다. 왜냐하면 예를 들어, ② 번 규칙이 ⑤ 번 규칙 앞에 있지 않기 때문이다 (⑤ 번 규칙은 ② 번 규칙의 전제조건을 제거한다).
두번째 단계에 있어서, DCOMP 는 부분적 순서를 상호작용하지 않는 것으로 바꾸려고 시도한다. 때때로, 이러한 변환작업은 가능하다. 이에는 두 가지 기본적인 방법이 있다. 즉, 위에서 말한 상호작용하지 않기 위한 조건 중의 하나를 만족하도록 순서를 제한하거나, 또는 어떠한 F-규칙이 이의 적용효과가 이 규칙의 추가자들의 하나의 순서를 조정하는 것에 의해 성취될 수 있다면 이러한 F-규칙 (이의 후손들까지) 을 제거할 수 있다.
예를 들어 그림 17 에서 ③ 규칙은 ② 규칙의 CLEAR(C) 조건의 제거자이다. 만일 ③ 규칙 앞에 ② 규칙이 있다면, ③ 규칙은 더 이상 이 조건의 제거자가 될 수 없다. 또한 ⑤ 규칙은 ④ 규칙의 HANDEMPTY 조건의 제거자이다. 이때 ④ 규칙을 ⑤ 규칙 앞에 있게 할 수 없다는 것은 분명하다. 왜냐하면 그래프 상의 부분적 순서에서 ④ 규칙은 이미 ⑤ 규칙의 조상으로 주어졌기 때문이다.
그러나, ⑤ 규칙과 ④ 규칙 사이에 ① 규칙이라는 추가자를 넣을 수 있다. 그렇지 않으면, ② 규칙이 ④ 규칙 앞에 있고 CLEAR(A) 조건의 어떤 제거자 뒤에 있을 경우, CLEAR(A) 가 F-규칙 ② 에 의해 추가되기 때문에 ⑤ 규칙을 제거할 수 있다.
DCOMP 는 첫번째 단계에서의 순서를 F-규칙들을 제거하거나 또는 더 많은 제한을 가함으로써 상호작용하지 않는 순서로 만들고자 한다. 적절한 조작을 찾는 일반적 문제는 오히려 더 어렵기 때문에 여기에서는 단순히 비형식적으로 이를 논의하겠다. 원래 해결 그래프에 추가되는 순서조건들은 그 자체가 모순이 없어야 한다. 그러나 우리의 예제에서 DCOMP 는 다음과 같은 단계를 거쳐 순서를 구성한다.
1) ④ 규칙 앞에 ② 규칙을 놓고, ⑤ 규칙을 제거한다. 이 때 ④ 규칙은 ② 규칙의 어떤 전제조건도 제거하지 않는 것을 주시하라. 또한 ② 규칙이 ③ 규칙 앞에 있으므로 ③ 규칙은 ② 규칙의 어떤 전제조건도 제거할 수 없다.
2) ④ 규칙 앞에 ① 규칙을 놓는다. 이때 ① 규칙은 ② 규칙 뒤에 ③ 과 ④ 규칙 앞에 있으므로 ① 규칙은 ② 규칙에 의해 제거되지만 ③ 과 ④ 규칙이 필요로 하는 조건들을 다시 정립한다.
이렇게 추가되는 조건들은 {unstack(C, A), stack(C, B), pickup(A), stack(A, C)} 에 대응되는 {2, 1, 4, 3} 이라는 순서를 제공한다.
이 경우에 있어서, 계획에 의한 F-규칙들의 순서는 완전히 순차적 (sequence) 이다. 실제, 이러한 블럭 세계의 예제에 이용되는 F-규칙들은 순차적인 순서에 따라서만 적용되어질 수 있다. 왜냐하면 로보트는 오직 한 개의 팔을 가지고 있고, 이 팔이 각각의 행동에 사용되기 때문이다. 이때, 로보트가 두 개의 팔을 가지고 있고, 각각의 팔이 F-규칙들에 의해 정의된 4 가지의 행동을 할 수 있다고 생각해 보자. 이러한 두 개의 팔을 가진 로보트 시스템의 규칙들은 이전의 F-규칙들의 정의에 1, 2 로 표시되는 각 팔의 숫자를 첨가하여 정의될 수 있다. 또한 HANDEMPTY 나 HOLDING 의 전제조건들도 팔의 숫자를 가지고 있어야 한다 (물론, 우리는 하나의 팔이 다른 팔을 잡는 것과 같은 상호작용은 허락하지 않는다). 그러면 두 개의 팔을 가진 로보트에 대한 F-규칙들은 다음과 같다.
1) pickup(x, h)
P&D : ONTABLE(x), CLEAR(x), HANDEMPTY(h)
A : HOLDING(x, h)
2) putdown(x, h)
P&D : HOLDING(x, h)
A
: ONTABLE(x), CLEAR(x), HANDEMPTY(h)
3) stack(x, y, h)
P&D : HOLDING(x, h), CLEAR(y)
A : HANDEMPTY(h), ON(x, y), CLEAR(x)
4) unstack(x, y, h)
P&D : HANDEMPTY(h), CLEAR(x),
ON(x, y)
A : HOLDING(x, h), CLEAR(y)
이러한 규칙들을 가지고 우리는 "1" 과 "2" 의 각 팔이 동시에 행동을 수행할 수 있도록 부분적으로 순서가 주어지는 계획을 생성해야 한다. 앞에서와 동일한 문제를 풀려고 해 보자. [즉, 그림 4 의 초기상태에서 목표는 [ON(A, C) ∧ ON(C, B)] 이다. 물론, 상태목록에서 HANDEMPTY 라는 서술은 [HANDEMPTY(1) ∧ HANDEMPTY(2)] 로 바뀌어진다]. 그림 18 에서 각 조건에 대한 추가자와 제거자들을 가진 DCOMP 의 첫단계 해답을 볼 수 있다. 그림 17 과 비교하여 볼 때, 두 개의 팔을 가졌기 때문에 HANDEMPTY 에 대한 제거자가 보다 적게 있음을 주의하라.

그림 18 두 개 팔을 갖는 문제의 첫단계 해결

그림 19 두 개 팔에 의한 블럭 문제의 부분적 순서화된 계획

그림 20 부분적 순서화된 계획의 목표 그래프
이 문제의 두번째 단계를 푸는 동안 DCOMP 는 ⑤ 규칙을 없애기 위하여 ④ 규칙앞에 ② 규칙을 놓는 순서를 제안할 것이다. 또한 ② 규칙의 조건 CLEAR(C) 를 제거하지 않도록 ③ 규칙 앞에 ② 규칙을 놓을 것이다. 이제 만일 ① 규칙이 ②, ③ 규칙 사이에 놓이게 되면, ③ 규칙의 CLEAR(C) 조건은 다시 성립된다. 이러한 제한들을 첨가하여 그림 19 에서와 같이 부분적으로 순서된 계획을 만들어 준다.
부분적으로 순서된 계획을 표현하기 위하여 AND/OR 그래프의 해결 그래프와 유사한 형태를 사용하는 것이 편리하다. 첫단계에서 만들어진 부목표들 사이에 상호작용이 없다면, 그 그래프 자체가 완전히 부분적으로 순서된 계획에 대한 충분한 표현이 된다. 만일 서로 동시에 수행되지 못할 상호작용이 있다면 해답은 그림 8 에서 10 을 통해서 표현된 것과 같을 것이다. 우리가 표현한 두 개의 팔을 가진 로보트에서 이런 상황은 어떤 경우가 되는지 살펴보자. 그림 20 은 우리가 그림 19 의 계획을 표현하는 하나의 방법을 보여준다. 목표조건에서 출발하여 계획을 따라 역방향으로 부목표들을 생성하는 과정을 볼 수 있다. 계획이 분리되는 것은 그 시점에서의 부목표의 조건들이 분리될 수 있기 때문이다. 그림 20 에서 "*" 로 표시된 곳에서 바로 그러한 분리가 일어난다. 이런 요소들은 "**" 로 표시된 곳에서 다시 합해질 때까지 서로 분리되어 해결될 수 있다. 첫번째 노드에서 CLEAR(C) 가 참으로, 두번째 노드에서 CLEAR(A) 가 참으로 역행됨에 주의하라. 그림 20 과 유사한 구조를 순서적 네트 (procedural nets) 라고 부른다 [Sacerdoti (1977)].
때때로 첫 단계 해답을 순서에 제약을 가함으로써 상호작용하지 않는 순서로 변환할 수가 없다. 이 경우에 두번째 단계의 작업은 전제조건의 제거를 피할 수 있는 부분적으로 순서화된 계획을 수립하지 못하게 된다. 우리는 여기서 두번째 단계의 작업이 가능한 한 제거의 경우가 적은 계획을 만들고, 남아있는 제거가 쉽게 해결될 수 있다는 것을 가정하자. 이러한 "근사한 계획" (approximate plan) 이 작성된 뒤에 DCOMP 는 3 번째 단계의 작업을 통하여, 제거조건을 해결하고 2 번째 단계의 (근사) 계획을 최종 해답이 상호작용하지 않도록 시도한다.
그러면, 세번째 작업에서 중요한 일은 주어진 계획을 수정하는 것이다. 계획을 수정하는 과정은 몇 가지 특별한 설명을 요구하고 따라서 이제부터 이것을 예를 들어 살펴 보자. 하나의 팔을 가진 로보트의 경우인 그림 4 의 초기상태로부터 목표 [CLEAR(A) ∧ HANDEMPTY] 를 성취하고자 한다. 그림 21 에서 첫 단계의 추가자와 제거자를 가진 결과를 볼 수 있다. 여기에서 추가제약조건을 사용하여 이러한 결과를 상호작용하지 않은 것으로 바꾸는 것은 분명히 불가능하다. 오직 하나의 F-규칙이 존재하고 그것은 0 번 결합규칙 (join) 의 전제조건을 제거한다. 이러한 상황에서 유일한 방법은 그 제거를 허용하고 CLEAR(A) 가 참이 되도록 하는 방법으로 HANDEMPTY 를 재정립하는 계획을 세우는 것이다.

그림 21 수선이 필요한 첫단계 해결
우리 전략은 ① 규칙과 join 규칙 사이에 P 라는 규칙을 집어 넣는다. P 에 대한 필요조건은 그것의 전제조건이 ① 규칙을 통하여 초기상태목록과 일치되는 조건들을 역행시켜야만 하고 CLEAR(A) 가 P 를 통하여 (① 규칙에 의해 성취될 수 있도록 하기 위하여) 변화되지 않으면서 역행되는 것이다. 여기서 우리가 찾는 해답의 구조는 그림 22 에서 볼 수 있다.

그림 22 수선된 해결 형태
만일, HANDEMPTY 에 putdown(x) 라는 B-규칙을 적용한다면 우리는 부목표 HOLDING(x) 를 얻게 된다. 이 부목표는 unstack(C, A) 를 통하여 {C/x} 치환에 의해 참 (T) 으로 역행된다. 더구나 CLEAR(A) 는 putdown(C) 를 통해 변하지 않은채 역행되고, 따라서 putdown(C) 는 적절한 추가규칙이 된다. 최종 해답은 그림 23 에 나타난다.

그림 23 최종 해답
추가되는 순서 제약으로도 상호작용이 제거되지 못하는 때 일반적인 상황은 이 마지막 예와 매우 비슷하다. 이러한 경우에 DCOMP 는 계획에서 가장 먼저 수정이 필요한 곳에 시도된다 (가장 초기상태에 가까운 계획에서부터).
이러한 수정과정은 전체 계획이 완전히 상호작용하지 않을 때까지 반복적으로 적용된다.
또다른 예제를 통해 수정과정을 살펴 보자. 이제 좀더 많이 상호작용하는 블럭 문제 즉, 그림 4 의 초기상태에서 목표가 [ON(A, B) ∧ ON(B, C)] 인 경우를 생각해 보자. 그림 23 에서 보듯이 첫단계작업의 결과는 어떤 추가순서계약을 가하여도 그 상호작용은 제거될 수 있다. 비록 ③ 규칙이 ④ 규칙의 전제조건을 제거하지만 즉, CLEAR(C) 를 제거하고 또한 ⑤ 의 전제조건도 HANDEMPTY 를 제거하더라도, 순서 3 → 5 → 4 → 2 → 1 은 좋은 근사 해답이다. 우리의 수정과정은 이러한 제거되는 조건들을 재성취하기 위한 것이며, 가장 최초의 것 HANDEMPTY 에 대하여 먼저 작업한다.
근사해의 수정은 그림 23 에 표현되어 있다. 초기상태의 어떠한 요소도 독립적으로 성취될 수 없기 때문에 우리는 초기복합목표를 분리하지 않았다. 역행은 반드시 새로운 후계자를 만들기 위해 사용되었고, 몇몇 목표요소는 참으로 역행되어 없어진 것을 주의해 살펴 보자. 여기에서, 우리는 B-규칙 화살표의 꼬리가 규칙의 추가목록에 있는 표현과 일치되는 조건을 가리키고 있다고 약속을 사용하였다. (*) 로 표시된 조건은 아직 정립되지 않은 근사계획의 조건들이다.
먼저, HANDEMPTY 를 정립하기 위하여 ③ 규칙과 ⑤ 규칙 사이에 수정을 집어 넣는 (이런 상황은 그림 22 에 나타나 있다). {C/x} 치환에 의한 putdown(x) 규칙은 적절한 수정이다. 그것의 부목표 HOLDING(C) 는 unstack(C, A) 를 통하여 참으로 역행된다. 더구나, 2 번 노드의 모든 조건들 (putdown(C) 에 의해 성취된 HANDEMPTY 는 제외) 은 putdown(C) 를 통해 역행될 때 변하지 않는다.
이제 우리는 다른 제거 전제조건, 즉 CLEAR(C) 를 수정하는 문제를 생각하자. 그러나 이 경우에는 CLEAR(C) 는 ⑤ 규칙을 통하여 역행될 때 변화하지 않고 있음에 주의하라. 그리고, 그것은 새로 추가된 규칙 putdown(C) 에 의해 참으로 역행된다. 그러므로 더 이상의 계획 수정은 필요없고, 다음의 해를 얻게 된다.
{unstack(C, A), putdown(C), pickup(B), stack(B, C), pickup(A), stack(A, B)}

그림 24 상호작용하는 블럭 문제의 첫 단계 해결
수정과정은 우리가 예에서 설명한 것보다도 더 복잡해질 수 있다. 만일 수정된 계획의 전제조건이 (마지막 예에서처럼) 어떤 일련의 엄격한 순서를 거쳐서만 역행된다면 그 과정은 직접 수행되지만, 그러나 부분적인 순서를 통해 역행된다면 어떻게 해야 하는가? 어떤 조건들은 부분적 순서와 모순이 없는 모든 일련의 순서에 대한 초기상태목록과 일치되는 조건들로 역행될 것이다. 어떠한 일련의 순서에 대해서도 그렇게 할 수 없는 경우에는 부분적인 순서에 추가 제약을 가할 수 있는데 그런 수정된 계획의 전제조건은 이것을 통하여 초기상태목록에 의하여 만족되는 조건까지 역행될 수 있다. 수정계획을 부분적 순서로 만드는 문제는 상당히 복잡하고 아직 어떤 적당한 방안이 없다.

그림 25 근사해

그림 26 두 레지스터 문제의 첫단계 해결
DCOMP 의 마지막 예로써, 두 레지스터의 내용을 바꾸는 문제를 다시 생각해 보자. 초기상태 [CONT(X, A) ∧ CONT(Y, B) ∧ CONT(Z, O)] 로부터 목표 [CONT(Y, A) ∧ CONT(X, B)] 를 성취하고자 한다. 첫단계 작업의 결과는 그림 26 에 나타나 있다. 추가자와 제거자는 앞에서와 마찬가지로 표시되어 있다. 첫단계의 해답은 어쩔 수 없이 제거된 것이 있다. ① 규칙은 ② 규칙의 전제조건을 제거하고 ② 규칙은 ① 규칙을 제거한다. 그것들은 둘 다 먼저 시행될 수 없다 ([Sacerdoti 77] 은 이런 유형의 모순을 "이중교차" (double cross) 라고 불렀다).
피할 수 없는 제거 모순은 규칙 중의 하나인 ② 규칙에 사용된 치환 때문에 일어났다. 만일 ② 규칙에서 Y 가 r1 과 치환되지 않는다면, ① 규칙은 CONT(r1, B) 를 제거하지 않게 된다. 그러면 ② 규칙에 의해 ① 규칙의 전제조건 CONT(X, A) 가 제거되지 않도록, ① 규칙이 ② 규칙 앞에 놓이게 된다. 이런 방법으로 DCOMP 는 ② 규칙의 전제조건 CONT(r1, B) 를 성립시킴으로써 계속해서 해답을 찾는다. 그러나 지금 {Y/r1} 치환은 불가하다.

그림 27 두 레지스터 문제의 해결
계속된 과정은 그림 27 의 임시적인 해답을 얻게 된다. 이러한 임시 해답으로부터 DCOMP 는 상호작용하지 않는 해답의 순서 3 → 1 → 2 를 계산할 수 있다. 최종 생성된 해답은 {assign(Z, Y, O, B), assign(Y, X, B, A), assign(X, Z, A, B)} 이 된다.
목표를 성취하는 계획을 수립하는 데에 지금까지 생각해온 것들은 모두 한 단계에서 작용하는 것들이었다. 예를 들어 역으로 작업할 때, 우리는 목표조건을 만족하기 위한 방법을 조사하고 그리고 모든 부목표를 성취하려고 하고, 다시 그런 식으로 작업했었다. 많은 실제 상황에서는, 단지 어떤 목표와 부목표조건들을 가정하고, 계획의 중요한 단계가 행해질 때까지 그것들을 풀려는 시도를 연기할 것이다. 사실 우리가 직면한 목표조건들과 그것들을 성취하기 위한 규칙들은 가장 세부적인 조건들과 가장 낮은 단계에서의 세분된 행동들, 주요조건들, 그리고 가장 높은 단계에서의 규칙들로서 단계적으로 구성될 것이다.
예를 들어 건물 축조 계획의 높은 단계 일로서 장소 준비, 기초작업, 구조화, 가열, 전기작업 등을 들 수 있다. 각각의 좀 더 세분화된 작업에 대하여 낮은 단계의 행동들이 필요하다. 가장 낮은 단계에서는 못박기, 전선벗기기 등과 같은 행동이 포함된다. 만일 전체 계획이 가장 세분화된 단계에서 종합되어야만 한다면, 그것은 거의 불가능할 정도로 길 것이다. 계층적으로 하나의 단계마다 계획을 생성하는 것은 각 단계에 적당한 길이의 계획을 제공하고, 따라서 유사한 작업들이 늘어나게 된다. 그러한 조작을 계층적 계획이라고 한다.
계층적으로 계획하는 하나의 간단한 방법은 조건들의 계층을 정하는 것이다. 낮은 단계의 조건들은 상대적으로 그보다 높은 단계의 조건들보다 덜 중요하고, 전자에서 정립된 대부분의 계획이 완성될 때까지 연기될 수 있다. 일반적인 생각은 먼저 가장 높은 단계의 조건들을 다루고 계획의 종합은 여러 단계에서 일어난다. 한번 높은 단계 조건들을 정립하기 위한 계획이 생성되면 다음 단계에서는 좀더 낮은 단계의 조건들을 정립하기 위한 계획이 생성되어 추가되고 그런 식으로 계속된다. 이 방법은 규칙들 자체가 등급에 따라 계층화될 필요가 없다. 우리는 여전히 하나의 규칙집합을 가질 수 있다.
계층적 계획은 (앞서 표현된 한 단계 방법의 어떤 것을 사용하더라도) 각 단계별로 계획을 구성함으로써 이루어진다. 각 단계이 작업이 이루어지는 동안, 어떤 조건들은 세부적인 것으로 간주되어 그보다 높은 단계의 작업이 끝날 때까지 연기된다. 세부적인 것으로 간주된 조건들은 (직각 모순이 없을 때에는) 그 단계에서 효율적으로 볼 수 있다. 그러나 갑자기 세부적인 것이 낮은 단계에서 이루어질 수 없다면 우리는 그것들을 성취하기 위하여 더 높은 단계의 계획을 수정할 수 있는 방법을 가져야만 한다.
수정작업은 STRIPS-형 문제 해결 시스템을 이용하고 상대적으로 직접 해결될 수 있다. 따라서, 기본문제 해결체계로서 STRIPS 를 사용하여 먼저 계층적 계획의 과정을 설명한다. 이런 식으로 STRIPS 가 사용될 때 이를 ABSTRIPS 라고 부른다.
예제로써 다시 목표 [ON(C, B) ∧ ON(A, C)] 를 사용하자. 그리고 초기상태는 그림 4 와 같다. 이 목표는 한 단계의 STRIPS 로도 해결되지만 우리는 이것을 여기에서 오직 어떻게 ABSTRIPS 가 작업하는지를 설명하기 위하여 사용한다.
우리가 사용하는 F-규칙은 우리가 사용했던 것들이다. 그러나 전제조건을 연기하기 위하여 우리는 조건들 (목표조건들도 포함) 의 계층을 정의해야만 한다. 실제로 이 계층화는 다양한 조건들을 성취하는 데에 따르는 본질적인 어려움을 반영하게 된다. 분명히 중요한 목표서술 식 ON 이 계층의 가장 높은 단계에 있어야 한다. 그리고 가장 정립되기 쉬우므로 아마도 HANDEMPTY 가 가장 낮은 단계에 있게 될 것이다. 이 간단한 예에서, 위의 두 단계와 중간단계로서 ONTABLE, CLEAR, HOLDING 의 서술식을 가진 세 단계만의 계층을 사용한다.
각 조건의 계층화 단계는 단순히 그 조건과 연관된 기준값 (criticality value) 으로써 표시된다. 작은 숫자는 낮은 단계 혹은 작은 기준을, 큰 숫자는 높은 단계 혹은 큰 기준을 표시한다. 전제조건 위에 기준값이 표시된 ABSTRIPS 의 F-규칙들은 다음과 같다.
1) pickup(x)
2
2
1
P&D
: ONTABLE(x), CLEAR(x), HANDEMPTY
A
: HOLDING(x)
2) putdown(x)
2
P&D : HOLDING(x)
A
: ONTABLE(x), CLEAR(x), HANDEMPTY
3) stack(x, y)
2
2
P&D : HOLDING(x), CLEAR(y)
A : HANDEMPTY, ON(x, y), CLEAR(x)
4) unstack(x,
y)
1
2
3
P&D : HANDEMPTY, CLEAR(x),
ON(x, y)
A : HOLDING(x), CLEAR(y)
기준값이 전제조건과 제거목록 표현 두 가지 모두에 나타나지만 추가목록에는 나타나지 않는 것에 주의해라. 어떤 F-규칙이 적용될 때, 추가목록의 모든 표현들이 상태목록에 추가된다.
이 예에서 ABSTRIPS 는 가장 높은 기준값, 즉 3 을 가진 조건들만 가지고 시작한다. 임계값 (threshold value) 보다 작은 기준값을 가진 모든 조건들은 무시된다. 우리의 목표는 3 의 값을 가진 두 개의 조건을 포함하므로, ABSTRIPS 는 그 중의 하나 즉, ON(C, B) 를 생각하고, 목표 스택에 stack(C, B) 를 추가한다 (만일 ABSTRIPS 가 먼저 다른 요소를 선택했다면, 나중에 다시 되돌아가야만 할 것이다. 독자는 이 경우를 스스로 해 보길 바란다). 스택에서 전체조건들의 기준값이 모두 2 이므로 이 단계에서는 무시되므로, (스택의) 아무 조건도 추가되지 않는다.
그러므로, ABSTRIPS 는 새 상태목록을 결과로 하는 F-규칙 stack(C, B) 를 적용할 수 있다. 다음에 다른 목표요소 ON(A, C) 를 생각하고, 목표 스택에 stack(A, C) 를 추가한다 (다시, 이 규칙의 전제조건은 무시된다). 그러면, ABSTRIPS 는 연속된 사태목록에 stack(A, C) 를 적용하여 완전한 목표와 일치되는 상태목록을 만든다. 이 단계에서는 ABSTRIPS 의 연산에 의해 생성된 해답이 그림 28 에 나타나 있다. 규칙의 제거표현이 보이지 않을 때, 상태목록으로 제거되어야만 하는 것들이 제거되지 않았음에 주의해라. 모순된 상태목록이 나올지 모르지만 이것은 문제되지 않는다.

그림 28 ABSTRIPS 의 첫단계에 대한 해결경로
세부적인 것들을 무시하여 얻어진 첫단계 해답은 {stack(C, B), stack(A, C)} 의 열이다 (다른 목표요소를 가지고 순서를 바꾸어 똑같이 작업하면 마찬가지로 {stack(A, C), stack(C, A)} 를 얻게 된다). 그러나 이 해답은 낮은 단계에서 문제점이 발생하여 적절한 순서를 정하기 위하여 다시 첫단계로 되돌려지게 된다). 우리의 첫단계 해답은 목표를 성취하는 높은 단계의 계획으로서 생각될 수 있다. 이러한 관점에서, 블럭 쌓기 동작이 가장 중요하며, 세부적으로 더 낮은 계획들이 생각되어진다.
이제 첫단계 해답, 즉 {stack(C, B), stack(A, C)} 를 가지고 낮은 단계를 생각해 보자. 이 두번째 단계에서 우리는 기준값이 2 이거나 혹은 그보다 더 큰 조건들을 생각한다. 이 때 우리는 이미 생각된 전제조건과 함께 높은 단계의 작업에서 사용된 F-규칙열을 포함하는 목표 스택을 가지고 이 단계의 작업을 시작함으로써 효과적으로 수행할 수 있다. 이때 최초의 목표 스택의 마지막 것이 바로 주요목표이다. 이 경우에 두번째 단계작업의 초기 목표 스택은 다음과 같다.
HOLDING(C) ∧
CLEAR(B)
stack(C, B)
HOLDING(A) ∧ CLEAR(C)
stack(A, C)
ON(C,
B) ∧ ON(A, C)
STRIPS 가 목표 스택을 가지고 작업을 하기 때문에 각각의 단계에서 세부적인 것을 완성시키기 위한 규칙 (rule) 의 수립은 쉽다. 높은 단계에서 내려온 계획은 낮은 단계에서 효율을 높이고, 조합으로 인한 어려움을 감소시키는 방향으로 제한을 가한다.
독자는 스스로 이 두번째 단계에서 생성되는 유일한 가능한 해답이 {unstack(C, A), stack(C, B), pickup(A), stack(A, C)} 열임을 알 수 있을 것이다. 만일 어떤 단계에서 해답이 찾아질 수 없다면, 과정은 다시 높은 단계로 되돌아가 또다른 해답을 찾아야 한다. 이런 경우에 우리의 두번째 과정은 잘 되었으며, HANDEMPTY 조건이 무시된 제약만 제외한다면 완전하다.
세번째 혹은 그 다음 단계에서 우리는 기준값을 1 로 놓고 계속해 나간다. 물론 두번째 단계에서의 F-규칙들과 그 모든 전제조건들이 포함된 목표 스택을 가지고 시작한다. 우리의 예에서 이 단계의 작업은 단지 가장 세분화된 단계에서까지도 두번째 단계의 해답이 정확하다는 것만을 보여주게 된다.
그러므로 ABSTRIPS 는 계층적 계획을 구성하는 완전한 직접적인 과정이다. 요구되는 것은 기준값이 정해짐으로써 서술식들의 중요성에 등급을 매기는 것뿐이다. 이 예보다 더 복잡한 문제에서는, ABSTRIPS 가 STRIPS 보다는 훨씬 더 효율적인 문제풀이 체계가 될 것이다.
이 특정한 계층적 문제 풀이에 있어서 몇 가지 변형이 있다. 먼저 기본 문제풀이 체계가 STRIPS 가 되어야 할 필요가 없다. 높은 단계에서 생성된 해답을 가지고, 어떤 단계에서는 사용될 수 있는 한, 어떤 문제 풀이 체계도 사용될 수 있다. 예를 들어 각 단계마다 적절한 수정과정을 통하여 DCOMP 나 또는 RSTRIPS 등을 사용할 수 있다.
이러한 계층적 계획 생성전략에 대한 조그만 변형은 오직 두 단계의 전제조건 기준값을 포함하고 있고, 기준값 단계에 약간씩 다른 방법을 사용한다. 이러한 변형이 중요하기 때문에, 아래와 같은 F-규칙을 사용하는 예를 가지고 어떻게 작업하는 지를 살펴 보자.
1)pickup(x)
P&D : ONTABLE(x), CLEAR(x),
P-HANDEMPTY
A : HOLDING(x)
2) putdown(x)
P&D : HOLDING(x)
A
: ONTABLE(x), CLEAR(x), HANDEMPTY
3) stack(x, y)
P&D : P-HOLDING(x), CLEAR(y)
A : HANDEMPTY, ON(x, y), CLEAR(x)
4) unstack(x,
y)
P&D : P-HANDEMPTY,
CLEAR(x), ON(x, y)
A : HOLDING(x),
CLEAR(y)
서술식 앞에 붙어 있는 P-접두사는 다음 더 낮은 단계에 이를 때까지 해당 전제조건의 정립이 연기됨을 표시한다. 이 전제조건들을 P-조건이라 부른다. 이러한 방법은 각각의 F-규칙에 대하여 어떤 전제조건이 가장 중요하며 (현재의 계획작업 중에 정립되도록), 어떤 것이 세부적인지 (즉시 더 낮은 단계에서 정립되도록) 구별하는 도구가 된다.

그림 29 P 조건을 사용한 첫 단계 STRIPS 해결
이 예에서 우리는 STRIPS 를 각 단계에서의 기본 문제 풀이 시스템으로 사용한다. 그림 4 의 초기상태로부터 목표 [ON(C, B) ∧ ON(A, C)] 를 정립하는 똑같은 문제를 생각해 보자. 그림 29 는 첫단계에서의 STRIPS 의 해답을 나타내고 있다. 세부적인 것들이 제거되지 않았기 때문에, 다시 상태목록이 모순성을 포함할 수 있음에 주의해라. 첫단계의 해답은 {stack(C, B), stack(A, C)} 열이다.
이제 방금 얻어진 F-규칙열과 그 전제조건들을 포함하는 목표 스택을 가지고 두번째 단계의 해답을 구해 보자. 그러나 먼저 연기된 P-조건들은 조건으로써 포함도어야 하고 이 단계에서 정립되어야 한다. 또한, 이러한 F-규칙들이 적용될 때, 상태목록에서 이러한 조건들을 제거하고, 새로운 규칙을 집어넣는 것은 위에서와 같다.
다음 단계의 초기 목표 스택은 아래에 주어져 있다. 전단계에서 내려온 F-규칙과 현단계에서 새로 추가된 F-규칙을 구분하기 위하여 내려온 F-규칙에 (*) 표시를 했다.
HOLDING(C) ∧
CLEAR(B)
*stack(C, B)
HOLDING(A) ∧ CLEAR(C)
*stack(A,
C)
[ON(C, B) ∧ ON(A, C)]
이 단계에서 STRIPS 의 해답은 {unstack(C, A), stack(C, B), pickup(A), stack(A, C)} 열이다. 이 단계에서 연기된 조건 즉, HANDEMPTY 가 있을지라도 이 해답열은 타당하다. 다음 단계에 의해서 계획에 새로 추가될 F-규칙은 없다. 이 단계에서의 문제 풀이 시스템은 단지 모든 세부적인 것이 포함되었을 때 두번째 단계 게획의 정확성을 증명하는 것에 불과하다.
1. right(x) 는 8-퍼즐에서 셀 x 의 오른쪽에 있는 셀을 나타낸다 (그러한 셀이 존재할 경우에). 이와 비슷하게 left(x), up(x), 그리고 down(x) 을 정의하여라. move B(공백) up, move B down, move B left, move B right 의 행동들을 다루는 STRIPS 규칙들을 적어 보아라.
2. 두 개의 STRIPS 규칙 pickup(x) 와 stack(x, y) 가 어떻게 결합되어 마크로-규칙 put(x, y) 가 될 수 있는지 묘사하여라. 새로운 규칙의 전제조건, 삭제 리스트, 첨가 리스트는 무엇인가? 구성요소들로부터 마크로-규칙을 생성하는 일반적인 프로시듀어를 명시할 수 있겠는가?
3. 그림 4 의 블럭 문제에서, 서술식 ABOVE 를 ON 을 가지고서 다음과 같이 정의한다.
ON(x, y) → ABOVE (x, y)
ABOVE(x, y) ∧ ABOVE(y, z) → ABOVE(x, z)
이러한 유도된 서술식의 출현에 의해 야기되는 프레임 문제들은 STRIPS F-규칙을 명시하는 데 어려움을 가지게 한다. 이러한 문제점과 어떤 구제책에 대해 서술하여라.
4.
"원숭이와 바나나" 문제는 계획 수립에 대한 인공지능 아이디어를 나타내는데
흔히 인용이 된다. 이 문제는 다음과 같이 서술된다.
상자 (box) 한 개와 바나나
(banana) 뭉치가 있는 방에 원숭이 한 마리가 있다. 바나나는 원숭이의 키로는 닿지
않는 천장에 달려 있다. 원숭이는 어떻게 바나나를 손에 넣을 수 있겠는가? 이 원숭이와
바나나 문제의 자세한 서술은 이 장의 2 절에 있다. STRIPS 가 다음과 같은 행동으로
구성된 계획을 수립하기 위해 이 문제는 어떻게 표현되어지는지를 보여라. 상자쪽으로
간다. 상자를 밀어 바나나가 걸려 있는 위치 아래에 놓는다. 상자 위에 오른다. 바나나를
잡는다.
5. 두 개의 레지스터의 내용을 교환하는 행동을 다루는 STRIPS 규칙을 적어라 (이 행동은 다른 추가의 레지스터를 사용함이 없이 직접 행해진다고 가정한다). 이 행동을 사용해서 레지스터 X, Y, Z 의 내용인 A, B, C 가 각각 C, B, A 의 내용으로 교환되는 프로그램을 유도하여라.
6. 그림 4 에 나타난 초기상태에서 출발하여, RSTRIPS 가 목표 [ON(B, A) ∧ ON(C, B)] 을 어떻게 이루는지를 보여라.
7. 이 장에서 언급한 계획 수립 시스템 중에 하나를 이용해서 다음의 블럭 쌓는 문제를 풀어라.

8. DCOMP 가 아래의 블럭 문제를 어떻게 푸는지 보여라.

상태와 행동을 나타내기 위해 5 절의 STRIPS 규칙과 서술식을 사용하여라.
9. 초기 블럭 문제 상황은 다음과 같이 묘사된다.
CLEAR(A)
ONTABLE(A)
CLEAR(B) ONTABLE(B)
CLEAR(C)
ONTABRE(C)
단지 한 개의 F-규칙이 있다. 즉 :
puton(x,
y)
P :
CLEAR(x), CLEAR(y), ONTABLE(x)
D
: CLEAR(y), ONTABLE(x)
A
: ON(x, y)
DCOMP 가 목표 [ON(A, B) ∧ ON(B, C)] 를 어떻게 푸는지 보여라.
10. RSTRIPS 와 DCOMP 의 "완전성 (completeness)" 에 대해 설명하여라. 다시 말해서, 이러한 계획 시스템들은 계획들이 존재할 경우에는 반드시 계획들을 구하게 되는가?