정리 증명 (Theorem Proving)

인공지능 원론 : 유석인, 교학사, 1988, Page 213~245

1. 서론

2. 비교흡수 부정 시스템 (resolution refutation system)

     (1) 비교흡수 (resolution)

     (2) 비교흡수 부정 (resolution refutation)

     (3) 비교흡수 (resolution) 과정 제어

     (4) 단순화 방법

     (5) 대답 유도과정

3. 규칙에 기초한 추론 (rule-based deduction)

     (1) 전향 (forward) 추론 시스템

     (2) 후향 (backward) 추론 시스템

     (3) 전향과 후향 시스템의 결합

연습문제

1. 서론

이 장에서는 정리 증명을 위해 이용되는 두 개의 시스템, 즉 비교흡수 부정 (resolution refutation) 시스템과 규칙에 기초한 연역 (rule-based deduction) 시스템에 대해 고찰한다.

비교흡수 부정 시스템은 어떤 목표문장이, 주어진 문장들의 집합으로부터 논리적으로 뒤따르고 있는지를 증명하기 위해 이 목표문장을 먼저 부정한 후 주어진 문장들과 합하여 새로운 집합을 만들고, 그 다음에 비교흡수 (2 절에서 언급) 과정을 이용해서 모순을 유도하는 시스템이다. 물론 이러한 방법이 논리적으로 정당하다는 것은 뒷절에서 증명된다. 비교흡수 부정 시스템의 중심적인 주제는 비교흡수방법을 명확히 이해하는데서 비롯된다. 비교흡수에 사용되는 문장들은 우선 적용가능한 표현형태 (절 (clause) 이라 하며 (1) 절에서 변환절차를 언급) 로 변환되어야 한다. 더우기 어떤 문장을 선택하여 비교흡수과정을 수행할 것인가 하는 제어방법 ((3) 절에서 자세히 언급) 은 시스템의 효율성을 증가시키는데 기여를 하게 된다.

인공지능 시스템에 의해 사용되는 지식의 대부분은 암시기호 (⇒) 를 사용해서 표현이 가능하다. 비교흡수 부정 시스템에서는 이러한 표현을 우선 절들의 표현으로 변환하여 사용한다. 그러나 이러한 변환과정에서는 암시적 표현에서 주어지는 어떤 유용한 제어정보를 잃어 버릴  수 있다. 예를 들어 절의 표현 (A ∨ B ∨ C) 는 암시적 표현 (~A ∧ ~B) ⇒ C, (~A ∧ ~C) ⇒ B, (~B ∧ ~C) ⇒ A, ~A ⇒ (B ∨ C), ~B ⇒ (A ∨ C), ~C ⇒ (A ∨ B) 등과 논리적으로는 같지만, 이러한 암시적 표현들에는 절의 표현에 나타나지 못하는 각기 다른 제어정보를 가진다. 비교흡수 부정 시스템과는 달리 규칙을 기초로 한 연역 시스템이란 암시적 표현 그 자체를 규칙으로 사용하는 시스템이다.

규칙을 기초로 한 연역 시스템에는 이와 같이 일반적 지식을 표현한 규칙 (rule) 들과 전체 데이터베이스 (global database) 를 이루는 특정한 지식을 표현한 사실들 (규칙들이 적용됨에 따라 전체 데이터베이스의 내용이 변해 감) 로부터 목표 wff 를 증명한다. 이러한 연역 시스템은 전향 (forward) 시스템과 후향 (backward) 시스템으로 분류된다.

전향 시스템이란, 전체 데이터베이스가 목표 wff 를 포함하게 될 때까지 전체 데이터베이스에 규칙 (F-규칙이라 함 ) 들을 적용시키는 것이며, 후향 시스템이란, 목표 wff 로 된 전체 데이터베이스에 규칙 (B-규칙이라 함) 들을 적용시켜 원래 주어진 사실들로 이루어진 전체 데이터베이스를 유도하는 시스템이다.

2. 비교흡수 부정 시스템 (resolution refutation system)

(1) 비교흡수 (resolution)

제 2 장에서 논리기호를 이용한 지식 표기방법에 대해 살펴보았다. 지식 표현인 잘 구성된 공식 (wff) 의 한 종류로 절 (clause) 이 있는데, 절이란 문자들의 논리합으로 구성된 wff 로 정의된다. 여기서 논할 비교흡수방법이란 이러한 절들에 적용되는 하나의 중요한 추론규칙이다. 비교흡수방법을 설명하기에 앞서 먼저 아래의 서술형 명제 wff 을 절들의 집합으로 변환시키는 과정을 살펴보자.

(∀x) {P(x) ⇒ {(∀y) [P(y) ⇒ P(f(x, y))] ∧ ~(∀y) [Q(x, y) ⇒ P(y)]}}

1) ⇒ 을 제거한다 : 이것은 X1 ⇒ X2 와 ~X1 ∨ X2 이 동치라는 사실을 이용한다. 위의 주어진 wff 를 변환시키면

(∀x) {~P(x) ∨ {(∀y) [~P(y) ∨ P(f(x, y))] ∧ ~(∀y) [~Q(x, y) ∨ P(y)]}}

2) ~의 영역을 축소한다 : 이것은 ~(~P) = P, ~(A ∧ B) = ~A ∨ ~B, ~(A ∨ B) = ~A ∧ ~B, ~(∀x) Px = (∃x) ~P(x), ~(∃x)P(x) = (∀x)~P(x) 등에 의해 이루어진다. 단계 1 로부터의 wff 를 변환시키면

(∀x) {~P(x) ∨ {(∀y) [~P(y) ∨ P(f(x, y))] ∧ (∃y) [Q(x, y) ∧ ~P(y)]}}

3) 변수들을 표준화한다 : 변수는 가상이름이고 wff 의 진리값에는 영향을 미치지 않으므로 각 한정사는 고유한 가상변수를 가질 수 있다. 즉 (∀x) [P(x) ⇒ (∃x)Q(x)] 는 (∀x) [P(x) ⇒ (∃y)Q(y)] 로 변형되어 변수 표준화를 이룬다. 단계 2 로부터의 wff 를 변화시키면

(∀x) {~P(x) ∨ {(∀y) [~P(y) ∨ P(f(x, y))] ∧ (∃w) [Q(x, w) ∧ ~P(w)]}}

4) 존재한정기호 (existential quantifier) 를 제거한다 : (∀y)[(∃x)P(x, y)] 라는 wff 를 우리말로 하면 '모든 y 에 대해 P(x, y) 를 만족시키는 y 에 종속되는 x 가 존재한다' 로 된다. 여기서 y 에 종속되어 결정되는 x 를 y 에 대한 어떤 함수로 표현해 g(y) 로 표현할 수 있다. 이와 같은 함수 g 를 스콜렘 함수 (Skolem function) 라 하며, 더우기 어떤 매개 변수도 가지지 않는 스콜렘 함수를 스콜렘 상수 (Skolem constant) 라 한다. 단계 3 으로부터의 wff 에 이를 적용시키면

(∀x) {~P(x) ∨ {(∀y) [~P(y) ∨ P(f(x, y))] ∧ [Q(x, g(x)) ∧ ~P(g(x))]}}

5) 프리닉스 형 (prenex form) 으로 변환한다 : 단계 4 를 행한 후의 wff 는 한정사 (quantifier) 로 전체한정기호 (universal quantifier) 들만 남고 이들 변수들은 이미 표준화되었으므로 이것들을 wff 의 제일 앞에 놓아 진리값에 영향을 줌이 없이 각 한정사의 영역을 wff 전체에 미치도록 할 수 있다. 이와 같이 하여 변환된 wff 를 프리닉스 형으로 표기되었다 한다. 또한 프리닉스 형의 wff 에서 한정사들로만 된 앞부분을 접두사 (prefix) 라 하고 나머지 뒷부분을 매트릭스 (matrix) 라 한다. 단계 4 로부터의 변환된 프리닉스 형은

(∀x)(∀y) {~P(x) ∨ {[~P(y) ∨ P(f(x, y))] ∧ [Q(x, g(x) ∧ ~P(g(x))]}}

6) 매트릭스를 논리곱의 정규형 (conjunctive normal form) 으로 변환한다. 논리곱의 정규형이란 문자 (literal) 들의 논리합으로 이루어진 유한집합에 대한 논리곱을 말한다. 단계 (5) 에서의 매트릭스는 분배규칙을 연속적으로 적용, (X1 ∨ (X2 ∧ X3)) 는 (X1 ∨ X2) ∧ (X1 ∨ X3) 로 함에 의해 다음과 같이 된다.

(∀x)(∀y) {[~P(x) ∨ ~P(y) ∨ P(f(x, y))] ∧ [~P(x) ∨ Q(x, g(x))] ∧ [~P(x) ∨ ~P(g(x))]}

7) 접두사를 생략한다 : 단계 6 에서 구한 wff 에서 접두사를 제거하고 공식에 나타나는 모든 변수는 전체 한정기호로 한정된 변수로써 가정한다.

8) ∧ 를 없앤다 : 즉 X1 ∧ X2 는 {X1, X2} 로 표현된다. 이와 같이 나타나는 각각의 독립된 인자를 절 (clause) 이라 부른다. 그러므로 단계 (7) 이 공식은 다음과 같은 절들의 집합으로 변환된다.

~P(x) ∨ ~P(y) ∨ P(f(x, y))

~P(x) ∨ Q(x, g(x))

~P(x) ∨ ~P(g(x))

9) 변수들을 조정한다 : 이것은 단계 (8) 에서 구한 어떠한 두 개의 절도 같은 이름의 변수가 나타나지 않도록 하기 위해서다. 그러므로 다음과 같이 변수 조정을 할 수 있다.

~P(x1) ∨ ~P(y) ∨ P(f(x1, y))

~P(x2) ∨ Q(x2, g(x2))

~P(x3) ∨ ~P(g(x3))

위의 9 가지 단계를 거쳐 wff 는 절들의 집합으로 변환이 된다. 만일 wff X 가 wff 들의 집합 S 에 논리적으로 뒤따르는 (logically follow) 것이라면 집합 S 에 있는 모든 wff 들을 절의 형태로 변환시킨 집합에 wff X 는 논리적으로 뒤따르는 것을 보일 수 있다. 그러므로 절의 표현만을 취급하는 비교흡수방법은 정리증명 시스템에서의 한 추론규칙으로 이용이 될 수 있음이 정당화 된다.

만일 변수를 가지지 않는 항이 절의 변수에 대치되어질 때 나타나는 표현을 본래 절의 기초예시 (ground instance) 라 한다. 예로서 일종의 단순한 절인 Q(A, f(B)) 는 Q(x, y) 의 한 기초예시이다. 비교흡수방법을 쉽게 이해하는 방법은 이러한 기초절들에 어떻게 비교흡수방법이 적용되는가 살펴 보는 것이 편리하다. 두 개의 기초 절, P1 ∨ P2 ∨ … ∨ P_N 과 ~P1 ∨ Q2 ∨ … ∨ Q_M 이 있다고 하자. P_i 와 Q_j 모두 서로 다른 것이라고 가정한다. 이 두 개의 부모절 (parant clause) 로부터 비교흡수 절 (resolvent) 이라는 새로운 절을 논리적으로 유도할 수 있다. 이 비교흡수절은 두 개의 절에 대해 논리합을 취하면 P1 ∨ ~P1 ∨ P2 ∨ … ∨ P_N ∨ Q2 ∨ … ∨ Q_M 이 되며 여기서 보수쌍 (complementary pair) 인 P1 ∨ ~P1 을 제거함에 의해 구해진다. 비교흡수방법의 흥미롭고 특수한 경우가 표 1 에 있다. 다음에는 이런 단순한 규칙이 변수를 지닌 절들에는 어떻게 확장되는지 살펴보자.

표 1

변수를 지닌 절에 대한 비교흡수방법은 제 2 장의 단일화 과정에서 언급한 치환 방법을 두 개의 부모절에 적용하여 이들이 보수문자 (complementary) 들을 서로 가지도록 함으로써 이루어진다. 공식화된 표현을 위해서 먼저 부모절을 문자들의 집합으로 표현한다면, 두 개의 부모절은 각기 {L_i}, {M_i} 와 같이 나타내지고 변수들은 따로 표준화되어 있다고 가정할 수 있다 (집합의 문자들을 서로 논리합을 이루고 있음). 더우기 {l_i} 와 {m_i} 는 각각 {L_i}, {M_i} 의 부분집합으로 {l_i} 와 {~m_i}  의 합에 대한 가장 일반적 단일화 (이를 s 라 하겠음) 가 존재한다고 하자. 그러면 이제 두 개의 절 {L_i} 와 {M_i} 는 비교흡수되어 다음과 같은 비교흡수절이 유도되어진다.

{{L_i} - {l_i} s ∪ {{M_i} - {m_i}}s

예로써 다음의 두 절에 대한 몇 개의 비교흡수절을 구해 보자.

P[x, f(A)] ∨ P[x, f(y)] ∨ Q(y)

~P[z, f(A)] ∨ ~Q(z)

여기서

{l_i} = {P[x, f(A)], P[x, f(y)]}, {m_i} = {~P[z, f(A)]} 라 하면 이의 비교 흡수절은

Q(A) ∨ ~Q(z)

이 된다.

두 개의 부모절로부터 유도되어진 비교흡수절은 또한 이 부모절에 논리적으로 뒤따르고 있음을 쉽게 보일 수 있다. 이를 기반으로 wff 들의 집합 S 에 논리적으로 뒤따르고 있는 wff 들은 이 wff 집합 S 에 비교흡수 부정방법을 적용해서 유도되어진다. 그러므로 정리 증명 시스템의 한 종류인 완전성을 지닌 비교흡수방법을 사용하는 비교흡수 부정 시스템의 이해는 이보다 더 효율적인 여러 정리 증명 시스템을 이해하는데 근본적인 기초를 제공하게 된다.

(2) 비교흡수 부정 (resolution refutation)

wff 의 집합 S 에 어떤 wff X 가 논리적으로 뒤따른다는 것을 증명하기 위해 비교흡수를 이용하는 비교흡수 부정방법은 먼저 집합 S 에 X 의 부정인 ~X 를 첨가하여 집합 P = S ∪ {~X} 을 형성한다. 이제 이 새로운 집합 P 로부터 비교흡수과정을 통해 유도되는 새로운 비교흡수절 R_i 을 유도하고, 집합 P 에 R_i 를 추가하여 나오는 새로운 집합에 대해 다시 비교흡수를 행하는 과정을 반복한다. 이 때 과정이 종결되는 시기는 새로이 유도되는 비교흡수절이 모순 (NIL 로 표기함) 을 나타내는 경우이며, 이로부터 wff X 는 집합 S 에 논리적으로 뒤따른다고 한다. 이와 같은 비교흡수 부정방법에 의해 정리 증명이 정당화되는 이유는 다음과 같은 논리로 설명된다.

wff 들로 구성된 집합 S 에 논리적으로 뒤따르는 wff X 가 있다고 가정하자. 그러면, 가정에 의해 S 을 만족하는 모든 해석 (interpretation) 은 또한 X 을 만족한다. 이것은 S 을 만족하는 어떠한 해석도 ~X 을 만족하지 못한다는 사실과 같다. 그러므로 위의 언급한 모든 해석들은 S 와 {~X} 를 동시에 만족시키지 못한다 (여기서 어떤 해석에 의해서도 만족되지 않는 wff 의 집합을 불만족 (unsatisfiable) 하다고 한다.).

실제적으로 X 가 S 에 논리적으로 뒤따른 wff 라면 S ∪ {~X} 는 불만족하다. 만일 비교흡수과정이 불만족한 집합에 반복적으로 적용이 되면 결국에는 모순 (NIL) 이 유도되는 것을 보일 수 있다. 그러므로 만일 X 가 S 에 논리적으로 뒤따르면 비교흡수과정에 의한 S ∪ {~X} 의 집합으로부터 NIL 절을 결국에는 유도하게 될 것이다. 역으로, 만일 NIL 이 집합 S ∪ {~X} 로부터 유도된다면 X 는 S 로부터 논리적으로 뒤따른다는 것을 보일 수 있다.

비교흡수 부정방법을 하나의 예를 통해 살펴보자. 먼저 wff 의 집합 S 가 다음과 같다고 할 때, I(z) ∧ ~R(z) 이 S 에 논리적으로 뒤따르는지를 증명하고자 한다.

1) ~R(x) ∨ L(x)

2) ~D(y) ∨ ~L(y)

3a) D(A)

3b) I(A)

먼저 목표 wff 인 I(z) ∧ ~R(z) 을 부정하여 아래의 형태와 같은 절을 구한다.

4) ~I(z) ∧ R(z)

1) ~ 4) 로 이루어진 집합으로부터 NIL 의 유도에 이르는 동안의 비교흡수과정을 나타내면 그림 1 과 같은 트리 형태가 된다.

그림 1  비교흡수 부정 트리

(3) 비교흡수 (resolution) 과정 제어

앞 절의 예에서 보듯이 모순절인 NIL 을 유도하기 위해 어떠한 두 개의 부모절을 선택해서 단계적으로 비교흡수과정을 수행하게 된다. 이와 같이 비교흡수되는 두 개의 절을 선택하는 방법에는 여러 가지가 있을 수 있다. 그 중에서 어떤 제어방식은 모순이 존재할 경우에는 언제나 이러한 존재를 증명하게 한다. 이러한 제어방법을 완전 (complete) 하다고 한다 (앞에서 논한 추론규칙의 논리적 완전성과는 별개의 개념임). 그러나 인공지능 응용분야에서는, 모순을 보다 효율적으로 구하는 것이 완전성보다 더 중요하게 받아들여지고 있다. 이제 앞절의 예를 이용하여 비교흡수과정 제어방식들을 살펴보자.

1) 나비-우선 (breadth-first) 방식

이 방식은 먼저 첫 단계에서 기초집합 S 로부터 모든 가능한 비교흡수절을 유도하고, 두번째 단계에서는, 이 유도된 절들과 첫 단계의 집합 S 를 합친 새로운 집합으로부터 다시 모든 가능한 비교흡수절을 유도하며, 그 다음에 세번째 단계 등으로 반복 수행하게 된다 (즉, i-번째 단계의 비교흡수절을 유도하는 두 개의 부모절 중의 하나는 (i - 1)-번째 단계에서 유도된 비교흡수절이다).

그림 2  나비-우선방식의 예

2) 세트-오브-서포트 (set of support) 방식

비교흡수가 가능한 두 개의 부모절 중의 하나는 증명하려는 목적 wff 의 부정된 형태로부터 생성되는 절이거나 또는, 그러한 절을 포함한 비교흡수과정에서 얻어지는 절이여야만 한다. 유도하려는 모순이 비교흡수하는 과정의 매 단계마다 포함되기 때문에 이 제어방식은 완전하게 된다. 그림 3 은 이 제어방식에 의한 비교흡수 부정 그래프를 보여준다. 이 방식은 나비-우선방식보다 적은 수의 절을 생성하지만 NIL 가지 이르기 위한 트리 상의 깊이는 증가하게 되는 경우도 있다.

그림 3  세트-오브-서포트 방식의 예

3) 단위-우선 (unit preference) 방식

이 방식은 비교흡수가 가능한 여러 부모절들 중에서 하나의 문자만으로 이루어진 절을 포함하는 부모절을 우선적으로 선택한다. 이러한 비교흡수과정에 의해 두 부모절 중 더 긴 부모절을 구성하고 있는 문자의 수보다 적은 수의 문자로 구성된 새로운 절을 얻을 수 있으므로 결국에는 빈 절인 NIL 을 빨리 유도하게 된다는 원리에서 효율성을 증가하게 된다. 그림 1 은 단위-우선방식을 이용한 예라고 할 수 있다.

4) 선형 입력형 (linear-input form) 방식

적어도 하나의 부모절은 기초집합에 포함된 절이어야 한다. 그림 4 는 이 방식을 보여 주는데 1 단계까지는 그림 2 와 같지만 2 단계부터는 다르다. 아래의 예에 보듯이 이 방식은 완전 (complete) 하지 않다. 기초집합이 다음과 같으면 그림 5 에서 증명되듯이 모순이 존재하므로 불만족 (unsatisfiable) 한 집합이다.

Q(u) ∨ P(A),

~Q(w) ∨ P(w),

~Q(x) ∨ ~P(x),

Q(y) ∨ ~P(y),

그러나 NIL 을 유도하기 위해서는 비교흡수되는 두 절이 모두 하나의 문자로 이루어진 단위절이거나, 비교흡수되어 완전히 NIL 이라는 빈 절이 생기도록 하는 절들이 있어야 하는데 이러한 성질을 지닌 두 개의 부모절을 이 제어방식으로는 구할 수 없다. 이와 같이 선형 입력형 제어방식은 완전하지는 못하다. 그러나 제어의 단순성과 효율성으로 인해 자주 이용이 된다.

그림 4  선형 입력형 방식의 예

그림 5  비교흡수 부정 트리

5) 조상절-선택형 (ancestry-filtered form) 방식

이는 선형-입력형 방식의 불완전성을 보완하기 위한 방식으로 각 비교흡수절의 두 부모절 중에 적어도 하나는 기초집합에 포함된 절이거나, 한쪽의 부모절이 다른 쪽 부모절의 조상절이라는 관계에 있으면 된다. 그림 5 는 조상절 선택형 제어방식을 이용한 비교흡수 부정 트리라 할 수 있다. 비교흡수절 NIL 의 한 부모절인 ^* 로 표기된 ~P(x) 는 다른 한 부모절인 P(A) 의 조상이다.

더우기 비교흡수에 이용되는 조상절들이 합병 (merge) 들이면 이 제어방식은 완전성을 가진다 ((1) 절에서 언급한 합병이란 하나의 문자로된 비교흡수절로 이것은 두 개의 부모절에 동시에 속해 있는 문자이다. 그림 5 의 ~P(x) 는 합병이다).

(4) 단순화 방법

때때로 절들로 이루어진 어떤 집합에서 몇 개의 절이 제거되거나 또는 절을 이루는 어떤 문자들이 제거될 수 있다. 이러한 단순화는 원래의 집합이 불만족한 집합이면 단순화가 된 후의 새로운 집합도 불만족함을 유지하는 방향으로 진행될 수 있다. 그러므로 이러한 단순화 방법의 적용은 비교흡수 부정방법의 수행과정에서 생겨나는 비교흡수절의 수를 줄이는데 도움을 준다.

1) 동치명제 (tautology) 의 제거

문자와 이것의 부정된 문자를 함께 포함하는 어떠한 절도 제거될 수 있다 (이러한 절을 동치명제라 함). 왜냐하면 동치명제를 포함한 불만족한 집합은 이것을 제거한 집합도 불만족한 것이기 때문이다. 예로서, P(x) ∨ B(y) ∨ ~B(y), P(f(A)) ∨ ~P(f(A)) 등은 제거되어도 무방하다.

2) 프로시쥬어의 부착  (procedure attachment)

때때로 문자나 이것의 부정을 기초집합에 포함시키는 것보다는 이 문자의 진리값을 계산해 버리는 것이 편리하다. 흔히 이러한 계산은 기초예시 (ground instance) 들에 해당된다. 예를 들어, 서술형 명제 E(x, y) 가 두 개의 숫자 x 와 y 사이의 크기가 같은지 여부를 나타낸다고 하면, 이것의 기초예시가 (예로서 E(7, 3) 과 같은) 수행과정시 생겨날 때마다 계산하여 참인지 거짓인지 결정해 버리고, E(x, y), ~E(x, y) 의 많은 형태의 기초예시들을 기초집합에 포함시키지 않음으로 해서 효율성을 증가시킨다. 여기에는 E(7, 3) 과 같은 표현의 진리값을 구하기 위한 프로시쥬어가 주어져야 한다. 이와 같이 서술형 명제와 이것의 실행을 행하는 컴퓨터 코드 사이를 연결해 주는 형태가 성립되는데 이것을 프로시쥬어의 부착이라 한다.

3) 포함 (subsume) 에 의한 제거

{L_i}s 가 {M_i} 의 부분집합이 되게하는 치환 s 가 존재한다면 절 {L_i} 는 절 {M_i} 을 포함한다 라고 정의한다. 예를 들어,

P(x) 는 P(y) ∨ Q(z) 를 포함하며,

P(x) 는 P(A) 를 포함하며,

P(x) 는 P(A) ∨ Q(z) 를 포함하며,

P(x) ∨ Q(A) 는 P(f(A)) ∨ Q(A) ∨ R(y) 를 포함한다.

불만족한 집합에서의 한 절이 다른 절에 의해 포함이 되면 이 포함되는 절이 제거되어도 불만족한 집합이 유지된다. 이와 같이 포함에 의한 제거는 비교흡수의 수를 줄이는데 상당한 효과를 준다.

(5) 대답 유도과정

많은 서술 논리 정리 증명 시스템에는 존재를 나타내는 변수가 결국 무엇으로 예시되는지 알고자 하는 경우가 있다. 예로서 기초집합 S 에 논리적으로 뒤따르는 (∃x)W(x) 가 있다면 x 가 무엇으로 예시되는가 하는 것이다. 이를 해결하기 위한 과정을 예를 들어 살펴보자.

"JOHN 이 가는 장소면 FIDO 도 반드시 그 장소에 간다." 는 사실이 주어졌을 때

"JOHN 이 학교에 가면 FIDO 는 어디에 가는가?" 라는 질문이 있다고 하자.

이것은 다음과 같이 표현된다.

(∀x)[AT(JOHN, x) ⇒ AT(FIDO, x)], AT(JOHN, SCHOOL),

(∃x)AT(FIDO, x)

여기서 증명하고자 하는 것은 목표 wff (∃x)AT(FIDO, x) 에서 x 가 무엇인가 하는 것이다. 이를 구하기 위해 (∃x)AT(FIDO, x) 의 부정인 (∀x)~AT(FIDO, x) 를 첨가하여 다음과 같은 기초집합이 형성된다.

~AT(JOHN, x) ∨ AT(FIDO, x), AT(JOHN, SCHOOL),

~AT(FIDO, x)

이 기초집합을 이용해 NIL 을 유도하는 비교흡수 부정 트리는 그림 6 과 같다. 그러나 (∃x)AT(FIDO, x) 에서 x 를 구하기 위해서는 ~AT(FIDO, x) 를 다시 한 번 부정한 AT(FIDO, x) 를 추가하여 논리합을 시킨다. 그러면 다음과 같은 기초집합이되며 이로부터 위에서와 같은 절차를 거쳐 비교흡수를 행하며, 결국에는 NIL 이 아닌 대답을 지닌 문장이 유도된다.

~AT(JOHN, x) ∨ AT(FIDO, x), AT(JOHN, SCHOOL),

~AT(FIDO, x) ∨ AT(FIDO, x).

위의 과정을 거친 대답 유도를 위한 트리는 그림 7 과 같으면 AT(FIDO, SCHOOL) 은 원하는 해답이 된다.

그림 6  비교흡수 부정 트리

그림 7  수정된 증명 트리

앞의 경우와는 달리 전체 한정에 의한 변수를 지닌 목표 wff 가 있는 경우를 살펴보자. 목표 wff 의 부정이 이루어지는 과정에서 이 변수는 존재변수가 되어 스콜렘함수 (skolem function) 로 대치된다.

이제 대답을 유도한 결과에서 이러한 스콜렘 함수가 어떻게 해석이 되는지 다음의 예를 통해 살펴 보자.

"모든 x 에 대해 x 는 p(x) 의 자식이다."

"모든 x 와 y 에 대해 x 가 y 의 자식이면 y 는 x 의 부모이다."

"모든 x 에 대해 x 의 부모는 누구인가?"

여기서 목표 wff (∀x)(∃y)P(y, x) 의 부정은 (∃x)(∀x)~P(y, x) 이 되며, x 는 스콜렘 함수로 대치되므로 ~P(y, A) 로 되어 대답 유도를 위한 기초집합은 아래와 같이 나타난다.

C(x, p(x)), ~C(x, y) ∨ P(y, x),

~P(y, A) ∨ P(y, A)

이제 대답 유도를 위한 증명 트리는 그림 8 처럼 된다. 여기서의 대답은 스콜렘 함수 A(상수 형태임) 을 지닌 P(p(A), A) 가 된다. 그러나 본래의 질문이 "모든 x 에 대해 x 의 부모는 누구인가? 즉 x 의 부모는 x 와 어떻게 연관되는 사람인가?" 이므로 A 의 해석을 상수가 아닌 모든 A 에 대해 P(p(A), A) 로 해석함이 타당하다.

그림 8  대답 유도를 지닌 증명 트리

하나의 예를 더 살펴보자. 기초집합 S 가 하나의 절 P(B, w, w) ∨ P(A, u, u) 와 목표 wff (∃x)(∀z)(∃y)P(x, z, y) 를 포함한다 하자.

이것의 비교흡수 부정 트리는 그림 9 와 같이 되며 대답 유도를 위한 증명 트리는 그림 10 과 같이 된다. 여기서 보면 스콜렘 함수 g(x) 대신에 변수 t 가 사용되었으며 결과적으로 P(A, t, t) ∨ P(B, z, z) 을 유도하였다. 그러나 P(A, t, t) 와 P(B, z, z) 은 같은 의미를 가진다.

그림 9  비교흡수 부정 트리

그림 10  수정된 증명 트리

결론적으로, 비교흡수방법을 이용한 대답 유도과정의 절차는 다음과 같다.

1) 먼저 비교흡수 부정 트리를 구한다 (여기서 단일화되는 부분에는 밑줄을 그어 표시한다.).

2) 목표 wff 의 부정형태에서 생기는 모든 스콜렘 함수들을 새로운 변수들로 대치 시킨다.

3) (2) 에 생긴 절과 이것의 부정된 절을 논리합시켜 동치명제 형태를 취한다.

4) (1) 에서 구한 트리 구조를 이용해서 (같은 단일화 과정) 수정된 증명 트리를 얻는다.

5) 증명 트리의 루트 노드에 있는 절이 구하고자 하는 대답 문장이 된다.

3. 규칙에 기초한 추론 (rule-based deduction)

(1) 전향 (forward) 추론 시스템

1) AND/OR 형태의 사실 (fact) 표현

전향 시스템은 사실의 집합으로 이루어진 초기의 전체 데이터베이스를 가진다. 이 사실들은 AND/OR 형태라 불리어지는 암시적 표현 (⇒) 이 없는 서술논리문 (predicate calculus) 으로 나타내어진다. 예로서 어떤 wff 를 AND/OR 형태로 전환하는 방법은 다음과 같다 :

(∃u)(∀v){Q(v, u) ∧ ~[[R(v) ∨ P(v)] ∧ S(u, v)]}

위와 같은 wff 에서 존재를 나타내는 존재한정기호 (∃) 는 스콜렘 함수에 의해 제거하고 전체한정기호 (∀) 는 생략하고 부정 심볼 (~) 은 이것의 영역이 한 개의 문자에 이를 때까지 드모르강 법칙을 이용하여 바꾸면, 다음과 같은 표현으로 변한다.

Q(v, A) ∧ {[~R(v) ∧ ~P(v)] ∨ ~S(A, v)]}

여기서 사실 표현이 다른 AND 결합에 같은 변수가 있지 않기 위해서 변수들을 표준화되면 다음과 같은 표현이 된다.

Q(w, A) ∧ {[~R(v) ∧ ~P(v)] ∨ ~S(A, v)}.

AND/OR 형태의 표현은 ∧ 와 ∨ 심볼에 의해 연결된 문자들의 부표현 (subexpression) 들로 구성되어진다.

2) 사실 표현을 나타내기 위한 AND/OR 그래프의 이용

AND/OR 그래프는 AND/OR 형태로 된 사실 표현을 나타내기 위해 이용이 될 수 있다. 예를 들면, 그림 11 은 앞에서 만든 AND/OR 형태의 사실 표현을 나타내고 있다. OR 결합에 관계된 부표현 (E₁ ∨ … ∨ E_k) 은 각 자식 노드들이 그들의 부모 노드에 k-연결자로 연결이 되어져 표현이 되고 AND 결합에 관련된 부표현 (E₁ ∧ … ∧ E_n) 은 각 지식 노드가 그의 부모 노드에 1-연결자에 연결이 되어서 표현되어진다. 이리하면 AND/OR 그래프의 잎 (leaf) 노드는 사실표현 내에 존재하는 해당 문자 (literal) 로 주어진다.

그림 11  사실 표현의 AND/OR 트리 표현

3) 규칙 적용에 의한 AND/OR 그래프의 변환

전방향 생성 시스템에 사용되는 규칙은 문제영역에 대한 일반적인 지식을 암시적인 wff 로 표현한 것이다. 이러한 wff 를 다음과 같이 제한된 형태로 구성하였다 하자. 즉,

L ⇒ W,

여기서 L 은 한 개의 문자이고, W 는 어떤 임의의 wff 이다. 이러한 형태의 wff 는 한정변수의 종류에 관계없이 암시적 심볼의 왼쪽에 국한된 한정변수를 먼저 "역" 으로 하고, 그 다음에 모든 존재한정변수들은 스콜렘하여 한정변수의 영역이 전 범위에 걸치도록 하는 형태로 바꿀 수 있다. 예를 들면, 다음과 같은 wff 는 이러한 단계를 거쳐 변환이 된다.

(∀x){[(∃y)(∀z)P(x, y, z)] ⇒ (∀u)Q(x, u)}

(1) (일시적으로) 암시적 심볼 "⇒" 을 없앤다.

    (∀x){~[(∃y)(∀z)P(x, y, z)] ∨ (∀u)Q(x, u)}

(2) 부정 심볼 "~" 을 진행시켜 첫번째 OR 결합에 있는 첫번째 문자에 관련된 한정 변수들을 "역" 으로 변환시킨다.

    (∀x){(∀y)(∃z)[~P(x, y, z)] ∨ (∀u)Q(x, u)}

(3) 존재한정변수를 스콜렘시킨다.

    (∀x){(∀y)[~P(x, y, f(x, y))] ∨ (∀u)Q(x, u)}

(4) 모든 전체한정변수를 없앤다.

    ~P(x, y, f(x, y)) ∨ Q(x, u)

(5) 암시적 심볼을 다시 나타낸다.

    P(x, y, f(x, y)) ⇒ Q(x, u)

이러한 암시적 심볼을 가진 규칙이 여기서 어떻게 AND/OR 그래프에 적용이 되는지 살펴보자. 먼저 변수를 가지지 않는 서술식의 경우를 생각하면, L ⇒ W 의 규칙이 있다고 할 때 사실 표현 F(L) 을 나타내는 AND/OR 그래프에 L ⇒ W 를 적용하여 새로운 사실 표현 F(W) 를 나타내는 AND/OR 그래프를 얻을 수 있다. 이 F(W) 를 표현하는 새로운 AND/OR 그래프상에서 잎 노드들로 끝나는 해결 그래프 (solution graphs) 들은 F(W) 로부터 생성되는 절 (clauses) 들을 나타내게 된다. 예를 들어 아래와 같은 규칙과 그림 12 에 주어진 변수가 없는 AND/OR 그래프를 생각해 보자.

그림 12  변수를 가지지 않는 AND/OR 그래프

그림 13  규칙 적용 후의 AND/OR 그래프

S ⇒ (x ∧ y) ∨ z

그림 12 에 S 로 명칭이 붙여진 노드는 S ⇒ (X ∧ Y) ∨ z 에 의해 새로운 형태의 AND/OR 그래프가 그림 13 처럼 나타나게 된다. 이 때 S 에 연결된 선을 비교선택 아크 (match arc) 라 한다.

규칙 S ⇒ [(X ∧ Y) ∨ Z] 은 다음과 같은 2 개의 절 (clause) 로 생각될 수 있다.

~S ∨ X ∨ Z, ~S ∨ Y ∨ Z

주어진 사실 표현 [(P ∨ Q) ∨ R] ∨ [S ∧ (T ∨ U)] 로부터 생성되는 절 (clause) 들 중에 S 를 포함하는 절들은 다음과 같다.

P ∨ Q ∨ S, R ∨ S

이들과 위의 규칙에서 생성되는 절들을 비교흡수 (resolution) 하면 다음과 같은 네 가지 절들이 유도된다.

X ∨ Z ∨ P ∨ Q, Y ∨ Z ∨ P ∨ Q, R ∨ Y ∨ Z, R ∨ X ∨ Z

위의 모든 절들은 그림 13 의 그래프의 잎 노드들로 구성되는 해결 그래프들로 나타내어 진다.

이와 같이 AND/OR 그래프는 사실과 규칙이 적용된 후의 유도되는 사실들은 알아내는데 매우 유용한 도구로써 사용될 수 있다.

앞에서 말한 설명은 사실 표현에 변수가 나타나지 않는 경우를 관한 것이며, 변수가 나타나는 표현에 관해서는 변수가 없는 종결조건을 살펴 본 이후에 거론하기로 한다.

4) 종결을 위한 목표 wff 의 사용

전방향 시스템의 목적은 주어진 사실과 규칙들로부터 어떤 목표 wff 를 증명하는 것이다. 이 때의 목표 wff 는 문자들의 OR 결합 형태로만 제한되어 진다. 이러한 제한은 나중에 설명되는 역방향 시스템과 복합된 시스템에서는 존재하지 않는다. 규칙 적용시와 마찬가지로 목표 문자는 AND/OR 그래프의 자손 노드로 첨가되어진다. 전방향 시스템은 목표 노드들로 이루어지는 해결 그래프를 포함하는 AND/OR 그래프가 생성될 대 성공적으로 끝난다.

5) 변수를 지니는 표현

이제부터 변수를 지니는 표현을 다루는 전향 추론 시스템을 살펴보자. 존재한정변수 혹은 전체한정변수들을 지닌 목표 wff 에 대해서는 사실이나 규칙에 대해 사용한 스콜렘 과정을 반대로 수행한다. 즉, 목표에 있는 전체한정변수들은 스콜렘 함수로 나타내어진다. 이는 비교흡수 부정 시스템에서 목표 wff 가 부정이 되어 첨가되어지는 것을 생각하면 쉽게 이해될 수 있다. 그 다음에 목표 wff 의 존재한정변수들은 삭제된다. 목표 wff 를 스콜렘한 후에는 두 개 이상의 OR 결합에 같은 변수가 나오지 않도록 문자들을 표준화시킨다. L ⇒ W 형태의 규칙이 AND/OR 그래프에 적용되는 과정을 다음의 예로서 살펴보자.

그림 14  변수를 포함하는 사실 표현의 AND/OR 그래프

{P(x, y) ∨ [Q(x, A) ∧ R(B, y)]}

이 사실의 AND/OR 그래프 표현은 앞의 그림 14 와 같다.

그림 15  변수를 지니는 규칙이 적용된 후의 AND/OR 그래프

P(A, B) ⇒ [S(A) ∨ X(B)] 를 AND/OR 그래프에 적용하면 그림 15 와 같이 된다.

이로부터 잎 노드들로 구성되는 해결 그래프들은 다음과 같은 두 개의 절로써 표현되어 진다.

S(A) ∨ X(B) ∨ Q(A, A), S(A) ∨ X(B) ∨ R(B, B)

이러한 절들을 유도하는데는 해결 그래프의 잎 노드에 문자들에 가장 일반적 단일화 (mgu) 인 u 를 적용하면 된다. 어떤 AND/OR 그래프에 하나 이상의 규칙이 가해진 후에는 하나 이상의 비교선택 아크가 생긴다. 특히 문자 노드로 종결되는 AND/OR 그래프의 어떤 해결 그래프는 여러 개의 비교선택 아크를 가질 수 있다. 이 여러 개의 비교선택 아크를 가지는 AND/OR 그래프로부터 유도되는 절들을 구하는 경우에는 일치하는 (consistent) 비교선택 아크의 치환으로 문자 노드에서 종결되는 해결 그래프만 선택하면 된다. 이와 같이 일치하는 해결 그래프에 의해 유도되는 절은 단일화 결합 (unifying composition) 이라 불리는 특별한 치환을 종료 (문자) 노드들의 OR 결합에 적용함으로써 구해 진다.

일치하는 치환과 치환의 단일화 결합은 다음과 같이 정의된다.

을 치환의 집합이라 하며 각 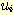는 다음과 같은 쌍의 집합이다.

여기서 t 들은 묶음 (term) 이고 v 들은 변수이다. 으로부터 두 개의 수식을 정의한다.

,

치환 이 일치한다 (consistent) 는 말은 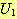과 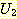가 단일화 가능하다는 말과 같다. 의 단일화 결합 u 는 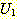과 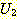의 가장 일반적 단일화를 말한다.

단일화 결합의 몇가지 예가 표 2 에 주어져 있다.

표 2  단일화 결합에 의한 치환

해결 그래프가 일치되는 비교선택 아크의 치환을 가진다는 것은 원래의 사실에 규칙들을 적용했을시 새로운 절들이 유도된다는 것을 말한다. 하나의 예를 살펴보자.

P(x) ∨ Q(x) 의 사실과 두 개의 규칙 P(A) ⇒ R(A), Q(B) ⇒ R(B) 의 AND/OR 그래프는 그림 16 과 같이 된다. 비록 이 그래프가 R(A), R(B) 로 이름이 붙여진 문자 노드를 가진 해결 그래프를 포함할지라도 이 그래프는 불일치된 치환을 포함한다. 그러므로 [R(A) ∨ R(B)] 는 그림 16 의 AND/OR 그래프에 의해 유도되는 절이 아니다.

그러나 그림 16 은 [R(A) ∨ Q(A)] 절의 표현을 나타낼 수 있다. R(A) 와 Q(x) 이름이 붙여진 문자 노드로 종결되는 해결 그래프에 일치되는 R(A) ∨ Q(x) 표현에 치환 {A/x} 을 적용하면 [R(A) ∨ Q(A)] 의 절이 얻어진다.

그림 16  불일치의 치환을 지닌 AND/OR 그래프

규칙과 목표 문자들에 의해 확장되는 AND/OR 그래프의 과정은 일치되는 해결 그래프가 모든 종료 노드에서 목표 노드를 가지는 순간에 성공적으로 종결이 된다. 이로부터 생성 시스템은 목표에 대한 OR 결합이 해결 그래프에 있는 목표 노드로 이름이 붙여진 문자의 OR 결합에 단일화 결합을 해서 얻어진다는 것을 알 수 있다. 이제 간단한 예를 들어 전향 생성 시스템의 작동을 설명한다. 다음과 같은 사실과 규칙들을 가지고 있다고 해보자.

       ~DOG(FIDO) ∨ [BARKS(FIDO) ∧ BITES(FIDO)]

R1 : ~DOG(x) ⇒ ~TERRIER(x)

R2 : BARKS(y) ⇒ NOISY(y)

그림 17  "Terrier" 문제의 AND/OR 그래프

이로부터 ~TERRIER(z) ∨ NOISY(z) 로 주어지는 목표 wff 를 증명하고자 한다. 여기서 z 는 존재한정변수이다. 이 문제의 AND/OR 그래프는 앞의 그림 17 과 같다. 이 AND/OR 그래프 안에서 일치되는 해결 그래프는 {FIDO/x}, {FIDO/y}, {FIDO/z} 의 치환을 가진다. 이 치환들의 단일화 결합은 {FIDO/x, FIDO/y, FIDO/z} 이 되며, 이것을 목표 문자들에 적용하면 다음과 같은 결과를 얻는다.

~TERRIER(FIDO) ∨ NOISY(FIDO)

이 표현은 우리가 증명하고자 하는 목표 wff 의 답이 되며 원하는 결과이다.

(2) 후향 (backward) 추론 시스템

1) AND/OR 형태의 목표 표현

후향 시스템은 목표 표현으로 아무런 제한도 받지 않는다. 전향 추론 시스템에서의 사실 표현의 전환과 유사하게 목표 표현의 wff 를 AND/OR 형태로 먼저 전환시킨다. 즉, 먼저 ⇒ 심볼을 제거하고 부정 심볼을 움직이며, 전체한정변수를 스콜렘시키고, 존재한정변수를 삭제한다 (한정변수의 변환이 전향 추론 시스템의 사실 표현의 경우와는 역이 도는 것을 유의할 것).

예를 들어 다음과 같은 목표 표현,

(∃y)(∀x) {P(x) ⇒ [Q(x, y) ∧ ~[R(x) ∧ S(y)]]}

은 아래처럼 전환이 된다.

~P(f(y)) ∨ {Q(f(y), y) ∧ [~R(f(y)) ∨ ~S(y)]}.

변수를 표준화시키면 다음과 같다.

~P(f(y)) ∨ {Q(f(y), y) ∧ [~R(f(y)) ∨ ~S(y)]}.

AND/OR 형태의 목표 wff 들은 AND/OR 그래프로서 표현이 되어진다. 그러나 목표 표현을 가진 k-연결자는 AND 결합으로 연관된 부표현들을 분리하는데 이용이 된다. 위의 보기의 AND/OR 그래프는 그림 18 과 같다.

그림 18  목표 wff 의 AND/OR 그래프 표현

이 그래프의 잎 노드들은 목표 표현의 문자들에 의해 이름이 붙여져 있다. AND/OR 그래프에서, 루트 (root) 노드의 자손을 부목표 (subgoal) 노드라고 한다. 이 목표 wff 로부터 생성되는 절들은 잎 노드에 종결되는 해결 그래프를 따라가면서 유도할 수 있다. 즉,

~P(f(z)),

Q(f(y), y) ∧ ~R(f(y)),

Q(f(y), y) ∧ ~S(y).

목표절들은 문자들의 AND 결합이며 이 절들의 OR 결합이 목표 wff 를 나타낸다.

2) 후향 시스템에서의 규칙 (B-규칙) 적용

B-규칙의 형태는 다음과 같이 제한이 된다.

W ⇒ L,

여기서 W 는 어떤 임의의 wff (AND/OR 형태에 있다고 가정함) 이고, L 은 하나의 문자이다. 목표 wff 를 나타내고 있는 AND/OR 그래프에 L 과 단일화될 수 있는 L' 로 이름이 붙은 문자 노드가 존재하면 위의 B-규칙을 적용할 수 있다. 이 규칙의 적용 후 나타나는 그래프는 L' 노드로부터 비교선택 아크로 이어지는 새로운 자손 노드 L 을 첨가한 형태가 되며, 이 새로운 자손 노드 L 을 첨가한 형태가 되며, 이 새로운 노드는 u 가 L 과 L' 의 가장 일반적 단일화 (mgu) 라 할 때 Wu 에 대한 AND/OR 그래프의 루트 노드가 된다. 위의 설명은 앞에서 설명한 전향 시스템에서의 F-규칙의 적용시와 비교해 볼 때 반대 (duality) 의 성질을 지니고 있다.

3) 종결 조건

후향 시스템에 의해 사용되는 사실 표현들은 문자들의 AND 결합의 형태에 한정된다. 후향 시스템에서의 종결조건은 AND/OR 그래프가 사실 노드에서 끝나는 일치된 (consistent) 해결 그래프를 포함하는 것이다. 여기서 일치된 해결 그래프는 비교 선택 아크의 치환들이 단일화 결합을 행하는 경우에 생긴다. 예를 들어 다음과 같은 사실과 규칙들이 있다고 하자.

F1 : F2 : F3 : F4 : R1 : R2 :   R3 : R4 : R5 :

DOG(FIDO) ~BARKS(FIDO) WAGS-TAIL(FIDO) MEOWS(MYRTLE) [WAGS-TAIL(x1) ∧ DOG(x1)] ⇒ FRIENDLY(x1) [FRIENDLY(x2) ∧ ~BARKS(x2)]            ⇒ ~AFRAID(y2, x2) DOG(x3) ⇒ ANIMAL(x3) CAT(x) ⇒ ANIMAL(x4) MEOWS(x5) ⇒ CAT(x5)

이로부터 다음과 같은 목표 표현을 증명하고자 한다.

(∃x)(∀y) {CAT(x) ∧ DOG(y) ∧ ~AFRAID(x, y)]

이 문제에서 일치되는 해결 그래프가 그림 19 에 나타나 있다. 이 해결 그래프의 일치성을 보이기 위해 해결 그래프에 있는 비교선택 아크에 분여진 모든 치환들로부터 단일화 결합을 시도한다. 그림 19 에서 ({x/25}, {MYRTLE/x}, {FIDO/y}, {x/y2, y/x2}, {F1DO/y}, {y/x1}, {F1DO/y} {F1DO/y}) 의 단일화 결합을 해야 한다. 그 결과는 {MYRTLE/x5, MYRTLE/x, FIDO/y, MYRTLE/y2, FIDO/x2, FIDO/x1} 이 된다. 이 단일화 결합을 목표 표현에 적용시키면 다음과 같은 해답을 얻게 된다.

[CAT(MYRTLE) ∧ DOG(FIDO) ∧ ~AFRAID(MYRTLE, FIDO)].

그림 19  후향 시스템의 일치되는 해결 그래프

(3) 전향과 후향 시스템의 결합

전향과 후향의 규칙을 기초로한 추론 시스템 각각이 저마다의 한계를 가진다. 후향 시스템의 경우, 어떠한 임의의 형태의 목표 표현도 가질 수 있는 반면에 사실 표현은 문자의 AND 결합이어야만 한다. 전향 시스템의 경우, 어떠한 임의의 형태의 사실 표현도 가능하지만 목표 표현은 문자들의 OR 결합이어야 한다. 그러면 위에서 말한 전향과 후향 시스템에서 나타나는 장점만을 가지는 시스템을 생각해 볼 필요가 있다.

둘을 결합한 시스템의 전체 데이터 베이스는 두 개의 AND/OR 그래프 구조를 가지며, 하나는 목표를, 하나는 사실을 나타낸다. 이 구조들은 앞에서 언급했듯이 B-규칙과, F-규칙에 의해 각각 수정이 되어진다. 이 결합된 시스템은 종결조건이 복잡하게 되는데, 종결이 되는 순간은 그래프에서 비교선택되는 모든 문자 노드들이 단일화되어지는 순간이다. 두 그래프 사이의 모든 가능한 비교선택이 이루어진 후, 목표 그래프의 루트 노드에 있는 표현이 사실 그래프의 루트 노드에 있는 표현과 규칙으로부터 증명이 되는지를 결정해야 한다. 이것이 증명될 때 결합된 시스템은 종결이 된다. 이 종결조건은 사실 노드와 목표 노드가 CANCEL 될 때 이루어진다. CANCEL 은 다음과 같이 순환적으로 정의된다.

1. n 이 사실 노드이고 m 이 목표 노드일 때 두 개의 노드 n 과 m 은 CANCEL 될 수 있다.

2. n 과 m 이 단일화되는 문자들에 의해 주어졌거나 또는 n 이 그의 자식들의 노드 {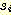} 에 k-연결자를 가지고 연결되어 있을 때 각각의 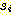노드가 m 과 CANCEL 될 수 있다면 두 개의 노드 n 과 m 은 CANCEL 될 수 있다.

예로서 그림 20 의 굵은 선은 사실 노드와 목표 노드가 CANCEL 되는 과정을 보여준다.

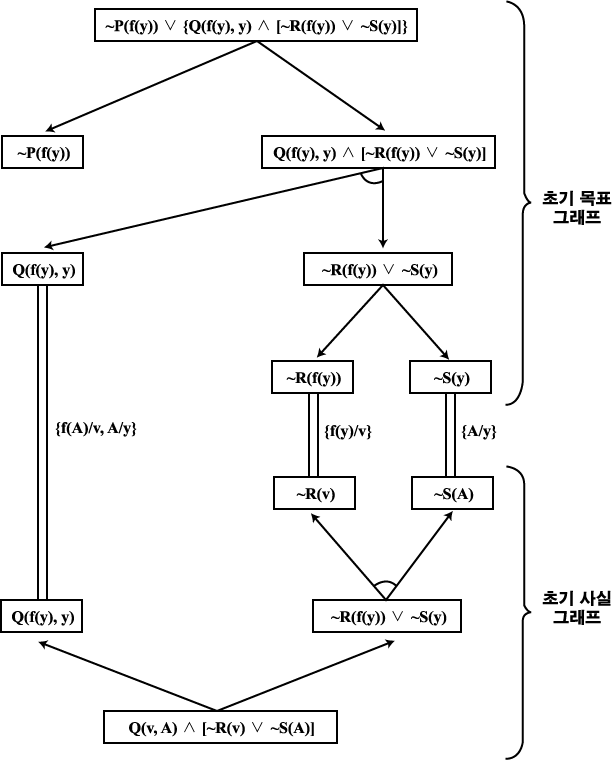
그림 20  CANCEL 그래프의 예

연습문제

1. 다음의 wff 들을 클로저 형태로 바꾸어라.

(a) (∀x) [P(x) ⇒ P(x)]

(b) {~{(∀x) P(x)}} ⇒ (∃x)[~P(x)]

(c) ~{(∀x) {P(x) ⇒ {(∀y) [P(y) ⇒ P(f(x, y))] ∧ ~(∀y) [Q(x, y) ⇒ P(y)]}}}

(d) (∀x)(∃y) {[P(x, y) ⇒ Q(y, x)] ∧ [Q(y, x) ⇒ S(x, y)]}

        ⇒ (∃x) (∀y) [P(x, y) ⇒ S(x, y)]

2. 결정은 건전 (sound) 함을 보여라. 즉, 두 클로저의 결정자는 논리적으로 두 클로저를 따른다는 것을 보여라.

3. 다음의 만족되지 않은 클로저들의 집합에 대해 일차적 입력형태 반복을 구하여라.

~P ∨ ~Q ∨ ~R
~S ∨ T
~T ∨ P
S
~R
~S ∨ U
~U ∨ Q

4. 아래의 어떤 클로저들이 P(f(x), y) 에 의해 포함 (subsume) 되는지 지적하여라.

(a) P(f(A), f(x)) ∨ P(z, f(y))

(b) P(z, A) ∨ ~P(A, z)

(c) P(f(f(x)), z)

(d) P(f(z), z) ∨ Q(x)

(e) P(A, A) ∨ P(f(x), y)

5. 다음의 각 공식은 항진 (tautologies) 임을 결정반복에 의해 보여라.

(a) (P ⇒ Q) ⇒ [(R ∨ P) ⇒ (R ∨ Q)]

(b) [(P ⇒ Q) ⇒ P] ⇒ R

(c) (~P ⇒ P) ⇒ P

(d) (P ⇒ Q) ⇒ (~Q ⇒ ~P)

6. 결정반복방법을 사용해서 다음의 wff 들의 유효성 (validity) 을 증명하라.

(a) (∃x) {[P(x) ⇒ P(A)] ∧ [P(x) ⇒ P(B)]}

(b) (∀z)[Q(z) ⇒ P(z)] ⇒ {(∃x) [Q(x) ⇒ P(A)] ∧ [Q(x) ⇒ P(B)]}

(c) (∃x)(∃y) {[P(f(x)) ∧ Q(f(B))] ⇒ [P(f(A)) ∧ P(y) ∧ Q(y)]}

(d) (∃x)(∀y)P(x, y) ⇒ (∀y)(∃x)P(x, y)

(e) (∀x){P(x) ∧ [Q(A) ∨ Q(B)]} ⇒ (∃x) [P(x) ∧ Q(x)]

7. 결정반복에 의해 wff (∃x)(Px)) 는 논리적으로 wff[P(A1) ∨ P(A2)] 로부터 따른다는 것을 보여라. 그러나 (∃x)(P(x)) 의 스클렘한 형태인, P(A) 는 [P(A1) ∨ P(A2)] 로부터 논리적으로 따르지 않는다. 여기에 대해 설명하여라.

8. 전체 데이터베이스에서의 결정규칙방식을 사용한 생성 시스템은 가환성 (commutative) 을 가진다는 것을 보여라.

9. 다음의 문장들을 규칙에 기초한 기하정리증명을 위한 생성규칙으로 나타내어라.

(a) Corresponding angles of two congruent triangles are congruent.

(b) Corresponding sides of two congruent triangles are congruent.

(c) If the corresponding sides of two triangles are congruent, the triangles are congruent.

(d) The base angles of an isoceles triangle are congruent.

10. 블력 문제의 상황이 다음의 wff 들의 집합에 의해 묘사된다.

ONTABLE(A)    CLEAR(E)
ONTABLE(C)    CLEAR(D)
ON(D, C)         HEAVY(D)
ON(B, A)         WOODEN(B)
HEAVY(B)        ON(E, B)

이러한 wff 들이 묘사하고자 하는 상황을 기술해보아라.

아래의 문장은 이러한 블럭 문제에 대한 일반적인 지식을 제공한다.

    Every big, blue block is on a green block.
    Each heavy, wooden block is big.
    All blocks with clear tops are blue.
    All wooden blocks are blue.

이러한 문장들을 암시적 표현으로 나타내어라. 더우기 "Which block is on a green block?" 을 풀기 위해서 B-규칙을 사용하여 일치하는 AND-OR 해결 트리를 그려라.