무정보 탐색

(Uninformed Search)

 

인공지능-지능형 에이전트를 중심으로 : Nils J.Nilsson 저서, 최중민. 김준태. 심광섭. 장병탁 공역, 사이텍미디어, 2000  (원서 : Artificial Intelligence : A New Synthesis 1998), Page 133~141 

 

상태공간의 설정 (Formulating the State Space)

암시적 상태공간 그래프의 구성요소 (Components of Implicit State-Space Graphs)

너비우선 탐색 (Breadth-First Search)

깊이우선 또는 되추적 탐색 (Depth-First or Backtracking Search)

반복적 깊이증가 (Iterative Deepening)

참고문헌 및 토론 (Additional Readings and Discussion)

 

 

상태공간의 설정

실제적인 문제들의 대부분은 탐색공간이 너무 크기 때문에 명시적인 그래프로 표현할 수 없다. 이 경우에는 계획하는 에이전트에서 설명한 기본적인 탐색 방법에 수정이 필요하다. 첫째, 이러한 문제들은 탐색 문제로 설정하는 방법에 있어서 매우 신중해야 한다. 둘째, 방대한 탐색 그래프를 암시적으로 (implicitly) 표현하는 방법이 있어야 한다. 셋째, 이런 방대한 그래프를 탐색하기 위한 효율적인 방법이 있어야 한다.

블록 쌓기와 같은 계획 문제에 있어서는, 여러 가지 상태 (state) 와 상태를 변화시키는 행동 (action) 을 표현하기 위한 자료 구조를 생각해내는 것이 그다지 어려운 일이 아니다. 하지만 일반적으로는 어떤 문제를 처리할 수 있을 만한 상태공간 그래프로 나타내 주는 표현 방법을 찾는 것이 어려운 일이다. 그렇게 하려면 대칭성을 고려하고, 관련 없는 부분을 단순화하며, 적절한 수준으로 추상화하는 등 문제에 대한 면밀한 분석이 필요하다. 유감스럽게도, 어떤 문제를 탐색 문제로 설정하는 것은 여전히 사람이 관여해야 하는 예술과도 같은 것이다.

블록 쌓기 문제 외에, 타일 맞추기 문제도 상태공간 탐색을 이용하여 행동 순서를 계획하는 방법을 보여주기 위하여 많이 사용된다. 다양한 예를 보이기 위하여 이장과 휴리스틱 탐색에서는 이 문제를 사용하기로 하자. 타일 맞추기의 가장 일반적인 경우는 15 퍼즐로서, 4×4 배열에 15 개의 타일이 있고 타일이 움직일 수 있는 하나의 빈자리가 있는 것이다. 이 문제의 임무는 초기의 타일 배치를 특정한 다른 배치로 바꾸어 줄 수 있는 타일 이동 순서를 찾는 것이다. 8 퍼즐은 이 문제의 축소된 경우로, 3×3 배열에 8 개의 타일이 있는 것이다. 그림 1 과 같이 타일의 배치가 바뀌도록 타일을 이동하는 것이 문제라고 가정하자.

 

그림 1 8 퍼즐에서의 시작과 목표 배치

이 문제에서 상태의 아이콘 표현으로 가장 쉬운 것이 1 에서 8 까지의 숫자와 빈자리를 나타내는 기호가 들어가 있는 3×3 배열일 것이다. 목표 상태는 그림 1 의 오른쪽 배치에 해당하는 배열이 된다. 각 상태 사이의 이동은 타일을 빈자리로 이동하는 것에 해당한다. 앞에 언급한 것처럼 어떤 문제를 상태공간으로 나타낼 때 여러 가지의 표현 방법이 있을 수 있다. 8 퍼즐에 있어서는 우선 1 을 위로, 1 을 아래로, 1 을 왼쪽으로, 1 을 오른쪽으로, 2 를 위로, ... 등 8×4 개의 서로 다른 이동을 생각할 수 있다 (물론 이들이 항상 모두 가능한 것은 아니다). 이보다 더 간결한 표현은 빈칸을 왼쪽으로, 빈칸을 위로, 빈칸을 오른쪽으로, 빈칸을 아래로 등 4 개의 서로 다른 이동만으로 나타내는 것이다. 시작 상태와 가능한 이동의 집합이 주어지면 시작 상태로부터 도달할 수 있는 상태들의 그래프가 암시적으로 정의된다. 위와 같은 표현 방법을 이용하면 8 퍼즐의 상태공간 그래프의 노드 수는 9! = 362,880 개가 된다 (8 퍼즐의 상태공간은 두 개의 그래프로 나뉘며, 한쪽 그래프에 있는 타일 배치는 다른 쪽 그래프에 있는 타일 배치로부터 도달될 수 없다).

암시적 상태공간 그래프의 구성요소

시작 상태로부터 행동을 취하여 도달될 수 있는 상태공간 그래프에서의 영역은 시작 상태의 정의와 각 행동들에 대한 정의에 의해 암시적으로 표현된다. 따라서 원칙적으로 암시적인 (implicit) 그래프 표현으로부터 명시적인 (explicit) 그래프를 만들어 내는 것이 가능하다. 그렇게 하려면 우선 시작 노드의 자식 노드들을 만들어내고 (모든 가능한 연산자들을 시작 노드에 적용하면 된다) 만들어진 자식 노드들의 자식 노드들을 다시 만들어내는 과정을 계속하면 된다. 너무 방대해서 자체를 명시적으로 나타낼 수 없는 그래프의 경우에는 탐색 과정에서 상태공간 중 목표까지의 경로를 찾는 데 필요한 부분만 명시적으로 만들어내야 한다. 탐색 과정은 목표 노드까지의 경로가 찾아지면 종료된다. 좀 더 공식적으로 이야기하면, 상태공간 그래프의 암시적인 표현에는 세 가지 기본 요소가 있다.

여기서는 크게 두 종류의 탐색 방법을 살펴볼 것이다. 그 중 한가지는 목표까지의 경로를 찾는 데 있어서 탐색공간의 어떤 한 부분을 다른 부분에 비해 선호할 만한 판단 근거가 없는 경우에 사용하는 방법이다. 이런 경우를 무정보 (uninformed) 탐색이라고 한다. 다른 한 가지는 탐색을 한 부분에 집중시킬 수 있도록 해주는 그 문제 고유의 정보가 있는 경우에 사용하는 방법이다. 이런 경우를 휴리스틱 (heuristic) 탐색이라고 한다. 우선 무정보 방법을 먼저 설명하고, 다음 장에 휴리스틱 방법을 설명하겠다.

너비우선 탐색

무정보 탐색에서는 각 노드에 문제에 대한 특별한 지식 없이 연산자를 적용한다 (물론 어떤 행동이 정당한지에 대한 지식은 가지고 있다). 가장 간단한 무정보 탐색 방법은 너비우선 탐색 (breadth-first search) 이다. 너비우선 탐색에서는 시작 노드에 모든 가능한 연산자를 적용하고, 다시 시작 노드의 모든 자식 노드들에 가능한 연산자를 적용하는 식으로 명시적인 상태공간 그래프를 만들어낸다. 탐색은 시작 노드에서부터 바깥쪽으로 균일하게 진행된다. 각 단계에서 노드에 모든 가능한 연산자를 적용시키므로, 이들을 하나의 그룹으로 묶어 후속자 함수 (successor function) 라고 한다. 어떤 노드에 후속자 함수를 적용하면 그 노드에 적용할 수 있는 모든 연산자를 적용했을 때 만들어지는 노드들의 전체 집합을 생성하게 된다. 어떤 노드에 후속자 함수를 적용하는 것을 그 노드를 확장 (expanding) 한다고 한다.

 

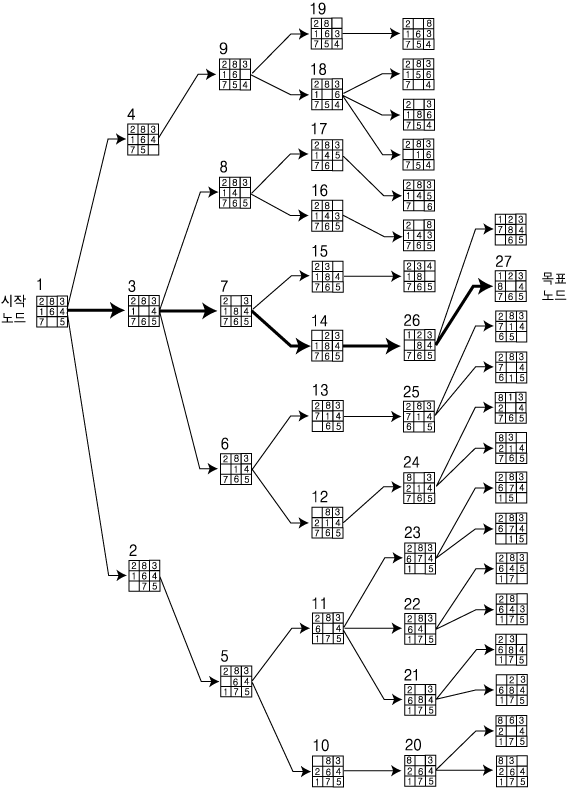
그림 2 8 퍼즐에 대한 너비우선 탐색

그림 2 는 8 퍼즐 문제를 풀기 위해 너비우선 탐색을 수행했을 때 만들어지는 노드를 나타낸다. 시작 노드와 목표 노드가 표시되어 있고, 각 노드 옆에 노드의 확장 순서를 나타내는 번호가 표시되어 있다. 같은 깊이에 있는 노드들은 정해진 순서에 의해 확장된다. 이 그림에서의 연산자 적용 순서는 빈칸을 왼쪽으로, 위로, 오른쪽으로, 아래로 순이다. 각각의 이동은 역방향으로도 가능하지만 자식으로부터 부모로의 아크는 나타내지 않았다. 해 경로 (solution path) 는 검은 선으로 나타내었다. 너비우선 탐색은 목표 노드가 찾아지면 목표 노드까지의 최단 경로가 찾아진다는 특성이 있다. 반면에 너비우선 탐색의 단점은 저장해야 하는 트리의 크기가 목표 노드의 깊이에 따라 지수적으로 증가한다는 것이다.

균일비용 탐색 (uniform-cost search) [Dijkstra 1959] 은 너비우선 탐색의 변형으로, 노드들이 시작 노드에서부터 같은 깊이 (depth) 의 등심선 (contour) 이 아닌 같은 비용 (cost) 의 등심선을 따라 확장되는 것이다. 만일 그래프의 모든 아크의 값이 동일하다면 균일비용 탐색은 너비우선 탐색과 같은 것이다. 균일비용 탐색은 또한 다음 장에서 설명할 휴리스틱 탐색의 특수한 경우라고 할 수도 있다. 너비우선 탐색과 균일비용 탐색에 대한 지금까지의 대략적인 설명으로 주요 개념은 다루었지만, 노드를 확장할 때 전에 이미 방문한 노드가 만들어지는 경우 등을 다루기 위해서는 좀 더 면밀하게 고려할 점들이 있다. 이런 상세한 내용들은 다음 장에서 보다 일반적인 알고리즘을 다룬 후에 이야기하겠다.

깊이우선 또는 되추적 탐색

깊이우선 탐색은 어떤 노드에 각 연산자를 적용하여 한번에 하나씩만 자식 노드를 만들어낸다. 각 노드에는 나중에 필요하게 되면 나머지 연산자들을 적용할 수 있도록 표시를 해둔다. 각 노드에서는 어떤 연산자를 먼저 적용하고 어떤 연산자들을 다음에 적용할 것인지에 대한 판단을 하여야 한다. 하나의 자식 노드가 만들어지면 다음에 적용할 것인지에 대한 판단을 하여야 한다. 하나의 자식 노드가 만들어지면 바로 그 노드의 자식 노드가 만들어지는 식으로 탐색이 진행된다. 탐색 과정이 시작노드에서부터 한없이 깊이 진행하는 것을 막기 위하여 깊이 제한(depth bound) 을 사용한다. 깊이 제한보다 더 깊이 있는 노드는 생성하지 않는다 (이 경우 적어도 하나의 목표 노드는 깊이 제한 안에 있다고 가정한 것이다). 이러한 제한을 두면 가까운 목표 노드를 포함하고 있지 않다고 판단되는 탐색 그래프의 영역을 무시할 수 있다.

 

그림 3 깊이우선 탐색에서 처음 몇 개 노드의 생성 과정

8 퍼즐에 깊이 제한을 5 로 한 경우에 대해 탐색 과정을 나타내어 보겠다. 여기서도 연산자의 적용 순서는 빈칸을 왼쪽, 위쪽, 오른쪽, 아래쪽의 순이고, 자식으로부터 부모로의 아크는 나타내지 않았다. 우선 그림 3a 에 처음 몇 개의 노드가 만들어지는 과정을 나타내었다. 각 노드의 왼쪽에 있는 숫자는 노드가 만들어진 순서를 나타내며, 아직 완전히 확장되지 않은 아크들도 나타나 있다. 노드 5 에서 목표 노드에 도달하지 못한 채로 깊이 제한에 도달했고, 따라서 가장 최근에 만들어졌으며 아직 완전히 확장되지 않은 노드인 노드 4 가 선택되어 다음 번 자식 노드인 노드 6 이 만들어진다 (그림 3b 를 보라). 이 시점에서 노드 5 는 더 이상 그 밑에 있는 노드들은 만들어내지 않을 것이므로 버려진다. 노드 6 도 깊이 제한에 도달했고 목표 노드가 아니므로, 다음 번으로 최근에 만들어졌으며 완전히 확장되지 않은 노드인 노드 2 가 선택되어 노드 7 을 만들고, 노드 3 과 그 자식 노드들은 더 이상 밑으로 진행하여 노드를 만들지 않을 것이므로 버린다. 노드 2 로 되돌아가는 것이 되추적 (backtracking) 의 예이다. 깊이 제한에 다시 도달한 상태가 그림 3c 의 그래프이다. 이 시점에서 목표 노드에 도달하지 못했으므로, 노드 8 의 다음 자식 노드를 만들 게 되며, 그 노드도 목표 노드는 아니다. 따라서 노드 8 과 모든 자식 노드들을 버리고 노드 7 의 다른 자식 노드를 만들기 위해 되돌아간다. 이러한 과정을 계속하면 최종적으로 그림 4 와 같은 그래프가 된다.

 

그림 4 깊이우선 탐색에서 목표 노드에 도달했을 때의 그래프

깊이우선 탐색에서는 그래프에서 현재 탐색중인 경로에 해당하는 부분과 그 경로상에 있는 완전히 확장되지 않은 노드에 대한 정보만을 저장하면 된다. 따라서 깊이우선 탐색의 메모리 필요량은 깊이 제한에 비례한다. 깊이우선 탐색의 단점은 목표 노드가 찾아졌을 때 목표까지의 최단 경로가 찾아진다는 것을 보장하지 못한다는 것이다. 또 다른 문제는 목표 노드가 하나인 경우, 그 부분이 탐색 과정에서 나중에 확장된다면 목표 노드가 아주 가까이 있더라도 방대한 탐색공간을 방문하게 된다는 것이다.

반복적 깊이증가

반복적 깊이증가 (iterative deepening) [Korf 1985, Stikel & Tyson 1985] 라는 기법은 깊이우선 탐색처럼 메모리 필요량이 깊이 제한에 비례하면서도 최단 경로로 목표 노드를 찾는 것을 보장하는 방법이다. 반복적 깊이증가 방법에서는 목표 노드가 찾아질 때까지 깊이 제한을 1 씩 증가시키면서 연속적인 깊이우선 탐색을 수행한다. 그림 5 에 반복적 깊이증가 탐색이 진행되는 예를 나타냈다.

 

그림 5 반복적 깊이증가 탐색 과정

놀랍게도 반복적 깊이증가 탐색을 수행할 때 확장되는 노드의 수는 너비우선 탐색에 의해 확장되는 노드의 수에 비해 그다지 많지 않다. 확장되는 노드의 수를 트리의 분기 계수 (branching factor) 가 이고 목표 노드가 깊이 에 있으며 마지막으로 만들어지는 노드라고 가정하고 계산해 보자. 너비우선 탐색에 의해 확장되는 노드의 수는 다음과 같다.

반복적 깊이증가 탐색에 의해 확장되는 노드의 수를 계산하기 위해 우선 깊이 까지의 완전한 깊이우선 탐색에 의해 확장되는 노드의 수를 알아보면 다음과 같다.

목표 노드가 깊이 에 있을 때 반복적 깊이증가 탐색은 번의 깊이우선 탐색을 수행해야 한다. 따라서 전체 깊이우선 탐색을 수행할 때 확장되는 노드의 총 합은 다음과 같다.

식을 단순화하면 목표 노드가 깊이 에 있을 때 반복적 깊이증가 탐색에 의해 확장되는 노드의 총 개수는 다음과 같다.

가 크면 비율은 가 된다. 분기 계수가 10 이고 목표 노드가 깊이 있는 경우, 반복적 깊이증가 탐색은 너비우선 탐색에 비해 약 11% 정도 더 노드를 확장할 뿐이다.
반복적 너비증가 (iterative broadening) 라는 또 다른 관련된 탐색 기법은 목표 노드가 많이 존재하는 경우에 유용하다. 이 방법에 대해서는 [Ginsberg & Harvey 1992, Harvey 1994] 를 참조하기 바란다.

참고문헌 및 토론

되추적 탐색을 개선할 수 있는 다양한 방법들로 종속 관계에 의한 되추적 (depen-dency-directed backtracking) [Stallman & Sussman 1977 (Stallman, R., and Sussman, G., "Forward Reasoning and Dependency-Directed Backtracking in a System for Computer-Aided Circuit Analysis," Artificial Intelligence, 9(2):135-196, 1977.)], 되도약 (backjumping) [Gaschnig 1979 (Gaschnig, J., "Performance Measurement and Analysis of Certain Search Algorithms," Carnegie-Mellon University Computer Science Tech. Report CMU-CS-79-124, Pittsburg, PA, 1979.)], 동적 되추적 (dynamic backtracking) [Ginsberg 1993 ({db} Ginsberg, M., "Dynamic Backtracking," Journal of Artificial Intelligence Research, 1:25-46, 1993.)] 등이 있다. 마지막 논문에서는 이러한 방법들을 비교하고 동적 되추적 방법의 장점을 설명하고 있다. 이러한 향상된 되추적 기법들은 일반적으로 제약조건 충족 (constraint-satisfaction) 문제에 많이 적용된다 (이 문제는 11 장에서 설명할 것이다).