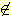 S" 로 표기된다. 집합은 중괄호 ({ }) 내에 소속 원소들을 열거함으로써
표시된다 ; 예를 들어, 정수 0, 1, 2 를 포함하는 집합은 다음과 같이 보여진다.
S" 로 표기된다. 집합은 중괄호 ({ }) 내에 소속 원소들을 열거함으로써
표시된다 ; 예를 들어, 정수 0, 1, 2 를 포함하는 집합은 다음과 같이 보여진다.계산 이론 개요
형식 언어와 오토마타 : Peter Linz 저서, 장직현. 김응모. 엄영익. 한광록 공역, 사이텍미디어, 2001 (원서 : An Introduction to Formal Languages and Automata. 3rd ed, Jones and Bartlett. 2001), Page 1 ~ 37
컴퓨터 과학은 매우 현실적인 학문이다. 이를 공부하는 사람들은 이론적인 고찰을 필요로 하는 문제보다는 현실적이고 실제로 유용한 문제들을 현저하게 좋아하는 경향을 가진다. 특히, 이러한 경향은 실세계에서 필요로 하는 복잡하고 어려운 응용 분야를 다루는 컴퓨터 과학도들에게서 두드러지게 나타난다. 이들은 자신이 원하는 해답을 구하는 데 도움이 된다고 판단할 경우에만 이론적인 문제에 관심을 갖는다. 컴퓨터를 필요로 하는 응용 분야가 없다면 컴퓨터에 대한 흥미도 없을 것이고, 따라서 이와 같은 자세가 잘못된 것이라 말할 수는 없을 것이다. 그러나 이러한 현실 지향적인 경향에서도, "왜 이론을 공부하는가?" 같은 질문이 제기될 수 있을 것이다.
이에 대한 첫 번째 답으로 이론은 학문 분야에 대한 일반적 본질을 이해할 수 있도록 개념 (concept) 과 원리 (principle) 를 제공한다는 점을 들 수 있다. 컴퓨터 과학 분야는 하드웨어 설계에서부터 프로그래밍에 이르기까지 넓은 범위의 다양한 토픽들을 포함하는 학문 분야이다. 실세계에서의 컴퓨터를 사용하는 데 있어서 성공적인 응용을 위하여 배워야할 많은 특정 세부사항들이 있어야 한다. 따라서 컴퓨터 과학은 매우 다양하고 광범위한 학문 분야이다. 이러한 다양성에도 불구하고 컴퓨터 과학 분야에는 몇 가지 공통적인 기본 원리가 존재하며, 이러한 기본 원리를 공부하기 위해서 우리는 컴퓨터와 계산 (computers and computation) 에 대한 추상적 모델 (abstract model) 을 설정하는 것이다. 이렇게 설정되는 모델은 하드웨어 및 소프트웨어에서 공통적으로 나타나는 특징들, 그리고 컴퓨터를 사용하여 작업을 진행하는 동안 접하게 되는 많은 복잡한 사항들에 필수적이고 중요한 특징들을 모두 표현한다. 비록 이러한 모델들은 실세계에 즉시 적용되기에는 너무 단순하지만, 이를 공부함으로써 우리가 얻는 통찰력에 의해 우리는 앞으로 해야 할 일들에 대한 기본적인 토대를 얻게 되는 것이다. 이와 같은 접근방식은 컴퓨터 과학 분야에만 국한되는 것은 아니다. 모델의 설정은 어느 과학 분야에나 필수적인 것이며, 그 분야의 실용성은 대부분 간단하면서도 강력한 이론과 법칙들이 존재하는가에 달려 있다.
명확하지는 않지만 위 질문에 대한 두 번째 답은 우리들이 이제부터 공부할 이론적인 개념들이 즉각적이고 중요한 분야에 응용가능하다는 것이다. 디지털 설계나 프로그래밍 언어, 컴파일러 분야 등이 확실한 예들이며, 이외에도 이론적인 개념들이 즉시 응용될 수 있는 여러 분야들이 존재한다. 이 책에서 공부하는 개념들은 컴퓨터 과학의 기초 분야인 운영체제 (operating system) 에서부터 최종 응용 분야라 할 수 있는 패턴 인식 등의 분야에까지 사용될 수 있을 것이다.
세 번째 답으로, 이론 분야에서는 지적인 사람들에게 매우 자극적이고 재미있는 주제들을 다루며, 수수께끼 같은 문제들을 제시함으로써 독자들의 공부 의욕을 돋군다는 점을 들 수 있다. 이는 본질적으로 문제해결 (problem-solving) 을 다루는 분야이며, 독자들은 밤잠을 설쳐가며 주어진 문제를 해결하는 데 시간을 투자하게 될 것이다. 앞으로 공부하면서 이러한 점들을 독자들이 수긍했으면 한다.
이 책에서는 컴퓨터와 그 응용들의 핵심적인 기능들을 표현하는 모델에 대해 공부하게 된다. 특히, 컴퓨터의 하드웨어를 모델링하기 위해 오토마타 (automata, automaton) 라는 개념을 소개한다. 오토마타란 디지털 컴퓨터에서 반드시 필요한 기능 모두를 갖춘 구조이다. 오토마타는 입력을 받아들이고, 출력을 산출하고, 약간의 임시 기억장소를 가질 수 있으며, 그리고 입력으로부터 출력으로의 변환 과정에서 필요한 결정들을 내릴 수 있다. 형식 언어 (formal language) 란 프로그래밍 언어들의 일반적인 특성들을 추상화한 개념이다. 형식 언어는 심볼 (symbol) 들의 집합과 이 심볼들을 조합하여 문장 (sentence) 이라 불리는 개체를 만드는 데 사용되는 형성규칙들로 구성된다. 다시 말해서, 형식 언어란 이 형성규칙들에 의해 생성되는 모든 문자열 (string) 들의 집합이라고도 할 수 있다. 우리가 이 책에서 공부하는 몇 가지 형식 언어들은 실제로 사용되는 프로그래밍 언어보다 단순 하지만 프로그래밍 언어에서와 동일한 핵심 기능들을 많이 가지고 있다. 우리는 형식 언어를 공부함으로써 프로그래밍 언어에 대해 많은 것들을 배우게 될 것이다. 마지막으로, 우리는 알고리즘 (algorithm) 이라는 용어에 대해 정확히 정의함으로써 기계적인 계산 (mechanical computation) 의 개념을 공식화할 것이며, 그러한 기계적 방법에 의해 해를 찾을 수 있는 (혹은 그렇지 못한) 문제들의 종류들에 대해 공부하게 될 것이다. 공부하는 과정에서, 우리는 이들 추상화 개념들간의 긴밀한 관계에 대해 알게 될 것이며, 그로부터 얻어낼 수 있는 결론들에 대해 연구하게 될 것이다.
제 1 장에서는, 이후의 공부를 위한 발판을 준비하기 위하여 이러한 기본 개념들을 복습한다. 1. 절에서는, 앞으로 필요한 수학에서의 주요 개념들을 살펴본다. 개념을 탐구하는데 있어서 많은 경우 직관 (intuition) 이 도움이 되겠지만, 결론을 유도해 낼 때에는 엄밀한 논증을 거치게 되며, 이 과정에서 전적으로는 아니더라도 수학적인 도구들을 사용하게 될 것이다. 이를 위해 독자들은 집합론 (set theory) 이나 함수 (function), 관계 (relation) 등에 대한 여러 가지 관련 용어들과 기본적인 결과들에 대해 잘 알고 있어야 한다. 또한 트리 (tree) 나 그래프 (graph) 구조도 자주 사용될 것이다. 그러나 라벨 그래프 (labeled graph) 나 유향 그래프 (directed graph) 의 정의 정도만 알고 있으면 문제없을 것이다. 아마도 꼭 필요한 것은 증명 과정을 따라갈 수 있는 능력과 올바른 수학적 논법에 대한 이해력이며, 이를 위해 연역법이나 귀납법, 귀류법 등의 기본적인 증명 기법들에 익숙해야 한다. 이 책에서는 독자들이 이러한 정도의 필요한 예비지식을 지니고 있다고 가정할 것이다. 1. 절에서는 앞으로 사용될 주요 결과들을 복습하고, 이후 논의에서의 수학적 표기법들을 규정하도록 한다.
2. 절에서는 언어 (language) 와 문법 (grammar), 그리고 오토마타와 관련한 주요 개념들을 살펴본다. 이러한 개념들은 이 책 전체에 걸쳐 여러 특정 형태로 보여질 것이다. 3. 절에서는 이러한 개념들이 컴퓨터 과학에서 얼마나 널리 사용되는지를 보이기 위하여 몇가지 간단한 응용들을 소개한다. 2. 와 3. 절에서의 논의는 수학적으로 엄밀하기 보다는 직관적일 것이며, 이는 앞으로 다루고자 하는 개념들을 우선 명확하게 독자들에게 제시하기 위해서이다. 이후에 각 개념들에 대한 보다 수학적이고 엄밀한 제시가 있을 것이다.
집합이란 원소 (element) 들의 모임이며, 소속성
(membership) 을 제외한 어떤 구조도 가지지 않는다. x 가 집합 S 의 원소임을 나타내기
위하여, "x ∈ S" 와 같이 표기한다. 또한, x 가 집합 S 의 원소가 아님을
나타내는 문장은 "x 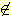 S" 로 표기된다. 집합은 중괄호 ({ }) 내에 소속 원소들을 열거함으로써
표시된다 ; 예를 들어, 정수 0, 1, 2 를 포함하는 집합은 다음과 같이 보여진다.
S" 로 표기된다. 집합은 중괄호 ({ }) 내에 소속 원소들을 열거함으로써
표시된다 ; 예를 들어, 정수 0, 1, 2 를 포함하는 집합은 다음과 같이 보여진다.
S = {0, 1, 2}
집합의 표현시에, 의미가 명확한 경우에는 생략 부호 (...) 를 사용할 수도 있다. 예를 들어, 집합 {a, b, ..., z} 는 영어 알파벳 중 모든 소문자들의 집합을 의미하며, 집합 {2, 4, 6, ...} 는 양의 정수들 중 짝수들의 집합을 의미한다. 필요에 따라서는, 짝수들의 집합을 다음과 같이 보다 명확하게 표기할 수도 있다.
S = {i : i > 0, i 는 짝수이다} (1)
이를 읽을 때 "S 는 0 보다 크고 짝수인 모든 i 들의 집합" 이라 하며, 이때 물론 i 가 정수임을 암시적으로 의미한다.
많이 사용되는 집합 연산들로는 합집합 (union, ∪), 교집합 (intersection, ∩), 차집합 (difference, -) 등이 있으며 다음과 같이 정의된다.
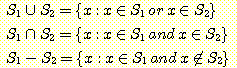
또 다른 기본적인 집합 연산은 여집합 (complementation)
이다. 집합 S 의 여집합은 S 에 속하지 않는 모든 원소들로 구성되며, 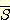 로 표기된다. 이 의미를 정확히 이해하기 위해서는, 모든 가능한 원소들의 집합인
전체 집합 (universal set) U 에 대해 알아야 한다. 전체 집합 U 가 정의되고 나면,
여집합은 다음과 같이 정의할 수 있다.
로 표기된다. 이 의미를 정확히 이해하기 위해서는, 모든 가능한 원소들의 집합인
전체 집합 (universal set) U 에 대해 알아야 한다. 전체 집합 U 가 정의되고 나면,
여집합은 다음과 같이 정의할 수 있다.
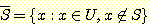
원소를 갖지 않는 집합은 공집합 (empty set, null set) 이라 불리며, Ø 으로 표기된다. 집합의 정의로부터 다음과 같은 사실들을 알 수 있다.
S ∪ Ø = S - Ø = S
S ∩ Ø = Ø
![]() = U
= U
![]() =
S
=
S
다음은 DeMorgan 법칙으로 알려진 유용한 항등식이다.
 (2)
(2)
 (3)
(3)
어떤 집합 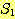 의 모든 원소들이 집합 S 의 원소이면 집합
의 모든 원소들이 집합 S 의 원소이면 집합 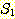 을 집합 S 의 부분집합 (subset) 이라 하며, 이를 다음과 같이 표기한다.
을 집합 S 의 부분집합 (subset) 이라 하며, 이를 다음과 같이 표기한다.
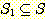
만일 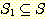 이면서 S 가
이면서 S 가 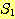 에 존재하지 않는 또 다른 원소를 포함하는 경우
에 존재하지 않는 또 다른 원소를 포함하는 경우 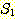 을 S 의 진부분 집합 (proper subset) 이라 하며, 이를 다음과 같이 표기한다.
을 S 의 진부분 집합 (proper subset) 이라 하며, 이를 다음과 같이 표기한다.

집합 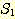 과
과 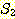 에 공통으로 속하는 원소가 없는 경우, 즉
에 공통으로 속하는 원소가 없는 경우, 즉 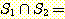 Ø 인 경우에는, 두 집합을 서로 소 (disjoint) 라 한다.
Ø 인 경우에는, 두 집합을 서로 소 (disjoint) 라 한다.
집합 내의 원소의 개수가 유한한 경우에는 이를 유한 집합 (finite set) 이라 하며, 그렇지 않은 경우에는 이를 무한 집합 (infinite set) 이라 한다. 유한 집합의 크기 (size) 란 그 집합 내의 원소의 개수를 의미하며 |S| 로 표기한다.
보통의 경우 한 집합은 여러 개의 부분집합을 가지게
된다. 한 집합 S 의 모든 부분집합들의 집합을 S 의 멱집합 (powerset) 이라 하며,
이는 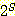 로 표기한다. 독자들은
로 표기한다. 독자들은 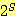 이 집합을 원소로 하는 집합임을 알 수 있을 것이다.
이 집합을 원소로 하는 집합임을 알 수 있을 것이다.
예제 1
집합 S 가 {a, b, c} 인 경우 이의 멱집합은 다음과 같다 :
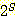 = {Ø, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}
= {Ø, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}
여기서 |S| = 3 이고 |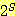 | = 8 이다. 이를 일반화하면 집합 S 가 유한 집합인 경우 다음이 성립함을 알
수 있다.
| = 8 이다. 이를 일반화하면 집합 S 가 유한 집합인 경우 다음이 성립함을 알
수 있다.

여러 경우에 한 집합의 원소들이 다른 여러 집합 원소들의 순서열 (ordered sequence) 인 경우를 볼 수 있다. 이러한 집합을 다른 집합들의 카티션 곱 (Cartesian product) 이라 한다. 두 개 집합의 카티션 곱인 경우에, 이 집합은 순서쌍 (ordered pair) 들의 집합이 되며, 이는 다음과 같이 표기할 수 있다.
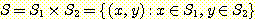
예제 2
두 집합 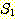 과
과 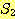 에 대해,
에 대해, 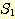 = {2, 4} 이고,
= {2, 4} 이고, 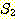 = {2, 3, 5, 6} 이라 하자. 이 경우
= {2, 3, 5, 6} 이라 하자. 이 경우
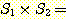 {(2, 2), (2, 3), (2, 5), (2, 6), (4, 2), (4, 3), (4, 5), (4, 6)}
{(2, 2), (2, 3), (2, 5), (2, 6), (4, 2), (4, 3), (4, 5), (4, 6)}
이 경우 하나의 순서쌍 내의 원소의 순서는 중요하다.
이 예에서 순서쌍 (4, 2) 는 집합  에 속하지만, 순서쌍 (2, 4) 는 집합
에 속하지만, 순서쌍 (2, 4) 는 집합  에 속하지 않음을 알 수 있다.
에 속하지 않음을 알 수 있다.
두 개 이상의 집합들에 대한 카티션 곱에 대해서도 자연스럽게 확장할 수 있으며, 이를 n 개 집합의 경우로 확장하면 다음과 같이 표기할 수 있다.
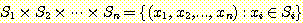
함수 (function) 란 한 집합의 원소들 각각에 대해 다른 집합의 유일한 원소로 배정하는 규칙을 말한다. f 가 한 함수를 표시한다면, 첫 번째 집합을 함수 f 의 정의역 (domain) 이라 하며, 두 번째 집합을 치역 (range) 이라 한다. 이러한 함수 f 를 다음과 같이 표기한다.
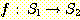
이는 함수 f 의 정의역이 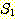 의 부분집합이고, 함수 f 의 치역이
의 부분집합이고, 함수 f 의 치역이 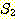 의 부분집합임을 의미한다. 만일 함수 f 의 정의역이
의 부분집합임을 의미한다. 만일 함수 f 의 정의역이 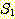 과 같은 경우에는 f 를 전체 함수 (total function) 라 하며, 그렇지 않은 경우에는
f 를 부분 함수 (partial function) 라 한다.
과 같은 경우에는 f 를 전체 함수 (total function) 라 하며, 그렇지 않은 경우에는
f 를 부분 함수 (partial function) 라 한다.
여러 응용에서, 관련된 함수들의 정의역과 치역은 양의 정수들의 집합이다. 더욱이, 우리는 때때로 이들 함수들이 인수들의 값이 아주 커질 때 어떻게 변화하는가에 관심이 있다. 그러한 경우 대부분 성장률 (growth rates) 에 대한 이해만으로 충분하고 일반적인 크기 순위 (order of magnitude) 표기법이 사용될 수 있다. f(n) 과 g(n) 을 정의역이 양의 정수들의 부분집합인 함수들이라 하자. 만일 다음의 부등식을 만족하는 양의 상수 c 가 존재하면, 모든 n 에 대하여,
f(n) ≤ cg (n)
f 의 순위가 g 의 순위보다 높지 않다고 한다. 우리는 이를 다음과 같이 표기한다.
f(n) = O(g (n))
이면, f 의 순위가 g 의 순위보다 낮지 않다고 하고 이를 다음과 같이 표기한다.
f(n) = Ω(g (n))
마지막으로, 다음의 부등식을 만족하는 상수들
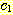 과
과 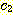 가 존재하면,
가 존재하면,
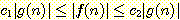
f 가 g 와 같은 크기 순위를 갖는다고 하고, 이를 다음과 같이 표기한다.
f(n) = θ(g (n))
이러한 크기 순위 표기법에서, 우리는 상수 계수와 낮은 순위의 항들은 무시한다. 그 이유는 n 이 커짐에 따라 그 값들은 전체 값에 비하여 보잘 것 없어지기 때문이다.
예제 3
다음의 함수에 대한
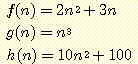
크기 순위 표기법은 다음과 같다.
f(n) = O(g (n))
g(n) = Ω(h (n))
f(n) = θ(h (n))
크기 순위 표기법에서, 심볼 = 는 등가 (equality) 의 개념으로 해석해서는 안되고 크기 순위의 식은 일반적인 수식과 같이 처리될 수 없다. 아래와 같은 유도는 의미가 없고 틀린 결과를 이끌어 낼 수 있다.
O(n) + O(n) = 2O(n)
그러나 만일 올바르게 사용하면, 크기 순위에 대한 논의는 유효할 것이다. 알고리즘 분석에 대한 것은 이 장의 뒷부분에서 확인하게 될 것이다.
함수는 다음과 같이 순서쌍들의 집합으로 표현될 수 있으며,
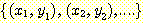
여기서  는 해당 함수의 정의역의 원소이고,
는 해당 함수의 정의역의 원소이고, 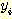 는 치역의 대응값이 된다. 이와 같이 순서 쌍들의 집합으로 함수를 표현하기
위해서는 각
는 치역의 대응값이 된다. 이와 같이 순서 쌍들의 집합으로 함수를 표현하기
위해서는 각  가 이 집합 내에서 순서쌍의 첫 번째 위치에 최대 한 번만 나타나야 한다. 이러한
조건이 만족되지 않는 경우에는 이 집합을 함수라 할 수 없으며, 이를 관계라 한다.
관계는 함수를 보다 일반화한 개념으로서 함수에서는 정의역의 각 원소는 정확히
치역의 한 원소와 대응이 되지만, 관계에서는 치역의 여러 원소들이 대응될 수 있다.
가 이 집합 내에서 순서쌍의 첫 번째 위치에 최대 한 번만 나타나야 한다. 이러한
조건이 만족되지 않는 경우에는 이 집합을 함수라 할 수 없으며, 이를 관계라 한다.
관계는 함수를 보다 일반화한 개념으로서 함수에서는 정의역의 각 원소는 정확히
치역의 한 원소와 대응이 되지만, 관계에서는 치역의 여러 원소들이 대응될 수 있다.
관계의 한 종류로 동치 관계 (equivalence relation) 를 들 수 잇는데 이는 등가 (equality, identity) 의 개념을 일반화한 개념이다. 하나의 순서쌍 (x, y) 가 동치 관계임을 표시하기 위해 다음과 같이 표기한다.
x ≡ y
여기서 ≡ 로 표기되는 관계는 다음과 같은 세 가지 성질을 만족하는 경우 동치 관계라 한다 : 반사성 (reflexivity rule)
모든 x 에 대해, x ≡ x
대칭성 (symmetry rule)
x ≡ y 이면 y ≡ x 이다.
전이성 (transitivity rule)
x ≡ y 이고 y ≡ z 이면, x ≡ z 이다.
예제 4
다음과 같은 음이 아닌 정수 집합에서의 관계를 생각해 보자.
x ≡ y
이고 오직 그럴 때에만
x mod 3 = y mod 3
이 관계에서 2 ≡ 5, 12 ≡ 0, 0 ≡ 36 등이 성립함을 알 수 있다. 이 관계는 반사성, 대칭성, 전이성 등이 모두 명백하게 성립하므로 동치 관계가 됨을 알 수 있다.
그래프란 두 개의 유한 집합, 즉 정점 (vertex)
들의 집합 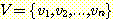 과 간선 (edge) 들의 집합
과 간선 (edge) 들의 집합  으로 이루어지는 구조를 말한다. 여기서 각 간선은 집합 V 에 있는 정점들의
쌍이며, 예를 들어, 간선
으로 이루어지는 구조를 말한다. 여기서 각 간선은 집합 V 에 있는 정점들의
쌍이며, 예를 들어, 간선
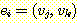
는 정점 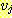 로부터 정점
로부터 정점 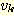 로의 간선이 된다. 이 경우 간선
로의 간선이 된다. 이 경우 간선 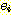 는
는 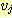 를 기준으로 했을 때는 진출 간선 (outgoing edge) 이라 하며,
를 기준으로 했을 때는 진출 간선 (outgoing edge) 이라 하며, 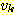 를 기준으로 했을 때는 진입 간선 (incoming edge) 이라 한다. 이와 같은 구조는
각 간선에 방향 (예를 들어,
를 기준으로 했을 때는 진입 간선 (incoming edge) 이라 한다. 이와 같은 구조는
각 간선에 방향 (예를 들어, 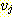 로부터
로부터 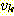 로) 을 지정하므로 유향 그래프 (directed graph, digraph) 라 한다. 그래프를
구성하는 요소, 즉 정점이나 간선에 라벨 (label) 을 지정할 수 있으며, 이러한 그래프를
라벨 그래프 (labeled graph) 라 한다. 이러한 라벨은 특별한 이름이나 또는 다른
정보일 수도 있다.
로) 을 지정하므로 유향 그래프 (directed graph, digraph) 라 한다. 그래프를
구성하는 요소, 즉 정점이나 간선에 라벨 (label) 을 지정할 수 있으며, 이러한 그래프를
라벨 그래프 (labeled graph) 라 한다. 이러한 라벨은 특별한 이름이나 또는 다른
정보일 수도 있다.
그래프는 다이어그램으로 편리하게 도식화할 수
있다. 여기서 정점은 원으로, 그리고 간선은 두 정점들을 잇는 화살로 표현된다.
예를 들어, 정점들의 집합이  이고 간선들의 집합이
이고 간선들의 집합이 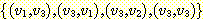 인 그래프는 그림 1 과 같이 그려질 수 있다.
인 그래프는 그림 1 과 같이 그려질 수 있다.
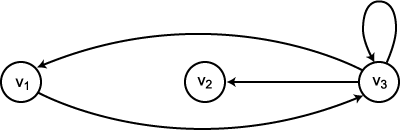
그림 1
일반적으로  과 같이 표현되는 간선들의 순서열을
과 같이 표현되는 간선들의 순서열을 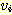 로부터
로부터  으로의 보행 (walk) 이라 하며, 보행의 길이 (length) 는 보행의 시작 정점으로부터
마지막 정점까지 지나게 되는 간선들의 수이다. 어느 간선도 중복하여 지나지 않는
보행을 경로 (path) 라 하며, 또한 어느 정점도 중복하여 지나지 않는 경로를 단순
경로 (simple path) 라 한다. 정점
으로의 보행 (walk) 이라 하며, 보행의 길이 (length) 는 보행의 시작 정점으로부터
마지막 정점까지 지나게 되는 간선들의 수이다. 어느 간선도 중복하여 지나지 않는
보행을 경로 (path) 라 하며, 또한 어느 정점도 중복하여 지나지 않는 경로를 단순
경로 (simple path) 라 한다. 정점 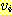 로부터 어느 간선도 중복하여 지나지 않고 자신에게로 돌아오는 보행을
로부터 어느 간선도 중복하여 지나지 않고 자신에게로 돌아오는 보행을 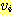 를 기지 (base) 로 하는 사이클 (cycle) 이라 한다. 한 사이클에서 기지 정점
외의 어느 정점도 중복하여 지나지 않는 경우 이를 단순 사이클 (simple cycle) 이라
한다. 그림 1 에서
를 기지 (base) 로 하는 사이클 (cycle) 이라 한다. 한 사이클에서 기지 정점
외의 어느 정점도 중복하여 지나지 않는 경우 이를 단순 사이클 (simple cycle) 이라
한다. 그림 1 에서 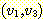 ,
,  는 정점
는 정점 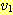 으로부터 정점
으로부터 정점 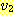 로의 단순 경로이다. 또한, 이 그림에서
로의 단순 경로이다. 또한, 이 그림에서  은 사이클이지만, 단순 사이클은 아니다. 그래프의 간선에 라벨을 지정하는 경우
보행의 라벨 (label of a walk) 이라는 개념을 생각할 수 있으며, 이는 경로를 지나는
동안 경유하게 되는 간선 라벨들의 순서열이 된다. 마지막으로, 한 정점에서 자기자신으로의
간선을 루프 (loop) 라 한다.
은 사이클이지만, 단순 사이클은 아니다. 그래프의 간선에 라벨을 지정하는 경우
보행의 라벨 (label of a walk) 이라는 개념을 생각할 수 있으며, 이는 경로를 지나는
동안 경유하게 되는 간선 라벨들의 순서열이 된다. 마지막으로, 한 정점에서 자기자신으로의
간선을 루프 (loop) 라 한다.
때에 따라서는 두 개의 정점간에 존재하는 모든
단순 경로 (또는 하나의 정점을 기지로 하는 모든 단순 사이클) 를 찾아내는 알고리즘이
필요할 경우가 있다. 효율성을 고려하지 않는다면 이를 위해 다음과 같은 명백한
알고리즘을 사용할 수 있다. 우선 주어진 정점 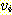 에서 시작하여 모든 진출 간선들, 즉
에서 시작하여 모든 진출 간선들, 즉 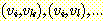 을 나열한다. 현재 정점
을 나열한다. 현재 정점 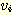 에서 시작한 길이가 1 인 모든 경로들이 정해진다. 다음으로 이렇게 도달한 정점
에서 시작한 길이가 1 인 모든 경로들이 정해진다. 다음으로 이렇게 도달한 정점
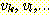 에 대해, 다시 진출 간선들을 나열하되 이미 한 번 경유한 정점은 다시 경유하지
않도록 제외한다. 이 과정이 끝나면 정점
에 대해, 다시 진출 간선들을 나열하되 이미 한 번 경유한 정점은 다시 경유하지
않도록 제외한다. 이 과정이 끝나면 정점 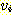 에서 시작하는 길이가 2 인 단순 경로가 모두 정해진다. 이 과정을 모든 경로를
얻을 때까지 반복한다. 정점들의 수가 단지 유한 개이기 때문에, 결국에는 정점
에서 시작하는 길이가 2 인 단순 경로가 모두 정해진다. 이 과정을 모든 경로를
얻을 때까지 반복한다. 정점들의 수가 단지 유한 개이기 때문에, 결국에는 정점 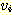 에서 시작하는 모든 단순 경로를 나열하게 된다. 이들 경로로부터 원하는 정점까지의
단순 경로들을 선정할 수 있다.
에서 시작하는 모든 단순 경로를 나열하게 된다. 이들 경로로부터 원하는 정점까지의
단순 경로들을 선정할 수 있다.
트리 (tree) 란 그래프의 한 종류이다. 트리는
사이클을 갖지 않고, 루트 (root) 라 불리는 특별한 하나의 정점을 가지는 유향 그래프이다.
이 루트로부터는 다른 모든 노드 각각으로 정확히 하나의 경로만이 존재하여야 한다.
이 정의는 트리의 루트는 진입 간선을 갖지 않음을 의미하고, 또한 트리에는 진출
간선을 갖지 않는 정점들이 존재함을 의미한다. 이들 정점들을 트리의 리프들 (leaves)
이라 한다. 트리에서 임의의 정점 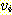 로부터
로부터 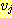 로의 간선이 존재하는 경우
로의 간선이 존재하는 경우 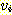 를
를 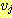 의 부모 (parent) 라 하고,
의 부모 (parent) 라 하고, 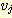 를
를 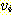 의 자식 (child) 이라 한다. 트리에서 한 정점의 레벨 (level) 이란 루트로부터
그 노드까지의 간선의 개수를 의미하며, 트리의 높이 (height) 란 해당 트리의 정점들
중 가장 큰 레벨을 갖는 정점의 레벨을 의미한다. 이러한 용어들은 그림 2 에 예시되어
있다.
의 자식 (child) 이라 한다. 트리에서 한 정점의 레벨 (level) 이란 루트로부터
그 노드까지의 간선의 개수를 의미하며, 트리의 높이 (height) 란 해당 트리의 정점들
중 가장 큰 레벨을 갖는 정점의 레벨을 의미한다. 이러한 용어들은 그림 2 에 예시되어
있다.
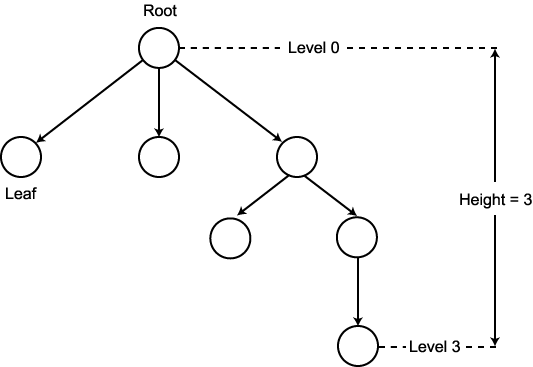
그림 2
때에 따라서는 트리의 각 레벨에 있는 노드들에 대해 순서를 부여하는 경우가 있으며, 이러한 경우의 트리를 순서 트리 (ordered trees) 라 한다.
그래프와 트리에 대한 보다 구체적인 사항들은 이산 수학에 대한 대부분의 서적에서 찾아볼 수 있다.
이 책을 읽기 위하여 필요로 하는 중요한 요구조건은 증명과정을 이해하는 능력이다. 수학적인 논의에서, 이미 인정된 연역 추론들이 사용된다. 많은 증명들은 단순히 그러한 연역 추론 단계들의 순서열이다. 아주 많이 사용되는 증명 기법으로는 귀납법 (proof by induction) 과 귀류법 (proof by contradiction) 등 두 가지가 있으며 다음은 이들에 대해 간단히 살펴보기로 한다.
귀납법이란 몇 개의 특정 사례 (instance) 가 참
(true) 이라는 사실들로부터 여러 문장들이 참임을 추론해 내는 기법을 말한다. 참임을
증명하고자 하는 문장들의 순서열 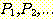 이 있다고 하자. 또한, 다음이 성립한다고 하자.
이 있다고 하자. 또한, 다음이 성립한다고 하자.
1. 임의의 k(k ≥ 1)
에 대해 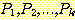 는 참이다.
는 참이다.
2. n ≥ k 인 모든 n
에 대해서 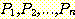 이 참인 사실이
이 참인 사실이 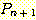 가 참임을 의미하도록 하는 문제
가 참임을 의미하도록 하는 문제
이 순서열에 있는 모든 문장이 참임을 보이기 위하여 귀납법을 사용할 수 있게 되었다.
귀납법에 의한 증명에서, 다음과 같은 주장을 할
수 있다 : 조건 1 로부터 문장들 중 첫 k 개 문장들이 참임을 알 수 있으며, 이에
조건 2 에 의하여 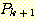 이 참임을 알 수 있게 된다. 따라서 우리는 문장들 중 첫 k + 1 개 문장들이
참임을 알 수 있으며, 이에 조건 2 를 다시 적용하면 또다시
이 참임을 알 수 있게 된다. 따라서 우리는 문장들 중 첫 k + 1 개 문장들이
참임을 알 수 있으며, 이에 조건 2 를 다시 적용하면 또다시 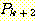 가 참임을 주장할 수 있게 된다. 계속해서 나머지도 참임을 주장할 수 있다.
이 과정이 분명하기 때문에 이러한 주장을 명백하게 계속 반복할 필요가 없다. 이러한
일련의 추론 과정은 어느 문장까지라도 연장될 수 있으며, 결국 모든 문장들이 참이
됨을 보이게 되는 것이다.
가 참임을 주장할 수 있게 된다. 계속해서 나머지도 참임을 주장할 수 있다.
이 과정이 분명하기 때문에 이러한 주장을 명백하게 계속 반복할 필요가 없다. 이러한
일련의 추론 과정은 어느 문장까지라도 연장될 수 있으며, 결국 모든 문장들이 참이
됨을 보이게 되는 것이다.
여기서 시작하는 문장들, 즉 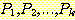 ㄹ,ㄹ 귀납법의 기저 (basis) 라 하며, 문장
ㄹ,ㄹ 귀납법의 기저 (basis) 라 하며, 문장 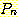 을
을 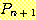 로 연결시키는 단계를 귀납 단계 (inductive step) 라 한다. 귀납 단계는
로 연결시키는 단계를 귀납 단계 (inductive step) 라 한다. 귀납 단계는 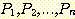 이 참이라는 귀납 가정 (inductive assumption) 에 의하여 일반적으로 쉽게 된다.
형식적인 귀납 논증에서는 이와 같은 세 부분들을 모두 명백하게 보여야 한다.
이 참이라는 귀납 가정 (inductive assumption) 에 의하여 일반적으로 쉽게 된다.
형식적인 귀납 논증에서는 이와 같은 세 부분들을 모두 명백하게 보여야 한다.
예제 5
이진 트리는 어떤 부모 노드도 셋 이상의 자식
노드를 가질 수 없는 트리를 말한다. 높이가 n 인 이진 트리의 리프 노드의 총
개수가 최대 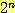 임을 증명해 보자.
임을 증명해 보자.
증명 : 높이가 n 인 이진 트리의 리프 노드의 최대 개수를 l(n) 이라 하면, 우리는 다음을 증명하면 된다.
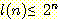
기저 : 높이가 0 인 이진 트리에 루트 외에
다른 노드가 존재할 수 없으므로, 즉 최대 한 개의 리프 노드만을 갖게 되므로,
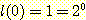 임은 명확하다.
임은 명확하다.
귀납 가정 : i = 0 , 1, ..., n 에 대해  임을 가정한다.
임을 가정한다.
귀납 단계 : 높이가 n 인 이진 트리로부터 높이가 n + 1 인 이진 트리를 만들어 내기 위해서 높이가 n 인 트리의 리프 노드들 각각에 대해 최대 두 개씩의 리프 노드를 추가로 생성할 수 있다. 따라서 다음이 성립한다.
l(n + 1) =2l(n)
여기에 귀납 가정을 적용하면 다음을 얻을 수 있다.
l(n + 1) ≤ 2 ×
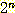 =
= 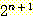
따라서, n + 1 인 경우에도 위 사실이 증명되었으며, n 은 임의의 수일 수 있으므로 위 문장은 모든 n 에 대해 참이 된다. ■
우리는 이 책에서 증명의 끝을 표시하기 위하여 심볼 ■ 을 사용하기로 한다.
예제 6
다음을 증명해 보자.
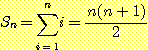 (4)
(4)
우선 우리는 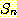 의 정의로부터 다음을 알 수 있다.
의 정의로부터 다음을 알 수 있다.
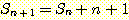
다음으로 윗식 (4) 가 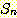 에 대해 성립한다는 귀납 가정을 하면 다음이 성립하게 된다
에 대해 성립한다는 귀납 가정을 하면 다음이 성립하게 된다
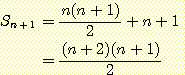
따라서, 식 (3) 는 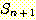 에 대해 성립하며, 이로써 귀납 단계가 완성된다. 식 (4) 는 n = 1 인 경우에도
명백하게 성립하므로 기저도 성립한 것이며, 결국 식 (4) 를 모든 n 에 대해서
증명한 것이 된다.
에 대해 성립하며, 이로써 귀납 단계가 완성된다. 식 (4) 는 n = 1 인 경우에도
명백하게 성립하므로 기저도 성립한 것이며, 결국 식 (4) 를 모든 n 에 대해서
증명한 것이 된다.
예제 6 에서 기저나 귀납 가정, 귀납 단계를 확인하는 데 있어서 약간 덜 형식적 (formal) 인 형태로 기술하였지만, 필수적으로 언급되어야 할 사항들은 모두 기술하였다. 앞으로의 논의가 지나치게 형식적이 되는 것을 피하기 위하여 예제 6 에서 따른 형태의 서술 방법을 주로 사용할 것이다. 만일 독자들이 증명을 이해하거나 구성하는 데 있어 어려움이 있다면 예제 5 에서 서술한 것처럼 보다 형식적이고 명확한 방법을 사용하기 바란다.
귀납적 추론 (inductive reasoning) 은 이해하기 어려울 수 있지만, 귀납법과 프로그래밍에서 사용되는 순환 (재귀, recursion) 개념간의 밀접한 연관성을 알 수 있게 해준다. 예를 들어, n 을 양의 정수라 할 때 임의의 함수 f(n) 에 대한 순환적 정의는 보통 두 부분으로 구성된다. 하나는 f(n + 1) 의 정의를 f(n), f(n - 1), ..., f(1) 으로 나타내는 부분이며, 이는 귀납법의 귀납 단계에 해당한다. 두 번째로는 순환으로부터 벗어나는 부분인데 이 부분에서는 f(1), f(2), ..., f(k) 를 비순환적으로 정의하게 된다. 이는 귀납법의 기저에 해당한다. 귀납법과 마찬가지로, 순환도 몇몇 초기값들과 문제 자체의 순환적 속성만 주어지면 문제의 모든 사례 (instance) 들에 대한 결론을 유도해 낼 수 있도록 한다.
귀류법은 다른 모든 경우가 성립되지 않을 때 자주 사용되는 또 다른 강력한 증명 기법이다. 어떤 문장 P 가 참임을 증명하고자 한다고 하자. 이때 우선 P 가 거짓이라 가정하고 그 가정으로 인해 어떤 사실들이 유도되는지를 확인한다. 만일, 이 가정으로 인해 틀린 결론이 유도된다면 처음의 가정이 잘못되었다고 판단할 수 있으며, 따라서 P 가 참이어야 한다고 결론짓게 되는 것이다. 다음은 고전적이면서도 멋진 귀류법의 예제이다.
예제 7
유리수 (rational number) 란 서로 소인 두
정수 n 과 m 의 분수로 표현되는 수를 말한다. 유리수가 아닌 실수를 무리수
(irrational number) 라 한다. 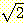 가 무리수임을 증명해 보자.
가 무리수임을 증명해 보자.
다른 모든 귀류법에서와 마찬가지로, 우선
우리가 증명하고자 하는 사실의 역을 가정하자. 여기서 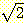 를 유리수라 가정하자. 따라서 아래와 같이 등식을 작성할 수 있다 :
를 유리수라 가정하자. 따라서 아래와 같이 등식을 작성할 수 있다 :
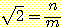 (5)
(5)
여기서 n 과 m 은 서로 소인 정수들이다. 식 (5) 를 다시 정리하면 다음과 같이 된다 :
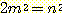
따라서, 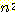 은 짝수이어야 한다. 이는 n 도 짝수이어야 함을 의미하고, 이에 따라 n = 2k
로 쓸 수 있으며, 이를 대입하면 다음과 같은 식을 얻게 된다 :
은 짝수이어야 한다. 이는 n 도 짝수이어야 함을 의미하고, 이에 따라 n = 2k
로 쓸 수 있으며, 이를 대입하면 다음과 같은 식을 얻게 된다 :

따라서,

따라서, m 은 짝수이다. 그러나 이는 n 과
m 이 서로 소이어야 한다는 우리의 가정과 모순된다. 결국, 식 (5) 에서의 m
과 n 은 존재하지 않으며, 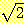 는 유리수가 아니다.
는 유리수가 아니다.
이 예제는 귀류법의 핵심적인 내용을 보여주고 있다. 어떤 가정을 함으로써 우리는 그 가정의 모순 또는 이미 거짓으로 알려진 사실에 도달하게 된다. 그 유도 과정의 모든 단계가 논리적으로 틀림이 없다면, 우리는 초기 가정이 잘못되었음을 결론짓게 되는 것이다.
1. 집합 S 의
크기에 대한 귀납법을 사용하여 집합 S 가 유한 집합이면  임을 증명하라.
임을 증명하라.
2. 집합 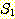 과
과 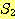 가 유한 집합이고,
가 유한 집합이고,  이고,
이고,  일 때 다음을 증명하라.
일 때 다음을 증명하라.
3. 집합 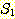 과
과 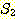 가 유한 집합이면,
가 유한 집합이면, 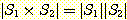 임을 증명하라.
임을 증명하라.
4. 아래와 같이 정의된 두 집합 사이의 관계가 동치 관계임을 증명하라.
 이고 오직 그럴 때에만
이고 오직 그럴 때에만 
5. 식 (2) 와 식 (3), 즉 DeMorgan 의 법칙을 증명하라.
6. 경우에 따라서는 합집합과 교집합 연산 기호를 합산 기호인 Σ 와 유사한 형태로 사용하기도 한다. 이를 합집합에 대해서는 다음과 같이 정의하며, 교집합에 대해서도 비슷하게 정의한다.
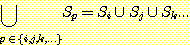
이 표기법을 사용하여, 일반적인 DeMorgan 의 법칙을 다음과 같이 기술할 수 있다 :
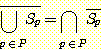
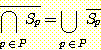
집합 P 가 유한 집합일 때 이 등식들을 증명하라.
7. 다음을 증명하라.

8. 다음을 증명하라.
 이고 오직 그럴 때에만
이고 오직 그럴 때에만 
9. 다음을 증명하라.
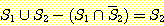
10. 다음을 증명하라.
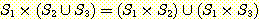
11. 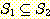 이면,
이면, 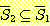 임을 증명하라.
임을 증명하라.
12. 두 집합 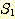 과
과 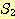 에 대해 다음을 만족하기 위한 필요충분 조건을 제시하라.
에 대해 다음을 만족하기 위한 필요충분 조건을 제시하라.
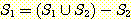
13. f(n) = O(g (n)) 이고 g(n) = O(f (n)) 이면, f(n) = θ(g (n)) 임을 증명하라.
14.  이지만
이지만 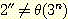 임을 증명하라.
임을 증명하라.
15. 다음의 크기 순위에 대한 결과가 성립함을 증명하라.
(a)
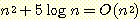
(b)
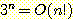
(c)
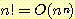
16. f(n) = O(g (n)) 이고 g(n) = O(h (n)) 이면 f(n) = O(h (n)) 임을 증명하라.
17.  이고
이고  이면 다음이 성립함을 증명하라.
이면 다음이 성립함을 증명하라.
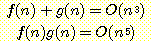
18. 연습문제 17 에서, g(n) / f(n) = O(n) 도 성립하는가?
19. 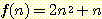 과
과  이라 하자. 다음의 주장에서 무엇이 잘못되었는가?
이라 하자. 다음의 주장에서 무엇이 잘못되었는가?
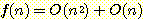
따라서
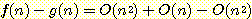
이다. 그러므로,
f(n) - g(n) = O(n)
이다.
20. 정점들의
집합이  이고 간선들의 집합이
이고 간선들의 집합이  인 그래프를 그림으로 그려보아라. 또한 이 그래프에서
인 그래프를 그림으로 그려보아라. 또한 이 그래프에서 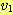 을 기지로 하는 사이클들을 모두 열거하라.
을 기지로 하는 사이클들을 모두 열거하라.
21. 그래프
G = (V, E) 에 대해 다음 주장을 증명하라 : 이 그래프의 정점들 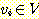 와
와  같에 보행이 존재하면, 이 두 정점간에는 길이가. |V| - 1 이하인 경로가 반드시
존재한다.
같에 보행이 존재하면, 이 두 정점간에는 길이가. |V| - 1 이하인 경로가 반드시
존재한다.
22. 어느 두
정점 사이에도 최대 하나의 간선이 존재하는 그래프에 대해 이 그래프에 n 개의 정점이
존재할 경우 간선의 최대 개수는 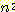 임을 증명하라.
임을 증명하라.
23. 다음의 식을 증명하라.
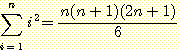
24. 다음을 증명하라.
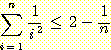
25. 모든 n
≥ 4 에 대해, 부등식  이 성립함을 보여라.
이 성립함을 보여라.
26. 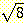 이 유리수가 아님을 증명하라.
이 유리수가 아님을 증명하라.
27.  가 무리수임을 증명하라.
가 무리수임을 증명하라.
28. 다음의 문장이 참인지 아닌지를 증명하라.
(a) 유리수와 무리수의 합은 무리수이어야 한다.
(b) 양수인 두 무리수의 합은 무리수이어야 한다.
(c) 유리수와 무리수의 곱은 무리수이어야 한다.
29. 모든 양의 정수는 소수 (prime number) 들의 곱으로 나타낼 수 있음을 증명하라.
30. 모든 소수들의 집합이 무한 집합임을 증명하라.
31. 소수 쌍 (prime pair) 은 차이가 2 인 두 개의 소수들로 구성된다. 소수 쌍들은 여러 개 있다. 예를 들어, 11 과 13, 17 과 19, 등등. 소수 세 원소 쌍 (prime triplet) 은 모두가 소수인 세 개의 수들 n, n + 2, n + 4 로 구성된다. 소수 세 원소 쌍들은 오직 (1, 3, 5) 와 (3, 5, 7) 임을 증명하라.
이 책에서 다루는 세 가지 주요한 주제는 언어 (languages), 문법 (grammars), 그리고 오토마타 (automata) 등이다. 우리는 이러한 개념들과 각 개념들간의 관계에 대해 깊이 공부하게 될 것이며, 본 절에서는 우선 각 용어들의 의미를 이해하고자 한다.
독자들은 이미 영어, 불어, 한국어 등과 같은 자연
언어 (natural languages) 의 개념과는 친숙할 것이다. 하지만, 우리들 대부분은 "언어"
라는
단어가 무엇을 의미하는지에 대해 정확히 설명하기 어려울 것이다. 사전에서는 언어를
어떤 생각이나 사실, 개념들을 표현할 수 있도록 해주는, 심볼들의 집합과 심볼을
다루는 규칙들의 집합을 수반하는, 시스템이라고 비형식적인 정의를 내리고 있다.
이러한 해설이 언어가 무엇인지에 대해 직관적인 이해를 도울 수는 있겠으나 형식
언어 (formal languages) 에 대한 공부를 위한 정의로서는 충분치 않으며, 우리에게는
언어라는 용어에 대한 좀더 정확한 정의가 필요하다.
우선 알파벳 (alphabet)
이라는
용어를 생각해 보자. 알파벳이란 하나 이상의 심볼들의 유한 집합이며, 보통 Σ 로
표현한다. 개개의 심볼들로부터 문자열 (string) 을 만들 수 있으며, 이는 주어진 알파벳에
속한 심볼들의 유한 길이의 순서열이다. 예를 들어, 알파벳이 Σ = {a, b} 라면, abab
나
aaabbba 등은 알파벳 Σ 에 대한 문자열이 되는 것이다. 앞으로 특별한 경우를 제외하고는
Σ 의 원소로 소문자 a, b, c, ... 등을 사용할 것이며, 문자열의 이름으로는 u,
v, w, ... 등을 사용할 것이다. 예를 들어, 다음은 이름이 w 인 문자열의 값이 abaaa
임을
나타낸다.
w = abaaa
두 문자열 w 와 v 의 접합 (concatenation) 은 문자열 w 의 오른쪽에 문자열 v 를 이어 부쳐서 얻어지는 문자열이다. 예를 들어,
w = a1a2...an
이고,
v = b1b2...bm
이면, w 와 v 의 접합 wv 는 다음과 같이 된다.
wv = a1a2...anb1b2...bm
문자열의 전도 (reverse) 는 문자열 내의 심볼들을 역순으로 배열함으로써 얻어진다. 예를 들어, w 가 위에서와 같은 문자열이라 할 때 이의 전도 wR 은 다음과 같이 된다.
wR = an...a2a1
문자열의 w 의 길이 (length) 는 해당 문자열 내의 심볼들의 개수이며, |w| 로 표기한다. 또한, 문자를 전혀 갖지 않는 문자열을 빈 문자열 (empty string) 이라 하며, λ 로 표기한다. 이에 따라 모든 문자열 w 에 대해 다음의 관계가 성립하게 된다 :
|λ| = 0
λw
= wλ = w
임의의 문자열 w 내에 존재하는 연속적인 문자들의 문자열을 부문자열 (substring) 이라 한다. 또한, 임의의 문자열 w 가 다음과 같이 구성되어 있는 경우
w = vu
부문자열 v 와 u 를 각각 문자열의 w 의 접두부
(prefix),
접미부 (suffix) 라 한다. 예를 들어, w = abbab 인 경우 {λ, a, ab, abb, abba, abbab}
는
w 의 모든 접두부들의 집합이며, bab 나 ab, b 등은 w 의 접미부가 된다.
길이
등과 같은 문자열 관련 간단한 성질들은 직관적이고, 아마도 면밀하게 조사할 필요가
없을 것이다. 예를 들어 v 와 u 를 문자열이라 했을 떼 이들의 접합의 길이는 각
문자열들의 길이의 합과 같게 되며, 다시 말해서 다음이 성립한다.
|uv|=|u|+|v| (6)
비록 이러한 관계를 명확히 알 수 있지만, 이를 정확하게 하고 증명할 수 있게 하는 것은 유용하다. 그렇게 할 수 있는 기술은 더욱 복잡한 상황에서 매우 중요하다.
예제 8
임의의 문자열 u 와 v 에 대해 식 (6) 이 성립함을 보여라. 이를 증명하기 위해, 우선 문자열의 길이에 대한 정의가 필요하다. 우리는 문자열의 길이를 다음과 같이 순환적인 형식으로 정의한다. 모든 a ∈ Σ 와 Σ 에 대한 임의의 문자열 w 에 대해,
|a| = 1
|wa| = |w| + 1
이 정의는 단일 심볼의 길이는 1 이고, 문자열에 하나의 문자를 덧붙일 때마다 길이가 1 씩 증가하게 된다는 직관적인 이해를 형식적으로 기술한 것이다. 이 형식적인 정의를 가지고 식 (6) 을 귀납법으로 증명한다.
정의에 의하여, 식 (6) 은 길이가 1 인 모든 문자열 v 와 임의의 길이의 문자열 u 에 대해 성립하게 되며, 이는 기저가 성립되었음을 의미한다. 귀납 가정 단계에서는 임의의 길이의 문자열 u 와 길이가 1, 2, ..., n 인 문자열 v 에 대해 식 (6) 이 성립한다고 가정한다. 이제 길이가 n + 1 인 문자열 v 에 대해 v = wa 라 하면 다음이 성립하게 된다.
|v| = |w| + 1
|uv| = |uwa| = |uw| + 1
귀납 가정에 의해서 (w 는 길이가 n 이므로)
|uw| = |u| + |w|
이고, 따라서
|uv| = |u| + |w| +1 = |u| + |v|
이 성립한다.
결국, 식 (6) 은 모든 문자열 u 와 길이가 n + 1 이하인 모든 문자열 v 에 대해 성립하게 되며, 이로써 증명이 완성된다.
문자열 w 에 대해  은 문자열 w 를 n 번 반복하여 얻어지는 문자열을 의미한다. 이에 대한 특별한
경우로 모든 문자열 w 에 대해 다음을 정의한다.
은 문자열 w 를 n 번 반복하여 얻어지는 문자열을 의미한다. 이에 대한 특별한
경우로 모든 문자열 w 에 대해 다음을 정의한다.

또한, 임의의 알파벳 Σ 에 대해, Σ 에 속한 심볼들을 0 개 이상 접합하여 얻어지는 모든 문자열들의 집합을 Σ* 로 표시한다. Σ* 에는 항상 빈 문자열 λ 가 포함되며, Σ* 에서 λ 를 제외한 집합을 Σ+ 는 다음과 같이 정의된다 :
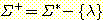
가정에 의하여 Σ 는 유한 집합이지만, Σ* 와 Σ+ 는 항상 무한 집합이 된다. 이는 이들 집합에 속하는 문자열들의 길이에 제한이 없기 때문이다.
언어란 일반적으로 Σ* 의 부분집합으로 정의되며, 임의의 언어 L 에 속하는 문자열을 언어 L 의 문장 (sentence) 이라 한다. 주어진 알파벳 Σ 에 대한 문자열들의 집합들은 모두 언어라 생각할 수 있기 때문에, 이 정의는 매우 광범위하다. 앞으로 특정 언어를 정의하는 또는 기술하는 방법에 대해 공부하게 될 것이며, 이에 따라 지금과 같은 광범위한 개념에 어느 정도의 언어 구조성을 가미할 수 있게 될 것이다. 우선 여기서 몇 가지 예를 보기로 하자.
예제 9
Σ = {a, b} 라 하면 Σ* 는 다음과 같이 된다.
Σ* = {λ, a, b, aa, ab, ba, bb, aaa, aab, ...}
이 경우 집합
{a, aa, aab}
는 Σ 에 대한 언어가 되며, 이 언어에 속하는 문장들의 개수가 유한하므로 이 언어를 유한 언어 (finite language) 라 부른다. 다음 집합 L 을 생각해 보자.

이 역시 Σ 에 대한 언어이다. 문자열 aabb 와 aaaabbbb 는 L 에 속하지만 문자열 abb 는 L 에 속하지 않는다. 이 언어 L 은 무한 언어 (infinite language) 이다. 우리가 관심을 갖게 되는 대부분의 언어들은 무한 언어이다.
언어들은 집합들이기 때문에, 두 언어에 대한 합집합, 교집합, 차집합 등이 정의될 수 있다. 또한 언어의 여집합은 Σ* 를 기준으로 정의된다. 즉 L 의 여집합은 다음과 같이 기술할 수 있다.
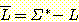
한 언어의 전도 (reverse of a language) 란 그 언어에 속하는 모든 문자열들의 전도들의 집합이다. 즉, 이 언어를 다음과 같이 기술할 수 있다.

두 언어 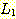 과
과 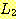 의 접합이란
의 접합이란 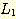 의 원소와
의 원소와 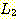 의 원소를 접합하여 얻어질 수 있는 모든 문자열들의 집합을 의미하며, 이를
다음과 같이 표현할 수 있다.
의 원소를 접합하여 얻어질 수 있는 모든 문자열들의 집합을 의미하며, 이를
다음과 같이 표현할 수 있다.
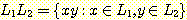
어떤 언어 L 을 n 번 접합하여 얻어지는 언어를
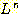 으로 표시하며, 이에 특별히 경우는 다음과 같다. 모든 언어 L 에 대하여,
으로 표시하며, 이에 특별히 경우는 다음과 같다. 모든 언어 L 에 대하여,


마지막으로, 특정 언어 L 에 대한 스타-폐포 (star-closure) 는 다음과 같이 정의되며,

양성폐포 (positive closure) 는 다음과 같이 정의된다.

예제 10
어떤 언어 L 이 다음과 같다면

언어 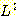 은 다음과 같이 된다.
은 다음과 같이 된다.

윗식에서 n 과 m 은 아무런 관계가 없음을
유의하라. 문자열 aabbaaabbb 는 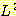 에 속한다.
에 속한다.
언어 L 의 전도는 다음과 같이 쉽게 표현될 수 있다.

하지만, 언어 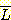 이나
이나 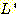 는 이와 같은 집합 표현방법으로 쉽게 표현하기 어렵다. 이를 포함한 복잡한
언어들에 대해 이와 같은 집합 형태로의 표현을 시도해 보면 집합 형태의 언어
표현방법이 갖는 제약점을 알 수 있을 것이다.
는 이와 같은 집합 표현방법으로 쉽게 표현하기 어렵다. 이를 포함한 복잡한
언어들에 대해 이와 같은 집합 형태로의 표현을 시도해 보면 집합 형태의 언어
표현방법이 갖는 제약점을 알 수 있을 것이다.
언어에 대해 수학적으로 연구하기 위하여 우리는
언어를 묘사하는 방법이 필요하다. 일상의 언어들은 부정확하고 (imprecise) 모호하기
(ambiguous) 때문에, 영어나 한국어 등의 자연 언어를 사용하여 비형식적으로 묘사하는
것은 적절하지 않다. 앞으로 우리는 서로 다른 상황에 적용할 수 있는 여러 가지의
언어 정의 기법들을 공부하게 될 것이다. 여기서는 일반적으로 많이 사용되는 강력한
기법인 문법에 대해 소개한다.
자연 언어의 하나인 영어에 대한 문법은 특정 문장이
적법하게 구성되었는가를 판단할 수 있게 해준다. 영문법의 대표적인 규칙 중의 하나는
"문장은 명사절(noun phrase)과 술부(predicate)로 구성된다"는 것이다.
이를 보다 정확하게 다음과 같이 표현할 수 있다.
<sentence> → <noun_phrase><predicate>
물론 실제 문장들을 다루는 데에 있어서 이 규칙만으로는 충분하지 않다. 위 규칙에서 새로 소개된 구조인 <noun_phrase>와 <predicate> 에 대한 정의가 마련되어야 한다. 이를 다음과 같이 정의하고,
<noun_phrase>
→ <article><noun>
<predicate>
→ <verb>
실제로 단어 "a" 와 "the"
를 <article> 에, "boy" 와 "dog" 을 <noun> 에,
그리고 "runs"와 "walks" 를 <verb> 에 대입시키면, "a
boy runs"와 "the dog walks" 등의 문장은 적절하게 구성되어 있는
문장인 것으로 판단할 수 있다. 만일 완전한 문법을 제공할 수만 있다면, 이론적으로
모든 적절한 문장들은 이와 같은 방식으로 설명될 수 있을 것이다.
이 예에서는
일반적인 개념에 대해 보다 간단한 개념들을 사용하여 정의하는 방법을 보여주고
있다. 즉, 최상위 단계의 개념에서, 여기서는 <sentence>, 시작하여 이를 계속
분해하면서 마지막으로 더 이상 분해할 수 없는 언어 구조들로 표현하는 것이다.
이러한 개념을 일반화하여 형식 문법(formal grammar)이라는 개념이 제시되는 것이다.
정의
1
문법 G 는 다음과 같은 네 원소 쌍 (quadruple) 으로 정의된다.
G = (V, T, S, P)
여기서 V 는 변수 (variable) 라 불리는 객체들의
유한 집합이다.
T 는 단말 심볼 (terminal symbol) 이라 불리는 객체들의 유한 집합이다.
S
는 V 의 특별한 원소이며, 시작 변수 (start variable) 라 불린다.
P 는 생성규칙
(production) 들의
유한 집합이다.
앞으로 V 와 T 는 공집합이 아니고, 서로 소 (disjoint) 임을 가정한다.
문법의 핵심은 생성규칙들이다 ; 생성규칙들은 해당 문법이 어떻게 하나의 문자열을 다른 문자열로 변환하는가를 규정하고, 이에 따라 주어진 문법에 대한 언어를 정의하게 되는 것이다. 앞으로 모든 생성규칙들은 다음의 형태를 갖는다고 가정한다.
x → y
여기서 x 는 (V∪T)+ 의 원소이고, y 는 (V∪T)* 의 원소이다. 생성규칙은 다음과 같은 방법으로 적용된다 : 다음과 같은 형태로 주어진 문자열 w 에 대하서
w = uxv
이 문자열에 생성규칙 x → y 가 적용될 수 있으며, x 를 y 로 대체하기 위하여 생성규칙을 사용하여 다음과 같은 문자열을 얻게 된다 :
z = uyv
이러한 과정을 다음과 같이 표현한다.
w ⇒ z
이에 대해 우리는 w 가 z 를 유도한다 (derive) 고 말하거나 또는 z 가 w 로부터 유도된다 라고 말한다. 문법의 생성규칙들을 임의 순서로 연속적으로 적용함으로써 계속 새로운 문자열들이 유도된다. 각 생성규칙들은 적용가능한 경우에 사용될 수 있고 또한 필요한 만큼 여러 번 적용될 수도 있다. 만일 다음과 같은 유도가 가능하다면,
w1 ⇒ w2 ⇒ … ⇒ wn
우리는 w1 이 wn 을 유도한다고 말하며, 이를 다음과 같이 표기한다.
w1 ![]() wn
wn
이 표현에서 * 는 w1 으로부터 wn 을 유도하기 위하여 명기되지 않은 수(0일 수도 있음)의 단계가 취해질 수 있음을 의미한다. 따라서
w ![]() w
w
도 항상 성립한다.
생성규칙들을 서로 다른
순서로 적용함으로써, 주어진 문법은 많은 문자열들을 생성할 수 있다. 이러한 모든
단말 문자열들의 집합을 주어진 문법에 의해 생성되는 또는 정의되는 언어라 한다.
정의
2
문법 G = (V, T, S, P) 가 주어지면 이에 의해 생성되는 언어 L(G) 는 다음과 같이 정의된다.
L(G) = {w ∈ T* : S
![]() w}
w}
만일 w ∈ L(G) 이면 다음과 같은 나열을
S ⇒ w1 ⇒ w2 ⇒ … ⇒ wn ⇒ w
문장 w 에 대한 유도 (derivation) 라 한다. 여기서 단말뿐 아니라 변수들로 구성된 문자열 S, w1, w2, ..., wn 등을 이 유도에서의 문장 형태 (sentential form) 라 한다.
다음 문법을 생각해 보자.
G = ({S}, {a, b}, S, P)
여기서 P 는 다음과 같이 주어진다.
S → aSb
S → λ
이 경우 다음 같은 유도가 가능하며,
S ⇒ aSb ⇒ aaSbb ⇒ aabb
따라서 다음과 같이 표기할 수 있다.
S ![]() aabb
aabb
문자열 aabb 는 G 에 의해 생성되는 언어에 속하는 문장이며, 반면에 aaSbb 는 문장 형태이다.
문법 G 가 언어 L(G) 를 완전하게 정의하지만, 주어진 문법으로부터 언어에 대한 명백한 묘사를 얻기는 그리 쉽지 않을 수도 있다. 그러나, 본 예제의 경우에는 문법 G 에 의해 생성되는 언어가 다음과 같이 묘사될 수 있음을 명확하게 짐작할 수 있으며 이를 증명하기도 쉽다.
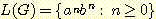
규칙 S → aSb 가 순환적임을 고려하면, 귀납법에 의한 증명을 할 수 있음을 쉽게 생각해 볼 수 있다. 우선 이 문법에 의해 생성되는 모든 문장 형태가 다음의 형태를 가짐을 보인다.
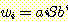 (7)
(7)
식 (7) 이 길이가 2i + 1 이하인 모든 문장
형태 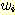 에 대해 성립한다고 가정하자. 이로부터 또 다른 (문장이 아닌) 문장 형태를
얻기 위해 적용할 수 있는 생성규칙은 S → aSb 뿐이다. 이를 적용하면 다음의
유도 과정이 이루어지며,
에 대해 성립한다고 가정하자. 이로부터 또 다른 (문장이 아닌) 문장 형태를
얻기 위해 적용할 수 있는 생성규칙은 S → aSb 뿐이다. 이를 적용하면 다음의
유도 과정이 이루어지며,
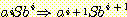
따라서 길이가 2i + 3 인 모든 문장 형태가 또한 식 (7) 의 형태임을 알 수 있다. 식 (7) 은 i = 1 일 때 명백하게 성립하며, 따라서 귀납법에 의해 모든 i 에 대해 성립한다. 마지막으로 문장을 얻기 위해서는 생성규칙 S → λ 를 적용해야 하며, 모든 가능한 유도과정은 다음뿐임을 알 수 있다.
S ![]()
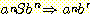
따라서 문법 G 는 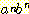 형태의 문자열들만을 유도하게 된다.
형태의 문자열들만을 유도하게 된다.
우리는 또한 이러한 형태의 문자열들이 모두 유도될 수 있음도 보여야 한다. 이는 아주 쉽다 ; 단순히 생성규칙 S → aSb 를 필요한 횟수만큼 적용하고, 마지막으로 생성규칙 S → λ 를 적용하면 된다.
예제
12
다음 언어를 생성시키는 문법을 만들어 보자.

이를 위해 예제 11 의 문법을 확장하는 방법을 사용할 수 있다. 필요한 것은 추가로 b 를 하나 더 생성하는 것이다. 이는 생성규칙 S → Ab 에다 다른 생성규칙들은 A 로 하여금 예제 11 에서의 언어를 생성하도록 함으로써 선택하면 된다. 이에 따라 문법 G = ({S, A}, {a, b}, S, P) 를 구성할 수 있고, 생성규칙들은 다음과 같다 :
S → Ab
A → aAb
A → λ
이 문법으로 몇몇 문장들을 생성해 봄으로써 원하는 언어가 생성될 수 있음을 독자들 스스로 확인하기 바란다.
위 예제들은 더 이상 언급이 필요 없을 정도로 쉬운 예제들이다. 하지만, 일반적으로 비형식적으로 묘사되는 언어에 대한 문법을 찾아내는 일이나 또는 주어진 문법에 의해 정의되는 언어에 대해 직관적인 특성을 찾아내는 일은 그리 쉽지 않다. 주어진 언어 L 이 특정 문법 G 에 의해 생성된다는 사실을 보이기 위해서는, 우선 (a) 모든 문자열 w ∈ L 이 문법 G 를 사용하여 시작 변수 S 로부터 유도될 수 있다는 사실과 (b) 이렇게 유도되는 모든 문자열들이 언어 L 에 속한다는 사실을 증명해야 한다.
예제
13
알파벳 Σ = {a, b} 라 하고 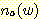 와
와  를 각각 문자열 w 에 있는 a 의 개수와 b 의 개수라 하자. 다음과 같은 생성규칙들을
가지는 문법 G 는
를 각각 문자열 w 에 있는 a 의 개수와 b 의 개수라 하자. 다음과 같은 생성규칙들을
가지는 문법 G 는
S → SS
S
→ λ
S → aSb
S
→ bSa
다음과 같은 언어를 생성하게 된다.
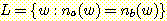
이 주장은 그리 명확하지는 않으며, 우리는 납득이 가는 논의를 제시하여야 한다.
우선, 문법 G 의 모든 문장 형태들에서 나타나는 a 와 b 의 개수가 같음은 쉽게 알 수 있다. 그 이유는 a 를 생성하는 생성규칙들, 즉 S → aSb 와 S → bSa 가 동시에 b 도 생성하기 때문이다. 따라서 L(G) 의 모든 원소들은 L 에도 속하게 됨을 알 수 있다. L 에 속하는 모든 원소들이 문법 G 에 의해 유도됨을 증명하는 것은 조금 더 어렵다.
우선 임의의 문자열 w ∈ L 이 가질 수 있는 여러 가지 형태를 고려하면서 이 문제를 전체적으로 살펴보기로 하자. 만일 문자열 w 가 a 로 시작하고 b 로 끝나는 문자열이라면 이는 다음의 형태를 가질 것이다.

여기서 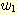 은 역시 L 에 속하는 문자열이 된다. 이러한 경우는 이 문자열에 대한 유도가
아래와 같이 시작되는 것으로 생각할 수 있다.
은 역시 L 에 속하는 문자열이 된다. 이러한 경우는 이 문자열에 대한 유도가
아래와 같이 시작되는 것으로 생각할 수 있다.
S ⇒ aSb
문자열 w 가 b 로 시작하고 a 로 끝나는 경우에도 비슷하게 생각해 볼 수 있을 것이다. 또한, L 에 속한 문자열 가운데 이러한 경우들 뿐만 아니라 같은 문자로 시작하고 끝나는 경우도 있을 수 있으며, 이러한 경우에 대해서도 고려해야 한다. 예를 들어, 문자열 aabbba 와 같은 경우가 그러하며, 이 때에는 이를 두 문자열 aabb 와 ba 의 두 문자열의 접합으로 볼 수 있고, 이들은 모두 L 에 속하는 문자열들이 된다. 일반적으로 언어 L 에 속하는 문자열들이 이와 같이 분리될 수 있을까? 정말 그렇다는 것을 확인해 보자. 주어진 문자열의 왼쪽에서부터 시작하여 a 를 만날 때에는 계산값에 +1 을 하고 b 를 만날 때에는 -1 을 한다고 가정해 보자 (물론 계산값은 처음에 0 에서 시작한다). 만일 문자열 w 가 a 로 시작하고 끝나는 경우 이 문자열이 L 에 속한다면 계산값은 왼쪽 끝 심볼 다음에서 +1 이 될 것이고 오른쪽 끝 심볼 직전에서는 -1 이 될 것이다. 따라서 이 계산값은 문자열 w 의 중간 어디에선가 0 이 되는 지점을 가져야 된다. 이는 문자열 w 가 다음의 형태를 갖게 됨을 의미한다.
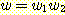
물론 여기서 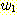 과
과 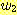 는 모두 L 에 속하는 문자열이다. 이 경우는 생성규칙 S → SS 로 해결될 수
있다.
는 모두 L 에 속하는 문자열이다. 이 경우는 생성규칙 S → SS 로 해결될 수
있다.
지금까지 L 에 속하는 모든 원소들이 문법
G 에 의해 유도됨을 직관적으로 언급하였으며, 이제 이에 대해 좀더 엄밀하게
귀납법을 사용하여 수학적으로 증명해 보도록 하자. |w| ≤ 2n 인 모든 문자열
w ∈ L 이 G 에 의해 유도된다고 가정하자. 이제 길이가 2n + 2 인 임의의 문자열
w ∈ L 을 선정한다. 이 문자열이  의 형태를 갖는다면,
의 형태를 갖는다면, 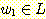 이 되고
이 되고 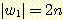 이 된다. 따라서 가정에 의해 다음이 성립한다.
이 된다. 따라서 가정에 의해 다음이 성립한다.
S ![]()
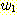
이에 따라
S ⇒ aSb ![]()
 = aSb
= aSb
이 가능해지며, 문자열 w 는 G 에 유도될 수
있다. 문자열 w 가 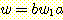 의 형태를 갖는 경우에도 성립함을 유사하게 증명할 수 있다.
의 형태를 갖는 경우에도 성립함을 유사하게 증명할 수 있다.
문자열 w 가 이러한 형태를 갖지 않는 경우,
즉 같은 심볼로 시작하고 끝나는 경우, 위에서 언급했던 계산하는 논의에 따라
이 문자열은 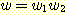 의 형태를 가져야 하며, 이때
의 형태를 가져야 하며, 이때 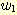 과
과 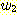 는 L 에 속하는 경우 문자열이고 길이는 모두 2n 이하가 된다. 따라서 다음의
유도과정이 가능함을 알 수 있다.
는 L 에 속하는 경우 문자열이고 길이는 모두 2n 이하가 된다. 따라서 다음의
유도과정이 가능함을 알 수 있다.
S ⇒ SS ![]()
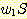
![]()
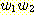 = w
= w
귀납 가정이 n = 1 인 경우에 명확하게 성립하므로, 증명의 기저 단계가 성립되었고, 따라서, 위 사실은 모든 n 에 대해서 성립하게 된다.
보통, 주어진 언어에 대하여 그 언어를 생성하는
문법이 여러 개 존재한다. 이들 문법은 서로 다르지만, 어떤 면으로는 동치 (equivalent)
이다. 우리는 두 개의 문법 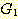 과
과  가 이 같은 언어를 생성하는 경우, 즉,
가 이 같은 언어를 생성하는 경우, 즉,

이면, 두 문법은 동치라고 한다. 앞으로 확인하게 되겠지만, 두 개의 문법이 동치임을 알아내는 것이 항상 쉬운 것은 아니다.
문법 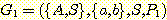 을 고려해 보자.
을 고려해 보자.  은 다음의 생성규칙들을 갖는다.
은 다음의 생성규칙들을 갖는다.
S → aAb|λ
A → aAb|λ
이 예제에서는 생성규칙들 중에서 좌변 (left-hand side) 이 같은 생성규칙들의 다른 우변들을 (right-hand sides) | 를 사용하여 분리하여 한 줄에 표기하는 간편한 약식 표기법을 소개하고 있다. 이 표기법에서 S → aAb|λ 는 S → aAb 와 S → λ 의 두 생성규칙을 나타낸다.
이 문법은 예제 11 에서 언급했던 문법 G 와 동치이다. 이들이 동치임은 다음을 증명함으로써 쉽게 보일 수 있다.

이 증명은 연습문제로 남겨둔다.
오토마타 (automaton) 란 디지털 컴퓨터에 대한 추상적 모델이며, 모든 오토마타들은 몇 가지 필수적인 기능들을 갖는다. 우선 오토마타는 입력을 받아들이는 장치를 갖는다. 입력은 주어진 알파벳에 대한 문자열이고 입력 파일 (input file) 에 저장되며, 오토마타는 이를 읽을 수는 있지만 변경할 수는 없다. 입력 파일은 셀 단위로 구분되며, 각 셀은 하나의 심볼을 저장할 수 있다. 입력 장치는 (EOF 조건을 검사함으로써) 입력 문자열의 마지막을 감지할 수 있다. 오토마타는 어떤 형태로든 출력을 생성할 수도 있다. 또한, 오토마타는 임시 기억장소 (storage) 를 가질 수 있다. 이 기억장소는 무한 개의 셀들로 구성되어 있으며, 각 셀은 주어진 알파벳 (이는 반드시 입력 알파벳과 같을 필요는 없다) 내의 한 심볼을 저장할 수 있다. 오토마타는 제어 장치 (control unit) 를 가진다. 이 제어 장치는 유한 개의 내부 상태 (internal state) 들 중 한 상태에 있을 수 있으며, 미리 정해진 규칙에 따라 상태를 바꿀 수 있다. 그림 3 은 일반적인 오토마타의 도식적인 표현을 보여준다.
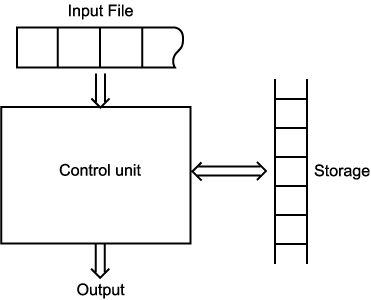
그림 3
오토마타는 이산 시간 (discrete time) 단위로 운영되는 것을 가정한다. 임의의 주어진 시간에 제어 장치는 어떤 내부 상태에 있게 되며, 입력 장치는 입력 파일의 특정 심볼을 읽어들인다. 다음 단계에서의 제어 장치의 내부 상태는 다음-상태 함수 (next-state function) 또는 전이 함수 (transition function) 에 의하여 결정된다. 이 전이 함수는 현재 상태, 현재의 입력 심볼, 현재 임시 기억장소에 저장된 내용 등에 따라 다음 상태를 결정한다. 한 단계에서 다음 단계로 전이가 발생하는 동안 출력이 생성되거나 임시 기억장소의 내용이 변화될 수 있다. 형상(configuration)이라는 용어는 제어 장치와 입력 파일, 그리고 임시 기억장소의 상태를 종합하여 언급할 때 사용한다. 오토마타가 한 형상으로부터 다음 형상으로 전이하는 것을 이동(move) 이라 한다.
이러한 일반적인 모델은 우리가 이 책에서 논의하는 모든 오토마타에 적용된다. 어떤 경우에도 유한-상태 제어장치 (finite-state control) 는 공통적이지만, 출력을 생성하는 방법이나 임시 기억장소와 관련한 성질은 오토마타마다 차이가 있다. 임시 기억장소의 성질은 각 형태의 오토마타에 대해 커다란 영향을 주게 된다.
이후부터는 오토마타를 결정적 오토마타 (deterministic automata) 와 비결정적 오토마타 (nondeterministic automata) 로 구분할 필요가 있다. 결정적 오토마타에서는 각 이동이 현재의 형상에 의해 유일하게 결정된다. 즉, 오토마타의 내부 상태, 입력, 그리고 임시 기억장소의 내용 등이 알려지면 그 오토마타의 이후 행동을 정확히 예측할 수 있게 되는 것이다. 비결정적 오토마타에서는 그렇지 않다. 비결정적 오토마타는 각 단계에서 여러 가지 이동이 가능하며, 따라서 정확히 하나의 가능한 행동만을 예측하기 보다는 가능한 행동들의 집합을 예측할 수 있을 뿐이다. 여러 형태의 오토마타에 대한 결정적 오토마타와 비결정적 오토마타간의 관계는 앞으로 우리가 공부하는 데 있어서 중요한 역할을 할 것이다.
출력이 단순히 "yes" 또는 "no" 로 제한되어 있는 오토마타를 인식기 (accepter) 라 한다. 입력 문자열이 주어졌을 때 인식기는 오로지 그 문자열을 승인 (accept) 하거나 거부 (reject) 하는 역할만을 수행한다. 이보다 더 일반적인 오토마타로 임의의 문자열을 출력으로 생성할 수 있는 오토마타를 변환기 (transducer) 라 부른다. 다음 절에서 간단한 변환기의 예들을 제시하겠지만, 이 장에서의 주된 관심은 인식기에 있다.
1. 모든 문자열
u 와 모든 n 에 대해  임을 사용하여 증명하라.
임을 사용하여 증명하라.
2. 위에서 비형식적으로 소개되었던 문자열의 전도는 다음과 같이 순환적인 규칙을 사용하여 보다 정확히 정의될 수 있다. 모든 a ∈ Σ, w ∈ Σ* 에 대해,
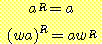
이를 이용하여, 모든 u, v ∈ Σ+ 에 대해, 다음이 성립함을 증명하라.

3. 모든 w ∈
Σ* 에 대해 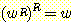 임을 증명하라.
임을 증명하라.
4. L = {ab, aa, baa} 라 하자. 다음 문자열들 중 어떤 것이 L* 에 속하는가 : abaabaaabaa, aaaabaaaa, baaaaabaaaab, baaaaabaa?
5. 예제 12 와 13 에서의 언어들을 고려해 보자. 어느 언어가 L = L* 를 만족하는가?
6.  를 만족하는 언어들이 존재하는가?
를 만족하는 언어들이 존재하는가?
7. 모든 언어
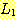 과
과 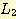 에 대해,
에 대해,
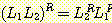
임을 증명하라.
8. 모든 언어
L 에 대해,  임을 증명하라.
임을 증명하라.
9. 다음의 주장이 옳은지 틀린지를 증명하라.
(a)
모든 언어 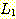 과
과 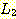 에 대해,
에 대해, 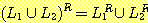
(b)
모든 언어 L 에 대해, 
10. 다음 언어를 생성하는 Σ = {a, b} 에 대한 문법을 찾아라.
(a) a 를 하나만 갖는 모든 문자열들
(b) a 를 하나 이상 갖는 모든 문자열들
(c) a 가 세 개 이하인 모든 문자열들
(d) a 가 세 개 이상인 모든 문자열들
각 경우에 대해, 당신이 제시한 문법이 정말로 지정된 언어를 생성함을 보여라.
11. 다음 생성규칙들을 갖는 문법에 의하여 생성되는 언어의 간단한 묘사를 제시하라.
S
→ aA
A → bS
S → λ
12. 다음 생성규칙들을 갖는 문법은 어떤 언어를 생성하는가?
S
→ Aa
A → B
B → Aa
13. 다음 각 언어들에 대해, 그 언어를 생성하는 문법을 찾아라.
(a)

(b)
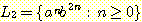
(c)

(d)
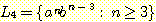
(e)
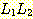
(f)
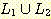
(g)
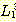
(h)
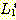
(i)
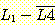
14. Σ = {a} 에 대한 다음 언어들을 생성하는 문법을 찾아라.
(a) L = {w : |w| mod 3 = 0}
(b) L = {w : |w| mod 3 > 0}
(c) L = {w : |w| mod 3 ≠ |w| mod 2}
(d) L = {w : |w| mod 3 ≥ |w| mod 2}]
15. 다음 언어를 생성하는 문법을 찾아라.

자신의 답에 대한 완벽한 근거를 제시하라.
16. 예제 13 의 표기법을 다음 언어들에 대한 문법을 찾아라. Σ = {a, b} 를 가정한다.
(a)

(b)
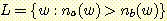
(c)
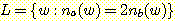
(d)
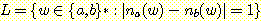
17. Σ = {a, b, c} 에 대해, 연습문제 16(a) 와 16(b) 를 답하라.
18. 예제 14
에서의 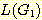 이 주어진 언어를 생성함을 증명하라.
이 주어진 언어를 생성함을 증명하라.
19. 다음 각 생성규칙들을 갖는 두 개의 문법이 동치인지를 보여라.
S → aSb|ab|λ
그리고
S → aAb|ab
A → aAb|λ
단, 두 문법 모두 S 가 시작 심볼이라 가정한다.
20. 문법 G = ({S}, {a, b}, S, P) 가 다음 생성규칙을 갖는다고 하자.
S → SS|SSS|aSb|bSa|λ
이 문법이 예제 13 에서 제시된 문법과 동치임을 보여라.
21. 지금까지는
모든 생성규칙들이 좌변에 하나의 변수만을 갖는 상대적으로 간단한 문법들의 예들만
제시되었다. 앞으로 우리가 확인하겠지만, 이러한 문법들은 매우 중요하다. 그러나
정의 1 은 더욱 일반적인 형태의 생성규칙도 허용한다.
다음과 같은 생성규칙을
갖는 문법 g = ({A, B, C, D, E, S}, {a}, S, P) 를 고려해 보자.
S
→ ABaC
Ba → aaB
BC → DC|E
aD → Da
AD → AB
aE
→ Ea
AE → λ
L(G) 에 속하는 문장을 세 개만 유도하라. 또한 이들로부터 L(G) 가 어떤 언어인지를 추측해 보아라.
우리가 형식 언어와 오토마타에 대한 추상적이고 수학적인 면들에 대해 많이 강조하고 있지만 이러한 개념은 컴퓨터 과학 분야에 널리 응용되고 있으며, 실제로 많은 특정 분야들을 연결하는 공통 주제이다. 본 절에서는 독자들이 이 책에서 공부하는 내용이 단순히 추상화 (abstraction) 들을 모아 놓은 것만이 아니라, 많은 중요한 실세계의 문제들에 대한 이해에 도움을 준다는 확신을 주기 위하여, 몇 가지 간단한 예제들을 소개하고자 한다.
형식 언어와 문법은 프로그래밍 언어와 관련해서 널리 사용된다. 프로그래밍을 하는 과정에서, 우리는 대부분의 경우 사용하는 언어에 대해 다소 직관적인 이해만을 바탕으로 작업하고 있다. 때때로, 사용하는 프로그래밍 언어에 대해 익숙하지 않은 기능을 사용하고자 할 때에는, 대부분의 프로그래밍 관련 서적에서 찾을 수 있는 해당 기능에 대한 구문 다이어그램 (syntax diagram) 등과 같은 자세한 설명을 참조하게 된다. 컴파일러를 개발할 때나 프로그램의 정확성 증명을 시도할 때에도, 거의 매 단계마다 그 언어에 대한 자세한 설명이 필요하게 되는 것이다. 프로그래밍 언어를 정확하게 정의하는 방법 가운데, 아마도 문법이 가장 널리 사용된다.
Pascal 이나 C 와 같은 대표적인 프로그래밍 언어를 묘사하는 문법은 매우 복잡하고 규모가 크다. 여기서는 간단한 예를 들기 위하여 이렇게 규모가 큰 언어의 일부분인 보다 작은 언어를 고려해 보자.
예제
15
Pascal 의 모든 적법한 식별자 (identifier) 들의 집합들은 하나의 언어이다. 비형식적으로 표현하면, 이 언어는 영문자로 시작하고 뒤이어 임의의 개수의 영문자나 숫자들이 오는 문자열들의 집합이다. 다음의 문법은 이러한 비형식적인 정의를 보다 명확하게 해준다.
<id> → <letter> <rest>
<rest>
→ <letter> <rest> | <digit> <rest> | λ
<letter>
→ a|b|ㆍㆍㆍ| z
<digit> → 0|1|ㆍㆍㆍ| 9
이 문법에서 <id>, <letter>, <digit>, <rest> 등은 변수이며, a, b, ..., z, 0, 1, ..., 9 등은 단 말들이다. 이를 이용하여 식별자 a0 를 유도하는 과정은 다음과 같다.
<id> ⇒ <letter> <rest>
⇒ a <rest>
⇒
a <digit> <rest>
⇒
a0 <rest>
⇒ a0
문법을 사용하여 프로그래밍 언어를 정의하는 것은 일반적이며 이는 매우 유용하다. 하지만, 편리한 또 다른 방법들이 있다. 예를 들어, 언어를 인식기를 사용하여 묘사할 수 있다. 이때 인식기가 승인하는 문자열들을 해당 언어에 속하는 것으로 한다. 이를 좀더 명확히 하기 위해서는 오토마타에 대한 좀더 형식적인 정의가 필요하다. 이는 곧 소개될 것이며, 당분간은 직관적인 방법으로 이에 대해 설명하기로 한다.
오토마타는 그래프로 표현될 수 있다. 여기서 정점들은 내부 상태들, 그리고 간선들은 상태간의 전이를 의미한다. 간선 위의 라벨은 해당 전이 중 발생하는 입력 또는 출력을 보여준다. 예를 들어, 그림 4 는 상태 1 에서 상태 2 로의 전이를 나타내고, 이 전이는 입력 심볼이 a 일 때 행해진다. 이러한 직관적인 이해를 가지고 Pascal 의 식별자들을 묘사하는 또 다른 방법을 살펴보자.
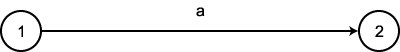
그림 4
예제
16
그림 5 는 Pascal 의 모든 식별자들을 승인하는 오토마타이다. 약간의 설명이 필요하다. 초기에 오토마타는 상태 1 에 놓인다고 가정한다 ; 우리는 이를 (다른 상태로부터가 아닌) 화살표를 그 상태에게로 그려서 표시한다. 항상 그렇듯이, 검사 대상 문자열은 왼쪽부터 오른쪽으로 한 번에 한 문자씩 읽혀진다. 첫 문자가 영문자일 경우에는 오토마타는 상태 2 로 전이하고 이후에 들어오는 영문자나 숫자들을 모두 받아들인다. 따라서 상태 2 는 이 인식기의 "yes" 상태를 나타낸다. 반대로, 첫 문자가 숫자일 경우에는 오토마타는 "no" 상태인 상태 3 으로 전이하고, 이후에 어떤 문자가 입력되든지 그 상태에 남아 있다. 여기서 우리는 영문자와 숫자 외의 어떤 다른 심볼도 입력되지 않음을 가정하고 있다.
주어진 프로그램을 한 언어로부터 다른 언어로 변환하는 컴파일러나 다른 번역기 (translator) 들은 위와 같은 예제에서 다룬 아이디어들을 널리 사용한다. 예제 15 에서처럼 프로그래밍 언어는 문법을 통해 명확히 정의되며, 문법과 오토마타는 프로그램 코드의 각 부분들이 프로그래밍 언어에서 규정한 조건들을 만족하면서 승인되는지를 결정하는 데에 기본적인 역할을 한다. 위 예제 16 은 이런 결정이 어떻게 이루어지는지에 대한 첫 힌트를 예시한 것이며, 이후의 예제들에서 이런 관찰을 좀더 확장할 것이다.
오토마타와 관련하여 또 하나의 중요한 응용 분야는
디지털 설계 분야이며, 이 분야에서는 변환기가 널리 사용되고 있다. 이 분야에 대해서는
이 책에서 광범위하게 다루지 않을 것이지만, 여기서 간단한 예제를 소개하려고 한다.
원칙적으로 모든 디지털 컴퓨터는 하나의 오토마타로 볼 수 있지만, 그러한 관점이
반드시 적절한 것만은 아니다. 컴퓨터의 주기억장치와 내부 레지스터들을 오토마타의
제어장치라 가정해 보자. 주기억장치와 내부 레지스터의 총 용량을 n 비트라 했을
때 이 오토마타는 모두 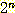 개의 내부 상태를 갖게 된다. 이때 n 의 값이 작다 하더라도 상태의 수는 다루기가
불가능할 정도로 굉장히 커지게 된다. 그러나 우리가 아주 더 작은 단위를 살펴보면,
이런 경우에 오토마타 이론이 유용한 설계 도구가 된다.
개의 내부 상태를 갖게 된다. 이때 n 의 값이 작다 하더라도 상태의 수는 다루기가
불가능할 정도로 굉장히 커지게 된다. 그러나 우리가 아주 더 작은 단위를 살펴보면,
이런 경우에 오토마타 이론이 유용한 설계 도구가 된다.
이진 가산기 (binary adder) 는 범용 컴퓨터 시스템의 주요한 부분들 중의 하나이다. 이러한 가산기는 수를 표현하는 두 개의 비트열 (bit string) 을 받아서 그들의 합을 출력으로 생성한다. 문제를 간단히 하기 위해서 양의 정수만을 대상으로 한다고 가정하고 다음과 같이 표현되는 비트열이

정수값
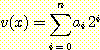
을 나타낸다고 가정한다. 이는 일반적인 이진수 표현의 역순이다.
순차 가산기 (serial adder) 는 이러한 두
개의 수  과
과  을 왼쪽에서부터 비트 단위로 처리한다. 각 비트의 합산은 합에 대한 비트와
다음 위치로 전해질 캐리 비트를 생성한다. 이 과정은 이진 가산 테이블 (그림
6) 과 같이 요약된다.
을 왼쪽에서부터 비트 단위로 처리한다. 각 비트의 합산은 합에 대한 비트와
다음 위치로 전해질 캐리 비트를 생성한다. 이 과정은 이진 가산 테이블 (그림
6) 과 같이 요약된다.
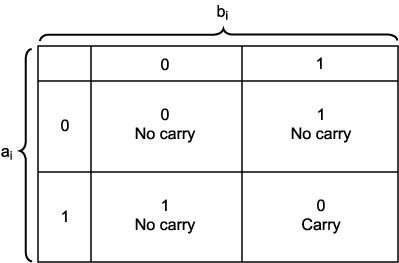
그림 6

그림 7
우리가 컴퓨터를 처음 배웠을 때 보았던 것과 같은 블록 다이어그램이 그림 7 에서 주어진다. 이 그림에서 네모 박스가 가산기이며, 두 비트를 입력받아 합산 비트와 캐리 비트를 출력한다. 이 다이어그램이 가산기가 어떤 일을 하는지에 대해서는 보여주고 있으나 이의 내부적인 처리 과정에 대해서는 설명하고 있지 않다. 오토마타 (여기서는 변환기) 는 이러한 내부 처리 과정을 명확하게 해줄 수 있다.
변환기로의 입력은 비트 쌍 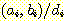 형태의 라벨을 붙인다. 한 단계에서 다음 단계로 전달되는 캐리 비트는 "carry"
와 "no carry" 로 표현되는 두 개의 내부 상태를 통해서 오토마타가
기억하고 있게 된다. 초기에는 오토마타가 "no carry" 상태에 있게
되며, 입력 비트 쌍 (1, 1) 을 만날 때까지 이 상태에 남아 있게 된다. 입력
비트 쌍 (1, 1) 을 만나게 되면 오토마타는 캐리를 생성하고, "carry"
상태로 전이된다. 캐리가 존재하면 다음 입력 비트 쌍이 읽혀질 때 합산에 고려된다.
그림 8 에서 순차 가산기에 대한 완전한 그래프를 보여주고 있다. 몇 가지 예를
적용해 봄으로써, 독자들 스스로 이 오토마타가 올바르게 작동하는 것을 확인하기
바란다.
형태의 라벨을 붙인다. 한 단계에서 다음 단계로 전달되는 캐리 비트는 "carry"
와 "no carry" 로 표현되는 두 개의 내부 상태를 통해서 오토마타가
기억하고 있게 된다. 초기에는 오토마타가 "no carry" 상태에 있게
되며, 입력 비트 쌍 (1, 1) 을 만날 때까지 이 상태에 남아 있게 된다. 입력
비트 쌍 (1, 1) 을 만나게 되면 오토마타는 캐리를 생성하고, "carry"
상태로 전이된다. 캐리가 존재하면 다음 입력 비트 쌍이 읽혀질 때 합산에 고려된다.
그림 8 에서 순차 가산기에 대한 완전한 그래프를 보여주고 있다. 몇 가지 예를
적용해 봄으로써, 독자들 스스로 이 오토마타가 올바르게 작동하는 것을 확인하기
바란다.
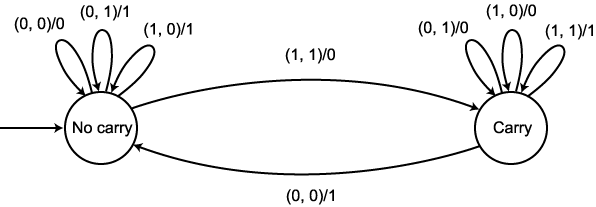
그림 8
이 예를 보면 오토마타가 디지털 회로에 대한 고수준의 기능적 묘사와 트랜지스터나 게이트, 플립플롭 등을 사용한 논리적인 구현간의 중간 단계의 역할을 함을 알 수 있다. 오토마타는 결정 논리 (decision logic) 를 명확하게 보여주면서도 명확한 수학적 조작을 가능하게 할 정도로 형식적이다. 이러한 이유로 디지털 설계 기법들은 오토마타 이론에서 나오는 개념들을 많이 사용하고 있다. 이에 관심 있는 독자들은 이 분야의 대표적인 책 (예를 들어, Kovahi 1978) 들을 참조하기 바란다.
1. C 에서의 정수 집합에 대한 문법을 제시하라.
2. C 에서의 정수에 대한 인식기를 설계하라.
3. C 에서의 모든 실수를 생성하는 문법을 제시하라.
4. 어떤 프로그래밍 언어에서, 식별자가 반드시 영문자로 시작해야 하고, 하나 이상 세 개 이하의 숫자를 가질 수 있으며, 영문자의 개수에는 제한이 없다고 하자. 이러한 식별자들의 집합을 생성하는 문법과 인식기를 제시하라.
5. Pascal 에서의 var 선언에 대한 문법을 제시하라.
6. 로마 숫자 표기법 (roman number system) 에서, 숫자들은 알파벳 {M, D, C, L, X, V, I} 에 대한 문자열로 표현된다. 이들 문자열이 적절히 구성된 로마 숫자인 경우에만 이를 인식하는 인식기를 설게하라. 문제를 간단히 하기 위하여 숫자 9 의 경우 이를 IX 로 표기하는 것과 같은 "빼기" 관계 ("subtraction" convention) 대신 VIIII 로 표기하는 "더하기" 관례 ("addition" convention) 을 사용한다고 가정하자.
7. 지금까지
우리는 오토마타가 이산 시간 단위의 프레임워크 기반으로 동작함을 가정하였지만,
이 관점은 우리들의 앞으로의 논의에서는 그리 크게 영향을 주지 않는다. 그러나
디지털 설계 분야에서는 시간이라는 개념을 특별하게 다루어야 한다.
컴퓨터 시스템에서는
서로 다른 구성요소들로부터 도착하는 신호 (signal) 들을 동기화하기 위하여 지연
회로 (delay circuitry) 를 필요로 한다. 단위-지연 변환기 (unit-delay transducer)
란 자신에게 들어오는 입력을 한 단위시간만큼 지연시켜 출력하는 기능을 하는 변환기이다.
즉, 변환기는 시간 t 에 하나의 심볼 a 를 입력받으면 이를 시간 t + 1 에 출력한다.
시간 t = 0 에는, 변환기는 아무 것도 출력하지 않는다. 결국, 변환기는 입력 문자열
 을 출력 문자열
을 출력 문자열 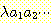 로 변환하는 것이다.
로 변환하는 것이다.
알파벳이 Σ = {a, b} 인 경우, 단위-지연 변환기가
어떻게 설계되어야 하는지를 보여주는 그래프를 그려라.
8. 자신에게
입력되는 문자열을 n-단위 시간만큼 지연시켜 출력하는 변환기를 n-단위 지연 변환기
(n-unit delay transducer) 라 한다. 즉, 이 변환기에는 입력 문자열  을 출력 문자열
을 출력 문자열  로 변환하는 것이며, 이 변환기는 처음 n 단위 시간 동안은 출력을 생성하지
않는다.
로 변환하는 것이며, 이 변환기는 처음 n 단위 시간 동안은 출력을 생성하지
않는다.
(a) 알파벳 Σ = {a, b} 에 대한 2-단위 지연 변환기를 구성하라.
(b)
n-단위 지연 변환기가 적어도  개의 상태를 가짐을 보여라.
개의 상태를 가짐을 보여라.
9. 양의 정수를 표현하는 이진 문자열에 대한 2 의 보수 (2's complement) 는 우선 각 비트들을 모두 보수로 바꾸고, 다음으로 이의 최하위 비트에 1 을 더하여 얻어진다. 주어진 이진 문자열을 2 의 보수로 변환하는 변환기를 설계하라. 이진수가 예제 17 에서와 같이 표현된다고 가정한다. 즉 하위 비트가 문자열의 왼쪽에 있다.
10. 이진수를 팔진수 (octal) 로 바꾸는 변환기를 설계하라. 예를 들어, 이진 문자열 001101110 에 대하여 156 이 출력되어야 한다.
11.  이 입력 비트 문자열이라 가정하자. 이 입력 문자열의 모든 3-비트 부문자열
(substring) 의 패리티 (parity) 를 계산하는 변환기를 설계하라. 이 변환기는 다음과
같은 출력을 생성하여야 한다.
이 입력 비트 문자열이라 가정하자. 이 입력 문자열의 모든 3-비트 부문자열
(substring) 의 패리티 (parity) 를 계산하는 변환기를 설계하라. 이 변환기는 다음과
같은 출력을 생성하여야 한다.
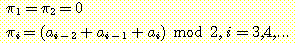
예를 들어, 입력 110111 에 대해서는 출력 000001 을 생성하여야 한다.
12. 비트 문자열
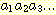 을 입력으로 받아, 매 세 개의 연속된 비트로 이루어진 이진 정수를 법 5 (modulo
5) 에 대하여 계산하는 변환기를 설계하라. 즉, 이 변환기는 다음을 만족하는 출력
을 입력으로 받아, 매 세 개의 연속된 비트로 이루어진 이진 정수를 법 5 (modulo
5) 에 대하여 계산하는 변환기를 설계하라. 즉, 이 변환기는 다음을 만족하는 출력
 을 생성하여야 한다.
을 생성하여야 한다.
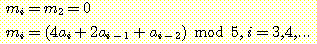
13. 일반적으로
디지털 컴퓨터는 모든 정보를, 특정 형태의 인코딩 기법을 사용하여, 비트 문자열로
표현한다. 예를 들어, 문자 정보는 잘 알려진 ASCII 코드를 사용하여 인코딩될 수
있다.
두 개의 알파벳 {a, b, c, d} 와 {0, 1} 에 대하여 다음과 같이 정의된
첫 번째 알파벳으로부터 두 번째 알파벳으로의 인코딩을 고려해 보자.
a → 00, b → 01, c → 10, d → 11
알파벳 {0, 1} 에 대한 문자열을 원래 메시지로 해독 (decode) 하는 변환기를 구성해 보라. 예를 들어, 입력 010011 은 출력 bad 로 변환되어야 한다.
14. 두 개의 양의 이진수 x 와 y 를 입력받아 출력으로 max (x, y) 를 생성하는 변환기를 설계하라.