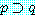
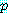
∴

타당성 증명 : 추론형식
기호논리학 : 소광희 지음, 경문사, 1985, Page 96~107
18. 변형 규칙
19. 추론형식과 대입규칙
1. 단순화규칙 (Rule of Simplification, Simp)
2. 교환규칙 (Rule of the Commutativity, Com)
3. 연언규칙 (Rule of Conjunction, Conj)
21. 선언적 삼단논법과 선언의 제 규칙
22. Modus Ponens 와 Modus Tollens
23. 가언적 삼단논법과 Dilemma
수많은 타당한 추론형식(valid argument form) 중 가장 기본이 되고 추론의 타당성 증명에 이용되는 형식을 설명하자.
(1) 서울은 한국의 수도이고 한국에서 가장 큰 도시이다.
(1)이 진이라면
(2) 서울은 한국의 수도이다.
도 진이다. 왜냐하면 (1)을 명제변수로 'pㆍq'라고 표시하면 (2)는 'p'로 표시되는데 'pㆍq'는 'p'와 'q'가 모두 진일 때만 진인 명제형식이기 때문이다. 즉 'pㆍq'가 진이라면 'p'도 반드시 진이어야 한다. 따라서 (1)→(2)는 다음과 같은 추론형식을 갖는 추론이다.
pㆍq
∴p
전제 'pㆍq'가 진이면 결론 'p'도 반드시 진이므로
이 추론형식은 타당한 추론형식이다. 따라서 이런 형식을 가진 모든 추론은 타당하다.
위의 추론은 그 한 예이다. 이 추론형식은 'pㆍq'가 진이라면 그것을 연언기호 왼쪽에
있는 명제 'p'로 단순화해도 진이라는 것을 의미하므로 이것을 단순화규칙(Rule of
Simplification)이라 부르고 'Simp'로 표시한다. 따라서 진인 명제로부터 단순화규칙에
의하여 도출된 명제는 그 진리성을 단순화 규칙으로부터 보증받는다고 하겠다.
한편
(1)이 진이라면 다음 명제도 진이라 여겨진다.
(3) 서울은 한국에서 가장 큰 도시이다.
(3)이 진인 것은 사실이지만, 그것을 (1)로부터 단순화규칙에 의하여 직접 도출할 수는 없다. 왜냐하면 단순화규칙은 연언(and) 의 왼쪽 명제의 타당성만을 보증하는데 (3)은 오른쪽 명제이기 때문이다.
그러나 (1)이 진이면 다음 명제도 진이다.
(4) 서울은 한국에서 가장 큰 도시이고 한국의 수도이다.
그러므로 (1)을 전제로 하고 (4)를 결론으로 하는 추론은 타당한 추론이다. (1)과 (4)를 명제변수로 표현하면 다음과 같은 타당한 추론형식을 얻는다.
pㆍq
∴qㆍp
이 추론형식은 연언(and, conjunction) 의 왼쪽 명제와 오른쪽 명제를 서로 교환하는 형식으로서, 전제가 진이면 결론도 반드시 진임을 의미한다. 이것을 연언의 교환규칙(Rule of the Commutativity of Conjunction)이라 하며 'Com'으로 표시한다. 따라서 진인 명제로부터 교환규칙에 의하여 도출된 명제의 진리성은 교환규칙이 보증해 준다고 하겠다. (3)은 (1)에서 직접 도출되는 것이 아니라 교환규칙에 의하여 (1)에서 (4)를 도출하고 다시 (4)를 단순화해서 얻은 명제이다.
다음의 두 명제가 각각 모두 진이라면,
(5) 서울은 한국의 수도이다.
(6) 서울은
한국에서 가장 큰 도시이다.
(5)와 (6)의 연언(and) 인 다음 명제도 반드시 진이다. 왜냐하면 연언은 두 원자명제가 모두 진이면 진이기 때문이다.
(7) 서울은 한국의 수도이고 한국에서 가장 큰 도시이다.
(5)와 (6)을 전제로 하고 (7)을 결론으로 하는 추론은 타당한 추론이며 다음의 추론형식을 갖는다.
p
q
∴ pㆍq
이것을 연언규칙(Rule of Conjunction)이라 부르며 'Conj'으로 표시한다.
이상의 제규칙들을 이용하여 다음 추론의 타당성을 증명해 보자.
(8) 연사는 열변(A)을 토하고 청중(B)은 졸고 있으나 시간(C)이 남았으니 연설(D)은 계속될 것이다. 그러므로 청중은 졸더라도 연설은 계속될 것이다.
(8)을 기호화하면
(9) ∴
BㆍD
1) (AㆍB)ㆍ(CㆍD) Pr
이다. 결론 'BㆍD'는 'B'와 'D'의 연언(and) 이므로 전제 '(AㆍB)ㆍ(CㆍD)'에서 'B'와 'D'를 분리시켜 각각 도출하고 이것들을 다시 'ㆍ'으로 결합하면 결론을 얻을 수 있다. 이러한 증명절차를 기호로 표시하면 다음과 같다.
(10) ∴
BㆍD
1) (AㆍB)ㆍ(CㆍD) Pr
2) AㆍB 1,
Simp
3) (CㆍD)ㆍ(AㆍB) 1,
Com
4) CㆍD 3,
Simp
5) BㆍA 2,
Com
6) DㆍC 4,
Com
7) B 5,
Simp
8) D 6,
Simp
9) ∴ BㆍD 7,
8, Conj
증명에 사용된 모든 명제들은 그 도출근거를 밝혀야 한다. 명제 1)의 오른쪽 끝에 있는 'Pr'는 그것이 전제임을 표시하고, 명제 2)의 '1, Simp'는 2)의 도출근거를 지시한다. 즉 명제 1)에서부터 단순화규칙(Simp)에 의하여 도출되었음을 의미한다. 명제 1)이 진이면 명제 2)도 진이라는 것을 단순화규칙이 보증한다. 이와 같은 방식으로 명제 3)은 1)로부터 교환규칙에 의하여 (1, Com), 4)는 3)을 단순화해서 (3, Simp), 5)는 2)를 교환해서 (2, Com), 6)은 4)를 교환해서 (4, Com), 7)은 5)를 단순화해서, 8)은 6)을 단순화해서, 9)는 연언규칙에 의하여 7)과 8)로부터 도출한 것이며 이때의 각 규칙들은 그것에 의해 도출된 명제들의 진리성을 보증해준다. 9)에서 '7, 8, Conj'은 '8, 7, Conj'으로 써서는 안 된다. '8, 7, Conj'으로써 도출된 명제는 'DㆍB'이지 'BㆍD'가 아니기 때문이다. 그러므로 연언규칙에 의하여 명제를 도출할 때는 'ㆍ'의 왼쪽과 오른쪽에 올 명제의 위치가 바뀌지 않도록 주의해야 한다. 그러나 8)과 7)을 연언해서도 다음과 같이 결론 'BㆍD'를 도출할 수는 있다.
10) DㆍB 8,
7, Conj
11) ∴ BㆍD 10,
Com
이처럼 증명의 방법은 여러 가지 있을 수 있겠으나 보다 효과적인 방법을 택해야 할 것이다.
가언명제를 전제로 하는 삼단론법을 전통적으로 가적 삼단론법(hypotheitical syllogism)이라 부르고 전가언적 삼단론법(wholly hypothetical syllogism)과 반 언적 삼단론법(partly hypothetical syllogism)의 2종류로 구분하여 왔다. 그러나 양자는 그 형식에 있어서 많은 차이가 있으므로 여기에서는 그 형식을 구별하기 위하여 소위 전가언적 삼단론법만을 가언적 삼단론법(§23)이라 부르고 반가언적 삼단론법은 Modus Ponens와 Modus Tollens로 나누어 설명하기로 한다.
'긍정식'이란 명칭은 Latin 어의 'Modus Ponens' (긍정의 식 ; modus=mode, ponere=to affirm)라는 말에서 유래한다. 가언명제인 제1전제의 전건을 정언명제인 제 2전제가 긍정함으로써 결론에서 후건을 긍정하는 추론형식이니 긍정적 긍정식(Modus Ponendo Ponens; the mode which, by affirming, affirms)이라고도 부른다. 기호로 표시하면 다음과 같다.
Modus Ponens(MP)
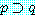
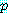
∴
이 추론형식의 타당성 여부는 '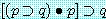 '의 진리표로써 밝혀진다.
'의 진리표로써 밝혀진다.
다음 진리표에서 보는 바와 같이,
'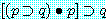 '는 Tautology이므로 Modus Ponens는 타당한 추론형식이다.
'는 Tautology이므로 Modus Ponens는 타당한 추론형식이다.
|
|
이런 형식을 가진 모든 추론은 Modus Ponens에 의하여 그 타당성을
보증받는다고 말할 수 있다. 따라서 우리는 추론의 타당성 증명에 이것을
이용할 수가 있다. |
(1) 흔히 어린이의 세계는 어른들의 세계와ㅏ 다르다(A)고 한다. 만일 그렇다면 어른들은 어린이의 세계를 이해(B)해야 할 것이다. 어른들이 어린이의 세계를 이해해야 한다면, 어린이의 생각을 무시(C)해서는 안된다. 어린이의 생각을 무시해서 안된다면 어린이를 인간(D)으로 인정해야 할 것이고 또 어린이의 세계가 어른들의 세계와 다르다면 어린이를 어린이의 입장(E)에서 대해야 할 것이다. 그러므로 어른들은 어린이를 인간으로 인정해야 하며 어린이의 입장에서 대해야 할 것이다.
기호로 표시하면 (1)은 다음과 같은 추론이다.
(2) ∴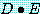
1) 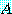 Pr
Pr
2) 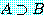 Pr
Pr
3) 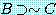 Pr
Pr
4) 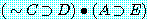 Pr
Pr
(2)의 증명은 다음 (3)과 같다.
|
(3) 1) |
∴ Pr |
부정식(Modus Tollens ; modus=mode, tollere=to deny; 부정의 식)은 후건을 부정함으로써(tollendo) 전건을 부정하는(tollens) 추론형식(modus)이므로 부정적 부정식(Modus Tollendo Tollens; the mode which, by denying, denies)이라고도 부른다. 그 형식은 다음의 왼쪽 식과 같고 그 타당성의 증명은 오른쪽 표와 같다.
|
Modus Ponens(MP) |
|
Modus Tollens를 이용해서 다음 추론을 증명해 보자.
(4) 김군이 산서용액(A)에 리트머스지를 넣으면 그것은 붉게(B) 될 것이고 알칼리성 용액(C)에 넣으면 푸르게(D) 변할 것이다. 그런데 김군은 산성용액이든가 알칼리성 용액에 넣을 것이다. 넣어 봤더니 그것은 푸르게 변하지 않았다. 그러므로 그것은 붉게 변하였을 것이다.
(4)를 기호화하여 증명하면 다음과 같다.
|
(5) 1) |
∴ Pr |
Modus Ponens와 Modus Tollens는 가끔 부당한 추론형식과 혼동되기 쉽다. 다음 예를 비교해 보자.
(6) 만일 이 물질이 우라늄이라면, 그것은 방사능을
가졌다. 그런데 이것은 우라늄이다. 그러므로 이것은 방사능을 가졌다.
(7)
만일 이 물질이 우라늄이라면, 이것은 방사능을 가졌다. 그런데 이 물질은 방사능을
가졌다. 그러므로 이것은 우라늄이다.
(6)과 (7)은 각각 다음과 같은 추론형식을 갖는다.
|
|
|
왼쪽 형식 즉 (6)의 형식은 전건을 긍정함으로써 후건을 긍정한 Modus Ponens이므로 (6)은 타당한 추론이다. 그러나 오른쪽 형식 즉 (7)의 형식은 후건을 긍정함으로써 전건을 긍정하는 형식이다. 이 형식은 타당한가? 이 추론의 진리표를 만들어 보자.
|
|
일부진이므로 부당하다는 것을 알 수 있다. 그러므로 (7)은 부당한 추론이다. 방사능을 가졌다고 해서(즉 후건을 긍정해도) 반드시 우라늄인 것은 아니다(즉 전건이 긍정되지는 않는다). 우라늄이 아니라 플루토늄일 수도 있지 않은가? |
그러므로 후건을 긍정함으로써 전건을 긍정하는 것은 잘못이다. 이것을 후건긍정의 오류(the fallacy of affirming the consequent)라고 부른다.
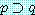
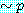
∴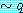
또 후건을 부정함으로써 전건을 부정하는 Modus Tollens는 타당한 형식이지만 위의 형식처럼 전건을 부정함으로써 후건을 부정하는 추론형식은 부당한 형식이다. 그 부당성은 왼쪽의 진리표로써 증명된다. 이것을 전건부정의 오류(the fallacy of denying the antecedent)라 한다. 다음과 같은 부당한 추론이 그 한 예이다.
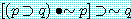
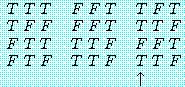
(8) 만일 그 동물이 고래라면, 그것은 포유동물이다. 그런데 그 동물은 고래가 아니다. 그러므로 그것은 포유동물이 아니다.
포유동물 중에는 고래만 있는 것이 아니다. 그러므로 고래가 아니라고해서 곧 포유동물이 아니라고 추론하는 것은 잘못이다.