
술어논리
(The Predicate Calculus)
인공지능-지능형 에이전트를 중심으로 : Nils J.Nilsson 저서, 최중민. 김준태. 심광섭. 장병탁 공역, 사이텍미디어, 2000 (원서 : Artificial Intelligence : A New Synthesis 1998), Page 255~267
명제논리는 표현상의 제약이 있다. 명제논리에서 아톰은 내부 구조를 가지고 전혀 가지고 있지 않은 스트링으로 본다. 장난감 블록에 관한 명제에서 ON_A_B 와 ON_B_C 는 전혀 다른 것이다. 이 책에서는 각 명제의 의미를 쉽게 알 수 있고, 기억하기에도 편리하도록 ON_A_B 나 ON_B_C 와 같은 의미 있는 단어로 표현하였지만, 이것을 각각 P124 나 Q23 으로 표현할 수도 있다.
실세계 (world) 에 대한 명제뿐만 아니라 실세계에 존재하는 객체 (object) 를 나타낼 수 있는 언어라면 더욱 유용할 것이다. 다시 말하자면 우리가 명제로 표현하는 객체와 우리가 표현하고자 하는 명제가 이름을 가지고 있는 언어가 필요하다. 장난감 블록세계 (이제부터는 이것을 간단히 "블록세계" 라고 부르기도 한다) 에서 ON_B_C ⊃ ¬CLEAR_C 와 같은 형태의 명제가 필요할지도 모른다. 여기서 CLEAR_C 는 블록 C 위에 아무 것도 없음을 의미한다. 여러 블록에 대하여 이러한 명제를 표현하려고 할때 각 블록에 대하여 별도의 명제로 표현하는 대신 x 와 y 가 임의의 블록을 나타낼 수 있는 변수라고 했을 때 On (x, y) ⊃ ¬Clear (y) 와 같이 표현하는 것이 훨씬 간결하다.
이 장에서는 이러한 장점을 지닌 일차 술어논리 (first-order predicate calculus) 라는 언어에 대하여 소개하고자 한다. 술어논리에서는 객체상수 (object constant), 관계상수 (relation constant), 함수상수 (function constant) 라는 기호가 사용된다. 이 언어는 실세계에 존재하는 사물과 실세계에 대한 명제를 표현하는 데 사용될 수 있다.
제한된 형태의 술어논리에 대하여 설명한 다음 나중에 이것을 확장하는 방식으로 술어논리에 대하여 설명하기로 한다. 이 책에서는 술어논리로 표현된 정형식은 Glypha 서체로 표현한다.
구성요소
예 : Aa, 125, 13B, Q, John, EiffelTower
예 : fatherOf¹, distanceBetween², times²
예 : B17³, Parent², Large¹, Clear¹, X11⁴
항
예 : fatherOf(John, Bill), times (4, plus (3, 6)), Sam
정형식
예 : Greaterthan (7, 2), P(A, B, C, D), Q
예 : [Greaterthan (7, 2) ∧ Lessthan (15, 4)] ∨ ¬Brother (John, Sam) ∨ P
(위의 예에서 나온 정형식은 어떤 의미를 생각하고 만든 것은 아니므로 각 정형식이 도대체 무슨 의미를 가지는가에 대해서는 고민할 필요가 없다.)
명제논리에서 두 개 이상의 논리곱 인자 (conjunct) 를 논리곱 (conjunction) 으로 연결하고 두 개 이상의 논리합 인자 (disjunct) 를 논리합 (disjunction) 으로 연결하는 등의 방법으로 확장한 것과 같은 방식으로 술어논리에서의 정형식도 확장할 수 있는데, 이 점에 대해서는 나중에 소개하기로 한다.
이제 우리는 명제뿐만 아니라 실세계에 존재하는 객체도 표현하는 데 사용할 수 있는 언어를 가지고 있다. 이 언어는 다음과 같은 특징을 지니고 있다.
술어논리로 표현된 식을 해석 (interpretation) 한다는 것은 객체상수를 객체로, 인자 수가 n 인 함수상수를 인자 수가 n 인 함수로, 인자 수가 n 인 관계상수를 인자 수가 n 인 관계로 사상하는 할당 (assignment) 을 말한다. 이러한 할당은 술어논리로 표현된 각 식에 대한 의미 (denotation) 라고 불린다. 객체상수의 할당을 한 객체들의 집합을 해석의 도메인 (domain) 이라고 한다.
아톰의 각 구성요소에 대한 해석이 주어졌다고 하자. 각 항 사이에 아톰이 의미하는 관계가 성립하는 경우에는 그 아톰은 참이 되며, 그렇지 않은 경우에는 거짓이 된다.
아톰이 아닌 정형식의 진리값은 명제논리에서 사용된 것과 같은 진리표에 의해 결정된다.
예 : A, B, C, Floor 로 이루어진 블록세계가 있다고 하자. 술어논리의 각 요소들을 실세계의 객체로 사상하는 할당을 하려고 한다. 그런데 우리는 실세계의 객체들 자체를 할당할 수 없기 때문에 실세계를 A, B, C, Floor 등과 같은 수학적인 구조로 생각한다 (실세계를 수학적인 구조로 생각한다는 것에 대하여 당황하지는 말자. 표현하고자 하는 실세계의 실체가 무엇이든 그것을 수학적인 구조로 간주하는 것은 아무런 문제가 되지 않는다).

그림 1 블록을 쌓아 놓은 모양
이러한 객체들 사이의 관계에 대해서도 생각해 보자. 예를 들어 On 이나 Clear 와 같은 관계를 생각해 보자. 이러한 관계는 n 튜플의 객체로 정의할 수 있다. 예를 들어 그림 1 과 같은 블록을 보면 이러한 블록세계에서 On 이란 관계는 <B, A>, <A, C>, <C, Floor> 란 객체의 쌍으로 주어진다. 마찬가지로 Clear 란 관계는 <B> 로 주어진다.
그래서 이 예의 경우 블록세계는 A, B, C, Floor 란 개체와 On, Clear 란 관계로 이루어진다. 이러한 블록세계를 술어논리로 나타내기 위하여 A, B, C, F1 란 객체상수와 On 이란 이항 관계상수와 Clear 란 단항 관계상수를 사용한다. 이와 같이 의미있는 단어를 사용하는 것은 기억하기에 편하도록 하기 위함이다. 어쩌면 G0045, G123 등과 같은 이름으로 관계상수를 나타내는 것이 교육적으로 더 좋을 수도 있다. 왜냐하면 술어논리에서 사용되는 각종 상수들은 이들 상수를 표현하는 데 사용된 단어의 사전적인 의미와 아무 상관이 없다는 것을 분명히 할 수 있기 때문이다.
표 1 술어논리와 실세계 사이의 사상
|
술어논리 |
실세계 |
|
A B C F1 On Clear |
A B C Floor On = {<B, A>, <A, C>, <C, Floor>} Clear = {<B>} |
표 1 은 여러 가지 가능한 해석 중 한 가지를 예로 든 것이다. 이러한 할당을 이용하여 다음과 같은 술어논리 정형식의 진리값을 결정할 수 있다.
<A, B> 는 On 이란 관계에 포함되지 않으므로 On (A, B) 는 거짓이다.
<B> 는 Clear 란 관계에 포함되므로 Clear (B) 는 참이다.
<C, Floor> 는 On 이란 관계에 포함되므로 On (C, F1) 은 참이다.
On (C, F1) 과 ¬On (A, B) 둘 다 참이므로 On (C, F1), ¬On (A, B) 도 참이다.
술어논리에서의 몇 가지 의미론적 개념에 대한 정의는 명제논리에서의 정의와 같다. 명제논리에서 정의한 것을 다시 살펴보자.
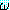 가 참이라면 Δ 은
가 참이라면 Δ 은 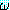 를 논리적으로 귀결한다 (entail) 고 하며 이것을
를 논리적으로 귀결한다 (entail) 고 하며 이것을  로 표기한다.
로 표기한다.술어논리식 (formula) 은 에이전트의 실세계에
대한 지식을 표현하는 데 사용될 수도 있다. 그러한 식들의 집합 Δ 를 에이전트의
지식베이스 (knowledge base) 라고 하며 식 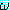 가 Δ 에 포함되어 있는 경우 우리는 에이전트가
가 Δ 에 포함되어 있는 경우 우리는 에이전트가 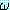 를 "안다" 고 말한다 (에이전트가
를 "안다" 고 말한다 (에이전트가 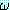 를 "믿는다" 고 하는 것이 보다 정확한 표현일 것이다).
를 "믿는다" 고 하는 것이 보다 정확한 표현일 것이다).
식의 집합으로 실세계의 지식을 표현한다고 하는 것이 어떤 의미가 있는지 좀 더 자세히 살펴보자. 예를 들어 다음과 같은 식은 블록세계에 대한 지식을 표현하고 있는가?
1. On (A, F1) ⊃ Clear (B)
2. Clear (B) ∧ Clear (C) ⊃ On (A, F1)
3. Clear (B) ∨ Clear (A)
4. Clear (B)
5. Clear (C)
윗식들을 만족하는 블록세계에 대한 해석, 즉 모델은 그다지 어렵지 않게 설정할 수 있다. 우리가 생각하고 있는 상황을 그림으로 나타내면 그림 2 와 같다. 이 그림의 각 경우에 대한 모델은 표 1 에서 보인 것과 같은 (객체에서 객체로의) 사상을 사용한다. 그러나 세 가지 모델에서 실세계의 관계상수에서 관계로의 사상은 다르다. 예를 들어, 그림 2 의 첫번째 상황에서 관계상수 Clear 는 Clear = {<C>, <B>} 라는 관계로 사상된다. 이와 같은 방법으로 나머지 두 상황에 대한 모델도 세울 수 있다.

그림 2 블록세계에서의 세 가지 상황
윗식에 대한 모델로서 위와 다른 것들도 있을 수 있다. 예를 들어 어떤 모델에서는 B 와 C 라는 별개의 술어논리 명칭이 실세계의 B 라는 하나의 객체를 나타내기도 한다. 또 다른 모델에서는 A, B, C 가 블록이 아니라 숫자를 나타내기도 한다.
이러한 대체 모델은 식들을 추가적으로 제공함으로써 제거될 수 있다. 예를 들어, 표 1 에서 주어진 것과 같이 객체상수에서 객체로의 할당을 가정하고 Clear(A) 라는 식을 추가함으로써 그림 2 에서 두 가지 모델을 제거할 수 있다. 명제논리에 대한 설명에서 언급한 바와 같이 식의 수가 많으면 많을수록 모델의 수는 줄어든다. 그러므로 식의 집합이 우리가 원하는 특정 실세계에 대한 "지식" 을 나타내도록 제한하려면 우리가 표현하고자 하는 실세계를 포함해야 할 뿐만 아니라, 우리가 표현하고자 하는 실세계가 아닌 것은 제외시킬 수 있을 정도로 충분한 식을 가지고 있어야 한다.
주어진 도메인의 모든 객체가 어떤 성질을 가지고 (또는 어떤 관계에 참여하고) 있음을 표현한다고 하자. 도메인의 크기가 유한한 경우에는 Clear(B1) ∧ Clear(B2) ∧ Clear(B3) ∧ Clear(B4) 와 같은 논리곱으로 표현할 수 있다. 그러나 도메인의 크기가 큰 경우에는 이러한 방식으로 표현하기란 번거로울 뿐만 아니라 도메인의 크기가 무한한 경우에는 이러한 방식으로 표현하는 것이 아예 불가능하다.
주어진 도메인에서 적어도 하나의 객체가 어떤 성질을 가지고 있음을 표현하려고 한다고 가정하자. 도메인의 크기가 유한한 경우에는 Clear(B1) ∨ Clear(B2) ∨ Clear(B3) ∨ Clear(B4) 와 같은 논리합으로 표현할 수 있다. 그러나 이 경우에도 역시 도메인의 크기가 크다든지 무한한 경우에는 위에서 언급한 것과 같은 문제가 발생한다.
이와 같은 표현상의 문제를 해결하기 위하여 도입된 것이 변수 기호 (varidable symbol) 와 한정사 기호 (quantifier symbol) 이다.
1. 변수 기호는 소문자로 이루어진 문자열로 표시하는 데 p, q, r, s, t, ..., p1, p2, ..., 등과 같이 주로 알파벳의 뒷부분에 나오는 문자들로 시작한다 (변수 기호나 함수 기호 모두 소문자로 표시하나 어떤 문자열이 변수 기호인지 함수 기호인지는 문맥에 따라 구분된다). 변수도 항의 일종이다. 그러므로 f(x, Bob, C17) 은 인자 수가 3 인 함수이다.
2. 한정사 기호는 ∀, ∃ 와 같은 부호로 나타내는데 전자는 전체 한정사 (universal quantifier) 라고 하며 후자는 존재 한정사 (existential quantifier) 라고 한다.
3. 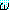 가 정형식을 나타내고 ξ 가 변수를 나타낸다면 (∀ξ)
가 정형식을 나타내고 ξ 가 변수를 나타낸다면 (∀ξ)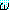 , (∃ξ)
, (∃ξ)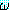 도 정형식이다. 여기서 ξ 는 한정을 받는 변수라고 하며
도 정형식이다. 여기서 ξ 는 한정을 받는 변수라고 하며 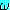 는 한정사의 한정 범위내에 있다고 말한다. ξ 는 변수를, Q 는 ∀ 또는 ∃ 를
나타낸다고 하자. (Qξ)
는 한정사의 한정 범위내에 있다고 말한다. ξ 는 변수를, Q 는 ∀ 또는 ∃ 를
나타낸다고 하자. (Qξ)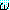 형태로 주어진 정형식에서
형태로 주어진 정형식에서 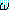 를 이루고 있는 항 중에는 ξ 라고 하는 변수가 포함되어 있는 경우가 보통이다.
를 이루고 있는 항 중에는 ξ 라고 하는 변수가 포함되어 있는 경우가 보통이다.
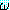 내의 모든 변수가 한정을 받는 경우 (Qξ)
내의 모든 변수가 한정을 받는 경우 (Qξ)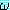 는 폐쇄식 (closed wff) 또는 폐쇄문 (closed sentence) 이라고 한다.
는 폐쇄식 (closed wff) 또는 폐쇄문 (closed sentence) 이라고 한다.
예 : (∀x) [P(x) ⊃ R(x)], (∃x) [P(x) ⊃ (∃y) [R(x, y) ⊃ S(f(x))]]
뒤에서 설명할 한정사의 의미론에 대하여 이해를
하면 (∀x) [(∀y)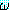 ] 와 (∀y) [(∀x)
] 와 (∀y) [(∀x)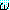 ] 이 같음을 보일 수 있을 것이다. 따라서 전체 한정사에 의해 한정을 받는 변수를
(∀x, y)
] 이 같음을 보일 수 있을 것이다. 따라서 전체 한정사에 의해 한정을 받는 변수를
(∀x, y)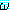 와 같이
와 같이 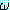 앞에 모아 둘 수도 있다. 이러한 식에서
앞에 모아 둘 수도 있다. 이러한 식에서 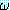 를 행렬 (matrix) 이라고 부른다. 존재 한정사의 경우에도 마찬가지이다. 그러나
전체 한정사와 존재 한정사가 동시에 나타난 경우에는 이들이 나타난 순서를 지켜야
한다. 따라서 (∀x) [(∃y)
를 행렬 (matrix) 이라고 부른다. 존재 한정사의 경우에도 마찬가지이다. 그러나
전체 한정사와 존재 한정사가 동시에 나타난 경우에는 이들이 나타난 순서를 지켜야
한다. 따라서 (∀x) [(∃y)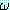 ] 는 (∃y) [(∀x)
] 는 (∃y) [(∀x)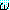 ] 와 다르다.
] 와 다르다.
정형식에서 한정사에 의해 한정을 받는 변수의
이름 자체에는 별다른 의미가 없으므로 어떤 변수를 다른 변수로 변경하더라도 정형식의
논리값은 변하지 않는다 (이것을 증명하려면 아래에서 설명할 한정사의 의미론에
대하여 이해를 해야 한다). 그러므로 (∀x)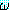 에서 모든 x 를 y 로 바꾸어 얻은 (∀y)
에서 모든 x 를 y 로 바꾸어 얻은 (∀y)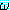 는 (∀x)
는 (∀x)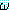 과 의미적으로 동등하다. 존재 한정사의 경우에도 마찬가지이다.
과 의미적으로 동등하다. 존재 한정사의 경우에도 마찬가지이다.
술어논리에서 변수를 한정함으로써 술어논리의 표현력을 높이듯이 관계나 함수를 나타내는 기호에 대해서도 한정할 수 있지 않을까 하는 의문을 가질 수도 있다. 그러나 여기서 다루고 있는 술어논리에서는 관계나 함수를 나타내는 기호에 대한 한정은 허용되지 않는다. 이와 같은 술어논리를 일차 술어논리라고 한다. 이차 혹은 고차 술어논리에서는 관계나 함수를 나타내는 기호에 대한 한정이 허용된다. 그러나 이러한 술어논리에서는 추론 방법이 매우 복잡하다.
주어진 도메인의 객체를 변수 ξ 에 할당하는 경우
모든 할당에 대하여 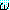 (ξ) 이 참값을 가질 때 (∀ξ)
(ξ) 이 참값을 가질 때 (∀ξ)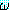 (ξ) 는 참값을 가진다고 한다.
(ξ) 는 참값을 가진다고 한다.
예 : 그림 2 와 같이 주어진 Clear 와 On 이 두 가지 해석을 가정하자. 각각의 해석에 대하여 (∀x) [On (x, C) ⊃ ¬Clear(C)] 의 진리값은 어떻게 되겠는가? 이것을 계산하기 위해 변수 x 를 A, B, C 또는 Floor 로 할당하고 각 해석에 대한 진리값을 알아본다. 예를 들어 변수 x 를 A 로 했을 때 On (x, C) ⊃ ¬Clear(C) 이 참값을 가지려면 <A, C> 가 관계 On 에 포함되지 않거나 <C> 가 관계 Clear 에 포함되지 않아야 한다. 사실 각 해석에서 <C> 는 관계 Clear 에 포함되지만 <A, C> 는 관계 On 에 포함되지 않으므로 변수 x 를 A 로 할당하면 주어진 식은 참값을 가지게 된다. 나머지 할당에 대한 진리값 계산은 각자가 해 보기 바란다.
주어진 도메인의 객체를 변수 ξ 에 할당할 때
적어도 하나 이상의 할당에 대하여 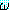 (ξ) 이 참값을 가지는 경우에 (∃ξ)
(ξ) 이 참값을 가지는 경우에 (∃ξ)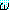 (ξ) 은 참값을 가진다고 한다.
(ξ) 은 참값을 가진다고 한다.
한정사에 대하여 드모르간의 법칙과 유사한 다음과 같은 동치 관계가 성립한다.
¬(∀ξ)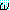 (ξ) ≡ (∃ξ)¬
(ξ) ≡ (∃ξ)¬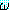 (ξ)
(ξ)
¬(∃ξ)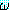 (ξ) ≡ (∀ξ)¬
(ξ) ≡ (∀ξ)¬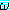 (ξ)
(ξ)
(∀ξ)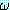 (ξ) ≡ (∀
(ξ) ≡ (∀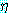 ξ)
ξ)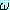 (
(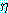 )
)
명제논리에서의 추론 규칙을 잘 확장하면 술어논리에서도 사용할 수 있다. 이러한 규칙으로는 모더스 포넌스 (modus ponens) 논리곱 (∧) 의 도입과 제거, 논리합 (∨) 의 도입과 제거, 부정 (¬) 제거, 논리융합 (resolution) 이 있다. 논리융합 규칙에 대한 일반화는 다음 장에서 다룰 것이다. 술어논리에서는 이들 규칙 외에 다음과 같은 중요한 추론 규칙도 포함되어 있다.
UI (Universal Instantiation, 전체 한정사 사례화)
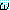 (ξ) 는 변수 ξ 를 가지는 임의의 정형식이고, α 는 임의의 상수 기호이며,
(ξ) 는 변수 ξ 를 가지는 임의의 정형식이고, α 는 임의의 상수 기호이며,
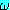 (α) 는
(α) 는 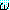 에서 ξ 를 α 로 대치한 것이라고 했을 때, (∀ξ)
에서 ξ 를 α 로 대치한 것이라고 했을 때, (∀ξ)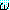 (ξ) 로부터
(ξ) 로부터 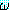 (α) 를 추론한다.
(α) 를 추론한다.
예 : (∀x)P(x, f(x), B) 로부터 P(A, f(A), B) 를 추론한다.
EG (Existential Generalization, 존재 한정사 일반화)
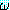 (α) 는 상수 기호 α 를 포함하고 있는 정형식이고
(α) 는 상수 기호 α 를 포함하고 있는 정형식이고 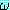 (ξ) 는
(ξ) 는 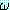 에서 모든 α 를 ξ 로 대치한 것이라고 했을 때
에서 모든 α 를 ξ 로 대치한 것이라고 했을 때 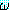 (α) 로부터 (∃ξ)
(α) 로부터 (∃ξ)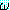 (ξ) 를 추론한다.
(ξ) 를 추론한다.
예 : (∀x) Q (A, g(A), x) 로부터 (∃y) Q (y, g(y), x) 를 추론한다.
UI 와 EG 둘 다 정당한 추론 규칙임을 보이는 것은 쉽다.
인공지능 분야에서 가장 큰 문제는 어떻게 말하느냐가 아니라 무엇을 말하느냐이다. 술어논리는 실세계에 대한 지식을 표현하고 추론하는 데 사용되는 언어에 지나지 않는다. 이렇게 표현된 지식은 뒤에서 설명할 논리적 연역 방법에 따라 이용된다.
실세계에 대한 지식을 표현하는 첫번째 단계는 그것을 객체, 함수, 관계로 개념화 (conceptualization) 하는 것이다. 실세계에 어떤 종류의 객체가 존재할 수 있는가에 대한 여러 가지 선택이 있을 수 있다. 우리가 원하는 대로 실세계를 자유롭게 개념화할 수 있지만 어떤 개념화가 다른 개념화보다 (항상 더 올바른 것이라는 의미는 아니지만) 더 유용할 수도 있다. 이러한 의미에서 개념화하는 이것을 수행하는 사람의 창의적인 능력을 요구한다.
두번째 단계에서는 객체, 함수, 관계를 수반하는 술어논리식을 만든다. 그리고 마지막으로 개념화하고자 하는 실세계에 의해 만족되는 정형식을 작성한다. 이러한 정형식은 다른 해석 (interpretation) 에 의해서도 만족될 수 있다. 그러나 이러한 점에 대해서는 신경을 쓸 필요는 없다. 다만 그러한 정형식들은 우리가 표현하고자 하는 실세계에 대한 지식 상태에서 볼 때 제외되어야 하는 해석에 의해 만족되지 않는다는 점에 대해서는 주의를 해야 한다.
실세계에 대하여 추론하고 실세계와 상호작용을 하는 에이전트를 설계할 때 실세계에 근거를 두고 개념화하는 것은 중요하다. 즉, 지식베이스에서 사용된 아톰 중 일부의 진리값은 실세계와 연결된 지각 작용 (perceptual mechanism) 에 의해 얻을 수 있어야 한다. 그러나 논리적인 방법으로 얻은 결론이 실세계와 관련이 있으려면 한다면 전체 구조는 인지에 근거를 두고 있어야 한다. 여기에 비하여 수학은 실세계에 근거를 둘 필요가 없다. 왜냐하면 수학에서 다루는 내용은 실세계에 대한 것이 아닐 수도 있기 때문이다.
인공지능 분야에서 술어논리를 사용하여 실세계에 대한 지식을 표현한 것은 John McCarthy [McCarthy 1958] 가 최초이다. [Guha & Lenat 1990, Lenat 1995, Lenat & Guha 1990] 에는 실세계에 대한 수백만 개의 상식을 표현하기 위한 대규모 프로젝트 (CYC 프로젝트) 에 대한 설명이 있다. [Nilsson 1991] 는 인공지능에서 논리학의 역할에 대하여 자세하게 설명하였다. [Genesereth & Nilsson 1987] 은 논리학 부분을 특히 강조한 인공지능 교재이다.
여기서는 실세계에 대한 지식을 개념화하는 과정을 예로 들어 설명하겠다. 사무실에서 짐꾸러미를 운반하는 에이전트를 설계한다고 가정하자. 우선 짐꾸러미의 성질을 나타내는 관계상수가 필요한데 이것을 Package(x) 로 나타내자. 다음엔 방 안에 있는 객체를 나타내는 관계상수가 필요한데 이것을 Inroom (x, y) 로 나타내자. 어떤 객체가 다른 객체보다 작다는 것을 나타내는 관계상수도 필요하다. 이러한 관계상수들을 이용하여 실세계에 대한 상황을 술어논리로 표현해 보자.
(∀x, y) {[Package (x) ∧ Package (y) ∧ Inroom (x, 27) ∧ Inroom (y, 28)] ⊃ Smaller (x, y)}
이 문장은 모호성 (ambiguity) 을 지니고 있다 (이러한 현상은 우리들이 일상적으로 사용하는 자연언어에서 발생한다). 따라서 이 문장의 의미는 다음과 같은 두 가지 식으로 표현할 수 있다 (두 식은 동치 관계가 아니다).
(∃y)(∀x) {[Package (x) ∧ Package
(y) ∧ Inroom (x, 27) ∧
Inroom
(y, 28)] ⊃ Smaller (x, y)}
(∀x)(∃y) {[Package (x) ∧ Package
(y) ∧ Inroom (x, 27) ∧
Inroom
(y, 28)] ⊃ Smaller (x, y)}
실세계에 대한 지식을 표현할 때 시간을 개념화해야 하는 경우도 있다. 예를 들어 "짐꾸러미 A 가 짐꾸러미 B 보다 먼저 도착하였다" 라는 문장을 생각해 보자. 이러한 문장을 개념화하려면 시간을 나타내는 객체와 이들 객체 사이의 순서를 나타내는 관계가 필요할 것이다. 어떤 객체의 도착시간을 나타내는 방법도 필요한데 이것을 Arrived (x, z) 로 나타내자. 여기서 x 는 도착한 객체를 나타내며 z 는 x 가 도착한 시간을 나타낸다. 이러한 관계상수를 이용하여 다음과 같은 표현이 가능하다.
(∃z1, z2) [Arrived (A, z1) ∧ Arrived (B, z2) ∧ Before (z1, z2)]
시간을 수반하는 개념화에 대한 자세한 설명은 18 장에서 다루기로 한다. 전산학 및 인공지능 분야에서 시간을 다루는 데 사용되어 온 것으로서 시간논리 (temporal logic) 란 것이 있다 [Emerson 1989, Shoham 1987].
개념화를 하는 도중 까다로운 문제가 수반되기도 한다. 예를 들어 "28 호실의 짐꾸러미에 우유가 2 리터 들어 있다." 라는 문장에서 "우유" 와 같은 소위 물질명사를 어떻게 다룰 것인가는 어려운 문제이다. 우유는 가령 "희다" 라는 성질을 가진 객체인가? 그렇다면 2 리터의 우유를 1 리터짜리 두 개로 나누면 이것을 (둘 다 흰) 두 개의 객체로 보아야 하는가 아니면 하나의 객체로 보아야 하는가? 이러한 의문점들은 현재도 연구가 계속되고 있는 분야 중의 하나이다.
이 책의 뒷부분에서는 상황이나 동작과 같은 무형물을 다루는 개념화도 객체로 취급하는 방법을 취할 것이며, "에이전트 A 는 짐꾸러미 B 가 28 호실에 있다는 것을 안다" 와 같이 한 에이전트가 다른 에이전트의 지식을 나타내도록 술어논리를 확장하는 것에 대해서도 소개할 것이다.
전술한 바와 같이 논리 문장 (logical sentence) 을 이용하여 지식을 표현하고 논리적 추론 절차를 이용하여 추론을 하는 것은 인공지능 분야에서 오랫동안 논란거리였다. [McDermott & Doyle 1980] 에서 이러한 논란에 대한 예들을 볼 수 있다. 이러한 논란은 [Tarski 1935 (Tarski, A., "Die Wahrheitsbegriff in den Formalisierten Sprachen," Studia Philosophica, 1:261-405, 1935.)] (영어판은 [Tarski 1956 (Tarski, A., Logic, Semantics, Metamathematics: Papers from 1923 to 1938, Oxford: Oxford University Press, 1956.)]) 의 논리언어 (logical language) 에 대한 정확한 의미론 (semantics) 과 (실세계에 대한 지식을 표현하는 데 필요하다고 보이는) 보다 유동적이고 문맥의존적인 의미 (meaning) 에 대한 개념 사이의 불일치와 관련이 있다.
타스키 의미론은 실세계의 개체를 객체상수와 연관시킨다. 다른 관점에서 소위 색인 함수적 (indexical functional) 표현의 필요성이 강조되기도 한다. Agre 와 Chapman [Agre & Chapman 1990 (Agre, P., and Chapman, D., "What Are Plans For?" Robotics and Autonomous Systems, 6:17-34, 1990. Also in [Maes 1990a (Maes, P. (ed.), Designing Autonomous Agents: Theory and Practice from Biology to Engineering and Back, Cambridge, MA: MIT Press, 1990.)]), p.21] 은 다음과 같이 말하고 있다.
전통적인 표현에서는 에이전트의 머리 속에 있는 기호와 객관적으로 개체화된 실세계 객체 사이의 "의미적" 일치를 가정하는 반면 우리들의 이론은 에이전트와 색인 함수적으로 개체화된 실세계 개체 사이의 인과 관계를 설명한다. 예를 들어 the-bee-I-am-chasing 은 Pengi 가 사용한 ([Agre & Chapman 1987 (Agre, P., and chapman, D., "Pengi: An Imple-mentation of a Theory of Activity," Proceedings of the Sixth National Conference on Artificial Intelligence (AAAI-87), pp.268-272, Menlo Park, CA: AAAI Press, 1987.)] 에 기술되어 있는) 개체들 중의 하나이다. 이 개체는 ("I" 라는) 에이전트와의 관계에 의해 정의되어 있다는 점에서 색인 개체화되어 있다.
그러나 다음 장에서 보듯이 많은 학자들은 인공지능을 표현하고 추론하는 데 (확장된) 논리 언어를 사용하였다.
[Enderton 1972 (Enderton, H., A Mathematical Introduction to Logic, New York: Academic Press, 1972.), Pospesel 1976 (Pospesel, H., Introduction to Logic: Predicate Logic, Englewood Cliffs, NJ: Prentice Hall, 1976.)] 은 논리에 대하여 다룬 두 권의 책인데 전자는 수학적으로 쓰여졌으며 후자는 평범하게 쓰여져 있다. 전체적인 개관에 대하여 알고 싶으면 [Barwise & Etchemendy 1993 (Barwise, J., and Etchemendy, J., The Language of First-Order Logic: Including the Macintosh Program~Tarski's World 4.0, Center for the Study of Language and Information (CSLI), Stanford, California, third revised and expanded edition, 1993.)] 을 참조하라. 이 책에는 예제 프로그램도 포함되어 있다.