
상황논리
(The Situation Calculus)
인공지능-지능형 에이전트를 중심으로 : Nils J.Nilsson 저서, 최중민. 김준태. 심광섭. 장병탁 공역, 사이텍미디어, 2000 (원서 : Artificial Intelligence : A New Synthesis 1998), Page 393~402
7 장에서 상태공간의 개념과 이 공간을 탐색하여 목표를 달성하기 위한 행동의 계획을 계산하는 방법에 대하여 소개하였다. 특히 7 장에서는 아이콘기반의 상태공간과 특징기반의 상태공간에 대한 탐색을 설명하였다. 이 장에서는 특징과 그들 사이의 제약 사항을 상세히 기술하는 언어를 이용하여 특징기반의 계획수립 방법을 좀 더 철저히 조사하고자 한다.
특징기반의 접근 방법을 이용하는 강점 중의 하나는 현재 해결해야 할 문제와 관계없거나 알려져 있지 않은 실세계의 상태에 대한 특성을 생략할 수 있다는 것이다. 이 점은 에이전트가 달성해야 할 목표조건을 에이전트의 행동을 이용하여 기술할 때 특히 중요하다. 만일 에이전트가 그림 1 과 같은 배치에서 출발하여 블록 B 위에 어떤 블록을 올려놓기 위한 계획을 수립한다고 하자 (이때 블록 B 위에는 어떤 블록이 와도 관계없고, 또한 블록 B 가 어디에 있는지도 관계없다고 하자). 이 목표는 간단하게 (∃x) On (x, B) 의 식으로 기술할 수 있다. 일반적으로 목표조건은 술어논리 (predicate calculus) 의 임의의 wff 를 가지고 기술될 수 있으며, 식으로 기술된 실세계 상태에 대해 목표가 만족되는지를 결정하기 위해, 그 식으로부터 목표 wff 를 증명할 수 있다.
이 장과 다음 장에서는 목표 wff 에 의해 표현되는 상태에 도달하기 위한 행동의 집합을 찾아내는 기법을 제시하고자 한다. 여기서는 상태와 행동에 대해 직접 추론을 하기 위해 술어논리의 도구를 이용한다. 모든 술어논리의 추론에서처럼 탐색은 여전히 필요하지만, 여기서는 실세계 상태의 모델의 공간에 대한 탐색이 아니라 논리 표현식의 공간에 대한 탐색을 하게 된다. 다음 장에서는 이와는 다른 대안으로, 연산자를 이용하여 상태 기술 (state description) 을 바꾸고, 탐색이 상태 기술의 공간에 대해 이루어지는 방법을 기술한다.
상황논리 (situation calculus) [McCarthy & Hayes 1969, Green 1969a] 는 상태, 행동 그리고 상태에 미치는 행동의 결과 등을 술어논리로 정형화시킨 것이다. 상태와 행동에 대한 지식은 일차 술어논리 (first-order predicate calculus) 의 식으로 표현되고, 연역 시스템 (deduction system) 을 이용하여 어떤 (목표) 특성을 만족시키는 상태가 존재하는가? 존재한다면 어떤 행동을 취하여 현재 상태를 그 상태로 변환시킬 수 있는가? 와 같은 질문을 하게 된다. 이 질의에 대한 대답이 바로 원하는 상태에 도달하기 위한 계획을 구성하게 된다. 상황논리는 초기의 AI 계획수립 시스템에서 주로 사용되었지만, 현재는 거의 사용되지 않고 있으며, 다음 장에서 논의할 방법들에게 대부분 자리를 내주었다. 하지만 상황논리의 형식 체계 (formalism) 는 행동의 결과를 포함하는 개념적 문제를 표출하고 명확히 하는 데 있어서 아직도 중요하다.
상황논리를 블록세계 예제를 이용하여 소개하고자 한다. 가령 그림 1 의 상태를 S0 이라고 하자. 일차 술어논리를 이용하면 S0 을 다음과 같은 식으로 기술할 수 있다.
On (B, A) ∧ On (A, C) ∧ On (C, F1) ∧ Clear (B) ∧ ㆍㆍㆍ

그림 1 블록의 배치
이 상태와 다른 상태들을 상황논리로 기술하기 위해서 이 책에서는 상태를 구체화시킨다 (reify). 즉, 상태를 실세계에 대한 개념화내에 존재하는 개체로 포함시킨다. 상태는 상수 기호 (S0, S1, S2 등으로 표현), 변수, 또는 함수식으로 나타낸다. 의도하는 관계가 성립하는 상태를 나타내는 항을 포함하도록 원자 wff (atomic wff) 를 바꾸고자 한다. 이에 따라 이러한 원자 wff 의 해석을 바꾸어서 원자 wff 가 상태에 대한 관계를 나타내도록 하고 이것을 변량 (fluent) 이라고 부른다. S0 의 상태에서 참이 되는 것을 나타내는 문장을 다음 식으로 나타낸다.
On (B, A, S0) ∧ On (A, C, S0) ∧ On (C, F1, S0) ∧ Clear (B, S0)
또한 다음과 같이 모든 상태에 대해 참인 명제도 가질 수 있다.
(∀x, y, s) [On (x, y, s) ∧ ¬(y = F1) ⊃ ¬Clear (y, s)]
(∀s) Clear (F1, s)
[Clear (x, s) 는 x 위에 어떤 물체를 올려놓을 수 있다는 것을 의미한다.] 이 일반 공리 (general axiom) 를 이용하여 S0 에 대한 여러 문장을 증명할 수 있다. 예를 들어 ¬Clear (A, S0) 와 Clear (F1, S0) 를 증명할 수 있다.
행동과 그 결과를 표현하기 위해 다음 단계를 이용한다.
1. 행동을 구체화한다 (즉, 행동이라는 물체가 있다고 가정한다). 따라서 행동을 상수 기호, 변수, 또는 함수식으로 개체에 대한 함수로 간주한다. 이 장의 예제에서는 행동이 블록에 대한 함수가 된다. 예를 들어 하나의 블록을 한 장소에서 다른 장소로 옮기는 행동을 고려해 보자. 블록 B 를 블록 A 에서 바닥으로 옮기는 행동을 move (B, A, F1) 의 식으로 나타낸다 (행동을 함수의 값에 의해 주어지는 "객체" 로 간주하라).
일반적으로 일련의 move 행동을 move (x, y, z) 의 스키마 (schema) 로 표현할 수 있으며 이때 x, y, z 를 스키마변수 (schema variable) 라고 한다. 이 변수에 상수 기호를 대입하면 행동의 실제 사례를 나타내는 식을 생성한다.
2. 행동과 상태를 상태로 대응 (map) 시켜 주는 함수를 나타내는 함수상수 do 를 가정한다. 만일 α 가 행동을, σ 가 상태를 나타낸다면 do (α, σ) 는 이 상태-행동의 쌍을 σ 의 상태에 대해 α 의 행동을 수행하여 얻어지는 상태로 대응시켜 주는 함수를 나타낸다.
3. 행동의 결과를 wff 로 표현한다. 어떤 형식화 (formulation) 에서는 각 행동-변량 쌍 (action-fluent pair) 에 대해 이러한 wff 가 두 가지 있다 (당분간 행동이 변량에 영향을 주지 못하는 쌍은 무시한다). 가령 {On, move} 의 쌍에 대한 두 가지 wff 는 다음과 같다.
[On
(x, y, s) ∧ Clear (x, s) ∧ Clear (z, s) ∧ (x ≠ z)
⊃ On (x, z,
do (move (x, y, z), s))]
[On
(x, y, s) ∧ Clear (x, s) ∧ Clear (z, s) ∨ (x ≠ z)
⊃ ¬On (x,
y, do (move (x, y, z), s))]
위의 식에 포함된 모든 변수는 전체적으로 한정된다 (universally quantified) 고 가정한다. 이 중 첫번째 식은 긍정 결과 공리 (positive effect axiom) 라고 하며 어떻게 행동이 변량을 참으로 만드는지를 기술한다. 두번째 식은 부정 결과 공리 (negative effect axiom) 라고 하며 어떻게 행동이 변량을 거짓으로 만드는지를 기술한다. 위의 예에서 결과 공리의 전제부 (antecedent) 는 행동을 적용시키기 위해 만족되어야 할 전제조건 (precondition) 을 기술한다. 또한 결론부 (consequent) 는 행동을 적용시킨 후 변량이 어떻게 바뀌는지를 기술한다.
앞에서 Clear 를 On 을 이용하여 정의하였지만 {Clear, move} 쌍에 대한 결과 공리를 작성할 수도 있다. 물론 이 결과 공리는 {On, move} 에 대한 정의나 결과 공리와 모순되지 않아야 한다. {Clear, move} 의 결과 공리는 다음과 같다.
[On (x,
y, s) ∧ Clear (x, s) ∧ Clear (z, s) ∧ (x ≠ z) ∧ (y ≠ z)
⊃ Clear
(y, do (move (x, y, z), s))]
[On (x,
y, s) ∧ Clear (x, s) ∧ Clear (z, s) ∧ (x ≠ z) ∧ (z ≠ F1)
⊃ ¬Clear
(z, do (move (x, y, z), s))]
이 예에서 전제부는 두 부분으로 이루어져 있다. 한 부분은 행동이 수행될 수 있는 전제조건을 표현하며, 다른 부분은 행동이 수행되었을 경우 공리의 결론부에 표현된 결과를 가지게 될 조건을 표현한다. 위의 긍정 결과 공리에서 두번째 부분은 (y ≠ z 이다 ( y = z 라고 하더라도 블록을 한 장소에서 같은 장소로 움직일 수 있기 때문에 행동이 수행될 수는 있지만 이 경우 결론부에 표시된 결과를 내지 못한다. 부정 결과 공리에서는 두번째 부분이 (z ≠ F1) 이다 (바닥은 항상 그 위에 아무 것도 없다 (clear) 고 가정하기 때문에 어떤 행동도 이를 부정으로 만들지 못한다).

그림 2 상태-행동쌍을 상태로 대응시킴
결과 공리가 어떻게 이용되는지를 설명하기 위해 그림 2 의 위에 있는 블록세계 상황을 고려하자. 이 상황은 {B/x, A/y, S0/s, F1/z} 의 치환 (substitution) 을 이용하면 결과 공리의 전제조건을 만족시킨다. 따라서 move (B, A, F1) 의 행동을 적용시켜 다음과 같은 결론부를 추론할 수 있다.
On (B, F1, do (move (B, A, F1 (, S0))
¬On (B, A, do (move (B, A, F1 (, S0))
Clear (A, do (move (B, A, F1 (, S0))
각각의 식은 do (move (B, A, F1), S0)) 을 행동 후 상태 항 (postaction state term) 으로 가지고 있다 (간결성을 위해 이 행동 후 상태를 S1 로 나타낸다). 그림 2 에서 행동을 적용시킨 후의 결과 상태와 이 상태를 기술하는 식을 보여주고 있다 (결과 공리에서 추론되는 식 외에도 S1 에서 참이 되는 다른 식들이 있다. 이런 식들이 어떻게 추론되는지는 잠시 후에 기술할 것이다).
하나의 행동이 완료된 후에도 그 행동이 허용하는
추론을 수행하기 전에 이미 존재했던 모든 식은 그대로 참이 된다는 것을 깨닫는
것이 중요하다 (블록 B 를 바닥으로 옮긴 후에도 S0 의 상태에서는 블록 B 가 블록
A 위에 있었다는 것이 여전히 성립한다. 마찬가지로 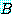 를 바닥으로 옮기기 전에도 do (move (B, A, F1), S0) 에 의해 나타나는 상태에서는
를 바닥으로 옮기기 전에도 do (move (B, A, F1), S0) 에 의해 나타나는 상태에서는
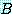 가 바닥에 있다는 것이 성립한다). 상황논리의 식은 그 식이 존재했던 상태에서는
항상 참이라는 의미에서 "상태가 없다 (stateless)" 고 한다.
가 바닥에 있다는 것이 성립한다). 상황논리의 식은 그 식이 존재했던 상태에서는
항상 참이라는 의미에서 "상태가 없다 (stateless)" 고 한다.
그림 2 에서 분명히 보았던 것처럼 do (move (B, A, F1), S0) 의 상태에서 참이 되는 모든 문장이 결과 공리에 의해 모두 추론될 수 있는 것은 아니다. 예를 들어 C 가 바닥에 있었다는 것과 블록 B 위에는 아무 것도 없었다는 사실처럼 옮기기 전에 참이었던 것이 옮긴 후에도 명백히 참으로 남아있는 사실이 존재한다. 행동은 전형적으로 지역적 결과만을 가지기 때문에 많은 변량들은 변하지 않은 채로 남게 된다. 이러한 불변성에 대한 추론을 하기 위해서는 각 행동과 그 행동의 결과로 변하지 않는 각 변량에 대한 프레임 공리 (frame axiom) 의 쌍이 필요하다. 예를 들어, {(move, On)} 쌍에 대해 프레임 공리는 다음과 같다.
[On (x, y, s) ∧ (x ≠ u)] ⊃ On (x, y, do (move (u, v, z), s))
(¬On (x, y, s) ∧ [(x ≠ u) ∨ (y ≠ z)]) ⊃ ¬On (x, y, do (move (u, v, z), s))
(어떤 행동이 이루어지기 전에 한 블록이 두번째 블록 위에 있었을 때, 그 행동이 두번째 블록에서 첫번째 블록을 제거하지 않는다면 행동이 일어난 후에도 그 블록이 두번째 블록 위에 계속 있게 된다. 행동이 이루어지기 전에 한 블록이 두번째 블록 위에 있지 않았을 경우, 그 행동이 두번째 블록 위에 첫째 블록을 올려놓지 않는다면 행동이 일어난 후에도 그 블록은 두번째 블록 위에 있지 않게 된다).
결과 공리와 마찬가지로 첫번째 프레임 공리를 긍정 프레임 공리 (positive frame axiom) 라 하고, 두번째 프레임 공리를 부정 프레임 공리 (negative frame axiom) 라 한다.
{(move, Clear)} 쌍에 대한 프레임 공리는 다음과 같다.
Clear (u, s) ∧ (u ≠ z) ⊃ Clear (u, do (move (x, y, z), s))
¬Clear (u, s) ∧ (u ≠ y) ⊃ ¬Clear (u, do (move (x, y, z), s))
(행동이 이루어지기 전에 블록 위에 아무 것도 없었다면, 그 행동이 그 블록 위에 다른 블록을 올려놓지 않을 경우 행동이 일어난 후에도 그 블록 위에는 계속적으로 아무 것도 없다. 행동이 이루어지기 전에 블록 위에 어떤 것이 놓여져 있었다면, 그 행동이 그 블록 위에 있는 블록을 제거하지 않을 경우 행동이 일어난 후에도 그 블록 위에는 계속적으로 어떤 것이 놓여져 있게 된다).
프레임 공리는 상태의 특성에 영향을 주지 않는 행동에 의해 상태가 변화되면, 그 상태의 특성이 계속 참을 유지한다는 것을 증명하는 데 이용된다. 예를 들어, {move, Clear} 프레임 공리 중의 하나를 이용해서 그림 1 에 있는 Clear (B, do (move (B, A, F1), S0)) 을 유추할 수 있다. 전형적으로 변량과 행동의 모든 조합에 대해서 프레임 공리의 쌍이 존재하기 때문에 실제 문제에서 행동이 상황논리의 식에 의해 실세계를 변화시키는지를 표현하는 것은 아주 어렵다.
프레임 공리의 수를 줄이거나 결과 공리로부터 프레임 공리를 자동으로 유추할 수 있는 방법에 대해서 많은 저자들이 탐구해왔다. 이러한 기법이 여기서 논의되지는 않을 것이며, 다만 이 방법들은 변량에 대해서 이루어질 수 있는 유일한 변화는 결과 공리에 명확하게 명시된 것뿐이라는 가정을 포함한다 ([Pednault 1986, Schubert 1990, Reiter 1991, Elkan 1992] 를 참조하라). 프레임 공리의 수를 줄일 수 있더라도 그들을 이용해서 일련의 여러 행동에 대해서 변하지 않는 변량을 추론하는 것은 계산적으로 부담이 많이 된다. 행동에 의해서 영향을 받지 않는 변량을 다루는 것에 관계된 여러 난제점들을 프레임 문제 (frame problem) 라고 불러왔다. 다음 장에서는 프레임 문제의 몇몇 관점을 다루는 하나의 접근 방법을 논의하고자 한다.
move 와 같이 행동을 기술하는 전이식 (transition formula) 의 전제부는 이상적인 경우에 대한 전제조건을 나타낸다. 만일 좀 더 정확하게 하기 위하여, 옮겨야 하는 객체가 아주 무겁지는 않아야 한다고 하자. 이 경우 ¬Too_heavy (x, s) 와 같은 추가적인 논리곱 인자를 전제조건에 추가해야 할 것이다. 이러한 신중한 고려는 ¬Glued_down (x, s), ¬Armbroken (s) 등과 같은 자격요건 (qualification) 을 무한정 추가할 수 있다. 중요한 자격요건을 모두 명시하는 데 대한 어려움 때문에 이 문제를 자격요건 문제 (qualification problem) 라 부른다. 비단조 추론 (nonmonotonic reasoning) 을 이용하여 자격요건문제에 대처하기 위한 노력이 있어 왔다. 기본적인 아이디어는 결과 공리가 자격요건이 추가되었을 때 제거될 수 있는 디폴트 결론 (default conclusion) 을 허용하는 것이다 (한 예로 [Dean & Wellman 1991, 63 쪽] 을 참조하라). 이러한 시도들이 모두 성공적이지만은 않았다.
또 다른 문제가 있다. 복잡한 도메인에서는 도메인의 일반 지식을 기반으로 객체에 대한 문장을 추론할 수 있다. 예를 들어, 로봇이 어떤 방 (room) 안에 있다면 그 로봇은 자신이 나르는 화물 (package) 도 그 방 안에 있다는 것을 추론할 수 있다. 화물의 위치에 대해서 결과 공리나 프레임 공리를 이용하여 추론하는 것보다는 로봇의 위치를 추론하고 나서 일반 지식을 이용하여 화물의 위치를 추론하는 것을 더 선호할 수 있다. 예를 들어, S0 의 상황에서 PA 가 화물을 나타내고 R1 이 방을 나타낸다고 할 때 In (PA, R1) 이라는 사실이 있다고 하자. 결과 공리를 이용할 경우 로봇이 다른 방 (가령 R2 로 표시하자) 으로 움직인 후 그 로봇은 자신이 새로운 상황에서 R2 에 있다고 결론지을 수 있다. 더 나아가 화물도 새로운 상황에서 R2 에 있다고 추론할 수도 있다. 하지만 새로운 상황에서 어떻게 프레임 공리가 화물이 R1 에 더 이상 있지 않다고 결론을 내리지 못하도록 할 수 있는가? 추론된 식 중에 추후의 상태 전이에서도 남아있는 것을 추적하는 것을 세분화 문제 (ramification problem) 라 한다. 세분화 문제를 다루는 여러 기법 [진리보존 프로시저 (truth maintenance procedure) 와 관련됨] 이 제시되었다.
프레임 문제나 자격요건 문제, 세분화 문제는 잠시
접어두고 상황논리가 원칙적으로 어떻게 추론 방법을 이용하여 일련의 행동을 계획하는
데 이용되는지 살펴보고자 한다. 목표 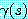 를 달성하는 계획을 생성하기 위해서
를 달성하는 계획을 생성하기 위해서 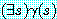 를 증명하고, 이것의 답이 되는 술어를 이용하여 상태를 생성하는 중첩된 행동의
함수로서 그 상태를 추출하고자 한다.
를 증명하고, 이것의 답이 되는 술어를 이용하여 상태를 생성하는 중첩된 행동의
함수로서 그 상태를 추출하고자 한다.
예를 들어, 그림 1 에 주어진 초기 상태 S0 에서 블록 B 를 바닥에 내려놓는 계획을 얻고자 한다고 가정하자. 이 계획을 계산하기 위해선 (∃s) On (B, F1, s) 를 증명해야 한다. 이 증명은 (∃s) On (B, F1, s) 의 부정인 (∀s) ¬On (B, F1, s) 와 S0 나 move 의 결과를 기술하는 식이 서로 모순이라는 논리융합 반박 (resolution refutation) 에 의해 이루어진다. 답변 술어 (answer predicate) 를 이용하여 증명 도중에 이루어진 치환을 얻어내려 한다. 이 문제를 위한 식은 다음과 같다.
¬On (B, F1, s) ∨ Ans (s)
On (B, A, S0)
On (A, C, S0)
On (C, F1, S0)
Clear (B, S0)
Clear (F1, S0)
[On (x, y, s) ∧ Clear (x, s) ∧ Clear (z, s) ∧ (x ≠ z)
⊃ On (x, z, do (move (x, y, z), s))]
마지막 식은 {On, move} 에 대한 긍정 결과 공리이다. 이것은 논리융합 반박을 수행할 수 있도록 절 형태 (clausal form) 로 변환되어야 한다. 반박을 수행할 때 동등술어 (equality predicate) 인 (x ≠ z) (¬(x = z) 를 나타내는 한 방법) 는 모든 변수에 값이 할당될 때까지 남겨둔다. 그리고 나서 전에 논의한 바와 같이 (A = A) 나 ¬(A = B) 와 같은 공리가 무한정 제공되어 논리융합에 이용된다고 가정한다. 위의 예제에 논리융합 반박을 이용하면 Ans (do (move (B, A, F1), S0)) 를 생성하게 되는데 이에 대한 증명은 독자들에게 맡긴다.
만일 목표를 달성하기 위해 여러 행동이 요구될 경우 행동 함수가 중첩될 수 있다. 예를 들어 그림 1 과 같은 초기 상태에서 시작하여 블록 A 를 블록 B 위에 올려 놓는 문제에 대한 결과는 Ans (do (move (A, C, B), do (move (B, A, F1), S0))) 가 될 것이다. 하지만 이 문제를 적절한 결과 공리와 프레임 공리를 이용하여 해결하려 한다면 이처럼 간단한 계획에 비해 증명에 드는 노력이 너무 크다. 이러한 프레임 문제의 측면은 상황논리를 이용하여 계획을 생성하는 대부분의 시도에 대한 장애물이 되어 왔다.
자격요건 문제는 [McCarthy 1977 (McCarthy, J., "Epistemological Problems in Artificial Intelligence," in Proceedings of the Fifth International Joint Conference on Artificial Intelligence (IJCAI-77), nl pp. 1038-1044, San Francisco: Morgan Kaufmann, 1977.)] 에서 처음 제기되었다. 비단조 추론 방법을 이용하여 프레임 문제와 자격요건 문제를 다루기 위한 여러 시도가 있어왔다. [Hanks & McDermott 1986 (Hanks, S., and McDermott, D., "Default Reasoning, Nonmonotonic Logics, and the Frame Problem," in Proceedings of the Fifth National Conference on Artificial Intelligence (AAAI-86), pp.328-333, Menlo Park, CA: AAAI Press, 1986. (Reprinted in Ginsberg, M. (ed.), Readings in Nonmonotonic Reasoning, pp.390-395, San Francisco: Morgan Kaufmann, 1987.)] 은 비단조 결론만 가지고는 어떤 변량이 변하고 어떤 것은 그대로 유지되는지 결정하기가 모호할 수 있다는 것을 발견하였다. 그 후 [Baker 1991 (Baker, A., "Nonmonotonic Reasoning in the Framework of Situation Calculus," Artificial Intelligence, 49:5-23, 1991.)] 과 [Shoham 1988 (Shoham, Y., Reasoning about Change: Time and Causation from theStandpoint of Artificial Intelligence, Cambridge, MA: MIT Press, 1988.)] 에서 이 문제가 거론되었다 (Baker 의 접근 방법에 대한 주석은 [Kartha 1994 (Kartha, G. N., "Two Counterexamples~Related to Baker's Approach to the Frame Problem," Artificial Intelligence, 69(1-2):379-391, 1994.)] 에 있다). 프레임 문제에 대한 또 다른 비단조 접근 방법에서는 후속자 상태 공리 (successor-state axiom) 를 이용하여 임의의 행동이 임의의 변량에 미치는 모든 변화를 제한하고 기술하였다 [Reiter 1991 (Reiter, R., "The Frame Problem in the Situation Calculus: A Simple Solution (Sometimes) and a Completeness Result for Goal Regression," in Lifschitz, V. (ed.), Artificial Intelligence and Mathematical Theory of computation: Papers in Honor of John McCarthy, pp.359-380, New York: Academic Press, 1991.)]. [Shanahan 1997 (Shanahan, M., Solving the Frame Problem: A Mathematical Investigation of the Commonsense Law of Inertia, Cambridge, MA: MIT Press, 1997.)] 은 프레임 문제에 대한 책이다.
에이전트 계획수립에 대한 최근의 대부분의 연구가 다음 장에 기술된 대안을 이용하지만, 상황논리와 이와 관련된 언어인 GOLOG (alGOl in LOGic) [Levesque, et al. 1997 (Levesque, H., Reiter, R., Lesprance, Y., Lin, F., and Scherl, R., "GOLOG: A Logic Programming Language for Dynamic Domains," Journal of Logic Programming, Special Issue on Reasoning about Action and Change, 31(1-3):59-83, 1997.)] 는 토론토 대학의 인지로봇 그룹의 로봇 연구의 기반이 되고 있다 [Scherl & Levesque 1993 (Scherl, R., and Levesque, H., "The Frame Problem and Knowledge Producing Actions," in Proceedings of the Eleventh National Conference on Artificial Intelligence (AAAI-93), pp.689-695, Menlo Park, CA: AAAI Press, 1993.)]