(7)
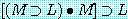
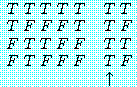
(8)
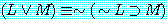
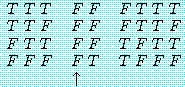
(9)
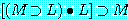
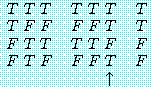
(10)
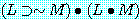
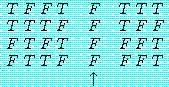
(11)
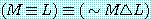
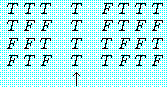
(12)
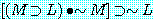
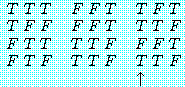
Tautology
논리식 혹은 합성명제에 있어 각 명제의 참·거짓의 모든 조합에 대하여 항상 참인 것을 항진(恒眞)명제(tautology) 라고 한다. 또 각 명제의 참·거짓에 관계없이 결과가 항상 거짓인 것을 모순(矛盾)명제(contradictory)라고 하며, 일부가 참, 거짓인 명제는 일부진명제(contingent)라고 한다.
Tautology : 소광희 : 진리표 에서 알 수 있는 바와 같이, 분자명제의 진리치를 결정하는 가능한 모든 조건은 여러 가지 경우가 있으나, 이에 따라 결정되는 전체 분자명제의 진리치는 진과 위 두 종류뿐이다. 전체 분자명제의 가능한 모든 진리치가 어떠냐에 따라 명제를 3가지 종류로 나눈다 ;
i) 가능한 모든 조건 아래에서 모든 진리치가 진이 되는 명제가 있는가 하면,
ii) 어떤 조건에서도 위인 진리치만 갖게 되는 명제도 있고,
iii) 조건이 달라짐에 따라 진일 때도 있고 위일 때도 있는 명제도 있다.
다음 명제의 진리표를 작성해 보자.
(1) 김군이 수학을 잘하면 그는 논리학도 잘하는데 만일 그가 수학을 잘한다면, 그는 논리학을 잘한다.
(2) 김군이 논리학이나 수학을 잘 한다는 것은, 만일 그가 논리학을 잘하지 못하면 수학을 잘 한다는 것이 거짓이 되기 위한 필요충분조건이다.
(3) 만일 김군이 수학을 잘하면 그는 논리학도 잘하는데 만일 그가 논리학을 잘한다면, 그는 수학을 잘한다.
(4) 만일 김군이 논리학을 잘하면 수학은 잘 하지 못할 것이나, 그는 논리학도 잘하고 수학도 잘한다.
(5) 김군이 수학을 잘 한다면 오직 그때에만 논리학을 잘한다는 것은 그가 수학을 잘 하지 못하든가 아니면 논리학을 잘하기(두 경우 다일 수는 없음) 위한 필요충분조건이다.
(6) 김군이 수학을 잘하면 그는 논리학을 잘하는데 만일 그가 수학을 잘하지 못한다면, 그는 논리학을 잘하지 못한다.
"김군은 수학을 잘한다"를 'M', "김군은 논리학을 잘한다"를 'L'이라 하여 위 명제들의 진리표를 만들면 각각 다음과 같다. 다음 진리표를 서로 비교 검토해 보면 (7)과 (11), (8)과 (10), (9)와 (12)는 전체명제의 진리치 (↑표한 종렬의 진리치) 가 어떤 공통적인 특징을 가지고 있음을 곧 알 수 있다.
|
(7) |
|
(8) |
|
|
(9) |
|
(10) |
|
|
(11) |
|
(12) |
|
먼저
(7)과 (11) 두 경우를 보면 진리치들은 모든 경우에 있어서 진 (T) 이다. 이것은 원자명제
즉 'M'과 'L'의 진리치에 상관없이 '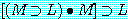 ' 과 '
' 과 '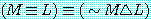 ' 은 항상 진임을 의미하니 이런 명제를 항진명제 (tautology) 라 한다. 일반적으로,
어떤 진리함수적 명제의 가능한 진리치가 모두 진일 때, 오직 그 때에만, 그 명제를
tautology 라 부른다. 항진명제는 그 논리적 형식상 결코 위가 될 수 없고 항상 진이어야만
한다.
' 은 항상 진임을 의미하니 이런 명제를 항진명제 (tautology) 라 한다. 일반적으로,
어떤 진리함수적 명제의 가능한 진리치가 모두 진일 때, 오직 그 때에만, 그 명제를
tautology 라 부른다. 항진명제는 그 논리적 형식상 결코 위가 될 수 없고 항상 진이어야만
한다.