Multilayer Perceptron
신경망 이론과 응용(1) : 김대수, 하이테크 정보, 1992, Page 91~142
3. Backpropagation 학습 알고리즘의 배경
(1) Delta rule 과 gradient descent method
5. Backpropagation 학습 알고리즘의 문제점 및 개선책
6. Multi layer perceptron의 적용 예
(6) 부정 문제 (The Negation Problem)
민스키 (Minsky) 의 파퍼트 (Papert) 가 1969 년 '퍼셉트론즈' (Perceptrons) 란 저서 [MIN69] 에서 퍼셉트론 모델을 수학적으로 철저히 분석하고 그 모델의 결정적인 단점들을 밝혀낸 이후 신경망에 관련된 연구는 약 20 년간 침체의 길을 걷게 되었다.
퍼셉트론과 같이 하나의 조정층 (single-adjustable layer) 으로 구성되는 모델들의 한계점들 때문에 입력층, 출력층 그리고 한 개 이상의 은닉층 (hidden layer) 을 쓰는 새로운 모델들이 1980 연대 중반에 제안되었으며, 특히 PDP (Parallel Distributed Processing) 그룹에 의한 폭 넓은 연구가 진행되었다 [RUM86]. 러멜하트 (Rumelhart) 등은 1980 연대 후반에 출판된 "Parallel Distributed Processing" (PDP) 란 저서를 통해 백프로퍼게이션 알고리즘을 널리 유행시켰다. 이 그룹에서 제안한 모델은 은닉층을 가진 다층 퍼셉트론에 백프로퍼게이션 (Backpropagation) 학습 알고리즘을 사용함으로써 선형 분리 문제 뿐만 아니라 여러 가지 문제점들을 해결할 수 있었으며 이로 인하여 십여년간 침체했던 신경망 연구가 새롭게 활기를 띠게 되었다.
Multilayer perceptron 은 입력층과 출력층 사이에 하나 이상의 중간층이 존재하는 신경망으로 <그림 1> 에 나타낸 것과 같은 계층구조를 갖는다. 이 때 입력층과 출력층 사이의 중간층을 은닉층 (hidden layer) 이라 부른다. 네트워크는 입력층, 은닉층, 출력층 방향으로 연결되어 있으며, 각 층내의 연결과 출력층에서 입력층으로의 직접적인 연결은 존재하지 않는 전방향(feedforward) 네트워크이다.
<그림 1> 다층 퍼셉트론의 구조
multi layer perceptron 은 단층 perceptron 과 유사한 구조를 가지고 있지만 중간층과 각 unit 의 입출력 특성을 비선형으로 함으로써 네트워크의 능력을 향상시켜 단층 perceptron 의 여러 가지 단점들을 극복했다. multi layer perceptron 은 층의 갯수가 증가할수록 perceptron 이 형성하는 결정 구역의 특성은 더욱 고급화된다. 즉 단층일 경우 패턴공간을 두 구역으로 나누어주고, 2 층인 경우 볼록산 (convex) 개구역 또는 오목한 폐구역을 형성하며, 3 층인 경우에는 이론상 어떠한 형태의 구역도 형성할 수 있다.
<그림 2> 에 단층, 2층, 3층 perceptron 들의 구조와 결정 구역을 나타내었다 [KHA90]. 이 그림에서 두 번째 열은 각 네트워크가 형성하는 결정 구역을 나타내고 다음 두 개의 열은 Exclusive-or 와 mesh 구역 문제에 대한 결정 구역을 예시한다. 그리고 맨 오른쪽 옅은 일반적인 결정 구역을 예시한다. 지금까지는 주로 계단형 (hard limiting) 의 비선형 (noolinear) 활성함수를 사용하고 출력 unit 가 하나인 multilayer perceptron 에 대하여 논의하였는데 이와 비슷한 결과가 시그모이드 비선형 활성함수를 적용한 한 개 이상의 출력 unit를 가진 네트워크에도 나타난다. 시그모이드 비선형 활성함수를 적용할 경우 결정 영역이 통상 직선이 아닌 완만한 곡선으로 경계지워지므로 행위의 분석이 약간 복잡하지만 미분이 가능하므로 오히려 은닉층을 학습할 수 있는 Backpropagation 학습 알고리즘을 수행할 수 있다. 대부분의 multilayer perceptron 은 backpropagation 학습 알고리즘을 사용하여 학습시킬 수 있다.
일반적인 multilayer perceptron 의 학습방법은 다음과 같다. 입력층의 각 unit 에 입력 데이터를 제시하면 이 신호는 각 unit에서 변환되어 중간층에 전달되고 최종적으로 출력층으로 나오게 된다. 이 출력값과 원하는 출력값을 비교하여 그 차이를 감소시키는 방향으로 연결강도를 조정하는 것이다. 그러나 중간층이 있으면 학습은 어려워 진다. 왜냐하면 어떤 연결강도가 오차를 유발 시키는지 알 수 없기 때문이다.
<그림 2> 층수와 결정 구역의 특성
Backpropagation 학습 알고리즘은 최소자승 (least mean square) 알고리즘의 비선형적인 확장이다. Backpropagation 학습 알고리즘은 미분의 반복규칙 (chain-rule) 을 여러번 반복적으로 적용하여 확률 근사치 프레임워크(stochastic-approximation framework) 와 관련지움으로써 유도해낼 수 있다.
러멜하트 (Rumelhart) 등은[RUM86] 1980 년대 후반에 출판된 "Parallel Distributed Processing"(PDP) 이란 저서에서 Backpropagation 알고리즘을 널리 유행시켰다. 이 책은 샌디에이고에 있는 캘리포니아 대학의 여러 심리학자들과 컴퓨터 관련 학자들의 신경망 관련 연구들을 요약한 것이다. 그 주요 맴버들로는 러멜하트 (David E, Rumelhart), 맥클란드 (James L.McClelland), 엘만 (Geoffrey L, Elman), 세즈오우스키 (Terrence J.Sejnowski), 스몰렌스키 (Paul Smolensky), 집서 (David Zipser) 등을 들 수 있으며 이 책은 신경망의 새로운 붐을 일으키는데 크게 기여했다.
PDP 연구팀은 일반화 델타 규칙 (generalized delta rule) 이라고 불리는 Backpropagation 알고리즘을 제안하였다. 이것은 민스키와 파퍼트가 상세히 분석한 perceptron 모델의 제한점들을 극복했으며, 이로써 십여년 간 침체했던 신경망 연구에 새로운 장을 열었다.
이 알고리즘은 많은 컴퓨터 관련 과학자들과 인지과학자들이 신경망 이론과 응용들을 통칭하여 즐겨 부르는 커넥셔니즘 (connectionism) 의 개가이다. 그 무렵 세즈노우스키 (Sejnowski) 는 Backpropagation 학습 알고리즘을 사용하여 텍스트 (text) 를 음성 (speech) 으로 합성하는 NETtalk 시뮬레이션에 사용하였다 [SEJ86]. Backpropagation 알고리즘이 소개된 PDP 책은 신경망에 관련된 참고 문헌으로 널리 사용되었으며 수 많은 Backpropagation 소프트웨어들이 개발되기 시작했다. 또한 주식 시장의 예측 등 기술적인 응용 분야에 대한 수 많은 시뮬레이션이 시도되었으며, 그 결과들이 학술대회에 보고되었다.
많은 사람들은 훈련을 통한 이 새로운 학습 방법이 기계지능(machine intelligence)의 새로운 장을 여는 놀라운 방법이라는 인식에서 공장 자동화, 실시간 음성인식, 다른 언어간의 번역, 로봇와 같은 분야들에의 응용 가능성을 매우 밝게 보았다. 일부 생리학자 (pysiologist) 들은 이 Backpropagation 알고리즘을 인간의 두뇌 및 중추신경 시스템으로까지 여겼다. 이와 더불어 Backpropagation 학습 알고리즘의 단점들도 드러났다. 첫째, 이 알고리즘은 수렴에 종종 실패하고 지역 최소값 (local minimum) 에 봉착한다. 둘째, Backpropagation 은 비지역성 (nonlocality), 동시성 (synchrony), 감독 (supervision) 과 긴 훈련 시간 등으로 생물학적인 신경망과는 상당한 차이점이 있다. 셋째, Backpropagation 은 불연속 시뮬레이션에서 항상 수렴하는 것은 아니다. 즉, 초기의 상태를 어떻게 선택하느냐에 따라 진동하거나 (oscillation), 최악의 경우에는 제멋대로 방황 (chaotic wandering) 하기도 한다.
어떤 Backpropagation 옹호론자들은 이 알고리즘이 연결강도 공간 (weight space) 의 시냅스에서 오차의 표면 (error surface) 이 기울기를 따라가는 (gradient descent) 방법으로 수행되기 때문에 만약 시뮬레이션의 간격을 충분히 작게 한다면 항상 수렴하게 된다고 주장한다. 그러나 이런 주장은 이 알고리즘의 통계적인 성질을 간과한 것이라고 볼 수 있다. Backpropagation 알고리즘은 그것이 수렴할 경우에도 지역 최소오류 (local minimum error) 에 수렴하기도 한다. 이 알고리즘의 옹호론자들도 이 점을 인정하지만, 그들 중 몇몇은 연결강도 공간의 차원이 매우 클 경우에는 지역 최소값이 거의 생기지 않는다는 주장이다. 이 점은 몇몇 차원의 Backpropagation 에서는 성공적인 시뮬레이션을 입증했다.
Backpropagation 에 대한 비판적인 시각은 많은 Backpropagation 연구가들이 서로 자기가 처음으로 Backpropagation 을 개발했다고 주장하는 데에도 문제가 있다. 이 Backpropagation 에 관한 기록을 보면 파커 (Parker) 가 80년대 초에 '학습 논리 (learning logic)' 로서의 이 알고리즘을 유도했고[PAR85], 웨보스 (werbos) 는 1974년 Harvard 대학의 박사학위 논문으로 'Dynamic feedback' 을 유도했다. 웨보스 [WER74] 는 Backpropagation 을 통계적으로 공식화했으며 이 알고리즘을 1970 년대와 1980 년대에 경기예측과 여러 문제들에 응용하였다. 이 알고리즘은 어쩌면 그 이전부터 존재했는지도 모른다.
또 다른 비평적인 관점으로는 Backpropagation 학습이 과연 새로운 것이었냐는 것이다. 그 문제는 누가 제일 먼저 이 알고리즘을 유도했느냐가 아니라 알고리즘이 이미 존재했던 것과 다르냐는 것이다. 화이트 (White) 는 Backpropagation 을 1950 년대에 확률 근사 (stochastic approximation) 로 귀착시켰다 [WHI89a, WHI89b]. 따라서 이 알고리즘은 새로운 종류의 학습 방법을 제시하지 못했다. 그 대신 Backpropagation 은 통계학이 오래전부터 탐구해놓은 추정 (estimation) 방법을 구현하는 계산적으로 효과적인 방법을 제시했다. 최근에 (1989) 화이트는 Backpropagation 알고리즘을 확률 근사의 한 특수한 경우인 것으로 귀착시켰다.
Backpropagation 학습 알고리즘의 기본 원리는 다음과 같다. 입력층의 각 unit 에 입력패턴을 주면, 이 신호는 각 unit에서 변환되어 중간층에 전달되고 최후에 출력층에서 신호를 출력하게 된다. 이 출력값과 기대값을 비교하여 차이를 줄여나가는 방향으로 연결강도를 조절하고, 상위층에서 역전파하여 하위층에서는 이를 근거로 다시 자기층의 연결강도를 조정해나간다.
지도학습에서는 입력 및 원하는 출력 (목포출력) 패턴 (백터) 이 네트워크에 제시된다. 네트워크는 입력층에 주어진 입력패턴이 출력층에 전파되면서 변한 출력패턴을 목표패턴과 비교한다. 네트워크에서 출력된 패턴이 목표패턴과 일치하는 경우에는 학습이 일어나지 않는다. 그렇지 않은 경우는 얻어진 출력패턴과 목표패턴의 차이를 감소시키는 방향으로 네트워크의 연결강도를 조절하여 학습을 한다. 네트워크에 은닉 unit 가 없는 경우는 델타 규칙과 동일하다. 즉 p 번째의 입력/목표출력 패턴이 제시되는 경우에 노드 i 에서 노드 j 로의 연결강도의 변화는 (식 1) 과 같이 표현된다.
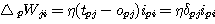 (식
1)
(식
1)
여기서 tpj 는 p 번째 목표출력 패턴의 j 성분, opj 는 p 번째 입력패턴으로부터 네트워크가 계산한 출력의 j 성분. δpj = tpj - opj 는 목표출력과 실제출력의 차 (오차), Δpwj 는 입력층 iunit 로부터 출력층 junit 에서 연결강도의 변화량이다.
델타 규칙을 유도하는 방법은 여러 가지가 제안되어
있으나 여기서는 최급하강법을 이용하여 유도하기로 한다.
델타 규칙은 입출력 함수가 선형의 unit 로부터
이루어진 네트워크에 대하여 모든 입력패턴으로부터 얻어지는 출력과 목표출력과의
오차의 제곱의 총합을 최소로 하도록 연결강도를 조정하는 것이다. 그러기 위해서는
p 번째 패턴의 쌍 (pair) 을 제시한 경우의 오차의 제곱을 각각의 견결강도 Δpwi
로 미분한 것이 델타 규칙에서의 연결강도 변화량에 비례하는
것을 나타내면 된다.
델타 규칙에 의해 연결강도의 변화가 연결강도
공간상에 주어지는 오차의 제곱을 높이로 하는 곡면에 대하여 최급하강을 한다. 즉,
오차의 제곱이 가장 많이 감소하는 방향으로 변화한다. 이것을 수식적으로 나타내면
다음과 같다.
패턴 p 에 대한
오차의 제곱은 (식 2) 와 같고 전체 패턴에 대한 오차의 제곱의 합은 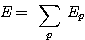 이다.
이다.
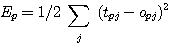 (식
2)
(식
2)
먼저, 델타 규칙이 E 내에서 최급하강법임을 알아보기 위해 각각의 Ep 에 대하여 (식 3)이 성립함을 보인다.
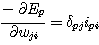 (식
3)
(식
3)
(식 3) 의 우변에 정수 η 를 곱한 것이 델타 규칙의 학습식 (식 1) 의 우변이 된다. 은닉 unit 가 없는 경우는 합성함수 반복규칙 (chain rule) 을 사용하여 좌변의 미분을 간단히 계산할 수 있다.
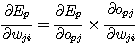 (식
4)
(식
4)
(식 2) 로부터 우변의 σEp/σopj 에 대한 미분을 계산하면 다음과 같다.
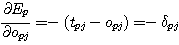 (식
5)
(식
5)
출력의 junit(uj) 의 값이 변화함에 따라 오차의 변화는 ∂pj 에 비례한다. 더욱이 선형 unit 를 사용하는 경우는 unit 의 출력과 입력의 관계가 (식 6) 과 같으므로 ∂σopj/∂wji 는 (식 7) 과 같다.
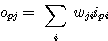 (식
6)
(식
6)
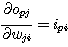 (식
7)
(식
7)
따라서 (식 4) 는 (식 8) 로 나타낼 수 있다.
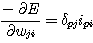 (식
8)
(식
8)
한편 (식 9) 에서와 같이 모든 패턴을 한번씩 제시한 후에 연결강도의 변화의 총합은 ∂E/∂wji 에 비례한다.
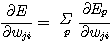 (식
9)
(식
9)
단, 이것은 모든 패턴에 대한 한 번의 학습이 끝날 때까지 연결강도를 변화시키지 않는 경우에 대해서만 유효하다. 각각의 패턴이 제시될 때마다 연결강도를 변화시키는 경우에는 처음에 제시된 패턴에 의한 연결강도의 변화가 뒤에 제시되는 패턴에 대하여 변화되는 연결강도에 영향을 주기 때문에 변화의 총합은 ∂Ep/∂wji 와 조금씩 차이가 있다. 그러나 이러한 경우에도 학습 계수 Л 를 충분히 작게하면 무시할 수 있어 델타규칙은 오차의 제곱의 총합을 E에 대해 최급하강법에 아주 근사하다. 실제로 Л 를 작게하면 E 를 최소화하는 wji 를 구할 수 있다.
은닉 unit 가 없는 경우는 오차의 제곱에 대한 곡면이 하나의 최소점을 갖는 포물선의 모양을 하고 있으므로 최급하강법에 의해 오차의 제곱을 최소로 하는 값을 얻을 수 잇다. 그러나 일반적으로 은닉 unit 가 있는 경우는 E의 미분을 구하는 것이 그리 쉽지 않을 뿐 아니라 오차의 제곱의 곡면도 일반적으로 간단하지 않아 최급하강법이 오차의 제곱에 지역 최소값을 나타내는 연결강도에 수렴할 가능성이 있다. 따라서 델타 규칙을 일반화하여야 한다.
먼저 준선형이라 부르는 임의의 비선형 입출력 함수를 갖는 unit 를 이용한다. 준선형 (semilinear) unit 는 unit 의 출력이 그 unit의 입력의 종합 (식 10) 에 대한 비감소이며 미분 가능한 함수이다. 즉 준선형의 unit 출력은 (식 11) 과 같다.
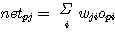 (식
10)
(식
10)
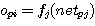 (식
11)
(식
11)
여기서 fi 는 비감소이며 미분 가능한 함수이다.
이하에서는 네트워크가 이러한 준선형의 입출력함수를 갖는 unit 들로 이루어진 경우에 대하여 일반화 델타 규칙을 정식화 한다. perceptron 등에서 사용한 선형입출력 함수는 미분이 불가능하여 이러한 조건을 만족하지 못함에 유의해야 한다.
델타 규칙에서와 같이 E 를 오차의 제곱의 총합으로 하고, 연결강도의 변화량은 (식 1) 과 (식 8) 에 의해 (식 12) 와 같이 된다.
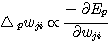 (식
12)
(식
12)
우변의 미분을 오차 입력의 총합에 관한 미분과 입력 총합의 연결강도에 관한 미분으로 나누어 바꿔 쓰면 (식 13) 과 같다.
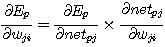 (식
13)
(식
13)
(식 10) 을 이용하여 (식 13) 의 두 번째의 미분을 계산하면 (식 14) 와 같다.
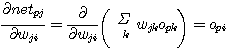 (식
14)
(식
14)
여기서 δpi 를 (식 15) 로 정의하면 (식 13) 은 (식 16) 으로 쓸 수 있다.
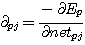 (식
15)
(식
15)
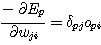 (식
16)
(식
16)
따라서 Ep 에 관한 최급하강을 하기 위해서는 통상의 델타 규칙과 같이 (식 17) 을 이용하여 연결강도를 변화시키면 된다.
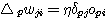 (식
17)
(식
17)
그러나 문제는 각각의 unit에 대하여 δpj 를 어떻게 정할 것인가 하는 것이다. 이하에서 δpj 를 재귀적으로 간단히 구하는 방법을 살펴본다.
(식 15) 를 합성함수의 미분공식을 이용하여 오차의 출력에 관한 미분과 출력의 입력 총합에 관한 미분으로 나누어 바꿔 쓰면 (식 18) 과 같다.
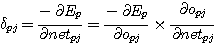 (식
18)
(식
18)
(식 11) 을 이용하여 (식 18) 의 두 번째의 미분을 계산하면 (식 19) 와 같다.
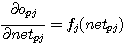 (식
19)
(식
19)
첫 번째의 미분계산은 경우에 따라 다르다. 먼저 unit uj 가 출력층의 unit 인 경우는 Ep 의 정의로부터 통상의 델타 규칙의 경우와 같이 (식 20) 으로 계산하면 된다.
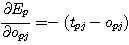 (식
20)
(식
20)
따라서 (식 18) 에 대입하여 얻은 출력층의 unit 에 관한 δpj 는 (식 21) 과 같다.
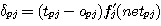 (식
21)
(식
21)
다음에 unit uj 가 출력층의 unit 가 아닌 경우에는 합성함수의 미분공식을 사용하여 (식 22) 와 같이 얻을 수 있다.
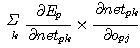 (식
22)
(식
22)
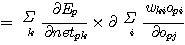
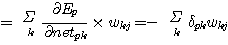
따라서 이 경우 δpj 는 (식 18) 과 (식 22) 에 의해 (식 23) 과 같이 된다.
 (식
23)
(식
23)
여기서 k 는 unit uj 의 출력을 받는 unit 전체를 나타낸다. (식 21) 과 (식 23) 을 이용하면 모든 unit uj 에 대한 δpj 를 재귀적으로 계산할 수 있다. 또한 (식 17) 을 이용하면 전체 unit에 대하여 연결강도의 변화량을 구할 수 있다.
위에서 유도한 결과는 3 개의 식으로 정리할 수 있다. 첫 번째, 일반화 델타규칙은 원래의 델타 규칙과 동일한 식이다. 즉, 연결강도의 변화 △pwji 는 그 연결의 종점 unit 에 관한 오차신호 δpj 와 그 연결의 시점 unit 의 출력 opi 의 곱에 비례한다.
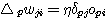 (식
24)
(식
24)
두 번째, 오차를 결정하는 식이다. 오차신호의 계산은 출력 unit 에 대한 오차를 초기값으로 하여 재귀적으로 수행된다. 먼저 출력 unit 에 대한 오차 신호는 델타 규칙과 거의 같으며, 네트워크 출력과 목표출력의 차이로부터 (식 25) 가 구해진다.
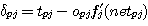 (식
25)
(식
25)
여기서 fj'(netpj) 는 준선형 입출력 함수의 미분계수이다.
세 번째, 은닉 unit 에 관한 오차신호는 unit 가 출력을 보내는 unit uk 의 오차신호 δpk 와 그 사이의 연결강도 wkj 를 이용하여 (식 26) 으로 구해진다.
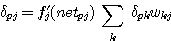 (식
26)
(식
26)
일반화 델타 규칙에 의한 학습은 두 개의 순서에 의해 이루어진다고 볼 수 있다. 첫째, 입력을 네트워크에 제시하면 이것이 네트워크의 전방향으로 전파되어 출력을 낸다 .이 출력과 목표출력과의 차이에 미분계수를 곱하여 출력 unit 에 대한 오차를 계산한다. 둘째, 오차신호가 네트워크의 역방향으로 전파되어 가면서 위의 식과 같이 각각의 unit 의 오차 신호가 계산되어, 이것을 바탕으로 연결강도를 수정한다.
일반적으로 많이 사용되는 연결강도의 변화 △wji 에 대한 수식은 (식 27) 과 같다.
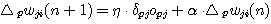 (식
27)
(식
27)
여기서 n 은 학습의 횟수, α 는 상수이며 α*△pwji(n) 은 오차진동을 적게하여 수렴속도를 빨리하기 위하여 첨가한 모멘텀항 (momentum term) 이다.
연결강도의 변경방법은 패턴을 제시할 때마다 연결강도를 변경하는 방법과 학습패턴을 전부 제시한 후 한꺼번에 변경하는 일괄 연결강도 변경 방법이 있다.
Backpropagation 학습 알고리즘은 기울기를 따라가는 (gradient descent) 방법의 하나인데 이 알고리즘의 단점중의 하나는 지역 최소값 (local minima) 에 빠질 염려가 있다는 것이다. 이를 개선하기 위하여 은닉 unit 수를 증가시키거나, 모멘텀항 α 의 이득 (gain) 항 Л 를 조절해 나가는 방식을 사용하거나 또는 연결강도의 초기값을 여러 가지의 임의 (random) 수를 주어 학습시킴으로써 좋은 결과를 택하는 방법도 있으나 획기적인 방안은 아직 고안되어 있지 않다.
이러한 단점외에도 Backpropagation 학습 알고리즘은 학습 과정이 수렴되기까지 아주 많은 양의 학습 데이터를 필요로 한다거나 기억된 패턴의 수정, 추가학습 등이 불가능하다는 등의 단점을 가지고 있다. 그럼에도 불구하고 multi layer perceptron 은 구현이 쉽고 학습이 어느 정도 가능하다는 이유로 해서 현재 가장 많이 사용되고 있다.
백프로퍼게이션 학습 알고리즘의 학습 과정은 다음과 같다.
|
■ 백프로퍼게이션 학습 알고리즘 학습 과정 ■ [1 단계] 네트워크의
상태를 결정하는 연결강도 wji, wkj
와 오프셋 (offsets) [2 단계] 학습 패턴을 설정한다. [3 단계] 학습
패턴의 값을 입력층 유니트에 제시하여 출력되는 값 opi,
입력층과 중간층 사이의 연결강도 wji 와 중간층
유니트 j 의 오프셋 [4 단계] 중간층
유니트의 출력 opj, 중간층과 출력층 사이의
연결 강도 wpk 와 출력층 유니트 k 의 오프셋
[5 단계] 학습패턴의 목표출력 tpk 와 실제 출력 opk 와의 차로부터 출력층 유니트 k 에 연결된 연결강도와 출력층 유니트 k 의 오프셋에 대한 오차 δpk 를 구한다. [6 단계] 오차 δpk 와 중간층과 출력층간의 연결강도 wkj 와 중간층의 출력 netpj 로부터 중간층 유니트 j 에 연결된 연결강도와 중간층 유니트의 오프셋에 대한 오차 δpj 를 구한다. [7 단계] 5
단계에서 구한 출력층 유니트 k 에서의 오차 δpk,
중간층 유니트 j 의 출력 opj, 정수 α 와의
곱을 더하여 중간층 유니트 j 와 출력층 유니트 k 에 연결된 연결강도
wkj 를 수정한다. 또 오차 δpk 와
정수 β 와의 곱을 더하여 출력층 유니트 k 의 오프셋 [8 단계] 중간층
유니트 j 의 오차 δpj, 입력층 유니트 i 의
출력 opi, 정수 α 와의 곱을 더하여 입력층
유니트와 중간층 유니트 j 에 연결된 연결강도 wji
를 수정한다. 또 오차 δpj 와 정수β 와의 곱을
더하여 중간층 유니트 j 의 오프셋 [9 단계] 다음 패턴을 학습시킨다. [10 단계] 모든 학습패턴에 대하여 전부 학습할 때까지 2 단계로 되돌아간다. [11 단계] 학습의 반복 획수를 센다. [12 단계] 학습의 반복 획수가 제한 횟수보다 작으면 2 단계로 되돌아간다. [13 단계] 종료 |
<그림 3> 백프로퍼게이션 학습 알고리즘의 학습과정
1 단계부터 13 단계까지의 처리를 흐름도 (flow chart) 로 나타내면 <그림 3> 과 같다. 지금까지의 설명으로부터 알 수 있듯이 3 단계부터 4 단계까지는 입력층으로부터 중간층을 거쳐 출력층에의 전방향 (forward) 처리이고, 5 단계와 6 단계는 오차를 구하는 과정이며, 7 단계부터 8 단계까지는 출력층으로부터 중간층, 입력층에의 역방향 (backward) 처리이다.
Backpropagation 학습 알고리즘은 다층의 구조를 갖는 복잡한 신경망 학습 알고리즘으로 최급하강법을 기본으로 한 매우 유용한 패턴인식 해법이다. 그러나 이 방법이 가지고 있는 몇가지 문제점이 있다.
첫 번째 문제점으로는 Backpropagation 학습 알고리즘이 지역 최소점에 빠질 가능성이 있다는 점이다. 오차함수는 연결강도가 만든 다차원 공간에서 비교적 간단한 모양을 하고 있는 것 같은 착각을 하기 쉬우나 반드시 그런 것만은 아니다. 예를 들면 <그림 4> 와 같이 뉴런이 은닉층의 3 개 뉴런과 접속하고 있고 이 뉴런의 출력값이 커짐에 따라 은닉층의 첫 번째 뉴런이 흥분하기 시작하고, 두 번째 뉴런이 흥분을 억제하기 시작하며, 세 번째 뉴런이 흥분하기 시작한다고 하자. 이 세 개의 뉴런이 출력층의 한 개 뉴런에 연결되어 있다고 하면 그 출력층의 뉴런은 첫 번째 뉴런의 출력에 대해서 올라갔다 내려갔다 하며 복잡한 변화를 한다. 여기서 첫 번째 뉴런에 들어오는 연결강도를 변화시키면 최종출력은 매우 복잡한 변화를 할 것이 예상된다. 이와같이 오차함수의 모양이 매우 복잡해질 것을 고려하면, 경우에 따라 오차 0의 한 개의 골짜기 이외에 몇 개의 골짜기가 있을 가능성이 있다. 이 상태를 <그림 5> 에 나타내었다. 최급하강법은 반드시 가장 낮은 골짜기를 목표로 하는 방법이 아니라 지금 있는 점에서 보아 가장 급경사면을 따라 내려가는 것이므로 오차가 0 이 아닌 지역 최소점에 머무를 가능성이 높다. 이와같은 전역적 최소점이 아닌 지역 최소점에서는 연결강도에 대한 오차함수의 미분계수가 0 이므로 그 곳에서 탈출할 수 없게되고 오차만 남게된다. 즉 원하는 패턴을 출력하지 못하는 상태에서 네트워크가 안정되어 버린다.
<그림 4> 연결강도의 변화에 따른 복잡한 출력의 예
<그림 5> 연결강도와 오차함수
두 번째 문제점은 Backpropagation 학습 알고리즘이 포화영역에서 잘 동작하지 않는다는 점이다. (식 25), (식 26) 로부터 뉴런의 포화영역에서는 f' 가 0 이 되므로 연결강도는 변화하지 않는다. 시뮬레이션 초기에는 연결강도의 값은 대개 0 부근의 값으로 초기화되지만 시뮬레이션이 진행됨에 따라 연결강도는 점점 커져 포화형 함수 f 의 입력 레벨도 크게 변화되어 사실상 계단 함수로 동작하게된다. 즉 대부분의 뉴런이 f' 가 거의 0인 포화영역에서 동작하게 된다. 이러한 상황에서 네트워크의 환경이 변한다면 네트워크는 이전의 것과는 다른 출력을 요청받게 된다. 그러나 f' 가 거의 0 이므로 연결강도는 거의 변할 수 없다. 물론 이런 경우에는 연결강도 전부를 어떤 계수로 축소한다든지 포화함수를 천천히 변화시킨다든지 등의 여러 가지 해결방법도 있지만 생물기관과 유사한 방법은 아직 찾아내지 못했다.
세 번째 문제점은 이 방법이 기본적으로 신호기 입력에서 출력까지 한 방향으로만 흘러가는 전방향(feedforward) 방식이라는 것이다. 실제 생물의 뇌에서는 내부에 무수히 많은 루프를 가지고 있으며 피드백(feedback)을 구성하고 있다. 더욱이 출력된 신호가 외부를 경유해서 입력에 피드백하는 경우도 많다. 이러한 시스템에서는 용이하게 발진이 일어나고, 그 생물은 발진을 잘 이용하여 정보를 처리한다. 그러나 Backpropagation 학습 알고리즘과 이밖에 현재 제안되고 있는 많은 신경망 패턴인식기는 전방향 방식을 원칙으로 하고 있어 앞으로 고차원의 시스템을 구현할 경우 문제가 될 것으로 예상된다.
이밖에 Backpropagation 학습 알고리즘을 사용할 때 문제가 되는 것은 다음과 같다.
① 학습이 완료되기까지 많은 횟수의 반복학습이 필요하다.
② 응용분야에 따라 학습 파라미터의 조절이 필요하다.
③ 추가 학습시 전체적인 재학습이 필요하다.
④ 학습의 완료시점을 예측할 수 없다.
①, ② 와 같은 문제점들을 해결하기 위하여 지금까지 제안된 방법들은 다음과 같으며 ③ 과 ④ 의 문제점은 피할 수 없다.
(1) 일괄 수정법
Backpropagation 학습 알고리즘은 학습패턴을 1 개 입력한 후 오차를 계산하여 연결강도와 임계값을 수정한다. 그러나 일괄 수정법은 학습패턴 각각에 대한 오차로부터 구한 연결강도와 임계값의 수정량을 평균하여 학습패턴 전체의 수정량을 계산한다. 이것을 이용하여 임계값을 일괄적으로 수정하는 방법이다. 이 방법은 수정횟수가 적으므로 학습시간을 단축시킬 수 있어 효과적이라고 생각될 수 있다. 그러나 수정량이 평균값으로 처리되어 미묘한 수정을 할 수 없어서 복잡한 문제에 적용하는 것은 어렵다.
(2) 출력값의 제한
각 unit 의 출력값은 시그모이드 함수에 의해 0 부터 1 까지의 값이 되지만 출력값이 0 또는 1 에 가까운 값이 되기 위해서 시그모이드 함수의 입력값은 아주 작은 값이나 아주 큰 값이 될 필요가 있다. 따라서 시그모이드 함수의 출력을 예를 들면 0.01 부터 0.99 가지의 값이므로 제한하는 방법이 있다. 이 방법은 중간층 unit의 출력값이 0 또는 1 이 되지 않으므로 연결강도의 수정이 계속 진행되어 학습이 종료되기 어렵다.
(3) 모멘텀 방법
Backpropagation 학습 알고리즘에서 연결강도와 오프셋의 수정량은 출력층에 의한 오차의 기여도에 따라 구해지지만 모멘텀 방법은 이전의 수정량도 고려하여 수정량을 결정하는 방법이다. 이 방법은 엄밀히 말하자면 최급하강법은 아니지만 오차로부터 구해진 수정량에 의한 오버 스프트를 억제하여 학습의 고속화에 유효한 것으로 알려져 있어 일반적으로 많이 사용되고 있다.
(4) 수정 모멘텀 방법
Backpropagation 학습 알고리즘에서 학습의 초기에는 수정방향이 임의적일 수 있으나 학습이 진행됨에 따라 점차 이전의 수정방향과 근사한 방향으로 수정이 될 것이다. 따라서 학습이 진행됨에 따라 모멘텀의 비중을 점차 크게 하여 학습의 고속화를 이루는 방법이다. 그러나 모멘텀의 비중을 너무 크게 하면 오차에 의한 수정이 일어나지 못하게 되므로 모멘텀의 비중 설정에 있어서 상한선을 설정해두는 것이 필요하다.
(5) 학습계수의 최적화 방법
학습 패턴수나 학습의 진행 상황에 따라 학습계수를 자동적으로 선택하여 학습의 효율화를 얻는 방법이다. 즉, 여러 개의 학습계수를 미리 준비하여 오차의 제곱을 구하고, 그 값이 최소가 되는 학습계수를 선택하여 연결강도와 오프셋을 수정하는 방법이다. 이 방법은 매번 여러 개의 학습계수를 사용하여 오차를 구하므로 계산량이 많은 문제점이 있다.
(6) 복잡도 방법
일반적으로 신경망을 복잡하게 하면 학습패턴에 대해서는 잘 처리할 수 있지만 문제의 성질을 적절히 일반화시키기에는 어려운 문제점이 있다. 특히 학습패턴에 노이즈가 포함되어 있는 경우 본질적이지 못한 패턴까지도 학습된다. 이러한 문제점을 해결하기 위해서는 네트워크의 자유도가 될 수 있는 한 작은 것이 좋다. 러멜하트 (Rumelhart) 는 이러한 점을 고려하여 Backpropagation 학습 알고리즘에 네트워크의 복잡도라는 새로운 요소를 추가한 복잡도 방법을 제안했다. 그가 제안한 복잡도 방법은 다음과 같다. 오차 (E), 복잡도 (compexity) 를 결합한 평가함수 (cost) 를 만들어 이것이 최소가 되도록 연결강도를 바꾸어가는 방법이다.
Cost = λ * E + (1 - λ) * Complexity
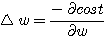
Complexity
= Cweight + C unit = 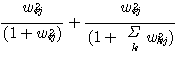
여기서 Cweight 는 연결강도의 정도에 따른 복잡도 비교이며 Cunit 는 unit 의 수에 의한 복잡도이다.
네트워크의 복잡도를 줄이는 방법은 다음과 같다.
* 네트워크의 연결수를 줄인다.
* 중간 unit의 수를 줄인다.
* 네트워크의 대칭성을 높인다.
* 연결강도를 나타내는 비트의 수를 늘린다.
(7) 선택적 재학습 방법
Backpropagation 학습 알고리즘의 학습 종료 시점은 전체 학습패턴의 오차합이 주어진 허용치보다 작아지는 때이다. 그런데 학습시켜야 할 패턴이 많은 경우에는 전체에 비하여 매우 적은 일부 학습패턴의 오차 때문에 학습 속도가 늦어지는 것을 볼 수 있다. 즉, 훈련이 잘 안되는 몇몇 학습패턴의 오차를 줄이기 위하여 전체 학습패턴을 계속 반복적으로 학습시켜야 하는데 이때 소모되는 노력이 매우 크다. 따라서, 좀 더 효과적인 학습 방법이 필요하다. 선택적 재학습 방법은 학습 과정에서 훈련이 잘 안되는 패턴을 집중적으로 재학습 시키는데, 이때 편중된 학습에 의하여 발생할 수 있는 기존의 학습된 패턴의 손실 정도를 조사함으로써 최적의 재학습을 할 수 있다. 선택적 재학습은 인간의 학습 과정과도 어느 정도 일치하는데, 새로운 사실을 배울 때 어려운 것을 보다 많이 반복하여 학습하는 것과 유사하다. 이것은 수학적으로는 명확하지 않지만 학습이 잘 되지 않는 패턴을 좀 더 집중적으로 학습에 참여시키고자 하는 것이며, 이와같은 방법을 사용하면 학습에 소요되는 시간을 줄일 수 있을 뿐만 아니라, 학습 결과 생성된 신경망 자체도 사용된 전체 학습패턴을 잘 일반화하여 인식률을 높일 수 있다.
(8) 연결강도 갯수의 축소
인공 신경망의 기능에 대한 연구는 많이 진행되고 있는데 비하여 그 구조에 대한 연구는 매우 미비한 실정이다. 대부분의 신경망 모델들은 모든 노드 사이를 연결시키는 방법을 사용하며, 특히 Backpropagation 과 같은 모델은 강 층사이의 노드를 모두 연결시킨다. 이러한 방법은 노드의 수가 몇 백개 미만인 간단한 문제에서는 상관 없지만, 노드의 수가 수만개 이상이 되는 실제 문제의 경우에는 매우 많은 계산이 필요하다. 일부에서는 이러한 문제를 해결하기 위하여 일반적인 네트워크 구조인 하이퍼 큐브 (hyper-cube) 나 사각 그리드 (rectanguar grid), 또는 링 (ring) 과 같은 구조를 도입한 CNN (Compact Neural Netword)과 RINN (Reduced Interconnections Neural Network) 등을 설계하고 구현하는 연구가 진행되고 있다. 또 다른 연구로는 네트워크의 구조를 초기에 임의로 구성하고, 여러 가지 매개변수를 조정하면서 검사 데이터에 대하여 원하는 기능을 할 때까지 구조를 변경하는 과정을 반복하는 방법을 사용하는 것도 있다. 하지만, 이와같은 신경망 설계 방법은 근본적으로 해결하고자 하는 문제의 성격을 고려하지 않는 구조이기 때문에 어느정도 효율의 손실을 감수해야만 하는 단점이 있다.
연결강도 갯수의 축소 방법은 학습후에 중요하지 않은 연결선을 제거하여 전체 연결선의 수를 줄임으로써 인식 속도를 높이는 것이다. Backpropagation 학습 알고리즘과 같은 모델의 노드가 하는 일은 단순히 입력값들의 가중된 합을 비선형 함수에 의하여 정규화시키는 것이므로, 이 때 값이 0혹은 0에 가까운 연결은 제거하여도 효율에는 큰 영향을 미치지 않는다. 이와같은 방법을 통하여 생성된 신경망은 연결선의 수가 감소되어 소형 컴퓨터에서 사용하기 용이할 뿐만 아니라 인식 과정의 속도도 높아지는 장점이 있다. 이때, 연결선을 제거함에 따른 속도의 개선과 성능 저하의 상호 관계를 분석하여 문제에 따른 최적의 신경망 구조를 선정한다.
제 2 장에서 설명한 XOR 문제는 은닉 unit 를 필요로 하는 고전적인 문제이다. <그림 6> 은 multilayer perceptron 을 이용하여 XOR 문제의 해를 구한 것이다. 이 때는 4 개의 입출력 패턴을 885 회씩 제시하여 학습한 후에 얻어진 것이다. 네트워크의 학습계수 Л 는 0.5 로 한다. <그림 6> 에서 화살표 위의 숫자는 연결강도를 나타내며 원내의 숫자는 오프셋 (offset) 이다. 이 해에서는 은닉unit와 출력 unit 두쪽 모두 양 (+) 의 오프셋을 가지고 있으므로 다른 unit 에 의해 억제되지 않는한 ON 이 된다.
은닉 unit 는 입력 unit 가 양쪽 모두 ON 이 아닌 경우에는 ON 이 된다. 그리고 은닉unit가 ON 일 경우에는 출력 unit 는 OFF 가 된다. 입력 unit에서 출력 unit로의 결합은 입력 unit 가 양쪽모두 ON 일 경우에만 출력 unit 가 OFF 가 된다. 네트워크를 이용하여 문제를 풀기 위해서는 수백회의 패턴의 제시와 연결강도의 수정이 필요하였다. <그림 6> 과 같이 하나의 은닉 unit를 사용한 경우외에 <그림 7> 과 같은 두 개의 은닉 unit 를 가지고 입력 unit 에서 출력 unit 로의 결합이 없는 네트워크에 관해서도 실험을 했다. 실험 결과 단지 두 번만이 국소점에 빠져 정확한 해를 구할 수 없었고 나머지 경우에는 모두 정확한 해를 구했다. 국소점에 빠졌을 때의 네트워크의 연결강도를 <그림 7> 에 나타냈으며 점선은 음 (negative) 의 연결강도를 나타낸다.
이 네트워크는 입력이 00 과 10 의 경우에 대해서는 정확한 값을 출력하지만 11 과 01 에 대해서는 출력 unit 의 총합은 0 이 되어 출력값은 0.5 가 된다. 이 네트워크의 상태는 학습계수를 0.25. 각각의 패턴을 6,587 회씩 제시한 후에 얻어졌다. 다른 문제에서는 더 많은 제시가 필요하겠지만 이 문제의 경우에는 더 이상 제시를 반복해도 연결강도의 크기가 증가할 뿐 성능의 향상은 없었다. 이와같은 국소점에 빠지는 빈도를 예상하는 것은 어려우나 몇 가지 문제를 해결한 경험에 의하면 이러한 것은 매우 드문 현상이라고 볼 수 있다. 참고로 이러한 일이 일어난 것은 수백 종류의 문제에 대한 많은 실험을 통해서 단 두 번의 경우에만 일어났을 뿐이다.
XOR 의 문제는 네트워크 학습에 관하여 여러 가지 특성을 조사하기 위한 테스트 케이스로서 매우 유용하다. 예를 들면 이브 쇼빈 (Yves Chauvin) 은 <그림 6> 타입의 네트워크를 사용해서 은닉 unit 의 수 및 학습계수의 변화가 학습의 속도에 주는 영향을 조사했다. 각각의 입력패턴에 대해서 출력의 오차가 0.01 이 될 때까지 245 회, 32 개의 은닉 unit 를 사용한 경우에는 120 회이다. 그의 실험 결과를 정리하면 학습시에 제시될 패턴의 횟수 P 는 P = 280 - 33logH 와 같이 된다. 여기서 H 는 은닉 unit 의 갯수이다. 그러므로 XOR 를 풀기 위해 필요한 패턴의 제시 횟수는 은닉 unit 의 개수 H 의 로그 (logarithm) 에 비례해서 감소한다고 할 수 있다. 이 관계는 H = 40 정도까지의 범위에서 성립되고 있다. 이러한 은닉 unit 의 갯수와 패턴 제시 횟수와의 관계는 거의 모든 문제에 대하여 일반적으로 성립했다. 쇼빈은 또한 은닉 unit 의 수를 8 개로 고정하고, 학습계수를 변화시켜서 학습속도의 변화를 조사해 학습계수가 0.1 일 때의 평균 450 회부터 학습계수가 0.75 일 때의 평균 68 회까지의 결과를 얻었다. 더 이상 학습계수를 크게 하면 학습이 불안정하게 되는 것도 실험결과 알아냈다. 그러나 위의 범위내에서 학습계수를 크게 하면 할수록 학습속도가 향상됨을 알아냈다.

<그림 6> 생성된 XOR 네트워크의 예
<그림 7> XOR 문제의 국소해
패리티 문제는 입력패턴이 홀수개의 1 을 포함한 경우에만 1 을 출력하는 문제이다. 이 문제는 아주 유사한 입력에 대해서 다른 출력을 내지 않으면 안되므로 네트워크를 이용하여 풀기에는 쉽지 않은 문제이다. XOR 문제는 입력 유니트 수가 2 개인 특수한 경우의 패리티 문제라고 할 수 있다 <그림 8> 과 같은 계층구조 네트워크를 이용하여, 입력의 크기가 2부터 8 까지의 경우를 실험해 보았다. 이와같은 모양의 네트워크를 사용할 경우에는 N 의 패리티 문제를 풀기 위해서는 적어도 N 개의 은닉 유니트가 필요하다. <그림 8> 은 네트워크가 학습한 해의 기본적인 원리를 나타내고 있다. 그림에서 실선으로 나타낸 연결은 연결강도가 +1 이며, 점선의 연결은 연결강도가 -1 이다. 유니트를 나타내는 원내의 숫자는 그 유니트의 오프셋이다. 각각의은닉 유니트는 입력 패턴 내의 1 의 갯수를 세는 것과 같은 역할을 한다.

<그림 8> 패리티 문제해의 원리적인 설명도
예를들면 <그림 8> 의 제일 왼쪽의 은닉 유니트는 한 개 이상의 입력 유니트가 ON 인 경우에 ON 이 되며 그 옆의 유니트는 2 개 이상의 ON 인 경우에 ON 이 된다. 모든 입력 유니트가 ON 인 경우에는 왼쪽부터 m 개 까지의 은닉 유니트가 ON 이 된다. 은닉 유니트로부터 출력 유니트에의 결합은 +1, -1 이번갈아 되어 있기 때문에 짝수개의 은닉 유니트가 ON 일 경우에는 출력 유니트에의 입력의 합이 0 이 되며, 홀수개의 은닉 유니트가 ON 일 경우에는 입력의 총합이 1 이 된다. <표 1> 은 실제의 실험에서 얻어진 해의 하나를 나타낸다. 이해는 16 가지의 입력패턴을 각각 2,825 회 제시한 후에 얻어진 것이며 학습계수는 0.5였다. 즉, ON 이 되는 은닉 유니트의 수는 입력 유니트 내에 OFF 인 것의 수와 같다. 그러나 원리적으로는 같은 것이다. 주의할 것은 은닉 유니트의 층에 나타나는 패턴이 입력패턴내의 ON 의 갯수만에 의한 것으로 되어있는 것이다. 이와같은 내부 표현이야말로 패리티 문제를 해결하는데 필요한 것이다.
<표 1>
|
Number of on Input Units |
|
Hidden Unit Pattern |
|
Output Value |
|
0 1 2 3 4 |
―→ ―→ ―→ ―→ ―→ |
1111 1011 1010 0010 0000 |
―→ ―→ ―→ ―→ ―→ |
0 1 0 1 0 |
에클리 (Ackley), 힌튼 (Hinton), 세즈노스키 (Sejnowski) [ACK85] 는 1985 년에 입력 유니트보다도 적은 수의 은닉 유니트를 사용하여 서로 직교하고 있는 입력패턴의 집합을 직교하고 있는 출력패턴의 집합에 대응시키는 문제를 다루었다. 이 경우, 은닉 유니트상의 각각의 내부 표현은 입력층상의 내부 표현보다 효율적으로 표현되어야 할 것이다.
N 개의 입력패턴과 출력패턴을 대응시키는 문제를 생각해보자. 은닉 유니트를 log2N 개 사용한다. 이 문제를 해결하기 위하여 네트워크는 N 개의 입력패턴의 각각을 은닉층에서 길이 log2N 의 이진부호로 표현하는 것을 학습할 것이다. <그림 9> 에 이 문제를 풀기 위하여 사용한 네트워크의 기본 구조를 나타내었다. 문제의 본질은 N 비트의 패턴을 log2N 비트의 패턴에 부호화하는 것과 그 부호를 복원하는 것의 학습이다. 백프로퍼게이션 학습 알고리즘을 사용하여 여러 가지 크기의 부호화 문제를 실험했다.
여기에서는 그 중에서 8 비트의 입력패턴, 3 개의 은닉 유니트를 사용한 예를 소개한다.

<그림 9> 부호화 문제를 풀기 위한 네트워크
문제는 <표 2> 에 나타낸 것처럼 항등사상의 학습이다. 즉, 입력패턴에서 ON 이 된 위치에 출력 유니트도 ON 이 되도록 하는 것이다. <표 3> 은 학습의 결과를 나타낸다. 네트워크는 은닉층에서의 표현에 중간값 (0.5) 을 사용한 것을 알 수 있다. 물론 은닉층에서 1 이나 0 의 값만 갖는 해를 가질 수도 있다. 실제로 그러한 해가 얻어지는 경우도 많다. 그러나 이 예에서는 네트워크를 될 수 있는 한 1 이나 0 의 값을 갖도록 하였으나 중간값을 갖는 해를 얻었다. 다음에 중간값을 갖지 않으면 안되는 문제에 대하여 검토해보자.
<표 2>
|
Input Patterns |
|
Output Patterns |
|
10000000 01000000 00100000 00010000 00001000 00000100 00000010 00000001 |
―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ |
10000000 01000000 00100000 00010000 00001000 00000100 00000010 00000001 |
<표 3>
|
Input Patterns |
|
|
|
Output Patterns |
||
|
10000000 01000000 00100000 00010000 00001000 00000100 00000010 00000001 |
―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ |
.5 0 1 1 0 .5 1 0 |
0 1 1 1 1 0 0 0 |
0 0 0 1 1 1 .5 .5 |
―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ |
10000000 01000000 00100000 00010000 00001000 00000100 00000010 00000001 |
<표 4>
|
Input Patterns |
|
Output Patterns |
|
00 01 10 11 |
―→ ―→ ―→ ―→ |
1000 0100 0010 0001 |
<표 4> 는 2 비트로 분산 표현된 입력을 4 비트 표현의 출력패턴에 대응시키는 문제를 나타낸다. 입력패턴간의 유사관계는 출력패턴간의 관계에 반영하지 않았다. 이 문제에 대하여 다음과 같은 구조적인 제약을 갖는 네트워크를 사용하여 실험하였다. 두 개의 입력 유니트는 하나의 은닉 유니트와만 결합하고, 은닉 유니트는 다른 4 개의 유니트와 결합하고 있다. 그리고 4 개의 은닉 유니트는 출력 유니트와 결합하고 있다. 따라서 이 네트워크는 먼저 4 개의 입력패턴의 각각을 하나의 은닉 유니트의 다른 값으로 변환하는 것을 학습하지 않으면 안된다. 이 4 개의 중간값은 다음의 4 개 은닉 유니트위의 분산적인 표현으로 변환하고, 출력 유니트위의 국소적인 표현으로 변환한다. 학습계수를 0.05, 패턴의 제시 획수를 5,226 로 하여 학습한 결과를 <표 5> 에 나타낸다. <표 5>에서 알 수 있듯이 각각의 입력패턴은 하나의 은닉 유니트의 다른 상태값에 대응되고 있다. 이들 값은 다음의 은닉층위의 분산적인 표현에 대응되고, 출력층의 4 비트 표현으로 변환되어 있다. 원리적으로 이 방법은 입력패턴의 수가 제한되어 있지 않지만, 입력패턴의 수가 많아지면 구별해야 할 상태값의 차이가 작아지므로 난이도가 높아진다.
<표 5>
|
Input Patterns |
|
Singleton Hidden Unit |
|
Remaining Hidden Units |
|
Output Patterns |
|||
|
10 11 00 01 |
―→ ―→ ―→ ―→ |
0 .2 .6 1 |
―→ ―→ ―→ ―→ |
1 1 .5 0 |
1 1 0 0 |
1 0 0 0 |
0 0 .3 1 |
―→ ―→ ―→ ―→ |
0010 0001 1000 0100 |
<그림 10> 은 학습 후의 네트워크를 나타낸다. 은닉 유니트로부터 출력 유니트로의 연결강도는 그림을 이해하기 쉽게하기 위하여 생략했다. 그림에서 실선은 양 (+) 을 나타내고, 점선은 음 (-) 을 나타낸다. 4 개의 중간값은 부호가 다른 아주 큰 값의 결합에 의해 얻어진다. 제 1 층에서 은닉층의 한쪽 결합은 은닉 유니트를 완전히 ON 으로 만들고, 다른 한쪽은 완전히 OFF 로 만든다. 두 개의 결합의 차이는 그다지 크지 않으므로 양쪽의 입력 유니트가 ON 인 경우에는 은닉 유니트는 0 과 0.5 사이의 값을 가진다. 양쪽 모두 OFF 인 경우는 은닉 유니트의 바이어스가 거의 0 이므로 0.5 를 조금 넘는 값을 가진다. 제 2 층에서 은닉층은 제 1 층의 은닉 유니트가 완전이 ON 일 경우에는 제일 오른쪽의 유니트만이 ON 이 되고 나머지는 OFF 가 된다. 또 전부가 OFF 인 경우에는 좌단 이외의 3 개가 ON 이 된다. 이밖의 2 개의 값에 관해서는 각각 다른 패턴이 출력되도록 결합되어 있다. 이처럼 네트워크의 학습은 매우 유연하다. 이러한 실험으로부터 은닉 유니트는 대부분 1 또는 0 의 값을 가지지만 경우에 따라서는 중간값을 갖는 것을 알 수 있다. 여기서 유니트가 1 또는 0 을 갖기 쉬운 성향은 시그모이드 함수가 S 자형을 하고 있어, 유니트의 입출력의 절대값이 크게 되면, 유니트의 값은 1 또는 0 으로 수렴하기 때문이다. 따라서 중간값을 갖기 위해서는 유니트 입력의 절대값이 그다지 크지 않은 값을 가져야 한다. 한편 일반화 델타 규칙에서는 모든 유니트가 같은 입출력 함수를 사용한다는 가정이 없으므로 중간값을 원하는 유니트에 관해서는 선형의 입출력 함수를 사용하고, 다른 유니트에서는 시그모이드를 사용하는 경우도 생각할 수 있다. 선형의 유니트는 강력한 동적영역 (dynamical range) 을 가지므로 보다 강력한 중간값 표현을 사용할 수 있다.

<그림 10> 중간값을 이용한 네트워크
대칭성 문제는 입력패턴의 중심대칭 여부를 판단하는 문제이다. 이 문제에 대하여 여러 가지 크기의 입력패턴과 은닉 유니트에 대하여 실험했다. 실험결과 입력패턴의 크기에 관계없이 2 개의 은닉 유니트만 있으면 대칭성 문제가 해결됨이 보였다. 네트워크가 발견한 내부 표현을 이해하기 위하여 입력패턴의 크기를 6 으로 한 예를 <그림 11> 에 나타내었다. 그림에서 중앙에 있는 6 개는 입력 유니트이며, 두 개의 은닉 유니트는 상하에 나타내었다. 또한 가장 오른쪽의 유니트는 출력 유니트이다. 이 해는 학습계수를 0.1, 각각의 패턴을 1,208 회씩 제시한 후 얻은 것이다. 그림을 보기 쉽게 하기 위하여 6 개의 입력 유니트를 중앙에 두고, 2 개의 은닉 유니트를 상하에 두었다. 대칭성을 판단하는 출력 유니트는 오른쪽에 그렸다. 해의 포인트는 중심 대칭의 위치에 있는 입력 유니트로부터 은닉 유니트에서의 연결강도가 크기가 같고 부호가 반대가 되어 있는 것이다. 그러므로 대칭적인 입력패턴이 주어지면 2 개의 은닉 유니트로의 입력의 총합이 0 이 된다. 은닉 유니트는 음 (-) 의 바이어스를 가지고 있으므로 이들의 유니트는 OFF 가 된다. 따라서 양 (+) 의 바이어스를 갖는 출력 유니트는 ON 이 된다.

<그림 11> 대칭성 문제에 사용한 네트워크
또 다른 주목할 점은 중심의 좌우에 있는 3 개의 연결강도의 크기의 비율이 대략 1:2:4 인 점이다. 이것에 의해 한쪽 3 개의 입력 유니트로부터 은닉 유니트로의 입력의 총합은 8 종류의 패턴에 대하여 전부 다른 값을 갖는다. 따라서 비대칭적인 입력패턴에 대하여 오른쪽 반으로부터의 은닉 유니트로의 입력과 왼쪽 반으로부터의 은닉 유니트로의 입력이 서로 상쇄되는 경우는 있을 수 없다. 마지막으로 2 개의 은닉 유니트는 각각의 입력 유니트로부터 부호가 서로 다른 연결강도를 가지고 있다. 이것에 의해 어떠한 비대칭적인 입력패턴에 대해서도 어느 쪽이든 1 개의 은닉 유니트는 ON 이 되고, 출력 유니트를 OFF 로 할 수 있다. 다시 말하자면, 네트워크의 구조는 입력패턴이 대칭인 경우는 은닉 유니트가 항상 OFF 가 되고, 비대칭인 경우에는 반드시 은닉 유니트의 1 개가 ON 이 되도록 되어 있다.
이 문제는 2 진수의 덧셈을 네트워크를 이용하여 수행하는 것이다. <그림 12> 는 문제의 기본 구조와 최소의 네트워크에 의한 해를 나타낸다. 네트워크는 4 개의 입력 유니트, 3 개의 출력 유니트, 2 개의 은닉 유니트들로 구성되어 있다. 2 개의 입력패턴 (2비트) 의 합이 출력패턴이 되도록 구성되어 있다. 입력층의 왼쪽에서 두 번째와 네 번째의 유니트가 하위 비트이고, 첫 번째와 세 번째의 유니트가 상위 비트이다. 우단의 은닉 유니트는 2 개의 상위 비트가 양쪽 모두 ON 이 되고, 좌단의 은닉 유니트는 2 개의 상위 비트가 모두 ON 이 되거나, 둘중 하나와 좌단의 은닉 유니트가 ON 인 경우에 ON 이 된다. <그림 12>에서 연결강도의 값을 나타내지 않은 것은 모두 1 이다. 점선은 억제성 (-) 의 연결강도를 나타내며, 원내의 숫자는 유니트의 바이어스이다. 출력의 최하위 비트는 입력의 2 개의 하위 비트의 XOR 를 값으로 한다. XOR 문제를 풀기 위하여 우단의 은닉 유니트가 사용되었다. 2 개의 하위 비트가 모두 ON 인 경우에는 은닉 유니트가 ON 이 되고, 출력의 최하위 비트는 억제되어 OFF 가 된다. 하위 비트 중에서 1 개만 ON 인 경우에는 은닉 유니트는 OFF 이고, 출력의 최하위 비트는 ON 이 된다. 출력의 중앙의 비트에 관해서는 좀 복잡하다. 이 비트는 입력의 상위 비트 2 개와 우단의 은닉 유니트를 합친 3 개의 유니트 중 홀수개가 ON 인 경우에 ON 이 되지 않으면 안된다.

<그림 12> 덧셈계산 (2 비트의 2 진수) 네트워크
네트워크의 동작 원리를 살펴보면 다음과 같다.
먼저, 좌단의 은닉 유니트는 입력의 상위 비트와 우단의 은닉 유니트로부터 입력을
받아 그 중에서 2 개 이상이 ON 일 경우에 ON 이 된다. 출력의 중앙 유니트는 같은
3 개의 유니트로부터 입력을 받고 또한 좌단의 은닉 유니트로부터 연결강도 -2 의
결합을 받고 있다. 따라서 3 개의 유니트 중 하나가 ON 인 경우에는 좌단의 은닉
유니트는 OFF 이므로 출력의 중앙 유니트는 ON 이 되고, 3 개 중에 2 개가 ON 인
경우에는 좌단의 은닉 유니트도 ON 이 되어 출력의 중앙 유니트에 억제적으로 적용하여
출력의 중앙 유니트는 OFF 가 된다. 더욱이 3 개 모두가 ON 인 경우는 좌단의 은닉
유니트로부터의 억제에 의해 3 개의 유니트의 입력의 합이 크게 되므로 중앙 유니트는
ON 이 되는 것이다.
출력의 최상위 비트는 왼쪽의 은닉 유니트가 ON 일 경우에만
ON 이 되면 된다. 이렇게 하여 <그림 12> 가 덧셈을 실현한 매우 컴팩트한
네트워크임을 알 수 있다. 이 네트워크의 구조는 문제의 크기가 커지더라도 기본적인
원리를 바꾸지 않고 일반화가 가능하다. 일반적으로 2 개의 m 비트의 2 진수를 덧셈하기
위해서는 2m 개의 입력 유니트와 m 개의 은닉 유니트, m + 1 개의 출력 유니트가
필요하다.
공교롭게도 이 문제에서는 지역 최소값이 관측되었다. 모든 입력 유니트는
모든 은닉 유니트에 연결되어 있고, 모든 은닉 유니트는 모든 출력 유니트와 결합되어
있으며 은닉 유니트들간에 서로 연결을 가지고 있는 구조의 네트워크를 사용했다.
네트워크는 <그림 12> 에 나타낸 것과 같은 본질적인 해를 얻은 경우도 있었지만
거의 비슷하게 지역 최소점에 빠졌다. 지역 최소점에 빠진 것은 출력의 최하위에
관한 XOR 문제가 그림에 나타낸 것과 같은 형태로 풀지 못한 경우이다. 즉 2 개의
은닉 유니트 중에서 상위의 은닉 유니트가 XOR 를 위하여 사용된다면 불가능하다.
결국 문제는, 두 번째의 출력 유니트에 관한 학습은 첫 번째의 출력 유니트에 관한 학습을 전제로 하고 있으므로, 첫 번째의 출력 유니트에 관한 XOR 의 학습으로 어느 쪽의 은닉 유니트를 사용할 것인가이다. 이렇게 하여 반정도는 틀린 은닉 유니트가 처음에 사용되어 학습이 실패하는 것이다. 이 경우 11 + 11 → 110 (3 + 3 = 6) 이 11 + 11 → 100 으로 잘못 계산되었으며, 다른 경우에는 정확한 계산을 했다. 이 문제의 특성은 은닉 유니트가 대등하지 않은 구조를 가지고 있다는 점이다. 다른 문제에서는 모든 은닉 유니트가 잠재적으로 등가이므로 이러한 문제는 일어나지 않는다. 그러나 이러한 문제에는 간단한 해결법이 존재한다. 즉 여유분의 은닉 유니트를 사용하면 된다. 이렇게 하면 처음에 틀린 선택을 한 경우라도 바른 해를 얻을 가능성이 남게 된다. 실제 2 비트의 덧셈에 관해서는 하나의 여분의 은닉 유니트를 준비하면 항상 바른 해를 얻을 수 있다. 그보다 사이즈가 큰 문제의 경우에는 2 개나 3 개가 필요하다. 3 개의 은닉 유니트를 사용한 2 비트의 덧셈의 예를 <그림 13> 에 나타냈다. <그림 13> 은 학습계수를 0.5, 학습 제시 횟수를 3,020 회 한 후의 상태이다. 알기 쉽게 하기 위하여 네트워크의 결합을 4 개로 나누어 나타냈다.

<그림 13> 덧셈을 하기 위해 학습된 네트워크
먼저 <그림 13> 의 (a) 에는 은닉 유니트에의
결합과 은닉 유니트간의 결합이 나타나 있다. 최하위의 은닉 유니트는 입력의 하위
비트 중에 하나라도 ON 이 있으면 OFF 가 된다. 바꾸어 말하면 이 유니트는 입력의
하위 비트가 둘다 OFF 인 것을 검출한다. 최상위의 은닉 유니트는 입력의 합이 2
이상의 경우에는 언제나 ON 이 되도록 되어있다. 중간의 은닉 유니트가 입력의 합이
3 이하일 경우에는 언제나 ON 이 되도록 되어 있다.
<그림 13> 의 (b) 는
한자리의 출력 유니트로의 결합을 나타낸다. 여기서는 XOR 의 경우가 계산되는 것을
알 수 있다. 먼저 양쪽의 하위 비트가 OFF 인 경우에는 은닉 유니트가 ON 이 되고
출력을 억제한다. 역으로 양쪽의 하위 비트가 ON 인 경우에는 이들의 유니트가 직접
출력 유니트를 억제한다. 하위 비트 중 하나만 ON 인 경우에는 출력 유니트의 바이어스에
의해 출력 유니트는 ON 이 된다. <그림 13> 의 (c) 는 중간의 출력 유니트로의
결합을 나타내고 <그림 13> 의 (d) 에는 최상위의 출력 유니트로의 결합을
나타낸다. 이러한 결합에 의해 덧셈이 올바르게 수행되고 있는 지를 확인하기는 그리
쉬운 일은 아니다. 지금까지 소개한 문제에서는 은닉 유니트의 역할을 분석하기가
그다지 어렵지 않았다. 그러나 은닉 유니트의 수가 필요 이상으로 많을 경우에는
분석하기가 매우 어려워진다. 이것은 네트워크가 내부 표현으로 국소적인 표현을
사용하는 경향이 적기 때문이며, 일반적으로 알려진 내부 표현은 분산적인 표현이
많다.
<표 6> 은 16 종류의 입력에 대한 은닉 유니트의 반응을 나타낸다.
<표 6>
|
Input Patterns |
|
Hidden Unit Patterns |
|
Output Patterns |
|
00 + 00 00 + 01 00 + 10 00 + 11 01 + 00 01 + 01 01 + 10 01 + 11 10 + 00 10 + 01 10 + 10 10 + 11 11 + 00 11 + 01 11 + 10 11 + 11 |
―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ |
111 110 011 010 110 010 010 000 011 010 001 000 010 000 000 000 |
―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ |
000 001 010 011 001 010 011 100 010 011 100 101 011 100 101 110 |
부정 문제는 n + 1 비트의 이진패턴을 입력하여
n 비트의 이진패턴을 출력하는 문제이다. n + 1 개의 입력 중 n 개는 출력에 대응하지만
나머지 하나는 특별한 역할을 한다. 즉 비트는 부정을 나타내는 비트로서 OFF 인
경우에는 남은 n 비트는 그대로 출력으로 나타나지만, ON 인 경우에는 남은 n 비트의
부정을 갖는 패턴을 출력하도록 해야 한다. 즉 문제는 부정 유니트와 다른 3 개의
입력 유니트의 각각의 XOR 를 취하는 것에 귀착한다. <표 7> 은 대응하는 패턴을
나타낸다. 여기에서는 좌단의 비트가 부정 비트이지만 네트워크는 그것을 알 수 없으므로
어떤 비트가 부정 비트인가도 학습하여야 한다. 입력 유니트로부터 모든 은닉 유니트와
출력 유니트에 결합이 있고, 은닉 유니트는 모든 출력 유니트와 결합한 네트워크를
사용하여 실험하는데 학습의 결과는 <그림 14> 에 나타냈다.
이 그림에서는
연결강도가 0 이 아닌 결합만을 나타냈다. 해답의 기본적인 구조는 이 그림에서 알
수 있듯이 부정 비트와 각각의 입력 비트와의 XOR 를 구하는 것이다. 오른쪽의 2
개의 입력 비트는 부정 유니트와 입력 유니트의 양쪽이 OFF 되는 것을 검출하는 은닉
유니트가 형성되어 있다. 남은 하나의 이력 비트는 부정 유니트와 입력 양쪽이 ON
되는 것을 검출하는 은닉 유니트가 형성되어 있다. 이 문제의 해는 학습계수를 0.25
로 하고 각각의 패턴을 5,000 회 정도 제시하여 얻었다.
<표 7>
|
Input Patterns |
|
Output Patterns |
|
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ ―→ |
000 001 010 011 100 101 110 111 111 110 101 100 011 010 001 000 |

<그림 14> 부정 문제로 학습된 네트워크
지금까지 다루었던 문제는 대칭성 판단을 제외하고 수치적인 문제였다. 여기에서는 보다 기하학적인 문제로서 T 와 C 를 평행이동과 회전에 관계없이 판별하는 문제를 다루겠다. <그림 15> 는 실험에 사용된 패턴을 나타낸다. T 와 C 의 패턴은 모두 5 개의 정방형으로 구성되어 있으며, 정방형 하나의 부분만 다르다. 더욱이 민스키와 파퍼트 [MIN69] 가 지적한 것처럼 이들의 패턴으로부터 2 개의 정방형을 선택하여 그들간의 거리의 집합을 만들면 정확히 일치한다. 그러므로 이것을 구별하기 위해서는 적어도 3 개 이상의 정방형의 조합을 보지 않으면 안된다. 이러한 이유로 민스키 등은 이 문제를 차수 3 (order three) 이라고 불렀다. 학습을 효과적으로 하기 위하여 지금까지와는 다른 구조의 네트워크를 사용하였다.

<그림 15> 실험에 사용한 입력패턴

<그림 16> T-C 판별 네트워크
<그림 16> 은 네트워크의 기본적인 구조를
나타낸다. 모든 입력 유니트로부터 은닉 유니트에 연결이 있는 것이 아니라, 2 차원으로
나열하였을 때 각각의 은닉 유니트는 입력층의 3 × 3 의 영역으로부터 입력을
받는다. 즉 그림에서 입력층에 나타낸 겹쳐진 각각의 정방형이 대응하는 은닉 유니트의
수용영역이 되어있다. 모든 은닉 유니트는 하나의 출력 유니트에 연결되어 있다.
입력에
나타낸 패턴이 T 일 경우에 출력 유니트의 값은 1, C 의 경우에는 0 을 갖도록 한다.
더욱이 학습이 장소에 따라 의존하지 않도록 모든 은닉 유니트는 같은 결합의 연결강도를
학습하도록 한다. 이렇게 하면 모든 은닉 유니트는 수용영역으로부터의 입력에 대하여
동일한 함수를 계산하게 된다. 이것에 의해 결과적으로 위치 불변성이 보장됨은 물론
입력층의 단의 영향 (edge effects) 도 피할 수 있다.
이러한 제약을 실현하기
위해서는 간단하게 델타 규칙으로 계산되는 각각의 유니트에 대한 결합의 수정량을
모두 더하여, 이것을 바탕으로 모든 유니트에의 연결강도를 같게 수정한다. 이 결과
모든 은닉 유니트는 동일한 특징추출기의 복제가 되어, 동일 특징추출기가 입력층의
다른 영역에도 많이 존재하는 것과 같다. 또 한 곳에서의 학습이 자동적으로 전체에
전파된다.
위와 같은 네트워크를 사용하여 여러 번 학습을 실험한 결과 여러 가지 해를 얻었다. 해를 이해하기 위해서는 어떠한 수용영역이 형성되었는가를 보면 된다. <그림 17> 은 여러 개의 수용영역을 나타낸다. <그림 17> 의 (a) 는 아주 국소적인 표현이다. ON 중심, OFF 주변형의 수용영역은 우수한 T 검출기가 되어있다. 왜냐하면 그림처럼 배치된 T 는 입력합 +1 을 갖지만 C 의 경우에는 어떻게 배치하여도 양 (+) 의 입력을 갖는 경우는 없다. 이 검출기를 사용하여 은닉 유니트의 바이어스를 적당히 설정하면 T 가 존재하는 경우에는 반드시 하나의 은닉 유니트가 ON 이 되고, C 의 경우에는 한 개도 ON 이 되지 않도록 할 수가 있다. 이것은 일종의 돌기검출로서 T 의 돌기부를 검출함으로서 T 와 C 를 식별한다. <그림 17> 의 (b) 에 나타낸 수용영역도 T 검출기의 일종이다. T 가 제시되면 하나의 은닉 유니트에의 입력이 +2 가 된다. C 의 경우에는 어떠한 은닉 유니트도 입력이 +1 을 넘지 못한다. 그림에 나타낸 것처럼 90 도 또는 270 도 회전시킨 T 의 경우에는 횡봉의 밑에 있는 은닉 유니트 중 하나가 +2 의 입력을 받는다. 나머지 두 개의 경우 (0 도와 180 도) 에는 T 의 돌출부분이 검출된다. <그림 17> 의 (c) 는 보다 분산적인 표현을 나타낸다. 그림에서 알 수 있듯이 T 가 제시되면 5 개의 은닉 유니트가 ON 이 되고, C 의 경우에는 3 개만이 ON 이 된다. 이 경우에도 T 의 돌기부분과 C 의 돌기부분의 차이가 검출에 이용되었다. 마지막으로 흥미로운 예를 <그림 17> 의 (d) 에 나타냈다. 이 경우에는 은닉 유니트의 바이어스를 +1 로 설정한다. 따라서 패턴이 조금이라도 수용영역에 포함이 되면 은닉 유니트는 OFF 가 된다. C 는 T 보다도 컴팩트하여 T 가 21 개의 은닉 유니트를 OFF 로 하는 것에 비하여 C 는 20 개를 OFF 시킴으로써 식별 가능하다. T-C 판별 문제는 8 개의 패턴을 약 5,000 ~ 10,000 회를 제시하여 해를 얻었다.

<그림 17> T-C 판별문제의 해로 얻어진 여러 가지 수용영역
단층 퍼셉트론의 문제점과 제한성이 민스키와 파퍼트 [MIN69] 에 의해 철저히 분석되고 난 후 퍼셉트론 모델에 관한 연구는 약 20 년간 거의 외면되어 왔다. 러멜하트 등이 PDP 모델을 고안하고난 후 다층 퍼셉트론에 대한 새로운 관심이 일어났다. 이 장에서는 다층 퍼셉트론 모델에 관한 설명과 더불어 백프로퍼게이션 학습 알고리즘에 관하여 살펴보았다. 또한 백프로퍼게이션 학습 알고리즘을 이용하는 여러 가지 적용 예들을 살펴보았다.
1 절에서는 머리말을, 2 절에서는 입력층, 은닉층
및 출력층을 가진 다층 퍼셉트론의 기본적인 구조와 층의 갯수에 따른 결정 구역의
특성을 살펴 보았다.
3 절에서는 백프로퍼게이션 학습 알고리즘의 배경을 살펴
보았다. PDP 그룹에 의한 생성 배경과 지역 최소값 수렴 등의 단점들을 기술하였으며,
이 알고리즘의 역사적인 배경을 살펴 보았다.
4 절에서는 백프로퍼게이션 학습
알고리즘에 대하여 기술하였다. 델타 규칙을 최급하강법을 이용하여 수식으로 유도하였다.
다음으로 일반화 델타 규칙을 유도하였으며 13 단계로 나눈 백프로퍼게이션 학습
알고리즘의 학습과정을 플로우 챠트와 더불어 기술하였다.
5 절에서는 백프로퍼게이션
학습 알고리즘의 3 가지 중요한 문제점들을 살펴보았으며 이러한 문제점을 해결하기
위한 일괄 수정법 등 8 가지 개선책을 기술하였다.
6 절에서는 다층 퍼셉트론의
적용 예들을 살펴 보았다. XOR 문제, 패리티 문제, 부호화 문제, 대칭성 문제, 덧셈
문제, 부정 문제, T-C 판별 문제 등의 서술과 더불어 시뮬레이션을 통한 결과들을
살펴 보았다.
◈ 생각할 점 ◈
1. 다층 퍼셉트론에서 층의 갯수에 따른 결정 구역은 어떻게 다른가?
2. 델타 규칙과 일반화 델타 규칙과의 유사성과 차이점들을 기술하시오.
3. 백프로퍼게이션 학습 알고리즘은 문자인식을 비롯하여 여러 분야들에 응용되고 있다. 그러나 이 알고리즘은 여러 가지 단점들도 가지고 잇다. 이들을 열거하고 간략히 설명하시오.
4. 은닉층의 갯수가 하나 이상인 퍼셉트론을 다층 퍼셉트론이라고 정의한다. 은닉층의 갯수가 늘어남에 따른 장단점들을 생각해 보시오.
5. 백프로퍼게이션 학습 모델의 단점중의 하나는 추가적인 학습이 불가능하다는 점이다. 이것은 무엇을 의미하는가?
6. 인간의 두뇌를 시뮬레이션하려는 것이 신경망 연구의 주된 목표중의 하나이다. 최근에 널리 쓰이고 있는 다층 퍼셉트론에서의 노드 연결과 인간의 신경세포와의 연결은 어떤 점에서 서로 다른가?
7. 단층 퍼셉트론에서 해결이 불가능한 XOR 문제가 다층 퍼셉트론에서 해결이 가능한 이유를 설명하고 해결까능한 네트워크의 연결강도들과 임계값을 제시하시오.