초기의 신경망 이론 및 모델
신경망 이론과 응용(1) : 김대수, 하이테크 정보, 1992, Page 59~86
2. 맥컬럭-피츠 (McCulloch-Pitts) 뉴런
3. 헵의 학습 규칙 (Hebbian Learning Rule)
8. 선형 분리 가능(Linear Separability)
9. Adaline (Adaptive Linear Neuron)
1940 연대에 시작된 신경망 관련 연구는 50 년이 지난 오늘날 많은 관심과 더불어 활발하게 진행되고 있다. 최초의 모델로 여겨지는 맥클럭-피츠 모델에서의 단순한 논리 구현과 '헵의 시냅스' 라고 알려진 연결강도 조정을 위한 생리학적 학습 규칙으로부터 시작된 신경망 이론은 1957 년 로젠블럿에 의해 발명된 '퍼셉트론' 모델에서 상당한 기대를 모았으나 1969 년 민스키와 파퍼트가 저술한 '퍼셉트론즈' 이후 약 20 년간 침체기를 맞이하게 되었다. 이 장에서는 초기의 신경망 이론과 모델들에 관해 그 배경과 예제들을 통하여 체계적으로 살펴보기로 한다.
초기의 신경 시스템 모델 중에서 아마도 가장 잘 알려진 것은 1943년 워렌 맥컬럭 (Warren McCulloch) 과월터 피츠 (Walter Pitts) 에 의해 제안된 모델일 것이다. 그들은 인간의 두뇌를 논리적 서술을 구현하는 이진 원소들의 결합으로 추측했는데, 이진 원소인 뉴런은 on이나 off 상태를 나타낸다. 맥컬럭과 피츠가 쓴 논문 [MCC43] 의 요약 부분 중의 첫 단원을 소개한다.
신경 활동의 '전부 아니면 전무 (All-or-Nothing)' 적인 특성 때문에 신경계의 일과 그들 사이의 관계들은 명제논리 (Propositional logic) 로 취급된다. 모든 망의 행동은 이러한 관점에서 기술될 수 있다. ...중략... 어떠한 조건들을 만족시키려는 논리적 표현에 대하여, 우리는 그것이 기술하는 방법대로 행동하는 망을 찾을 수 있다.
이 논문의 가장 중요한 결과는 그러한 신경망들이 완벽하게 일반적이어서 어떤 유한한 논리적 표현도 실현할 수 있다는 점이다. 이 모델은 명백히 실용적인 의미를 내포하는데 그러한 뉴런들을 합쳐서 강력하고도 범용적인 컴퓨터 장치를 마들 수 있다. 이외에도 1943년 그 당시에 맥컬럭-피츠 모델과 같은 프로젝트가 펜실베니아 대학의 Moore School of Engineering 에서도 진행중 이었다. 맥컬럭과 피츠는 이 논문을 쓰는 데 단지 3 개의 문헌만 참조하였는데 모두가 수학적인 논리를 다룬 책들이다. 맥컬럭과 피츠는 뉴런의 오퍼레이션을 지배하는 5 개의 가정 (assumptions) 을 하였다. 그 가정들은 컴퓨터 과학자들에게 맥컬럭과 피츠의 뉴런으로 알려지게 되었는데 다음과 같다 [MCC43].
① 뉴런의 활동은 '전부 아니면 전무' 의 과정이다.
② 어떤 뉴런을 흥분되게 (excited) 하려면 2개 이상의 고정된 수의 시냅스가 일정한 시간내에 활성화 (activated) 되어야 한다.
③ 신경 시스템에서 유일하게 의미있는 시간지연 (delay) 은 시냅스에서의 지연 (synaptic delay) 이다.
④ 어떠한 억제적인 (inhibitory) 시냅스는 그 시각의 뉴런의 활성화(activation)를 절대적으로 방지한다.
⑤ 네트워크의 연결 구조는 시간에 따라 바뀌지 않는다.
예를 들면, 만약 두 개의 자극적인 (excitatory) 입력 a, b 를 가진 단순한 뉴런이 있고 임계값이 1이라고 하자. 시각이 t일 때 처음 a, b 가 비활성적 (inactive) 이라면 시각 t + 1 일 때의 뉴런은 두 개의 비활성적인 시냅스의 합이 0 이므로 비활성적이다. 만약 a 가 활성적이고 b 가 비활성적인 경우 시각 t + 1 일 때 뉴런의 상태는 활성적이게 된다. 왜냐하면 비활성적인 시냅스와 활성적인 시냅스의 합은 1 인데 이 값이 임계값과 같기 때문이다. 만약 b 가 활성적이고 a 가 비활성적인 경우, 그리고 a, b 모두가 활성적인 경우에도 그 뉴런은 활성적이게 된다.
이와같이 두 개의 자극적인 입력을 가지고 임계값이 1 인 뉴런은 논리적 'OR' 연산을 수행하게 된다. 만약 위와 같은 뉴런에다 임계치만 2 로 줄 경우, 이 뉴런은 논리적 'AND' 를 수행하는데 이 경우 a, b 둘다 활성적인 경우만 이 뉴런이 활성적이게 된다.
앞에서 살펴본 바와 같이 맥컬럭과 피츠의 뉴런은 단순한 임계 논리를 수행할 수 있다. 그들의 신경 활동 법칙인 '전부 아니면 전무'는 어떠한 명제도 뉴런의 활동으로 표현될 수 있다는 것을 보여 준다. 단순한 명제들간의 네트워크 연결을 통하여 대단히 복잡한 명제들을 만들 수 있다. 어떤 유한한 논리적 표현도 맥컬럭과 피츠의 뉴런들로 구현될 수 있다는 것이 이 논문을 더욱 중요하게 만들었다.
<그림 1> 은 명제 논리로 나타낸 맥컬럭과 피츠의 네트워크이다. 여기에서 번호가 적힌 큰 원은 뉴런의 몸체이고 작고 검은 원은 자극성 연결이며 작은 원은 억제성 연결을 나타낸다.
<그림 1> 명제 논리로 나타낸 맥컬럭과 피츠 네트워크
이 맥컬럭과 피츠의 네트워크는 네트워크내의 단순한 요소들의 연결을 통하여 무한한 컴퓨팅 능력을 가진다는 점에서 매우 고무적인 것이다. 그 요소들이 신경생리학에 의거했기 때문에, 인간의 두뇌가 잠재적으로는 논리와 계산을 처리할 수 있는 강력한 장치인 것을 암시해 주었다. 이러한 논리 요소 네트워크의 결과는 데이터와 프로그램을 지정하여 작동하는 현대 디지털 컴퓨터의 논리적인 윤곽을 처음으로 그려낸 폰 노이만 (John von Neumann) 에게도 중요한 영향을 끼쳤다. 폰 노이만의 유명한 기술 문서 (1945년) 에 따르면,
모든 디지털 컴퓨팅 장치는 각각 평형 상태에 있는 '요소 (element)' 와 같은 릴레이를 가지고 있다. 그러한 요소들은 2개 또는 그 이상의 별개의 상태 (state) 를 가진다. 중략... 그 릴레이 행위는 요소가 지시된 형태의 자극을 받을 때마다 자극을 발산한다. 고등 동물들의 뉴런들은 틀림없이 위의 감각들을 가진 요소라고 할 수 있다. ...중략. W.Pitts 와 W.S.McCulloch 를 따라... 중략. 우리는 뉴런의 기능의 더 복잡한 양상은 여기서 더 언급하지 않기로 한다.
맥컬럭과 피츠의 이 논문이 끼친 영향과 중요성은 매우 크다고 할 수 있다. 신경 시스템이 기본적인 처리 요소들인 뉴런들과 그들의 연결들로 주어졌을 때 실제로 무엇이 가능한가를 이해하려는 시도이다.
맥컬럭과 피츠의 이론 [MCC43, MCC5, PIT47] 에 대한 증명이나 표현은 이해하기가 매우 어려우며 후에 인간 두뇌 활동의 정확한 모델링은 아닌 것이 판명되었지만 그 중요성은 결코 간과될 수 없을 것이다.
생물학적인 신경 시스템은 그들이 가져야 할 지식이나 능력들이 모두 사전(事前)에 프로그램된 것은 아니다. 생물학적인 지식이나 능력은 계속적인 학습을 통하여 이루어지며 일정한 기간 동안 일어난 학습과정은 새로운 지식이 들어왔을 때 네트워크를 다시 수정하여 계선한다.
1949 년 캐나다의 심리학자인 도날드 헵 (Donald Hebb) 은 그의 저서인 'The Organization of Behavior' [HEB49] 에서 '헵의 시냅스' 라고 알려진 시냅스의 연결강도 조정을 위한 생리학적 학습 규칙을 기술했는데 이 책은 1949년경의 신경심리학에 대해 폭넓고 깊이있게 기술하고 있다. 그는 이 책의 도입 부분에서 복잡한 두뇌 모델링에 대해 '커넥셔니즘 (connectionism)' 이란 말을 처음으로 사용하였다.
헵은 여러 가지 중요한 아이디어를 제공했다. 첫 번째, '헵의 시냅스' 라고 알려진 것에 대한 분명한 서술이다. 그러나 수학적으로 엄밀한 표현은 아니다. 둘째, 헵은 신경 시스템의 '분산된 (distributed)' 표현 방식을 날카롭게 지적하고 있다. 이 아이디어는 즉, 어떤 것을 표현하기 위하여 여러개의 뉴런들이 참여해야 한다는 것이다. 셋째, 헵은 그가 'cell assemblies' 라고 부르는 것의 형태를 공리화 하였다. 그 기본적인 아이디어는 신경 시스템에서의 정보 표현을 형성하는 한편 서로 연결되고 자기강화 (self-reinforcement) 를 하는 뉴런의 부분 집합에 관한 것으로, 하나의 셀 (cell) 은 문맥에 따라 한 개 이상의 assembly 에 속할 수도 있다.
그러면 "우리는 어떻게 학습하는가?" 에 대한 비교적 간단한 학습이론에 대하여 살펴보자. 이에 대한 기본적인 학습이론은 1949 년 헵 (D.D. Hebb) 의 'The Organizaion of Behavior' [HEB49] 란 저서에서 처음으로 논의되었는데 중심적인 아이디어는 다음과 같다.
두 개의 뉴런 A, B 가 서로 반복적이고 지속적으로 점화 (firing) 하여 어느 한쪽 또는 양쪽 모두에 어떤 변화를 야기한다면 상호간의 점화의 효율은 점점 커지게 된다.
헵의 기본적인 아이디어를 수식으로 표현해 보자. 한 유니트 ui 가 다른 유니트 uj로부터 입력을 받으면 두 유니트 모두 활성화된 상태에서 uj 에서 ui 로의 연결강도 wij 는 더욱 더 강해진다. 이것을 식으로 나타내면,
Δwij = лaioi (식 1)
여기서 л 는 학습률을 나타내는 비례상수이고, ai 는 뉴런 i 의 출력이며, oj 는 뉴런 j 의 출력이다. 일반적으로,
H(oj(t). wij) = oj(t)
g(ai(t). ti(t)) =л(ti(t)-ai(t)) (식 2)
로 나타낸다. 여기에서 ti(t) 는 ui 의 교사입력이고, h 는 연결강도 wij 의 함수이며, g 는 교사입력 ti 의 함수를 나타낸다. 이것을 바로 위드로우-호프 (Widrow-Hoff) 법칙이라고 하는데, 학습의 양은 실제 활성화량의 목표입력과의 차이에 비례하기 때문에 델타 규칙 (Delta rule) 이라고도 한다.
Δwij = л(ti(t) - ai(t)) * oj(t) (식 3)
이것은 퍼셉트론의 학습 규칙으로 사용되고 그로스버그 (Grossberg) 모델에서는 다음의 식이 사용된다.
Δwij = лai(t) (oj(t) - wij) (식 4)
위에서 살펴본 바와 같이 헵의 학습 규칙은 나중에 개발된 다른 신경망 모델들의 학습 규칙의 토대가 된다는 것을 알 수 있다. <그림 1>는 헵의 뉴런 연결을 나타낸다.
<그림 1> 헵의 뉴런 연결
1957년 미국의 프랭크 로젠블럿 (Frank Rosenblatt) 에 의해 발명된 퍼셉트론은 처음 소개되었을 때 상당한 센세이션을 불러일으켰다. 퍼셉트론은 비교적 정확히 기술된, 계산에 의한 최초의 신경망 모델이었으며 여러 분야에 걸쳐 커다란 영향을 끼쳤다. 로젠블릿은 원래 심리학자였으며 퍼셉트론은 그러한 심리학적인 요구에 부응하는 것이었다. 또한 퍼셉트론이 잠재적으로 복잡한 적응행위를 할 수 있는 학습 머신이라는 점은 엔지니어들에게는 매우 매력적인 것이었다.
그가 기술한 퍼셉트론 모델은 매우 복잡했다. 퍼셉트론, 그리고 그것과 유사한 모델들은 분석하기가 매우 어려웠으나 학습 머신으로서의 능력과 제한점에 대한 통찰력을 제공해 주었다. 퍼셉트론 이후의 연구 개발은 대부분 엔지니어와 물리학자들에 의해 진행되었다.
그러나 그의 중요한 논문 [ "Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms", by Frank Rosenblatt, 1962. ]은 읽기가 매우 어려웠다. 그는 퍼셉트론을 기술할 때 여러 개의 버전 (version) 으로 기술했으며 각 버전마다 제 나름대로 이름을 붙였기 때문에 혼란을 가져 왔다. 퍼셉트론에 대한 분석 또한 쉽지 않았다. 여러 가지 옵션과 변수와 학습 규칙들이 제대로 정리되지 않은 채 소개되어 이해에 상당한 혼란을 주었다.
로젠블럿은 노이즈가 포함되어 있거나 완전하지 않은 연결이 있을 때의 퍼셉트론의 능력에 대해서도 기술하였는데, 메모리가 여러 곳에 분산되어 있어 손상에 대해 영향을 적게 받는다는 주장이었다.
몇 년이 지난 후 이 연구 논문은 논문으로서는 아이디어를 스케치한 것에 불과하다고 여겨졌다. 퍼셉트론이 많은 분류 (classification) 를 학습할 수 있다는 그 유명한 퍼셉트론 수렴정리 (Perceptron convergence theorem) 에 대한 증명이나 그것에 대한 인식조차 없었다. 단지 학습 가능성에 대한 몇가지 통계적인 계산만이 포함되었고 나중에 밝혀진 대로 학습 가능성에 대한 제한성을 간과하고 있었다.
최초의 신경망 장치인 마크Ⅰ퍼셉트론은 1957년에 제작되었으며 1958에 성공적인 시범을 보였다 [ROS58a, HEC90]. 이와 관련하여 관련자료[HEC90]를 통하여 초기의 퍼셉트론 연구를 엿볼 수 있다.
<그림 3> 은 퍼셉트론과 마크 I 퍼셉트론 신경망 컴퓨터를 발명한 프랭크 로젠블럿과 400 (20 × 20) 개의 화소 (pixel) 를 가진 마크 I 퍼셉트론 이미지 센서를 나타낸다.

<그림 3> 로젠블럿과 마크 I 퍼셉트론 이미지 센서
<그림 4> 는 마크 I 퍼셉트론 프로젝트 엔지니어인 차알스 위트만 (Charles Wightman) 이 영상입력 시스템을 조정하고 있는 사진이다. 그림에서 "C" 라고 인쇄된 문자가 20 × 20 의 CdS 행렬의 사진 전송기에 초점이 맞추어져 있다. 이 400 개의 입력은 퍼셉트론 신경망의 입력값으로 쓰여지며 A, B, C 등의 문자 클래스로 분류된다.

<그림 4> 마크 I 퍼셉트론 이미지 입력장치
<그림 5> 는 마크 I 의 8 개의 모터/전위차계로 이루어진 격자선반을 나타내는데 각각의 모터/전위차계는 하나의 연결강도 조정에 쓰인다. 여기서 퍼셉트론 학습 규칙은 아날로그 회로로 구현되었다.

<그림 5> 마크 I 퍼셉트론의 연결강도 조절 장치
마크 I 퍼셉트론 패치 보드 (patch board) 는 <그림 6> 에 나타나 있다. 여기서는 퍼셉트론의 원하는 패턴학습의 능력을 시험하기 위하여 정확한 선의 연결 (wiring)을 하지 않고 임의의 연결 패턴을 사용하였다.

<그림 6> 마크 I 퍼셉트론 패치 보드
로젠블럿 (Frank Rosenblatt) 에 의해 1950 년대
말에 발명된 단층 퍼셉트론 [ROS58a, ROS58b, ROS61] 은 위드로우 (B. Widrow)[WID60]
의
ADALINE 과 MADLINE 등의 모델과 더불어 1960년대 초에 집중적으로 연구되었으며 이
모델들은 지금의 패턴인식 연구의 바탕이 되었다. 이 장치들의 기본 요소는 임계논리
유니트 (TLU:Threshold Logic Unit) 인데 이것은 맥컬럭-피츠 뉴런의 특별한 타입의
하나이다. 그는 특정한 생물 기관에 국한되지 않는 일반적인 지능시스템 (Inteligent
system) 의 기본적인 성질들을 규명하고자 하는 노력의 일환으로 단층 퍼셉트론을
제안했다. <그림 7> 은 단층 퍼셉트론의 구조를 나타낸다.
<그림 7> 단층 퍼셉트론의 구조
첫 번째 센서층은 단순히 환경의 센서 역할을 담당한다. 이 센서층에서 생성된 신호들은 두 번째 층인 결합층과 연결되어 있다. 만약 센서층의 입력이 이진수라면 결합층은 논리회로와 같이 작용한다. 세 번째 층인 반응층은 학습을 담당하는데 결합층과 반응층 사이의 연결들은 가변적인 연결강도로 이루어져 있다.
결합층에서 반응층으로의 결합은 Adaline 의 통계적인 저항과 비슷한 가변 연결로 되어 있다. Adaline 과의 뚜렷한 차이는 반응층의 요소가 임계장치라는 것이다. 즉, 그것은 식별함수에 의해 입력값에 좌우되는 안정된 두 개의 출력상태(0 또는 1)만 가진다.
임계논리 유니트는 여러개 (n) 의 입력을 가지고 있으며 뉴런 입력의 연결강도 (synaptic strength) 와 유사한 기능을 하는 실수값 연결강도와 연계되어 있다. 임계논리 유니트의총 입력은 n차원의 백터인데 각각의 입력백터 컴포넌트 (component) 는 연관된 연결강도와 곱해지며 n 개의 이 값들은 모두 합해진다. 이 합이 임계값을 초과하면 출력은 1이 되고 그렇지 않으면 0이 된다. 이를 수식으로 표현하면 출력은 (식 1) 의 진리값으로 나타내진다 [HIN89].
출력값 y = 1 |
if Σ ifi*wi > θ |
(식 5) |
|
0 otherwise |
여기에서 fi 는 i 번째 입력선의 값이고 wi 는 i 번째의 연결강도이며 θ 는 임계값이다.
로젠블럿과 위드로우가 얼마나 서로 영향을 받았는지는 알 수 없으나 Adaline 은 후에 적응적 안테나 (Adaptive antenna) 와 같은 통신공학에 주로 응용되었으며 퍼셉트론은 이론적인 신경과학에 결정적인 영향을 끼쳤다.
컴퓨팅 장치로서의 퍼셉트론의 유용성은 구조적인 단순함에 있다. 병렬 계산의 단순한 개념은 <그림 8> [MIN69] 에 나타나 있다.
<그림 8> 퍼셉트론의 병렬 계산
로젠블럿의 퍼셉트론 이후 신경망이 무엇이든지 할 수 있는 듯이 보였던 시절이 있었다. 수백개의 알고리즘이 제시되었고, 학습 머신에 대한 관심과 열기가 대단하였다. 그러나 1969 년에 출판된 민스키 (Minsky) 와 파퍼트 (Papert) 에 의한 '퍼셉트론즈 (Perceptrons)' 란 저서 [MIN69, MIN88] 가 출간되고부터 신경망 연구에 대한 열기는 급격히 냉각되었다. 퍼셉트론즈는 퍼셉트론 모델에 대해 철저한 분석을 하였으며 또한 퍼셉트론 모델의 한계성에 대해서도 논리 정연하게 파헤쳤다. 퍼셉트론즈는 형식에 크게 매이지 않으면서도 우아한 형태로 간결하게 쓰여졌다.
퍼셉트론즈는 주어진 데이터의 선형 분리 문제도 해결할 수 없다는 등의 퍼셉트론 모델의 제한점에 관하여 예리하게 분석하였다. 특히 단층 퍼셉트론은 선형 분리의 단순한 예인 XOR 문제도 해결할 수 없었다. 민스키와 파퍼트는 퍼셉트론 모델들의 계산적인 제한점들에 관한 연구를 수학과 계산 이론에 입각하여 증명하였다.
퍼셉트론 모델의 쇠퇴 요인에는 '퍼셉트론즈'란 책 이외에 다른 요소들도 포함되어 있다. 신경망 분야 개척자의 한 사람인 위드로우 (Bernard Widrow) 에 의하면, 인공적으로 인간의 두뇌 (Chunk of Brain) 를 묘사하려는 아이디어에 대하여 많은 사람들의 저항이 있었다는 것이다. 따라서 초기 단계부터 과학적인 의구심을 내포하고 있었다. 또 다른 요인으로는 로젠블럿의 퍼셉트론 모델이 그 당시 신문 지상을 통하여 지나칠 정도로 환상적으로 소개되었다는 점이다. 두뇌 모델이 극적인 뉴스거리가 되었으며 기자들은 과학적인 이해도 없이 인공적인 두뇌 모델에 대한 가능성을 대서특필했다.
퍼셉트론즈의 출현은 그 당시 신경망에 대한 견해는 한마디로 "퍼셉트론에 관한 연구 논문은 과학적인 가치가 결여되어 있다" 또는 "퍼셉트론에 관련된 수백가지의 프로젝트와 실험 결과들은 일반적으로 지극히 실망스럽다" 등의 부정적인 견해를 보였다.
그리하여 1980 년대의 다층 퍼셉트론이 나올 때까지 단층 퍼셉트론에 대한 관심은 오랫동안 멀어졌다.
신경망에서 쓰이는 계산요소 또는 노드는 비선형적이며 대개 아날로그인데 현재의 디지털 회로에 비하여 속도면에서 매우 느리다. 가장 간단한 노드는 <그림 9>에서 보는 바와 같이 N 개의 입력을 받아 N 개의 연결강도의 벡터들과 곱해져서 특정한 출력함수 (또는 전이함수 (transfer function)) 를 거쳐 출력을 내게 된다. 노드는 내부적인 임계값이나 오프셋 θ, 그리고 비선형 함수의 형태에 따라 특징지워진다. 신경망에서 많이 사용되는 대표적인 비선형 함수로는 계단함수 (hard limiter), 임계논리 (threshold logic) 그리고 S 자 형태의 시그모이드 (sigmoid) 형 등이 있는데 이는 <그림 10> 에 나타나 있다. 그 중에서 가장 많이 쓰이는 것은 시그모이드 함수이다. 이들보다 더욱 복잡한 노드의 형태는 시간적인 총합 (temporal integration) 또는 시간에 종속적인 것들, 그리고 단순한 합이 아닌 복잡한 수학적 연산을 포함하는 것들이다.
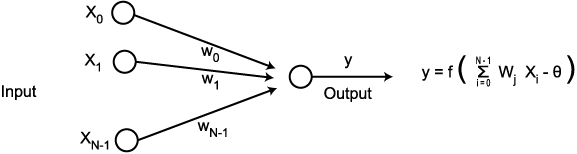
<그림 9> 기본적인 노드에서의 입ㆍ출력
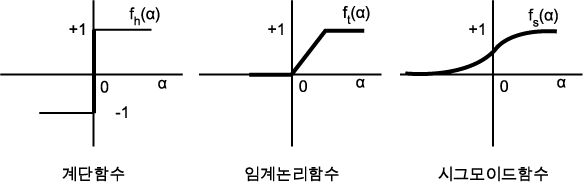
<그림 10> 3 가지 대표적인 비선형함수
연결강도를 조정하는 최초의 퍼셉트론 학습 과정은 로젠블럿에 의해 개발되었으며 이래와 같이 기술될 수 있다[LIP87].
|
< 퍼셉트론 학습 과정 > [단계 1] 연결강도들과 임계값을 초기화한다. wi(0)(0 ≤ i ≤ N - 1) 와 θ 를 임의수 (random number) 로 정한다. 여기에서 wi(t) 는 시각 t 일 때 입력 i 로부터의 연결강도를 나타내고 θ 는 출력 노드의 임계값을 나타낸다. [단계 2] 새로운 입력과 기대되는 출력을 제시한다. 새로운 연속값 (continuous value) 입력 xo, x1, ... xN-1 과 기대되는 출력 d(t) 를 제시한다. [단계 3] 실제의 출력값을 계산한다. N-1 y(t) = fh(Σwi(t)xi(t) - θ) (식 2) t=0 [단계 4] 연결강도를 조정한다. wi(t+1) = wi(t) + Л[d(t) - y(t)xi(t) (식 3) (0 ≤ i ≤ N - 1) |
|||
d(t) = |
+1 입력이 A 클래스로부터일 때 |
(식 4) |
|
-1 입력이 B 클래스로부터일 때 |
|||
|
|
|
|
|
Л는 0.0 에서 1 사이의 값이고 d(t) 는 현재의 입력에 대해 기대되는 정확한 출력값인데 입력이 어느 클래스 (A, B) 에 속하는지에 따라 좌우된다. 네트워크에 의해 정확한 결정이 되었을 때에는 연결강도는 조정되지 않으며 이 경우에 학습을 마친다. [단계 5] 단계 2 로 가서 반복 수행한다. |
|||
퍼셉트론의 학습 과정은 입력행렬과 결정 유니트 (decision unit) 사이에 한 개 이상의 가변적인 연결강도를 가진 장치들에 응용될 수 없다. 여러 층의 가변 연결강도를 가진 장치는 단층 연결강도 장치보다 인간 두뇌에 더 유사하고 보다 복잡한 판별을 할 수 있는 것은 자명하지만 이것은 단순한 퍼셉트론의 가장 주요한 특징인 자동학습 (automatic learning) 이 부족하다.
퍼셉트론의 제한점은 처음부터 명백했다. 이 모델은 기본적인 논리 연산인 exclusive-or(XOR) 함수를 수행해 내지 못한다. 이런 심각한 제한점을 모른 채 많은 사람들은 민스키와 파퍼트가 [MIN69] 가 패턴인식 장치로서의 퍼셉트론의 한계성을 매우 철저하게 분석하기 전에는 아주 희망적인 인식 모델로 여겼다.
퍼셉트론의 학습 과정에서 심리적으로 비현실적인 점은 반응이 정확할 때 어떤 학습도 일어나지 않는다는 점이다. 만족스런 심리학적 학습 모델은 'positive' 학습인데 이는 학습 중에 실수를 했을 때보다 정확하게 맞았을 때 더욱 학습 효과가 많다는 것으로 광범위한 실험이 이 점을 입증하고 있다. 이러한 점에서 퍼셉트론은 학습 모델로서는 비현실적이다. 인간의 자각력은 매우 복잡한 활동이다. 단층 퍼셉트론은 분명히 이를 만족시키지 못하며 부적당한 모델이라고 할 수 있다. 그러나 이 퍼셉트론 모델은 나중에 백프로퍼게이션 (Backpropagation) 모델과 같은 다층 퍼셉트론 모델의 기반이 되어 문자인식을 비롯한 여러 분야에 폭넓게 응용되었으며 신경망 연구의 새로운 장을 열게 된 결정적인 계기가 되었기에 이 퍼셉트론의 기여는 매우 크다고 할 수 있다.
퍼셉트론의 가장 주된 기능적인 제한점은 출력 유니트가 선형 분리 가능한 패턴들만을 분류할 수 있다는 것이다. 선형 분리 기능이란 패턴 클래스가 하나의 직선에 의해 두 개의 영역으로 나뉘어지는 것을 말하는데 <그림 11> 은 선형 분리 기능의 일반적인 개념을 그림으로 나타낸 것이다. 여기서는 4 가지 경우를 보여 주는데 첫 번째는 분리 가능' 이며 나머지는 '선형 분리 불가능' 이다.
Exclusive-or(XOR) 함수는 선형 분리가 가능하지 않은 패턴분류 문제의 대표적인 예이다. <그림 12> 는 네 개의 입력 패턴들이 하나의 직선에 의하여 2 개의 영역으로 나뉘어질 수 없음을 보여주고 있다.
<그림 11> 선형 분리 가능의 일반적인 개념
<그림 12> XOR 함수
이 모델은 Bernard Widrow (Stanford Computer Science) 가 개발한 모델이다. Adaline(Adaptive Linear Neuron) 은 신경세포의 초기 모델로서 적응형 선형결합기와 양자의 회로를 직렬로 접속한 것이다. Adaline 을 신경세포와 비교하면 적응형 연결강도는 시냅스, 입력벡터의 성분은 축색돌기 (axon) 의 입력, 양자화된 출력은 축색의 출력에 각각 대응한다. Adaline 의 출력은 실제의 신경세포에서 일어나는 것과 매우 유사하다. 적응형 선형결합기의 출력은 각각의 입력에 연결강도를 곱하여 합한 ( s = Σxiwi ) 입력신호의 선형결합이다. 입력신호와 연결강도는 벡터이며, 출력신호는 입력신호 벡터와 연결강도 벡터의 내적이다. 적응형 선형결합기의 출력은 0 이나 1 의 둘 중 하나로 결정된다. Adaline의 구조는 그림 13 과 같다.
<그림 11> Adaline 의 구조
양자화 회로에서는 적응형 선형결합기로부터 출력된 값을 다음과 같은 식을 이용하여 양자화한다.
|
출력값 y = |
+1 if s ≥ 0 |
|
|
-1 if s < 0 |
Adaline의 학습은 입력-출력을 쌍으로 순차적으로 제시하여 원하는 출력값이 나오도록 연결강도 (wi) 를 바꾸어가는 것이다. 일반적으로 Adaline의 학습은 1959년에 Widrow 와 Hoff [WID60] 가 제안한 LMS (Least Mean Square) 알고리즘을 사용한다. LMS 알고리즘을 이용한 연결강도의 변화량은 다음과 같다.
Δwi = xi (T-y) (식 10)
여기서 Δwi 는 학습률, xi 는 I 유니트의 입력값, T 는 목표값, y 는 Adaline 의 출력값이다.
Adaline의 주요 응용분야는 다음과 같이 나누어 볼 수 있다.
① 시스템 모델링 ② 통계적 예측 ③ 노이즈 제거 ④ 전화 회로에서 에코(echo) 제거 ⑤ 미지 시스템의 역모델링
⑥ 채널 이퀄라이저(channel equalizer) ⑦ 적응 신호 처리(adaptive signal processing)
Adaline 의 구현에 있어서의 델타 규칙에 서브 루틴은 다음과 같다 [CAU88]
/* Global storage variables and arrays
/* The Adaline has NUMROWS*NUMCOLS
/* total weights kept in matrix
double adaline[NUMROWS][NUMCOLS];
double input1[NUMROWS][NUMCOLS];
double input2[NUMROWS][NUMCOLS];
double answers[NUMROWS];
double insize1, insize2;/*Magnitude of each input pattern
/* adjust_wts (pattnum, res)
/* Adjust the weights of the ADALINE according to
/* the Widrow-Hoff learning law (the Delta rule):
/* w_new = w_old + (BETA*Error*Input)/[(Input)*(Input)]
adjust_wts(patt, res)
int pat; /*number of the pattern being input
double res; /*actual output
{
double error, w_old, w_new;
double in, insize;
double beta;
beta = BETA;
error = answer[patt]-res;/*error=ideal out-actual out*/
for(row=0; row<NUMROWS;row++)
{
for(col=0; col<NUMCOLS; col++)
{
switch(patt)
{
case 0:
in =input1[row][col];
insize =insize1;
break;
case 1:
in =input2[row][col];
insize =insize2;
break;
}
w_old =adaline[row][col];
w_new=w_old+beta*error*in/insize;
adaline[row][col]=w_new;
}/*end for each column
}/*end for each row
return;
}/*end adjust_wts
Adaline 은 하나의 뉴런에 상응하여 선형 분리 가능한 논리함수만이 실현 가능하다. 따라서 일반적으로 대부분의 논리함수는 실현이 불가능하다. 그러나 Adaline 의 조합이나 다량의 Adaline 을 이용하여 네트워크를 구성함으로써 비선형분리 함수를 구현할 수 있다. 이러한 생각을 바탕으로 만들어진 것이 Madaline 이다.
1960년대에 제안된 Madaline 의 구조는 1 층에는 많은 입력 유니트들로 구성되어 있고, 2층에는 ADN, OR, 다수결소자 (MAJ : Majority Votetaker) 등의 고정논리 디바이스로 구성되어 있다. Madaline 시스템의 기본적인 구조는 그림 14 와 같다.
그림 14 Madaline 시스템
그 후, 1980년대에 전방향 (feedforward) 3층 네트워크가 제안되었다. 학습은 일반적으로 다층일 경우 Rumelhart 등이 제안한 백프로퍼게이션 (Backpropagation) 알고리즘 [RUM86] 을 사용하지만 Madaline 의 경우는 각 유니트 양자화가 계단함수 (hard limiter) 를 사용하므로 미분이 불가능하여 사용할 수 없다. 따라서 Adaline 의 학습 알고리즘을 확장한 Madaline rule Ⅱ(or MR Ⅱ) 를 사용한다.
MR Ⅱ 의 기본 아이디어는 과거의 입력패턴에 관하여 학습이 끝난 응답을 될 수 있는 한 교란되지 않게 하기 위하여 다른 유니트에 영향을 가장 적게 미치는 유니트에 책임을 전가시키는 것이다. 학습의 목표는 입력패턴과 목표값을 제시하여 잘못된 응답의 갯수를 될 수 있는 대로 억제시키는 것이다. Madaline 은 패턴인식에의 응용이 가능하고 화상인식에서 위치 변화와 회전등에 적응력이 강한 신경망을 구성할 수 있다.
제 2 장에서는 초기의 신경망 이론 및 모델들에 관하여 살펴 보았다. 1943 년 워렌 맥컬럭과 월터 피츠에 의해 처음 제안된 모델에서는 인간의 두뇌를 논리적 서술을 구현하는 이진 원소들의 집합으로 생각했다. 그들의 5 가지 가정에 입각한 맥컬럭과 피츠의 뉴런은 단순한 임계 논리를 수행할 수 있었으며 네트워크내의 단순한 요소들의 연결이 무한한 컴퓨팅 능력을 가질 수 있다는 점에서 매우 고무적이었다. 맥컬럭-피츠 모델은 현대 디지털 컴퓨터의 논리적 윤곽을 처음으로 디자인한 폰 노이만에게도 큰 영향을 끼쳤다.
헵은 '헵의 시냅스' 라고 알려진 시냅스의 연결강도 조정을 위한 생리학적 학습 규칙을 연구하였다. 그의 학습이론은 비록 체계적이지는 못했지만 지금까지 뉴런의 상호 작용에 관한 한 큰 영향력을 미치고 있다.
1 절에서는 머리말을, 2 절에서는
맥컬럭-피츠 모델에 관하여 설명하였으며, 3 절에서는 헵의 학습 규칙에 관하여 기술하였다.
4
절에서는 로젠블럿이 창안한 퍼셉트론에 관하여 기술하였다. 단층 퍼셉트론의 구조
및 퍼셉트론의 생성되었을 때의 배경 및 쇠퇴 원인들을 살펴보았으며, 5 절에서는
신경망의 3 가지 대표적인 비선형 함수들을 살펴보았고, 퍼셉트론의 학습 과정은
6 절에서 기술하였다.
7 절에서는 퍼셉트론의 한계점들을 살펴 보았고, 8 절에서는
퍼셉트론의 가장 주된 제한점인 선형 분리 가능에 대하여 살펴보았다. 9 절에서는
Adline 모델을 기술하였고 10 절에서는 여러개의 Adaline 들의 집합 모델인 Madaline
에 대하여 설명하였다.
◈ 생각할 점 ◈
1. 맥컬럭과 피츠의 네트워크는 복합적인 명제 논리를 어떻게 표현하는가? 예를 들어 설명하시오.
2. 헵의 학습 규칙이 그 이후에 나온 신경망 모델들의 학습 규칙의 토대가 되는 이유는 무엇인가?
3. 퍼셉트론의 중요성과 장점들에 대하여 기술하시오.
4. 1960 연대에 선풍적인 관심과 기대를 모았던 퍼셉트론이 침체기를 맞이한 결정적인 계기는 무엇이며 퍼셉트론의 제한점들은 무엇인가?
5. 비선형 함수는 어떤 것들이 있으며 각각의 특징은 무엇인가?
6. '선형 분리 가능' 이란 무엇을 의미하며 퍼셉트론에서는 XOR 함수의 구현이 왜 불가능한가?
7. 퍼셉트론을 프로그래밍하여 구현하시오.