Nonparametric Decision Making
Pattern Recognition and Image Analysis : Earl
Gose. Richard
Johnsonbaugh. Steve Jost 저서, Prentice
Hall, 1996, Page 149~193
실세계의 대부분의 문제에서 관심사가 어떤 type의
density function을 가지는지를 모르는 경우가 많다.이러한 경우에는 일련의 sample들에 대한 임의의 density를
사용하여 맞추는 방법을 사용하는데 이것을 Nonparametric Decision Making
이라고 한다. 이것은 density의 일반적인 형태를 추측할 만한 충분한 근거를 갖고
있지 못할 때 사용한다.
sample data로부터 정확한 parameter를 구하여 parametric
decision function으로부터 각 class들의 분포를 파악하는 것이 아니라, sample로부터
확률적 parameter를 구하지 않고 각 class들의 분포 type을 모르는 상태에서 곧바로
classification을 수행한다.
분포 type을 모를 때 근사적인 parametric decision
function을 사용하는 것이 histogram 과 kernal 이며 이와는 전혀 다른 방법이 nearist neighbour
classification 방법이다.
도수분포를 나타내는 그래프를 말하며 기둥그래프 ·기둥모양 그림 등이라고도 한다. 관측한 데이터의 분포의 특징이
한눈에 보이도록 기둥 모양으로 나타낸 것이다. 가로축에 각 계급의 계급간격을 나타내는 점을 표시하고, 이들 계급간격에 대한 구간 위에 이 계급의
도수에 비례하는 높이의 기둥을 세운다. ..........
각 class 에 대한 probability density function
(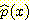 )을 모를 때 근사적인
)을 모를 때 근사적인 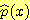 를 구하는 방법으로서 변수
를 구하는 방법으로서 변수 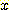 의 범위를 모든 data를 포함하는 유한갯수의 interval 로 나누어서 막대그래프로
표시한 것이다. 이때 의 각 interval을 cell 또는 bin 이라고 부른다. 각 histogram을
연결하여 density function 의 추정치로서 사용하려면 histogram 하의 합계
면적이 1 이어야 한다. 각 interval을
의 범위를 모든 data를 포함하는 유한갯수의 interval 로 나누어서 막대그래프로
표시한 것이다. 이때 의 각 interval을 cell 또는 bin 이라고 부른다. 각 histogram을
연결하여 density function 의 추정치로서 사용하려면 histogram 하의 합계
면적이 1 이어야 한다. 각 interval을  라 하고 전체 sample 의 수를
라 하고 전체 sample 의 수를 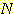 이라 하면 각 bin 의 면적은
이라 하면 각 bin 의 면적은 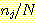 이고 그 interval 의 폭에 따라 나뉘어져 density 의 높이는
이고 그 interval 의 폭에 따라 나뉘어져 density 의 높이는  이 된다. 일단 근사치 density function 이 구해지면 Bayes'
정리를 사용하여 decision을 하게된다.
이 된다. 일단 근사치 density function 이 구해지면 Bayes'
정리를 사용하여 decision을 하게된다.
변수 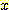 가 연속이든 이산이든 그 범위를 interval로 나누고 같은 방법을 사용하게 된다.
각
가 연속이든 이산이든 그 범위를 interval로 나누고 같은 방법을 사용하게 된다.
각  의 값을 가지는 sample 의 부분이 분포
의 값을 가지는 sample 의 부분이 분포  의 추정치
의 추정치  로 사용되고 그 합은 1 이 될 것이다.
로 사용되고 그 합은 1 이 될 것이다.
bin 의 크기를 적절하게 하는 것이 중요하며 너무
크면 그래프가 너무 rough 하게 되며 작으면 너무 변화가 심하게 된다. 이러한 histogram을
잘 만들면 원래의 probability density function을 구해 낼 수도 있다.
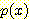
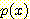
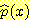
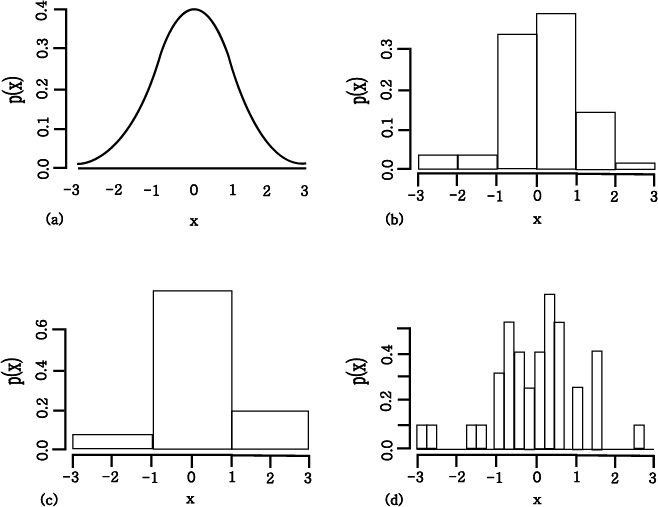
(a) 50 개의 임의의 수들로 이루어진
true normal density (b) 6 개의 interval을 가진 50 개의 normally distributed 임의의
수들에 대한 histogram (c) 3 개의 interval 의 경우 (d) 24 개의 interval
의 경우.
Example 4.1 다른 크기의 interval을 가진 density
histogram 의 구축
grapefruit volumes을 위한 density
function 의 histogram 근사치를 구해보자. 100 개의 grapefruit 을 volume  에 따라서 다음과 같은 data 가 측정되었다.
에 따라서 다음과 같은 data 가 측정되었다.
|
 의 interval 의 interval
|
interval 길이
|
sample 의 수
|
sample 들의 비율
(=area)
|
rectangle
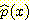 의 높이 의 높이
|
|
[0, 4)
[4, 6)
[6,
7)
[7, 8)
[8, 10]
|
4
2
1
1
2
|
10
30
30
20
10
|
0.1
0.3
0.3
0.2
0.1
|
0.025
0.150
0.300
0.200
0.050
|
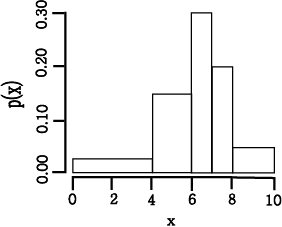
각 rectangle 의 높이는 interval
길이로 나누어진 sample 의 비율과 같다. 예를들면 0 에서 4 까지의 interval 의
경우 rectangle 의 높이는 0.1/(4-0)=0.025 이다. 결과적인 density 는 그림과 같다.
이것은 density histogram 이기 때문에 rectangle 면적의 합은 1 이어야 한다.
rectangle 의 높이는 단순한 예측치이기
때문에 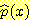 와 같이 표현한다. sample 이 많은 구간에서는 bin 의 크기가 작고, 적은 구간에서는
bin 의 크기가 크다는 것을 알 수 있다.
와 같이 표현한다. sample 이 많은 구간에서는 bin 의 크기가 작고, 적은 구간에서는
bin 의 크기가 크다는 것을 알 수 있다.
Example 4.2 histogram 과 Bayes' 정리를 사용한
classification
다음 data를 사용하여 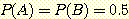 일 때,
일 때, 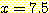 의 sample 이 class
의 sample 이 class 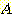 에 속하는지
에 속하는지 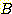 에 속하는지를 분류하라.
에 속하는지를 분류하라.
다음 data 는 class 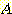 에서 선택된 60 개의 임의의 sample 의 feature
에서 선택된 60 개의 임의의 sample 의 feature 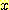 의 값이다.
의 값이다.
|
0.80
2.01
2.96
4.10
4.47
5.64
|
0.91
2.18
2.97
4.12
4.61
5.85
|
0.93
2.27
3.17
4.18
4.64
5.99
|
0.95
2.31
3.17
4.20
4.89
6.29
|
1.32
2.40
3.38
4.23
4.96
6.42
|
1.53
2.61
3.67
4.27
5.12
6.53
|
1.57
2.64
3.73
4.27
5.15
6.70
|
1.63
2.64
3.83
4.39
5.33
6.78
|
1.67
2.67
3.99
4.40
5.33
7.18
|
1.74
2.85
4.06
4.46
5.47
7.22
|
다음 data 는 class 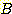 에서 선택된 60 개의 임의의 sample 의 feature
에서 선택된 60 개의 임의의 sample 의 feature 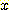 의 값이다.
의 값이다.
|
3.54
5.60
6.33
6.90
7.61
8.33
|
3.88
5.77
6.41
6.92
7.67
8.36
|
4.24
5.87
6.43
7.03
7.68
8.44
|
4.30
5.94
6.49
7.08
7.68
8.45
|
4.30
5.95
6.52
7.18
7.78
8.49
|
4.70
6.04
6.58
7.29
7.96
8.75
|
4.78
6.05
6.60
7.33
8.09
8.76
|
4.97
6.15
6.63
7.41
8.12
9.14
|
5.21
6.19
6.65
7.41
8.20
9.20
|
5.42
6.21
6.75
7.46
8.22
9.86
|
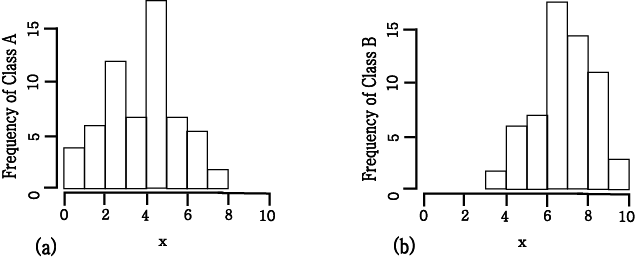
(a) class
A 를 위한 feature 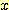 의 histogram (b) class B
의 histogram (b) class B
위의 그림은 class 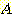 와
와 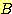 를 위한
를 위한 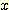 의 각 interval에서 sample들의 histogram 이다.이것을 density function 으로
변환하기 위해서, 이러한 수들이 sample 들의 전체의 수(60) 와 interval width (1)
로 나누어져야 한다.
의 각 interval에서 sample들의 histogram 이다.이것을 density function 으로
변환하기 위해서, 이러한 수들이 sample 들의 전체의 수(60) 와 interval width (1)
로 나누어져야 한다.
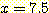 인 sample을 분류하기 위해, 7.5 에서 두 개의 histogram 의 높이를 비교한다.
왜냐하면 7.5를 포함하는 class interval 은 classes
인 sample을 분류하기 위해, 7.5 에서 두 개의 histogram 의 높이를 비교한다.
왜냐하면 7.5를 포함하는 class interval 은 classes 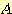 와
와 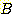 에 대하여 [7, 8] 구간이기 때문이다.
에 대하여 [7, 8] 구간이기 때문이다. 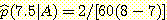 이며
이며 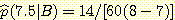 이다. 여기서 Bayes' 정리를 사용하여
이다. 여기서 Bayes' 정리를 사용하여
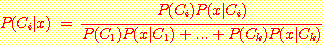
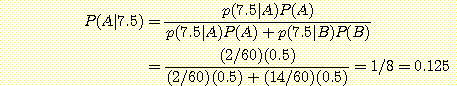
또한 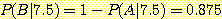 이다. 그러므로
이다. 그러므로  이다.
이다.
따라서 그 sample 은 class 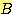 로 분류되어야 한다.
로 분류되어야 한다.
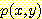
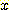
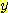
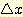 and
and 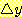
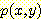
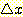
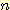




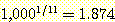

...........
예를 들면
spike 집합이나 delta 함수의 경우와
같이 각 sample 값이 매우 좁은 폭과 큰 높이를 가지는 경우 각 spike 면적의 합이 1 이 되도록 하여 true
density function의 매우 거친 근사치를 구할 수 있다. 각 spike 의 면적은 전체 sample의
수에 의해 나누어진
해당 포인트의 sample 의 수이다.
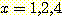 에 놓여있는 sample 들의 density를 추정하는 delta 함수 의 예 (그림 1)를 들어보자.
이러한 continuous density function 의 근사치는 의사 결정에서는 유용하게 사용될
수 없는 것이다. 그러나 그 delta 함수가 사각이나 삼각 또는
정규밀도함수 와 같은 kernel 이라고 불리는 다른 함수로 바꾸어 진다면 그들의 합계
면적이 1 이 되도록 하는 더 부드럽고 만족스런 추정을 할 수가 있다(smoothening).
에 놓여있는 sample 들의 density를 추정하는 delta 함수 의 예 (그림 1)를 들어보자.
이러한 continuous density function 의 근사치는 의사 결정에서는 유용하게 사용될
수 없는 것이다. 그러나 그 delta 함수가 사각이나 삼각 또는
정규밀도함수 와 같은 kernel 이라고 불리는 다른 함수로 바꾸어 진다면 그들의 합계
면적이 1 이 되도록 하는 더 부드럽고 만족스런 추정을 할 수가 있다(smoothening).
Example 4.3 삼각 kernel 의 사용
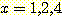 의 sample을 가지는 경우의 삼각 kernel을 사용한 추정 density function을 (그림
2) 에서 볼 수 있고, 삼각 사각 정규 분포 kernel을 사용하여 표준편차 1을 가지게
하는 경우는 (그림 3) 에서 볼 수 있다. .....
의 sample을 가지는 경우의 삼각 kernel을 사용한 추정 density function을 (그림
2) 에서 볼 수 있고, 삼각 사각 정규 분포 kernel을 사용하여 표준편차 1을 가지게
하는 경우는 (그림 3) 에서 볼 수 있다. .....
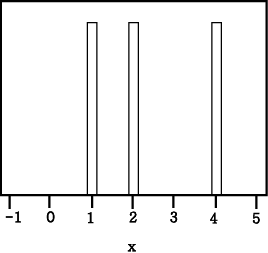
그림1 : 3 개의 delta functions
에 의해 구해진 근사치 density. 각 bar 의 높이와 폭은 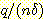 ,
, 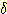 이다.
이다.
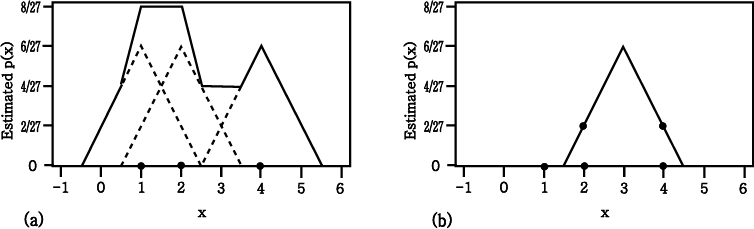
그림 2 : (a) kernel 방법을 사용해서
추정 확률 분포함수 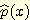 를 계산하는 것으로 kernels (점선) 과 그 합계 (실선) 를 볼 수 있다. 실선
면적의 합은 1 이다.
(b) window 방법을 사용해서
를 계산하는 것으로 kernels (점선) 과 그 합계 (실선) 를 볼 수 있다. 실선
면적의 합은 1 이다.
(b) window 방법을 사용해서 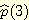 를 계산하면
를 계산하면  와 같다.
와 같다.
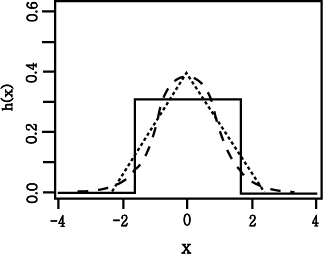
그림 3 : 3개의 kernel functions,
rectangular
(실선), triangular (점선), normal (dashed). 각 영역의 합은 1 이고
표준편차도 1 이다.
 에 있는 sample을 분류하기 위해서는 전체 밀도
에 있는 sample을 분류하기 위해서는 전체 밀도 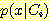 가 필요하지는 않고
가 필요하지는 않고 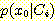 에서의 값만 필요하다. (그림 2, b) 의 경우처럼
에서의 값만 필요하다. (그림 2, b) 의 경우처럼  에서
에서 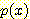 를 가정해 보자. 결과는 물론
를 가정해 보자. 결과는 물론  에서 모든 kernel 함수의 높이의 합과 같을 것이다. 이런 결과를 얻는 또 다른
방법은
에서 모든 kernel 함수의 높이의 합과 같을 것이다. 이런 결과를 얻는 또 다른
방법은  의 중앙 근처에서 kernel 함수를 반영하는 window 함수를 만드는 것이다. 그리고
이 window 에 포함된 각 sample point 의 높이를 합하는 것이다. 대칭적인
kernel 함수가 보통 사용된다. (그림 2, b)에서 window 함수는 sample 두 개를 포함하고
있고 각각의 높이는 2/27 이며
의 중앙 근처에서 kernel 함수를 반영하는 window 함수를 만드는 것이다. 그리고
이 window 에 포함된 각 sample point 의 높이를 합하는 것이다. 대칭적인
kernel 함수가 보통 사용된다. (그림 2, b)에서 window 함수는 sample 두 개를 포함하고
있고 각각의 높이는 2/27 이며 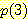 의 추정치
의 추정치 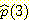 는 4/27 이다. 이것은 kernel 방법을 사용한 (그림 2, a) 와 같은 값이다.
는 4/27 이다. 이것은 kernel 방법을 사용한 (그림 2, a) 와 같은 값이다.
histogram 의 경우와 마찬가지로
kernel 이나 window 방법을 사용하는 경우에도 적절한 width 나 표준편차를 선택하는
문제는 중요하다. width 가 너무 크면 미세한 구조를 잃을 수가 있고 너무 작으면
최종 근사값이 충분히 smoothen 되지 않을 것이다.
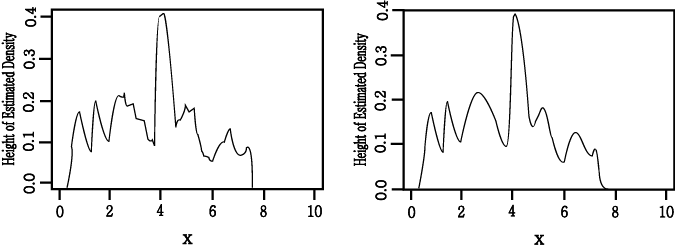
그림 4 : 추정 density functions
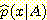 (a)
삼각(triangular) kernel (b) normal kernel. normal kernel
이 삼각 kernel보다 더 부드럽다.
(a)
삼각(triangular) kernel (b) normal kernel. normal kernel
이 삼각 kernel보다 더 부드럽다.
분류하고자 하는 class 의 종류에 대해서는 알고
있지만 sample 들 각각에 대한 probability density function을 알지 못하는 상태에서
사용한다. 굳이 각 sample 에 대한 확률적 parameter들을 구하지 않고 sample의
값을 그대로 좌표에 표시하여 reference set에서 가장 유사(similar)하거나 거리
상으로 가까운 (nearest) class 에 속하는 것으로 분류하는 방법이다.
nearest 의 의미는 무엇인가? 그것은 smallest
Euclidean distance, absolute difference, maximum distance, Minkowski distance
등으로 나눌 수 있다.
(1) Euclidean distance
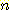 -차원의 feature space 로 구성된 경우라 하면 두 개의 포인트
-차원의 feature space 로 구성된 경우라 하면 두 개의 포인트  와
와 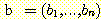 사이의 기하학적 거리는 다음과 같이 구해질 수 있다. 이것은 피타고라스 정리를
사이의 기하학적 거리는 다음과 같이 구해질 수 있다. 이것은 피타고라스 정리를
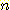 -차원으로 확장한 것이다.
-차원으로 확장한 것이다.
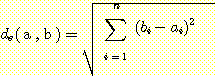
이 방법은 가장 흔하게 사용되는 거리 측정 방법이지만
항상 최고의 방법은 아니다. 각 차원에서 합계되기 전에 제곱을 하기 때문에 계산이
복잡하고 dissimilarity 가 큰 경우가 강조될 수 있다.
(2) absolute difference
두 포인트의 차이를 그대로 표현하여 계산하기가
쉽다. city block distance, Manhattan metric, taxi-cab distance 라고도 표현된다.
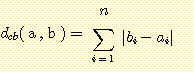
(3) maximum distance
feature 들 중에서 가장 유사하지 않은 (거리가
많이 떨어진) 부분이 강조되는 것이다.
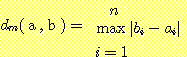
(4) Minkowski distance
거리를 측정하는 (1), (2), (3) 방법을 종합한
방법이다. 여기서  은 조정가능한 parameter 로서 그 값이 1 이면 absolute difference 와 같고,
2 이면 Euclidean distance 랑 같다.
은 조정가능한 parameter 로서 그 값이 1 이면 absolute difference 와 같고,
2 이면 Euclidean distance 랑 같다.
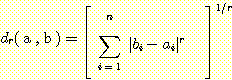
.........
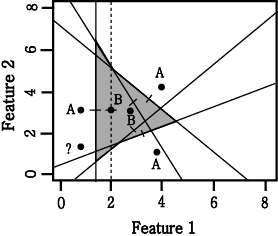
다음 그림은 class A에서 3 개, class B에서 2
개의 sample을 가지는 경우의 feature space 이다. 어떤 class에 속하는지 알려지지
않은 sample이 (1,1) 좌표에 있을 경우 Euclidean distance 의 방법을 써서 가장
가까이 있는 class는 (1,3)에 위치한 class A 이다. 따라서 class A 에 속하는 것으로
한다
........
nearest neighbor classifier 의 성능은 Bayesian
classifier(density function을 알고 있는 경우) 에 비해 항상 좋지 않다. 그 이유는
Bayesian 은 항상 가장 확실한 class를 선택하기 때문이다. 그 이유는 크게 2 가지가
있다.
1. sample 의 좌표에서 가장 가까이 있는 class로
분류하기 때문에 실제로 분류되어 있는 class 와는 차이가 있을 수 있다.
2. 기존 분류되어 있는 class 의 좌표는 대개 전문가에
의해 그 좌표가 결정되는데 그 것 조차도 정확하지 않을 수 있다.
class 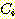 , feature vector
, feature vector 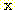 , 어떤
, 어떤 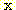 에서도 정확하게 분류될 확률
에서도 정확하게 분류될 확률  , 확률 밀도
, 확률 밀도 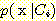 의 경우에 정확하게 분류될 확률의 기대값은 다음과 같다.
의 경우에 정확하게 분류될 확률의 기대값은 다음과 같다. 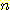 -차원 공간
-차원 공간 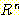 에서
에서
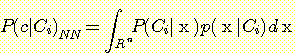
 를 Bayes' 정리로 바꾸면
를 Bayes' 정리로 바꾸면
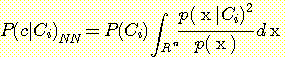
다음식은 모든 class에 대한 mixture density 이다.
즉 전체 모집단에 대한 density 이다.
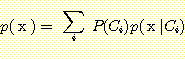
따라서
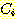 의 member 가 부정확하게 분류될 확률 즉 각 class의 error 확률은 다음과 같다.
의 member 가 부정확하게 분류될 확률 즉 각 class의 error 확률은 다음과 같다.
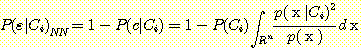
다음 식에 의해 또다른 유용한 식이 구해진다.
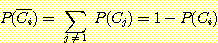
따라서
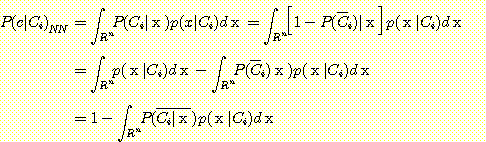
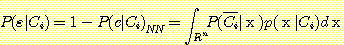 .
.
Bayes' 정리를 대입하면
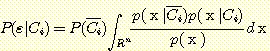 .
.
전체 error 확률을 얻기위해 위에서
구한 각 class의 error 확률이 각 class의 사전확률과 가중되고 합하면 다음식이
얻어진다.
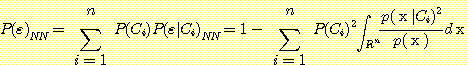 .
.
위와 같이 각 class의 density function과
사전 확률을 알면 nearest neighbor 방법의 예상되는 error 율을 구할 수 있다. 실제로
density를 알 경우에는 분류법으로 Bayes' 정리를 사용할 것이다. 그러나
Bayes' 정리를 사용한 방법과 density를 모르는 경우의 nearest neighbor 방법을
사용한 경우의 error 율을 비교하는 것은 흥미있는 일이다.
Example 5 Estimation of error rates for
nearest neighbor and Bayesian classification for two classes with equal prior
probabilities.
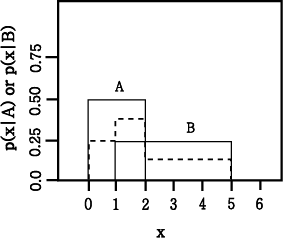
Figure 9 : Two uniform density
functions and the mixture density. The mixture density is dashed.
다음 그림과 같이 classes
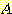 와
와 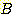 의 사전 확률이 각각 0.5 이고 class
의 사전 확률이 각각 0.5 이고 class 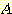 는 범위
는 범위 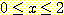 에서 ,
에서 , 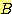 는 범위
는 범위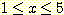 에서 uniformly distributed 되었다고 가정하자. nearest neighbor를 사용한
경우의 각 class 의 error 율은 어떻게 되며 Bayesian error 율과는 어떻게 비교되는가?
density 는 그림과 같으며
에서 uniformly distributed 되었다고 가정하자. nearest neighbor를 사용한
경우의 각 class 의 error 율은 어떻게 되며 Bayesian error 율과는 어떻게 비교되는가?
density 는 그림과 같으며 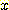 는 0에서 1, 1 에서2, 2 에서 5, 0 으로 구분된다. 위에서 구한 각 class를
위한 error 확률에 density를 대입하면 class
는 0에서 1, 1 에서2, 2 에서 5, 0 으로 구분된다. 위에서 구한 각 class를
위한 error 확률에 density를 대입하면 class 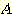 ,
, 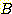 의 error 확률은 다음과 같다.
의 error 확률은 다음과 같다.
전체의 error 율은 다음과 같다.
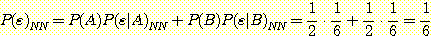 .
.
Bayesian classification
은 항상 가장 확실한 class를 선택한다. 따라서 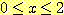 라면 class A ,
라면 class A , 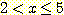 라면 class B 분류된다. 따라서
라면 class B 분류된다. 따라서  ,
, 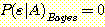 . 전체 error 율은 다음과 같다.
. 전체 error 율은 다음과 같다.
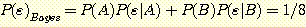
위의 예제에서 nearest neighbor error 율은
Bayesian error 율에 비해 4/3 배이다.
Example
5 could also have been solved by inspection of Figure 9 : The half of the 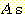 lying between
lying between  and
and  will be classified correctly, and the half of the
will be classified correctly, and the half of the 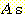 that overlap the density of
that overlap the density of 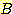 have a 1/3 probability of being called
have a 1/3 probability of being called 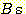 (because
(because  ), so
), so 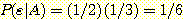 . Also, the left 1/4 of the
. Also, the left 1/4 of the 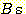 have a 2/3 probability of being called
have a 2/3 probability of being called 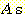 so
so 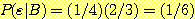 . Thus
. Thus  .
.
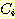
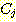
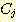 s
s 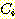 s
s 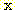
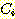

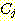
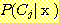
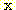
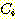
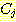
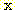
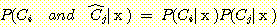
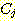
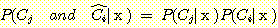
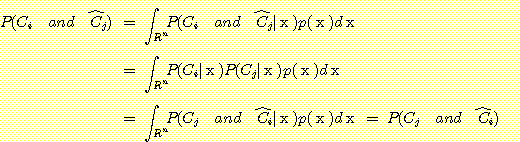
Figure 4.10 : (a) Density functions for Example
4.6. (b) The density functions multiplied by the prior probabilities of their
classes.
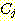
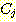
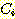
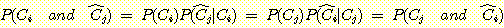
 and
and 
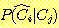 and
and 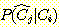
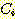 non-
non-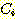 non-
non-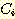
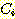
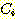 s
s 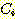 s
s 
Example 4.6
 and
and 

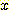
 and
and 
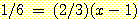 and
and 
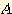 if
if 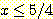 , and
, and 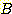 if
if 
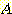
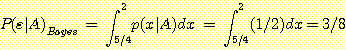
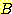
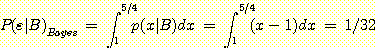
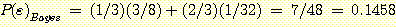
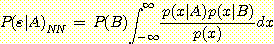
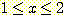
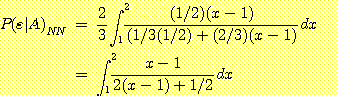
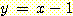
 1/3 2/3
1/3 2/3

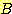
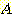
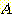

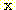
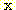
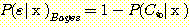 , (10)
, (10)
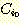
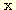
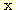
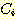
 ,
, 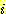

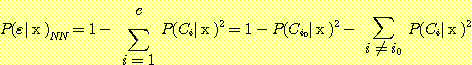 (11)
(11)
Substituting 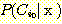 from (10),
from (10),
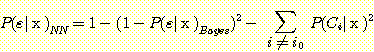
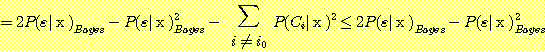 (12)
(12)
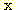
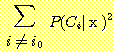
in (12). Since
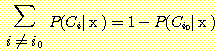 ,
,




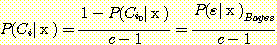 . (13)
. (13)
Substituting (13) for  in (12) produces the inequality
in (12) produces the inequality
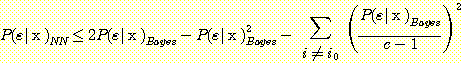
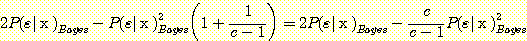 . (14)
. (14)
The term  equals 2 when there are two classes and it approaches 1 as the number of
classes becomes large.
equals 2 when there are two classes and it approaches 1 as the number of
classes becomes large.
Since (14) is true at all values of 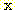 , it can be used to compare the overall error rates
, it can be used to compare the overall error rates
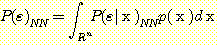 (15)
(15)
and
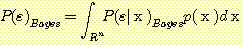 (16)
(16)
Multiplying (14) by 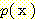 and integrating gives
and integrating gives
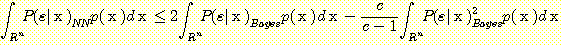
or
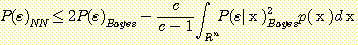 . (17)
. (17)
the integral of a nonnegative quantity
must be greater than or equal to 0, so
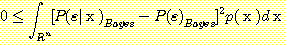
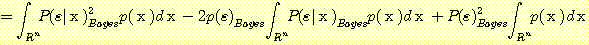
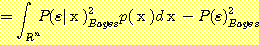
thus
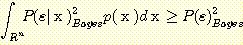 . (18)
. (18)
Substituting the integral from (18)
into (17) gives
 . (19)
. (19)
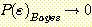 or
or 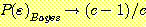
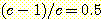
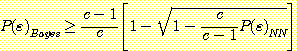 . (20)
. (20)
When  , this becomes
, this becomes
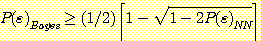 ,
,
so when 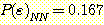 ,
,
 .
.
Nearest neighbor 방법중에서 일반적으로
사용되는 것은 단하나의 가장 가까운 이웃 만으로 구하는 것이 아니라 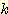 개의 가까운 이웃중에서 "선출하여 (votes)" 미지의 샘플들을 분류하는
것이다. 이러한 k-nearest neighbor 분류과정은 흔히
개의 가까운 이웃중에서 "선출하여 (votes)" 미지의 샘플들을 분류하는
것이다. 이러한 k-nearest neighbor 분류과정은 흔히 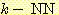 이라고 표현된다. 만일 각 클래스에 대해 에러비용 (costs of error) 가 같다면,
미지의 샘플이 속하는 것으로 추정되는 클래스는
이라고 표현된다. 만일 각 클래스에 대해 에러비용 (costs of error) 가 같다면,
미지의 샘플이 속하는 것으로 추정되는 클래스는 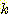 개의 가장가까운 이웃 집단중에서 가장 흔하게 표현되는 (most
commonly represented) 클래스를 선택하는 것이다. 예를들면 그림 4.8
에서처럼 3개의 이웃이 있다면, 미지의 샘플 (1, 1) 은 B 클래스에 속하는 것으로
분류된다. 왜냐하면 3개의 가장가까운 이웃은 클래스 A 의 (1, 3) 과 클래스 B 의
두개의 샘플로 구성되기 때문이다.
개의 가장가까운 이웃 집단중에서 가장 흔하게 표현되는 (most
commonly represented) 클래스를 선택하는 것이다. 예를들면 그림 4.8
에서처럼 3개의 이웃이 있다면, 미지의 샘플 (1, 1) 은 B 클래스에 속하는 것으로
분류된다. 왜냐하면 3개의 가장가까운 이웃은 클래스 A 의 (1, 3) 과 클래스 B 의
두개의 샘플로 구성되기 때문이다.
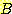
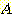
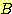
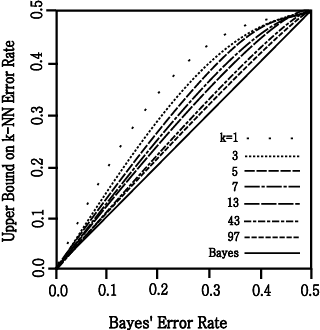
Figure 11 : Upper bounds
on the k-NN error rate as a function
of the Bayesian error rate
for two classes.
The k-nearest Neighbor Technique
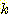
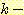 NN
NN 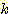 (1,1)
(1,1) 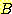
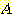 (1, 3)
(1, 3) 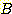
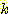 -nearest
-nearest 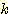
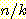
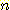

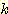

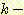 NN
NN 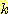 -nearest
-nearest 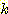

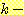 NN
NN 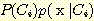
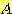
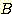
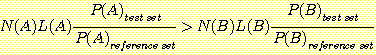

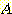 s
s 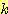
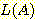
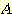
 and
and 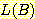

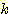
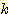
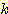
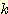

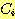
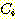
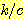
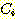
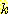
 ,000 1,000,000
,000 1,000,000 
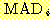
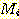
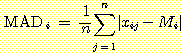
 by
by 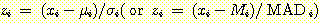
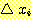
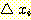
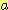
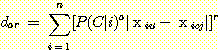

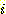
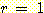 and
and 
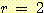 and
and 
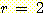 and
and 
 and
and 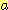
Example 4.7
242 1570.20
to 0.35 


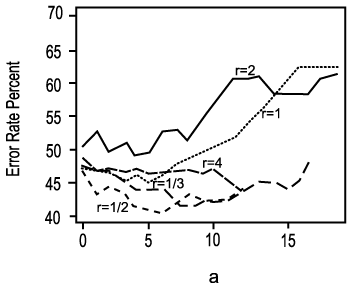
Figure 4.12 : Performance of variants
of the nearest neighbor decisin rule [Wu]. 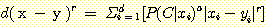
 of
of 







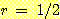
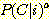

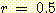
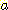 5.5 0.35/0.20 = 1.75
5.5 0.35/0.20 = 1.75 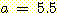
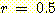
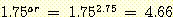
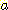
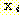

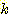
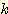
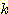

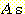
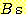
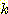
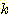

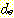
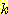


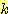

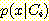
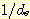

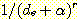
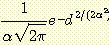
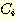
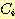
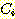
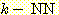
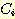
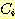
분류하고자 하는 class들 사이의
decision boundary 의 기능적 형태(즉 그것이 몇차원이지)를 알고 있다고 가정하고
class들을 가장 잘 분류하는 decision boundary를 찾는 방법이다. 예를들면 2 개의
class를 분류하기 위해 선형 decision boundary 가 사용되며 각 sample 이 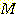 개의 feature를 가진다면 discriminant function(식별함수) 는 다음의 형태를
가진다.
개의 feature를 가진다면 discriminant function(식별함수) 는 다음의 형태를
가진다.
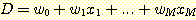
이 식에서  은 두 class를 분류하는 decision boundary 식이다. 가중치
은 두 class를 분류하는 decision boundary 식이다. 가중치  은 training set에서 좋은 성능을 내기위해 선택된다. feature vector
은 training set에서 좋은 성능을 내기위해 선택된다. feature vector 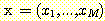 를 가지는 sample 이 하나의 class로 분류되고
를 가지는 sample 이 하나의 class로 분류되고  이라면 class 1,
이라면 class 1,  이라면 class -1 이라고 부른다고 하자. 만일
이라면 class -1 이라고 부른다고 하자. 만일 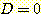 이라면 sample x 는 분류될 수 있다.
이라면 sample x 는 분류될 수 있다.
기하학적으로 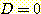 은
은 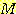 -차원 feature space를 2 영역으로 나누는 decision boundary 방정식이다.
-차원 feature space를 2 영역으로 나누는 decision boundary 방정식이다.  에서 class1,
에서 class1,  에서 class -1을 구분하는 decision boundary 가 존재한다면 두 class 는 linearly
separable 하다고 한다.
에서 class -1을 구분하는 decision boundary 가 존재한다면 두 class 는 linearly
separable 하다고 한다.
그림 ......
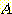 and
and 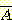
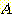

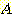











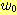
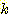
adaptive
decision boundary algorithm 은 다음의 단계로 구성된다.
- 가중치
 을 0 이나 작은 임의의 수로 초기화 한다. 가중치를 잘 선택하면 존재할
수 있는 완전한 해에 빠르게 수렴할수 있다.
을 0 이나 작은 임의의 수로 초기화 한다. 가중치를 잘 선택하면 존재할
수 있는 완전한 해에 빠르게 수렴할수 있다.
- training set에서 다음 sample
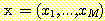 을 선택한다.
을 선택한다.  또는 -1 이
또는 -1 이 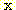 의 true class 가 되도록
의 true class 가 되도록  의 바람직한 class를
의 바람직한 class를 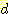 라고 한다.
라고 한다.
-
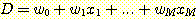 를 계산한다.
를 계산한다.
- 만일
 라면 ,
라면 , 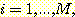 에 대하여
에 대하여 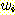 를
를 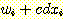 로 바꾼다.여기서
로 바꾼다.여기서  는 가중치를 조정하기 위한 step size를 조절하는
양의 상수이다.
는 가중치를 조정하기 위한 step size를 조절하는
양의 상수이다.  이라면
이라면 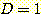 이고
이고  이라면
이라면  이다. 또한
이다. 또한 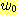 를
를 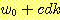 로 바꾸는데
로 바꾸는데 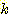 는 양의 상수이다. 만일
는 양의 상수이다. 만일 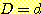 이라면 가중치에는 변화를 주지 않는다.
이라면 가중치에는 변화를 주지 않는다.
- training set 에서의 각 sample 에 대해
2에서 4 의 단계를 반복한다. 끝나면 전체 training set을 통해 다시 수행한다.
training 과정을 통해서 전체 sample에 대해 분류가 되면 멈춘다. 만일 2
개의 class가 선형으로 분리가 되지 않는다면 이러한 과정은 절대 끝나지
않기 때문에 부가적인 stopping
rule이 필요하다. 최대로 반복가능한 횟수를 정하든가, 평균 error 율이
감소하는 것이 멈춰지면 알고리즘이 종료되든가 한다.
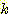
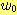
적절한 방향으로 가중치를 조정해가는
과정을 보자. 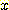 가 잘못 분류되었다면
가 잘못 분류되었다면  의 새로운 값은 다음과 같을 것이다.
의 새로운 값은 다음과 같을 것이다.
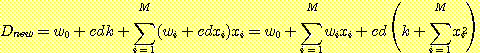
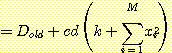
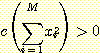 이며
이며  ,
,  이면
이면  이고
이고  이면
이면  이다.
이다.
이 알고리즘에서 가중치를
조정하는 것은 부정확하게 분류된 sample을 정확하게 되도록 decision boundary를
이동하는 것을 의미한다. 하나의 sample에 대한 adaptation 후에는 새로운  가 계산될 필요는 없으며 다음 sample로 이동한다.
가 계산될 필요는 없으며 다음 sample로 이동한다.
Example 4.8 하나의 수치 feature
(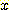 ) 를 사용하여 sample들을 분류하는 decision boundary를 찾는 것을 보여준다.
training sample은 다음과 같다.
) 를 사용하여 sample들을 분류하는 decision boundary를 찾는 것을 보여준다.
training sample은 다음과 같다.
여기서 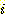 는 sample의 수이고
는 sample의 수이고 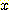 는 1차원 feature 이며
는 1차원 feature 이며 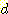 는 분류할 class이다. 상수
는 분류할 class이다. 상수  와
와 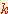 는 1로 주어진다(적당히 주어진다?). 가중치
는 1로 주어진다(적당히 주어진다?). 가중치 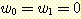 에서 시작한다. 첫번째 sample
에서 시작한다. 첫번째 sample  을 사용하여
을 사용하여  를 얻었다.
를 얻었다.  이라면 class 1,
이라면 class 1,  이라면 class -1 이라고 부른다고 가정하였다. 그러나
이라면 class -1 이라고 부른다고 가정하였다. 그러나  이고 따라서 sample 은 잘못 분류되어(error) 새로운 가중치를 적용해야 한다.
이고 따라서 sample 은 잘못 분류되어(error) 새로운 가중치를 적용해야 한다.
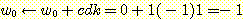
 .
.
이 새로운 가중치가 다음 table의
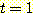 일 때 볼 수 있다. 여기서
일 때 볼 수 있다. 여기서  는 반복 횟수이다. 알고리즘은 계속 반복되어
는 반복 횟수이다. 알고리즘은 계속 반복되어 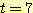 과
과 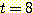 에서야 정확하게 분류된다. 왜냐하면 decision boundary는
에서야 정확하게 분류된다. 왜냐하면 decision boundary는  즉
즉  에서 얻어지기 때문이다. 마지막 decision boundary는
에서 얻어지기 때문이다. 마지막 decision boundary는 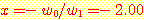 이다. 이 data로부터 만족스런 decision boundary는 -4 와 -1 사이에
있다는 것을 알 수 있다.
이다. 이 data로부터 만족스런 decision boundary는 -4 와 -1 사이에
있다는 것을 알 수 있다.
|

|
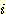
|
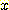
|
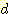
|
Old 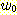
|
Old 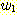
|

|
Error?
|
New 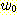
|
New 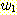
|
|
1
2
3
4
5
6
7
8
|
1
2
1
2
1
2
1
2
|
-4
-1
-4
-1
-4
-1
-4
-1
|
-1
1
-1
1
-1
1
-1
1
|
0
-1
0
0
1
1
2
2
|
0
4
3
3
2
2
1
1
|
0
-5
-12
-3
-7
-1
-2
1
|
Yes
Yes
No
Yes
No
Yes
No
No
|
-1
0
0
1
1
2
2
2
|
4
3
3
2
2
1
1
1
|
Example 4.9 2 개의 수치 feature를
가진 sample을 분류하는 decision boundary를 찾는 것이다. training sample은 다음과
같다.
|
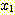
|
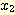
|
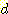
|
|
2
3
5
50
65
35
|
10
8
2
25
30
40
|
1
1
1
-1
-1
-1
|
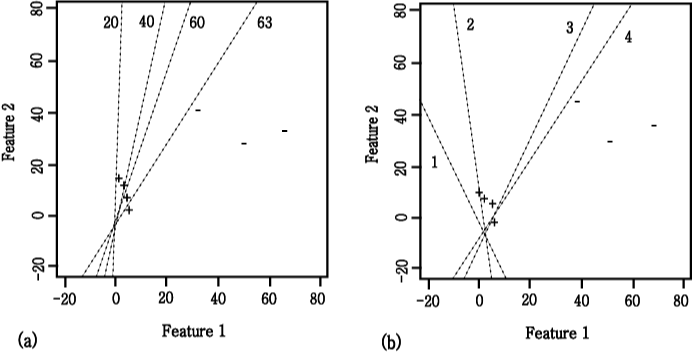
위의 예제에 대하여 얻어진 decision
boundary 의 위치이다.
(a) 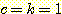 의 경우에 training set 에 대하여 20, 40, 60, 63 회의 알고리즘의 반복으로
얻어지는 decision boundary 의 변화되는 그림이다. 좌표(5,2) 가 정확히 분류될
때 까지 계속된 것이다. feature를 정규화 시키지 않고 정확한 가중치를 얻는데 381
step 또는 약 63 회의 반복이 필요하였다.
의 경우에 training set 에 대하여 20, 40, 60, 63 회의 알고리즘의 반복으로
얻어지는 decision boundary 의 변화되는 그림이다. 좌표(5,2) 가 정확히 분류될
때 까지 계속된 것이다. feature를 정규화 시키지 않고 정확한 가중치를 얻는데 381
step 또는 약 63 회의 반복이 필요하였다.
(b)
 ,
, 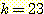 (feature의 평균절대값) 의 경우에 1, 2, 3, 4 회의 알고리즘의 반복으로 얻어진
그림이다. 단지 4 번만에 알고리즘이 수렴한 것을 볼수있다.
(feature의 평균절대값) 의 경우에 1, 2, 3, 4 회의 알고리즘의 반복으로 얻어진
그림이다. 단지 4 번만에 알고리즘이 수렴한 것을 볼수있다.
.......
2 개 이상의 class가 있을 때 각 class 에 대한 분리된 선형 discriminant function을 유도하여
그 중 가장 큰 discriminant function을 가지는 class를 선택하는 것이다. 만일 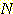 개의 class 와
개의 class 와 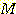 개의 변수를 가진다면 선형 discriminant function 집합은 다음과 같다.
개의 변수를 가진다면 선형 discriminant function 집합은 다음과 같다.


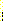
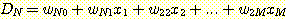 .
.
변수  는 비선형 함수 일 수 있으며
는 비선형 함수 일 수 있으며 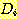 가 가중치
가 가중치  집합의 선형 함수일 때 비선형 discriminant function 가 사용될 수도 있다.
집합의 선형 함수일 때 비선형 discriminant function 가 사용될 수도 있다.
sample 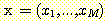 를 분류하기 위해 위의 식과 같은 discriminant function을 계산하여 sample을
가장 큰
를 분류하기 위해 위의 식과 같은 discriminant function을 계산하여 sample을
가장 큰 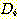 를 가지는 class
를 가지는 class 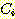 로 분류한다. 이러한 discriminant function 에 가중치를 적용하는 방법은 선형
decision boundary에서 가중치를 찾는 방법과 같다. 이러한 기술은 해가 존재한다면
모든 data를 완벽하게 분류하는 가중치 집합으로 수렴하는 것을 보장한다.
로 분류한다. 이러한 discriminant function 에 가중치를 적용하는 방법은 선형
decision boundary에서 가중치를 찾는 방법과 같다. 이러한 기술은 해가 존재한다면
모든 data를 완벽하게 분류하는 가중치 집합으로 수렴하는 것을 보장한다.
sample
x 가 class 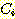 로 분류되어야 하는데
로 분류되어야 하는데 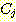 로 잘못 분류되었을 경우 2 개의 같은 discriminant function (
로 잘못 분류되었을 경우 2 개의 같은 discriminant function (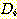 와
와 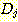 )를 위한 새로운 가중치가 다음과 같이 구해진다.
)를 위한 새로운 가중치가 다음과 같이 구해진다.


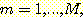 일 때
일 때

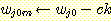
즉 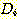 의 가중치를 증가시켜서
의 가중치를 증가시켜서 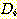 의 값이 최대값에 가까워 지도록 증가시켜야 한다. 반대로
의 값이 최대값에 가까워 지도록 증가시켜야 한다. 반대로 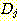 의 가중치는 감소시켜서
의 가중치는 감소시켜서 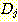 의 값을 줄여준다. 다른 discriminant function 의 값을 변화시킬 필요는 없다.
왜냐하면 잘 못 분류되지 않았기 때문이다.
의 값을 줄여준다. 다른 discriminant function 의 값을 변화시킬 필요는 없다.
왜냐하면 잘 못 분류되지 않았기 때문이다.
가중치를 변화시키는 간단한 방법으로
완벽한 분류가 가능한 기술이다. 그러나 error 없이 data를 분류할 만한 가중치 조합이
없을 경우에는 최선의 가중치를 찾는 것을 보장하지는 않는다. 그러나 경험적으로
보면 그것은 대개 좋은 절충안에 도달한다.
하나의 선형 discriminant function
은 feature space를 discriminant function이 가장 큰 값을 가지는 region 으로 분할한다.
data를 분류하기 위해 region들 간의 decision boundary 의 위치를 계산할 필요는
없다. 그러나 이러한 region들이 어떤 형태를 하고 있는지를 보는 것은 흥미롭다.
다음 예제는 3 개의 class를 위한 decision region 들을 보여준다.
Example 4.10 Finding the decision
regions resulting from three discriminant functions.
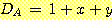

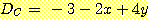
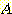 and
and 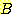

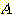
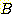

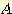



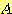
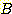
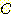
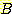
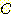

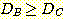

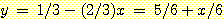
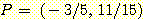
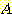
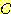

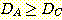
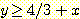
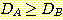
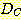
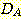
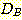
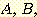 and
and 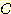
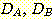 , and
, and 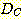
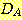
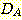

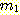 and
and 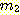

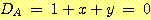
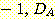 +1
+1 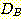 +2 and
+2 and 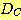 -2
-2
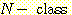
 9ㆍ8/2 = 36
9ㆍ8/2 = 36
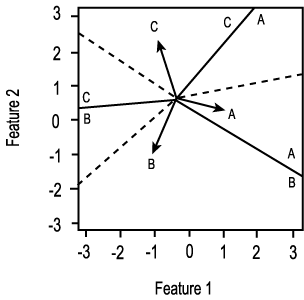
Figure 4.15
 and
and 

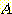

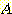 and
and 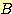
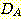 nd
nd 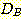
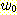
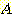 and
and 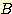 (where
(where  )
) 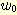

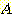 and
and 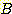 in
in 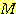

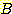 and
and 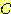
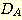 and
and 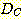
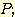
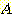 and
and 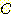
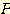
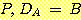 and
and  thus
thus 
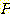
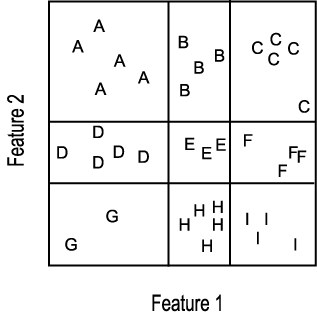
Figure 4.16
비록 adaptive decision boundary
와 adaptive discriminant function 이 상당히 매력적인 방법이지만 완벽하게 분류하기
위해서는 알고리즘을 위한 feature space에서 class 들이 linearly
separable 해야만 한다. 또한 class 들이 hyperplane 으로 분리 되더라도
decision boundary를 찾기위해서는 많은 반복 (many iteration)이
요구된다. 또한 adaptive 알고리즘이 training data를 정확하게 분류하는 최초의
가중치 집합을 발견할 때 종료되지만, 무엇이 좋은 decision boundary 인지에 대한
직관적인 (intuitive notion) 것과 같지 않을 수 있다. 즉 좋은
decision boundary 가 아닌데 종료될 수 있다. 예들들면 다음 그림의 (b)에서
4 번만에 얻어진 adaptive decision boundary 보다는 직관적으로 + 와 - 를 구분하는
수직 decision boundary 가 더 좋다는 것을 직관적으로 알 수 있다.

minimum squared error 분류 방법은
iteration을 요구하지도 않고, linearly separable을 요구하지도 않는다. adaptive
decision boundary 방법을 사용한 것보다 더 직관적으로 그럴 듯한 decision boundary를
찾아내지만 완전한 하나의 해를 찾아내는 것을 보장하지는 않는다. minimum squared
error 에서는 class의 수에 상관없이 단 하나의 discriminant function을 사용한다.
만일 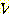 개의 sample 과
개의 sample 과 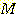 개의 feature 가 있다면,
개의 feature 가 있다면, 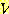 개의 feature vector 가 있을 것이다.
개의 feature vector 가 있을 것이다.
 ,
,  .
.
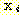 의 true class를
의 true class를 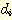 라고 할 때 그것은 어떤 수치값도 가질 수 있다. 우리는 단 하나의 linear discriminant function
(
라고 할 때 그것은 어떤 수치값도 가질 수 있다. 우리는 단 하나의 linear discriminant function
(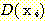 ) 을 위한 가중치 집합
) 을 위한 가중치 집합 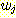 ,
,  을 찾고자 한다.
을 찾고자 한다.
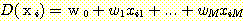
여기서 모든 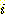 에 대해
에 대해  이다. 실제로 그러한 가중치 값은 존재하지 않지만 단지 적절하게 적절하게 가중치
이다. 실제로 그러한 가중치 값은 존재하지 않지만 단지 적절하게 적절하게 가중치
 를 선택하는 것이다. 즉 목표치 (desired values
를 선택하는 것이다. 즉 목표치 (desired values 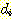 ) 와 출력치 (actual values
) 와 출력치 (actual values 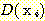 ) 간의 차이의 제곱의 합이 최소가 되도록 하는 것이다. 그 값
) 간의 차이의 제곱의 합이 최소가 되도록 하는 것이다. 그 값 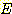 는 다음과 같이 구해진다.
는 다음과 같이 구해진다.
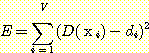
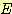
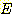

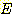
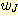
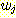
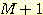
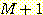

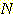
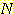 or
or 
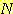
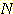
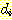
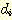
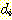
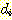
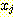
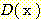
Example 11 The minimum squared
error procedure.
Inserting this data and (24) into
(25) produces

 .
.
Computing the partial derivatives
of 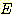 with respect to
with respect to 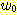 ,
, 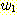 , and
, and 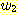 and setting each one equal to zero produces
and setting each one equal to zero produces
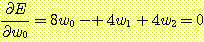 ,
,
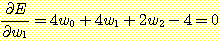 ,
,
and
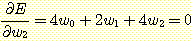 .
.
Solving for 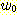 ,
, 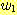 , and
, and 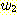 results in
results in 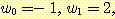 and
and  . Substituting these weights into equation (24) gives the discriminant function
. Substituting these weights into equation (24) gives the discriminant function
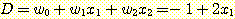 .
.
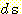
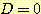
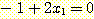 or
or 
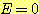
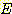
Example 12 Comparison of the
minimum squared error decision boundary with the adaptive decision boundary.
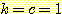
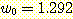 ,
,  , and
, and 
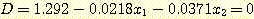
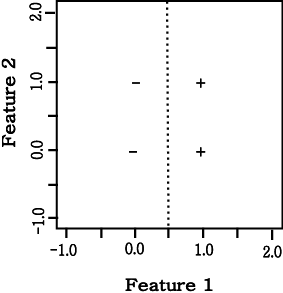
Figure 17 : The minimum squared
error decision boundary for Example 11.
..........
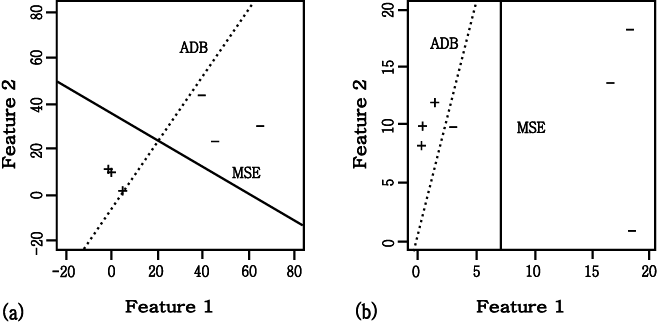
위 그림에서 (a) 에서는 minimum
squared error (MSE) 방법이 adaptive decision boundary
(ADB) 방법보다 더 좋은 결과를 보인다. (b) 에서는 boundary 로서 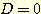 를 사용하여 ADB 가 MSE 보다 더 좋은 결과를 보여준다.
를 사용하여 ADB 가 MSE 보다 더 좋은 결과를 보여준다.
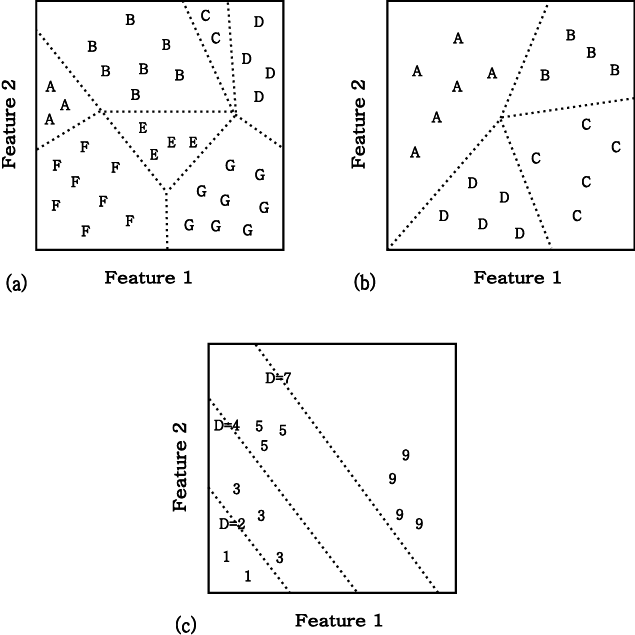
위 그림 (a) 에서는 각 class에 대해
하나의 adaptive linear decision boundary 를 사용하여 완벽하게 구분된 class들이다.
필요한 boundary 들만을 보여준다. (b)에서는 각 class 에 대해 하나의 adaptive discriminant function 을
사용하여 완벽하게 구분된다.
(c)에서는 1, 3, 5, 9 의 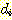 값을 가지는 minimum squared error 을 사용하여 완벽하게 구분된다.
값을 가지는 minimum squared error 을 사용하여 완벽하게 구분된다.
...............
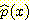 )을 모를 때 근사적인
)을 모를 때 근사적인 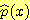 를 구하는 방법으로서 변수
를 구하는 방법으로서 변수 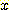 의 범위를 모든 data를 포함하는 유한갯수의 interval 로 나누어서 막대그래프로
표시한 것이다. 이때 의 각 interval을 cell 또는 bin 이라고 부른다. 각 histogram을
연결하여 density function 의 추정치로서 사용하려면 histogram 하의 합계
면적이 1 이어야 한다. 각 interval을
의 범위를 모든 data를 포함하는 유한갯수의 interval 로 나누어서 막대그래프로
표시한 것이다. 이때 의 각 interval을 cell 또는 bin 이라고 부른다. 각 histogram을
연결하여 density function 의 추정치로서 사용하려면 histogram 하의 합계
면적이 1 이어야 한다. 각 interval을  라 하고 전체 sample 의 수를
라 하고 전체 sample 의 수를 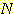 이라 하면 각 bin 의 면적은
이라 하면 각 bin 의 면적은 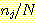 이고 그 interval 의 폭에 따라 나뉘어져 density 의 높이는
이고 그 interval 의 폭에 따라 나뉘어져 density 의 높이는  이 된다. 일단 근사치 density function 이 구해지면 Bayes'
정리를 사용하여 decision을 하게된다.
이 된다. 일단 근사치 density function 이 구해지면 Bayes'
정리를 사용하여 decision을 하게된다. 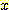 가 연속이든 이산이든 그 범위를 interval로 나누고 같은 방법을 사용하게 된다.
각
가 연속이든 이산이든 그 범위를 interval로 나누고 같은 방법을 사용하게 된다.
각  의 값을 가지는 sample 의 부분이 분포
의 값을 가지는 sample 의 부분이 분포  의 추정치
의 추정치  로 사용되고 그 합은 1 이 될 것이다.
로 사용되고 그 합은 1 이 될 것이다.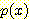
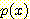
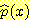
 에 따라서 다음과 같은 data 가 측정되었다.
에 따라서 다음과 같은 data 가 측정되었다.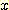 의 interval
의 interval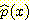 의 높이
의 높이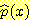 와 같이 표현한다. sample 이 많은 구간에서는 bin 의 크기가 작고, 적은 구간에서는
bin 의 크기가 크다는 것을 알 수 있다.
와 같이 표현한다. sample 이 많은 구간에서는 bin 의 크기가 작고, 적은 구간에서는
bin 의 크기가 크다는 것을 알 수 있다.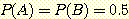 일 때,
일 때, 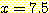 의 sample 이 class
의 sample 이 class 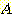 에 속하는지
에 속하는지 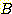 에 속하는지를 분류하라.
에 속하는지를 분류하라. 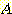 에서 선택된 60 개의 임의의 sample 의 feature
에서 선택된 60 개의 임의의 sample 의 feature 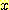 의 값이다.
의 값이다.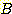 에서 선택된 60 개의 임의의 sample 의 feature
에서 선택된 60 개의 임의의 sample 의 feature 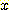 의 값이다.
의 값이다.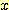 의 histogram (b) class B
의 histogram (b) class B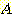 와
와 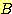 를 위한
를 위한 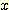 의 각 interval에서 sample들의 histogram 이다.이것을 density function 으로
변환하기 위해서, 이러한 수들이 sample 들의 전체의 수(60) 와 interval width (1)
로 나누어져야 한다.
의 각 interval에서 sample들의 histogram 이다.이것을 density function 으로
변환하기 위해서, 이러한 수들이 sample 들의 전체의 수(60) 와 interval width (1)
로 나누어져야 한다.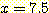 인 sample을 분류하기 위해, 7.5 에서 두 개의 histogram 의 높이를 비교한다.
왜냐하면 7.5를 포함하는 class interval 은 classes
인 sample을 분류하기 위해, 7.5 에서 두 개의 histogram 의 높이를 비교한다.
왜냐하면 7.5를 포함하는 class interval 은 classes 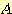 와
와 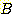 에 대하여 [7, 8] 구간이기 때문이다.
에 대하여 [7, 8] 구간이기 때문이다. 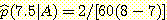 이며
이며 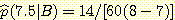 이다. 여기서 Bayes' 정리를 사용하여
이다. 여기서 Bayes' 정리를 사용하여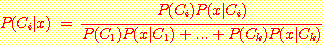
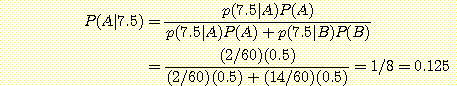
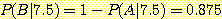 이다. 그러므로
이다. 그러므로  이다.
이다.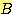 로 분류되어야 한다.
로 분류되어야 한다.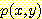
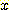
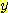
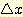 and
and 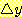
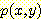
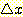
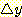
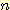




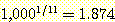

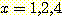 에 놓여있는 sample 들의 density를 추정하는 delta 함수 의 예 (그림 1)를 들어보자.
이러한 continuous density function 의 근사치는 의사 결정에서는 유용하게 사용될
수 없는 것이다. 그러나 그 delta 함수가 사각이나 삼각 또는
정규밀도함수 와 같은 kernel 이라고 불리는 다른 함수로 바꾸어 진다면 그들의 합계
면적이 1 이 되도록 하는 더 부드럽고 만족스런 추정을 할 수가 있다(
에 놓여있는 sample 들의 density를 추정하는 delta 함수 의 예 (그림 1)를 들어보자.
이러한 continuous density function 의 근사치는 의사 결정에서는 유용하게 사용될
수 없는 것이다. 그러나 그 delta 함수가 사각이나 삼각 또는
정규밀도함수 와 같은 kernel 이라고 불리는 다른 함수로 바꾸어 진다면 그들의 합계
면적이 1 이 되도록 하는 더 부드럽고 만족스런 추정을 할 수가 있다(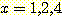 의 sample을 가지는 경우의 삼각 kernel을 사용한 추정 density function을 (그림
2) 에서 볼 수 있고, 삼각 사각 정규 분포 kernel을 사용하여 표준편차 1을 가지게
하는 경우는 (그림 3) 에서 볼 수 있다. .....
의 sample을 가지는 경우의 삼각 kernel을 사용한 추정 density function을 (그림
2) 에서 볼 수 있고, 삼각 사각 정규 분포 kernel을 사용하여 표준편차 1을 가지게
하는 경우는 (그림 3) 에서 볼 수 있다. .....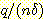 ,
, 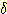 이다.
이다. 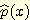 를 계산하는 것으로 kernels (점선) 과 그 합계 (실선) 를 볼 수 있다. 실선
면적의 합은 1 이다.
(b) window 방법을 사용해서
를 계산하는 것으로 kernels (점선) 과 그 합계 (실선) 를 볼 수 있다. 실선
면적의 합은 1 이다.
(b) window 방법을 사용해서 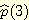 를 계산하면
를 계산하면  와 같다.
와 같다.  에 있는 sample을 분류하기 위해서는 전체 밀도
에 있는 sample을 분류하기 위해서는 전체 밀도 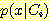 가 필요하지는 않고
가 필요하지는 않고 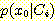 에서의 값만 필요하다. (그림 2, b) 의 경우처럼
에서의 값만 필요하다. (그림 2, b) 의 경우처럼  에서
에서 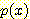 를 가정해 보자. 결과는 물론
를 가정해 보자. 결과는 물론  에서 모든 kernel 함수의 높이의 합과 같을 것이다. 이런 결과를 얻는 또 다른
방법은
에서 모든 kernel 함수의 높이의 합과 같을 것이다. 이런 결과를 얻는 또 다른
방법은  의 중앙 근처에서 kernel 함수를 반영하는 window 함수를 만드는 것이다. 그리고
이 window 에 포함된 각 sample point 의 높이를 합하는 것이다. 대칭적인
kernel 함수가 보통 사용된다. (그림 2, b)에서 window 함수는 sample 두 개를 포함하고
있고 각각의 높이는 2/27 이며
의 중앙 근처에서 kernel 함수를 반영하는 window 함수를 만드는 것이다. 그리고
이 window 에 포함된 각 sample point 의 높이를 합하는 것이다. 대칭적인
kernel 함수가 보통 사용된다. (그림 2, b)에서 window 함수는 sample 두 개를 포함하고
있고 각각의 높이는 2/27 이며 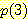 의 추정치
의 추정치 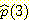 는 4/27 이다. 이것은 kernel 방법을 사용한 (그림 2, a) 와 같은 값이다.
는 4/27 이다. 이것은 kernel 방법을 사용한 (그림 2, a) 와 같은 값이다. 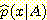 (a)
삼각(triangular) kernel (b) normal kernel. normal kernel
이 삼각 kernel보다 더 부드럽다.
(a)
삼각(triangular) kernel (b) normal kernel. normal kernel
이 삼각 kernel보다 더 부드럽다.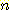 -차원의 feature space 로 구성된 경우라 하면 두 개의 포인트
-차원의 feature space 로 구성된 경우라 하면 두 개의 포인트  와
와 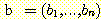 사이의 기하학적 거리는 다음과 같이 구해질 수 있다. 이것은 피타고라스 정리를
사이의 기하학적 거리는 다음과 같이 구해질 수 있다. 이것은 피타고라스 정리를
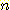 -차원으로 확장한 것이다.
-차원으로 확장한 것이다. 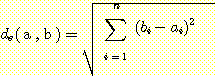
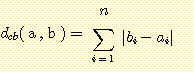
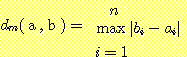
 은 조정가능한 parameter 로서 그 값이 1 이면 absolute difference 와 같고,
2 이면 Euclidean distance 랑 같다.
은 조정가능한 parameter 로서 그 값이 1 이면 absolute difference 와 같고,
2 이면 Euclidean distance 랑 같다. 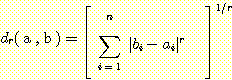
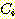 , feature vector
, feature vector 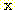 , 어떤
, 어떤 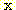 에서도 정확하게 분류될 확률
에서도 정확하게 분류될 확률  , 확률 밀도
, 확률 밀도 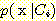 의 경우에 정확하게 분류될 확률의 기대값은 다음과 같다.
의 경우에 정확하게 분류될 확률의 기대값은 다음과 같다. 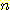 -차원 공간
-차원 공간 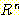 에서
에서 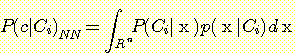
 를 Bayes' 정리로 바꾸면
를 Bayes' 정리로 바꾸면 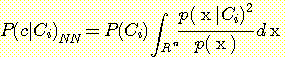
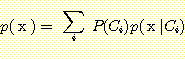
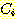 의 member 가 부정확하게 분류될 확률 즉 각 class의 error 확률은 다음과 같다.
의 member 가 부정확하게 분류될 확률 즉 각 class의 error 확률은 다음과 같다.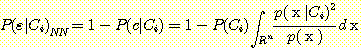
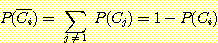
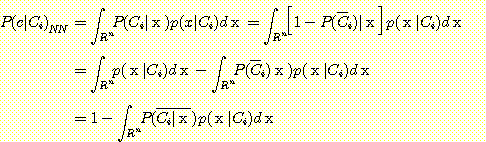
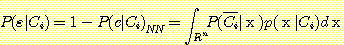 .
.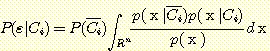 .
. 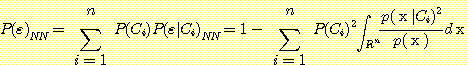 .
. 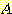 와
와 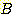 의 사전 확률이 각각 0.5 이고 class
의 사전 확률이 각각 0.5 이고 class 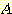 는 범위
는 범위 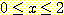 에서 ,
에서 , 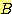 는 범위
는 범위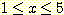 에서 uniformly distributed 되었다고 가정하자. nearest neighbor를 사용한
경우의 각 class 의 error 율은 어떻게 되며 Bayesian error 율과는 어떻게 비교되는가?
density 는 그림과 같으며
에서 uniformly distributed 되었다고 가정하자. nearest neighbor를 사용한
경우의 각 class 의 error 율은 어떻게 되며 Bayesian error 율과는 어떻게 비교되는가?
density 는 그림과 같으며 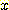 는 0에서 1, 1 에서2, 2 에서 5, 0 으로 구분된다. 위에서 구한 각 class를
위한 error 확률에 density를 대입하면 class
는 0에서 1, 1 에서2, 2 에서 5, 0 으로 구분된다. 위에서 구한 각 class를
위한 error 확률에 density를 대입하면 class 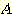 ,
, 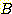 의 error 확률은 다음과 같다.
의 error 확률은 다음과 같다. 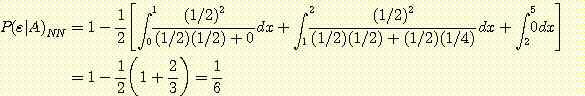
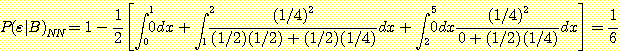
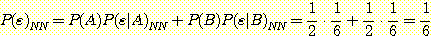 .
.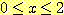 라면 class A ,
라면 class A , 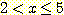 라면 class B 분류된다. 따라서
라면 class B 분류된다. 따라서  ,
, 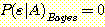 . 전체 error 율은 다음과 같다.
. 전체 error 율은 다음과 같다. 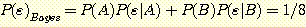
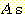 lying between
lying between  and
and  will be classified correctly, and the half of the
will be classified correctly, and the half of the 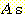 that overlap the density of
that overlap the density of 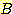 have a 1/3 probability of being called
have a 1/3 probability of being called 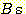 (because
(because  ), so
), so 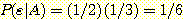 . Also, the left 1/4 of the
. Also, the left 1/4 of the 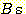 have a 2/3 probability of being called
have a 2/3 probability of being called 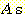 so
so 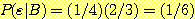 . Thus
. Thus  .
.
 s
s 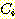 s
s 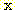
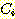

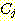
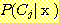
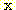
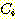
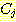
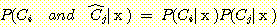
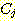
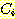
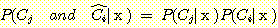
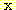
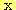
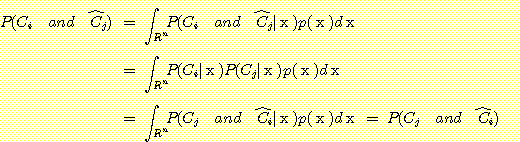

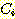
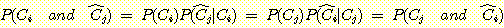
 and
and 
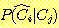 and
and 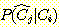
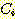 non-
non-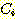 non-
non-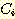
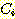
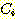 s
s 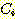 s
s 
 and
and 

 and
and 
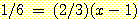 and
and 
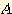 if
if 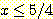 , and
, and 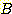 if
if 
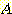
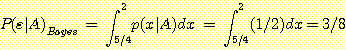
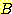
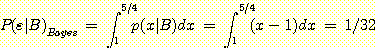
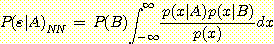
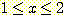
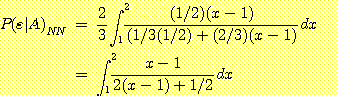
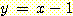
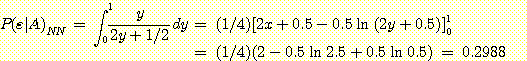
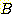 1/3 2/3
1/3 2/3
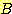
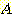
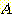

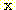
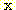
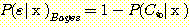 , (10)
, (10)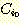
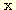
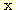
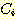
 ,
, 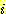

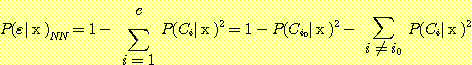 (11)
(11)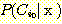 from (10),
from (10),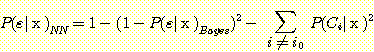
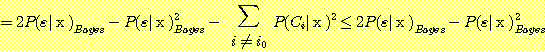 (12)
(12)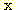
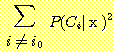
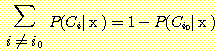 ,
,



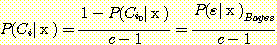 . (13)
. (13) in (12) produces the inequality
in (12) produces the inequality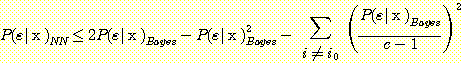
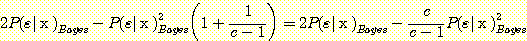 . (14)
. (14) equals 2 when there are two classes and it approaches 1 as the number of
classes becomes large.
equals 2 when there are two classes and it approaches 1 as the number of
classes becomes large.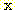 , it can be used to compare the overall error rates
, it can be used to compare the overall error rates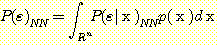 (15)
(15)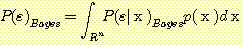 (16)
(16)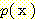 and integrating gives
and integrating gives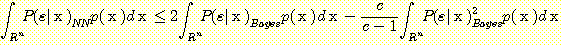
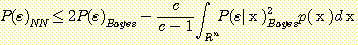 . (17)
. (17)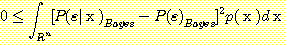
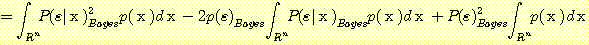
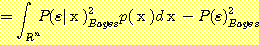
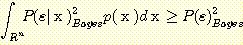 . (18)
. (18) . (19)
. (19)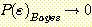 or
or 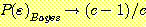
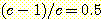
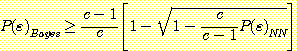 . (20)
. (20) , this becomes
, this becomes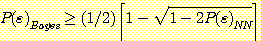 ,
,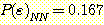 ,
, .
.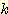 개의 가까운 이웃중에서 "선출하여 (votes)" 미지의 샘플들을 분류하는
것이다. 이러한 k-nearest neighbor 분류과정은 흔히
개의 가까운 이웃중에서 "선출하여 (votes)" 미지의 샘플들을 분류하는
것이다. 이러한 k-nearest neighbor 분류과정은 흔히 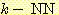 이라고 표현된다. 만일 각 클래스에 대해 에러비용 (costs of error) 가 같다면,
미지의 샘플이 속하는 것으로 추정되는 클래스는
이라고 표현된다. 만일 각 클래스에 대해 에러비용 (costs of error) 가 같다면,
미지의 샘플이 속하는 것으로 추정되는 클래스는 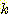 개의 가장가까운 이웃 집단중에서 가장 흔하게 표현되는 (most
commonly represented) 클래스를 선택하는 것이다. 예를들면 그림 4.8
에서처럼 3개의 이웃이 있다면, 미지의 샘플 (1, 1) 은 B 클래스에 속하는 것으로
분류된다. 왜냐하면 3개의 가장가까운 이웃은 클래스 A 의 (1, 3) 과 클래스 B 의
두개의 샘플로 구성되기 때문이다.
개의 가장가까운 이웃 집단중에서 가장 흔하게 표현되는 (most
commonly represented) 클래스를 선택하는 것이다. 예를들면 그림 4.8
에서처럼 3개의 이웃이 있다면, 미지의 샘플 (1, 1) 은 B 클래스에 속하는 것으로
분류된다. 왜냐하면 3개의 가장가까운 이웃은 클래스 A 의 (1, 3) 과 클래스 B 의
두개의 샘플로 구성되기 때문이다. 
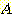

 NN
NN  (1,1)
(1,1) 
 (1, 3)
(1, 3) 
 -nearest
-nearest 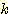
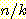
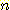

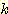

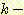 NN
NN 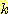 -nearest
-nearest 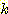

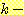 NN
NN 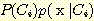
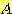
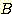
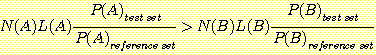

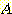 s
s 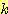
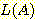
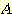
 and
and 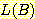

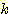
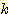
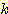
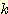

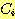
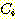
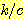
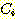
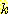
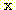 ,000 1,000,000
,000 1,000,000 
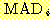
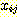
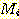
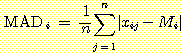
 by
by 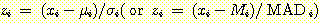
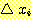
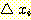
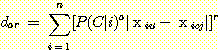

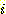
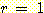 and
and 
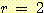 and
and 
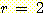 and
and 
 and
and 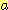
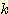



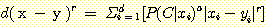
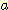 of
of 







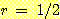
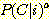

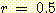
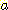 5.5 0.35/0.20 = 1.75
5.5 0.35/0.20 = 1.75 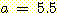
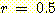
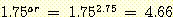
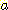
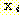

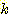
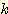
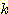

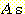
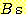
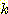
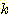

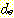
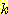


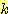

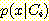
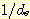

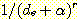
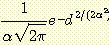
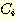
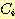
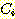
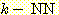
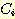
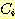
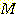 개의 feature를 가진다면 discriminant function(식별함수) 는 다음의 형태를
가진다.
개의 feature를 가진다면 discriminant function(식별함수) 는 다음의 형태를
가진다.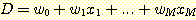
 은 두 class를 분류하는 decision boundary 식이다. 가중치
은 두 class를 분류하는 decision boundary 식이다. 가중치  은 training set에서 좋은 성능을 내기위해 선택된다. feature vector
은 training set에서 좋은 성능을 내기위해 선택된다. feature vector 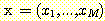 를 가지는 sample 이 하나의 class로 분류되고
를 가지는 sample 이 하나의 class로 분류되고  이라면 class 1,
이라면 class 1,  이라면 class -1 이라고 부른다고 하자. 만일
이라면 class -1 이라고 부른다고 하자. 만일 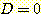 이라면 sample x 는 분류될 수 있다.
이라면 sample x 는 분류될 수 있다. 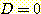 은
은 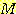 -차원 feature space를 2 영역으로 나누는 decision boundary 방정식이다.
-차원 feature space를 2 영역으로 나누는 decision boundary 방정식이다.  에서 class1,
에서 class1,  에서 class -1을 구분하는 decision boundary 가 존재한다면 두 class 는 linearly
separable 하다고 한다.
에서 class -1을 구분하는 decision boundary 가 존재한다면 두 class 는 linearly
separable 하다고 한다. 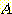 and
and 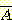












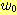
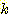
 을 0 이나 작은 임의의 수로 초기화 한다. 가중치를 잘 선택하면 존재할
수 있는 완전한 해에 빠르게 수렴할수 있다.
을 0 이나 작은 임의의 수로 초기화 한다. 가중치를 잘 선택하면 존재할
수 있는 완전한 해에 빠르게 수렴할수 있다. 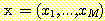 을 선택한다.
을 선택한다.  또는 -1 이
또는 -1 이 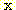 의 true class 가 되도록
의 true class 가 되도록  의 바람직한 class를
의 바람직한 class를 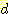 라고 한다.
라고 한다.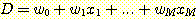 를 계산한다.
를 계산한다.  라면 ,
라면 , 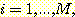 에 대하여
에 대하여 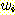 를
를 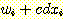 로 바꾼다.여기서
로 바꾼다.여기서  는 가중치를 조정하기 위한 step size를 조절하는
양의 상수이다.
는 가중치를 조정하기 위한 step size를 조절하는
양의 상수이다.  이라면
이라면 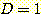 이고
이고  이라면
이라면  이다. 또한
이다. 또한 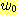 를
를 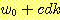 로 바꾸는데
로 바꾸는데 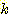 는 양의 상수이다. 만일
는 양의 상수이다. 만일 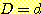 이라면 가중치에는 변화를 주지 않는다.
이라면 가중치에는 변화를 주지 않는다.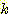
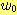
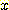 가 잘못 분류되었다면
가 잘못 분류되었다면  의 새로운 값은 다음과 같을 것이다.
의 새로운 값은 다음과 같을 것이다. 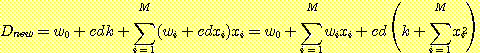
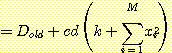
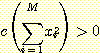 이며
이며  ,
,  이면
이면  이고
이고  이면
이면  이다.
이다.  가 계산될 필요는 없으며 다음 sample로 이동한다.
가 계산될 필요는 없으며 다음 sample로 이동한다. 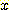 ) 를 사용하여 sample들을 분류하는 decision boundary를 찾는 것을 보여준다.
training sample은 다음과 같다.
) 를 사용하여 sample들을 분류하는 decision boundary를 찾는 것을 보여준다.
training sample은 다음과 같다.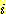
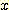
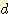
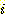 는 sample의 수이고
는 sample의 수이고 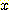 는 1차원 feature 이며
는 1차원 feature 이며 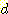 는 분류할 class이다. 상수
는 분류할 class이다. 상수  와
와 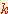 는 1로 주어진다(적당히 주어진다?). 가중치
는 1로 주어진다(적당히 주어진다?). 가중치 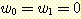 에서 시작한다. 첫번째 sample
에서 시작한다. 첫번째 sample  을 사용하여
을 사용하여  를 얻었다.
를 얻었다.  이라면 class 1,
이라면 class 1,  이라면 class -1 이라고 부른다고 가정하였다. 그러나
이라면 class -1 이라고 부른다고 가정하였다. 그러나  이고 따라서 sample 은 잘못 분류되어(error) 새로운 가중치를 적용해야 한다.
이고 따라서 sample 은 잘못 분류되어(error) 새로운 가중치를 적용해야 한다.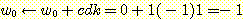
 .
.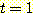 일 때 볼 수 있다. 여기서
일 때 볼 수 있다. 여기서  는 반복 횟수이다. 알고리즘은 계속 반복되어
는 반복 횟수이다. 알고리즘은 계속 반복되어 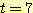 과
과 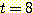 에서야 정확하게 분류된다. 왜냐하면 decision boundary는
에서야 정확하게 분류된다. 왜냐하면 decision boundary는  즉
즉  에서 얻어지기 때문이다. 마지막 decision boundary는
에서 얻어지기 때문이다. 마지막 decision boundary는 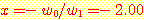 이다. 이 data로부터 만족스런 decision boundary는 -4 와 -1 사이에
있다는 것을 알 수 있다.
이다. 이 data로부터 만족스런 decision boundary는 -4 와 -1 사이에
있다는 것을 알 수 있다. 
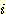
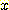
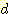
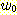
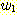

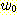
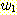
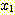
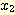
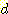
 의 경우에 training set 에 대하여 20, 40, 60, 63 회의 알고리즘의 반복으로
얻어지는 decision boundary 의 변화되는 그림이다. 좌표(5,2) 가 정확히 분류될
때 까지 계속된 것이다. feature를 정규화 시키지 않고 정확한 가중치를 얻는데 381
step 또는 약 63 회의 반복이 필요하였다.
의 경우에 training set 에 대하여 20, 40, 60, 63 회의 알고리즘의 반복으로
얻어지는 decision boundary 의 변화되는 그림이다. 좌표(5,2) 가 정확히 분류될
때 까지 계속된 것이다. feature를 정규화 시키지 않고 정확한 가중치를 얻는데 381
step 또는 약 63 회의 반복이 필요하였다. ,
, 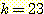 (feature의 평균절대값) 의 경우에 1, 2, 3, 4 회의 알고리즘의 반복으로 얻어진
그림이다. 단지 4 번만에 알고리즘이 수렴한 것을 볼수있다.
(feature의 평균절대값) 의 경우에 1, 2, 3, 4 회의 알고리즘의 반복으로 얻어진
그림이다. 단지 4 번만에 알고리즘이 수렴한 것을 볼수있다.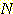 개의 class 와
개의 class 와 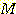 개의 변수를 가진다면 선형 discriminant function 집합은 다음과 같다.
개의 변수를 가진다면 선형 discriminant function 집합은 다음과 같다.

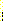
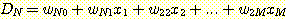 .
. 는 비선형 함수 일 수 있으며
는 비선형 함수 일 수 있으며 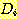 가 가중치
가 가중치  집합의 선형 함수일 때 비선형 discriminant function 가 사용될 수도 있다.
집합의 선형 함수일 때 비선형 discriminant function 가 사용될 수도 있다.
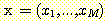 를 분류하기 위해 위의 식과 같은 discriminant function을 계산하여 sample을
가장 큰
를 분류하기 위해 위의 식과 같은 discriminant function을 계산하여 sample을
가장 큰 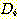 를 가지는 class
를 가지는 class 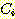 로 분류한다. 이러한 discriminant function 에 가중치를 적용하는 방법은 선형
decision boundary에서 가중치를 찾는 방법과 같다. 이러한 기술은 해가 존재한다면
모든 data를 완벽하게 분류하는 가중치 집합으로 수렴하는 것을 보장한다.
로 분류한다. 이러한 discriminant function 에 가중치를 적용하는 방법은 선형
decision boundary에서 가중치를 찾는 방법과 같다. 이러한 기술은 해가 존재한다면
모든 data를 완벽하게 분류하는 가중치 집합으로 수렴하는 것을 보장한다.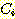 로 분류되어야 하는데
로 분류되어야 하는데 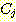 로 잘못 분류되었을 경우 2 개의 같은 discriminant function (
로 잘못 분류되었을 경우 2 개의 같은 discriminant function (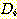 와
와 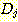 )를 위한 새로운 가중치가 다음과 같이 구해진다.
)를 위한 새로운 가중치가 다음과 같이 구해진다. 

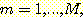 일 때
일 때 
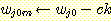
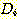 의 가중치를 증가시켜서
의 가중치를 증가시켜서 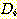 의 값이 최대값에 가까워 지도록 증가시켜야 한다. 반대로
의 값이 최대값에 가까워 지도록 증가시켜야 한다. 반대로 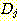 의 가중치는 감소시켜서
의 가중치는 감소시켜서 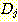 의 값을 줄여준다. 다른 discriminant function 의 값을 변화시킬 필요는 없다.
왜냐하면 잘 못 분류되지 않았기 때문이다.
의 값을 줄여준다. 다른 discriminant function 의 값을 변화시킬 필요는 없다.
왜냐하면 잘 못 분류되지 않았기 때문이다. 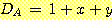

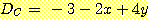
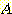 and
and 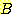





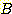
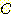
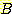
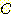

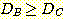

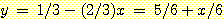
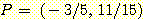
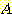
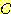

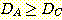
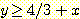
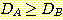
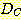
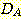
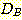
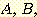 and
and 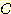
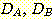 , and
, and 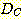
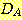
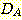

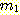 and
and 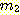

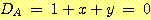
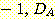 +1
+1 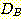 +2 and
+2 and 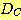 -2
-2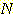
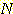
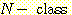
 9ㆍ8/2 = 36
9ㆍ8/2 = 36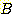

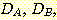 and
and 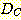

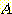

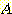 and
and 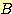
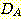 nd
nd 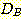
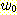
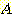 and
and 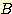 (where
(where  )
) 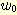

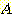 and
and 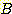 in
in 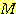

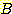 and
and 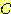
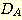 and
and 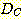
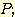
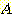 and
and 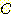
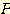
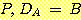 and
and  thus
thus 
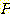

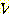 개의 sample 과
개의 sample 과 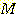 개의 feature 가 있다면,
개의 feature 가 있다면, 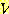 개의 feature vector 가 있을 것이다.
개의 feature vector 가 있을 것이다. ,
,  .
.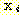 의 true class를
의 true class를 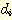 라고 할 때 그것은 어떤 수치값도 가질 수 있다. 우리는 단 하나의 linear discriminant function
(
라고 할 때 그것은 어떤 수치값도 가질 수 있다. 우리는 단 하나의 linear discriminant function
(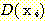 ) 을 위한 가중치 집합
) 을 위한 가중치 집합 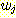 ,
,  을 찾고자 한다.
을 찾고자 한다. 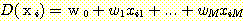
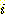 에 대해
에 대해  이다. 실제로 그러한 가중치 값은 존재하지 않지만 단지 적절하게 적절하게 가중치
이다. 실제로 그러한 가중치 값은 존재하지 않지만 단지 적절하게 적절하게 가중치
 를 선택하는 것이다. 즉 목표치 (desired values
를 선택하는 것이다. 즉 목표치 (desired values 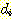 ) 와 출력치 (actual values
) 와 출력치 (actual values 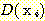 ) 간의 차이의 제곱의 합이 최소가 되도록 하는 것이다. 그 값
) 간의 차이의 제곱의 합이 최소가 되도록 하는 것이다. 그 값 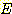 는 다음과 같이 구해진다.
는 다음과 같이 구해진다.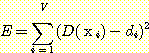
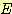
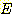

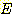
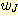

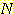 or
or 
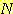
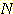
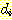
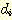
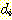
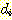
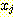
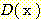
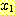
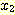
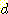

 .
.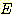 with respect to
with respect to 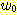 ,
, 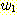 , and
, and 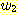 and setting each one equal to zero produces
and setting each one equal to zero produces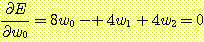 ,
,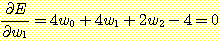 ,
,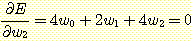 .
.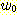 ,
, 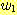 , and
, and 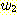 results in
results in 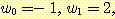 and
and  . Substituting these weights into equation (24) gives the discriminant function
. Substituting these weights into equation (24) gives the discriminant function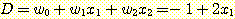 .
.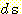
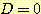
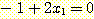 or
or 
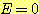
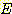
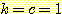
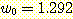 ,
,  , and
, and 
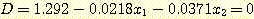
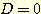 를 사용하여 ADB 가 MSE 보다 더 좋은 결과를 보여준다.
를 사용하여 ADB 가 MSE 보다 더 좋은 결과를 보여준다.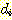 값을 가지는 minimum squared error 을 사용하여 완벽하게 구분된다.
값을 가지는 minimum squared error 을 사용하여 완벽하게 구분된다.