시각 시스템의 영상처리와 분석
로봇공학 : Saeed B. Niku 저, 김정하, 염영일 역, 사이텍미디어, 2002 (원서 : Introduction to Robotics : Analysis. Systems. Applications, Prentice Hall, 2001), Page 281 ~ 346
시각 시스템과 영상처리, 패턴인식 등에 관련된 작업은 매우 큰 작업이며 이에 관한 다양한 하드웨어, 소프트웨어에 관련된 연구주제도 매우 많다. 이러한 정보는 1950년대부터 지속적으로 축적되어 왔으며, 산업분야와 경제분야와 같은 다른 분야에서도 관심을 가지면서 성장해 왔다. 매년 발표되는 엄청난 숫자의 보고서를 보면 그것이 얼마나 유용한 기술인지 알 수 있다. 이러한 기술들이 다른 응용분야에서는 부적당할 수도 있으나, 이 장에서는 영상처리와 분석을 위한 몇몇 기본적인 내용을 공부할 것이고, 어떤 목적을 위해 개발된 몇 가지 예제를 언급할 것이다 이 장에서는 유용한 모든 시각 루틴을 다루지는 못하였고 다만 서론적인 내용만 다루었다. 흥미를 가진 사람은 다른 참고서적을 찾아보기 바란다.
다음에 이어지는 몇 개의 절에서 기초적인 용어의 기본정의와 사용할 개념을 기술하였다.
영상처리는 추후에 영상분석과 분석 결과를 사용하기 위해 영상 (image) 을 준비하는 과정이다. 예를 들면 카메라나 비슷한 기술(스캐너 같은)을 통해 획득된 영상은 영상분석루틴에 의해 사용될 수 있는 상태로 존재하지 않는다. 어떤 영상은 잡음을 줄여 개선해야 하고, 어떤 영상은 단순화해야 하며, 또 다른 영상은 향상시키고, 변환되고, 나누어지고, 필터링되어야 할 것이다. 영상처리 (image processing) 는 향상시키거나, 간단히하거나, 강화하거나 심지어는 영상을 바꾸는 루틴이나 기술의 집합이다.
영상분석 (image analysis) 은 영상처리를 통하여 미리 획득된 영상에서 정보를 추출하고 물체나 물체가 놓인 환경에서 그 물체를 검출해내기 위한 통합된 처리과정을 말한다.
실제의 모든 화면 (scene) 은 3차원이나, 영상은 2차원이나 3차원이 된다. 2차원 영상은 화면의 깊이나 특징이 필요하지 않을 때 주로 사용되나. 예를 들면 물체의 윤곽이나 물건의 반면 영상 (silhouette) 을 정의한다고 고려해 보자, 그 경우 물체 위의 임의의 위치에서의 깊이를 결정할 필요는 없을 것이다. 또 다른 예로는 실장된 회로판의 검사를 위한 시각 시스템의 사용이다. 여기서도 모든 부품이 평면에 고정되어 있으므로 다른 부품간의 연관된 깊이를 알 필요가 없으며 표면에 대한 정보도 필요하지 않다. 따라서 2차원으로도 영상분석과 검사는 충분할 것이다.
3차원 영상처리는 동작감지, 깊이측정, 원거리 감지, 상대위치, 항법운행 등의 작업을 다룬다. CAD/CAM 에 관련한 작업도 3차원 영상처리가 필요하며, 또한 많은 검사와 물체인식 작업이 필요하다. 단층사진 (CT: computed tomography) 에서도 3차원 영상처리를 필요로 한다. 단층사진에서는 X선이나 초음파는 한 번에 한 면의 영상을 얻는 데 사용되고, 추후에 획득된 모든 영상은 물체의 내부특성에 대한 3차원 영상을 생성하는 데 사용된다.
대부분의 3차원 시각 시스템은 많은 화면이나 하나의 화면이나 마찬가지로 영상으로 생성하는 데 문제점을 가지고 있다. 이 화면들로부터 정보를 추출해내기 위해 영상처리 기술이 인공지능 (artificial intelligence) 기술과 융합된다. 특성이 알려진 곳(예를 들어 조명 조절) 에서 시스템이 작업을 할 때에는 높은 정밀도와 빠른 작업속도로 기능을 수행할 수 있다. 이에 반하여, 환경이 알려져 있지 않거나, 잡음이 있거나, 제어가 불가능할 경우(예를 들어 수중에서의 작동) 에는, 시스템은 부정확해지고 부가적으로 정보를 처리해야 하므로 처리속도가 느려지게 될 뿐만 아니라 3차원 좌표계를 다루어야 한다.
영상 (image) 은 검은색과 흰색 또는 색상뿐만 아니라 프린트 형태나 디지털 형태로써 실제 화면을 표현하는 방식이다. 인쇄된 영상은 다양한 색상(컬러인쇄나 명암인쇄처럼) 이나 무채색 (gray scale), 또는 단 한가지의 색에 의해 인쇄된다. 예를 들면, 실제 하프톤 (halftone) 으로서 함께 사진을 출력하기 위해서는 현실적인 영상의 구현이 가능한 다양한 회색의 잉크를 사용해야 한다. 그러나 대부분의 인쇄에서는 단 한 가지 색만이 사용된다(신문이나 복사기에서 검은색의 잉크만 사용되어지는 것처럼). 이러한 경우에는 검은색 부분과 흰색 부분의 비율을 변화시켜 모든 하프톤을 만들어 낸다(검은 점의 크기). 인쇄할 부분이 작은 부분으로 나뉘진다고 가정해 보자. 각각의 부분에서 잉크가 있는 부분의 양이 희고 빈 공간에 비해 더 작다면 밝은 회색으로 보일 것이다(그림 1의 예제를 참조). 검은 잉크 지역이 흰 지역보다 많으면 그것은 어두운 회색으로 보일 것이다. 인쇄할 점의 크기를 바꿈으로써 다양한 그레이 단계를 생성할 수 있고 무채색의 그림을 인쇄할 수 있다.
인쇄된 영상과는 달리 텔레비전과 디지털 영상은 세분된 화소 (pixel 또는 picture cell) 로 나누어지고(3차원 영상에서는 volume cells 또는 voxel 이라 한다), 각 화소의 크기는 모두 같으나 그레이 영상을 만들기 위해 빛의 강도 (intensity) 가 바뀌게 된다. 여기서는 주로 디지털 영상에 대해서 논의하므로 크기가 같으며 빛의 강도가 변하는 화소에 대해서 항상 논의할 것이다.
[그림 1] 인쇄된 영상 안의 음영단계 표현의 예. 인쇄물에서 단지 한 가지 색의 잉크가 사용되었다. 희색과 검은색의 비율은 다른 음영단계를 만든다.
영상 카메라에는 보통 아날로그와 디지털의 두 가지 종류가 존재한다. 아날로그 카메라는 흔하지는 않지만 아직도 주위에서 쓰여지고 있다. 이는 텔레비전 방송국에서 기준장비로써 사용되기도 한다. 디지털 카메라는 아주 흔하고 서로 비슷하다. 비디오 카메라는 비디오 테이프 녹화장치가 있는 디지털 카메라이다. 반면에, 그것이 녹화기능이 없다면 다른 카메라의 영상획득 장비와 같다. 획득된 영상이 아날로그이든지, 디지털이든지 상관없이 시각 시스템은 결국 영상을 디지털화하며 디지털 형태로 모든 데이터가 이진화되어 컴퓨터 파일이나 메모리칩에 저장된다.
아날로그 카메라와 디지털 카메라가 어떻게 영상을 획득하는지 잠깐 살펴보기로 한다.
비록 아날로그 카메라가 더 이상 평범한 것은 아니나 대부분의 텔레비전은 아직도 아날로그이므로 텔레비전의 작동방식을 알게 되면 카메라의 작동방식을 이해할 수 있을 것이다. 그러므로 아날로그와 디지털 카메라 모두 검토해 보자.
비디콘 카메라 (vidicon camera) 는 영상을 아날로그 전기신호로 바꿔주는 아날로그 카메라이다. 신호나 시간에 따라 변화하는 전압(혹은 전류)은 저장이 가능하며 디지털화와 방송도 가능하고 영상으로 재구성될 수도 있다. 그림 2는 비디콘 카메라의 개요를 보여주고 있다. 렌즈를 사용해서 스크린에 두 개의 층으로 구성된 화면이 투사된다. 투명한 금속성 필름과 광전도성 모자이크 (phoconductive mosaic) 는 빛에 대해 매우 민감하다. 모자이크는 빛의 변화와 세기에 따라 저항이 변함으로써 반응한다. 그것 위에 영상을 투영한 결과, 모든 위치의 저항의 크기는 빛의 세기에 따라 변화한다. 전자총 (electron gun) 은 연속적인 음극광선 (cathode beam: 끊임없이 이어지는 음전하가 있는 전자) 을 만들고 서로 수직인 콘덴서 2쌍 (편향기: deflector) 을 통해 보낸다. 콘덴서의 각 쌍에 대한 전하에 따라서 전자빔 (electron beam) 은 위로 또는 아래로 또는 왼쪽이나 오른쪽으로 편향되고 광전도성의 모자이크에 투사된다. 전자빔이 모자이크를 때리는 순간, 전하가 금속성 필름으로 유도되고 출력포트에서 정확히 계측이 가능해진다. 출력에 측정되는 전압은 V = IR 이며, 여기서 I는 전류(전자빔의)이고 R은 관련된 모자이크의 저항이다.
이제 계획된 경로를 통하여 두 콘덴서의 전하를 변화시킴으로써 모자이크를 주사할 수 있도록 위, 아래와 양옆으로 광선이 편향할 수 있다고 가정해 보자 (래스터 스캔이라고 불리는 과정). 빔이 영상을 주사할 때마다 출력은 모자이크의 저항에 비례하거나 빛의 세기에 비례한다. 출력전압을 지속적으로 읽어들임으로써 아날로그 방식의 영상표현을 구현할 수 있다.
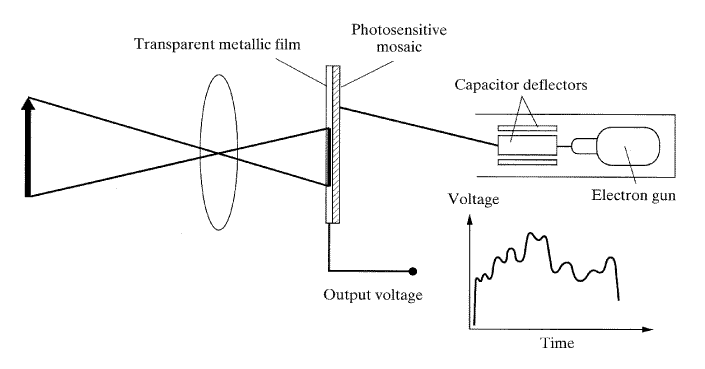
[그림 2] 비디콘 카메라의 개략도
텔레비전의 동영상을 만들기 위해서는 영상이 초당 30회 뿌려지고 재현된다. 인간의 눈은 약 1/10초의 일시적인 이력현상 (temporary hysteresis effect) 을 가지고 있기 때문에 초당 30번 바뀌는 영상이 연속적인 것으로 지각되어 움직이는 것으로 보이는 것이다. 영상은 서로 얽힌 240선을 가진 두 개의 부 영상 (subimage) 으로 나누어진다. 따라서 텔레비전 영상은 1초에 30번 반복하는 480선으로 구성되어 있다. 빔을 모자이크의 최상단에 되돌려 주기 위해 45개의 선이 추가되어 총 525선을 만들면서 사용되나 대부분의 다른 나라에서는 625선이 기준이다. 그림 3은 비디콘 카메라의 래스터 스캔 (raster scan) 을 보여주고 있다.
방송되는 신호는 보통 주파수 변조방식 (FM: frequency modulation) 으로 방송된다. 즉, 전송신호의 주파수는 신호의 진폭을 말한다. 신호가 방송되고, 수신기를 통해 수신하며 시간에 의존하는 가변전압을 생성하는 원래의 신호로 복조된다. 예를 들어 텔레비전 수상기에서 영상을 재현하기 위해 이 전압이 영상으로 변환되어야 한다. 이를 위해, 전압이 비디콘 카메라에서 전자총과 유사한 편향 콘덴서와 함께 음극선과 (CRT: cathod-ray tube) 으로 공급된다. 텔레비전에서의 전자빔 강도는 신호의 전압에 비례하고 카메라에서 보았던 방법과 비슷한 방식으로 주사된다. 그러나 텔레비전 수상기에서는 빔이 강도에 비례하여 빛을 발생하는 인 (phosphorous) 성분을 가진 물질 위에 투사되어 영상을 재생한다.
컬러영상에서는 투사된 영상이 빨강. 녹색.청색의 세 개의 색 (RGB) 으로 분해된다. 세 가지 색 중 같은 과정이 각각의 색을 기준으로 한 영상에 대해서 반복되는 동시에 세 개의 연속 신호가 생성되고 또한 방송된다. 텔레비전 수상기에서는 세 개의 전자총이 스크린에 RGB로써 연속적인 세 개의 영상을 재생하나 RGB색으로 빛을 내어 반응하는 스크린의 작은 세 가지 화소를 제외하고는 전체의 스크린에서 반복된다. 어떤 시스템에서도 컬러영상은 RGB의 영상으로 나누어지고 세 개의 독립적인 영상으로 다루어진다.
만약 신호를 방송하지 않는다면, 다음 사용을 위해 디지털화되어 기록되거나(추후에 논의될 것이다)또는 모니터에 직접 방송된다.
[그림 3] 비디콘 카메라의 레스터 스캔 묘사
디지털 카메라는 고체 (solid-state) 기술에 기초를 둔다. 다른 종류의 카메라와 같이, 렌즈부는 카메라의 영상지역 위에 관심분야를 투사하기 위해 사용된다. 카메라의 주요 부분은 photosites 라고 하는 수십만 개의 매우 작은 감광영역이 인쇄된 고체 실리콘 웨이퍼 영상영역이다. 각 웨이퍼의 작은 영역은 화소이다. 영상영역 위에 영상을 투영할 때, 웨이퍼의 각 화소의 위치에 전하는 그 위치의 빛의 세기에 비례해서 전하가 발생한다(따라서 디지털 카메라를 전하결합장치 (CCD) 또는 전하통합장치 (CID) 라 한다).연속적으로 읽어들인 전하들의 집합은 영상 화소 (image pixel) 로 표현된다(그림 4).
웨이퍼는 단위인치(3/16 X 1/4)의 영역에 520,000개 정도의 화소를 가질 수 있다. 각각의 전하를 측정하기 위한 모든 화소의 직접적인 배선은 분명히 불가능하다. 이러한 큰 수의 화소를 읽어들이기 위해, 초당 30회의 속도로 전하가 각 photosite 옆에 위치한 광학상으로 독립된 시프트 레지스터 (shift register) 로 움직이고, 또한 출력배선으로도 움직인 후에 읽을 수 있게 된다[1,2]. 따라서 초당 30번마다 화소에 위치한 모든 전하가 순서대로 읽히며 저장된다. 그림 5(a)에서 나타낸 바와 같이 출력은 영상을 불연속적으로 표현하게 된다. 그림 5(b)는 VHS 카메라의 CCD 요소이다.
가시광선용의 CCD 카메라와 마찬가지로 파장이 긴 적외선 카메라는 적외선이 방출되는 모습을 텔레비전의 영상처럼 생성한다[3].
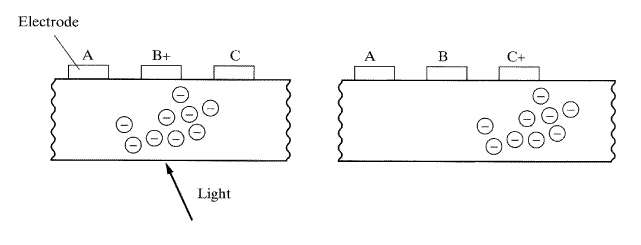
[그림 4] 디지털 카메라의 영상획득은 각각의 화소의 위치에서 각 화소에 빛의 충전현상에 관계 있다. 다음에 전하들을 광학적으로 독립된 시프트 레지스터들로 이동함으로써 읽는다. 그리고 전하들을 알고 있는 비율로 읽는다.
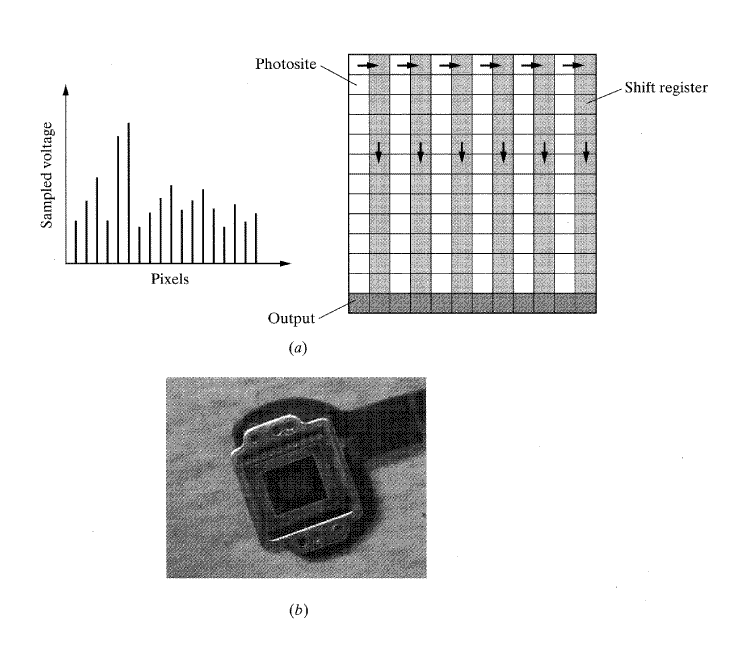
[그림 5] (a) 영상 데이터 수집 모델, (b) VHS 카메라의 CCD 소자.
앞서 언급한 대로, 검출전압 (sample voltage) 은 먼저 A/D컨버터(ADC)로 디지털화되고 컴퓨터 저장장치에 TIFF, JPG, Bitmap 등의 영상형식으로 저장되거나 모니터에 출력된다. 영상이 디지털화되었기 때문에 각 화소의 밝기의 강도를 나타내는 정보는 0과 1의 집합으로 저장된다. 디지털 영상 (digitized image) 은 각 화소에 빛의 강도를 표현하기 위해 순차적인 0과 1의 집합으로 저장된 컴퓨터 파일 이외에는 아무런 의미가 없다. 그 파일은 프로그램으로써 접근이 가능하고 읽기와 조작이 가능하며 다른 형태로 변환해서 쓸 수도 있다. 일반적으로 비전 루틴은 이 정보에 접근하고 자료에 어떤 기능을 수행하거나 결과를 표시하거나 조작된 결과를 새로운 파일로서 저장한다.
각 화소 위치에서 다른 명암도 (gray level) 를 가지고 있는 영상을 그레이 영상 (gray image) 이라고 한다. 명암값 (gray value) 은 디지타이저 (digitizer) 에 의해 디지털화되고 0과 1로 구성된 자료열 (string) 이후에 연속적으로 출력되거나 저장된다. 컬러영상은 빨강,초록, 파란색의 세 영상이 겹쳐지고 그레이 영상과 마찬가지로 각 색상의 변화하는 빛의 강도에 따라서 얻을 수 있게 된다. 이와 마찬가지로 영상이 디지털화되면 각 색상마다 빛의 강도를 위해 0과 1의 자료열을 갖게 된다. 이진영상 (binary image) 은 영상에서 각 화소의 가장 밝거나, 가장 어두운 값, 즉 0또는 1이 된다. 이진화 영상을 얻기 위한 대부분의 경우에 그레이 영상은 영상의 히스토그램 (histogram) 을 사용하거나 임계값 (threshold) 이라 불리는 차단값 (cut-off value) 에 의해 변환된다. 히스토그램이 다른 명암도의 분배를 결정한다. 최소의 일그러짐과 함께 차단 단계를 최상으로 결정할 수 있는 임계값을 고르고, 그 임계값으로 0(또는 "off")을 명암도가 임계값 아래에 있는 모든 화소에 할당하고, 1(또는 ”on")을 명암값이 임계점보다 위에 있는 모든 화소에 할당하기 위해 사용한다. 임계값이 변하면 이진영상도 변하게 되며 이진영상의 장점은 그것이 컬러영상이나 그레이 영상보다 훨씬 더 적은 메모리를 필요로 하고 훨씬 더 빨리 처리할 수 있다는 것이다.
영상처리와 영상분석에 관련한 과정은 주파수영역 (frequency domain) 과 공간영역 (spatial domain) 에 기초를 둔다. 주파수영역 처리과정에서는 주파수 스펙트럼이 영상을 변경하고 분석, 처리하는 데 이용된다. 이 경우, 각각의 화소와 화소의 내용은 사용되지 않는다. 그 대신에 전체 영상의 주파수 표현이 처리과정에 사용된다. 공간영역의 처리과정에서는 영상이 각각의 화소에 적용된다. 따라서 각각의 화소들이 처리과정에 직접적인 영향을 받는다. 위의 두 기술은 모두 중요하고, 강력하고, 서로 다른 목적을 위해 사용된다. 비록 두 가지의 기술이 다르게 사용되나 서로 관련되어 있다. 예를 들어 공간필터 (spatial filter) 가 영상의 잡음을 줄이는 데 사용된다고 가정해 보자, 그 결과 영상의 잡음은 줄어들 것이나 잡음이 줄어드는 동안에 영상의 주파수 스펙트럼 또한 영향을 받게 된다.
다음 몇 개의 절에서는 주파수와 공간영역에 대해 몇 가지 기본적인 사항을 논의할 것이다. 비록 일반적이기는 하지만 모든 장을 이해하는 데 도움이 될 것이다.
수학이나 다른 과목에서 배운 내용을 상기해 보면, 모든 주기적인 신호는 다음 식과 같이 다른 주기와 진폭을 가지는 많은 Sine과 Cosine함수로 분해가 가능하다는 것을 알 수 있다.
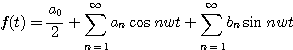(1)
만약 Sine함수와 Cosine함수를 더한다면 다시 원래의 신호를 재생할 수 있다. 식 (1)은 푸리에 급수 (Fourier series) 이며 방정식에 나타난 다른 주파수들의 집합을 신호의 주파수 스펙트럼 (frequency spectrum) 또는 주파수 내용 (frequency content) 이라 부른다. 물론 신호가 진폭-시간 영역에 있지만 주파수 스펙트럼은 진폭-주파수 영역에 있다. 이 개념에 대한 이해를 돕기 위해 예를 들어보자.
f(t) = sin (t)과 같은 간단한 Sine함수를 갖는 신호를 고려해 보자. 이 신호가 고정 진폭과 단일 주파수로 구성되었으므로 주파수영역에서 신호를 도시해 보면 그림 6에서처럼 하나의 선으로 표현이 가능할 것이다. 만약 주어진 주파수와 폭을 가지고 그림 6(b)와 화살표로 표현되게 함수를 그린다면, 똑같은 Sine 함수를 재생할 수 있을 것이다. 그림 7의 그래프는 서로 비슷하며 f(t) = ∑ n=1,3...15(1/n) sin(nt)와 같이 표현할 수 있다. 또한 주파수는 주파수-진폭 영역에서도 그려진다. f(t)에 포함된 주파수의 개수가 증가하면 합계는 2차 함수에 근접한다.
이론상 Sine함수로 구형파 (square wave) 를 만들기 위해서는 무한 개의 Sine함수가 더해져야 한다. 구형과 함수는 예리한 변화를 보이는데, 이는 많은 수의 주파수들이 급격히 변화한다는 것을 의미한다(충격, 펄스, 구형파 또는 이 함수에서 비롯된 합성함수들). 변화가 예리할수록 이를 구현하기 위한 주파수의 수는 증가한다. 따라서 어떤 예리한 변화를 포함한 비디오 신호나 세부적인 정보(빠르고 정밀도가 높은 변화하는 신호)는 주파수 스펙트럼에서 많은 주파수를 가지게 될 것이다.
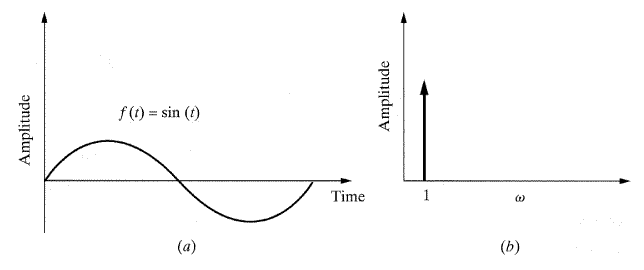
[그림 6] 단순한 Sine함수의 시간과 주파수영역에서의 그래프
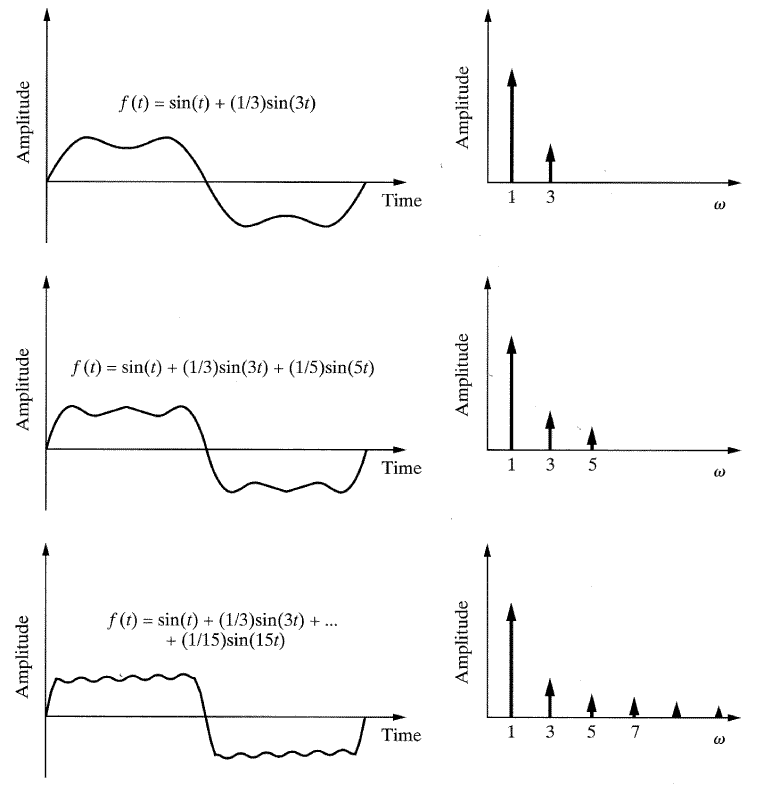
[그림 7] 주파수들이 규정된 Sine함수의 시간과 주파수영역의 그래프. 주파수의 수가 증가함에 따라 결과신호는 사각함수에 가까워진다.
불연속적인 신호에서도 이와 비슷한 해석이 적용될 것이다(방정식은 푸리에 변환을 사용하고 때로는 빠른 푸리에 변환 (FFT: Fast Fourier Transform)을 사용한다). 비록 이 책에서 푸리에 변환에 대해서 상세하게 논의하지는 않을 것이나 임의의 신호의 근사한 주파수 스펙트럼을 충분히 찾을 수 있을 만큼은 논의하였다. 이론상, 스펙트럼에는 비록 무한한 개수의 주파수들이 있으나 일반적으로 스펙트럼 안에서 주가되는 몇 개의 주파수는 더 큰 진폭을 가진다. 이러한 주된 주파수 (고조파: Harmonic) 는 신호를 구분하는 데 사용되고 음성인식이나 형상 또는 물체인식 등에 사용된다.
영상이 주사된 그대로 화소의 위치(x축 위에서)나 시간에 반하는 영상 화소 (image pixel) 의 명암값(y축 위에)을 순서대로 그리는 것을 고려해 보자 (5 절을 참조). 결과는 그림 8에서 보여주고 있는 것처럼 각 화소의 빛의 강도 (intensity) 를 보이는 변화하는 진폭에 대한 불연속적인 시간 도표일 것이다. 현재 우리가 9번째 행에 위치하고 129-144열의 화소를 보고 있다. 136화소의 강도가 주변 화소들에 비해 많이 다르기 때문에 그것을 잡음이라 생각할 수 있다(일반적으로 잡음은 주변 환경에 속하지 않는 정보이다). 134와 141화소의 강도 또한 이웃 화소와 다르며 이는 물체와 배경 사이의 전이를 의미한다. 따라서 이러한 화소를 통해 물체의 윤곽 (edge) 을 표현할 수 있다.
비록 불연속 (디지털화된) 신호에 대해서만 다루고 있지만, 이 신호는 진폭과 주파수가 다른 많은 Sine함수와 Cosine함수로 변환이 가능하고, 만약 그들이 서로 더해지면 신호는 재생될 것이다. 앞에서 논의한 바와 같이 천천히 변하는 신호(연속하는 화소 사이의 명암값의 변화가 작은 경우)를 재생할 경우에는 적은 수의 Sine함수와 Cosine함수가 필요하며 주파수도 낮을 것이다. 반면에, 빠르게 변하는 신호(화소간 명암도의 차이가 큰 경우)는 재생하는데 많은 주파수를 필요로 하고 주파수도 높을 것이다. 잡음과 윤곽은 어느 한 화소값 (pixel value) 이 이웃하는 화소값과 상이하게 다른 실제 예이다. 이러한 잡음과 윤곽은 전형적인 주파수 스펙트럼보다 더 큰 주파수들을 생성하는 반면에, 명암도가 천천히 변하는 화소들의 집합은 물체를 나타내고 스펙트럼의 더 낮은 주파수에 관여한다.
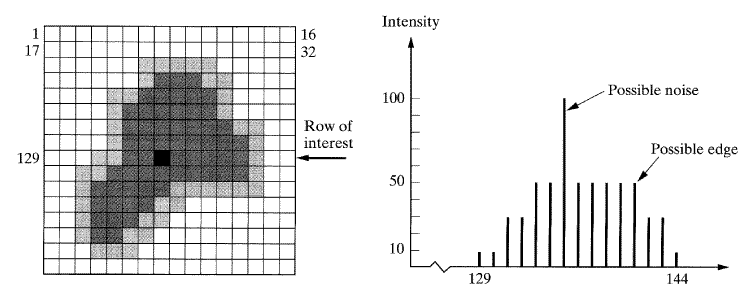
[그림 8] 영상의 세기 그래프에서 잡음과 윤곽 정보. 화소의 강도가 주위의 다른 화소들의 강도와 많이 다르다면 윤곽이나 잡음으로 고려할 수 있다.
하지만 만약 고주파 신호가 저역통과필터 (low-pass filter)를 지나가게 된다면-필터는 저주파가 통과할 때는 진폭을 줄이지 않고 통과하게 하나 고주파수가 통과할 때에는 진폭을 많이 줄인다 - 필터는 잡음과 윤곽을 포함한 모든 고주파의 영향을 감소시킬 것이다. 이것은 비록 저역통과필터가 잡음을 줄여서 영상을 부드럽게는 만들지만 윤곽을 줄임으로써 영상의 선명도가 감소된다는 것을 의미한다. 반면에, 고역통과필터는 저주파수 진폭을 많이 줄여서 고주파수의 영향을 분명히 증가시킬 것이다. 이 경우에는 잡음과 윤곽은 홀로 남겠지만 천천히 변화하는 부분은 영상에서 사라질 것이다.
어떻게 푸리에 변환이 응용되는지를 보기 취해 한번 더 그림 8의 데이터를 살펴보자. 9열 화소의 명암값이 그림 9(a)에서 반복된다. 처음 4개의 고조 주파수를 위해 명암값의 간단한 1차 근사 푸리에 변환[4]을 수행하였고, 그림 9(b)에 나타낸 것과 같이 신호가 재구성되었다. 두 개의 그래프를 비교해 보면 디지털의 불연속 신호도 재구성이 가능하고 심지어는 신호의 정확성은 적분방법뿐만 아니라 Sine함수와 Cosine함수의 수에 좌우된다는 것을 알 수 있다.
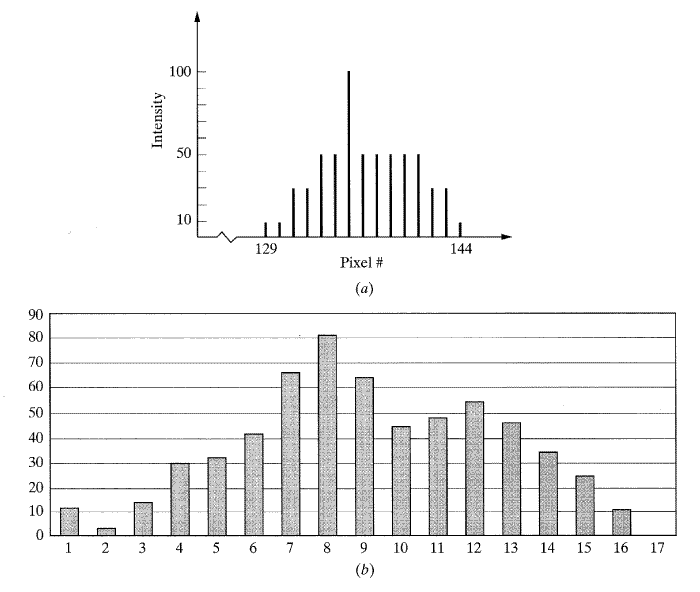
[그림 9] (a) 신호, (b) (a)신호의 스펙트럼의 1차 주파수의 4개만 이용하여 푸리에 변환으로부터 재구성된 이산신호
공간영역에서는 각각의 화소에 포함되는 정보에 접근하고 연산을 수행한다. 따라서 영상은 연산의 직접적인 영향을 받는다. 시각 시스템에서 사용하는 대부분의 처리방식은 공간영역 안에서 사용된다. 공간영역에서 가장 자주 쓰이고 가장 평범한 기술 중의 하나는 많은 다른 작업, 즉 필터링, 윤곽추출, 사진술, 기타 등등에 적용이 가능한 회선마스크 (convolution mask) 이다. 다음에는 마스크의 종류에 상관없이 회선 마스크의 기본 원리를 살펴보기로 한다. 그 후에 회선 마스크의 원리를 다른 목적에 적용해 볼 것이다.
영상이 화소로 구성되며, 각각의 화소는 자신만의 명암도와 색상정보를 가지고 영상을 집합적으로 구성한다고 생각해 보자. (명암도가 0과 1로 디지털화되지 않지만 아날로그값으로 표시된다고 가정하자). 예를 들어 그림 10의 영상이 A,B,C ...등의 기호로서 화소의 값을 가지는 보다 큰 영상의 일부분이라고 가정해 보자. 또한 값들이 각각의 화소에서 m1,..,m9으로 표현되는 값을 가지는 3 X 3마스크 (mask) 가 존재한다고 가정하자.
영상 위에 마스크를 적용하는 것은 첫 번째로 마스크를 영상의 좌상 모퉁이의 위에 중첩시키고 각 화소값과 상응하는 마스크의 값과의 곱을 모두 더한 값을 취한 후 표준값으로 나눈다. 이는 다음과 같이 표현이 가능하다.
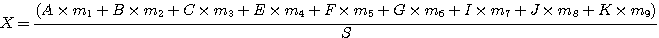(2)
여기서 S는 다음과 같다.
S = ㅣm1 + m2 +m3 + ...+m9ㅣ (3)
S는 표준화된 값이다. 하지만 만약 총합이 0이 되면 "1" 을 사용한다.
이 연산의 결과 X가 중첩된 블록의 중심에서 화소의 값을 대신할 것이다. 이 경우 X는 F의 값을 대신할 것이다(X →Fnew). 일반적으로는 수를 대신하게 하는 것은 원본 파일을 변경하지 않기 위해 새로운 파일에서 수행된다. 마스크는 오른쪽으로 1화소만큼 이동하고 새로운 파일에서 G값을 대신할 새로운 값인 X를 찾기 위해서 다음과 같은 연산이 반복된다.
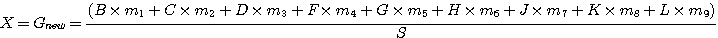
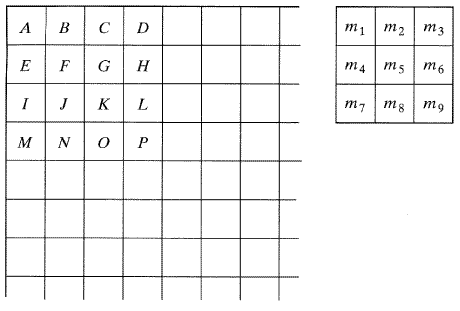
[그림 10] 영상에 중첩된 회선 마스크는 영상 화소를 화소로 변환 시킬 수 있다. 각 단계는 마스크에 있는 각 셀에 상당하는 화소에 화소의 값과 마스크에 있는 셀의 값을 곱하고 그 수를 더하여 관심영역의 중심에 있는 화소를 대신하는 평균화된 수로 나눔으로써 중첩시키는 단계로 구성되어 있다. 마스크는 화소단위로 움직이며 연산은 과정이 완전히 끝날 때까지 계속된다.
다음 마스크는 1화소 더 이동하고, 화소의 모든 열의 내용이 바뀔 때까지 계속해서 연산된다. 영상이 완전히 영향을 받을 때까지 계속해서 다음 열을 연산한다. 결과로 나온 영상은 약간 또는 매우 심하게, 마스크의 m값에 따른 연산의 결과로 받은 영향의 특성을 보일 것이다. 첫 번째와 마지막의 행과 열들은 영향을 받지 않으며 무시된다. 어떤 시스템에서는 첫 번째와 마지막의 행과 열에 0을 대입한다.
화소의 R행과 C열에 있는 영상 I(R,C), 마스크에서 n행과 n열에 있는 마스크 M(n,n)에 의해 블록의 중심에 있는 화소값 (Ix,y)new 는 다음에 의해 계산된다.
|
|
[그림 11] 회선 마스크의 예
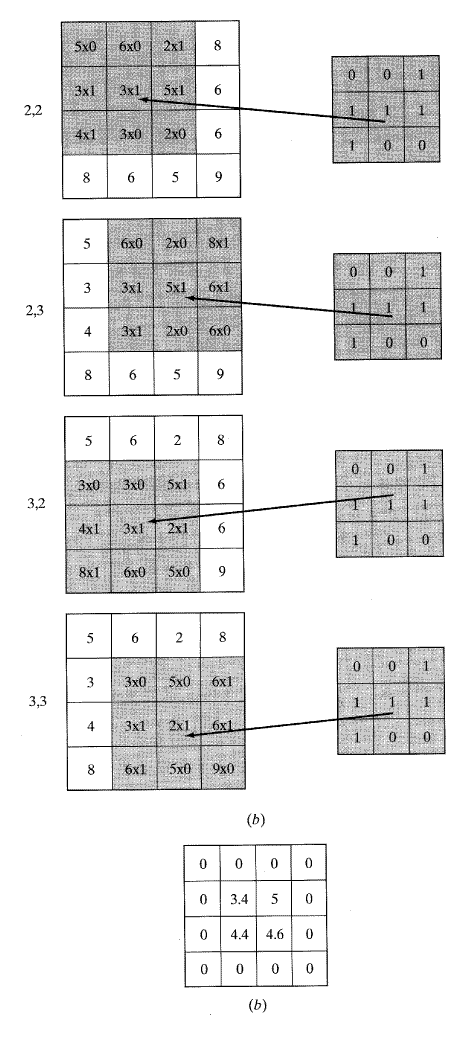
[그림 12] (a) 마스크를 영상 셀 위에 올려놓기, (b) 연산 결과.
|
|
|
(4) |
|
S |
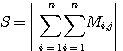(만약 합이 0이 아니면) (5)
만약 합이 0이면 S=1 이 된다.
표준화 (normalizing) 과 크기인수 (scaling factor) 인 S는 임의의 값이고 영상의 포화 (saturation) 를 막기 위해 사용된다. 따라서 사용자는 항상 이 수를 영상포화가 없도록 영상을 얻기 위해 조절할 수 있다.
|
예제 1 |
회선 마스크에 주어진 값들과 그림 11에 나타낸 값을 가진 영상의 화소를 고려해 보자. 주어진 화소의 새로운 값을 계산하라.
[해답] 첫 번째와 마지막 행과 열에 0을 대입한다. 왜냐하면 그것들은 회선 마스크에 의해 영향을 받지 않기 때문이다. 남아 있는 화소에는 마스크를 영상의 남아 있는 셀에 중첩시킬 것이고 그림 12(a)와 같이 새로운 화소값을 계산하기 위해 식 (2)와 (3)을 사용하여 그림 12(b)와 같은 결과를 얻을 것이다. 영상에 남아 있는 각각의 요소에 마스크를 중첩하면 다음의 수식을 얻을 수 있다.
2,2: 5(0)+6(0)+2(1)+3(1)+3(1)+5(1)+4(1)+3(0)+2(0)/5 = 3.4
2,3: 6(0)+2(0)+8(1)+3(1)+5(1)+6(1)+3(1)+2(0)+5(0)/5 = 5
3,2: 3(0)+3(0)+5(1)+4(1)+3(1)+2(1)+8(1)+6(0)+5(0)/5 = 4.4
3,3: 3(0)+5(0)+6(1)+3(1)+2(1)+6(1)+6(1)+5(0)+9(0)/5 = 4.6
영상처리와 분석에서 사용되는 보통의 루틴과 기술을 다음에 고려한다.
영상처리를 유용하게 하기 위해, 영상은 진폭뿐만 아니라 공간적으로 디지털화되어야 한다. 공간적인 디지털화는, 각 화소는 빛의 강도에 의해 읽힌다는 5.2절에서 언급한 처리 과정이다. 개별적으로 표현되고 읽히는 화소들이 많을수록 카메라와 영상의 해상도는 좋아진다. 빛의 강도를 같은 간격으로 검출하는 것을 샘플링이라 한다. 샘플링이 비율이 클수록 화소 데이터의 수는 커지며 해상도도 높아지게 된다.
그림 13은 같은 영상을 (a) 432 × 576, (b) 108 × 144, (c) 54 × 72, (d) 27 × 36 화소로 샘플링한 결과를 보여주고 있다. 샘플링 비율이 감소하면 영상의 투명성이 떨어지게 된다. 각 화소값에서 읽어들인 전압과 전하는 아날로그값이며 디지털화되어야 한다. 각 화소의 빛에 강도값의 디지털화를 양자화 (quantization) 라고 부른다. 사용하는 비트수에 따라서 영상의 해상도가 바뀌게 된다. n이 비트수일 때 가능한 명암도의 총 가지수 (possibility) 는 2n 이다. 1비트 AD컴버터(ADC) 에서는 단지 두 가지의 조합만이 있다: off, on 또는 0,1(이 경우는 이진영상이라 한다). 8비트 ADC로 양자화를 한다면 명암도의 최대 가지수는 256개이다. 따라서 영상은 256개의 다른 명암도를 가지게 된다. 양자화와 샘플링 해상도는 서로 독립적이다. 예를 들면 고해상도 영상이 이진영상으로 바뀔 수도 있으므로 양자화에는 오직 두종류만 있다(0 또는 1, 흑 또는 백, off 또는 on). 같은 화상을 8비트의 256개의 다른 명암을 가진 스펙트럼을 가진 것으로 양자화할 수 있다. 그림 14는 같은 영상이 (a) 2 레벨, (b) 4 레벨, (c) 8 레벨, 그리고 (d) 원래 44레벨로 양자화된 것을 보여주고 있다.
[그림 13] 영상의 다른 샘플링값에 따른 효과 : (a) 432 × 576, (b) 108 × 144, (c) 54 × 72, (d) 27 × 36 화소. 해상도가 감소함에 따라 영상의 선명도는 감소한다.
[그림 14] 2, 4, 8 과 44 의 음영단계로 양자화된 영상. 양자화 해상도가 증가함에 따라 영상은 더 부드러워진다.
화소에서 검출된 빛이 양자화될 때는 화소의 위치와 빛을 표현하는 0과 1의 문자열이 생성된다. 영상을 저장하기 위한 총 메모리는 총 샘플 개수와 각 디지털화된 샘플에 필요한 메모리의 곱이다. 영상이 커지거나 해상도가 높아지거나 또는 명암도의 수가 증가하면 더 큰 메모리가 필요하게 된다.
|
예제 2 |
256 × 256 화소의 영상을 고려해 보자. 영상의 총 화소수는 256 × 256 = 65,536이다. 영상이 이진영상인 경우에는 각 화소당 0과 1같이 1비트가 필요하다. 따라서 영상을 기억하기 위한 총 메모리는 65,536비트가 필요하며, 이는 8비트가 1바이트 (byte) 이므로 8,192바이트가 된다. 만약 각 화소가 256가지의 다른 회색 농도를 위해 8비트로 디지털화된다면 65,536 × 8 =524,288비트 또는 65,536바이트가 필요하게 된다. 만약 컬러영상이라면, 빨강, 녹색, 파랑의 각 색마다 65,536바이트가 필요하게 된다 초당 30개의 영상이 나오는 컬러 동영상의 경우 메모리는 초당 65,536 × 3 × 30 = 5,898,240바이트를 필요로 한다. 이것은 단지 영상 화소들의 기록을 위한 필요한 메모리이며 색인정보와 다른 부가정보는 포함하지 않은 메모리이다.
그림 15가 무엇을 나타내는 영상인지 알아볼 수 있는가? 물론, 이 그림은 16 × 16의 저해상도이므로 실물이 무엇인지 예측하기는 매우 어렵다. 이러한 간단한 그림은 샘플링 비율과 샘플링으로 얻은 정보 사이의 관계를 나타낸다. 이 관계를 이해하기 위해 샘플링과 관련한 몇몇 기본적인 사항에 대해 논의할 것이다.
[그림 15] 낮은 해상도 (16 × 16)의 영상
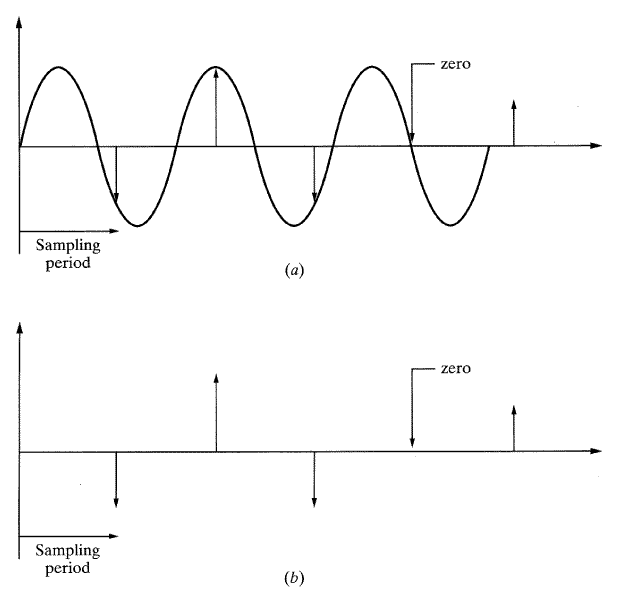
[그림 16] (a) 주파수 f를 가진 Sine함수 신호, (b) fs의 비율로 샘플링한 크기.
그림 16(a)에서 나타낸 바와 같이 주파수 f 를 갖는 간단한 Sine함수의 곡선을 생각해보자. 신호가 fs의 비율로 샘플링된다고 가정해 보자. 이는 샘플링 회로가 fs의 주파수로 신호의 진폭을 읽는다는 것을 말한다. 그림 16(b)의 화살표는 상당하는 샘플의 진폭을 말한다.
지금 샘플된 데이터를 신호를 재구성하기 위해 사용한다고 가정해 보자(이는 CD플레이어 같은 음원 (sound source) 에서 샘플링하고 스피커를 통해 샘플링된 데이터로 사운드 신호를 재구성하는 것과 비슷하다). 이때 우연히 같은 신호가 재구성될 가능성도 있을 수 있다. 그러나 그림 17을 볼 때 같은 자료에서 원래의 신호와는 전혀 다른 신호가 재건될 가능성이 더 크다. 위의 두 신호 모두 유효한 것이지만 다른 많은 신호들도 유효한 것은 마찬가지이며 샘플링된 데이터로부터 재구성될 수 있다. 이러한 정보의 손실을 주파수중복 (aliasing) 이라 하며 심각한 문제를 일으킬 수 있다.
샘플링 원리 (sampling theorem) 를 참조하면, 주파수중복 (aliasing) 을 막기 위해서 추출된 샘플링 주파수는 신호에서 보이는 가장 큰 주파수보다 적어도 두 배는 커야 한다. 이때는 주파수 중복이 없이도 원래의 신호를 재구성할 수 있다. 신호의 주파수 스펙트럼으로부터 현재 신호의 고주파를 결정할 수 있다. 푸리에 변환 (Fourier transform) 을 이용하면 많은 주파수를 포함하는 주파수 스펙트럼을 얻을 수 있다. 그러나 여기서 알 수 있듯이, 주파수가 높을수록 진폭은 작아진다. 시스템 전체를 나타내는 주파수에 큰 영향을 주지 않는 저주파수는 무시되며 일반적으로 관심 있는 최대주파수만 선택된다. 이 경우 신호의 샘플링 비율은 적어도 최대주파수보다 두 배는 되어야 한다. 실제로 샘플링 비율은 주파수중복이 일어나지 않을 만큼 큰 값으로 정해진다. 주파수들은 보통 최대주파수보다 4~5배 가량 크다. 예로서 CD플레이어를 생각해 보자. 이론상으로 인간의귀는 약 20,000 Hz까지의 센서의 샘플링 비율은 적어도 40,000 Hz 정도로 두 배 정도가 클 것이다. 실제로 CD플레이어는 75,000 Hz까지 샘플링 비율을 취한다. 더 낮은 샘플링 비율의 사운드는 왜곡될 것이다.
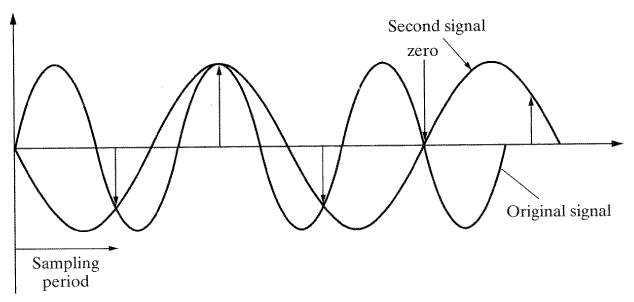
[그림 17] 샘플링된 데이터로부터 재구성된 신호. 샘플링된 데이터로부터 하나 이상의 신호가 재구성될 수 있다.
그림 18의 예는 샘플링 비율이 신호의 고주파보다 낮은 경우를 보여주고 있다. 비록 신호의 저주파수는 재구성되지만 원래의 고주파 성분은 제거된다. 이는 오디오 신호나 비디오 신호를 포함한 모든 신호에서 발생될 것이다.
역시 영상에서도 샘플링 비율(이는 영상의 해상도로 변환된다)이 낮다면 샘플 데이터는 모든 필요한 항목을 가지지 못할 것이고 영상 정보를 잃게 되고 원래 영상과 같게 재구성되지 못한다. 그림 15의 영상은 매우 낮은 비율로 샘플링되었고 정보 또한 잃어버렸다. 이것은 무슨 영상인지 말할 수 없는 이유이다. 하지만, 만약 샘플링 비율을 높인다면 영상을 알아볼 수 있을 만큼 충분한 정보를 얻을 수 있을 것이다. 고해상도나 샘플링 비율이 높아지면 더 많은 정보를 전송할 수 있으므로 보다 세밀하게 영상을 인식할 수 있다. 그림 19는 그림 15와 같은 그림이나 2, 4, 16배의 더 높은 해상도를 가지고 있다. 만약 로봇에게 부품을 집도록 명령하기 위해서는 시각 시스템에서 볼트와 너트 사이의 차이점을 인식할 수 있어야 한다. 볼트를 나타내는 정보는 너트의 정보와는 매우 다르기 때문에 저해상도 영상으로도 부품을 구별해낼 수는 있다. 그러나 차가 움직이는 동안에 차량 번호판을 인식하기 위해서는 차량 번호판의 숫자를 추출해내기 위한 충분한 정보를 가진 고해상도의 영상이 필요할 것이다.
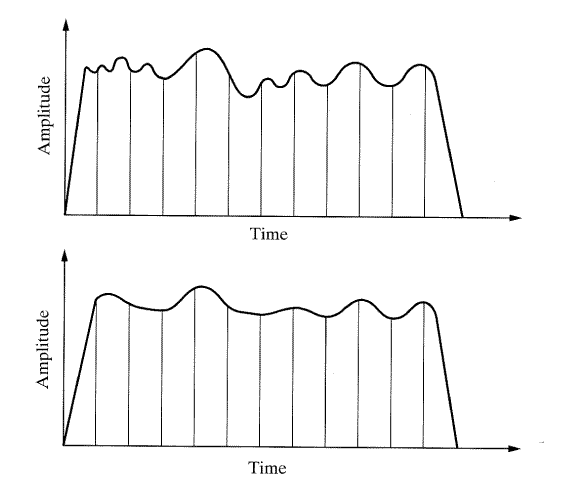
[그림 18] (a)의 원래 신호는 신호의 높은 주파수보다 낮은 주파수로 샘플링되었다. 재구성된 신호(b)는 원래 신호의 높은 주파수부분을 가지고 있지 않을 것이다.
[그림 19] 그림 15 영상의 높은 해상도 표현.(a) 32 × 32, (b) 64 × 64 (c) 256 × 256.
이미 언급하였듯이 영상처리 기술은 영상분석을 위해 영상을 강화시키고 향상시키거나 심지어는 변경하는 데 사용된다. 보통 영상처리 정보는 영상으로부터 추출되지 않는다. 잘못되거나 무의미한 정보를 제거하려는 의도는 중요하나 영상을 개선하는 데 반드시 유효한 것은 아니다. 예제에서 보여주듯이 물체가 움직이는 동안에 획득된 영상은 선명하지 않다. 물체에 관한 정보(성질, 형상, 위치, 방위 등)가 결정되기 전에 영상에서 흐릿한 부분을 줄이거나 삭제가 가능한지 검토하는 것이 매우 바람직하다. 조명이 반사되어 손상된 영상이나 어두운 빛 때문에 잡음이 있는 영상을 생각해 보자. 모든 경우에서 영상을 개선하고 영상분석루틴을 사용하기 전에 이를 위한 준비를 하는 것은 매우 바람직하다. 이와 마찬가지로, 거리, 차, 그림자 등이 표현된 매우 상세한 도시 일부분의 영상을 고려해 보자. 이러한 영상에서 정보를 추출하는 것은 윤곽을 제외한 모든 불필요한 항목이 제거된 영상에서보다 더 어려울 것이다.
영상처리는 히스토그램 분석, 이진화, 마스킹, 윤곽추출, 분할, 영역확장과 모델링 등으로 세분화될 수 있다. 다음 절에서는 이의 몇몇 과정과 그 응용에 대해 공부할 것이다.
히스토그램은 각 명암도 (gray level) 에서 영상 화소의 총 개수를 나타낸다. 히스토그램 정보는 임계값을 포함한 다른 많은 처리과정에서 이용된다. 예를 들어 히스토그램 정보는 영상이 이진수 값으로 변환될 때 차단점을 찾는 것을 도와준다. 또한 영상에 어떤 우세한 명암도가 있는지를 결정하는 데 이용될 수 있다. 예를 들어 영상의 잡음이 시스템상의 문제로 인해 많은 화소가 유일한 잡음의 명암도를 가진다고 가정해 보자. 이때 히스토그램은 잡음을 제거하거나 중화하기 위해 잡음이 있는 명암도가 어떤지 결정하는 데 이용될 수 있다.
그림 20(a)에서처럼 모든 명암도의 화소 중에서 비교적 근사한 값을 가진 두 화소를 밀집되도록 구성한다고 가정해 보자. 이 영상에서 모든 화소의 명암값 (gray value) 은 4단위 간격으로 120에서 180 명암도 사이의 값을 갖는다(0부터 255까지 16단계로 양자화 된다). 그림 10(c)는 상대적으로 분명히 낮은 범위인 120부터 180까지의 명암도의 화소를 갖는 히스토그램이다. 그 결과 영상이 선명하지 않고 세밀하지 못하다. 영상에서 보이는 16명 암도로 히스토그램을 균일화하고 이 명암도가 120부터 180의 명암도를 4단위 간격으로 표현하는 것 대신에 0부터 255의 명암도를 17단위의 간격으로 전개된다고 가정해 보자.
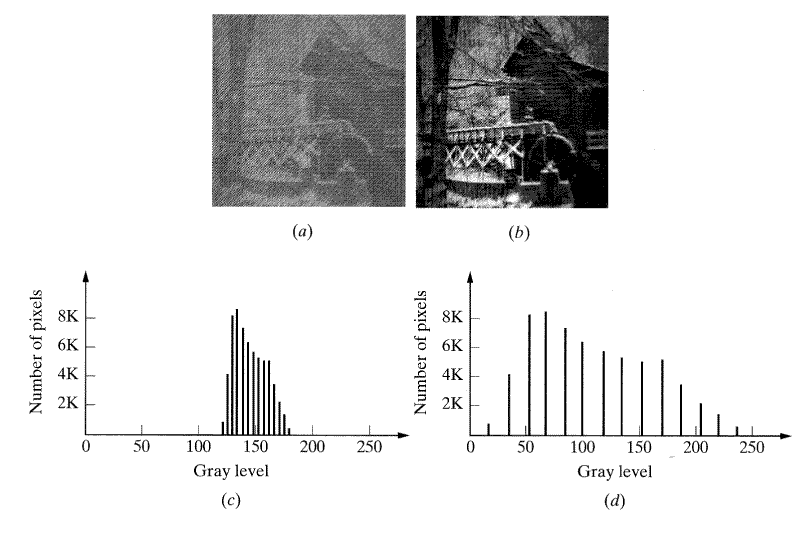
[그림 20] 히스토그램 평활화 효과와 개선된 영상
[표 1] 그림 20의 영상 (a), (b)에서의 실제 음영값과 화소의 개수
|
Levels |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
화소개수 |
0 |
750 |
5,223 |
8,147 |
8,584 |
7,769 |
6,419 |
5,839 |
5,392 |
5,179 |
5,185 |
3,451 |
2,078 |
1,692 |
341 |
0 |
|
(a) 경우 |
0 |
17 |
34 |
51 |
68 |
85 |
102 |
119 |
136 |
153 |
170 |
187 |
204 |
221 |
238 |
256 |
|
(b) 경우 |
120 |
124 |
128 |
132 |
136 |
140 |
144 |
148 |
152 |
156 |
160 |
164 |
168 |
172 |
176 |
180 |
균일화로 인해 영상은 그림 20(b)에서 보여주듯이 방대하게 개선되며, 이것의 히스토그램을 그림 20(d)에 나타내었다. 각 명암도에서 화소의 개수는 위의 두 경우 모두 같으나 명암도는 확산됨을 알 수 있다. 명암값은 표 1에 주어져 있다.
[그림 21] 256개의 음영단계를 가진 영상을 (b) 100, (c) 150의 값으로 이진화한 것.
임계화 (thresholding) 는 임계값으로서 임의의 명암도를 선택하여 영상을 임계값과 일일이 비교하여 두 부분(레벨)으로 분리하는 과정을 말하며 분리한 후에는 임계값 보다 높은지(on 또는 1, 영역에 포함됨), 낮은지(off 또는 0, 영역에 포함되지 않음)에 따라 화소를 다른부분이나 레벨로 할당한다. 임계화는 한 레벨이나 여러 개의 레벨을 같이 수행할 수 있으며 영상은 선택된 임계값을 기준으로 "층 (layer)"으로써 분할된다. 적당한 임계값을 선정하는 것을 돕기 위해 많은 다양한 기술, 즉 이진영상을 위한 간단한 루틴에서부터 복잡한 영상을 위한 고급 기술이 제안되었다. 이진영상을 위해 사용된 초기의 방법은 물체는 밝은 부분으로, 배경은 완전히 어둡게 표현되었다. 이러한 방식은 산업현장에서 조명을 제어가 가능하게 해주었으나 다른 환경에서는 가능하지 않다. 이진영상에서의 화소는 on 또는 off이므로 임계값을 선택하기가 쉽고 직선적이다. 다른 경우에서 영상은 다중 명암도를 가지고 있을 것이고 히스토그램은 여러 모드의 분포를 보일 것이다. 이 경우에는 계곡이 임계값으로 결정된다. 보다 진보된 기술에서는 통계학적인 정보와 영상 화소의 분포특성까지도 임계값을 구하는 데 이용된다. 그림 21은 256 명암도의 원본 영상과 100과 150의 명암도로 이진화한 결과를 나타낸다.
임계화는 영상을 이진값으로 변환하거나 필터링 연산, 마스킹, 그리고 윤곽추출과 같은 많은 연산에 이용된다.
때로는 이웃하는 화소끼리 어떻게 서로 연결되었는지, 또는 서로 어떻게 관련되어 있는지를 결정해야 한다. 연결성 (connectivity) 은 같은 성질을 가지는 동일 물체에서 같은 영역에 존재하는 것과 같이 같은 속성을 가지는지 정립하는 것이다. 이웃하는 화소의 연결성을 확립하기 위해서는 연결경로 (connectivity path)를 설정해야 한다. 예를 들어 똑같은 열과 행에 있는 화소만 연결되는지 아닌지, 또는 연결될 때 대각선에 위치한 화소도 연결되는지 결정해야 한다.
2차원 영상처리와 분석을 위한 세 가지 기본적인 연결경로가 있다. +4- 또는 ×4- 연결성이나, H6- 또는 V6-연결성 그리고 8-연결성이 그것이다. 3차원에서 Voxels (Volume Cells)사이의 연결성 범위는 6부터 26이다. 다음의 용어는 그림 22에 관하여 다음과 같이 정의된다.
|
a |
b |
c |
|
d |
p |
e |
|
f |
g |
h |
[그림 22] 화소의 이웃 연결성
+4-연결성: 화소 p에 대해서 p의 위, 아래, 왼쪽, 오른쪽 4개의 화소 (소위 b, g, d, e)에 관하여 분석할 때 +4-연결성이 적용된다.
×4-연결성: 화소 p에 대해서 p의 대각선의 4개 화소 (a, c, f, h)에 관하여 분석할 때 4-연결성이 적용된다.
p(x,y)를 위해 적절한 화소는 다음과 같다.
• +4-연결성에 대해: (x +1, y), (x - 1, y),(x, y, + 1),(x, y - 1) (6)
• ×4-연결성에 대해: (x + 1, y + 1), (x + 1, y -1)
(x - 1, y + 1), (x -1, y -1) (7)
H6-연결성: 화소 p에 대해서 p의 위와 아래 행에서 이웃하는 6개의 화소(a,b,c,f,g,h)에 관하여 분석할 때 H6-연결성이 적용된다.
V6-연결성: 화소 p에 대해서 p의 오른쪽과 왼쪽 열에서 이웃하는 6개의 화소(a, d, f, c, e, h)에 관하여 분석할 때 V6-연결성이 적용된다.
p(x, y)를 위해 적절한 화소는 다음과 같다:
• H6-연결성에 대해: (x -1, y + 1), (x, y, + 1), (x + 1, y +1)
(x -1, y - 1), (x, y, - 1), (x + 1, y -1) (8)
• V6-연결성에 대해: (x -1, y + 1), (x - y, y), (x - 1, y - 1)
(x +1, y + 1), (x + 1, y), (x + 1, y - 1) (9)
8-연결성: 화소 p에 대해서 p의 주변에 있는 8개의 모든 화소(a, b, c, d, e, f, g, h)에 관하여 분석할 때 8-연결성이 적용된다.
일반적인 화소 p(x, y)를 위해 적절한 화소는 다음과 같다:
(x -1, y - 1),(x,y - 1), (x +1,y -1), (x - 1, y)
(x +1, y), (x - 1, y + 1), (x, y +1), (x + 1, y + 1) (10)
지금까지는 일반적인 사항과 영상처리와 분석에서 사용되는 기본적인 기술에 대해서 공부하였다. 다음에는 특정한 응용프로그램을 위해 사용된 특별한 기술을 논의할 것이다.
|
예제 3 |
그림 23에 나타낸 영상에서, 화소(4,3)에서부터 시작해서 +4-, ×4-, H6-, V6-, 8-연결성 규칙에 의서하여 서로 접속하고 있는 것에 따라 찾을 수 있는 모든 연속하는 화소를 검색하라.
[해답] 그림 24는 5개의 연결성을 찾은 결과를 보여주고 있다. 각 방법을 위한 검색을 위해서 우선 한 화소를 선정하고 찾고자 하는 검색방법의 원리에 근거하여 다른 이웃하는 화소와의 연결성을 찾고 작업이 완료될 때까지 계속한다. 나중에 같은 규칙을 영역 확장과 같은 다른 목적을 위해 사용하게 될 것이다.
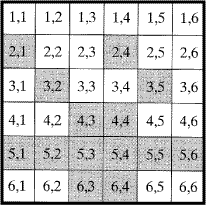
[그림 23] 예제 3의 영상
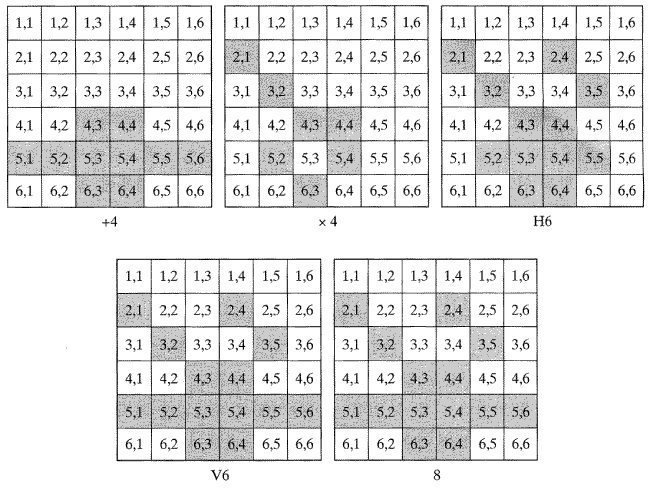
[그림 24] 예제 3의 연결성 검색 결과
다른 신호처리의 경우와 같이 시각 시스템에도 잡음이 있다. 몇몇의 잡음은 시스템의 원인, 더러운 렌즈, 전자부품의 고장, 나쁜 성능의 메모리칩과 낮은 해상도가 원인이 될 수 있다.다른 원인들은 특별히 정해져 있지 않고 주변환경이나 조명이 좋지 않으면 발생한다. 순 효과 (net effect) 는 잡음을 제거하거나 줄이기 위한 전처리과정이 필요한 영상을 말한다. 게다가, 때때로 영상은 하드웨어와 소프트웨어, 둘 다 맞지 않아서 발생할 수 있으므로 영상을 분석하기 이전에 개선되거나 향상되어야 한다. 하드웨어에서는 탑재된 칩을 정정하는 것이 영상 센서를 통한 결함이 있는 영상이 있을 경우, 한 번은 시도된다[5]. 이 방법에서는 가장 가까운 이웃화소를 판독한 결과가 잘못된 화소라고 판명된 화소와 대체된다. 그러나 일반적으로 소프트웨어적인 방법은 모든 필터링에 사용된다.
필터링 기술은 두 개의 분야로 나뉘어진다: 주파수 관련 기술 (frequency-related technique) 은 신호의 푸리에 변환을 연산하는 반면에 공간영역 기술 (spatial-domain technique) 은 영상의 부분적이나 전체적으로 화소 수준에 영향을 미친다. 다음 내용은 영상에서 잡음을 줄이기 위해 많은 다른 연산방법을 요약한 것이다.
10절에서 언급했듯이, 마스크 (mask) 는 필터링 연산이나 잡음제거를 포함한 많은 다른 목적으로 사용된다. 9절에서는 윤곽뿐만 아니라 잡음이 신호 스펙트럼에서 더 높은 주파수를 야기함을 언급하였다. 저주파수가 변동이 그리 크지 않은 경우에 높은 주파수를 가진 화상이 감쇄되므로 마스크가 저역통과필터와 같은 역할을 하게 구성하는 것이 가능 해진다. 따라서 잡음은 줄어든다.
이웃평균
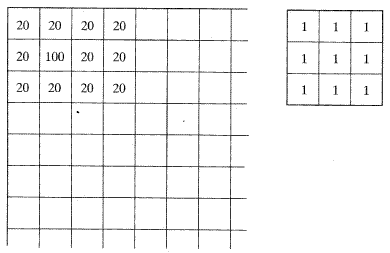
이웃평균 (neighborhood averaging) 은 영상에서 잡음을 감소시키는 데 사용되나 영상의 선명도 (sharpness) 또한 감소시킨다. 그림 25에서 나타낸 지시된 명암도를 가진 상징적인 영상뿐만 아니라 이에 상당하는 값을 가진 3 × 3 마스크를 고려해 보자. 모든 화소가 일일이 20의 명암값을 가진다고 볼 수 있을 것이다. 100의 명암값을 가지는 화소는 주위의 화소와 다르기 때문에 그것은 잡음으로 볼 수 있다. 표준화된 값 9 (마스크의 모든 값들의 합)와 더불어 영상의 구석에 마스크를 적용하면 다음의 수식을 얻을 수 있다.
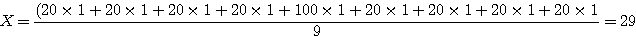
지시한 구석에 마스크를 적용한 결과 100의 값을 갖는 화소는 29로 바뀌고, 잡음화소와 주변화소의 큰 차이(100 대 20)는 대폭 줄어들게(29 대 20) 되므로 잡음은 감소하게 된다.
[그림 25] 이웃평균 마스크
[그림 26] 영상의 이웃평균
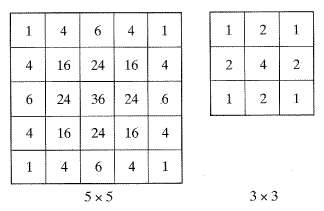
[그림 27] 5 × 5 와 3 × 3 가우시안 평균필터
이러한 특성으로 마스크는 저역통과필터의 역할을 한다. 이어한 연산을 통해서 영상에 새로운 명암도(29)가 생성되고 히스토그램도 변경됨을 숙지해야 한다. 이와 마찬가지로, 평균화 저역통과필터는 윤곽의 선명도를 감소시키고 영상을 더 부드럽게 하며 초점이 흐려진다. 그림 26은 원래의 영상(a)과 잡음으로 손상된 영상(b), 3 × 3 의 평균필터 응용 후의 영상(c), 5 × 5 의 평균필터 응용 후의 영상(d)을 보여주고 있으며, 3 × 3필터보다 5 × 5필터가 더 좋음을 알 수 있지만 좀더 많은 처리과정이 필요하다.
그림 27에서 나타낸 것처럼, 가우시안 (Gaussian) 평균필터(등방형 저역통과필터라 함)와 같은 또 다른 평균필터가 있다. 이 필터도 다른 필터와 마찬가지로 영상을 개선시키나 약간 다른 결과를 낳는다
이 기술에서는 여러 개의 같은 화면이 동시에 평균화된다. 카메라는 같은 화면의 영상을 얻어야 하므로 화면에서의 모든 동작은 멈추어야 한다. 따라서 소요시간뿐만 아니라 연산에 맞지 않는 기술도 빠르게 변해야 한다. 영상평균화 (image averaging) 는 영상의 숫자가 늘어날수록 더욱 효과적이다. 이는 근본적으로 무작위 잡음에 대해서는 매우 유용하며 잡음이 체계적이라면 다중영상에 대한 영상처리 결과와 같으며 그 결과 영상을 평균화하는 것은 잡음을 감소시키지 못하게된다. 만약 취득한 영상 A(x,y)가 무작위 잡음 N(x,y)를 가진다고 가정하면, 무작위 잡음의 합이 0이 되므로 목표영상 I(x,y)는 평균영상에서 찾아 낼 수 있을 것이다. 이는 다음 수식으로 표현이 가능하다.
A(x,y)=I(x,y) + N(x,y)
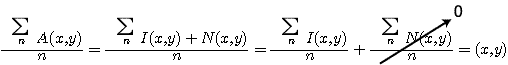(11)
비록 영상평균화가 무작위 잡음을 줄이기는 하지만, 평균을 이루는 이웃화소와는 달리 영상이 흐려지거나 초점이 흐릿해지지 않는다.
영상에서 푸리에 변환이 계산될 때, 주파수 스펙트럼은 잡음에 대해 깨끗한 주파수를 보여줄 것이며, 대부분의 경우 적당한 필터링에 의해 선택적으로 여과될 것이다.
평균이웃화소를 사용함에 있어서 가장 큰 문제점 중의 하나는 잡음을 제거할 때 필터가 윤곽도 흐리게 한다는 점이다. 중간값 필터 기술의 다른 점은 화소의 값이 주어진 화소 주변의 마스크에 있는 화소의 중간값(주어진 화소에 8개의 주변값을 더한)으로 대체된다는 것이다. 중간값은 집합에서 절반은 아래, 절반은 위로 만드는 중간값(또한 50%)이다. 평균값과는 달리 중간값은 집합의 임의의 한 화소값에 독립적이므로 중간값 필터는 전체적인 영상의 선명도를 감소시키거나 물체를 흐리게 하지 않으면서 잡음을 보다 강력하게 제거할 수 있다. 그림 25의 영상에 중간값 필터를 적용한다고 가정해 보자. 이때 오름차순으로 분류된 값은 20,20,20,20,20,20,20,20,100이 될 것이며, 중간값은 순서에 따라 5번째인 20이 된다. 중심 화소의 값을 20과 바꾸면 완벽하게 잡음이 없어지게 될 것이다. 물론 잡음이 항상 쉽게 제거되지는 않지만, 이 예제는 중간값 필터의 효과가 평균화하는 효과와 매우 다를 수 있다는 것을 보여주고 있다. 중간값 필터가 새로운 명암도를 만들지는 않지만, 그것들이 영상의 히스토그램을 변경시킨다는 점은 숙지해야 한다.
만약 중간값 필터가 여러 번 적용된다면 영상에 결 (grainy) 을 만드는 경향이 있다. 그림 28(a)를 고려해 보자. 명암도가 오름차순으로 1, 2, 3, 4, 5, 6, 7, 8, 9로 정렬되어 있다. 중간값은 5이고, 연산 결과의 영상은 (b)에 나타내었다. 영상이 화소 집합원소가 비슷한 값으로 구성되어 영상에 결이 생기게 된 것을 관찰해 보자.
[그림 28] 메디안 필터의 적용
[그림 29] (a) 원본 영상, (b) 같은 영상에 임의의 가우시안 잡음 추가, (c) 3 × 3 중간값 필터를 사용하여 개선된 영상, (d) 7 × 7 중간값 필터를 사용하여 개선된 영상
그림 29는 원래의 영상 (a)과 정해지지 않은 가우시안 (Gaussian) 잡음을 가지고 더럽혀진 영상(b), 3 × 3의 중간값 필터로 향상된 영상(c), 7 × 7의 중간값 필터로 향상된 영상(d)을 보여주고 있다.
윤곽추출 (edge detection) 은 영상을 처리하고 그 결과를 선으로 묘사하는 영상을 출력하는 결과를 나타내는 기법과 루틴을 통틀어 칭하는 일반적인 이름이다. 그 선은 평면의 횡단면, 평면의 교차점, 질감, 선과 컬러뿐만 아니라 그림자와 질감을 표현한다. 어떤 기법들은 수학 지향적이고 몇몇은 경험적이고 몇몇은 기술적이다. 위에 언급한 모든 기법들은 마스크와 임계값을 통하며 화소 모임과 화소의 명암도 사이의 차이점을 연산한다. 최종결과는 저장시에 메모리를 적게 차지하는 선으로 그려지거나 유사하게 표현되며, 이 방식은 처리도 손쉽고 연산비용과 저장비용도 저렴하다. 윤곽추축은 분할 (segmentation) 과 물체인식 (object recognition) 과 같은 하위처리단계에서도 필요하다. 윤곽추출 없이 겹쳐진 부분들을 찾고 지름과 면적과 같은 특성을 계산하거나 팽창하는 영역에서 부품을 탐색하는 것은 거의 불가능하다. 윤곽추출의 다른 기법은 다소 다른 결과를 나타내므로 신중하게 선택하고 현명하게 사용되어야 한다.
초기에 언급한 것처럼 잡음과 윤곽은 스펙트럼에서 높은 주파수들을 생성하므로 고역통과필터에 의해 분리될 수 있다. 마스크는 저주파 성분을 줄이며 고주파에는 영향을 미치지 않는 고역통과필터와 같은 역할을 하도록 설계(라플라시안1 필터라고 함)되었으므로 영상의 여백으로부터 잡음과 윤곽을 분리한다. 그림 30의 영상과 라플라시안1이라 불리는 마스크를 고려해 보자. 마스크는 음의 수들을 가지고 있다. 마스크를 영상의 모서리에 적용시킨 결과는 다음과 같다.
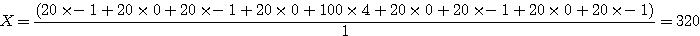
표준화 인자는 1이며, 따라서 100의 값은 320으로 치환되고 원래의 차이가 두드러질 것이다(100 대 20에서 320 대 20으로). 마스크가 이러한 차이(높은 주파수)를 강조하므로 고역통과필터라 할 수 있다. 이는 영상에서 물체의 잡음이나 윤곽이 더 효율적으로 보인다는 것을 의미한다. 그림 31은 몇 가지 다른 고역통과필터를 나타내고 있다.
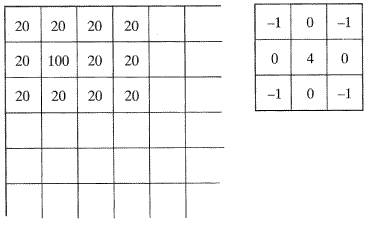
[그림 30] 전형적인 고역통과 윤곽추출 마스크(라플라시안1)
[그림 31] 다른 고역통과필터
여전히 다른 마스크들은 변화율의 사용을 통하여 영상에 미분효과를 준다. 이 경우에 주위 화소 사이의 수평과 수직 변화율이 계산되고 누승되어 총합의 제곱근을 찾을 수 있다. 수학적으로는 다음과 같이 쓸 수 있다.
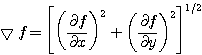(12)
식 (12)는 화소간의 강도에 대한 차이값들의 절대값을 계산하는 것이다. 그림 32에 나타낸 세 개의 마스크[6,7,8,9,10]는 소벨 (Sobel), 로버트 (Roberts), 그리고 프리윗 (Prewitt) 윤곽추출기 (edge detector) 라 하며 같은 변화율의 미분을 수행하나 서로 약간씩 다른 결과를 나타내며, 제일 많이 사용되는 방식이다. 이 방식들이 영상에 적용되면 두 쌍의 마스크들이 x, y 방위의 변화율을 계산하여 더해져서 임계값과 비교된다. 그림 33의 (a)는원본영상이고, (b)는 라플라시안1을 적용한 영상, (c)는 라플라시안2, (d)는 소벨, (e)는 로버트 윤곽추출을 한 것이다. 다른 영상을 처리한 결과는 영상의 히스토그램과 선택된 임계값이 최후 결과에 가장 영향을 미치므로 다를 수도 있다. 몇몇의 루틴은 사용자가 임계값을 변화시킬 수도 있으나 일부는 그렇지 않다. 각각의 경우에 사용자는 어느 루틴이 최적인지 선정해야 한다.
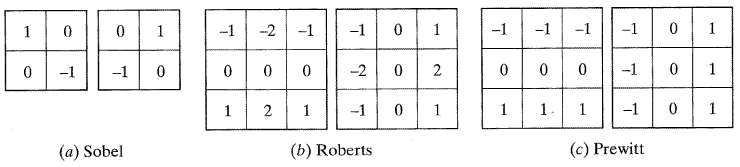
[그림 32] 소벨, 로버트, 프리윗 윤곽추출기
[그림 33] (a) 원본영상, (b) 라프라시안1로 윤곽추출, (c) 라프라시안2, (d) 소벨, (e) 로버트 윤곽추출기.
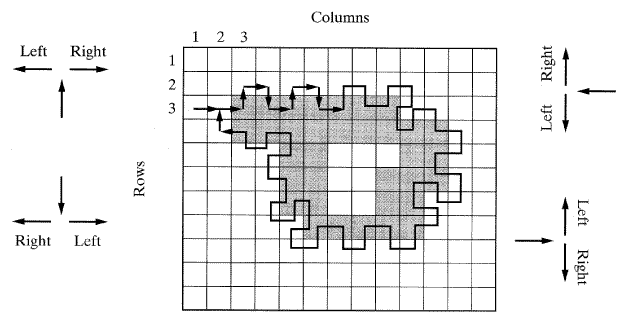
[그림 34] 윤곽추출을 위한 좌-우 검색기법[11]
실행이 간단하며 연속적인 윤곽을 생성할 수 있는 다른 간단한 루틴들도 이진영상을 위해 사용이 가능하다. 예를 들면[11] 이 책에서 제안하는 검색기법 중의 하나인 좌우동시 검색 (L-R: dubbed left-right) 인 이 방식은 얼룩같이 보이는 이진영상에서 물체를 빠르고 효율적으로 윤곽을 검출할 수 있다. 그림 34와 같은 이진영상을 상상해 보자. 음영화소 (gray pixel) 들은 켜지고(또는 물체를 표현) 백색화소 (white pixel) 들은 꺼졌다(또는 배경을 표현)고 가정해 보자. 포인터가 하나의 화소에서 다른 화소로 임의의 방향(위, 아래, 오른쪽 왼쪽)으로 이동이 가능하다고 가정해 보자. 포인터가 "켜진" 화소에 도착하면 왼족으로 방향을 전환하고 포인터가 "꺼진" 화소에 도착했을 때 오른쪽으로 방향을 전환한다. 물론 "왼쪽" 과 "오른쪽" 의 의미는 포인터의 방위에 따라 다른 방향을 의미하게 된다. 화소 1,1에서 출발하여 1,2로 움직이고 행의 끝까지 움직이고 다음의 2행, 3행 등으로 움직인다. 포인터가 첫 번째 "켜진" 화소를 3,3에서 발견하여 왼쪽으로 방향을 바꾸고 다시 "꺼진" 화소를 만나 오른쪽으로 두 번 돌고, 다음에 왼쪽으로 돌고 계속해 나가며 첫 번째 화소를 다시 만날 때까지 계속된다. 포인터가 지나간 화소들의 집합은 하나의 연속된 윤곽이다. 다른 윤곽들은 새로운 화소를 가진 연속된 과정으로써 찾을 수 있다. 이 예제에서 윤곽은 화소 3,3; 3,4; 3,5; 3,6; ...3,9; 4,9; 4,10; 4,11,... 이 된다.
마스크는 영상에서 어떤 특성을 강하게 강조하는 데도 사용할 수 있다. 예를 들면 마스크는 수평선, 수직선, 사선들을 강조하도록 설계될 수 있다. 그림 35는 각각의 세 가지 경우의 마스크를 보여주고 있다. 그림 36은 원본 영상(a), 수직 마스크(b), 수평 마스크(c), 사선 마스트(d)를 적용한 결과를 보여주고 있다.
[그림 35] 수평, 수직, 원형 강조 마스크
[그림 36] (a) 원본 영상. (b) 수직 마스크 효과, (c) 수평 마스크, (d) 원형 마스크
대부분의 윤곽추출에 있어서 윤곽은 연속적이 아니라는 것을 알 수 있을 것이다. 그러나 많은 응용프로그램에서 연속적인 윤곽이 선호되고 필요하다. 예를 들면, 추후에 더 자세히 살펴볼 내용이지만, 영역확대에 있어서 영역이나 지역으로 정의된 윤곽은 영역확장 루틴이 영역을 검출하고 영역으로 표시하기 이전에 반드시 연속이어야 하며 완전해야 한다. 뿐만 아니라 끊어진 선을 연결하거나 물체를 탐지하기 위해 탐지한 윤곽선의 기울기를 계산할 수 있어야 한다. 허프변화 (Hough transform)[12]은 선의 기울기를 포함하여 선위의 다른 화소들간의 기하학적인 관계를 결정하는 데도 사용된다. 예를 들면 점의 무리형태로 변환시키므로 추후에 물체를 인식하는 화상으로 진보시키는 데 도움이 된다. 허프변환은 영상공간을 임의의 평면에 무한한 직선이 존재하는 (r,θ) 공간으로 바꾸는 것에 기초한다. 원점을 지나는 어떤 선이라도 보통의 경우에는 x축에 관한 θ 의 각을 가질 것이고, 원점에서 r만큼 떨어진 곳에 있을 것이다.(r,θ) 평면으로의 변환(이를 허프평면이라 한다)에서 보이는 이러한 값은 허프변환이다. 선택적으로 xy 평면에 있는 기울기 m과 절편 c를 가진 직선은 x와 y로 표현된 m과 c의 허프평면으로 변환이 가능하다. 그러므로 xy평면에 있는 특별한 경사도와 절편을 가진 직선은 허프평면의 점으로 변환될 것이다. 점을 통과하는 모든 직선들은 허프평면에서 하나의 선으로 변환 될 것이다. 만약 점들의 집합이 동일 선상에 있다면 그것의 허프변환은 모두 교차할 것이다. 특별한 경우의 이러한 성질을 자세히 보면 화소의 집합이 직선 위에 있는지를 알 수 있다. 허프변환은 또한 한 선의 방위와 각을 결정하는 데 사용될 수 있다. 그래서 평면상의 물체의 방위는 물체상의 직선의 방위를 계산함으로써 결정할 수 있다.
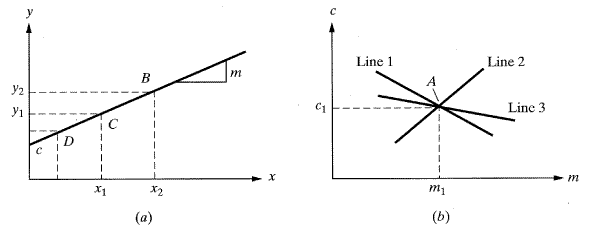
이를 좀더 명확하게 이해하기 위해, 그림 37에 있는 하나의 직선을 가진 xy평면을 고려해 보자. 그 선은 기울기 (m) 와 절편 (c) 으로 표현이 가능하다.
y = mx + c (13)
식 (13) 또한 m과 c를 기준으로 쓰여졌다.
c = -xm + y (14)
여기서 mc평면상의 x와 y는 기울기와 절편이 된다.
분명히, m과 c를 가진 식 (13)에 의해 주어진 선은 mc (허프)평면의 하나의 점 A처럼 보일 것이다. 이는 직선 위의 모든 점이 기울기가 같고 절편 m, c를 가지며, 그 평면에서 똑같은 위치를 가지기 때문이다. 직선(직선 위의 점도 마찬가지임)이 이 방정식으로 그려지든지 극좌표계(r,θ)에서 그려지든지 결과는 같다. 이렇게 허프평면의 점이 라인과 그 위의 모든 점을 나타낸다.
그림 37(b)에서 허프평면을 고려해 보자. 두 직선이 점 A에서 교차된다. 식 (14)로부터 직선 1은 기울기와 교점 x 과 y을 가지며 xy평면의 C점에서 볼 수도 잇다. 이와 마찬가지로 직선 2도 xy평면에서 B로서 표현이 가능하므로 mc평면에서 교차한다면 그들이 xy평면에서 직선을 구성할 수 있다는 것을 의미한다. 만약 세 번째 직선이 똑같은 점에서 교차한다면 그것은 xy평면의 같은 직선 위에 있을 것이다. 결과적으로, 만일 xy평면의 수많은 점이 같은 직선위에 있다면 그 점들은 mc평면의 교차직선을 구성하게 된다. 이러한 특성은 수많은 점이 같은 직선 위에 있는지 아닌지를 결정하는 데 사용된다. 예를 들어, 만일 xy평면상의 5개의 점을 선정하고 그 점들이 같은 직선 위에 존재한다면 이 점에 상응하는 직선이 mc평면에서의 똑같은 점에서 교차할 것이다. 물론, 직선의 기울기와 절편을 사용하여 직선에 점을 추가하여 연속으로 만들 수도 있고 형상을 제거할 수도 있다.
[그림 37] 허프변환
|
예제 4 |
다음은 5개 점의 좌표이다.
|
y |
x |
|
3 |
1 |
|
2 |
2 |
|
1.5 |
3 |
|
1 |
4 |
|
0 |
5 |
허프변환을 이용하여 어느 점이 같은 직선 위에 있는지 결정하라. 또한 그 직선의 기울기와 절편을 구하라.
[해답] 물론, 임의의 두 점은 직선 위에 존재한다. 따라서 최소한 세 개의 점이 직선위에 존재할 것이다. 점들의 그래프를 보면 위의 질문은 매우 쉽다는 것을 알 수 있다. 그러나 컴퓨터 비전에서는 컴퓨터는 영상을 이해할 수 없으며 지능도 가지고 있지 않으므로 연산이 되어야 한다. 영상을 담고 있는 컴퓨터 파일은 수천 개의 점을 가지고 있다. 따라서 인간이나 컴퓨터 모두 어느 점이 직선 위에 있고, 어느 점이 직선 위에 없는지를 구분하는 것은 불가능하다. 허프변환을 통해서 어느 점이 직선 위에 있는지 결정한다. 다음의 표는 mc평면에서의 직선을 요약한 것이며 XY평면에서의 상당하는 점도 표현되어 있다.
|
Y |
x |
XY |
mc |
|
3 |
1 |
3 = m1 + c |
c = -1m + 3 |
|
2 |
2 |
2 = m2 + c |
c = -2m + 2 |
|
1.5 |
3 |
1.5 = m3 + c |
c = -3m + 1.5 |
|
1 |
4 |
1 = m4 + c |
c = -4m + 1 |
|
0 |
5 |
0 = m5 + c |
c = -5m + 0 |
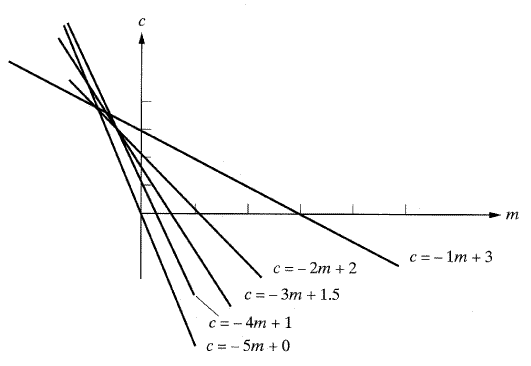
그림 38은 mc평면에서의 5개의 상당하는 직선을 보여주고 있다. 세 개의 직선은 교차하고 있으며, 다른 직선은 그렇지 못하다. 후반부 직선들은 1,3과 5,0에 상당하는 직선이다. 직선의 기울기와 절편은 각각 -0.5와 3의 직선상의 점을 나타낸다. 이 직선들은 다른 점에서 교차하며 두 점으로써 하나의 직선을 이룬다. 여기서 어느 직선의 교차점이 허프변환 분석에서 주된 관심사가 되어야 하는지 결정한다. 이와 마찬가지로 직선이나 점 대신에 아날로그형의 원과 점이 생성될 수도 있다. 점 위의 모든 점들은 허프평면에서 교차하는 원에 상당하게 된다(보다 자세한 내용은 참고문헌 [7]을 참고하도록 하자).
[그림 38] 예제 4의 허프변환
허프변환은 많은 바람직한 특성을 가지고 있다. 예를 들면 영상의 각 점이 독립적으로 다루어지기 때문에 모든 점이 비슷한 처리방법으로 동시에 병렬처리가 가능하다. 이는 허프변환이 실시간 처리에 가장 유용한 이유이다. 각 점들은 최종적인 연산에 큰 영향을 끼치지 않으므로 무작위 잡음에 둔감하다. 그러나 허프변화은 연산 집중적인 성격을 가지고 있다. 연산수를 줄이는 것은 직선이 실제로 한 점에서 교차하고 있는지 결정하기 위해 필요하며 직선이 서로 교차하고 있다면 원(또는 경계)을 정의하여 그 안에서는 일반적으로 교차하고 있다고 하는 가정을 내려야 한다. 허프변환은 물체인식이나 다른 작업들을 위해 효율성과 유용성을 증가시키기 위해서 많은 수정된 형태가 고안되었다.
분할 (segmentation) 은 영상을 영상의 요소로 세분하는 다양한 기술을 통틀어 칭하는 고유의 이름이다. 분할의 목적은 영상에서 다른 목적을 위해 사용이 가능한 보다 작은 독립체 (entity) 들을 포함한 정보로 나누는 것이다. 예를 들면 영상은 화변 (scene) 의 윤곽 또는 작은 영역으로 분할이 가능하다. 이 각각의 독립체는 더 진보된 영상처리나 표현, 인증 등에 사용된다. 분할은 윤곽추출, 영역확장, 배경분석 등에 사용되지만 이에 국한되지는 않는다.
초기의 분할 루틴은 다면체와 같은 간단한 기하학적 모델의 윤곽추출을 기초로 삼았다. 물체의 3차원 분석에서 원통, 원뿔, 구, 육면체와 같은 모델이 주로 사용된다. 비록 이러한 형태와 특징이 실제 물체와 정확히 일치되지는 않는다 하더라도 초기의 개발단계에서는 보다 정교한 루틴이나 기술을 개발하기 위한 초석이 되었다. 이는 또한 복잡한 형상이나 물체를 처리할 수 있는 루틴을 개발하는 방안을 제공하였다. 예를 들면 매우 적은 처리과정으로도 실린더상에 원뿔을 가진 형태로 나무를 모델링할 수 있으며 나무의 모델을 가진 최종적인 그림에 일치시키는 것이 가능하다. 따라서 나무는 원뿔과 실린더의 높이 등과 같은 몇 개의 정보로써 표현이 가능해진다. 나무에 포함된 모든 정보를 표현하는 것은 상대적으로 유동적이다.
영역확장 (region growing) 과 영역분리 (region splitting) 는 분할의 기법들이고 윤곽추출루틴이다. 이러한 기법들을 통해 물체검출과 같은 보다 진보된 분석에 사용될 수 있는 비슷한 성질을 가진 요소들이나 부분들로 영상을 다른 부분으로 나누려는 시도가 행해지고 있다. 윤곽추출기 (edge detector) 가 배경의 분할된 선을 찾는 동안 영역에 의한 색, 평면과 명암도 (gray level), 조각부분들은 자연스럽게 완벽하게 닫혀진 경계를 나타낼 것이다(다른 분할 기법을 살펴보려면 참고문헌 [14]를 보라).
영역분할을 위해서는 두 가지 접근법이 사용된다. 하나는 명암도 범위와 같은 유사한 속성이나 다른 유사성을 통한 영역을 확장시키고 평균 유사성이나 공간적 관계를 통해 영역을 연관시킨다. 또 다른 하나의 기법은 영역분리이며, 이는 영상의 세밀한 차이점을 이용해서 보다 작은 영역으로 분리시키는 것이다.
영역분리 (region splitting) 기법 중의 하나는 임계값이다. 영상은 임계값이나 임계범위와 비교하여 이웃화소의 닫힌 영역으로 분할된다. 임계값 아래의 수치(또는 값의 범위 사이)를 가지는 어떤 화소는 주어진 영역에 속하나 범위밖에 속하게 될 수도 있다. 임계값은 영상을 같거나 유사한 속성을 지닌 화소들의 무리나 또는 영역의 집합으로 분리할 것이다. 일반적으로 이것이 간단한 기법이라 하더라도 이는 적당한 임계값의 선택이 어렵기 때문에 그리 유용하지는 못하다. 결과는 임계값에 매우 의존하게 되며 임계값이 변할 때 결과도 따라서 변하게 된다. 그러나 임계값은 역광과 같은 상황에서는 매우 유용하며 일정한 영역을 가진 영상에도 매우 유용한 기법이다.
영역확장 (region growing) 의 첫 번째 핵심영역은 몇몇의 특별한 선택법에 기초하여 형성된다(핵심영역은 분할 초기에 형성된 화소들의 작은 무리이다. 핵심영역은 결정이 합금 안에서 하는 역할과 같이 보통 작고 성장하고 융합된다). 결과는 많은 수의 작은 영역을 생성한다. 계속하여 이들 영역들은 몇몇 다른 성질이나 규칙에 기초하여 좀더 큰 영역으로 통합된다. 비록 이러한 규칙들이 많은 작은 영역을 융합하여 보다 부드러운 영역의 집합을 생성 하지만 구멍이나 보다 작은 영역이나 특별한 빛의 강도를 가진 영역과 같은 융합되지 않아야 할 특성도 융합하는 불필요한 융합도 발생하게 된다.
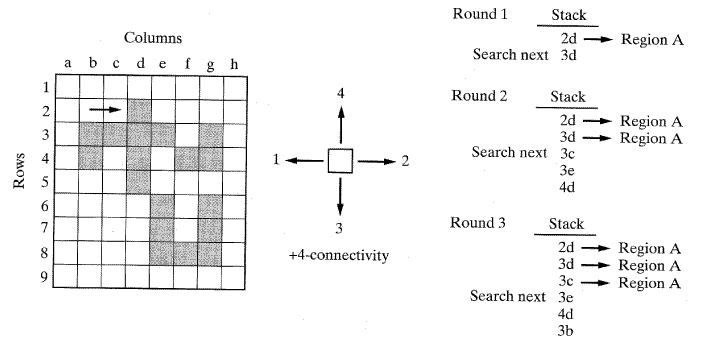
이진영상의 확장하는 영역을 위한 간단한 탐색기법(또는 명암도를 위한 임계값을 적용하는 것은 물론)으로는 부기 (bookkeeping) 를 사용하여 같은 영역에 속하는 모든 화소는 찾는 접근방식이다[15]. 그림 39는 이진영상을 보여준다. 각각의 화소는 한 쌍의 일련번호를 가지고 있다. 포인터가 위에서부터 시작하고 영역을 출발하여 핵심화소를 찾는다고 가정하자. 어느 영역에도 속하지 않은 핵심화소를 바로 찾을 수 있으며 프로그램에서 이 영역에 번호를 부여한다. 이 핵심화소에 연결된 모든 화소들은 같은 영역의 번호를 가지게 되며 스택에 위치하게 된다. 이는 스택의 모든 화소가 검색되어 스텍이 모두 비워질 때까지 계속된다. 포인터는 새로운 번호를 가진 영역에서 새로운 핵심을 찾기 위해 계속 검색할 것이다.
확장영역에서 사용할 연결성 (connectivity) 의 형태를 결정하는 것은 매우 중요하며, 그 형태에 따라 최종 결과가 결정된다. 16절에서 논의한 +4-, ×4-, H6-, 8- 연결성이 영역확장을 위해 사용되어질 수 있다. 그림 39에서 첫 번째 핵심화소를 2d에서 찾았다. +4-연결성을 선택하였다고 가정하자. 그러면 프로그램상에서 핵심화소 주위의 4개의 상응되는 화소들을 검사하여 화소들의 연결성을 결정할 것이다. 만약 "켜진 (on)" 화소가 있다면 스택에 위치의 일련번호가 저장되고 그 셀은 영역번호 (A)를 부여받는다. 그리고 포인터는 스택에서 다음 셀인 아래쪽의 3d로 움직인다. 이곳에서 셀 주위 화소들의 연결성을 다시 검사하고 "켜진" 화소의 일련번호가 검색용 스택에 저장되고 셀은 영역 A로 지정되고 이러한 과정은 스택의 다음 번호인 3c를 위해 반복된다. 이 과정은 스택이 빌 때까지 계속된다.
+4-연결성에서 포인터가 4f와 6e의 화소를 얻었다면 이 화소들은 같은 영역으로 지정되지 않는다는 것을 숙지해야 한다. +4-, ×4-, H6- 또는 8-연결성을 기준으로 한다면 두 영역 모두가 영역 A 의 부분이 된다. 반면에, 포인터는 소위 다음 영역인 B영역, C영역의 새로운 화소를 찾을 때까지 계속한다.
[그림 39] 검색기법에 기본을 둔 영역확장
형태 (morphology) 명령은 물체의 형상을 구분하는(그러므로 형태론이라 할 수 있다) 명령의 종류에 속한다. 이는 다양한 이진연상이나 흑백영상에서의 농밀화 (thickening), 팽창, 수축, 세선, 열기, 닫기, 채우기와 같은 다양한 연산명령이 있으며, 이런 명령들은 명상의 분석에 사용되며 영상에 나타나는 외부정보를 줄이는 데도 사용된다. 예를 들어 그림 40의 이진영상에서 막대그림은 하나의 볼트를 나타내고 있다. 추후에 자세히 살펴보겠지만, 모멘트 방정식은 볼트의 방위를 계산하는 데 사용된다. 그러나 볼트의 막대그림에 같은 방정식이 적용될 수 있으나 이것이 보다 효율적이다. 따라서 볼트를 골격화하거나 막대그림으로 변환하는 것이 바람직하다.
[그림 40] 볼트의 이진영상과 막대 표현
농밀화 (thickening) 명령은 작은 구멍이나 물체의 경계부분의 결함을 채우고 경계를 부드럽게 만든다. 그림 40의 예를 보면 농밀화 명령은 볼트의 나사부분의 외형을 줄여줄 것이다. 이것은 골격화와 같은 다른 연산명령을 물체에 적용할 때 중요하게 된다. 초기의 농밀화는 나중에 보겠지만 나사산으로부터 야기된 가느다란 선들의 생성을 막을 것이다. 그림 41은 세 번의 농밀화 명령을 볼트의 나사산에 적용한 후의 결과를 보여주고 있다.
팽창 (dilation) 에서, 8방향으로 물체화소(물체)와 연결된 배경화소는 물체화소로 변환된다. 결과적으로 연산처리가 수행될 때마다 화소층이 효과적으로 더해진다. 물체와 연결된 8개의 화소에 수행된 팽창연산 때문에 중복된 팽창은 물체의 형태를 변화시킬 수 있다. 그림 42(b)는 그림 42(a)를 네 번 팽창시킨 결과를 보여주고 있다. 여기서 볼 수 있는 것처럼 물체들은 하나의 형태로 겹쳐진다. 계속된 팽창명령의 적용은 물체들을 하나의 형태로 변환할 수 있고 구멍도 사라지지만 나중에는 물체들을 더 이상 인식할 수 없을 수도 있다.
[그림 41] 확장명령을 세 번 적용함으로써 볼트의 나사산이 제거되었고 윤곽이 부드러워졌다.
[그림 42] 팽창명령의 효과. (a)에 보이는 물체가 네 번의 팽창연산을 수행한 결과 (b) 로 변환되었다.
침식 (erosion) 연산은 배경화소에 인접한 8개의 물체화소를 제거한다. 이 연산명령이 수행될 때마다 물체화소의 최외곽층이 효과적으로 침식된다. 그림 43(b)는 그림 43(a)의 이진영상에 세 번 침식연산을 수행한 뒤의 결과이다. 침식명령은 물체 주위의 한 화소를 제거하므로 물체는 연산을 한 번 수행할 때마다 가늘어지게 된다. 그러나 침식은 형태를 표현하기 위한 다른 모든 요구사항들은 무시한다. 물체의 주변화 구멍으로부터 한 화소를 제거할 것이고, 결국 물체의 형태가 없어질 때까지 한 화소씩 제거할 것이다. 그림 (c)는 7회 반복한 것을 보이고 있다. 여기서 볼트는 완벽히 사라졌고 너트는 곧 사라질 것이다. 침식연산을 너무 많이 수행하게 되면 물체를 소실하게 될 것이다. 다시 말하면, 만약 물체의 주변에 한 화소를 더하는 것과 같은 침식연산을 거꾸로 행하면 침식된 물체는 원래의 물체와는 상이할 것이다. 사실, 물체가 한 화소 정도 침식되면 침식연산의 결과는 원형을 이루거나 사각형을 이루게 된다. 따라서 침식연산으로 인한 영상의 손실을 보상할 수 없다. 예를 들면, 만일 영상에서 가장 큰 물체를 검출하기 원하는 경우, 연속적인 침식연산으로 다른 모든 물체를 제거하면 가장 큰 물체만 남게 된다. 따라서 보고자 하는 물체를 확인할 수 있다.
골격 (skeleton) 은 임의의 위치에서 모든 물체의 두께를 한 화소로 줄여 물체를 표현하는 방식이다. 골격화 (skeletonzation) 는 침식의 변형된 형태로써, 침식에서는 물체의 두께가 0으로 변하고 최종적으로는 물체가 사라지지만 골격화는 물체의 두게가 1화소로 변화하고 연산을 종료한다. 또한 침식에서는 반복횟수가 사용자에 의해서 선택되지만 골격화 연산에서는 연산과정이 자동적으로 모든 두께가 1화소가 될 때까지 계속된다(프로그램은 연산의 결과로서 새로운 결과가 생성되지 않을 때 종료한다). 골격화의 최종 결과는 물체의 막대 그림이 되며 때때로 윤곽보다 훨씬 좋은 표현방법이다. 그림 44(b)는 그림 44(a)의 물체를 골격화한 결과이다. 빗살무늬는 물체가 농밀화 연산으로 부드럽게 변환되지 않았기 때문에 발생하였다. 그 결과, 모든 나사산들은 1화소로 감소하고 빗살무의를 생성하였다. 그림 45는 농밀화 연산으로 인해 나사산의 두께가 사라지고 깨끗한 골격이 생성된 모습을 보여주고 있다. 그림 45(c)는 골격화한 것을 7회 팽창한 결과를 보여주고 있다. 여기서 볼 수 있듯이 팽창된 물체는 원래의 것과 같지 않다. 작은 나사가 더 큰 볼트만큼 얼마나 커졌는지 숙지하도록 하자.
비록 골격화의 팽창은 원래 물체의 형상과 다른 모습을 보인다 할지라도 다른 방법보다는 일반적으로 우수하므로 골격화가 사용된다. 물체의 막대 표현이 발견되면 일치를 위해서 물체에 대한 사전 지식과 비교할 수 있다.
[그림 43] (a) 물체의 침식효과, (b)3번, (c) 7번 반복 수행.
[그림 44] 농밀화 연산이 없는 영상의 골격화 효과. 볼트의 나사산이 빗살무늬로 생성되었다.
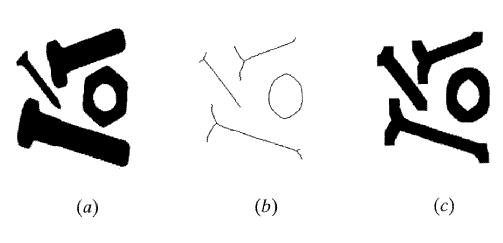
[그림 45] (a) 물체의 골격화에서, (b) 농밀화 연산을 수행한 후의 모습. (c)는 골격화 영상을 팽창시킨 모습을 보여주고 있다.
열기연산은 침식연산 다음의 팽창연산을 말하며, 물체의 볼록한 면을 제한적으로 부드럽게 한다. 열기연산은 골격화 이전의 중간연산으로 사용될 수 있다.
닫힘연산은 팽창연산 다음의 침식연산을 말하며, 물체의 볼록산 면을 제한적으로 부드럽게 한다. 열기연산과 같이 골격화 이전의 중간연산으로 사용될 수 있다.
채움 명령은 표면(물체)의 구멍들을 채운다. 그림 46에서, 너트의 구멍은 구멍이 사라 질 때까지 표면의 화소들로 채워졌다.
[그림 46] 채움 명령의 결과처럼 너트의 구멍은 전면물체의 화소들로 채워졌고, 그 결과 구멍은 사라졌다.
다른 명령들에 대한 정보는 시각 시스템 생산업체의 참고문헌에서 찾을 수 있다. 각 회사마다 다른 명령어를 사용하며 그들이 만든 유일한 소프트웨어를 포함한다.
명암 형태 명령 (gray morphology operation) 들은 명암영상 (gray image)에서 동작하는 것을 제외하고는 이진 형태 명령과 매우 비슷하다. 보통 3 × 3 마스크는 0 또는 1 인 마스크의 각각의 셀에 명령을 적용하기 위해 사용된다. 명암영상이 밝은 부분이 봉우리 형태를 ,어두운 부분이 계곡 형태를 가진 다층으로 구성된 3차원 영상이라 가정해 보자. 마스크는 화소와 화소 사이를 이동하면서 영상에 적용된다. 마스크가 영상의 명암값에 일치될 때마다 아무런 변화가 발생되지 않는다. 만일, 화소의 음영값이 일치되지 않으면 다음에 나오는 명령에 따라 선택된 명령으로 값이 변화될 것이다.
이 경우, 각각의 화소는 최소연산자 (min operator) 로 알려진 물체에 효과적으로 침식연산을 수행할 수 있는 3 × 3의 주변 화소에서 가장 어두운 값으로 치환된다. 물론 결과는 마스크의 셀 값이 0인지 1인지에 따라 좌우된다. 명암 형태 침식은 어두운 물체들간의 밝은 직선을 제거한다.
이 경우, 각각의 화소는 최대연산자 (max operator) 로 알려진 물체에 효과적으로 팽창연산을 수행할 수 있는, 3 × 3의 주변 화소에서 가장 밝은 값으로 치환된다.물론 결과는 마스크의 셀 값이 0인지 1인지에 따라 좌우된다. 명암 형태 팽창은 어두운 물체들간의 밝은 직선을 제거한다.
영상분석 (image analysis) 은 영상으로부터 정보를 추출하는 데 사용되는 명령이나 기법을 통틀어 말한다. 이러한 명령과 기법들은 물체인식, 특성추출, 영상 안에서의 위치, 크기, 방위 등의 성질분석, 길이의 정보추출을 말한다. 어떤 기법들은 뒤에서 논의하겠지만 다양한 목적을 위해 사용된다. 예를 들어 모멘트 방정식 (moment equation) 은 물체인식뿐만 아니라 물체의 위치와 방위를 계산하는 데 사용된다.
일반적으로 영상처리 명령들은 이미 영상에 적용되었거나 필요로 할 때 미래의 분석을 위해 준비하고 개선하기 위해 사용하는 것이 가능하다. 영상분석 명령과 기법은 이진영상화와 명암영상에 모두 쓰인다. 이 기법들 중의 몇몇을 다음에 다루고 있다.
영상에 있는 물체는 자신의 특성에 의해 인식이 가능하며, 이 특성에는 명암의 히스토그램, 면적과 같은 형태학적 형상, 경계선 구멍의 개수 등과 편심량 (eccentricity), 코드의 길이, 모멘트 등이 있으나 반드시 이에 국한되는 것은 아니다. 대부분 추출된 정보는 참조표 (lookup table) 에 있는 물체의 초기정보와 비교된다. 예를 들면 영상에 두 개의 물체가 있다고 가정하자, 한 물체는 두 개의 구멍을 가지며, 다른 하나는 한 개의 구멍을 가지고 있다. 이전에 언급한 명령들을 수행함으로써 각 부품에 구멍이 몇 개인지 결정할 수 있으며, 이 두 부품을 참조표와 비교함으로써 각각 구분할 수 있다. 얼마나 많은 구멍이 있는지를 참조표에 있는 구멍에 관한 정보와 두 부품(여기서 두 부분을 영역 1과 영역 2로 명한다)을 비교함으로써 결정이 가능하고, 두 부품을 구분하는 것도 가능하다. 또 다른 예로는, 알고 있는 부품의 모멘트를 다른 각도에서 분석할 때 축에 대한 부품의 모멘트는 이 각들을 계산하기 위해 존재하며 결과 데이터는 참조표에 모아진다. 후에 계산된 영상에 있는 부품의 모멘트가 같은 축에 관계되고 참조표 안의 정보와 비교한다면 영상 안의 부분의 각은 추정될 수 있다.
다음에 물체인식을 위해 몇 가지 기법과 다른 형상에 대하여 논의할 것이다.
다음의 형태학적 특징은 물체인식과 판별에 사용이 가능하다.
a. 평균, 최대, 또는 최소 명암값은 영상 안의 물체 또는 다른 부분을 판별하는 데 사용이 가능하다. 예를 들면 영상이 세 부분으로 나누어져 있다고 가정하자. 각각은 다른색 또는 배경을 가지고 있으며, 영상에서 다른 명암값을 만들 것이다. 만약 물체의 평균, 최대 또는 최소 명암값을 히스토그램의 맵핑을 통하여 찾을 수 있다면 물체는 이 정보와 비교하여 인식이 가능해진다. 다른 경우에는 하나의 특수한 명암값이 존재하여도 부품을 이식하는 데 충분하다.
b.물체의 경계, 면적, 그리고 직경뿐만 아니라 물체의 구멍개수와 다른 형태학적 특징들도 물체를 판별하는 데 사용이 가능하다. 물체의 경계는 윤곽추출루틴을 적용함으로써 찾을 수 있다. 그 다음에는 경계의 화소수를 센다. 18절의 좌우검색(L-R)기법도 누산기에서 물체의 경로에 있는 화소의 수를 셈으로써 물체의 경계를 계산할 수 있다. 물체의 영역도 영역확장 기술을 이용하여 계산할 수 있다. 모멘트 방정식 또한 사용이 가능하며 이는 추후에 자세히 논의할 것이다. 원형이 아닌 물체의 지름은 물체의 정의된 지역을 관통하는 어떤 선의 임의의 두 점 사이의 최대거리로 정의한다.
c. 물체의 형상비율 (aspect ratio) 은 그림 47에서 보는 바와 같이 물체에 대한 닫힌 사각형의 폭과 넓이의 비율이다. 최소형상비율 (minimum aspect ratio)을 제외하고 모든 형상비율은 방위에 민감하다. 그래서 최소형상비율은 일반적으로 물체를 판별하는 데 사용된다.
d. 두께는 다음의 두 식 중에서 하나로 정의가 가능하다.
1. 
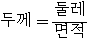(15)
2. 
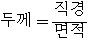(16)
e. 모멘트는 특별히 중요하기 때문에 다음 절에서 논의하였다.
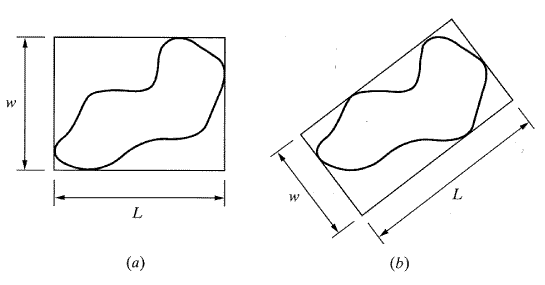
[그림 47] 물체의 각도 비율, (b)에서 최소 형상 비율을 보여준다.
이진영상 (binary image) 안에 물체가 있다고 가정해 보자. 물체는 켜진 화소들로 표현되고 배경을 꺼진 화소들로 표현된다. 이 효과는 이진 형태 안에서 영상을 표현하거나 또는 후광 (backlighting) 으로부터 얻어질 수 있다. 이제 일반적인 모멘트 방정식 (moment equation)을 고려해 보자.
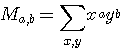(17)
여기서 Ma,b 는 a와 b를 각각의 화소의 좌표로 하는 물체의 모멘트이며, 그림 48에서처럼 x와 y는 각 영상 안에서 켜지는 화소들의 좌표축이며 a, b의 다승으로 켜진다. 이 경우에 식 (17)에 기초한 루틴은 우선 각 화소가 물체에 속해 있는지(켜져 있다) 아닌지를 결정하며, 만약 속해 있다면, 화소의 위치좌표를 주어진 a, b값까지 상승시킬 것이다. 전체 영상에서 이 연산의 총합은 a,b값을 가지는 물체의 특별한 모멘트가 된다. M0,0은 a = 0, b = 0을 갖는 물체의 모멘트이다. 이는 모든 x, y값들은 0제곱을 한다는 것이다. M0,2의 의미는, x값은 0제곱을 모든 y값은 2제곱을 한다는 것이다.0과 3사이의 모든 값의 조합은 일반적이다.
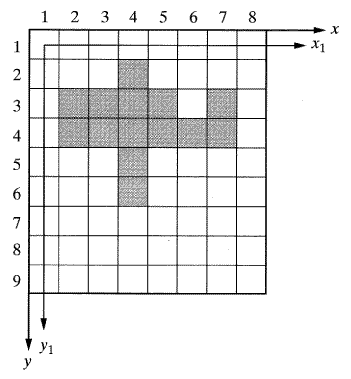
[그림 48] 영상의 모멘트를 계산하라. 물체에 속한 화소들을 위해, 화소의 좌표들은 모멘트 지수들에 의해 높은 좌표로 상승해간다. 그래서 계산된 값들의 합은 영상의 특유한 모멘트이다.
거리 x,y는 영상의 모서리의 가상 좌표계 (fictitious coordinate) 에서나 영상의 첫 번째 행과 열로 구성된 좌표에서 측정된다. 화소의 수를 셈으로써 거리가 측정되므로 첫 번재 행과 열을 이용해서 좌표축을 생성하는 것이 보다 논리적이다.그러나 이 경우에는 모든 거리가 행과 열 화소의 중심선으로부터 측정되어야 한다. 예를 들면 두 번재 줄에서 첫 번째로 "켜진 (on)" 화소는 I2,4이다. x1y1 좌표계에서 화소의 x거리는 3일 것이다. 반면에,xy 촤표계에서는 같은 거리가 4가 된다(좀더 정확하게는 3.5). 같은 거리가 사용되는 한, 선택은 그리 중요하지 않다.
앞서 언급한 것을 기초로 하여 보면 모든 수의 0제곱은 1이다. 즉, 모든,x0,y0은 1이다. 따라서 모멘트 M0,0은 많은 "켜진" 화소 1의 합이다. "켜진" 화소의 수를 계산하면 그것이 물체의 면적이 된다. 즉, 모멘트 M0,0은 물체의 면적을 말한다. 이 모멘트는 물체의 특징을 결정하거나 다른 면적을 가지고 있는 다른 물체로부터 구별하는데 사용 될 수 있다. 특히 모멘트M0,0은 또한 영상 안의 물체의 면적을 계산하는데 사용될 수 있다.
이와 마찬가지고 M0,1은 ∑x0y1이거나 1 × y 의 합이다. 이는 x축으로부터 떨어진 거리와 각 화소의 면적을 곱한 것의 총합을 말한다. 이것은 x축과 관계된 면적의 첫 번째 모멘트와 유사하다. 그 다음 x축과 관계된 면적의 중심의 위치는 다음 식으로부터 계산할 수 있다.
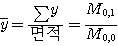(18)
단순히 두 모멘트를 나눔으로써 물체의
면적의 중심좌표인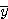 
를 계산할 수 있다. 이와 마찬가지로 y 축에 대한 면적의 중심위치는 다음의
수식으로 찾을 수 있다.
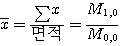(19)
이 방법으로 물체는 물체방위에 무관하게 영상 안에서 위치하게 된다(방위는 면적의 중심의 위치는 변하지 않는다). 물론 이 정보는 물체를 위치하거나 로봇에서 물체를 잡는 데 사용할 수 있다.
이제 M0,2 와 M2,0을 고려해 보자. M0,2는 ∑x0y2 이며 x축과 관계된 면적의 2차 모멘트 (second moment) 를 의미한다. 이와 마찬가지로, M2,0는 y축과 관계된 면적의 2차 모멘트이다. 여기서 알 수 있듯이, 그림 48에서 물체의 관성모멘트는 중심축에 대하여 물체가 회전함에 따라 분명하게 변할 것이다. 다른 방향인 x축에 대한 면적의 모멘트를 계산한다고 가정한다. 각 방향은 고유의 값을 생성하므로, 이러한 값들을 포함한 참조표 (loopup table) 는 후에 물체의 방위를 판별하는 데 사용 가능하다. 따라서 만약 다른 방향에서 알고 있는 물체의관성모멘트의 값을 가진 참조표가 있다면, 물체의 다음 방향은 테이블 안에 값을 가진 그것의 2차 모멘트를 비교함으로써 추정할 수 있다. 물론 물체가 영상 내에서 평행이동하였다면 관성모멘트도 변할 것이나 물체의 면적중심의 좌표를 알고 있다면, 물체의 위치와는 상관 없이 평행축 이론 (parallel axes theorem) 을 간단히 적용하여 면적중심의 2차 모멘트를 계산할 수 있다. 그 결과로 모멘트 방정식을 사용하여 물체의 위치와 방위를 판단할 수 있다. 게다가 부품을 집어 올리는 데 사용할 수 있다.
다른 모멘트들도 유사하게 사용된다 예를 들어 M1,1은 면적의 관성의 내적을 나타내며 물체를 판별하는 데 사용될 수 있다. M0,3, M3,0, M1,2 등과 같은 높은 차수의 모멘트는 물체와 물체의 방위를 판별하는데 사용될 수 있다. 그림 49(a)에서처럼 모양이 비슷한 두 개의 물체가 있다고 생각해 보자. 물체의 2차 모멘트, 면적, 경계 또는 다른 형태학적인 특성들은 물체를 판별하는 데 그다지 유용하지 않을 것처럼 유사하거나 가깝다. 이 경우에 두 물체 사이의 미소한 차이는 물체의 식별을 가능하게 해주는 고차 모멘트를 통해서 확대시킬 수 있다. 그림 49(b)에서처럼 작은 비대칭성 물체에 대해서도 적용할 수 있다. 물체의 방위는 고차 모멘트로 찾을 수 있다.
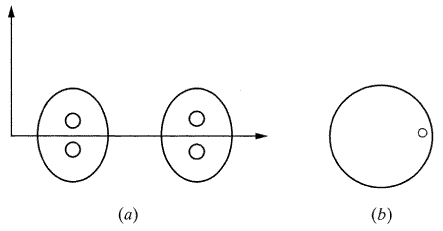
[그림 49] 물체간의 미소한 차이나 작은 비대칭성 물체는 고차 모멘트로 식별할 수 있다.
불변모멘트 (moment invariant) 는 물체의 방위와 위치의 독립과 그것의 다른 모멘트에 기초한 척도이다. 7개의 다른 불변모멘트 중 하나는 다음과 같다.
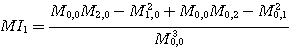(20)
(나머지 6개의 불변모멘트를 보려면 참고문헌 [6]을 참고하기 바란다.)
|
예제 5 |
그림 50의 낮은 해상도 영상에 간단한 물체가 있다. 면적을 계산하고 x1, y1 축에 관계된 물체의 2차 관성모멘트를 계산하라.
[그림 50] 예제 5 에서 사용된 영상
[해답] x1,y1축으로부터 각 화소의 거리를 측정한다. 그리고 측정값을 모멘트 방정식에 대입하여 다음을 얻을 수 있다.
M0,0=∑x0y0=12(1)=12
M1,0=∑x1y0=∑x=2(1)+1(2)+3(3)+3(4)+1(5)+2(6)=42
M0,1=∑x0y1=∑y=1(1)+5(2)+5(3)+1(4)=30
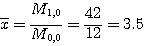그리고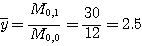 
M2,0=∑x2y0=∑x2=2(1)2+1(2)2+3(3)2+3(4)2+1(5)2+2(6)2=178
M0,2=∑x0y2=∑y2=1(1)2+5(2)2+5(3)2+1(4)2=82
보다 높은 해상도를 가진 영상에도 이와 같은 처리절차가 사용되나 더 많은 화소들을 다루어야 한다. 그러나 컴퓨터 프로그램으로는 별다른 어려움 없이 많은 화소들을 다룰 수 있다.
[그림 51] 예제 6에서 사용된 영상
|
예제 6 |
어떤 응용분야에서의 시각 시스템은 정사각형이나 사각형의 8 × 8의 영상을 사용한다.정사각형은 치밀한 3 × 3화소나 속이 빈 4 × 4 또는 치밀한 3 × 4의 사각형도 있다. 가이드, 지그 (jig)를 통하여 그림 51에서 물체들이 기준축에 항상 평행하다는 것을 알 수 있고 물체의 왼쪽 낮은 모서리는 항상 1,1화소에 있다. 모멘트 방정식을 이용하여 부품을 구별하고자 한다. 모멘트 방정식에서 가장 작은 a와 b값을 찾고 각 부품에서 상당하는 값을 구하라. 상응되는 축으로부터 거리를 위한 각 화소의 절대 좌표계를 사용하라.
[해답] 모멘트 방정식을 이용하여 각각의 물체를 위한 한 집합을 찾을 때까지 다른 모멘트를 계산한다.
|
구멍이 있는 사각형 |
완전 사각형 |
옆이 긴 사각형 |
긴 사각형 |
|
M0,0 = 12 |
M0,0 = 9 |
M0,0 = 12 |
M0,0 = 12 |
|
M0,1 = 30 |
M0,1 = 18 |
M0,1 = 24 |
M0,1 = 30 |
|
M1,0 = 30 |
M1,0 = 18 |
M1,0 = 30 |
M1,0 = 24 |
|
M1,1 = 75 |
M1,1 = 36 |
M1,1 = 60 |
M1,1 = 60 |
|
M0,2 = 94 |
M0,2 = 42 |
M0,2 = 56 |
M0,2 = 90 |
각각의 물체를 위한 고유의 해답을 산출한 모멘트 항목의 가장 낮은 집합은 M0,2이다.물론M2,0도 유사한 값을 갖는다.
|
예제 7 |
그림 52의 나사의 영상에서 면적,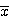
, 
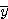, M0,2, M2,0, M1,1, M2,0
@
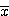, M0,2 @
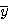와 불변모멘트를 계산하라. M0,2 @
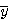의 의미는 중심 y축에 대한 M0,2 이다. 이와 마찬가지로, M2,0@
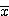는 중심 x축에 대한 관성모멘트이다.
[그림 52] 예제 7 에서 사용된 영상
[해답] 모멘트.마크로 (moments.macro) 라 하는 마크로는 Optimas™ 6.2 비전 소프트웨어에서 모멘트를 계산하기 위해 사용되었다. 이 프로그램에서 거리는 모멘트를 위해 길이의 단위가 아닌 화소의 수의 단위로 사용된다. 수평, 30°, 45°, 60°, 그리고 수직방향의 5개의 경우에 대한 연산 결과가 다음에 나타나 있다. 연산 결과에서 미소한 변화는 회전으로 인해 발생한다. 영상의 부품이 회전할 때마다. 영상의 모든 점이 Sine 함수와 Cosine함수로 변환되므로 영상은 다소 변하게 되나 결과는 아무런 변화가 발생하지 않는다. 예를 들면 한 장소에서 부품이 회전하면 면적의 중심의 위치는 변화하지 않으며 불변모멘트 (moment invariant) 는 일정하다. 또한, 불변모멘트는 상수이며 중심축에 대한 관성모멘트 정보를 이용하여 부품의 방위를 찾을 수 있다. 이 정보는 현재 물체판별에도 사용이 가능하며 로봇 제어기에 직접 교시되어 로봇 팔을 적당한 방위로 위치하거나 부품을 집는 명령을 내릴 수 있다.
|
|
수평방향 |
30° |
45° |
60° |
수직방향 |
|
면적 |
3713 |
3747 |
3772 |
3724 |
3713 |
|
127 |
123 |
121 |
118 |
113 |
|
102 |
105 |
106 |
106 |
104 |
M0,2 |
38.8 E6 |
34.6 E6 |
46.4 E6 |
47.6 E6 |
47.8 E6 |
M2,0 |
67.6 E6 |
62.6 E6 |
59 E6 |
53.9 E6 |
47.8 E6 |
M1,1 |
48.1 E6 |
51.8 E6 |
52 E6 |
49.75 E6 |
43.75 E6 |
불변모멘트 |
7.48 |
7.5 |
7.4 |
7.3 |
7.48 |
M2,0 @ |
7.5 E6 |
5.7 E6 |
3.94 E6 |
2.07 E6 |
0.264 E6 |
M0,2 @ |
0.264 E6 |
2.09 E6 |
3.77 E6 |
5.7 E6 |
7.5 E6 |
비록 모멘트.마크로 프로그램이 다른 소프트웨어에 직접 사용될 수 없다고 하더라도 다음에 보이는 리스트에서 얼마나 프로그램이 간단히 이와 같은 모멘트 연산을 수행하는지 살펴볼 것이다. 프로그램의 엑셀 (excel) 부분은 단순한 엑셀의 방정식이며 모든 화소의 좌표를 구하고 총합을 구하는 연산을 수행한다. 다음은 프로그램의 내용이다.
/* MOMENTS.MAC 프로그램, Saeed Niku 작성, 1998년도, 저작권 있음.
/* 이 마크로는 Optimas 시각 시스템에서 동영상을 검사하고 주어진 임계값을 가지는 모든 화소의 좌표를 기록한다. 또한 바로 엑셀의 워크시트 (worksheet) 에 모멘트를 결정하는 결과를 기입한다. 모멘트. 마크로는 다시 읽혀지고 그 데이터가 표시된다. DDE 명령은 엑셀과 Optimas 마크로 사이의 데이터 통신을 수행한다. 만일, 좌표계의 수가 20,000개 이상의 화소라면 아래의 DDEPoke 명령을 바꾸어 주어야 한다.*/
BinaryArray = GetPixelRect (ConvertCalibTopixels(ROI));
INTEGER NewArray[,]; Real MyArea; Real XBar; Real YBar;
Real Mymoment02; Real Mymoment20; Real Mymoment11; Real VariantM;
Real MyMXBar; Real MyMYBar;
For(XCoordinate = 0; XCoordinate <= (VectorLength(BinaryArray[0,])-1;
XCoordinate++)
{
For(YCoordinate
= 0; YCoordinate <= (VectorLength(BinaryArray[,0]-1); YCoordinate++)
{
if(BinaryArray[YCoordinate,
XCoordinate] > 100)
{
NewArray
:: XCoordinate : YCoordinate;
}
}
}
hChanSheet1 = DDEInitiate("Excel," "Sheet1");
DDEPoke(hChanSheet1," R1C1:R20000C2,"NewArray);
DDETerminate(hChanSheet1);
Show("Pleaxe Enter to Show Values");
hChanSheet1 = DDEInitiate("Excel," "Sheet1");
DDERequest(hChanSheet1, "R1C14," MyArea);
DDERequest(hChanSheet1, "R2C14," YBar);
DDERequest(hChanSheet1, "R3C14," XBar);
DDERequest(hChanSheet1, "R4C14," Mymoment02);
DDERequest(hChanSheet1, "R5C14," Mymoment20);
DDERequest(hChanSheet1, "R6C14,"
Mymoment11);
DDETerminate(hChanSheet1);
VariantM = (MyArea*Mymoment20*1000000.0-XBar*XBar
+MyArea*Mymoment02*1000000.0-YBar*YBar)/(MyArea*MyArea*MyArea);
MyMyBar = (Mymoment20*1000000.0-MyArea*XBar+XBar)/1000000.0;
MyMyBar = (Mymoment02*1000000.0-MyArea*YBar+YBar)/1000000.0;
MacroMessage("Area=,"MyArea,"\n,""XBar=,"XBar,"\n,"
"YBar=,"YBar,"\n,"
"Moment20,"x10^6,""\n""Moment11="
,Mymoment11,"x10^6,""\n""Invariant
1=",VariantM);
MacroMessage("Moment20@Xbar=,"MyMXBar,"x10^6,""\n"
"Moment02@Ybar=,"MyMYBar,"x10^6");
물체인식을 위한 또 다른 기법은 모델 (model) 또는 형판 (template) 또는 정합 (matching) 이다. 만약 화면 (scene) 위에 적당한 선이 그려진 거시 발견되었다면 지리적 (topological) 또는 구조적 요소인 선(또는 면)의 총 수, 꼭지점과 연결점 등을 모델과 일치시킬 수 있다. 회전, 이동, 크기 변화 (scaling) 와 같은 좌표변화 (coordinate transformation) 은 물체와 모델 사이에서 위치, 방위 또는 깊이의 차이로부터 얻어진 결과를 토대로 모델과 물체 사이의 차이점을 제거하는 데 사용될 수 있다. 이 기법은 정합 (matching) 을 위해 필요한 모델의 사전 지식으로부터 제한을 받게 된다. 따라서 만약 물체가 모델과 다르다면 이는 일치가 안 된 것이며 물체를 인식하지 못하게 된다. 또 다른 주요한 제한요인은 다른 물체가 보고자 하는 물체를 가로막고 있는 경우이며, 이때에도 모델과는 일치하지 못하게 된다.
아날로그 신호를 연산하는 푸리에 변환과 비슷하게 산재된 점들(화소와 같은)의 집합의 이산 푸리에 변환 (DFT: discrete fourier transform) 을 통하여 연산될 수 있다. 이는 만약 윤곽추출과 같은 방법으로 영상 안의 물체의 윤곽을 찾았다면 윤곽의 이산화소들도 DFT 연산에서 사용될 수 있다. DFT 연산의 결과는 보고자 하는 점의 공간적 관계를 표현하는 주파수영역에서 주파수와 진폭의 집합을 나타낸다[16].
평면상의 점 형태의 DFT 계산을 위해 각각의 점들을 x + iy 로 표현하는 평면인 복소평면 (complex-number plane) 이라 가정하자. 만약 점들의 집합을 둘러싼 윤곽이 임의의 화소에서 시작하여 완전하게 주위를 감싸고 있고 점들의 위치가 측정이 가능하다면 이 정보로써 상당하는 주파수 스펙트럼 집합에 대한 연산을 할 수 있다. 이러한 주파수들은 참조표에서 가장 가능성 있는 물체의 주파수와 일치하는 것을 찾아서 원래의 물체를 결정한다. 아직 공개되지 않은 실험 중에서, 8개의 주파수를 일치시키는 것은 원래의 물체를 찾는 데에 충분하다는 결과를 보여주고 있으며 보다 큰 평면에서 비행기의 형태를 결정하는 16개의 주파수가 필요하다. 이 기법의 장점은, 풀에 변환은 크기, 위치, 방위를 쉽게 표준화할 수 있다. 단점으로는 완벽한 물체의 윤곽이 있어야 한다는 것이다. 물론 허프변환과 같은 다른 기법들은 물체의 끊어진 윤곽을 재현하는 데 사용될 수 있다.
단층촬영 (computed tomography) 은 검사하는 부품의 물성의 밀도분포를 결정하는 기술이다. 컴퓨터 단층촬영에서의 물체의 밀도분포 3차원 영상은 X선이나 초음파와 같은 다른 촬영기법을 통해 얻어진 수많은 2차원 영상으로부터 재현된다. 컴퓨터 단층촬영에서의 부품은 겹쳐진 조각면 (slice) 들이 순서대로 구성되었다고 가정한다. 각 조각면의 분배된 밀도의 영상은 물체 주위를 반복적으로 촬영한다. 부품의 일부분만이 사용된다 할지라도 360°의 완벽한 범위의 촬영이 선호된다. 컴퓨터에 데이터가 저장되고 그 후에 데이터들은 부품의 밀도분포 영상으로 변환되어 CRT에 보여진다. 단층촬영은 물체 내부의 맵핑에 매우 유용한 기법이다.
비록 이 기법이 이미 언급된 다른 기법들과 매우 다르다고 하더라도 물체인식을 위한 가능한 방법 중의 하나이다. 단독으로나 또는 다른 기법과의 연계를 통하는 경우의 단층 촬영은 매우 비슷한 물체의 인식분야에서는 거의 독보적이라 할 수 있다. 특히 의료분야에서 단층촬영은 의료로봇과 결합되어 사용될 수 있다. 이 로봇은 사람 몸의 내부장기의 3차원 맵핑을 통하여 외과수술을 직접 수행할 수 있다.
영상에서의 깊이에 대한 정보는 두 가지 기본적인 방법을 통해 추출된다. 한 가지 방법은 시각 시스템과 영상처리기법이 융합된 거리측정기 (range finder) 를 이용하는 것이다. 이 방식에서의 영상은 거리측정기로부터 얻어진 주위에 있는 다른 부품 사이의 거리나 각각의 물체의 위치나 물체의 일부분에 대해 획득한 정보를 토대로 분석된다. 또 다른 방법은 쌍안경 (binocular) 이나 스테레오 비전 (stereo vision) 을 사용하는 것이다. 이 방법은 인간과 동물처럼 두 개의 카메라로 동시에 장면을 보거나 한 대의 카메라로 장면의 영상을 찍고 어떤 거리만큼 움직이고 또 다른 영상을 찍어 연속적인 영상이 생성되도록 반복하는 것이다. 이 명령을 수행하는 동안 영상이 변하지 않으면 결과는 여러 대의 카메라를 이용하여 획득된 것과 같을 것이다. 영상에 있는 특정 위치와 관계된 두 대의 카메라의 위치가 약간 다르므로 두 대의 카메라는 약간 다른 영상을 만든다. 두 영상 사이의 차이를 분석하고 측정함으로써 깊이 정보를 얻을 수 있게 된다.
영상분석 (scene analysis) 은 카메라나 이와 유사한 장치를 통해 획득된 영상의 완벽한 화면의 분석을 의미한다. 다시 말하면, 영상 (image) 은 장치의 해상도 제한범위 내에서 장면 (scene) 의 완벽한 복사본이라 할 수 있다. 이 경우, 영상에서 정보를 획득해내는 데 보다 많은 처리과정이 있을수록 보다 더 많은 정보가 획득될 수 있다. 예를 들면 장면 내의 물체를 정의하기 위해서, 영상은 이진화나 윤곽검출에 의해 분리되는 것처럼 여과되고 강화되어야만 한다. 그리고 부품은 영역확장을 통해서 분리되며 부품의 특성추출이나 형판 또는 참조표의 정보와의 비교를 통하여 판별된다. 이와 같은 비교를 통하여 맵핑은 물체나 장면의 표면 형태의 밑그림을 참조하며, 영상은 보통 저해상도에서는 이산적인 거리측정의 집합으로 구성된다. 마지막 영상은 불규칙적인 위치에 있는 물체 위의 점의 위치관계와 연결된 선들의 집합이다. 이미 영상이 얇게 나뉘어져 있으므로 맵핑 분석에서는 연산처리가 쉬우나 화면에서 추출할 수 있는 정보도 적어지게 된다. 각 기법은 각각의 장점과 이점과 한계점이 있으며 운항분야뿐만 아니라 다양한 목적으로 사용이 가능하다.
거리측정과 깊이분석은 특수조명 또는 능동적 범위 측정[22], 다중영상, 화면분석 등과 같은 다양한 기법으로 수행된다. 인간은 영상의 다른 요소 사이에 깊이나 위치관계에 관한 정보를 추출하기 위해서 여러 기법들을 조합하여 사용한다. 인간은 2차원 영상에서 비슷한 요소의 크기 변화와 선의 소멸, 그림자, 배경의 밀도 변화, 명암으로부터 유용한 정보를 추출할 수 있다. 다양한 인공지능기법들은 사실 인간이 어떤 것을 행하는 것을 이해하는 것을 얻기 위해 학습하는 것에 기초하고 있기 때문에 대부분의 깊이측정방법은 인간의 명령과 유사하게 설계되었다[17].
영상은 이상적인 렌즈를 통하여 영상 평면으로 장면이 투영된 것이다. 그래서 영상 위의 모든 점은 화면 위의 점과 일치할 것이다. 그러나 평면상의 점의 거리는 투영하게 되면 소실되고 화면에서 이 정보를 회수할 수 없게 된다. 만약 두 개의 영상이 한 화면을 표현한다면 두 영상의 비교를 통해 영상 평면으로부터 다른 점들의 공간적인 깊이관계를 추출할 수 있다[18,19]. 인간은 두 영상을 비교함으로써 자동적으로 위와 같은 작업을 수행하고 3차원 영상을 형성한다[20,21]. 깊이측정을 위한 입체영상은 실제적으로 2.5차원의 영상으로 간주되고 3차원 영상을 형성하기 위해서는 보다 많은 영상이 요구된다.
다중영상을 사용하는 깊이측정은 두 가지 연산처리가 필요하다:
1. 화면에서 같은 점에 해당하는 점의 위치는 두 영상에서 한 쌍을 이룬다. 이것을 일치 (correspondence) 또는 불균형 (disparity) 이라 한다. 이것은 한 영상에서 몇 개의 점이 영상에서 보이지 않을 수도 있으며, 두 영상에서 공간적 관계나 크기가 달라서 생기는 시각적인 왜곡 때문에 다루기가 어려운 명령이다.
2. 화면에 있는 물체의 점의 깊이나 위치를 삼각측량법 (triangulation) 이나 다른 기법으로 결정한다.
일반적으로, 만약 두 대의 카메라(또는 하나의 카메라의 위치관계를 두 번 사용하여 두 장의정적인 영상을 얻는다)가 정밀하게 조정되었다면, 상응점들이 충분히 검출되는 한 삼각측량법은 상대적으로 간단하다.
일치점 (correspondence point) 들은 두 영상의 모서리나 작은 부분 등의 특징 부분을 일치시켜 결정할 수 있다. 일치점들은 그들의 위치에 따라서 정합 (matching) 에 있어서 문제가 발생한다. 그림 53에 있는 두 개의 점 A와 B를 고려해 보자. 각각의 경우, 두 카메라는 (a) 와 (b) 처럼 표시를 볼 것이다. 결과적으로 표시는 서로 다르게 위치하게 될 것이다.
입체영상에서의 깊이측정 정확도는 두 영상 사이의 각에 따라 좌우되며 두 영상이 불균형하게 된다. 그러나 불균형하면 할수록 보다 넓은 지역에 대한 검색이 필요하게 된다. 정확도를 높이고 연산시간을 줄이기 위해서 같은 화면을 가진 다중영상이 사용된다[18]. 이와 비슷한 기법이 Stanford Cart에서 사용되었다.Stanford Cart의 항법 시스템은 거리와 장애물을 검출하기 위한 다중영상을 획득하는 카메라를 축에 고정시켜 사용하였다.
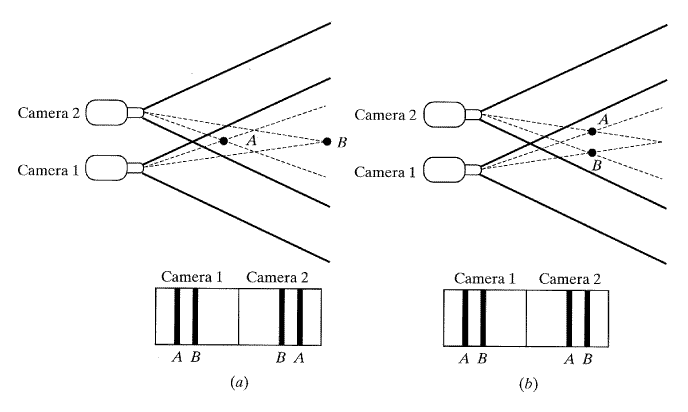
[그림 53] 스테레오 영상에서 대응문제
인간은 화면에 있는 물체의 위치, 크기, 방위에 관한 정보를 추출하기 위해 세부적인 내용들도 이용한다. 이러한 세부적인 내용 중의 하나는 다른 표면의 그림자이다. 비록 분할 명령과 같은 다른 명령에서는 다른 표면 위의 그림자의 감도가 미세하게 변한다면 명령의 수행이 매우 어려워지게 되는 원인이 되며 물체의 형상이나 깊이에 관한 정보를 추출하는 데 간접적으로 사용할 수 있다. 그림자는 물체의 방위와 반사된 빛 사이의 관계이다. 만약 이 관계를 알 수 있다면 물체의 위치와 방위에 관한 정보를 추론할 수 잇다 그림자를 이용하여 깊이를 측정하는 것은 물체의 반사율에 대한 지식과 빛의 근원에 대한 정확한 지식이 필요하므로 이에 대한 응용은 제한적이고 어렵다.
깊이분석을 위해 사용되는 또 다른 정보의 근원은 배경의 변화율을 이용하거나 깊이의 변화로 인한 배경의 변화를 이용하는 것이다. 이러한 변화는 일정하다고 가정된 배경 자신이 변화한 결과이며 평면의 방위 변화(변화율 조정)나 거리(원근법이라 불리우는)가 변화한 결과이기도 하다. 하나의 예는 벽에서 벽돌의 크기 변화를 알아차리는 것이다. 벽돌크기의 변화율을 계산함으로써 깊이가 추정될 수 있다.
[그림 54] 깊이측정에서 빛의 응용, 빛이 구성하는 평면이 물체를 비춘다. 빛이 비추는 평면과 다른 각을 가지고 위치한 카메라는 곡선과 같은 빛이 물체에서 반사된 것을 볼 수 있을 것이다. 선의 곡률이 깊이를 계산하는 데 사용된다.
깊이측정을 위한 또 다른 방법은 특별한 결과를 낳는 특수조명기법을 사용하는 것이다. 이러한 기법의 대부분은 특별한 조명과 환경의 조절이 가능한 산업응용분야를 위해 설계되었다. 이 기술의 이론적인 배경은, 만약 직선조명이 평평한 표면에 투영되었다면 빛은 평면과 빛의 근원의 위치와 방위 관계에 관하여 직선을 생성할 것이다. 그러나 만약 면이 편평하지 않고 관측기가 평면이 아닌 빛의 다른 평면의 빛의 줄기를 본다면, 곡선이나 끊어진 직선이 관측될 것이다(그림 54 참조). 반사된 빛의 분석을 통해서 물체의 그림자, 위치, 방위에 대한 정보를 추출 있다. 어떤 시스템에서는 두 개의 빛줄기가 아무것도 없는 테이블 위에 사용되고 표면 위에서 정확하게 교차할 것이다. 물체가 나타나면 두 개의 빛줄기는 반사된다. 이 반사된 빛이 카메라에서 검출되고 물체의 특징을 검출하고 결과를 나타내는 루틴을 선택한다. 이 기법을 바탕으로 개발된 상업적 시스템은 GM이 개발한 COMSIGHT™라 하는 시스템이다. 이 기법의 단점은 조사된 빛들에 대해서 단지 점에 관한 정보만 추출한다는 것이다. 따라서 완벽한 영상정보를 얻기 위해서는 물체의 전체 또는 화면을 검색해야 한다.
전자적 영상은 많은 양의 정보를 포함하고 있으므로 큰 대역폭을 가지는 데이터 전송선을 필요로 한다. 영상의 시간적, 공간적 해상도와 초당 영상수, 그리고 흑백 또는 컬러의 수를 위한 요구는 영상의 성능에 대한 요구에 의해 결정된다. 최근 데이터 전송과 저장기법은 영상 전송능력과 인터넷을 통한 전송을 포함하여 상당히 진보하였다.
비록 다른 많은 데이터 압축기법이 있지만 그들 중 몇 개만이 시각 시스템과 관련이 있다(일반적으로 데이터 전송에 관한 주제는 이 책의 범주를 벗어나며, 여기서 다루지 않기로 한다). 영상 데이터 압축기법들은(프레임을 포함한)프레임 내부와(프레임 사이의)프레임 내부방법으로 나누어진다.
펄스 코드 변조 (PCM: pulse code modulation) 는 보통 나이키스트 속도 (속도 (rate) 는 주파수 중복 (aliasing) 을 막는다)에서 아날로그 신호를 추출하는 자주 쓰이는 데이터 전송기법이며 여기서 양자화된다. 양자기 (quantizer) 는 N개의 단계(8 bit 영상 양자화) 를 갖는데, 여기서 N은 2의 N승이다. 만약 N이 8이라면 28은 256개의 다른 명암도를 가진 양자화를 생성한다. 이 범위는 텔레비전 영상 형식이나 시각 시스템에서도 매우 평범하다. 다른 응용 분야에서는 (예를 들면 항공이나 의료분야) 210이나 212의 높은 해상도를 사용한다.
의사무작위 양자화 디더링 (pusedorandom quantization dithering) 기법[24]은 원본 영상과 같은 수준의 영상을 나타내기 위하여 무작위 잡음값을 화소에 추가하여 비트수를 감소시키는 것이다. 양자화에서 만약 비트수가 디더링 없이 감소된다면 윤곽선이 생성될 것이다. 영상에서 사용 가능한 명암값이 작기 때문에 영사의 명암윤곽은 그것을 지형도 (topological map) 처럼 만든다(11 절과 그림 14를 참조). 이러한 윤곽선들은 적은 대역폭 (broadband) 의 의사무작위 (pseudorandom) 또는 디더 (dither) 라 하는 비균일한 잡음을 샘플링 이전의 신호에 더함으로써 없어질 수 있다. 디더는 원래의 양자화 레벨에 대한 윤곽선을 제거하면 화소가 진동하게끔 한다. 다시 말하면, 윤곽선은 무작위로 평균값에 대해 작은 진동이 발생되게 한다. 적당한 잡음의 양은 시스템이 비트수를 줄이는 동안에도 같은 해상도를 유지시켜 준다.
또 다른 데이터 압축방식은 하프토닝 (halftoning) 을 사용하는 것이다. 이 기법은 화소당 샘플수를 증가시킴으로써 효과적으로 화소가 분산되는 것이다. 대신에 모든 샘플은 1비트 양자화를 통하여 흑백으로 양자화된다. 인간의 눈은 화소의 그룹을 평균을 내기 때문에 영상은 여전히 이진영상이 아닌 음영으로 보인다.
예측코딩 (predictive coding) 은 고속영상에서 새로운 정보만이 전송되고 양자화되고 샘플링될 필요가 있다는 이론적인 배경을 가진 기술의 분류에 속한다. 이러한 형태의 영상들은 많은 화소들이 영상의 수가 많음에도 변함없이 남아 있다. 따라서, 단지 연속적인 영상 변화가 전송되었다면 데이터 전송은 확연하게 줄어들 것이다.
예상기 (predictor) 는 이전 영상으로부터 획득된 정보를 근거로 각 화소의 최적값을 예측하는 데 사용된다. 쇄신값 (innovation) 은 실제 화소값과 예측값 사이의 차이를 나타낸다. 예측값은 시스템을 통해 전송되어 이전의 영상을 업데이트 (update) 한다. 만약 영상에서 많은 화소가 변함없이 같다면 쇄신값은 거의 없고 전송은 감소한다. 대부분의 영상들은 빠르게 반복되고 화면의 요소들은 빠르게 움직이지 않고 임의의 영상의 배경과 같은 큰 부분은 변하지 않으므로 예측코팅이 유용하게 사용된다.
보이저 2호 (Voyager 2 Spacecraft) 의 데이터 전송량을 줄이려는 목적으로 보이저 2호가 우주에 있는 동안 컴퓨터가 다른 프로그램 방식으로 다시 프로그램되었다. 우주여행 초기 단계에는 보이저의 시스템은 화소당 256개 단계의 명암정보를 전송할 수 있게 설계되었다. 그것은 똑같은 데이터 길이에 대해 에러검출코드나 고정코드 없이도 한 영상을 전송하는데5,120,000비트가 필요하다. 천왕성에 근접하여 비행하기 시작하였을 무렵에는 시스템은 화소의 절대 밝기 값보다 연속적인 화소의 차이값만을 전송하도록 다시 프로그램되었다. 따라서, 만약 연속적인 화소들 사이에서 차이가 없다면 어떤 정보도 전송되지 않는다. 우주와 같은 환경의 배경은 본래 검은색이고 많은 화소들의 주변과 유사한 값을 가지므로 데이터 전송은 약 60%가 감소하였다[25]. 다른 고정된 배경정보의 예는 TV 뉴스 장치와 영화장치, 그리고 산업용 영상 등이 있다.
상시영역 양자화 (constant-area quantization) 또는 CAQ[26,27]에서는 낮은 대비영역과 높은 대비영역을 비교하여 낮은 해상도에서 보다 적은 펄스를 전송하여 데이터 전송을 줄인다. 실제로는 영역의 대비가 높을수록 보다 높은 주파수를 가지는 장점이 있으나 낮은 대비 영역보다 정보를 더 많이 전송해야 한다.
이 방법은 연속되는 영상 사이에 조재하는 정보가 여유롭는 장점이 있다. 프레임 사이 (interframe) 의 프로그램 기법과 프레임 내부 (intraframe) 의 기술의 차이점은 한 영상안의 정보를 이용하는 것보다는 수많은 영상의 정보전송량을 줄이는 데 있다.
이러한 목적을 이루기 위해 수신기에 있는 프레임 메모리 (frame memory) 를 사용하는 간단한 기법이 사용된다. 프레임 메모리는 영상을 유지하고 계속해서 모니터에 영상을 출력한다. 화소의 정보가 변한다면 프레임 메모리에서 상당하는 위치에서 정보가 바뀌므로 전송비율은 확연히 줄어든다. 이 기법의 단점은 순식간에 움직이는 물체에서는 깜박거림이 있다는 것이다.
영상을 처리하기 이전에 디지털화하고 저장하는 등의 다양한 많은 기법들이 고안되었다. 다른 경우에는, 비록 영상이 저장되지 않았다고 하더라도 영상처리루틴은 루틴종료 이전에 긴 연산시간이 필요하다. 이는 영상을 얻는 시간과 결과를 얻는 시간 사이에 시간이 필요하다는 의미이다. 이것은 위와 같은 결정이 결과에 영향을 끼치지 않을 때 수용할 수 있다. 그러나 실시간 영상처리 (real-time processing) 를 위해서는 결과가 실시간, 또는 충분히 짧은 시간이 실시간이라 고려되면 유효하다. 두 가지 다른 접근방법이 실시간 영상 처리를 위한 방법으로 고려된다. 하나는 실시간과 같이 아주 빠른 시간에 연산처리가 가능한 전용 하드웨어를 설계하는 것이다[28]. 또 다른 하나는 하드웨어(일부분이라 할지라도)와 소프트웨어의 효율성을 증가시키는 것이다. 따라서 처리과정과 필요한 연산을 줄이면 요구되는 계산량이 적어지므로 실시간에 가까워질 것이다. 대부부의 과정이 실제적으로 실시간이 아니지만 시스템에서 변화속도, 결정시간을 비교하면 처리시간은 실시간만큼 충분히 빠를 것이다.
경험적 학습법 (heuristic) 은 현재상황을 토대로 의사결정을 가능하게 하기 위하여 반 지능적 시스템 (semiintelligent system)을 위한 개발법의 집합이다. 경험적 학습법은 이동로봇과 결합하여 사용되나 많은 분야에서 응용되고 있다.
이동로봇이 미로에서 움직이고 있다고 가정해 보자. 또한, 로봇이 한 점에서 출발하고 벽과 같은 장애물에 도달하면 제어기에 신호를 주는 센서를 장착하였다고 가정해 보자. 이점에서, 제어기는 다음에 무엇을 해야 할 지를 결정해야 한다. 로봇이 물체를 만났을 때 첫 번째해야 하는 규칙은 왼쪽으로 회전하는 것이라 하자. 로봇이 계속 주행하면서 다른 벽면에 도달한다면 왼쪽으로 회전하고 계속 주행할 것이다. 로봇이 왼쪽으로 세 번을 회전하면 처음 출발했던 곳에 도착할 것이다. 이 경우에도 계속해서 왼쪽으로 돌아야만 하는 것인가?분명히 로봇은 끝나지 않는 무한루프를 돌고 있을 것이다. 두 번째 규칙은 첫 번째 점을 만났을 때 오른쪽으로 회전하는 것이다. 이제 로봇이 왼쪽으로 회전하여 더 이상 주행할 수 없는 막다른 곳에 도착했다고 상상해 보자. 그 다음은 어떻게 해야 하는 것일까? 세 번째 규칙은 아마도 다른 루트를 찾을 때까지 경로를 다시 추적하는 것이다. 여기서 알 수 있듯이, 로봇이 경험해야 하는 수많은 상황들이 있다. 설계자는 이러한 상황을 고려하여 의사결정 방법을 준비해야 한다. 이러한 규칙의 집합은 어떻게 로봇의 운동을 지능적으로 결정할 것인가를 결정하는 제어기를 위한 학습방법의 기초가 된다. 그러나 제어기는 실제로 의사결정을 하는 것이 아니라 단순히 이미 구성된 의사결정을 선택하는 것이므로 이 지능화는 실제 지능화가 아니라는 것을 숙지해야 한다. 만약 기본적인 법칙에서 벗어나는 새로운 상황을 만난다면 제어기는 어떻게 반응해야 하는지 알 수 없게 된다[29].
시각 시스템은 다양한 응용분야와 함께 때때로 로봇구동이나 로봇에도 결합되어 사용된다. 시각 시스템은 보통 작업환경의 정보가 필요한 곳에 사용되며, 검사, 운항,부품의 판별, 부품조립과 통신 등의 작업에 사용되기도 한다.
전자회로기판을 생산하는 자동생산라인이 있다고 가정해 보자. 이 과정에서 중요한 부분 중의 하나는 동작 전후의 보드의 변화된 형상을 검사하는 것이다. 시각 시스템의 가장 평범한 응용분야는 부품의 위치를 영상을 통하여 검사하는 것이다. 그 후에 영상처리 명령은 영상을 수정, 개선, 그리고 변경하는 데 사용한다. 그리고 처리된 영상을 메모리의 영상과 비교한다. 만약 두 영상이 일치한다면 그 부품은 인정할 수 있게 된다. 반면에, 부품이 다르면 거부되거나 수정되나. 일반적으로 영상처리와 분석과정은 앞에서 언급한 과정들로 만들어진다. 대부분의 상업용 시각 시스템은 시스템을 쉽게 구성할 수 있도록 마크로 (macro) 라고 하는 추가된 루틴을 가지고 있다.
항법장치에서 장면은 보통 올바른 길, 장애물 또는 다른 요소를 찾기 위해 분석된다. 다른 성능으로는, 시각 시스템은 조작자에게 거리로부터 운동을 제어할 수 있도록 정보를 제공한다. 이러한 구성은 원격로봇 분야에서는 매우 평범한 내용이며 우주분야의 응용도 마찬가지이다[30]. 몇몇의 의료분야에서도 마찬가지로 외과의사가 장치를 조작하여 간단한 검사와 검출장비로 혈관 촬영도 (angiogram) 를 만들 수 있다.자동항법 (autonomous navigation) 분야는 거리 탐지기나 스테레오비전, 또는 시각 시스템으로 깊이측정을 해야만 한다.또한 로봇이 주위환경을 운항할 수 있도록 행동학습규칙 (heuristic rule of behavior) 이 필요하다.
또 다른 응용분야[31,32]는, 값싼 레이저 다이오드가 카메라 옆에 장착된다. 투영된 레이저는 카메라에서 검출되어 화면상의 길이를 측정하거나 카메라를 조절하는 데 사용된다. 이 두 경우에, 레이저 빛의 밝기와 물결효과때문에 영상은 넓고 밝은 원형의 점이 생긴다. 화면의 나머지 부분에서 이 점을 제거해내기 위해서 히스토그램과 임계값 명령이 사용된다. 이어서, 원이 판별되고 원의 중심이 남아 있다면 골격화된다. 원의 중심을 나타내는 화소의 위치는 삼각측량법을 통해 영상의 깊이나 카메라를 조절하는 데 사용된다.
이러한 단순한 예들은 모두 위에서 언급했던 것과 관계된다. 비록 많은 루틴들이 가능하다고 할지라도 시각 시스템에 관한 기본적인 지식을 통하여 시각 시스템을 응용하고 적응하는 것을 계속할 수 있게 한다.
간단한 시각 시스템을 구성할 수 있는 다양하고 값싼 디지털 카메라가 상점에서 많이 팔리고 있다. 이러한 종류의 카메라들은 간단하고 작고 가벼우며 컴퓨터로 획득이 가능한 간단한 영상을 제공할 수 있고 시각 시스템을 개발하는 데 사용된다. 사실 대부분의 카메라는 획득 소프트웨어와 디지털화하는 프로그램이 제공된다. 일반적인 VHS비디오 카메라는 Snappy™와 같은 상품과 연계되어 영상을 디지털화하고 컴퓨터에 저장할 수 있다. 또한 일반 디지털카메라로 영상을 획득하고 그 영상을 컴퓨터에 저장할 수도 있다. 이 경우 나중에 영상을 분석하기 위해 영상을 획득하였다고 하더라도 카메라에서 컴퓨터로 다운로드하는데 여러 가지 절차가 있으므로 이 영상을 즉시 사용하는 것은 불가능하다.
이 장에서 논의한 내용과 유사하고 다양한 기능을 가지 어도비 포토샵™(Adobe Photoshop™) 과 같은 간단한 프로그램들이 많이 있다. 추가되는 푸틴들은 C와 같은 평범한 컴퓨터 언어로 개발된다. 최종적인 시스템은 몇 가지 영상처리에 관련된 일을 수행할 수 있는 간단한 시각 시스템일 것이다. 이 시스템은 독립적으로 작업을 수행하거나 3축 로봇과 연계되어 사용할 수도 있으며 부품을 집거나 판별하는 루틴을 포함할 수도 있고, 이동로봇과 이와 비슷한 장비를 개발할 수도 있다.
이 장에서 나타낸 모든 영상은 캘리포니아 공과대학의 기계공학 로봇 실험실에 있는 시각 시스템으로 획득한 것이다. 이 시각 시스템은 MVS909™, Optimas™ 6.2로 구성되었다. 이 책을 읽는 독자들도 다른 프로그램 언어와 시스템을 이용하여 영상파일을 처리할 수 있는 자신만의 시각 시스템을 개발할 수 있을 것이다. 이러한 시스템은 엑셀 (Excel™), 랩뷰 (LabView™) 등이며 다른 개발 시스템이다.
이 장에서는 응용을 위해 영상획득과 영상처리, 변경, 개선, 강화 등과 영상분석, 영상으로부터 데이터 추출을 통한 영상의 분석들을 공부하였다. 시각 시스템은 다양한 응용분야와 제조분야를 포함하며 감시분야와 항법, 그리고 로봇분야에도 사용이 가능하다. 시각 시스템은 유연하고 저렴하여 쉽게 사용할 수 있는 강력한 시스템이다.
다양한 목적을 가지고 사용되는 셀 수 없이 많은 루틴들이 존재한다. 대부분의 루틴은 특별한 목적과 응용분야를 위해 제작되지만 회선 마스크와 같은 기본적인 방법들은 많은 분야의 루틴에 응용이 가능하므로 이러한 방식들을 집중적으로 익혀야 하며 이를 통해서 이 책을 읽는 독자들은 스스로 다른 응용분야를 위해서 다른 루틴을 사용하고 개발하며 선택할 수 있는 안목을 가지게 될 것이다. 기술의 발전은 시각 시스템과 비전분석 분야에 큰 기회를 주었다. 미래에도 이러한 경향은 계속 될 것임에 틀림 없을 것이다.
