신경망 : Neural Networks : Nils J.Nilsson

기계가 학습할 수 있는 방법에 대해서는 이 책의 다른 부분에서 논의될 것이다. 이 장에서는 S-R (stimulus-response) 기계에 의하여 수행될 동작을 선택 (selection) 하는 계산이, 관련된 입력-행동의 쌍으로 구성된 학습 예제로부터 어떻게 학습될 수 있는지를 살펴본다. 사용될 수 있는 계산 구조가 많지만, 여기서는 조정 가능한 가중치를 가진 TLU (threshold logic unit) 로 구성된 네트워크에 초점을 맞춘다. 학습은네트워크의 동작 계산 (action computing) 성능이 받아들여질 수 있을 때까지 네트워크내의 가중치를 조정함으로써 이루어진다. 이전 장에서 언급된 바와 같이 이 TLU 네트워크는 생물학적 뉴런의 특성 중 일부를 모델로 했기 때문에 신경망이라고부른다. 여기서는 신경망과 두뇌 및 그 일부분이 어떻게 작동하는지에 대해서는 서술하지 않을 것이다. 그 대신, 단지 흥미롭고 유용한 공학적 도구로서 신경망을 살펴볼 것이다.

다음의 학습 문제를 생각해 보자. 구성 성분이 x_i, i = 1, ..., n 인 n 차원 벡터 X 의 집합 Ξ 가 주어졌다. 이 벡터들은 반응형 에이전트의 지각처리 요소에 의하여 계산된 특성 벡터일 수도 있다. 앞에서 언급한 바와 같이, 구성 성분은 실수나 부울(Boolean) 값을 갖는다. Ξ 의 각 X 에 대하여, 알맞은 행동 a 가 무엇인지 알 수 있다. 이 행동은 입력의 집합에 답하여 교사가 수행한 것을 학습자가 관찰한 것일 수 있다. 이 연관된 행동은 때때로 벡터의 라벨 (label) 또는 부류 (class) 라고 불린다. 입력의 집합과 이와 연관된 라벨은 소위 훈련집합 (training set) 을 구성한다. 기계 학습 문제는 훈련 집합의 요소에 만족스럽게 답하는 함수 f(X) 를 찾는 것이다. 보통은 f 에 의하여 계산된 행동이 Ξ 내의 가능한 한 많은 벡터에 대한 라벨과 일치하기를 바란다. 그 라벨이 입력 벡터와 함께 주어졌기 때문에, 학습 과정이 감독된다고 말한다.

우리가 훈련 집합에 대해 적절하게 답하는 함수를 찾는다고 할지라도, 훈련중에 본적이 없는 입력에 대하여도 올바르게 답할 것이라는 믿음에 대한 근거가 있는가? '그럴 것이다' 라는 믿음을 뒷받침하는 실험적인 증거 이외에도, 훈련 집합이 접할 가능성이 있는 다른 입력을 대표한다면 이 다른 입력은 아마도 대략 맞는 출력을 생성하리라는 것을 (어떤 조건하에서) 보여주는 이론이 있다. 이 주제에 대한 더 많은 것은 probably approximately correct (PAC) 학습 이론에 대한 문헌을 참고하라 [Kearns & Vazirani 1994, Haussler 1988, Haussler 1990]. 실제로, 비슷한 (그러나 지금까지 본 적 없는) 입력에 대하여 학습된 함수 f 의 정확성이 어떠할 것인가를 평가하는 다양한 방법이 있다. 이 장의 후반부에 이러한 방법 중 몇 가지를 설명할 것이다.

2. 단일 TLU 의 훈련

(1) TLU 의 기하학적 표현

우선 하나의 TLU 의 가중치가 어떻게 조정 또는 훈련되어 어떤 훈련 집합에 대해 알맞은 출력을 낼 수 있는가를 살펴볼 것이다. TLU 가 행동을 결정하기 위해 사용된다면, 그것의 입력은 가중합이 계산될 수 있는 숫자가 되어야 한다. 만약 지각 처리 시스템이 범주 특성을 산출한다면, 이것은 어떠한 방법으로든 숫자로 부호화되어야 할 것이다. 물론, 그것의 동작을 계산하기 위해 TLU 를 사용하는 반응형 기계는 TLU 의 두 가지 가능한 출력에 따라 단지 두 가지 동작만을 할 수 있을 것이다. 하나의 TLU 는 퍼셉트론 (Perceptron) 또는 Adaline (adpative linear element) 으로 불리어져 왔다. 이들의 유용성은 Rosenblatt 과 Widrow 에 의하여 광범위하게 연구되었다 [Rosenblatt 1962, Widrow 1962]. TLU 의 훈련은 그것의 가변 가중치를 조정함으로써 이루어진다. TLU 가 입력에 대해 어떻게 응답하는지를 기하학적으로 이해함으로써 TLU 훈련을 더 잘 이해하게 될 것이다.

TLU 는 가중치와 임계치에 의하여 정의된다. 가중치 (w₁, ..., w_i, ..., w_n) 은 가중치 벡터 W 에 의하여 표현될 수 있다. TLU 외 임계치는 θ 로 나타낸다 .여기서 입력 벡터 X 는 수지 성분 (가중합이 계산될 수 있는) 으로 구성되어 있다고 가정한다. TLU 는 벡터의 내적, s = X • W 가 θ 보다 크면 1 을 출력하고 그렇지 않으면 0 을 출력한다. TLU 는 그림 1 에서 보이는 바와 같이 입력 벡터 공간을 선형 경계로 나눈다. 2 차원에서의 경계는 직

그림 1. TLU 의 기하학적 표현

선이고 3 차원에서는 평면이다. 고차원에서 선형 경계를 이동하여 초평면 (hyperplane) 이라고 불린다. 초평면은 벡터를 X • W - θ > 0 을 만족하는 것과 X • W - θ < 0 을 만족하는 것으로 분리한다. 초평면 자체의 식은 X • W - θ = 0 이다. 임계치 θ 를 조정함으로써 초평면 경계의 위치를 (원점에 대하여) 변경할 수 있고, 가중치를 조정함으로써 초평면의 방향을 조정할 수 있다.

(2) 확장 벡터

TLU 의 가중치를 조정하기 위해 제안된 방법이 몇 가지 있다. TLU 의 임계치가 항상 0 과 같다는 관례를 받아들인다면 이것에 대한 설명은 간단하다. 그 대신 (n + 1) 차원의 확장 벡터 (augmented vector) 를 사용함으로써 임의의 임계치가 얻어질 수 있다. 확장 입력 벡터의 (n + 1) 번째 성분은 항상 1 의 값을 갖는다. 확장 가중치 벡터의 (n + 1) 번째 성분 n + 1 은 원하는 임계값 θ 의 음수값과 같게 설정된다. 후에 X-W 표시법을 사용할 때, (n + 1) 차원의 확장 벡터를 가정한다. 그러면 TLU 의 출력은 X • W ≥ 0 일 때 1 의 값을 갖고, 그렇지 않으면 0 의 값을 갖는다.

(3) 경사 하강법

TLU 가 훈련 벡터에 대하여 알맞게 답하도록 훈련시키는 문제에 접근하는 한 가지 방법은 가중치를 조정하여 최소화될 수 있는 에러 함수를 정의하는 것이다. 보통 사용되는 에러 함수는 제곱 에러 (squared error) 이다.

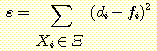
여기서 f_i 는 입력 X_i 에 대한 TLU 의 실제 응답이고 d_i 는 원하는 응답이며, 훈련 집합 내의 모든 벡터에 대하여 합을 구한다. 고정된 Ξ 에 대하여 ε 는 (f_i 를 통하여) 가중치에 의존한다는 것을 알 수 있다. ε 의 최소값을 기울기하강 (gradient descent) 에 의한 탐색 과정을 수행함으로써 찾을 수 있다. 기울기 하강을 수행하기 위해 "가중치 공간" 에서 ε 의 기울기를 계산하고 음의 기울기 (내리막길) 를 따라 가중치 벡터를 움직인다. ε 의 기울기를 정의한 대로 계산할 때의 한 가지 문제는 ε 가 Ξ 내의 모든 입력 벡터에 의존한다는 것이다. 주로 TLU 가 한번에 Ξ 의 한 원소에 대하여 시도하고 가중치를 조절한 다음, Ξ 의 다른 원소에 대하여 시도하는, 즉 라벨이 붙여진 입력 벡터의 열 Ξ 를 사용하는 점진적 훈련 과정 (incremental learning process) 이 선호된다. 물론, 점진적 훈련의 결과는 소위 일괄 학습(batch learning) 의 결과를 근사하는 것이기는 하나 근사값은 보통 아주 효과적이다. 여기서는 점진적 방법에 대해 설명한다.

원하는 출력이 d 일 때 f 의 출력을 내는 하나의 입력 벡터 X 에 대한 제곱 에러는다음과 같다.

ε = (d - f)²

가중치에 대한 ε 의 기울기 (gradient) 는

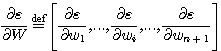
이다 (벡터 W 에 대한 어떤 값 ø 의 기울기는 때때로 로 표시된다).

ε 의 W 에 대한 의존은 완전히 내적 s =X • W 를 통한 것이기 때문에 다음과 같은 연쇄 법칙 (chain rule) 을 사용할 수 있다.

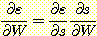
, 이므로,

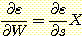
이다. 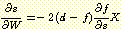임에 주목하라. 따라서

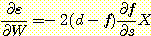
그러나 s 에 대한 f 의 편미분을 구하려 할 때 문제가 되는 것은 임계 함수 (threshold function) 의 존재 때문에 TLU 의 출력 f 는 s 에 대하여 연속적으로 미분가능하지 않다는 점이다. 내적에서의 아주 작은 변화는 f 를 전혀 변화시키지 않고, f 가 변할 때 이것은 0 에서 1로 혹은 반대로 갑자기 변한다. 이 문제를 다루는 두 가지 방법을 앞으로 살펴볼 것이다. 하나는 임계 함수를 무시하고 f = s 로 놓는 것이고 다른 하나는 임계 함수를 미분 가능한 비선형의 다른 함수로 바꾸는 것이다.

(4) Widrow-Hoff 방법

1 이라고 표시된 모든 훈련 벡터는 정확히 1 의 내적값을 나타내고, 0 이라고 표시된 모든 벡터는 -1 의 내적값을 나타내도록 가중치 조정을 시도한다고 가정하자, 이러한 경우 f = s 를 사용하면 제곱 에러는, ε = (d -f)² = (d - s)² 이고, 이다. 따라서 기울기는 다음과 같다.

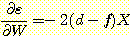
음의 기울기를 따라 가중치 벡터를 움직이고, 인수 2를 학습률 매개변수 (learning rate parameter) c 에 통합하면, 가중치 벡터의 새로운 값은

W ← W + c (d - f) X

로 주어진다. (d - f) 가 양수일 때는 입력 벡터의 일부를 가중치 벡터에 더한다. 이것은 내적값을 크게 하고 (d - f) 를 작게 한다. (d - f) 가 음수일 때는 입력 벡터의 일부를 가중치 벡터에서 뺀다. 이것은 반대 효과를 가져온다. 이 방법은 Widrow-Hoff 또는 델타 (delta) 규칙으로 알려져 있다 [Widrow & Hoff 1960]. (수치적인 방법에 익숙한 사람은 Widrow-Hoff 방법이 선형 방정식을 풀기 위한 완화법 (relaxation method) 의 하나임을 알 수 있을 것이다.) 물론 (f = s 를 사용하여) 제곱 에러를 최소로 하는 가중치의 집합을 찾은 후에 f 가 0 또는 1 의 값을 나타내도록 하기 위해 임계 함수를 다시 넣을 수 있다.

(5) 일반화된 델타 방법

미분 불가능한 임계 함수를 다루는 또 다른 방법은 Werbos [Werbos 1974] 에 의하여 제안되었고, 몇몇 연구자들, 예를 들면 [Rumelhart, et al. 1986] 에 의하여 독립적으로 연구가 진행되었다. 이 방법은 임계 함수를 시그모이드 (sigmoid) 라고 하는 S 자 모양의 미분 가능한 함수로 바꾸는 것이다. ([Russell & Norvig 1995, p. 595] 는 이러한 생각을 하게 된 것이 [Bryson & Ho 1969] 덕분이라고 한다.) 보통, 사용되는 시그모이드 함수는

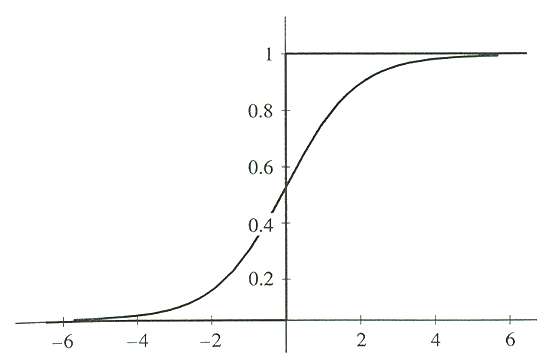
그림 2. 시그모이드 함수

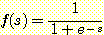이다 (여기서 s 는 입력이고, f 는 출력이다). 그림 2 는 임계 함수의 출력과시그모이드 함수의 출력을 보여준다.

시그모이드 함수를 선택함으로써 다음과 같은 편미분이 가능하다.

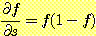
이 식을 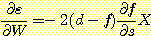에 대입하면

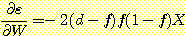
가 되고, 이것은 일반화된 델타 방법 (generalized delta procedure) 이라고 알려진 다음과 같은 가중치 변경 규칙을 만든다.

W ← W + c (d - f) f (1 - f) X

Widrow-Hoff 규칙과 일반화된 델타 규칙을 비교하면 다음과 같은 차이점이 있다.

1. Widrow-Hoff 규칙에서는 원하는 출력 d 가 1 또는 -1 인 반면, 일반화된 델타 방법에서는 1 또는 0 이다.

2. Widrow-Hoff 규칙에서는 실제 출력 f 가 내적 s 와 같지만 일반화된 델타 규칙에서는 시그모이드 함수의 출력이다.

3. 일반화된 델타 방법에서는 시그모이드 함수 때문에 덧붙여진 항 f (1 - f) 가 존재한다. 시그모이드 함수에서 f (1 - f) 는 0 부터 1 까지 변한다. f 가 0 일 때 f (1 - f) 도 0 이고 f 가 1 일 때도 f (1 - f) 는 0 이다. f 가 1/2 일 때 (즉, 시그모이드의 입력이 0 일 때) f (1 - f) 는 최대값 1/4 을 갖는다. 시그모이드 함수는 어떤 퍼지 초평면을 구현한 것이라고 생각할 수 있다. 이 퍼지 초평면에서 멀리 떨어진 입력에 대해 f (1 - f) 는 0 에 가까운 값을 갖고, 일반적인 델타 규칙은 원하는 출력에 관계없이 가중치를 거의 혹은 전혀 변화시키지 않는다. 가중치 변화는 단지 초평면을 둘러싸는 퍼즈 (fuzz) 영역 (변화가 f 에 많은 영향을 주는 유일한 곳) 내에서 일어나고, 이 변화는 에러를 수정하는 방향이다.

일반화된 델타 규칙이 가중치의 집합을 발견한 후에, 원한다면 시그모이드 함수는 한계 함수로 대체될 수 있다.

(6) 에러 수정 절차

다음 방법에서는 임계 요소를 유지하고 (시그모이드로 대체하는 대신에) TLU 가 잘못 답할 때, 즉 (d - f) 의 값이 1 또는 -1 의 값을 가질 때 가중치 벡터를 조정한다. 이것은 에러 수정 절차라고 불린다. 가중치 변경 규칙은 다음과 같다.

W ← W + c (d - f) X

다시 말하면, 에러를 수정하는 방향으로 가중치가 변경된다. 그리고 학습률 매개변수 c의 값에 따라 실제로 에러를 수정할 것이다. 이 규칙과 Widrow-Hoff 규칙의 차이점은 에러 수정에서 d 와 f 는 모두 0 또는 1 인데 반해, Widrow-Hoff 규칙에서 d 는 +1 (또는 -1) 이고, f = s 는 내적값이다.

Ξ 내의 모든 입력 벡터에 대하여 올바른 출력을 내는 어떤 가중치 벡터 W 가 존재한다면, 한정된 개수의 입력 벡터가 제시된 후에 에러 수정 절차는 그 가중치 벡터를 찾을 것이고, 그러면 더 이상의 가중치 변화가 일어나지 않는다는 것을 증명할 수 있다 (이 절차가 입력의 순서 Σ 로부터 단지 한정된 수의 예제가 제시된 후에 종료된다는 것이 보장된다 하더라도 증명에서는 각 입력 벡터가 Σ 내에 무한번 나타나야 한다). 선형적으로 구별되지 않는 입력 벡터의 집합에 대하여 에러 수정 절차는 결코 종료되지 않을 것이므로 어떤 에러 기준에 의하여 판단된 가장 좋은 가중치 벡터를 찾는데 사용할 수 없다. 그러나 Widrow-Hoff 와 일반적인 델타 방법은 최소 에러가 0 이 아닐지라도 최소의 제곱 에러 해를 찾을 것이다.

전형적으로 구별되는 함수의 예는 2장에서 살펴보았다. 경계선을 따라가는 로봇의 행동에 대한 규칙의 생성을 상기해 보자. 예를 들어 이러한 것 중 하나는 다음과 같다.

감지 입력에 대하여 표시하면, 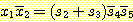이다. 이 함수는 선형적으로 구분되고 자극반응 에이전트 그림 6 에서 나타낸 TLU 에 의하여 표현될 수 있다. 그러므로 올바르게 분류된 감지 벡터의 충분히 큰 집합에 대해 오차 수정 훈련을 하면 로봇이 동쪽으로 움직여야

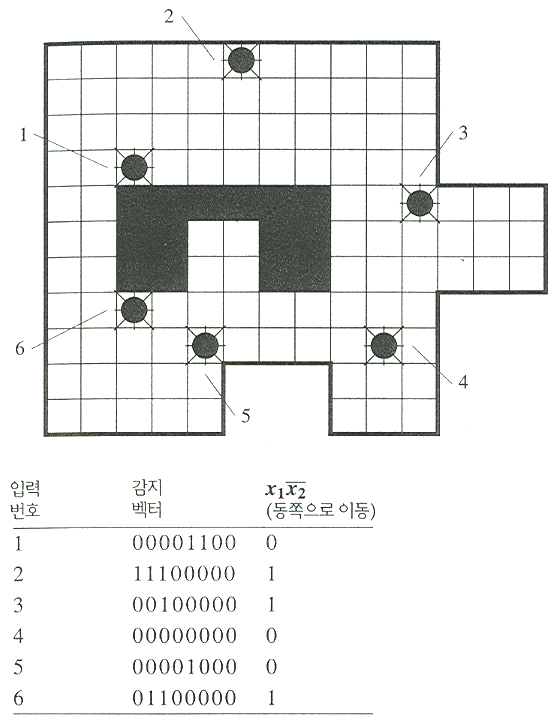
그림 3. 동쪽으로 움직일 때의 학습을 위한 훈련 집합

하는 입력과 그렇지 않은 입력을 구별할 수 있는 TLU 를 생성할 것이다. 그 결과 그림 3 과 같은 훈련 벡터의 집합을 만들 수 있다. 독자들도 이러한 것과 추가적으로 라벨이 붙은 입력 벡터를 사용하여 에러 수정 절차를 시도해 보고 싶을 것이다 (s₉ ≡ 1 입력과 w₉ 가중치 요소를 포함시키는 것을 잊지 말아야 한다). 훈련된 TLU 는 그것이 훈련하는 동안 보지 못한 입력에 대하여 어떻게 작동할까? TLU 가 만족할만하게 수행하기 전에 얼마나 많은 입력 벡터가 훈련 집합에 필요한가?

에러 수정 절차에 대한 추가적인 예비 지식, 관련 논문, 증명 그리고 예제에 대해서는 [Nillsson 1965] 를 참조하라.

3. 신경망

(1) 동기

하나의 TLU 에 의하여 학습될 수 없는 자극과 반응의 집합이 종종 존재한다 (아마도 훈련 집합이 선형적으로 구분되지 않을 것이다). 이러한 경우에 여러 개의 TLU 로 구성된 신경망이 올바른 답을 낼 수 있다. TLU 신경망에 의하여 구현된 함수는 각 TLU 의 가중치뿐만 아니라 그것의 구조에 따라 결정된다. 전방향 신경망 (feedforward network) 에는 싸이클이 없다. 전방향 신경망에서 어떤 TLU 의 입력도 (0 또는 그 이상의 중간 TLU 를 통해서 그 TLU 의 출력에 의존하지 않는다. 전방향이 아닌 신경망을 순환 신경망 (recurrent network) 이라고 한다. 뒷장에서 순환 신경망의 예를 살펴볼 것이다. 전방향 신경망의 TLU 가 단지 j - 1 층의 TLU 로부터 입력을 받는 j 층의 요소가 되도록 층으로 배열된다면, 그 신경망을 다층 전방향 신경망 (layered feedforward network) 이라고 한다. (짝수 패리티라고 불리는)

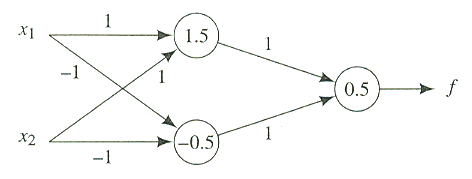
그림 4. 짝수 패리티 함수를 구현한 TLU 신경망

함수 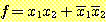을 구현한 그림 4 의 신경망은 두 개의 (가중치의) 층을 가진 다층 전방향 신경망이다 (어떤 사람들은 TLU 의 층을 세고 또한 입력을 층에 포함시킨다;그들은 그림 4 의 신경망을 3 층의 신경망이라고 부를 것이다).

다음 절에서는 다층 전방향 신경망을 훈련시키는 일반적인 방법을 설명할 것이다. 이것을 역전파 방법 (backpropagation procedure) 이라고 하고 경사 하강법을 사용한다. 가중치 벡터에 대하여 에러 함수의 편미분을 계산할 것이기 때문에 신경망내의 모든 임계 함수를 시그모이드 함수로 바꾼다 (훈련 후에 시그모이드 함수를 한계 함수로 다시 대체할 수 있다).

(2) 표기법

그림 5 는 일반적인 k 층 전방향 시그모이드 유닛 신경망을 나타낸다. 마지막 층에 있는 것을 제외한 모든 시그모이드 유닛은 그것의 출력이 단지 간접적으로만 최종 출력에 영향을

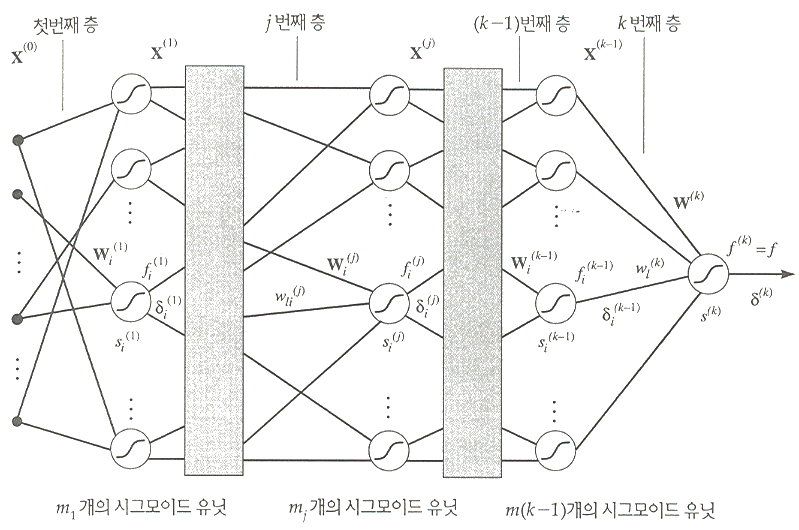
그림 5. 시그모이드 유닛의 k 층 신경망

주기 때문에 은닉 유닛 (hidden unit) 이라고 불린다. 그림 5 의 신경망은 단지 하나의 출력 유닛을 갖고 있다. 입력의 행동 또는 범주가 두 개 이상일때는 복수 개의 출력 유닛이 사용될 수 있다 (복수 개의 출력 유닛이 사용되면, 출력 벡터를 범주로 변환시키기 위한 디코딩 방법이 필요하다. [Brain, et al. 1962] 는 최대 이동 레지스터열 (maximal shift-register sequence) 에 기반한 코드를 사용했고, [Dietterich & Bakiri 1991, Dietterich & Bakiri 1995] 는 비슷한 에러 수정 코드의 사용을 연구하였다).

그림 5 에 몇 가지 유용한 표기법을 제시하였다. 입력 특성이 입력 벡터의 성분인 것처럼, 시그모이드 유닛의 각 층은 우리가 벡터의 성분으로 얻는 출력을 갖게 된다. 시그모이드의 j 번째 (1 ≤ i < k) 층은 출력으로 벡터 X^(j) 를 갖는다. 그러면 이 벡터는 (j + 1) 번째 층의 각 시그모이드의 입력이 된다. 입력 벡터는 X⁽⁰⁾ 로 표시되고 (k 번째 층의 TLU 의) 최종 출력은 f 이다. 각 층의 각 시그모이드는 (그것의 입력과 연결되는) 가중치 벡터를 갖는다. j 번째 층의 i 번째 시그모이드 유닛은 W_i^(j) 로 표시되는 가중치 벡터를 갖는다. 전과 같이, 연관된 가중치 벡터의 마지막 성분은 임계 가중치 (threshold weight) 로 가정한다. j 번째 층의 i 번째 시그모이드 유닛의 가중합 입력은 s_i^(j) 로 표시된다. 시그모이드 유닛에 대한 입력은 활성화 (activation) 라고 하고 다음과 같이 주어진다.

s_i^(j) = X^(j-1) • W_i^(j)

j 번째 층의 시그모이드 유닛의 개수는 m_j 로 표시된다. 벡터 W_i^(j) 는 성분 w_1,^(j)_i l = 1, ..., m_(j-1) + 1 을 갖는다.

(3) 역전파 방법

앞으로 에러의 제곱 함수 ε = (d - f)² 의 기울기 (gradient) 를 계산할 것이다. 이 경우 기울기가 계산되는 가중치 벡터는 네트워크상의 모든 가중치로 구성되어야 한다. 하지만 각 시그모이드의 모든 가중치에 대해 ε 의 편미분을 구하는 것이 더 쉽다. 가중치 벡터 W_i^(j) 에 대한 ε 의 편미분은 다음과 같다.

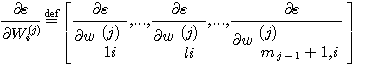
여기서 w_li^(j) 는 W_i^(j) 의 l 번째 구성요소를 의미한다.

이전과 마찬가지로 W_i^(j) 에 대한 ε 의 종속성은 전적으로 s_i^(j) 를 통하여 이루어지므로 연쇄 법칙을 이용하여 다음과 같이 표현할 수 있다.

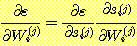
또한 s_i^(j) = X^(j-1) • W_i^(j) 이므로 W_i^(j), 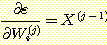이다. 따라서

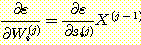
로 표현된다.

이제, 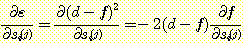이므로

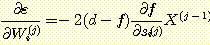
이다.

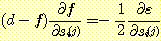의 값은 이 계산에서 중요한 역할을 한다. 여기서는 이것을 δ_i^(j) 로 표현하자. 각각의 δ_i^(j) 는 신경망의 출력에 대한 에러 제곱값이 얼마나 해당 시그모이드 함수의 입력값의 변화에 민감한지를 의미한다. 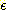의 기울기는 다음과 같이 δ' 의 값으로 표현될 수 있다.

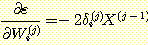
음의 기울기 방향으로 가중치 벡터를 변화시켜가므로 신경망의 가중치 변화에 대한 기본적인 법칙은 다음과 같다.

W_i^(j) ← W_i^(j) + c_i^(j) δ_i^(j) X^(j+1)

여기서 c_i^(j) 는 이 가중치 벡터에 대한 학습률 상수 (learning rate constant) 이다 (흔히, 네트워크내에서 모든 가중치 벡터에 대한 학습률 상수는 일정하다). 이 규칙이 단일 TLU 나 시그모이드 유닛에 대한 학습 방법에서 사용되었던 것과 아주 유사하다는 것을 알 수 있다. 가중치 벡터는 입력 벡터의 상수배 만큼을 더함으로써 수정된다.

(4) 출력층에서의 가중치 변화 계산

이제 δ_i^(j) 를 계산해 보자. 정의에 의해 다음과 같은 식을 얻을 수 있다.

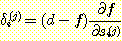
우선 최종 출력 시그모이드 유닛에서의 가중치 변화를 계산하기 위해 δ^(k) 를 계산해 보자.

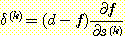
f는 시그모이드 함수이고 s^(k) 는 이것의 입력이므로 와 같은 식을 얻을 수 있다. 따라서,

δ^(k) = (d - f) f (1 - f)

이다. 그리고 최종 출력층에서의 단일 유닛에 대한 역전파 가중치 변화는 다음과 같이 표현된다.

W^(k) ← W^(k) + c^(k) (d - f) f (1 - f) X^(k-1)

만약 최종 시그모이드 유닛이 네트워크상에서 유일한 것이고 X^(k-1)= X 라면, 이 결과는 일반화된 델타 규칙에서 유도된 것과 동일한 것이다.

(5) 중간층에서의 가중치 변화 계산

δ 에 대한 표현을 사용하여 신경망에서 각 가중치 벡터의 변화를 계산하는 방법을 비슷한 방식으로 구해낼 수 있다.

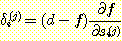
다시 한번 연쇄 법칙을 이용하자. 최종 출력 f 는 (j + 1) 번째 층에 있는 시그모이드 입력값의 합에 의해 s_i^(j) 에 종속적이다.

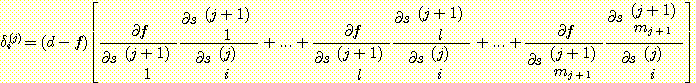
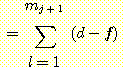
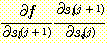
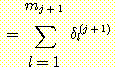
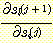
여기에서도 여전히 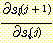를 계산해야 한다. 이것을 하기 위하여 우선 다음과 같은 식을 보자.

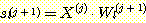
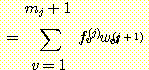
가중치는 s 에 종속적이지 않으므로 다음과 같이 표현된다.

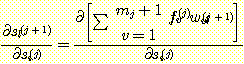
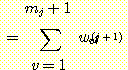
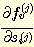
이제 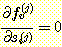인 경우, v = i 가 아니라면 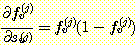이 된다. 따라서 다음이 성립된다.

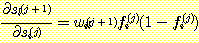
이다. 이 결과를 δ_i^(j) 에 대한 식에 이용하면 다음과 같은 결과를 얻게 된다.

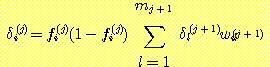
위의 식은 δ 에 대한 재귀 방정식이다 (이 식이 에러 함수에 독립적이라는 사실은 매우 흥미롭다. 에러 함수는 명시적으로 단지 δ^(k) 의 계산에만 영향을 미칠 뿐이다). j + 1 층에 대한 δ_i^(j+1) 값의 계산이 끝난 후 이 식을 이용하여 δ_i^(j) 의 값을 계산해낼 수 있다. 기초가 되는 출발점은 δ^(k) 이다. 이 값은 이미 다음과 같이 구해졌다.

δ^(k) = (d - f) f (1 - f)

δ 에 관한 이 식을 일반화된 가중치 변경 규칙에 사용할 수 있다. 즉,

W_i^(j) ← W_i^(j) + c_i^(j) δ_i^(j) X^(j-1)

이다. 이 규칙은 일견 복잡해 보이지만 직관적이고 합리적으로 설명될 수 있는 규칙이다. δ^(k) = (d - f) f (1 - f) 의 값은 네트워크내에서 모든 가중치 조정의 양이나 부호를 조절한다 (최종 출력이 0 이나 1 에 도달할 때는 조정량이 감소한다. 그 이유는 이들이 f 에 대해 감쇠 효과를 가져오기 때문이다). δ 에 관한 재귀 방정식이 보여 주듯이 j 번째 층의 시그모이드 유닛으로의 입력 가중치 조정은 이러한 조정이 출력 유닛 시그모이드의 출력값, 즉 f^(j) (1 - f^(j)) 에 대해 가지는 효과에 비례한다. 이들은 또한 시그모이드 유닛의 출력값의 변화가 최종 출력에 대해 미치는 평균 효과에 비례한다. 이러한 평균 효과는 j 번째 층의 시그모이드 유닛의 출력 가중치와 (j + 1) 번째 층의 시그모이드 유닛의 출력값의 변화가 최종 출력에 미치는 영향에 의존적이다. 이러한 계산은 단순히 δ 를 역방향으로 가중치를 통하여 역전파시킴으로써 구현될 수 있다. 그래서 이 알고리즘을 역전파 알고리즘이라고 한다. 역전파 알고리즘과 이의 응용에 대해서 좀더 자세히 알고 싶다면 [Chauvin & Rumelhart 1995] 를 참조하라.

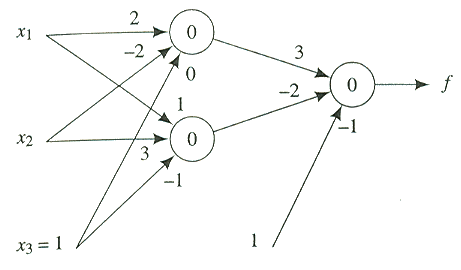
그림 6. 역전파 방법에 의하여 훈련된 신경망

역전파 과정의 예로서 그림 6 의 신경망을 한 단계 훈련시켜 보자. 초기의 가중치로 주어진 값을 가지고 시작한다. 목적 함수는 두 개의 이진 변수에 대한 짝수 패리티 함수이다. 임계치 입력을 포함한 입력과 목표값은 다음과 같다.

1. x₁⁽⁰⁾ = 1, x₂⁽⁰⁾ = 0, x₃⁽⁰⁾ = 1, d = 0

2. x₁⁽⁰⁾ = 0, x₂⁽⁰⁾ = 0, x₃⁽⁰⁾ = 1, d = 1

3. x₁⁽⁰⁾ = 0, x₂⁽⁰⁾ = 1, x₃⁽⁰⁾ = 1, d = 0

4. x₁⁽⁰⁾ = 1, x₂⁽⁰⁾ = 1, x₃⁽⁰⁾ = 1, d = 1

처음의 입력 벡터는 (1, 0, 1) 이고 이 입력값에 의해 첫번째 층의 출력값은 f₁⁽¹⁾ = 0.881 와 f₂⁽¹⁾ = 0.500 이며, 최종 출력값은 f = 0.665 가 된다. 기초값에 대한 식을 이용하여 δ⁽²⁾ = -0.148 을 계산할 수 있다. 두번째 층의 가중치를 통하여 이러한 δ 의 역전파는 δ₁⁽²⁾ = -0.047, δ₂⁽¹⁾ = 0.074 값이 계산된다. 다음으로 학습률을 1 로 잡았을 때 가중치 조정 공식을 이용하면 각 가중치는 다음과 같이 변경된다.

W₁⁽¹⁾ = (1.953, -2.000, -0.047)

W₂⁽¹⁾ = (1.074, 3.000, -0.926)

W⁽²⁾ = (2.870, -2.074, -1.148)

비록 f₂⁽¹⁾ = 0.500 로 가중치 변경에 가장 민감하게 되지만 x₂⁽⁰⁾ = 0 이므로 w_2,⁽⁰⁾₂ 이나 w_1,⁽¹⁾₂ 에는 어떠한 변화도 일어나지 않았음을 주목하자. 첫번째 층의 가중치에 대한 조절은 f₁⁽¹⁾ 과 f₂⁽¹⁾ 양쪽의 값을 감소시키게 된다. 이는 두번째 층의 가중치에 대한 변경과 더불어 f 와 입력 벡터에 대한 에러값을 감소시킨다. 이는 이 훈련 과정을 계속해서 반복해야 함을 의미한다.

4. 일반화, 정확도, 과다 학습

이전에 제시된 신경망의 학습 예는 매우 비전형적이다. 주어진 예는 차원이 낮기 때문에 모든 가능한 입력 벡터를 훈련시킬 수 있었다. 그림 4 에 따르면, 이 모든 예를 정확히 학습할 수 있는 가중치의 집합이 존재한다. 대부분의 응용 문제에서는 차원이 매우 높아서 보통 100 이나 그 이상이 되기도 한다. 100 개의 이진 요소에 대해서는 2¹⁰⁰ 개의 가능한 입력 벡터가 존재한다. 이들 중 아주 일부만을 훈련을 위해 사용할 수가 있다. 그리고 비록 네트워크가 전체 훈련 집합을 정확하게 분류해낼 수 있다고 하더라도 (사실 있을 법하진 않지만 (성능은 항상 잡음에 의하여 제한된다. 예를 들어 잡음 감지로부터 유도되었다면, 입력 벡터의 몇 가지 요소는 잡음이다. 혹은 훈련 집합의 어떤 입력 벡터는 때로는 라벨이 되어있지 않을지도 모른다. 처음의 잡음을 속성 잡음 (attribute noise) 이라고 부르고, 두번째 잡음을 분류 잡음 (classification noise) 이라고 한다)) 다른 입력 벡터도 잘 분류해낼 수 있다는 보장을 할 수 있는 것은 아니다. 네트워크가 훈련 집합에 포함되지 않은 입력 벡터에 대해서도 올바르게 분류해낼 수 있다면 이 네트워크는 일반화 (generalize)되었다고 한다. 일반화 능력은 이러한 분류의 정확도 (accuracy) 에 의해 측정된다. 여기서는 어떻게 일반화 정확도를 측정할 수 있는지에 대해 간단히 설명한다.

왜 신경망이 일반화 능력이 있다고 기대하게 되는 것일까? 그것은 곡선 적합화 (curve fitting) 와 어느 정도 연관이 있다. 직선이나 혹은 저차원의 다항 함수를 데이터에 적합화시키려 할 때, 데이터에 대한 곡선의 적합도가 매우 좋고 또한 많은 데이터가 존재한다면, 우리는 데이터간에 존재하는 관계를 찾았다고 확신한다. 이 적합화된 곡선은 적합화 과정에서 사용되지 않은 새로운 데이터에 대한 값을 예측하는데 사용될 수 있다. 만약 직선이 데이터에 잘 들어맞지 않는다면 아마 2차 곡선이나 다른 곡선을 사용하려고 할 것이다. 유사한 상황이 신경망에도 적용된다. 신경망은 입력값에 대해 비선형적이고 복잡한 함수를 계산해낸다. 만약 이러한 입력의 분류가 신경망에 의해 구해질 수 있는 함수와 유사한 함수라면, 그리고 아주 많은 양의 훈련 데이터에 대해 훈련된 신경망의 적합화가 아주 좋다면, 훈련 과정은 입력과 그 유형 사이의 존재하는 함수 관계를 파악했다고 생각할 수 있다. 이 경우 새로운 입력에 대한 일반화가 잘 된다.

훈련 입력 벡터의 수는 네트워크의 자유도 (가변 가중치의 개수) 보다 더 커야 한다는 사실은 매우 중요하다. 다시 한번 곡선 적합화는 유용하게 사용된다. m 개의 데이터가 존재하고 직선이 이 데이터에 적합하지 않다면, 어떤 (m - 1) 차 다항식이 주어진 데이터에 완벽하게 적합하다고 판별될 수 있다. 그러나 m 개의 데이터 위치에 상관없이 그러한 적합화가 가능하므로, 이것은 그 데이터에 대한 특별한 어떤 것을 찾아내었다고 말하기는 어렵다. 대신 주어진 데이터에 과다 학습되었다고 할 수 있다. 만약 그 데이터가 잡음이 많은 데이터라면 (아마도 직선은 잡음이 전혀 없는 데이터에 적합할 지도 모른다) 여분의 추가 자유도는 잡음에 필연적으로 적합화된다. 곡선 적합화에서 잘 알려져 있는 것처럼 데이터의 개수는 적합화를 위해 사용되는 다항 함수의 차원의 개수보다 아주 커야 한다. 그리고 주어진 데이터가 충분하다면 오캄의 원리 (Occam's razor principle) 는 적당하게 데이터에 적합화되는 가장

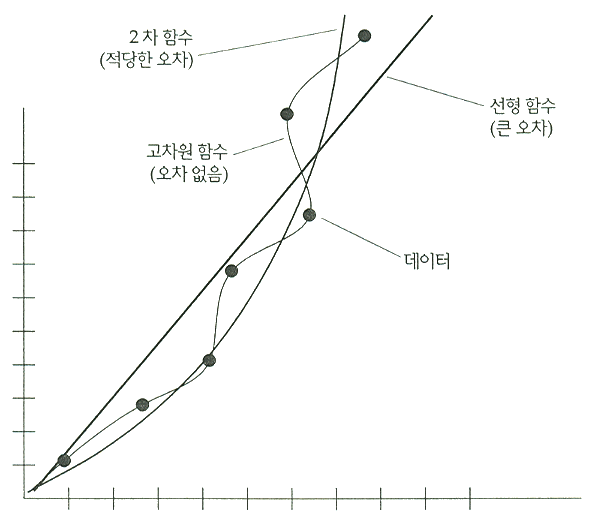
그림 7. 곡선 적합화

낮은 차원의 다항함수를 선택할 것을 지시한다. 그럼 7 은 곡선 적합화를 위한 이러한 개념을 보여준다. 2차원 함수는 선형 함수보다 데이터에 적합하며 다차원 함수에서처림 데이터에 대한 과다 학습도 하지 않는다. 같은 원리가 신경망의 학습에도 적용된다.

n 개의 입력 유닛과 h 개의 은닉 유닛, 1 개의 출력 유닛을 가진 2 층 신경망을 생각해 보자. 이러한 신경망은 nh + h = (n + 1)h 의 가변 가중치를 가진다. 입력 차원이 고정되어 있다면 자유도는 은닉 유닛의 개수에 의해 조절된다. 훈련 집합에 대한 분류 오차 백분율은 그것의 최소값에 도달할 때까지 은닉 유닛의 수가 증가할수록 계속 떨어질 것이다 (물론 훈련 집합이 선형적으로 분리된다면, 우리는 단 하나의 은닉 유닛만을 가지고도 0 에러를 얻을 수 있

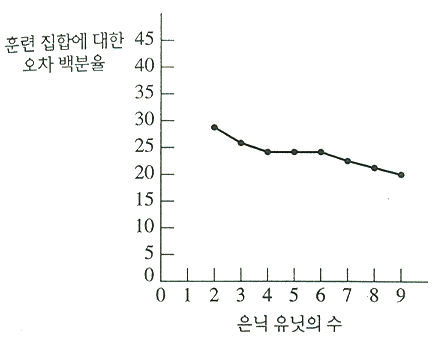
그림 8. 오차 대 은닉 유닛의 수 ([Duda, Hart, & Stork 1998] 의 변형임)

다). 그림 8 은 은닉 유닛의 개수에 대한 함수로서의 학습 에러에 대한 전형적인 예를 보여준다. 그러나 이전에 언급한 바와 같이 과다 학습을 회피하기 위해서 우리는 nh + h = (n + 1)h 가 훈련 입력 벡터의 개수에 근접할 정도의 많은 은닉 유닛을 원하지는 않는다.

오차가 아주 작다고 하더라도 일반화는 좋지 않을 수도 있다. 훈련 집합에 있는 입력이 아닌 훈련 집합과 같은 확률 분포로부터 추출된 입력에 대한 오차율을 추정하는 여러 가지 방법이 있다. 이러한 오차율을 확률론에서는 표본 외 집합에 대한 오차율 (out-of-sample-set error rate) 이라 한다. 아마 가장 단순한 방법은 입력 벡터를 두개의 집합으로 분리하여 훈련을 위해 그들 중 하나만을 사용하는 방법일 것이다. 이때 사용된 집합을 훈련 집합 (training set) 이라고 한다. 훈련이 끝난 후 검증 집합 (validation set) 이라 불리는 또 다른 집합을 이용하여 표본 외 집합에 대한 오차율을 계산하는 것이다. 만약 양쪽에 있는 데이터의 개수가 아주 많다면 검증 집합에 대한 오차율은 일반화 정확도와 아주 가까울 것이다 (물론 실제적인 표본 외 오차율이라고 하기는 어렬다. 왜 그럴까?). 경험이 많은 설계자는 흔히 훈련 집합으로 전체의 2/3 를 쓰고 검증 집합으로는 나머지 1/3 을 쓴다.

일반화의 정확도를 측정하는 또 다른 방법으로 널리 쓰이는 방법은 교차 검증 (cross validation) 이다. 여기서는 주어진 훈련 데이터를 k (흔히 10) 개의 폴드 (fold) 라 불리는 서로 다른 부분 집합으로 분리한다. 검증 집합으로 이 중 하나만을 쓰고 훈련을 위해 나머지 k - 1 개의 데이터 집합을 사용한다. 이것을 k 번 반복하는데 각 시도 때 마다 검증 집합으로 서로 다른 폴드를 선택하고 나머지로 훈련을 한다. 각각의 검증 집합에 대한 오차율을 계산할 수 있고, 표본 외 오차율의 추정치로서 이들 오차율의 평균값을 취한다. m 을 주어진 데이터의 개수라고 할 때, k = m 인 (여기서 m 은 사용 가능한 라벨된 벡터의 개수이다) 특별한 경우에 이것을 leave-one-set 교차 검증이라고 한다. 실험상의 결과로 10 겹 교차 검증 (10-fold cross validation) 이 가장 그럴듯한 일반화 정확도를 산출해냄을 알 수 있다.

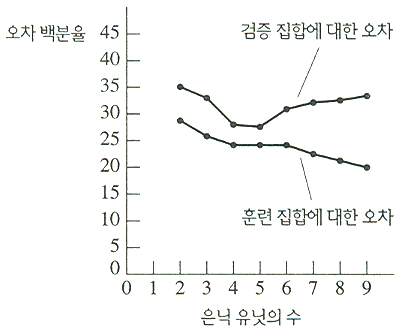
그림 9. 일반화 오차의 기대치 대 은닉 유닛의 수

([Duda, Hart, & Strok 1998] 의 변형임)

그림 9에서 검증 집합에 의해 측정된 표본외 오차율 추정이 은닉 유닛의 개수에 따라 다양함을 알 수 있다. 은닉 유닛의 개수가 증가함에 따라 과다 학습의 영향으로 검증 집합에 대한 오차율이 증가하기 시작함을 주목하기 바란다.

참고문헌 및 토론

신경망은 패턴인식, 자동 제어, 뇌기능 모델링 등 여러 실제 문제에 적용되어 왔다. 전형적인 예는 필기체 문자 (우편번호) 인식 문제 [LeCun, et al. 1989 (LeCun, Y., Boser, B., Denker, J., Henderson, D., Howard, R., Hubbard, W., and Jackel, L., "Backpropagation Applied to Handwritten Zip Code Recognition," Neural Computation, 1(4), 1989.)], 음성인식 [Waibel, et al, 1988 (Waibel, A., Hanazawa, T., Hinton, G., Shikano, K., and Lang, K., "Phoneme Recognition: Neural Networks versus Hidden Markov Models," in Proc. of the International Conf. on Acoustics, Speech and Signal Processing, New York, 1988.)], 기록 문서에 의해 제시된 단어의 발음을 학습하는 문제 [Sejnowski & Rosenberg 1987 (Sejnowski, T., and Rosenberg, C., "Parallel Networks That Learn to Pronounce English Text," Complex Systems, 1:145-168, 1987.)] 등이다. 그러나 이러한 응용 문제에 대한 신경망의 설계와 학습은 아직도 많은 경험과 실험이 요구된다는 사실이 강조되어야만 한다. 가장 훌륭한 연구 논문과 결과들이 Neural Information Processing Systems (NIPS) 국제 학회에 발표되며 이러한 발표 논문은 Advances in Neural Information Processing Systems 라는 이름으로 출판된다.

언급된 것처럼 신경망의 기본적인 단위인 TLU 는 초공간상에서 입력 벡터 공간을 분할한다. 만약 훈련 집합의 두 부분 집합이 교차하지 않는다면 한 개의 초평면으로 이러한 분할은 가능하다. 분할 평면은 이 장에서 언급된 훈련 방법이나 혹은 선형 프로그래밍 방법에 의해 구해질 수 있다. 이러한 선형 프로그래밍 방법은 다항 함수적인 복잡도를 가진다고 알려져 있다 [Karmarkar 1984 (Karmarkar, N., "A New Polynomial-Time Algorithm for Linear Programming," Combinatorica, 4(4):373-395, 1984.)].

여기서는 단지 다층 전방향 신경망만을 다루었다. 순환 신경망의 행동 분석은 더욱 복잡하지만 [Hertz, Krogh, Palmer 1991 (Hertz, J., Krogh, A., and Palmer, R., Introduction to the Theory of Neural Computation, Reading, MA: Addison-Wesley, 1991.)] 에서는 동적 시스템의 물리적 현상에 대한 분석을 이용하여 이를 잘 설명하고 있다. 역전파 알고리즘은 [Pineda 1987 (Pineda, F. J., "Generalization of Back-Propagation to Recurrent Neural Networks," Physical Review Letters, 59:2229-2232, 1987.), Almeida 1987 (Almeiida, L. B., "A Learning Rule for Asynchronous Perceptrons with Feedback in a Combinatorial Environment," in M. Caudill and C., Butler (eds.), IEEE First International Conference on Neural Networks, San Diego, 1987, vol. II, pp.609-618, New York: IEEE, 1987.), Rohwer & Forrest 1987 (Rohwer, R., and Forrest, B., "Training Time-Dependence in Neural Networks," in Caudill, M., and Butler, C. (eds.), IEEE First International Conference on Neural Networks, San Diego, 1987, vol. II, pp.701-708, New York: IEEE, 1987.)] 에 의해 순환 신경망의 경우까지 적용될 수 있도록 확장되고 일반화되었다. 이 알고리즘에 관한 읽을 만한 논문으로는 [Hertz, Krogh, Palmer 1991, pp.172-176 (Hertz, J., Krogh, A., and Palmer, R., Introduction to the Theory of Neural Computation, Reading, MA: Addison-Wesley, 1991.)] 이 있다.

신경망은 기계 학습에서 사용되는 수많은 구조 중의 하나일 뿐이다. 또 다른 것으로는 결정트리 (decision tree) 가 있는데 이는 트리의 구성이 신경망보다 훨씬 이해하기가 쉽기 때문에 많은 사람들에 의해 선호된다. 인공지능에서는 Quinlan 이 ID3 [Quinlan 1979 (Quinlan, J., "Discovering Rules from Large Collections of Examples: A Case Study," in Michie, D. (ed.), Expert Systmes in the Microelectronic Age, Edinburgh: Edinburgh University Press, 1979.)] 와 C4.5 [Quinlan 1993 (Quinlan, J. R., C4.5: Programs for Machine Learning, San Francisco: Morgan Kaufmann, 1993.)] 를 사용한 결정트리 학습 방법을 고안해내었다 [Quinlan 1993 (Quinlan, J. R., C4.5: Programs for Machine Learning, San Francisco: Morgan Kaufmann, 1993.)]. 비슷한 학습 방법이 통계학자들 [Brieman, et al. 1984 (Breiman, L., Friedman, J., Olshen, R., and Stone, C., Classification and Regression Trees, Belmont, CA:Wadsworth, 1984.)] 에 의해 독자적으로 제안되기도 했다.

이 책에서는 다른 여러 기계 학습 방법을 보여줄 것이다. 그렇지만 여기서는 그 주제에 대한 정보를 얻기 위한 소스를 일단 몇가지 공급하고자 한다. 주요 연례 학회로서는 Inter-national Conference on Machine Learning (ICML) 이 있는데 발표 논문집 또한 발행된다. 계산 학습 이론에 관한 논문은 Workshops on Computational Learning Theory (COLT) 의 논문집에서 볼 수 있다. 주요 저널로는 Machine Learning 이 있고, 중요한 교재로서는 [Mitchell, T. 1997 (Mitchell, T., {Machine Learning}, New York: McGraw-Hill, 1997.), Langley 1996 (Langley, P., Elements of Machine Learning, San Francisco: Morgan Kaufmann, 1996.), Weiss & Kulikowski 1991 (Weiss, S., and Kulikowski, C., Computer Systems That Learn, San Francisco: Morgan Kaufmann, 1991.)] 등이 있다. [Fu 1994 (Fu, L. M., Neural Networks in Computer Intelligence, New York: McGraw-Hill, 1994.), Haykin 1994 (Haykin, S., Neural Networks: A Comprehensive Foundation, New York: Macmillan College Publishing, 1994.), Hertz, Krogh, Palmer 1991 (Hertz, J., Krogh, A., and Palmer, R., Introduction to the Theory of Neural Computation, Reading, MA: Addison-Wesley, 1991.)] 등도 신경망에 있어 좋은 책이다. [Shavlik & Dietterich 1990 (Shavlik, J., and Dietterich, T. (eds.), Readings in Machine Learning, San Francisco: Morgan Kaufmann, 1990.)] 은 논문 모음집이고, [Dietterich 1990 (Dietterich, T., "Machine Learning," in Traub, J., et al. (eds.), Annual Review of Computer Science, 4:255-306, 1990.)] 은 기계 학습 분야의 훌륭한 자료를 제공해 준다.