
계획수립
(Planning)
인공지능-지능형 에이전트를 중심으로 : Nils J.Nilsson 저서, 최중민. 김준태. 심광섭. 장병탁 공역, 사이텍미디어, 2000 (원서 : Artificial Intelligence : A New Synthesis 1998), Page 405~434
1. STRIPS 계획수립 시스템 (STRIPS Planning System)
(1) 상태와 목표의 기술 (Describing States and Goals)
(2) 순방향 탐색 방법 (Forward Search Methods)
(3) 재귀적 STRIPS (Recursive STRIPS)
(4) 실행시간 조건을 포함한 계획 (Plans with Run-Time Conditionals)
(5) 서스만 이상 (The Sussman Anomaly)
(6) 역방향 탐색 방법 (Backward Search Methods)
2. 계획공간과 부분 순서 계획수립 (Plan Spaces and Partial-Order Planning)
3. 계층적 계획수립 (Hierarchical Planning)
(2) 계층적 계획수립과 부분 순서 계획수립의 결합 (Combining Hierarchical and Partial-Order Planning)
5. 참고문헌 및 토론 (Additional Readings and Discussion)
프레임 문제를 해결하는 좋은 방법 중의 하나는 상태공간 접근 방법과 상황논리의 접근 방법을 혼합하는 것이다. 7 장에서 특징기반의 상태공간을 논의할 때 가정한 것처럼 이 혼합은 실세계 상태의 집합을 기술하는 술어논리의 식 자체가 상태의 일종이라는 가정을 한다. 예를 들어, 블록세계에서 그림 1 에 보인 것과 같이 블록 C 위에 블록 A 가 있고, 다시 그 위에 블록 B 가 놓여진 실세계 상태는 다음과 같이 기술된다.
On (B, A)
On
(A, C)
On (C, F1)
Clear (B)
Clear (F1)

그림 1 하나의 상태 기술
이 식은 실세계 상태의 한 집합을 기술하는데, 그 이유는 이 식이 의도하는 관계가 참인 모든 상태에 대해서 식이 만족되기 때문이다. 만일 다른 블록이 존재하고 그 블록이 가령 색깔과 같은 다른 특성을 가졌을 때는 상태를 기술할 때, 그 블록이 존재하고 블록이 색깔을 가지는 모든 상태를 포함해야 할 것이다.
이 장에서 앞으로 논의하게 될 초기의 계획수립 방법에서는 실세계 상태의 집합을 기술하는 식을 에이전트의 행동에 따라 변할 수 있는 자료 구조로 간주한다. 목표를 만족하는 실세계 상태의 집합을 기술하는 하나의 자료 구조를 찾기 위해, 이 자료 구조의 공간을 탐색하기 위한 방법을 기술할 것이다. 이 자료 구조에 대한 상태 공간 탐색을 할 경우, 이 자료 구조는 계획수립 과정의 상태가 된다. 계획수립과 정의 상태와 실세계 상태를 구별하기 위해 앞으로 전자를 상태 기술 (state description) 이라고 할 것이다.
관심을 둘 필요가 없는
몇몇 기술적인 어려움을 피하기 위해, 행동 전 상태 기술 (before-action state description)
과 행동 후 상태 기술 (after-action state description) 모두를 기초 리터럴 (ground
literal) 의 논리곱 (또는 집합) 으로 제한한다. 하지만 한 가지 예외가 허용되는데,
상태 기술이 모든 상태에서 참이 되는 임의의 식 (예를 들어, On (x, y) ⊃ (y =
F1) ∨ ¬Clear (y)) 을 포함할 수 있다는 것이다. 목표는 리터럴의 논리곱 (존재
한정사가 사용될 수 있음) 으로 제한한다. 앞으로 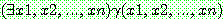 형태의 목표 wff 는 간단히
형태의 목표 wff 는 간단히 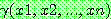 으로 쓰고 모든 변수는 존재 한정 (existential quantification) 이 되어 있다고
가정한다. 물론 여러 가지 방법을 이용해서 이러한 제한을 두지 않을 수도 있지만,
제한을 한다 하더라도 흥미로운 계획 수립 문제들을 얼마든지 해결할 수 있다.
으로 쓰고 모든 변수는 존재 한정 (existential quantification) 이 되어 있다고
가정한다. 물론 여러 가지 방법을 이용해서 이러한 제한을 두지 않을 수도 있지만,
제한을 한다 하더라도 흥미로운 계획 수립 문제들을 얼마든지 해결할 수 있다.
주어진 목표 wff 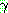 에 대한 탐색 방법에서는
에 대한 탐색 방법에서는  를 만족하는 상태 기술 로 표현되는 실세계 상태를 생성하는 일련의 행동을
갖고자 한다. 이때 상태 기술이 목표를 만족시킨다 (satisfy) 고 한다. 제한된 상태와
목표 wff 에 대하여
를 만족하는 상태 기술 로 표현되는 실세계 상태를 생성하는 일련의 행동을
갖고자 한다. 이때 상태 기술이 목표를 만족시킨다 (satisfy) 고 한다. 제한된 상태와
목표 wff 에 대하여  가 성립하는 경우는 치환 σ 가 존재하여
가 성립하는 경우는 치환 σ 가 존재하여  가
가 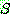 에 나타나는 모든 기초리터럴의 논리곱이 될 때이다.
에 나타나는 모든 기초리터럴의 논리곱이 될 때이다.  가 성립하는지 아닌지를 입증하려면 먼저
가 성립하는지 아닌지를 입증하려면 먼저 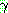 의 처음 리터럴을
의 처음 리터럴을 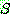 의 리터럴로 단일화 시키고 (unify), 여기서 생성돤 단일화 치환 (unifying
substitution) 을
의 리터럴로 단일화 시키고 (unify), 여기서 생성돤 단일화 치환 (unifying
substitution) 을 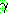 의 나머지 리터럴에 적용시킨 다음에 하면 된다 (이 과정은 PROLOG 해석기에
절 (cluse) 이 몸체 (body) 가 사실 (fact) 과 단일화될 수 있는지 거꾸로 목표에서
진행하는 순방향 탐색 (forward search) 거꾸로 목표에서 시작하여 초기 상태로 진행되는
역방향색 (backward search) 이 있다. 어떤 저자들은 순방향 탐색을 전진 계획수립
(progression planning) 이라 하고 역방향 탐색을 회귀계획 수립 (regression planning)
이라고 한다. 순방형 탐색에 대해서 먼저 논의하고자 한다.
의 나머지 리터럴에 적용시킨 다음에 하면 된다 (이 과정은 PROLOG 해석기에
절 (cluse) 이 몸체 (body) 가 사실 (fact) 과 단일화될 수 있는지 거꾸로 목표에서
진행하는 순방향 탐색 (forward search) 거꾸로 목표에서 시작하여 초기 상태로 진행되는
역방향색 (backward search) 이 있다. 어떤 저자들은 순방향 탐색을 전진 계획수립
(progression planning) 이라 하고 역방향 탐색을 회귀계획 수립 (regression planning)
이라고 한다. 순방형 탐색에 대해서 먼저 논의하고자 한다.
상태 기술의 공간에
대해서 순방향을 탐색을 하기 위해서는 행동에 상응하는 연산자 (operator) 가 필요한데
이 연산자는 행동 전 상태 기술을 행동 후 상태 기술로 바꾼다. 이 탐색은 목표 wff
인  에 대하여
에 대하여  를 만족하는 상태 기술
를 만족하는 상태 기술  를 생성하면 성공적으로 끝나게 된다. 이 연산자들은 (STRIPS [Fikes &
Nilsson 1971, Kikes, Hart & Nilsson 1972] 라 불리는 시스템의 연산자에 기반을
둔다. STRIPS 연산자는 다음과 같이 세 부분으로 구성된다.
를 생성하면 성공적으로 끝나게 된다. 이 연산자들은 (STRIPS [Fikes &
Nilsson 1971, Kikes, Hart & Nilsson 1972] 라 불리는 시스템의 연산자에 기반을
둔다. STRIPS 연산자는 다음과 같이 세 부분으로 구성된다.
1. 연산자의 전제조건 (precondition) 으로 불리는 기초 리터럴의 집합 PC. 연산자에 대응되는 행동은 PC 에 있는 모든 리터럴이 행동 전 상태 기술에도 있는 그런 상태에서만 수행될 수 있다.
2. 삭제 리스트 (delete list) 라 불리는 기초 리터럴의 집합 D.
3. 추가 리스트 (add list) 라 불리는 기초 리터럴의 집합 A.
행동 후 상태 기술을 생성하기 위해서는 먼저 행동 전 상태 기술에서 D 에 있는 리터럴을 제거하고 A 에 있는 리터럴을 추가한다. D 에서 언급되지 않은 모든 리터럴은 행동 후 상태 기술로 이월된다. 이 이월 (carryover) 을 STRIPS 가정 (STRIPS assumption) 이라고 부르며 프레임 문제를 해결하는 한 가지 방법이 된다.
STRIPS 연산자는 대개 행동 스키마에 대응되는 스키마에 의해 정의된다. STRIPS 규칙 (STRIPS rule) 이라 불리는 연산자 스키마는 자유변수를 가지며, 이 규칙의 기초 사례 (ground instance) 가 실제 연산자에 대응된다. 자유변수 x, y, z 를 가지는 STRIPS 규칙의 한 예를 들면 다음과 같다.
move (x, y, z)
PC
: On (x, y) ∧ Clear (x) ∧ Clear (z)
D : Clear (z), On (x, y)
A :
On (x, z), Clear (y), Clear (F1)
(여기서 Clear (F1) 의 식을 추가 리스트에 명시적으로 포함시켰는데, 이것은 만일 z 가 F1 이라면 Clear (F1) 이 삭제되므로 Clear (F1) 이 항상 참이려면 그것이 추가 리스트에 있어야 하기 때문이다). 블록 B 를 블록 A 에서 바닥 (floor) 으로 옮기는 행동에 대한 이 STRIPS 규칙의 한 사례를 그림 2 에서 보여주고 있다.
STRIPS 규칙 자체의
전제조건은 목표를 표현하는 형태, 즉 리터럴의 논리곱은 형태를 가진다는 것에 유의할
필요가 있다. PC 가 목표 wff 로 해석될 때, PC 에 있는 자유변수는 존재 한정되어
있다고 가정한다. PC 의 한 기초 사례 (목표로 간주되는) 가 어떤 상태 기술에 의해
만족된다면 STRIPS 규칙의 한 사례를 그 상태 기술 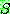 에 적용할 수 있다. 전에 언급한대로, 이러한 사례는 PC 에 있는 각 리터럴을
상태기술에 있는 리터럴과 차례대로 단일화시켜 얻을 수 있는데, 이때 단일화 치환을
PC 의 나머지 리터럴에 적용시킨다. 그리고 나서, 적용 가능한 연산자 사례 (applicable
operator instance) 는 위 과정의 결과로 얻어진 치환을 STRIPS 규칙의 모든 요소에
적용하여 얻을 수 있다. 규칙은 이러한 치환을 적용하여 그 결과가 항상 그 규칙의
기초 사례가 되도록 작성되어야 한다. 즉, D 나 A 에는 PC 에 나타나지 않는 자유변수가
있을 수 없다. 그림 2 에서 STRIPS 연산자의 적용을 설명하고 있다.
에 적용할 수 있다. 전에 언급한대로, 이러한 사례는 PC 에 있는 각 리터럴을
상태기술에 있는 리터럴과 차례대로 단일화시켜 얻을 수 있는데, 이때 단일화 치환을
PC 의 나머지 리터럴에 적용시킨다. 그리고 나서, 적용 가능한 연산자 사례 (applicable
operator instance) 는 위 과정의 결과로 얻어진 치환을 STRIPS 규칙의 모든 요소에
적용하여 얻을 수 있다. 규칙은 이러한 치환을 적용하여 그 결과가 항상 그 규칙의
기초 사례가 되도록 작성되어야 한다. 즉, D 나 A 에는 PC 에 나타나지 않는 자유변수가
있을 수 없다. 그림 2 에서 STRIPS 연산자의 적용을 설명하고 있다.
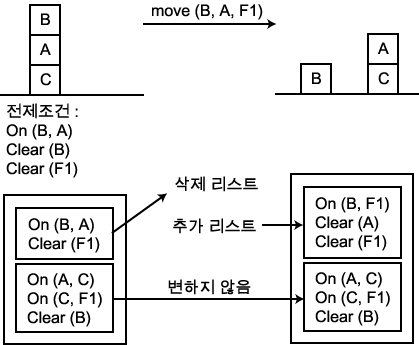
그림 2 STRIPS 연산자

그림 3 순방향 탐색
순방향 탐색 방법에서는
STRIPS 규칙의 사례를 목표 wff 를 만족시키는 상태 기술이 얻어질 때까지 적용하여
새로운 상태 기술을 생성한다. 그림 3 에 순방향 탐색에 의해 생성된 탐색 그래프의
일부를 나타내었다. 상태 기술에 있는 대부분의 리터럴은 STRIPS 연산자를 적용시켜도
변하지 않기 때문에 변화된 것만 추적한다면 순방향 탐색을 경제적으로 구현할 수
있다 (목표 상태까지의 비용을 추정하는 적절한 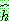 와 행동의 비용을 반영하는 적절한
와 행동의 비용을 반영하는 적절한 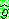 를 이용하여 A* 탐색을 사용할 수도 있다). 상황 논리와 비교하면
행동을 수행한 후에도 어떤 관계는 변하지 않는다는 것을 증명할 필요가 없다는 것에
유의해야 한다. STRIPS 가정이 이것을 처리해 준다.
를 이용하여 A* 탐색을 사용할 수도 있다). 상황 논리와 비교하면
행동을 수행한 후에도 어떤 관계는 변하지 않는다는 것을 증명할 필요가 없다는 것에
유의해야 한다. STRIPS 가정이 이것을 처리해 준다.
어떤 규칙의 어떤 사례를 적용해야 하는지에 대한 휴리스틱이 없다면 순방향 탐색은 상태 기술과 규칙의 숫자가 많은 실제 응용에서는 비현실적이다. 순방향 탐색을 좀더 효율적으로 만드는 한 가지 방법은 목표 상태 기술로 가는 탐색에 초점을 맞출 수 있는 탐색공간의 섬 (islands) 을 구별해내는 것이다. 다음 절에서 섬을 구별하고 활용하기 위한 방법을 기술한다.
우리가 여기서 가정하는 것과 같이 목표조건이 리터럴의 논리곱으로 구성되었을 때는 분할정복 (divide-and-conquer) 휴리스틱을 이용하여 순방향 탐색을 할 수 있다. 먼저, 논리곱 인자 (conjunct) 중의 하나를 해결하고, 그 다음에 다른 논리곱 인자를 하나씩 계속 해결한다. 논리곱 인자 중 하나가 만족된 상태 기술은 탐색공간의 하나의 섬 (island) 을 나타낸다. 우선적으로 이 섬의 방향으로 작업을 수행하는데, 대응되는 논리곱 인자가 만족되는 상태 기술을 생성하는 연산자를 적용시킨다. 그리고 나서, 또 다른 섬을 향해 작업을 수행하고, 이러한 과정을 계속한다. 물론 나중에 구한 논리곱 인자에 의해 전에 구한 논리곱 인자가 철회될 (disachieved) 수도 있다.
AI 역사에서 초기에
개발된 범용 문제 해결자 (General Problem Solver, GPS) 라 불리는 시스템 [Newell,
Shaw, & Simon 1959, Newell & Simon 1963] 에서 이러한 방법으로 탐색공간
섬을 활용하였다. 이 섬을 달성하는 연산자는 "수단 목표 분석" (means-ends
analysis) 이라 불리는 과정에 의해 식별된다. STRIPS 규칙을 이용해 계획수립 시스템에
적용되는 것과 같이 이 기법은 목표조건에 있는 논리곱 인자들의 한 사례를 선택하고,
또한 그것을 달성하게 될 STRIPS 규칙의 한 사례를 선택하게 된다. 그리고 나서,
그 규칙을 적용하는 데 필요한 전제조건을 부목표 (subgoal) 로 생성하고, 그 부목표가
만족될 때까지 같은 섬 식별 방법을 이용하여 재귀적으로 (recursively) 작업을 수행한다.
그리고 나서, 섬의 상태 기술을 생성하는 연산자를 적용시키고 또 다른 섬을 식별하고,
이런 식으로 계속 진행한다. 이 프로시저는 STRIPS 라 불리는 재귀적 프로그램의
기초가 된다. STRIPS 는 논리곱 목표식인 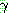 를 다음과 같이 해결한다.
를 다음과 같이 해결한다.
STRIPS (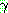 ). 이 프로시저는 기초 리터럴의 집합으로 구성된 전역 (global) 자료 구조인
). 이 프로시저는 기초 리터럴의 집합으로 구성된 전역 (global) 자료 구조인
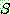 를 이용한다. 이 자료 구조는 초기 상태 기술로 초기화되고 프로시저에
의해, 그리고 프로시저 도중에 변경된다.
를 이용한다. 이 자료 구조는 초기 상태 기술로 초기화되고 프로시저에
의해, 그리고 프로시저 도중에 변경된다.
1.
repeat STRIPS 의 주루프는 목표 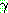 를 만족시키는 상태 기술이 생성될 때까지 반복된다. 9 번 단계의 종료 검사에
를 만족시키는 상태 기술이 생성될 때까지 반복된다. 9 번 단계의 종료 검사에
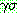 의 논리곱 인자 중 일부 (없을 수도 있음) 가
의 논리곱 인자 중 일부 (없을 수도 있음) 가 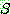 에 나타나는 치환
에 나타나는 치환 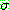 [공치환 (empty substitution) 일 수도 있음] 가 생성된다. 검사를 수행할 때
여러 치환을 시도할 수 있으며, 따라서 이 검사가 하나의 되추적점 (backtracking
point) 이 될 수 있다.
[공치환 (empty substitution) 일 수도 있음] 가 생성된다. 검사를 수행할 때
여러 치환을 시도할 수 있으며, 따라서 이 검사가 하나의 되추적점 (backtracking
point) 이 될 수 있다.
2.
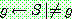 를 만족하는
를 만족하는 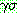 의 한 요소. 또 다른 선택이며 따라서 되추적점이 된다. "수단 목표 분석"
의 용어에 따르면
의 한 요소. 또 다른 선택이며 따라서 되추적점이 된다. "수단 목표 분석"
의 용어에 따르면 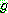 는 목표를 달성하기 위해 "줄여야" (reduce) 하는 차이 (difference)
로 간주된다.
는 목표를 달성하기 위해 "줄여야" (reduce) 하는 차이 (difference)
로 간주된다.
3.
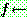 리터럴 λ 를 포함하는 추가 리스트를 가진 STRIPS 규칙. 이때 λ 는 mgu
리터럴 λ 를 포함하는 추가 리스트를 가진 STRIPS 규칙. 이때 λ 는 mgu 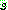 에 의해
에 의해 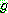 와 단일화된다. 이러한 규칙이 여러 개가 있을 수 있기 때문에 또 다른
되추적점이 된다.
와 단일화된다. 이러한 규칙이 여러 개가 있을 수 있기 때문에 또 다른
되추적점이 된다. 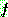 는 차이를 줄이는 데 연관 (relevant) 된 연산자이다.
는 차이를 줄이는 데 연관 (relevant) 된 연산자이다.
4.
 . 치환
. 치환 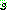 를 이용한
를 이용한 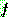 의 사례이다.
의 사례이다. 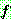 이 기초 사례일 필요는 없으며, 따라서 전제조건이 변수를 가질 수 있다.
이 기초 사례일 필요는 없으며, 따라서 전제조건이 변수를 가질 수 있다.
5.
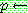 (치환
(치환 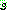 로 사례화된)
로 사례화된) 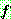 의 전제조건식.
의 전제조건식.
6.
STRIPS (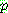 ). 부목표를 만족시키는 상태 기술을 생성하는 재귀 호출. 이 호출이 이루어지면
일반적으로
). 부목표를 만족시키는 상태 기술을 생성하는 재귀 호출. 이 호출이 이루어지면
일반적으로 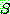 가 변경된다.
가 변경된다.
7.
 에서 적용시킬 수 있는
에서 적용시킬 수 있는 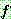 의 기초 사례.
의 기초 사례.
8.
 을
을 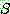 에 적용시킨 결과.
에 적용시킨 결과. 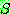 는 항상 기초리터럴의 논리곱으로 구성된다.
는 항상 기초리터럴의 논리곱으로 구성된다.
9.
until 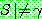 .
.
9 번 단계에서는 항상
전체 목표인 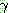 에 대하여 검사를 수행한다. 만일
에 대하여 검사를 수행한다. 만일 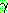 의 논리곱 인자 중 하나가 다른 논리곱 인자를 만족시키는 과정에서 철회되면,
이 과정이 종료되기 전에 첫째 인자를 다시 만족시켜야 하거나 첫째 인자가 철회되지
않는 다른 경로를 되추적해야 한다.
의 논리곱 인자 중 하나가 다른 논리곱 인자를 만족시키는 과정에서 철회되면,
이 과정이 종료되기 전에 첫째 인자를 다시 만족시켜야 하거나 첫째 인자가 철회되지
않는 다른 경로를 되추적해야 한다.
이 알고리즘 기술에서 명시적으로 언급하지는 않았지만 계획을 구성하는 일련의 목표 달성 연산자는 성공적으로 수행된 알고리즘을 추적 (trace) 하여 추출할 수 있다. 이들은 다시 에이전트가 수행할 수 있는 행동에 대응되는데, 단번에 (ballistically) 수행되거나, 감지/계획/행동 주기를 가지고 수행된다.
알고리즘이 어떻게
작동하는지를 다음 예제를 통해 설명하고자 한다. 가령 초기에 그림 1 에서 제시된
것과 같은 상황에 대해서 On(A, F1) ∧ On (B, F1) ∧ On (C, B) 의 목표를 달성하려
한다고 하자. 9 번 단계의 목표 검사에서는 어떤 논리곱 인자가 초기 상태 기술에
의해 만족되는지 알지 못한다. 가령 STRIPS 가 On (A, F1) 을 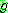 로 선택한다고 가정하자. 규칙 사례 move (A, x, F1) 이 추가 리스트에 On (A,
F1) 을 가지고 있으며, 따라서 규칙의 전제조건인 Clear (A) ∧ Clear (F1) ∧ On
(A, x) 를 달성하기 위해 STRIPS 를 재귀적으로 호출한다. 재귀적 호출의 9 번 단계의
검사에서 C/x 의 치환을 생성하는데, 이 치환은 Clear (A) 를 제외한 나머지 인자를
초기 상태에 대해 만족시킨다. 이 Clear (A) 리터럴이 선택되고, 규칙 사례 move
(y, A, u) 가 이것을 달성하기 위해 선택된다.
로 선택한다고 가정하자. 규칙 사례 move (A, x, F1) 이 추가 리스트에 On (A,
F1) 을 가지고 있으며, 따라서 규칙의 전제조건인 Clear (A) ∧ Clear (F1) ∧ On
(A, x) 를 달성하기 위해 STRIPS 를 재귀적으로 호출한다. 재귀적 호출의 9 번 단계의
검사에서 C/x 의 치환을 생성하는데, 이 치환은 Clear (A) 를 제외한 나머지 인자를
초기 상태에 대해 만족시킨다. 이 Clear (A) 리터럴이 선택되고, 규칙 사례 move
(y, A, u) 가 이것을 달성하기 위해 선택된다.
다시 이 규칙의 전제조건이 Clear (y) ∧ Clear (u) ∧ On (y, A) 를 달성하기 위해 STRIPS 를 재귀적으로 호출한다. 이 두번째 재귀 호출의 9 번 단계에서는 B/y, F1/u 의 치환을 생성하여 전제조건의 각 리터럴을 초기 상태에 나타나는 리터럴로 만들어 준다. 따라서 이 두번째 재귀적 호출에서 빠져나와서 move (B, A, F1) 의 연산자를 적용시켜 초기 상태를 다음으로 변경시킨다.
On (B, F1)
On
(A, C)
On (C, F1)
Clear (A)
Clear (B)
Clear (F1)
이제 첫번째 재귀 호출로 돌아가서 9 번 단계의 검사 (즉, Clear (A) ∧ Clear (F1) ∧ On (A, x)) 를 다시 수행한다. 이 검사는 C/x 의 치환에 따라 변경된 상태 기술에 의해 만족되며, 따라서 첫째 재귀 호출에서 빠져나와 move (A, C, F1) 연산자를 적용시켜 다음과 같은 세번째 상태 기술을 생성한다.
On (B, F1)
On
(A, F1)
On (C, F1)
Clear (A)
Clear (B)
Clear (C)
Clear (F1)
이제 다시 주프로그램의 9 번 단계의 검사를 수행한다. 원래 목표에서 새로운 상태 기술에 나타나지 않은 논리곱 인자는 On (C, B) 뿐이다. 주프로그램을 다시 재귀적으로 수행하면 move (C, F1, B) 의 전제조건은 이미 만족되었기 때문에 이것을 적용시켜 주목표를 만족시키는 상태 기술을 생성할 수 있고, 이제 모든 과정은 종료된다.
지각 과정 (perceptual process) 에 의한 계획 수행 동안에 상태 기술을 다듬을 수 있다면 상태 기술에서 허용하는 식의 종류를 약간 일반화할 수 있다. 상태 기술식에 리터럴의 논리합을 허용하면 어떻게 되는지 고려해 보자. 구체적으로 말하면, 가령 한 상태 기술이 On (B, A) ∨ On (B, C) 의 wff 를 가진다고 가정하자. 이 wff 는 B 가 A 위에 있거나 또한 B 가 C 위에 있다는 것을 의미하지만 시스템은 계획이 생성되는 시점에서는 둘 중 어느 것이 맞는지 알지 못한다. 이와 같은 상태 기술에 적용될 수 있는 STRIPS 연산자와 그 연산자의 결과는 On (B, A) 나 On (B, C) 중 어느 것이 만족되는지에 의존하지는 않는다. 이들 연산자에 대해서 상태 기술에 논리합이 있는 것은 문제가 되지 않으며, 이 논리합은 행동 후 상태 기술로 바로 전달된다.
하지만 어떤 연산자는 On (B, A) 나 On (B, C) 중의 하나를 전제조건으로 가질 수 있다. 이런 연산자에 대응하는 행동을 수행하기 위해서는 그 행동이 수행될 때 (즉, 실행시간에) 어떤 논리합 인자가 만족되는지를 시스템이 알아야 한다. 아마도 지각과정에서 이에 대한 결정을 할 수 있을 것이다. 만일 그렇다면, 연산자를 적용하는 시점에서 계획에 실행시간 조건 (run-time conditional) 을 삽입할 수 있다. 실행시간 조건 후의 계획을 세울 때는 계획수립 과정이 연산자 전제조건을 만족시킬 수 있는 논리합 인자의 수만큼의 가지 (branch) 로 쪼개진다. 각 가지는 별개의 상태 기술과 연산자를 가진다. 위의 예제에서 보면 한 가지에서는 추후의 행동이 수행되었을 때의 실세계에서 On (B, A) 가 참이 된다 (또는 참이 될 것이다) 고 가정하고, 다른 가지에서는 On (B, C) 가 참이 된다 (또는 참이 될 것이다) 고 가정한다. 각 가지는 문맥 (context) 이라 부른다. 계획수립시에는 문맥이 나뉘는 시점의 실세계 상태를 설명하는 상태기술이 어느 것인지 알지 못하지만 그들 중 하나인 것만은 명확하다. 각 문맥에 대해 별도의 계획이 생성된다. 그리고 나서, 실행시에 시스템이 둘 이상의 문맥으로 나뉘어지는 상황에 접했을 때는, 지각 과정에서 어느 논리합 인자가 참읹를 결정하고 수행은 적절한 경로를 따라 진행된다. 복잡한 문제에서는 여러 개의 분기 문맥이 있을 수 있다.
때로는 이전 행동의 결과에 따라 지각 과정에서 실세계의 어느 논리합 인자가 참인지를 필요할 때 결정할 수 있다. 더 일반적으로는 시스템이 정보수집 행동 (information-gathering action) 에 대응하는 연산자를 사용하여 그 정보를 얻기 위한 계획을 세워야 한다. 위의 예제에서 On (B, A) 나 On (B, C) 중 어느 것이 참인지 결정하기 위해서는 시스템이 블록 위의 글자를 읽을 수 있는 행동을 수행해야 할 것이다. 이 행동은 STRIPS 연산자에 의해 기술될 수 있는데 이 연산자의 결과는 "know-which" 를 명시하는 정형적 방법을 포함한다. 실행시간 조건은 이제 이 know which 를 전제조건으로 가지게 된다.
그림 4 에 있는 블록세계 문제에 대해 재귀적 STRIPS 를 적용해 보자. 목표조건은 On (A, B) ∧ On (B, C) 이다. STRIPS 는 두 논리곱 인자 중 하나를 먼저 만족시켜야 한다. 만일 On (A, B) 가 선택되었다고 하자. 먼저 C 를 A 에서 분리시켜 바닥에 놓는다. 그리고 나서 A 를 B 위로 옮긴다. 하지만 다른 논리곱 인자인 On (B, C) 를 만족시키기는 과정에서 On (A, B) 를 원상태로 되돌리기 (undo) 때문에 이를 다시 만족시켜야 한다. 만일 On (B, C) 가 먼저 선택되었다고 하자. 이 경우는 B 를 C 위로 옮기면 되지만 다른 논리곱 인자인 On (A, B) 를 만족시키는 과정에서 On (B, C) 를 원상태로 되돌리게 되고 따라서 다시 만족시켜야 한다. 따라서, 어느 것을 먼저 선택한다고 해도 연산자의 수를 최소로 가지는 계획을 만들지 못한다. 이러한 특별한 블록 세계 문제를 제안한 사람의 이름을 따서 서스만 이상 (Sussman anomaly) 이라고 한다 [Sussman 1975].
이 문제를 재귀적 STRIPS 로 풀기 어려운 이유는 깊이우선 (depth-first) 탐색 방법처럼 한번에 하나의 논리곱 인자에만 집중하기 때문이다. 만일 순방향 탐색이 너비우선 (breadth-first) 전략을 사용한다면 최단의 계획을 찾을 수 있다. 하지만 앞에서 지적한 바와 같이 너비우선 순방향 탐색은 실제 상황에서는 매우 많은 계산을 요구하기 때문에 실행 불가능하다.
하나의 대안으로는 너비우선과 역방향 탐색을 시도해 보는 것이다. 이 방법은 계산상으로 순방향 탐색에 비해 효율적인데 왜냐하면 일반적으로 초기 상태 기술에 있는 기초 리터럴의 수보다 목표 wff 에 있는 논리곱 인자의 수가 적기 때문이다. 다음 절에서 역방향 탐색에 대해 다루고자 한다.

그림 4 서스만 이상
STRIPS 규칙을 이용하여
목표 상태로부터 역방향 탐색을 할 수 있다. 이를 위해서는 STRIPS 규칙을 통해 목표
wff 를 회귀시켜 (regress) 부목표 (subgoal) wff 를 생성해야 한다. STRIPS 규칙
α 를 통한 식 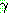 의 회귀 (regression) 는 다음을 만족시키는 가장 약한 식 (weakest formula)
의 회귀 (regression) 는 다음을 만족시키는 가장 약한 식 (weakest formula)
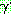 이 된다. 즉, 만일
이 된다. 즉, 만일 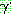 이 α 의 사례를 적용시키기 전에 어떤 상태 기술에 의해 만족되면 (또한
이 α 의 사례를 적용시키기 전에 어떤 상태 기술에 의해 만족되면 (또한 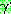 이 α 의 사례의 전제조건을 만족시키면),
이 α 의 사례의 전제조건을 만족시키면), 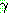 는 α 의 사례를 적용시킨 후에도 그 상태 기술에 의해 만족된다 (
는 α 의 사례를 적용시킨 후에도 그 상태 기술에 의해 만족된다 ( 일 경우
일 경우  이
이  보다 더 약하다고 한다. 예를 들어 P ∨ Q 는 P 보다 약하고, P 는 P∧ Q 보다
약하다).
보다 더 약하다고 한다. 예를 들어 P ∨ Q 는 P 보다 약하고, P 는 P∧ Q 보다
약하다).

그림 5 STRIPS 연산자를 통한 논리곱의 회귀
회귀 계산은 기초 리터럴의 논리곱으로 된 목표에서 출발하여 STRIPS 연산자 (STRIPS 규칙의 기초 사례) 를 통해서만 회귀하게 된다면 매우 간단하다. 이 경우 모든 회귀도 기초 리터럴의 논리곱이 된다. 그림 5 는 목표 기술로부터 역방향 탐색을 이용하는 한 예를 보여주고 있다. 여기서의 문제는 B 가 A 위에 있고, A 가 C 위에, C 가 바닥 위에 있는 상태로부터 A 가 B 위에, B 가 C 위에, C 가 바닥 위에 있는 상태를 달성하는 것이다. 이 문제에서는 목표에 있는 논리곱 인자 중 하나를 달성하는 임의의 연산자를 통하여 목표조건인 On (C, F1) ∧ On (B, C) ∧ On (A, B) 를 회귀시키게 된다. 부목표 wff 를 생성하기 위해 move (A, F1, B) 를 통해 회귀한다고 하자. 이 연산자는 논리곱 인자 중 하나인 On (A, B) 를 달성하므로 On (A, B) 는 부목표에 포함될 필요가 없다. 하지만 목표 기술에 있지 않은 이 연산자의 모든 전제조건은 부목표에 포함되어야 한다. 이 경우 Clear (B), Clear (A), On (A, F1) 이 여기에 해당된다. 목표 wff 에 있는 다른 두 논리곱 인자, 즉 On (C, F1) 과 On (B, C) 는 이 연산자에 의해 추가되거나 삭제되지 않으므로 단순히 이 연산자를 통과하여 부목표에 나타나게 된다. 그림 5 에 나타난 것처럼 역방향 탐색의 또 다른 대안은 move (B, F1, C) 를 통해 목표 wff 를 회귀시키는 것이다. 역방향 탐색은 (A* 와 비슷한 방법을 이용하여) 현재의 상태 기술에 의해 만족되는 부목표가 생성될 때까지 진행된다.
만일 어떤 리터럴의 집합이, 삭제 리스트에 그 리터럴 중 하나가 포함된 연산자에 의해 회귀된다면 어떤 현상이 발생할지 알아보는 것도 흥미로울 것이다. 리터럴 λ 가 어떤 연산자에 의해 삭제된다면 이 연산자가 그 리터럴을 만족시킬 방법이 없다. 따라서 λ 를 삭제하는 연산자를 통해 λ 를 포함하는 임의의 논리곱을 회귀시킨 결과는 항상 F 가 된다. 물론, F 는 만족시키기가 불가능하기 때문에 검색을 할 때 F 를 포함하는 상태 기술로부터 역방향으로 시도할 필요는 없다.
완전히 사례화되지 않은 규칙, 즉, 스키마변수를 아직도 포함하는 규칙을 통해 목표를 회귀시키는 것이 때로는 현명할 수 있다. 그림 5 에서 On (A, B) 를 달성하는 한 가지 방법으로 move (A, F1 B) 를 이용하였다. 왜 A 를 바닥으로부터 옮기도록 결정하였는가? A 를 어떻게든 다른 곳으로부터 옮겨와야 하는 것은 맞지만 왜 하필이면 바닥으로부터 옮기도록 했어야 하는가? 아마도 다른 곳으로부터 옮기는 더 좋은 계획이 있을 수도 있다. 이에 대한 결정을 미루는 한 가지 방법은 이동 연산자의 "from place" 부분을 임시로 지정하지 않은 채로 남겨두는 것이다. 이런 방법은 최소 개입 계획수립 (least commitment planning) 의 한 사례가 된다. 일부만 사례화된 (partially instantiated) 연산자 move (A, x, B) 를 통해 목표를 회귀시켜 "from place" 부분을 지정하지 않고 남겨둔다. 그림 6 에서 이 회귀의 결과를 보여주고 있다. 이 결과는 이전의 것과 거의 같은데 한 가지 다른 것은 전제조건의 하나인 On (A, x) 가 변수를 포함하고 있다는 것이다. 부목표로 해석되는 이 리터럴은 상태기술의 기초 리터럴과 단일화시켜 만족될 수 있다. 변수를 포함하는 부목표의 공간에 대해 역방향 탐색을 하려면, 변수를 다른 변수나 상수로 사례화시키는 추가 연산자를 허용해야 한다. 이를 위한 하나의 휴리스틱으로는 변수를 포함하는 리터럴이 초기 상태 기술에 있는 리터럴과 단일화될 수 있을 때까지 사례화를 미루는 것이다.

그림 6 하나의 변수를 포함하는 STRIPS 규칙을 통한 논리곱의 회귀

그림 7 역방향 탐색
때로 변수에 제약조건을 부여하기 위해 여러 추론 과정이 사용될 수 있다. 그림 6 에서 설명된 예제에서는 A 가 옮기고자 하는 블록이므로 On (A, x) 의 변수가 x 가 A 와 같을 수 없다. x 가 C 가 될 수도 없는데 그 이유는 A 를 다른 곳에서 B 로 옮기는 것이기 때문이다. 또한 x 가 C 가 될 수도 없는데 그 이유는 약간 미묘하다. 만일 x 가 C 라면 부목표의 논리곱인자 중 하나가 On (A, C) 가 될 것이다. 하지만 블록 B 와 블록 A 가 동시에 C 위에 있을 수 없기 때문에 이 경우 목표에 있는 On (B, C) 를 부목표의 On (B, C) 로 회귀시킬 수 없다 (STRIPS 의 재귀적 호출에 이용된 부목표는 회귀에 의해 생성된 부목표와는 다르다는 것에 유의하라).
완전히 사례화되지 않은 STRIPS 규칙을 통해서 목표와 부목표를 회귀시키는 전체 프로시저는 복잡하며 [Nilsson 1980, pp.288ff] 에 조금 더 상세히 설명되어 있다. 역방향 탐색에 대한 간단한 예제를 그림 7 에서 보여주고 있다. 이 경우 변수들이 F1 로 사례화되었는데 이것은 변수들의 제약조건을 보면 다른 값으로 사례화될 수 있는 가능성이 없기 때문이다. 초기 상태 기술에 의해 만족되는 부목표가 생성되면 탐색이 종료된다. 그리고 나서, 주목표를 초기 상태에 의해 만족되는 부목표와 연결시키는 일련의 규칙이 모두 읽혀지고, 탐색 과정에서 발견된 사례화를 수행함으로써 목표를 달성하는 계획의 연산자로 사례화된다. 더 복잡한 예제는 [Nilsson 1980, pp.292-296] 에 나와 있다.
회귀를 이용한 역방향 탐색은 순방향 탐색보다 더 효율적이지만 변수가 나타나기 때문에 더 복잡하다. 소규모의 간단한 블록세계 문제에서는 큰 어려움 없이 변수를 사례화할 수 있지만, 훨씬 더 큰 규모의 복잡한 문제에서 이 방법이 도메인 한정적인 휴리스틱을 사용하지 않고도 계산상으로 수행 가능한지는 의심스럽다.
너비우선의 순방향 또는 역방향 탐색에서는 목표의 논리곱 인자를 만족시킬 때 특별한 순서를 두지 않는다. 서스만 이상은 각 논리곱 인자를 해결하는 데 필요한 단계를 교차배치 (interleave) 하는 것이 최선책인 문제의 한 예제이다. 최종 계획에서의 단계들의 순서에 대한 결정을 미루는 것은 최소 개입 계획수립의 또 다른 사례이며, 식의 공간을 탐색하기보다는 계획의 공간을 탐색하는 것이 최선책일 수 있다. 계획 공간에서는 계획의 단계들이 부분 순서적 (partially ordered) 일 수 있다. 이 계획수립 전략을 부분 순서 계획수립 (partial-order planning, POP) 이라고 하며 다음 절에서 다루게 된다 (부분 순서적인 단계를 가진 계획을 비선형 계획 (nonlinear plan) 이라고도 한다).

그림 8 상태공간 탐색과 계획공간 탐색의 대비
계획 생성을 위한 두 가지 서로 다른 접근 방법이 그림 8 에 설명되어 있다. 식의 공간을 탐색 (순방향) 할 때는 STRIPS 규칙이 식의 집합에 적용되어 식의 후속자 (successor) 집합을 생성하고, 이 과정은 목표식을 만족시키는 상태 기술이 생성될 때까지 계속된다. 하지만 계획의 공간을 탐색할 때는 후속자 연산자가 STRIPS 규칙이 아니고, 불완전하고 사례화되지 않은 또는 불충분한 계획을 좀더 명확한 계획으로 변환시키는 연산자가 되며, 초기 상태 기술을 목표조건을 만족시키는 상태 기술로 바꾸어주는 수행 가능한 계획이 생성될 때까지 탐색이 계속된다. 계획공간 탐색의 연산자들은 계획을 다른 계획으로 변환시키기 위해 다양한 수단을 이용한다. 이러한 수단에는 (a) 계획에 단계를 추가, (b) 계획에 이미 포함된 단계를 재배치, (c) 완전 순서화된 계획을 부분적으로 순서화된 계획으로 변환, (d) 계획 스키마 (사례화되지 않은 변수 포함) 를 그 스키마의 사례로 변환하는 것 등을 포함한다. 이런 계획 변환 연산자의 일부에 대한 예가 그림 9 에 나타나 있다.

그림 9 계획변환 연산자
계획공간 탐색 방법을 서스만 이상 (그림 4) 에 적용시켜 설명해 보자. 여기서는 체계적, 비선형적 계획수립 (systematic, nonlinear planning, SNLP) 기법 [McAllester & Rosenblitt 1991] 과 NONLIN [Tate 1977] 에 기초하여 설명하고자 한다. 계획의 기본 구성요소는 STRIPS 규칙이다. 이 규칙은 두 가지 유형의 노드를 가진 그래프 구조로 표현되는데, 타원형 노드는 STRIPS 규칙의 이름으로 표식 (label) 이 붙고, 상자형 노드는 이 규칙의 전제조건과 결과 리터럴로 표식이 붙는다. 이러한 그래프 구조가 그림 10 에 나타나 있다. 그래프의 윗부분에 있는 상자는 결과이고, 아래에 있는 상자는 전제조건이다.

그림 10 STRIPS 규칙의 그래프 표현
목표 wff 와 초기 상태의 리터럴은 finish 와 start 로 불리는 가상의 규칙 그래프로 표현된다. finish 규칙의 전제 조건은 전체 목표이고 결과는 Nil 이 된다. start 연산자의 결과는 초기 상태 기술에 있는 모든 리터럴이고, 전제조건은 T 이다. 서스만 이상에 대한 이 두 그래프를 그림 11 에서 설명하였다.
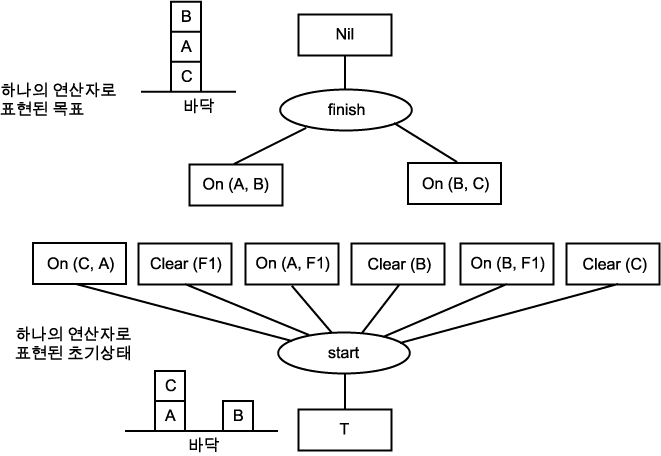
그림 11 finish 와 start 규칙의 그래프 표현
초기 계획 구조 (어떤 계획 변환 연산자도 적용시키지 않은) 는 그림 11 에서 보여준 것과 같은 (연결되지 않은) start 와 finish 규칙으로만 구성된다. 물론 이것은 매우 불완전한 것이다 (계획이 완전하다는 것이 무엇을 의미하는지는 나중에 정의하고자 한다).
이제 계획의 탐색은 계획변환 연산자들 중 하나를 초기 계획 구조에 적용시키는 것으로부터 시작한다. 이 단계에서 채택될 수 있는 변환 중 하나는 초기 계획 구조에 목표의 논리곱 인자 중 하나를 만족시킬 수 있는 규칙을 추가하여 확장하는 것이다. 가령 규칙 사례 move (A, y, B) 를 추가하여 On (A, B) 를 만족시키기로 하자. 이 사례에 대한 그래프 구조를 초기 계획 구조에 추가한다. 이 규칙을 추가하면 On (A, B) 가 달성될 수 있을 것이라고 판단했기 때문에 규칙의 결과 상자를 finish 규칙의 전제 조건 상자에 연결시킨다. 이 결과가 그림 12 에 나타나 있다. 여기서 블록 A 가 어디로부터 옮겨지는지에 대한 언급은 아직 하지 않았다는 것에 유의하라.

그림 12 초기 상태의 다음 단계의 계획 구조
이 단계에서 여러 계획 변환이 가능하다. Clear (B) 를 연결시킬 수도 있다. 또는 move (A, y, B) 의 전제조건인 Clear (A) 를 만족시키도록 시도할 수 있다. 이 조건은 A 위에 있는 어떤 물체 (u 의 사례) 를 다른 곳 (v 의 사례) 으로 옮기는 규칙 사례 move (u, A, v) 를 삽입하여 만족시킬 수 있다. 그리고 나서 u 를 C 로, 그리고 v 를 F1 으로 사례화시켜 초기 상태에 있는 식에 대한 연결을 확립할 수 있다. 이러한 일련의 계획 변환 (plan-alteration) 단계의 결과로 그림 13 에 나타난 것과 같은 계획 구조를 생성할 수 있다.

그림 13 중간 단계의 계획 구조
이 단계에서 알 수 있는 것은, 두 move 연산자의 전제조건들이 그 연산자가 적용될 때 만족된다는 것이다. 아직 불완전한 계획을 표현하는 그래프 구조에 있는 두 move 연산자에는 내재된 순서가 있다. 이후에 계획 과정을 기술할 때는 move 연산자의 이 두 경우를 인용하려고 한다. 이러한 이유로 그림 13 에 이 둘에 대해 a 와 b 의 표식을 붙였다. b 가 a 보다 먼저 와야 한다는 사실은 b < a 라는 표기법에 의해 명확하게 표현하는데 여기서 < 는 이전 (before) 을 나타낸다. 이때 On (C, F1) 과 Clear (F1) 의 두 상자는 move 연산자의 생산품 (product) 이지만 이후에 다른 연산자에 의해 소비되지 (consumed) 않는다는 것에 주의하라. 이들은 계획의 나중 단계에서 반드시 참이 되어야 하는 조건에 모순되지 않는 한 계획에는 아무런 해를 끼치지 않는다.
다음으로 다른 주목표 논리곱 인자인 On (B, C) 를 어떻게 만족시켜야 할지를 고려해 보자. 이 조건은 B 를 어딘가로부터 C 위로 옮기는 규칙 사례인 move (B, z, C) 에 의해 달성될 수 있다. 따라서 이 단계를 계획 구조내에 추가하면 된다. 그 후 z 를 F1 로 사례화하여 초기 조건과 연결시킬 수 있다. 결과적으로 그림 14 와 같은 계획 구조가 나타난다.

그림 14 후반 단계의 계획 구조
이제 연산자 a, b, c 를 포함하는 계획 구조를 갖게 되는데, 이들 연산자는 부분적으로만 순서가 매겨져 있다 (only partially ordered). 지금까지는 계획 단계의 순서에서 c 가 어디에 와야 하는지에 대해서 아무런 언급을 하지 않았다. 부분 순서 계획에서는 한 연산자가 잘못하여 적절하지 않을 때 수행되어 다른 연산자가 필요로 하는 전제조건을 원사태로 되돌릴 수 있기 때문에 이때 발생하는 문제를 고려해야 한다. 이런 가능성은 계획 구조 그래프에서 위협 아크 (threat arc) 로 나타낸다. 그림 15 에 있는 그래프 구조를 고려해 보자. 굵은 회색 화살표가 위협 아크이다. 위협 아크는 연산자 (타원형) 노드에서부터 (a) 그 연산자의 삭제 리스트에 있고, (b) 그 연산자 노드의 후손이 아닌 전제조건 (상자) 노드에게로 화살표가 그려진다. 그림 15 에서 보면, 연산자 move (A, F1, B) 는 move (B, F1, C) 의 전제조건인 Clear (B) 를 삭제한다. 이런 면에서 move (A, F1, B) 는 move (B, F1, C) 를 위협한다고 보는데, 왜냐하면 앞 연산자가 먼저 수행되면 뒤 연산자를 수행할 수 없기 때문이다. 위협 아크는 연산자의 순서에 대해 제약 사항을 줌으로써 제거되어야 (discharged) 한다. 하나의 계획은 모든 위협 아크를 제거하는 일관된 순서 제약 집합을 찾을 수 있을 때까지는 완성된 것이 아니다. 위의 예제에서 이러한 일관된 순서 제약의 집합은 (c < a, b < c) 이다. 물론 그래프 구조 자체가 (b < a) 라는 제약을 암시하고 있으며, 이것은 다른 모든 순서 제약과 일관된다. 따라서 그림 15 의 계획 구조는 (b < c < a) 의 전체 순서 (total order) 를 구성한다. 이 계획은 모든 위협 아크가 제거되고 연산자 (finish 연산자를 포함하는) 들이 요구하는 모든 전제 조건이 그 연산자가 적용될 때 만족되기 때문에 완전하다. 따라서 최종 계획은 {move (C, A, F1), move (B, F1, C), move (A, F1, B)} 가 된다.

그림 15 위협 아크 추가
이미 10 장에서 계층적 탐색 프로시저에 대해 언급하였다. 여러 연구원들이 STRIPS 규칙에 기반을 둔 계층적 계획자를 개발하였다. 이 중 하나인 ABSTRIPS 시스템 [Sacerdoti 1974] 은 STRIPS 규칙의 전제조건에 있는 각 논리곱 인자에 한계값 (criticality number) 을 부여한다. 달성하기가 쉬울수록 그 논리곱 인자의 한계값은 내려간다. ABSTRIPS 에서는 이 한계값을 사용해서 다음과 같이 단계적으로 계획을 수립한다.
1. 한계의 모든 전제조건이 어떤 임계갑 (threshold value) 이하인 것은 참이라고 가정하고 이 가정에 기반을 두고 계획을 수립한다. 근본적으로 가장 달성하기 어려운 논리곱 인자를 제외한 다른 모든 논리곱 인자의 달성은 미루어진다.
2. 한계 임계값 (criticality threshold) 을 1 만큼 낮추고, 단계 1 에서 개발한 계획을 안내자로 삼아 임계값보다 작은 한계의 전제조건은 참이라고 가정하는 계획을 개발한다.
3. 이런 식으로 계속한다.
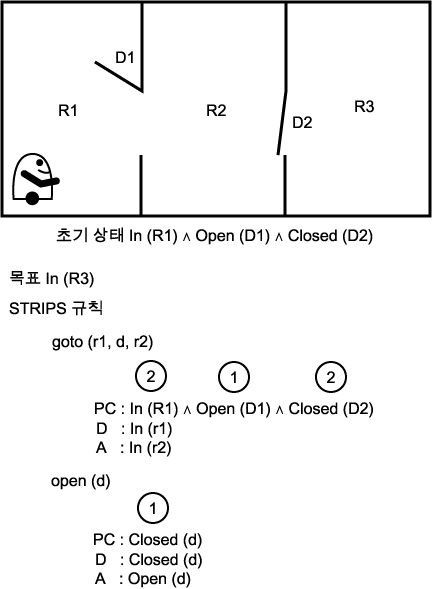
그림 16 ABSTRIPS 를 위한 계획수립 문제
ABSTRIPS 의 아이디어를 예제를 하나 들어 설명하고자 한다. 이번에는 한 방에서 다른 방으로 이동하는 로봇을 이용한다. 그림 16 에 초기 상황과 목표, 규칙이 정의되어 있다. goto (r1, d, r2) 규칙은 로봇을 방 r1 에서 방 r2 로 문 d 를 통과해서 움직이게 하는 행동 스키마를 모델링한다. open (d) 규칙은 문 d 를 여는 것이다. 한계값은 이 규칙들의 전제조건에 있는 해당 리터럴 위에 원으로 나타낸다. 특히 문을 여는 것이 문을 통과하는 것에 비해 상대적으로 쉽다고 가정하면, open (d) 가 1 의 한계값을 갖는다.
먼저, 추상 계획 (이제까지 논의된 계획수립 방법 중 하나를 사용하는) 을 구축한다. 이때 한계값이 1 인 모든 전제조건은 이미 만족되었다고 가정한다. 이 추상 단계에서 In (R3) 를 달성하는 계획은 {goto (R1, D1, R2), goto (R2, D2, R3)} 이다. 다음으로 추상 계획에 있는 첫번째 연산자의 전제조건을 달성하기 위한 좀더 자세한 계획을 구축하고, 이 연산자를 적용하여 추상 계획의 두번째 연산자의 전제조건을 달성하고, 이런 식으로 계속 진행한다. 이 연산자들의 전제조건은 탐색공간에 있는 섬으로 간주할 수 있는데, 이 섬들은 첫번째 단계인 추상적 계획수립 과정에서 발견된다. 하지만 이 전제조건을 만족시킬 때 한계 임계값을 1 만큼 낮추어서 한계값이 1 인 모든 전제조건도 만족되도록 한다. 결과적으로 {goto (R1, D1, R2), open (D2), goto (R2, D2, R3) 의 계획이 생성된다. 일반적으로 두 개 이상의 한계값을 가질 수도 있는데, 이때에는 계획수립 과정이 여러 추상 단계를 거쳐 내려가게 된다.
ABSTRIPS 에서 사용되는 계획개발 과정 (plan-development process) 은 길이우선 (length first) 이다. 즉, 각 추상 단계에서 먼저 완전한 계획을 개발하고 나서, 아래의 더 상세한 단계로 내려가서 그곳에서의 완전한 계획을 개발하는 것이다. 이 길이우선의 계획 개발에 대한 대안도 있다. 예를 들어, 탐색공간에 있는 일련의 섬을 식별하기 위해서는 최상위 단계에서 완전한 계획을 개발할 수도 있다. 이러한 섬은 첫째 단계의 여러 연산자의 전제 조건일 수 있다. 그리고 나서, 다음 단계에서 첫째 섬에 대해서만 완전한 계획의 첫 부분을 개발할 수 있다. 이런 과정은 가장 낮은 단계에 있는 첫째 섬에 대한 완전한 계획이 만들어질 때까지 계속된다. 여기서 가장 상세한 단계에서는 계획의 첫째 연산자가 초기 상태에서 수행될 수 있는 행동에 대응된다고 가정한다. 이러한 깊이우선 (depth first) 의 계획수립 과정은 감지/계획/행동 주기 (sense/plan/act cycle) 를 이용하는 상황에 적합하다. 처음 행동을 수행하여 결과로 나타나는 상태를 인식한 후 계획재수립 (replanning) 에 의해 과정을 반복하는데, 이때 이전 계획의 좀 더 추상적인 단계를 안내자로 이용하게 된다.
계층적 계획수립 (hierarchical planning) 은 9 장에서 기술한 기법, 즉 실제 문제에서 사용되는 휴리스틱 함수의 값을 얻기 위해서는 그 문제에 대한 단순화되고 완화된 버전을 먼저 해결한다는 기법의 한 사례이다. 추상적 계획수립 과정의 각 단계는 그 아래 단계의 단순화된 버전으로 간주될 수 있다 ([Pearl 1984, p.131-132] 에서 Pearl 은 자신이 제안한 단순화 모델과 ABSTRIPS 간의 관계를 언급하고 있다).
NOAH, SIPE, O-PLAN [Sacerdoti 1977, Wilkins 1988, Currie & Tate 1991] 과 같은 계획수립 시스템은 부분 순서 계획공간 계획수립을 계층적 계획수립과 결합하고 있다. 이 시스템들은 이미 언급한 계획공간 연산자 (변수의 사례화, STRIPS 규칙의 추가 등등) 외에도 추상 계획을 상세 정도의 아래 단계에 있는 계획과 서로 연결시키는 연산자를 포함한다. 이 접합 (articulation) 은 앞에서 고려한 계획공간 연산자에 비유될 수 있다. 예를 들어, 블록세계에서 사용된 move 규칙은 pickup 과 putdown 와 같은 좀 더 원시적인 규칙의 연속으로 구성될 수 있다. 이 하위단계 규칙들은 일반적으로 좀더 구체적인 전제조건을 가지게 되는데, 이 전제조건들은 그 단계에서 완전한 계획을 만들기 위해 다른 하위 단계 규칙의 삽입을 요구한다 (그림 17 을 참조). 이 과정은 모든 연산자 (또는 적어도 첫째 연산자) 가 수행 가능한 원시 행동 (primitive action) 에 대응될 때까지 계속된다.

그림 17 계획의 접합
17 장에서 추론 시스템에 대한 새로운 규칙을 학습할 때 EBG 를 이용한 것처럼 이미 존재하는 일련의 STRIPS 규칙으로 구성된 새로운 STRIPS 규칙을 학습할 때도 STRIPS 를 이용할 수 있다. 이러한 학습된 규칙들은 더 복잡한 계획을 생성하기 위해 사용될 수 있다. 물론 앞에서 언급한 것과 같은 효용성 문제 (utility problem) 에 봉착하게 된다. 학습된 규칙이 자주 사용되지 않고, 계획수립의 수고를 덜지 못하고, 사용하는 데 비용이 많이 든다면 쓸모가 없을 것이다. 예제를 하나 들어서 새로운 규칙을 학습하는 기법을 설명하고자 한다.

그림 18 두 블록을 내려놓는 문제
그림 18 에 나타난 것과 같이 블록의 배치를 바꾸는 문제를 고려해 보자. 초기에는 블록 A 가 블록 B 위에 있고, 블록 B 는 블록 C 위에 있으며, 이 초기 상태로부터 A 와 B 가 모두 바닥 위에 놓이는 목표 상태를 달성하려고 한다. 이제까지 논의된 모든 계획수립 방법에서는 {move (A, B, F1), move (B, C, F1)} 를 계획으로 생성하게 될 것이다. 이때, 이 계획을 새로운 STRIPS 규칙의 형태로 저장할 가치가 있겠는가? 에이전트가 이 구체적인 문제를 자주 풀어야 한다면 그럴지도 모른다. 이 계획은 맨 위의 두 블록 (이름은 상관없이) 을 블록의 스택에서 같은 목표 지점으로 옮기도록 일반화될 수 있다면 더욱 높은 효용성을 가질 수 있다. 계획을 구축하는 것은 블록의 이름에 의존하지 않기 때문에 EBG 와 유사한 과정을 통해 객체상수인 A, B, C 대신에 변수 기호를 가진 계획 스키마를 생성할 수 있다. 하지만 이러한 두 단계 계획에서 목표 지점은 바닥이어야 하기 때문에 객체상수 F1 은 일반화될 수 없다.

그림 19 블록 내려놓기에 대한 삼각형 테이블
이 계획 일반화 과정
(plan-generalization process) 에는 계획에 있는 전제조건과 결과에 대한 정보가
이용된다. 이러한 정보를 표현하는 편리한 방법 중 하나는 삼각형 테이블 (triangle
table) [Fikes, Hart, & Nilsson 1972] 을 이용하는 것이다. 블록 내려놓기 문제에
대한 테이블을 그림 19 에 나타내었다. 테이블의 각 열 (column) 의 맨 위에는 계획에
포함된 연산자 중 하나가 오게 되는데 계획에 나타나는 순서에 따라 배치한다. 부분
순서 계획수립에서처럼 가상의 start 와 finish 연산자를 가정하는 것이 편리하다.
이 테이블은 각 연산자에 대한 전제조건과 각 연산자가 무엇을 만족시키는지를 표시한다.
각 연산자 바로 아래에 있는 셀은 연산자에 의해 추가되는 리터럴 (반복될 수 있음)
을 가진다. 각 연산자의 왼쪽에 있는 셀은 그 연산자의 전제조건이 되는 리터럴을
가진다. 테이블의 셀은 테이블의 맨 위 행 (row) 을 1 로 할 때의 행 위치 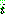 와 테이블의 맨 왼쪽 열을 1 로 할 때의 열 위치
와 테이블의 맨 왼쪽 열을 1 로 할 때의 열 위치  로 색인된다. 구체적으로 말한다면, 셀
로 색인된다. 구체적으로 말한다면, 셀 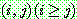 는 연산자
는 연산자  의 전제조건으로 요구되는 것 중에
의 전제조건으로 요구되는 것 중에 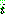 연산자에 의해 추가되는 리터럴과
연산자에 의해 추가되는 리터럴과 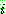 와
와  의 연산자를 적용해서 남게 되는 리터럴을 가진다. 따라서 start 연산자의 아래에
있는 셀은 초기 상태 기술에 있는 리터럴과 추후에 오는 연산자가 필요로 하거나
또는 목표조건에 있는 논리곱 인자를 만족시키는 리터럴을 포함한다. finish 연산자의
왼쪽에 있는 셀은 목표조건을 만족시키는 리터럴을 가진다.
의 연산자를 적용해서 남게 되는 리터럴을 가진다. 따라서 start 연산자의 아래에
있는 셀은 초기 상태 기술에 있는 리터럴과 추후에 오는 연산자가 필요로 하거나
또는 목표조건에 있는 논리곱 인자를 만족시키는 리터럴을 포함한다. finish 연산자의
왼쪽에 있는 셀은 목표조건을 만족시키는 리터럴을 가진다.
계획 일반화 프로시저의 다음 단계에서는 삼각형 테이블에 있는 모든 객체상수를 변수 기호로 바꾼다. 한 객체상수가 여러 번 나올 때는 같은 변수 기호로 바꾼다. 그리고 나서 이 과정은 모든 규칙의 전제조건이 그 규칙의 한 사례가 적용될 때 만족되도록 결과 계획 스키마 (resulting plan schema) 의 가장 일반적인 사례를 찾는다. 각 규칙의 전제조건들은 첫째 조건부터 차례로 검사되며, 만일 그 전제조건을 만족시키기 위해 치환이 필요가 있는 경우 해당 치환이 만들어진다. 블록 내려놓기 문제에 대한 결과 삼각형 테이블 스키마가 그림 20 에 나타나있다.

그림 20 블록 내려놓기에 대한 삼각형테이블 스키마
삼각형 테이블 형태로 된 일반화된 계획 스키마를 MACROP (매크로 연산자의 의미임) 라 부른다. 이것은 더 긴 계획을 생성하기 위해 STRIPS 규칙으로 사용될 수 있다. 1 번 열에 있는 리터럴의 논리곱은 MACROP 의 전제조건이 되고, 3 번 행에 있는 리터럴은 추가 리스트에 있는 리터럴이 된다 (삭제 리스트를 계산하려면 개별적 규칙들의 삭제 리스트를 분석해야 한다). 일반화 과정 자체에 대한 내용과 계획의 수행을 감시하는 데 대한 삼각형 테이블의 이용이 [Fikes, Hart, & Nilsson 1972] 에서 논의되었다.
MACROP 를 학습하는 것 외에 구체적인 계획을 구축하기 위한 시도가 미래의 계획수립 노력을 줄이는 제어전략 정보를 생성할 수 있다. 예를 들어, 앞의 문제에서 On (A, F1) ∧ On (B, F1) 의 논리곱을 달성하기 위해서는 On (A, F1) 의 논리곱 인자를 먼저 달성하는 것이 중요하다 (On (B, F1) 을 먼저 달성하기 위해 B 위에 아무 것도 없도록 하려면 A 를 다른 블록 위로 옮기고 나서, 다시 바닥으로 옮겨야 한다). Minton 의 PRODIGY 시스템은 EBG 를 이용하여 이같은 제어 정보를 학습할 수 있었다 [Minton 1988] (부분 계산 (partial evaluation) 에 기초를 둔 대안은 [Etzioni 1993] 에 나와 있다).
계획수립에 있어서 또 다른 유형의 학습으로는 규칙 자체의 결과를 학습하는 것이다. 에이전트는 많은 수의 사용 가능한 행동을 가질 수 있지만 이 행동의 결과나 또는 이 행동이 어떤 조건에서 수행될 수 있는지에 대한 것은 모를 수 있다. 해결하기는 어렵지만 중요한 문제인 행동 모델 (action model) 의 학습이 [Shen 1994, Gil 1992, Wang 1995, Benson 1997] 에 의해 이루어졌다. [Benson 1997] 에서는 학습된 연산자를 이용하여 구축된 계획을 나타내기 위해 목적 반응적 (teleo-reactive, T-R) 프로그램 표현을 이용하였다. 2 장에서 언급한 대로 T-R 표현은 계획 수행을 더욱 견고하게 만든다.
[Lifschitz 1986 (Lifschitz, V., "On the Semantics of {STRIPS}," in Georgeff, M., and Lansky, A. (eds.), Reasoning about Actions and Plans: Proceedings of the 1986 Workshop}, Timberline, Oregon, pp.1-9, San Francisco: Morgan Kaufmann, 1986. (Also in Allen, J., Hendler, J., and Tate, A. (eds.), Readings in Planning, pp.523-530, San Francisco: Morgan Kaufmann, 1990.))] 은 STRIPS 의 초기 설명이 타당하지 않고 무의미한 공식화를 방지하는 데 필요한 정확성과 제약 사항들이 결핍되어 있다고 언급하였다. 또한 이 문제를 피하기 위해 요구되는 STRIPS 의 사용 언어에 대한 제약 사항을 논의하였다 (이 책에서 사용한 식은 이 제약 사항을 따르고 있다). [Pednault 1986 (Pednault, E. "Formulating Multiagent, Dynamic-World Problems in the Classical Planning Framework," in Georgeff, M., and Lansky, A. (eds.), Reasoning about Actions and Plans: Proceedings of the 1986 Workshop, Timberline, Oregon, pp.47-82, San Francisco: Morgan Kaufmann, 1986. (Also in Allen, J., Hendler, J., and Tate, A. (eds.), Readings in Planning, pp.675-710, San Francisco: Morgan Kaufmann, 1990.)), Pednault 1989 (Pednault, E., "ADL: Exploring the Middle Ground between STRIPS and the Situation Calculus," in Brachman, R., Levesque, H., and Reiter, R. (eds.), Proceedings of the First International Conference on Principles of Knowledge Representation and Reasoning (KR-89), pp.324-332, San Francisco: Morgan Kaufmann, 1989.)] 에서는 조건부 결과 (conditional effects) 를 가진 규칙을 이용해서 Lifschitz 가 언급한 문제를 방지하고 다중 에이전트 계획을 공식화할 수 있는 STRIPS 의 버전이 제시되었다. [Bylander 1994] 에서는 STRIPS 의 명제 연산자에 의한 계획수립이 최악의 경우 (worst case) 에 실질적으로 처리가 불가능하다는 것을 증명하였다 (평균 경우 (average case) 분석에 대해서는 [Bylander 1993 (Bylander, T., "An Average Case Analysis of Planning," in Proceedings of the Eleventh National Conference on Artificial Intelligence (AAAI-93), pp.480-485, Menlo Park, CA: AAAI Press, 1993.)] 을 참조하라). [Erol, Nau, & Subrahmanian 1992 (Erol, K., Nau, D., and Subrahmanian, V., "On the Complexity of Domain-Independent Planning," in Proceedings of the Tenth National Conference on Artificial Intelligence (AAAI-92), pp.381-386, Menlo Park, CA: AAAI Press, 1992.)] 는 STRIPS 와 같은 유형의 계획수립 시스템의 복잡도에 대한 철저한 분석을 제안하고 있다.
[Gupta & Nau 1992 (Gupta, N., and Nau, D., "On the Complexity of Blocks-World Planning," Artificial Intelligence, 56(2/3):223-254, 1992.)] 는 실세계의 상태와 목표가 기초 원자 (ground atom) 의 논리곱으로 기술되는 블록세계 문제에서 최적의 (최단의) 계획을 찾는 것은 일반적으로 NP-hard 임을 증명하였다 (그럼에도 불구하고 [Chapman 1989 (Chapman, D., "Penguins Can Make Cake," AI Magazine, 10(4):45-50, 1989.)] 는 단순한 반응형 시스템 (reactive system) 이라도 적절한 감지 술어 (sensory predicate) 를 갖춘다면 블록세계 작업을 빨리 수행할 수 있다는 것을 보였다).
역방향 탐색에서 요구되는 과정인 STRIPS 규칙을 통한 목표의 회귀를 이용하는 방법이 [Waldinger 1975 (Waldinger, R., "Achieving Several Goals Simultaneously," in Elcock, E., and Michie, D. (eds.), Machine Intelligence 8, pp.94-138, Chichester, England: Ellis Horwood, 1975.)] 에서 소개되었다.
[Blum & Furst 1995 (Blum, A., and Furst, M., "Fast Planning through Planning Graph Analysis," in Proceedings of the Fourteenth International Joint Conference on Artificial Intelligence (IJCAI-95), pp.1636-1642, San Francisco: Morgan Kaufmann, 1995.)] 는 STRIPS 규칙으로 기술된 계획수립 문제를 경로 찾기 방법으로 해결하기 위해 계획수립 그래프 (planning graph) 라 불리는 구조로 변환하였다. [Kautz & Selman 1996 (Kautz, H., and Selman, B., "Pushing the Envelope: Planning, Propositional Logic, and Stochastic Search," in Proceedings of the Thirteenth National Conference on Artificial Intelligence (AAAI-96), pp.1194-1201, Menlo Park, CA: AAAI Press, 1996.), Kautz, McAllester, & Selman 1996 (Kautz, H., McAllester, D., and Selman, B., "Encoding Plans in Propositional Logic," in Proceedings of the Fifth International Conference on Principles of Knowledge Representation and Reasoning (KR-96), pp.374-384, San Francisco: Morgan Kaufmann, 1996.)] 은 WALKSAT 로 문제 해결을 하기 위해 계획수립 그래프를 명제논리 PSAT 문제로 변환하는 방법을 제안하고 있다. 또한 계획수립 문제를 PSAT 문제로 직접 코드화하는 새로운 기법도 제안하였다. [Ernst, Millstein, & Weld 1997 (Ernst, M., Millstein, T., and Weld, D., "Automatic SAT-Compilation of Planning Problems," in Proceedings of the Fifteenth International Conference on Artificial Intelligence (IJCAI-97), pp.1169-1176, San Francisco: Morgan Kaufmann, 1997.)] 은 효율적인 확률적 언덕오르기 (stochastic and hill-climbing) 탐색 기법을 이용한 신축적인 (scalable) 계획수립 방법을 결과로 내는 매우 중요한 연구이다.
Sacerdoti 의 NOAH 시스템 [Sacerdoti 1975 (Sacerdoti, E., "The Non-linear Nature of Plans," in Proceedings of the Fourth International Joint Conference on Artificial Intelligence (IJCAI-75), pp.206-214, San Francisco: Morgan Kaufmann, 1975. (Reprinted in Allen, J., Hendler, J., and Tate, A. (eds.), Readings in Planning, pp.162-170, San Francisco: Morgan Kaufmann, 1990.))], Sacerdoti 1977 (Sacerdoti, E., A Structure for Plans and Behavior, New York: American Elsevier, 1977.)] 과 Tate 의 INTERPLAN [Tate 1977 (Tate, A., "Generating Project Networks," in Proceedings of the Fifth International Joint Conference on Artificial Intelligence (IJCAI-77), pp.888-893, San Francisco: Morgan Kaufmann, 1977. (Reprinted in Allen, J., Hendler, J., and Tate, A. (eds.), Readings in Planning, pp.291-296, San Francisco: Morgan Kaufmann, 1990.))] 은 최초의 부분 순서 계획자였다. Chapman 의 TWEAK 시스템 [Chapman 1987 (Chapman, D., "Planning for Conjunctive Goals," Artificial Intelligence, 32(3):333-377, 1987.)] 은 부분 순서 계획자를 최초로 정형화하였고, 여러 가지 중요한 개념을 소개하였다. 그는 원자 목표조건 (atomic goal conditions) 의 논리곱을 달성하기 위한 부분 순서 계획을 찾는 문제는 NP-hard 임을 보였다.
McAllester 와 Rosenblitt 의 부분 순서 계획자의 SNLP 공식화는 [Soderland & Weld 1991 (Soderland, S., and Weld, D., "Evaluating Nonlinear Planning," Technical Report TR-91-02-03, University of Washington Department of Computer Science and Engineering, Seattle, WA, 1991.)] 에서 구현되었다. 이 구현은 UCPOP [Penberthy & Weld 1992 (Penberthy, J., and Weld, D., "UCPOP: A Sound, Complete Partial-Order Planner for ADL," in Proceedings of the Third International Conference on Principles of Knowledge Representation and Reasoning (KR-92), pp.103-113, San Francisco: Morgan Kaufmann, 1992.)] 으로 이어졌다. [Ephrati, Pollack, & Milshtein 1996 (Ephrati, E., Pollack, M., and Milshtein, M., "A Cost-Directed Planner: Preliminary Report," in Proceedings of the Thirteenth National Conference on Artificial Intelligence (AAAI-96), pp.1194-1201, Menlo Park, CA: AAAI Press, 1996.)] 은 계획공간 연산자를 선택하기 위해 A* 유형의 탐색을 이용하였다. 부분 순서 계획자와 전체 순서 계획자의 비교가 [Minton, Bresina, & Drummond 1994 (Minton, S., Bresina, J., and Drummond, M., "Total-Order and Partial-Order Planning: A Comparative Analysis," Journal of Artificial Intelligence Research, 2:227-262, 1994.)] 에서 이루어졌다. 최소 개입 계획수립과 부분 순서 계획수립 방법에 대한 문헌조사는 [Weld 1994 (Weld, D., "An Introduction to Least Commitment Planning," AI Magazine, 15(4):27-61, 1994.)] 를 참조하라.
[Christensen 1990 (Christensen, J., "A Hierarchical Planner That Generates Its Own Hierarchies," in Proceedings of the Eighth National Conference on Artificial Intelligence (AAAI-90), pp.1004-1009, Menlo Park, CA: AAAI Press, 1990.), Knoblock 1990 (Knoblock, C. A., "Learning Abstraction Hierarchies for Problem Solving," in Proceedings of the Eighth National Conference on Artificial Intelligence (AAAI-90), nl pp.923-928, Menlo Park, CA: AAAI Press, 1990.)] 은 자동으로 연산자 계층 구조를 학습하는 방법을 개발하였다. [Tenenberg 1991 (Tenenberg, J., "Abstraction in Planning," in Allen, J., Kautz, H., Pelavin, R., and Tenenberg, J. (eds.), Reasoning about Plans, Ch.~4, San Francisco: Morgan Kaufmann, 1991.)] 은 계층적 계획자에서 필요한 추상화를 연구하였다. [Erol, Hendler, & Nau 1994 (Erol, K., Hendler, J., and Nau, D., "HTN Planning: Complexity and Expressivity," in Proceedings of the Twelfth National Conference on Artificial Intelligence (AAAI-94), pp.1123-1128, Menlo Park, CA: AAAI Press, 1994.)] 는 또 다른 계층적, 부분 순서 계획자이다.
[Dean & Wellman 1991 (Dean, T., and Wellman, M., Planning and Control, San Francisco: Morgan Kaufmann, 1991.)] 은 AI 계획수립과 시간적 추론 방법을 현대의 제어 이론과 잘 통합한 책이다. 이러한 중립 입장을 다른 방향에서 접근한 것이 [Ramadge & Wonham 1989 (Ramadge, P., and Wonham, M., "The Control of Discrete Event Systems," Proc. of the IEEE, 77(1):81-93, 1989.)] 에 의한 이산적 이벤트 시스템에 대한 연구이다. 시간적 추론과 계획 수립에서의 역할에 대한 추가 논의는 [Allen, et al. 1990 (Allen, J., Hendler, J., and Tate, A. (eds.), Readings in Planning, san Francisco: Morgan Kaufmann, 1990.)] 을 참조하라. [Zweben & Fox 1994 (Zweben, M., and Fox, M. (eds.), Intelligent Scheduling, San Francisco: Morgan Kaufmann, 1994. endbiblio endlist)] 는 여러 가지 계획수립과 탐색 방법을 스케줄링 문제에 적용시켰다. [Wilkins, et al. 1995 (Wilkins, D. E., Myers, K., Lowrance, J., and Wesley, L., "Planning and Reacting in Uncertain and Dynamic Domains," Journal of Experimental and Theoretical Artificial Intelligence, 7(1):197-227, 1995.)] 는 계획수립 방법을 확장하여 불확실성을 포함하는 응용에 적용시켰다.
계획수립에 대한 많은 중요한 논문들이 [Allen, et al. 1990 (Allen, J., Hendler, J., and Tate, A. (eds.), Readings in Planning, san Francisco: Morgan Kaufmann, 1990.)] 의 편집서에 포함되어 있다. 학습과 계획수립에 대한 논문들은 [Minton 1993 (Minton, S. (ed.), Machine Learning Methods for Planning, San Francisco: Morgan Kaufmann, 1993.)] 에 나와 있다. Practical Planning 이라는 이름의 책은 SPIE 시스템과 그 응용에 대해 기술하고 있다 [Wilkins 1988 (Wilkins, D. E., Practical Planning: Extending the Classical AI Planning Paradigm, San Francisco: Morgan Kaufmann, 1988.)].
계획수립에 대한 논문은 주요한 AI 저널과 학회 논문집에 정기적으로 실린다. AI 계획수립 시스템(AI Planning Systems, AIPS) 에 대한 국제학회도 있다. 계획수립과 스케줄링 기법의 최근 응용에 대한 예제들이 [Tate 1996 (Tate, A. (ed.), Advanced Planning Technology, The Technological Achievements of the ARPA/Rome Laboratory Planning Initiative, Menlo Park, CA: AAAI Press, May 1996.)] 에 나와 있다.