만약 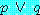 와
와 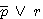 가 모두 참이면
가 모두 참이면 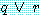 은 참이다. (1)
은 참이다. (1)
Proof
확률증명 (probabilistic proof) 은 하나의 예가 확률이론의 방법에 의해 존재한다는 것이 보여지는 증명을 의미하며 - 어떤 정리가 '아마도' 참일 것이다 라는 주장에 의한 것이 아니다. 후자의 추론 형식을 '가능성 주장 (plausibility argument)' 라고 부른다 ; Collatz conjecture 의 경우에서 처럼 참된 증명과는 거리가 멀다는 것이 명확하다. 확률증명은 존재 (existence) 정리를 보여주는 여러 방법중 하나로서, 구축에 의한 증명과는 다르다.
예를들면 "어떤 X 가 f(X) 를 만족한다" 를 증명하고자 한다면, existence or nonconstructive 증명은 f(X) 를 만족하는 X 가 존재한다 는 것을 증명할 것이지만, 그러한 X 가 어떻게 얻어지는 지를 말하지 않는다. 그러나 constructive 증명에서는 그렇게 할 것이다.
참이라고 생각되지만 아직 증명되지는 않은 문장을 추측 (conjecture) 라고 부른다.
때때로 어떤 문장이 주어진 공리 집합으로부터 아마도 증명될 수 없을 것이라는 것을 증명하는 것은 가능하다 ; continuum hypothesis 를 그 예로서 들 수 있다. 대부분의 공리 시스템에서, 증명될 수도 없고 반증될 수도 없는 문장들이 존재한다. 괴델의 불완전성 정리 (Incompleteness Theorem) 를 참고하라. .... (Wikipedia : Mathmatical proof)
..... 이 기술은 다음과 같은 하나의 법칙에 의존한다.
만약 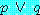 와
와 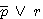 가 모두 참이면
가 모두 참이면 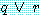 은 참이다. (1)
은 참이다. (1)
(1) 의 특별한 경우는 다음과 같다.
만약 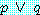 와
와 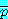 가 참이면
가 참이면  는 참이다.
는 참이다.
만약 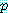 와
와 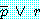 이 참이면
이 참이면  은 참이다. (2)
은 참이다. (2)
이것은 추론이나 정리 증명의 많은 컴퓨터 프로그램의 기초 (basis) 이다. ... (Richard Johnsonbaugh, 1999)
term :
증명 (Proof) 도출법 (Resolution) 정리증명 (Theorem Proving)
paper :
증명 (Proof) 분해증명 (Resolution Proof) : Richard Johnsonbaugh