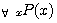 를 얻는다.
를 얻는다.Inference Rule
기존의 논리식으로부터 새로운 논리식을 생성하는 과정을 추론 규칙 (Inference Rule) 이라고 한다. 추론 규칙에 의해 새로 생성된 논리식이 기존의 논리식 집합과 논리적인 모순이 없어야만, 우리는 그 추론 규칙을 논리계산에서 이용할 수 있다.
추론규칙 |
항진명제의 형식 |
명제 |
P ∴P ∨ Q |
P ⇒ (P ∨ Q) |
가산 (or 에서의 add) |
P ∧ Q ∴P |
(P ∧ Q) ⇒ P |
단순화 (and 에서 simplification) |
P P → Q ∴ Q |
[P ∧ (P → Q)] ⇒ Q |
긍정식(Modus Ponens) |
| P → Q ∼Q ∴ ∼P |
[∼Q ∧ (P → Q)] ⇒ ∼P |
부정식(Modus Tollens) |
P ∨ Q ∼P ∴ Q |
[(P ∨ Q) ∧ ∼P] ⇒ Q |
선언 3단 논법 (or에서 syllogism) |
P → Q Q → R ∴ P → R |
[(P → Q) ∧ (Q → R)] ⇒ (P → R) |
가언 3단 논법 (hypothetical syllogism) |
P Q ∴ P ∧ Q |
(P ∧ Q) ⇒ (P ∧ Q) |
결합 (conjunction) |
(P → Q) ∧ (R → S) P ∨ R ∴ Q ∨ S |
[(P → Q) ∧ (R → S) ∧ (P ∨ R)] ⇒Q ∨ S |
구성적 딜레마 (constructive dilemma) |
(P → Q) ∧ (R → S) ∼Q ∨ ~S ∴ ∼P ∨ ∼R |
[(P → Q)∧(R → S)]∧(∼Q∨~S) ⇒(∼P ∨ ∼R) |
파괴적 딜레마 (destructive dilemma) |
명제함수와 정량자 (Quantifier) 를 사용하는 술어논리 에서는 명제논리 와 다른 추론규칙을 추가로 정할 필요가 있다. 전칭기호와 존재기호를 첨삭하여 추론을 유도 할 수 있게 하는 네 가지의 규칙이 있다.
(1) 전칭의 특정화(US, Universal Specialization) : 만일, ∀xP(x) 형태의 명제가 참이라 하면, 전칭기호는 생략되어 논의영역 내의 임의의 대상 C 에 대해 참임 P(c) 를 얻을 수 있다.
∀xP(x)
∴ P(c)
예) 논의영역이 행성이고, P(x)는 '행성은 움직이고 있다'를 뜻할 때,
∀xP(x) (모든 행성은 움직이고 있다.)
∴ P(c)
(2) 전칭의 일반화(UG, Universal
Generalization) : 명제 P(c)에 대하여 참이라면 전칭기호를 붙여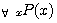 를 얻는다.
를 얻는다.
P(c)
∴∀xP(x)
예) 논의영역이 신입생이고, P(x) 는 'x는 교양과목을 수강한다'를 뜻할 때,
P(아무개)
∴∀xP(x)
(3) 존재의 특정화(ES, Existential Specialization) : ∃xP(x) 형태의 명제가 참이라 하면, P(c) 가 참이 되게 하는 논의영역 내의 한 요소 c가 존재한다.
∃xP(x)
∴ P(c)
여기서 유의하여야 할 점은 c는 전칭의 특정화에서와 같이 임의의 값이 아니라, 반드시 ∃xP(x)를 만족하는 요소이다. 예를 들면, 논의영역을 사람이라고 하고, F(x)를 'x는 여자이다', M(x)를 'x는 남자이다'라고 할 때, ∃xF(x)와 ∃xM(x)는 모두 참이다. 그러나 F(c) ∧ M(c) 는 논의영역 내의 c에 대하여 거짓이다 참이 되려면 논의영역 내의 요소 c와 d에 대해 F(c) ∧ M(d) 이어야 한다.
(4)
존재의 일반화(EG, Existential Generalization) : 만일 P(c) 가 논의영역 내의
한 요소 c 에 대하여 참이라 하면, 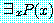 또한 참이다. 즉,
또한 참이다. 즉,
P(c)
∴∃xP(x)
예) 다음 추론을 증명하여 보아라.
∃xG(x) ∧ H(x)) → ∃G(x) ∧ ExH(x)
(1) ∃xG(x) ∧ H(x)) : 전체
(2) G(c) ∧ H(c) : ES
(3) G(c) : (2) 항의 단순화
(4) H(c) : (2) 항의 단순화
(5) ∃xG(x) : (3) 항과 EC
(6) ∃xH(x) : (4) 항과 EC
(7) ∃G(x) ∧ ExH(x) : (5), (6) 항의 결합
예) 1.34 다음의 추론을 기호화한 후 정확성 여부를 판정하여라.
사탕은 몸에 해롭다. S(x) : x는 사탕이다.
사탕이 있다. H(x) : x는 몸에 해롭다.
그러므로 몸에 해로운 것이 있다.
위의 추론을 기호화하면
∀xS(x) → H(x))
∃xS(x)
∴ ∃xH(x)
이 추론의 증명은 다음과 같다.
(1) ∃xS(x) : pr (전제)
(2) S(a) : (1)항과 ES
(3) ∀xS(x) → H(x)) ; pr (전제)
(4) S(a) → H(a) : (3)항과 US
(5) H(a) : (2), (4)항과 긍정식
(6) ∃H(x) : (5)항과 EG ................... (소광희 1985)
term :
추론규칙 (Inference Rule) 논리 (Logic) 명제논리 (Propositional Logic) 술어논리 (Predicate Logic) 기호 논리학 (Symbolic Logic) 추론 (Reasoning) 추론 규칙 (Inference Rule) 논리식(wff) 정량자 (Quantifier) 전문가시스템 (Expert System)
site :
paper :
video :
컴퓨터과학이 여는 세계 - 추론규칙을 이용한 논리증명 예 : SNU : 이광근 : 2016/03/07 ... 동영상 82개