 , 분류하고자 하는 class를
, 분류하고자 하는 class를  , 전체 모집단에서 변수
, 전체 모집단에서 변수  에 대한 확률분포를
에 대한 확률분포를 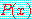 , 임의의 sample 이 class
, 임의의 sample 이 class  에 속할 사전확률
에 속할 사전확률 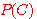 , class
, class  에서 변수 값
에서 변수 값  가 얻어질 조건부 확률
가 얻어질 조건부 확률 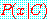 이 주어진다.
이 주어진다.Bayes' Theorem
베이즈 정리는 Thomas Bayes 가 ‘우연이라는 원칙으로 문제를 해결하는 방법에 관한 논문’ (Essay towards solving a problem in the doctrine of chances) 에 발표한 이론이다 ....
조건부 확률에서는 새로운 정보를 알았을 때 확률의 개선이 일어나게 된다. 가끔 우리는 어떤 실험결과에서 나온 정보를 이용하여 어떤 사건의 처음 확률을 개선시킬 수 있는데, 여기서 처음 확률은 사전확률 (prior probability) 이라 하고, 개선된 확률을 사후확률 (posterior probability) 이라고 하며, 이러한 확률의 개선을 이룩하는 것이 베이즈의 정리 (Bayes' theorem) 이다. 이러한 확률의 개선과정은 다음 그림과 같다.
|
사전확률 |
|
새로운 정보 |
|
베이즈 정리의 |
|
사후확률 |
|
|
|
|
Bayes' 정리를 이용한 의사 결정은 feature 값이 주어진 상태에서 가장 가능성이 있는 class를 선택하는 것을 말한다. 즉 Bayes' 정리를 이용하여 class membership 의 확률이 계산된다 (Earl Gose 1996).
변수 값을  , 분류하고자 하는 class를
, 분류하고자 하는 class를  , 전체 모집단에서 변수
, 전체 모집단에서 변수  에 대한 확률분포를
에 대한 확률분포를 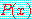 , 임의의 sample 이 class
, 임의의 sample 이 class  에 속할 사전확률
에 속할 사전확률 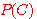 , class
, class  에서 변수 값
에서 변수 값  가 얻어질 조건부 확률
가 얻어질 조건부 확률 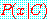 이 주어진다.
이 주어진다.
우리가 얻고자 하는 것은 변수 값 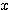 가 주어진 상황에서 sample 이 class
가 주어진 상황에서 sample 이 class 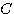 에 속할 사후확률 즉
에 속할 사후확률 즉 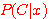 을 구하는 것인데, 이를 위해
을 구하는 것인데, 이를 위해 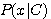 ,
, 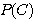 ,
, 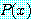 값이 주어진다.
값이 주어진다.
class 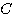 에 속하면서 하나의 변수값
에 속하면서 하나의 변수값 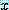 (single feature)를 가지는 경우의 확률은 다음과 같다.
(single feature)를 가지는 경우의 확률은 다음과 같다.
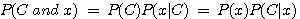
위의 식을 다시 정리하면 다음과 같은 Bayes' 정리가 된다. (하나의 변수만 있을 경우)
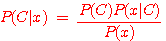
term :
베이즈 정리 (Bayes' Theorem) Thomas Bayes 베이즈확률 (Bayesian Probability) 베이즈 네트워크 (Bayesian Network) 나이브 베이즈 분류 (Naive Bayesian Classification) 베이즈추론 (Bayesian Inference) 확률 (Probability) 통계학 (Statistics) 수학 (Mathematics) 인공지능 (Artificial Intelligence)
site :
Wikipedia : Bayes' theorem 위키백과 : 베이즈정리
paper :
Bayes' Theorem : Earl Gose 외
video :
뇌과학으로 본 인공지능의 현주소와 미래 - 1부 : afoofa Jung : 박문호 : 2016/04/07
뇌과학으로 본 인공지능의 현주소와 미래 - 2부 : afoofa Jung : 박문호 : 2016/04/07